Significance
Oscillators, widely found in nature, form the basis of a wide variety of actuating and signal processing mechanisms. While the ability to mimic arrays of oscillators and control their coupling is a central goal in the field of bioinspired soft materials, this has been difficult to achieve. Using Marangoni forces generated during spatially inhomogeneous illumination of photothermally responsive particles, we demonstrate a scheme for optically trapping arrays of particles at air–water interfaces that can incite a range of oscillatory and spinning behaviors. When multiple objects are arranged in proximity, they exhibit complex, collective behavior emerging from geometry-dependent interparticle coupling. This route to achieving collective motion is expected to open opportunities in the study of active materials.
Keywords: coupled oscillation, Marangoni forces, active matter
Abstract
Cyclic actuation is critical for driving motion and transport in living systems, ranging from oscillatory motion of bacterial flagella to the rhythmic gait of terrestrial animals. These processes often rely on dynamic and responsive networks of oscillators—a regulatory control system that is challenging to replicate in synthetic active matter. Here, we describe a versatile platform of light-driven active particles with interaction geometries that can be reconfigured on demand, enabling the construction of oscillator and spinner networks. We employ optically induced Marangoni trapping of particles confined to an air–water interface and subjected to patterned illumination. Thermal interactions among multiple particles give rise to complex coupled oscillatory and rotational motions, thus opening frontiers in the design of reconfigurable, multiparticle networks exhibiting collective behavior.
Motion in living systems often relies on coupled dynamics of oscillatory and active networks (1–4). Examples spanning a wide range of size scales include the swimming of lamprey coordinated by oscillatory neuronal networks and the synchronized rotation of flagella coupled by hydrodynamic interactions (5, 6). Synthetic platforms that mimic key elements of these natural systems promise new fundamental understanding and next-generation active material systems: recent advances include chemomechanical oscillators built upon the Belousov–Zhabotinsky reaction (7, 8), synthetic genetic circuits (9), self-regulatory microfluidic devices (10–12), and organic chemical reactions (13). However, in most synthetic systems that rely on complex chemical or biochemical reactions, the nature of interactions between different elements is typically hardwired with limited ability to dynamically adjust coupling parameters. Similar limitations on geometric reconfigurability and tunability of coupling are found in physical particle oscillator networks, such as in acoustically levitated oscillators (14). In contrast, the effectiveness of natural control systems stems from oscillatory elements that can reconfigure their interactions rapidly, as observed in transitions of insect flight modes or animal gait patterns (2, 15). Therefore, developing simple yet versatile experimental platforms that mimic adaptive and active living systems with synthetic components remains a critical challenge.
As an important step in this direction, we describe particles at fluid interfaces, driven by two-dimensional (2D) patterns of light, as a powerful approach to coupled motion across easily tunable geometries. In nature, insects such as Microvelia secrete chemicals to generate gradients in surface tension and propel themselves across water surfaces (i.e., Marangoni propulsion) (16). This concept has been exploited to drive translation and rotation of objects on fluid surfaces using both chemical (17, 18) and light-induced photothermal (19–21) gradients. Some of us previously demonstrated how photothermal Marangoni forces incite oscillatory motion of interfacially adsorbed particles, but as this approach relied on the use of curved droplets and permitted only very coarse “patterns” of light defined by the field of view of a microscope objective, it was not amenable to the study of multiparticle systems with well-controlled geometries (22). Indeed, the rational design of systems exhibiting reconfigurable Marangoni interactions between multiple particles remains elusive. In contrast, optical tweezers operating by momentum transfer offer spatial control over trapped objects in almost limitless arrangements (23–25), enabling oscillatory motion of colloids via continuous repositioning of traps (26) and sustained rotation of particles by transferring spin angular momentum (27). However, scaling this platform to larger collections of particles is challenging, since the high-intensity light (∼106 W/cm2) required (28) becomes problematic over large areas and can drive large temperature increases. Here, we show that the Marangoni forces developed during illumination of hydrogel nanocomposite disks (HNDs), consisting of polymer gels with patterned gold nanoparticles (Au NPs), can incite a gamut of coordinated and reconfigurable multiparticle behavior at very modest light intensities (∼1 W/cm2). Arbitrary gray-scale light patterns provide optical boundary conditions to define coupled systems of HNDs, culminating in a versatile materials toolbox of active matter exhibiting complex rhythmic motion.
Results
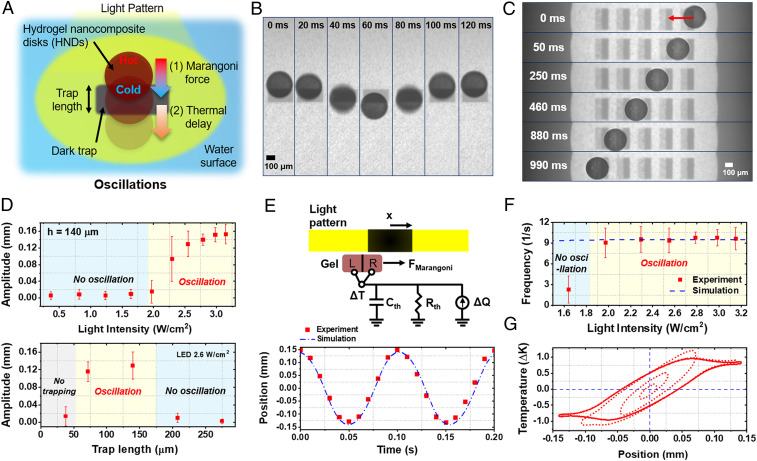
We first consider the behavior of circular HNDs uniformly loaded with Au NPs under a pattern of light containing a nonilluminated rectangular trap region; the resultant sustained oscillatory motion of the HNDs is illustrated in Fig. 1A. The HNDs are fabricated with a diameter of 300 μm and thickness of ∼6 μm by lithographic patterning of the photo cross-linkable copolymer (poly(diethylacrylamide-co-N-(4-benzoylphenyl)acrylamide-coacrylic acid)) (SI Appendix, Fig. S1) (29). The Au NPs, grown in situ by photoreduction of embedded Au salts, absorb light because of their surface plasmon resonance (30), thereby generating localized heat in proportion to the light intensity and the NP absorbance. Offsetting an HND from the center of the trap causes differential heating across its diameter (SI Appendix, Fig. S2) and a greater surface tension on the colder (less illuminated) portion, which acts to restore the disk to the center of the trap. However, a temporal lag in the thermal response causes the HND to overshoot the optical-trap midpoint before the temperature gradient reverses direction, giving rise to sustained oscillatory motion, as seen in the time-lapse images of Fig. 1B and Movie S1. This behavior is sensitive to the trap dimensions, as summarized in Fig. 1D—as the length of the trap approaches the HND diameter, stable trapping with no oscillation is observed, whereas small traps (≲50 μm) do not provide sufficient Marangoni restoring force to retain the HNDs within the trap. Oscillations persist over extended time periods (at least 400 s) with minimal changes in amplitude or frequency (SI Appendix, Fig. S3). Furthermore, for trap dimensions that support sustained oscillations, there is a threshold light intensity for the illuminated regions surrounding the trap, above which oscillations are observed. Dividing the trap pattern into two regions of different light intensity generates asymmetric oscillations, with higher amplitude toward the darker side (SI Appendix, Fig. S4). A series of such asymmetric traps drive directional stochastic hopping of oscillating HNDs between traps, with the HND spending varying intervals of time in each trap (Fig. 1C, SI Appendix, Fig. S4, and Movie S1).
Fig. 1.
Oscillation of HNDs confined to Marangoni traps. (A) Schematic diagram of the trap geometry that drives oscillatory motion. (B) Time-lapse images of an HND undergoing oscillation within a symmetric trap. (C) Directed stochastic hopping along a row of asymmetric traps (Movie S1). (D) Amplitude of HND oscillations with varying light intensity and trap length. (E) Schematic diagram of the model (Top), and a comparison of experimental and simulated displacement for two cycles of oscillatory motion (Bottom). Light-emitting diode power = 2.8 W/cm2, trap length 140 μm. (F) Comparison between simulated and experimental frequencies with varying light intensity. (G) Simulated phase portrait of the oscillator showing position versus temperature difference.
To further elucidate the mechanism underlying oscillation of trapped HNDs, we adapt our previously developed model to treat each HND as a two-element lumped thermal system (22). The differential heat generation ΔQ(x) between the left and right halves of the HND is calculated based on the pattern of the light and instantaneous center position x and is used to determine the resulting time-varying temperature difference ΔT, considering heat loss due to transient motion and thermal mass of the HNDs. Effective mass, drag coefficients, and overall absorption fraction from the wide-spectrum white light are treated as adjustable parameters as these variables cannot be calculated easily; this also serves to compensate for oversimplifications in the model (16). As an exemplary result (Fig. 1E), the simulations closely match the observed time dependence of HND position. The trend of increasing oscillation amplitude with light intensity is also recovered from the simulation (SI Appendix, Fig. S5). However, we note that the threshold intensity for oscillation from simulations (∼0.5 W/cm2) is lower than observed experimentally (>1.5 W/cm2). Given that a similarly high threshold intensity is also observed here for the propulsion of Marangoni swimmers under uniform illumination (SI Appendix, Fig. S6), as well as in previous reports on Marangoni spinners and colloids (20, 31), we speculate that redistribution of small amounts of surface-active impurities in the presence of temperature gradients, or perhaps hysteresis in the gel–water–air contact line position (32, 33), suppress motion at low intensity.
At light intensities greater than ∼2 W/cm2, the frequency of HND oscillations becomes constant, as shown in Fig. 1F. This behavior is also seen in the analytical thermal circuit model (derived in the Materials and Methods section) as the frequency beyond a threshold light intensity becomes , where ηeff is the effective damping coefficient, meff is the effective mass of the HND, Cth is thermal capacitance, and Rth is thermal resistance. The increase of Cth at high intensity by convective heat loss at higher velocity (h(); is velocity) nearly balances a decrease of Rth (∼1/h()), thus defining an oscillation frequency independent of intensity. This interpretation does not apply to the low light-intensity regime (with low particle velocities), which arises from the simplifying assumption that the parameters ηeff and meff are velocity independent. A simulated phase portrait of position versus temperature difference during the onset of oscillations and convergence to a stable oscillator limit cycle in Fig. 1G provides valuable insights into these systems: when the HND is located in the center of the trap (i.e., x = 0 mm), the substantial temperature difference of ∼0.5 K that persists across the HND drives its movement beyond the trap center. This latent temperature difference reflects the “RC” delay time (τth = CthRth) of the thermal circuit model and drives stable oscillation modes. Although the lumped thermal model used in these simulations is clearly an oversimplification, we note that the predicted magnitude of the temperature difference across the disk in Fig. 1G is well matched to analytical calculations considering the experimental geometry in detail (SI Appendix, Fig. S2). While temperature increase of up to ∼1 K is generated in the vicinity of an HND, the overall heat generation is negligible (only ∼1 mW per HND).
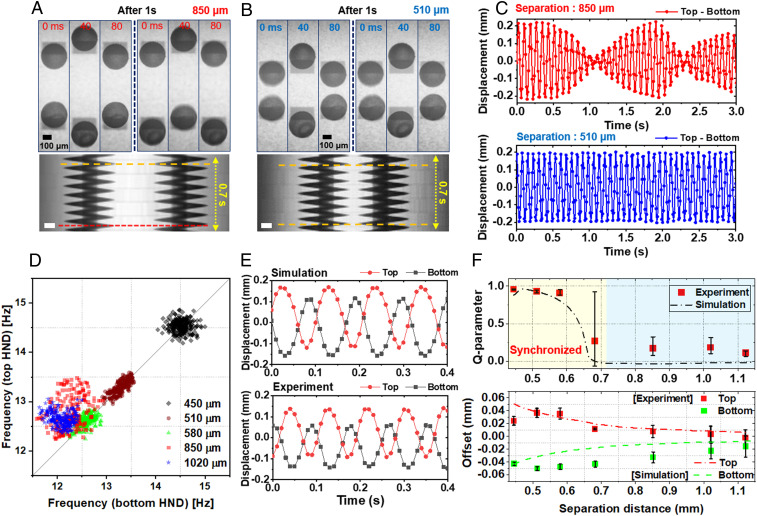
We next turn to systems of multiple coupled oscillators, which can be prepared in any selected geometry by the design of an optical-trap pattern. When two HNDs are trapped at large separation distances (Fig. 2A and Movie S2), they each oscillate at their own natural frequency, which is found to vary by as much as 20% due to imperfections in HND shape and/or variations in position of the pinned three-phase contact line that alter their effective mass and drag. However, when the HNDs are trapped in close proximity, frequency locking with antiphase synchronization emerges, as seen in Fig. 2B. This transition from uncoupled oscillation to antiphase synchronization is also seen in the plots of relative displacement (Fig. 2C), where the beat pattern observed at large HND separation disappears at close proximity. Variation of the separation distance reveals that the transition occurs when the trap spacing is between 580 and 850 µm, as shown in Fig. 2 C and D and SI Appendix, Fig. S7. Upon synchronization, a further reduction in the trap spacing (or stronger coupling) leads to an increase in the oscillation frequency, as seen in Fig. 2D. The number of HNDs in this experimental system is limited by the threshold light intensity required for oscillations, which sets the minimum size of HNDs that can exhibit Marangoni motions for a given light intensity (see derivation in Materials and Methods).
Fig. 2.
Distance-dependent coupling of two oscillators. Time-lapse images showing oscillation of two HNDs confined to traps with center-to-center distances of 850 μm (A) and 510 μm (B). Bottom images are kymographs (0.7 s) of the coupled oscillations. The yellow (red) dashed lines indicate antiphase (in-phase) synchronization. (Scale bars, 100 μm.) Time step for each image is 40 ms. (C) Differences in displacements of the coupled HNDs with separation distances of 850 μm (Top) and 510 μm (Bottom). (D) Instantaneous frequency relationship of the two coupled HND oscillators with varying trap separation. (E) Temporal motion of the HNDs from simulation and experiment for a trap separation distance of 510 μm. (F) Q-parameter and center offsets of the oscillations with respect to trap separation.
Oscillator synchronization is suspected to originate largely from the radial temperature gradients generated by neighboring HNDs, such that each HND experiences an additional repulsive Marangoni force from the neighboring HND, though hydrodynamic interactions may also play an important role. This leads to a time-varying HND–HND repulsion that drives synchronization and fixes an antiphase relationship when HNDs are closely spaced. Two oscillators coupled through repulsive interactions are known to synchronize to an antiphase state (34, 35). This repulsive interaction also manifests in an outward shift in the center of oscillation of each HND from the center of its trap as shown in Fig. 2E. Once the HNDs are synchronized, further decreasing their separation distance increases the offset between the oscillation center and trap center, as shown in Fig. 2F, which is consistent with repulsive interactions between closely positioned HNDs.
Here, we adopt a simplified first-order approach to simulate coupling between two disks based on the temperature increase around each HND due to thermal conduction, which scales as ∼1/r, where r is the distance from the heat source. Thus, the resulting temperature difference across a neighboring HND, and resulting inter-HND repulsion, scales as ΔT ∼ (∂/∂r)T(r) ∼ 1/r2 (36). This is supported by experiments using optical traps when the HNDs are held stationary (and therefore do not experience hydrodynamic interactions). As the traps are brought closer together, the two HNDs are pushed away from their respective trap centers, revealing the presence of Marangoni repulsion (SI Appendix, Fig. S8). However, further work is needed to incorporate both thermal and hydrodynamic interactions in the simulation, as the latter likely plays an important role as well. Moreover, we expect that our approach can be readily extended to oil/water interfaces, which may provide another handle to modulate the relative importance of hydrodynamic effects and interfacial tension gradients. The synchronization-to-random phase transition is observed in both simulation and experimental results and is quantified using an order parameter Q (26). The Q parameter denotes the quality of synchronization between two oscillators, where Q lies between 1 (antiphase) and −1 (in phase); the value is close to 0 when the oscillators are uncorrelated. Phase locking is observed at an HND separation distance of 0.6 mm or below, as indicated by high Q values (>0.9) (Fig. 2F). Experimentally, we find an increase in oscillation frequency as the separation becomes small (SI Appendix, Fig. S9), a trend that is not captured by the simulation, suggesting potential additional interactions at shorter distances that are absent from the model (e.g., hydrodynamic interactions between the HNDs or crosstalk due to scattered light).
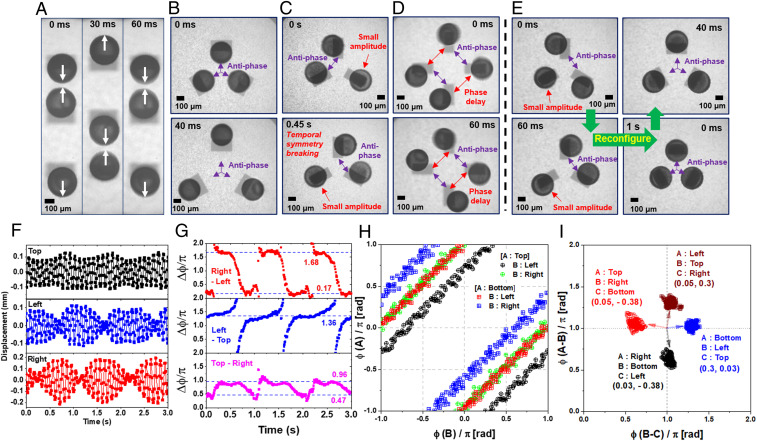
Coupling multiple HND oscillators in various arrangements of optical traps yields systems exhibiting more complex dynamics. First, three HNDs in serial traps show extended coupling, such that the top and bottom oscillators exhibit nearly in-phase coupling, connected by an antiphase oscillator in the middle, as seen in Fig. 3A, Movie S2, and SI Appendix, Fig. S10. When three traps are positioned at the vertices of an equilateral triangle with side lengths of 580 μm and oscillatory axes oriented toward the center of the triangle, synchronization occurs with all HNDs simultaneously moving radially inward and outward (Fig. 3B and Movie S3).
Fig. 3.
Reconfigurable multi-HND oscillators. (A) Time-lapse images of three serially coupled HNDs, showing in-phase coupling between the first and third HNDs. (B–D) Time-lapse images of dynamic 2D patterns from 2D coupled oscillators. (E) Reconfiguration of the optical traps for coupling transition from a ring network to all-antiphase radial synchronization. (F) Displacements of the HNDs in a three-body ring network with time. (G) Phase difference between HNDs in a three-oscillator ring network. (H) Phase-phase plot for HND pairs in a four-oscillator ring network. (I) Phase difference map for HND pairs in a four-oscillator ring network.
The tendency of two neighboring oscillators to exhibit antiphase synchronization leads to interesting collective dynamics when multiple oscillators are configured into a ring. When a group of N identical oscillators are arranged in a ring such that each oscillator is coupled to its two neighbors, the simplest group of resulting oscillator states are splay states where each pair of oscillators is separated by a constant phase difference (), yielding an integral number (k) of phase rotations around the ring (34). However, a splay state with perfectly antiphase synchronization between neighboring oscillators is inherently impossible when an odd number of HNDs are configured into a ring, leading to a geometrically frustrated system (37). Experimentally, we observe complex phase dynamics when HNDs are arranged in a three-oscillator ring structure, the smallest of frustrated geometries (Fig. 3C). Experimental results demonstrate that the oscillator network relieves frustration through time-varying, symmetry-breaking transitions with periodic changes in oscillation amplitudes and phase relationships between neighboring HNDs (Fig. 3F and SI Appendix, Fig. S11); for example, in Movie S3, one sees that the amplitude of oscillations of the bottom-right HND is nearly zero at 18 s, and gradually increases to attain maximum amplitude at 21 s, and then returns to small amplitude oscillations by 24 s. By tracking the instantaneous phase relationship between neighboring HNDs (Fig. 3G), we see that each HND pair exhibits quasi-stable states with repetitive transitions between these states of temporary stability. It is also evident from Fig. 3 F and G that the period of transient phase stability for a pair of HNDs is reflected in their respective amplitudes—that is, during transitions in and out of transient phase stability, the oscillation amplitudes drop to their lowest levels. We expect that the time spent by a pair at each transiently stable state is sensitive to the intensity of coupling with the third oscillating HND.
Importantly, this platform allows for real-time reconfiguration of oscillatory networks; for example, a three-oscillator HND network can be switched from a frustrated state to parallel antiphase synchronization simply by altering the orientation of the traps, as shown in Fig. 3E. This is shown in Movie S3, where the three-HND network originally exhibits frustrated oscillations (starting at 26 s). When switched to parallel coupling (at 42 s), all HNDs stop oscillating in the original ring configurations and adapt to this new trap configuration, gradually increasing their oscillation amplitudes until steady, synchronized amplitudes are attained (at about 46 s).
When HNDs are configured into a four-oscillator ring with a trap separation distance of 680 μm, they exhibit full frequency synchronization (Fig. 3D and Movie S3). The linearity and unity slope of the phase maps in Fig. 3H indicate that each neighboring pair of HNDs adopts a fixed phase relationship during the oscillation cycle. Strikingly, however, the HNDs are not perfectly symmetric in an antiphase relationship with each neighbor. As seen in the offsets in Fig. 3H, they instead form two clusters of nearly antiphase synchronization (top-right and bottom-left pairs), but the top-left and bottom-right pairing does not exhibit a phase relationship of π (SI Appendix, Fig. S12). This is more clearly illustrated in the plot of the instantaneous phase offset for each HND pair (Fig. 3I); a perfectly antiphase symmetric system would have all points at the (1, 1) region of the map. While further investigation is needed to fully understand the origin of this behavior, we suspect that it is more favorable than perfect antiphase coupling between all particles, since it requires the closest separations to be attained by only two, rather than all four, of the neighboring HND pairs.
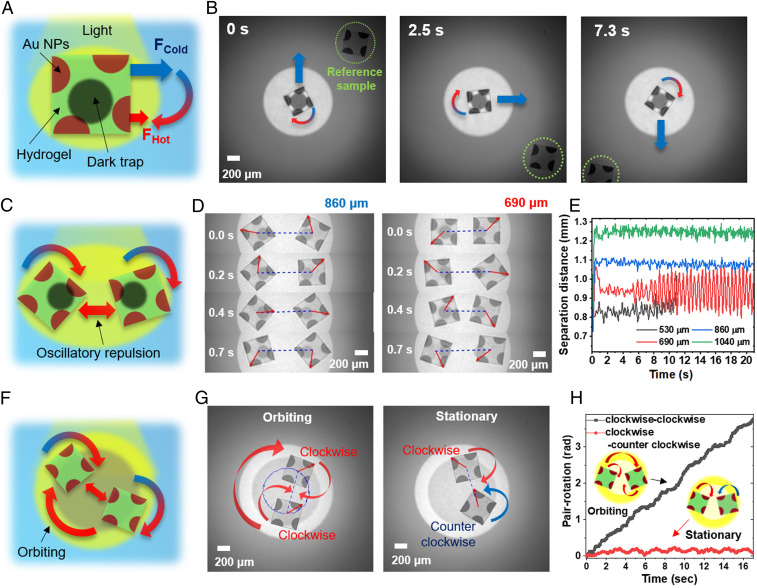
We next consider how spatial programming of Au NP locations within the hydrogel disks, coupled with Marangoni optical traps, gives rise to additional modes of coupled particle motion. Fig. 4A shows a square hydrogel film with a chiral pattern, comprising off-center semicircular Au NP features along each side. This structure exhibits rotational motion under nonstructured illumination, driven by the temperature difference along each side of the HND (SI Appendix, Fig. S13 and Movie S4), which generates a Marangoni torque. We note that while the rotating HND is pushed toward the edge of the illuminated region due to an intensity gradient, it stops at the edge of the pattern with a portion of the disk exposed to light. Although the origin of the effect is not well understood, we suspect that a slight deswelling of HND due to the temperature increase induces out-of-plane deformation, creating an additional contribution to the surface energy that favors location of the distorted edge in the lower surface tension (illuminated) environment, thereby balancing the Marangoni repulsion. The angular velocity of an HND spinner scales linearly with light intensity beyond the threshold value (SI Appendix, Fig. S13), consistent with the observations for the HND oscillations. Also, by positioning a (nonilluminated) circular trap at the center of the disk, the spinning disk can be translated along the fluid interface by moving the microscope stage. The navigation of the spinning HNDs with a circular trap is made possible by the overlap between the repositioned dark trap and the Au NP–embedded region and the associated decrease in local heat generation, thereby directing the HND along the translating trap (Fig. 4B). Furthermore, by providing a gradient intensity of light as a global energy landscape for Marangoni propulsion, an arbitrary translational trajectory of the spinning disk can be programmed (SI Appendix, Fig. S14). A spiral light pattern with higher intensity at the center causes the HND to move outward from the center toward the periphery as it spins, as shown in Movie S4 (at 22 s).
Fig. 4.
Active HND spinners. (A) Schematic diagram of square-shaped HNDs containing chiral Au NP patterns to create light-driven spinners. (B) Time-lapsed images showing rotational and translational motions with moving trap pattern (Movie S4). (C) Schematic diagram of HND spinners coupled by two trap patterns. (D) Time-lapse images of spinning HNDs trapped with center-to-center separation distances of 690 and 860 μm. (E) Separation distances of the centers of HNDs versus time. (F) Schematic diagram of HND spinners in a circular well. (G) Images of two clockwise rotating HNDs (Left) and clockwise and counterclockwise rotating HNDs (Right) under circular optical confinement (Movie S5). (H) Pair-rotation angles versus time for the same and opposite-directional HND spinners under optical confinement.
Collective motion driven by active constituents is evident in many living systems, from corotation of individually spinning Volvox algae to spiral vortex formation of swimming, circularly-confined bacteria (38, 39). With this inspiration, we extend the experimental system to demonstrate HND rotation in an arbitrarily defined optical boundary. As shown in Fig. 4 C–E, two spinners trapped at a separation distance of 1,040 µm rotate individually in an uncoupled manner. As shown in Movie S5, as the trap separation distance is reduced to 690 µm, the HNDs show oscillatory separation while the individual HNDs spin (gradually increasing in amplitude from 22 s to about 29 s). Notably, the left HND rotates faster than the right one, which likely reflects sample-to-sample variations resulting from the fabrication process; for example, roughness of the edges resulting from photolithographic fabrication. This could be interpreted as two rotating HNDs that periodically bring two Au NP patches (that are repulsive) into close proximity, resembling the coupled oscillation of circular HNDs at short separation distances. Two spinners can be confined within a gray-scale pattern of light with a higher light intensity outside the circle that acts as an optical wall (Fig. 4 F–H). Since the two HNDs experience Marangoni repulsion, they are pushed toward the edge of the optical wall to maximize separation distance. When the two HNDs rotate in the same direction, they co-orbit inside the optical barriers. Over time, thermal repulsion results in oppositely positioned HNDs within the circle, with HND chirality defining the direction of net torque, since one edge is subjected to the higher intensity portion of the circular light pattern. On the other hand, two HNDs with opposite chirality counter rotate but show little, if any, co-orbiting in the circular trap (SI Appendix, Fig. S15). These observations were consistent across four separate measurements with two clockwise rotating HNDs and three measurements with one clockwise and one counterclockwise disks. This coupling of optical boundaries and NP patterns allows an approach to gain versatile control of active-matter movement and interactions under geometric confinement.
Discussion
In summary, 2D patterns of light were employed to optically trap photothermally active polymer nanocomposite structures at an air–water interface, leading to a reconfigurable platform for coupled particle motion. This system enables diverse assemblies of active matter such as coupled oscillator networks with dynamic patterns of serial or parallel coupling, radially synchronized motion, and frustrated ring networks. Furthermore, patterning of the Au NPs in the hydrogel disk enables active spinning motion where both rotational and translational motions are programmed by light patterns. Optical confinement of light-pumped active spinners excites oscillatory modes in particle separation or chirality-dependent multiparticle orbital motion superimposed on the rotational motion of each individual particle. Overall, this platform provides a versatile set of experiments for exploring coupled dynamics of light-driven motion with arbitrary boundary conditions, which may serve to validate existing, and inspire the development of new, theoretical descriptions of complex coupled motions.
Materials and Methods
Chemicals.
Azobisisobutyronitrile (AIBN), acrylic acid (AAc), poly(vinyl alcohol) (PVA, 13 to 23 kDa, 87% hydrolyzed), 4-methyl-2-pentanone (4MP), and 1,4-dioxane were purchased from Aldrich and used as received, except for AIBN, which was recrystallized from methanol. N,N-diethylacrylamide (DEAM) was purchased from TCI America, and inhibitors were removed by passage through basic alumina. Hexanes was purchased from Fisher Scientific. Benzophenone acrylamide (AAmBP) and rhodamine B methacrylate (RhBMA) were prepared following literature procedures (30, 40).
Copolymer Synthesis.
Poly(diethylacrylamide-co-N-(4-benzoylphenyl)-acrylamide-coacrylic acid) (PDEAM) was synthesized according to a published procedure (30). Briefly, DEAM (3.0 g), AAmBP (0.45 g), AAc (0.037 g), RhBMA (0.01 g), and AIBN (0.01 g) were dissolved in 1,4-dioxane (20 mL) and added to a sealed vial in an inert atmosphere glove box. The solution, while protected from light, was heated up to 80 °C and polymerized for 20 h, then cooled to room temperature. The resulting polymer solution was precipitated into hexane and dried under vacuum [yield: 3.4 g, gel permeation chromatography (tetrahydrofuran eluent) with poly(methyl methacrylate) calibration standard: Mn = 24 kDa, Ɖ = 2.3].
Fabrication of HNDs and Optical-Trapping Experiments.
The HND fabrication procedure was adapted from a previous report (30). Si wafers were coated with PVA by spin coating 4 to 8 wt.% aqueous PVA solution at 5,000 rpm for 60 s. To prepare the drop-casting solution, 100 μL diethylene glycol was mixed with 7.5 mL 1-propanol. Then, 0.01 g AuCl3 ⋅ 3H2O was dissolved in the 1-propanol solution (750 μL). In a separate vial, 0.05 g PDEAM copolymer was dissolved in 0.5 mL 1-propanol. The solution for drop casting was prepared by mixing the polymer solution and gold salt solution, followed by filtration through a 0.45 μm membrane. The resultant solution (30 to 35 μL) was then drop cast onto a PVA-coated Si wafer (1 × 1 cm) and dried for 12 to 48 h in a closed dark jar, followed by 5 to 10 min in an oven (55 °C). In order to pattern the hydrogel networks, the dried film was transferred to the microscope stage and exposed to the patterned UV light (365 nm, 0.17 W/cm2, 60 s) through an objective lens using a digital micromirror device (DMD) array. The Au NP patterning process was performed by photoexposure (400 nm, 2.24 W/cm2, 500 to 800 s). Any residual uncrosslinked polymers and unreacted salts were removed by immersing the sample in a 9:1 (volume) mixture of the 4MP:hexane solution for 90 s. Finally, by immersing the Si wafer in water and dissolving the sacrificial layer, the patterned HNDs were floated to the top in pure water by following the previously reported procedure (41). Subsequently, thoroughly washed Petri dishes (Fisher Scientific, catalog no. FB0875713A) were filled with pure water, and the HNDs were transferred to them immediately prior to the experiments. The Petri dishes with the floating HNDs were transferred to the translational stage of the inverted microscope (Nikon ECLIPSE Ti) equipped with a white light source (Lumencor Spectra light-emitting diode) and the DMD array. The experiments were performed by illuminating the HNDs with patterned light of intensity typically in the range 1 to 3 W/cm2. Spatial nonuniformity in light intensity at the sample plane was characterized using an sCMOS camera (Hamamatsu ORCA Flash) to capture an image with all mirrors on the DMD in the on position. Subsequently, uniform intensity was achieved within a given spatial region by turning each mirror on with a probability inversely proportional to the local intensity during each projected frame (except for the first movie of Movie S4, which shows how an HND is pushed away from the center to the outer region by a light intensity gradient). Although this yields local variations in light intensity on the size scale of the DMD pixel array (3.4 µm at the sample plane), the much larger size HND features lead to an effectively uniform intensity. Before starting oscillation experiments, the HNDs were coarsely positioned using a manual probe and then directed to the desired location by using a nonoscillatory optical trap formed via a gradient of light intensity. MATLAB was used to analyze the translational motion of the HND, and rotational motions of chiral HNDs were analyzed with Tracker software. Pair correlations for the coupled HND oscillators were quantified by using the Q parameter as described in the previous literature (26),
| [1] |
where t is time, x1 and x2 are the positions of the HNDs with respect to their trap positions, and Δ is the duration of the evaluation. Temperature profiles of the stationary-state HNDs were estimated by using a Green’s function approach, assuming that the temperature profiles were equilibrated by conduction in the water (SI Appendix, Figs. S2 and S13) (36).
Lumped Element Modeling of Oscillators.
Oscillation of HNDs was modeled using a lumped thermal model in conjunction with the equation of motion including Marangoni forces and viscous drag. This approach was adapted from our previously reported method (22) with modifications to account for the flat fluid interface, optical-trap patterns, and multiparticle interactions. Briefly, HNDs were simplified as squares broken into two discrete elements (left and right halves), and the transient temperature difference between the elements was calculated by using linear superposition of diffusive heat transfer (at zero velocity) and velocity-dependent convective heat transfer through the gel/water surface (42). The overall velocity-dependent convection coefficient, , under a flat-plate approximation is given by the following:
| [2] |
where kw is the heat conduction coefficient of the water, a is the width of the gel, µ is the dynamic viscosity of the water, L is the characteristic size (L ∼ a, the HND size), Pr is the Prandtl number as (cpµ/kw), cp is the specific heat capacity, ρw is the density of the water, and is the velocity. Then, the thermal resistance and capacitance, which are functions of the velocity-dependent convection coefficient, were calculated as described below (22):
| [3] |
| [4] |
where Rth is the thermal resistance, and Cth is the thermal capacitance in the lumped thermal circuit. Also, ρm is the density of the gel, A is the surface area of the lumped element (half the area of the gel), and t is the thickness. Then, the equations of motion were coupled with transient thermal difference between elements as shown below:
| [5] |
| [6] |
| [7] |
where u1 is the position, u2 the velocity, u3 the temperature difference between elements, the derivative of surface tension with respect to temperature, the heat generation difference between two elements, the effective mass of the object (), the effective viscous drag coefficient of the object (, ), and the scaling factor for the effective mass and drag. The scaling parameter was obtained by fitting the simulation result with the experimental result to account for the mass of water and recirculation flow during oscillation.
Finally, in the case of coupled oscillation, since the temperature difference between the two elements induced by a nearby heat source scales as ∼1/r2, the following thermal coupling term was added to the equation to connect two sets of differential equations for oscillation as below:
| [8] |
where r is the separation distance between two oscillators, and is the thermal coupling coefficient, which was fit to the observed Q values with respect to the separation distance. The sign () is determined from the initial configuration of the two oscillator positions. For example, the oscillator trapped on the left uses the positive sign and the one on the right is negative. In addition, the average frequency differences (∼9%) in oscillator pairs at large separation distance were setup by tuning the effective mass coefficient on each oscillator to resemble the experimental system (SI Appendix, Fig. S9).
Threshold Light Intensity for Oscillation.
For small HND displacements about the center of the trap, the differential heat input can be written as where . Here, I0 is the light intensity, α is the absorption coefficient of the HNDs, and W is the characteristic out-of-plane width of the HNDs. The temperature difference (ΔT) between the lumped elements resulting from the differential heat input can be calculated based on the thermal circuit shown in Fig. 1E and results in the following equation:
| [9] |
The equation of motion of the HND is as follows:
| [10] |
Assuming a periodic solution of the form , and substituting for T from Eq. 9, the above equation becomes the following:
| [11] |
During sustained oscillation, the imaginary component of the above equation is exactly 0. It is noteworthy that when the imaginary component is positive, this system behaves like a damped oscillator resulting in a gradual drop in the amplitude. Whereas when the imaginary component is negative (e.g., at the startup of oscillations with small amplitude oscillations), the amplitude of oscillation increases until an amplitude-limiting nonlinearity in the system brings the imaginary component to 0 at steady oscillation. This implies that during sustained oscillation, from Eq. 11,
| [12] |
Substituting for , the expression for the minimum threshold light intensity for sustained oscillation at a frequency ω can be expressed as follows:
| [13] |
At the onset of oscillation during startup (and when ω ),
| [14] |
Specifically, for a square HND of side a, with = 0.5, the threshold current density can be simplified to the following: .
Furthermore, during steady oscillation, Eq. 11 can be rewritten as follows:
| [15] |
Therefore, the final settling frequency can be written as follows:
| [16] |
where , the thermal time constant of the system.
Note that the equation of motion, Eqs. 10 and 11, resembles that of a damped harmonic oscillator. However, the restoring force results from the Marangoni force—which unlike a restoring spring—is not instantaneous. This is due to the thermal delay; that is, the delay between the HND displacement and the resulting temperature rise. Therefore, as seen in Eq. 11, the restoring Marangoni force has real and imaginary components. In other words, the real part of the restoring Marangoni force Re() acts as an instantaneous “spring,” and the imaginary part Im() counters the inherent viscous damping of the system. From Eq. 11, the ratio of the real and imaginary components of the Marangoni force is Re/Im() = . When Im() exactly balances the viscous damping term , the settling frequency of this system simply reduces to Eq. 16 as the Re() = . It is evident from the third term in Eq. 11 that the thermal components of this system control both the mechanical resonance of the HND and the thermal response times. When the settling frequency is less than the thermal cutoff frequency (), the differential heat generated effectively acts as a thermal spring, with a dominant Re component of the total Marangoni force . Furthermore, the maximum value of the Im component of Marangoni force that compensates the damping loss is attained when the frequency of oscillations matches the thermal cutoff frequency (); beyond this frequency, the magnitudes of both the Re and Im components of the Marangoni force drop rapidly. Finally, it is evident from Eq. 16 that the final settling frequency of the HND increases with faster thermal dynamics. Likewise, higher damping in the system results in stable oscillation at higher frequencies.
Supplementary Material
Acknowledgments
We thank Ji-Won Kim and Ian Hunter for helpful discussions. This work was supported by the Army Research Office through Grants W911NF-21-1-0068 (to R.C.H.) with additional support from the National Science Foundation through the Brandeis Materials Research Science and Engineering Center (MRSEC, DMR‐2011846) and Chemistry program (NSF-CHE, 1904660, to T.E.).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2024581118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or supporting information.
References
- 1.Goulding M., Circuits controlling vertebrate locomotion: Moving in a new direction. Nat. Rev. Neurosci. 10, 507–518 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Deora T., Singh A. K., Sane S. P., Biomechanical basis of wing and haltere coordination in flies. Proc. Natl. Acad. Sci. U.S.A. 112, 1481–1486 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Satterlie R. A., Reciprocal inhibition and postinhibitory rebound produce reverberation in a locomotor pattern generator. Science 229, 402–404 (1985). [DOI] [PubMed] [Google Scholar]
- 4.Zhang H. P., Be’er A., Florin E.-L., Swinney H. L., Collective motion and density fluctuations in bacterial colonies. Proc. Natl. Acad. Sci. U.S.A. 107, 13626–13630 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Polin M., Tuval I., Drescher K., Gollub J. P., Goldstein R. E., Chlamydomonas swims with two “gears” in a eukaryotic version of run-and-tumble locomotion. Science 325, 487–490 (2009). [DOI] [PubMed] [Google Scholar]
- 6.Grillner S., Neurobiological bases of rhythmic motor acts in vertebrates. Science 228, 143–149 (1985). [DOI] [PubMed] [Google Scholar]
- 7.Yoshida R., Ueki T., Evolution of self-oscillating polymer gels as autonomous polymer systems. NPG Asia Mater. 6, e107 (2014). [Google Scholar]
- 8.Fang Y., Yashin V. V., Levitan S. P., Balazs A. C., Pattern recognition with “materials that compute”. Sci. Adv. 2, e1601114 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Prindle A., et al., A sensing array of radically coupled genetic ‘biopixels’. Nature 481, 39–44 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.He X., et al., Synthetic homeostatic materials with chemo-mechano-chemical self-regulation. Nature 487, 214–218 (2012). [DOI] [PubMed] [Google Scholar]
- 11.He X., Friedlander R. S., Zarzar L. D., Aizenberg J., Chemo-mechanically regulated oscillation of an enzymatic reaction. Chem. Mater. 25, 521–523 (2013). [Google Scholar]
- 12.Wehner M., et al., An integrated design and fabrication strategy for entirely soft, autonomous robots. Nature 536, 451–455 (2016). [DOI] [PubMed] [Google Scholar]
- 13.Semenov S. N., et al., Autocatalytic, bistable, oscillatory networks of biologically relevant organic reactions. Nature 537, 656–660 (2016). [DOI] [PubMed] [Google Scholar]
- 14.Dolev A., Davis S., Bucher I., Noncontact dynamic oscillations of acoustically levitated particles by parametric excitation. Phys. Rev. Appl. 12, 034031 (2019). [Google Scholar]
- 15.Andersson L. S., et al., Mutations in DMRT3 affect locomotion in horses and spinal circuit function in mice. Nature 488, 642–646 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bush J. W. M., Hu D. L., WALKING ON WATER: Biolocomotion at the interface. Annu. Rev. Fluid Mech. 38, 339–369 (2006). [Google Scholar]
- 17.Pena-Francesch A., Giltinan J., Sitti M., Multifunctional and biodegradable self-propelled protein motors. Nat. Commun. 10, 3188 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kitahata H., Hiromatsu S.-i., Doi Y., Nakata S., Rafiqul Islam M., Self-motion of a camphor disk coupled with convection. Phys. Chem. Chem. Phys. 6, 2409–2414 (2004). [Google Scholar]
- 19.Okawa D., Pastine S. J., Zettl A., Fréchet J. M. J., Surface tension mediated conversion of light to work. J. Am. Chem. Soc. 131, 5396–5398 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Maggi C., Saglimbeni F., Dipalo M., De Angelis F., Di Leonardo R., Micromotors with asymmetric shape that efficiently convert light into work by thermocapillary effects. Nat. Commun. 6, 7855 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Miniewicz A., Bartkiewicz S., Orlikowska H., Dradrach K., Marangoni effect visualized in two-dimensions Optical tweezers for gas bubbles. Sci. Rep. 6, 34787 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hauser A. W., Sundaram S., Hayward R. C., Photothermocapillary oscillators. Phys. Rev. Lett. 121, 158001 (2018). [DOI] [PubMed] [Google Scholar]
- 23.Ashkin A., Dziedzic J. M., Bjorkholm J. E., Chu S., Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 11, 288–290 (1986). [DOI] [PubMed] [Google Scholar]
- 24.Dufresne E. R., Grier D. G., Optical tweezer arrays and optical substrates created with diffractive optics. Rev. Sci. Instrum. 69, 1974–1977 (1998). [Google Scholar]
- 25.Reicherter M., Haist T., Wagemann E. U., Tiziani H. J., Optical particle trapping with computer-generated holograms written on a liquid-crystal display. Opt. Lett. 24, 608–610 (1999). [DOI] [PubMed] [Google Scholar]
- 26.Kotar J., Leoni M., Bassetti B., Lagomarsino M. C., Cicuta P., Hydrodynamic synchronization of colloidal oscillators. Proc. Natl. Acad. Sci. U.S.A. 107, 7669–7673 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lehmuskero A., Ogier R., Gschneidtner T., Johansson P., Käll M., Ultrafast spinning of gold nanoparticles in water using circularly polarized light. Nano Lett. 13, 3129–3134 (2013). [DOI] [PubMed] [Google Scholar]
- 28.Friese M. E. J., Nieminen T. A., Heckenberg N. R., Rubinsztein-Dunlop H., Optical alignment and spinning of laser-trapped microscopic particles. Nature 394, 348–350 (1998). [Google Scholar]
- 29.Christensen S. K., Chiappelli M. C., Hayward R. C., Gelation of copolymers with pendent benzophenone photo-cross-linkers. Macromolecules 45, 5237–5246 (2012). [Google Scholar]
- 30.Kim H., et al., Light-driven shape morphing, assembly, and motion of nanocomposite gel surfers. Adv. Mater. 31, e1900932 (2019). [DOI] [PubMed] [Google Scholar]
- 31.Dietrich K., Jaensson N., Buttinoni I., Volpe G., Isa L., Microscale Marangoni surfers. Phys. Rev. Lett. 125, 098001 (2020). [DOI] [PubMed] [Google Scholar]
- 32.Michelin S., Lauga E., Phoretic self-propulsion at finite Péclet numbers. J. Fluid Mech. 747, 572–604 (2014). [Google Scholar]
- 33.Chen J. Z., Troian S. M., Darhuber A. A., Wagner S., Effect of contact angle hysteresis on thermocapillary droplet actuation. J. Appl. Phys. 97, 014906 (2005). [Google Scholar]
- 34.Matheny M. H., et al., Exotic states in a simple network of nanoelectromechanical oscillators. Science 363, eaav7932 (2019). [DOI] [PubMed] [Google Scholar]
- 35.Tsimring L. S., Rulkov N. F., Larsen M. L., Gabbay M., Repulsive synchronization in an array of phase oscillators. Phys. Rev. Lett. 95, 014101 (2005). [DOI] [PubMed] [Google Scholar]
- 36.Baffou G., Quidant R., Girard C., Thermoplasmonics modeling: A Green’s function approach. Phys. Rev. B Condens. Matter Mater. Phys. 82, 165424 (2010). [Google Scholar]
- 37.Goldstein D., Giver M., Chakraborty B., Synchronization patterns in geometrically frustrated rings of relaxation oscillators. Chaos 25, 123109 (2015). [DOI] [PubMed] [Google Scholar]
- 38.Lushi E., Wioland H., Goldstein R. E., Fluid flows created by swimming bacteria drive self-organization in confined suspensions. Proc. Natl. Acad. Sci. U.S.A. 111, 9733–9738 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Drescher K., et al., Dancing volvox: Hydrodynamic bound states of swimming algae. Phys. Rev. Lett. 102, 168101 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Barber D. M., Crosby A. J., Emrick T., Mesoscale block copolymers. Adv. Mater. 30, e1706118 (2018). [DOI] [PubMed] [Google Scholar]
- 41.Bae J., et al., Programmable and reversible assembly of soft capillary multipoles. Mater. Horiz. 4, 228–235 (2017). [Google Scholar]
- 42.Jafarpur K., Yovanovich M. M., Laminar free convective heat transfer from isothermal spheres: A new analytical method. Int. J. Heat Mass Transf. 35, 2195–2201 (1992). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or supporting information.