Communication consumes 35 times more energy than computation in the human cortex, but both costs are needed to predict synapse number

Significance

Engineers describe the human brain as a low-energy form of computation. However, from the simplest physical viewpoint, a neuron’s computation cost is remarkably larger than the best possible bits per joule—off by a factor of $10^8$. Here we explicate, in the context of energy consumption, a definition of neural computation that is optimal given explicit constraints. The plausibility of this definition as Nature’s perspective is supported by an energy audit of the human brain. The audit itself requires modifying conventional perspectives and calculations revealing that communication costs are 35-fold computational costs.

Abstract

Darwinian evolution tends to produce energy-efficient outcomes. On the other hand, energy limits computation, be it neural and probabilistic or digital and logical. Taking a particular energy-efficient viewpoint, we define neural computation and make use of an energy-constrained computational function. This function can be optimized over a variable that is proportional to the number of synapses per neuron. This function also implies a specific distinction between adenosine triphosphate (ATP)-consuming processes, especially computation per se vs. the communication processes of action potentials and transmitter release. Thus, to apply this mathematical function requires an energy audit with a particular partitioning of energy consumption that differs from earlier work. The audit points out that, rather than the oft-quoted 20 W of glucose available to the human brain, the fraction partitioned to cortical computation is only 0.1 W of ATP [L. Sokoloff, Handb. Physiol. Sect. I Neurophysiol. 3, 1843–1864 (1960)] and [J. Sawada, D. S. Modha, “Synapse: Scalable energy-efficient neurosynaptic computing” in Application of Concurrency to System Design (ACSD) (2013), pp. 14–15]. On the other hand, long-distance communication costs are 35-fold greater, 3.5 W. Other findings include 1) a $10^8$-fold discrepancy between biological and lowest possible values of a neuron’s computational efficiency and 2) two predictions of $N$, the number of synaptic transmissions needed to fire a neuron (2,500 vs. 2,000).

The purpose of the brain is to process information, but that leaves us with the problem of finding appropriate definitions of information processing. We assume that given enough time and given a sufficiently stable environment (e.g., the common internals of the mammalian brain), then Nature’s constructions approach an optimum. The problem is to find which function or combined set of functions is optimal when incorporating empirical values into these function(s). The initial example in neuroscience is ref. 1, which shows that information capacity is far from optimized, especially in comparison to the optimal information per joule which is in much closer agreement with empirical values. Whenever we find such an agreement between theory and experiment, we conclude that this optimization, or near optimization, is Nature’s perspective. Using this strategy, we and others seek quantified relationships with particular forms of information processing and require that these relationships are approximately optimal (1–7). At the level of a single neuron, a recent theoretical development identifies a potentially optimal computation (8). To apply this conjecture requires understanding certain neuronal energy expenditures. Here the focus is on the energy budget of the human cerebral cortex and its primary neurons. The energy audit here differs from the premier earlier work (9) in two ways: The brain considered here is human not rodent, and the audit here uses a partitioning motivated by the information-efficiency calculations rather than the classical partitions of cell biology and neuroscience (9). Importantly, our audit reveals greater energy use by communication than by computation. This observation in turn generates additional insights into the optimal synapse number. Specifically, the bits per joule optimized computation must provide sufficient bits per second to the axon and presynaptic mechanism to justify the great expense of timely communication. Simply put from the optimization perspective, we assume evolution would not build a costly communication system and then not supply it with appropriate bits per second to justify its costs. The bits per joule are optimized with respect to $N$, the number of synaptic activations per interpulse interval (IPI) for one neuron, where $N$ happens to equal the number of synapses per neuron times the success rate of synaptic transmission (below).

To measure computation, and to partition out its cost, requires a suitable definition at the single-neuron level. Rather than the generic definition “any signal transformation” (3) or the neural-like “converting a multivariate signal to a scalar signal,” we conjecture a more detailed definition (8). To move toward this definition, note two important brain functions: estimating what is present in the sensed world and predicting what will be present, including what will occur as the brain commands manipulations. Then, assume that such macroscopic inferences arise by combining single-neuron inferences. That is, conjecture a neuron performing microscopic estimation or prediction. Instead of sensing the world, a neuron’s sensing is merely its capacitive charging due to recently active synapses. Using this sampling of total accumulated charge over a particular elapsed time, a neuron implicitly estimates the value of its local latent variable, a variable defined by evolution and developmental construction (8). Applying an optimization perspective, which includes implicit Bayesian inference, a sufficient statistic, and maximum-likelihood unbiasedness, as well as energy costs (8), produces a quantified theory of single-neuron computation. This theory implies the optimal IPI probability distribution. Motivating IPI coding is this fact: The use of constant amplitude signaling, e.g., action potentials, implies that all information can only be in IPIs. Therefore, no code can outperform an IPI code, and it can equal an IPI code in bit rate only if it is one to one with an IPI code. In neuroscience, an equivalent to IPI codes is the instantaneous rate code where each message is $IP{I}^{-1}$. In communication theory, a discrete form of IPI coding is called differential pulse position modulation (10); ref. 11 explicitly introduced a continuous form of this coding as a neuron communication hypothesis, and it receives further development in ref. 12.

Results recall and further develop earlier work concerning a certain optimization that defines IPI probabilities (8). An energy audit is required to use these developments. Combining the theory with the audit leads to two outcomes: 1) The optimizing $N$ serves as a consistency check on the audit and 2) future energy audits for individual cell types will predict $N$ for that cell type, a test of the theory. Specialized approximations here that are not present in earlier work (9) include the assumptions that 1) all neurons of cortex are pyramidal neurons, 2) pyramidal neurons are the inputs to pyramidal neurons, 3) a neuron is under constant synaptic bombardment, and 4) a neuron’s capacitance must be charged 16 mV from reset potential to threshold to fire.

Following the audit, the reader is given a perspective that may be obvious to some, but it is rarely discussed and seemingly contradicts the engineering literature (but see ref. 6). In particular, a neuron is an incredibly inefficient computational device in comparison to an idealized physical analog. It is not just a few bits per joule away from optimal predicted by the Landauer limit, but off by a huge amount, a factor of $10^8$. The theory here resolves the efficiency issue using a modified optimization perspective. Activity-dependent communication and synaptic modification costs force upward optimal computational costs. In turn, the bit value of the computational energy expenditure is constrained to a central limit like the result: Every doubling of $N$ can produce no more than 0.5 bits. In addition to 1) explaining the $10^8$ excessive energy use, other results here include 2) identifying the largest “noise” source limiting computation, which is the signal itself, and 3) partitioning the relevant costs, which may help engineers redirect focus toward computation and communication costs rather than the 20-W total brain consumption as their design goal.

Results

Energy Audit.

Adenosine triphospate use for computation and communication.

Microscopic energy costs are based on bottom–up calculations for adenosine triphosphate (ATP) consumption (9). A total of 36,000 J/mol ATP (13) implies watts. As derived below, computation consumes ca. 0.1 ATP-watts per cortex or 1/200th of the nominal and oft-quoted 20 W that would be produced by complete oxidation of the glucose taken up by the brain (1). Fig. 1 compares cortical communication costs to computational costs. Also appearing is an energy consumption labeled ($SynMo{d}^{+}$). What ref. 14 calls “housekeeping” is a hypothesis on its part; an alternative hypothesis is inspired by and consistent with results from developing brain (15). This category seems to be dominated by costs consistent with synaptogenesis (e.g., growth and process extension via actin polymerization and via new membrane incorporation, membrane synthesis and its axo- and dendro-plasmic transport, and astrocytic costs); a small fraction of $SynMo{d}^{+}$ is time-dependent “maintenance.” Here $SynMo{d}^{+}$ is calculated by subtracting the bottom–up calculated communication and computation ATP consumption from available ATP, a top–down empirical partitioning (Table 1).

Fig. 1.

Computation costs little compared to communication. Communication alone accounts for more than two-thirds of the available 4.94 ATP-W (Table 1), with slightly more consumption due to WM than to GM (big pie chart). Computation, the smallest consumer, is subpartitioned by the two ionotropic glutamate receptors (bar graph). $SynMo{d}^{+}$ includes astrocytic costs, process extension, process growth, axo- and dendro-plasmic transport of the membrane building blocks, and time-independent housekeeping costs (although this last contributor is a very small fraction). The small pie chart subpartitions GM communication. See Results and Materials and Methods for details. WM communication includes its maintenance and myelination costs in addition to resting and action potentials.

Table 1.

Rudimentary partitioning, glucose to ATP

Brain/region (weight, g)	Watts (complete oxidation)	Unoxidized (equivalent watts)	Heat watts	ATP-watts
Whole brain (1,495)	17.0	1.86	8.89	6.19
Cerebellum (154)	1.77	0.19	0.93	0.65
Other regions (118)	1.65	0.18	0.87	0.60
Forebrain cortex (1,223)				4.94
White (590)	5.07	0.56	2.66	1.85
Gray (633)	8.45	0.93	4.43	3.09

See Materials and Methods and SI Appendix, Tables S1–S8 for details and citations.

For some, the rather large cost of communication might be surprising but apparently is necessary for suitable signal velocities and information rates (1, 16–19). Combining gray matter (GM) communication costs with the total white matter (WM) costs accounts for 71%, 3.52 W (Fig. 2), of the total 4.94 ATP-watts per cortex, compared to 2% for computation. Supposing that all WM costs are essentially communication costs (including oligodendrocyte/myelination costs), then the ratio for communication vs. computation is 35:1.

Fig. 2.

Energy use increases linearly with average firing rate, but for reasonable rates, computation (Comp) costs much less than communication (Comm). Comparing the bottom (red) curve (GM communication costs) to the top (blue) curve (GM communication cost plus computational costs) illustrates how little computational costs increase relative to communication costs. The y-intercept value is 1.09 W for resting potential. The open circle plotting $SynMo{d}^{+}$ + GMComm + Comp adds the 1.32 W of GM $SynMo{d}^{+}$ to the 1.77 W of GMComm + Comp at 1 Hz. The solid circle, labeled WMComm + GMComm, shows the value of the combined communication cost, cortical GM at 1 Hz, and the total cortical white matter cost. See Materials and Methods for further details.

Computation costs in the human brain.

The energy needed to recover ion gradients from the total excitatory synaptic current flows per IPI determines the cost of computation for that IPI. Various quantitative assumptions feeding into subsequent calculations are required (Materials and Methods and SI Appendix), but none are more important than the generic assumption that the average firing rate of each input to a neuron is the same as the average firing rate out of that neuron (4). Via this assumption, and assuming $10^4$ synapses per neuron and a 75% failure rate, the aggregate effects of inhibition, capacitance, and postsynaptic ${\mathrm{K}}^{+}$ conductances are implicitly taken into account. This aggregation is possible since increases of any of these parameters merely lead to smaller depolarizations per synaptic activation but cause little change in synaptic current flow per excitatory synaptic event. Indeed, such attenuating effects are needed to make sense of several other variables. A quick calculation helps illustrate this claim.

An important starting point for computational energy cost is the average number of excitatory synaptic activations to fire a cortical neuron. Assume the neuron is a pyramidal neuron and that its excitatory inputs are other pyramidal neurons. Therefore, the mean firing rate of this neuron is equal to the mean firing rate of each input. Thus, the threshold will be the number of input synapses times the quantal success rate (4); i.e., ca. $10^4\cdot 0.25=\mathrm{2,500}=N$ because on average each input fires once per IPI out. Even after accounting for quantal synaptic failures, inhibition is required for consistency with 2,500 excitatory events propelling the 16-mV journey from reset to threshold. Activation of AMPA receptors (AMPARs) and NMDA receptors (NMDARs) provides an influx of three Na${}^{+}$ for every two ${\mathrm{K}}^{+}$ that flow out. With an average total AMPAR conductance of 200 pS, there are 114.5 pS of Na${}^{+}$ per synaptic activation (SA). Multiplying this conductance by the 110-mV driving force on Na${}^{+}$ and by the 1.2-ms SA duration yields 15.1 fC per SA. Dividing this total Na${}^{+}$ influx by 3 compensates for the two ${\mathrm{K}}^{+}$ that flow out for every three Na${}^{+}$ that enter; thus, the net charge influx is 5.04 fC per SA. We assume that the voltage-activated, glutamate-primed NMDARs increases this net flux by a factor of 1.5, yielding 7.56 fC per SA (see Materials and Methods and SI Appendix, Tables S3–S5 for more details and the ATP costs). Taking into account the 2,500 synaptic activations per IPI yields 18.9 pC per IPI. Using a 750-pF value for a neuron’s capacitance, this amount of charge would depolarize the membrane potential 25.2 mV rather than the desired 16 mV. Thus, the excitatory charge influx must be opposed by inhibition and ${\mathrm{K}}^{+}$ conductances to offset the total 7.56-fC net positive influx. Most simply, just assume a divisive inhibitory factor of 1.5. Then the numbers are all consistent, and the average depolarization is 6.4 $\mathrm{\mu }$V per synaptic activation. Because each net, accumulated charge requires one ATP to return the three Na${}^{+}$ and two ${\mathrm{K}}^{+}$, the computational cost of the 16-mV depolarization is $6.67\cdot 10^{-12}$ J per neuron per spike; i.e., required computational power for each neuron spike of cortex $6.67\cdot 10^{-12}\cdot 1.5\cdot 10^{10}=0.10$ W.

Communication costs.

As quantified in Materials and Methods (also SI Appendix, Tables S3 and S5), the GM long-distance communication cost of 1.67 W (Fig. 1) includes the partitioned costs of axonal resting potentials (APs) and presynaptic transmission (neurotransmitter recycling and packaging, vesicle recycling, and calcium extrusion). The neurotransmission costs assume a 1-Hz mean neuron firing rate and a $75\%$ failure rate. Next using ref. 14, the calculation assumes one vesicle is released per nonfailed AP. Differing from ref. 14 while closer to earlier work (9), assume there is the same Ca influx with every AP (20). Further, also use a more recent measurement of Na${}^{+}$-${\mathrm{K}}^{+}$ overlapping current flows of the AP, 2.38 (21). Of all of the difficult but influential estimates, none is more challenging and important than axonal surface area (Materials and Methods).

Firing rate.

In regard to average firing rate, we postulate an average value of one pulse per neuron per decision-making interval (DMI), which we assume as 1 s.

As Fig. 2 indicates, the combined WM and GM communication cost at 1 Hz is 3.52 W. Computational costs are only a very small fraction of frequency-dependent costs. Calculation of $SynMo{d}^{+}$ is not possible and, as explicated in Discussion, we discredit the ouabain manipulation others (9, 22) use to estimate it. The value here is arrived at by differencing the calculated and measured costs from the available energy (SI Appendix, Fig. S1).

Using a firing rate of 1 Hz and $1.5\cdot 10^{10}$ neurons per cortex, a bottom–up calculation for the excitatory postsynaptic ion flux per AP per cortex yields 0.10 W. The linear relationship between firing rate and energy consumption has a substantial baseline energy consumption of 1.09 W (y-axis intercept). Apparently resting axon conductance (23) is required for a resting potential and stable behavior (24). In the case of the dendrite, computational costs are zero at zero firing rate, a theoretical limit result which, as argued earlier, is a nonsense practical situation. However, dendritic leak is assumed to be essentially zero since we assume, perhaps controversially (cf. ref. 9), that a cortical neuron is under constant synaptic bombardment and that all dendrosomatic conductances are due to synaptic activation and voltage-activated channels. That is, a neuron resets after it fires and immediately starts depolarizing until hitting threshold.

Computational costs are very sensitive to failure rates, which for Fig. 2 are fixed at 75%, whereas communication is only slightly sensitive to the synaptic failure rate (see below for more details).

An energy-use partitioning based on glucose oxidation.

The oft-repeated brain energy consumption of 20 W is not simply the cost of computation and communication, thus requiring an appropriate partitioning (Table 1). The 17 W of glucose potential energy from recent positron emission tomography (PET) scan research (25) replaces Sokoloff’s 20 W from the 1950s. The PET scan research produces regional per-gram values, and these values are scaled by the regional masses (26), allowing regional estimates (SI Appendix, Table S1). Arguably, 11% of the total glucose uptake is not oxidized (27) (some arteriovenous differences obtain a smaller percentage; SI Appendix). After removing the 8.89 W for heating, there are only 6.19 ATP-W available to the whole brain. The regional partitioning implies cerebral gray consumes 3.09 ATP-W, which is split between computation, communication, and $SynMo{d}^{+}$. After direct calculation of communication and computational costs, the remaining GM energy is allocated to $SynMo{d}^{+}$.

A specialized partitioning.

The ultimate calculation of bits per joule requires a bipartite partition of action potential-driven costs: Those independent of $N$, $A≔{\mathcal{E}}_{\mathtt{\text{WMAP}}}+{\mathcal{E}}_{\mathtt{\text{GMAxAP}}}+{\mathcal{E}}_{\mathtt{\text{SynModGrow}}}\approx 1.23+0.45+1.08=2.76$ J/s per cortex vs. those scaled by $N$, $B≔{\mathcal{E}}_{\mathtt{\text{COMP}}}+{\mathcal{E}}_{\mathtt{\text{Pre}}}+{\mathcal{E}}_{\mathtt{\text{NSynMod}}}+{\mathcal{E}}_{\mathtt{\text{PreNaAP}}}\approx 0.10+0.11+0.11+0.02=0.34$ J/s per cortex. For the three constituents of $A$, WMAP is white matter action potential dependent; GMAxAP is gray matter action potential dependent; and SynModGrow is action potential dependent and combines all of the functions that underlie synaptogenesis and nonsynaptic, firing-dependent maintenance. For the four $N$-proportional functions, COMP is postsynaptic ionotropic activation, Pre is presynaptic ${\mathrm{C}\mathrm{a}}^{2+}$ and transmitter release functions, PreNaAP is partial presynaptic depolarization driven by the axonal AP, and NSynMod is $N$-proportional synaptic modifications including synaptic metabotropic activation. Note that ${\mathcal{E}}_{{\mathtt{\text{SynMod}}}^{+}}={\mathcal{E}}_{\mathtt{\text{SynModGrow}}}+{\mathcal{E}}_{\mathtt{\text{NSynMod}}}+{\mathcal{E}}_{\mathtt{\text{Plus}}}\approx 1.08+0.11+0.12$, where ${\mathcal{E}}_{\mathtt{\text{Plus}}}$ is the time-dependent maintenance cost. As in ref. 8, the purely time-dependent costs, e.g., ${\mathcal{E}}_{\mathtt{\text{Plus}}}$ and resting potential, are charged to the decision-making process of the system, not to an individual neuron. Finally, to use $A$ and $B$, they are rescaled to joules per IPI per neuron (divide by the number of neurons firing in 1 s) and, additionally for $B$, a rescaling to dependence on synapse number (multiply by $N÷\mathrm{2,500}$; thus, $\mathcal{E}\left(\mathrm{\Lambda },T\right)≔\left(A+N\cdot B/\mathrm{2,500}\right)\cdot E\left[T\right]÷n$, where $E\left[T\right]$ is the average IPI and $n$ is the number of cortical neurons.

A Baseline for Maximally Efficient Computation.

A simplistic model relates physics to neuroscience.

For the sake of creating a baseline, initial comparison, and for further understanding of just what “computation” can mean, suppose a neuron’s computation is just its transformation of inputs to outputs. Then, quantifying the information passed through this transformation (bits per second) and dividing this information rate by the power (W = J/s) yields bits per joule. This ratio is our efficiency measure. In neuroscience, it is generally agreed that Shannon’s mutual information (MI) is applicable for measuring bit rate of neural information processing, neural transformations, or neural communication (3, 4, 28–33). Specifically, using mutual information and an associated rate of excitatory postsynaptic currents of a single neuron produces a comparison with the optimal bits per joule for computation as developed through physical principles. To understand the analogy with statistical mechanics, assume the only noise is wideband thermal noise, k$\mathcal{T}\hspace{0.17em}\approx 4.3\cdot 10^{-21}$ J (Boltzmann’s constant times absolute temperature, $\mathcal{T}=310$ K). The bits per joule ratio can be optimized to find the lowest possible energetic cost of information, which is ${\left(k\mathcal{T}\ln 2\right)}^{-1}$, the Landauer limit (34).

To give this derivation a neural-like flavor, suppose a perfect integrator with the total synaptic input building up on the neuron’s capacitance. Every so often the neuron signals this voltage and resets to its resting potential. Call the signal $V_{sig}$ and, rather unlike a neuron, let it have mean value (resting potential) of zero. That is, let it be normally distributed $\mathcal{N}\left(0,{\sigma }_{sig}^2=E\left[V_{sig}^2\right]\right)$. The thermal noise voltage fluctuation is also a zero-centered normal distribution, $\mathcal{N}\left(0,{\sigma }_{noise}^2\right)$. Expressing this noise as energy on the membrane capacitance, $\frac{C_m{\sigma }_{noise}^2}{2}=\frac{k\mathcal{T}}{2}\Rightarrow {\sigma }_{noise}^2=\frac{k\mathcal{T}}{C_m}$ (35–37). Then using Shannon’s result, e.g., theorem 10.1.1 in ref. 38, the nats per transmission are $\frac{1}{2}\ln \left(1+\frac{{\sigma }_{sig}^2}{{\sigma }_{noise}^2}\right)=\frac{1}{2}\ln \left(1+\frac{C_{m}E\left[V_{sig}^2\right]}{k\mathcal{T}}\right)$ (with natural logarithms being used since we are performing a maximization, thus nats $:\hspace{0.17em}=$ bits$\cdot \ln 2$). Converting to bits, and calling this result the mutual information channel capacity, $C_{MI}={\left(2\ln 2\right)}^{-1}\ln \left(1+\frac{C_{m}E\left[V_{sig}^2\right]}{k\mathcal{T}}\right)$.

Next we need the energy cost, the average signal joules per transmission developed on the fixed $C_m$ by the synaptic activation, $\mathcal{E}≔\frac{C_{m}E\left[V_{sig}^2\right]}{2}$. Dividing the bits per second $C_{MI}$ by the joules per second $\mathcal{E}$ yields the bits per joule form of interest: $\frac{C_{MI}}{\mathcal{E}}=\frac{2}{\left(C_{m}E\left[V_{sig}^2\right]\right)}\cdot \frac{1}{2\ln 2}\ln \left(1+\frac{C_{m}E\left[V_{sig}^2\right]}{k\mathcal{T}}\right)$. This ratio is recognized as the monotonically decreasing function $\frac{\ln \left(1+x\right)}{cx}\hspace{0.17em}$ with $x,c>0$. Therefore, maximizing over $E\left[V_{sig}^2\right]$ but with the restriction $E\left[V_{sig}^2\right]>0$, this is a limit result implying an approach to zero bits per second. That is,

$\underset{E\left[\underset{sig}{\overset{2}{V}}\right]\to 0}{lim}\frac{C_{MI}}{\mathcal{E}}=\frac{1}{C_{m}E\left[V_{sig}^2\right]}\frac{1}{\ln 2}\frac{C_{m}E\left[V_{sig}^2\right]}{k\mathcal{T}}={\left(k\mathcal{T}\ln 2\right)}^{-1}\approx 3.37\cdot 10^{20}$bits per joule.

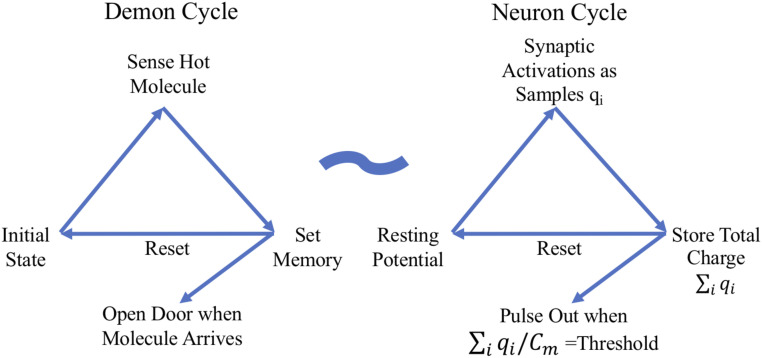
Two comments seem germane. First, physicists arrived at this value decades ago in their vanquishing of Maxwell’s demon and its unsettling ability to create usable energy from randomness (34). In their problem, the device (the demon) is not obviously computational in the neural sense; the demon just repeatedly 1) senses, 2) stores, and 3) operates a door based on the stored information and then 4) erases its stored information as it continues to separate fast molecules from the slower ones (39, 40) (Fig. 3). Moreover, even after simplifying this cycle to steps 1, 2, and 4, physicists do see the demon’s relevance to digital computation. Such a cycle is at the heart of modern computers where computation occurs through repetitive uses, or pairwise uses, of the read/write/erase cycles. For example, bit shifting as it underlies multiplication and the pairwise sensing and bit setting (then resetting) of binary, Boolean logical operations reflect such cycles. Thus, as is well known from other arguments (34, 41), the limit result of physics sets the energy-constraining bound on nonreversible digital computation. Regarding step 3, it would seem that if the demon communicates and controls the door as slowly as possible (i.e., the limit of time going to infinity), there is no need to assign an energy cost to these functions.

Fig. 3.

Maxwell’s demon cycle is analogous to the neuron’s computational cycle. The initial state in the demon cycle is equivalent to the neuron at rest. The demon sensing fast molecules is analogous to the synaptic activations received by the neuron. Whereas the demon uses energy to set the memory and then opens the door for a molecule, the neuron stores charge on the membrane capacitance (${\mathrm{C}}_{\mathrm{m}}$) and then pulses out once this voltage reaches threshold. Simultaneous with such outputs, both cycles then reset to their initial states and begin again. Both cycles involve energy being stored and then released into the environment. The act of the demon opening the door is ignored as an energy cost; likewise, the neuron’s computation does not include the cost of communication. Each ${\mathrm{q}}_i$ is a sample and represents the charge accumulated on the plasma membrane when synapse $i$ is activated.

Despite a nonsurprising qualitative comparison, there is a second insight. Compared to the estimates here of a neuron cycling from reset to firing to reset, this physics result is unimaginably more efficient, not just 5 or 10 times more, but $10^8$-fold more efficient. Suppose that the computational portion of a human cortical neuron has capacitance $C_m\approx 750$ pF (obtained by assuming the human neuron’s surface area is about three times a rat’s pyramidal value of 260 pF) (42) and suppose this neuron resets to $V_{rst}=-0.066$ V while the firing threshold is $V_{\theta }=-0.050$ V. Then in the absence of inhibition, the excitatory synaptic energy needed to bring a neuron from reset to threshold is $\frac{1}{2}{C}_m\left(V_{rst}^2-V_{\theta }^2\right)\approx 1.4\cdot 10^{-12}$ J per spike. Assuming 4 bits per spike, the bits per joule are $2.9\cdot 10^{12}$. Compared to the optimal limit set by physics, this efficiency value is $10^8$ times less energy efficient, a seemingly horrendous energy efficiency for a supposedly optimized system.

The disagreement reorients our thinking.

In the context of understanding neural computation via optimized energy use, this huge discrepancy might discourage any further comparison with thermal physics or the use of mutual information. It could even discourage the assumption that Nature microscopically optimizes bits per joule. But let us not give up so quickly. Note that the analogy between the four-step demon and an abstract description of neural computation for one IPI is reasonable (Fig. 3). That is, 1) excitatory synaptic events are the analog of sensing, 2) these successive events are stored as charge on the plasma membrane capacitance until threshold is reached, at which point 3) a pulse-out occurs, and then 4) the “memory” on this capacitor is reset and the cycle begins anew. Nevertheless, the analogy has its weak spots.

The disharmony between the physical and biological perspectives arises from the physical simplifications that time is irrelevant and that step 3 is cost-free. While the physical simplifications ignore costs associated with step 3, biology must pay for communication at this stage. That is, physics looks at each computational element only as a solitary individual, performing but a single operation. There is no consideration that each neuron participates in a large network or even that a logical gate must communicate its inference in a digital computer in a timely manner. Unlike idealized physics, Nature cannot afford to ignore the energy requirements arising from communication and time constraints that are fundamental network considerations (43) and fundamental to survival itself (especially time) (18, 19).

According to the energy audit, the costs of communication between neurons outweigh computational costs. Moreover, this relatively large communication expense further motivates the assumption of energy-efficient IPI codes (i.e., making a large cost as small as possible is a sensible evolutionary prioritization). Thus, the output variable of computation is assumed to be the IPI or, equivalently, the spike generation that is the time mark of the IPI’s endpoint.

Furthermore, any large energy cost of communication sensibly constrains energy allocated to computation. Recalling our optimal limit with asymptotically zero bits per second, it is unsustainable for a neuron to communicate minuscule fractions of a bit with each pulse out. To communicate the maximal bits per spike at low bits per second leads to extreme communication costs because every halving of bits per second requires at least a doubling of the number of neurons to maintain total bits per second which in turn requires more space. This space problem arising from a larger number of neurons is generally recognized as severely constraining brain evolution and development as well as impacting energy use (44–49). Such an increase of neuron numbers moves neurons farther away from each other. In turn, axons must be longer for the same connectivity. Moreover, to prevent increased communication delays requires wider axons to compensate for the longer axons. Such delays undermine the timely delivery of information (18, 19), which we assume has evolved to its own optimization for any one species. (See SI Appendix for a more fully developed model including assumptions. This model shows that communication costs rise much more than computational costs decrease.) This space problem, arising from a larger number of neurons, is generally recognized as severely constraining brain evolution and development as well as impacting energy use (44–49). It is better for overall energy consumption and efficiency to compute at a larger, computationally inefficient bits per IPI that will feed the axons at some requisite bits per second, keeping neuron number at some optimal level. To say it another way, a myopic bits per joule optimization can lead to a nonsense result, such as zero bits per second and asymptotically an infinite number of neurons.

Nevertheless, assuming efficient communication rates and timely delivery that go hand in hand with the observed communication costs, there is still reason to expect that neuronal computation is as energy efficient as possible in supplying the required bits per second of information to the axons. The problem then is to identify such a computation together with its bits per joule dependence and its inferred bits per second.

A Neurally Relevant Optimization.

How close is the optimized $N$ bits per joule to 2,500?

The computations of this section combined with the earlier energy audit imply an efficiency of ca. $1.4\cdot 10^{12}$ bits per computational joule and fewer than 7.5 bits per IPI for neurons completing their first IPI. Comparing the curves of Fig. 4, the bits per joule maximization that accounts for all spike-dependent costs produces the agreeable result $N\approx \mathrm{2,000}$, which is not far from the 2,500 derived earlier. By comparison, the purely computational perspective of costs, Fig. 4B, indicates the exponentially increasing efficiency is reached as a limit $N\to 0$. Fig. 4A also indicates the optimization result is robust around the optimizing $N$, changing little over a sevenfold range; likewise, bits per IPI are robust. In sum for $N=\mathrm{2,000}$, the neuron computational efficiency is inferior to the demon by ca. $10^8$ but is optimal when other costs are considered. In fact, more detailed considerations below suggest slightly downgrading bit-rate estimates.

Fig. 4.

Bits per joule per neuron at optimal $N$. (A) The bits per joule function, Eq. [1], is concave and reaches a maximum when $N$ is ca. 2,000. This efficiency decreases little more than 5% over a sevenfold range away from this 2,000. At this optimum there are 7.48 bits per spike. (B) The optimal $N$ implies $1.4\cdot 10^{12}$ bits per computational joule. B is calculated by changing Eq. [1]’s denominator to $E\left[T\right]N\cdot B÷\left(\mathrm{2,500}\cdot n\right)$ instead of $E\left[T\right]\left(A+N\cdot B/\mathrm{2,500}\right)÷n$.

Using the notation $\mathrm{\Lambda }$ for the random variable (RV) of the total, unfailed input intensity (events per second) to a neuron and $\widehat{\mathrm{\Lambda }}$ the RV that is the neuron’s estimate, Fig. 4A illustrates the concave function being maximized,

$$\begin{array}{ll}\hfill & \frac{I\left(\mathrm{\Lambda };T\right)}{\mathcal{E}\left(\mathrm{\Lambda },T\right)}=\frac{I\left(\mathrm{\Lambda };\widehat{\mathrm{\Lambda }}\right)}{\mathcal{E}\left(\mathrm{\Lambda },T\right)}\hfill \\ \hfill & =\frac{{\log }_2\left(\ln \left(\frac{{\widehat{\lambda }}_{mx}}{{\widehat{\lambda }}_{mn}}\right)\right)+\frac{1}{2}{\log }_2\left(\frac{{\left(N+1\right)}^2}{N}\right)-\frac{1}{2}{\log }_2\left(2\pi e\right)}{\left(A+N\cdot B/\mathrm{2,500}\right)\cdot E\left[T\right]÷n},\hfill \end{array}$$ [1]

where $I\left(\mathrm{\Lambda };T\right)$ and its equivalent $I\left(\mathrm{\Lambda };\widehat{\mathrm{\Lambda }}\right)$ are the bits per IPI of information gain (8). This gain arises from an additive neuron communicating its implicitly estimated latent variable’s value $\widehat{\mathrm{\Lambda }}=\widehat{\lambda }$ as a first-hitting time, $T=t$ (i.e., RV $T$ producing one particular realization, $t$). The denominator, previously introduced at the end of the energy audit, is the joules per IPI per neuron as a function $N$. The ratio $\frac{{\widehat{\lambda }}_{mx}}{{\widehat{\lambda }}_{mn}}$ is essentially the ratio of the maximum rate of synaptic activation to the baseline rate.

$I\left(\mathrm{\Lambda };T\right)$, derived in ref. 8, requires Corollary 2 (below) for conversion to I($\mathrm{\Lambda };\widehat{\mathrm{\Lambda }}$). Moreover, attending this result are the related results, Lemma 2b and Corollary 1, which enhance our understanding of the neuron’s computation. Just before these mathematical developments, we recall and interpret some results of ref. 8, one of which sheds light on the $10^8$ discrepancy with the demon result.

Deeper insights into the defined computation.

As noted in the Introduction and developed in detail elsewhere (8), the neuron’s computation is an estimation of its scalar latent variable $\mathrm{\Lambda }=\lambda$. $I\left(\mathrm{\Lambda };T\right)=E_{\mathrm{\Lambda },T}\left[\frac{p\left(T|\mathrm{\Lambda }\right)}{p\left(T\right)}\right]$ is the information gain for a Bayesian performing estimation (50). Written this way, the relative entropy starts with the prior $p\left(t\right)$ and via sampling, i.e., synaptic activations, implicitly arrives at a likelihood $p\left(t|\lambda \right)$. The form of this conditional probability density is a maximum-entropy development, which is the best distribution in the sense of maximizing a gaming strategy (51). The maximum-entropy constraints are energy and unbiasedness. This likelihood also carries all of the information of sampling.

Defining 1) $\theta$ as threshold to fire, 2) $E\left[V_{syn}\right]$ as the average size of the synaptic event arriving at the initial segment, and 3) $E\left[V_{syn}^2\right]$ as its second moment, from equations 12 and 6 of ref. 8, $p\left(t|\lambda \right)=\frac{\theta }{\sqrt{\pi \lambda t^{3}E\left[V_{syn}^2|\lambda \right]}}\exp \left(2\frac{\theta E\left[V_{syn}|\lambda \right]}{E\left[V_{syn}^2|\lambda \right]}-\frac{\lambda tE{\left[V_{syn}|\lambda \right]}^2}{E\left[V_{syn}^2|\lambda \right]}-\frac{{\theta }^2}{\lambda tE\left[V_{syn}^2|\lambda \right]}\right)$.

While the only consistent marginal distribution we have yet to discover is $p\left(\lambda \right)={\left(\lambda \log \left(\frac{{\lambda }_{mx}}{{\lambda }_{mn}}\right)\right)}^{-1}$ with $0<{\lambda }_{mn}<\lambda <{\lambda }_{mx}<\infty$, which is enough to infer the form of $p\left(t\right)$ and of $p\left(\lambda |t\right)$.

Importantly, the IPI, $t$, is a sufficient statistic, which is information equivalent to the likelihood $p\left(t|\lambda \right)$ and so is the latent RV estimate, $\widehat{\lambda }=\frac{N^2}{\left(N+1\right)t}$. The conditional mean-squared error of the estimate is $E\left[{\left(\widehat{\mathrm{\Lambda }}-\mathrm{\Lambda }\right)}^2|\lambda \right]=\frac{{\lambda }^2\left(N+2\right)}{{\left(N+1\right)}^2}$ as Corollary 1 here demonstrates. Thus, we not only define a neuron’s computation, but also can understand its performance as a statistical inference.

Parsing Eq. [1], the information rate increases at the rate of ca. $\frac{1}{2}{\log }_2\left(N\right)$ while energy consumption increases in proportion to $N$. This disadvantageous ratio and the large optimizing $N$ help explain the demon’s superior efficiency. Moreover, increasing the noncomputational demands such that $A÷B$ increases leads to a larger optimal value of $N$ and vice versa. Regardless, Corollaries 1 and 2 of the next subsection clearly show that the energy devoted to computation, or other $N$-dependent energy consumers, restricts the precision of a neuron’s estimation and restricts the information a neuron generates when the neuron is required to be energy optimal.

Mathematical derivations.

As an approximation of a result in ref. 52, assume an empirical distribution of synaptic weights such that the second noncentral moment is equal to twice the mean squared (e.g., an exponential distribution). Note also that $\theta$ can be written as the product $N$, the average number of synaptic increments, multiplied by the average synaptic incrementing event $E\left[V_{syn}|\lambda \right]$ (with inhibition and capacitance taken into account) (8). That is, $\theta =N\cdot E\left[V_{syn}|\lambda \right]$. Putting this assumption to work, we obtain a simplification, and there are two new corollaries based on the above $p\left(t|\lambda \right)$.

$\mathit{\text{Lemma 1}}$.

$p\left(t|\lambda \right)=N{\left(2\pi \lambda t^3\right)}^{-1/2}\exp \left(-\frac{\lambda t}{2}-\frac{N^2}{2\lambda t}+N\right)$.

$\mathit{\text{Proof}}$:

Start with $p\left(t|\lambda \right)$ given earlier, substitute using $\theta =N\cdot E\left[V_{syn}|\lambda \right]$, and then note that $\frac{E{\left[V_{syn}|\lambda \right]}^2}{E\left[V_{syn}^2|\lambda \right]}=\frac{1}{2}$.

At this point there is an instructive and eventually simplifying transform to create $p\left(\widehat{\lambda }|\lambda \right)$ from $p\left(t|\lambda \right)$. The transform arises from the unbiased requirement, one of the constraints producing the earlier optimization results (8). As a guess suppose the unbiased estimate is $\widehat{\lambda }=\frac{N^2}{\left(N+1\right)t}$ or equivalently $t=\frac{N^2}{\left(N+1\right)\widehat{\lambda }}$ and then use this relation to transform $p\left(t|\lambda \right)$ to $p\left(\widehat{\lambda }|\lambda \right)$.

$\mathit{\text{Lemma 2a}}$.

$p\left(\widehat{\lambda }|\lambda \right)=\sqrt{N+1}{\left(2\pi \lambda \widehat{\lambda }\right)}^{-1/2}\exp \left(-\frac{\lambda N^2}{2\left(N+1\right)\widehat{\lambda }}-\frac{\widehat{\lambda }\left(N+1\right)}{2\lambda }+N\right)$.

$\mathit{\text{Lemma 2b}}$.

$E\left[\widehat{\mathrm{\Lambda }}|\lambda \right]=\lambda =\frac{N^2}{N+1}\cdot E\left[T^{-1}|\lambda \right]$.

So $\widehat{\lambda }=\frac{N^2}{\left(N+1\right)t}$ is indeed the desired unbiased estimate, which has a particular mean-squared error.

Corollary 1.

$E\left[{\left(\widehat{\mathrm{\Lambda }}-\mathrm{\Lambda }\right)}^2|\lambda \right]=\frac{{\lambda }^2\left(N+2\right)}{{\left(N+1\right)}^2}$.

$\mathit{\text{Proofs}}$:

See Materials and Methods.

As Corollary 1 shows, devoting more energy to computation by increasing $N$ reduces the error of the estimate. Specifically, the standard deviation decreases at the rate of $1/\sqrt{N}$. Of course, computational costs increase in direct proportion to $N$.

Corollary 1 adds additional perspective to our definition of a neuron’s computation as an estimate. Furthermore, the new likelihood, $p\left(\widehat{\lambda }|\lambda \right)$, is particularly convenient for calculating information rates, a calculation which requires one more result. That result is the marginal distribution of $\widehat{\mathrm{\Lambda }}$. Because the only known consistent density (and arguably the simplest) is $p\left(\lambda \right)={\left(\lambda \log \left(\frac{{\lambda }_{mx}}{{\lambda }_{mn}}\right)\right)}^{-1}$, the estimate’s marginal density is simply approximated via the following:

Lemma 3.

$p\left(\widehat{\lambda }\right)={\int }_{\lambda mn}^{\lambda mx}p\left(\lambda \right)p\left(\widehat{\lambda }|\lambda \right)d\lambda \approx {\left(\widehat{\lambda }\ln \left(\frac{{\lambda }_{mx}}{{\lambda }_{mn}}\right)\right)}^{-1}$,where the approximation arises by the near identity of the integral to $p\left(\lambda \right)$ assuming the range of $\lambda$ and $\widehat{\lambda }$ is the same. Moreover, the lack of $\widehat{\lambda }$ bias for all conditioning values of $\lambda$ hints that the approximation should be good. In fact, using Mathematica at its default precision, numerical evaluation of ${\int }_{\lambda mn}^{\lambda mx}p\left(\lambda \right)p\left(\widehat{\lambda }|\lambda \right)d\lambda$ indicates zero difference between this integral and ${\left(\widehat{\lambda }\ln \left(\frac{{\lambda }_{mx}}{{\lambda }_{mn}}\right)\right)}^{-1}$.

The information rate per first IPI can now be evaluated.

$\mathit{\text{Corollary 2}}$. $E_{T,\mathrm{\Lambda }}\left[{\log }_2\frac{p\left(T|\mathrm{\Lambda }\right)}{p\left(T\right)}\right]=E_{\widehat{\mathrm{\Lambda }},\mathrm{\Lambda }}\left[{\log }_2\frac{p\left(\widehat{\mathrm{\Lambda }}|\mathrm{\Lambda }\right)}{p\left(\widehat{\mathrm{\Lambda }}\right)}\right]={\log }_2\left(\ln \left(\frac{{\widehat{\lambda }}_{mx}}{{\widehat{\lambda }}_{mn}}\right)\right)+\frac{1}{2}{\log }_2\left(\frac{{\left(N+1\right)}^2}{2\pi eN}\right)+\frac{1}{2}{E}_{\widehat{\mathrm{\Lambda }},\mathrm{\Lambda }}\left[{\log }_2\left(\frac{\widehat{\mathrm{\Lambda }}}{\mathrm{\Lambda }}\right)\right]\approx {\log }_2\left(\ln \left(\frac{{\lambda }_{mx}}{{\lambda }_{mn}}\right)\right)+\frac{1}{2}{\log }_2\left(\frac{{\left(N+1\right)}^2}{2\pi eN}\right)$.

$\mathit{\text{Proof}}$:

$E_{\widehat{\mathrm{\Lambda }},\mathrm{\Lambda }}\left[{\log }_2\frac{p\left(\widehat{\mathrm{\Lambda }}|\mathrm{\Lambda }\right)}{p\left(\widehat{\mathrm{\Lambda }}\right)}\right]=h\left(\widehat{\mathrm{\Lambda }}\right)-h\left(\widehat{\mathrm{\Lambda }}|\mathrm{\Lambda }\right)\approx h\left(\mathrm{\Lambda }\right)-h\left(\widehat{\mathrm{\Lambda }}|\mathrm{\Lambda }\right)$.

Limitations on the information rate.

The bit/rate calculated above is arguably naive, even beyond the fact that we are assuming there is such a thing as an average neuron. First, under physiological conditions, humans are constantly making decisions, including novel sensory acquisitions (e.g., a saccade and new fixation). Suppose that such a decision-making interval and sensory reacquisition occur every second. Then, many neurons do not complete even their first IPI. Such neurons make a much smaller information contribution, although still positive. To maintain average firing rate, suppose half the time a neuron completes one IPI, one-quarter of the time two IPIs, one-eighth of the time three IPIs, etc., per decision-making interval. Thus, half the time a neuron does not complete a first IPI, one-quarter of the time a neuron completes a first IPI but not a second one, etc. Each noncompleted IPI has a bit value. Combining the contributions for complete and incomplete IPIs produces a bit value of 5.1 bits per second for a 1-Hz neuron. See Materials and Methods for details.

Shot noise is potentially deleterious to bit rate as well. As a crude approximation of shot noise affecting the signal, suppose Shannon’s independent additive Gaussian channel, i.e., the mutual information, is $\frac{1}{2}{\log }_2\frac{{\sigma }_{signal}^2+{\sigma }_{noise}^2}{{\sigma }_{noise}^2}$. In biophysical simulations, depending on synaptic input intensity, it takes 50 to 250 NaV 1.6 activations to initiate an AP (42). Using this range as a Poisson noise and 2,500 as the Poisson signal, the capacity is much smaller than the rate of information gain, 2.8 to 1.7 bits per second. In fact, simulations with this biophysical model produce 3 bits per IPI (42). This value is probably an underestimate by about one bit because the model did not contain inhibition; without inhibition, synaptic excitation rates are limited to less than 750 events to reach threshold vs. the 2,500 here allowed by inhibition and dendrosomatic surface area.

Discussion

Results contribute to our understanding of computation in the brain from the perspective of Nature. Essentially, Results analyze a defined form of neural computation that is 1) based on postsynaptic activation and that is 2) a probabilistic inference (8). From this defined perspective, the corresponding bits per joule are maximized as a function of $N$. This value of $N$ is 2,000, close enough to 2,500 to substantiate the latter’s use in the audit. Likewise, it only changes the estimated synapses per neuron from 10,000 to 8,000 given a 75% failure rate.

As first introduced into neuroscience in ref. 1 and later emphasized by ref. 6, a certain class of bits per joule optimizations can proceed if the denominator joule term consists of two parts: a constant joule-consumption term added to a term in which the joule consumption depends on the variable being optimized. Typically, this denominator consists of 1) a constant energy-consumption term that is independent of firing-rate, such as resting potential, and 2) a firing-rate dependent term. However, here resting potential is charged to the decision-making process and does not appear in the equation while both denominator terms are dependent on the mean firing rate. Importantly, only the second $B$ multiplied term of the denominator varies with $N$. This particular denominator allows the $N$-based optimization of Fig. 4A. By way of contrast and to relate to the demon’s optimization, Fig. 4B calculates the computational bits/computational joules, using the single-denominator term of computational cost. As a result of this simplistic viewpoint of energetic costs, which aligns with the demon’s viewpoint, Fig. 4B visualizes how the $10^8$ discrepancy arises as the value of $N$ moves away from the optimized $N$ value toward zero synapses and zero computational energy consumption.

From Fig. 4B and its bits per joule formulation, we see that if Nature selects for smaller $N$, this form of computational efficiency increases exponentially. Indeed, a two-synapse neuron with 10,000-fold less surface area and a 1,000-fold decrease in the voltage between reset and threshold misses the demon’s value only by 10-fold. However, using such neurons leads to other larger cost increases if communication time is to remain constant. For a particular semiquantitative analysis establishing this point, see SI Appendix.

One reason why the bits per joule per spike of Eq. [1] (Fig. 4A) increase so slowly as $N$ increases is that the synaptic inputs are assumed to be unclocked, asynchronous, and therefore approximately Poissonian (11). Unlike energy costs that grow in proportion to $N$, the slow information growth at the rate $2^{-1}\ln \left(N\right)$ seems unavoidable (3). Indeed, for visual sensing, ref. 32 notes a similar difference in growth rates.

Although the basis of our theory is IPI coding, this hypothesis has some relevance to optimization theories based on rate coding (3, 6). Specifically, each input to a neuron is a non-Poisson point process with an implicit rate. However, the union of these inputs is, to a good approximation, Poisson (11). This union of input lines creates the neuron’s latent RV $\mathrm{\Lambda }$. Thus, each neuron is estimating the intensity of a local-population rate code over the time of each of its IPIs. This may explain the similarity of bit-rate estimates between models since, as calculated in Results and Materials and Methods, the randomness underlying this approximately Poisson signal is itself the largest source of uncertainty (i.e., entropy). Finally, the rate-code approach (3, 6) might claim a greater generality as it applies to many pulses whereas the current IPI theory applies with exactitude only to the first IPI. The theory requires extensive work for application to later IPIs in cortex where neurons are receiving feedback during the generation of later IPIs, which feedback can change the value of the neuron’s initial input.

Human and Rodent Energy Audits.

The per-neuron values here are relatively close to those obtained by Herculano-Houzel (26). Her value for the gray matter energy use of human cortex is $1.32\cdot 10^{-8}\hspace{0.17em}\mathrm{\mu }$mol of glucose per neuron per minute, which converts to $2.26\cdot 10^{-10}$ W per neuron in terms of ATP. Our value is 1.94 $\cdot 10^{-10}$ W per neuron (SI Appendix, Table S3). This small, 16% difference is not surprising since she uses the older glucose values of slightly more than 20 W per brain, and we use her regional brain weight values and cell counts.

The top–down part of the audit can do no more than limit the total ATP available among the defined uses of ATP. This value is then subject to partitioning across specific, functional consumers.

Staying as close to ref. 9 as sensible, newer values are used [e.g., for conversion of glucose to ATP (13) and for the overlapping Na-K conductances of the AP (21)]. Species differences also create unavoidable discrepancies, including average firing rate; the fraction of the time that the glutamate-primed NMDARs are voltage activated; and, more importantly, the surface area of rodent axons vs. human axons. Other discrepancies arise from differences in the partitioning of energy consumers. After removing WM costs, our partitioning of GM creates three subdivisions: computation, communication, and $SynMo{d}^{+}$. Although the partitioning of energy consumption is at variance with refs. 1 and 9, this is not a problem because partitioning is allowed to suit the question. On the other hand, estimating the cost of $SynMo{d}^{+}$ is problematic (see ouabain comments below). Moreover, the optimization here requires a subpartitioning of $SynMo{d}^{+}$. This subpartitioning is 1) costs based on mean firing rate exclusive of $N$ dependence, 2) costs based on mean firing rate multiplied by $N$, and 3) purely time-dependent costs. Here the costs of synaptic modification, including metabotropic receptor activation and postsynaptically activated kinases, do not fall within the present definition of computation but are activity-dependent $SynMo{d}^{+}$ costs.

An earlier human GM energy audit (22) comes to a different conclusion than the one found here. Although our more contemporary empirical values and more detailed analysis point to many initial disagreements with this study, these initial disagreements offset each other; thus, ref. 22 concludes that the GM has 3.36 ATP-W available, within 10% of our 3.09. On the other hand, there are two rather important disagreements: 1) the postsynaptic current associated with the average presynaptic spike arrival and 2) the total noncomputational and noncommunication energy expenditures. Regarding disagreement 1, the relative postsynaptic currents per spike differ by nearly 14-fold, and this difference arises from three sources. First, in ref. 22 synaptic success rates are 2-fold greater than the rate used in ref. 9 and here. Second, the number of synapses is 2.2-fold greater (we use newer values from normal tissue). Third, average synaptic conductance per presynaptic release is 3-fold greater than the values here (again we use newer values) (52). See Materials and Methods and SI Appendix for details underlying all of our numbers.

Disagreement 2 arises because ref. 22 concludes that 50% of ATP goes to processes independent of electrical potentials (i.e., independent of computation plus communication). The earlier work bases its values on ouabain studies. While there is no argument that ouabain poisons the Na-K ATPase pump preventing it from metabolizing ATP, there is clear evidence that ouabain activates other functions known to increase ATP consumption. Ouabain increases spontaneous transmitter release (53) and depolarizes neurons. One must assume until shown otherwise that these two effects stimulate many ATPases and ATP-consuming processes that would not normally occur at rest. These include internal CaATPases to handle Ca${}^{+}2$ influx (54); vesicle recycling and transmitter packaging; metabotropic receptor activation; and possibly even synaptic modification that demands actin polymerization, membrane construction, protein insertion, and transport of the synthesized membrane to the ends of dendrites and axons. In sum, any increases of ATP consumption will lead to underestimates of ATP used for the electrical potential and an overestimate of the ATP devoted to what we call $SynMo{d}^{+}$.

Our ultimate problem with ref. 22 is the two calculations of $N$ that it implies. Taking ref. 22’s values of failure rate and synapse number implies that $N=\mathrm{8,750}$ while applying ref. 22’s costs to the optimization of Eq. [1] produces $N\approx 300$. In contrast, our two values are closer to agreeing, 2,500 vs. 2,000.

General Relevance of Results.

Outside of neuroscience.

Because there is some interest (55, 56) outside of neuroscience to reproduce neurally mediated cognition on a limited energy budget, the energy audit here brings increased specificity to a comparison between the evolved biological and the human engineered perspective. In particular, engineers often tout brain function as consuming energy at what they consider a modest 20 W given the difficulty they have in reproducing human cognition. Here we provide a more precise set of comparisons. Our computation can be compared to the job performed by the central processing unit. Communication has its two major forms defined here, axonal costs and presynaptic functions, which must be compared to communication into and out of memories plus the communication of clock pulses. Perhaps maintenance can be compared to memory refresh costs. However, comparing power conversion loss by a computer to the heat generation of intermediary metabolism is challengeable since heating is fundamental to mammalian performance. A better comparison might be between the cost of cooling a computer and the biological heating cost.

Inside neuroscience.

Although the primary goal of the energy audit is an estimate of the cost of computation per se, the audit also illuminates the relative energetic costs of various neural functions. Notably for humans, the audit reveals that axonal resting potential costs are greater than the firing-rate costs. This axonal rest expense is directly proportional to the leak conductance and axonal surface area. Thus, of all of the parameters, these two might benefit the most from better empirical data. Regarding these large, leak-associated costs, two additional points seem relevant. First, regarding functional MRI studies that measure regional brain metabolism, the small increases of oxygen consumption over baseline consumption (57) are consistent with the high, continuous cost of axonal leak.

Second, arguing from her data and data of other studies (26), Herculano-Houzel presents the intriguing hypothesis that average glucose consumption per cortical neuron per minute is constant across mammalian species. Qualitatively, this idea is consistent with the increase in neuron numbers along with the decrease of firing rates found in humans vs. rats. However, it seems that the hypothesis can be quantitatively correct only if axonal leak conductance in humans is much lower than in animals with smaller brains and presumably shorter axons of smaller diameters. This topic deserves more detailed exploration.

Hopefully the work here motivates further empirical work, especially using primates, to improve the energy audit and the calculations that ensue. Such empirical work includes better surface area measurements and a better idea about the NMDAR off-rate time constant. Finally, going beyond the average neuron, perhaps someday there will be energy audits for the different cell types of cortex.

Materials and Methods

Partitioning Glucose by Region and by Metabolic Fate.

This section explains the top–down calculations of Table 1. The glucose-uptake values combine the regional uptakes, reported in terms of per 100 g of tissue from Graham et al. (25) as copied into our SI Appendix, Table S1 along with the reported regional masses from Azevedo et al. (58). We choose this uptake study because of its use of the [${}^{11}$C]glucose tracer and its straightforward application to obtain regional net glucose uptakes. Multiplying regional masses by uptake values, and converting to appropriate units as in SI Appendix, Table S1, yields the first “Watts” column of Table 1. These glucose watts are calculated using 2.8 MJ/mol (59). The regional uptakes are combined to produce the brain total as illustrated in SI Appendix, Fig. S1.

Following the flow diagram of SI Appendix, Fig. S1, next we remove the nonoxidized glucose from regional and total uptakes. We use an oxygen–glucose index (OGI) value of 5.3 (out of 6 possible oxygen molecules per one glucose molecule). We assume the OGI is constant across regions and that we can ignore other, non-${\mathrm{C}\mathrm{O}}_2$ carbons that enter and leave the brain. Thus, these simple glucose watts are split into oxidized and nonoxidized as produced in Table 1 and illustrated in SI Appendix, Fig. S1.

As the energy source, the oxidized glucose is then partitioned into two different metabolic fates: heating and ATP. Again we assume this process is constant across regions and that the brain does not differ too much from other regions which have been studied in greater depth. The biological conversion is calculated using Nath’s torsional mechanism, which yields 37 ATP molecules per molecule of glucose and 36,000 J/mol of ATP at $\mathrm{37}\hspace{0.17em}°$C.

Computation Costs.

Our “on average” neuron begins at its reset voltage and then is driven to a threshold of −50 mV and then once again resets to its nominal resting potential of −66 mV. Between reset and threshold, the neuron is presumed to be under constant synaptic bombardment with its membrane potential, $V_m$, constantly changing. To simplify calculations, we work with an approximated average $V_m,\hspace{0.17em}{V}_{ave}$ of −55 mV; this approximation assumes $V_m$ spends more time near threshold than reset. (Arguably the membrane potential near a synapse which is distant from the soma is a couple of millivolts more depolarized than the somatic membrane voltage, but this is ignored.) To determine the cost of AMPAR computation, we use the ion preference ratios calculated from the reversal potential and use the total conductance to obtain a Na${}^{+}$ conductance of 114.5 pS per 200 pS AMPAR synapse as seen in SI Appendix, Table S4. [The ion-preference ratios used for the calculations in SI Appendix, Table S4 are calculated from the reported reversal potential value of −7 mV (60) and the individual driving forces at this potential, -90-(-7)=-83 mV for ${\mathrm{K}}^{+}$ and 55-(-7)=62 mV for Na${}^{+}$.] Multiplying the conductance by the difference between the Na${}^{+}$ Nernst potential and the average membrane potential ($V_{Na,Nern}-V_{ave}$) yields a current of 12.5 pA per synapse. Multiplying this current by the SA duration converts the current to coulombs per synaptic activation, and dividing this by Faraday’s constant gives us the moles of Na${}^{+}$ that have entered per synaptic activation. Since one ATP molecule is required to pump out three Na${}^{+}$ molecules, dividing by 3 and multiplying by the average neuron firing rate and success rate yield $1.29\cdot 10^{-20}$ mol-ATP per synapse per second. Multiplying by the total number of synapses ($1.5\cdot 10^{14}$) implies the rate of energy consumption is 0.069 W for AMPAR computation. When NMDARs are taken into account, the total computational cost is 0.10 W (assuming that NMDAR’s average conductance is half as much as AMPAR’s).

SI Appendix, Table S4 lists the excitatory ion fluxes mediated by AMPARs and NMDARs. The cost of the AMPAR ion fluxes is straightforward. The cost of the NMDAR ion fluxes depends on the off-rate time constant as well as the average firing rate. That is, if this off-rate time constant is as slow as 200 ms and the IPI between firings of the postsynaptic neuron is 500 ms or more (such as the 1-s interval that comes from the 1.0-Hz frequency used in the following calculations), then most glutamate-primed NMDARs will not be voltage activated. Thus, in contrast to the rat where the AMPAR and NMDAR fluxes are assumed to be equal, here we assume the ion fluxes mediated by NMDARs are half those of the AMPARs and multiply the AMPAR cost by 1.5 to obtain the final values in SI Appendix, Table S4.

The spike generator contributes both to computation and to communication; fortunately, its energetic cost is so small that it can be ignored.

Communication Costs.

SI Appendix, Table S5 provides an overview of the communication calculations, which are broken down into resting potential costs, action potential costs, and presynaptic costs. The following sections explain these calculations, working toward greater and greater detail.

In general, the results for communication costs are built on less-than-ideal measurements requiring large extrapolations. For example, there do not seem to be any useable primate data. The proper way to determine surface area is with line-intersection counts, not point counts, and such counts require identification of almost all structures. As the reader will note in SI Appendix, use of mouse axon diameters produces much larger surface areas assuming fixed volume fractions, thus raising communication costs and decreasing the energy available for computation and $SynMo{d}^{+}$.

Resting potential costs.

The cost of the resting potential itself is simply viewed as the result of unequal but opposing Na${}^{+}$ and ${\mathrm{K}}^{+}$ conductances. If other ions contribute, we just assume that their energetic costs eventually translate into Na${}^{+}$ and ${\mathrm{K}}^{+}$ gradients. The axonal resting conductance uses the recent result of 50 k$\omega \hspace{0.17em}{\mathrm{c}\mathrm{m}}^2$ (23). With our surface area of $21.8\cdot 10^6\hspace{0.17em}{\mathrm{c}\mathrm{m}}^2$ (includes axonal boutons; SI Appendix, Table S6), this produces a total conductance of 436 S. The driving voltage for each ion is determined by subtracting the appropriate Nernst potential from the assumed resting membrane potential of −66 mV. Using Nernst potentials of +55 mV and −90 mV for Na${}^{+}$ and ${\mathrm{K}}^{+}$, respectively, just assume currents are equal and opposite at equilibrium. Thus, conductance ratios derive from the equilibrium: $-24$ mV $\cdot g_K=-121$ mV $\cdot g_{Na}$, implying $g_K=5.04\hspace{0.17em}{g}_{Na}$, and further implying $\frac{g_{Na}}{g_{Na}+g_K}=\frac{1}{6.04}$. The Na${}^{+}$ conductance times the driving voltage yields the Na${}^{+}$ current, 0.121 V $\cdot \frac{1}{6.04}\cdot 436$ S = 8.73 A. Scaling by Faraday’s constant implies the total Na⁺ influx; then divide by 3 to obtain moles of ATP required to pump out this influx, 3.02 $\cdot 10^{-5}$ mol ATP per second. Multiplying by 36,000 J/mol ATP yields 1.09 W, the resting potential cost.

Plasma membrane leak is a major energy expenditure, 22% of ATP-W here compared to 13% in ref. 9. Here, however, we emphasize that this cost is 66% of gray matter communication costs. The differences in percentages arise from different interpretations of a functioning neuron and of the meaning of certain measurements. Our distinction between the costs of reset differs from their cost of resting potentials: Here resting cost is entirely axonal and essentially continuous across time. Their resting cost is dendrosomatically based and deviates from our assumption that a neuron is under constant synaptic bombardment.

Action potential costs.

Action potential costs are calculated from Na${}^{+}$ pumping costs (SI Appendix, Table S5). The coulombs to charge a 110-mV action potential for the nonbouton axon start with the product of the total GM axonal capacitance, 14.6 F; the peak voltage; and the firing rate, 1 Hz; i.e., $14.6\cdot 0.11\cdot 1.0=1.61$ A. To account for the neutralized currents observed by Hallerman et al. (21), multiply this by 2.28, yielding 3.66 A.

Bouton costs, although clearly part of an axon, are calculated separately from the axon. As will be detailed later, our approximation of surface areas treats all presynaptic structures as bouton terminaux, and rather than assume tapering for impedance matching purposes, presume an abrupt transition of diameters. Importantly, we assume that a bouton mediates a calcium spike and that this spike requires only a 0.02-V depolarization to be activated. Altogether, the rate of Na⁺ coulomb charging for boutons is $6.34$ F $\cdot 0.02$ V $\cdot 1$ Hz = 0.13 A.

The sum of axonal spike Na${}^{+}$ and bouton charging determines the Na${}^{+}$ to be pumped. Faraday’s constant converts coulombs per second to moles of charge per second, yielding a Na${}^{+}$ flux of $3.9\cdot 10^{-5}$ mol/s. Dividing by 3 converts to ATP moles per second; multiplying this value by Nath’s 36,000 J/mol ATP yields the total action potential cost of 0.47 W.

To calculate bits per joule requires WMAP costs. Assume that the oligodendrocytes (especially myelogenesis) are using energy solely to support the AP. Then we approximate that two-thirds of the 1.85-W energy goes to WMAP, 1.23 W.

The action potential values here largely agree with ref. 18, but there are a number of important differences. They use an old, nonmammalian value for overlap. The neutralized current flux of the AP in mammals is 2.28 (21) at the initial segment, far from the multiplier of 4 they use. Furthermore, the plotted values in ref. 18, figure 7A are not adjusted for overlap. Ref. 18, figure 7A uses an axonal length of 1 $\mathrm{\mu }$m; therefore, for the axonal diameter plot point of 0.5$\mathrm{\mu }$m, the surface area is $\pi /2\cdot 10^{-12}$ m${}^2=1.57\cdot 10^{-8}\hspace{0.17em}{\mathrm{c}\mathrm{m}}^2$. This implies a capacitance of $1.57\cdot 10^{-14}$ F. Then the total charge needed for 0.1-V polarization is $1.57\cdot 10^{-15}$ C. Multiplying by the number of charges per coulomb yields $1.57\cdot 10^{-15}\cdot 6.24\cdot 10^{18}=9.8\cdot 10^3\approx 10^4$ Na${}^{+}$, the plotted value of figure 7A in ref. 18. Thus, the neutralized Na${}^{+}$ flux was somehow lost when the y axis was labeled. With this understanding, our values differ from ref. 18 only because the calculations here use the mammalian measured overlap of 2.28.

Presynaptic AP costs.

The presynaptic transmitter-associated costs are mostly based on the values of Attwell and Laughlin (9) and of Howarth et al. (14). The assumptions include an assumed 25% success rate of vesicular release for each cortical spike ($1.5\cdot 10^{14}$ spikes per second under the 1-Hz and $1.5\cdot 10^{14}$ synapses assumptions). However, in contrast to Howarth et al. (14), which uses a number supported by observations in calyx of Held (61) and in cell cultures (62), the observations of Stevens and Wang (20) in CA1 hippocampal pyramidal neurons indicate that the same calcium influx occurs for both synaptic successes and failures. Because adult hippocampal synapses seem a better model of cerebral cortical synapses than calyx or tissue culture synapses, we use the hippocampal observations. Therefore, the 1-Hz firing rate produces a ${\mathrm{C}\mathrm{a}}^{2+}$ cost that is more than eightfold greater than the cost of vesicle release (VR) events (SI Appendix, Table S5). The ${\mathrm{C}\mathrm{a}}^{2+}$ influx per action potential is $1.2\cdot 10^4\hspace{0.17em}{\mathrm{C}\mathrm{a}}^{2+}$ per vesicle, and assuming 1 ATP is required to pump out each ${\mathrm{C}\mathrm{a}}^{2+}$, the ${\mathrm{C}\mathrm{a}}^{2+}$ cost is $1.2\cdot 10^4$ ATPs per vesicle. Multiplying this by $1.5\cdot 10^{14}$ APs per second for the gray matter, dividing by Avogadro’s number, and finally multiplying by 36 kJ/mol ATP yields a total presynaptic ${\mathrm{C}\mathrm{a}}^{2+}$ cost of 0.11 W.

The cost per vesicle release is determined by adding the packaging and processing costs and then multiplying by the number of glutamate molecules per vesicle as in refs. 9 and 14. Adding the cost of membrane fusion and endocytosis yields a total of 5,740 ATPs per vesicle (14). This value is multiplied by the VR events per second and divided by Avogadro’s number to obtain $3.57\cdot 10^{-7}$ ATP mol/s. Converting to watts yields a presynaptic transmitter release cost of 0.01 W and a total presynaptic cost of 0.12 W for the GM.

Synapse counts.

Both computation and communication costs depend on the number of cortical synapses. For the approach taken here, computational costs scale in a one-to-one ratio to synaptic counts while communication costs scale proportionally, but with a smaller proportionality constant.

The calculations use the Danish group’s synapse counts of $1.5\cdot 10^{14}$ (63). The alternative to the numbers used here reports an 80% larger value (64); however, their human tissue comes from nominally nonepileptic tissue from severely epileptic patients. Since the incredibly epileptic tissue is likely to stimulate the nearby nonepileptic tissue at abnormally high firing rates, we find the data’s import questionable.

Estimation of surface areas from mouse and rabbit data.

Here volume-fraction data are used to estimate axon and presynaptic surface areas. As far as we know, there are two journal-published, quantitative electron microscopic studies of cerebral cortex that are suitable for our purposes: one in rabbit (65) and one in mouse (66). (Although structural identifications do not neatly conform to our simplifying cylindrical assumptions, we can still use their data to direct and to check our estimates.)

Chklovskii et al. (66) report a 36% volume fraction for small axons, 15% for boutons, 11% for glia, 12% for other, and 27% for dendrites and spines as read from their graph in their figure 3. They purposefully conducted their evaluations in tissue that lacked cell bodies and capillaries. Because cortical tissue does contain cell bodies and capillaries, this will produce a small error for the average cortical tissue. More worrisome is the size of “other,” half of which could be very small axons.

The quantification by Schmolke and Schleicher (65) examines the rabbit visual cortex. Their evaluation partitions cortex into two types of tissue: that with vertical dendritic bundling and that which lacks dendritic bundling (they do not seem to report the relative fraction of the two types of cortex, but we assume the tissue without bundling dominates over most of cortex). For boutons and axons, respectively, they report volume fraction values within bundles of 17 and 20% and values between bundles of 26 and 29%.

The 30% axonal volume fraction used in SI Appendix, Table S6 is a compromise between the ref. 66 value of 36% and the two values from ref. 65. The average of the within-bundle and between-bundle volume fractions from ref. 65 is used for boutons. Specifically, the approximated human volume fractions are 1) 22% boutons; 2) 30% small axons; 3) 11% glia; 4) 5% neuronal somata; 5) 3% vasculature; and 6) 29% dendrites, spineheads, and spine-stems, totaling 100%. (It is assumed that standard fixation removes almost all of the physiological extracellular space and, naively, shrinkage/swelling has little relative effect on these values.) The calculations are essentially unaffected by the two conflicting bouton volume fractions since the difference between the two possible calculations is negligible.

SI Appendix, Table S6 lists the critical values, the intermediate values for the cylindrical model to fit the data, and finally the implications for the relevant membrane capacitance.

Cylindrical model approximations for axons and boutons.

Axons.

By making a cylindrical assumption and assuming the average small axon’s diameter is $0.50\hspace{0.17em}\mathrm{\mu }$m (radius = $0.25\cdot 10^{-4}$ cm), a small extrapolation of a cross-species result in the cerebellum (67), we can estimate the total surface area of these unmyelinated axons using the 30% volume fraction to calculate the length of an average axon, $L_{ax}$. The total volume (cm${}^3$) occupied by all such axons is $L_{ax}\cdot 1.5\cdot 10^{10}\cdot \pi {\left(0.25\cdot 10^{-4}\right)}^2$. Dividing this volume by the volume of the GM (632 ${\mathrm{c}\mathrm{m}}^3$) must equal the volume fraction, 0.3. Solving yields $L_{ax}=6.44$ cm. Then net surface area is calculated using this length and the same diameter and number of neurons, $6.44\cdot 1.5\cdot 10^{10}\cdot \pi \cdot 0.5\cdot 10^{-4}=1.52\cdot 10^7\hspace{0.17em}{\mathrm{c}\mathrm{m}}^2$. For an independent calculation of axon length based on light microscopic data, see SI Appendix.

Boutons.

The surface area estimates also treat boutons (Btn) as uniform cylinders of a different diameter. Assume that cortical presynaptic structures in humans are no bigger than in any other mammalian species. To determine bouton surface area, assume a bouton diameter ($d_{pb}$) $1.1\hspace{0.17em}\mathrm{\mu }m$ and height ($h_{pb}$) $1.0\hspace{0.17em}\mathrm{\mu }$m. Denote the total number of synapses in the gray matter as $n_{gm}$ ($1.5\cdot 10^{14}$). (Note that the cylinder area of interest has only one base.) Then, with the formulation $A_{pb}=n_{gm}\pi \left(d_{pb}{h}_{pb}+{\left(\frac{1}{2}{d}_{pb}\right)}^2\right)$, the bouton surface area works out to $A_{pb}=1.5\cdot 10^{14}\pi \left(1.1\hspace{0.17em}\mathrm{\mu }\text{m}\cdot 1.0\hspace{0.17em}\mathrm{\mu }\text{m}+{\left(0.55\hspace{0.17em}\mathrm{\mu }\text{m}\right)}^2\right)=6.61\cdot 10^6\hspace{0.17em}{\mathrm{c}\mathrm{m}}^2$ (SI Appendix, Tables S6 and S7).

We assume a bouton accounts for only one synapse. However, larger boutons can contact multiple, distinct postsynaptic neurons. Thus, the small cylinders, as individual synapses, are an attempt to approximate such presynaptic configurations. See SI Appendix, Table S8 for more details and for the effect of overestimating areas.

Oxidized vs. Nonoxidized Glucose.

Arteriovenous blood differences indicate that insufficient oxygen is consumed to oxidize all of the glucose that is taken up by the brain. Supposing glucose is the only energy source, it takes six ${\mathrm{O}}_2$s for complete oxidation. The calculations use an OGI value of 5.3 (68). Other values from arteriovenous differences are found in the literature (69–71). Even before these blood differences were observed, Raichle’s laboratory proposed as much as $20\%$ of the glucose is not oxidized (27).

Glucose to ATP Based on Nath’s Theory.

SI Appendix, Table S2 offers the reader a choice between Nath’s torsional conversion mechanism of glucose to ATP (13, 72, 73) and the conventional conversion to ATP based on Mitchell’s chemiosmotic theory (74). According to Nath, the minimum number of ATP molecules produced per molecule of glucose oxidized is 32, and this includes mitochondrial leak and slip (13). Nath’s calculations are based on free-energy values under physiological conditions. However, his calculations are recent while the standard model has been taught for decades, although not without controversy (75). The standard textbook number for this conversion is 33 ATPs per molecule of glucose before accounting for mitochondrial proton leak and slip. Since leak is often assumed to consume 20% of the energy that might have gone to ATP production in oxidative phosphorylation (9, 76), the Mitchell conversion number is reduced from 33 to 27 molecules of ATP (2 ATPs are produced by glycolysis and 2 by the Krebs cycle, so this 20% reduction applies only to the ATP produced in the electron transport chain).

$SynMo{d}^{+}$.

Here $SynMo{d}^{+}$ is not directly calculated. Rather it is the residual of the energy available after removing the above uses. The assumed subpartitioning occurs as follows. Assume 10% of this goes to time proportional costs; assume the postsynaptic fraction, accounting for metabotropic activations, receptor modification, and actin polymerization–depolymerization cycles, equals 0.134 W, which is activity and synapse number dependent. The remainder, devoted to synaptogenesis and firing-rate dependent axonal and dendritic growth (e.g., membrane construction, protein insertion, and axo- and dendro-plasmic transport) is just activity dependent.

Proofs.

The proof of Lemma 2a is just a textbook change of variable from one density to another (77), where $dt=\frac{N^2}{\left(N+1\right){\widehat{\lambda }}^2}d\widehat{\lambda }$; to prove Corollary 1 and the first equality of Lemma 2b, use Lemma 2a to calculate the appropriate conditional moments, which Mathematica obliges; to prove the second equality of Lemma 2b, use Lemma 1 to calculate the indicated conditional moment.

Parameterizing the marginal prior $p\left(\lambda \right)$.

As derived from first principles (8), the only known, consistent marginal prior of the latent RV is $p\left(\lambda \right)={\left(\lambda \ln \left(\frac{{\lambda }_{mx}}{{\lambda }_{mn}}\right)\right)}^{-1}$ where the bounds of the range of this RV, and thus its normalizing constant, are the subject of empirical observations and the required definition $\lambda \in \left(0<{\lambda }_{mn}<{\lambda }_{mx}<\infty \right)$.

From the energy audit, use the 1-Hz average firing rate. Then $E\left[\mathrm{\Lambda }\right]$, the mean marginal total input firing rate, is $10^4$/s. Now suppose that the rate of spontaneous release is 1 Hz over these $10^4$ synapses, giving us ${\lambda }_{mn}=1$. With one unknown in one equation, $E\left[\mathrm{\Lambda }\right]=\frac{{\lambda }_{mx}-{\lambda }_{mn}}{\ln \left(\frac{{\lambda }_{mx}}{1}\right)}=\mathrm{10,000}$, Mathematica produces ${\lambda }_{mx}\approx \mathrm{116,672}$, and the prior is fully parameterized.

Adjusting the bit-rate calculation for multiple IPIs per DMI.

The 7.48 bits per IPI apply only to a neuron’s first IPI. Later spikes are worth considerably less using the current simplistic model of a fixed threshold and no feedback. Moreover, while maintaining the average firing rate, we might suppose that only half the time a neuron completes a first IPI, half of these complete a second IPI, and so on. Thus, the average number of spikes per DMI remains nearly one. With a fixed threshold, the bit values of the later spikes are quite small. The values of the second through fourth spikes are $\left\{\frac{1}{2}{\log }_2\left(\frac{2N}{N}\right),\hspace{0.17em}\frac{1}{2}{\log }_2\left(\frac{3N}{2N}\right),\hspace{0.17em}\frac{1}{2}{\log }_2\left(\frac{4N}{3N}\right)\right\}$, which gives ca. 0.35 bits. However, complementing the completion of the first IPI is, half the time, the bit contribution of an uncompleted IPI, $0.5\cdot 1$ and for the one-quarter of the time a neuron produces a first IPI but not a second one, and so on for later IPIs. The summed value of these nonfirings approaches 1 bit. Then, $7.48/2+0.35+1\approx 5.1$ bits.

Shot noise can affect bit rate but not as much as the signal.

As measured in the biophysical simulations (42), the most deleterious degradation of a neuron’s computation arises not from thermal noise or shot noise (43), but from the neuron’s input signal itself. Here is a calculation consistent with this biophysical observation.

Using stochastic NaV 1.2 and NaV 1.6 channels in a biophysical model of a rat pyramidal neuron, it is possible to observe shot noise and to estimate the number of such channels that are activated at threshold. With relatively slow depolarization, there are fewer than 250 channels on when threshold is reached, and this number of channels seems to contribute less than 1.6 mV (figure 5 in ref. 42). Thus modeling channel activation as a Poisson process with rate 250 and individual amplitudes of 6.4 $\mathrm{\mu }$V, Campbell’s theorem (78) produces the variance; this variance is less than $250\cdot {\left(6.4\cdot 10^{-6}\right)}^2=1.02\cdot 10^{-8}$. The same calculation for the input excitation yields a variance of $\mathrm{2,500}\cdot {\left(6.4\cdot 10^{-6}\right)}^2=1.02\cdot 10^{-7}$, a $10:1$ ratio.

Numerically based optimization calculations.

Optimizing the bits per joule equation uses Mathematica. Treat $N$, the average number of events per IPI, as a continuous variable. Then to optimize, take the derivative, $dN$, of the single-neuron, single-IPI bit per joule formulation. Set the numerator of this derivative equal to zero and solve for $N$ using Mathematica’s NSolve.

Data Availability

All study data are included in this article and/or SI Appendix.