Parameterizing neural power spectra into periodic and aperiodic components

Abstract

Electrophysiological signals exhibit both periodic and aperiodic properties. Periodic oscillations have been linked to numerous physiological, cognitive, behavioral, and disease states. Emerging evidence demonstrates the aperiodic component has putative physiological interpretations, and dynamically changes with age, task demands, and cognitive states. Electrophysiological neural activity is typically analyzed using canonically-defined frequency bands, without consideration of the aperiodic (1/f-like) component. We show that standard analytic approaches can conflate periodic parameters (center frequency, power, bandwidth) with aperiodic ones (offset, exponent), compromising physiological interpretations. To overcome these limitations, we introduce a novel algorithm to parameterize neural power spectra as a combination of an aperiodic component and putative periodic oscillatory peaks. This algorithm requires no a priori specification of frequency bands. We validate this algorithm on simulated data, and demonstrate how it can be used in applications ranging from analyzing age-related changes in working memory to large-scale data exploration and analysis.

INTRODUCTION

Neural oscillations are widely studied, with tens-of-thousands of publications to date. Nearly a century of research has shown that oscillations reflect a variety of cognitive, perceptual, and behavioral states^1,2, with recent work showing that oscillations aid in coordinating interregional information transfer^3,4. Notably, oscillatory dysfunction has been implicated in nearly every major neurological and psychiatric disorder^5,6. Following historical traditions, the vast majority of the studies examining oscillations rely on canonical frequency bands, which are approximately defined as: infraslow (< 0.1 Hz), delta (1–4 Hz), theta (4–8 Hz), alpha (8–12 Hz), beta (12–30 Hz), low gamma (30–60 Hz), high frequency activity (60–250 Hz), and fast ripples (200–400 Hz). Although most of these bands are often described as oscillations, standard approaches fail to assess whether an oscillation—meaning rhythmic activity within a narrowband frequency range—is truly present (Fig. 1A,B).

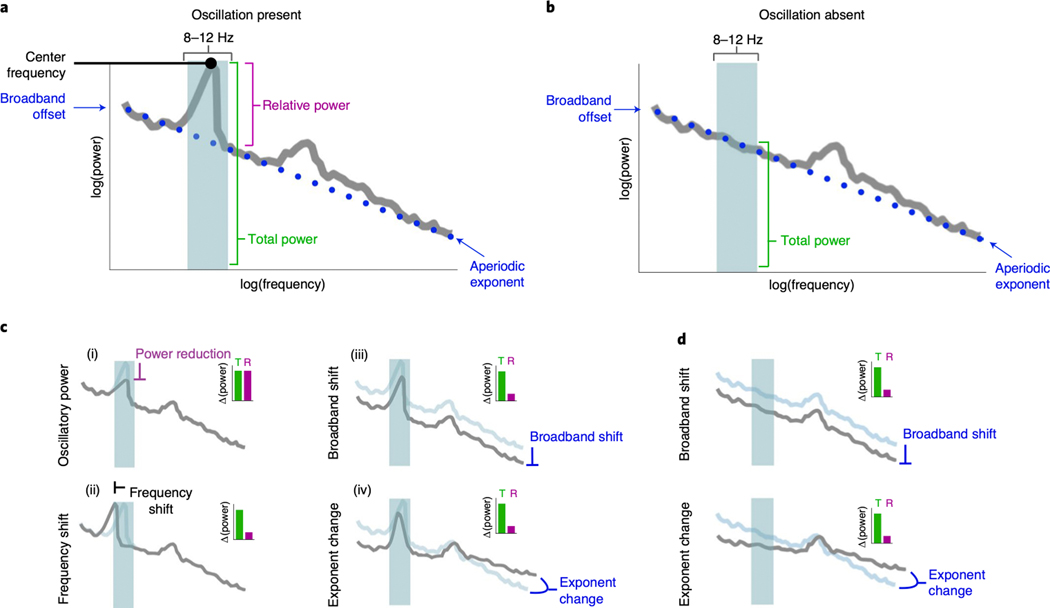
Figure 1 |. Overlapping nature of periodic and aperiodic spectral features.

(A) Example neural power spectrum with a strong alpha peak in the canonical frequency range (8–12 Hz, blue shaded region) and secondary beta peak (not marked). (B) Same as A, but with the alpha peak removed. (C-D) Apparent changes in a narrowband range (blue shaded region) can reflect several different physiological processes. Total power (green bars in the inset) reflects the total power in the range, and relative power (purple bars in the insets) reflect relative power of the peak, over and above the aperiodic component. (C) Measured changes, with a peak present, including: (i) oscillatory power reduction; (ii) oscillation center frequency shift; (iii) broadband power shift, or; (iv) aperiodic exponent change. In each simulated case, total measured narrowband power is similarly changed (inset, green bar), while only in the true power reduction case (i) has the 8–12 Hz oscillatory power relative to the aperiodic component actually changed (inset, purple bar). (D) Measured changes, with no peak present. This demonstrates how changes in the aperiodic component can be erroneously interpreted as changes in oscillation power when only focusing on a narrow band of interest.

In the frequency domain, oscillations manifest as narrowband peaks of power above the aperiodic component (Fig. 1A)^7,8. Examining predefined frequency regions in the power spectrum, or applying narrowband filtering (e.g., 8–12 Hz for the alpha band) without parameterization, can lead to a misrepresentation and misinterpretation of physiological phenomena, because apparent changes in narrowband power can reflect several different physiological processes (Fig. 1C,D). These include: (i) reductions in true oscillatory power^9,10; (ii) shifts in oscillation center frequency^11,12; (iii) reductions in broadband power^13–15, or; (iv) changes in aperiodic exponent^8,16–19. When narrowband power changes are observed, the implicit assumption is typically a frequency-specific power change (Fig. 1C.i), however, each of the alternative cases can also manifest as apparent oscillatory power changes, even when no oscillation is present (Fig. 1D). That is, changes in any of these parameters can give rise to identical changes in total narrowband power (Fig. 1C,D).

Even if an oscillation is present, careful adjudication between different oscillatory features—such as center frequency and power—is required. Variability in oscillation features is ignored by many approaches examining predefined bands and, without careful parameterization, these differences can easily be misinterpreted as narrowband power differences (Fig. 1C). For example, there is clear variability in oscillation center frequency across age²⁰, and cognitive/behavioral states^11,12. Oscillation bandwidth may also change, but this parameter is underreported in the literature. Thus, what is thought to be a difference in band-limited oscillatory power could, instead, reflect center frequency differences between groups or conditions of interest^21,22 (Fig. 1C.ii).

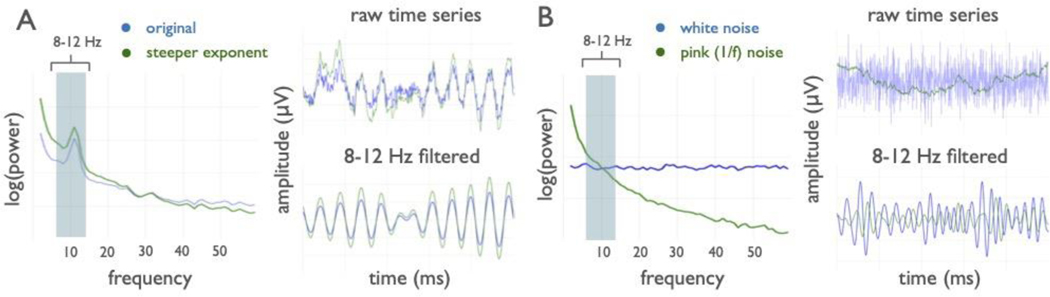
Interpreting band-limited power differences is further confounded by the fact that oscillations are embedded within aperiodic activity (represented by the dotted blue line in Fig. 1A). This component of the signal stands in contrast to oscillations in that it need not arise from any regular, rhythmic process²³. For example, signals such as white noise, or even a single impulse function, have power at all frequencies despite there being, by definition, no periodic aspect to the signal (Extended Data Fig. 1B). Due to this aperiodic activity, pre-defined frequency bands or narrowband filters will always estimate non-zero power, even when there is no detectable oscillation present (Fig. 1B, Extended Data Fig. 1).

In neural data, this aperiodic activity has a 1/f-like distribution, with exponentially decreasing power across increasing frequencies. This component can be characterized by a 1/f^χ function, whereby the χ parameter, hereafter referred to as the aperiodic exponent, reflects the pattern of aperiodic power across frequencies, and is equivalent to the negative slope of the power spectrum when measured in log-log space²⁴. The aperiodic component is additionally parameterized with an ‘offset’ parameter, which reflects the uniform shift of power across frequencies. This aperiodic component has traditionally been ignored, or is treated as either noise or as a nuisance variable to be corrected for, such as is done in spectral whitening²⁵, rather than a feature to be explicitly parameterized.

Ignoring or correcting for the aperiodic component is problematic, as this component also reflects physiological information. The aperiodic offset, for example, is correlated with both neuronal population spiking^13,14 and the fMRI BOLD signal¹⁵. The aperiodic exponent, in contrast, has been related to the integration of the underlying synaptic currents²⁶, which have a stereotyped double-exponential shape in the time-domain that naturally gives rise to the 1/f-like nature of the power spectral density (PSD)¹⁹. Currents with faster time constants, such as excitatory (E) AMPA, have relatively constant power at lower frequencies before power quickly decays whereas for inhibitory (I) GABA currents power decays more slowly as a function of frequency. This means that the exponent will be lower (flatter PSD) when E>>I, and larger when E<<I¹⁹. Thus, treating the aperiodic component as “noise” ignores its physiological correlates, which in turn relate to cognitive and perceptual^17,27 states, while trait-like differences in aperiodic activity have been shown to be potential biological markers in development²⁸ and aging¹⁸ as well as disease, such as ADHD²⁹, or schizophrenia³⁰.

To summarize, periodic parameters such as frequency^11,12, power^9,10, and potentially bandwidth, as well as the aperiodic parameters of broadband offset^13–15 and exponent^8,16–19, can and do change in behaviorally and physiologically meaningful ways, with some emerging evidence suggesting they interact with one another³¹. Reliance on a priori frequency bands for oscillatory analyses can result in the inclusion of aperiodic activity from outside the true physiological oscillatory band (Fig. 1C.ii). Failing to consider aperiodic activity confounds oscillatory measures, and masks crucial behaviorally and physiologically relevant information. Therefore, it is imperative that spectral features are carefully parametrized to minimize conflating them with one another and to avoid confusing the physiological basis of “oscillatory” activity with aperiodic activity that is, by definition, arrhythmic.

To better characterize the signals of interest, and overcome the limitations of traditional narrowband analyses, we introduce an efficient algorithm for parameterizing neural PSDs into periodic and aperiodic components. This algorithm extracts putative periodic oscillatory parameters characterized by their center frequency, power, and bandwidth; it also extracts the offset and exponent parameters of the aperiodic component (Fig. 2). Importantly, this algorithm requires no specification of narrowband oscillation frequencies; rather, it identifies oscillations based on their power above the aperiodic component.

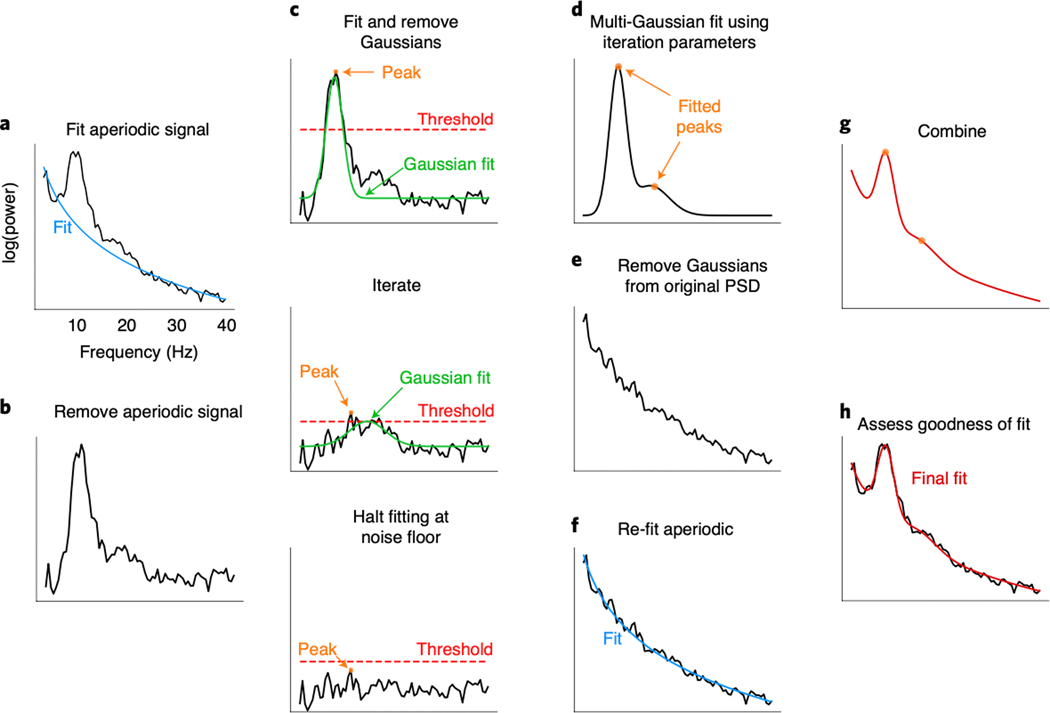
Figure 2 |. Algorithm schematic on real data.

(A) The power spectral density (PSD) is first fit with an estimated aperiodic component (blue). (B) The estimated aperiodic portion of the signal is subtracted from the raw PSD, the residuals of which are assumed to be a mix of periodic oscillatory peaks and noise. (C) The maximum (peak) of the residuals is found (orange). If this peak is above the noise threshold (dashed red line), calculated from the standard deviation of the residuals, then a Gaussian (solid green line) is fit around this peak based on the peak’s frequency, power, and estimated bandwidth (see Methods). The fitted Gaussian is then subtracted, and the process is iterated until the next identified point falls below a noise threshold or the maximum number of peaks is reached. The peak-finding at this step is only used for seeding the multi-Gaussian in D, and, as such, the output in D can be different from the peaks detected at this step. (D) Having identified the number of putative oscillations, based on the number of peaks above the noise threshold, multi-Gaussian fitting is then performed on the aperiodic-adjusted signal from B to account for the joint power contributed by all the putative oscillations, together. In this example, two Gaussians are fit with slightly shifted peaks (orange dots) from the peaks identified in C. (E) This multi-Gaussian model is then subtracted from the original PSD from A. (F) A new fit for the aperiodic component is estimated—one that is less corrupted by the large oscillations present in the original PSD (blue). (G) This re-fit aperiodic component is combined with the multi-Gaussian model to give the final fit. (H) The final fit (red)—here parameterized as an aperiodic component and two Gaussians (putative oscillations)—captures >99% of the variance of the original PSD. In this example, the extracted parameters for the aperiodic component are: broadband offset = −21.4 au; exponent = 1.12 au/Hz. Two Gaussians were found, with the parameters: (1) frequency = 10.0 Hz, power = 0.69 au, bandwidth = 3.18 Hz; (2) frequency = 16.3 Hz, power = 0.14 au, bandwidth = 7.03 Hz.

We test the accuracy of this algorithm against simulated power spectra where all the parameters of the periodic and aperiodic components are known, providing a ground truth against which to compare the algorithm’s ability to recover those parameters. The algorithm successfully captures both periodic and aperiodic parameters, even in the presence of significant simulated noise (Fig. 3). Additionally, we show that algorithm performs comparably to expert human raters who manually identified peak frequencies in both human EEG and non-human local field potential (LFP) spectra (Fig. 4). Finally, we demonstrate the utility of algorithmic parameterization in three ways. First, we replicate and extend previous results demonstrating spectral parameter differences between younger and older adults at rest (Fig. 5). Next, we find a novel link between the aperiodic component and behavioral performance in a working memory task (Fig. 6). Finally, by leveraging large-scale analysis of human magnetoencephalography (MEG) data, we map the spatial patterns of oscillations and aperiodic activity across the human neocortex, demonstrating how this method can be used at scale (Fig. 7).

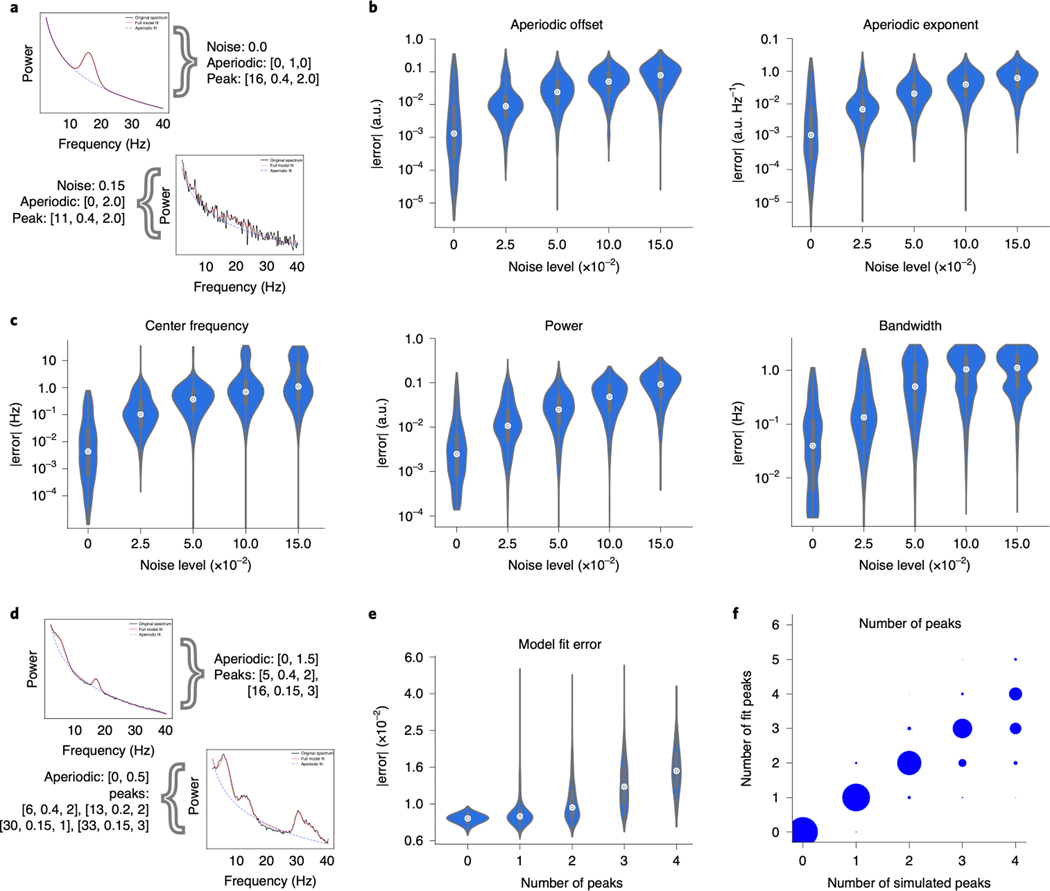
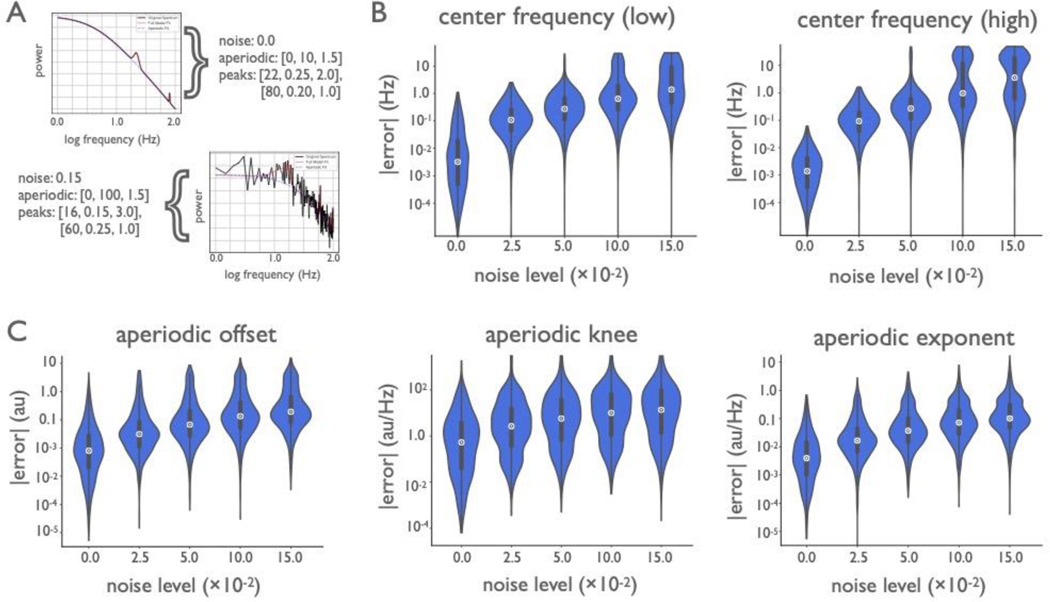
Figure 3 |. Algorithm performance on simulated data.

(A-C) Power spectra were simulated with one peak (see Methods), at five distinct noise levels (1000 spectra per noise level). (A) Example spectra with simulation parameters are shown (black), as aperiodic [offset, exponent] and periodic [center frequency, power, bandwidth]. Spectral fits (red), for the one-peak simulations in a low- and high-noise scenario. Simulation parameters for plotted example spectra are noted. (B) Median absolute error (MAE) of the algorithmically identified aperiodic offset and exponent, across noise levels, as compared to ground truth. (C) MAE of the algorithmically identified peak parameters—center frequency, power, and bandwidth—across noise levels. In all cases, MAE increases monotonically with noise, but remains low. (D-F) A distinct set of power spectra were simulated to have different numbers of peaks (0–4, 1000 spectra per number of peaks) at a fixed noise level (0.01; see Methods). (D) Example simulated spectra, with fits, for the multi-peak simulations. Conventions as in A. (E) Absolute model fit error for simulated spectra, across number of simulated peaks. (F) The number of peaks present in simulated spectra compared to the number of fitted peaks. All violin plots show full distributions, where small white dots represent median values and small box plots show median, first and third quartiles, and ranges. The algorithm imposes a 6.0 Hz maximum bandwidth limit in its fit, giving rise to the truncated errors for bandwidth in C. Note that the error axis is log-scaled in B,C,E.

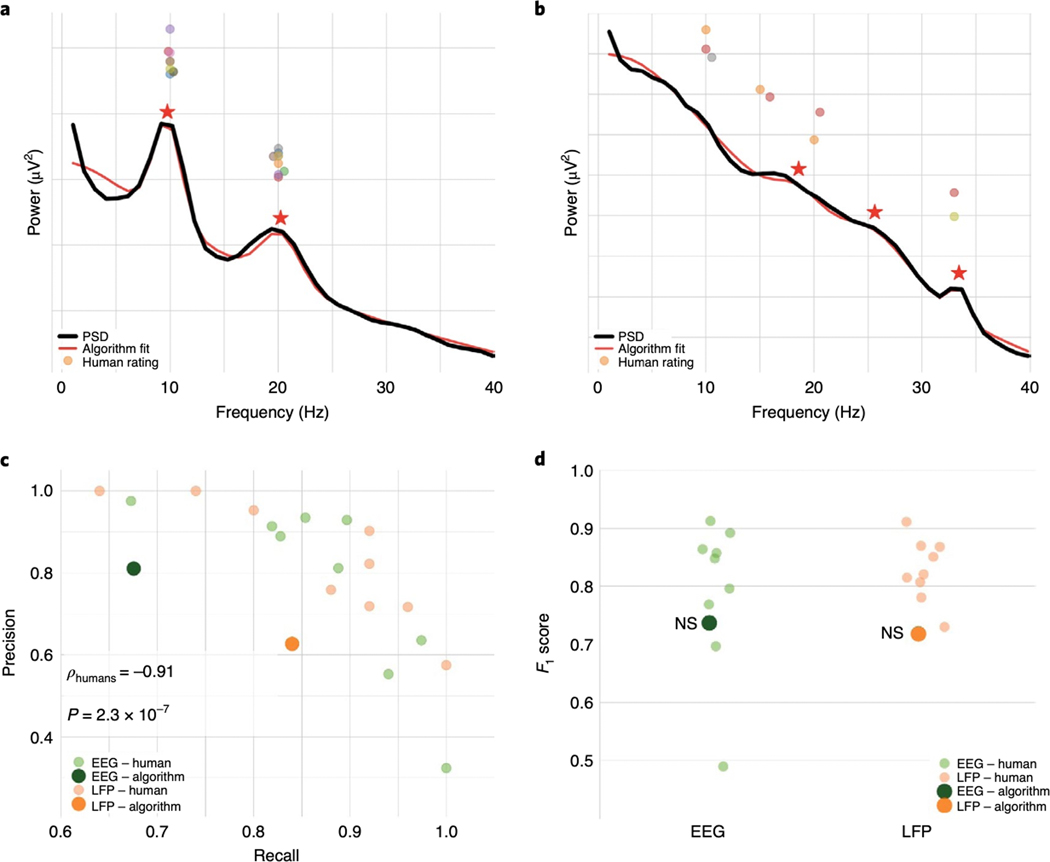
Figure 4 |. Algorithm performance compared to human raters on real EEG and LFP data.

(A,B) Examples of two different EEG spectra labeled by expert human raters, highlighting cases of strong (A) and weak (B) consensus amongst raters. The black line is the PSD of real data against which center frequency estimates were made. The red line is the algorithm fit; the red stars are the center frequencies identified by the algorithm. The dots are each individual expert’s center frequency rating(s). Note that even when human consensus was low, with many identifying no peaks, as in B, the algorithm still provides an accurate fit (in terms of the R² fit and error). Nevertheless, the identified center frequencies in B would all be marked as false positives for the algorithm as compared to human majority rule, penalizing the algorithm. (C) Human raters show a strong precision/recall tradeoff, with some variability amongst raters. Inset is Spearman correlation between precision and recall. (D) Despite the penalty against the algorithm for potential overfitting, as in B, it performs comparably to the human majority rule. n.s.: algorithm not significantly different from human raters.

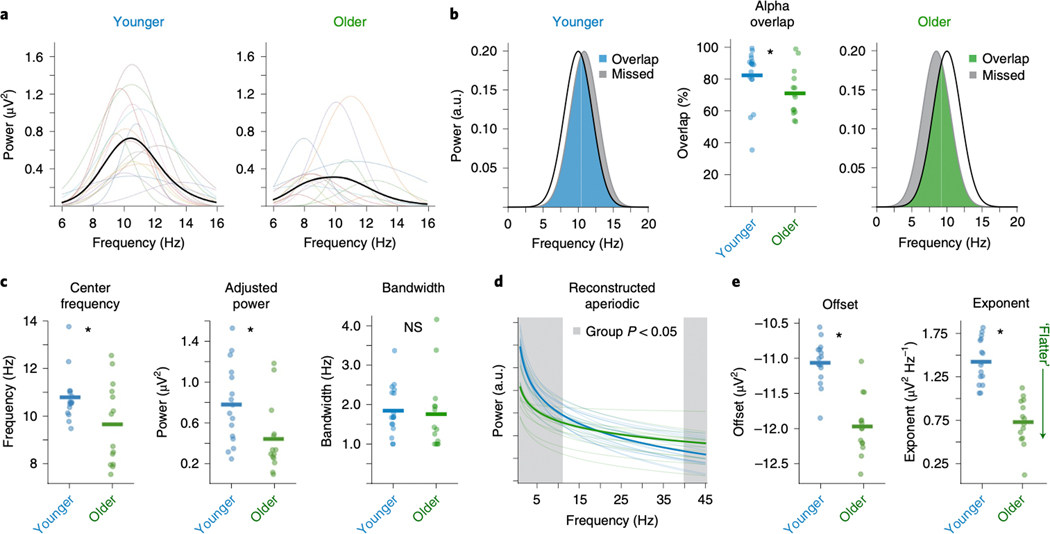
Figure 5 |. Age-related shifts in spectral EEG parameters during resting state.

(A) Visualization of individualized oscillations as parameterized by the algorithm, selected as highest power oscillation in the alpha (7–14 Hz) range from visual cortical EEG channel Oz for each participant. There are clear differences in oscillatory properties between age groups that are quantified in C. (B) A comparison of alpha captured by a canonical 10 ± 2 Hz band, as compared to the average deviation of the center frequency of the parameterized alpha, for the younger group (left, blue) and older group (right, green). In this comparison, the canonical band approach captures 84% of the parameterized alpha in the younger adult group, and only 71% in the older adult group, as quantified in the middle panel, reflecting a significant different (p=0.031). Red represents the alpha power missed by canonical analysis, which disproportionately reflects more missed power in the older group. (C) Comparison of parameterized alpha center frequency (p=0.036), aperiodic-adjusted power (p=0.018), and bandwidth (p=0.632), split by age group. (D) Comparison of aperiodic components at channel Cz, per group. For this visualization, the aperiodic offset and exponent, per participant, were used to reconstruct an “aperiodic only” spectrum (removing the putative oscillations). Red shaded regions reflect areas where there are significant power differences at each frequency between groups (p < 0.05 uncorrected t-tests). In this comparison, significant group differences in both aperiodic offset (p<0.0001) and exponent (p=0.0001) (E) drive group-wise differences that otherwise appear to be band-specific in both low (< ~10 Hz) and high (> ~40 Hz) frequencies, when analyzed in a more traditional manner. Bars in B, C, E represent mean values while stars indicate statistically significant difference, (two-sided paired samples t-test, uncorrected) at p < 0.05. n.s. not significant.

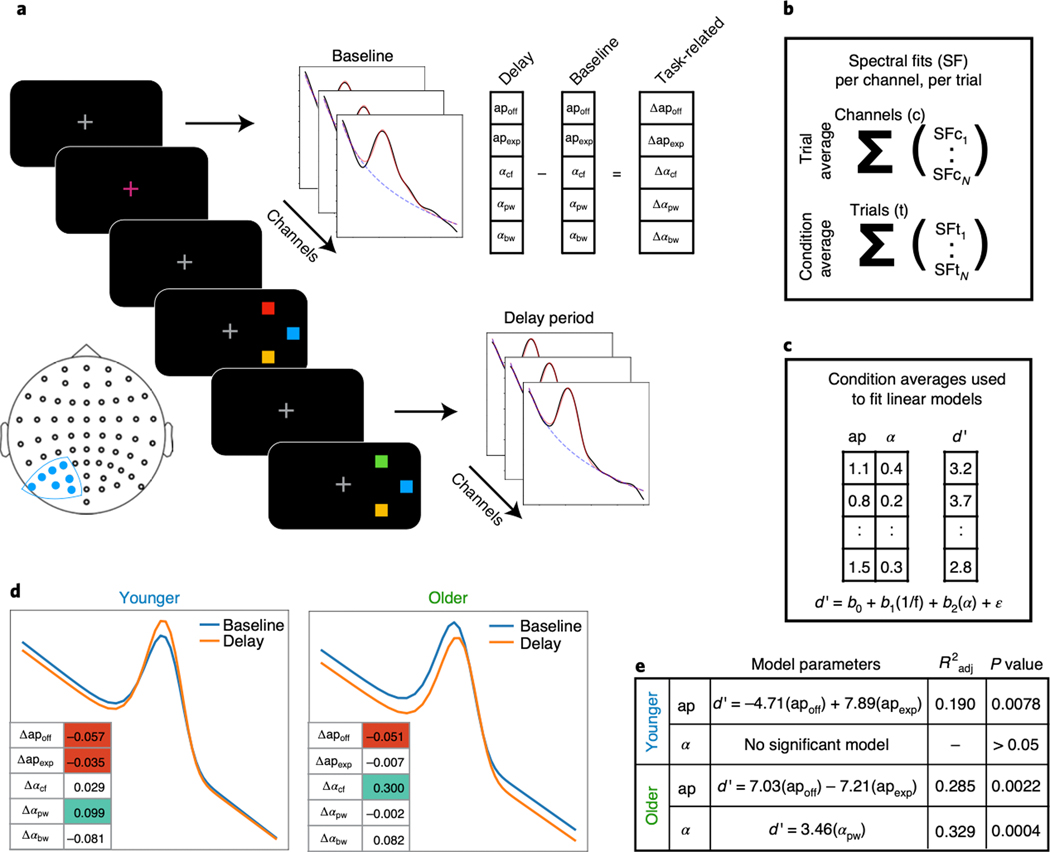
Figure 6 |. Event-related spectral parameterization of working memory in aging.

(A) Contralateral electrodes (filled blue dots on the electrode localization map) were analyzed in a working memory task, with spectral fits to delay period activity per channel, per trial, as well as to the pre-trial baseline period (see Methods). Task-related measures of each spectral parameter were computed by subtracting the baseline parameters from the delay period parameters. (B) Parameters were collapsed across channels, to provide a measure per trial, and collapsed across trials, to provide a measure per working memory load (condition). (C) For this analysis, condition average spectral parameters were used to predict behavioral performance, measured as d’, per condition. (D) The average evoked difference in spectral parameters, between baseline and delay periods, for each group, presented as spectra reconstructed from the spectral fits, including aperiodic and oscillatory alpha parameters. The inset tables present the changes in each parameter, shaded if significant (one sample t-test, p < 0.05; green: positive weight; red: negative weight). For further details of the statistical comparisons, see Supplementary Table 1. (E) Parameters for regression models predicting behavioral performance for each group. All behavioral models use the evoked spectral parameters from A. Note that all models also include an intercept term, and a covariate for load. Models were fit using ordinary least squares, and the model r-squared and results of F-test for model significance are reported (see Methods).

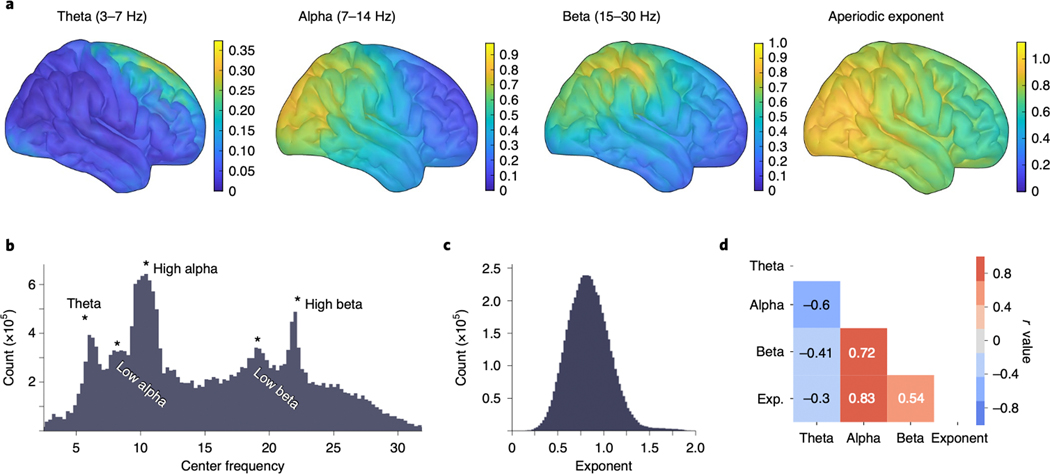
Figure 7 |. Large-scale analysis of MEG resting state data uncovers cortical spectral features.

Spectral parameterization was applied to a large MEG dataset (n=80 participants, 600,080 spectra). (A) Oscillation topographies reflecting the oscillation score: the probability of observing an oscillation in the particular frequency band, weighted by relative band power, after adjusting for the aperiodic component (see Methods). These topographies quantify the known qualitative spatial distribution for canonical oscillation bands theta (3–7 Hz), alpha (7–14 Hz), and beta (15–30 Hz). (Right) The topography of resting state aperiodic exponent fit values across the cortex. Group exponent—calculated as the average (mean) exponent value, per vertex, across all participants—shows that the aperiodic exponent is lower (flatter) for more anterior cortical regions. (B) The distribution of all center frequencies, extracted across all participants (n = 80), roughly captures canonical bands, though there is substantial heterogeneity. Peaks in the probability distribution are labeled for approximate canonical bands. (C) The distribution of aperiodic exponent values, fit across all vertices and all participants. (D) Correlations between the oscillation topographies and the exponent topography (as plotted in A) show that theta is spatially anti-correlated with the other parameters.

RESULTS

Algorithm performance against simulated data

To investigate algorithm performance, we simulated realistic neural PSDs with known ground truth parameters. These simulated spectra consist of a combination of Gaussians, with variable center frequency, power, and bandwidth; an aperiodic component with varying offset and exponent; and noise. Algorithm performance was evaluated in terms of its ability to reconstruct the individual parameters used to generate the data (Fig. 3; see Methods). Individual parameter accuracy was considered, since the algorithm, without using the settings to limit the number of fitted peaks, can arbitrarily increase R² and reduce error. Thus, overall fit error should not be the sole method by which to assess algorithm performance, and should be considered together with the number of peaks fit. This is because, in the extreme, if the algorithm fits a peak at every frequency then the error between the center frequency of the true peak and the closest identified peak will be artificially low. In addition, global goodness-of-fit measures such as R² or mean squared error are not directly related to accuracy of individual parameter estimation.

Common analyses seek to identify and measure the most prominent oscillation in the power spectrum. To assess algorithm performance at this task, we began by simulating a single spectral peak with varying levels of both noise and aperiodic parameters (Fig. 3A). Algorithm performance is assessed by the absolute error of each of the reconstructed parameters: aperiodic offset and exponent (Fig. 3B), as well as center frequency, power, and bandwidth of the largest peak (Fig. 3C). Note that power as returned by the algorithm always refers to aperiodic-adjusted power—that is the magnitude of the peak over and above the aperiodic component.

Simulated aperiodic exponents ranged between [0.5, 2.0] au/Hz, and the median absolute error (MAE) of the algorithmically identified exponent remained below 0.1 au/Hz, even in the presence of high noise, with MAE increasing monotonically across noise levels (Fig. 3B). Spectral peaks were simulated with center frequencies between [3, 34] Hz, with peak power between [0.15, 0.4] au above the aperiodic component, and bandwidths between [1, 3 Hz] (see methods for full details). When identifying center frequency, MAE was within 1.25 Hz of the true peak for all tested noise levels. For peak power MAE remained below 0.1 au, and for bandwidth MAE was within 1.25 Hz, for even the largest noise scenarios. In both cases MAE increased monotonically with noise (Fig. 3A). Note that for bandwidth, a default algorithm parameter limits maximum bandwidth to 8.0 Hz (see Methods), which likely reduces MAE.

Another use case for the algorithm is to identify multiple oscillations (Fig. 3D–F). Here we assess performance as overall fit error, considered in combination with whether the algorithm finds the correct number of oscillations. In the presence of multiple simulated peaks (Fig. 3D), the median fit error increases monotonically as the number of peaks increases (Fig. 3E). Multiple simulated peaks can differ significantly in power and can overlap, increasing fit error. Despite this, the modal number of fit peaks matches the number of true simulated peaks (Fig. 3E,F).

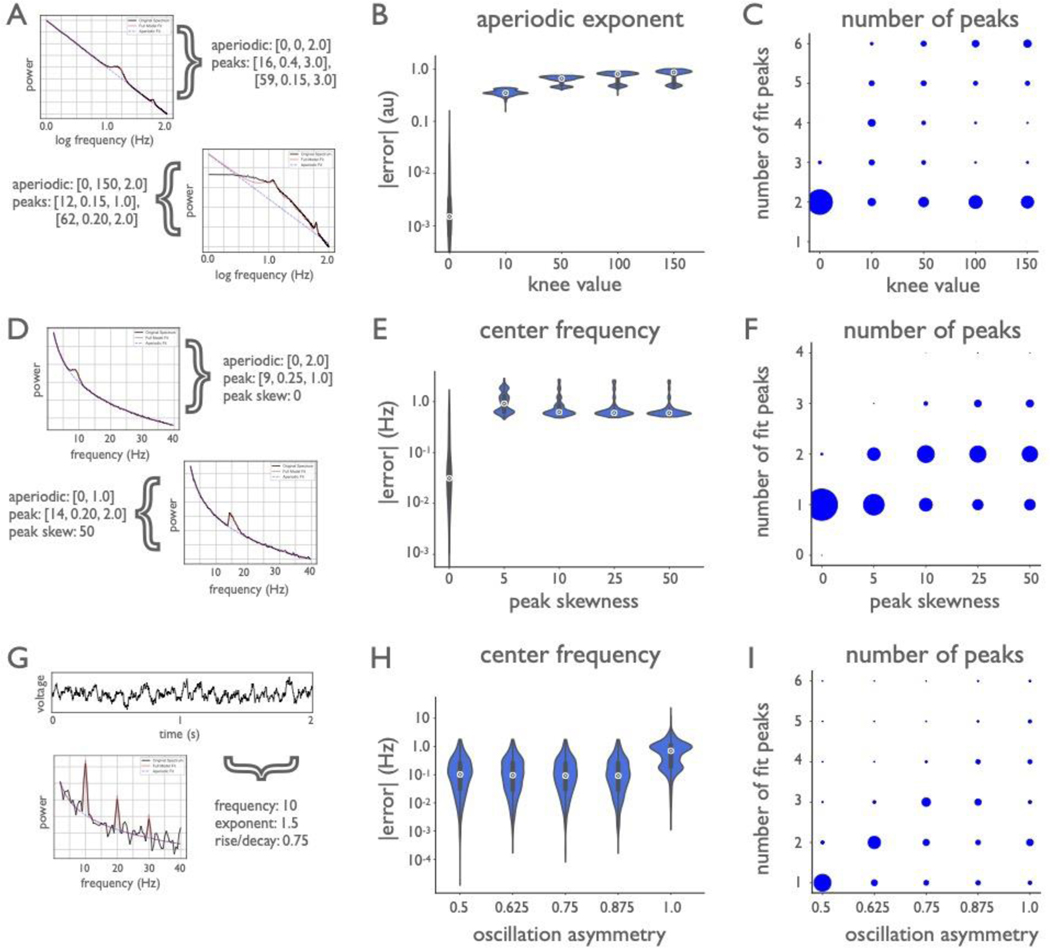
Additional simulations tested algorithm performance across broader frequency ranges (Extended Data Fig. 2). For the frequency range of 1–100 Hz, MAE was below 1.5 Hz for low frequency peaks (3–34 Hz), and below 4 Hz for high frequency peaks (50–90 Hz), across noise levels (Extended Data Fig. 2B). Across larger frequency ranges, spectra often exhibit a ‘knee’, or bend in the aperiodic component of the data^24,32 (see Methods). Knee values were simulated between [0, 150] au, and MAE for the recovered parameters was below 15 au, while maintaining good performance for offset (MAE below 0.2) and exponent (MAE below 0.15) (Extended Data Fig. 2C). Finally, the robustness of the algorithm was assessed against violations of model assumptions, including fitting no knee when a knee is present, non-Gaussian peaks, and non-sinusoidal oscillations (Extended Data Fig. 3).

Algorithm performance against expert human labeling

Next, we examined algorithm performance against how experts identify peaks in PSDs. Because it is uncommon for human raters to manually measure the other spectral features parameterized by the algorithm, human raters experienced in oscillation research (n=9) identified only the center frequencies of peaks in human EEG and non-human primate LFP PSDs (Fig. 4A,B). For many spectra there was strong consensus (e.g., Fig. 4A), but not for all (e.g., Fig. 4B). Performance was quantified in terms of precision, recall, and F₁ score, the latter of which combines precision and recall with equal weight (see Methods). This is a conservative approach that underestimates the abilities of the algorithm (which is optimized to best fit the entire spectrum, not just a peak’s center frequency). Also important is that the definition of surrogate ground truth used here means that when human raters show disagreement regarding the center frequency of putative oscillations, the algorithm will be marked as incorrect (Fig. 4B).

Human labelers were relatively consistent in peak labeling for both EEG and LFP datasets, as evidenced by above-chance recall for each rater with the majority (Fig. 4C). Despite the disadvantages outlined above, the algorithm identified a similar number of peaks as the raters for both EEG (n=64 PSDs; humans, algorithm: 1.81, 1.71; t₆₃=0.77, p=0.44) and LFP (n=42 spectra, humans, algorithm: 1.05, 1.10; t₄₁=−0.47, p=0.64). The algorithm had comparable precision as humans for both EEG (humans, algorithm: 0.77, 0.81; z=0.18, p=1.0) and LFP (humans, algorithm: 0.83, 0.63; z=−1.44, p=0.38). The algorithm had slightly lower recall compared to humans for EEG (humans, algorithm: 0.87, 0.68; z=−2.15, p=0.092), and comparable recall for LFP (humans, algorithm: 0.86, 0.84; z=−0.22, p=0.99).

Raters also demonstrated a strong precision/recall tradeoff (Spearman ρ=−0.91, p=2.2×10⁻⁷) (Fig. 4C). Such a tradeoff is common in search and classification, as most strategies to improve recall come at the cost of precision, and vice versa. For example, one could achieve perfect precision by marking only the most obvious, largest power, peak, but at the cost of failing to recall all other peaks. Or one could achieve perfect recall by marking every frequency as containing a peak, but at the cost of precision. For this reason, we assessed overall performance using the F₁ score, which equally weights precision and recall. The algorithm had comparable F₁ scores as humans for EEG (humans, algorithm: 0.79, 0.74; z=−0.44, p=0.96), and slightly lower F₁ scores for LFP (humans, algorithm: 0.83, 0.72; z=−2.16, p=0.087) (Fig. 4D).

Age-related differences in spectral parameters

The practical utility of the algorithm was assessed across several EEG and MEG applications. First, we replicated and extend previous work looking at age-related differences in spectral parameters, such as alpha oscillations and aperiodic exponent, including how individualized parameters differ with aging (Fig. 5); then we examined whether task-related parameters are altered by working memory and aging (Fig. 6). To test this, we analyzed scalp EEG data from younger (n=16; 20–30 years; 8 female) and older adults (n=14; 60–70 years; 7 female) at rest and while performing a lateralized visual working memory task (see Methods).

Resting state analyses.

Resting state alpha oscillations and aperiodic activity, as parameterized by the algorithm, were compared between age groups. First, we quantified how much individualized alpha parameters differed from canonical alpha. To do this, participant-specific alpha oscillations were reconstructed based on individual peak frequencies from channel Oz and were compared against a canonical 10 Hz-centered band. We observed considerable variation across participants (Fig. 5A,B, see Methods), as well as a significant difference between groups (overlap with canonical alpha: younger=84%, older=71%; t₂₈=2.27, p=0.031; Cohen’s d=0.83) (Fig. 5B). Note that this manifests as a difference in alpha power between groups when using the canonical band analyses, though this is partly driven by more of older adult’s alpha lying outside the canonical 8–12 Hz alpha range.

Older adults had lower (slower) alpha center frequencies than younger adults (younger=10.7 Hz, older=9.6 Hz; t₂₈=2.20, p=0.036; Cohen’s d=0.79) and lower aperiodic-adjusted alpha power (younger=0.78 μV², older=0.45 μV²; t₂₈=2.52, p=0.018; Cohen’s d=0.93), though bandwidth did not differ between groups (younger=1.9 Hz, older=1.8 Hz; t₂₈=0.48, p=0.632; Cohen’s d=0.17) (Fig. 5C). The mean aperiodic-adjusted alpha power difference between groups was 0.33 μV²/Hz whereas, when comparing total (non aperiodic-adjusted) alpha power, the mean difference was 0.45 μV²/Hz. This demonstrates that, though alpha power changes with age, the magnitude of this change is exaggerated by conflating age-related alpha changes with age-related aperiodic changes.

Regarding aperiodic activity, older adults had lower aperiodic offsets (younger=−11.1 μV², older=−11.9 μV²; t₂₈=6.75, p<0.0001; Cohen’s d=2.45) and lower (flatter) aperiodic exponents (younger=1.43 μV²/Hz, older=0.75 μV²/Hz; t₂₈=7.19, p<0.0001; Cohen’s d=2.63) (Fig. 5E). Participant-specific aperiodic components were reconstructed based on individual offset and exponent parameter fits from channel Cz, and used to compare frequency-by-frequency differences between groups (Fig. 5D). From reconstructions, significant differences were found between groups in the frequency ranges 1.0–10.5 Hz and 40.2–45.0 Hz (p<0.05, uncorrected t-tests at each frequency band). This demonstrates, in real data, how group differences in what would traditionally be considered to be oscillatory bands can actually be caused by aperiodic—non-oscillatory—differences between groups (c.f., Fig. 1).

Working memory analyses.

To evaluate whether parameterized spectra can predict behavioral performance, we analyzed a working memory task from the same dataset, in which participants had to remember the color(s) of briefly presented squares over a short delay period. We then attempted to predict behavioral performance, measured as d’, from periodic and aperiodic parameters calculated as a difference measures between baseline and delay period (see Methods for task and analysis details). Ordinary least squares linear regression models were fit to predict performance, and model comparisons were done to examine which spectral parameters and estimation approaches best predicted behavior (Fig. 6A–C). The most consistent model for predicting behavior across groups (adjusting for the number of parameters in the model) was one using only the two aperiodic parameters (offset and exponent; younger: F_{(4, 46)}=3.94, p=0.0078, R_adj²=0.19; older: F_{(4, 37)}=5.10, p=0.0023, R_adj²=0.29). In the older adult group, the aperiodic-adjusted alpha power model was also a significant predictor (F_{(3, 38)}=7.70, p=0.0004, R_adj²=0.33), performing better than a model using canonical alpha measures (F_{(3, 38)}=5.18, p=0.0042, R_adj²=0.23). In the younger adult group, neither measure of alpha power significantly predicted behavior (Fig. 6E). This result highlights that, while traditional analyses of such tasks typically focus on alpha activity³³, we find that the more accurate prediction of behavior is from aperiodic activity, a pattern that may be misinterpreted as alpha dynamics in canonical analyses, in particular when there are spectral parameter differences between groups.

Spatial analysis of periodic and aperiodic parameters in resting state MEG

Finally, we parameterized a large dataset (n=80, 600,080 spectra) of source-reconstructed resting state MEG data to quantify how spectral parameters varies across the cortex. When collapsed across all participants and all cortical locations, the distribution of center frequencies for all algorithm-extracted oscillations partially recapitulates canonical frequency bands, wherein the most common frequencies are centered in the theta, alpha, and beta ranges (Fig. 7B). Notably, however, there are extracted oscillations across all frequencies, so while canonical bands do capture the modes of oscillatory activity, they are not an exhaustive description of periodic activity in the human neocortex.

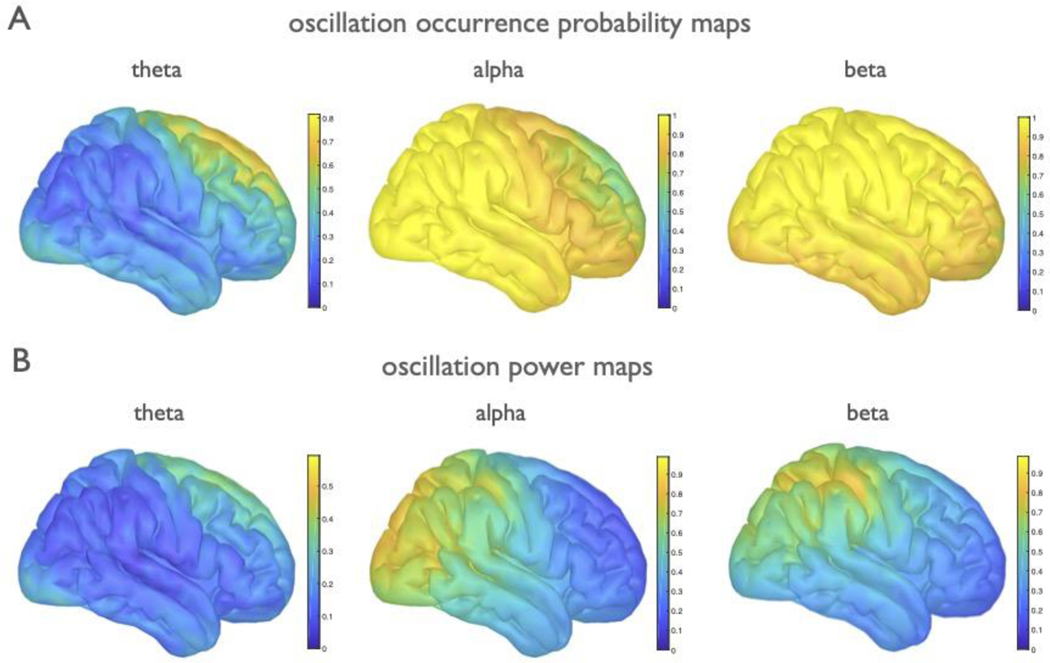
Because extracted peaks are broadly consistent with canonical bands, we clustered them post hoc into theta (3–7 Hz), alpha (7–14 Hz), and beta (15–30 Hz) bands. When examined across the cortex, we find that the aperiodic-adjusted oscillation band power also recapitulates well-documented spatial patterns³⁴, where theta power is concentrated at the frontal midline, alpha power is predominantly distributed over posterior and sensorimotor areas, and beta power is focused centrally, over the sensorimotor cortex (Extended Data Fig. 4B). However, prior reports using canonical methods may be at least partially driven by aperiodic activity, because they do not separate or quantify if, or how often, oscillations are present over and above the aperiodic component. To address this, we quantified how often an oscillation was observed, for each band, across the cortex (Extended Data Fig. 4A). These two metrics were then combined into an “oscillation score” measure (see Methods), which is a composite of the group-level oscillation occurrence probability weighted by the relative power of algorithmically identified parameters (Fig. 7A).

The oscillation score allows us to examination the variability of periodic activity across participants. For example, the oscillation scores approaching 1.0 in both alpha and beta indicate a very high degree of consistency in these bands (a maximum score of 1.0 tells us that every participant has an oscillation of maximum relative power in the same location). We find that alpha and beta are ubiquitous across the cortex, though their relative power is concentrated in specific regions (Extended Data Fig. 4). By contrast, theta is more variable, with max oscillation scores <0.4 indicating significant variability in theta presence, and its relative power. Theta oscillations are only sometimes observed in frontal regions at rest (Extended Data Fig. 4) and are almost entirely absent in visual regions.

The explicit parametrization of each feature allows us to examine how each parameter varies across the cortex. Note, for example, that the consistency of oscillation presence and relative power do not imply that these oscillations are consistent in their center frequency, because we also see significant variation of peak frequencies (Fig. 7B). We also show that, while the aperiodic exponent has a mean value of 0.828 (Fig. 7C), there is spatial heterogeneity such that highest exponent values are found in posterior regions, and the exponent gets gradually smaller (flatter) as it moves anteriorly (Fig. 7A). We also examined relationships between parameters, calculated as correlations between the spatial topographies of oscillation scores per parameter (Fig. 7D). The strongest observed relationships were a negative correlation between theta and alpha (r=−0.60, p<0.0001) and a positive correlation between alpha and the aperiodic exponent (r=0.83, p<0.0001). Collectively, these analyses allow us to verify patterns of aperiodic-adjusted periodic activity, and quantify, for the first time, the consistency of occurrence of oscillations. In addition, the spatial topography of the aperiodic exponent is important to note when exploring topographies of presumed oscillations derived from narrowband analyses, given that the aperiodic component can drive observed spatial differences.

DISCUSSION

Despite the ubiquity of oscillatory analyses, there are several analytic assumptions that impact the physiological interpretation of prior oscillation research. Standard approaches for quantifying oscillations presume that oscillations are present, which may not be true (Extended Data Fig. 1), and often rely on canonical frequency bands that presume that spectral power implies oscillatory power. These assumptions overlook the existence of aperiodic activity, which is itself dynamic, and so cannot be simply ignored as stationary noise. Aperiodic activity also has interesting demographic, cognitive, and clinical correlates, as well as physiological relevance, and so should also be explicitly parameterized and analyzed. Here we introduce a novel method for algorithmically extracting periodic and aperiodic components in electro- and magnetophysiological data that addresses these often-overlooked issues in cognitive and systems neuroscience.

We demonstrate this method with a series of applications, and highlight methodological points and novel findings. We show how apparent age-related differences in oscillatory power can be partially driven by shifts in oscillation center frequency (Fig. 1C). Specifically, we find that canonical alpha band analyses (e.g., analyzing the 8–12 Hz range) fail to capture all of the oscillatory power within individual participants, and are systematically biased between groups²² (Fig. 5B). In our data, canonical alpha analyses miss a greater proportion of power in older adult’s true alpha activity compared to younger adult’s alpha, due to the fact that older adults tend to have slower (lower frequency) alpha²⁰ (Fig. 5A,B). This is important, as traditional analyses using fixed bands fail to address inter-individual differences, which has methodological consequences, and also ignores that variations in peak-frequencies within oscillation bands have functional correlates and are of theoretical interest¹².

We also show how apparent oscillation power can be influenced by changes in the aperiodic exponent, for example in the case of age-related changes in the aperiodic exponent (Fig. 5D,E). Thus, though we replicate often-described age-related alpha power changes²⁰, we find the magnitude of this effect, when analyzed for alpha power specifically, is more subtle than previously reported. This is because age-related changes in the aperiodic component also shift total narrowband alpha power, despite the fact that power in a narrowband oscillation has not changed relative to the aperiodic process⁶ (Extended Data Fig. 1A). We conclude that periodic activity is not the sole driver of the apparent ~10 Hz power differences in aging; and that the magnitude of alpha power differences have been systemically confounded by concomitant differences in aperiodic activity.

We also examined the utility of spectral parameterization in a cognitive context, analyzing EEG data from a visual working memory task (Fig. 6). While such studies often focus on oscillatory activity, in particular visual cortical alpha³³, recent computational work shows the importance of excitation/inhibition (EI) balance in working memory maintenance³⁵. Given that the aperiodic exponent partially reflects EI balance¹⁹, and is systematically altered in aging¹⁸, we hypothesized that the aperiodic component would predict working memory performance. We find that, across groups, event-related changes in the aperiodic parameters, rather than just oscillatory alpha, most consistently predict individual working memory performance. In contrast, delay period alpha parameters tracked behavior among older, but not younger, adults. This suggests that there are categorical differences between groups regarding which spectral parameters track working memory outcomes, and that these features are easy to conflate—or miss—without explicit spectral parameterization, and highlights a novel finding of aperiodic activity predicting working memory performance in human EEG data.

Finally, we applied the algorithm to a large collection of MEG data, mapping periodic and aperiodic activity across the cortex (Fig. 7). Notably while these results broadly recapitulate expected patterns of activity^36,37, the explicit parameterizations reveal features not possible with traditional approaches. For example, we show that: 1) there is a large amount of variability, for example, of oscillatory peak frequencies (Fig. 7B); 2) there are band-specific patterns of the detectability of oscillatory peaks (Extended Data Fig. 4A) and aperiodic-adjusted power (Extended Data Fig. 4A), and; 3) there is a gradient across the cortex of the aperiodic exponent³⁶. These findings highlight how traditional analyses are not adequately accounting for the rich variation present in neural data because they use fixed frequency bands, they do not account for the presence of aperiodic activity, and they overlook variability in oscillation presence and in oscillatory features.

This work raises interesting possibilities for how to interpret common findings. Intriguingly, when examined in the time-domain, differences in the aperiodic exponent manifest as raw voltage differences (Extended Data Fig. 1A). It may be that observed differences between conditions, for example in event-related spectral perturbations or evoked potentials, are partially explainable by, or related to, differences in aperiodic exponent. This consideration is particularly important when comparing between groups, given that the aperiodic exponent varies across groups, including aging¹⁸ (Fig. 5D,E) and disease^29,30.

The observation of within subject changes of the aperiodic exponent also has implications regarding the ubiquitous negative correlation between low frequency (<30 Hz) and high frequency (>40 Hz) activity³⁸, observed here in the EEG data (Fig. 5D). This is often interpreted as a push/pull relationship between low frequency oscillations and gamma, however spectral parameterization offers a different interpretation: a see-saw-like rotation of the spectrum at around 20–30 Hz due to a change in aperiodic activity. This results in decreased power in lower frequencies with a simultaneous increase in higher frequency power. Here it would be a mischaracterization to say that there was a task-related decrease in low frequency oscillations, because that need not be the feature that was truly altered; instead, the aperiodic exponent changed, manifesting as the spectrum “rotating” around a specific frequency point. This has been observed to occur in a task-related manner in human visual cortex¹⁷.

Across the gamma range, there can be both narrowband activity and broadband shifts³⁹. There may also be high variability of narrowband frequencies within participants such that averaging across those bands decreases detectability overall statistical power⁴⁰. Parameterizing spectra allows for detecting narrowband peaks, and inferring whether narrow- and/or broadband aspects of the data are changing. This may also be useful for analyses such as phase-amplitude coupling (PAC), which have provided a powerful means for probing the potential mechanisms of neural communication^4,41,42. These analyses typically rely on fixed frequency bands, which is problematic given that multiple-oscillator PAC exhibits different phase coupling frequencies by cortical region⁴². Using spectral parameterization to characterize oscillatory components may allow for better identifying phase coupling modes across brain regions, task, and time, thus increasing the specificity and accuracy of cross-frequency coupling analyses.

Altogether, the parameterization algorithm provides a principled method for quantifying the neural power spectrum, increasing analytical power by disentangling periodic and aperiodic components. This allows researchers to take full advantage of the rich variability present in neural field potential data, rather than treating that variability as noise. These spectral features reflect distinct properties of the data, but may also be inter-related, given the evidence that the aperiodic exponent and band powers can be correlated^43,44. This highlights the need for careful parameterization to adjudicate between individual spectral features and their relationship to cognitive, clinical, demographic, and physiological data.

Though the algorithm itself is agnostic to underlying physiological generators of the periodic and aperiodic components, it can be leveraged to investigate theories and interpretations of them. For example, changes in the aperiodic exponent may relate to a shift in the balance of the transmembrane currents in the input region, such as a shift in EI balance¹⁹. In oscillations, traditional canonical frequency band analyses commit researchers to the idea that those predefined bands have functional roles, rather than considering the underlying physiological mechanisms that generate different spectral features. Spectral parameterization across scales, and in combination with other measures, may allow us to better link macroscale electrophysiology to microscale synaptic and firing parameters⁴⁵, providing a better understanding of the relationship between microscale synaptic dynamics and different components in field potential signals, from microscale LFP, to mesoscale intracranial EEG, to macroscale EEG and MEG²⁶.

While there are other methods for measuring periodic and aperiodic activity, none jointly parameterize aperiodic and periodic components. Some methods focus on identifying individual differences in oscillations, however, they are mostly restricted to detecting the peak frequency within a specific sub-band¹¹. This has resulted in a broad literature looking at variation within canonical bands, most commonly peak alpha frequency within and across individuals^11,12. However, such approaches often assume only one peak within a band, do not generalize across broad frequencies, and/or ignore aperiodic activity⁴⁶, perpetuating the conflation of aperiodic and periodic processes. Other approaches attempt to control for the aperiodic component when identifying oscillations, but do not parameterize both the aperiodic and periodic features together. Often, these methods treat the aperiodic component as a nuisance variable, for example by correcting for it via spectral whitening²⁵, rather than a feature to be explicitly modeled and parameterized.

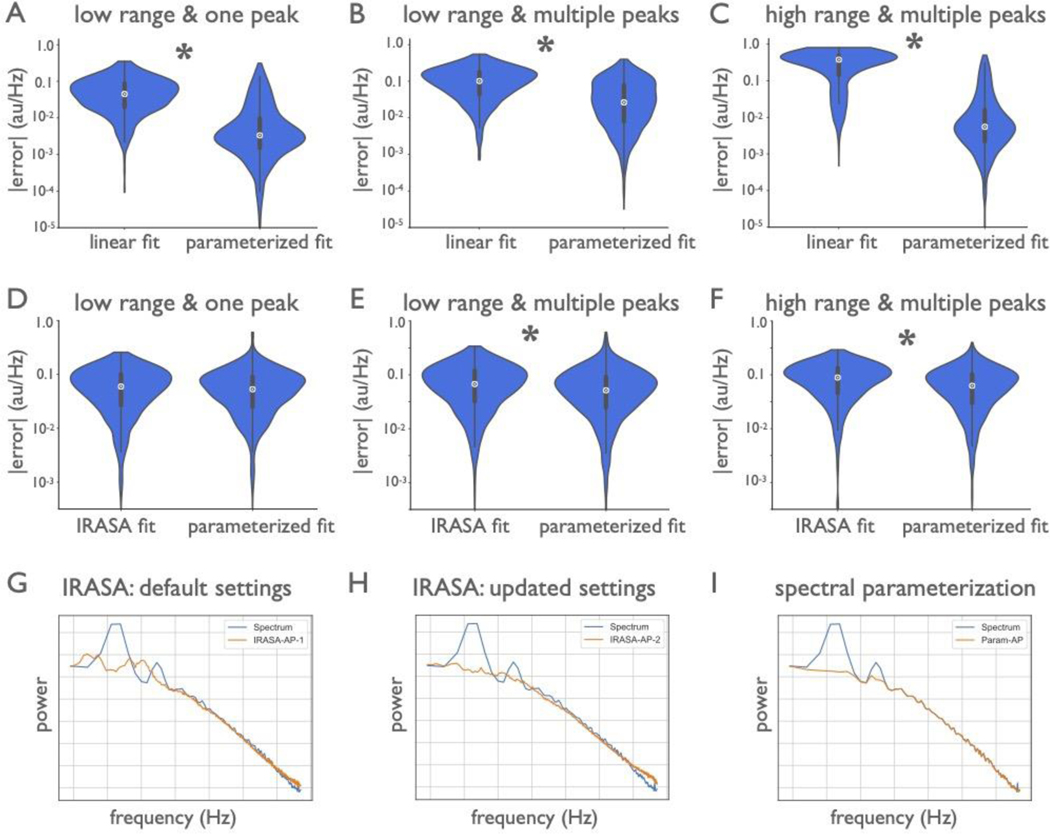
A time-domain approach called BOSC (Better OSCillation Detector)⁴⁷ uses a simple linear fit to the PSD to determine a power threshold in an attempt to isolate oscillations, though this does not explicitly parameterize the aperiodic component for analysis. The irregular-resampling auto-spectral analysis (IRASA) method is a decomposition method that seeks to explicitly separate the periodic component from self-similar aperiodic activity through a resampling procedure⁴⁸. This approach does not parameterize aperiodic or periodic components, but can be combined with model fitting of the isolated components. However, as the original authors noted, IRASA smears multi-fractal components⁴⁸ (knees). Neither of these methods (BOSC, IRASA), currently allow for the same range of measurements as power spectrum parameterization (see Supplementary Modeling Note), though future work could seek to integrate these different methods. In direct comparisons of comparable measures, we find that spectral parameterization is at least as performant, and typically better and more generalizable than BOSC or IRASA (Extended Data Fig. 5; Supplementary Modeling Note). Other methods, such as principal component variants, require manual component selection¹⁴. Collectively, the current method addresses existing shortcomings by explicitly parameterizing periodic and aperiodic signals, flexibly fitting multiple peaks and different aperiodic functions, without requiring extensive manual tuning or supervision.

There are some practical considerations to keep in mind when applying this method. The model, as proposed, is applicable to multiple kinds of datasets, ranging from LFP to EEG and MEG. Different modalities, and different frequency ranges, may require different settings for optimal fitting, and fits should always be evaluated for goodness-of-fit. In particular, we find that it is important for the aperiodic component to be fit in the correct aperiodic mode, reflecting if a knee should be fit (Extended Data Figs. 2,3). Detailed notes and instructions for applying the algorithm to different modalities, assessing model fits, and tuning parameters are all available in the online documentation. There are also caveats to consider when interpreting model parameters. Notably, while the presence of power above the aperiodic component is suggestive of an oscillation, a spectral peak does not always imply a true oscillation at that frequency⁴⁹. For example, sharp wave rhythms, such as the sawtooth-like waves seen in hippocampus or the sensorimotor mu rhythm, will manifest as narrowband power at harmonics of the fundamental frequency⁴⁹ (Extended Data Fig. 3G–I). Similarly, the lack of an observed peak over and above the aperiodic component does not definitively imply the complete absence of an oscillation. There could be very low power oscillations, highly variable oscillatory properties, and/or rare burst events or within a long time series, that do not exhibit as clear spectral peaks. To address these possibilities, spectral parameterization can be complemented with time-domain analysis approaches²¹.

In conclusion, application of our algorithm shows that different physiological processes, including changes in the exponent or offset of the aperiodic component or periodic oscillatory changes, are often conflated⁵⁰. Our approach allows for disambiguating distinct changes in the data by parameterizing aperiodic and periodic features, allowing for investigations of how these features relate to cognitive functioning in health, aging, and disease, as well as their underlying physiological mechanisms. The proposed algorithm is validated on simulated data, and demonstrated with a series of data applications. Because of the speed and ease of the algorithm and the interpretability of the fitted parameters, this tool opens avenues for the high-throughput, large-scale analyses that will be critical for data-driven approaches to neuroscientific research.

METHODS

Algorithm development and analyses for this manuscript were done with the Python programming language. The code for the algorithm and for the analyses presented in this paper are openly available (https://github.com/specparam-tools/specparam; see Code Availability statement). The name of the Python module stands for ‘spectral parameterization’.

Algorithmic parameterization

The parameterization method presented herein quantifies characteristics of electro- or magneto-physiological data, in the frequency domain. While many methods can be used to calculate the power spectra for algorithmic parametrization, throughout this investigation we use Welch’s method⁵¹. The algorithm conceptualizes the PSD as a combination of an aperiodic component^52,53, with overlying periodic components, or oscillations⁷. These putative oscillatory components of the PSD are characterized as frequency regions of power over and above the aperiodic component, and are referred to here as “peaks”. The algorithm operates on PSDs in semilog-power space, which is linearly spaced frequencies, and log-spaced power values, which is the representation of the data for all of the following, unless noted. The aperiodic component is fit as a function across the entire fitted range of the spectrum, and each oscillatory peak is individually modeled with a Gaussian. Each Gaussian is taken to represent an oscillation, whereby the three parameters that define a Gaussian are used to characterize the oscillation (Fig. 2).

This formulation models the power spectrum as:

$$P=L+\mathrm{ }\sum _{n=0}^N{G}_n\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left(1\right)$$ (1)

where power, P, representing the PSD, is a combination of the aperiodic component, L, and N total Gaussians, G. Each G_n is a Gaussian fit to a peak, for N total peaks extracted from the power spectrum, modeled as:

$$G_n=a\mathrm{*}exp\left(\frac{{-\left(F-c\right)}^2}{{2w}^2}\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left(2\right)$$ (2)

where a is the power of the peak, in log₁₀(power) values, c is the center frequency, in Hz, w is the standard deviation of the Gaussian, also in Hz, and F is the vector of input frequencies.

The aperiodic component, L, is modeled using a Lorentzian function, written as:

$$L=b-\log \left(k+F^{\chi }\right)\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left(3\right)$$ (3)

where b is the broadband offset, χ is the exponent, and k is the “knee” parameter, controlling for the bend in the aperiodic component^24,32, with F as the vector of input frequencies. Note that when k=0, this formulation is equivalent to fitting a line in log-log space, which we refer to as the fixed mode. Note that there is a direct relationship between the slope, a, of the line in log-log spacing, and the exponent, χ, which is χ = -a (when there is no knee). Fitting with k allows for parameterizing bends, or knees, in the aperiodic component that are present in broad frequency ranges, especially in intracranial recordings²⁴.

The final outputs of the algorithm are the parameters defining the best fit for the aperiodic component and the N Gaussians. In addition to the Gaussian parameters, the algorithm computes transformed ‘peak’ parameters. For these peak parameters, we define: (1) center frequency as the mean of the Gaussian; (2) aperiodic-adjusted power—the distance between the peak of the Gaussian and the aperiodic fit (this is different from the power in the case of overlapping Gaussians that might share overlapping power), and; (3) bandwidth as 2std of the fitted Gaussian. Notably, this algorithm extracts all these parameters together in a manner that accounts for potentially overlapping oscillations; it also minimizes the degree to which they are confounded and requires no specification of canonical oscillation frequency bands.

To accomplish this, the algorithm first finds an initial fit of the aperiodic component (Fig. 2A). This first fitting step is crucial and not trivial, as any traditional fitting method, such as linear regression, or even robust regression methods designed to account for the effects of outliers on linear fitting, can still be significantly pulled away from the true aperiodic component due to the overwhelming effect of the high power oscillation peaks. To account for this, we introduce a procedure that attempts to fit the aperiodic aspects of the spectrum only. To do so, initial seed values for offset and exponent are set to the power of the first frequency in the PSD and an estimated slope, calculated between the first and last points of the spectrum (calculated in log-log spacing, and converted to a positive value, since χ = -a). These seed values are used to estimate a first-pass fit. This fit is then subtracted from the original PSD, creating a flattened spectrum, from which a power threshold (set at the 2.5 percentile) is used to find the lowest power points among the residuals, such that this excludes any portion of the PSD with peaks that have high power values in the flattened spectrum. This approach identifies only the data points along the frequency axis that are most likely to not be part of an oscillatory peak, thus isolating parts of the spectrum most likely to represent the aperiodic component (Fig. 2A). A second fit of the original PSD is then performed only on these frequency points, giving a better estimate of the aperiodic component. This is, in effect, similar to approaches that have attempted to isolate the aperiodic component from oscillations by fitting only to spectral frequencies outside of an a priori oscillation¹⁸, but does so in a more unbiased fashion. The percentile threshold value can be adjusted if needed, but in practice rarely needs to be.

After the estimated aperiodic component is isolated, it is regressed out, leaving the non-aperiodic activity (putative oscillations) and noise (Fig. 2B). From this aperiodic-adjusted (i.e., flattened) PSD, an iterative process searches for peaks that are each individually fit with a Gaussian (Fig. 2C). Each iteration first finds the highest power peak in the aperiodic-adjusted (flattened) PSD. The location of this peak along the frequency axis is extracted, along with the peak power. These stored values are used to fit a Gaussian around the central frequency of the peak. The standard deviation is estimated from the full-width, half-maximum (FWHM) around the peak by finding the distance between the half-maximum powers on the left- and right flanks of the putative oscillation. In the case where there are two overlapping oscillations, this estimate can be very wide, so the FWHM is estimated as twice the shorter of the two sides. From FWHM, the standard deviation of the Gaussian can be estimated via the equivalence:

$$std=\frac{FWHM}{2\sqrt{2ln2}}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left(4\right)$$ (4)

This estimated Gaussian is then subtracted from the flattened PSD, the next peak is found, and the process is repeated. This peak-search step halts when it reaches the noise floor, based on a parameter defined in units of the standard deviation of the flattened spectrum, re-calculated for each iteration (default = 2std). Optionally, this step can also be controlled by setting an absolute power threshold, and/or a maximum number of Gaussians to fit. The power thresholds (relative or absolute) determine the minimum power beyond the noise floor that a peak must extend in order to be considered a putative oscillation. Once the iterative Gaussian fitting process halts, in order to handle edge cases, Gaussian parameters that heavily overlap (whose means are within 0.75std of the other), and/or are too close to the edge (<= 1.0std) of the spectrum, are then dropped. The remaining collected parameters for the N putative oscillations (center frequency, power, and bandwidth) are used as seeds in a multi-Gaussian fitting method (Python: scipy.optimize.curve_fit). Each fitted Gaussian is constrained to be close to (within 1.5std) of its originally guessed Gaussian. This process attempts to minimize the square error between the flattened spectrum and N Gaussians simultaneously (Fig. 2D).

This multi-Gaussian fit is then subtracted from the original PSD, in order to isolate an aperiodic component from the parameterized oscillatory peaks (Fig. 2E). This peak-removed PSD is then re-fit, allowing for a more precise estimation of the aperiodic component (Fig. 2F). When combined with the equation for the N-Gaussian model (Fig. 2G), this procedure gives a highly-accurate parameterization of the original PSD (Fig. 2H; in this example, >99% of the variance in the original PSD is accounted for by the combined aperiodic + periodic components). Goodness-of-fit is estimated by comparing each fit to the original power spectrum in terms of the median absolute error (MAE) of the fit as well as the R² of the fit.

The fitting algorithm has some settings, that can be provided by the user, one of which defines the aperiodic mode, with options of ‘fixed’ or ‘knee’, which dictates whether to fit the aperiodic component with a knee. This parameter should be chosen to match the properties of the data, over the range to be fit. The algorithm also requires a setting for the relative threshold for detecting peaks, which defaults to 2, in units of standard deviation. In addition, there are optional settings, which can be used to define: (1) the maximum number of peaks; (2) limits on the possible bandwidth of extracted peaks, and; (3) absolute, rather than relative, power thresholds. The algorithm can often be used without needing to change these settings. Some tuning may be useful for tuning algorithmic performance to different datasets with potentially different properties, for example, data from different modalities, data with different amounts of noise, and/or for fitting across different frequency ranges. Detailed description and guidance on these settings and if and how to change them can be found in the tool’s documentation. All parameter names, as well as their descriptions, units, default values, and accessibility to the API are also presented in Supplementary Table 2.

Code for this algorithm is available as a Python package, licensed under an open source compliant Apache-2.0 license. The module supports Python >= 3.5, with minimal dependencies of numpy and scipy (>= version 0.19), and is available to download from the Python Package Index (https://pypi.python.org/pypi/specparam/). The package is openly developed and maintained on GitHub (https://github.com/specparam-tools/specparam/). The project’s repository includes the codebase, a test-suite, instructions for installing and contributing to the package, and the documentation materials. The documentation is also hosted on the documentation website (https://specparam-tools.github.io/), which includes tutorials, examples, frequently asked questions, a section on motivations for parameterizing neural power spectra, and a list of all the functionality available. On contemporary hardware (3.5 GHz Intel i7 MacBook Pro), a single PSD is fit in approximately 10–20 ms. Because each PSD is fit independently, this package has support for running in parallel across PSDs to allow for high-throughput parameterization.

Simulated PSD creation and algorithm performance analysis

Power spectra were simulated following the same underlying assumption of the fitting algorithm—that PSDs can be reasonably approximated as a combination of an aperiodic component and overlying peaks, that reflect putative periodic components of the signal. The equations used in the algorithm and described in the methods for the fitting procedure were used to simulate power spectra, such that for each simulated spectrum, the underlying parameters used to generate it are known. On top of the simulated aperiodic component with overlying peaks, white noise was added, with the level of noise controlled by a scaling factor. The power spectra were therefore simulated as an adapted version of equation (1):


$$P=L+\mathrm{ }\sum _{n=0}^N{G}_n+\mathrm{‎}m\epsilon \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\left(5\right)$$ (5)

Where P is a simulated power spectrum, L and G_n are the same as described in equations (2) and (3) respectively, ‎ε is white noise, applied independently across frequencies, and m is a multiplicative scaling factor of that noise.

For all simulations, the parameterization algorithm was used with settings of {peak_width_limits=[1,8], max_n_peaks=6, min_peak_height=0.1, peak_threshold=2.0, aperiodic_mode=‘fixed’}, except where noted. For each set of simulations, 1000 power spectra were simulated for each condition. The algorithm was fit to each simulated spectrum, and estimated values for each parameter were compared to ground truth values of the simulated data. Deviation of the parameter values was calculated as the absolute deviation for the fit value from the ground truth value. We also collected the goodness-of-fit metrics (error and R²) and the number of fit peaks from the spectral parameterizations.

For the first set of simulations, power spectra were generated across the frequency range of 2–40 Hz, with a frequency resolution of 0.25 Hz (Fig. 3A–F). The aperiodic component was generated with y-intercept (offset) parameter of 0, and without a knee (k=0). Exponent values were sampled uniformly from possibilities {0.5, 1, 1.5, 2}. Oscillation center frequencies came from the range of 3–34 Hz (1 Hz steps), with each center frequency sampled as the observed probability of center frequencies at that frequency in real data, namely the MEG dataset described in this study. For simulations in which there were multiple peaks within a single spectrum (Fig. 3D–F), center frequencies were similarly sampled at random, with the extra constraint that a candidate center frequency was rejected if it was within 2 Hz on either side of another center frequency already selected for the simulated spectrum, such that individual spectra could not have superimposed peaks. Peak powers and bandwidths were sampled uniformly from {0.15, 0.20, 0.25, 0.4} and {1, 2, 3} respectively, independent of their center frequency.

A set of power spectra were generated with one peak per spectrum across five noise levels {0.0, 0.025, 0.05, 0.10, 0.15} (Fig. 3A–C). In these simulations, the center frequency, power, and bandwidth of the fit peak, as well the aperiodic exponent, were compared to the ground truth parameters. In order to compare ground truth parameters to the spectral reconstructions, which potentially included more than one peak, the highest power peak was extracted from the spectral fit to use for comparison. In another set of simulations, PSDs were created with a varying number of peaks – between 0 and 4 – with a fixed noise value of 0.01 (Fig. 3D–F). For these simulations, the performance of the algorithm was examined in terms of the fit error across the number of peaks, as well by comparing the number of simulated peaks to the number of peaks in the spectral fit.

Simulated power spectra to test across a broader frequency range were generated across the frequency range of 1–100 Hz, with a frequency resolution of 0.5 Hz (Extended Data Fig. 2 A–C). These spectra were created with knees, using knee values of {0, 10, 25, 100, 150}, sampled with equal probability, with offset and exponent values sampled as done previously. For these spectra two peaks were added, one in the low frequency range, sampled as previously described, with an additional peak sampled with a center frequency sampled, with even probability, from between 50 and 90 Hz (in 1 Hz) steps, with the same sampled power and bandwidth values as used previously. These spectra were generated across different noise levels, as before. Spectra were fit using the same algorithm settings as before, except for aperiodic mode being set to ‘knee’. Parameter reconstruction was evaluated, with the addition of calculating the accuracy of the reconstructed knee parameter.

Additional simulations were created to evaluate the model performance with respect to violations of model assumptions (Extended Data Fig. 3A–I). To examine violations of the aperiodic model assumptions, a set of spectra were also simulated with knees (Fig. 3A–C) but were fit in the ‘fixed’ aperiodic mode, using the same settings as before. Simulations were created as described above for simulations including knees, except that in order to evaluate the influence of knee parameters, spectra were simulated and grouped by knee values, for values of {0, 10, 50, 100, 150}, using a fixed noise level of 0.01. For these simulations, performance was primarily evaluated in terms of reconstruction accuracy of the aperiodic exponent, and in the number of fit peaks.

To examine model violations of the periodic component, power spectra were also simulated using asymmetric peaks in the frequency domain (Extended Data Fig. 3D–F). For these simulations, peaks were simulated as skewed gaussians, in which an additional parameter is used that controls the skewness of the peaks (simulated in code with `scipy.stats.skewnorm`). These simulations were created across the frequency range of 2–40 Hz, with a fixed noise value of 0.01. Each spectrum contained a single peak, with peak parameters sampled as in the prior simulations for this range. A skew value was added to the peak, across conditions with skew values of {0, 5, 10, 25, 50}. For these simulations, performance was primarily evaluated in terms of reconstruction accuracy of the peak center frequency, and in the number of fit peaks.

In addition, time series simulations were created with non-sinusoidal oscillations (Extended Data Fig. 3G–I), to investigate how the algorithm performs with asymmetric cycles and the resulting power spectra. Simulations were created as time series signals of oscillations of asymmetric cycles combined with aperiodic activity, using the simulation tools in the NeuroDSP Python toolbox⁵⁴. Time series were simulated as 10 second segments at a sampling rate of 500 Hz. The aperiodic component of the signal was simulated as a 1/f signal, with exponent values sampled from the same values as above. The periodic component of the data was an asymmetric oscillation, with a peak frequency sampled as above. These oscillations were created with varying across rise-decay symmetry values⁴⁹ of {0.5, 0.625, 0.75, 0.875, 1.0}. Note that a value of 0.5, with a symmetric rise and decay is a sinusoid, whereas values approaching 1 are increasingly sawtooth-like. The full signal was a combination of the two components, from which power spectra were calculated, using Welch’s method (2 second segments, 50% overlap, Hanning window). The power spectrum models were then fit across the frequency range of [2, 40], using the same settings as above. For these simulations, performance was primarily evaluated in terms of reconstruction accuracy of the peak center frequency, and in the number of fit peaks.

Finally, simulated data were also used to compare spectral parameterization to other related methods (Extended Data Fig. 5), which are described and reported in the Supplementary Modeling Note. For the method comparison simulations, we considered three test cases: signals with an aperiodic component and one oscillation over the frequency range of 2–40 Hz; signals with aperiodic activity and multiple (three) oscillations, also across 2–40 Hz; and signals with two peaks over a broader frequency range (1–100 Hz), in which the aperiodic component included a knee. For all comparisons between methods, paired samples t-tests were used to evaluate the difference between the distributions of errors for each method, and effect sizes were calculated with Cohen’s d. Statistical comparisons were computed on log-transformed errors, because the distributions are approximately log-normal.

Spectral parameterization was first compared to the aperiodic fit as performed using the BOSC method⁴⁷, which is a linear fit of the log-log power spectrum (Extended Data Fig. 5A–C). For these measures, power spectra were directly simulated, with parameters sampled as previously described. We also compared measurements of aperiodic fitting to IRASA⁴⁸ (Extended Data Fig. 5D–F). Since IRASA operates on time series, simulated data in this case were created as time series, as previously described, creating 10-second signals with a sampling rate of 1000 Hz. Aperiodic time series with a knee were created using a previously described physiological time series model¹⁹. Periodic and aperiodic parameters were sampled as previously described, except for the knee time series, for which the aperiodic exponent is always 2, due to the time series model. IRASA decomposition was applied directly to the simulated time series. Spectral parameterization was applied to power spectra computed from the simulated time series, using Welch’s method (1 second segments, 50% overlap, Hanning window). Finally, as an example real data case, we used an example real data spectrum of LFP data from rat hippocampus, available from the openly available HC-2 database⁵⁵, to which spectral parameterization and IRASA were applied (Extended Data Fig. 5G–I).

Human labelers versus algorithm

In addition to simulated power spectra, randomly selected EEG (n = 64) and LFP (n = 42) PSDs were labeled by the algorithm and by expert human raters (n = 9). PSDs were calculated using Welch’s method⁵¹ (1 second segments, 50% overlap, Hanning window). These PSDs were then fit and labeled from 2 to 40 Hz. Note that human labeling was done only for the center frequencies of putative oscillations on the PSDs that had the aperiodic component still present, as this is the most common human PSD parameterization approach. This misses all other features that the algorithm can also parameterize (power, bandwidth, offset, and exponent). Raters gave a high/low confidence rating to their labels, to provide a human analog for overfitting, and all plots and analyses use only results from the high-confidence ratings (including low-confidence ratings significantly impairs human label performance). Comparisons of the average number of peaks fit to each spectrum were done using independent-samples t-tests, where for each spectrum we counted the number of peaks identified by the algorithm, and compared that number across all spectra to the average number of peaks the human raters found per spectrum.

In order to estimate a putative “truth” for real physiological data where ground truth is unknown, we used a majority rule approach wherein a “consensus truth” criterion was calculated for each PSD separately by estimating the majority consensus for each identified peak. Specifically, for each PSD, all peaks identified by every human labeler were pooled, and the frequency of identification was established for each peak. Those peaks that were identified by the majority of labelers (n > 4) within 1.0 Hz of one another were set as the putative truth for that PSD. All human labelers, and the algorithm, were then scored against this putative truth. Precision, recall, and F₁ scores for human raters and the algorithm were calculated for each rater across all PSDs. Accuracy measures were then averaged across human labelers and compared the those of the algorithm. Normally, precision is calculated as the number of true positives divided by the total of true positives and false positives. However, because ground truth is unknown, “true positive” and “false positive” here are defined relative to the consensus truth. Similarly, recall is calculated as the number of true positives divided by the total of true positives and false negatives. The F₁ score is a weighted measure of accuracy that combines precision and recall. This metric is used because precision can be artificially very high while recall is very low; for example, it is possible to inflate precision by simply identifying a peak at every point along the frequency axis, thus no peaks would ever be missed, but recall would be severely impacted. If no peaks were found, precision and recall were all set to 0. Correct rejections were not included in performance estimates; had they been included, every non-peak that was correctly identified as such (most of the power spectra) would be marked as a correct rejection, skewing performance results. For those instances when a human labeler or the algorithm identified no peaks in the PSD, precision and recall values were set to 0 if the putative truth contained any peaks, and to 1 if there was no consensus among human labelers on any of the peaks (i.e., the putative truth criterion was 0 peaks). Thus, the majority rule scoring system did not penalize either human labelers or the algorithm for correctly rejecting false positives. All reported p values are Bonferroni corrected for the three correlated comparisons (precision, recall, and F₁) performed for each modality (EEG and LFP). Comparisons of these measures across PSDs were assessed using the z-score, where the algorithm’s precision, recall, and F1 scores were compared to the distribution of the raters’ scores. For the Spearman correlation, rater precision and recall on both EEG and LFP data were included.

Algorithmic analysis of EEG, LFP, and MEG data

Analyzed data are from openly available and previously reported datasets. Samples sizes were determined by the size of available datasets, without using power analyses, but our sample sizes are similar to those reported in previous publications for the EEG^18,33,56, LFP^57,58, and MEG^31,34,36 datasets. In the analyzed datasets, there were no experimentally defined groups requiring assignment, and thus no randomization or blinding procedures were used. Where relevant, analyzed distributions were tested for normality, to test validity of the applied statistical tests, and full distributions of data are also shown.

Scalp EEG data.

Electroencephalography (EEG) data from a previously described study³³ were re-analyzed here. Briefly, we collected 64-channel scalp EEG from 17 younger (20–30 years old) and 14 older (60–70 years old) participants while they performed a visual working memory task as well as a resting state period. All participants gave informed consent approved by the University of California, Berkeley Committee on Human Research. Participants were tested in a sound-attenuated EEG recording room using a 64+8 channel BioSemi ActiveTwo system. EEG data were amplified (−3dB at ~819 Hz analog low-pass, DC coupled), digitized (1024 Hz), and stored for offline analysis. Horizontal eye movements (HEOG) were recorded at both external canthi; vertical eye movements (VEOG) were monitored with a left inferior eye electrode and superior eye or fronto-polar electrode. All data were referenced offline to an average reference. All EEG data were processed with the MNE Python toolbox⁵⁹, the algorithm described herein, and custom scripts. These data have previously been reported³³, though all analyses presented here are novel using our new algorithmic approach.

EEG task and stimuli.

Participants performed a visual working memory task. They were instructed to maintain central fixation and asked to respond using the index finger of their right hand. The visual working memory paradigm was slightly modified from the procedures used in Vogel and Machizawa (2004)⁵⁶ as previously outlined⁶⁰, where additional task details can be found. Participants were visually presented with a constant fixation cross in the center of the screen throughout the entire duration of the experiment. At the beginning of each trial, this cross would flash to signal the beginning of the trial. This was followed 350 ms later by one, two, or three (corresponding to the load level) differently colored squares for 180 ms, lateralized to either the left or right visual hemifield. After a 900 ms delay, a test array of the same number of colored squares appeared in the same spatial location. Participants were instructed to respond with a button press to indicate whether or not one item in the test array had changed color compared to the initial memory array. Each participant performed 8 blocks of 40 trials each, with trials presented in random order in terms of side and load.

EEG behavioral data analysis.

Behavioral accuracy was assessed using a d’ measure of sensitivity which takes into account the false alarm rate to correct for response bias (d’ = Z(hit rate)-Z(false alarm rate)). To avoid mathematical constraints in the calculation of d’, we applied a standard correction procedure, wherein, for any participants with a 100% hit rate or 0% false alarm rate, performance was adjusted such that 1/(2N) false alarms were added or 1/(2N) hits subtracted where necessary.

EEG Pre-processing.

Each participant’s EEG data were first filtered with a highpass filter at 1 Hz, and then decomposed using ICA⁶¹. Any ICA components that significantly correlated with HEOG and/or VEOG activity were automatically identified and rejected. A two-minute segment of data from the beginning of the recording was extracted and analyzed as resting state data. Trials were epoched from −0.85 to 1.10 seconds relative to stimulus onset. All incorrect trials and trials with artifacts were excluded from subsequent analysis. The AutoReject procedure was used to estimate thresholds and automatically reject any trials with artifacts, as well as to interpolate bad channels⁶².

EEG resting state data analysis.

Power spectra were calculated for all channels, using Welch’s method⁵¹ (2 second windows, 50% overlap),, for a two-minute segment of extracted resting state data from the beginning of the recording. These power spectra were fit using the algorithm, using the settings {peak_width_limits=[1,6], max_n_peaks=6, min_peak_height=0.05, peak_threshold=1.5, aperiodic_mode=‘fixed’}. The average R² of spectral fits was 0.96, reflecting good fits, though one participant from the younger group was considered an outlier, with R² and absolute error of the fit more than 2.5 standard deviations away from the mean; this participant was dropped from further analyses in the resting condition. Estimated periodic spectral parameters were analyzed from a posterior channel of interest, Oz, chosen to capture visual cortical alpha activity. Aperiodic parameters were analyzed from channel Cz.

T-tests were performed to evaluate differences between age groups. For visualization purposes, periodic and/or aperiodic components were reconstructed for each participant’s fitted parameters. To explore if aperiodic differences could drive frequency-specific power differences, t-tests were run at each frequency, comparing between younger and older adult group, for the power values from the reconstructed aperiodic-only signal. To compare participant-specific fits to canonical band analyses, the overlap of a Gaussian centered at 10 Hz with a +/−2 Hz bandwidth (reflecting the common 8–12 Hz alpha range) was calculated with the individualized center frequency per participant, using a fixed +/−2 Hz bandwidth range. All t-tests are two-tailed.

EEG task data analysis.

For task analyses, data were analyzed from visual cortical alpha electrodes contralateral to the hemifield of visual stimulus presentation (right hemifield stimuli: {P3, P5, P7, P9, PO3, PO7, O1}; left hemifield stimuli: {P4, P6, P8, P10, PO4, PO8, O2}). Only correct trials were analyzed, and trials were collapsed across presentation side. Trials were split up into the three segments of interest: baseline [−0.85 to −0.35 sec], early trial segment [0.10 to 0.60 sec], and late trial segment [0.50 to 1.00 sec].

For spectral parameterization analyses, PSDs were calculated across each segment, for each channel, and spectra were fit, using the same settings as the rest data. Fitted parameters were then averaged across channels, to arrive at one set of parameters per trial, per participant. For comparison, two canonical alpha band analyses were run, one in which trial data were filtered to the alpha range (8–12 Hz), and another in which the data were filtered +/− 2 Hz around an individualized alpha center frequency⁶³, identified as the frequency of peak power between the range 7–14 Hz. These filtered copies of the data were then epoched and Hilbert transformed to calculate analytic alpha amplitude. Average analytic alpha was calculated across each time segment. Evoked measures of each parameter (i.e., canonical alpha, aperiodic-adjusted alpha power, and aperiodic offset and exponent) were calculated, in which the value of the parameter in the late trial was baseline-corrected by the measure of the parameter from the pre-trial baseline period for each investigated parameter.

To investigate which estimation technique (canonical band estimation vs. spectral parameterization) and which spectral parameter(s) best predicted behavior, regression models were used to predict d’, per load, from canonical or spectral parameterization output measures, separately for each age group. We used a baseline behavioral model, predicting d’ from the memory load (the number of presented items in the trial), and all models also used load as a covariate. To compare which features best predicted behavior, we predicted separate models, using 1) canonical alpha, 2) canonical alpha measured at an individualized frequency, 3) parameterized alpha, 4) parameterized aperiodic features. These models are described as:

$$d^{\mathrm{\text{'}}}=b_0+b_1\left(load\right)+\mathrm{ }\epsilon \text{ baseline model}$$

$$d\mathrm{\text{'}}={b_0+b}_1\left(load\right)+b_2\left({\alpha }_{pw\left(c\right)}\right)+\mathrm{ }\epsilon \text{ canonical alpha model}$$

$$d\mathrm{\text{'}}={b_0+b}_1\left(load\right)+b_2\left({\alpha }_{pw\left(cif\right)}\right)+\mathrm{ }\epsilon \text{ individualized canonical alpha model}$$

$$d\mathrm{\text{'}}={b_0+b}_1\left(load\right)+b_2\left({\alpha }_{pw\left(p\right)}\right)+\mathrm{ }\epsilon \text{ parameterized alpha model}$$

$$d\mathrm{\text{'}}={b_0+b}_1\left(load\right)+b_2\left({ap}_{exp}\right)+b3\left({ap}_{off}\right)+\mathrm{ }\epsilon \text{ aperiodic model}$$

In the above, ${\alpha }_{pw}$ represents alpha power, and c, icf, p represent ‘canonical’, ‘canonical with individualized frequency’, and ‘parameterized’, respectively, and $ap$ represents aperiodic, with exp and off denoting exponent and offset respectively. All models were fit as ordinary least squares linear models. Model fitting and comparisons were done using the statsmodels module in Python. The F-test for overall significance of the model was used to evaluate whether each model provided a significant fit.

LFP data.

LFP data used for algorithm validation came from two male rhesus monkeys (Maccaca mulatta) 4 to 5 years of age, collected for a previously reported experiment (methodological details can be found in the corresponding manuscript⁵⁷). All procedures were carried out in accord with the US National Institutes of Health guidelines and the recommendations of the University of California, Berkeley Animal Care and Use Committee. Neuronal responses were recorded from PFC using arrays of 8–32 tungsten microelectrodes. Local field potentials were recorded with a 1 kHz sampling frequency and analyzed offline. LFP were isolated from the band-passed (0–100 Hz) recordings, and spectral fits were done on a channel-by-channel basis using Welch’s method and the same settings used for the EEG analyses described above.

MEG data.

Open-access resting-state MEG data, as well as corresponding T1-weighted MRIs for each participant, were accessed from the young adult dataset from the Human Connectome Project (HCP) database⁶⁴. Briefly, a subset of 95 participants from the HCP had MEG recordings. Of this group, 80 participants met our quality control procedures and were included in the analyses here (ages 22–35; 35 female). Participants were excluded due to missing resting state recordings, missing anatomical scans needed for source projection, or due to excessive artifacts. One participant was rejected post fitting due to being an outlier on goodness-of-fit and/or aperiodic parameters (more than 3 standard deviations from the group mean). For each participant, the first available rest recording was used, comprising approximately 6 minutes of eyes open, resting state data. Full details of the data collection are available elsewhere⁶⁵.

MEG data were pre-processed following best-practice guidelines⁶⁶, using the Brainstorm software toolbox⁶⁷. Cardiac and eye related artifacts (blinks and saccades) were automatically detected from ECG and EOG traces respectively and removed from the data using signal-space projections (SSP) from data segments selected from around each artifactual event⁶⁸ using default parameters in Brainstorm. All MEG data were manually inspected for any remaining artifacts, and any contaminated segments were marked as bad, and not included in any further analysis. Cleaned, pre-processed resting state data were then epoched into 5 second segments.

Using the segmentation procedures available in Freesurfer⁶⁹, each participants’ T1-weighted anatomical MRI scan was used to construct scalp and cortical surfaces. Individual high-resolution surfaces were downsampled to 7501 vertices using Brainstorm to serve as cortical reconstructions for MEG source imaging. Structural MRI images were co-registered with the MEG recordings using anatomical landmarks (nasion, and pre-auricular points) and digitized head points available from the recording, which were automatically aligned in Brainstorm, and then manually checked and tuned, as needed.

For source-projection, the overlapping-sphere technique⁷⁰ for forward modeling of the neural magnetic fields was used, using perpendicularly oriented current dipoles for each individual’s anatomy⁷¹. Source projections were calculated using Brainstorm’s weighted minimum norm estimate (wMNE) applied to the preprocessed sensor data. Empty room recordings, also available from the HCP, were used as an empirical estimate of the noise for each MEG sensor, in the wMNE projection. For group analysis, individual source maps were then geometrically registered to the ICBM152 brain template, a non-linear average of 152 participants⁷², using Brainstorm’s multilinear registration technique.

For each epoch, a PSD was estimated using an adapted version of Welch’s method, which averaged across the individual FFTs using the median⁷³, as opposed to the mean, in order to deal with the skewed nature of power value distributions⁷³, using a window size of 2 seconds. For each participant, at every vertex, a PSD was calculated from source-projected data, on the group template brain. Power values were then averaged across all available epochs to obtain one PSD per vertex, per individual.

Following pre-processing, source projection, and spectral analysis, we had PSD representations of resting state activity at each of 7501 vertices for each of the 80 participants, projected on a template brain. Each of these spectra were then fit across the frequency range [2, 40], with settings {peak_width_limits=[1,6], max_n_peaks=6, min_peak_height=0.1, peak_threshold=2, aperiodic_mode=‘fixed’}, providing an aperiodic exponent and offset value per vertex as well as a list of extracted peaks (if found) per vertex, per participant. In rare cases, the algorithm can fail to converge on a solution and thus does not provide a fit. This was the case for a total of 4 spectra out of 600,080. For any spectrum for which this happened, that vertex for that participant was set as having no detected peaks, and the aperiodic exponent was interpolated as the mean value of all successful fits from that participant.

To analyze and visualize the putative oscillation results, all extracted peaks were post hoc sorted into pre-defined oscillation bands of theta (3–7 Hz), alpha (7–14 Hz), and beta (15–30 Hz). These ranges were chosen to capture the approximate clusters of peaks in the extracted data (see Fig. 7B). To do so, per vertex and per participant, peak output parameters were selected, for each band, if they corresponded to a peak with a center frequency within the band limits. If there was no peak within that range, that vertex was set as having no oscillation in that band. If more than one peak was found for the given range, the highest power peak was selected. From this band-specific data, we then created group maps for each oscillation band across all vertices. For each band we extract two maps: an oscillation power map as well as an oscillation probability map, which is the percent of the group that had a peak within that band at that vertex.

We then calculated a power-normalized “oscillation score”. To do so, for each band, the average peak power value at each vertex, across all participants, was divided by the maximum average power value from the distribution of all vertices, such that the vertex that displays the highest band power across the group receives a score of 1, and every other vertex receives a normalized score between 0 and 1. This power ratio was then multiplied, vertex-by-vertex, with the oscillation probability topography. The resultant oscillation score is a bounded measure that can take values between 0 and 1, whereby a maximal score of 1 reflects that every participant has an oscillation in the specified band at the specified vertex, and that oscillation has the greatest average power at that vertex. Scores lower than 1 reflect increased variation in the presence and/or relative power of oscillations across the group.

Note that oscillation scores lower than 1 cannot, by themselves, be disambiguated in terms of where the variability lies. For example, an oscillation score of approximately 0.5 could reflect either a location in which oscillations tend to be of maximal power, but are only observed across approximately half the group, or oscillations that are consistent across the entire group, at about half the maximal power, or some middle ground between the two. These situations can be disambiguated by examining both the oscillation probability and power ratio maps separately. We then calculated the Pearson correlation between the topographies of oscillation scores for each band as well as the correlation between each band’s oscillation score and the aperiodic exponent topography.

Reporting Summary.

Further information on the research design and methods is available in the Life Sciences Reporting Summary.

Data Availability Statement

All empirical behavioral and physiological data reported and analyzed in this manuscript are secondary uses of data that has previously been published and/or was accessed from openly available data repositories.

Simulated Data.

A copy of the simulated data, as well as the code to regenerate it, is available in the GitHub repository: https://github.com/TomDonoghue/SimParam

EEG Data.

Data was analyzed from a previously described study³³

MEG Data.

Open-access MEG data was analyzed from the Human-Connectome Project^64,65, which is described on the project site (https://www.humanconnectome.org/), and available through the data portal (https://db.humanconnectome.org/).

LFP Data.

Local field potential data was analyzed from rhesus monkey from a previously described study⁵⁷. Additional LFP data from rats was accessed from the HC-2 dataset⁵⁵, which is available from the ‘Collaborative Research in Computational Neuroscience (CRCNS) data sharing portal (https://crcns.org/).

Code Availability Statement

Custom code used in this manuscript is predominantly using the Python programming language, version 3.7. In addition, some pre-processing of MEG data was done in Matlab (R2017a), using the Brainstorm package (https://neuroimage.usc.edu/brainstorm/).

Algorithm Code.

The algorithm code is openly available and released under the Apache 2.0 open-source software license. The code for the algorithm is available on GitHub (https://github.com/specparam-tools/specparam), and from PyPi (https://pypi.org/project/specparam/), and includes a dedicated documentation site (https://specparam-tools.github.io/).

Analysis Code.

All the code used for the analyses is openly available, and indexed on Github (https://github.com/specparam-tools/Paper). This includes all the code used for the simulations (https://github.com/TomDonoghue/SimParam), the EEG analyses (https://github.com/TomDonoghue/EEGParam) and for the MEG analyses (https://github.com/TomDonoghue/MEGParam).

SUPPLEMENTARY MODELING NOTE

Algorithm comparison against other approaches

A key focus of the proposed algorithm has been to contextualize it in relation to approaches and standard methods that are typically used within research on oscillations. There are also other methods that do consider aperiodic neural activity, such as BOSC⁴⁷ and IRASA⁴⁸. They do so, however, in ways that differ substantially from spectral parameterization, rendering it difficult to employ direct comparisons between the different methods. Overall, one of the key differences between them and the method proposed here is that it considers the aperiodic activity to be a signal that should be directly parameterized, while most other approaches treat it as a nuisance variable²⁵ and/or have different conceptions and goals with respect to the data. In this section, related methods, focusing on IRASA and BOSC, are discussed and compared, including descriptions of the differences between these methods.

First, a brief summary of how each method differs in their conceptual approach:

Spectral Parameterization, as proposed, is a model fitting method.

A mathematical model is used to parameterize periodic and aperiodic activity. It is applied to the frequency domain, and returns parameter estimates for all fitted components.

BOSC estimates relative oscillatory power.

BOSC is applied to, and analyzed in, the time domain, measuring occurrence and relative power of rhythms, using a threshold computed from a linear aperiodic fit applied in the spectral domain. This method measures adjusted power of oscillations, in the time domain, but does not explicitly parameterize periodic or aperiodic activity.

IRASA is a decomposition method.

IRASA decomposes self-similar from non-self-similar activity. It is applied to the time domain, and returns decompositions of the data in the frequency domain. The IRASA method does not parameterize components, though it is typically used in conjunction with a linear fitting procedure of the log-log spectrum.

Overall, these methods are different in their goals, applications, and assumptions, and this complicates simple, direct comparisons. However, because each of these methods employs a measure of aperiodic activity, accuracy for fitting the aperiodic component can be directly compared in simulated data (Extended Data Fig. 5). Notably, as discussed here, a key difference between the methods is the conceptual model embodied and employed by each of these methods.

BOSC.

Though related, the design, goals, and outputs of the BOSC method are quite different from spectral parameterization, and BOSC does not return measures that are directly comparable to the majority of the parameters fit by the proposed algorithm. BOSC is designed to compute aperiodic-adjusted oscillatory power in the time domain. To do so, it applies a linear fit to the log-log power spectrum to learn a threshold value, that is then applied in the time-domain, to compute oscillatory power over the threshold. Simulated power spectra were used to compare median absolute error (MAE) between spectral parameterization (param) and the linear log-log fits (linear), as used in BOSC (Extended Data Fig. 5A–C). Spectral parameterization outperforms the default linear aperiodic fit in BOSC, across all tested situations (see Methods) including a low frequency range with one peak (MAE_param=0.003, MAE_linear=0.045; t₉₉₉=53.86, p=1.1×10⁻²⁹⁷; Cohen’s d=1.58) a low frequency range with multiple peaks (MAE_param=0.026, MAE_linear=0.102; t₉₉₉=37.22, p<6.7×10⁻¹⁹¹; Cohen’s d=0.95) and a high frequency range with two peaks and an aperiodic knee (MAE_param=0.006, MAE_linear=0.377; t₉₉₉=62.47, p=0.0; Cohen’s d=2.30). Overall, the linear fitting approach for aperiodic activity used by BOSC is significantly biased by oscillatory peaks, and also does not consider, or deal with, multi-fractal data, such as knees, and is outperformed by spectral parameterization.

However, the overall goal of BOSC is not to parameterize aperiodic activity, and the aperiodic fit it uses is not intended as an optimized measure of aperiodic activity, but rather as a heuristic fit for its main goal of computing a relative measure of oscillatory power. Since BOSC operates on the time domain, it does not parameterize oscillations in the same was as spectral parameterization, and the periodic measures it returns are not directly comparable to anything measured and returned by the spectral parameterization algorithm. BOSC also implicitly uses a particular model of aperiodic activity: fitting a linear fit to the log-log spectrum, which is equivalent to the ‘fixed’ aperiodic mode (though it is not fit in the same way). This is a limited model that does not generalize to properties seen in neural data, such as aperiodic knees. Using this particular aperiodic model is not a requirement of the BOSC method, per se, and so an interesting topic for future work could be to integrate the BOSC time-domain approach with different models and approaches for spectral fitting, such as allowed for by the proposed algorithm.

IRASA.

IRASA is a decomposition technique that separates putative components of the data. Technically, it separates fractal (self-similar) activity from non-self-similar activity, with the goal of disentangling oscillations from true 1/f^χ activity. The resampling procedure it employs makes assumptions about the nature of the aperiodic activity, specifically that it is self-similar. This is consistent with true 1/f activity – however, it does not readily extend to the cases often observed in neural data, in which there is a ‘knee’ in the aperiodic component of the data. These ‘knees’ in the data are described in the original IRASA paper⁴⁸ as ‘multi-fractal breakpoints’, and it was noted that the IRASA method blurs these breakpoints. Relatedly, IRASA, as predominantly a decomposition technique, does not propose a model for parameterizing the separated components. It is typically used with a linear fit applied to the estimated 1/f^χ component, after IRASA has been used to try and remove the non-self-similar features (putative oscillations). This is equivalent to our ‘fixed’ (no knee) model. Notably, IRASA does not (without additional developments) parameterize periodic components, and so there are no direct comparisons available for this aspect of our fitting approach, nor does it generalize to other observed forms of the aperiodic component.

Spectral parameterization, as proposed here, does not make as strict assumptions about the nature of the aperiodic activity. Rather it simply tries to find the best fit to the oscillation-removed aperiodic component, applying the selected aperiodic fit function, without requiring the same assumptions of overall self-similarity. These differences in the applications and models between our approach and IRASA limit the range of direct comparisons that can be made. IRASA also operates on time domain data, which is different from spectral parameterization. Therefore, for comparisons, plausible time series were simulated with known aperiodic components (such as was done for the comparisons in Extended Data Fig. 3G–I). IRASA was applied to the simulated time domain data and compared to spectral parameterization applied to power spectra computed from the simulated time series (Extended Data Fig. 5A–C). Note that IRASA does not explicitly parameterize the resulting aperiodic component, so an extra parameterization step must be taken to compare approaches. For the low frequency range, with one or multiple peaks, the common linear fit that is typically used with IRASA was applied. In the data with one simulated oscillation, the two methods perform comparably (MAE_param=0.053, MAE_irasa=0.060; t₉₉₉=0.75, p<0.45; Cohen’s d=0.03). In the case of multiple peaks, spectral parameterization has a modest performance benefit (MAE_param=0.052, MAE_irasa =0.068; t₉₉₉=5.52, p<4.3×10⁻⁸; Cohen’s d=0.23).

Additionally, time series data with a knee were simulated using a physiological time series model¹⁹. For this case, the typical linear fit that is often used with IRASA is ill-posed for the nature of the aperiodic component, and as expected, performs very poorly (MAE_irasa=0.67). This is due to a model mismatch, however IRASA does not propose any general model for parameterizing the aperiodic component. For a fairer comparison, the IRASA-derived aperiodic component was fit with the knee model definition proposed here. Note that this approach is something of a hybrid, as it relies on the spectral parameterization model to give a good parameterization of the IRASA results, but is the clearest way to compare across methods in this case. In data with an aperiodic knee, spectral parameterization outperforms the IRASA decomposition (MAE_param=0.063, MAE_irasa=0.090; t₉₉₉=8.45, p<9.7×10⁻¹⁷; Cohen’s d=0.35). In addition, the way that IRASA distorts aperiodic components with knees creates a systematic bias in the measured aperiodic parameters. In the simulated data, which has a true exponent value of 2, the median estimated exponent using IRASA is 1.91, as compared to 1.97 using spectral parameterization. This reflects a systematic bias in the direction of the errors due to the distortion from the IRASA method when applied to data that is not strictly self-similar.

These differences between the methods can also be visualized using a real data example, demonstrating that these limitations do have practical relevance. As an illustrative example, rodent hippocampal data is shown, demonstrating a case in which there is a prominent theta oscillation, its harmonic, and a knee in the aperiodic component (Extended Data Fig. 5G–I). IRASA, at default settings, has difficulty separating out the large peaks, leaving non-aperiodic activity in the decomposed aperiodic component (Extended Data Fig. 5G). These larger peaks can be increasingly removed by increasing the amount of resampling, however, this additional resampling further blurs the aperiodic activity that IRASA separates, due to the knee (Extended Data Fig. 5H). By comparison, the periodic-removed component from our proposed algorithm can simultaneously address large peaks and variable model forms of the aperiodic component (Extended Data Fig. 5I). Overall, IRASA performs well in some contexts, and is a useful and interesting decomposition approach, however a key issue is that the resampling procedure of IRASA assumes the precise fractal nature of aperiodic activity, which does not generalize to common use cases in real neural data.

Extended Data

Extended Data Figure 1 |. False oscillatory power changes and illusory oscillations.

(A) Here we took a real neural PSD (blue) and artificially introduced a change in the aperiodic exponent, similar to what is seen in healthy aging¹⁸. This PSD was then inverted back to the time domain (right panels). The exponent change manifests as amplitude differences in the time domain. This affects apparent narrowband power when an a priori filter is applied. This is despite the fact that the true oscillatory power relative to the aperiodic component is unaffected. (B) Even when no oscillation is present, such as the case with the white and pink (1/f) noise examples here (blue and green, respectively), narrowband filtering gives rise to illusory oscillations where no periodic feature exists in the actual signal, by definition.

Extended Data Figure 2 |. Algorithm performance on simulated data across a broader frequency range.

(A-C) Power spectra were simulated across the frequency range (1–100 Hz), with two peaks, one in a low range, and one in a high range (see Methods), across five distinct noise levels (1000 spectra per noise level). (A) Example power spectra with simulation parameters as aperiodic [offset, knee, exponent] and periodic [center frequency, power, bandwidth] (B) Absolute error of algorithmically identified peak center frequency, separated for the low (3–35 Hz) and high range (50–90 Hz) peaks. (C) Absolute error of algorithmically identified aperiodic parameters, offset, knee, and exponent. All violin plots show full distributions, where small white dots represent median values and small box plots show median, first and third quartiles, and ranges. Note that the error axis is log-scaled in B,C.

Extended Data Figure 3 |. Algorithm performance on simulated data that violate model assumptions.

(A-C) Power spectra were simulated across a broader frequency range (1–100 Hz), with two peaks, one in a low range, and one in a high range (see Methods), across five distinct knees values (1000 spectra per knee value), with a fixed noise level (0.01). Power spectra were parameterized in the ‘fixed’ aperiodic mode (without a knee) to evaluate how sensitive performance is to aperiodic mode. (A) Example power spectra with simulation parameters as aperiodic [offset, knee, exponent] and periodic [center frequency, power, bandwidth], showing spectra with knee values of 0 and 150, both fit in the ‘fixed’ aperiodic mode. (B) Absolute error of algorithmically identified aperiodic exponent, across spectra with different knee values. Notably, exponent reconstruction is high when spectra with knees are fit without a knee parameter. (C) The number of peaks fit by the model, across knee values. Note that all spectra in this group have two peaks, indicating here that the presence of knee’s in ‘fixed’ mode leads to overfitting peaks. (D-F) A distinct set of simulations were created in which power spectra were created with asymmetric or skewed peaks (see Methods), across five distinct skew levels (1000 spectra per skew level). (D) Example simulated spectra, showing two different skew levels. (E) Absolute error of algorithmically identified peak center frequency, across peak skewness values. (F) The number of peaks fit by the model, across peak skewness. Note that all spectra in this set have one peak. (G-I) A distinct set of simulations, in which time series were generated with asymmetric oscillations in the time domain, from which power spectra were calculated (see Methods), across five distinct levels of oscillation asymmetry (1000 spectra per asymmetry value). (G) Example simulation of an asymmetric oscillation, simulated in the time domain, and the associated power spectrum. Note that the power spectrum displays harmonic peaks. (H) Absolute error of algorithmically identified peak center frequency, across oscillation asymmetry values. (I) The number of peaks fit by the model, compared across oscillation asymmetry values. Note that these simulations all contained one oscillation in the time domain. All violin plots show full distributions, where small white dots represent median values and small box plots show median, first and third quartiles, and ranges. Note that the error axis is log-scaled in B,E,H.

Extended Data Figure 4 |. Oscillation band occurrences and relative powers in the MEG dataset.

(A) The proportion of participants for whom an oscillation peak was fit, at each vertex, per band. (B) The group level relative power, per band. For each participant, the oscillation power within the band was normalized between 0 and 1, and then averaged across all participants, such that a maximal relative power of 1 would indicate that all participants have the same location of maximal band-specific power. Note that alpha and beta have maximal values approaching 1, reflecting a high level of consistency in location of maximal power, whereas in theta the values are lower, reflecting more variability. The “oscillation score” metric, as presented in Fig. 7, is the result of multiplying the occurrence probability map with the power maps.

Extended Data Figure 5 |. Methods comparison of measures of the aperiodic exponent.

(A-C) Comparisons of spectral parameterization to a linear fit (in log-log space), as used in BOSC⁴⁷, on simulated power spectra (1000 per comparison). (A) Comparison of a linear fit and spectral parameterization on a low frequency range (2–40 Hz) with one peak. (B) Comparison across the same range with multiple (3) peaks (C) Comparison across a broader frequency range (1–150 Hz) with two peaks and an aperiodic knee. In all cases (A-C), spectral parameterization outperforms the linear fit. (D-F) Comparisons of spectral parameterization to IRASA⁴⁸. Groups of simulations mirror those used in (A-C). Note that for these simulations, the data were simulated as time series (1000 per comparison) (see Methods). IRASA and spectral parameterization are comparable for the one peak cases (D), but spectral parameterization is significantly better in the other cases (E,F). Note that as IRASA has both greater absolute error and a systematic estimation bias (see Supplemental Modeling Note). (G-I) Example of IRASA and spectral parameterization applied to real data. (G) The IRASA-decomposed aperiodic component, using default settings, in orange, is compared to the original spectrum, in blue. There are still visible non-aperiodic peaks, meaning IRASA did not fully separate out the periodic and aperiodic components. (H) The IRASA-decomposed aperiodic component, with increased resampling. This helps remove the peaks, but also increasingly distorts the aperiodic component, especially at the higher frequencies, due to its multi-fractal properties (the presence of a knee). (I) The isolated aperiodic component from spectral parameterization (computed as the peak-removed spectrum), showing parameterization can account for concomitant large peaks and knees, providing a better fit to the data. All violin plots show full distributions, where small white dots represent median values and small box plots show median, first and third quartiles, and ranges. Note that the error axis is log scaled in (A-F). * indicates a significant difference in between the distributions of errors between methods (paired samples t-tests). Discussion of these methods and results are reported in the Supplemental Modeling Note.