Evaluating medical capacity for hospitalization and intensive care unit of COVID-19: A queue model approach

Abstract

Background

The surge of COVID-19 pandemic has caused severe respiratory conditions and a large number of deaths due to the shortage of intensive care unit (ICU) in many countries.

Methods

We developed a compartment queue model to describe the process from case confirmation, home-based isolation, hospitalization, ICU, recovery, and death. By using public assessed data in Lombardy, Italy, we estimated two congestion indices for isolation wards and ICU. The excess ICU needs were estimated in Lombardy, Italy, and other countries when data were available, including France, Spain, Belgium, New York State in the USA, South Korea, and Japan.

Results

In Lombardy, Italy, the congestion of isolation beds had increased from 2.2 to the peak of 6.0 in March and started to decline to 3.9 as of 9^th May, whereas the demand for ICU during the same period has not decreased yet with an increasing trend from 2.9 to 8.0. The results showed the unmet ICU need from the second week in March as of 9^th May. The same situation was shown in France, Spain, Belgium, and New York State, USA but not for South Korea and Japan. The results with data until December 2020 for Lombardy, Italy were also estimated to reflect the demand for hospitalization and ICU after the occurrence of viral variants.

Conclusion

Two congestion indices for isolation wards and ICU beds using open assessed tabulated data with a compartment queue model underpinning were developed to monitor the clinical capacity in hospitals in response to the COVID-19 pandemic.

Introduction

The outbreak of emerging infectious diseases could pose a great threat to challenge clinical capacity and medical resources when the first wave of infectiousness is not well controlled and the second or later waves of epidemic turn into a large-scale community outbreak. The novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), the virus that causes coronavirus disease 2019 (COVID-19), had caused 115 million confirmed cases and claimed more than 2.5 million lives as of 28 Feb. 2021.¹ It has been still affecting many countries even during the period of vaccination distribution. A lethal disease can not only result in a large number of casualties but also bring high demand for critical medical resources.

The influence of the latter is particularly critical in the early period of COVID-19 pandemic. As indicated in the accompanying article of this special issue, the COVID-19 outbreak had started as a local epidemic in Wu-Han in December 2019,² spread to South Korea, Iran, and Italy on 20 Feb. 2020 and subsequently expanded to Washington in the United States of America (USA) in mid-March 2020, the foci that caused further spread to their continents by the end of March 2020. Among the COVID-19 cases accumulated in the first two months in China, 5% were admitted to intensive care units (ICUs), 2.3% underwent invasive mechanical ventilation, and 1.4% had died.³ The fatality among confirmed cases raised to 6.9% globally (265861 deaths out of 3855809 confirmed cases) by 9 May 2020.¹ Grasselli et al. reported the emergency call for critical care utilization demand by mid-March in Lombardy region of Italy.⁴ High demand of mechanical ventilation (88%) and high fatality within one month (26%) among the Italian ICU admitted patients with COVID-19 in Lombardy region was reported.⁵ Therefore, it is necessary to develop a useful medical need index for the preparedness of critical medical equipment.

Owing to its high contagiousness, the number of confirmed cases increased dramatically in the first week of the epidemic in the community, leading to the shortage of respiratory equipment and ICUs in the origin countries of each continent, and even neighboring countries. It is of paramount importance to monitor the medical requirement for the COVID-19, including quarantine beds, and ICUs in hospitals, in order to avoid deaths of COVID-19. In this study, we aim to develop the medical need index to measure the congestion in hospitals with a compartment model, which is further decomposed into two queue models for hospitalization and ICU admission with data from countries, where open assessed daily reported data were available, such as Italy, South Korea, France, Japan, Belgium, Spain and New York State in the USA.

Materials and methods

The compartment queue model for clinical management of COVID-19 patients

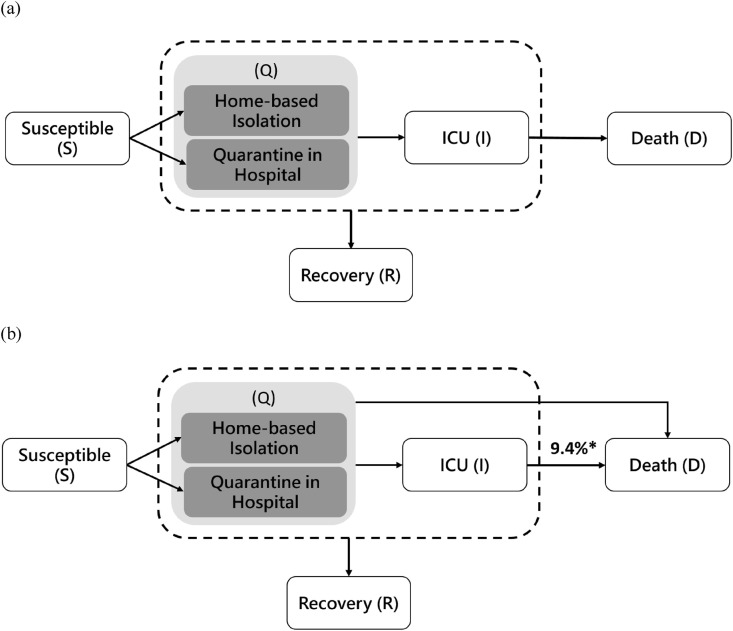
We developed a compartment queue model for the patient flow from the confirmation of COVID-19 case, self-quarantined and self-isolated, admission to hospitals, transferred to ICU, and discharge due to recovery or death for the clinical management of COVID-19 patients in response to pandemic resulting from SARS-CoV-2 infection (Fig. 1 -a). This model is composed of six compartments, including susceptible (S), self-quarantine and self-isolation at home (Q₁) and hospital (Q₂), ICU admission (I), recovery (R), and death (D), where Q₁, Q₂, and I are transient states, and D and R are two absorbing states. We assume that death is only through ICU. This model is applied to Lombardy region, Italy. For other countries, the two states of quarantine and isolation (Q₁ and Q₂) are combined into one state (Q) due to the limited data source.

Figure 1.

Clinical management model.

Design with the queue process for hospitalization and ICU

Given the built-in compartment model as mentioned above, we propose two queue processes, the arrival to and the departure from both hospitalization (Q₂) and ICU (I). Therefore, we also propose two traffic intensity ratios (TIRs) for evaluating the congestion of hospitalization and ICU. They are in a similar manner of traffic intensity of ratio of arrival to departure as in queue model as follows,

$$\text{The}\text{first}\text{TIR}\text{for}\text{hospitalization:}{\rho }_H=\frac{P_{SQ2}}{P_{Q2R}}$$

$$\text{The}\text{second}\text{TIR}\text{for}\text{ICU:}\frac{1}{{\rho }_I}=\frac{P_{ID}}{P_{Q2I}},$$

where P_SQ2 is the transition probability from S to Q₂ (the probability of being infected with SARS-CoV-2 and quarantined in hospital), P_Q2R is the transition probability from Q₂ to R (the recovery rate among hospitalization), P_Q2I is the transition probability from Q₂ to I (the probability of transferring to ICU from hospitalization state), and P_ID is the transition probability from I to D (the death rate among patients in ICU).

Note that, unlike the quarantine beds, we use the inverse traffic intensity for ICU because its destination is death, which means that the departure from ICU is a worse scenario. The higher the value of the TIR for hospitalization and ICU, the more demand is required to meet an increasing COVID-19 cases due to the spread of SARS-CoV-2 with which the region/country is faced.

Data sources

In order to assess the needs for isolation wards and ICU in this study, we searched for public available web-based sources on the utilization of ICU due to SARS-CoV-2 infection, and recruited data from Belgium, France, Japan, Lombardy in Italy, New York State in the USA, Spain, and South Korea as analytic data.6, 7, 8, 9, 10, 11 The majority of data source were derived from the official website from public health authority, such as Ministero della Salute, Italy, and Ministry of Health, Labor and Welfare, Japan. In particular, the region-specific data enables us to study the situation in Lombardy, Italy, where the first and worse region affected by COVID-19 in Italy. The reported data included daily counts of SARS-CoV-2 test and patients with COVID-19 in different status, including newly COVID-19 confirmed, home-based isolation, quarantine in hospital, ICU admission, recovery, and death. For countries other than Italy, data on home-based isolation and quarantine in hospitals were reported in the same category.

The study period started from the earliest date when data of ICU were available (17 Feb. 2020 for Japan, 22 Feb. 2020 for South Korea, 28 Feb. 2020 for France, 2 Mar. 2020 for Spain, 3 Mar. 2020 for Italy, 14 Mar. 2020 for Belgium, and 27 Mar. 2020 for the USA) until the end of data can be accessed (8 Dec. 2020 for Italy and 17 Apr. 2020 for the remaining countries). Although the starting date of study period was 31–49 days behind the first reported case in each country, the lag only consisted of first few cases which would not affect the urgent medical utilization that might cause medical system crushed. It should be noted that the classification of week in the following analysis is based on successive seven dates from the initial index date and is not exactly the same as that based on the calendar.

Statistical analysis

We assumed the departing probabilities from any given state in one day follow the multinomial distribution with the transition probabilities of disease progression (per day), $P_{ij}$, where $i,j\in \left\{S,Q_1,Q_2,I,D,R\right\}$, and used the Bayesian Markov Chain Monte Carlo algorithm to estimate the transition probabilities between each state. We started with non-informative prior in the beginning of each country and then applied the sequential Bayesian approach to the empirical data. This means that we used the posterior probability obtained in the previous week as the informative priors to form the posterior probability in conjunction with the likelihood formed by the data of the current week. The daily count of different compartments from open accessed data followed Poisson distribution, of which the mean was the abovementioned dynamic compartment size.

In order to estimate the extra needs for ICU, we applied the estimated P_ID from the first week, and calculated the expected number of death without being admitted to ICU (Fig. 1-b).

Results

Estimates of transition probabilities

Table 1 shows the estimated results of transition probabilities in Lombardy, Italy from 3 Mar. to 8 Dec. 2020. The odds of being quarantined in hospital for being infected with SARS-CoV-2 (P_SQ2) was dynamic and increased from 14.7% (95% CI = 12.6%–16.8%) in the first week to 20.2% (95% CI = 18.9%–21.5%) in the second week, and lasted around one month and then decreased to 9.7% (95% CI = 9.5%–9.9%) in the tenth week (3-9 May 2020). Note that this figure was lowest (0.1%, 95% CI = 0.1%–0.1%) during the Period II (1 Jul.-30 Sep. 2020), and increased slightly to 0.7% (95% CI = 0.7%–0.8%) during the Period III (1 Oct.-8 Dec. 2020). The recovery rate (P_Q2R) decreased with time from 6.7% (95% CI = 6.1%–7.4%) in the first week to 2.5% (95% CI = 2.4%–2.5%) in the seventh week and then remained stable. During the Period II (1 Jul.-30 Sep. 2020), it still showed 2.6% (95% CI = 2.6%–2.6%), but rose to 3.4% (95% CI = 3.3%–3.4%) during the Period III (1 Oct.-8 Dec. 2020). The probability of ICU (P_Q2I) transferred from hospitalization increased from 3.4% (95% CI = 2.2%–4.7%) in the first week, reached to the peak of 4.1% (95% CI = 3.5%–4.6%) in the second week and lasted for around one month and then fell to 3.4% (95% CI = 3.3%–3.5%) in the tenth week (3-9 May 2020). In both Period II (1 Jul.-30 Sep. 2020) and Period III (1 Oct.-8 Dec. 2020), the figures were still stable (3.2% and 3.1%, respectively). The death rate from ICU (P_ID) was the lowest (9.4%; 95% CI = 7.7%–11.4%) in the first week and rose dramatically to the maximum 30.4% (95% CI = 29.7%–31.2%) between the fourth and fifth week and then declined gradually to 27.0% (95% CI = 26.6%–27.4%) in the tenth week (3-9 May 2020) and sustained throughout the Period II (1 Jul.-30 Sep. 2020). After then, the death rate dropped to 24.7% (95% CI = 24.4%–25.0%) during the Period III (1 Oct.-8 Dec. 2020).

Table 1.

Estimated transition probability of clinical management model in Italy-Lombardy.

Date	Susceptible → Quarantine in Hospital (PSQ2)	Quarantine in Hospital → Recovery (PQ2R)	Quarantine in Hospital → ICU (PQ2I)	ICU → Death (PID)	TIR for hospitalization (${\rho }_H)$	TIR for ICU ($1/{\rho }_I)$	Predicted number of beds needed (per week)	Predicted number of ICU beds needed (per week)
Period I (3 Mar.-30 Jun. 2020)
3-7 Mar.	14.7% (12.6%,16.8%)	6.7% (6.1%,7.4%)	3.4% (2.2%,4.7%)	9.4% (7.7%,11.4%)	2.2 (1.9,2.6)	2.9 (1.9,4.3)	2289 (2251,2302)	469 (442,498)
8-14 Mar.	20.2% (18.9%,21.5%)	4.1% (3.9%,4.3%)	4.1% (3.5%,4.6%)	19.9% (18.6%,21.2%)	5.0 (4.6,5.4)	4.9 (4.4,5.6)	4715 (4674,4755)	887 (857,916)
15-21 Mar.	19.9% (19.0%,20.8%)	4.2% (4.1%,4.3%)	4.1% (3.8%,4.4%)	28.0% (27.0%,28.9%)	4.8 (4.5,5.0)	6.8 (6.4,7.3)	8072 (8024,8120)	1717 (1680,1754)
22-28 Mar.	20.2% (19.4%,21.1%)	3.6% (3.5%,3.6%)	4.0% (3.8%,4.2%)	30.4% (29.7%,31.2%)	5.7 (5.4,5.9)	7.6 (7.2,8.0)	11939 (11875,12008)	2330 (2291,2370)
29 Mar.-4 Apr.	19.4% (18.7%,20.0%)	3.2% (3.2%,3.3%)	3.9% (3.7%,4.0%)	30.3% (29.7%,30.9%)	6.0 (5.8,6.2)	7.9 (7.5,8.2)	12275 (12230,12325)	2375 (2345,2406)
5-11 Apr.	17.0% (16.5%,17.6%)	2.9% (2.8%,2.9%)	3.7% (3.6%,3.9%)	28.5% (28.0%,29.1%)	5.9 (5.7,6.1)	7.6 (7.4,7.9)	12688 (12640,12737)	2050 (2027,2075)
12-18 Apr.	14.2% (13.9%,14.6%)	2.5% (2.4%,2.5%)	3.6% (3.5%,3.7%)	27.7% (27.2%,28.1%)	5.8 (5.6,6.0)	7.8 (7.5,8.0)	11529 (11487,11573)	1651 (1634,1667)
19-25 Apr.	12.3% (12.0%,12.6%)	2.4% (2.4%,2.5%)	3.5% (3.4%,3.6%)	27.3% (26.9%,27.7%)	5.0 (4.9,5.2)	7.9 (7.6,8.1)	9695 (9660,9730)	1287 (1274,1299)
26 Apr.-2 May	10.6% (10.4%,10.8%)	2.2% (2.2%,2.2%)	3.5% (3.4%,3.5%)	27.1% (26.7%,27.5%)	4.8 (4.7,5.0)	7.8 (7.6,8.1)	7705 (7674,7738)	952 (944,961)
3-9 May	9.7% (9.5%,9.9%)	2.5% (2.5%,2.5%)	3.4% (3.3%,3.5%)	27.0% (26.6%,27.4%)	3.9 (3.8,4.0)	8.0 (7.7,8.2)	6435 (6413,6458)	734 (727,741)
10-16 May	8.6% (8.5%,8.8%)	2.5% (2.5%,2.5%)	3.3% (3.3%,3.4%)	27.1% (26.7%,27.5%)	3.4 (3.4,3.5)	8.1 (7.9,8.3)	5478 (5458,5499)	553 (548,559)
17-23 May	7.8% (7.6%,7.9%)	2.5% (2.5%,2.5%)	3.3% (3.2%,3.4%)	27.2% (26.9%,27.6%)	3.1 (3.1,3.2)	8.3 (8.0,8.5)	5271 (5247,5296)	445 (440,449)
24-30 May	7.3% (7.2%,7.4%)	2.6% (2.6%,2.6%)	3.3% (3.2%,3.3%)	27.2% (26.8%,27.6%)	2.8 (2.8,2.9)	8.4 (8.2,8.6)	4369 (4352,4385)	380 (376,384)
31 May-6 Jun.	6.9% (6.8%,7.0%)	2.6% (2.6%,2.6%)	3.2% (3.2%,3.3%)	27.2% (26.8%,27.5%)	2.7 (2.6,2.7)	8.5 (8.3,8.7)	4122 (4102,4142)	292 (289,295)
7-13 Jun.	6.6% (6.5%,6.7%)	2.6% (2.6%,2.6%)	3.2% (3.1%,3.2%)	27.2% (26.9%,27.6%)	2.5 (2.5,2.6)	8.6 (8.4,8.8)	3195 (3181,3209)	233 (230,235)
14-20 Jun.	6.2% (6.1%,6.3%)	2.7% (2.7%,2.7%)	3.2% (3.1%,3.2%)	27.3% (26.9%,27.6%)	2.3 (2.3,2.4)	8.6 (8.5,8.9)	2098 (2089,2108)	149 (147,150)
21-30 Jun.	5.5% (5.5%,5.6%)	2.8% (2.8%,2.8%)	3.2% (3.1%,3.2%)	27.3% (26.9%,27.6%)	2.0 (2.0,2.0)	8.6 (8.4,8.8)	521 (517,525)	41 (41,41)
Period II (1 Jul.-30 Sep. 2020)
1 Jul.-30 Sep.	0.1% (0.1%,0.1%)	2.6% (2.6%,2.6%)	3.2% (3.1%,3.2%)	27.0% (26.6%,27.3%)	0.04 (0.03,0.04)	8.5 (8.3,8.7)	24 (23,25)	4 (4,4)
Period III (1 Oct.-8 Dec. 2020)
1 Oct.-8 Dec.	0.7% (0.7%,0.8%)	3.4% (3.3%,3.4%)	3.1% (3.0%,3.1%)	24.7% (24.4%,25.0%)	0.22 (0.21,0.23)	8.1 (7.9,8.3)	617 (616,618)	106 (105,106)

The probabilities of ICU admission (P_QI) in France, Spain, and Belgium reached to the highest value (approximately 4.0%) during 21-27 Mar. 2020 (Table 2 ) and declined to 1.1%–1.6% gradually during 11-17 Apr. 2020. For New York State (USA), South Korea, and Japan, the probabilities of ICU admission were relatively low and even lower than 1% during 11-17 Apr. 2020. After entering the ICU, the difference in death rates across countries was remarkable. The death rates were consistently higher in France (from 9.5% to 11.7%) and New York State (from 14.3% to 13.9%) but increased with time in Belgium (from 7.8% to 24.8%) and decreased with time both in Spain (from 23.4% to 6.8%) and South Korea (from 25.6% to 5.6%). The death rates in Japan were moderate with variation between 1.3% and 6.6%.

Table 2.

Estimated transition probability of clinical management model for ICU demands in France, Spain, Belgium, New York State (USA), South Korea, and Japan until 17 Apr. 2020.

	Quarantine → ICU (PQI)	ICU → Death (PID)	Available ICU beds	Predicted number of ICU beds needed (per week)
France
29 Feb.-6 Mar.	2.9% (1.5%,4.7%)	9.5% (3.7%,17.3%)	1514	33 (27,40)
7-13 Mar.	1.7% (1.3%2.2%)	13.5% (10.6%,16.9%)		167 (154,180)
14-20 Mar.	3.9% (3.6%,4.2%)	9.8% (8.8%,10.9%)		1329 (1301,1357)
21-27 Mar.	4.0% (3.8%,4.2%)	10.1% (9.6%,10.6%)		3847 (3792,3902)
28 Mar.-3 Apr.	3.5% (3.4%,3.7%)	12.6% (12.2%,13.0%)		7133 (7059,7206)
4-10 Apr.	2.5% (2.4%,2.7%)	13.7% (13.3%,14.0%)		7637 (7564,7711)
11-17 Apr.	1.4% (1.3%,1.5%)	11.7% (11.4%,12.0%)		6391 (6322,6459)
Spain
6-13 Mar.	5.8% (5.0%,6.6%)	23.4% (19,4%,27,8%)	905	349 (324,375)
14-20 Mar.	3.1% (2.9%,3.4%)	24.3% (22.7%,25.9%)		1498 (1450,1548)
21-27 Mar.	3.9% (3.8%,4.1%)	23.6% (22.9%,24.4%)		5593 (5505,5685)
28 Mar.-3 Apr.	2.5% (2.4%,2.7%)	16.7% (16.2%,17.1%)		7290 (7215,7372)
4-10 Apr.	1.6% (1.5%,1.6%)	10.2% (9.9%,10.5%)		8056 (7992,8118)
11-17 Apr.	1.1% (1.1%,1.1%)	6.8% (6.6%,7.0%)		8297 (8232,8366)
Belgium
14-20 Mar.	2.7% (2.0%,3.4%)	7.8% (5.4%,10.6%)	363	138 (128,149)
21-27 Mar.	3.9% (3.3%,4.4%)	10.2% (8.9%,11.4%)		779 (756,802)
28 Mar.-3 Apr.	2.6% (2.3%,2.9%)	13.1% (12.2%,14.0%)		2489 (2460,2519)
4-10 Apr.	2.2% (2.0%,2.4%)	21.3% (20.3%,22.3%)		5129 (5085,5174)
11-17 Apr.	1.6% (1.5%,1.8%)	24.8% (23.8%,25.9%)		7422 (7374,7472)
New York State (USA)
27 Mar.-3 Apr.	1.2% (1.1%,1.2%)	14.3% (13.8%,14.9%)	490	4022 (3963,4081)
4-10 Apr.	0.9% (0.8%,0.9%)	15.9% (15.4%,16.4%)		5746 (5674,5820)
11-17 Apr.	0.5% (0.4%,0.5%)	13.9% (13.5%,14.3%)		5568 (5497,5638)
South Korea
22-28 Feb.	0.7% (0.7%,0.9%)	25.6% (13.3%,41.2%)	1091	21 (17,28)
29 Feb.-6 Mar.	0.3% (0.2%,0.4%)	16.1% (10.8%,22.5%)		65 (59,72)
7-13 Mar.	0.1% (0.1%,0.2%)	6.9% (4.5%,9.7%)		96 (90,102)
14-20 Mar.	0.06% (0.03%,0.1%)	6.4% (4.2%,8.9%)		55 (52,60)
21-27 Mar.	0.2% (0.1%,0.3%)	10.7% (7.8%,14.2%)		58 (52,63)
28 Mar.-3 Apr.	0.1% (0.04%,0.3%)	8.6% (6.0%,11.6%)		53 (48,59)
4-10 Apr.	0.2% (0.04%,0.4%)	8.6% (6.0%,11.9%)		54 (48,59)
11-17 Apr.	0.1% (0.03%,0.3%)	5.6%% (3.6%,8.2%)		53 (48,59)
Japan
17-28 Feb.	4.1% (1.7%,6.7%)	3.0% (0.6%,7.2%)	1851	20 (17,23)
29 Feb.-6 Mar.	1.5% (0.7%,3.1%)	1.3% (0.1%,3.4%)		27 (24,33)
7-13 Mar.	1.1% (0.7%,2.1%)	6.6% (3.5%,10.5%)		29 (26,35)
14-20 Mar.	1.1% (0.7%,1.9%)	5.0% (2.7%,7.9%)		50 (44,56)
21-27 Mar.	0.9% (0.7%,1.4%)	3.5% (1.8%,5.7%)		56 (49,63)
28 Mar.-3 Apr.	0.8% (0.7%,1.0%)	4.4% (2.6%,6.8%)		63 (56,72)
4-10 Apr.	0.7% (0.7%,0.8%)	4.8% (3.1%,6.8%)		119 (109,128)
11-17 Apr.	0.7% (0.7%,0.8%)	5.4% (3.7%,7.4%)		203 (190,217)

Traffic intensity ratios (TIRs) and number of beds needed

Table 1 also shows the estimated TIR for hospital (${\rho }_H$) was 2.2 (95% CI = 1.9–2.6) in the first week (3-7 Mar. 2020) and the corresponding predicted number of beds needed (per week) was 2289 (95% CI = 2251–2302) in Lombardy, Italy. After then, the TIR became more congested, and the highest value reached to 6.0 (95% CI = 5.8–6.2) in the fifth week. The maximum of number of beds needed increased to 12688 beds (95% CI = 12640–12737) in the sixth week. Afterwards, the TIR was relieved and the number of beds needed also declined. During the Period II (1 Jul.-30 Sep. 2020) and Period III (1 Oct.-8 Dec. 2020), the TIRs were lowered to less than 1 (0.04 vs. 0.22, respectively) and the number of beds needed (per week) were 24 and 617, respectively.

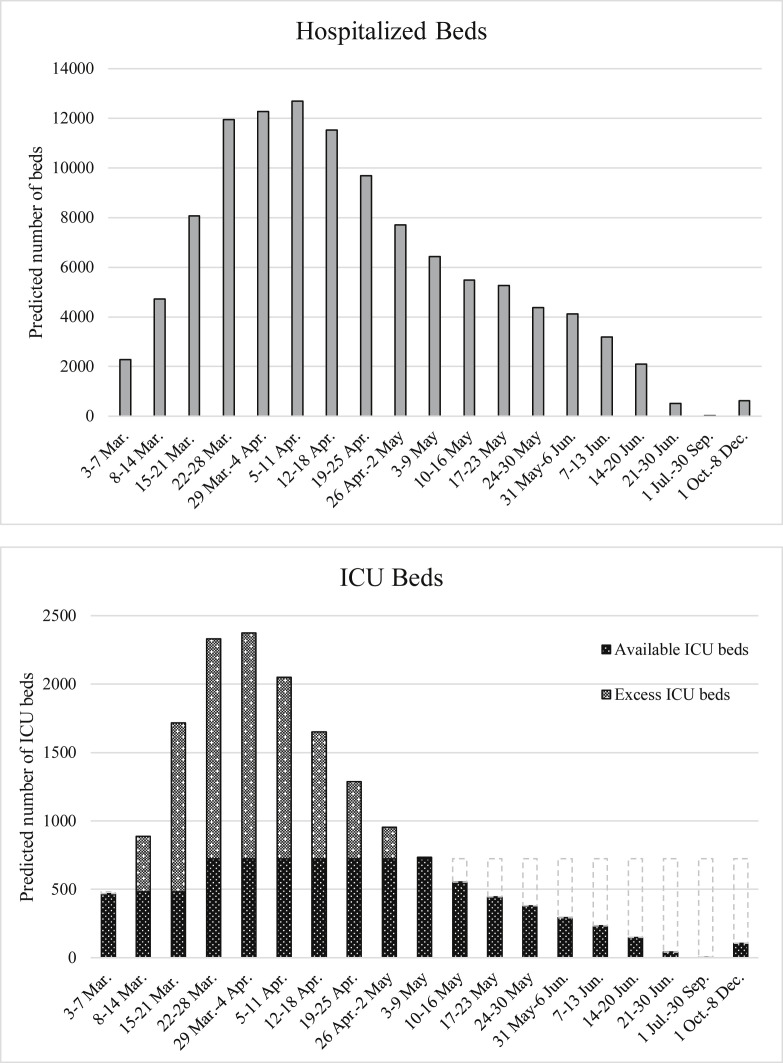
For the demand of ICU beds in Lombardy, Italy, the estimated results in Table 1 show that the TIR for ICU beds ($1/{\rho }_I$) increased from 2.9 (95% CI = 1.9–4.3) in the first week to 7.9 (95% CI = 7.5–8.2) in the fifth week, and the number of ICU beds needed was merely 469 (95% CI = 442–498) in the first week but reached to 2375 (95% CI = 2345–2406) in the fifth week, reaching the highest demand of ICU beds. After then, the quantity of ICU beds needed has been slow down and declined to 734 (95% CI = 727–741) until the tenth week (Fig. 2 ), and the TIR for ICU kept stable between 7.6 and 8.0. The rate of requiring critical care beds was 12.5 per 100,000 inhabitants in Italy, so the expected available ICU beds was 482 (80% occupancy rate) before 19 Mar. 2020 but extended to 724 after then. Therefore, after the second week, the predicted number of ICU beds was insufficient (Fig. 2) even though the total ICU capacity has been expanded. However, after the 11th week (10-16 May 2020), the expected number of ICU beds was lower than available 724 ICU beds. In addition, the number of ICU beds (per week) during the Period II (1 Jul.-30 Sep. 2020) and Period III (1 Oct.-8 Dec. 2020) was 4 and 106, respectively.

Figure 2.

Predicted number of beds needed and ICU beds needed in Lombardy, Italy.

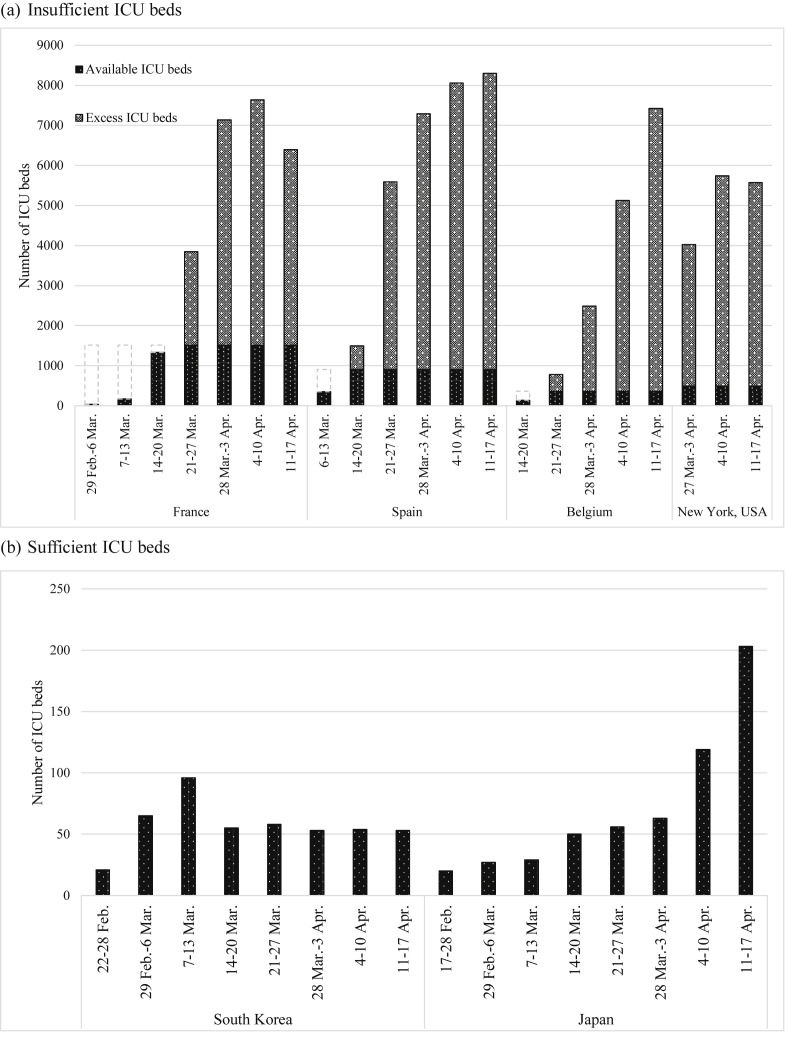
For France, Spain, and Belgium, the number of ICU beds needed increased dramatically (Fig. 3 ). The demand of ICU was no longer affordable after 14 Mar. 2020 in Spain, and after 21 Mar. 2020 in France and Belgium. The number of ICU beds needed increased in Spain (8297; 95% CI = 8232–8366) and Belgium (7422; 95% CI = 7374–7472), but were reduced gradually in France (6391; 95% CI = 6322–6459) during 11-17 Apr. 2020. For New York State (USA), the demand of ICU beds was far from available beds but improved slightly later on. The capacities in South Korea and Japan were still above par. The number of ICU beds needed was lower than 100 beds although it has been increasing gradually in Japan.

Figure 3.

Predicted number of ICU beds needed in Lombardy (Italy), France, Spain, Belgium, New York State (USA), Korea, and Japan.

Discussion

In this study, we estimated the process of patient flow from the confirmation of COVID-19 to the discharge from hospitals or death, and further developed two indices for the congestion of isolation wards and ICU beds in hospitals in response to the surge of patients in critical condition due to COVID-19. In Lombardy, Italy, the probability of entering into hospital for quarantine increased and reached to the highest value during the second to fourth week, and the similar trend was noted in the probability of entering into ICU. It may explain the reason of decreased recovery rate and increased fatality. In the capacity of hospitalization, the congestion of isolation beds has increased by the early of April, but started to relieve in mid-April 2020. The similar trend on the demands for ICU were notably observed as well. In other countries, the same situation was seen in France, Spain, Belgium, and New York State (USA) but not for South Korea and Japan.

The reduction in the expected number of bed and ICU in period II was mainly attributed to the containment of the epidemic during this period but a decrease in those expected figures in period III (second wave of pandemic) is possibly due to the adapted policy for the optimal allocation of mild COVID-19 to self-quarantine and self-isolation because there was a surge of epidemic during this period around the world. It is important to study the potential latent impact, such as delayed care, on the possible unmet isolation wards and ICU need in the face of the second or even the third wave of pandemic.

The developed congestion indices in our study for both isolation wards and ICU can be used as an early index for the disease severity. We found that both indices were poor in Italy in March, which was consistent with the high fatality they had in March. A slight decline of index of hospitalization in early April could expect a medical burden relief. This has been shown in the lowered ICU needs in the following weeks, and further reduction of fatality. The developed index was further used to estimate the ICU needs. By using the Bayesian approach, we can take priors from the previous week into account and update the information week by week to get the robust results. For other countries, unmet need of ICU was observed from the week of 21 Mar. 2020 in France, 10 Mar. 2020 in Spain, and 20 Mar. 2020 in Belgium. We found that the probabilities from quarantine to ICU among these countries were averagely greater than 3%. However, the preparedness of ICU was sufficient in South Korea and Japan. This can explain the fact that although South Korea experienced a rapid surge of confirmed cases in the third week of February, the fatality was low as of 9 Apr. 2020. The same phenomenon was observed in Japan. Although the probabilities from quarantine to ICU in New York State (USA) were relatively low, the demand of ICU was still insufficient, which may result from not applicable information of ICU before 26 Mar. 2020 or the rapid test for mass screening.

Worries have been raised for the unpreparedness of current health system in response to an infectious disease pandemic, even in developed countries. In a suggestion for the preparedness of the US health care system for the pediatric surge due to an infectious disease pandemic, Antony et al. pointed out that the use of mathematical modeling for the estimation of hospital admissions and resources needed in the catchment area can facilitate as a planning tools for equipment, supply, and medication.¹² In this study, we applied the compartment model to evaluate the demand of quarantine beds and ICU beds. The compartment model has been widely used in the healthcare management field. It can describe the movement of patient flows and assess the cost within the hospital system. The information can be provided for health service managers, clinicians, and policy makers to optimize bed occupancy and utilize the cost allocation efficiently.13, 14, 15 In addition, the demand for bed, the length of stay, and the number of patients in each state can be forecasted by the compartment model to improve the management of hospitalization in more cost-efficient way.^{16 , 17} Several studies also used computer simulation models to address the bed or ICU bed allocation to hospital services.^{18 , 19} Currently, the Institute for Health Metrics and Evaluation used an individual-level microsimulation model to forecast deaths from COVID-19, daily bed and ICU occupancy, and ventilator use over the next 4 months for all US states.²⁰

There are two limitations in this study. Firstly, data on the numbers of home-based isolation (Q₁) and quarantine in hospital (Q₂) were indistinguishable from the total confirmed cases (shown as state “Q” in Fig. 1) in France, Spain, Belgium, New York, South Korea, and Japan. Therefore, the probability of ICU admission from quarantine (P_Q2I) were unavailable for the calculation of the TIR for ICU in these countries. Secondly, data in France, Spain, Belgium, New York, South Korea, and Japan cannot be accessed after mid-April 2020. Therefore, we could not apply our methods to second or third wave in these countries.

In conclusion, the developed the compartment queue model for the clinical management in terms of medical resources by using open assessed tabulated data enables one to foresee the clinical capacity and its possible impact on the primary outcome of death.

Declaration of competing interest

The authors have no conflicts of interest relevant to this article.