Abstract
Understanding temporal regulation of development remains an important challenge. Whereas average, species-typical timing of many developmental processes has been established, less is known about inter-individual variability and correlations in timing of specific events. We addressed these questions in the context of postembryonic development in Caenorhabditis elegans. Based on patterns of locomotor activity of freely moving animals, we inferred durations of four larval stages (L1-L4) in over 100 individuals. Analysis of these data supports several conclusions. Individuals have consistently faster or slower rates of development because durations of L1 through L3 stages are positively correlated. The last larval stage, the L4, is less variable than the earlier stages and its duration is largely independent of the rate of early larval development, implying existence of two distinct larval epochs. We describe characteristic patterns of variation and correlation, as well as the fact that stage durations tend to scale relative to total developmental time. This scaling relationship suggests that each larval stage is not limited by an absolute duration, but is instead terminated when a subset of events that must occur prior to adulthood have been completed. The approach described here offers a scalable platform that will facilitate the study of temporal regulation of postembryonic development.
Graphical Abstract
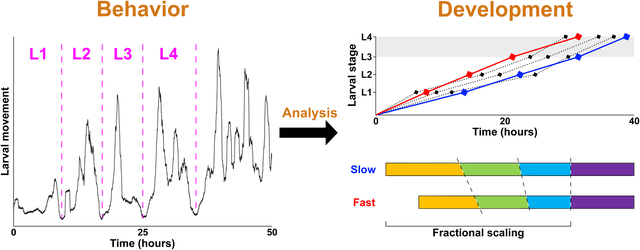
Introduction
As is true for other Ecdysozoa (Telford et al., 2008), postembryonic development of nematodes is organized into several discrete stages, separated by molts. Upon completing embryonic development, C. elegans progress through four larval stages (L1-L4) prior to larval-to-adult transition (Byerly et al., 1976). Between L1 and adulthood, freely moving larvae execute stage-specific developmental programs that increase the total (in hermaphrodites) number of somatic nuclei from 558 to 959 (Sulston et al., 1983), produce ~2,500 germline nuclei (Hirsh et al., 1976), while allowing the worms to grow on average from ~250 to ~1,000 μm in length (Byerly et al., 1976; Hirsh et al., 1976).
Larval stages have similar organization – the multi-hour periods of growth are capped by short periods of ecdysis, during which the old cuticle is shed (Singh and Sulston, 1978). Particular developmental events (e.g. cell divisions, deaths, migration, etc.) occur at specific times (Sulston and Horvitz, 1977) and transitions between larval stages are characterized by dramatic upheavals in gene expression (Frand et al., 2005; Hendriks et al., 2014; Snoek et al., 2014; Turek and Bringmann, 2014). Genetic analysis of timing of developmental events led to discovery of heterochronic mutants (Ambros and Horvitz, 1984), including the now-classic miRNAs lin-4 (Lee et al., 1993) and let-7 (Reinhart et al., 2000), as well as their targets (Slack et al., 2000; Wightman et al., 1993), and other genes (Abbott et al., 2005; Abrahante et al., 2003; Antebi et al., 1998; Jeon et al., 1999; Monsalve et al., 2011; Moss et al., 1997; Rougvie and Ambros, 1995) that regulate timing of developmental transitions (Rougvie and Moss, 2013).
Approximate population-average timeline of development is sufficient for analysis of the overall order of events; these estimates were made in the early days of C. elegans research (Byerly et al., 1976; Hirsh et al., 1976), but remain relevant today. They do not, however, permit inferences of inter-individual variation of developmental rates or more involved analyses of co-dependence of different developmental events and stages. Direct observation of developmental progression is time-demanding and labor-intensive, necessarily limiting numbers of animals that can be followed simultaneously. High-throughput approaches relying on a variety of technologies have been developed (Gritti et al., 2016; Keil et al., 2017; Nika et al., 2016; Olmedo et al., 2015; Uppaluri and Brangwynne, 2015), including methods that allow long-term observation (Stroustrup et al., 2016; Zhang et al., 2016). Some of these platforms could be used to analyze progression of development in individual animals. One promising approach is based on the periodic nature of the locomotor activity during postembryonic development – episodes of ecdysis at the end of each larval stage are preceded by periods of lower activity, called lethargus, that last ~1–2 hours (Singh and Sulston, 1978). Therefore, identifying periods of lower activity from continuous recordings could yield estimates of larval stage duration (Raizen et al., 2008), even though individuals are not uniformly inactive during lethargus (Iwanir et al., 2013). Recently, Stern et al. reported behavioral analysis of several hundred continuously monitored singled hermaphrodites over a period that extended from the onset of L1 to beyond the L4/adult transition (Stern et al., 2017). Taking advantage of these data, we set out to assess inter-individual variability and relationships between different stages of postembryonic development.
Materials and Methods
Primary data and inference of stage durations.
All primary data were generated and reported by Stern et al. (Stern et al., 2017). These data consisted of series of coordinates inferred from sequentially recorded frames that sampled, at 3 Hz, movement of individual larvae, produced by mothers whose ages were synchronized to within 1 day. Recordings were carried out at 22°C. Each X-Y coordinate (~6 × 105 per animal, spanning from L1 to adulthood) represents “center of mass” of an image of moving individual animal in a given frame (Stern et al., 2017). We obtained these coordinates from Mendeley (https://data.mendeley.com/datasets/3j6fsr634d/1). From coordinates corresponding to pairs of sequential frames, we calculated Euclidian distances that represented “displacements” over 1/3 second.
Typical velocity of C. elegans in the presence of food is ~30–100 μm/s (Ramot et al., 2008) for larvae that range between ~250 and ~1,000 μm (Byerly et al., 1976; Hirsh et al., 1976). We therefore reasoned that displacements over 1/3 sec (in the data we analyzed, these averaged ~4–5 μm) largely reflect minor changes in body posture, including head movements (Nagy et al., 2014; Yemini et al., 2013), rather than genuine locomotion. Because displacements between neighboring frames were a) highly variable and b) small with respect to animal size and average velocity, we experimented with effectively reducing recording frequency by calculating displacements between frames n and n+x, where x varied from 2 to 100 We refer to this process as reduction. We found that reduction to a sampling frequency of 0.1 Hz was a reasonable compromise between de-noising the data and sampling sufficiently frequently to retain finer features of locomotor activity. This level of data reduction is equivalent to recording activity at 1 frame per 10 sec, which has been empirically found to be an appropriate frequency based on different considerations (Huang et al., 2017; Nelson et al., 2013; Raizen et al., 2008). Because the 30X-reduced activity profiles were still quite noisy (Figure S1C), we tested whether sliding windows of various length that shifted by 1 displacement value at a time could generate smoother curves without removing features essential for identifying periods of lower activity. We found windows of ~333 frames of 30X-reduced activity (10,000 frames of primary, unreduced data) to be useful for this task; such frames cover ~55.5 minutes of developmental time.
We operationally defined midpoints of periods of reduced locomotor activity as transitions between larval stages. Because shapes of activity profiles during periods of reduced activity were irregular and varied across stages (Figure 1C) as well as among worms, we developed an algorithm to estimate their width. We started by identifying four activity minima per profile (i.e., per worm), each corresponding to one period of reduced activity. Because activity during the L1 stage was low in some animals, we ignored minima in the first 500 minutes of the recordings. Next, we drew horizontal lines (never more than 20) at 2.5 μm intervals, starting at the minimum for each period of lower activity. Intersections of these lines with the activity profile defined the width of the period of lower activity at that vertical level. Finally, we averaged midpoints of these width estimates thus obtaining provisional estimates of stage boundaries; these were further corrected in two ways.
Figure 1. Inferring duration of larval stages from high-content behavioral tracking data.
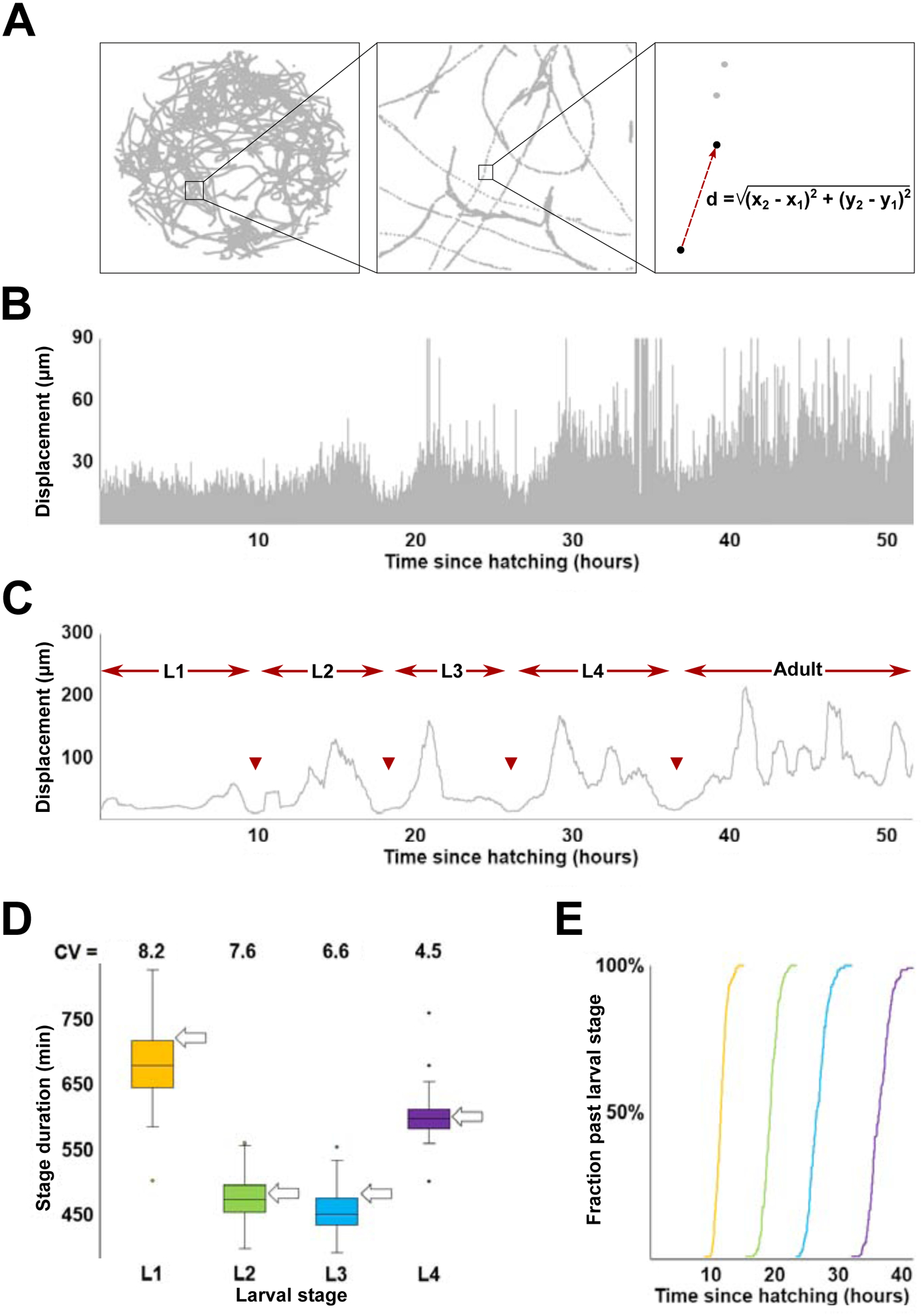
(A) Track of a single C. elegans hermaphrodite over the course of an ~50 hour recording. The right-most box shows calculation of displacement as distance between centers of mass of the tracked worm between two sequential frames. (B) Activity profile (i.e., plot of all consecutive displacements) of the worm shown in (A). Note that due to fluctuations in locomotor behavior, the ~600,000 displacements shown here exaggerate local extremes – vast majority of displacement values are considerably lower (mean ~4–5 μm) than the outline. See Figure S1 for more detail. (C) Activity profile of the worm shown in (A) produced from displacement values sampled at 0.1 Hz and smoothened (55.5 min). Arrowheads indicate boundaries between larval stages defined as mid-points of periods of reduced activity. (D) Inferred durations and coefficients of variation (CV; expressed as %) of L1-L4 larval stages. Arrows indicate stage durations (at 22°C; recordings analyzed in this study were collected at the same temperature) as shown in (https://www.wormatlas.org/hermaphrodite/introduction/Introframeset.html). (E) Transition times (sample N=125) between (L1, L2, L3, L4) larval stages.
First, the original data (Stern et al., 2017) contained missing frames incurred for technical reasons. Although there were few such frames (<0.4% of the total), we added their duration (1 frame = 1/3 second) to the estimates of stages during which they occurred. No extended runs of missing frames occurred sufficiently close to provisional boundaries between stages to meaningfully impact our ability to estimate them. Second, the algorithm that calculated smoothened activity profiles assigned value for each window based on the average of displacement values before (50%) and following (50%) it. Because this effectively shortened duration of the L1 by ½ of the sliding window size, we added this time to provisional estimates of duration of this stage.
Computation of activity, correlations, and randomized developmental time series.
We used two metrics to evaluate worm activity. First, we added all sequential displacements within a relevant stage. Activity defined in this way will be greater over longer time intervals. For this reason, there was a strong, but entirely uninformative correlation between activity and stage duration. We therefore computed correlations between stage duration and measures of activity that were normalized by stage duration. These latter quantities are equivalent to average velocities over the duration of a larval stage. Second, we calculated roaming fractions, as described previously (Ben Arous et al., 2009; Churgin et al., 2017; Flavell et al., 2013; Stern et al., 2017). Roaming fraction reflects the percentage (over a larval stage or entire postembryonic development) of behavioral episodes (each of a certain of defined duration) that were classified as roaming (as opposed to dwelling). For analysis in Figure 2C, activity profiles were manually classified into one of three categories (by two independent operators, with high concordance).
Figure 2. Relationship between the rate of development and locomotor activity.
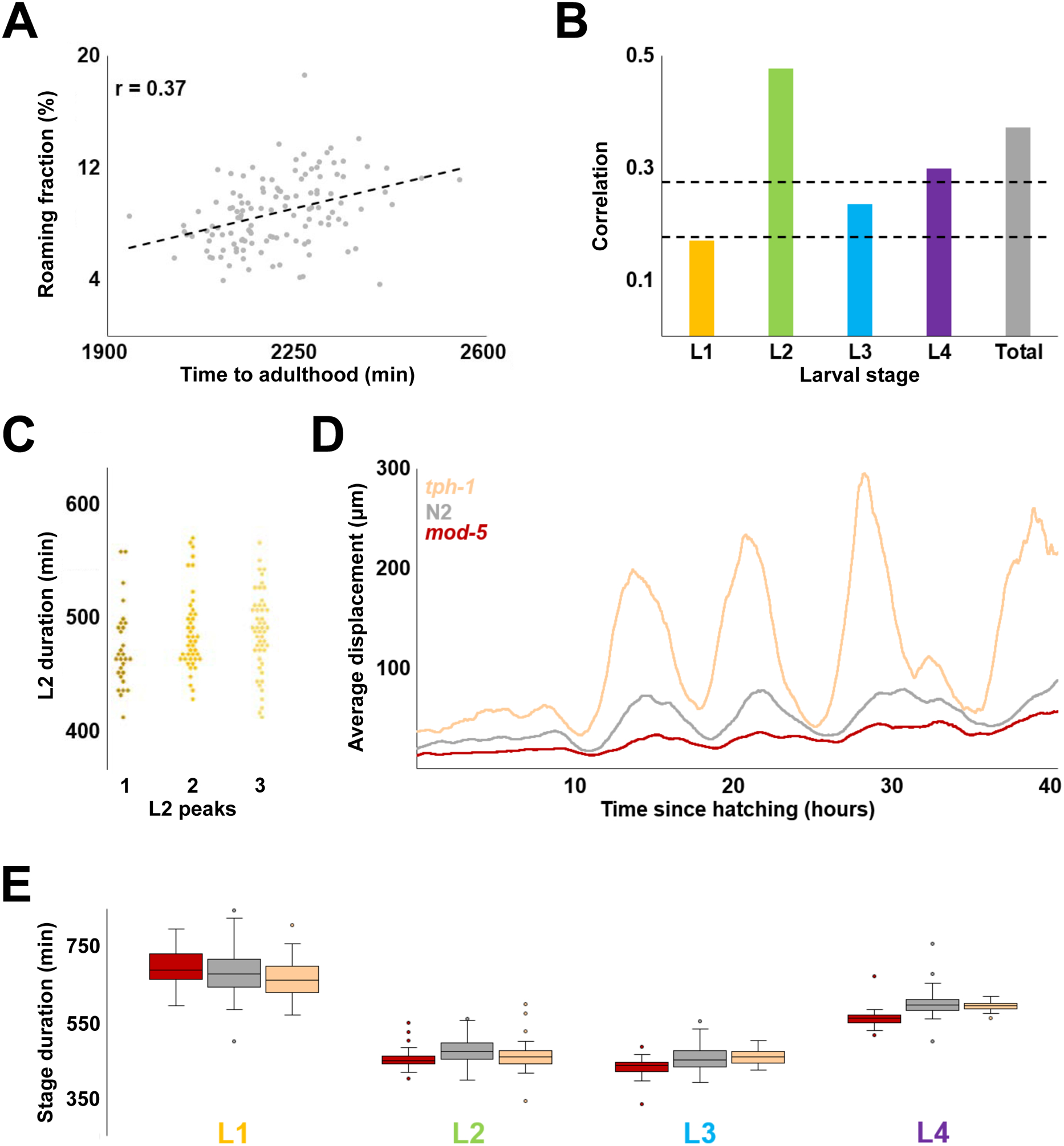
(A) Correlation between total developmental time and locomotor activity (measured as roaming fraction) for 125 wild type N2 worms. (B) Correlation between roaming fraction and stage duration for each larval stage; “total” shows the same value as in (A). Dashed lines denote two and three standard deviations above the expected correlation between two random sets of 125 uncorrelated variables. (C) Durations of L2 stages from each of the three categories activity profiles classified by overall shape (each diamond is one individual). Of the three possible pairwise comparisons (Kolmogorov-Smirnov test) only one – 1 peak vs 3 peak – had a p-value < 0.017 (0.05 after the Bonferroni correction for 3 comparisons is 0.017). The observed value – 0.015 – indicated at best a marginal difference. (D) Population average activity profiles of tph-1(mg280) (N=47), wild type N2 (N=125), and mod-5(n822) (N=41). (E) Inferred stage durations of tph-1, N2, and mod-5 animals.
To evaluate several hypotheses against a null model of random association between stage durations, we generated 10,000 artificial data sets, each containing 125 developmental time series. Each time series was composed from an L1, an L2, an L3, and an L4, each randomly drawn from the set of empirically estimated values described in the section above.
Perez et al. reported (their Extended Data Fig. 2k) progress of development for larvae obtained from age-synchronized mothers (Perez et al., 2017). They found that the fastest developing larvae were ~6 hours ahead of the slowest. Sample sizes ranged from 50 to 70 individuals. For comparison, we analyzed a sample of 125 larvae and inferred the difference of ~10 hours between the fastest and the slowest developers. Smaller samples underestimate the difference between the fastest and the slowest developers. To estimate the extent of this effect, we drew, at random, 10,000 sets of 60 developmental times (from the 125 total that we estimated for N2 larvae). We found that the mean difference between the slowest and fastest developers in these samples was ~8 hours, which is shorter than the ~10 hours estimated from the whole set of 125 and only slightly greater than >6 hours evident from the data of Perez et al.
Statistical analyses.
Data analyses were carried out using custom-written code (https://github.com/denisfaer/c-elegans-codes), Excel, and R package (https://cran.r-project.org/package=dgof). To evaluate variability across samples that in some instances had substantially different means, we routinely used coefficient of variation (CV), computed as standard deviation divided by the sample mean. Because standard deviation is susceptible to effects of outlier values, we used methods for comparing variation that were less affected by the extremes. We computed interquartile variability (based on Q2 and Q3 only), interdecile variability (2–9th deciles), or median absolute deviation of all data. In all cases, our conclusions regarding lower variability of L4 duration and less variable fractional stage durations (compared to absolute stage durations) held. One standard deviation of the correlation between two random sets of N values (expected to equal zero) is approximately , or ~0.09 for N=125. To account for multiple comparisons, we conservatively considered as significant only correlations >0.27 (three standard deviations), which correspond to p-values less than ~1.5×10−3. For comparing empirical data to results of permutation tests (using 10,000 randomly generated data sets) we considered as p-values the fractions of instances (out of 10,000) that were more extreme than the empirical values. In the box plots in all figures, the middle line is the median, top and bottom of the box encompass 2d and 3rd quartiles, and the whiskers represent the bulk of the fitted normal distribution.
Results
High-content behavioral tracking data can reveal temporal progression of development in individual C. elegans
To investigate long-term behavioral patterns in C. elegans hermaphrodites, Stern et al. continuously monitored individuals singled from hatching and freely moving on hard agar surfaces within relatively large (~10 mm, i.e. >10 times larger than the length of larvae) arenas (Stern et al., 2017). An advantage of relying on these data to ascertain larval stage duration, compared to more invasive methods or ones that restrain larvae during development, is that in this paradigm larvae moved freely and experienced minimal disturbance. Animals were observed from the onset of movement during early L1 stage until early adulthood, in the presence of E. coli food.
Although complete tracks generated over the entire duration of a recording were highly convoluted, coordinates of “centers of mass” captured in adjacent frames (i.e., 1/3 seconds apart) could be used to compute a quantity that characterizes animals’ movement; we refer to this quantity as displacement (Figure 1A). Plotting all (~6 × 105) sequential displacements for a given individual, provides a dynamic picture of movement activity of that animal over the entire duration of larval development (Figure 1B). Such plotting alone could reveal approximate periods of lower activity, at least in some individuals. Although some periods of low activity likely reflect lethargus episodes surrounding molts (Raizen et al., 2008), displacements vary considerably between frames (Figure S1A), making it challenging to computationally identify periods of lower activity, particularly in some individuals (Figure S1B). To overcome these limitations and to leverage the power of inter-individual comparisons, we implemented a method for identifying periods of lower activity from the somewhat noisy activity data (like those shown in Figure 1B). We generated activity profiles for all 125 wild type N2 individuals in the data set. In every case, the profiles had four well-articulated periods of lower activity that by timing and duration approximately corresponded to lethargus periods. In all 125 activity profiles we identified mid-points within periods of lower activity and designated corresponding times as boundaries between adjacent larval stages (Figure 1C).
Our estimates of durations of larval stages (Figure 1D) closely matched those previously obtained from direct observations (Gritti et al., 2016; Hirsh et al., 1976; Monsalve et al., 2011). Discrepancies between average estimates in our study and previously reported values were minor (<1 hour compared to 8–11 hour stage durations) and could be due to rounding of prior estimates, to minute differences in cultivation conditions (e.g., between 20°C and 25°C, temperature increase of 1°C accelerates larval development by ~2 hours (Gouvea et al., 2015)), or to other difficult-to-control factors. Our estimates matched well those previously made from the same data (Stern et al., 2017), while the fractions of overall developmental time occupied by L1-L4 were virtually identical between our analysis and that of Raizen et al. (Raizen et al., 2008), even though recordings were conducted at different temperatures (see more on this below). Durations of individual larval stages could be used to compute transition times between larval stages for the entire population (Figure 1E). Despite the relatively modest variation overall (coefficient of variation (CV) of timing of L4/adult transition is ~4.6%), the slowest developing individual reached adulthood ~10.1 hours later than the fastest, a considerable difference given the ~36.9 hour average duration of larval development.
Developmental rate is substantially decoupled from behavioral activity
We tested whether our estimates of duration of larval stages were correlated with the locomotor activity data from which they were derived. We found at best a modest correlation between duration of larval development and activity, which was computed as sum of displacements divided by time (Figure S2A; see Materials and Methods). Duration of the L2 stage was correlated with activity, while L4 showed marginal correlation and L1 and L3 stages showed none (Figure S2B). It is possible that locomotor activity per se is not the appropriate measure to evaluate correlation between behavior and duration of larval development. We therefore tested whether fraction of time devoted to roaming, a related but distinct measure (see Materials and Methods) was better suited for the task. We found that the overall correlation was slightly higher, with L2 (and possibly L4) showing evidence of correlation (Figure 2A, B).
As we examined activity profiles of individual animals, we noticed that despite diversity of shapes, these profiles displayed repeated patterns of higher and lower activity within larval stages, often in stereotyped, albeit complex ways (Figure S2C). We reasoned that shapes of activity profiles may reflect some currently unknown feature(s) of behavior. If so, it is possible that individuals displaying different activity profiles might develop at different rates. To test this idea, we focused on the L2 stage because we expected it to offer the best chance of identifying a relationship, if one exists, between activity and duration of development. We manually classified the 125 animals in the data set into one of three categories by the shape of L2 activity profiles. We found no appreciable differences between the three categories with respect to the duration of L2 stages (Figure 2C).
The method described here could be used to analyze temporal unfolding of larval developmental in mutants (Figure S2D). Even in cases of noisy activity profiles (Figure S2E), we were able to infer total duration of larval development (Figure S2F). Our estimates were consistent with the ones made previously (Stern et al., 2017). As an additional test of whether there exists a relationship between locomotor activity and duration of larval development, we examined two mutants (Figure 2D). The first is in the tph-1 gene (Sze et al., 2000) that encodes a serotonin biosynthetic enzyme tryptophan hydroxylase and is consequently defective in serotonergic signaling. The second mutation affects the serotonin reuptake transporter gene mod-5, effectively increasing serotonergic signaling (Ranganathan et al., 2001). Compared to wild type, these two mutant strains are known to have exacerbated and reduced exploratory behavior, respectively (Flavell et al., 2013; Stern et al., 2017). Consistent with prior analysis (Stern et al., 2017), despite having an approximately five-fold difference in activity (Figure S2G), the two mutants have nearly indistinguishable average durations of all larval stages (Figure 2E). It is possible that tph-1 and mod-5 mutations proportionally scale both developmental rate and activity (see more on this below). Still, the most plausible interpretation of these results is that no simple relationship exists between activity and rate of larval development.
Inferring temporal organization of larval development
The principle advantage of well-resolved developmental time series obtained from individual animals, compared to population averages, is that they could be used to explore inter-individual variability and relationships between different larval stages. Durations of L1-L4 larval stages were distributed approximately normally, with only a small number (~3 out of 125) of extreme outliers (Figure 3A). Same was true for total (i.e., L1+L2+L3+L4) durations of larval development (Figure 3B). We wondered whether animals that developed much slower or much faster than average did so because of one or two abnormally fast or slow larval stages. We therefore compared durations of all larval stages between 20 animals with the fastest and 20 animals with the slowest development. We found that the two populations had nearly nonoverlapping distributions of L1 through L3, but indistinguishable L4s (Figure 3C). Largely the same relationships were observed when the fastest and slowest individuals were excluded from the analysis (Figure S3A). We draw two conclusions from these results. First, animals develop at characteristic rates that are somewhat stable during the first three larval stages. Second, the duration of the L4 is independent of those rates.
Figure 3. Correlations between stage durations.
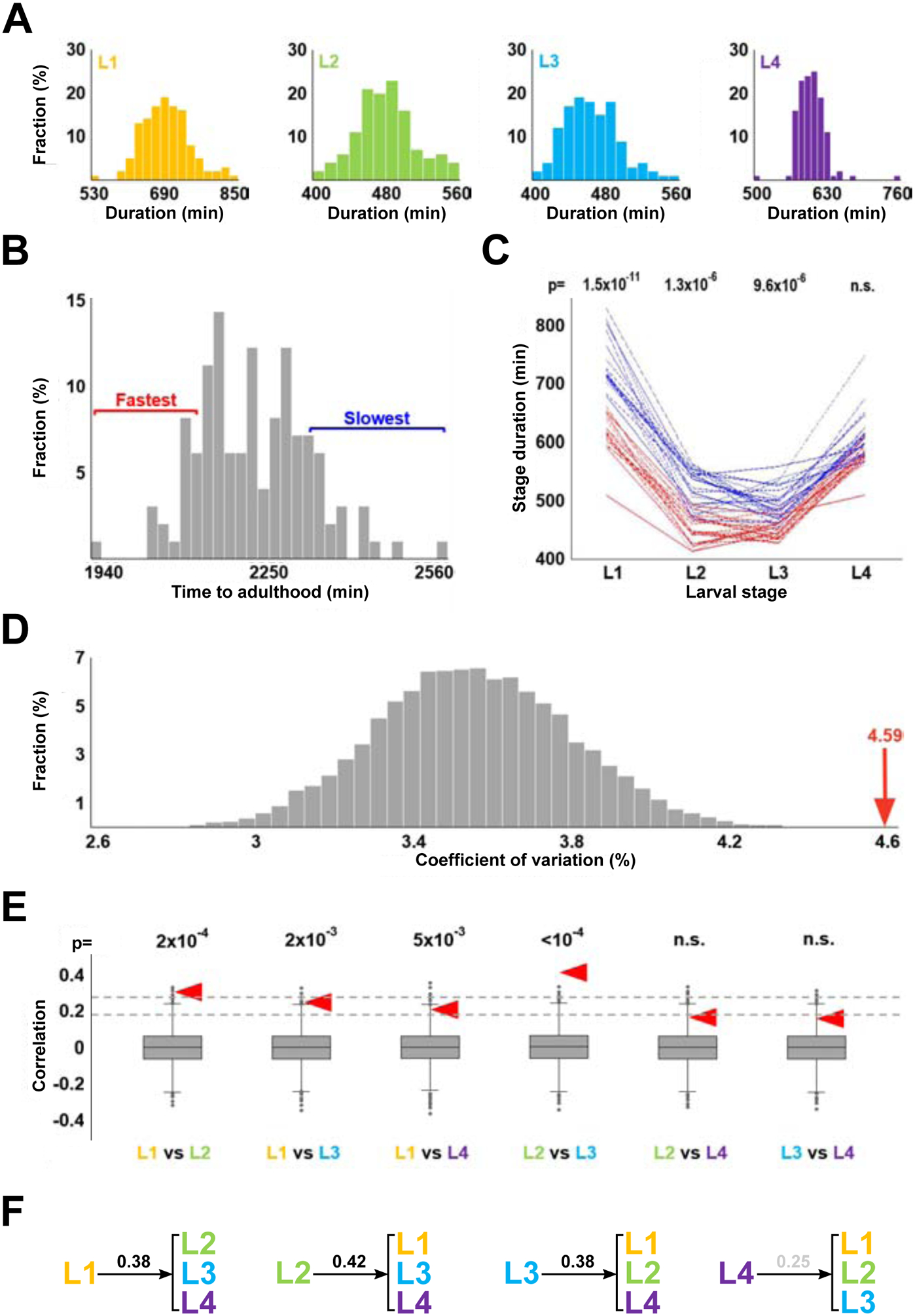
(A) Histograms showing stage durations of wild type N2 animals (N=125). Durations of L1, L2, and L3 stages (as well as total durations of development; not shown) are consistent with being sampled from normal distributions (according to Shapiro-Wilk tests). Durations of L4 could be made normal if as few as 3 extreme outliers were removed. (B) Histogram of total developmental times of wild type N2 animals (N=125). Red and blue brackets denote 20 fastest and slowest developmental times, respectively. (C) Stage durations of the 20 fastest and 20 slowest developing worms (by time to reach adulthood). p-values shown above each stage are results of the Kolmogorov-Smirnov test comparing durations of that stage for the 20 fastest and 20 slowest developing worms. (D) Coefficients of variation of total duration of development in 10,000 sets of 125 artificial developmental time series constructed from randomly selected stage durations. Red arrow represents the coefficient of variation of the total durations of development of the 125 empirical activity profiles. (E) Correlation of stage durations in 10,000 artificial data sets. Null hypothesis is that compared variables are independent, and thus their correlation is 0. Dashed lines denote two and three standard deviations from this expected correlation. Red arrowheads show correlation values obtained from the empirical dataset. p-values above each comparison are the fractions of instances (out of 10,000) in which CVs of randomly permuted data are greater than those from the empirical dataset. (F) Correlation coefficients between duration of an indicated larval stage and the duration of the remaining three stages. Correlation coefficient for L4 is shown in grey because it is lower than three standard deviations from the expected correlation of two random sets of variables (N=125).
To systematically explore the apparently nonrandom associations between larval stage durations, we computationally generated 10,000 data sets, each containing 125 combinations of L1, L2, L3, and L4 stage durations that were randomly selected from respective empirical data. Each combination of L1-L4 simulated a developmental time series of an individual animal, while each set of 125 combinations matched in size the empirical data set analyzed here.
For each set of the 125 simulated developmental time series we computed coefficient of variation (CV) of total larval development times. We thus obtained 10,000 values of CVs on the assumption that each developmental time series is randomly assembled from an L1, an L2, an L3, and an L4 (Figure 3D). Because the CV of the empirical data (4.59) is considerably greater than expected on the assumption of random association (p<10−4), correlations must exist between stage durations. Of the six possible pairwise comparison of the four larval stages, two – L1 vs L2 and L2 vs L3 – showed significant positive correlation (Figure 3E), although only the latter remained significant when extreme values were removed from consideration (Figure S3B). In addition, we observed correlation between duration of the L1 stage and the remainder of larval development (L2+L3+L4); same was true for L2 and L3, but not the L4 (Figure 3F). In all comparisons, correlations involving the L4 tended to be lower than those involving other stages.
Fractional scaling of developmental time series
One possible mechanism that could control duration of postembryonic development in C. elegans is “absolute timer” that allots specific time to each larval stage, variation being a consequence of intrinsic and extrinsic noise. Although normal distributions of L1-L4 (Figure 3A) and total (Figure 3B) durations would be expected under this scenario, correlations we detected between stages (Figure 3C–F) are inconsistent with the strict version of the model. Instructively, our estimates of the fractions of total time of postembryonic development devoted to L1-L4 (0.31, 0.21, 0.21, 0.27, respectively) are indistinguishable from those obtained in several independent studies that relied on different methodologies and were conducted at different temperatures (Byerly et al., 1976; Gritti et al., 2016; Hirsh et al., 1976; Keil et al., 2017; Raizen et al., 2008). We therefore studied “fractional” stage durations, such that for each individual, fractional duration of a stage is equal to absolute duration of that stage divided by total developmental time.
In the empirical set of 125 individuals, CVs of fractional durations were lower than those of the absolute durations from which they were derived (compare CVs in Figure 4A vs Figure 1D). We considered a possibility that the lower variability of fractional stage durations was trivially due to the way in which these quantities were calculated from absolute stage durations. We used two numerical approaches to examine this issue. 1) We compared the variability of fractional stage durations between the 10,000 randomized sets (same sets as analyzed in Figure 3) and the empirical data; we found that the latter were less variable, particularly in the L2 and L3 stages (Figure 4B). 2) We used the set of 10,000 randomly generated data to test whether variability of absolute stage durations was always higher than the variability of fractional stage durations. We found that for L1-L3, absolute stage durations were almost always more variable than relative stage durations, whereas for L4 the two tended to be the same (Figure 4C). However, the difference between variation of absolute and relative stage durations was consistently greater in the empirical data (Figure 4C). When all four stages of postembryonic development were considered together, the difference between variability of absolute vs fractional stage duration was dramatically and significantly (p<10−4) greater for empirical than for permuted data (Figure 4D).
Figure 4. Fractional scaling of developmental time.
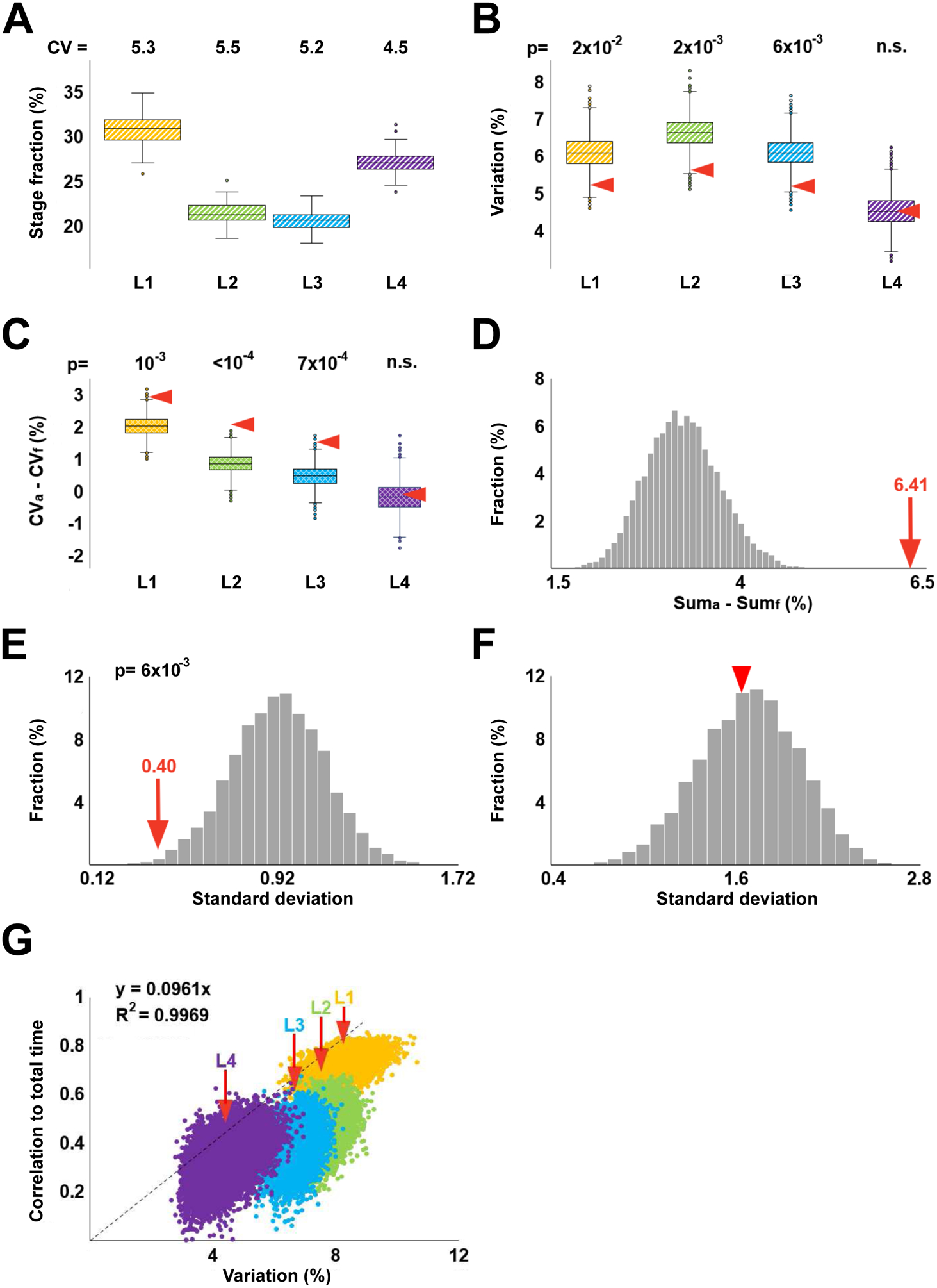
(A) Fractional durations of larval stages calculated based on data in Figure 1D. Shown above are CVs (expressed as %) of L1-L4 stages. (B) Coefficients of variation of fractional stage durations from 10,000 randomly permuted sets. Arrowheads denote coefficients of variation of the empirical stage durations. (C) For each of the 10,000 randomly permuted sets, the CV of fractional durations (CVf) of a given stage was subtracted from the CV of absolute duration (CVa) of this stage; distributions of resulting values are represented as boxplots. Red arrowheads indicate CVa-CVf for the empirical data set. (D) The histogram in grey shows the following values for each of the 10,000 randomly permuted sets: (CVaL1 + CVaL2 + CVaL3 + CVaL4) − (CVfL1 + CVfL2 + CVfL3 + CVfL4). Red arrow indicates the same quantity obtained for the empirical data set. (E) Distribution of standard deviations of CVs of fractional stage durations from 10,000 randomly permuted data sets. p-value shows that only 58 of 10,000 values from permuted data are lower than the CV of fractional stage durations from the empirical dataset (red arrow). (F) Distribution of standard deviations of CVs of absolute stage durations from 10,000 randomly permuted data sets. Red arrowhead marks CV from the empirical dataset. (G) Pairs of ci, si values from each of 10,000 randomly permuted data sets compared to values of the empirical data set (indicated by red arrows). The four larval stages are depicted in different colors. The dashed line, the equation that describes it, and the R2 value are to demonstrate that si ≈ 10ci. In panels B, C, and E, p-values are the fractions of instances (out of 10,000) in which randomly permuted data were more extreme than those from the empirical dataset. In panel D, no value was as high as 6.41, indicating a conservatively estimated p < 10−4.
We also noted that unlike CVs of absolute stage durations that declined from L1 to L4 (Figure 1D), CVs of fractional stage durations were quite similar (Figure 4A). In fact, the standard deviation of these four values (5.28, 5.45, 5.17, 4.54%) was significantly lower than the same quantity in the 10,000 data sets that were generated by randomly permuting stage durations of L1 through L4 (Figure 4E), whereas the same was not true for standard deviation of absolute stage durations (Figure 4F). Therefore, two observations regarding our empirical data are true – A) fractional stage durations are less variable across individuals than absolute stage durations and B) variability of fractional stage durations is more similar across stages than variability of absolute stage durations.
The numerical tests described above suggested that observations A) and B) reflected some underlying properties of the empirical data and were not trivially due to the way in which relative stage durations were computed from absolute stage durations. Still, we sought a better understanding of observations A) and B) and therefore analytically derived the relationship between relevant quantities (derivation is shown in Figure S4):
where ri and ci are CVs of fractional and absolute stage durations, respectively, for ith larval stage; c is the CV of total (L1+L2+L3+L4) absolute developmental time; and si is the correlation between absolute duration of ith larval stage and absolute total time. The above relationship is approximate and holds for ri, c, ci ≪ 1.
With respect to the observation A), the analytical relationship above confirms that ri could be greater, smaller, or equal to ci. The fact that in our data ri tends to be lower than ci reflects particular properties of durations of C. elegans larval stages. With respect to the observation B), it can be seen that if ci = 2csi, then ri ≈ c and r1 ≈ r2 ≈ r3 ≈ r4. In the empirical data we analyzed, for all four larval stages, ci = 2csi to within 16% of the value of ci, whereas in the 10,000 randomized data sets such modest deviations were essentially never observed (0, 0, 0, and 7 times for L1, L2, L3, and L4, respectively). The marked differences between the empirical and randomly permuted data are illustrated in Figure 4G – for all four larval stages, empirical values of ci/si reside effectively outside respective permuted distributions. Moreover, the values of ci/si are similar for L1-L4 (si ≈ 10ci), resulting in a nearly linear relationship in Figure 4G, as would be expected if ci = 2csi. It is not currently clear why ci ≈ 2csi. Our analysis suggests that ci ≈ csi if durations of larval stages were perfectly correlated, whereas ci ≈ 4csi if they were uncorrelated. The simplest interpretation of ci ≈ 2csi is that stage durations are somewhat correlated. It will be interesting to determine whether the coefficient 2 is due to happenstance or a deeper, yet to be discovered relationships of stage durations.
Discussion
Understanding mechanisms that regulate the temporal progression of development is an important problem, with much yet to be learned (Ebisuya and Briscoe, 2018). Species-typical average times are sufficient for addressing some questions, such as establishing timelines of specific developmental programs and studying molecular perturbations that alter them. Other mechanistic insights will require explicit consideration of inter-individual variation. Examples include understanding how timing of specific developmental events scales across individuals and environmental conditions. Although our study is focused on C. elegans, it is possible to estimate durations of discrete developmental stages in other species, such as Drosophila (Schumann and Triphan, 2020). We believe that the approaches we presented here would be useful for analyzing those data as well as any other multistage developmental processes for which high-resolution temporal measurements could be made for a large number of individuals.
We relied on minimal and apparently reasonable assumptions to infer duration of larval stages of individual C. elegans hermaphrodites from continuous measurements of their locomotor activity. One assumption that remains to be tested is whether our operational definition of stage boundaries (as midpoints of periods of reduced activity) yielded systematically different estimates of stage durations compared with ecdysis, which actually marks transition between stages. Our estimates of average stage durations are highly concordant with those obtained previously. Estimates of population-wide averages are robust and the sample of 125 individuals is ample for the task. However, although this is among the largest sets used for inferring developmental timing in C. elegans, future studies should be designed to be considerably larger to more fully capture individual-to-individual variability and to infer stage correlations, both features being susceptible to the effects of outlying values. Precision of the method also requires that provisions be made to explicitly account for batch effects that inevitably arise from multiple and difficult-to-control sources of variability. Our experience suggests that a reasonable tradeoff for larger sample sizes would be recording frequency ~0.1 Hz, which is more than an order of magnitude lower than those commonly used in studies of behavior.
Our analysis of individual timelines revealed several features of postembryonic development that could not have been identified if substantially fewer individuals were studied or if only population-average metrics were considered. These findings coalesce around three main ideas:
First, the dramatic increase in body length (~4X; (Hirsh et al., 1976)) and volume (~10X; (Uppaluri and Brangwynne, 2015)), that occur during larval development in C. elegans, require voracious food consumption. Our analyses suggest that only during the L2 stage the rate of development is correlated with overall locomotor activity, which reflects foraging behavior (Calhoun et al., 2014; Flavell et al., 2013). This somewhat surprising result may imply that even in the animals that display the highest levels of exploratory activity, nutrient intake is sufficiently high to permit fast larval development. Alternatively, appropriate features of exploratory behavior that could predict developmental rate remain to be discovered as are environmental conditions that would make exploratory activity rate-limiting for postembryonic development. The final commitment to reproductive development (as opposed to dauer) occurs in L2 (Schaedel et al., 2012), which may require higher sensitivity to nutrition during this stage and thus help to explain the tighter coupling between activity and rate of development.
Second, there appears to be two separable phases during postembryonic development – one comprised of the first three larval stages (L1-L3) and the second of the L4. Absolute durations of L1-L3, unlike durations of the L4s, are significantly different between fast and slow developing animals (Figure 3C). Durations of L1-L3 are at least somewhat correlated to each other, but far less so to L4 (Figure 3D, E). Another way to illustrate the dichotomy between L1-L3 on the one hand and L4 on the other hand, can be seen in a comparison, using fractional stage durations, of developmental progression of 20 fastest vs 20 slowest developers. Fractions of overall development time devoted to L1, L2, and L3 were indistinguishable between these two groups, whereas L4 distributions were essentially nonoverlapping (Figure 5A). This observation is opposite to what we found when analyzing the same data using absolute stage durations (Figure 3C). The simplest hypothesis to account for these findings is that the dichotomy between L1-L3 and L4 reflects two different underlying processes, one for each of these two epochs, that are at least somewhat decoupled. It is not currently clear what these processes might be, but an intriguing possibility is that duration of L1-L3 may reflect some aspect of somatic development, whereas the L4 may be dominated by germline production.
Figure 5. Temporal organization of postembryonic development in C. elegans.
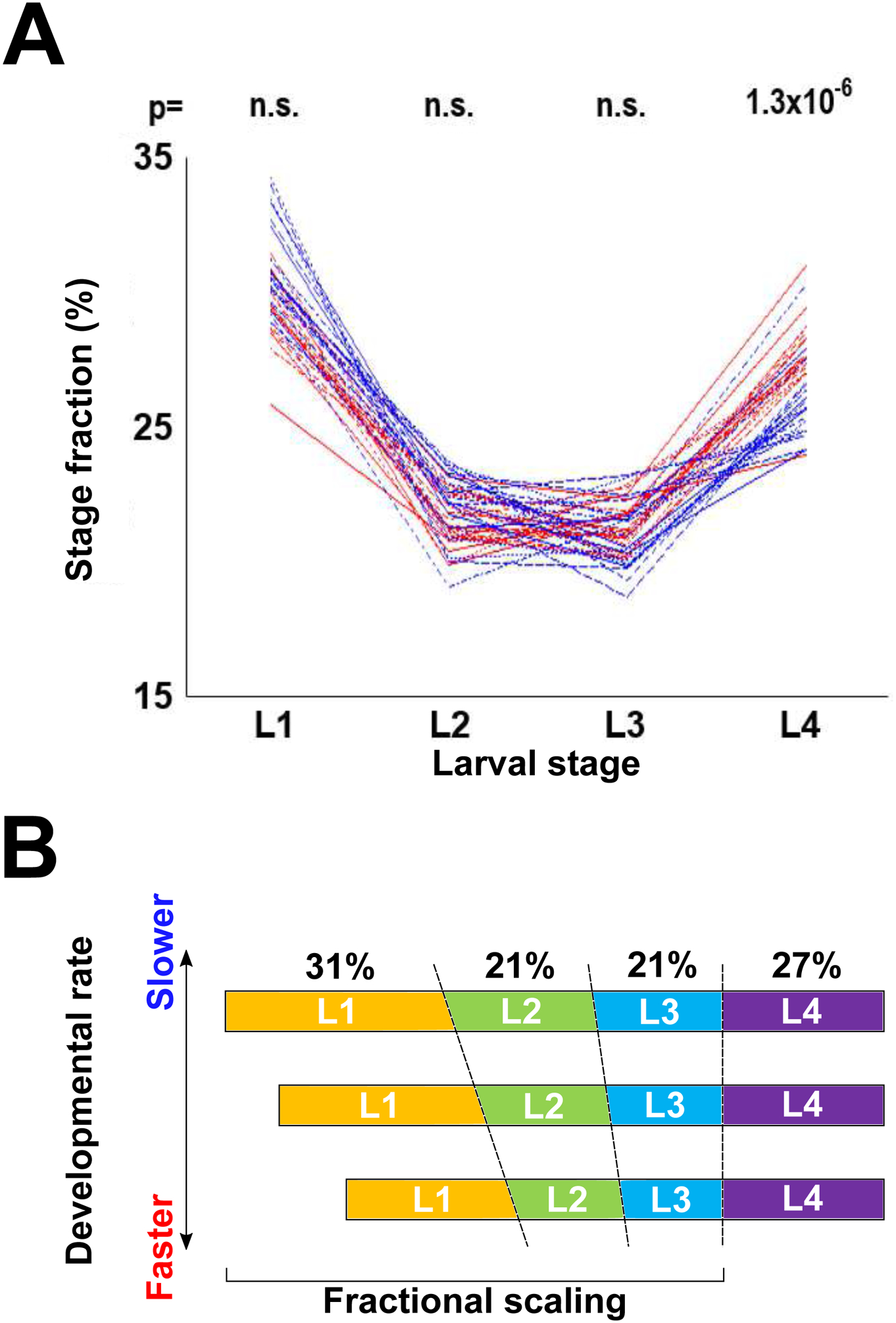
(A) Fractional stage durations of the 20 fastest and 20 slowest worms to reach adulthood. p-values shown above each stage are results of the Kolmogorov-Smirnov test comparing durations of that stage for the 20 fastest and 20 slowest developing worms. Compare with Figure 3C. (B) Model of temporal organization of postembryonic development in C. elegans. The three profiles shown correspond to a slow, intermediate, and fast developing individuals. Despite differences in absolute duration of development, fractions of overall developmental time devoted to each larval stage are conserved, primarily due to proportional scaling of L1-L3. Absolute duration of the L4 stage is less variable among individuals.
Third, some animals develop consistently faster than others at least in part because absolute durations of the first three larval stages are somewhat positively correlated (Figure 3D). We argue that these correlations arise from scaling of durations of the first three larval stages with respect to the total duration of development. A recent study used an entirely different set of measurements to estimate timing of developmental events in C. elegans (Filina, 2020). These authors found evidence of substantial individual-to-individual variability of developmental timing (~10 hours between fastest and slowest larvae to reach the L4-to-adult transition, which is the same as we report here) as well as temporal scaling, that is, an observation that despite variability in absolute developmental stage durations, relative timing of specific events is highly similar across individuals.
What could be the source of individual-to-individual variability of developmental timing? One possible explanation might be the difference in maternal provisioning of oocytes because offspring of young (Day 1) mothers reach the L4-to-adult molt ~2 hours slower than offspring of Day 2 mothers and ~4 hours slower than offspring of Day 3 mothers (Perez et al., 2017). However, these values refer to ~median developmental times. When maternal ages were synchronized to within ~1 day (Day 1, Day 2, and Day 3), larvae still developed at different rates – the gap between the fastest and the slowest developing larvae in each of these three categories was greater than 6 hours (Perez et al., 2017). For comparison, the gap between the fastest and the slowest developers in the set of 125 individuals we analyzed in this study was ~10 hours, same as in (Filina, 2020), and was ~8 hours when sample size was reduced to match those of Perez et al. (see Materials and Methods). We concluded that although we could not assign precise maternal age to the larvae in our study, this variable made a modest contribution to the observed differences in developmental rates and that other sources of variation likely exist.
A plausible mechanism to account for the observation of fractional scaling of developmental time could be a “sizer” model that stipulates that in C. elegans molts occur once larvae reach a certain volume/weight (Uppaluri and Brangwynne, 2015), akin to size-related checkpoints that are critical in postembryonic development in insects (Nijhout, 2003; Rewitz et al., 2013). Developmental rates differ among animals, but a size constraint that is a fraction of a size required to attain adulthood (or a highly correlated proxy) would impose proportional scaling on developmental time, such that fractional durations would be relatively constant across individuals and environmental conditions. Absolute duration of the L4 stage shows little correlation with the three earlier stages, but it is more tightly constrained, therefore contributing less to the variability of the overall developmental time (Figure 5B). Our analyses suggest that a study of mechanisms that control scaling of L1-L3 stages, duration of the L4 stage, and relationship between variability and developmental timing, is likely to be fruitful.
Supplementary Material
Highlights:
Behavioral tracking data reveal rates of development in individual C. elegans
Correlations among larval stage durations result in faster or slower development
Individual rates of development are decoupled from behavioral activity
Durations of larval stages scale as a fraction of total time to adulthood
Acknowledgments
We thank R. Morimoto for generous hospitality and S. Stern for sharing data and advice. IR and VG are grateful to Marshall Butler. This work was funded in part by the NSF (IOS-1755244) and NIH (R01GM126125) grants to IR.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abbott AL, Alvarez-Saavedra E, Miska EA, Lau NC, Bartel DP, Horvitz HR, Ambros V, 2005. The let-7 MicroRNA family members mir-48, mir-84, and mir-241 function together to regulate developmental timing in Caenorhabditis elegans. Dev Cell 9, 403–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abrahante JE, Daul AL, Li M, Volk ML, Tennessen JM, Miller EA, Rougvie AE, 2003. The Caenorhabditis elegans hunchback-like gene lin-57/hbl-1 controls developmental time and is regulated by microRNAs. Dev Cell 4, 625–637. [DOI] [PubMed] [Google Scholar]
- Ambros V, Horvitz HR, 1984. Heterochronic mutants of the nematode Caenorhabditis elegans. Science 226, 409–416. [DOI] [PubMed] [Google Scholar]
- Antebi A, Culotti JG, Hedgecock EM, 1998. daf-12 regulates developmental age and the dauer alternative in Caenorhabditis elegans. Development 125, 1191–1205. [DOI] [PubMed] [Google Scholar]
- Ben Arous J, Laffont S, Chatenay D, 2009. Molecular and sensory basis of a food related two-state behavior in C. elegans. PLoS One 4, e7584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byerly L, Cassada RC, Russell RL, 1976. The life cycle of the nematode Caenorhabditis elegans. I. Wild-type growth and reproduction. Dev Biol 51, 23–33. [DOI] [PubMed] [Google Scholar]
- Calhoun AJ, Chalasani SH, Sharpee TO, 2014. Maximally informative foraging by Caenorhabditis elegans. Elife 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churgin MA, McCloskey RJ, Peters E, Fang-Yen C, 2017. Antagonistic Serotonergic and Octopaminergic Neural Circuits Mediate Food-Dependent Locomotory Behavior in Caenorhabditis elegans. J Neurosci 37, 7811–7823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ebisuya M, Briscoe J, 2018. What does time mean in development? Development 145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filina O, Haagmans R, van Zon JS, 2020. Temporal scaling in C. elegans larval development. bioRxiv 2020.09.21.306423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flavell SW, Pokala N, Macosko EZ, Albrecht DR, Larsch J, Bargmann CI, 2013. Serotonin and the neuropeptide PDF initiate and extend opposing behavioral states in C. elegans. Cell 154, 1023–1035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frand AR, Russel S, Ruvkun G, 2005. Functional genomic analysis of C. elegans molting. PLoS Biol 3, e312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gouvea DY, Aprison EZ, Ruvinsky I, 2015. Experience Modulates the Reproductive Response to Heat Stress in C. elegans via Multiple Physiological Processes. PLoS One 10, e0145925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gritti N, Kienle S, Filina O, van Zon JS, 2016. Long-term time-lapse microscopy of C. elegans post-embryonic development. Nat Commun 7, 12500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hendriks GJ, Gaidatzis D, Aeschimann F, Grosshans H, 2014. Extensive oscillatory gene expression during C. elegans larval development. Mol Cell 53, 380–392. [DOI] [PubMed] [Google Scholar]
- Hirsh D, Oppenheim D, Klass M, 1976. Development of the reproductive system of Caenorhabditis elegans. Dev Biol 49, 200–219. [DOI] [PubMed] [Google Scholar]
- Huang H, Singh K, Hart AC, 2017. Measuring Caenorhabditis elegans Sleep During the Transition to Adulthood Using a Microfluidics-based System. Bio Protoc 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iwanir S, Tramm N, Nagy S, Wright C, Ish D, Biron D, 2013. The microarchitecture of C. elegans behavior during lethargus: homeostatic bout dynamics, a typical body posture, and regulation by a central neuron. Sleep 36, 385–395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeon M, Gardner HF, Miller EA, Deshler J, Rougvie AE, 1999. Similarity of the C. elegans developmental timing protein LIN-42 to circadian rhythm proteins. Science 286, 1141–1146. [DOI] [PubMed] [Google Scholar]
- Keil W, Kutscher LM, Shaham S, Siggia ED, 2017. Long-Term High-Resolution Imaging of Developing C. elegans Larvae with Microfluidics. Dev Cell 40, 202–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee RC, Feinbaum RL, Ambros V, 1993. The C. elegans heterochronic gene lin-4 encodes small RNAs with antisense complementarity to lin-14. Cell 75, 843–854. [DOI] [PubMed] [Google Scholar]
- Monsalve GC, Van Buskirk C, Frand AR, 2011. LIN-42/PERIOD controls cyclical and developmental progression of C. elegans molts. Curr Biol 21, 2033–2045. [DOI] [PubMed] [Google Scholar]
- Moss EG, Lee RC, Ambros V, 1997. The cold shock domain protein LIN-28 controls developmental timing in C. elegans and is regulated by the lin-4 RNA. Cell 88, 637–646. [DOI] [PubMed] [Google Scholar]
- Nagy S, Raizen DM, Biron D, 2014. Measurements of behavioral quiescence in Caenorhabditis elegans. Methods 68, 500–507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson MD, Trojanowski NF, George-Raizen JB, Smith CJ, Yu CC, Fang-Yen C, Raizen DM, 2013. The neuropeptide NLP-22 regulates a sleep-like state in Caenorhabditis elegans. Nat Commun 4, 2846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nijhout HF, 2003. The control of body size in insects. Dev Biol 261, 1–9. [DOI] [PubMed] [Google Scholar]
- Nika L, Gibson T, Konkus R, Karp X, 2016. Fluorescent Beads Are a Versatile Tool for Staging Caenorhabditis elegans in Different Life Histories. G3 (Bethesda) 6, 1923–1933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olmedo M, Geibel M, Artal-Sanz M, Merrow M, 2015. A High-Throughput Method for the Analysis of Larval Developmental Phenotypes in Caenorhabditis elegans. Genetics 201, 443–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez MF, Francesconi M, Hidalgo-Carcedo C, Lehner B, 2017. Maternal age generates phenotypic variation in Caenorhabditis elegans. Nature 552, 106–109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raizen DM, Zimmerman JE, Maycock MH, Ta UD, You YJ, Sundaram MV, Pack AI, 2008. Lethargus is a Caenorhabditis elegans sleep-like state. Nature 451, 569–572. [DOI] [PubMed] [Google Scholar]
- Ramot D, Johnson BE, Berry TL Jr., Carnell L, Goodman MB, 2008. The Parallel Worm Tracker: a platform for measuring average speed and drug-induced paralysis in nematodes. PLoS One 3, e2208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranganathan R, Sawin ER, Trent C, Horvitz HR, 2001. Mutations in the Caenorhabditis elegans serotonin reuptake transporter MOD-5 reveal serotonin-dependent and -independent activities of fluoxetine. J Neurosci 21, 5871–5884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinhart BJ, Slack FJ, Basson M, Pasquinelli AE, Bettinger JC, Rougvie AE, Horvitz HR, Ruvkun G, 2000. The 21-nucleotide let-7 RNA regulates developmental timing in Caenorhabditis elegans. Nature 403, 901–906. [DOI] [PubMed] [Google Scholar]
- Rewitz KF, Yamanaka N, O’Connor MB, 2013. Developmental checkpoints and feedback circuits time insect maturation. Curr Top Dev Biol 103, 1–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rougvie AE, Ambros V, 1995. The heterochronic gene lin-29 encodes a zinc finger protein that controls a terminal differentiation event in Caenorhabditis elegans. Development 121, 2491–2500. [DOI] [PubMed] [Google Scholar]
- Rougvie AE, Moss EG, 2013. Developmental transitions in C. elegans larval stages. Curr Top Dev Biol 105, 153–180. [DOI] [PubMed] [Google Scholar]
- Schaedel ON, Gerisch B, Antebi A, Sternberg PW, 2012. Hormonal signal amplification mediates environmental conditions during development and controls an irreversible commitment to adulthood. PLoS Biol 10, e1001306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schumann I, Triphan T, 2020. The PEDtracker: An Automatic Staging Approach for Drosophila melanogaster Larvae. Front Behav Neurosci 14, 612313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh RN, Sulston JE, 1978. Some observations on molting in Caenorhabditis elegans. Nematologica 24, 63–71. [Google Scholar]
- Slack FJ, Basson M, Liu Z, Ambros V, Horvitz HR, Ruvkun G, 2000. The lin-41 RBCC gene acts in the C. elegans heterochronic pathway between the let-7 regulatory RNA and the LIN-29 transcription factor. Mol Cell 5, 659–669. [DOI] [PubMed] [Google Scholar]
- Snoek LB, Sterken MG, Volkers RJ, Klatter M, Bosman KJ, Bevers RP, Riksen JA, Smant G, Cossins AR, Kammenga JE, 2014. A rapid and massive gene expression shift marking adolescent transition in C. elegans. Sci Rep 4, 3912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern S, Kirst C, Bargmann CI, 2017. Neuromodulatory Control of Long-Term Behavioral Patterns and Individuality across Development. Cell 171, 1649–1662 e1610. [DOI] [PubMed] [Google Scholar]
- Stroustrup N, Anthony WE, Nash ZM, Gowda V, Gomez A, Lopez-Moyado IF, Apfeld J, Fontana W, 2016. The temporal scaling of Caenorhabditis elegans ageing. Nature 530, 103–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sulston JE, Horvitz HR, 1977. Post-embryonic cell lineages of the nematode, Caenorhabditis elegans. Dev Biol 56, 110–156. [DOI] [PubMed] [Google Scholar]
- Sulston JE, Schierenberg E, White JG, Thomson JN, 1983. The embryonic cell lineage of the nematode Caenorhabditis elegans. Dev Biol 100, 64–119. [DOI] [PubMed] [Google Scholar]
- Sze JY, Victor M, Loer C, Shi Y, Ruvkun G, 2000. Food and metabolic signalling defects in a Caenorhabditis elegans serotonin-synthesis mutant. Nature 403, 560–564. [DOI] [PubMed] [Google Scholar]
- Telford MJ, Bourlat SJ, Economou A, Papillon D, Rota-Stabelli O, 2008. The evolution of the Ecdysozoa. Philos Trans R Soc Lond B Biol Sci 363, 1529–1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turek M, Bringmann H, 2014. Gene expression changes of Caenorhabditis elegans larvae during molting and sleep-like lethargus. PLoS One 9, e113269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uppaluri S, Brangwynne CP, 2015. A size threshold governs Caenorhabditis elegans developmental progression. Proc Biol Sci 282, 20151283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wightman B, Ha I, Ruvkun G, 1993. Posttranscriptional regulation of the heterochronic gene lin-14 by lin-4 mediates temporal pattern formation in C. elegans. Cell 75, 855–862. [DOI] [PubMed] [Google Scholar]
- Yemini E, Jucikas T, Grundy LJ, Brown AE, Schafer WR, 2013. A database of Caenorhabditis elegans behavioral phenotypes. Nat Methods 10, 877–879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang WB, Sinha DB, Pittman WE, Hvatum E, Stroustrup N, Pincus Z, 2016. Extended Twilight among Isogenic C. elegans Causes a Disproportionate Scaling between Lifespan and Health. Cell Syst 3, 333–345 e334. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


