Dopamine signals as temporal difference errors: Recent advances

Abstract

In the brain, dopamine is thought to drive reward-based learning by signaling temporal difference reward prediction errors (TD errors), a “teaching signal” used to train computers. Recent studies using optogenetic manipulations have provided multiple pieces of evidence supporting that phasic dopamine signals function as TD errors. Furthermore, novel experimental results have indicated that when the current state of the environment is uncertain, dopamine neurons compute TD errors using “belief states” or a probability distribution over potential states. It remains unclear how belief states are computed but emerging evidence suggests involvement of the prefrontal cortex and the hippocampus. These results refine our understanding of the role of dopamine in learning and the algorithms by which dopamine functions in the brain.

Introduction

A novice cook is purchasing tomatoes at the farmer’s market. He picks out a bunch of different tomatoes: some still green, some just turning red, and some deep red. After eating these tomatoes, he realizes that the deep red tomatoes are the tastiest, and he seeks out only ripe tomatoes in the future.

Animals must learn to predict the value of potential outcomes in order to survive. Dopamine is thought to play a critical role in associative learning by signaling the error between actual and predicted values. Here we will discuss many recent works which have strengthened the idea that dopamine carries an error signal between actual and expected value. In addition, we will discuss an expanded theoretical framework for reinforcement learning in the brain and its possible implementation.

Dopamine as a temporal difference error signal

Temporal difference (TD) learning is a computer learning theory that has been a cornerstone in understanding how dopamine may drive learning [1,2]. In TD learning, the agent attempts to learn accurate value predictions for each “state” s. States represent the environment, or task space, in a way that is useful to the animal as it performs the current task. In TD learning, each state represents the environment at a single moment in time, such that value predictions and updates may be made continuously in time. Value is defined as the discounted sum of future reward:

$$V(s_t)=\sum _{\tau =t}^{\infty }{\gamma }^{\tau -t}r(s_{\tau })$$ (1)

Where s_t is the state s that the agent occupies at the current time t, r(s_τ) is the reward at time τ, and γ is a discount factor that decrements future rewards. Because the states and transitions between them are represented as a Markov process (Figure 1a), Equation 1 can be written recursively using the Bellman equation:

$$V(s_t)=r(s_t)+\gamma V(s_{t+1})$$ (2)

Figure 1 ∣. Evidence for dopamine as a TD error signal.

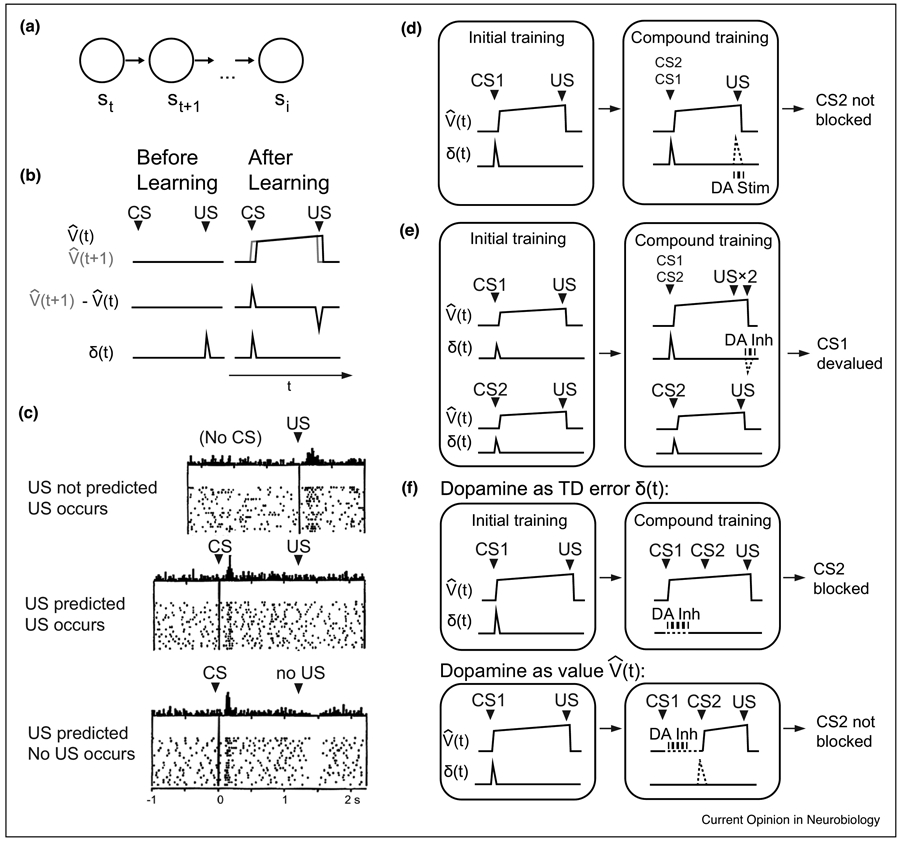
(a) In temporal difference learning, the agent proceeds through ‘states’ s. (b) Value signal, temporal difference of value signal, and error signal δ produced by a simple TD model. (c) Firing pattern of a putative dopaminergic neuron during a classical-conditioning task. From Schultz, Dayan, and Montague 1997 [3]. (d) Dopaminergic stimulation (DA stim) at the time of the US allows a cue that would otherwise be blocked to be learned. This can be modeled as dopaminergic stimulation signaling a positive TD error at the time of the US (dotted line). Based on Steinberg et al, 2013 [5]; Keiflin et al, 2019 [6]. (e) Dopaminergic inhibition (DA inh) at the time of the expected second US in an overexpectation paradigm led to the ‘un-reminded’ CS (CS1) being devalued. This can be modeled as dopaminergic inhibition signaling a negative TD error at the time of the ‘overexpected’ US (dotted line). Based on Chang et al, 2017 [25]. (f) If dopamine signals a TD error, inhibition at the time of a learned CS1 should not affect the value prediction based on CS1, thereby blocking learning of additional value for CS2. If dopamine signals value, dopaminergic inhibition following CS1 should allow learning to occur for CS2 (dotted lines). Experimental results from Maes et al, 2020 [14], supported the hypothesis that dopamine signals a TD error rather than value.

The model’s value prediction $\widehat{V}(s_t)$ for each state is therefore bootstrapped to the value prediction at the subsequent state $\widehat{V}(s_{t+1})$:

$$\widehat{V}(s_t)=r(s_t)+\gamma \widehat{V}(s_{t+1})$$ (3)

As an agent proceeds from timestep t to timestep t + 1, it receives information on reward r(s_t) received at timestep t, as well as undergoing the transition to state s_t+1. Even though $\widehat{V}(s_{t+1})$ is still an estimate, the right side of Equation 3 represents the most current estimation for state s_t because it incorporates new information about reward obtained after timestep t. Therefore, the value prediction $\widehat{V}(s_t)$ must be updated to reflect any discrepancy between the left and right sides of Equation 3:

$${\delta }_t=r_t+\gamma \widehat{V}(s_{t+1})-\widehat{V}(s_t)$$ (4)

Where δ_t is the temporal difference error at timestep t. δ_t can be intuitively understood as the discounted temporal derivative of the value function, plus reward (Figure 1b). δ_t is used to update $\widehat{V}(s_t)$ according to the following update rule,

$$\widehat{V}(s_t)\leftarrow \widehat{V}(s_t)+\alpha {\delta }_t$$ (5)

where α is the learning rate (0 < α < 1). Some important aspects of TD learning can be highlighted through the trial-by-trial process of learning an association between a conditioned stimulus (CS) and a rewarding unconditioned stimulus (US) separated by a constant interstimulus interval (ISI). On the first trial, there are no value predictions, resulting in a positive prediction error δ_t due to unpredicted reward (US) received at time t. This results in a value update that produces a positive $\widehat{V}(s_t)$ at time t. On the subsequent trial, there will be a positive prediction error δ_t at time t – 1, because $\gamma \widehat{V}(s_{t+1})$ is now positive, thereby increasing $\widehat{V}(s_{t-1})$. In this way, the prediction errors and resulting value updates will tile backward during the ISI interval until the value prediction spans the ISI. After learning, so long as the CS cannot be reliably predicted, the temporal derivative of the value function will immediately become positive after the CS, producing a positive prediction error δ_t at the time of the CS. However, because the value function spans only the time to reward, the temporal derivative of the value function is negative at precisely the time of reward, canceling excitation from reward. If reward does not arrive, there is a dip at the time of usually delivered reward. This set of responses emerge in both TD error signals and dopaminergic neurons after training on a CS-US association: excitation at the time of a learned CS, decreased excitation at the time of a predicted reward relative to an unpredicted reward, and a negative response at the time of an omitted reward [3,4] (Figure 1b-c). This striking resemblance between TD error signals and dopaminergic firing led to the proposal that dopamine neurons drive associative learning [3].

There is mounting causal evidence in rodents that dopaminergic signals function as TD errors in the brain. Normally, associative learning is ‘blocked’ if a CS already predicts a reward. In other words, if a new CS is repeatedly presented alongside a learned CS in anticipation of the same reward, conditioned responding is not observed when the new CS is presented alone. Because the original CS already predicts the reward, no new learning occurs for the new CS. A study by Steinberg et al showed that optogenetically activating dopamine neurons in the ventral tegmental area (VTA) at the time of a US, during the blocking phase of a classical conditioning experiment, elicited conditioned responding associated with a CS that should have otherwise been blocked [5] (Figure 1d). This result can be modeled as reinstating a TD error at the time of the US (when the US should have been fully predicted), allowing the prediction error to potentiate the value prediction of the otherwise-blocked CS. More recently, Keiflin et al also demonstrated that optogenetically activating VTA dopamine neurons at the time of the US potentiates responding to the CS [6]. Keiflin et al. utilized a reward upshift paradigm, in which a CS would not be blocked so long as the amount of reward was increased. In one arm of the study, dopaminergic neurons were optogenetically activated rather than increasing the amount of reward. The CS, which would have been otherwise blocked in the absence of optogenetic stimulation at the time of the US, later elicited conditioned responding as if it had been paired with upshifted reward. This result could also be explained by modeling dopamine as a TD error at the time of the US, which potentiated the value prediction of the otherwise-blocked CS.

In TD learning, dopamine responses to US “shift” to the CS after learning. A key prediction of TD learning is that CS dopamine responses develop through the activation of dopamine neurons during the US. Indeed, recent studies in monkeys and rats demonstrated that optogenetic stimulation of VTA dopamine neurons seconds after a CS presentation can cause an increase in a CS dopamine response [7], or even generate a CS response without a natural reward [8].

In addition to the above experiments which optogenetically activated dopamine neurons at the time of the US, there is also evidence that dopamine functions as a TD error based on experiments that optogenetically inhibited dopamine neurons at the time of the US. One work by Chang et al utilized a heightened over-expectation paradigm, in which animals learned to separately associate two CS’s with 3 reward pellets [9] (Figure 1e). Animals should then ‘over-expect’ 6 pellets when these cues were presented together in the compound training phase, and neither cue should be devalued. During compound conditioning, one of the two rewarded cues was also presented alone with 3 pellets as a reminder of that ‘reminded’ cue’s learned value. However, dopamine was inhibited during consumption of the last 3 of the 6 pellets, resulting in less conditioned responding during probe trials of the non-reminded cue. This result could be explained by modeling optogenetic inhibition as a negative TD error following presentation of the compound cue, thereby decrementing the value associated with the non-reminded cue. Other studies with different conditioning paradigms have utilized optogenetic inhibition at the time of the US in a learned CS-US association to produce results consistent with some aspects of extinction [10] and devaluation of a new cue added to the previously learned CS [11]. An experiment by Parker et al used a two-armed bandit task in mice [12]. Optogenetically inhibiting dopamine neurons at the time of the outcome biased choice behavior away from the lever after which inhibition was applied. A more recent study showed that optogenetic inhibition as well as activation during the US can bias the animal’s choice behavior in future trials but not when it was applied before the US [13]. These results demonstrate that dopamine activities can bias the animal’s choice behaviors both positively and negatively, and defined a critical window during which their activity reinforces preceding behaviors. In summary, there is evidence that both optogenetic excitation and inhibition at the time of the US can increase and decrease conditioned responding and bias choice behavior to an antecedent CS, consistent with a TD error.

Fewer studies have tested whether dopamine activation at the time of the CS represents a TD error. One recent study by Maes et al aimed to directly test this hypothesis [14]. The authors sought to identify whether the CS dopamine response is most consistent with signaling a TD error versus signaling the value of upcoming rewards, an idea which has arisen in some proposals [15]. The authors used a blocking paradigm in which the animal was initially conditioned to associate CS 1 with a reward (Figure 1f). In the blocking phase, CS 1 was presented first for several seconds, followed by CS B for several seconds, followed by the same reward. Normally, CS 2 should be blocked. However, the authors optogenetically inhibited dopaminergic neurons at the beginning of CS 1. The authors used computational modeling to argue the following: if dopamine carries a value signal, assuming that optogenetic inhibition blocked the entire value signal carried forward from CS 1, CS 2 should not be blocked. In contrast, if dopamine carries a TD error in the prediction of value, the value signal should still carry forward following CS 1 and block accrual of value prediction for CS B because reward would be fully predicted. Maes et al found conditioned responding to be most consistent with dopamine as a TD error signal, versus a value signal. This work has some caveats. For instance, if CS dopamine carries a value signal, briefly inhibiting dopamine at the beginning of CS A could allow value to rebound following a termination of the light pulse, thereby blocking value accrual of CS B. It is unclear exactly how dopaminergic signaling was affected by the optogenetic inhibition in the absence of recording dopamine neurons. Nonetheless, the experimental design is compelling. Future experiments similarly grounded by divergent model predictions depending on the proposed computational role of dopamine, combined with dopaminergic recordings, would help decipher the signal carried by dopaminergic activation at the CS.

Model-based features for reinforcement learning

A classic adaptation of temporal difference learning to dopaminergic signaling in the brain assumes that the agent learns a value approximation that is a weighted linear combination of stimulus features x_i(t):

$$\widehat{V}(t)={\sum }_i{w}_i{x}_t(i)$$ (6)

where w_i is a predictive weight associated with feature i. A traditional feature representation is a complete serial compound (CSC) representation that tracks elapsed time relative to observable stimuli (Figure 2a). In CSCs, x_t(1) would be a vector of zeros, except for a value of 1 for a single timepoint t. x_t(2) would be an identical vector, except that the value of 1 would occur at timepoint t + 1. In this way, the x_t(i) CSC features show serial activations that tile time intervals. CSC features x_t(i) are possibly signaled by cortex, and the weights w_i are possibly contained in the corticostriatal synapse.

Figure 2 ∣. Belief state TD model.

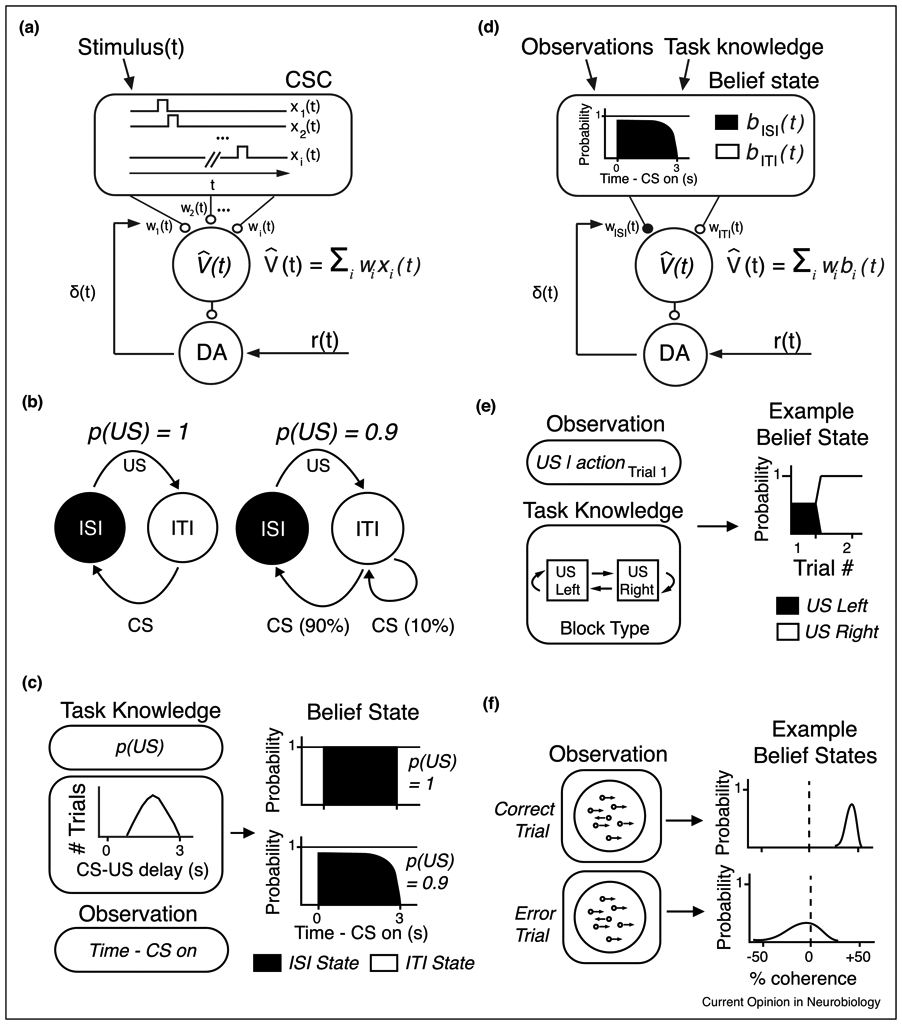
(a) Complete Serial Compound (CSC) schematic for implementing TD learning in the brain. Value is computed as the linear sum of features (each “CSC” component, indexed from 1-i) multiplied by their weights. (b) Semi-Markov schematic for computing a belief state under fully observable versus partially observable task conditions. Adapted from Daw et al. (2006) [17]. (c) In a task invoking variable delay times and particular reward contingencies (illustrated for 100%- and 90%-rewarded contingencies), the agent uses its observation of time passed since cue onset in addition to its knowledge of reward timing/contingency to compute a probability distribution over possible states, which is called a belief state. (d) Belief state TD model schematic. Value is computed as the linear sum of belief in each state (probability of each state), multiplied by each state’s respective weights (e) Based on observation of the first trial type within a block, an agent may use its knowledge of the task structure to compute a belief state. Based on Bromberg-Martin et al. (2010) [20]. (f) Based on ambiguous sensory stimuli (random dot motion), the agent may compute a belief state over possible coherences and direction of movement. Adapted from Lak et al. (2017) [24].

The weights are updated according to the following learning rule:

$$\Delta w_i=\alpha x_t(i){\delta }_t$$ (7)

where α is a learning rate and δ_t is the TD error from Equation 3. The CSC and closely related models that incorporate temporal uncertainty [16] are compatible with many features of dopamine RPE signals, as well as timing-related aspects observed in endogenous dopamine signals such as delay discounting.

More recently, experimental evidence has pointed to a richer feature representation for reinforcement learning in the brain. Value is computed as a weighted sum of stimulus features that correspond to an inferred probability distribution over states, or ‘belief state’ [17, 18] (Figure 2d):

$$\widehat{V}(t)=\sum _i{w}_i{b}_t(i)$$ (8)

where b_t(i) represents the belief state (i.e. the probability of being in the state i) at time t, with i indexing individual states, and w_i being a predictive weight associated with state i. More precisely, the belief state is the probability of being in state i, given all the previous observations (o_t, o_t−1, ⋯, o₁) and actions (a_t−1, a_t−2, ⋯ , a₁,),

$$b_t(i)=P(s_t=i,\mid o_t,a_{t-1},o_{t-1},a_{t-2},\cdots ,a_1,o_1).$$ (9)

As formulated in (9), the current belief b_t(i), in principle, depends on all the previous observations and actions. However, using the Bayes rule and the Markov assumption (future outcomes only depend on the current state but not the past), the equations (9) can be rewritten in a recursive form such that the current belief b_t(i) can be computed based only on the current observation o_t, the belief at the previous time step b_t–1(j) and the probability of transitioning from state j to state i given an action a_t–1 that was just taken,

$$b_t(i)=k\cdot P(o_t\mid s_t=i)\cdot \sum _{j}p(j,a_{t-1},i)\cdot b_{t-1}(j)$$ (10)

where k is a normalization constant (to make the total probability to be 1), and i represents the current states and j the previous states [18], P(o_t∣s_t = i) is the likelihood of the new observation o_t in state i. The term p(j, _t–1, i) connects two states (i and j) with certain probabilities. This transition probability and the reward function (i.e. the information about when reward will occur in the environment, r(s_t)) constitute a “model” of the world (or a task). In this sense, computing belief states necessitates a model of the world.

After “experiencing” belief states, states’ weights are updated proportional to the probability with which the agent ‘believes’ it occupies a particular state:

$$\Delta w_i=\alpha b_i(t){\delta }_t$$ (11)

A TD model with a belief state began as a theoretical proposal to gracefully equip the TD model for uncertain conditions. This proposal also happened to also account for some experimental findings that the classic TD model could not account for, such as dopamine neurons failing to show a reward omission response if reward was delivered early (perhaps reflecting an inferred switch in task state after reward receipt) [19]. In addition, it would account for the finding that dopamine neurons reflected inferred values of cues after block changes [20]. In this task, a monkey’s saccade to one of two targets would lead to reward. Following an un-signaled block shift, the rewarded and unrewarded targets would switch. After an animal experienced lack of reward on the previously rewarded side, dopaminergic neurons showed excitation to the previously unrewarded cue on the following trial. This result could be explained by the belief state shifting to reflect the block switch, thereby appropriately assigning higher value to the newly rewarded cue even prior to it being experienced in the new block (Figure 2e). More recently, experiments explicitly designed to test dopamine signaling under ambiguous task conditions, or ‘state uncertainty’ have favored a belief state TD model [13,21-24].

One set of experiments involves variable reward timings [21]. On any given trial, reward may arrive as early as 1.2s, or as late as 2.8s, following the CS. In one task, reward arrived in 100% of trials: although reward timing was variable, the reward always arrived. In the other task, reward arrived in 90% of trials: in addition to timing variability, there was also uncertainty as to whether reward would arrive at all. One could conceive of the task as comprising two states: an interstimulus interval (ISI) during which reward is expected, and an intertrial interval (ITI) during which reward is not expected (Figure 2b). Whereas the CS would clearly signal entry into the rewarded (ISI) state in the 100%-rewarded task, there was state uncertainty in the 90%-rewarded task due to the possibility of reward omission. As time passes following the CS and no reward arrived in the 90%-rewarded task, the belief state would shift to eventually favor the non-rewarded state (meaning that an increasingly smaller probability would be assigned to the ISI), resulting in a smaller value prediction as time passed (Figure 2c). There was a striking difference in dopaminergic signaling between the two tasks. In the 90%-rewarded task, dopaminergic RPEs were largest for the latest rewards. In other words, because the belief state gradually shifted to favor the possibility of a reward omission trial if the animal was kept waiting for reward, TD errors were larger for rewards delivered later, only in the 90%-rewarded task.

Other recent experimental results can also be explained by the belief state TD model. Two studies in primates and mice, respectively, use a belief state to model right/left choice behavior (perceptual decisions) following presentation of an ambiguous stimulus (random dot motion or moving gratings, respectively) [13, 24]. In these tasks, a belief state can be defined as a distribution over the relevant stimulus parameter (e.g. motion coherence and direction in [24] and stimulus contrast in [13]) given the subject’s estimate on the stimulus in a given trial (i.e. “stimulus belief state”, Figure 2f). In a belief state TD model, the agent represents a subjective estimate of a stimulus using a probability distribution over a stimulus parameter (i.e. belief states), instead of a point estimate. Using this stimulus belief states, the agent then computes the probability of the stimulus being on a particular side in order to choose an action. This belief state TD model was compared against an alternative TD model which does not have belief states nor a subjective estimate of the current stimulus altogether (“traditional TD model). That is, this alternative model does not have access to the subjective estimate of the stimulus which contributed to a decision process, but associated the presented stimulus directly with reward. Their modeling showed that in the belief state TD model, the value prediction would be increasingly divergent for correct and error trials, for increasing coherences. On a high-coherence ‘correct’ trial, the probability of a correct response given the sensory percept (akin to sensory confidence), would be high, because the random dot motion sampled by the animal would be statistically likely to fall far from the decision boundary for that trial. This would correspond to a positive dopaminergic response at the time of that stimulus. On a high-coherence ‘incorrect’ trial, the animal would have had to sample random dot motion relatively closer to the decision boundary, as the probability of observing high-coherence in the incorrect direction is very low. Therefore, sensory confidence would be low on high-coherence ‘incorrect’ trials. This would correspond to a smaller dopaminergic response at the time of the stimulus for high-coherence incorrect trials. Importantly these divergent predictions for ‘correct’ and ‘error’ trials rely on the animal comparing its observation to belief about the underlying noisy stimulus. By contrast, the traditional TD model exhibited identical predictions for ‘correct’ and ‘error’ trials at various coherences. Thus, the belief state TD model better explained the observed dopamine responses. It remains to be tested whether a model that has access to the subjective estimate of stimulus, but does not have stimulus belief state (i.e. probability distribution over a stimulus parameter), can equally explain the data.

Finally, another study providing support for the belief state TD model also showed that dopamine responses appear to subtract inferred values [22]. In this study, blocks consisted of identical trials of a cue followed by either ‘big’ or ‘small’ rewards. On rare blocks, rewards were of intermediate size. After experiencing one of these intermediate rewards, the dopamine signal at the time of the reward on the subsequent trial appeared to subtract either the value of the ‘big’ or ‘small’ reward from the value of the received intermediate reward. If the animal’s belief state favored the value of a larger intermediate reward as most likely to belong to a ‘big’ reward block, the reward prediction error at the time of reward should be smaller than if an average value for the cue was subtracted (which would be the prediction for traditional TD learning).

These recent studies highlight that the dopamine system can employ a “hybrid” of model-free and model-based processes. Traditionally, a model-free reinforcement learning referred to the learning process that directly associates the value with observable states (often called “cached values”). As discussed above, computing a belief state depends on having a model of the environment, or more specifically, the transition probabilities across states (p(j, a_t–1, i)). For instance, in the variable timing task described above, a model could be as simple as knowing there are two states (ISI and ITI) and a set of transition probabilities between them. This model is needed in order to compute a posterior probability distribution over states (the belief state, b_t(i)) (Equation 10). Downstream of this model-based state representation and resulting belief state, the belief state TD model still ‘caches’ values, which means that it stores values by experiencing the states. In contrast to traditional model-free reinforcement learning, the states are no longer restricted to observable states and can be ‘experienced’ by assigning them an inferred probability and updating weights proportional to the probability occupying the state (Equations 7). Thus, the model-free TD update rules (Equations 3,4) remain unchanged, despite the upstream computation of value relying on a model of the environment or model-based feature representations. This is different from a separate, recent proposal that dopaminergic signals represent errors in the animal’s model of the environment [25,26]: for instance, by driving learning of an association between two unrewarded sensory cues. While temporal difference errors provide errors useful for updating the representation of value, it is unclear how they could be separated from signals carrying errors in sensory features of the environment.

It should also be noted that the belief-state TD model differs from fully model-based reinforcement learning, which uses a model of the environment to compute values for various states by “mentally” simulating a sequence of actions. Consider a maze in which an animal receives different rewards at each possible exit [27]. The animal simulates mental paths through the maze and computes values for states (each corresponding to various locations in the maze). If the animal is hungry, states in the maze leading to food rewards would have greater value, even in the absence of the animal experiencing those states while it is hungry. In this way, value does not have to be cached through direct experience in a particular state. This contrasts with the belief state TD model, in which the animal must infer that it is in a particular state, experience the outcome in that state, and thereby update the state’s value (cached value). One classic example of model-based reinforcement learning is the two-step task [28]. In this task, the subject chooses between two symbols, each of which lead another set of choices that are rewarded with slowly drifting probabilities. Each initially presented symbol leads with high probability to a particular second set of choices (a ‘common’ transition). The critical trials occurred if a subject were to choose an initial set of symbols and then experience the rare transition to a second set of symbols that resulted in reward. In the traditional model-free framework, the subject should be more likely to choose the same initial choice because the choice led to a reward. In contrast, in the model-based framework, the subject should be more likely to choose the opposite choice because they know the opposite choice would be more likely to undergo the ‘common’ transition to the rewarded choices. This requires updating the value of a state (the initially chosen symbol) that was not experienced, rather than simply caching value based on rewards received subsequent to that state. Both human subject behavior and blood-oxygen level dependent fMRI signal in the ventral striatum (thought to be a proxy for dopaminergic signaling), reflected both model-free and model-based contributions to a varying extent in individual subjects. Therefore, dopamine signals may reflect an element of model-based RPEs, which has also been recently proposed in studies involving rodents [26, 29]. However, whether such model-based RPEs would be used separately for updating certain types of states, or whether model-based RPEs would be used in parallel with model-free RPEs, remains to be further studied.

A model-based feature representation could provide a flexible platform for reinforcement learning in the real world. In the original example of picking tomatoes, now imagine the cook encounters an odd-looking greenish tomato he has never seen before. In TD learning with model-free states, he would need to buy the odd tomato, taste it, and assign a value to that particular tomato. In contrast, with a model-based state representation, he could compute a belief state based on tomatoes he has already tasted: perhaps he is 70% sure that the odd tomato is a delicious heirloom variety, and 30% sure it is simply an un-ripened tomato. Without having to taste it, he could already compute a value prediction based on past experiences; if he does taste it, he can use the experience to continue learning about varieties he already knows about. After all, two tomatoes rarely look exactly the same and it would be impractical to learn new values for every new variety. In this way, model-based feature representation can compress the dimensions of the complex real world into previously experienced stimuli.

State representation for reinforcement learning

In the belief state TD model, value is a linear combination of belief in ‘states’, where states represent some task-relevant aspect of the environment that can help an animal predict reward. It is not known how the brain computes a belief state. Also relevant to the belief state TD model, as well as other proposals that rely on a world model to compute value [30], is how and where the brain generates a state representation. Although this is an area of active investigation, we will discuss some recent studies of the prefrontal cortex and the hippocampus that begin to address these questions.

The prefrontal cortex (PFC) is a candidate for computing a belief state. One study used a two-armed bandit task in which the arms corresponding to high and low probabilities, respectively, would switch suddenly [31]. This switch was not signaled and had to be inferred by the monkey. Monkeys’ behavior indicated rapid shifts in preferred arm some time after switches occurred, which was accompanied by swift shifts in PFC activity. Interestingly, behavioral reversal on a particular trial could be predicted by PFC activity at the preceding trial. These findings suggest that PFC reflects the animal’s dynamic beliefs about the state of the task. Another study used a ‘hidden state’ foraging task [32]. Mice traveled between 2 reward ports, either of which could deliver reward with 70% probability. Only one of the two ports could deliver reward at any one time during the task; the ‘rewarded’ port would occasionally switch. If animals successfully inferred the state of the task, receiving a reward at a port would unequivocally confirm that the currently rewarded port was indeed the port just approached by the animal, and that the animal should continue to exploit that port. This contrasts with the prediction from an entirely ‘model-free’ system, where the value of a newly rewarded port would have to gradually accrue with each subsequent reward receipt at that port, and failures would gradually decrement this learned value. Mice behaved in a manner that reflected inferred beliefs based on task parameters: after receiving reward at a newly rewarded port, they continued exploiting that port, and shifted to the other port upon experiencing failures irrespective of the number of rewarded trials experienced. Inactivation of the OFC caused the mice to behave in a ‘model-free’ manner: if the mice had experienced many reward trials at the port, they had to gradually ‘unlearn’ the port’s value through a greater number of failures. This result suggests that the OFC may be important for representing the animal’s beliefs about the task.

Dopaminergic recordings while inactivating prefrontal cortical regions have strengthened the case that the PFC may compute a belief state relevant for reinforcement learning. One recent study used the aforementioned paradigm in which reward was delivered on 90% of trials at a variable delay [33]. Upon inactivating the mPFC, dopamine neurons signaled as if the belief state were fixed in time. Importantly, this effect was specific to the 90%-rewarded task: in a 100%-rewarded version of the variable delay task (in which the state of the environment was unambiguously signaled by the CS), inactivating the mPFC had no effect on dopamine signaling. Thus, the mPFC may convey a belief state to the subcortical circuitry, exclusively in tasks that implicate state uncertainty. Another study investigated the effect of OFC inactivation on dopaminergic signaling [34]. Upon ipsilateral inactivation of the OFC, dopamine neurons failed to signal prediction errors sensitive to inferred changes in CS value, which occurred following block changes. Another recent study suggested a role for the mPFC in representing inferred value, which multiplexes information about cached value with inferred state [13]. In this study, mPFC signals reflected the inferred values of the CS, scaled by sensory confidence computed based on a belief state. Inactivating the mPFC caused dopaminergic signals to increase in magnitude, as if the value prediction became smaller. This contrasted with another study in which mPFC inactivation with muscimol during an unambiguous, fixed delay task caused no changes in dopaminergic signaling [35], suggesting that the mPFC may come into play during tasks that implicate a belief state (e.g. tasks with state uncertainty).

One possible pathway by which mPFC conveys state-relevant information to dopamine neurons is through the nucleus accumbens (NAc). Recent studies have shown specific task-related activity in prelimbic cortex (PL) neurons projecting to the NAc [36-38]. For instance, some PL→NAc neurons multiplex spatial with social information; these cells fired only when the animal was both in a specific location and near another animal [36]. In a different task, PL→NAc neurons distinguish between an animal’s choice of action [37]. Conveying such specific state- and action-relevant information in corticostriatal neurons would allow dopamine to assign value to very specific states, or state-action pairings: for instance, establishing a preference for social interaction while in a specific corner of its enclosure. As many excitatory inputs converge in the NAc, including mPFC inputs that specify state variables, the NAc remains a plausible neural basis of learned value representation through dopaminergic adjustment of the corticostriatal synapse.

While prefrontal regions have been implicated in computing a belief state or inferred values, another line of work deals with the role of the hippocampus in state representation. One study modeled CA1 place cells as representing not the current location, but a probability distribution over potential subsequent locations, or ‘predictive map’ of an agent’s states [39]. Other studies have shown the spatial remapping of a subpopulation of CA1 cells to reflect reward location [40], with cells in deeper layers preferentially adapting their receptive fields to reflect salient aspects of the environment such as reward location [41]. The hippocampus may represent task-relevant states in dimensions other than location. For example, studies have examined hippocampal blood-oxygen level dependent (BOLD) signals in tasks requiring configural learning [42, 43]. This has traditionally been an area of weakness for TD learning algorithms without an explicit state representation, which struggle to assign values to cue AB versus that are different from the sum of values for cues A and B alone. BOLD signals in the hippocampus depended on the degree to which configural versus elemental strategies were used, suggesting that the hippocampus may be involved in determining the appropriate state to update (AB versus A alone, for instance) [43]. Finally, the hippocampus contains ‘time’ cells that scale their receptive fields to tile various interstimulus intervals [44,45], giving rise to the proposal that the hippocampus houses a ‘temporal map’ that could be deployed for reinforcement learning involving time intervals [46]. Therefore, the hippocampus could provide a basis for state representation with respect to multiple dimensions of the environment, including location, time, and cue configuration.

It is not known how either the brain could generate an appropriate belief state representation, or an appropriate state representation. One possible mechanism draws inspiration from a proposal for learning about state space during vocal learning in the songbird [47]. This proposal highlights the importance of neural song ‘replay’ in premotor regions, and comparison of this replay with auditory cortical memories of tutor song. This provides an opportunity for assessing temporal coincidences between the two brain regions, through spike-timing dependent mechanisms and Hebbian plasticity. If the brain actively attempts to anticipate state transitions (e.g. it tries to predict reward timing, after a CS), temporal coincidences that commonly occur during the task may potentiate an appropriate way of representing states. Another mechanism for honing an appropriate feature representation could rely on dopamine. For instance, mesocortical dopaminergic release could manipulate cortical circuits through local changes in spike-timing dependent plasticity (STDP) rules [48-50], specifically around the time of rewards. This type of temporally precise feedback could potentiate representation of states and beliefs that precede the animal accruing reward, allowing an optimal state representation and downstream action policy to emerge over time. Interestingly, a recent proposal using a recurrent ‘prefrontal-like’ Advantage Actor-Critic network (where the Advantage function resembles a TD error) was able to recapitulate animal behavior on many classic reinforcement learning tasks, including a ‘two-step’ tasked that requires model-based feature representation for optimal performance [51]. This suggests that dopaminergic signals conveyed to the prefrontal cortex may be useful in honing an appropriate feature representation for reinforcement learning and behavior. In summary, little is known about how a feature representation is formed, but proposals based on existing data could implicate a spike-timing rule based on anticipated temporal coincidences, or feedback from dopamine itself. Experiments focused on understanding the role of dopaminergic → PFC projections, particularly in behavioral tasks that require inference for optimal performance [52], are an interesting direction for future work.

Conclusion

The hypothesis that dopamine acts as a TD error signal has accrued increasing causal evidence. In addition, experiments testing dopaminergic signaling under ambiguous circumstances have suggested that upstream circuits cache value based on inferred ‘belief’, or probability, that the brain assigns to task states. How the brain arrives on a state representation of the environment, or how it computes belief over these states, are critical next questions for understanding the neural implementation of reward-based learning.

Highlights.

• Optogenetic activation and inactivation of dopamine neurons mimic TD error signals as predicted from reinforcement learning models.

• When the current state is uncertain, TD errors are computed based on a belief state, or a probability distribution over states.

• Computing a belief state requires a model of the world, or a representation of “task states”.

• The medial prefrontal cortex and the hippocampus may play an important role in computing TD errors using belief states.