Abstract
Analysis of time-to-event data, otherwise known as survival analysis, is a common investigative tool in ophthalmic research. For example, time-to-event data is useful when researchers are interested in investigating how long it takes for an ocular condition to worsen or whether treatment can delay the development of a potentially vision-threatening complication. Its implementation requires a different set of statistical tools compared to those required for analyses of other continuous and categorial outcomes. In this installment of the Focus on Data series, we present an overview of selected concepts relating to analysis of time-to-event data in eye research. We introduce censoring, model selection, consideration of model assumptions, and best practice for reporting. We also consider challenges that commonly arise when analyzing time-to-event data in ophthalmic research, including collection of data from two eyes per person and the presence of multiple outcomes of interest. The concepts are illustrated using data from the Laser Intervention in Early Stages of Age-Related Macular Degeneration study and statistical computing code for Stata is provided to demonstrate the application of the statistical methods to illustrative data.
Keywords: survival analysis, time-to-event, age-related macular degeneration, biostatistics
From understanding the natural history of ophthalmic conditions to evaluating the effect of interventions on the time to an outcome in clinical trials, survival analysis has an important role to play in the acquisition of knowledge in vision science. Also known as time-to-event analysis, this statistical framework is used to measure the association between an exposure or intervention and the rate of events or length of time until an outcome of interest is observed. More recently, this approach has also been applied to measuring distance-to-event. For example, distance of axon regeneration has been used to compare interventions following nerve damage.1 In this installment of the Focus on Data series, we present an overview of the concepts and best practice for reporting and interpreting the results of survival analyses in eye research. We start with a description of our illustrative example, taken from the Laser Intervention in Early Stages of Age-Related Macular Degeneration (LEAD) study. Then we discuss censoring, survival probability, and the hazard function. An overview of model selection will be presented with a focus on the assumptions required for valid interpretation, before briefly introducing competing risks and dealing with data from two eyes per person. These concepts will then be applied to our illustrative data. A simulated dataset, along with statistical computing code for Stata, has been provided in the Supplementary Material.
Illustrative Example
The LEAD study was a multicenter randomized clinical trial that investigated the effect of a subthreshold nanosecond retinal laser treatment on the time to development of late age-related macular degeneration (AMD) among participants with bilateral large drusen.2 Participants were randomized to either laser or sham treatment, which was applied to only one eye per person every six months for up to 30 months. The outcome of interest was the time to develop late AMD, either of the atrophic or neovascular type, and both eyes were assessed for progression every six months up to 36 months. Below, as an illustrative example, we explore the association between pigmentary abnormalities of the retinal pigment epithelium (hypopigmentation or hyperpigmentation) detected on color fundus photography at baseline, and the time from baseline to the date that late AMD was first detected. This association was explored among participants in the sham treatment group only to avoid effect modification by the laser intervention.
Censoring
Although the presence or absence of late AMD is recorded as a binary variable, the time taken for an eye to progress from an earlier stage to the late stage of AMD is described as time-to-event data. Time-at-risk usually begins at randomization in clinical trials and at the time of exposure in observational studies. In observational studies, time of exposure may be defined as the date of diagnosis or treatment, or at the baseline visit in a cohort study. Time-at-risk ends when the outcome is reached or at the time of censoring.
Censoring is common when dealing with time-to-event data. In the LEAD study, right censoring occurred for participants who did not progress to late AMD before withdrawal, loss to follow-up, or the end of the study (participants B-F in Fig. 1). This is referred to as right-censored data because only the lower bound of the time-at-risk is known. Censored participants are still included in the analyses and are counted among the number of people at risk for the outcome until the last date that their status is known. This is in contrast to analyses of binary outcome data observed at a fixed timepoint (e.g., the proportion of participants with late AMD at three years). In analyses that do not use time-to-event data, outcomes from participants who have not experienced the event of interest before being lost to follow-up are treated as missing, introducing a potential source of bias.
Figure 1.
Illustration of time-at-risk. Participants B and E were censored at the end of the study and participants C, D, and F were censored during the study period. Participant G was not included in the study at all. Participants A, B, D, and G progressed to the outcome of interest before death; however, the event was recorded during the study only for participant A.
The LEAD study was also subject to interval censoring. When late AMD was detected, the exact date of onset was usually not known, other that it occurred between the previous and current study visits. In the presence of interval-censored data, the date at which the outcome is first detected or a date midway between the two study visits may be treated as the event date (known as right-point and mid-point imputation, respectively). As with any imputation method, there is an associated risk of bias. Statistical techniques are available to model this uncertainty when estimating the survival function but are seldom used.3
Much less common is left censoring, that is, the occurrence of the outcome event prior to the start of analysis time. Left censoring may occur if analysis time is only measured after an interim event has been observed, for example, in the case of a delay between assessing participant eligibility and the date of treatment randomization (when measurement of time-to-event should commence). Left truncation (i.e., excluding people from enrollment if the outcome event has already occurred), on the other hand, is more common in epidemiological research and can result in selection bias.
For valid interpretation of results, either the assumption that censoring is not related to the outcome (i.e., noninformative censoring) is required, or statistical techniques should be used to adjust for this association.4 Noninformative censoring may be a valid assumption among people who withdraw from a study after moving away from the study area. However, if people were unable to attend study visits due to poor vision secondary to the outcome of interest, the assumption of non-informative censoring would not be valid. It can be difficult to assess whether censoring caused by loss to follow-up is related to the outcome because outcome status is usually unknown among participants with right censoring. It is important to consider this potential source of bias and whether drop out could be related to the intervention or exposure of interest.5
Survival, Failure and Hazard Functions
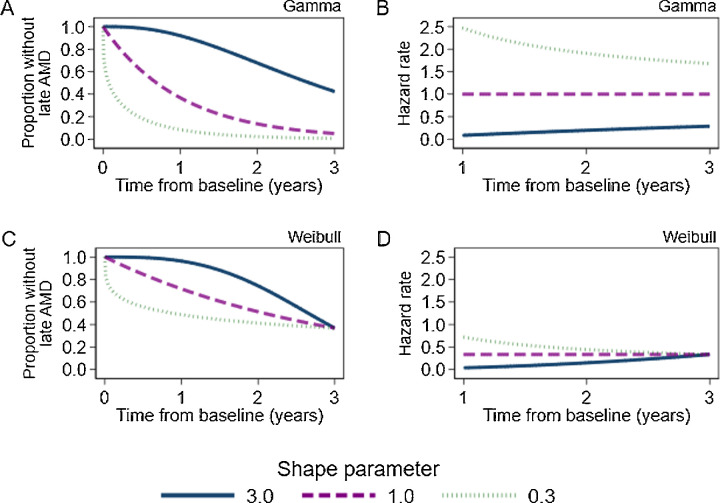
The survival function models the probability of a person remaining event free until a given time (see Fig. 2 for two examples of models with different event time distributions). The Kaplan-Meier estimator is an example of a nonparametric approach to estimating the survival function. Nonparametric methods do not require any assumptions to be made about the changes in the rate of the outcome over time. The Kaplan-Meier estimate is derived from the number of events (such as progression to late AMD), the number of people at risk (i.e., those who had not been censored or reached the endpoint before that time), and the survival probability immediately before that time (see Supplementary Material for formulae). At baseline, time-at-risk equals zero for all participants and the survival function equals one (because all participants have not yet experienced the outcome). The survival function decreases as time progresses and more participants experience the outcome of interest. The failure function is equal to one minus the survival function and is interpreted as the cumulative proportion of participants who have experienced the outcome.
Figure 2.
Theoretical survival functions and hazard rates from a gamma distribution (A and B) and a Weibull distribution (C and D, scale parameter = 3) and varying values of the shape parameter. These distributions are equal to the exponential distribution when the shape parameter is equal to one.
The hazard function represents the instantaneous risk of occurrence for the outcome at a given time. It represents how likely it is that the event occurs in the next instant, given that it has not occurred up to this point in time. The hazard function may decrease over time if events are more likely to be observed in the initial study period, or increase if events occur more frequently at the end of the study period. The ratio of the hazard rate between two groups is known as the hazard ratio (HR), and this ratio is often of interest in analyses of time-to-event data. The HR describes the relative increase or decrease in the rate of events in one group of participants compared to another. An HR >1 indicates a higher rate of events among the intervention group compared to the reference group, whereas an HR <1 indicates a lower rate of events among the intervention group compared to the reference group.
The log-rank test is a nonparametric test used to assess whether Kaplan-Meier survival functions differ between groups defined by exposure or intervention status. It is based on the number of outcomes observed in each group and the number of outcomes expected under the null hypothesis of no difference.6 The log-rank test is commonly used because it is easily implemented. However, this test does not provide an estimate of the magnitude of difference between groups such as a HR or incidence rate ratio.
Cox Proportional Hazards Model
The Cox proportional hazards model is a semiparametric approach to assessing time-to-event data. The term semiparametric refers to the fact that researchers do not need to make any assumptions about the shape of the underlying hazard function. Estimates of HRs from Cox regression models are valid under the proportional hazards assumption, as discussed below. Unadjusted Cox regression models provide similar statistical power to detect an intervention effect to that of the log-rank test. However, additional power is obtained when strong predictors of the rate of events are included as covariates in a Cox model.7 Power is diminished for Cox regression and the log-rank test if hazards are nonproportional.
If researchers are only interested in the proportion of participants who have experienced an event by a given time and the timing of events is not important (e.g., the proportion of individuals who progressed to late AMD by the end of the three-year study period), binary outcome data can be used to compare intervention or exposure groups via estimation of odds ratios, risk ratios, or risk differences. However, analyses of binary data address different research questions to analyses of time-to-event data. Therefore, estimates from analyses of binary data (e.g., odds ratios) cannot be directly compared to those from time-to-event analyses, such as HRs. Time-to-event analyses are particularly useful when a similar proportion of events has been observed in each study group by the end of the follow-up period, but the events tended to occur earlier in one group than another.
Model Covariates
Any model covariates should be selected a priori according to biological plausibility, either as confounders of the exposure-outcome relationship or as strong predictors time to event.
Unlike when using linear or logistic regression, time-varying covariates, i.e., variables with values that change between visits, can be incorporated into analyses of time-to-event data using time-dependent (or updated-covariate) methods.8 It should be noted that joint models of longitudinal and survival data may provide more efficient and less biased estimates of the effect of an intervention on time to event in the presence of correlation between the time-dependent variable and the outcome of interest.9,10 Researchers are urged to seek statistical advice when considering this approach.
Age is a special type of time-varying covariate. Because everyone increases in age at the same rate, including baseline age as a covariate is usually sufficient to adjust for confounding. Age can also be used as the time scale, rather than time from baseline visit.11,12 This is particularly useful in long-term cohort studies with a wide range of ages at baseline.
Accelerated Failure-Time Models
Accelerated failure-time (AFT) models use a fully-parametric approach to assess time-to-event data. These models have not been as widely used as log-rank or Cox models in the past because assumptions are required to be made about the shape of the survival function (i.e., whether the survival curve approximates a known distribution such as Weibull or gamma, as seen in Fig. 2). These assumptions can be tested, as demonstrated in the illustrative example. AFT modes can be used to estimate the ratio of time to event between exposure groups. A negative time coefficient indicates decreased time to event (i.e., a higher incidence rate) on average among the intervention group compared to the reference group, whereas a positive coefficient indicates the time to event will be greater (i.e., a lower incidence rate) among intervention group compared to the reference group. Weibull and exponential models are examples of AFT models, which also can be used to estimate HRs. A more flexible model, known as the Royston−Parmar model, has become more common in recent years and is particularly suited to predicting time to disease progression.13 AFT models can facilitate estimation of survival times and incidence beyond the range of the observed study period (whereas Cox models cannot).
Assessment of the Proportional Hazard Assumption
For valid interpretation of HRs, it is essential that the proportional hazards assumption is met, i.e., that the relative difference in the rate of events between categories remains constant for the entire study duration. Although the hazard rates may change over time, it is assumed that the HRs do not.
The proportional hazards assumption should be assessed following the log-rank test, and for each variable included in Cox, Weibull and exponential models. A log-log plot (Fig. 3) can be generated to graphically assess this assumption. Approximately parallel lines suggest a valid proportional hazards assumption, whereas lines that converge or diverge indicate a violation of the assumption. The proportional-hazards assumption can be assessed statistically (as demonstrated in the illustrative example). However, this test often has insufficient statistical power to detect a violation of the proportional hazards assumption, so graphical methods to assess proportionality are preferred.14 Small degrees of nonproportionality will have minimal impact interpretation of the estimates. However, strategies such as stratification or inclusion of time-varying coefficients should be considered in the case of obvious violations of the assumption, for example, in the case of a delayed treatment effect.
Figure 3.
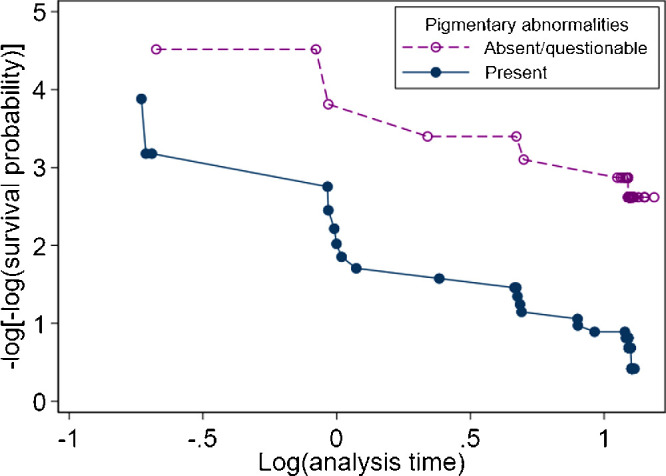
Graphical assessment (log-log plots) of the proportional-hazards assumption for pigmentary abnormality status when investigating time to late age-related macular degeneration among the sham treatment group from the LEAD study.
Competing Risks and Recurrent Events
Late AMD was defined as the presence of either atrophic or neovascular AMD in the LEAD study. Detection of atrophy can be difficult after neovascularization has developed in the macula, so neovascular AMD is a competing risk for atrophic AMD. An inferior approach to investigating the effect of an exposure on the time to atrophic AMD is to censor participants at the time of neovascular AMD detection. This censoring is informative, that is, the participants who are censored because of the detection of neovascular AMD are likely to have poorer ophthalmic health than those who do not have neovascular AMD, and this is a potential source of bias. Therefore it is recommended that competing risk regression be used, although interpretation of HRs from these models may not be intuitive.15,16 In Fine and Gray's subdistribution hazard model,15 participants who experience the competing event are still counted among those at-risk for the event of interest, even though these participants can no longer be observed to experience the event of interest.16 Therefore the HR from this model is interpreted as the relative difference in the effect on the cumulative incidence function (or the event rate for the outcome of interest) between exposure categories among participants who are either event free or have experienced the competing event.16
Not all events of interest are terminal and may, in fact, be recurrent. For example, an eye undergoing treatment for neovascular AMD may fluctuate between different levels of visual impairment. The probability of transitioning between states of visual impairment can be assessed via a multistate model when each state is distinctly defined.17 Researchers are urged to seek statistical advice when considering this approach.
Data on Two Eyes From One Person
For epidemiological studies in which a person-level exposure (such as diet or exercise) is of primary interest, disease status is often categorized per-person according to the eye with the most severe disease.18 On the other hand, eye-specific data on interventions and outcomes may be available in clinical trials. Collecting data from two eyes per person may be less resource intensive than collecting data on one eye per person with double the number of participants. However, given the likely similarity between the two eyes of one person, data from these two eyes (which share the same environment and genes) may not contribute as much statistical information as would two eyes from two separate people. The methods so far presented provide valid estimates and confidence intervals under the assumption that the outcome from each eye is independent. In the presence of correlated outcomes (i.e., outcomes from two eyes of the same person), these methods are likely to provide confidence intervals that are narrower than they should be. Methods for analyzing data with clustered observations (e.g., eyes within people or patients within hospitals) include the use of shared frailty models and the use of robust (sandwich) standard errors to account for this clustering.19 The correlation between clustered individuals is modeled when shared frailty models are applied. When clustering is accounted for using robust standard errors, the estimates will be the same as those from the equivalent model fitted with regular standard errors, but the confidence intervals and P values will change.
Reporting
Methods for handling censored observations, assessment of model fit and model assumptions should always be described. It is important to report the number of people who were lost to follow-up, dropped out or died during the study so readers can consider the potential for bias associated with censoring. The time-to-event summary statistics that we recommend reporting are listed in the Table. Time-at-risk is rarely distributed symmetrically around the mean, so the median (i.e., the time required for the outcome to be observed for half the participants) is often used as a summary measure. Incidence rates and HRs should be reported with 95% confidence intervals (CI) to allow readers to assess the precision of the estimates. When graphing survival or failure plots, it is good practice to include a risk table that gives the number of people or eyes at risk at selected timepoints below the plot and to plot confidence intervals around each curve (as seen in Fig. 4). Compliance with reporting guidelines such as STROBE (observational studies), CONSORT (trials), and ARRIVE (animal research) is recommended to facilitate transparent and reproducible research, regardless of the statistical approach used.20–22
Table.
Summary of Indications for Use of Survival Analysis Methods
| Approach | Method | Indication for Use |
|---|---|---|
| Non-parametric | Number (%) of events | All studies |
| Number (%) of participants lost to follow-up/withdrawn | All studies | |
| Total and median follow-up time | All studies | |
| Incidence rate | All studies | |
| Median survival time | All studies in which the outcome of interest is observed for more than 50% of the participants | |
| Kaplan-Meier survival or failure plots | All analyses of categorical exposures Continuous exposures will need to be categorized before plotting survival or failure functions | |
| Log-rank test | When there are no exposure-outcome confounders The magnitude of the exposure-outcome association does not need to be quantified | |
| Semiparametric | Cox regression model | To quantify the relative hazard of the event occurring (hazard ratio) The distribution of event times is not of interest |
| Fully parametric | Accelerated failure-time models (e.g., Generalized gamma, Weibull, lognormal, exponential) | To estimate an acceleration factor rather than a hazard ratio When the proportional hazards assumption is not valid, or To extrapolate estimates of survival beyond the study period |
| Fully or semiparametric | Time-varying coefficients | The effect of the exposure changes over time (i.e., hazards are non-proportional, e.g., a delayed treatment response or attenuation of treatment effect over time) |
| Time-varying covariates | The exposure changes over time | |
| Competing risk regression | The outcome of interest is not able to be observed after the occurrence of a separate but related event | |
| Log-log plot | To assess the proportional hazards assumption after the log-rank test or Cox, Weibull, or exponential models | |
| Stratification | There is evidence of nonproportional hazards for a model covariate other than the primary exposure The magnitude of the covariate-outcome association doesn't need to be estimated | |
| Shared frailty model | There are nonindependent observations (e.g., two eyes from one person) | |
| Joint longitudinal and survival data | In the presence of a time-dependent variable which is correlated with the event of interest and the degree of correlation is of interest. | |
| Multistate model | A person can transition between more than two states It is assumed that the future transition only depends on the present state |
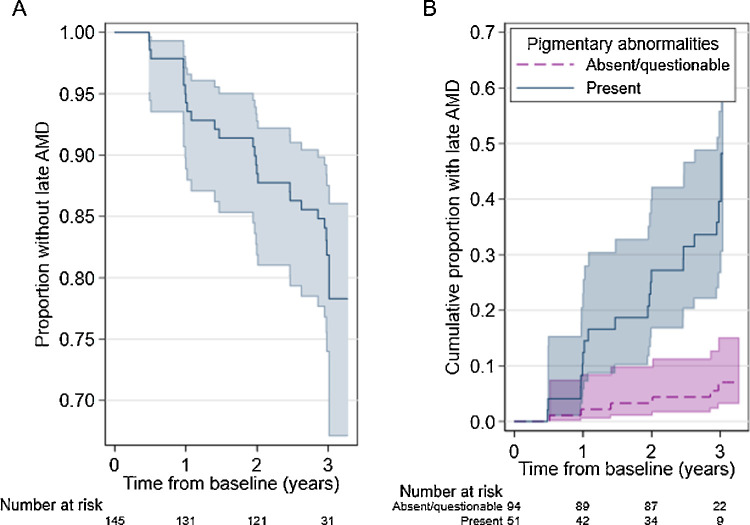
Figure 4.
(A) Survival function for study eyes in the sham treatment arm of the LEAD trial. (B) Failure function by pigmentary abnormality status. The functions derived using the Kaplan-Meier estimator at each timepoint. The shaded area represents the 95% CI.
Example From the LEAD Study
There were 145 participants randomized to the sham treatment group in the LEAD study (77% female, age at baseline 51-89 years). Definite retinal pigmentary abnormalities were detected in the study eye among 51 (35%) of these participants at baseline (see Supplementary Table S4 for participant characteristics by exposure status). Twelve participants (8%) were lost to follow-up and were censored at the last study visit they attended (n = 6, 6% with no/questionable pigmentary abnormalities; n = 6, 12% with definite abnormalities). Participants were followed for a total of 384 years and there were 25 study eyes which progressed to late AMD during the study period (n = 6, 6% with no/questionable pigmentary abnormalities; n = 19, 37% with definite abnormalities), resulting in an incidence rate of 6.5 events per 100 person-years, 95% CI 4.4, 9.6). Median survival time could not be reported because only 17% of study eyes progressed to late AMD during the study period.
Sex, age, and smoking status at baseline were hypothesized to be predictors time to late AMD and chosen as model covariates a priori. The estimated HR for baseline pigmentary abnormality status among study eyes from the covariate-adjusted Cox model was 8.86 (95% CI 3.48, 22.59). This is interpreted as an 8.9-fold increase in the rate of progression to late AMD for eyes with pigmentary abnormalities compared to those without (see Fig. 4B). Assessment of the log-log plot (Fig. 3) suggests that there was no major violation of the proportional hazards assumption for this variable (proportional hazards test of Schoenfeld residuals: P = 0.978 for pigmentary abnormality status, p-value between 0.301 and 0.767 for covariates).
AFT models were then explored to investigate whether a better fit to the observed data could be obtained. First, a generalized gamma model was fit. Statistical tests of the model parameters implied that a more parsimonious model could provide sufficient fit (i.e., tests of κ = 0 for lognormal, κ = 1 for Weibull, κ = 1 and ln [σ] = 0 for exponential distributions, see values in Supplementary Table S7). Among each of the models (including the Cox model), the Weibull model provided the best fit as indicated by Akaike's information criterion and the Bayesian information criterion (see values in Supplementary Table S8). The covariate-adjusted HR for pigmentary abnormalities derived from the Weibull model was estimated to be 9.39 (95% CI 3.67, 24.00). This is greater than the estimate from the Cox model presented above. However, in the presence of smaller effect sizes, estimates are expected to be similar between Cox and Weibull models. The exponentiated time metric coefficient (e−1.35) was 0.26 (95% CI 0.13, 0.53) which is interpreted as a 74% decrease in the time to late AMD among those with pigmentary abnormalities compared to those without. The shape parameter was greater than one, indicating that the hazard of progressing to late AMD increased with time from baseline. Estimates from this model suggest it would take 13.7 years for 50% of the participants without pigmentary abnormalities to progress to late AMD (median survival time, 95% CI 3.1, 24.3 years), whereas it would only take 3.9 years for 50% of the participants with pigmentary abnormalities to progress (95% CI 2.5, 5.3).
After including fellow eyes, pigmentary abnormalities were detected at baseline in 88 out of 290 eyes in the sham treatment group (30%). Thirty-one of these eyes (35%) progressed to late AMD prior to the end of the study compared to 12 (6%) of the 202 eyes without pigmentary abnormalities. The adjusted HR for pigmentary abnormalities estimated via a Weibull model including two eyes per participant with shared frailty by person was 8.73 (95% CI 4.13, 18.46).
Of the 25 study eyes that developed late AMD, 20 (80%) had the atrophic type and 5 (20%) had neovascular AMD. The rate of progression to atrophic AMD among those who were event free or had progressed to neovascular AMD was estimated via competing risk regression to be more than 15 times greater for those with pigmentary abnormalities compared to those without (adjusted HR 15.26, 95% CI 4.31, 54.04). As a comparison, the adjusted subdistribution HR for neovascular AMD was 1.52, 95% CI 0.26, 9.01.
Conclusions
Time-to-event analyses should be considered for longitudinal studies in which actual, or even approximate, event times can be recorded. As with any statistical analysis, attention should be paid to the assumptions required for valid inference, and all relevant information should be reported to allow readers to assess potential sources of bias.
Supplementary Material
Acknowledgments
The authors thank the LEAD study group for granting access to their data to be used as an illustrative example.
Supported by the Victorian Government, the National Health & Medical Research Council of Australia (project grant no.: APP1027624 [RHG, CDL]; and fellowship grant nos.: GNT1103013 [RHG], APP1104985 [ZW]); and Bupa Health Foundation, Australia (RHG). Ellex R&D Pty Ltd, Adelaide, Australia, provided partial funding of the central coordinating center.
Disclosure: M.B. McGuinness, None; J. Kasza, None; Z. Wu, None; R.H. Guymer, Advisory board Roche, Genentech, Bayer, Novartis, Apeliis
References
- 1. Witzel C, Reutter W, Stark GB, Koulaxouzidis G.. N-Propionylmannosamine stimulates axonal elongation in a murine model of sciatic nerve injury. Neural Regen Res . 2015; 10: 976–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Guymer RH, Wu Z, Hodgson LAB, et al.. Subthreshold nanosecond laser intervention in age-related macular degeneration: The LEAD randomized controlled clinical trial. Ophthalmology . 2019; 126: 829–838. [DOI] [PubMed] [Google Scholar]
- 3. Gómez G, Calle ML, Oller R, Langohr K.. Tutorial on methods for interval-censored data and their implementation in R. Statistical Modelling . 2009; 9: 259–297. [Google Scholar]
- 4. Templeton AJ, Amir E, Tannock IF.. Informative censoring—a neglected cause of bias in oncology trials. Nature Rev Clin Oncol. 2020; 17: 327–328. [DOI] [PubMed] [Google Scholar]
- 5. Clark TG, Bradburn MJ, Love SB, Altman DG.. Survival Analysis Part IV: Further concepts and methods in survival analysis. Br J Cancer . 2003; 89: 781–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Goel MK, Khanna P, Kishore J.. Understanding survival analysis: Kaplan-Meier estimate. Int J Ayurveda Res . 2010; 1: 274–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. European Medicines Agency. Guideline on adjustment for baseline covariates in clinical trials . London: The European Medicines Agency London, UK; 1 September 2015. [Google Scholar]
- 8. Dekker FW, de Mutsert R, van Dijk PC, Zoccali C, Jager KJ.. Survival analysis: time-dependent effects and time-varying risk factors. Kidney Int . 2008; 74: 994–997. [DOI] [PubMed] [Google Scholar]
- 9. Ibrahim JG, Chu H, Chen LM.. Basic concepts and methods for joint models of longitudinal and survival data. J Clin Oncol . 2010; 28: 2796–2801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Grand MK, Vermeer KA, Missotten T, Putter H.. A joint model for dynamic prediction in uveitis. Stat Med . 2019; 38: 1802–1816. [DOI] [PubMed] [Google Scholar]
- 11. McGuinness MB, Finger RP, Karahalios A, et al.. Age-related macular degeneration and mortality: the Melbourne Collaborative Cohort Study. Eye (Lond) . 2017; 31: 1345–1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Pencina MJ, Larson MG, D'Agostino RB. Choice of time scale and its effect on significance of predictors in longitudinal studies. Stat Med . 2007; 26: 1343–1359. [DOI] [PubMed] [Google Scholar]
- 13. Quartilho A, Gore DM, Bunce C, Tuft SJ.. Royston−Parmar flexible parametric survival model to predict the probability of keratoconus progression to corneal transplantation. Eye . 2020; 34: 657–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Hess KR. Graphical methods for assessing violations of the proportional hazards assumption in Cox regression. Stat Med . 1995; 14: 1707–1723. [DOI] [PubMed] [Google Scholar]
- 15. Fine JP, Gray RJ.. A proportional hazards model for the subdistribution of a competing risk. J Am Stat Assoc . 1999; 94(446): 496–509. [Google Scholar]
- 16. Austin PC, Fine JP.. Practical recommendations for reporting Fine-Gray model analyses for competing risk data. Stat Med . 2017; 36(27): 4391–4400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Putter H, Fiocco M, Geskus RB.. Tutorial in biostatistics: competing risks and multi-state models. Stat Med . 2007; 26: 2389–2430. [DOI] [PubMed] [Google Scholar]
- 18. McGuinness MB, Guymer RH, Simpson JA.. Invited commentary: Implications of analysis unit on epidemiology of multimodal imaging–defined reticular pseudodrusen: when 2 eyes are better than 1. JAMA Ophthalmol . 2020; 138: 477–478. [DOI] [PubMed] [Google Scholar]
- 19. Austin PC. A tutorial on multilevel survival analysis: methods, models and applications. Int Stat Rev . 2017; 85: 185–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Vandenbroucke JP, von Elm E, Altman DG, et al.. Strengthening the reporting of observational studies in epidemiology (STROBE): explanation and elaboration. PLoS Med . 2007; 4(10): e297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Percie du Sert N, Ahluwalia A, Alam S, et al.. Reporting animal research: explanation and elaboration for the ARRIVE guidelines 2.0. PLoS Biol . 2020; 18(7): e3000411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Moher D, Hopewell S, Schulz KF, et al.. CONSORT 2010 explanation and elaboration: updated guidelines for reporting parallel group randomised trials. BMJ . 2010; 340: c869. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.