Effect of Aging on the Viscoelastic Properties of Hippocampal Subfields Assessed with High-Resolution MR Elastography

Abstract

Age-related memory impairments have been linked to differences in structural brain parameters, including the integrity of the hippocampus (HC) and its distinct hippocampal subfields (HCsf). Imaging methods sensitive to the underlying tissue microstructure are valuable in characterizing age-related HCsf structural changes that may relate to cognitive function. Magnetic resonance elastography (MRE) is a noninvasive MRI technique that can quantify tissue viscoelasticity and may provide additional information about aging effects on HCsf health. Here, we report a high-resolution MRE protocol to quantify HCsf viscoelasticity through shear stiffness, μ, and damping ratio, ξ, which reflect the integrity of tissue composition and organization. HCsf exhibit distinct mechanical properties—the subiculum had the lowest μ and both subiculum and entorhinal cortex had the lowest ξ. Both measures correlated with age: HCsf μ was lower with age (P < 0.001) whereas ξ was higher (P = 0.002). The magnitude of age-related differences in ξ varied across HCsf (P = 0.011), suggesting differential patterns of brain aging. This study demonstrates the feasibility of using MRE to assess HCsf microstructural integrity and suggests incorporation of these metrics to evaluate HC health in neurocognitive disorders.

Introduction

Aging leads to brain tissue degeneration (Morrison and Hof 1997; Fjell et al. 2009; López-Otín et al. 2013) and concomitant impairments in multiple cognitive processes (Park et al. 2002), including sizeable impacts on memory performance (Levy 1994; Persson et al. 2006). Identifying how structural brain health is affected by aging is critical to understanding the neural basis of age-related cognitive decline and neurodegenerative disorders. The hippocampus (HC), a brain structure associated with age-related decline in memory performance, is of particular interest (Petersen et al. 2000; Persson et al. 2006). Although the HC exhibits global age-related atrophy (West 1993; Petersen et al. 2000; Raz et al. 2005; Du et al. 2006), it is a heterogeneous structure comprised of distinct subfields including the dentate gyrus (DG), cornu ammonis 1–3 (CA1-3), and the subiculum (SUB); whereas the greater HC complex includes the ERC, which connects the HC to the neocortex (Duvernoy 2005; Lavenex and Lavenex 2013). The hippocampal subfields (HCsf) have distinct cellular architecture (Andersen et al. 2007; Malykhin et al. 2010), fiber anisotropy (Shepherd et al. 2007), molecular profiles (Small et al. 2004), and functional specialization for different aspects of declarative memory (Shing et al. 2011; Tamnes et al. 2014; Zammit et al. 2017). Additionally, although several papers have demonstrated distinct patterns of apparent brain aging among the subfields, there has been little consensus as to which HCsf are primarily affected by age or if the subfields differentially decline across the lifespan (Mueller et al. 2007; La Joie et al. 2010; Pereira et al. 2014), which is likely due to lack of sensitivity of volumetric measures to hippocampal microstructure affected by aging. Thus, advanced in vivo imaging methods capable of sensitively assessing HCsf integrity may improve the characterization of age-related structural decline.

One such promising technique is magnetic resonance elastography (MRE), which is a magnetic resonance imaging (MRI) method to noninvasively quantify tissue viscoelastic mechanical properties in vivo (Muthupillai et al. 1995; Manduca et al. 2001). Viscoelastic measures are sensitive to the underlying microstructural integrity of brain tissue and reflect the distribution and organization of neurons, axons, and extracellular matrix (Schregel et al. 2012; Freimann et al. 2013; Klein et al. 2014). Several neurological conditions, including Alzheimer’s disease (Murphy et al. 2016; Hiscox et al. 2020b), multiple sclerosis (Wuerfel et al. 2010; Streitberger et al. 2012), frontotemporal dementia (Huston III et al. 2016), and amyotrophic lateral sclerosis (Romano et al. 2014) have been shown to affect the viscoelastic properties of the brain. Previous MRE studies have also shown that aging affects brain viscoelasticity (Sack et al. 2011; Arani et al. 2015; Hiscox et al. 2018; Kalra et al. 2019). One study estimated a 0.3–1.0% decrease in brain stiffness per year (Sack et al. 2011), which is enhanced in older age (Arani et al. 2015). The observed negative correlation of brain stiffness with age represents lower brain tissue integrity at older age. MRE studies also revealed age-related tissue stiffness effects in the individual brain lobes (Arani et al. 2015) and subcortical gray matter structures (i.e., HC, amygdala, putamen, etc.) (Hiscox et al. 2018). However, these studies only considered larger substructures of the brain, whereas property differences with age in smaller regions (i.e., HCsf) may yield more information about aging effects in critical structures that relate to cognitive outcomes.

To accurately and reliably measure viscoelasticity of the HCsf in vivo, high-resolution MRE methods are needed owing to their small size (~200–600 mm³ volume each (Daugherty et al. 2016)). In a recent report, we provide the first evidence of differences in HCsf viscoelasticity among younger adults (Daugherty et al. 2020) that is consistent with the known cytoarchitecture and evidence from the rat HC (Elkin et al. 2010, 2011), though this work used a 1.6 mm isotropic resolution that likely limited the accuracy of the HCsf property measures. Innovations in MRE sequences have increased the spatial resolution achievable in brain MRE that allow for improved accuracy of property estimates in smaller brain structures (Johnson et al. 2014; Johnson et al. 2016a). Here we adopt an imaging protocol capable of achieving MRE displacement data at 1.25 mm isotropic resolution. Previous work has also focused on the ability to resolve the inherently heterogeneous nature of brain tissue mechanical properties with MRE (McGarry et al. 2012, 2013; Barnhill et al. 2017; Murphy et al. 2020), thus further improving localized property estimates. Combining high-resolution imaging and inversion methods tailored for examining the HCsf regions may allow for a more sensitive, reliable, and accurate depiction of HCsf health.

In this cross-sectional study, we addressed three main aims: (1) develop and test a high-resolution, HCsf-specific MRE protocol that can measure the viscoelastic properties of the HCsf, i.e., shear stiffness (μ) and damping ratio (ξ); (2) characterize and compare the viscoelastic properties among four HCsf studied; and (3) determine how HCsf viscoelasticity is related to age in adults. Based on previous animal studies, we hypothesize that the HCsf will exhibit unique viscoelastic mechanical characteristics (Elkin et al. 2010; Finan et al. 2012; Elkin and Morrison 2013). Additionally, the cytoarchitectural profile of each HCsf may influence differential age-related microstructural changes (Duvernoy 2005; Mueller et al. 2007; Pereira et al. 2014; Daugherty et al. 2016), and thus we predict that the viscoelasticity of each HCsf will exhibit a different relationship withage.

Materials and Methods

Participants

Fifty-seven adult men and women aged 23–81 years were recruited and completed the neuroimaging protocol for assessing HCsf mechanical properties, as illustrated in Figure 1. The sample included 54 total participants (mean age: 54.1 ± 17.7 years; male/female: 30/24; right-handed/left-handed: 52/2). Three individuals were excluded for low octahedral shear-strain based signal-to-noise ratio (OSS-SNR), a measure of MRE quality, as OSS-SNR > 3 is considered sufficient for stable inversion (McGarry et al. 2011). Exclusion criteria for all participants were history of neurological conditions, head trauma, or psychiatric disorders, and contraindications for receiving an MRI scan (e.g., claustrophobia, metal in the body, pregnancy, etc.). The study was approved by the Institutional Review Board of the University of Delaware and all participants provided written informed consent prior to participation.

Figure 1.

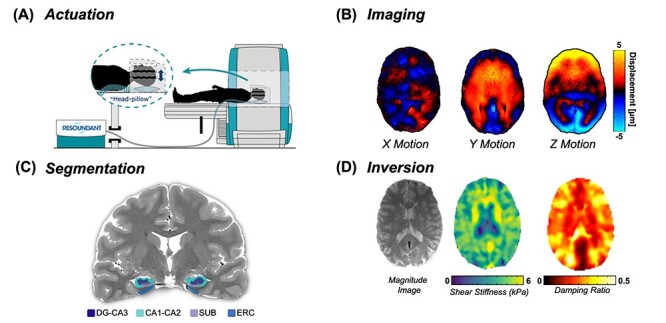
Overview of the high-resolution, HCsf-specific MRE protocol. (A) Vibrations are delivered from an active driver to a head pillow-driver to generate harmonic shear waves; (B) shear waves are imaged using a high-resolution MRE sequence; (C) HCsf regions are segmented using Automated Segmentation of Hippocampal Subfields (ASHS) into the dentate gyrus/cornu ammonis 3 (DG-CA3), cornu ammonis 1–2 (CA1-CA2), subiculum (SUB), and the entorhinal cortex (ERC); (D) the nonlinear inversion algorithm (NLI) calculates the shear stiffness (μ) and damping ratio (ξ) property maps for each HCsf region from displacement data using the HCsf segmentations as spatial priors via soft prior regularization (SPR).

MRE Imaging and Reconstruction

All participants completed an MRI session using a 3 T Siemens Prisma Scanner with a 64-channel head coil (Siemens Healthineers; Erlangen, Germany). The imaging session included a 3D multiband, multishot spiral imaging MRE sequence (Johnson et al. 2016a) that imaged micron-level displacements at 1.25 mm isotropic resolution. Imaging parameters included: repetition time (TR)/echo time (TE) = 3360/70 ms, 240 × 240 mm² field-of-view (FOV); 192×192 matrix; 8 in-plane constant-density spiral shots (Glover 1999) with 14.1 ms readout time per shot (4693 data points with 3 μs sampling); 96 axial 1.25 mm thick slices (24 volumes of 4 simultaneously excited slices each); undersampling both in-plane (4 k_xy-shots acquired, R_xy = 2) and through-plane (2 k_z-planes acquired, R_z = 2). The total acquisition time was 10 minutes 45 seconds. A commercial pneumatic driver system and soft pillow driver (Resoundant, Rochester, MN) was used to induce brain tissue deformation at a frequency of 50 Hz, which has been used in our previous works. Higher vibration frequencies lead to faster attenuation of waves, which decreases amplitude in center of the brain, though higher frequencies also result in shorter wavelengths and more deformation per voxel, which is the useable signal in MRE. The 50 Hz vibration was chosen to balance wavelength with wave amplitude in order to provide sufficient information for the NLI algorithm. The resulting motion was mapped to the phase of the MRE images through flow-compensated motion encoding gradients, and the phase images were used to generate full vector displacement fields (Manduca et al. 2001). PowerGrid (Cerjanic et al. 2016) was used to reconstruct imaging data using an iterative algorithm that includes SENSE parallel imaging (Pruessmann et al. 2001), correction for field inhomogeneities (Sutton et al. 2003), and correction for nonlinear motion-induced phase errors (Liu et al. 2005; Johnson et al. 2014).

HCsf Segmentation

The imaging protocol also included structural scans for segmentation of individual HCsf, including a HC-aligned T₂-weighted turbo spin echo (TSE) structural scan with 0.4 × 0.4 × 2.0 mm³ resolution (180 × 180 mm² FOV; 448×448 matrix; TR/TE = 8780/78 ms; 30 coronal slices) and a T₁-weighted magnetization-prepared rapid gradient-echo (MPRAGE) structural scan at 0.9 mm isotropic resolution (240 × 240 mm² FOV; 256×256 matrix; TR/TE = 2300/2.32 ms; 192 sagittal 0.9 mm thick slices). These structural scans were segmented using the fast version of the Automated Segmentation of the Hippocampal Subfields (ASHS) software (v. February 2017) in combination with the UPenn PMC Atlas (v. November 2016) to provide individual masks of DG-CA3, CA1-CA2, SUB, and ERC for each participant (Yushkevich et al. 2014). The masks of each HCsf were then registered to MRE space from native T₁ space using FMRIB’s Linear Image Registration Tool in FSL (Jenkinson et al. 2002). Each HCsf region was then thresholded to create binary masks which were visually inspected to ensure there was no overlap between them. The average number of voxels included in each HCsf mask across all subjects were: DG-CA3 = 728 voxels; CA1-CA2 = 1069 voxels; SUB = 421 voxels; and ERC = 502 voxels.

Mechanical Property Estimation

A nonlinear inversion (NLI) algorithm was used to estimate viscoelastic mechanical properties from imaged displacement data (Van Houten et al. 1999; McGarry et al. 2012). Outcome measures include the complex shear modulus (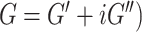, comprising the storage modulus (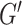) and loss modulus (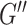). From the shear modulus we calculate the viscoelastic parameters shear stiffness (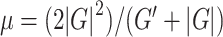) (Manduca et al. 2001), which describes the resistance of a material to a shear stress, and damping ratio (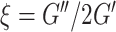) (McGarry and Van Houten 2008), which describes the relative viscous-to-elastic behavior of the material and is related to how motion is attenuated. We have previously reported these parameters in MRE studies of the HC (Johnson et al. 2016b; Schwarb et al. 2016, 2017; Hiscox et al. 2018) as they generally relate to the composition and organization of neural tissue microstructure (Sack et al. 2013). Soft prior regularization (SPR), an approach that promotes mechanical homogeneity in regions of interest during inversion by incorporating prior anatomical information, was also applied to each individual HCsf mask (McGarry et al. 2013). SPR has previously been shown to improve measurement repeatability in subcortical gray matter structures (Johnson et al. 2016b).

HCsf-Specific Inversion

We tailored the MRE process for estimating HCsf properties by using a combination of different NLI parameters on a subset of participants. The NLI inversion parameters examined were 2 SPR weightings (α = 10⁻¹⁰ and 10⁻¹²) and 2 spatial filtering (SF) widths (1.5 and 0.9 mm). A higher SPR weighting more strongly penalizes heterogeneity across the region to potentially reduce influence of neighboring regions (McGarry et al. 2013). Lower SF width reduces smoothing across subzones between global iterations, and thus allows more spatial variation in the mechanical property solution. Since we are fixing our imaging resolution based on the ratio of SF width and voxel resolution, using the lowest achievable resolution (1.25 mm isotropic resolution) works best for imaging the HCsf regions. Previous MRE studies with NLI used a default SF width of 1.5 mm, which was chosen to ensure stability of inversion results from displacement data at a 2 mm isotropic resolution (McGarry et al. 2012). However, improving the imaging resolution to 1.25 mm supplies 4 times more motion measurements. This means that applying a lower SF width may achieve sharper MRE property maps while maintaining stability of the MRE measures. This is important for taking advantage of the high-resolution data used in this work (McGarry et al. 2017).

We first investigated measurement repeatability through data collected on 4 participants (age: 25–29 years; male/female: 2/2; all right-handed) over 4 separate scanning sessions. We inverted MRE data using NLI 4 times with all combinations of SPR and SF and calculated the coefficient of variation (CV; standard deviation divided by the mean then turned into a percentage) for each parameter pair for both μ and ξ. We next assessed measurement sensitivity to determine which NLI combination could best differentiate HCsf mechanical properties. We used a subset of healthy adults younger than 50 years (N = 17; age: 31.2 ± 8.0 years; male/female: 10/7; all right-handed), as previous MRE protocol development has been tested on similar younger adult samples not expected to exhibit large age-related differences in properties (Murphy et al. 2013; Johnson et al. 2016b). It is expected that individual HCsf regions exhibit different viscoelasticity based on their unique cytoarchitecture (Duvernoy 2005), thus we investigated which parameter combination could best differentiate between the subfield viscoelastic measures. We quantified sensitivity in 2 ways: (1) the variance across all HCsf within each participant, and (2) the minimum difference between any 2 HCsf within each participant. Together, large variances and large minimum differences would indicate greater sensitivity, i.e., will be more able to differentiate among all HCsf regions, and thus may be more sensitive to age-related effects in HCsf properties to be tested on the full sample. The sensitivity analysis consisted of two 2 × 2 within-subjects ANOVAs for μ and ξ, independently, to compare the effects of SPR and SF on sample variances and minimum differences.

Validating HCsf Property Estimates

We performed a simulation study to examine the accuracy of HCsf μ and ξ estimates. In brief, realistic brain simulations were created by assigning material property distributions in a known geometry generated from 1 of our participants (51-year-old female). Next, we used a finite element solver to calculate expected displacements with boundary conditions supplied by the actual MRE data from the same participant, added 2% noise, then inverted these displacements with the proposed NLI parameters to determine accuracy (McGarry et al. 2020). Material properties of the HCsf and surrounding tissue were chosen randomly from a range of values from the average population, with a total of 10 property distributions investigated. Accuracy in each HCsf, for both μ and ξ, was determined as recovered properties minus truth (i.e., true property values assigned).

HCsf Property Analyses

We aimed to determine (1) if HCsf differed in viscoelasticity, (2) if HCsf viscoelasticity related to age, and (3) if the relationship of viscoelasticity with age was different among HCsf. A general linear mixed model (LMM) was used to test if the HCsf exhibited different properties and displayed age-related differences. Separate models were used for μ and ξ. An unstructured residual covariance matrix chosen for all models was based on minimizing the Akaike and Bayesian information criteria simultaneously. The models included between-subject effects of age and sex, and HCsf region as a 4-level within subject factor, as well as an interaction (age × HCsf) that tested the hypothesis of differential age effects. Omnibus effects were further evaluated by pairwise comparisons with Bonferroni correction to determine differences between HCsf in a post hoc analysis. To examine the age × HCsf interaction, post hoc comparisons were made using a Steiger z-test (Steiger 1980) to determine how the relationships of viscoelasticity with age differ between HCsf. Sex is included as a covariate in the model as sexual dimorphism in human brain mechanical properties has been reported previously (Sack et al. 2009; Arani et al. 2015; Hiscox et al. 2020a). We also performed partial correlations, adjusting for age, between HCsf MRE and volume measures to determine any relationships between the 2 measures.

All assumptions for all models were tested and remedied as appropriate. The assumptions of the model included assessing data normality for both the raw data and the residual values using the Kolmogorov–Smirnov test (Lilliefors 1967), while residuals were calculated and used to screen for outliers. We considered an outlier threshold as 2 times the interquartile range; no outliers were detected in our sample. Statistically significant effects were determined at P < 0.05. The degrees of freedom (df) for the independent variables and error df in this model was determined from a Satterthwaite approximation (Gaylor and Hopper 1969; Keselman et al. 1999). All statistical analyses were performed using IBM SPSS Statistics for Mac, version 26.0.0 (IBM Corp., Armonk, NY, USA).

Results

Measurement Reliability

Figure 2 provides an overview of the NLI parameter combination effects on μ and ξ property maps. The repeatability analysis revealed that the CVs of μ estimates were in the range of 2.7–8.8%, across all regions, whereas the CVs of ξ estimates ranged from 6.8% to 22.8%. SPR had minimal effect on CV estimates for both μ and ξ, with 10⁻¹² being slightly better than 10⁻¹⁰ (see Table 1). The μ estimates reveal that 0.9 mm SF produced slightly more uncertainty, though still comparable to previously reported repeatability for μ of larger regions (Johnson et al. 2016b). Conversely, SF width had a much larger impact on ξ estimates, with 1.5 mm having smaller CVs (6.8–12.4%) than 0.9 mm (13.8–22.8%).

Figure 2.

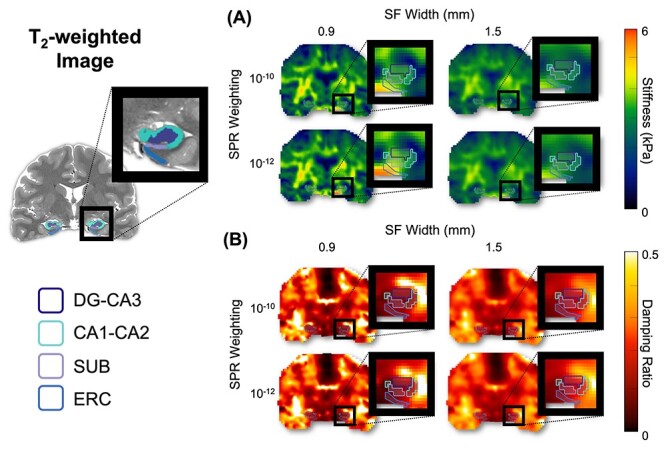
Example property maps, at a single slice in one subject, created from NLI with different combinations of SPR weighting (10⁻¹² and 10⁻¹⁰) and SF width (0.9 and 1.5 mm): (A) stiffness, μ, and (B) damping ratio, ξ. Masks generated for each HCsf region are shown.

Table 1.

HCsf MRE repeatability results for both shear stiffness (μ) and damping ratio (ξ), quantified by coefficient of variation (CV), for each individual HCsf region and NLI parameter combination

	Stiffness				Damping ratio
SPR	10 −10	10 −12	10 −10	10 −12	10 −10	10 −12	10 −10	10 −12
SF (mm)	1.5	1.5	0.9	0.9	1.5	1.5	0.9	0.9
DG-CA3	4.2%	4.5%	8.1%	7.5%	7.7%	6.8%	13.8%	15.6%
CA1-CA2	4.2%	2.9%	8.2%	8.8%	10.4%	7.4%	17.0%	18.8%
SUB	3.8%	2.7%	5.9%	6.3%	12.4%	8.4%	21.7%	22.8%
ERC	4.2%	5.0%	6.7%	6.9%	9.4%	9.4%	15.9%	16.2%
Average	4.1%	3.8%	7.2%	7.4%	10.0%	8.0%	17.1%	18.4%

Note: SPR, soft prior regularization weighting; SF, spatial filtering width (mm).

For μ sensitivity, the SF × SPR interaction was not significant for either minimum difference [F(1,16) = 0.035, P = 0.854] or sample variance [F(1,16) = 0, P = 0.987]. The SF width had a significant effect on both the minimum difference [F(1,16) = 7.15, P = 0.017] and variance of HCsf μ [F(1,16) = 12.5, P = 0.003] (see Table 2). The lower SF yielded greater minimum difference and variance compared with the higher SF. There was not a significant main effect of SPR weighting on minimum difference [F(1,16) = 0.112, P = 0.742] or variance [F(1,16) = 0.697, P = 0.416] for HCsf μ.

Table 2.

HCsf MRE sensitivity results for both shear stiffness (μ) and damping ratio (ξ), quantified by minimum difference and variance between subfields for each NLI parameter combination of SPR weighting and SF width

	Stiffness				Damping ratio
SPR	10 −10	10 −12	10 −10	10 −12	10 −10	10 −12	10 −10	10 −12
SF (mm)	1.5	1.5	0.9	0.9	1.5	1.5	0.9	0.9
MD mean	0.037	0.042	0.069	0.071	0.009	0.009	0.012	0.012
MD SD	0.027	0.027	0.088	0.055	0.006	0.006	0.010	0.011
SV mean	0.023	0.027	0.077	0.081	0.0008	0.0011	0.0010	0.0015
SV SD	0.018	0.019	0.088	0.067	0.0006	0.0008	0.0011	0.0016

Note: SPR, soft prior regularization weighting; SF, spatial filtering width (mm); MD, minimum difference; SV, sample variance; SD, standard deviation.

For ξ sensitivity, the SF × SPR interaction was not significant for either minimum difference [F(1,16) = 0.030, P = 0.864] or variance [F(1,16) = 3.34, P = 0.087]. Effect of SF width was also not significant for minimum difference [F(1,16) = 4.35, P = 0.053] or variance [F(1,16) = 3.12, P = 0.097]. For SPR weighting, the effect on minimum difference was not significant for HCsf ξ [F(1,16) = 0.484, P = 0.497], but sample variance at 10⁻¹² was significantly greater than at 10⁻¹⁰ [F(1,16) = 20.0, P < 0.001].

When considering both repeatability and sensitivity, we determined the NLI parameter combination most appropriate for examining HCsf properties by balancing repeatability and sensitivity. This was determined by dividing the sample variance (sensitivity) by the average CV (inverse of repeatability) for each parameter combination and choosing the maximum value. For HCsf μ, this was SPR weighting of 10⁻¹² and SF width of 0.9 mm; for ξ it was SPR weighting of 10⁻¹² and SF width of 1.5 mm. Although the lower SF width did have more uncertainty for stiffness, it greatly increased sensitivity. Conversely, the greater SF width of 1.5 mm increased stability for ξ without sacrificing sensitivity.

Table 3 shows the results of the simulation study comparing recovered properties with simulated truth for μ and ξ when using the chosen inversion parameters. The average error in estimates of μ is −0.24 ± 0.21 kPa, indicating that HCsf stiffness is underestimated. The average error in estimates of ξ is 0.051 ± 0.027 kPa, indicating that HCsf damping ratio is overestimated. In both cases, the recovered values tend toward the simulated background value which has lower μ and higher ξ.

Table 3.

Results of simulation study on recovered HCsf properties μ and ξ presented as average mean error (recovered minus truth)

HCsf	Stiffness, μ (kPa) mean error	Damping ratio, ξ mean error
DG-CA3	−0.14	0.018
CA1-CA2	−0.34	0.040
SUB	−0.25	0.077
ERC	−0.26	0.069
Mean	−0.25 ± 0.21	0.051 ± 0.027

HCsf Viscoelastic Properties

Before performing the LMM analysis, an independent sample t-test revealed no statistically significant differences between males and females in both μ and ξ (all P > 0.05). However, the effect size (Cohen 1992) was moderate in some measures and variable across regions: sex differences in μ ranged from small (d = −0.05 in SUB) to moderate (d = 0.25 in DG-CA3), whereas ξ demonstrated a similar range (d = −0.17 in SUB to d = −0.39 in DGCA3). Therefore, we included sex as a covariate in all LMM analyses.

Figure 3 presents the observed values for HCsf μ and ξ. Our analysis revealed that the HCsf significantly differed in μ [F(3,52) = 3.03, P = 0.037, partial-η² = 0.156], after adjusting for sex, and that sex was not significant [F(1,51) = 0.97, P = 0.329, partial-η² = 0.009]. Post hoc pairwise comparisons with Bonferroni correction (Fig. 3A) found that SUB had significantly lower mean μ than CA1-CA2 (P < 0.001), DG-CA3 (P = 0.001), and ERC (P < 0.001). We also found CA1-CA2 had significantly greater μ than DG-CA3 (P = 0.016). There were no significant differences between the other 2 HCsf pairs (all P > 0.05).

Figure 3.

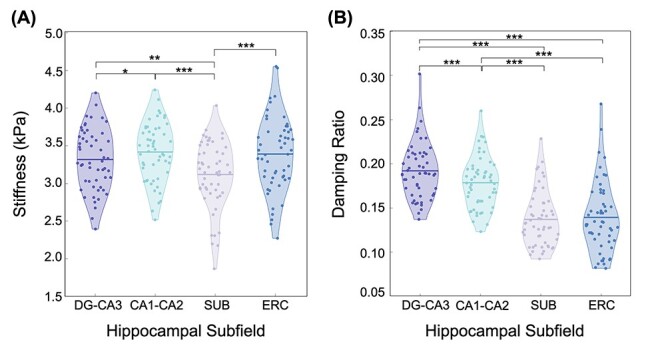
Individual HCsf viscoelasticity as quantified by (A) μ and (B) ξ for DG-CA3 (dark purple), CA1-CA2 (light blue), SUB (light purple), and ERC (dark blue). Individual subject μ and ξ values are indicated by the dots on both plots, whereas the mean value for each subfield is indicated by the solid horizontal lines on each plot. Post hoc tests with Bonferroni correction were performed to determine significant individual differences between the subfield pairs (^*: P < 0.05; ^**: P < 0.01; ^***: P < 0.001).

The models for ξ violated the assumption of normality, but after a log₁₀ transformation was applied to ξ all assumptions were satisfied. After adjusting for sex, the HCsf significantly differed in ξ [F(3,52) = 30.3, P < 0.001, partial-η² = 0.643]; the effect of sex was not significant [F(1,51) = 1.37, P = 0.248, partial-η² = 0.026]. Post hoc pairwise comparisons with Bonferroni correction (Fig. 3B) revealed that all HCsf pairs were significantly different in ξ (P < 0.001), except between SUB and ERC (P = 1.00). After performing a back transformation on the log₁₀-transformed data, we determined that DG-CA3 had the highest mean ξ, followed by CA1-CA2, with SUB and ERC having the lowest ξ. Table 4 shows the average μ and ξ across all subjects.

Table 4.

Overview of μ and ξ values for each subfield region, presented as mean ± standard deviation (SD) across all subjects, as well as the annual change per year for both μ and ξ in each HCsf region

HCsf	Stiffness, μ (kPa)		Damping ratio, ξ
	Mean ± SD	Annual change	Mean ± SD	Annual change
DG-CA3	3.32 ± 0.41	−0.011	0.192 ± 0.032	0.0006
CA1-CA2	3.42 ± 0.39	−0.011	0.179 ± 0.029	0.0008
SUB	3.12 ± 0.45	−0.011	0.137 ± 0.031	0.0008
ERC	3.39 ± 0.49	−0.014	0.139 ± 0.040	0.0006

Age-Related Differences in HCsf Viscoelasticity

In addition to analyzing HCsf property differences, we further considered (1) the effect of age on HCsf μ and ξ (2) the age × HCsf region interaction using the same LMM to determine whether each subfield region exhibits a differential relationship with age. The analysis revealed a significant effect of age on the HCsf μ [F(1,51) = 23.8, P < 0.001, partial-η² = 0.319] (Fig. 4A), whereas there was no significant age × HCsf interaction effect on μ [F(3,52) = 0.522, P = 0.669, partial-η² = 0.029]. Similarly, there was a significant effect of age on HCsf ξ [F(1,51.5) = 10.3, P = 0.002, partial-η² = 0.167] (Fig. 5A) and a significant age × HCsf interaction effect on ξ [F(3,52) = 4.13, P = 0.011, partial-η² = 0.206]. Individual plots of μ (Fig. 4B–E) and ξ (Fig. 5B–E) of each HCsf region versus age are shown with 95% confidence interval bounds around the slope of the linear fit line, and Table 4 presents the annual change of each parameter. Neither sex nor sex × HCsf interaction were related to HCsf viscoelasticity differences (all P > 0.05). Additionally, there were no significant relationships between HCsf MRE (both μ and ξ) and volume measures across all subfields (all P > 0.05).

Figure 4.

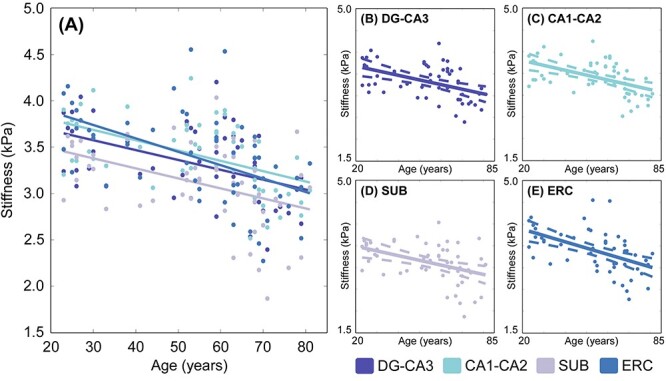
(A) Relationship between age and HCsf μ. (B–E) Individual plots for each HCsf region for μ with 95% confidence interval boundaries around the slope. There is a significant linear negative relationship between μ and age (P < 0.001) across allHCsf.

Figure 5.

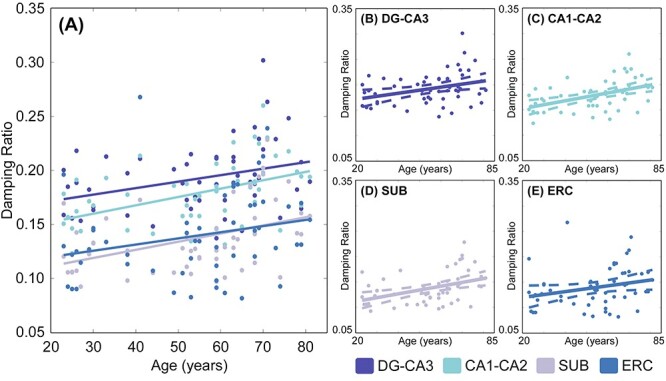
(A) Relationship between age and HCsf ξ. (B–E) Individual plots for each HCsf region for ξ with 95% confidence interval boundaries around the slope. There is a significant linear positive relationship between ξ and age (P = 0.002) across all HCsf. The HCsf also exhibited differential relationships with age, as indicated by a significant age × HCsf interaction (P = 0.011).

Table 5 presents Steiger z-test comparisons of the relationships of ξ with age between each of the HCsf pairs as a post hoc analysis of the significant age × HCsf interaction. CA1-CA2 displayed a stronger positive relationship with age than DG-CA3 (z = 2.21, P = 0.027) and ERC (z = 2.09, P = 0.037), whereas the SUB also had a stronger positive relationship with age compared with ERC (z = 2.06, P = 0.039). There were no significant differences in the relationships with age seen among the other HCsf pairs (P > 0.05).

Table 5.

Summary of the z-scores generated from Steiger’s z-test, which was used to determine the significant correlations for each HCsf pair in the damping ratio (ξ) age × HCsf interaction results; significantly different relationships with age are indicated by ^*(P < 0.05)

Damping ratio
	DG-CA3	CA1-CA2	SUB	ERC
DG-CA3	−
CA1-CA2	−2.21*	−
SUB	−1.13	0.62	−
ERC	0.66	2.09*	2.06*	−

Discussion

In this study, we have developed and tailored the first high-resolution MRE protocol to specifically analyze the mechanical properties of HCsf—the smallest brain structures measured with MRE to date. We combined displacement data at a high spatial resolution and tuned NLI parameters to increase the repeatability and sensitivity of MRE property measures. Concurrently, we assessed the impact of healthy aging on the viscoelasticity of each individual subfield region using MRE data acquired from participants aged between 23 and 81 years.

The repeatability analysis revealed that the chosen NLI parameter combinations resulted in repeatable estimates of both μ and ξ across all HCsf (CV range: 6.3–9.4%). These repeatability measures are similar to those previously reported for gray matter structures in the range of 2–7% (Johnson et al. 2016b). The slightly greater CV range for the HCsf property estimates is likely due to the HCsf being smaller structures than previously investigated. Overall, our results demonstrated that measurements are more repeatable with more SF (i.e., greater SF widths). The purpose of SF is to reduce the effects of noise and displacement measurement variation on the viscoelastic property outcomes (McGarry et al. 2012), and greater SF reduces the errors from noise and thus increases repeatability (McGarry et al. 2012, 2013), though it also results in smoother property maps with a loss in contrast recovery of smaller regions. This is reflected in higher estimates of HCsf μ at 0.9 mm compared with 1.5 mm SF width (3.29 vs. 3.02 kPa average across all regions) as the HC is stiffer than the surrounding tissue. Similarly, HCsf ξ estimates are lower at 0.9 mm compared with 1.5 mm SF width (0.147 vs. 0.163 average across all regions) as the HC is less viscous than the surrounding tissue.

The sensitivity analysis demonstrated that smaller SF widths significantly increased both the minimum difference and sample variance in HCsf property measurements. This is likely due to reduced smoothing of property maps, as too much smoothing can blur properties across regional boundaries and reduce the apparent differences in viscoelasticity between neighboring HCsf regions (McGarry et al. 2012, 2013). SPR uses segmentations of anatomical structures as prior information to reduce smoothing across region boundaries, while maintaining smooth properties within regions to allow higher contrast recovery of small structures while maintaining stability. Our analysis also revealed that sample variance in ξ estimates was significantly increased at a 10⁻¹² SPR weighting. Interestingly, this indicates that a lower SPR weighting may be more suitable in differentiating between the small HCsf regions, compared with the greater SPR weighting of 10⁻¹⁰, although higher weightings have been used in previous studies of subcortical gray matter structures (Johnson et al. 2016b). The HCsf are smaller substructures that closely neighbor one another, which may explain why an SPR weighting of 10⁻¹² provides higher variance in this application.

We chose NLI parameters for estimating HCsf properties by balancing measurement repeatability and sensitivity. We used the metric of sample variance divided by CV and chose the parameter combination that maximized this value. For estimating HCsf μ, this analysis indicated using a lower SF width of 0.9 mm, as this resulted in much higher sample variance without much higher CV. Conversely, for estimating HCsf ξ, the higher SF width of 1.5 mm is used as it critically increased repeatability without sacrificing sensitivity. This resulted in separate inversion parameters for both μ and ξ, indicating 2 inversions may need to be performed from the dataset. However, NLI can incorporate different SF widths for 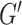and 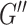, which may help achieve the desired performance in estimating μ and ξ in a single inversion (McGarry et al. 2012). The metric used to choose inversion parameters both weighs sensitivity and repeatability performance, but also can account for changes in measurement variance due to noise and how it is affected by filtering and SPR, which are expected to affect both performance outcomes. We also note that estimated properties from NLI can become unstable and diverge with noisy data, though we have demonstrated they are very stable for data with OSS-SNR > 3 (McGarry et al. 2011), which was confirmed for all data in this study.

In addition to repeatability and sensitivity estimated from in vivo data, the simulation study was performed to provide an assessment of accuracy compared with a known ground truth, as determining accuracy of MRE estimates is impossible for the in vivo brain. Our estimates of HCsf μ measurement error of 0.25 kPa on average are consistent with previous simulation (McGarry et al. 2015, 2020) and phantom studies (Solamen et al. 2018), with stiffness of HCsf underestimated due to incomplete contrast recovery in small regions (Johnson et al. 2013). The average HCsf ξ measurement error of 0.051 is proportionally larger, but again is consistent with previous phantom results indicating poorer performance in estimating ξ (Solamen et al. 2018), as well as simulation where the loss modulus (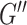) is more difficult to recover than the storage modulus (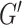) (McGarry et al. 2020), which would manifest as more error in ξ. The challenge in recovering 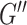, and thus ξ, is likely due to mismatch between the data and the model of viscous behavior of the brain, which can require additional regularization to stabilize the results (McGarry et al. 2012). This is reflected in our protocol for estimating HCsf ξ that incorporates more regularization (i.e., greater SF widths) to stabilize results, even with filter widths greater than the nominal imaging resolution, in order to balance measurement accuracy, repeatability, and sensitivity.

We were able to use the recommended inversion parameters to analyze the data from our entire sample and demonstrate that the individual HCsf are mechanically distinct, with each region exhibiting different μ, ξ, or both μ and ξ than each of the other regions, on average. Our findings are consistent with previous works that describe how the HCsf differ in their cytoarchitectural properties and contain unique cellular configurations (Duvernoy 2005; Lavenex and Lavenex 2013), which are likely to give rise to differences in viscoelasticity. More specifically, we found that the ERC and CA1-CA2 are the stiffest HCsf, whereas the SUB is the softest. These results are supported by ex vivo rodent studies which reveal that the HCsf possess unique viscoelastic properties, and that the CA1 region was reported to be stiffer than the CA3 region (Elkin et al. 2010; Finan et al. 2012). We recently reported preliminary findings through an in vivo MRE study of HCsf properties, though the stiffness did not significantly differ between regions (Daugherty et al. 2020). However, the same study also found higher ξ values in the CA1-CA2 region and lower ξ values in the SUB region. Our results also showed SUB had the lowest ξ (as well as ERC, which was not tested in the previous study), though we find that the DG-CA3 region had highest ξ. We expect that the differences between our results are likely due to that study using a small sample of N = 20 males only with ages that ranged from 18 to 33 years, while our sample was larger and had a wide age range from 23 to 81 years. Additionally, differences could result from our HCsf-specific protocol using a T₂-TSE HC scan necessary for robustly segmenting the whole HCsf, and not just the body, for use with the higher resolution MRE (1.25 mm isotropic). We also note that there is considerable variability in the properties across the population and that while subfields have significantly different average properties, relative properties between subfields are not uniform across all individuals.

Both HCsf mechanical properties correlated with age—lower μ and higher ξ with increasing age—which suggests lower brain tissue integrity in advanced age. The negative correlation between μ and age in all HCsf regions is consistent with previous MRE findings of other brain regions, including the total HC (Sack et al. 2011; Arani et al. 2015; Hiscox et al. 2018; Kalra et al. 2019; Takamura et al. 2019). Stiffness is thought to reflect brain tissue neuronal composition, myelination, and network strength, with higher stiffness indicative of a greater cellular matrix integrity (Freimann et al. 2013; Sack et al. 2013; Klein et al. 2014) and increased myelin content (Weickenmeier et al. 2016). Conversely, neuronal degeneration may contribute to less stiffness in old age (Sack et al. 2011; Arani et al. 2015).

In parallel with this finding, the positive correlation of ξ with age in the HCsf regions is likely related to differences in microstructural tissue organization (Sack et al. 2013). Most MRE studies of the aging brain have not reported ξ, though one previous study from our group did not find a significant difference in hippocampal ξ between young and older adults (Hiscox et al. 2018). However, a general trend for higher ξ in older adults was evident in that work and lack of statistical significance is likely due to the smaller sample size (N = 24); here, in a larger sample, we identify significant age-related differences in ξ in each HCsf. Additionally, previous studies from our group have reported a relation between hippocampal ξ and memory performance, such that higher ξ is strongly associated with poorer memory performance (Schwarb et al. 2016, 2017; Johnson et al. 2018; Schwarb et al. 2019; Hiscox et al. 2020c). Most recently, we found a relationship between relational memory and DG-CA3 ξ (Daugherty et al. 2020), which is consistent with the functional specialization of that region. Our results of increasing HCsf ξ with older age agree with these reported structure–function relationships in that higher ξ would indicate lower structural integrity of neural tissue.

The differential relationships of HCsf viscoelasticity with age suggests that specific HCsf measures may be highly sensitive to early stages of age-related degeneration of HCsf microstructure, which is presumed to precede shrinkage. Previous volumetric imaging studies have observed differential age-related differences in volumes between HCsf (Mueller et al. 2007; Pereira et al. 2014; Wisse et al. 2014; Raz et al. 2015; Daugherty et al. 2016). For example, across the lifespan (age 8–82 years), CA1-CA2 volume displays a negative, linear effect of age, whereas nonlinear age effects in DG-CA3 are attenuated in late life, and there was little age-related variability in ERC and SUB volumes in adulthood (Daugherty et al. 2016). This suggests that volumetric measures may be insensitive to microstructural changes in the ERC and SUB, which are understood to be among the earliest sites of Alzheimer’s-related pathology (Mueller et al. 2007; Wisse et al. 2014). The sensitivity of MRE within these regions as shown in this report, as well as other larger regions that are vulnerable to neurodegeneration (Sack et al. 2011; Arani et al. 2015), underscore the promising future applications of the method in clinical translational study.

In this work, we analyzed linear relationships between HCsf viscoelasticity and age, despite visual inspection of μ and ξ data suggesting potential nonlinear trends with age. A previous MRE study indicated that stiffness may exhibit a quadratic relationship with age (Sack et al. 2011), and volumetric studies have found greater hippocampal volume loss in older age (Raz et al. 2005). We only tested linear age-related differences due to the limitations of the study design; nonlinear age effects signal a variable rate of change across the lifespan, which cannot be accurately estimated with cross-sectional observations that conflate between-person differences with estimates of time-dependent change (Hofer and Sliwinski 2001). Future longitudinal studies should evaluate possible nonlinear changes in HCsf viscoelastic properties across the lifespan.

This study had several additional limitations. We were not able to directly relate our MRE measures to the underlying microstructural changes in the HCsf regions, which is a limitation broadly affecting brain MRE studies, and thus we can only speculate on the microstructural correlates. There is a need for more animal brain MRE studies with associated histological analysis to understand the neurobiological bases of viscoelastic properties, especially in typical aging animals, similar to the recent study on the developing rodent brain by Guo et al. (2019). Future studies may also gain further insight by relating these MRE measures to measurement outcomes from other MRI modalities, such as relaxometry, diffusion-weighted imaging, and arterial spin labeling, or metrics such as beta-amyloid deposition (Rodrigue et al. 2009) and metabolic function (Small et al. 2011), both of which have previously been associated with HCsf volume decline in healthy aging (Reilly et al. 2003; Small et al. 2011; Hsu et al. 2015).

Conclusion

In this study, we have demonstrated the feasibility of performing MRE of the HCsf through the development of a high-resolution MRE protocol. We show that the tailored approach can differentiate between the HCsf to reveal changes in HCsf viscoelasticity throughout the lifespan. Supporting previous work, we found that advanced age correlates with lower μ and higher ξ, and extend this to the study of the HCsf for the first time. Furthermore, we demonstrate that the relations between viscoelastic properties and age differ between HCsf regions. Future studies should build on these results by examining longitudinal data in the same participants, examining the relationship between HCsf viscoelasticity and specific domains of memory performance, and the application of HCsf MRE to be used as clinical measures for characterizing hippocampal health in patients with neurological conditions such as Alzheimer’s disease and mild cognitive impairment.

Funding

National Institutes of Health (R01-AG058853, R01-EB027577, and K01-AG054731), Delaware INBRE (P20-GM103446), Delaware Cardiovascular COBRE (P20-GM113125), and Delaware Neuroscience COBRE (P20-GM103653).