Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2021 May 10.
Published in final edited form as: Eur J Clin Nutr. 2018 Oct 12;73(2):200–208. doi: 10.1038/s41430-018-0337-1

A machine learning approach relating 3D body scans to body composition in humans

James D Pleuss 1, Kevin Talty 1, Steven Morse 1, Patrick Kuiper 1, Michael Scioletti 1, Steven B Heymsfield 2, Diana M Thomas 1
PMCID: PMC8108117  NIHMSID: NIHMS1695673  PMID: 30315314

Abstract

A long-standing question in nutrition and obesity research involves quantifying the relationship between body fat and anthropometry. To date, the mathematical formulation of these relationships has relied on pairing easily obtained anthropometric measurements such as the body mass index (BMI), waist circumference or hip circumference to body fat. Recent advances in 3D body shape imaging technology provides a new opportunity for quickly and accurately obtaining hundreds of anthropometric measurements within seconds, however, there does not yet exist a large diverse database that pairs these measurements to body fat. Herein, we leverage 3D scanned anthropometry obtained from a population of United States Army basic training recruits to derive four sub-populations of homogenous body shape archetypes using a combined principle components and cluster analysis. While the Army database was large and diverse, it did not have body composition measurements. Therefore, these body shape archetypes were paired to an alternate smaller sample of participants from the Pennington Biomedical Research Center in Baton Rouge, LA that were not only similarly imaged by the same 3D scanning machine, but also had concomitant measures of body composition by dual energy X-ray absorptiometry body composition . With this enhanced ability to obtain anthropometry through 3D scanning quickly of large populations, our machine learning approach for pairing body shapes from large datasets to smaller datasets that also contain state of the art body composition measurements can be extended to pair other health outcomes to 3D body shape anthropometry.

Keywords: Cluster Analysis, Principle Components, 3D body image scan, Human Solutions, body composition

INTRODUCTION

Anthropometric measures in adult humans have been used for centuries to quantify and categorize body types and shapes (1). In more recent history, indices formulated by algebraic combinations of anthropometric measurements such as the body mass index (BMI), have been experimentally correlated to percent body fat and other components of body composition (2–5). These indices (6–8) rely on manual measurements that are relatively simple to obtain in large scale epidemiology studies or through national health surveys (5, 9). However, manual measurements are prone to inter-rater reliability error, are labor intensive, and are restrictive in scope, i.e., e limited to what is feasible to quickly measure (10, 11).

The advent of 3D body image scanning technology has increased our capacity to obtain an extraordinary number of accurate body measures within seconds (12–15). These 3D scanned anthropometry measurements have been validated against carefully collected manual measurements (12, 13). However, pairing data obtained from 3D body imaging scanning technology to adiposity and other body composition outcomes remains challenging. Such a study requires a research facility with access to a 3D body image scanner and an accurate body composition measurement technology such as the dual energy X-ray absorptiometry (DXA) or magnetic resonance imaging (MRI). Even with access to such equipment, research facilities still will likely recruit participants from the regional location of the facility.

The Leipzig Research Center for Civilization Diseases in Leipzig, Germany has been developing a database that consists of 3D body human body image scans in local residents acquired through the Human Solutions technology since 2011 (16). From this data, Löffler-Wirth et al. (16) applied machine learning to identify 13 different body shape archetypes from this data. Löffler-Wirth et al. (16) apply a neural network approach called self-organizing maps (SOM) to transform this high dimensional 3D data to low dimensional representations in the form of body shape archetypes that can be visualized.

Here we add to the work in (16) three-fold. Our Human Solutions database, which was acquired from Human Solutions 3D body image scans employed by the United States Army for the purpose of automatic and accurate uniform sizing in basic training recruit, is racially and geographically diverse. The United States Army represents the largest branch of the United States military and employs Soldiers from all 50 states (17). Forty three percent of active duty personnel are non-white race/ethnicities and seventeen percent are female (18).

Second, we combine a principle components analysis (PCA) and cluster analysis (CA) to develop four homogenized populations that represent distinct body shape archetypes. As pointed out in (16), PCA alone or CA alone does not outperform self-organized maps, however, the application of these techniques in sequence can reduce the number of archetype sub-populations. Identification of these archetypes then allows us to pair body composition measurements from a separate and smaller database to them.

Finally, a smaller sample of Human Solutions scanned participants from the Pennington Biomedical Research Center (PBRC) in Louisiana were assigned to their respective body shape archetypes. These PBRC participants also had DXA measured body composition which then could be analyzed within each body shape archetype. Our method of using descriptive data algorithms like PCA and CA to homogenize sub-populations and then pair to health outcomes can be utilized in the nutrition field to relate conclusions from “big data” to smaller datasets that contain measurements that are much more challenging or expensive to collect.

METHODS

Study Design

There were three main questions this study was designed to address. 1) Are there natural quantifications of collinearities within the 3D imaged body shape measures? For example, it is known that limb length and height are strongly correlated (19, 20). We seek the pairwise strength of the correlations between all of the body measures. 2) Do body shapes aggregate into distinct sub-populations; that is, are there archetype body shapes that can be algorithmically identified? 3) How does body composition differ between the archetypes?

Resolution of questions 1 and 2 using machine learning requires a large and diverse population sample. To address questions 1 and 2, we used Human Solutions body scan data from over 10,000 basic training recruits assessed at Fort Jackson, South Carolina. Study design question 1 was evaluated by conducting PCA (21) on the data. After completing PCA, study design question 2 was assessed from data using a k-means cluster analysis (22) on the principle components previously identified in results to question one.

Question 3 requires rigorously and carefully collected body composition data on subjects that had been simultaneously scanned using the 3D body image scanner. For this purpose, we used 3D body image scan measurements in 148 subjects obtained by the Human Solutions machine at the Pennington Biomedical Research Center (PBRC) that also had DXA measured body composition. The principal component loadings from the Fort Jackson data were then applied to the Human Solutions measurements of the PBRC participants. After the loading, the participants from the PBRC study were assigned to clusters developed from the Fort Jackson data. The distributions of body composition within each cluster was then compared against the remaining clusters.

Subjects

Fort Jackson Basic Training Recruits

Data from Fort Jackson, South Carolina was used to answer the first two questions in our study design. Fort Jackson currently trains 50% of the US Army’s basic combat training load including 60% of the female population entering the Army each year (23). US Army basic training recruits (N=20,896 soldiers, 28% female) were scanned for uniform fitting using the 3D body imaging scanner, Human Solutions of North America (Mooresville, NC) Vitus Smart XXL 3D body scanner at Fort Jackson, SC from February 1, 2017 to October 27, 2017. Recruits were instructed on scanning posture; however, the scanning was not supervised. A database consisting of 161 anthropometric measurements per soldier, obtained from Human Solutions, was retained in spreadsheet form. Human Solutions anthropometric measurements are consistent with and have been successfully validated against research protocol manual anthropometry measurements (12, 13). Age was not available in the database; however, basic training recruits are generally between the ages of 17 to 21 years. Individual race/ethnicity information was also not available, however, a 2010 report on overall basic training recruit demographics published total recruit percentages of 18.9% black, 4.8% Asian, 0.8% Native American, and 11.9% Hispanic (24).

Pennington Biomedical Research Center (PBRC)

Subjects between the ages of 5 and 79 years were recruited that were good health with an absence of major chronic diseases. Subjects were excluded if they were underweight (BMI < 18.5 kg/m2, over 136 kg, pregnant, had edema or dehydration. Subjects would report to PBRC to be scanned by the Human Solutions of North America (Mooresville, NC) Vitus Smart XXL 3D body scanner. Subjects also underwent a DXA scan during the same visit. Imaged measurements, DXA body composition data, and demographic variables were retained from adults over the age of 18. The study was approved by the Institutional Review Board of Pennington Biomedical Research Center (PBRC-12021), and all subjects signed an informed consent and Health Insurance Portability Act authorization form before participation. The study is registered on Clinicaltrials.gov (NCT02118675).

Mathematical Methods

A workflow outlining mathematical procedures appears in Figure 1. Human Solutions Fort Jackson data was first prepared for analysis and after pre-processing, a combined PCA and CA were performed. The literature does not currently provide formal justification methods for extending a CA developed on one population to an alternate population. As a result, before extending the CA to PBRC data, we triangulated several methods that justify this extension here. Finally, we analyze body composition in the PBRC dataset on the Fort Jackson identified clusters.

FIGURE 1:

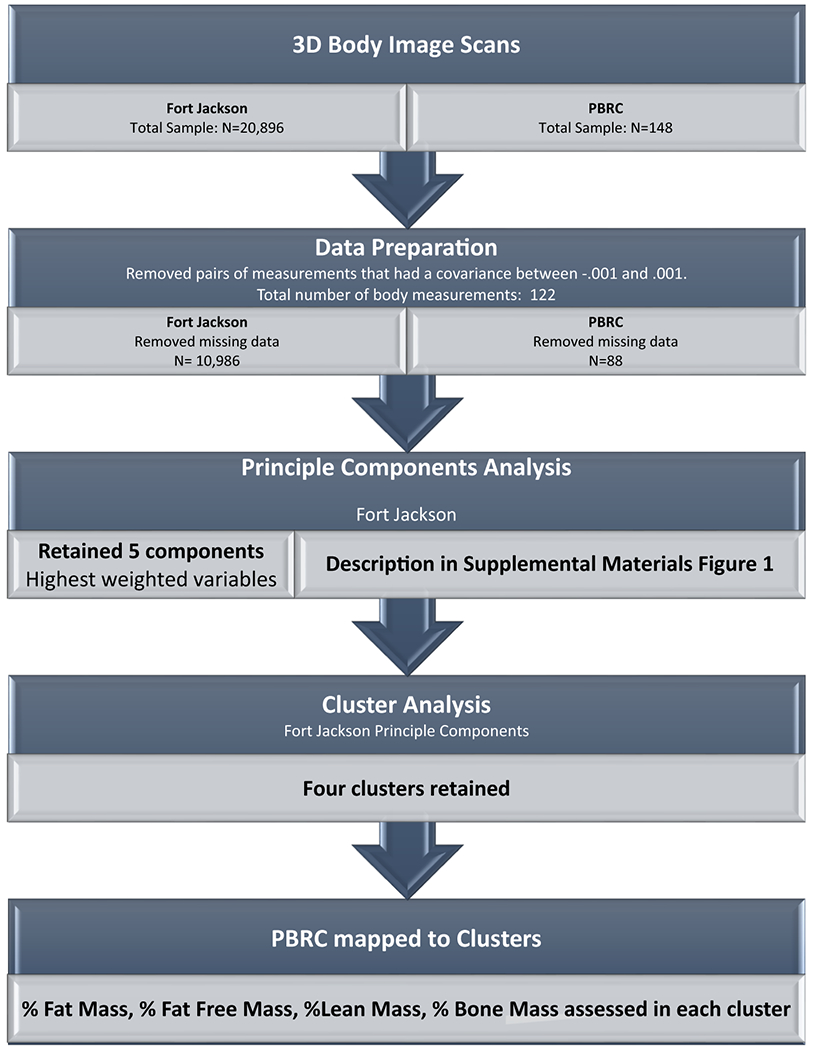
FIGURE 1:

Open in a new tab

Study design workflow

All data preparation, analysis, and modeling was performed using the statistical package R (R Core Team (2013)). Descriptive statistics were determined using the RStudio package, “psych”, and the “describe” command.

Data Preparation

Missing measurements in Human Solutions data typically occur when subjects are incorrectly postured within the scanner. Because the Fort Jackson recruits were not supervised during the body scans, some recruits are missing measurements. Any recruit that was missing a measurement was removed from the database. There did not exist any missing 3D body scan body site measurements in the PBRC database, however, some subjects did not have paired DXA measurements. Only subjects that had both body scans and DXA measurements were retained.

Only one of any symmetric body measurement pairs such as left and equivalent right arm measurements were retained. This analysis was systematically performed by eliminating one of the pair of variables that had a covariance between −0.001 and 0.001. The analysis reduced the original set of anthropometric measurements from 161 to 137 measures. This removal was performed because highly correlated variables interfere with the theoretical basis, specifically matrix formation, of the cluster analysis.

Clustering (CA) and Principle Component Analysis (PCA) are sensitive to variable measures with differing units. To account for this, some preprocessing of the Fort Jackson data was done using the R package “caret” using the “preProcess″ command to scale and center each of the 137 measurements (21). The “scale” command divides each measurement value by the standard deviation of that variable. The “center” command re-centers the measurement by subtracting the variable mean from each measurement. These same preprocessing measures were then applied to the PBRC subject measurements.

Principle Components Analysis (PCA)

Some body shape measurements are collinear. For example, height and leg length are strongly correlated. To account for these collinearities, a PCA of the Fort Jackson dataset was performed using the R package “stats”. A scree plot was formed to identify how many principle components explain an acceptable amount of variance. The first PCA did not consider gender, however a second PCA was performed that included gender as a variable. A gender-specific PCA was not performed since this would double the number of components and clusters. Separating the small sample in PBRC into these clusters would result in substantially smaller samples invalidating any potential conclusion that could be made. Moreover, performing a gender specific PCA would eliminate the possibility of males and females belonging to the same cluster, an outcome that carries some interesting discussion with it as to the other defining characteristics within these clusters. We preferred our analysis to allow for this possibility.

Cluster Analysis (CA) on the Fort Jackson study

Three different k-means cluster analyses were performed (22). Each k-means cluster analysis was conducted using the “kmeans” package in R.

First, a k-means CA was performed on the first five principle components retained in the PCA (see above section). A k-means CA was also performed directly on the 137 different measurements obtained from Human Solutions. A final k-means CA was performed using only the top weighted variables in the five principle components retained in the PCA. The best CA method is the one that provides the most homogeneous clustering, which is determined by the minimal average distance over clusters from the cluster centroid to each observation within the cluster. Because many of the body shape variables are correlated, comparison of these three clustering methods used the Mahalanobis metric (25) which accounts for correlated data within the clustering algorithms.

A scree plot on the optimal cluster was formed to identify the number of clusters to retain. Four clusters were retained from the CA performed on the principle components on the Fort Jackson population sample.

Cluster assignment of the PBRC study subjects

The loading of the five principle components described above were first retained in order to assign PBRC subjects the same principle components as the ones formed by the Fort Jackson population sample. The same CA was then done on the PBRC subjects using the principle component loadings from the Fort Jackson dataset.

Extension of Models from Fort Jackson to PBRC population samples

Similar to the caution required for extending a regression model beyond the population sample it was developed on, extending our analysis on the Fort Jackson population to the PBRC study needs to be justified. Unlike regression, we do not require both populations to be similar, since a CA does not rely on governing assumptions like regression does (26). Instead we need to verify that cluster homogeneity is preserved in the second population. To preserve homogeneity across population samples, we first need to justify applying the same loading from the PCA and then we need to confirm that homogeneity of the clusters is retained.

In order to confirm that the principle component loading structure developed on the Fort Jackson is extended to the PBRC population we need to demonstrate that the variables in both populations are similarly correlated. This was tested by evaluating the correlation of variables that yield the first principle component. Only the first principle component requires this comparison as all other principle components are orthogonal to the first.

Homogeneity of the clusters in the PBRC sample was evaluated by comparing the average Euclidean distance of each observation to its cluster center over all clusters in the Fort Jackson and PBRC datasets to determine whether the PBRC clusters were within the measured range of the Fort Jackson clusters. Specifically, the average Euclidean distance from the cluster centroid to cluster elements were computed in the Fort Jackson clusters and then compared to the analog average distances in the PBRC sample. Euclidean distance was used instead of Mahalanobis distance because the small sample in the PBRC dataset creates a singularity in its respective covariance matrix, eliminating the ability to perform Mahalanobis measurements.

Finally, similar distributions and range of body shape variables within clusters of one population sample to the other provide additional confirmation of the extension from the Fort Jackson population to the PBRC study. For example, if average and full range of BMI in the first cluster was normal for the Fort Jackson population, the average and full range of BMI should also be normal for the first cluster in the PBRC population. To this end, we calculated BMI group means and standard deviations within each cluster for both samples. We then compared the cluster specific mean and variance for each population.

Comparison of BMI across clusters

Mean BMI values were computed for each cluster in both the Fort Jackson and PBRC datasets. Pairwise 2-tailed t-tests of BMI were performed between each of the four clusters retained from the CA. The significance threshold was set to P<0.05. Adjustments for the number of cluster comparisons were made using the Bonferroni correction (P<0.05/6).

Comparison of body composition measures between clusters in the PBRC study

Percent fat mass, fat free mass, lean mass, and bone mass were computed from the DXA measurements. Mean values were calculated and then compared between clusters using 2-tailed t-tests. Similar to the BMI comparison, the significance threshold was set to P<0.05 with application of the Bonferroni correction adjustments for the number of cluster comparisons.

RESULTS

Subject Characteristics

After data preparation, the Fort Jackson sample contained N=10,986 subjects and PBRC consisted of N=88 subjects. Descriptive statistics for the Fort Jackson and PBRC population samples appear in Table 1.

Table 1:

Subject Characteristics. Data is reported as mean ± SD.

Males Females Combined
Fort Jackson
Age 17-21 17-21 17-21
BMI 25.60 ± 3.99 23.73 ± 2.93 25.08 ± 3.82
N 8717 2269 10,986
PBRC
Age 34.5 ± 20.2 33.6 ± 17.1 34.0 ± 18.7
BMI 27.21 ± 6.44 27.96 ± 6.22 27.58 ± 6.33
N 45 43 88
Open in a new tab

Principle Components Analysis (PCA)

After evaluation of the PCA scree plot (Figure 2 A), we opted to retain five principle components. The highest weighted variables in each of the five principle components were Human Solutions code 9800, body weight (kg), Human Solutions code 0691, distance from the iliac crest to the floor (m), Human Solutions code 6030, distance from the narrowest part of the waist to the top of the buttocks (m), Human Solutions code 5080, distance from the narrowest part of the waist to the highest point in the buttocks (m), Human Solutions code 0630, deviation from the narrowest part of the waist to the wall (m) (Supplemental Online Materials Figure 1). The PCA results involving number of components and which variables held the highest weight did not alter after including gender (Supplemental Online Materials Figure 2).

FIGURE 2:

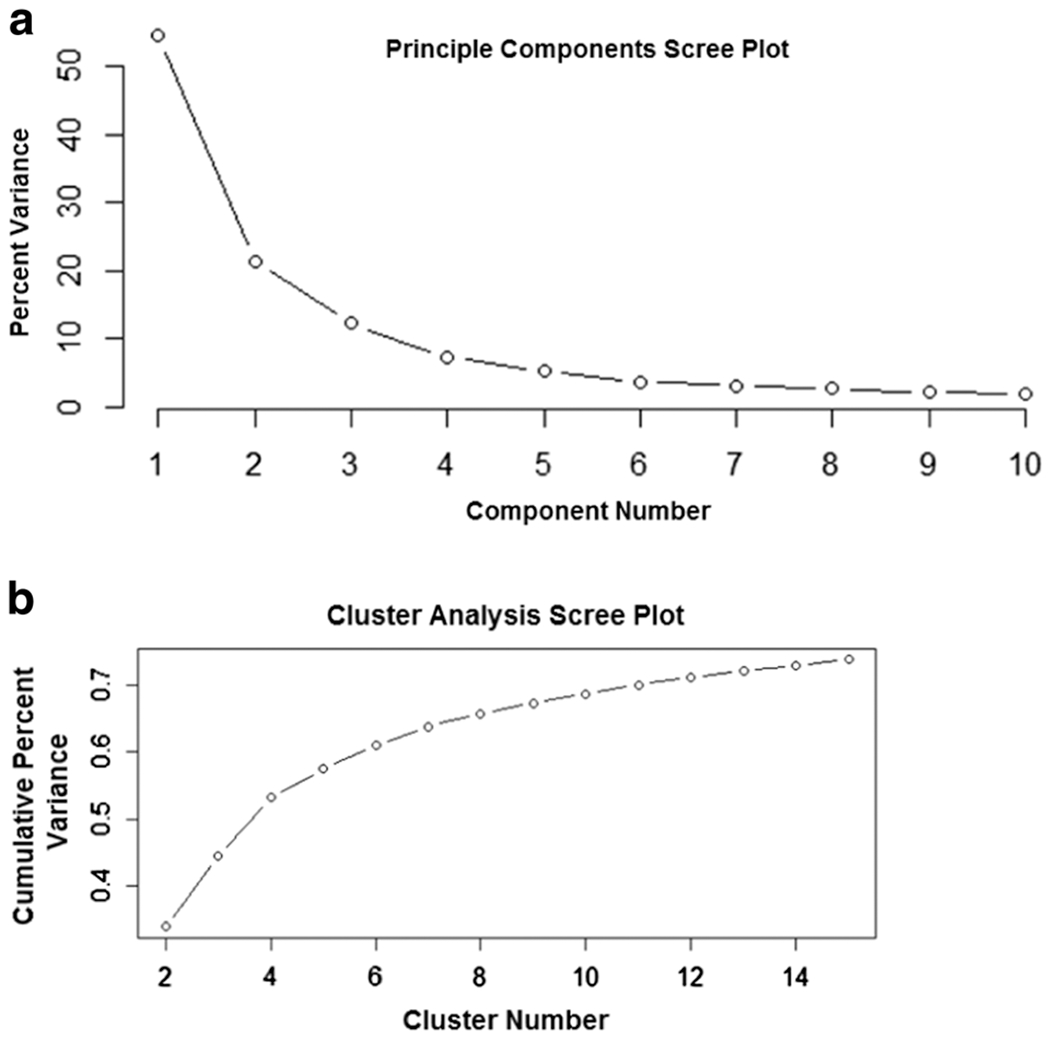
FIGURE 2:

Open in a new tab

Scree plots for the PCA and cluster analysis. Panel A depicts the percent of total variance explained in the Fort Jackson dataset by each principle component. The vertical axis represents the percent of the variance and the horizontal axis is the principle component number. Panel B is the percent of total variance in the Fort Jackson dataset that is explained with the addition of each cluster. The vertical axis represents the cumulative percent of the variance explained and the horizontal axis is the cluster number.

Cluster Analysis (CA)

The average squared Mahalanobis distance for clustering on the five principle components was 137.99. The average squared Mahalanobis distance for clustering using only the highest weighted variables on the five principle components was 139.90. The average squared Mahalanobis distance for clustering using all 137 body measurement variables was 138.01. Since clustering on the five principle components yielded the smallest average squared Mahalanobis distance, all further analysis was performed using the results of the CA on principle components.

Based on the scree plot cluster results (Figure 2 B), we selected to retain four clusters for analysis. Subject characteristics in each cluster for both the Fort Jackson and PBRC datasets appear in Table 2. Cluster specific weight (kg), BMI (kg/m2) and height (cm) are similar across the two datasets. Cluster 3 in the PBRC dataset has a higher percentage of females in comparison to the Fort Jackson dataset. Similar CA scree plots and cluster assignments were derived using the gender included PCA components (Supplemental Online Materials Figure 3).

Table 2:

Cluster specific subject characteristics for the Fort Jackson and PBRC studies. Summary of body composition measures within each cluster for the PBRC cohort is provided. The high fat-low fat free mass group is associated with Cluster Number 3 while the low fat-high fat free mass group is associated with Cluster Number 4. Cluster Number 2 represents individuals with a higher BMI and lower % fat mass than Cluster Number 3. Cluster Number 1 is largely populated in both Fort Jackson and PBRC by females.

Cluster 1 Cluster 2 Cluster 3 Cluster 4
Fort Jackson
Age (years) 17-21 17-21 17-21 17-21
Height (cm) 163.02±5.28 181.39±5.34 171.38±4.59 177.67±5.01
Weight (kg) 59.61±6.82 93.28±9.38 76.92±8.09 70.04±7.03
BMI (kg/m2) 22.95±2.62 29.07±3.14 26.81±2.94 22.72 ±2.28
N (% male) 2642 (29) 2404 (99) 2757 (97) 3183 (91)
Average Euclidean Distance 13.01 ± 3.89 9.77 ± 2.68 9.21 ± 2.40 13.21 ± 3.28
PBRC
Age (years) 28.73±16.0 43.4± 16.9 39.9± 19.5 27.4±15.4
Height (cm) 159.85±7.20 178.87±8.92 166.68 ±6.31 176.28±2.81
Weight (kg) 59.74±8.84 100.33±13.08 82.10±6.23 72.33±5.34
BMI (kg/m2) 23.52±3.10 31.64±4.58 29.78±3.86 23.28±1.65
N (% male) 26 (8) 27 (81) 23 (48) 12 (92)
Average Euclidean Distance 13.23 ± 3.98 9.10± 2.07 8.55 ± 1.46 11.93 ± 3.11
% Fat Mass 31.49±7.06 33.11±10.46 36.46±9.08 19.32±7.28
% Fat Free Mass 69.18±7.28 67.30±10.99 64.03±9.41 81.79±7.46
% Lean Mass 65.41±6.98 63.80±10.52 60.61±9.04 77.67±7.04
% Bone Mass 3.76±0.46 3.51±0.59 3.42±0.47 4.12±0.47
Open in a new tab

Evaluation of Fort Jackson derived principal component loadings and cluster assignments to PBRC study

Figure 3 Panel A represents a three-dimensional plot with each cluster color coded (Cluster 1= blue, Cluster 2 = green, Cluster 3 = yellow, and Cluster 4 = pink) describing the relationship between the highest weighted variables in the first three principle components (Supplemental Materials Figure 2) in the Fort Jackson dataset. The plot depicts the distinct separation of the cluster regions. Figure 3 Panel B is the analog plot for the same three variables in the PBRC data. The range and cluster delineation in Figure 3 Panel B is similar to the range and cluster delineation in Figure 3 Panel A. Additionally, the points in both plots follow the same general plane indicating that the variables are correlated in the same way even though they come from two different datasets.

FIGURE 3:

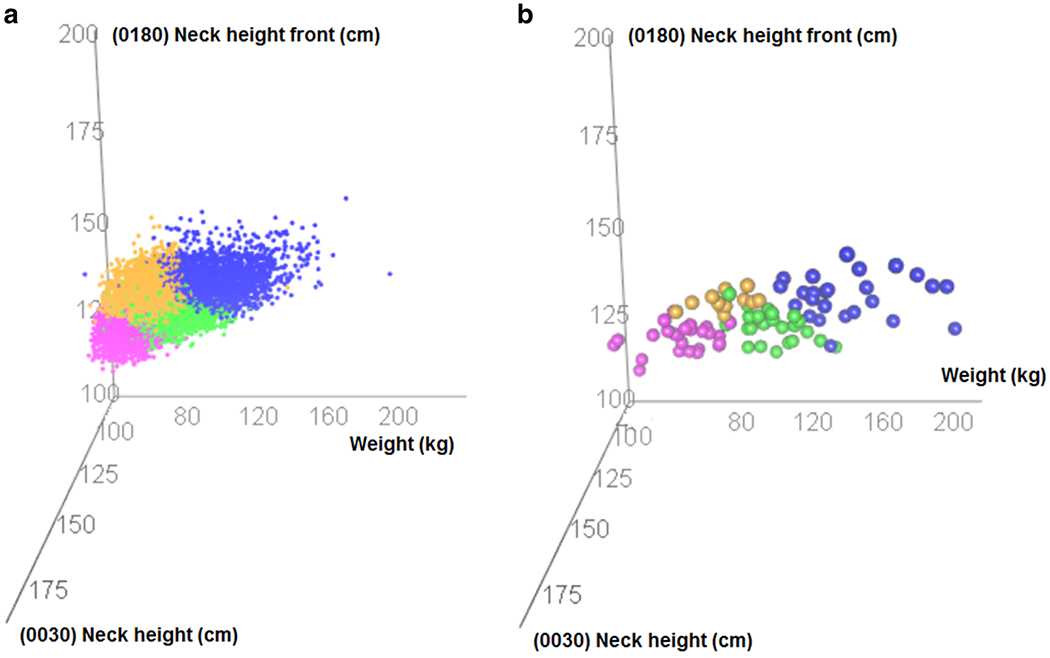
FIGURE 3:

Open in a new tab

Three dimensional scatterplots of top weighted variables in the first three principle components in the Fort Jackson dataset (Panel A) and the PBRC dataset (Panel B). The cluster delineation and the range of data is similar in both plots. The axis label descriptions relying on Human Solutions measurements (neck height and neck height front) appear in Supplemental Materials Figure 2.

Average cluster specific Euclidean distance for the Fort Jackson and PBRC datasets appear in Table 2. The PBRC dataset yielded smaller average Euclidean distance from the cluster centroid than the Fort Jackson counterpart for three of the four clusters.

Comparison of BMI across clusters

The Bonferroni correction adjustment yielded a significance threshold of P=0.008. For both, the Fort Jackson and PBRC datasets, the two-sided t-test revealed that mean BMI (kg/m2) in Cluster 1 was significantly different than the mean BMI (kg/m2) in Clusters 2 and 3 (P<0.008). Similarly mean BMI (kg/m2) was significantly different in Cluster 4 when compared with Clusters 2 and 3. Cluster 1 BMI (kg/m2) was significantly different than Cluster 3 BMI (kg/m2) in the Fort Jackson sample before Bonferroni corrections (P=0.009), however, did not hold after correction. Summary statistics of the pairwise t-test comparisons appear in the Supplemental Materials.

Comparison of body composition across clusters

The Bonferroni correction adjustment yielded a significance threshold of P=0.008. The two-sided t-test revealed that mean percent body fat in Cluster 4 was significantly different than the mean percent body fat in Clusters 1-3 (P<0.008). Mean percent body fat in Cluster 1 and 3 differed when the significance threshold was set as 0.05, however this was not retained after Bonferroni correction. Summary statistics of the t-test comparisons appear in the Supplemental Materials.

DISCUSSION

Human Solutions 3D body imaging and similar technology (12, 13), can automatically and accurately provide hundreds of anthropometry measurements within seconds, which presents an opportunity to predict body composition using state-of-the-art machine learning and statistical techniques. Direct prediction using standard approaches like regression depends upon research facilities to grow a database containing 3D scans and measured body composition in the same subjects. Conducting a study in this manner will take time, be expensive, and be restricted to subject samples recruited from the local vicinity of the research facility. The purpose of this study was to circumvent these challenges by identifying homogenous sub-populations of 3D imaged body shapes in a large diverse dataset and pairing these findings to a smaller independent sample that contained 3D imaged body shapes with simultaneously measured body composition.

Our study reduced Human Solutions 3D body scans into four distinct subpopulations (Figure 3) using a combined PCA and CA. The combined PCA and CA was found to be superior to using CA alone by comparison of Mahalanobis distance across each cluster. Specifically, the PCA-CA combination algorithm yielded to most homogenous clusters. Once homogenous clusters were identified, we were able to characterize these sub-populations by their body composition using data obtained at PBRC.

There were four distinct clusters that were characterized. The first can be loosely described as normal weight females, the second represents males classified with obesity with higher percent body fat, the third represents males and females classified as overweight with higher percent body fat, and the fourth as males with low percentage body fat. Interestingly, while Cluster 1 and 4 did not have statistically different BMI, the two clusters did differ in percent body fat.

Our study adds to the self-organized map analysis performed on Human Solutions 3D scans by Löffler-Wirth et al. (16), which identified 13 body shape archetypes. Because the PBRC dataset was smaller, sample sizes assigned to the 13 body shape archetypes would have resulted in even smaller sample sizes which would have made body composition characterization prohibitive. With a larger health outcome database, a similar pairing to health outcomes could be performed as we have done here using the Löffler-Wirth body shape archetypes.

Study strengths

Nationally represented and racially diverse 3D body scan dataset

A major strength of our study was the application of Human Solutions 3D body image scans from the United States Army basic training recruits at Fort Jackson resulted in representation from every one of the 50 states of the US. The dataset also was racially and ethnically diverse. Our dataset differs from traditional measurements collected at research sites which is restricted to subjects recruited locally.

Extension of PCA and CA to a second dataset

Special analysis had to be performed to justify the PCA-CA from Fort Jackson to the PBRC study. This is because the United States Army adheres to BMI standards that basic training recruits must satisfy in order to enlist (27). Thus, outside a small minority of exceptions, recruits have a normal weight BMI. Moreover, basic training recruits are between the ages 17 to 21 years old. In order to extend our CA to the PBRC dataset which contained older subjects from Baton Rouge, LA that were not held to the United States Army Body Composition standards we note several important points and justifications. First, age was not used to determine the cluster assignments in the Fort Jackson dataset. Second, the majority of the Human Solutions measurements are length measurements such as forearm length or leg length. By adulthood, these lengths are static.

However, the Human Solutions scans also contain body circumference measurements which are highly correlated to adiposity which are a function of age (5, 28). The justification for extending the conclusions was supported by similar BMI distributions within clusters between the two datasets. By computing ranges and distances, we also found that cluster homogeneity was preserved across the two datasets. Future studies that choose to employ the pairing application we have performed here can apply the same process to justify such an extension.

Study Limitations

Our study has several limitations. First, the PBRC population sample is small. This limited our ability to separate the population by gender in the PCA and to consider more clusters. As more data is acquired at different sites that are using the Human Solutions technology, we anticipate a more robust analysis within clusters.

Second, any analysis that is dependent on one type of machine, for example, Human Solutions, is restricted to the specific machine. There are many new and advancing 3D body image scanning technologies that are rapidly becoming available. Some of the technologies are cheaper and available for individual consumers using smart phones (29–31) while others are more sophisticated and focus on accuracy and rapid image acquisition. It is unlikely that the measurements or image quality will ever be standardized. Therefore, either individual technology specific studies analyzing data would need to be performed as we and others have done (16) or a partial automatic analysis software analysis could be made available.

Because the analysis presented here is not readily tractable, delivering the final predictions for direct clinical applications also represents a challenge. We advocate for programming predictions directly in the Human Solutions device so that outcomes can be provided directly upon scan.

CONCLUSIONS

Three-dimensional body scan image data offers a wealth of human anthropometric data that can be quickly and accurately obtained in large populations. A cluster analysis can pair these large datasets to health outcomes that are difficult to collect from smaller sized datasets. The results of these analyses can be clinically deployed in either software or directly within the 3D scanning device.

Supplementary Material

1695673_Supp_Fig1
1695673_Supp_Fig2

Acknowledgments

Funding:

This work was partially supported by two National Institutes of Health NORC Center Grants P30DK072476, Pennington/Louisiana; and P30DK040561, Harvard; and R01DK109008, Shape UP! Adults.

Abbreviations:

BMI

body mass index

DXA

dual energy X-ray absorptiometry

MRI

magnetic resonance imaging

PCA

principle components analysis

CA

cluster analysis

Footnotes

Conflict of Interest Statement: The authors have no conflicts of interest to declare.

References

  • 1.Dublin LI, Lotka AJ, Metropolitan Life Insurance Company. Statistical Bureau., Metropolitan Life Insurance Company. Twenty-five years of health progress; a study of the mortality experience among the industrial policyholders of the Metropolitan Life Insurance Company 1911 to 1935. New York, San Francisco etc.: Metropolitan Life Insurance Company; 1937. xi, 611 p. incl. illus. (maps) tables, diagrs. p. [Google Scholar]
  • 2.Heo M, Kabat GC, Gallagher D, Heymsfield SB, Rohan TE. Optimal scaling of weight and waist circumference to height for maximal association with DXA-measured total body fat mass by sex, age and race/ethnicity. Int J Obes (Lond). 2013;37(8):1154–60. [DOI] [PubMed] [Google Scholar]
  • 3.Heymsfield SB, Chirachariyavej T, Rhyu IJ, Roongpisuthipong C, Heo M, Pietrobelli A. Differences between brain mass and body weight scaling to height: potential mechanism of reduced mass-specific resting energy expenditure of taller adults. J Appl Physiol (1985). 2009;106(1):40–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Heymsfield SB, Peterson CM, Thomas DM, Heo M, Schuna JM Jr., Hong S, et al. Scaling of adult body weight to height across sex and race/ethnic groups: relevance to BMI. Am J Clin Nutr. 2014;100(6):1455–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Bouchard C BMI, fat mass, abdominal adiposity and visceral fat: where is the ‘beef’? Int J Obes (Lond). 2007;31(10):1552–3. [DOI] [PubMed] [Google Scholar]
  • 6.Motamed N, Rabiee B, Hemasi GR, Ajdarkosh H, Khonsari MR, Maadi M, et al. Body Roundness Index and Waist-to-Height Ratio are Strongly Associated With Non-Alcoholic Fatty Liver Disease: A Population-Based Study. Hepat Mon. 2016;16(9):e39575. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Tian S, Zhang X, Xu Y, Dong H. Feasibility of body roundness index for identifying a clustering of cardiometabolic abnormalities compared to BMI, waist circumference and other anthropometric indices: the China Health and Nutrition Survey, 2008 to 2009. Medicine (Baltimore). 2016;95(34):e4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Maessen MF, Eijsvogels TM, Verheggen RJ, Hopman MT, Verbeek AL, de Vegt F. Entering a new era of body indices: the feasibility of a body shape index and body roundness index to identify cardiovascular health status. PLoS One. 2014;9(9):e107212. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.The National Health and Nutrition Examination Survey (NHANES) Anthropometry Procedures Manual. (CDC) CfDC January 2007. [Google Scholar]
  • 10.Nordhamn K, Sodergren E, Olsson E, Karlstrom B, Vessby B, Berglund L. Reliability of anthropometric measurements in overweight and lean subjects: consequences for correlations between anthropometric and other variables. Int J Obes Relat Metab Disord. 2000;24(5):652–7. [DOI] [PubMed] [Google Scholar]
  • 11.Wang J, Bartsch G, Rahgavan SS, Yurik T, Peng G, Chen L, et al. Reliability of body circumference and skinfold measurements by observers trained in groups. Int J Body Comp Res. 2004;2:31–6. [Google Scholar]
  • 12.Kuehnapfel A, Ahnert P, Loeffler M, Broda A, Scholz M. Reliability of 3D laser-based anthropometry and comparison with classical anthropometry. Sci Rep. 2016;6:26672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Soileau L, Bautista D, Johnson C, Gao C, Zhang K, Li X, et al. Automated anthropometric phenotyping with novel Kinect-based three-dimensional imaging method: comparison with a reference laser imaging system. Eur J Clin Nutr. 2016;70(4):475–81. [DOI] [PubMed] [Google Scholar]
  • 14.Koepke N, Zwahlen M, Wells JC, Bender N, Henneberg M, Ruhli FJ, et al. Comparison of 3D laser-based photonic scans and manual anthropometric measurements of body size and shape in a validation study of 123 young Swiss men. PeerJ. 2017;5:e2980. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Stewart AD, Klein S, Young J, Simpson S, Lee AJ, Harrild K, et al. Body image, shape, and volumetric assessments using 3D whole body laser scanning and 2D digital photography in females with a diagnosed eating disorder: preliminary novel findings. Br J Psychol. 2012;103(2):183–202. [DOI] [PubMed] [Google Scholar]
  • 16.Loffler-Wirth H, Willscher E, Ahnert P, Wirkner K, Engel C, Loeffler M, et al. Novel Anthropometry Based on 3D-Bodyscans Applied to a Large Population Based Cohort. PLoS One. 2016;11(7):e0159887. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Reynolds G, Shendruk A. Demographics of the U.S. Military: Council on Foreign Relations; 2018. [Available from: https://www.cfr.org/article/demographics-us-military.
  • 18.Army Demographics FY16 Profile. 2016 [Available from: https://m.goarmy.com/content/dam/goarmy/downloaded_assets/pdfs/advocates-demographics.pdf.
  • 19.Yun DJ, Yun DK, Chang YY, Lim SW, Lee MK, Kim SY. Correlations among height, leg length and arm span in growing Korean children. Ann Hum Biol. 1995;22(5):443–58. [DOI] [PubMed] [Google Scholar]
  • 20.Bogin B, Varela-Silva MI. Leg length, body proportion, and health: a review with a note on beauty. Int J Environ Res Public Health. 2010;7(3):1047–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Jolliffe IT. Principal component analysis. 2nd ed. New York: Springer; 2002. xxix, 487 p p. [Google Scholar]
  • 22.DeGregory KW, Kuiper P, DeSilvio T, Pleuss JD, Miller R, Roginski JW, et al. A review of machine learning in obesity. Obes Rev. 2018;19(5):668–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.US Army Training Center, Fort Jackson [Available from: http://jackson.armylive.dodlive.mil/about/.
  • 24.Military Recruitment 2010: National Priorities Projet; 2011. [Available from: https://www.nationalpriorities.org/analvsis/2011/militarv-recruitment-2010/.
  • 25.Varmuza K, Filzmoser P. Introduction to multivariate statistical analysis in chemometrics. Boca Raton: CRC Press; 2009. xiii, 321 p. p. [Google Scholar]
  • 26.Freedman D, Pisani R, Purves R. Statistics. 4th ed. New York: W.W. Norton & Co.; 2007. [Google Scholar]
  • 27.Army Regulation 600-9 The Army Body Composition Program. In: DoD, editor. Washington DC: The Department of the Army; 2013. [Google Scholar]
  • 28.Gallagher D, Heymsfield SB, Heo M, Jebb SA, Murgatroyd PR, Sakamoto Y. Healthy percentage body fat ranges: an approach for developing guidelines based on body mass index. Am J Clin Nutr. 2000;72(3):694–701. [DOI] [PubMed] [Google Scholar]
  • 29.Heymsfield SB, Bourgeois B, Ng BK, Sommer MJ, Li X, Shepherd JA. Digital anthropometry: a critical review. Eur J Clin Nutr. 2018;72(5):680–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Bourgeois B, Ng BK, Latimer D, Stannard CR, Romeo L, Li X, et al. Clinically applicable optical imaging technology for body size and shape analysis: comparison of systems differing in design. Eur J Clin Nutr. 2017;71(11):1329–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Pradhan L, Song G, Zhang C, Gower B, Heymsfield S, Allison D, et al. , editors. Feature Extraction from 2D Images for Body Composition Analysis. IEEE International Symposium on Multimedia (ISM); 2015; Miami, FL, USA: IEEE [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1695673_Supp_Fig1
NIHMS1695673-supplement-1695673_Supp_Fig1.docx (30.4KB, docx)
1695673_Supp_Fig2
NIHMS1695673-supplement-1695673_Supp_Fig2.docx (64.6KB, docx)

RESOURCES