Psychometric analysis of the Adult Separation Anxiety Symptom Questionnaire: Item functioning and invariance across gender and time

Abstract

The Adult Separation Anxiety Symptom Questionnaire (ASA-27) is the most widely used self-report assessment of adult separation anxiety (ASA). Despite its widespread use, relatively little is known about its psychometric properties, specifically whether it is unidimensional, its degree of precision (or information) across latent levels of ASA, the functioning of individual items in general and of DSM-derived versus non-DSM-derived items in particular, and whether the measure is invariant across gender and time. We addressed these issues in a sample of 509 adult women and 407 adult men from the local community participating in a longitudinal study of temperament and psychopathology in children. Two items from the ASA-27 were removed so that the measure met the item response theory (IRT) assumption of unidimensionality. Findings from a graded response model for categorical items suggested that the ASA-27 assesses ASA most reliably at moderate to high levels and that the DSM-derived items were more closely related to latent ASA than the non-DSM-derived items. Invariance tests employing single-factor confirmatory factor analysis models suggested that the measure is partially invariant across gender and time at the unique factor level, with fewer than 7% of parameters freed in both cases; this implies that the means and variances of the latent factors and differences in the observed responses are attributable to true differences in ASA. Future work should replicate these findings in a sample that includes individuals with a wider range of ASA severity and may consider removing additional items that provide little or redundant information.

The Adult Separation Anxiety Symptom Questionnaire (ASA-27; Manicavasagar, Silove, Wagner, & Drobny, 2003) is the most widely used self-report measure of adult separation anxiety (ASA). The ASA-27 has been studied as a moderator of treatment response (Aaronson et al., 2008; Kirsten, Grenyer, Wagner, & Manicavasagar, 2008), linked to biological markers of psychiatric disorders (Costa et al., 2009; Eapen et al., 2014; Pini et al., 2005), used to establish convergent validity (Cyranowski et al., 2002; Shear, Jin, Ruscio, Walters, & Kessler, 2006), examined in relation to personality (Mertol & Alk, 2012; Pini et al., 2010; Pozzi et al., 2014; Silove, Marnane, Wagner, Manicavasagar, & Rees, 2010), and employed in studies of separation anxiety disorder comorbidity (Dell’Osso et al., 2011, 2012; Tasdemir, Tamam, Keskin, & Evlice, 2015), familial aggregation (Manicavasagar, Silove, Rapee, & Waters, 2001), and continuity (Manicavasagar, Silove, Curtis, & Wagner, 2000). Despite its widespread use, an in-depth analysis of the measure’s psychometric properties has not been conducted. This is a particularly important and timely topic given the recent change to the separation anxiety disorder criteria in DSM-5 to allow the disorder to be diagnosed after age 18, which will likely lead to increased use of this measure in both research and clinical settings. This study addresses several important issues related to the psychometric functioning of the ASA-27.

The ASA-27 and the notion that separation anxiety can be diagnosed in adulthood were developed by Manicavasagar’s and Silove’s group over the course of several studies. The first paper presented case reports of three patients suffering from putative primary ASA and suggested that it may be an overlooked clinical problem (Manicavasagar & Silove, 1997).

Additional studies systematically examined the phenomenology, onset, and course of ASA, as well as patterns of comorbidity, in community (Manicavasagar, Silove, & Curtis, 1997) and clinical samples (Manicavasagar et al., 2000), and the familial and developmental factors uniquely associated with ASA (Manicavasagar et al., 2001; Manicavasagar, Silove, Wagner, & Hadzi-Pavlovic, 1999). Studies since then have shown that ASA is prevalent in both community and clinical samples (Shear et al., 2006; Silove, Marnane, Wagner, Manicavasagar, et al., 2010), impairs beyond comorbid disorders (Pini et al., 2010; Shear et al., 2006), and negatively affects treatment outcomes (Aaronson et al., 2008; Kirsten et al., 2008; Miniati et al., 2012; see Bogels, Knappe, & Clark, 2013 for a review of ASA).

Items included in the ASA-27 were identical to those in the Adult Separation Anxiety Semi-Structured Interview (ASA-SI), which were drawn from attachment theory, clinical impressions, and open-ended interviews conducted in a qualitative study and also included modified versions of the separation anxiety criteria for youth in DSM-IV (Manicavasagar et al., 1997, 2003). The authors reported a high degree of concordance in frequency of endorsement between the interview and the self-report measure in adults who responded to a media campaign about experiencing anxiety about separation from attachment figures (Manicavasagar et al., 1997).

In the study finalizing the self-report measure, the ASA-27 showed favorable psychometric properties with a mixed clinical and community sample (Manicavasagar et al., 2003). A principle components analysis yielded a strong first factor accounting for 45% of the variance, with all items loading positively on the factor (0.38 to 0.80), and the measure had good test-retest reliability (0.86) over an average span of three weeks and high internal consistency (Cronbach’s alpha=0.95; inter-item correlations ranging from 0.10 to 0.74). Using diagnoses from the ASA-SI as the criterion, a cut-off score of 16 exhibited 97% sensitivity and 66% specificity. This self-report measure was the first, and remains one of the only, to focus on symptoms and phenomenology of ASA as opposed to attachment problems or specific forms of separation anxiety, like from mother to child, which is often the focus of similar measures for adults (Manicavasagar et al., 2003).

Psychometric Properties of ASA-27: Classical Test Theory Approach

Since the original study, several others have confirmed the measure’s favorable psychometric properties using a classical test theory approach. The measure shows convergent validity with interview assessments of ASA and childhood separation anxiety (Cyranowski et al., 2002) and internal consistency estimates ranging from 0.89 to 0.93 in a variety of samples, including cross-culturally with Turkish and Bangla translations of the measure (Dirioz, Alkin, Yemez, Onur, & Eminagaoglu, 2011; Islam & Khanam, 2017; Kirsten et al., 2008; Kohlhoff, Barnett, & Eapen, 2015). The original and subsequent studies, however, have largely examined the psychometric properties at the level of the total score, consistent with a classical test theory approach, which assumes that variation in sum scores is attributable to true differences in levels of ASA, systematic error affecting all reporters equally, and normally distributed random error (Magno, 2009). One partial exception compared means at the item level for patients with ASA disorder versus patients with other anxiety disorders; 16 items had higher means in the ASA disorder group (Manicavasagar et al., 2000). While this study examined how groups may answer items differently, it did not directly test whether the item properties themselves differed across groups. Consequently, it cannot be known whether the differences reflect true differences in levels of ASA or differences arising from measurement properties.

Benefits of IRT

Item response theory provides an alternative conceptualization of responses on the ASA-27, wherein an individual’s probability of endorsing an item on the ASA-27 is construed as both a function of the individual’s level of ASA and of the items’ properties. This approach has several benefits over sum score approaches. At the test (and item) level, it allows the standard error of the estimate—or, in the language of IRT, the information—to vary across levels of the latent construct (Thomas, 2011). For example, it may be empirically determined that the ASA-27 has less error, or provides more information, at the mid-level of a trait, but has more error at extreme values. This information can be readily translated for clinical and research purposes: a clinician can have more confidence in an ASA-27 assessment when an individual’s score falls in a range with high precision, and researchers can use the degree of measurement error in the expected range of scores to determine whether the ASA-27 would be suitable for their sample.

At the item level, IRT models also estimate item discrimination parameters, which index the strength of the relationships between items and the latent trait (ASA) and denote their abilities to discriminate between people at varying levels on that trait. Discrimination parameters weight items in order to estimate a person’s standing on the latent trait, such that different combinations of the same number of items can be combined to produce different factor scores, unlike sum scores which weight all items equally (Thomas, 2011). Given the relative newness of diagnosing separation anxiety disorder in adulthood, using IRT methods to identify which ASA-27 items are most closely related to the latent construct of interest may also enrich our understanding of the adult form of this disorder. This study will use IRT to determine, in particular, whether the ASA-27 items that were based on DSM criteria for youth separation anxiety disorder are more or less central than other items drawn from clinical impressions and attachment theory.

IRT models also estimate item difficulties, or the level of ASA associated with a 0.5 probability of endorsing a response category. In a clinical context, difficulty can be construed as severity (Thomas, 2011). The range of item difficulty parameters not only show which level(s) of the latent trait the measure adequately assesses, but also order symptoms in terms of relative severity. Like the item discrimination parameters, this information can develop our understanding of separation anxiety in adulthood, and particularly which symptoms can be expected to be present in more or less severe forms. Clinicians may also find it useful when locating the degree of ASA in their clients; that is, a client who describes experiencing symptoms queried by items with high difficulty parameters is likely to have a more severe form of ASA than one who describes symptoms queried by items with low difficulty parameters.

Meeting the Assumptions of IRT

Before an IRT model can be fit to any data, however, three assumptions must be met. First, the measure must be unidimensional. In the case of the ASA-27, this means that the relationships among items should be due to levels of ASA and not to other factors (Reise, Moore, & Haviland, 2013). Alternatively, if a measure assesses multiple constructs or dimensions, data can be modeled using a multidimensional IRT model, in which case the assumption of unidimensionality does not apply. The developers of the ASA-27 (Manicavasagar et al., 2003) and an independent study (Dirioz et al., 2011) find that the measure is unidimensional, so we likewise adopt a unidimensional model for the current study. Second, all items must be locally independent, which means that items should not have residual relationships after ASA is taken into account (Reise et al., 2013). Items violating this assumption tend to have certain properties that make them likely to elicit identical responses (Steinberg & Thissen, 1996). These two assumptions are interrelated in that when all items are locally independent, the measure is also unidimensional. The last assumption is that all items must be monotonic, which means that the probability of endorsing a higher response category increases as the level of ASA increases (Reeve et al., 2007; Reise et al., 2013).

These assumptions not only optimize conditions for IRT models, however; they also have utility, regardless of whether IRT is used, for empirically supporting or refuting common and implicit interpretations of scores. For example, researchers and clinicians typically view sum scores derived from the ASA-27 as indicative of ASA rather than of some other factor that may be related to, but distinct from, ASA, like talkativeness. However, if the ASA has an unacknowledged multidimensional structure or pairs of locally dependent items, researchers cannot know which of the multiple constructs is giving rise to item responses and, in turn, sum scores (Steinberg & Thissen, 1996). A similar problem with interpreting sum scores arises when items are not monotonic. If people with lower levels of ASA more frequently endorse the top response categories on some ASA-27 items compared to people with higher levels of the trait, the resulting sum score differences will not correspond meaningfully to differences in the latent trait of interest. Finally, the assumptions are relevant for interpreting internal consistency statistics. Researchers generally interpret internal consistency as indexing how reliably the items assess the single general construct of ASA. This interpretation may be invalid if locally dependent items consistently measure some factor besides the construct of interest and thereby artificially inflate the internal consistency statistic (Steinberg & Thissen, 1996). Ensuring that the ASA-27 meets these assumptions therefore substantively aids interpretation of total scores and reliability in addition to laying the groundwork for IRT modeling. The current study will evaluate these three assumptions for the ASA-27.

ASA-27 Across Gender and Time

Several studies using the ASA-27 report that women have higher levels of ASA compared to men (Aaronson et al., 2008; Silove, Marnane, Wagner, & Manicavasagar, 2010; Silove, Marnane, Wagner, Manicavasagar, et al., 2010). However, it is unknown whether this reflects true quantitative differences of latent ASA levels. It may instead reflect qualitative differences in the construct itself as assessed by the ASA-27 or scaling differences in women versus men, which would render a quantitative comparison of means across the two groups meaningless (Liu et al., 2017). In order to meaningfully compare men’s and women’s ASA-27 scores, measurement invariance of the ASA-27 across genders must be established.

In a similar manner, evaluating the longitudinal measurement invariance of the ASA-27 can reveal whether observed differences across assessment occasions are due to true changes in levels of ASA or to qualitative changes in the construct being measured or its scaling. Indeed, establishing longitudinal measurement invariance is a prerequisite for questions about change (e.g., Widaman & Conger, 2011). To date, no previous studies have reported on repeated administrations of the ASA-27, aside from its test-retest reliability over a few weeks (Manicavasagar et al., 2003). Because separation anxiety has only recently been recognized as a disorder of adulthood, and there is virtually no information available about its course and response to treatment, it is particularly important and timely to begin exploring the longitudinal performance of the ASA-27.

Consequently, in addition to providing detailed information about the psychometric properties of the ASA-27 using IRT methods, the current study will draw on confirmatory factor analysis (CFA) approaches to determine the degree to which the measure is invariant, or unbiased, in how it assesses ASA across gender and time. The two frameworks can be used in tandem because the specific CFA and IRT models used in this paper are formally equivalent (Millsap, 2010; Takane, Leeuw, & Angeles, 1987). We opted to use CFA methods for evaluating measurement invariance, rather than differential item functioning as is customary within the IRT framework, for two reasons. First, a formal procedure for testing measurement invariance using CFA with ordered categorical variables has been clearly delineated (Liu et al., 2017; Millsap & Yun-Tein, 2004), whereas there are a variety of differential item functioning methods in IRT which may lead to divergent conclusions (Millsap, 2006). Second, CFA measurement invariance techniques support inferences about whether mean differences across groups or time reflect bias or true differences, which has substantive implications for past and future studies using this measure. In contrast, IRT differential item functioning methods focus on single items, which may make them more suitable for measurement development. The current paper will estimate two series of four hierarchically nested multigroup and longitudinal CFAs for ordered categorical variables with an increasing number of equality constraints across gender and time.

Method

Participants

The study sample includes 509 adult women and 407 adult men from the local community who completed a self-report measure of separation anxiety symptoms on one or two occasions. These adults are from 609 families in an ongoing longitudinal study of children’s temperament and psychopathology. Of the 609 families, 559 families were recruited at the first wave of the study when children were 3 years old, and 50 additional minority families were recruited at the second wave 3 years later to increase racial/ethnic diversity (see Bufferd, Dougherty, Carlson, Rose, & Klein, 2012 for details). Parents provided written informed consent after receiving a description of the study. The study was approved by the human subjects review committee at Stony Brook University, and families were compensated.

Only the primary caretaker completed the ASA-27 at the second wave; this included 384 women. Data from the small number of male primary caretakers who completed the ASA-27 at wave 2 (n = 39) are not included in this report in order to facilitate clear conclusions from the longitudinal invariance test; had they been included, these results would have technically reflected both genders, but characterizing them as such would have been misleading due to the small proportion of men. Both caretakers completed the measure at the third wave; after two men with outlying ASA-27 total scores over eight standard deviations above the mean (79 and 81) were removed, this included 482 women (54.2%) and 407 men (45.8%; n=889). Five hundred and nine women completed the ASA-27 at wave 2 and/or wave 3; of these, 357 (70.1%) completed the ASA-27 at both assessments, 27 (5.3%) at wave 2 only, and 125 (24.6%) at wave 3 only. In total, the current study includes 1273 reports on the ASA-27. Seven items for women at wave 2 were missing responses for one case, and one item was missing responses for five cases. There were no missing data at wave 3. Assessment waves were approximately three years apart.

The majority of women were married or living with their child’s biological parent at wave 2 (85.9%) and wave 3 (84.4%), as were the majority of men at wave 3 (91.7%). Women were 39.1 years old on average at wave 2 (SD=4.9; range=22.8-51.8) and 41.8 years old on average at wave 3 (SD=4.8; range=25.9-53.5). At wave 3, men were 44.3 years old on average (SD=5.7, range=29.1-61.1). At both waves, approximately half of the women had at least a 4-year college degree (wave 2: 54.95%; wave 3: 56.3%), as did just under half of men at wave 3 (47.4%). The larger study’s main focus is on children’s psychopathology. Thus, parents’ race and ethnicity were not collected, and participating children’s race and ethnicity are used instead as proxies; 88.3% of women and 92.6% of men had children who were White, and 12.4% of women and 11.3% of men had children who were Hispanic or Latino. Missing data on demographic variables were due to failure to respond (valid cases range=94.8-100.0%).

Participants included in versus excluded from the sample for the current study were compared on all demographic variables. Significant differences were found for two variables: participants included in the sample were more likely to be living with/married to the child’s biological parent (109/888 [87.7%] versus 49/98 [50.0%]; χ²(1, N=986)=90.56, p<.001) and more likely to have graduated college (464/888 [52.3%] versus 31/96 [32.3%]; χ²(1, N=984)=13.02, p<.001).

Measure

ASA.

The ASA-27 is a 27-item self-report measure of separation anxiety symptoms experienced as an adult (over age 18; Manicavasagar et al., 2003). Items are rated on a four-point scale (1=This happens very often; 4=This has never happened), reverse coded, and subtracted by 1 so that response categories were 0-3. Cronbach’s α was .89 at wave 2 and .92 at wave 3.

Data Analysis

First, a single-factor CFA with ordered categorical indicators was fit to men’s and women’s ASA-27 data at wave 3. This model is equivalent to a normal ogive (probit) unidimensional graded response model (Millsap, 2010; Muthen & Muthen, 2018; Samejima, 1969; Takane et al., 1987), which is an extension of the 2-parameter logistic model for polytomous items (Thomas, 2011). The variance of the latent factor was set to 1 and the mean was set to 0 for model identification, while all other parameters were freely estimated.

Next, we evaluated whether the data met the IRT assumptions of unidimensionality, local independence, and monotonicity. Model fit of the initial single factor CFA was used as one index of unidimensionality. Comparative fit index (CFI) and Tucker-Lewis index (TLI) values greater than .95 and root mean squared error of approximation (RMSEA) values less than .06 suggest good model fit (Hu & Bentler, 2009). The polychoric correlation matrix was also subjected to principle components analysis (PCA) and the ratio of the first to second eigenvalues was examined. Larger ratios indicate greater unidimensionality. Pairs of items were reviewed for possible local dependence (LD) when residual correlations were greater than .20 (Reeve et al., 2007) and when the expected change in chi-square model fit or expected parameter change (EPC) from the modification indices were large and much higher relative to others (Hill et al., 2007). Pairs of items with relatively higher discrimination parameters were also flagged for possible local dependence (Orlando & Bryce, 2007). When local dependence was ambiguous, models were estimated with and without the potentially dependent items and local dependence was supported when item discrimination parameters changed markedly (Hill et al., 2007). When local dependence was established, the item with the lower discrimination parameter was removed. Finally, violations of monotonicity were tested using the Mokken package in R (Van der Ark, 2007); the program default of .03 was used as a cutoff.

The minimum number of items were removed until assumptions were met. IRT difficulty parameters were calculated by dividing item thresholds by item discrimination parameters, the latter of which are identical to factor loadings in this parameterization (Asparouhov & Muthen, 2016). Subsequently, the test information curve was plotted, along with the item characteristic and information curves, which were plotted separately for items that were derived based on DSM-criteria versus those that were not as indicated by the developers of the measure (Manicavasagar et al., 2003). The MODEL CONSTRAINT command was then used to test whether DSM-derived items were on average more closely related to the latent construct of ASA than non-DSM items. We also used cut-offs proposed by Baker (2001) to describe the item discrimination levels: 0.65-1.34 for moderate discrimination and 1.35-1.69 for high discrimination.

Next, CFA models were fit separately to men’s and women’s data at wave 3 to ensure the single-factor model fit well in both groups (Byrne, Shavelson, & Muthén, 1989). We use CFA language when discussing these models (loadings and thresholds) as opposed to IRT language (discrimination and difficulty parameters) to be consistent with the existing literature from each framework. The conclusions that can be drawn from models with varying levels of invariance for categorical indicator models differ from those permitted by invariance models for continuous indicators, because the continuous responses for the ordered categorical models are latent and inferred based on item thresholds and distributional assumptions rather than observed (see Liu et al., 2017). For example, comparisons at the level of observed categorical indicators require that unique factor, or strict, invariance is established, whereas only strong invariance is necessary for the same conclusions using continuous indicator models.

Measurement invariance by gender was tested by fitting a series of four hierarchically nested multiple group CFA models with increasing invariance constraints (Liu et al., 2017; Millsap & Yun-Tein, 2004; Muthén & Asparouhov, 2002). First, a baseline configural invariance model was fit. For model identification, the factor loading of one item (the marker variable) was constrained to 1 in both groups, one threshold per item and two thresholds for the marker variable were constrained to equality across groups, and, in the reference group only, the item residuals were constrained to 1 and the factor mean to 0; all other parameters were freely estimated. Item 14 was chosen as the marker variable because it loaded strongly on the factor in the separate CFAs for women at both waves and men at wave 3, and thus has a meaningful metric (Liu et al., 2017), and because its loading, threshold, and residual parameters were invariant across gender and time. For all other items, the first threshold was constrained to equality since there were the most cases in response categories 0 and 1 for all items unless modification indices suggested misfit in these threshold constraints; in these cases, an alternative threshold that exhibited invariance was constrained (Liu et al., 2017). Next, a loading or weak measurement invariance model was fit, which constrained all item loadings to equality across groups, followed by a threshold or strong measurement invariance model, which additionally constrained all item thresholds to equality. Finally, a unique factor or strict invariance model was fit which also constrained all unique factor item residuals to equality.

As each set of equality constraints were added, the degree of invariance was evaluated. Previous work has employed changes in fit statistics like the CFI (e.g., .01) and RMSEA (e.g., .015; Chen, 2007; Cheung & Rensvold, 2002); however, their performance for evaluating invariance with ordered categorical indicators estimated has not been systematically evaluated so they are not yet recommended in this context (Liu et al., 2017; Sass & Marsh, 2014). An alternative is the likelihood ratio test for comparing nested models with categorical indicators (DIFFTEST in Mplus; Asparouhov & Muthen, 2016). Despite the fact that this test may exhibit inflated Type I error rates (Sass & Marsh, 2014), we opted to take a conservative approach and deemed models invariant when the DIFFTEST was significant. CFI and RMSEA values were also used to determine whether the models continued to show good fit overall (e.g., Lin, Hirschfeld, & Margraf, 2018). Finally, a novel sensitivity analysis was employed to determine the practical impact of the additional levels of constraints (Liu et al., 2017). In this sensitivity analysis, discrepancies between the model-estimated proportion of cases in each response category for the less versus more restrictive models were calculated, and items were flagged if the discrepancy exceeded 5% for any response category. When models failed to exhibit invariance, partial invariance was tested. Constrained parameters were freed one by one according to modification indices until the above criteria were met (Byrne et al., 1989). If at least 80% of the constrained parameters were invariant, models were deemed partially invariant.

In a similar manner, a series of longitudinal CFAs with increasing invariance constraints were fit to women’s data at waves 2 and 3. Again in accordance with Liu and colleagues (2017), for the baseline model, in order to identify the variance and mean structure of the latent factor, the loading of a marker variable was constrained to 1 at both waves and the mean of the latent factor was constrained to 0 at wave 2 only. Additionally, one threshold per item plus a second for the marker variable were constrained to equality across waves, the unique residual item variances were constrained to 1 at wave 2 only, and the same items were permitted to covary across waves (e.g., item 6 at wave 2 with item 6 at wave 3), as were the latent factors. The invariance of the slope and thresholds of the marker variable and the other thresholds for each item that were necessary for identification were verified by the modification indices for the baseline model. The measurement model constrained the loading and threshold parameters to be identical across time, and the unique factor invariance model additionally constrained the unique variances at the third wave to equality by setting them to 1 to match the unique variances at wave 2.

All IRT and CFA models were estimated in Mplus 8 (version 1.6; Muthen & Muthen, 2012-2018) using a probit link, theta parameterization (so that variances for the categorical indicators could be specified, an option that is only available in Mplus using the theta parameterization), and the robust weighted least squares estimator (WLSMV; Flora & Curran, 2004), which is suitable for ordered categorical data. Although the correlation between ASA total scores within dyads was small and non-significant (r=0.06, n=405, p=0.26), for the models including both men and women, standard errors were adjusted for potential non-independence of observations (i.e., clustering within families) using a sandwich estimator (Muthen & Muthen, 2012-2018). The R package MplusAutomation was used to extract model fit statistics and parameters (Hallquist & Wiley, 2018) and descriptive statistics were computed in R Studio (version 1.2.1335; R Core Team, 2016)

Results

Descriptive Statistics

The mean total ASA score for women at wave 2 was 11.94 (SD=9.29; range: 0-60). For men at wave 3 it was 8.10 (SD=8.46, range: 0-54) and for women at wave 3 it was 10.34 (SD=9.61; range: 0-59). The average inter-item polychoric correlation for women at wave 2 was 0.37 (SD=0.14; range: 0.00 to 0.90), the average for men at wave 3 was 0.50 (SD=0.14; range: −0.01 to 0.99), and the average for women at wave 3 was 0.46 (SD=0.14; range: 0.07 to 0.91).

IRT Analysis

Assumptions.

An initial single-factor ordered categorical CFA model including all items from the ASA-27 was fit to men’s and women’s data at wave 3. The fit of this model, the residual correlations between the model estimated and observed polychoric correlations, and the modification indices were examined to determine whether the data met the IRT assumptions of unidimensionality and local independence. While the fit suggested unidimensionality (CFI=.957, TLI=.953, RMSEA=.049 [.045-.052]), two pairs of items exhibited strong local dependence (Supplementary Table 1). Specifically, for the first pair (items 21 and 24), which query panic symptoms, modification indices suggested that adding a covariance would substantially improve model fit. The second pair (items 10 and 26), which query talkativeness, had a large residual correlation. The pairs of items query narrow constructs and use similar wording, which make them likely to elicit similar responses. The item with the lower discrimination parameter in each pair was removed (items 21 and 26).

Several other pairs of items exhibited possible local dependence, so the item with the lower discrimination parameter in each pair was removed iteratively (Supplementary Table 1). However, the changes in discrimination parameters and model fit were negligible in every case, which suggested that the remaining items were locally independent. The unidimensionality and local independence of these 25 items were further supported by other indices: the single-factor CFA fit the data well (CFI=.966, TLI=.963, RMSEA=.042 [90% CI=.038-.046], SRMR=.051), the 1:2 eigenvalue ratio was large (12.81:1.28 [10.04]), and the average residual correlation was low (M=.047, SD=.035; range=.000-.201). In addition, no items significantly violated the monotonicity assumption.

Test and item properties.

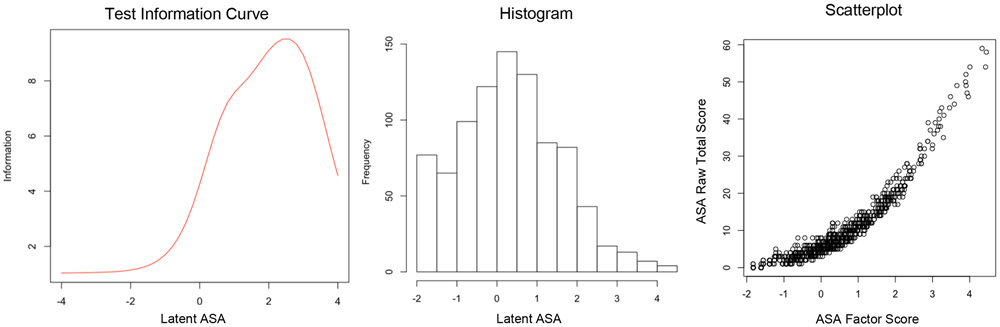
The total information curve shows that the ASA-27 provides the most information, or assesses with the least error, at approximately 2.5 SDs above the mean of latent ASA and that it provides very little information below −1 SDs (Figure 1). Information was reliable at the equivalent of alpha of .88 or greater from approximately 1 to 3 SDs (Thissen, 2000). The histogram depicts the number of cases at all levels of latent ASA and the scatterplot of factor scores against sum scores depicts the impact of weighting items by the discrimination parameters (Figure 1). At lower levels of latent ASA (approximately 1 SD and below), the sum and factor scores are less strongly related. Items 14, 17, 18, and 24 were highly discriminating, and all other items except item 1 were moderately discriminating (Table 1; Baker, 2001). The three sets of difficulty parameters were quite variable (1: −2.59 to 2.00; 2: 0.00 to 3.19; 3: 1.50 to 3.85; these parameters are based on item thresholds and demarcate response categories 0 from 1, 1 from 2, and 2 from 3).

Figure 1.

Test information curve for the ASA-27, histogram of ASA factor scores, and scatterplot of raw v. factor scores for men and women at wave 3

Notes: N=889. ASA=Adult separation anxiety. ASA-27=Adult Separation Anxiety Questionnaire.

Table 1.

Graded response model item parameters in men and women

Item		a	SE	b-1	b-2	b-3	DSM-IV
1b	More secure at home with attachments	0.42	0.05	−2.59	0.00	1.50	--
2ab	Difficulty staying away from home for hours	0.84	0.08	1.53	2.97	3.61	A-4
3	Carries around object for security/comfort	0.58	0.06	1.56	2.77	3.28	--
4a	Extreme stress when leaving home for trip	1.02	0.08	0.58	2.19	2.86	A-1
5ab	Nightmares about separation from attachments	1.00	0.07	0.94	2.68	3.18	A-7
6a	Extreme stress before leaving someone close for trip	1.30	0.09	0.77	2.24	2.84	A-1
7	Very upset when usual daily routine is disrupted	0.94	0.06	0.20	2.26	3.28	--
8b	Worries about relationship intensity with attachments	1.13	0.08	0.74	2.05	2.84	--
9a	Physical symptoms before leaving home for work/activity	0.82	0.07	1.51	3.11	3.74	A-8^
10b	Talks a lot to keep attachments around	0.76	0.06	1.15	2.68	3.85	--
11	Concerned about where attachments are going when separated	1.09	0.08	0.78	2.32	3.00	--
12ab	Difficulty sleeping alone at night	0.88	0.07	0.53	2.07	2.84	A-6
13b	Falls asleep better with voices or TV	0.63	0.05	0.61	2.06	2.92	--
14ab	Very distressed thinking about being away from attachments	1.43	0.11	0.81	2.11	2.70	A-1
15a	Nightmares about separation from home	1.27	0.17	1.91	2.82	3.07	A-7
16a	Worries about attachments coming to serious harm	1.00	0.07	0.07	2.18	2.87	A-2
17b	Very upset when changes to usual daily routine interfere with contact with attachments	1.43	0.11	0.82	2.20	3.02	--
18b	Worries a lot about attachments leaving	1.53	0.11	0.68	1.98	2.57	--
19	Sleeps better with lights on in home/bedroom	0.77	0.09	2.00	3.19	3.63	--
20ab	Avoids being home alone when attachments are out	1.19	0.12	1.68	2.59	3.15	A-5
21ab	*Panic symptoms when thinking about separation from attachments	--	--	--	--	--	A-8
22b	Anxious about not speaking to close attachments on phone regularly	1.26	0.11	1.05	2.35	3.15	--
23b	Afraid would not be able to cope if attachments left	1.13	0.08	0.88	2.28	3.16	--
24ab	Panic symptoms when separated from attachments	1.43	0.17	1.72	2.74	3.19	A-8
25ab	Worrying about events causing separation from attachments	1.15	0.10	1.40	2.54	3.36	A-3
26	*Attachments mention he/she talks a lot	--	--	--	--	--	--
27	Worries relationship so close it causes others problems	1.06	0.12	1.87	3.09	3.73	--

Notes: N=889. a=discrimination parameter. b-1=difficulty parameter between response categories 0 and 1. b-2=difficulty parameter between response categories 1 and 2. b-3=difficulty parameter between response categories 2 and 3. All items loaded significantly on the factor at p<.001.

^*Excluded based on local dependence.

^aItems based on DSM-IV criteria (Manicavasagar et al., 2000); the particular DSM-IV criteria was determined by authors of current study.

^bItems significantly discriminate at p<.05 between ASA and other anxiety disorder patients (Manicavasagar et al., 2000).

^{^}A-8 does not include physical symptoms when separation from home occurs/is anticipated, only separation from major attachment figures.

Using the MODEL CONSTRAINT command, the difference between the average discrimination parameters for the DSM-derived items and the non-DSM-derived items was tested. The DSM-derived discrimination parameters were higher on average (b = 1.11, SE=.05) than the non-DSM derived discrimination parameters (b=.98, SE=.04; b_diff=.13, SE=.04, p<.001). This indicates that the DSM-derived items are more strongly associated with the latent trait, ASA.

The DSM-derived versus non-DSM-derived item sets provide comparable information, despite the DSM-derived set having one fewer item, though neither set provides sufficient information across the entire range of latent ASA (Supplementary Figure 1). The steepness of the item characteristic curves for the first response category for the DSM-derived items indicate that these items discriminate well starting from approximately −1 SD up to 2.5 SD. The non-DSM derived items’ first response categories discriminate across approximately the same range, but several items have shallower slopes indicating poorer discrimination (i.e., 1, 3, 13, 19). Overall, neither set of items discriminate well at lower levels of ASA. Indeed, people with the lowest (−4 SD) and average (0) levels of latent ASA are equally likely to endorse the lowest response option for most items. The curves for response categories 2 and 3 for several items in the non-DSM set are relatively shallow, whereas all curves for the DSM-derived set are fairly peaked. Finally, the curves from the fourth response category are similar but both sets do not reach a probability of endorsement of 1, even at the highest levels of latent ASA. This indicates that the measure may discriminate at higher levels of ASA not represented in the sample.

Measurement Invariance

Gender.

Separate single-factor CFAs for men and women at wave 3 using the same 25-item set fit the data well (men: CFI=.977, TLI=.975, RMSEA=.037 [90% CI=.030-.044], SRMR=.58; women: CFI=.965, TLI=.962, RMSEA=.044 [90% CI=.038-.050], SRMR=.059). The baseline configural invariance multiple group model fit to both genders simultaneously also fit well (Table 2). The model continued to fit well but the DIFFTEST was significant (see Supplementary Table 2 for complete set of models); items 1, 12, and 19 were the largest source of misfit. The loading for item 1 was higher in women (b=.41, SE=.09) compared to men (b=.24, SE=.05), suggesting that feeling more secure with attachment figures when at home is more strongly related to ASA in women. Similarly, item 12, which queries difficulty sleeping alone at night, was more strongly related to ASA in women (b=.79, SE=.10) than men (b=.63, SE=.08) as was item 19 (women: b=.82, SE=.12; men: b=.50, SE=.10); this item asks about sleeping better with lights on. After releasing these constraints (3/24 [12.5%] loadings freed), the model demonstrated partial loading invariance. Next, threshold constraints were added, and the model again fit well overall but the DIFFTEST was significant, meaning full threshold invariance was not established. The first thresholds for items 17 (upset when changes to routine interfere with contact) and 25 (worrying about events causing separation) were identified by modification indices. Both parameters were higher in women (item 17: b=1.89, SE=.20; item 25: b = 2.04, SE=.22) compared to men (item 17 b =1.12, SE=.16; item 25 b = 1.48, SE=.15), suggesting that women with higher levels of ASA have a similar probability of endorsing the first response categories for these items as men with lower levels of ASA. Partial threshold invariance was achieved with these constraints freed (2/49 [4.1%] thresholds freed). Finally, when constraints were added to item residuals in the strict unique factor model, the model fit well but the DIFFTEST was again significant, so the residual for item 19 was freed (1/25 residuals; 4.0%). The model then exhibited partial unique factor invariance. This item residual was larger in women (b=1.64, SE=.33) than men (constrained to 1), suggesting less variance was explained by the ASA factor in women. In total, 6.5% (6/92) of parameters were freed. The sensitivity analysis comparing each partially invariant model to its lesser constrained counterpart indicated that none of the probabilities for response categories were discrepant by 5% or more, which suggests that the constraints had little practical impact.

Table 2.

Invariance of ASA-27 across gender and time

	Model	Invariance	df	CFI	TLI	RMSEA	Δχ2 a	Δdf	p	Freed parameters
Gender	Baseline (Configural)	Full	550	.971	.969	.041	--	--	--	--
	Loading (Metric/Weak)	Partial	571	.972	.971	.039	31.09	21	.07	λ: 1, 12, 19
	Threshold (Scalar/Strong)	Partial	618	.975	.976	.036	63.36	47	.06	λ: 1, 12, 19; τ: 17-1, 25-1
	Unique Factor (Strict)	Partial	642	.979	.981	.032	32.73	24	.11	λ: 1, 12, 19; τ: 17-1, 25-1; δ: 19
Time	Baseline	Full	1149	.962	.960	.026	--	--	--	--
	Loading	Partial	1172	.962	.960	.026	33.87	23	.07	λ: 19
	Threshold	Partial	1218	.963	.963	.025	60.81	46	.07	λ: 19 τ: 1-1, 1-2, 18-1
	Unique Factor	Partial	1241	.965	.965	.024	35.17	23	.05	λ: 19; τ: 1-1, 1-2, 18-1; δ: 1, 3

Notes:

^aDIFFTEST. λ (lambda)=loading. τ (tau)=threshold. δ (delta)=residual. Analysis excludes items 21 and 26 due to local dependence with other items.

Time.

Separate CFA models using women’s data only fit well at the two assessments three years apart (wave 2: CFI=.939, TLI=.933, RMSEA=.052 [90% CI=.045-.058]; wave 3: CFI=.965, TLI=.962, RMSEA=.044 [90% CI=.039-.050]), as did the configural baseline longitudinal CFA model (Table 2). Next, the loadings were constrained to equality. This model continued to fit the data well overall, but the DIFFTEST was significant, so full loading invariance was not achieved (see Supplementary Table 2 for complete set of models). Item 19 (sleeping better with lights on) was identified as contributing to misfit. When the equality constraint was released for this item (1/24 [4.2%] loadings freed), the model exhibited partial loading invariance. The loading was higher for women at wave 3 (b=.81, SE=.11) compared to wave 2 (b=.26, SE=.06). Subsequently, a threshold invariance model was fit. Again, the model fit the data well but the DIFFTEST was significant. To achieve partial threshold invariance, the first threshold of items 1 and 18 were freed. Modification indices then suggested freeing the second threshold for item 24; however, doing so caused the item’s third threshold to be lower than its second threshold at wave 3, which is problematic, so the parameter constraint with the next largest modification index was freed instead. This was threshold 2 for item 1 (3/49 [6.1%] thresholds freed). Both thresholds for item 1 (feel more secure at home with attachment figures) were lower at wave 2 (1-1 b=−1.07, SE=.09; 1-2: b=.05, SE=.07) compared to wave 3 (−1 b=−1.93, SE=.29; 1-2: b=−.34, SE=.11), which indicates that women at wave 2 with lower levels of ASA have the same probability of endorsing response categories 1 and 2 as women with higher levels at wave 3. In contrast, the first threshold for item 18 (worries about attachments leaving) was higher at wave 2 (b=.88, SE=.12) compared to wave 3 (b=.29, SE=.11). Finally, the unique factor invariance model was fit which constrains all item residuals to equality. The model fit well but the DIFFTEST was significant. The residuals for items 1 and 3 were freed and partial unique factor invariance was achieved (2/25 [8.0%] residuals freed). For both items, the residuals were over two times larger at wave 3 (item 1: b=2.14, SE=.67; item 3: b=2.12, SE=.47) compared to wave 2 (constrained to 1), suggesting less variance was explained by latent ASA for these items at wave 3. In total, 6.5% (6/92) of parameters were freed. Again, the sensitivity analysis revealed that all discrepancies in proportions of model-estimated proportions were smaller than 5%.

Discussion

We conducted a thorough psychometric analysis of the ASA-27, the most widely used self-report measure of ASA. This effort is timely in that the disorder was recently recognized by DSM-5 as a clinical problem that can occur in adulthood, and researchers and clinicians alike may be increasingly interested in its assessment. Overall, the measure assessed ASA well at ASA levels above but not below the mean and demonstrated partial unique factor (or strict) invariance across both gender and time.

Item Response Theory Assumptions: Substantive Benefits

Meeting the assumptions of unidimensionality, local independence, and monotonicity is both a prerequisite condition for IRT modeling and facilitates evaluations of whether common interpretations of sum scores and reliability estimates are permissible. We determined that the ASA-27 did not meet the assumption of local independence in our sample, and consequently removed one item from each of two locally dependent pairs (21 and 24; 10 and 26). Had we retained all items in these pairs of items, the measure’s reliability estimate may have been artificially inflated, as it would reflect how these items consistently measure constructs (talkativeness and panic symptoms) besides the construct of interest per se (ASA), and the sum scores would have reflected some combination of individual differences in the construct of interest and in these unacknowledged secondary constructs.

We identified and removed the locally dependent items on statistical grounds, but removing them also aligns with past studies. Specifically, removing item 26 (“Have people close to you mentioned that you ‘talk a lot’?”) was consistent with work reporting that this item had the lowest correlation with the ASA-27 total score in a community sample (Manicavasagar et al., 1997), did the poorest job of discriminating between anxiety disorder patients with versus without ASA disorder (Manicavasagar et al., 2000), and had the lowest loading (or tied for lowest) on the first factor in two principle components analyses (Dirioz et al., 2011; Manicavasagar et al., 2003). There was also some evidence that item pair 21 and 24 were locally dependent in a past study, which used a Turkish translation of the measures, in that these two items loaded very strongly and more strongly than other items (Dirioz et al., 2011; Orlando & Bryce, 2007). However, these two items did not load exceptionally highly in a mixed community/clinical sample using the English version (Manicavasagar, Silove, Wagner, & Drobny, 2003), so future work will need to replicate this finding.

Test & Item Functioning

After meeting the IRT assumptions, we subsequently found that the ASA-27 provided the most accurate assessment, or most information, at high levels of latent ASA. We showed this in several ways, including the test information and individual item curves which peaked near the upper end of latent ASA and the strong positive relationship between total raw scores and model-estimated factor scores starting at about two SDs above the mean depicted in a scatterplot. In the same vein, the ASA-27 did not appear to be a reliable measure of the lowest levels of ASA. This can be seen by the test information curve, which shows negligible information levels below −1 SD (this includes 142 cases, or 16.0% of our sample); the weak relationship between total and factor scores below the mean of latent ASA, which shows that differences between individuals at low levels are less meaningful than differences between individuals at high levels; and the fact that the item difficulties for response categories 0-1 are all greater than the mean except item 1, which indicates that an individual must have higher than average levels of latent ASA in order to have a 50% chance of endorsing the second lowest response category instead of the lowest response category on nearly all items.

Given that we used a community sample, and the lowest levels of ASA are probably represented, it is notable that the ASA-27 items were not able to discriminate in this range. This means that when a total score is used in a typical fashion (e.g., as a predictor in a regression model), one- or two-point differences between low total scores based on the items currently included in the ASA-27 are given the same weight as one- or two-point differences between high total scores even though the precision for the former is much lower. This limited range of precision suggests a need for items with lower difficulty parameters. These items could either query less severe aspects of ASA, which, given the disorder’s newness, may still need to be defined, or could use alternative wording in order to lower the threshold for endorsement (e.g., change “Very upset” in item 7 to “Somewhat frustrated”). Eliminating items with poor discrimination parameters may be another means for mitigating this problem.

The low precision as lower levels of ASA suggest that the ASA-27 is most suitable for assessing individuals who have average to high levels of ASA relative to others in a community sample, or that it may be an acceptable measure for use with clinical populations (Thomas, 2011). Thomas (2011) notes, “Such scales [that have information functions that peak near a cutoff on the impaired end of a latent distribution] can only make reliable discriminations within narrow regions of latent distributions and are not appropriate for dimensional classifications of patients along entire continuums,” (p. 296) and suggests they could be dichotomized around the band of precision to classify cases from non-cases.

The difficulty parameters in the item-level analysis also show which items individuals with more severe ASA are more likely to endorse compared to those with lower levels. We consider here the difficulty parameters for response categories two versus three and three versus four in particular because Manicavasagar et al. (1997) considered items positive if either of these top categories were endorsed. Specifically, items 2, 9, 19, and 27 were among the items with the top five highest difficulty parameters for these two categories. They query a range of aspects of ASA: sleeping better with the lights on, worrying about relationships being so close it causes problems, having difficulty staying away from home for several hours, and experiencing physical symptoms before leaving home for work or activity. What ties them together may be that three of the four involve behavior or anxiety-responses to behavior, compared to many other items on the scale which query emotional states like distress or worry. While the fourth does query worry, it is also the only item on the scale that asks about potential impairment in particular. Clients who present with these symptoms may be more likely to be experiencing high levels of ASA compared to clients who present with other symptoms.

Comparing DSM to Non-DSM-Derived Items

The developers of the scale based some items on adaptations of criteria for separation anxiety in youth from DSM-IV (Manicavasagar et al., 1997). Our analysis suggests that these criteria are central for understanding disorder presentation in adults. We found that the DSM-derived items were more discriminating than the non-DSM-derived items on average, which means that the former have a stronger relationship to the underlying construct measured by the ASA-27. At the same time, of the four items which were highly discriminating, two were DSM-derived (item 14: very distressed thinking about being away from attachments; item 24: panic symptoms when thinking about separation from attachments) and two were not (item 17: very upset when changes to usual daily routine interfere with contact with attachments; item 18: worries a lot about attachments leaving). This highlights the significance of some aspects of ASA that are not captured explicitly by DSM criteria.

Invariance by Gender and Over Time

Our analysis suggests that the ASA-27 shows partial unique factor invariance across gender. This is the categorical indicator counterpart to strict invariance with continuous indicators. Of 92 loading, threshold, and item residual parameters, 86 (93.5%) were constrained to equality in the final partial unique factor invariance model. This small degree of invariance is particularly notable given that it was evaluated by the conservative DIFFTEST. Moreover, the sensitivity analysis revealed that there was virtually no practical impact of increasing constraints. Since partial unique factor invariance was achieved, we can conclude that, for the most part, the differences in factor means and variances are attributable to true differences in latent ASA rather than to measurement bias of the ASA-27 (Liu et al., 2017). We can additionally conclude that, for the most part, the differences in the continuous latent responses, which underlie the observed categorical responses, and the differences in the categorical indicators themselves and thus the sum scores, are attributable to differences in the latent factor. This suggests that the higher levels of ASA in women observed in the current study and past work using the ASA-27 (Aaronson et al., 2008; Silove, Marnane, Wagner, & Manicavasagar, 2010; Silove, Marnane, Wagner, Manicavasagar, et al., 2010) can tentatively be interpreted as reflecting true differences in the latent ASA, as opposed to differences in the measurement properties or structure of the ASA-27. The gender differences in loadings and thresholds may be due to differences in socially acceptable expressions of anxiety.

The longitudinal invariance test in women likewise suggests that the ASA-27 demonstrates partial unique factor invariance across a three-year interval. Like the gender invariance analysis, the vast majority of parameters (93.5%) were constrained to equality across time in the final unique factor model, so the differences in the means and variances of the latent factors and of the observed ordered-categorical indicators can tentatively be interpreted as reflecting true differences in latent ASA across time. The sensitivity analysis again indicated very little practical impact of the constraints on model-estimated response category proportions. While establishing longitudinal invariance is an important prerequisite for posing questions about change in ASA, whether these results hold after treatment or significant loss events needs to be tested in future research.

Since modification indices are used to identify the equality constraints that should be released, and thus models may be susceptible to overfitting to noise in a given sample, we refrain from extensive interpretation about the specific parameters that were freed in the multigroup gender and longitudinal models. We do note, however, that equality constraints for items 1 and 19 contributed to misfit in both invariance tests. This may indicate that the data from wave 3 women, which were included in both invariance tests, were anomalous in some fashion, or that these items are biased across time or gender. They may be candidates for removal if future work replicates these findings. Until then, researchers may consider administering the full measure and assessing unidimensionality in their own samples. If these items are identified as problematic in independent samples, researchers may consider eliminating them from sum score calculations.

Study Strengths and Limitations

The current study has several notable strengths. First, the psychometric analysis goes into much greater depth than previous analyses of this widely-used measure, and it provides insight into how the test functions as a whole, as well as into how individual items function. Additionally, by framing the assumptions of IRT in terms of their practical benefits, and by testing differences in DSM- versus non-DSM derived items, the analysis had both psychometric value in terms of the ASA-27 and conceptual value in terms of advancing thinking about ASA. We also had a relatively large sample and reports from men and women and reports at two measurement occasions, which permitted us to test questions about invariance. Finally, we employed a cutting-edge sensitivity analysis on the practical impact of adding invariance constraints (Liu et al., 2017).

Alongside these strengths, the study limitations must be acknowledged as well. Several issues regarding sampling and generalizability must be noted. The sample was made up of mostly White and non-Hispanic adults who were married and had young children, so results may not generalize to other racial or ethnic groups, single adults, or people without children or with older children. In addition, there was evidence of attrition bias for the wave 3 assessment, so whether the results generalize to individuals who are not in a relationship or have not completed college is unknown (although this is somewhat tempered by the similarity with the wave 2 results, which did not exhibit attrition bias, but included women only). In the same vein, since the sample was drawn from the community, we cannot be certain that the results would generalize to a clinical sample, despite the fact that IRT parameters are theoretically sample-invariant. The longitudinal invariance testing was also conducted in women only, so whether changes in latent levels of ASA or item responses over time reflect true change in men is still unknown. In addition, the substantive meaning of the partial gender and longitudinal invariance can be somewhat difficult to determine, in part, because the loading, threshold, and item residual parameters are interdependent; for example, freeing a loading may permit that item’s residual to be constrained to equality in the more restrictive model. Moreover, as in the case in all types of structural equation models, using modification indices to identify the parameters to free may be prone to fitting to idiosyncratic noise in the sample as opposed to reflecting true differences at the population level. For these two reasons, we encourage readers to focus on how, in general, the measure was invariant, rather than on the meaning of the specific non-invariant item parameters until they are replicated in an independent sample. Finally, because we removed two items in order to achieve unidimensionality and thereby reduce bias in parameter estimation, our results must be applied to the use of the full scale cautiously.

Conclusion

The ASA-27 is a widely-used self-report measure of the newly-recognized clinical problem, ASA. In a community sample, it assesses ASA most reliably at higher than average levels and least reliably below the mean. The ASA-27 showed partial invariance at the unique factor level across gender and time, with less than 7% of parameters freed in both cases, which implies that the means and variances of the latent factors and differences in the observed responses can be attributable to true differences in ASA. Future work should replicate these findings in a sample that includes individuals with a wider range of ASA severity and may consider removing additional items that provide little or redundant information.

Public Significance Statement:

The ASA-27, the most widely-used self-report measure of ASA, can reliably distinguish among individuals in the community when they have ASA levels at or above, but not below, the average. In general, men’s and women’s ASA-27 sum scores can be validly compared, as can women’s scores across three years.