Abstract
Convolutional Neural Networks (CNNs) have been utilized for to distinguish between benign lung nodules and those that will become malignant. The objective of this study was to use an ensemble of CNNs to predict which baseline nodules would be diagnosed as lung cancer in a second follow up screening after more than one year. Low-dose helical computed tomography images and data were utilized from the National Lung Screening Trial (NLST). The malignant nodules and nodule positive controls were divided into training and test cohorts. T0 nodules were used to predict lung cancer incidence at T1 or T2. To increase the sample size, image augmentation was performed using rotations, flipping, and elastic deformation. Three CNN architectures were designed for malignancy prediction, and each architecture was trained using seven different seeds to create the initial weights. This enabled variability in the CNN models which were combined to generate a robust, more accurate ensemble model. Augmenting images using only rotation and flipping and training with images from T0 yielded the best accuracy to predict lung cancer incidence at T2 from a separate test cohort (Accuracy = 90.29%; AUC = 0.96) based on an ensemble 21 models. Images augmented by rotation and flipping enabled effective learning by increasing the relatively small sample size. Ensemble learning with deep neural networks is a compelling approach that accurately predicted lung cancer incidence at the second screening after the baseline screen mostly 2 years later.
Keywords: Radiomics, ensemble classification, Convolutional Neural Network, Lung Nodule, NSCLC
1. Introduction
Lung cancer is often diagnosed at a late stage of the disease where the survival rates are dismal; the five-year relative survival rate for all lung cancers is 19% [1, 2]. Early diagnosis of lung cancer is a foremost priority for improving patient survival and outcomes. The National Lung Screening Trial (NLST) [3] compared low-dose helical computed tomography (LDCT) and standard chest radiography (CXR) for three annual screens and reported a 20% relative reduction in lung cancer mortality for LDCT compared to CXR. As such, lung cancer screening by LDCT is an effective modality for mitigating lung-cancer mortality and currently is the only option for those who are at high-risk. Lung cancer screening for high-risk individuals typically detects a large number of indeterminate pulmonary nodules, of which only a fraction will ever be diagnosed as cancer. As such, accurate and reproducible biomarkers to predict which indeterminate pulmonary nodules will be diagnosed as cancer would have direct translational implications as a tool for clinical purposes to improve the lung cancer screening for nodule detection.
Conventional quantitative radiomics features (size, shape, and texture) and image-based features (deep features, blobs, and, curves) can be generated and then analyzed using machine learning algorithms for classification analyses including risk prediction, diagnostic discrimination, and prognosis [4]. Deep learning is an emerging machine learning approach, which has been applied to classification of lung nodules and tumors [5, 6]. To generate generic features (blobs, edges, etc.) from an image, different convolutional kernels are applied over the input image and then those generic feature-based images are passed through some fully connected neural layers. This category of neural network is called a convolutional neural network (CNN) which has achieved high accuracy on image data [7]. Hu et al. [8] surveyed four deep neural network architectures (CNN, autoencoders, deep belief network and fully connected network) for detection and diagnosis of various cancers. Many machine learning approaches have been proposed for lung cancer classification. Cao et al. [9] proposed a multi-kernel based feature selection approach along with imbalanced learning. The feature selection approach was based on pairwise feature similarities. Data oversampling was conducted to mitigate the effect of imbalance problem. The proposed approach was evaluated using different classifiers and compared with other feature selection algorithms. Causey [10] proposed a non-invasive method using CT data to predict malignancy of lung nodules by CNN. They divided the patients in the LIDC dataset into 5 levels (1- less likely to be malignant, 2 and 3- intermediate malignant, 4- moderately malignant, 5- highly likely to be malignant) and combined both image and quantitative radiomics features to predict malignancy. They achieved 0.993 AUC with 95.2% accuracy when differentiating level 1 tumors from the remaining ones. Whereas, differentiating level 1 and 2 from the other levels yielded 0.984 AUC and 94.6% accuracy. Nishio et al. [11] developed an approach to classify benign, primary, and metastatic lung cancer. They evaluated the effectiveness of a deep CNN for lung cancer classification and compared the performance of a CNN with the machine learning models built on quantitative radiomics features. Liu et al. [12] proposed a multi-view and multi-scale CNN for lung nodule classification. There were 12 different views and 3 different scales utilized to generate different images as input to the CNN. This approach yielded 92.1% and 90.3% accuracy on the LIDC and ELCAP [13] dataset respectively. Carvalo et al. [14] utilized index basic and standardized taxic weights to show the different patterns between malignant and bengin tumors and then finally used a CNN for classification. Zuo et al. [15] proposed a multi-resolution CNN to classify lung nodules. The multi-resolution CNN was used to generate features of various resolutions from network layers of different depth for nodule classification. Most of the studies [9, 10, 12, 14] in lung cancer analysis have used the LIDC-IDRI dataset [16] for classification which has mostly contrast enhanced CT scans as opposed to NLST scans used in this study which are non-contrast and low dose.
Ensemble learning [17, 18, 19] is an approach for creating multiple different learned models and then integrating the outcomes into a single classification model. The final ensemble model typically generates improved classification compared to a single model by reducing the variance obtained from individual models. In a previous study [20], the authors utilized ensemble learning for predicting lung nodule malignancy, which improved the classification accuracy from 76.79% [21] to 86% and AUC from 0.81 to 0.9.
In this study, we generated additional CNN models by using different random weight initializations for training and then utilized the ensemble of CNN classifiers to predict lung cancer incidence from LDCT screening images. Classification performance between different image augmentation approaches was also compared. The maximum accuracy from this work was 90.29% with 0.96 AUC, a marked increase from past results [20, 21].
2. Methodology
2.1. Dataset
We obtained deidentified data from the National Cancer Institute Cancer Data Access System. The data included patient demographics, clinical covariates, and LDCT images. The NLST was a multi-center trial with subjects randomly assigned to be imaged by LDCT or x-ray (CXR). The study compared LDCT versus x-ray (CXR) for early detection of lung cancer [22, 3] among high-risk individuals who were current or former smokers with a minimum of 30-pack years of smoking and an age range of 55-74 years. Former smokers had to have quit within 15 years [22, 3, 23]. Our overall study was a nested case-control approach which included nodule positive controls and screen-detected incident lung cancers with matched demographics from the NLSTs LDCT arm. The original description of lung cancer and nodule-positive cohorts was described in Schabath, et. al. [24, 25]. At T1, 85 screen-detected incident lung cancers (SDLC) were diagnosed and at T2, a separate group of 85 SDLC cases were diagnosed. Both lung cancer case groups had nodules at T0 that were followed across time. Then 328 nodule-positive controls had nodules (never diagnosed as cancer) that were followed from T0 to T2 and had similar matched demographics as the cases diagnosed as lung cancer. We didn’t include any ground glass nodules in our study.
The incident lung cancer patient and nodule positive controls for this study were divided into two cohorts: Cohort 1 (training cohort. which consisted of 85 incident lung cancers diagnosed at T1 and 176 nodules positive control for a total of 261 cases) and Cohort 2 (test cohort, which consisted of 85 incident lung cancers diagnosed at T2 and 152 nodules of 85 incident lung cancers diagnosed at T2 and 152 nodules positive control for a total of 237 cases). Selection of the two cohorts is shown in Figure 1. Table 1 shows nodule size by category. There was no significant difference statistically between the incident lung cancers diagnosed and positive controls with respect to smoking history, age, sex, race, and ethnicity. As previously described in [21] the T0 nodules were identified and segmented using Definiens Software [26] by a radiologist with more than 9 years of experience
Figure 1:
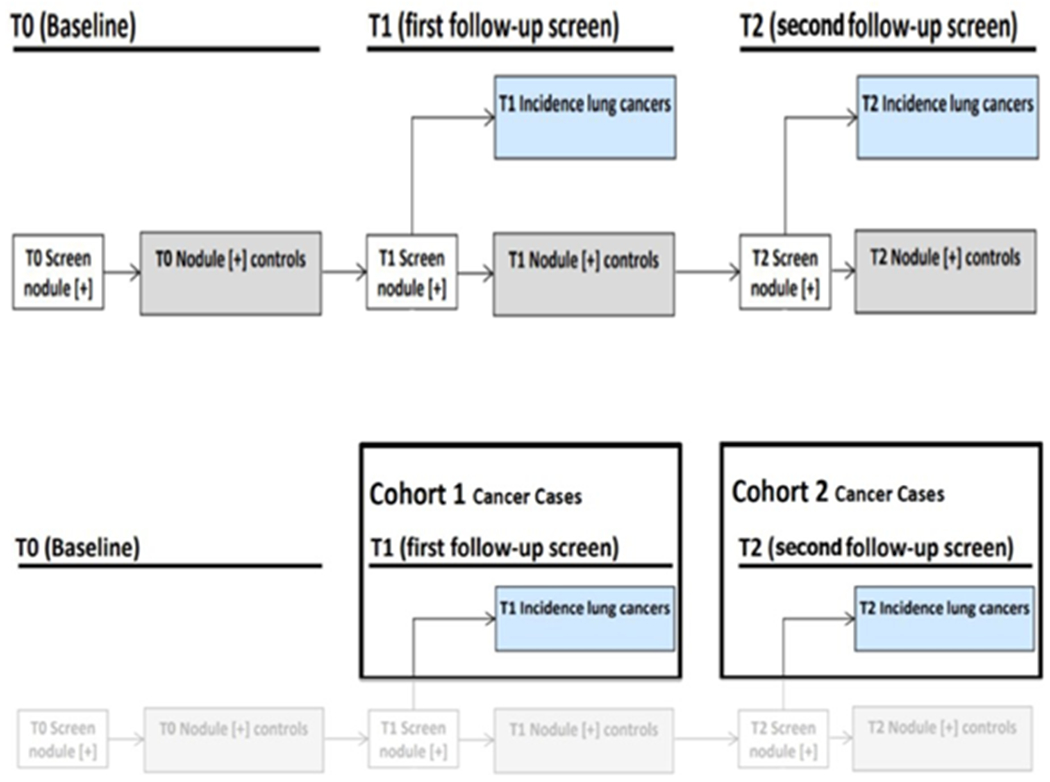
(top row)NLST study schematic, (bottom row)Flowchart of selection of cohort 1 and cohort2 from NLST study
Table 1.
Number of cases after splitting using various Clinical criteria
| Measurements | Cohorts | Min | Max | Ave |
|---|---|---|---|---|
| Cohort 1 SDLC | 3.32 | 28.64 | 12.1 | |
| DiamLoetnegre (tmm) | Cohort 1 PC | 2.24 | 27.45 | 8.1 |
| Cohort 2 SDLC | 2.04 | 48.62 | 12.1 | |
| Cohort 2 PC | 3.52 | 30.54 | 8.6 | |
| Cohort 1 SDLC | 0.02 | 10.76 | 0.81 | |
| Volume (cm3) | Cohort 1 PC Cohort 2 SDLC |
0.02 0.01 |
4.94 23.64 |
0.3 1.63 |
| Cohort 2 PC | 0.02 | 6.55 | 0.32 |
Abbreviations: PC = positive control; Min= Minimum; Max= Maximum; Ave = Average
2.2. Convolutional Neural Network
A CNN [27] is a multi-layer neural network architecture with convolutional, and typically max pooling, plus fully connected layers. With more than 1 hidden layer, they are deep networks trained via “deep learning”. The convolutional layers enable the deep neural network to learn appropriate features. In our previous study [28], a tuned pre-trained VGG-S model (> 10 million parameters) was analyzed, but the results obtained were not as good as using only quantitative features [21]. The VGGS model had many weights with respect to the number of images in our dataset. To avoid overfitting the data, smaller CNN architectures were generated and analyzed. For this study, three smaller CNN architectures (less weights) were designed. They were built using Keras [29] with a Tensorflow [30] backend. Each model had less weights than larger CNN models (VGG, ResNet, etc). Each model had a significantly smaller number of weights compared to most models available for transfer learning. The goal was a diverse set of classifiers that did not overfit. More weights in a CNN network can provide a robust and complex classifier, but also requires more data to train, otherwise overfitting is likely to occur.
CNN architecture 1 had two convolution layers followed by two max-pooling layers and finally two fully connected layers before a final classification layer. Leaky ReLU (alpha=0.01) was added after the convolution layer output to add non-linearity. The total number of parameters was 841,681. CNN architecture 2 had the same initial layers (convolution and max-pooling layers) as in CNN architecture 1; however, after the first fully connected (fc) layer, a Long-Short-Term Memory (LSTM) layer [31] was used in place of the second fc layer followed by a final classification layer. LSTM is a recurrent neural network architecture that can store useful information for future calculation and has different gate types to allow for memory. In CNN architecture 2, we took advantage of the unique architecture of LSTMs and assessed whether a stateless LSTM could provide improved classification performance. The total number of parameters in CNN architecture 2 was 845,033. CNN architecture 3 was a cascaded CNN architecture that was modified from the CNN architecture utilized by Li et al. [32] . Initially, there were two branches in the network and the same input image was sent through both branches. The left branch has only a max-pooling layer, whereas the right branch has 2 convolution layers and each convolution layer is followed by one max-pooling layer. The output of both the right and left branches were merged together and then fed to another convolution and max-pooling layer, followed by the final classification layer. Combining the resized image directly with a set of convolved images provides more image specific raw information. Before the final classification layer, the convolution layer preserved generic information (e.g. size, shape) for malignant and control positive cases and could provide more information for better classification performance. CNN3 had 40k parameters, whereas CNN1 and CNN2 had 845k parameters. The reduction of parameters in CNN3 from CNN1 and CNN2 was 96%. [28]. Table 2 and 3 show the parameters and layers for each CNN architecture. Although our CNN architectures were small and shallow, to further reduce overfitting L2 regularization along with dropout [33] was utilized before the final classification layer for all three CNN architectures. The CNN architectures along with pre-trained weights can be accessed from (https://github.com/hellorp1990/CNN-architectures).
Table 2.
Parameters for CNN architectures 1 and 2
| CNN architecture 1 | CNN architecture 2 | ||
|---|---|---|---|
| Layers | Parameters | Layers | Parameters |
| Input | 100×100 | Input | 100×100 |
| Conv1 | 64×5×5,pad 0,stride 1 | Conv1 | 64×5×5,pad 0,stride 1 |
| Leaky ReLU | alpha=0.01 | Leaky ReLU | alpha=0.01 |
| Max Pool 1 | 3×3, stride 3, pad 0 | Max Pool 1 | 3×3, stride 3, pad 0 |
| Conv2 | 64×2×2,pad 0,stride 1 | Conv2 | 64×2×2,pad 0,stride 1 |
| Leaky ReLU | alpha=0.01 | Leaky ReLU | alpha=0.01 |
| Max Pool 2 | 3×3, stride 3, pad 0 | Max Pool 2 | 3×3, stride 3, pad 0 |
| Dropout | 0.1 | Dropout | 0.1 |
| FC 1+ReLU | 128 | FC 1+ReLU | 128 |
| FC 2+ReLU | 8 | LSTM 1 + ReLU | 8 |
| L2 regularizer | 0.01 | L2 regularizer | 0.01 |
| Dropout | 0.25 | Dropout | 0.25 |
| FC 3+Sigmoid | 1 | FC 3 + Sigmoid | 1 |
| Total parameters | 841,681 | Total parameters | 845,033 |
Table 3.
Parameters of CNN architecture 3
| Layers | Parameters |
|---|---|
| Left BRANCH | |
| Input | 100×100 |
| Max Pool 1 | 10×10 |
| Dropout | 0.1 |
| Right BRANCH | |
| Conv1 | 64×5×5,pad 0,stride 1 |
| Leaky ReLU | alpha=0.01 |
| Max Pool 2 | 3×3, stride 3, pad 0 |
| Conv2 | 64×2×2,pad 0,stride 1 |
| Leaky ReLU | alpha=0.01 |
| Max Pool 3 | 3×3, stride 3, pad 0 |
| Concatenate Left and Right Branch | |
| Conv 3 | 64×2×2, pad 0, stride 1 |
| Max Pool 4 | 2×2, stride 2, pad 0 |
| L2 regularizer | 0.01 |
| Dropout | 0.1 |
| FC 1+Sigmoid | 1 |
| Total parameters | 39,553 |
2.3. Data Augmentation
Cohort 1 was used as the training set, which included 85 incident lung cancers and 176 nodule positive controls. Data augmentation was applied to increase the sample size of the training set before training a CNN. The dataset was augmented first by rotating between 0-360 degrees with a gap of 12-degrees and flipping (vertically) as one approach (72 augmented images were generated from each original image). Elastic deformation [34, 35, 36], was also utilized for image augmentation. In [37], the authors showed improvement with elastic augmentation for automated cell counting inspiring us to try it. Strength of the displacement, height and width of grid was chosen empirically as 3 for elastic deformation using software from [38], to keep the similarity (Structural Similarity Index) between original and augmented images less than 85%. After elastic deformation augmentation, we utilized 12-degree rotations and flipping and added the original images (261 cases from Cohort 1) for training the CNN (72 augmented images were generated from each original image). In this case, we utilized both original (261 cases) as well as elastic augmented image for training and validation. This was a second augmentation approach. Three original nodule images along with elastic augmented images are shown in Figure 2.
Figure 2:
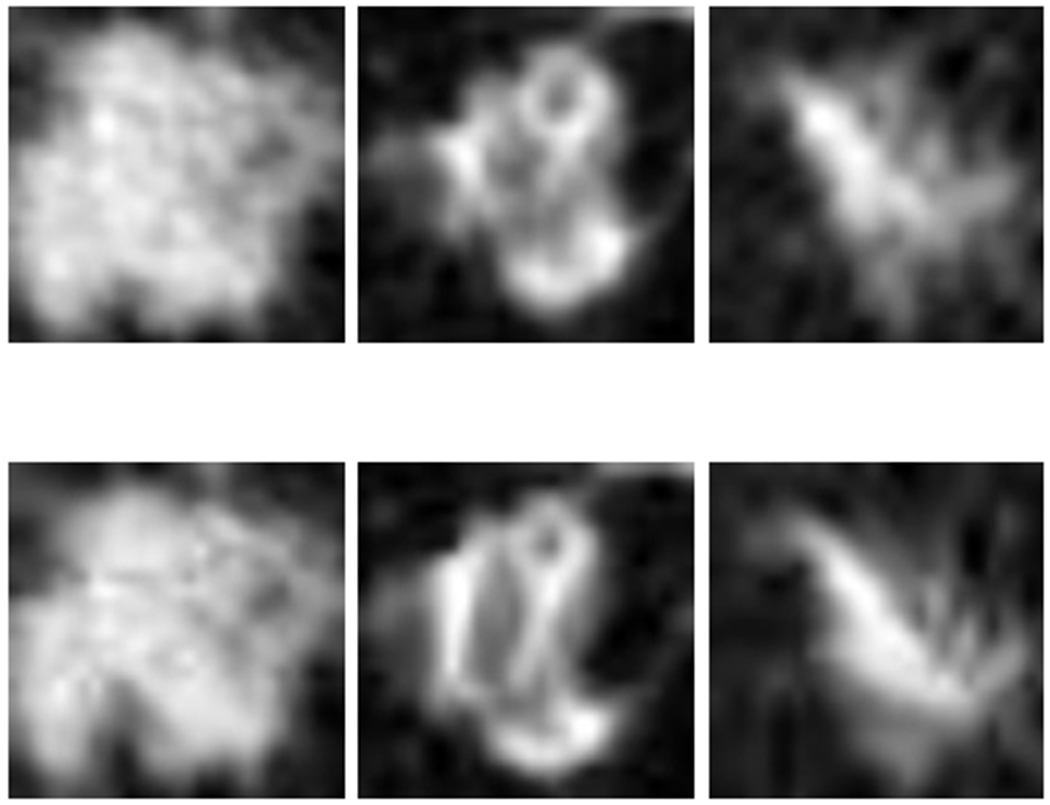
Examples of lung nodule images: Top row: original, Bottom row: elastic deformed images.
2.4. Ensemble Learning
The machine learning procedure that integrates diverse classifier models to create a single (better performing) learned model is called ensemble learning [17]. Ensembles have been used for image understanding [39], as well as brain signal (EEG, BCI) analysis [40, 18]. The ensemble model is often more stable, robust and accurate than the base learners. Ensembles reduce variance among base learners to produce improved classification. In this study, we trained each CNN using seven different initializations to obtain different starting random weights. For combination, we used an averaging approach (obtain pseudo probabilities from each base learner which are then averaged to generate a final probability) to produce a final prediction from our ensemble. We compared the ensemble approach result against training individual models using one of the previously discussed image augmentation strategies.
To reduce the training complexity, we explored snapshot ensembles [41, 42]. We trained a CNN once and took models from intermediate epochs to create an ensemble. The triangular cyclic learning rate (step size 20) with base and max learning rate of 0.00001 and 0.0001 was used for snapshot learning [43]. While training a CNN we chose 7 epochs (epoch 40 to 100 with a gap of 10) for an ensemble. Seven such epochs were taken for the 3 CNNs, and the performance of the ensemble of 21 classifiers was calculated over the test set with the outputs averaged to produce a final ensemble prediction.
3. Experiments and Results
For each imaging study, the slice which contained the most area of the nodule was chosen, and a rectangular region that mostly covered the nodule was extracted. In Figure 3 there is an interpolated nodule as well as the lung slice containing the largest nodule outlined in red. The input size for our CNN architectures was 100×100 and the largest nodule size was 104×104. A bi-cubic algorithm was used for resizing the nodule images. Our designed CNN architectures were trained for 100 epochs. Cohort 1 was used for a training set, and Cohort 2 was used as a separate test set. Cohort 1 data was randomly divided into 70% for training and 30% validation. As previously discussed, for training the CNN two different image augmentations were applied to generate more training images from Cohort 1: flip and rotate and elastic deformation was applied to both the 70% of data used for training and 30% of data used for validation. Each of the three CNN architectures were trained using different initializations with the same training and validation set. The learning rate was 0.0001, and a batch size of 16 was chosen for training and validation. As we have only 2 classes (SDLC and positive control cases), a sigmoid function for activation was utilized in the final classification layer. For performance evaluation, accuracy and area under the re-ceiver operator characteristic curve (AUROC) [44] were calculated from predictions on the unseen and separate Cohort 2 data.
Figure 3:
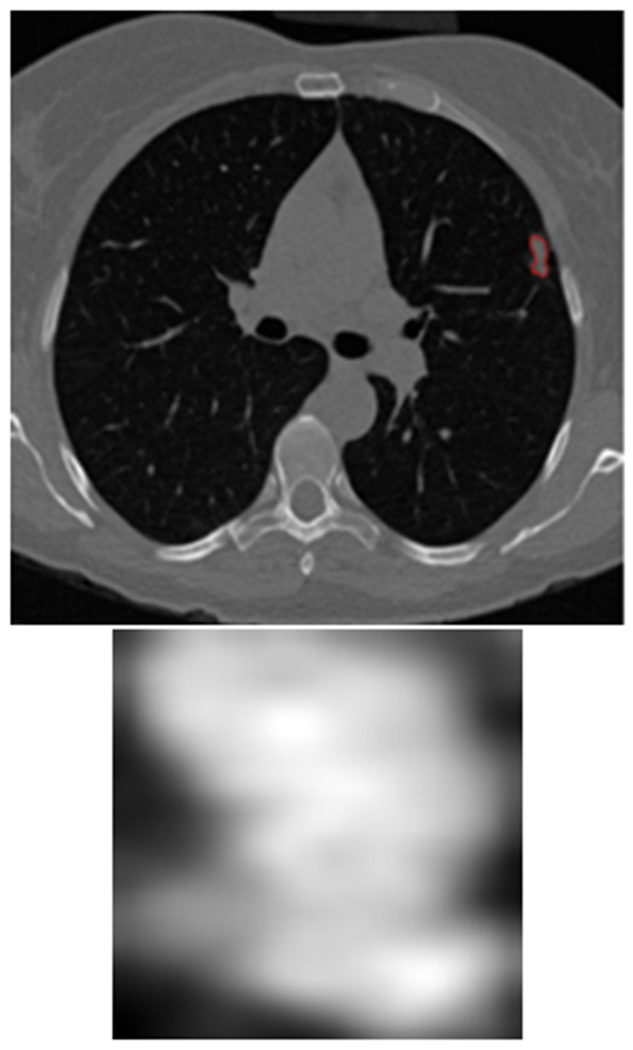
(top) the lung nodule inside the lung image was outlined by red and (bottom) generated nodule region
Each of the three CNN architectures was trained using seven different initializations, yielding 21 models. Figure 4 and 5 show the variations in accuracy for each CNN type in the ensemble while training using different initializations with two image augmentation approaches and without image augmentation. We also utilized the Grad-Cam [45] algorithm to display the areas in the input image which are relevant for prediction analysis. The Grad-cam algorithm was applied on the CNNs trained on images generated by flipping and rotation. We found that for every CNN architecture trained using seven different initializations activated different regions of the input image. Figure 6 presents the input image and the Grad-Cam algorithm output from three CNN architectures.
Figure 4:
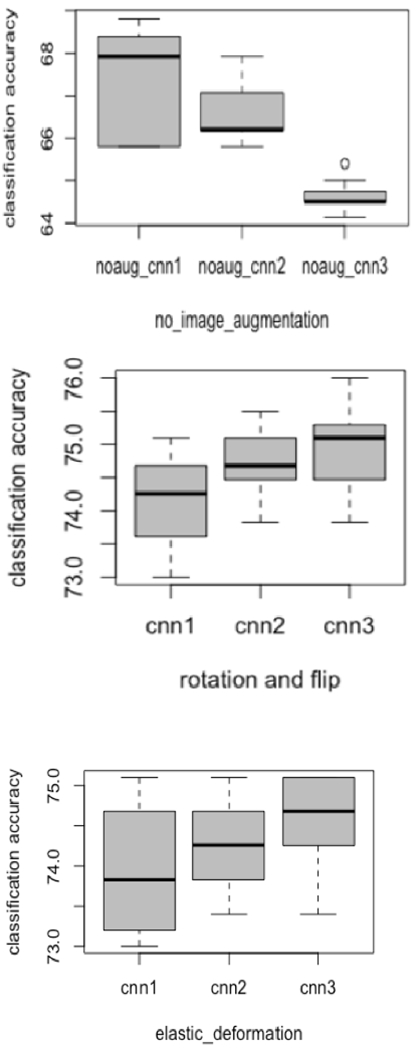
Box plots variations for each CNN while training using different initializations
Figure 5:
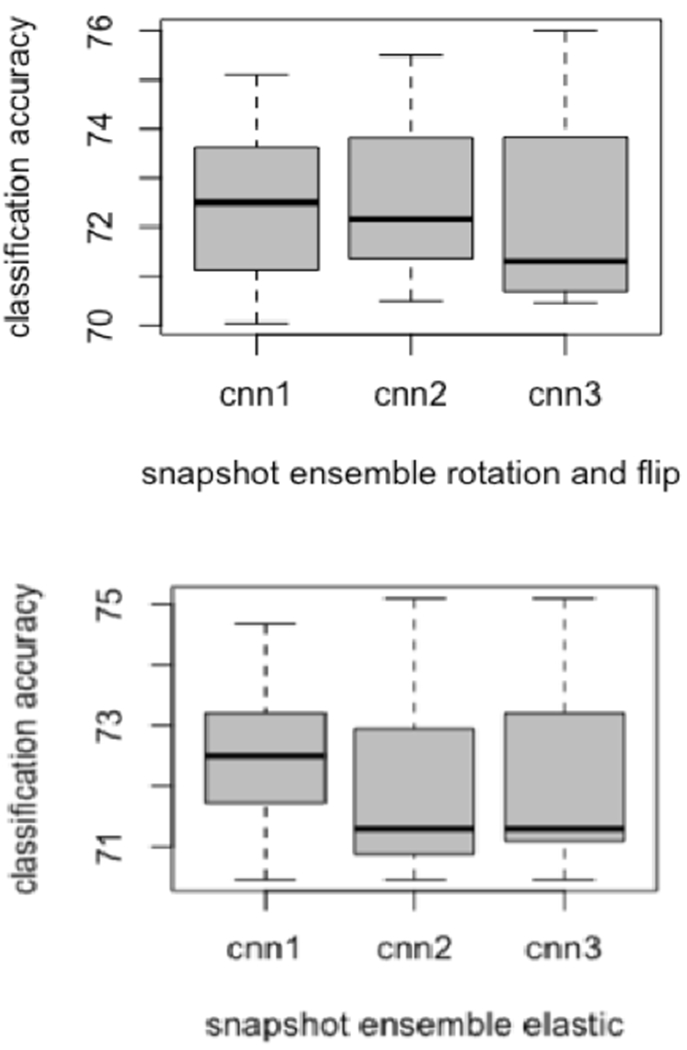
Box plots variations for each CNN while training using snapshot ensemble
Figure 6:

Examples of lung nodule images after Grad-Cam: First column: CNN1; Second Column: CNN2; Third Column: CNN3; Bottom Row: Original nodule image and the colormap.
With the original images only (no augmentations) the ensemble of these models achieved 74.68% accuracy with 0.78 AUC as shown in Table 4. Augmentation was performed by training each CNN architecture with the images generated by flipping and rotation and seven different initializations for random initial weights. For each of the initializations, the model with the best performance on the validation data was used for prediction on Cohort 2. An ensemble result from the seven models was created using averaging for every CNN architecture. We found that the ensemble enhanced classification performance. We also made an ensemble of 21 models (3 CNN architectures with seven different initializations) and observed a further improvement in classification performance. The ensemble of 21 models with images augmented with flipping and rotation achieved the best results of 90.29% accuracy with 0.96 AUC (95% confidence interval, 0.93-0.98; True positive rate (TPR)=0.73, False negative rate (FNR)= 0.27, False positive rate (FPR)= 0). The results are shown in Table 4. We also examined how similar the predictions obtained by these models were. The pearson correlation coefficient was calculated along with the standard deviation across all the 7 models. We analyzed only the models trained on images generated by flipping and rotation image augmentation. The 7 models from the CNN1 architecture had a maximum and minimum correlation of 0.96 and −0.03 respectively with a standard deviation of 0.19. Similarly, the 7 models from the CNN2 architecture had a maximum and minimum correlation of 0.95 and −0.12 respectively with a standard deviation of 0.21. Whereas, 7 models from the CNN3 architecture had a maximum and minimum correlation of 0.9 and −0.1 respectively with a standard deviation of 0.3. From the 21 models from CNN1, CNN2 and CNN3 had a maximum and minimum correlation of 0.96 and −0.1522 with 0.24 standard deviation.
Table 4.
VGG16 and ResNet50 Tuned Architecture
| VGG16 | ResNet50 |
| Output from the final Convolution layer | Output from base model |
| Fully Connected 1: 512, ReLU, Dropout=0.5 | Global Average Pooling |
| Fully Connected 2: 512, ReLU, Dropout=0.5 | Dropout =0.5 |
| Fully Connected 3: 1, Sigmoid | Fully Connected 1: 1, Sigmoid |
Our smaller CNN architectures were also compared with tuned VGG16 and ResNet50 architectures from [46]. We used the ImageNet trained weights in the lower layers for both architectures, and only modified the parameters of the upper layers. The tuned VGG16 and ResNet50 CNN architectures are presented in Table 5. The tuned CNN architectures were trained on images generated by flipping and rotation. Each of the CNN architectures were trained using seven different initializations. Figure 7 presents the variations in accuracy. From the ResNet50 architecture, we achieved 73.41% maximum and 69.62% minimum accuracy. Similarly, from the tuned VGG16 architecture, 73% maximum and 69.19% minimum accuracy was obtained. The maximum and minimum accuracy of the tuned VGG16 and ResNet architecture was found to be lower than our smaller CNN architectures. Then an ensemble of CNNs were generated. From the 7 ResNet50 models, 82.27% accuracy (0.89 AUC, TPR= 0.66, FNR= 0.34, FPR= 0.08) was achieved. Whereas, 81.43% accuracy (0.88 AUC, TPR= 0.66, FNR = 0.34, FPR= 0.1) was obtained from 7 ensemble VGG16 architectures. Seven models from the tuned ResNet50 architecture had a maximum and minimum correlation of 0.96 and −0.05 respectively with a standard deviation of 0.3. Wheras, 7 models from tuned VGG16 architecture had a maximum and minimum correlation of 0.98 and −0.11 respectively with a standard deviation of 0.38. The VGG16 and ResNet50 model had many weights with respect to the number of images in our dataset, which resulted in lower performance.
Table 5.
Results from various ensemble approaches
| Different Image Augmentation | CNN Architecture 1 Ensemble of 7 models Accuracy (AUC) | CNN Architecture 2 Ensemble of 7 models Accuracy (AUC) | CNN Architecture 3 Ensemble of 7 models Accuracy (AUC) | Ensemble of 21 models Accuracy (AUC) | ||
| No Augmentation | 70.46% (0.74) TPR=0.4, FNR=0.6, FPR=0.125 | 70.04% (0.74) TPR=0.38, FNR=0.62, FPR=0.125 | 69.62% (0.72) TPR=0.33, FNR=0.67, FPR=0.1 | 74.68% (0.78) TPR=0.44, FNR=0.56, FPR=0.0.08 | ||
| Rotation and Flipping Augmentation | 84.80% (0.89) TPR=0.63, FNR=0.37, FPR=0.03 | 87.34% (0.89) TPR=0.66, FNR=0.34, FPR=0.01 | 87.34% (0.95) TPR=0.67, FNR=0.33, FPR=0.02 | 90.29% (0.96) TPR=0.73, FNR=0.27, FPR= 0 | ||
| Elastic | Deformation | 82.30% (0.9) TPR=0.66, FNR=0.34, FPR=0.086 | 83.50% (0.92) TPR=0.67, FNR=0.33, FPR=0.072 | 79.32% (0.86) TPR=0.59, FNR=0.41, FPR=0.092 | 86.91% TPR=0.68, FNR=0.32, FPR=0.03 | (0.95) |
| Rotation and Flipping Augmentation (Snapshot) | 83.54% (0.89) TPR=0.635, FNR=0.365, FPR=0.066 | 81.85% (0.87) TPR=0.612, FNR=0.383, FPR=0.066 | 82.7% (0.88) TPR=0.6235, FNR=0.3765, FPR=0.06 | 85.65% TPR=0.65, FNR=0.35, FPR=0.03 | (0.91) | |
| Elastic Deformation (Snapshot) | 80.16% (0.82) TPR=0.624, FNR=0.376, FPR=0.1 | 79.32% (0.82) TPR=0.56, FNR=0.44, FPR=0.08 | 79.32% (0.83) TPR=0.61, FNR=0.39, FPR=0.1 | 83.96% TPR=0.64, FNR=0.36, FPR=0.05 | (0.86) | |
Figure 7:
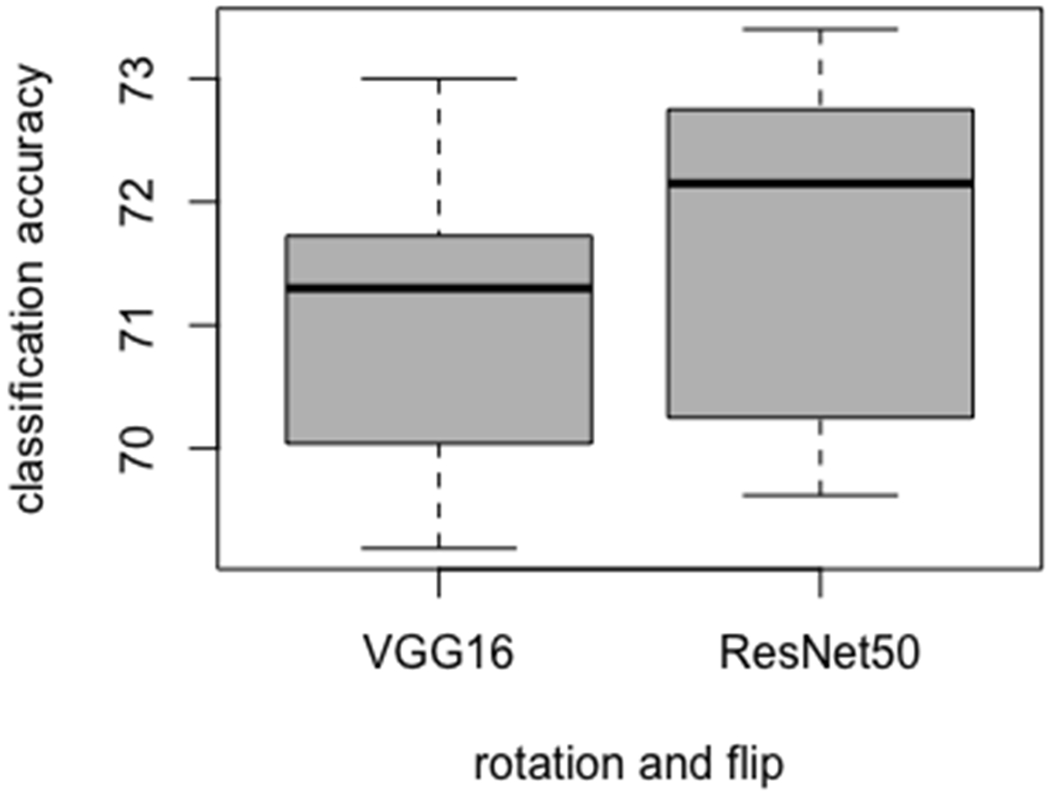
Box plot variations for tuned VGG16 and ResNet50
The previously described elastic transformation approach was also applied for data augmentation, and each of the CNN architectures was trained using seven different initializations. An ensemble was created for each CNN architecture separately, and an ensemble of 21 models was also generated. Using an ensemble of 21 models, the best results achieved were 86.91% accuracy with 0.95 AUC (TPR= 0.68,FNR= 0.32, FPR= 0.03) by augmenting images using elastic deformation followed by rotation and flipping.
A Snapshot ensemble was also created for all three CNN architectures after data augmentation. For every CNN, 7 epochs (epoch 40 to 100 with a gap of 10) were chosen for an ensemble. Afterwards, 21 models (7 models from 3 CNN architectures) were used for an ensemble and the best results achieved were 85.65% accuracy with 0.91 AUC (TPR= 0.65, FNR= 0.35, FPR= 0.03) by augmenting images using flipping and rotation.
We compared the improvement in accuracy and AUCROC of our best result with previous studies using only conventional radiomics approaches [21], ensembles of classifiers [20], and an ensemble of CNNs without any image augmentation with the results are shown in Table 6. In [20], the authors achieved 86.91% accuracy with 0.94 AUC (TPR= 0.7, FNR = 0.3, FPR= 0.04) using averaging after combining three CNNs. The accuracy improvement here is over 3% from previous results and a 0.02 AUC increase was obtained. Using only quantitative features [21] we achieved just 76.79% accuracy with 0.81 AUC (TPR=0.67, FNR= 0.33, FPR= 0.18). The McNemar Test was applied for accuracy improvement analysis, where the AUROC significance test was calculated by the standard error (SE). The statistical analysis outcomes are shown in Table 6. The best ensemble performance was often statistically significantly better than other approaches.
Table 6.
Statistical significance test among various approaches
| Significance Test | AUC comparison (Using Standard Error) | Accuracy comparison (Using McNemar test) |
| Quantitative features [18] vs ensemble of 21 CNN (rotation and flipping augmentation) | 0.81 (SE: 0.0273) vs 0.96 (SE: 0.0119) * | 76.79% vs 90.29% * |
| Quantitative features [18] vs ensemble of 21 CNN (elastic augmentation) | 0.81 (SE: 0.0273) vs 0.95 (SE: 0.0134) * | 76.79% vs 86.91% * |
| Quantitative features [18] vs ensemble of 21 CNN (snapshot ensemble-rotation and flipping) | 0.81 (SE: 0.0273) vs 0.91 (SE: 0.0184) * | 76.79% vs 85.65% * |
| Quantitative features [18] vs ensemble of 21 CNN (snapshot ensemble elastic deformation) | 0.81 (SE: 0.0273) vs 0.86 (SE: 0.0233) † | 76.79% vs 83.96% † |
| Ensemble of 21 CNN (without augmentation) vs ensemble of 21 CNN (rotation and flipping augmentation) | 0.78 (SE: 0.0294) vs 0.96 (SE: 0.0119) * | 74.68% vs 90.29% * |
| Ensemble of 21 CNN (without augmentation) vs ensemble of 21 CNN (elastic deformation) | 0.78 (SE: 0.0294) vs 0.95(SE: 0.0134) * | 74.68% vs 86.91% * |
| Ensemble of 21 CNN (without augmentation) vs ensemble of 21 CNN (snapshot ensemble-rotation and flipping) | 0.78 (SE: 0.0294) vs 0.91 (SE: 0.0184) * | 74.68% vs 85.65% * |
| Ensemble of 21 CNN (without augmentation) vs ensemble of 21 CNN (snapshot ensemble-elastic deformation) | 0.78 (SE: 0.0294) vs 0.86 (SE: 0.0233) * | 74.68% vs 83.96% * |
| Ensemble of different models [17] vs ensemble of 21 CNN (rotation and flipping augmentation) | 0.94 (SE: 0.0148) vs 0.96 (SE: 0.0119) † | 86.91% vs 90.29% † |
| Ensemble of different models [17] vs ensemble of 21 CNN (elastic deformation) | 0.94 (SE: 0.0148) vs 0.95 (SE: 0.0134) † | 86.91% vs 86.91% † |
| Ensemble of different models [17] vs ensemble of 21 CNN (snapshot ensemble rotation and flipping augmentation) | 0.94 (SE: 0.0148) vs 0.91 (SE: 0.0184) † | 86.91% vs 85.65% † |
| Ensemble of different models [17] vs ensemble of 21 CNN (snapshot ensemble elastic deformation) | 0.94 (SE: 0.0148) vs 0.86 (SE: 0.0233) † | 86.91% vs 83.96% † |
SE = Standard Error;
Statistical significance was analyzed at p= 0.05; Statistically significant and Not significant at p=0.05 is represented respectively by *and†
4. Discussion and Conclusions
In this study we utilized an ensemble of CNNs and two different image augmentation approaches to predict which baseline nodules detected in lung cancer screening would be diagnosed as lung cancer in a follow-up screening interval. Though lung nodules can be classified and predicted by a CNN effectively, [10, 11, 15, 20], the classification performance can be further enhanced by ensemble learning. Our analyses revealed that using an ensemble of 21 models and augmenting images using only rotation and flipping yielded the best accuracy of 90.29% (AUC = 0.96 AUC) to predict which baseline nodules would be diagnosed as lung cancer at the second screen beyond the baseline, mostly 2 years later. The next best approach used elastic deformation-based image augmentation with an ensemble of 21 CNNs (Accuracy = 86.91% with AUC = 0.95). An ensemble of 21 CNNs without any image augmentation yielded an accuracy of 74.68% accuracy (AUC = 0.78) Thus, image augmentation enabled significant improvement in accuracy and AUC. We also compared our approach using two tuned CNN architectures (VGG16 and ResNEt50). Using the 7 ResNet models, 82.27% accuracy (0.89 AUC, TPR= 0.66, FNR= 0.34, FPR= 0.08) was achieved. Whereas, 81.43% accuracy (0.88 AUC, TPR= 0.66, FNR = 0.34, FPR= 0.1) was obtained from 7 ensemble VGG16 architectures.
In [20], the authors utilized pseudo-probabilities from three CNNs to form an ensemble and obtained enhanced performance. Motivated by this observation, more CNN models were generated for the ensemble. Training each of the three CNN architectures with seven different initializations was our approach to generate more dissimilar base learner models. This created an ensemble of twenty-one models. A larger ensemble enabled further enhancement of the classification performance. Training a CNN with different seeds gives different weights and then convolution operations generate different feature maps and the final calculations for classification change as well. This approach generates different CNN models with variations in performance (Fig. 4 and 5), which helped in generating further improved classification performance when combined as an ensemble. Training multiple CNNs with different initializations is time-consuming even with a GPU. To counter this problem, a snapshot ensemble was chosen for analysis.
Image augmentation by flipping and rotation keeps the original shape and size of the nodule, whereas the elastic augmentation displaces each pixel which generates a deformed nodule image. We speculate that after elastic deformation, some nodules would no longer be clearly like those that became malignant nor the control nodules. We found that with the flip and rotation image augmentation 85.65% accuracy (0.91 AUC) was achieved using the snapshot ensemble whereas, 83.96% accuracy (0.86 AUC) was obtained from elastic augmentation. These results showed improvement over no image augmentation and over a quantitative approach [21]. However, training multiple CNNs with different initializations showed better classification performance than a snapshot ensemble. The snapshot ensemble did have an advantage of 7 times reduction in wall clock time over training multiple CNNs. To our knowledge this is the first work to report on a snapshot ensemble for radiomics analysis.
In a recent study [47] that utilized a large number of lung cancer screening subjects (N = 42,290) with an end-to-end approach they found 0.944 and 0.874 AUC on the NLST dataset for predicting cancer after one follow-up and two follow-ups (typically at 1 year and 2 years), respectively. From our study, we obtained 0.960 AUC for predicting cancer that will be discovered on the second follow-up (typically 2 years later), which was an improvement over the 0.874 AUC in [47]. By comparison, the best models obtained from our study were compared with the radiomics model, and CNN models and the results shown in Table 6. Traditional radiomics features and CNNs were used previously successfully for classifying future lung cancer incidence from nodules non-invasively. The best result from our current work was 90.29% accuracy with 0.96 AUC (95% confidence interval, 0.93-0.98; True positive rate (TPR)=0.73, False negative rate (FNR)= 0.27, False positive rate (FPR)= 0), which was significantly better than our radiomics approach of 76.79% accuracy with 0.81 AUC [21] and a single CNN model of 76% accuracy with 0.87 AUC from [48] and 86.9% accuracy (0.94 AUC,TPR= 0.7, FNR = 0.3, FPR= 0.04) from three CNN ensemble [20]. Our accuracy and AUC were solid improvements over those in [20], though not statistically significantly.
Size is an effective factor for the prediction of malignancy in the lung nodule. The positive-screened nodule should be > 6 mm in diameter according to both the National Comprehensive Cancer Network (NCCN) and the American College of Radiology (ACR) [49]. We divided the Cohort2 into three subsets based on the longest diameter: < 6mm (small nodules), 2: 6mm, and < 16mm (intermediate nodules) and 2: 16mm (large nodules) as mentioned in [25]. Table 7 shows the number of cases in each subset after spitting using size. Here we broke down our best performing model (90.29% accuracy and 0.96 AUC) with respect to size categories. Large nodules (2: 16mm) had TPR: 0.94, true negative rate (TNR): 1. Whereas, from the intermediate nodules ( 2: 6mm, and < 16mm) and small nodules (< 6mm) had a TPR of 1 and 0.48 respectively ; and TNR of 1 and 1. There are less small nodules and they are more difficult to predict. For real screening patient population, we can divide the nodules with respect to size information and then apply our model as mentioned in [50].
Table 7.
Number of cases of Cohort1 and Cohort2 after splitting using size criteria
| Nodule type | <6 mm | 2: 6 and <16 mm | 2: 16mm |
| Cancer | 23 | 43 | 19 |
| Non-cancer | 21 | 123 | 8 |
In the NLST study [3], in T2, only 5.2% cases (211 out of 4054) had confirmed lung cancer. This makes it a highly imbalanced problem. That’s why we chose an ensemble model. The ensemble model is often more stable, robust and accurate than the base learners. Individual models may have more FPR or FNR, but the ensemble model will reduce that. From this study, our model achieved FNR of 0.27 and FPR of 0. Even other models in our paper had very low FPR <0.1.
We do acknowledge some limitations of this study. For this study, we used 2-D slices instead of 3-D volumes our 2-D approach loses some information compared to 3-D; however, our results are significantly better than those using a 3-D approach shown in Table 6. With the small data available, a 3-D approach will re’quire more parameters and we believe the tradeoff from having more parameters will not let us improve performance until more data is available. Our training and test data sets were fairly small. Given the modest limitations to this work, we applied a rigorous training and testing analysis to identify an ensemble that is highly predictive of lung nodules becoming cancer in the future for the lung cancer screening setting. Our study utilized a semi-automatic segmentation approach which was a limitation for our study
In conclusion, we found that image augmentation by rotation and flipping was very powerful for augmentation. Ensemble learning is a compelling approach with deep neural networks for lung nodule malignancy prediction to significantly enhance the classification results by utilizing diverse models.
Acknowledgments
This research partially supported by the National Institute of Health under grants (NIH U01 CA143062), (NIH U24 CA180927) (U01-CA186145), (U01-CA196405), and (NIH U01 CA200464), National Science Foundation under award number 1513126, by the State of Florida Dept. of Health under grant (4KB17).
Footnotes
Conflict of Interest
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- [1].Siegel RL, Miller KD, Jemal A, Cancer statistics, 2015, CA: a cancer journal for clinicians 65 (1) (2015) 5–29. [DOI] [PubMed] [Google Scholar]
- [2].Melton N, Lazar JF, Moritz TA, A community-based pulmonary nodule clinic: Improving lung cancer stage at diagnosis, Cureus 11 (3) (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Team NLSTR, Reduced lung-cancer mortality with low-dose computed tomographic screening, New England Journal of Medicine 365 (5) (2011) 395–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Gillies RJ, Kinahan PE, Hricak H, Radiomics: images are more than pictures, they are data, Radiology 278 (2) (2015) 563–577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Deepak S, Ameer P, Brain tumor classification using deep cnn features via transfer learning, Computers in biology and medicine 111 (2019) 103345. [DOI] [PubMed] [Google Scholar]
- [6].Zhu Z, Albadawy E, Saha A, Zhang J, Harowicz MR, Mazurowski MA, Deep learning for identifying radiogenomic associations in breast cancer, Computers in biology and medicine 109 (2019) 85–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Krizhevsky A, Sutskever I, Hinton G, Imagenet classification with deep convolutional neural networks, in: Advances in Neural Information Processing Systems, 2012, pp. 1097–1105. [Google Scholar]
- [8].Hu Z, Tang J, Wang Z, Zhang K, Zhang L, Sun Q, Deep learning for image-based cancer detection and diagnosis a survey, Pattern Recognition 83 (2018) 134–149. [Google Scholar]
- [9].Cao P, Liu X, Yang J, Zhao D, Li W, Huang M, Zaiane O, A multi-kernel based framework for heterogeneous feature selection and oversampling for computer-aided detection of pulmonary nodules, Pattern Recognition 64 (2017) 327–346. [Google Scholar]
- [10].Causey JL, Zhang J, Ma S, Jiang B, Qualls JA, Politte DG, Prior F, Zhang S, Huang X, Highly accurate model for prediction of lung nodule malignancy with ct scans, Scientific reports 8 (1) (2018) 9286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Nishio M, Sugiyama O, Yakami M, Ueno S, Kubo T, Kuroda T, Togashi K, Computer-aided diagnosis of lung nodule classification between benign nodule, primary lung cancer, and metastatic lung cancer at different image size using deep convolutional neural network with transfer learning, PloS one 13 (7) (2018) e0200721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Liu X, Hou F, Qin H, Hao A, Multi-view multi-scale CNNs for lung nodule type classification from ct images, Pattern Recognition 77 (2018) 262–275. [Google Scholar]
- [13].Welch HG, Woloshin S, Schwartz LM, Gordis L, Gøtzsche PC, Harris R, Kramer BS, Ransohoff DF, Overstating the evidence for lung cancer screening: the international early lung cancer action program (i-elcap) study, Archives of internal medicine 167 (21) (2007) 2289–2295. [DOI] [PubMed] [Google Scholar]
- [14].de Carvalho Filho AO, Silva AC, de Paiva AC, Nunes RA, Gattass M, Classification of patterns of benignity and malignancy based on CT using topology-based phylogenetic diversity index and convolutional neural network, Pattern Recognition 81 (2018) 200–212. [Google Scholar]
- [15].Zuo W, Zhou F, Li Z, Wang L, Multi-resolution cnn and knowledge transfer for candidate classification in lung nodule detection, Ieee Access 7 (2019) 32510–32521. [Google Scholar]
- [16].Armato III SG, McLennan G, Bidaut L, McNitt-Gray MF, Meyer CR, Reeves AP, Zhao B, Aberle DR, Henschke CI, Hoffman EA, et al. , The lung image database consortium (LIDC) and image database resource initiative (IDRI): a completed reference database of lung nodules on CT scans, Medical physics 38 (2) (2011) 915–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Duin RP, The combining classifier: to train or not to train?, in: Object recognition supported by user interaction for service robots, Vol. 2, IEEE, 2002, pp. 765–770. [Google Scholar]
- [18].Zheng X, Chen W, You Y, Jiang Y, Li M, Zhang T, Ensemble deep learning for automated visual classification using EEG signals, Pattern Recognition (2019) 107147. [Google Scholar]
- [19].Fergus P, Selvaraj M, Chalmers C, Machine learning ensemble modelling to classify caesarean section and vaginal delivery types using cardiotocography traces, Computers in biology and medicine 93 (2018) 7–16. [DOI] [PubMed] [Google Scholar]
- [20].Paul R, Hall L, Goldgof D, Schabath M, Gillies R, Predicting nodule malignancy using a cnn ensemble approach, in: 2018 International Joint Conference on Neural Networks (IJCNN), IEEE, 2018, pp. 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Hawkins S, Wang H, Liu Y, Garcia A, Stringfield O, Krewer H, Li Q, Cherezov D, Gatenby RA, Balagurunathan Y, et al. , Predicting malignant nodules from screening ct scans, Journal of Thoracic Oncology 11 (12) (2016) 2120–2128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].N. L. S. T. R. T. W. committee:, Aberle DR, Adams AM, Berg CD, Clapp JD, Clingan KL, Gareen IF, Lynch DA, Marcus PM, Pinsky PF, Baseline characteristics of participants in the randomized national lung screening trial, Journal of the National Cancer Institute 102 (23) (2010) 1771–1779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Alahmari SS, Cherezov D, Goldgof DB, Hall LO, Gillies RJ, Schabath MB, Delta radiomics improves pulmonary nodule malignancy prediction in lung cancer screening, IEEE Access 6 (2018) 77796–77806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Schabath MB, Massion PP, Thompson ZJ, Eschrich SA, Balagurunathan Y, Goldof D, Aberle DR, Gillies RJ, Differences in patient outcomes of prevalence, interval, and screen-detected lung cancers in the ct arm of the national lung screening trial, PloS one 11 (8) (2016) e0159880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Cherezov D, Hawkins SH, Goldgof DB, Hall LO, Liu Y, Li Q, Balagurunathan Y, Gillies RJ, Schabath MB, Delta radiomic features improve prediction for lung cancer incidence: A nested case– control analysis of the national lung screening trial, Cancer medicine 7 (12) (2018) 6340–6356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].X. Definiens Developer, 2.0. 4 user guide, Definiens AG, Munich, Germany: (2009). [Google Scholar]
- [27].Zeiler MD, Fergus R, Visualizing and understanding convolutional networks, in: European conference on computer vision, Springer, 2014, pp. 818–833. [Google Scholar]
- [28].Paul R, Hawkins SH, Schabath MB, Gillies RJ, Hall LO, Goldgof DB, Predicting malignant nodules by fusing deep features with classical radiomics features, Journal of Medical Imaging 5 (1) (2018) 011021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Chollet F, et al. , Keras: The python deep learning library, Astrophysics Source Code Library (2018). [Google Scholar]
- [30].Abadi M, Barham P, Chen J, Chen Z, Davis A, Dean J, Devin M, Ghemawat S, Irving G, Isard M, et al. , Tensorflow: A system for large-scale machine learning, in: 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), 2016, pp. 265–283. [Google Scholar]
- [31].Gers FA, Schraudolph NN, Schmidhuber J, Learning precise timing with lstm recurrent networks, Journal of machine learning research 3 (Aug) (2002) 115–143. [Google Scholar]
- [32].Li H, Lin Z, Shen X, Brandt J, Hua G, A convolutional neural network cascade for face detection, in: Proceedings of the IEEE conference on computer vision and pattern recognition, 2015, pp. 5325–5334. [Google Scholar]
- [33].Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R, Dropout: a simple way to prevent neural networks from overfitting, The Journal of Machine Learning Research 15 (1) (2014) 1929–1958. [Google Scholar]
- [34].Rueckert D, Sonoda LI, Hayes C, Hill DL, Leach MO, Hawkes DJ, Nonrigid registration using free-form deformations: application to breast mr images, IEEE transactions on medical imaging 18 (8) (1999) 712–721. [DOI] [PubMed] [Google Scholar]
- [35].Sorokin DV, Peterlik I, Tektonidis M, Rohr K, Matula P, Nonrigid contour-based registration of cell nuclei in 2-d live cell microscopy images using a dynamic elasticity model, IEEE transactions on medical imaging 37 (1) (2018) 173–184. [DOI] [PubMed] [Google Scholar]
- [36].Perez F, Vasconcelos C, Avila S, Valle E, Data augmentation for skin lesion analysis, in: OR 2.0 Context-Aware Operating Theaters, Computer Assisted Robotic Endoscopy, Clinical Image-Based Procedures, and Skin Image Analysis, Springer, 2018, pp. 303–311. [Google Scholar]
- [37].Alahmari SS, Goldgof D, Hall L, Phoulady HA, Patel RH, Mouton PR, Automated cell counts on tissue sections by deep learning and unbiased stereology, Journal of chemical neuroanatomy 96 (2019) 94–101. [DOI] [PubMed] [Google Scholar]
- [38].Bloice MD, Roth PM, Holzinger A, Biomedical image augmentation using augmentor, Bioinformatics (2019). [DOI] [PubMed] [Google Scholar]
- [39].Kuehlkamp A, Pinto A, Rocha A, Bowyer KW, Czajka A, Ensemble of multi-view learning classifiers for cross-domain iris presentation attack detection, IEEE Transactions on Information Forensics and Security 14 (6) (2019) 1419–1431. [Google Scholar]
- [40].Silva VF, Barbosa RM, Vieira PM, Lima CS, Ensemble learning based classification for BCI applications, in: 2017 IEEE 5th Portuguese Meeting on Bioengineering (ENBENG), IEEE, 2017, pp. 1–4. [Google Scholar]
- [41].Huang G, Li Y, Pleiss G, Liu Z, Hopcroft JE, Weinberger KQ, Snapshot ensembles: Train 1, get m for free, arXiv preprint arXiv:1704.00109 (2017). [Google Scholar]
- [42].Wen L, Gao L, Li X, A new snapshot ensemble convolutional neural network for fault diagnosis, IEEE Access 7 (2019) 32037–32047. [Google Scholar]
- [43].Smith LN, Cyclical learning rates for training neural networks, in: 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), IEEE, 2017, pp. 464–472. [Google Scholar]
- [44].Hajian-Tilaki K, Receiver operating characteristic (roc) curve analysis for medical diagnostic test evaluation, Caspian journal of internal medicine 4 (2) (2013) 627. [PMC free article] [PubMed] [Google Scholar]
- [45].Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D, Batra D, Grad-cam: Visual explanations from deep networks via gradient-based localization, in: Proceedings of the IEEE international conference on computer vision, 2017, pp. 618–626. [Google Scholar]
- [46].Zamzmi G, Paul R, Salekin MS, Goldgof D, Kasturi R, Ho T, Sun Y, Convolutional neural networks for neonatal pain assessment, IEEE Transactions on Biometrics, Behavior, and Identity Science 1 (3) (2019) 192–200. [Google Scholar]
- [47].Ardila D, Kiraly AP, Bharadwaj S, Choi B, Reicher JJ, Peng L, Tse D, Etemadi M, Ye W, Corrado G, et al. , End-to-end lung cancer screening with three-dimensional deep learning on low-dose chest computed tomography, Nature medicine (2019) 1. [DOI] [PubMed] [Google Scholar]
- [48].Paul R, Hawkins S, Schabath MB, Gillies RJ, Hall LO, Goldgof DB, Predicting malignant nodules by fusing deep features with classical radiomics features, Journal of Medical Imaging 5 (1) (2018) 011021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Wood DE, Kazerooni E, Baum SL, Dransfield MT, Eapen GA, Ettinger DS, Hou L, Jackman DM, Klippenstein D, Kumar R, et al. , Lung cancer screening, version 1.2015, Journal of the National Comprehensive Cancer Network 13 (1) (2015) 23–34. [DOI] [PubMed] [Google Scholar]
- [50].Paul R, Schabath MB, Gillies R, Hall LO, Goldgof DB, Hybrid models for lung nodule malignancy prediction utilizing convolutional neural network ensembles and clinical data, Journal of Medical Imaging 7 (2) (2020) 024502. [DOI] [PMC free article] [PubMed] [Google Scholar]


