Dynein self-organizes while translocating the centrosome in T-cells

Abstract

T-cells massively restructure their internal architecture upon reaching an antigen-presenting cell (APC) to form the immunological synapse (IS), a cell–cell interface necessary for efficient elimination of the APC. This reorganization occurs through tight coordination of cytoskeletal processes: actin forms a peripheral ring, and dynein motors translocate the centrosome toward the IS. A recent study proposed that centrosome translocation involves a microtubule (MT) bundle that connects the centrosome perpendicularly to dynein at the synapse center: the “stalk.” The synapse center, however, is actin-depleted, while actin was assumed to anchor dynein. We propose that dynein is attached to mobile membrane anchors, and investigate this model with computer simulations. We find that dynein organizes into a cluster in the synapse when translocating the centrosome, aligning MTs into a stalk. By implementing both a MT-capture-shrinkage and a MT-sliding mechanism, we explicitly demonstrate that this organization occurs in both systems. However, results obtained with MT-sliding dynein are more robust and display a stalk morphology consistent with our experimental data obtained with expansion microscopy. Thus, our simulations suggest that actin organization in T-cells during activation defines a specific geometry in which MT-sliding dynein can self-organize into a cluster and cause stalk formation.

INTRODUCTION

The response of the immune system to foreign invaders relies to a large extent on the action of cytotoxic T lymphocytes (T-cells). These cells directly attack and kill virus-infected cells, as well as endogenous (pre-) cancerous cells (Pennock et al., 2013). The recognition and elimination of these cells are a complex multistep process that involves major cellular rearrangement, directed force generation, signaling, and precise coordination of these mechanisms (Angus and Griffiths, 2013; Dieckmann et al., 2016). After a T-cell recognizes an antigen-presenting cell (APC), a cell–cell contact is initiated that eventually leads to the elimination of the APC. During this cell–cell contact, both the centrosomal microtubule (MT) network and the actin network, composing most of the cellular architecture, are drastically remodeled (Geiger et al., 1982; Kupfer et al., 1983; Kuhn and Poenie, 2002; Billadeau et al., 2007; Gomez and Billadeau, 2008; Yi et al., 2013). During this remodeling, the centrosome translocates to the center of the immunological synapse (IS), allowing cytolytic granules to be transported there easily for subsequent cytolysis (Ritter et al., 2015; Stinchcombe et al., 2006). Simultaneously, the membrane contacting the APC takes on a structured spatial organization.

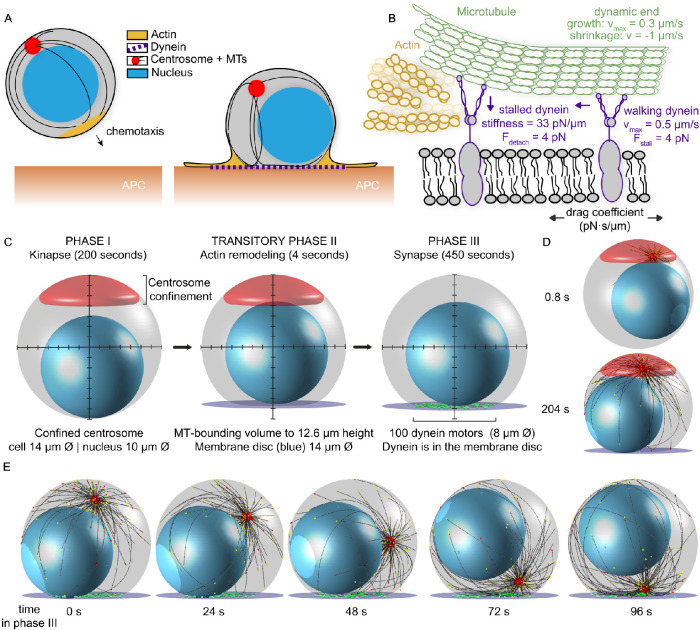
T-cells can move chemotactically toward a target in a “kinapse” form (Roig-Martinez et al., 2019). This form is defined as a state in which the cell’s leading edge contains actin lamellipodia and the centrosome is located behind the nucleus. When the cell finds an APC, it transitions to form the immunological synapse (IS), a cell–cell interface for an efficient and targeted attack. At this interface, actin lamellipodia spread to form a radially symmetric structure with a filamentous-actin retrograde flow to the periphery, with an inner contractile actomyosin ring (hereafter actin ring; Murugesan et al., 2016). With the formation of this actin ring structure, the center of the IS becomes actin-depleted. This actin depletion allows cytoplasmic dynein I (hereafter dynein) to be recruited to the IS (Sanchez et al., 2019). The dynein molecules, in turn, can pull on the MTs and translocate the centrosome to the IS (Figure 1A; Combs et al., 2006; Yi et al., 2013).

FIGURE 1:

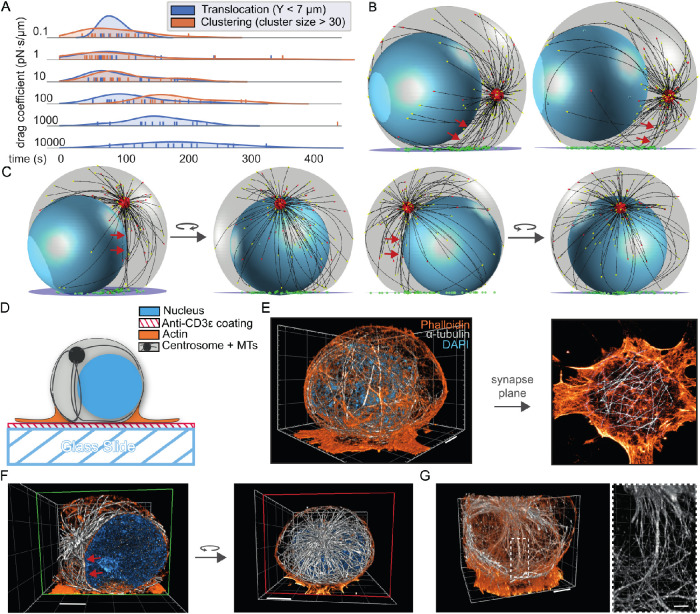
A model for T-cell attack with dynein molecules mobile in the synaptic membrane. (A) Cytoskeletal remodeling during the IS formation of a T-cell. The chemotactic cell moves toward the APC with a leading edge of actin (yellow), its centrosome (red) is behind the nucleus (blue), and the MTs (black) reach around in the cell. Upon encountering the APC, actin spreads to form a dense ring, and the centrosome translocates toward the IS. A MT bundle forms perpendicular to the synapse and resembles a stalk. (B) Model for dynein during centrosome translocation in T-cells. Dynein molecules are mobile in the membrane, with lateral mobility that is parameterized with a drag coefficient. When bound to a MT and encountering the actin-rich boundary, a dynein molecule stalls and detaches from the MT filament. (C) The three phases of our computational T-cell model. The centrosome is not shown, for clarity. The MT-bounding volume is shown in gray, the nucleus in blue, and the centrosome-confinement space in red. In phase II, the MT-bounding volume changes and the IS is introduced with the dynein-confining synaptic membrane (purple). In phase III, the centrosome is released from the confinement space and dynein molecules (green) are added to the synaptic membrane. (D) Snapshots of the computational model at initialization (upper) and in phase II (lower). The centrosome is shown in red and MTs are shown in black. The different colors of the arrowheads at the MT tips indicate the dynamic state of the MT: stalled in red and growing in yellow. (E) Snapshots at different time points of phase III of our computational simulation. In this run, the centrosome is translocated within 96 s.

Simultaneous with these cytoskeletal rearrangements, the membrane at the IS undergoes a major reorganization to form several supramolecular activation clusters (SMACs; Monks et al., 1998; Lin et al., 2005; Alarcón et al., 2011). These clusters form concentric rings with different molecular compositions: a center (cSMAC) enclosed by a peripheral ring (pSMAC) and a distal ring (dSMAC). How these three processes—actin spreading, centrosome translocation, and IS formation—are precisely coordinated is difficult to determine. A recent experimental study suggests the following order: first actin spreads and clears the center; then T-cell receptor microclusters (TCR-MCs) form the beginning of the cSMAC. Subsequently, the centrosome is translocated toward the IS, and then the rest of the IS-membrane organization forms (Ritter et al., 2015).

For successful T-cell activation, the exact mutual timing and dependency between the constituent cellular processes are likely critical. However, their precise coordination and molecular mechanisms are mostly unknown. Although it is known that centrosome translocation is mediated by dynein motors, it is still elusive how this organization is precisely orchestrated and what role the MT network and associated proteins play (Kuhn and Poenie, 2002; Combs et al., 2006; Hooikaas et al., 2020). A recent study showed that T-cell centrosome translocation displayed a defining phenomenon, where a MT bundle formed perpendicular to the IS and this structure shrank during centrosome translocation (Yi et al., 2013). This MT bundle, termed the “stalk,” was proposed to be the major force transmitter between the centrosome and the dynein motors located in the IS. The morphology suggested that dynein induces the shrinkage of this stalk in a process termed MT-capture-shrinkage—an uncommon form of MT–dynein force generation, where the end of a MT is captured by dynein that is able to pull on the MT by inducing controlled shrinkage of the MT (Laan et al., 2012). The biophysical properties of this form of dynein-mediated force generation are poorly understood, and the extent to which it occurs in T-cells is still elusive.

The MT stalks connecting the IS to the centrosome were found to end in the center of the synapse (Yi et al., 2013). Therefore, it is logical to assume that the major source of dynein-mediated force generation is located there. However, during actin reorganization, this region of the synapse becomes actin-depleted, which makes it difficult to imagine how these dynein molecules could be statically anchored, as assumed by previous computational studies (Kim and Maly, 2009; Hornak and Rieger, 2020). Alternatively, dynein could be anchored to mobile proteins embedded in the membrane, which is supported by recent findings that actin depletion is required for dynein recruitment (Sanchez et al., 2019). We propose a model in which dynein is mobile in the membrane and thus will drag itself through the membrane while exerting force on the MTs. In this way, dynein molecules will reorganize in the synapse to be under the centrosome, sliding the MT and themselves until they reach a position on the MT where they experience sufficient force to stall or to unbind. Another consequence of the actin reorganization is the dense actin ring that forms around the IS and excludes MTs from the peripheral volume. Presumably, dynein can still move under this dense actin structure, but needs to be detached from MTs. We explicitly take these geometric boundary conditions into account (Figure 1B).

The mobile dynein model has multiple consequences, which we investigate in this study. Increased mobility of dynein molecules decreases the time for centrosome translocation and MT decoration by dynein molecules. Our simulations show that dynein reorganizes in the synapse as a consequence of its own pulling force and forms clusters. This self-organizing clustering can align MT filaments to a stalk, a phenomenon that was thus far only attributed to MT-capture-shrinkage dynein (Yi et al., 2013). With our simulations, we explicitly demonstrate that dynein molecules that slide MT can produce forces perpendicular to the IS and form stalks. We qualitatively compare the morphology of the stalks in our simulations with experimental microscopy images of T-cells and find similarities in the attachment of MTs at the synapse. This confirms that the model with mobile dynein that slides MTs provides a plausible mechanism underlying the observed stalks.

RESULTS

A general T-cell model in three dimensions with Cytosim

To study the dynamic rearrangement of molecules and molecular structures during T-cell polarization, we introduce a computational model based on Cytosim (Nedelec and Foethke, 2007). The Cytosim framework allows for modular agent-based simulations of cytoskeletal systems using overdamped Langevin equations. Our previous T-cell model (Hooikaas et al., 2020) was extended to three spatial dimensions and to include mobile dynein in the IS.

The T-cell simulation was run in three phases: first, a 200-s initialization phase, representing the kinapse form, followed by a short 4-s transitory phase, modeling the actin reorganization. Subsequently, we added dynein to simulate 450 s of the polarization phase, describing the transition to the synapse form (Figure 1C). By using such a long initialization phase, we guaranteed that the highly dynamic MT network reached a steady-state length distribution before polarization started. The kinapse form during initialization consists of a spherical cell with a nucleus and a centrosome. The centrosome is confined to a spherical cap. The numerical values of the parameters describing the MT dynamics were estimated from TIRF microscopy data of EB3-GFP comets in polarized T-cells (Hooikaas et al., 2020), using a classic two-state MT dynamics model, in which the MT can be in a growing state and in a shrinking state. In the growing state, the MT polymerization rate decays exponentially with the force. The transition from the growing state to the shrinking state is characterized by a catastrophe rate, which is different for a freely growing end and for an end exposed to a large force (see Materials and Methods). We use 150 MTs, which is in the range of the number of MTs previously estimated in these cells (Hooikaas et al., 2020). Other numerical parameters were chosen according to literature values and are listed in Table 1.

TABLE 1: .

Overview of key parameters used in the simulation. All configuration files are available; see Material and Methods.

Parameter	Value	Description/Reference
MT parameters
Polymerization speed	0.3 µm/s	( Hooikaas et al., 2020)
Depolymerization speed	1 µm/s	( Hooikaas et al., 2020)
Rigidity	20 pN/µm	( Gittes et al., 1993)
Stall force	5 pN	Describes the modulation of growth speed and catastrophe rate by antagonistic force ( Dogterom and Yurke, 1997)
Catastrophe rate	0.058 s–1, 0.15 s–1	Matched to WT data of Hooikaas et al. (2020)
MT-bounding volume
Viscosity	0.1 pN.s/µm2	Internal viscosity of T-cells. As for most blood cells, it is usually estimated to be lower than that of somatic cells. Different values of internal viscosity for Jurkat cells have been reported ( Khakshour et al., 2015; Daza et al., 2019).
Elasticity	100 pN/µm	This typical stiffness is used for the interaction of MTs with the nucleus.
Radius	7 µm	( Hooikaas et al., 2020)
Synapse fraction	0.9	This corresponds to a synapse cutting off 10% of the height of the cell (1.4 µm).
Interpolation distance	1 µm
Centrosome parameters
First anchoring stiffness	500 pN/µm	Rotational stiffness on the MTs at the center of the centrosome, as proposed previously ( Letort et al., 2016).
Second anchoring stiffness	500 pN/µm	Rotational stiffness on the MTs exerted at the periphery of the centrosome, as proposed previously ( Letort et al., 2016).
Number of MTs	150	( Hooikaas et al., 2020)
Dynein parameters
Walking speed	0.5 µm/s	( Ohashi et al., 2019)
Number	100
Stall force	4 pN	( Belyy et al., 2016)
Binding rate	5 s–1	A typical value used for modeling ( Leduc et al., 2004; Xu et al., 2012; Klumpp et al., 2015; Feng et al., 2018)
Unbinding rate	0.05 s–1	The unbinding rate of the dynein–dynactin–BicD2 complex ( McKenney et al., 2014; Ohashi et al., 2019).
Initialization	Random on synapse	Dynein is initialized on the synapse and part of the interpolated curve connecting the synapse to the rest of the cell. The region is defined as being within 1.6 µm of the synapse along the vertical axis.
Effective stiffness	33 pN/µm	The stiffness of the dynein anchor, dynein–membrane binder, and membrane binder–synaptic membrane are all modeled as 100 pN/µm in series. This corresponds to an effective stiffness of ∼33 pN/µm.
Confinement to membrane	100 pN/µm
Lattice occupation	4 nm	Width of the lattice that can only contain a single dynein
Site shift	2 nm	This is lower than the measured step size of dynein in vitro ( Gennerich et al., 2007; Elshenawy et al., 2019). We consider this as a rather effective value to take backstepping and binding sites on different protofilaments into account.
System parameters
Dimensionality	3D
Number of repeats	15 per condition

In the transitory phase, we take the shape change of the T-cell by actin reorganization into account. Actin forms a dense structure along the periphery of the IS and is depleted in the center (Murugesan et al., 2016; Sanchez et al., 2019). This very dense actin ring hinders MTs from entering. As a consequence, MTs can only encounter a central part of the IS and move in a subvolume of the cell bounded by the actin ring. We model this MT-bounding volume as a sphere with a 7-μm radius cut by a plane, in such a way that the resulting intersection has a 4-μm radius. This intersection of the MT-bounding volume defines the plane representing the cell–cell interface in which the IS forms. To avoid sharp kinks at the intersection, we interpolate the corner continuously. We introduce a flat disk with a 7-μm radius that represents the IS, centered and connected to the flat side of the MT-bounding volume. Of this disk, only a central circular region with a 4-μm radius is accessible to MTs, as we assume that the rest of this cellular region is inaccessible because of the dense actin ring (Figure 1C).

Modeling dynein mobility based on actin geometry

After a 4-s simulation of the transitory phase with actin reorganization, we add dynein motors to the IS membrane disk and start the polarization phase. The transitory phase is necessary to ensure that MTs cannot attach to dynein molecules while relaxing to the newly formed space (Figure 1D).

Dynein is implemented as a molecular motor in Cytosim. It can bind stochastically to a nearby MT, walk along it, and stochastically unbind from it. The walking velocity decreases linearly with the force that is exerted on dynein and reaches zero under stall force. The force-dependent detachment of dynein from the MT filament is described by an unbinding rate that increases exponentially with the force. To avoid multiple dynein molecules occupying the same space on the MT, we used the Cytosim implementation of a digital walker. This model includes steric interactions by assuming discrete binding sites on the MT and thus can generate traffic jams (Lera-Ramirez and Nédélec, 2019). We assume that dynein molecules are anchored to proteins in the membrane of the IS, represented by Cytosim beads. The overdamped motion of these beads is restricted to the separate membrane disk space and the degree of mobility is defined by a drag coefficient.

With the shape, MT, and dynein definitions, we implicitly take the dense actin edge of the IS into account: membrane-anchored dynein can move in the whole synaptic interface, but MTs are excluded from the periphery. If the tip of a MT is pushed toward the edge, it slides along the dense actin structure upward from the synaptic plane, while dynein molecules remain in the synaptic membrane. Therefore, any dynein molecule at the periphery of the synapse, walking along a MT, will experience an increasing force that induces stall and eventually detachment from the MT (Figure 1B).

When simulating our model with mobile dynein, confined to the membrane disk, we consistently find that the centrosome is translocated to the synapse membrane (Figure 1E; Supplemental Video V1). To characterize the consequences of dynein mobility in this model, we ran simulations with a range of different numerical values for dynein’s drag coefficient in the membrane.

Video S1.

Download video file ^{(8.6MB, mp4)}

Supplemental Video V1 A side view of a full simulation run with 1 pN.s/μm drag on dynein, snapshots are shown in Figure 1E.

Dynein mobility decreases centrosome translocation time

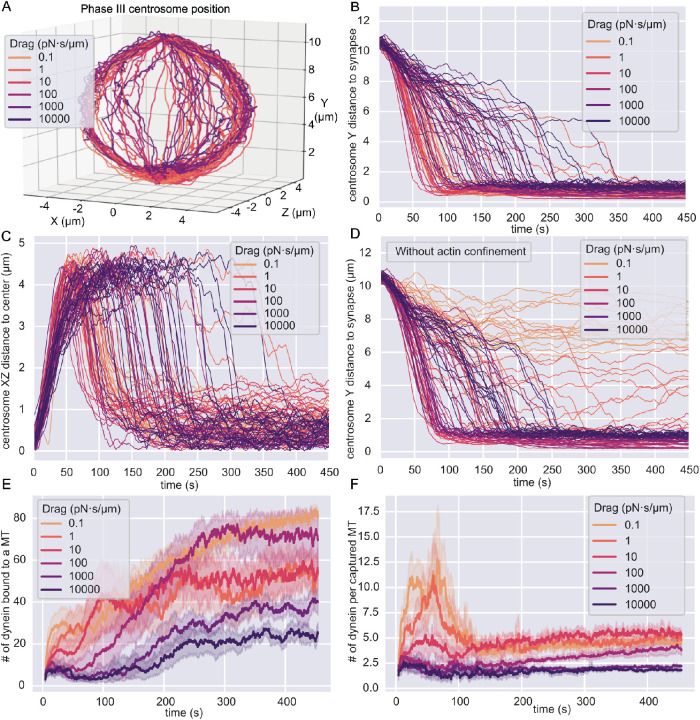
We chose a wide range of drag coefficients, of which the lower bound, 10^–1 pN·s/µm, matches the mobility for cytosolic objects and the upper bound, 10⁴ pN·s/µm, mimics statically anchored dynein molecules on the time scale of our simulations. In these simulations, dynein motors consistently translocate the centrosome to the IS and simultaneously center the centrosome in the synaptic plane (Figure 2A). To further analyze centrosome translocation and centering separately, we decomposed the centrosome trajectories into the height above the IS and the radial distance in the XZ plane from the central axis (Figure 2, B and C).

FIGURE 2:

Centrosome translocation in different models. In all figures, the colors indicate different numerical values for the drag coefficient of dynein molecules in the membrane. The time given in B–F represents the time in phase III. (A) Three-dimensional trajectories of the center of the centrosome. Each line represents one simulation. (B) The height above the synapse as the Y-component of the position of the centrosome’s center as a function of time. Each line is the result from one simulation. Increasing dynein’s drag coefficient, as indicated by the different colors, prolongs the time for the centrosome to translocate to the IS. (C) The radial distance from the centrosome’s center to the central axis of the cell as a function of time. Each line represents one simulation. (D) The Y-component of the position of the centrosome above the IS as a function of time in simulations without the actin ring. In this model, dynein molecules can move on the surface of the MT-bounding volume. (E) The total number of dynein molecules bound to MTs as a function of time averaged over all simulations for a specific drag coefficient. The 95% confidence interval is the shaded area. (F) The number of dynein molecules bound to MTs normalized by the number of MTs that are anchored by at least one dynein. This quantity is averaged over all simulations for a specific drag coefficient and gives a relative measure of MT decoration by dynein. The 95% confidence interval of the average is the shaded area.

In simulations with lower drag coefficients for dynein, the centrosome needed less time to reach the IS than in cases with relatively static dynein molecules (Figure 2B). Under sufficiently high-drag conditions, where dynein is practically statically anchored, we saw that the centrosome first slowly approached the middle of the cell ∼7 µm above the IS and then switched to a faster translocation phase, characterized by a steep slope of the trajectory. We suspected that the first phase was a dynein-independent relaxation of the centrosome to a new position after we released it from its initial confinement. To test this hypothesis, we ran simulations of a system without dynein and found that the centrosome relaxed to a position with a Y value of ∼7 µm above the IS (Supplemental Figure S1, A and B). This Y value corresponds to the equatorial plane of the MT-bounding volume, which is the widest part (S1B). These MTs are under the least stress, as they have the most space to form the centrosomal aster. We concluded that the first slow phase in the full model is independent of dynein, implying that MT capture by dynein is slower when dynein is immobile. Interestingly, simulations with the lowest drag parameter of 0.1 pN·s/µm displayed more noise in the translocation trajectory, which resulted in slower translocation.

Inspection of the radial distance as a function of time revealed that most of the centrosome centering in the synaptic plane occurred immediately after the translocation toward the IS (Figure 2C). Because the 4-µm radius of the synapse plane is smaller than the 7-µm radius of the spherical part of MT-bounding volume, the centrosome will always move toward the longitudinal axis while approaching the synapse and moving around the nucleus. However, we saw that most of the centrosomes eventually relaxed to a position closer than 1 µm from the synapse center.

A major geometrical constraint in our model is imposed by the dense actin ring separating the MT-bounding volume from the space in which the dynein molecules operate. To analyze the effect of this actin geometry on the centrosome translocation, we simulated a reduced model, in which we do not constrain dynein to the IS. Instead, dynein can move on the entire surface of the MT-bounding volume. However, we still initialized the dynein molecules at the IS. Traces from these simulations show that the Y distance of the centrosome above the IS does not decrease as a function of time for dynein with low drag coefficients (Figure 2D). Instead, the centrosome remains several micrometers above the IS and does not fully translocate. In this situation, dynein molecules leave the IS and move in the surface of the MT-bounding volume toward the centrosome, anchoring the MT network in such a way that the centrosome is positioned at the side of the volume and not close to the IS (Supplemental Figure S1C).

Dynein mobility increases initial MT decoration after capture

Previous studies suggest that the initial capture of MT by dynein plays an important role in the translocation of the centrosome (Sarkar et al., 2019). Therefore, we further sought to dissect the consequence of dynein’s mobility in the membrane on the initial capture of MT. We analyzed the number of dynein molecules attached to the MTs as a function of time (Figure 2E). During the polarization phase III, the number of MT-attached dyneins first increases and then saturates. The initial increase can be explained by the increasing number of available MT, as the MT-rich centrosome moves closer to the IS. After the centrosome has landed on the IS, the number of available MT is constant, and the number of attached dynein molecules saturates. We also see that dynein molecules immediately bind to MTs in the first time step after we initialize them. This successful initial capture is probably a consequence of the shape change that we introduce in the transitory phase. By introducing the flat IS, we shrink the MT-bounding volume on this side and force the MT to relax into a smaller space. This shape change increases the contact of MTs with the IS, and therefore MTs are immediately in the close vicinity for dynein molecules to bind to. Even though initial capture is present under all conditions, the attachment of dynein to MTs is faster for dynein molecules with a lower drag coefficient that display high mobility.

The drag-dependent capture phenomenon can be explained by the reorganization of mobile dynein molecules. On the MT, they localize as directly under the centrosome as the centrosomal and MT stiffnesses allow. We see the effect that larger dynein mobility causes them to diffuse more and thus find MTs earlier. To further investigate this effect, we looked at the number of dynein molecules per MT that has at least one dynein bound. This quantity represents a measure of dynein “decoration” on captured MTs (Figure 2F). The time evolution of this measure of decoration suggests that the average number of dyneins per captured MT increases much more quickly in systems with low dynein drag in the membrane. The measure of decoration decreases quickly as the initially caught MT filaments either go into shrinkage or detach completely from dynein and relax away, or dynein detaches and quickly attaches to other, nearby MTs. The last case is likely when the centrosome is close to the synaptic membrane and the MTs originating from the centrosome provide a dense network for dynein molecules to bind to.

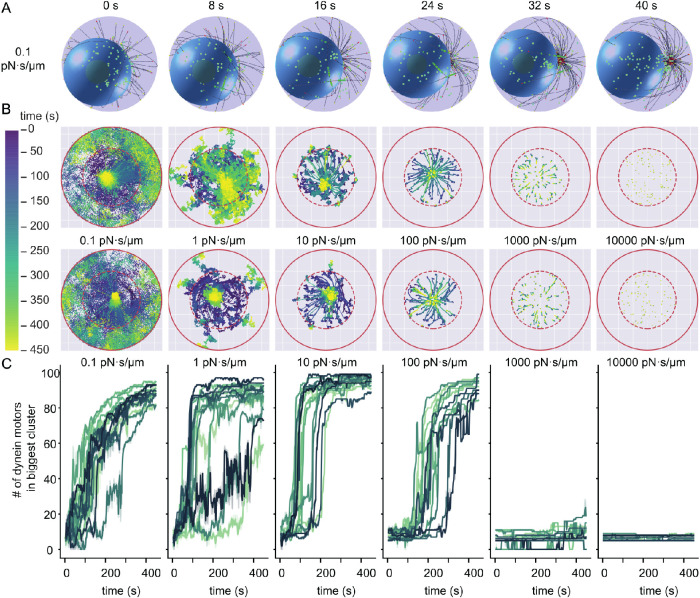
Dynein self-organizes into clusters over time

Because we allow dynein to be mobile in the IS, our simulations show a reorganization in the synapse plane for dynein with lower drag coefficients (Figure 3A). To investigate the reorganization of dynein molecules over time, we tracked the positions of all dynein motors in the membrane (Figure 3B; Supplemental Video V2). These tracks show that for sufficiently low drag parameters, dynein molecules can self-organize into a single cluster. Here, we use the term cluster to describe the localization of dynein molecules close to each other. These clusters are a result of a preferred positioning and not aggregates formed by attractive forces. Besides the occurrence of these clusters, a consequence of high mobility is that a fraction of dynein molecules diffuse away into a region under the dense actin ring, where MTs can no longer reach and bind to them. Analyzing the force on the dynein motors perpendicular to the IS plane indicates that the more mobile, clustering dynein molecules are under a perpendicular force on the order of 10 pN (Supplemental Figure S2).

FIGURE 3:

Dynein self-organizes into clusters in the synapse. All time measurements are in phase III. (A) Snapshots of a simulation with a drag coefficient of 0.1 pN·s/µm. The viewing plane is the plane of the IS. At 32 s a cluster of dynein (green) molecules is visible. (B) The movement of dynein molecules in the synapse membrane. The positions of dynein molecules at all time points in phase III are shown and the time evolution is encoded by the color gradient. The boundary of the 14 µm–diameter synapse is represented by a red circle and the boundary of the 8 µm–diameter area of initialization by a red dashed line. This initialization area is roughly comparable to the edge of the MT binding region. Two example simulations per drag coefficient are shown in the two rows. (C) The number of dynein molecules in the biggest dynein cluster as a function of time. The colors encode different runs of our simulations. To reduce the noise, we average the trajectories over a window of 1.6 s and show the 95% confidence interval as the shaded area.

Video S2.

Download video file ^{(8.4MB, mp4)}

Supplemental Video V2 Views of phase III for all drag conditions, shown from under the synapse. The dynein movement of these runs is shown in the top row in Figure 3B.

To show that the formation of clusters is general, we quantify it using a density-based clustering algorithm from the scikit-learn library based on DBSCAN (Ester et al., 1996; Pedregosa et al., 2011). This algorithm identifies regions in which points are closely packed together by assigning a point to a cluster if it is close to many points of that cluster. We choose this algorithm because no prior knowledge of the number of clusters is necessary; it identifies arbitrary-shaped clusters and accounts for noise in the data. Applying this method to the position of dynein molecules for every time step reveals how clusters develop during the simulation. Inspection of the size of the largest cluster as a function of time shows that the cluster does not form if the dynein drag coefficient is higher than 1000 pN·s/µm (Figure 3C). Most simulations with lower values for the drag coefficient clearly formed clusters, except for a few cases where many dynein motors diffused outside of the MT binding range.

Dynein clusters occur for different microtubule–dynein interactions

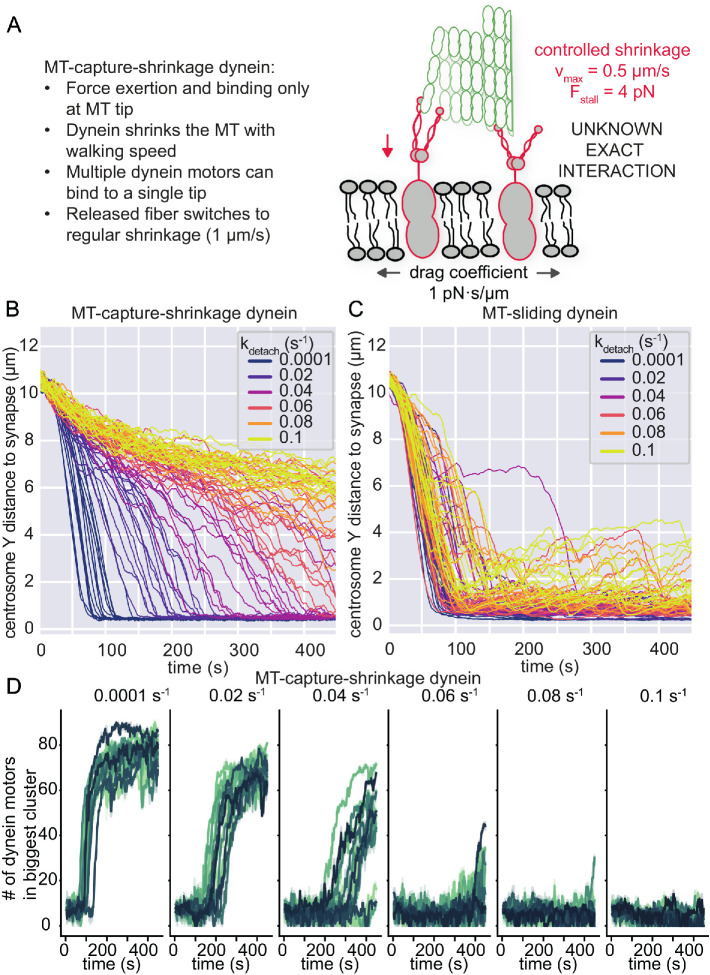
To investigate if cluster formation also occurs for a different MT–dynein interaction mechanism, we implemented a basic MT-capture-shrinkage dynein in Cytosim (Figure 4A). MT-capture-shrinkage is a different form of dynein-mediated force generation on the MT. A dynein molecule catches the dynamic end of a MT and causes controlled MT depolymerization while remaining attached to the MT filament (Laan et al., 2012). The precise coordination of this mechanism and its biophysical properties is mostly unknown and poorly understood. Therefore, we did not attempt to define a precise molecular mechanism for this process but rather extended the MT-sliding dynein that we used earlier, with minimal assumptions, to make the comparison between MT-capture-shrinkage dynein and MT-sliding dynein as simple as possible. Thus, our MT-capture-shrinkage dynein motors have the same binding/unbinding dynamics and force dependency in processivity as the MT-sliding dynein motors. However, the main difference is that binding and force generation for MT-capture-shrinkage dynein are only possible within 100 nm of the MT tip, and force generation is done by shrinking the MT filament. When all dynein molecules unbind from the tip, the MT switches to its regular shrinkage phase with a speed of 1 µm/s.

FIGURE 4:

MT-capture-shrinkage also shows dynein clusters in the IS, but is unable to reliably translocate the centrosome. (A) A minimal model of MT-capture-shrinkage dynein for centrosome translocation in T-cells. Dynein molecules induce a form of controlled shrinkage of the MT and pull on it by holding onto the shrinking MT tip. These dynein molecules are attached to mobile anchors in the membrane, with a lateral mobility that is parameterized by a drag coefficient, fixed to 1 pN·s/µm. (B) Traces of the position of the centrosome as a function of time in the Y direction for MT-capture-shrinkage dynein. Different colors indicate different values of the unbinding rate k_detach. (C) Traces of the position of the centrosome as a function of time in the Y direction for MT-sliding dynein. Different values of the unbinding rate are indicated by the different colors. (D) The number of dynein molecules in the biggest cluster of dyneins as a function of time from simulations with MT-capture-shrinkage dynein. The colors encode different runs of our simulations. To reduce the noise, we average the trajectories over a window of 1.6 s and show the 95% confidence interval as the shaded area. For each panel, the unbinding rate is given on the top.

Replacing the MT-sliding dynein with MT-capture-shrinkage dynein in our simulations suggested that the centrosome translocation and centering occur only for numerical values of the unbinding rate lower than 0.04 s^–1 (Figure 4B). For larger values of the unbinding rate, the Y-distance of the centrosome above the IS does not sufficiently decrease within our simulation time to accomplish translocation. In comparison, the MT-sliding dynein produces consistent translocation in the same timeframe for the full range of unbinding rates we tested (Figure 4C). However, we do notice that at higher unbinding rates, the translocated state can be less stable with MT-sliding dynein, as the noise in the centrosome position increases after a while. We see in the radial distance that the translocating runs of both force generation processes cause a degree of centrosome centering; however, here we see again that the noise in the polarized state of the MT-sliding dynein is higher with the increasing unbinding rate (Supplemental Figure S3, A and B). However, the higher degree of noise in radial distance may resemble centrosomal oscillations that were measured (Kuhn and Poenie, 2002). Taken together, the centrosome trajectories and cluster formation show that our simulations with MT-sliding dynein are more robust for different values of the unbinding rate than a MT-capture-shrinkage mechanism (Supplemental Figure S3C). Thus, we do not believe that this specific form of capture-shrinkage, as modeled, can translocate and center the centrosome, due to its high sensitivity to the unbinding behavior.

In the simulations with the MT-capture-shrinkage dynein that do display centrosome translocation, we also found that dynein self-organizes into clusters in the IS (Figure 4D). In the case of the MT-sliding dynein, the occurrence of clusters is more stable when the unbinding rate is changed, which is due to all runs polarizing (Figure S3C). In both implementations of the dynein–MT interactions, the dynein motors form clusters. These dynein clusters can generate the force to pull down the centrosome. However, some of these clusters only appeared after the centrosome had already translocated. We further investigate how the clustering contributes to centrosome translocation with the MT-sliding dynein model, as this showed more robustness.

Early clustering by dynein can cause stalk formation

To analyze if dynein clustering and localized force generation indeed occur before centrosome translocation, we compared the timescale for cluster formation with the timescale of centrosome translocation (Figure 5A). Because the MT-capture-shrinkage dynein is more sensitive to a particular choice of parameters, we limited this analysis to simulations with the MT-sliding dynein. We define the time scale for cluster formation as the time that dynein molecules need to form a cluster that contains more than 30 of the total of 100 dynein molecules. The time scale for centrosome translocation was quantified as the time until the centrosome reached the widest part of the cell, ∼7 µm above the IS. A comparison of these time scales indicates that in the simulations with a drag coefficient lower than 10 pN·s/µm clustering occurs before or during centrosome translocation. In this case, dynein molecules form a cluster for force generation that could align MTs in such a way that a low stalk appears (Figure 5B). The angle between this lower stalk and the IS is smaller than the angle of a complete perpendicular stalk, but displays a clear direction toward a single point at the membrane, forming the shortest distance between the anchoring point and the centrosome.

FIGURE 5:

Stalk formation in the model mimics stalk formation in cells. (A) Comparison of the typical time scales for clustering and centrosome translocation for different drag coefficients. The first time point at which the centrosome is less than 7 µm away from the IS is shown in blue and the time point when the cluster size is over 30 dynein motors is shown in orange. To estimate a probability density, a Gaussian kernel density is overlaid. (B) Snapshots of a simulation in which dynein clusters align MTs in such a way that stalks appear late during centrosome translocation, indicated by the red arrowheads. (C) Snapshots of simulations, together with rotated views to illustrate apparent stalk formation. The stalks are highlighted with the red arrowheads. These stalks are not uniform bundles, but rather appear so because of the viewing angle. (D) Diagram of the experimental setup. T-cells were fixed 3 min after activation on anti-CD3e coated coverslips and visualized using TREx. (E) Left panel: volumetric rendering of Jurkat T-cell stained for α-tubulin (gray), phalloidin (orange), and DAPI (cyan). Right panel: actin and microtubule organization at the immunological synapse of the same cell. (F) Left panel: same cell as shown in E; green plane indicates the portion that is clipped out. Red arrows point to apparent stalk formation. Right panel: rotated view; clipping plane is indicated in red. (G) Left panel: volumetric rendering of T-cell with a stalk consisting of a MT bundle. Right panel: zoomed-in region around the stalk, showing that the stalk does not end perpendicular to the immunological synapse. Scale bars (corrected to indicate preexpansion dimensions): E, F, G left panel ∼2 µm, G zoomed-in region ∼1 µm.

Lower stalks form more often in our simulations than stalks that appear at the start of the polarization phase, where the centrosome is still in the kinapse location. These high stalks can also be found visually (Figure 5C). However, we do see that these are often not true bundles, but partially dependent on particular viewing angles to see the alignment of multiple MTs toward the clustering dynein molecules.

In vitro morphology is consistent with the computational model

To validate the results of our computational model, we compared the morphology of different cellular structures from the simulation with experimental microscopy data. We examined Jurkat T lymphocyte cells, which we activated on a glass slide coated with anti-CD3ε antigen to mimic the APC as previously described in Parsey and Lewis (1993), Bunnell et al. (2001), and illustrated in Figure 5D. This method does not induce chemotaxis in the T-cells, so the kinapse form of the T-cell is not guaranteed before activation. To clearly visualize the MT network in these cells, we used tenfold robust expansion microscopy (TREx), where samples are physically expanded before imaging to better resolve the fine structure (Damstra et al., 2021). We achieved tenfold expansion and thus can clearly identify the intracellular architecture of actin, MTs, and the nucleus (Figure 5E; Supplemental Video V3). Notably, the MT network in the experimental system is more dense than in our simulations, as we see more MTs wrapping around the nucleus in the microscopy data.

Video S3.

Download video file ^{(1.8MB, mp4)}

Supplemental Video V3 Video showing the 3D volume of the TREx T cell data.

The actin stain clearly shows the geometry of the cell imposed by the actin network. The actin edge forms a very thin layer that is much wider than the cell body (Figure 5E). Inspecting the actin network from the synapse plane, we see that the actin ring stretches much further than the main cell body, and that there are no MTs present in this actin-rich part of the cell (Figure 5E). Thus, we clearly identify a geometry that supports our assumption that membrane-bound molecules cannot easily escape the IS, and our shape definitions thus match experimental observations.

In our simulations, stalks are difficult to define, and the identification of stalks can be dependent on viewing angles. Similarly, in the microscopy data, we can also find stalks that appear to end perpendicular to the synapse from one angle but appear more spread out when the viewing angle is changed (Figure 5F). We also find some MT bundles that clearly resemble stalks, especially when the centrosome is translocated further (Figure 5G). Interestingly, these bundled MTs do not abruptly end perpendicularly at the synapse, but split apart, and the separate MTs make sharp bends and follow along the synaptic plane. This MT configuration is favorable for MT-sliding dynein, and probably not expected from a MT-capture-shrinkage mechanism, in which MTs should end directly at the IS.

DISCUSSION

We propose a model for the mobility of dynein during T-cell polarization that is implicitly determined by actin organization. This reorganization of actin during IS formation results in a geometry that confines mobile dynein molecules to the synaptic membrane. We have shown that this model can reproduce multiple aspects of T-cell centrosome translocation. Most notably, mobile dynein molecules can accumulate into clusters in the synaptic membrane. Such a dynein cluster can form a MT bundle perpendicular to the synapse: a stalk, which was previously proposed to be a defining feature of centrosome translocation (Yi et al., 2013). We defined a stalk as a qualitative morphological feature, because we were unable to analyze MT bundles quantitatively in the experimental data and in the simulations. Our simulation showed only a relatively small number of MT filaments contributing to the stalk, making a quantitative criterion based on such a small number very difficult. Because of experimental limitations, we were not able to draw significant quantitative conclusions on the formation of MT bundles. Stalks can only appear in the model if enough dynein molecules converge before the centrosome translocates. Some factors of our model definition may hinder stalk formation in our current model, such as the rigid attachment at the centrosome and relatively short MT network. Additionally, in cells, it is likely that MT-bundling proteins can stabilize stalks, which we ignored in our simulations.

The dynein clusters form without any explicitly defined attractive forces between dynein motors and are caused by the mobility of dynein and the organization of the MT network. The accumulation of dynein motors at a translocated centrosome is a relatively intuitive process: the minus end–directed-motion of dynein along the MT propagates the predefined MT organization to the arrangement of dyneins on the molecular scale. Strikingly, we also observe that dynein molecules accumulate before the centrosome is fully translocated. This process happens when dynein molecules bound to MTs are dragged in the membrane to a point at which they mostly experience forces perpendicular to the IS. At this point, dynein either stalls or is about to unbind from the MT. The location where this process happens is defined by the initial angle of the MT anchor on the centrosome, the filament length, and its rigidity and dynein mechanics, but is likely under the centrosome as the MT is pulled taut. We term this pretranslocation clustering a self-organization process because this organization cannot directly be predicted from the properties of the individual parts without considering all their interactions and dissipative dynamics in the system as a whole (Karsenti, 2008). In the real biological system, the clustering of dynein molecules in the membrane could be enhanced by several additional mechanisms. Anchoring proteins in the membrane could attract each other because of membrane-induced interactions (Dan et al., 1993; Aranda-Espinoza et al., 1996). Through these attractive forces, microdomains in the membrane could emerge and contribute to the overall organization concurrent with the SMAC formation (Simons and Ikonen, 1997). Although these processes may contribute to the molecular organization in the IS, we did not include them in our study in order to be able to focus on how the system self-organizes without any explicitly defined clustering mechanism.

We built our main model with MT-sliding dynein, where dynein exerts force by walking on the MT. We also investigated the previously proposed model for stalk formation with MT-capture-shrinkage dynein, in which dynein binds to the ends of MTs and exerts force by inducing shrinkage of the MT filaments (Laan et al., 2012; Yi et al., 2013). The model for mobile MT-capture-shrinkage dynein was significantly less robust and required very low unbinding rates to translocate the centrosome in comparison to the MT-sliding dynein. However, our simple implementation of MT-capture-shrinkage dynein probably does not reflect all biophysical aspects of the mechanism. Because this mechanism is still poorly understood, we did not intend to develop a fully specific model. We aimed to introduce a different form of dynein’s force generation that is adequate to compare to the MT-sliding mechanism. Even though the mechanism of shrinkage gives a different translocation behavior of the centrosome, the MT-capture-shrinkage dynein still formed clusters when it was able to translocate the centrosome. These results suggest that the ability of dynein to form clusters may be independent of the precise interaction mechanism of dynein with the MTs.

In our experimental data, we see that stalks do not always form and that the constituent MT filaments do not end abruptly at the synapse but make a sharp bend. These observations are in agreement with our simulations with MT-sliding dynein. Interestingly, the bending of MTs at the synapse is a consequence of our dynein description. For the MT-capture-shrinkage dynein, one would expect that MTs abruptly end at the surface of the synapse. Although the simulated results from our MT-sliding model are consistent with our experimental observations, we cannot exclude a mixture of different mechanisms being active in centrosome translocation as previously suggested (Hornak and Rieger, 2020). Our results suggest that in the MT-sliding model the MTOC can be translocated for a larger range of parameter values for the unbinding rate of dynein from the MTs than in the MT-capture shrinkage model. It is possible that the two mechanisms work together, where the MTOC is robustly translocated through MT-sliding and the translocated state is stabilized by a MT-capture shrinkage mechanism. However, we also believe it may be possible that there is no MT-capture shrinkage dynein in the T-cell. To further gain insights into and distinguish between these mechanisms, it will be valuable to experimentally determine the precise time evolution of the centrosome and molecular rearrangements in the immunological synapse.

We parameterized the MT dynamics from fits to experimental data that were acquired with TIRF microscopy at the immunological synapse. Although the MT dynamics are consistent with these measurements, MTs in our simulations are shorter than we observe in the data from the expanded samples. This inconsistency could originate from locally different MT dynamics or location-dependent microtubule modifications. Our simplified MT model does not account for any other MT-associated proteins that may influence dynamics and is independent of MT location. A different parameterization leading to longer MTs would add a lot of computational complexity. However, a denser MT network will probably lead to more MTs contributing to stalks and more efficient capture, while it may also induce a force-balanced system that is unable to translocate the centrosome (Kim and Maly, 2009; Hooikaas et al., 2020; Hornak and Rieger, 2020).

The mobility of dynein in our model is dependent on the confinement of dynein to the synaptic membrane. If we remove the implicit actin geometry from the simulations and only confine dynein molecules to the surface of the MT-bounding volume, the centrosome will not be translocated to the IS. In this case, a dynein molecule that is bound to a MT is never forced by the geometry to unbind and will move away from the IS on the cell surface toward the centrosome. This process results in translocation of dynein molecules toward the centrosome, instead of translocation of the centrosome toward dynein. However, it is possible that not only the actin ring, but also other factors confine dynein in the synaptic membrane. The geometry that we introduced in our model is supported by our experimental data. Staining for MT and actin, we found examples of cells that show that the edge of the cell is dense in actin and excludes MT. Therefore, we believe that limiting MTs to a spherelike space representing only a part of the whole cell, as implemented in our simulations, is a valid approximation of the system.

In contrast to previous studies, we introduce a model in which dynein is attached to a mobile anchor in the membrane. These anchors have to sustain the forces generated by dynein without getting extracted from the membrane. In addition to the dynein-generated forces, rearrangements of the MT network can stretch these MT-dynein-membrane linkers and result in forces on the anchors that are above dynein’s stall force. We measure some of the forces on dynein to be above 10 pN; however, because we define the characteristic detachment force of dynein from the MT as 4 pN, the membrane anchor will not be exposed to these forces for an extended period of time. Dynein thus probably detaches from the MT before a substantial force can pull it from the anchor, or the anchor out of the membrane. From several experimental studies, the existence of dynein molecules strongly anchored to the membrane seems plausible. Different studies have reported membrane invaginations in the center of the immunological synapse within the first minutes after T-cell activation (Singleton et al., 2006; Yi et al., 2013). These invaginations suggest that a force is strongly coupled to the membrane and pulls it toward the center of the cell. Most likely, this force is generated by multiple membrane-anchored dynein molecules pulling on the MT network. Stable dynein anchoring to the membrane during force production has been reported in other biological systems (Kotak et al., 2012; Schmidt et al., 2017). Contrasting these models, however, we assume that the dynein anchors in the T-cell are very mobile, because of the highly dynamic environment of the IS.

We speculate that the mobile anchor for dynein may be the T-cell receptor microclusters (TCR-MCs). These TCR-MCs move in the membrane toward the center of the IS. This movement has been linked to dynein activity after the T-cell has polarized (Hashimoto-Tane et al., 2011; Hashimoto-Tane and Saito, 2016). From this data and other reported links between TCR-MCs and the MT network (Lasserre and Alcover, 2010; Martín-Cófreces et al., 2011), the role of TCR-MCs as dynein anchors seem plausible. As a direct consequence, the centralization of dynein would correspond to TCR-MC clustering and occur with early formation of the central supramolecular activation cluster (cSMAC), which is TCR-enriched (Dustin, 2014). The linking of TCR-MCs to the mobile dynein molecules would also spatially limit dynein to a central region of the IS, as actin dynamics has been shown to push the TCR-MCs toward the actin-depleted center (Murugesan et al., 2016).

The reorganization of a T-cell when it attacks an APC is tightly orchestrated, and the precise coordination and interplay of the involved cellular processes is still elusive. Here, we used computer simulations to investigate the consequences of different molecular mechanisms and how they contribute to T-cell reorganization. Considering the influence of actin on the geometry and allowing dynein to move in the IS, we found that MT-sliding dynein molecules self-organize into clusters that contribute to MT stalk formation. The morphology of these stalks agrees with our experimental data. In conclusion, our study elucidates how the interplay of the actin geometry, dynein dynamics, and MTs result in centrosome translocation, a critical process during T-cell activation.

METHODS

Shape and initial state

The simulation uses two instances of the Cytosim object SpaceHemisphere, as described in (Hooikaas et al., 2020). One instance defines the volume which contains the MTs and the nucleus and the other space initially confines the centrosome. A custom Cytosim SpaceCylinderY is used to describe a disk in which the dynein molecules are located. This space encodes a cylinder wrapped around the Y-axis and is a rewritten version of the existing cylinder spaces in Cytosim wrapping around the X- or Z-axis.

The MT-bounding volume is modeled as a sphere with a radius of 7 µm for the first 200 s. During this time, the centrosome is confined to a spherical cap comprising the top 20% of the MT-bounding sphere. At the start of the simulation, the centrosome and nucleus, a sphere with a 5-µm radius, are initialized at random positions in their bounding volumes. The centrosome starts with a slightly nonuniform MT length distribution (exponentially distributed around 1 µm) to further seed some slight randomness in the simulations.

We model the centrosome as a sphere with a 0.5-µm radius and 150 MTs attached. The number of MTs has been estimated from previous experimental data (Hooikaas et al., 2020). Each MT has two Hookean spring stiffnesses that force the centrosome into an asterlike conformation. The first stiffness is located at the centrosome center, while the second connects a single point on the centrosome surface to the MT (Letort et al., 2016). This second link enforces a radial asterlike conformation. The MT filaments and the centrosome cannot cross through each other or the nucleus.

At 200 s of simulation, the MT network is considered to be in a steady-state, and we introduce the IS by intersecting the MT-bounding sphere with a plane at 10% of the height, resulting in a cell of width 14 µm and height 12.6 µm. The flat bottom describes the synapse plane. To avoid artifacts from the intersecting corners, we interpolate between the plane and the original sphere. MTs that are pushed into the plane will bend and slide up on the side of the cell, without getting stuck at the corner.

We allow the MTs to relax into the new space for 4 s, to avoid unrealistic capture by dynein molecules at the IS. We release the centrosome from its confinement and add dynein to the disk. This disk that describes the IS is a cylinder space 10 nm thick and 14 µm wide, located at the flat bottom of the MT-bounding volume. Each of the 100 dynein molecules is attached to a mobile Cytosim bead initialized on the surface of the disk. The initial positions of the beads, within this 4-µm radius, are randomly drawn from a uniform distribution.

Dynein motors

We are using the digital walker form of a motor in Cytosim (Lera-Ramirez and Nédélec, 2019) to simulate dynein, because this implementation uses a discrete lattice on the MT to simulate walking motors. We used these digital walkers to prevent dynein molecules from accumulating at the same optimal position on the MT.

Dynein molecules stochastically bind to MTs in their proximity with a binding rate of 5 s^–1. They walk along MTs in a force-dependent manner, described by a linear force–velocity relation with an unloaded speed of 0.5 µm/s and a stall force of 4 pN. They stochastically detach from MTs with an exponentially increasing unbinding rate defined by a characteristic detachment force of 4 pN and by an unloaded unbinding rate of 0.05 s^–1. The unbinding rate is estimated from single-molecule measurements of dynein (McKenney et al., 2014; Ohashi et al., 2019). This low value gives clear behavior in the model to allow a functional analysis of mobility without a large number of molecules. If a dynein molecule is attached to a shrinking MT, and the MT’s end reaches the dynein molecule, it immediately unbinds from the filament. Dynein’s elasticity is considered as a linear spring with stiffness k = 100 pN/µm, which combines with the stiffness of the membrane binder and the membrane itself to ∼33 pN/µm. Our choice of numerical values to describe dynein’s force-dependent dynamics is biologically reasonable and produces a robust centrosome translocation. However, we cannot rule out the possibility that unknown factors in vivo dramatically change these values, which have mostly been determined in in vitro experiments. Dynein’s force-dependent unbinding rate could depend on the geometry and thus change its processivity, which limits the force generation (Khataee and Howard, 2019; Brenner et al., 2020; Pyrpassopoulos et al., 2020).

Our minimal implementation of a MT-capture-shrinkage dynein is an extension of the MT-sliding dynein, as explained. Because the MT-sliding dynein can bind simultaneously to a single MT, we do include this cooperativity as well in the MT-capture-shrinkage dynein, and multiple dynein molecules can bind to the same MT tip. The shrinking speed increases with the number of engaged dyneins and is bounded by a maximum value of 0.5 µm/s. When all MT-capture-shrinkage dyneins release from the tip, the MT switches to its regular shrinkage state with 1 µm/s.

Microtubule simulation

We use a classical two-state model to describe the growth and shrinkage of MTs, as implemented in Cytosim and used for previous studies (Dogterom and Yurke, 1997; Janson et al., 2003; Letort et al., 2016; Lacroix et al., 2018). This model includes force-dependent MT growth and catastrophe. The MT can be in a shrinking state with a constant depolymerization speed and in a growing state with a force-dependent polymerization speed. The polymerization speed decreases exponentially with force, v_growth = v₀e^–F/Fstall, in which v₀ is the force-free polymerization speed and F_stall is the characteristic stall force (Dogterom and Yurke, 1997). The transition from the growing state to the shrinking state is described by the force-dependent catastrophe rate, 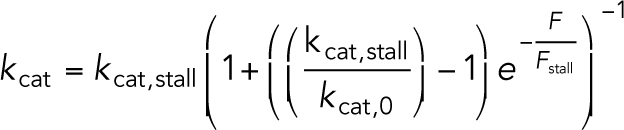(Janson et al., 2003), in which k_cat,stall is the catastrophe rate under stall and k_cat,0 is the catastrophe rate for a freely growing MT. We estimated the numerical values of the parameters from data on MT dynamics from (Hooikaas et al., 2020). This estimate resulted in a free-growing catastrophe rate k_{cat,free-growing} = 0.058 s^–1 and a catastrophe rate under stall k_cat,stall = 0.15 s^–1, and no rescue events where a shrinking MT switches to growth. We ignore any MT-associated proteins that could influence the MT dynamics and map the measured dynamics onto the simplified two-state model. The simulations based on these parameters do not reproduce the dense MT network observed in our TREx data. Nevertheless, instead of using the strong assumption of a static MT network as in previous studies (Kim and Maly, 2009; Hornak and Rieger, 2020), we include this dynamic MT network, which is important to accurately study the major rearrangement processes while the T-cell attacks.

Data visualization and analysis

Plots were made using Seaborn and its subsidiary Python libraries, Pandas, NumPy, and MatPlotLib/PyPlot. All confidence intervals represent 95% confidence intervals of the mean.

The cluster analysis was done with the SciPy scikit-learn DBSCAN algorithm (Ester et al., 1996; Pedregosa et al., 2011). The DBSCAN algorithm depends on two parameters: a distance “epsilon” and “min_samp,” the minimum number of points defining a cluster. Epsilon was set to 0.5 µm, as this reproduced clusters visually, and for min_samp we used the SciPy default value 5. A point is considered a core point of a cluster if within a circle with radius epsilon around this point at least min_samp points, including the point itself, are found. We searched for dense clusters of dynein positions in every separate time frame (0.4 s) in each run. The traces, shown in Figure 3B, take into account only the largest cluster that is found and are averaged over four time frames (a total of 1.6 s) with a shaded area as the confidence interval. This averaging procedure reduces the noise of separate clustering attempts and shows the general trend more clearly.

T-cell culture and tenfold robust expansion microscopy

Jurkat T-cells (clone E6.1) were grown in RPMI 1640 medium w/L-glutamine (Lonza) supplemented with 9% fetal bovine serum and 1% penicillin/streptomycin. To activate T-cells, 1.5 mm–thick coverslips (Marienfeld, 107032) were coated with poly-D-lysine (Thermo Fisher Scientific, A3890401), washed with phosphate-buffered saline (PBS), and incubated overnight at 4°C with 10 μg/ml mouse monoclonal anti-CD3 antibodies (clone UCHT1, StemCell Technologies, #60011) in PBS. Cells were spun down for 4 min at 1000 rpm and resuspended in fresh prewarmed RPMI 1640 medium, after which cells were incubated on the coated coverslips for 3 min before fixation. For fixation, the cells were preextracted for 1 min with prewarmed (37°C) extraction buffer composed of MRB80 (80 mM K-PIPES pH 6.8, 4 mM MgCl₂, 1 mM EGTA) supplemented with 0.35% Triton X-100 and 0.2% glutaraldehyde. After extraction, cells were fixed for 10 min with pre-warmed (37°C) 4% PFA in PBS. After fixation, cells were washed with PBS and permeabilized using PBS supplemented with 0.2% Triton X-100. Epitope blocking and antibody labeling steps were performed in PBS supplemented with 3% BSA. Labeling with primary antibodies was performed overnight at 4°C. After washing with PBS, labeling with secondary antibodies was performed for 3 h at RT. For immunofluorescence staining, we used a rabbit monoclonal antibody against α-tubulin (clone EP1332Y, Abcam, ab52866) in combination with goat anti-rabbit IgG (H+L) Alexa Fluor 488 (Molecular Probes, a11034).

For TREx, we followed the TREx protocol (Damstra et al., 2021). In short, samples were postfixed overnight at room temperature (RT) with 0.1 mg/ml acryloyl X-SE (Thermo Fisher, A20770) in PBS. To visualize actin, cells were washed twice with PBS and incubated with a polymerizable fluorescent phalloidin derivative, actin TREx (Chrometra, fluorophore 561), for 1 h at RT. The cells were quickly rinsed and immediately processed for gelation. For gelation, a monomer solution was prepared, containing 1.1 M sodium acrylate (Sigma-Aldrich, 408220), 2.0 M acrylamide (AA) (Sigma-Aldrich, A4058), and 0.009% N,N’-methylenebisacrylamide (BIS) (Sigma-Aldrich, M1533) in PBS. Gelation of the monomer solution was initiated with 0.15% ammonium persulfate and 0.15% tetramethylethylenediamine, and 170 µL was transferred to a silicone mold with an inner diameter of 13 mm (Sigma-Aldrich, GBL664107) attached to a parafilm-covered glass slide, with the sample put cell-down on top to close off the gelation chamber. The sample was transferred directly to a 37°C incubator for 1 h to fully polymerize the gel. After gelation, the gel was transferred to a 12-well plate and digested in TAE buffer (containing 40 mM Tris, 20 mM acetic acid, and 1 mM EDTA) supplemented with 0.5% Triton X-100, 0.8 M guanidine-HCl, and 7.5 U/ml proteinase-K (Thermo Fisher, EO0491) for 4 h at 37°C, supplemented with DAPI. The gel was transferred to a Petri dish, water was exchanged twice after 30 min, and the sample was left in water to expand overnight in MiliQ. Before imaging, the cells were trimmed and mounted.

All TREx images were acquired using a Leica TCS SP8 STED 3× microscope equipped with an HC PL APO 86x/1.20W motCORR STED (Leica 15506333) water objective for TREx. A pulsed white laser (80 MHz) was used for excitation. The internal Leica GaAsP HyD hybrid detectors were used with a time gate of 1 ≤ tg ≤ 6 ns. The setup was controlled using LAS X and run without stimulated emission depletion. For 3D visualization and rendering Arivis, Vision4D (Arivis AG) was used. For Figure 5, E–G, raw datasets were imported into Arivis, a discrete Gaussian filter with smoothing radius of 2 was applied, and these datasets were used for volumetric renders and clipping. For the phalloidin channel, gamma was adjusted manually to increase the visibility of dense actin ring and more sparse actin surrounding the cell. Figure 5E, right panel is a maximum projection of 10 frames (z-spacing: 0.35 µm).

Reproduction of simulations and code availability

A configuration file is provided and the full code of the Cytosim version used in this paper is on http://doi.org/10.5281/zenodo.4478879. Cytosim is modular and extendable and we invite everyone to work further on this.

Abbreviations used:

APC

antigen-presenting cell

IS

immunological synapse

MT

microtubule

SMAC

supramolecular activation cluster

TCR-MCs

T-cell receptor microclusters

TREx

tenfold robust expansion microscopy.