Latent Factor Structure and Measurement Invariance of the NIH Toolbox Cognition Battery in an Alzheimer’s Disease Research Sample

Abstract

Objective

This study investigated the latent factor structure of the NIH Toolbox Cognition Battery (NIHTB-CB) and its measurement invariance across clinical diagnosis and key demographic variables including sex, race/ethnicity, age, and education for a typical Alzheimer’s disease (AD) research sample.

Method

The NIHTB-CB iPad English version, consisting of seven tests, was administered to 411 participants aged 45 to 94 with clinical diagnosis of cognitively unimpaired, dementia, mild cognitive impairment (MCI), or impaired not MCI. The factor structure of the whole sample was first examined with exploratory factor analysis (EFA) and further refined using confirmatory factor analysis (CFA). Two groups were classified for each variable (diagnosis or demographic factors). The confirmed factor model was next tested for each group with CFA. If the factor structure was the same between the groups, measurement invariance was then tested using a hierarchical series of nested two-group CFA models.

Results

A two-factor model capturing fluid cognition (executive function, processing speed, and memory) versus crystalized cognition (language) fit well for the whole sample and each group except for those with age < 65. This model generally had measurement invariance across sex, race/ethnicity, and education, and partial invariance across diagnosis. For individuals with age < 65, the language factor remained intact while the fluid cognition was separated into two factors (1) executive function / processing speed and (2) memory.

Conclusions

The findings mostly supported the utility of the battery in AD research, yet revealed challenges in measuring memory for AD participants and longitudinal change in fluid cognition.

Introduction

Solid and convenient cognition measures are beneficial for research on Alzheimer’s disease (AD) to help characterize the associated longitudinal trajectory of cognitive decline and identify mild cognition change at the pre-clinical stage. The NIH Toolbox Cognition Battery (NIHTB-CB) provides a standardized set of measures to assess multiple domains of cognitive function and serves as a common currency for cross-study comparisons (Gershon et al., 2013). As shown in Table 1, the adult version (age ≥ 18) of the battery includes seven tests and measures multiple cognitive domains (Weintraub et al., 2013). The NIHTB-CB has many advantages as it is: (1) applicable across the lifespan; (2) brief; (3) non-proprietary; (4) based on state-of-the-art test theories and technology; and (5) available in both English and Spanish versions (Mungas et al., 2014). The validity and utility of the battery has been shown in cognitively unimpaired adults (Heaton et al., 2014; Mungas et al., 2014; Weintraub et al., 2013), and clinical samples with spinal cord injury (Carlozzi, Goodnight, et al., 2017; Cohen et al., 2017), traumatic brain injury (TBI; Carlozzi, Goodnight, et al., 2017; Nitsch et al., 2017; Tulsky, Carlozzi, et al., 2017; Tulsky, Holdnack, et al., 2017), stroke (Carlozzi, Goodnight, et al., 2017; Carlozzi, Tulsky, et al., 2017; Nitsch et al., 2017; Tulsky, Holdnack, et al., 2017), and intellectual disabilities (Hessl et al., 2016). In addition, a study including adults with varied cognitive statuses provided supportive findings for the validity of NIHTB-CB in assessing neurocognitive domains related to dementia (Hackett et al., 2018). Furthermore, for the cognitively unimpaired adult population, uncorrected, age-corrected, and fully-demographically-corrected normative standards have been developed for both English and Spanish versions (Casaletto et al., 2015, 2016). All of its unique features provide support that NIHTB-CB could potentially be a promising instrument in measuring cognition for AD research.

Table 1.

Tests of the NIH Toolbox Cognition Battery (NIHTB-CB) Adult Version (Age ≥ 18)

Test	Abbreviation	Cognition domain	Score type	Possible score range
Flanker Inhibitory Control and Attention	Flanker	Attention, executive function	Computed	0 – 10
Dimensional Change Card Sort	DCCS	Executive function	Computed	0 – 10
Pattern Comparison Processing Speed	Processing Speed	Processing speed	Raw	0 – 130
List Sorting Working Memory	Working Memory	Working memory	Raw	0 – 26
Picture Sequence Memory	Episodic Memory	Episodic memory	IRT theta	Unlimited
Picture Vocabulary	Vocabulary	Language (vocabulary)	IRT theta	Unlimited
Oral Reading Recognition	Reading	Language (reading)	IRT theta	Unlimited

Note. Score type = the name of score type exported from the iPad; IRT = Item Response Theory. For Flanker and DCCS, an accuracy score and a reaction time score are first calculated. The accuracy score is calculated as 0.125 * the number of correctly answered trials. The reaction time score is calculated as a function of the log (base 10) of the median reaction time using only correct trials with time length between 100ms and 3SD away from the participant’s mean time. The computed score is equal to the accuracy score if the participant has an accuracy rate ≤ 80%, and is the sum of the accuracy score and the reaction time score otherwise. For Processing Speed and Working Memory, the raw score is the number of items correctly answered. For Episodic Memory, Vocabulary, and Reading, scoring is based on the Item Response Theory (IRT). IRT models the probability of a correct response to an item given the underlying latent cognitive ability. The theta score represents the latent cognitive ability level (NIH & Northwestern University, 2006–2016). Higher score indicates better performance for each test. Two supplemental tests were also provided for the NIHTB-CB, including Auditory Verbal Learning Test (AVLT; Rey) Immediate Recall (trials 1, 2, 3) measuring learning, and Oral Symbol Digit Test measuring processing speed. However, these two tests were not included in this study.

Understanding the latent factor structure of NIHTB-CB specifically for its application to AD research samples is necessary for correct interpretation of findings from AD studies using the battery. A factor analysis of NIHTB-CB on cognitively unimpaired adults identified five factors, including executive function / processing speed (EF-PS), working memory, episodic memory, vocabulary, and reading. A subsequent second-order factor analysis on the same data showed the differentiation of fluid cognition (EF-PS, working memory, episodic memory) versus crystalized cognition (vocabulary, reading) (Mungas et al., 2014). The five-factor model has been validated in clinical samples with acquired brain injuries (TBI and stroke; Tulsky, Holdnack, et al., 2017). Both studies included other neuropsychological tests considered as gold standard measures in addition to NIHTB-CB, as their goal was to define convergent and discriminant validity of the battery based on its similarity and difference in factor loading patterns compared to the standard measures. Another factor analysis (Hackett et al., 2018) which included the NIHTB-CB battery only was conducted on a mixed sample of participants who were cognitively unimpaired, with subjective cognitive decline (SCD), mild cognitive impairment (MCI), and dementia due to AD. Episodic Memory and Working Memory tests were excluded because they were too challenging for participants with cognitive impairment and yielded low completion rates. However, the supplemental AVLT Immediate Recall and Symbol Digit tests were included. Two factors were identified capturing fluid and crystalized cognition. However, when AD participants were excluded from the analysis, tests measuring the fluid cognition instead loaded on two separate factors capturing EF-PS and memory respectively, while the crystalized cognition factor remained unchanged. Based upon the literature, the first goal of this study was to investigate the factor structure of NIHTB-CB in its application to a typical AD research sample with a wide range of cognition status including the cognitively unimpaired, MCI, and dementia. Different from the previous studies, the factor analysis was performed on the NIHTB-CB battery only including all seven tests listed in Table 1. The focus was to understand the underlying structural relations of multiple cognition domains and capture cognitive processes as a related and organized neuropsychological system.

The evaluation of measurement invariance between the cognitively unimpaired versus impaired is important for defining the utility of a battery for AD research. Variant factor structure would imply qualitative changes in the underlying neuropsychological system as the disease progresses, whereas invariant factor structure would suggest a quantitative decline in the same cognitive spectrum (Hayden, Plassman, & Warren, 2011). Although measurement invariance of NIHTB-CB has not been tested, the finding of different numbers of factors between the analyses including versus excluding AD participants by Hackett et al. (2018) suggested the possibility of variant factor structure across clinical diagnosis. The second goal of this study was to evaluate measurement invariance of NIHTB-CB between cognitively unimpaired versus impaired groups including MCI and dementia.

Previous studies have found demographic differences in cognitive performance, including differences across age, sex, race/ethnicity groups, and education level, either using NIHTB-CB (Casaletto et al., 2015, 2016; Flores et al., 2017) or other cognition measures (Collie, Shafiq-Antonacci, Maruff, Tyler, & Currie, 1999; Norman, Evans, Miller, & Heaton, 2000; Norman et al., 2011). Measurement invariance across these key demographic variables is necessary to confirm that differences in the cognition test scores truly represent demographic differences in the cognition abilities being tested (Dowling, Hermann, La Rue, & Sager, 2010). Moreover, measurement tools that allow fair comparison across different demographic groups are fundamental to address health equity issues (Victorson et al., 2013). Previous research on demographic invariance in cognition measures for older adults has mainly focused on race/ethnicity and related culture or language factors (Mungas, Widaman, Reed, & Tomaszewski Farias, 2011; Siedlecki et al., 2010; Tuokko et al., 2009). Research is significantly lacking in testing measurement invariance across multiple demographic variables or specifically for an AD research sample. Furthermore, in our literature review, the only demographic measurement invariance testing on NIHTB-CB for adults was age invariance in the cognitively unimpaired (Mungas et al., 2014). The third goal of this study was to test measurement invariance of NIHTB-CB across four major demographic variables, including sex, race/ethnicity, age, and education, in its application to an AD research sample. These four demographic variables were employed in deriving the fully demographically corrected normative standards for NIHTB-CB (Casaletto et al., 2015, 2016), which implies the significance of these variables in cognition variability. Findings of the invariance testing will be informative for the application of NIHTB-CB and its norms to AD research, and the interpretation of demographic differences in measured cognitive abilities found in a study.

In summary, this study investigated the factor structure of NIHTB-CB and its measurement invariance across clinical diagnosis groups and key demographic variables for a mixed sample of older adults with unimpaired cognition, MCI, and dementia. Findings will help evaluate the battery’s utility for AD research.

Method

Participants

The study included 411 participants from the Wisconsin Alzheimer’s Disease Research Center (ADRC). ADRC participants were recruited from memory diagnostic clinics and community. Women and men aged 45 and older with decisional capacity were eligible for enrollment. Exclusion criteria included major medical conditions (e.g., advanced congestive heart failure, kidney failure, severe untreated sleep apnea, HIV/AIDS), major neurologic disorders (e.g., significant ischemic or hemorrhagic stroke, multiple sclerosis, history of brain surgery), major psychiatric conditions (e.g., major Axis I disorder or addictive disorder), or lack of a study partner. Table 2 summarizes the sample demographics.

Table 2.

Sample Characteristics (n=411)

Variable	Subgroup	n (%)
Sex	Male	171 (41.6)
	Female	240 (58.4)
Race	White	329 (80.1)
	African American	61 (14.8)
	American Indian or Alaska Native	18 (4.4)
	Asian	1 (0.2)
	Other	1 (0.2)
	Unknown	1 (0.2)
Hispanic	No	402 (97.8)
	Yes	4 (1.0)
	Unknown	5 (1.2)
Education	Less than high school or GED	6 (1.5)
	High school or GED	138 (33.6)
	Bachelor	123 (29.9)
	Master	96 (23.4)
	Doctorate	48 (11.7)
Diagnosis	Cognitively unimpaired	317 (77.1)
	Dementia due to AD	40 (9.7)
	Dementia due to other causes	3 (0.7)
	MCI due to AD	32 (7.8)
	MCI due to other causes	7 (1.7)
	Impaired not MCI	12 (2.9)

Note. Age ranged 45–94 years, with M = 66.3, SD = 9.8. All four participants with Hispanic ethnicity had white race.

ADRC Visit and Test Administration

The ADRC participants undergo annual or biennial clinical and cognitive assessment at an academic medical center in Madison, Wisconsin. (Visit frequency was based on age and clinical diagnosis). For the purposes of this study, we used cross-sectional data collected at a single time visit. The National Alzheimer’s Coordinating Center (NACC) Uniform Data Set (UDS) (Besser et al., 2018) was collected at each visit. Between March 14, 2016 and March 08, 2017, the iPad English version of NIHTB-CB was administered at one visit immediately after completion of the NACC UDS neuropsychological battery version 3 (Weintraub et al., 2018). The study protocol was approved by the University of Wisconsin Institutional Review Board. Informed consent was obtained from each participant prior to the study.

Clinical Diagnosis

Following each ADRC visit, a clinical diagnosis was made at the Consensus Diagnosis Conference by a multidisciplinary team of geriatricians, neurologists, and neuropsychologists with expertise in dementia following NIA-AA Criteria (Albert et al., 2011; McKhann et al., 2011). The diagnosis was based on the comprehensive clinical and cognitive assessment results acquired at the visit, and was not determined by biomarkers. Cognition measures independent from NIHTB-CB were used for diagnosis, including the NACC UDS neuropsychological battery and AVLT (Schmidt, 1996). The sample included 77.1% unimpaired and 22.9% impaired individuals with varied severity levels and causes (Table 2).

Statistical Analyses

Evaluating the factor structure of the whole sample

Exploratory factor analysis (EFA) with the oblique geomin rotation was first performed on the whole sample with a focus on identifying the number of factors (Yates, 1987). Given seven tests, a maximum of three factors can be extracted (Muthén & Muthén, 2009). The number of factors was chosen based on the following criteria: (1) the number of eigenvalues greater than one; (2) good model fit; (3) the model solution having a clear factor structure with each test loaded on a single factor, i.e., the test had a significant and high loading on one factor, but low loading(s) on the other factor(s); (4) clinical meanings; and (5) model parsimony (Fabrigar & Wegener, 2012). Confirmatory factor analysis (CFA; Bollen, 1989) was next applied to further refine and confirm the factor structure identified by EFA with a focus on the relations between the tests (i.e., observed indicators) and the latent factors.

Testing factorial invariance across groups

As summarized in Table 3, invariance was tested in five dimensions, across clinical diagnosis, sex, race/ethnicity, age, and education, respectively, by comparing two groups in each dimension. The CFA model confirmed on the whole sample was first tested for each group separately. If the CFA fit well for both groups split by a specified variable, factorial invariance was next tested with a hierarchical series of nested two-group CFA models in the following order: (1) Configural invariance requires that the two groups have the same pattern of freely estimated and fixed at zero parameters, whereas all freely estimated parameters are allowed to differ across groups. Confirmed configural invariance serves as the baseline model and implies that the same latent constructs are measured for both groups. (2) Based on configural invariance, metric (weak) invariance requires that the factor loadings, i.e., slopes or regression coefficients of the tests on the latent constructs, are equal across groups. Under confirmed metric invariance, latent factor variances and covariances are comparable across groups, and group difference in the ratios of factor variances and the correlations of latent factors are thus interpretable. (3) Scalar (strong) invariance additionally requires equal indicator intercepts, i.e., difficulty levels of the tests. Under confirmed scalar invariance, latent factor means are also comparable and group difference in the latent factor means is thus interpretable. (4) Residual variance (strict) invariance additionally requires equal indicator residual variances. Under confirmed strict invariance, the unique factors contribute equally across groups, and thus the group differences in the means and variances of the indicators are entirely attributable to the group differences in the latent factors. Based on strict invariance, (5) factor variance-covariance invariance and (6) factor mean invariance were further tested in order (Meredith, 1993; Meredith & Teresi, 2006; Vandenberg, 2002; Vandenberg & Lance, 2000; Widaman & Reise, 1997). Models (1 to 4) test measurement invariance and evaluate whether the relations between the tests and the latent constructs are same across groups. Scalar invariance is required to confirm measurement invariance, and allows meaningful comparison in the latent constructs between groups. Strict invariance is more desirable but is usually difficult to achieve. Models (5, 6) test structural invariance and evaluate group differences in the variabilities, correlations, and levels of the latent constructs being measured (Byrne, Shavelson, & Muthén, 1989; Vandenberg & Lance, 2000).

Table 3.

Classification of Clinical Diagnosis and Demographic Groups for Invariance Testing

Variable	Group	n
Diagnosis	Cognitively unimpaired	317
	Dementia / MCI a	82
Sex	Male	171
	Female	240
Race / Ethnicity	Under represented groups (URG)	90
	Non-URG	314
Age	< 65 years	165
	≥ 65 years	152
Education	Without bachelor’s degree (low)	144
	With bachelor’s degree (high)	267

Note. Because of the limited sample size in each impaired group, dementia and MCI due to all causes were combined into one group, whereas the impaired not MCI were excluded from the invariance testing. Due to a similar consideration, race/ethnicity groups were classified as underrepresented groups (URG) versus non-URG. Following the NIH definition (NIH Diversity in Extramural Programs, 2019), a participant was classified as URG if s/he self-reported primary, secondary, or tertiary race as African American, American Indian or Alaska native, Native Hawaiian or other Pacific Islander, or self-reported Hispanic ethnicity. A participant was classified as non-URG if s/he self-reported only White or Asian in primary and secondary races and self-reported No to Hispanic ethnicity. A participant was classified as URG unknown and not included for the invariance testing, if s/he self-reported other or unknown in race or ethnicity. Age was classified as a binary variable, < 65 versus ≥ 65, since around 65 is commonly considered as the start of late adulthood. Because age is the biggest risk factor for dementia/MCI, and in the current sample age was highly associated with the incidence rate of dementia/MCI, 6.8% for participants < 65 versus 31.5% for those ≥ 65, p < .0001 (Fisher’s exact test), age invariance was tested only for cognitively unimpaired participants. Education level was classified into low (without bachelor’s degree) versus high (with bachelor’s degree) education groups, as these two groups would likely have access to different occupations, involving different cognitive demands and leading to different social economic status.

^a72 out of the 82 dementia / MCI participants had AD as a cause.

Model estimation

Analyses were performed on raw scores (Bowden, Cook, Bardenhagen, Shores, & Carstairs, 2004). These were the “computed” scores for Flanker and DCCS, “raw” scores for Processing Speed and Working Memory, and “theta” scores for Episodic Memory, Vocabulary, and Reading. (Explanation of these scores is provided in the note under Table 1). (NIH & Northwestern University, 2006–2016). Two extremely high scores (22.7 and 35.7) for Vocabulary and one (36.1) for Reading were excluded from the analysis, because the tests may not reliably measure these individuals’ abilities, given lack of items with high difficulty levels. Such items are needed to appropriately assess the highest functioning individuals. Models were tested with Mplus version 8 (Muthén & Muthén, 1998–2017) using the full information maximum likelihood (FIML) sandwich estimator with robust standard errors (MLR) which handles missingness and nonnormality (Enders, 2010; Wang & Wang, 2012; Yuan & Bentler, 2000). The description of model identification and sample Mplus codes are provide in the supplemental material.

Assessing model fit

Model fit was evaluated based on multiple indices in order to make best use of the available data and draw the most robust conclusion. Overall model fit was assessed using fit indices including the comparative fit index (CFI; Bentler, 1990), the root mean squared error of approximation (RMSEA) with 90% confidence interval (Steiger & Lind, 1980), and the standardized root mean squared residual (SRMR; Bentler, 1995). Model fit was considered adequate by meeting the following criteria: CFI ≥ 0.95, RMSEA ≤ 0.08, SRMR ≤ 0.08 (Browne & Cudeck, 1992; Hu & Bentler, 1998, 1999). Misfit in individual parameters was evaluated using model modification indices (MI), which are the amount of reduction in the model χ² if a parameter fixed at zero or constrained equal across groups were freely estimated (Steiger, Shapiro, & Browne, 1985). A parameter was freed by using the threshold MI >10 as a start (Wang & Wang, 2012). However, parameters with MI close to 10 were also freed if the model fit needed further improvement and the freed parameter had an estimate sufficiently different from zero. For factorial invariance testing with nested two-group CFAs, a more restricted invariance model was selected if the overall model fit was acceptable, and it was similar in model fit compared with the less restricted invariance model it nested within. Model fit difference was assessed using the Satorra-Bentler (SB) scaled correction χ² difference test (Satorra & Bentler, 2001) and change in CFI. Because the χ² test can be overly sensitive for sample sizes above 150 (Dowling et al., 2010) and to adjust for inflated type I error rate associated with multiple comparisons (i.e. five model comparison pairs across the six invariance levels), a more-conservative significance level of p < 0.01 (i.e. 0.05/5) was adopted. Insignificant χ² difference tests (i.e., p ≥ 0.01) and ΔCFI ≤ 0.01 (Cheung & Rensvold, 2002) were considered as the criteria for similar model fit. Partial invariance (Byrne et al., 1989; Millsap & Kwok, 2004) was examined by allowing part of the constrained parameters to differ across groups, if this was suggested by large MIs and led to improved model fit. Under partial invariance, at least two invariant indicators per factor were required to confirm measurement invariance and meaningful comparisons across groups (Dowling et al., 2010; Mungas et al., 2011).

Results

Descriptive Statistics

Univariate descriptive statistics and Pearson correlations of the tests are provided in Tables 4 and 5 for the whole sample and each diagnosis group, and provided in the supplemental Tables S1 and S2 for each demographic group. The dementia/MCI group generally had higher missing rates, lower averages, greater variabilities, and lower correlations than the cognitively unimpaired group.

Table 4.

Means, Standard Deviations, and Ranges of the Test Scores for the Whole Sample and Each Diagnosis Group

	The whole sample			Cognitively unimpaired			Dementia / MCI
Test	% Missing	M (SD)	Range	% Missing	M (SD)	Range	% Missing	M (SD)	Range
Flanker	1.2%	7.4 (1.2)	2.8 – 9.6	0.3%	7.8 (0.8)	4.6 – 9.6	4.9%	6.0 (1.5)	2.8 – 8.3
DCCS	2.2%	7.4 (1.5)	1.5 – 10.0	0.3%	7.9 (1.0)	2.4 – 10.0	8.5%	5.6 (1.9)	1.5 – 9.3
Processing Speed	1.5%	37.3 (9.2)	4.0 – 57.0	0.6%	39.8 (7.1)	17.0 – 57.0	4.9%	28.1 (10.6)	4.0 – 52.0
Working Memory	3.6%	15.9 (3.6)	4.0 – 24.0	0.3%	16.9 (2.7)	10.0 – 24.0	17.1%	11.6 (3.9)	4.0 – 19.0
Episodic Memory	9.2%	−0.8 (0.9)	−2.2 – 1.6	1.3%	−0.7 (0.8)	−2.2 – 1.6	40.2%	−1.8 (0.4)	−2.2 – −0.4
Vocabulary	1.5%	6.6 (2.2)	−0.5 – 11.9	0.9%	7.1 (2.0)	−0.5 – 11.9	3.7%	5.2 (2.1)	−0.2 – 9.9
Reading	1.7%	6.5 (2.7)	−7.0 – 11.5	0.9%	7.0 (2.3)	−1.3 – 11.5	4.9%	5.0 (3.1)	−7.0 – 9.7

Note. Reasons for missingness included the following: (1) The participant was unable to complete the test because of limited cognitive abilities or other limitations such as poor vision or hearing; (2) The test was automatically skipped if the participant failed on the sample items before the test; (3) The participant refused the test; (4) There was lack of time to administer the test. In addition, two extremely high scores (22.7 and 35.7) for Vocabulary and one (36.1) for Reading were excluded from the analysis, because the tests may not reliably measure these individuals’ abilities, given lack of items with high difficulty levels. Such items are needed to appropriately assess the highest functioning individuals. The Vocabulary and Reading tests are administered with the Computer Adaptive Testing (CAT) format, and are scored based on the Item Response Theory (IRT). With CAT, the next item an individual receives depends on her/his response to the previous item. CAT allows that a test is tailored to an individual’s ability level, and thus the battery can be applicable to individuals with a broad range of ability levels, which in turn, can reduce the chances in the floor and ceiling effects. However, lack of items with very high (or low) difficulty levels for individuals with extremely high (or low) abilities would result in unreliable scores for these individuals.

Table 5.

Pearson Correlations of the Test Scores for the Whole Sample and Each Diagnosis Group

The whole sample (ns: 370 to 403)
Test	1	2	3	4	5	6	7
1. Flanker	-
2. DCCS	0.67 (401)	-
3. Processing Speed	0.67 (403)	0.64 (400)	-
4. Working Memory	0.62 (395)	0.57 (393)	0.54 (394)	-
5. Episodic Memory	0.40 (372)	0.37 (371)	0.33 (373)	0.45 (372)	-
6. Vocabulary	0.39 (403)	0.37 (399)	0.30 (402)	0.43 (394)	0.34 (371)	-
7. Reading	0.40 (399)	0.36 (395)	0.32 (400)	0.45 (389)	0.30 (370)	0.76 (398)	-
Lower diagonal: cognitively unimpaired (ns: 311 to 316)
Upper diagonal: dementia / MCI (ns: 48 to 77)
Test	1	2	3	4	5	6	7
1. Flanker	-	0.39 (74)	0.70 (76)	0.57 (67)	0.27 (48)	0.08 (77)	0.14 (74)
2. DCCS	0.57 (316)	-	0.50 (74)	0.31 (66)	0.03 (48)	0.11 (74)	0.10 (71)
3. Processing Speed	0.40 (315)	0.49 (315)	-	0.44 (67)	0.16 (49)	0.04 (77)	0.16 (75)
4. Working Memory	0.35 (316)	0.42 (316)	0.37 (315)	-	0.35 (48)	0.11 (68)	0.15 (64)
5. Episodic Memory	0.25 (313)	0.23 (313)	0.23 (313)	0.29 (313)	-	0.02 (49)	0.13 (48)
6. Vocabulary	0.28 (314)	0.24 (314)	0.18 (313)	0.33 (314)	0.22 (311)	-	0.66 (75)
7. Reading	0.30 (313)	0.28 (313)	0.22 (313)	0.39 (313)	0.19 (311)	0.74 (311)	-

Note. Insignificant correlations (p > .05) are underscored. Sample sizes are included in the parentheses () after the correlations. The dementia/MCI group had much smaller sample sizes than the cognitively unimpaired group. Thus the comparison should be based on the effect size of the correlations rather than the p-values. In addition, the pairwise missing rate was consistently higher for the dementia/MCI group than the cognitively unimpaired group. The missing rate was similar between different correlation coefficients (i.e., different pairs of tests) for the cognitively unimpaired. However, it varied for the dementia/MCI group and was most substantial for the correlations that involved memory tests. This missing pattern implied a systematic restriction in the samples such that only the relatively less impaired in the dementia/MCI group was included in the correlation estimation and comparison, and this restriction was most severe for correlations that involved memory tests. As a result, different subsamples of the dementia/MCI group were being compared between different correlations.

EFA and CFA for the Whole Sample

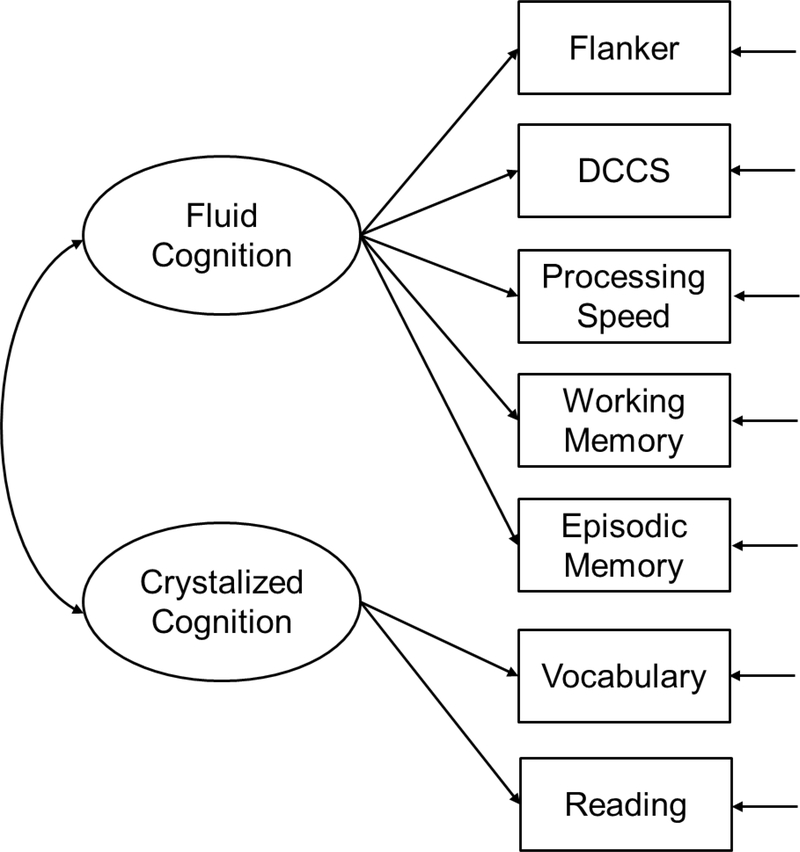
EFA yielded two eigenvalues (3.98, 1.13) greater than one. Supplemental Figure S1 provided the scree plot of all eigenvalues. As shown in Table 6, the one-factor solution had unacceptable model fit, whereas standard errors could not be computed for the three-factor solution due to model identification issues. In contrast, the two-factor solution yielded good model fit and a clear fluid-crystalized cognition factor structure as depicted in Figure 1 (Heaton et al., 2014). This model was next confirmed by CFA, as evidenced by its excellent overall model fit, all MIs < 10, and all factor loadings being large (0.60 to 0.90), positive, and significant (Table 7).

Table 6.

Factor Loadings, χ² Test, and Model Fit Indices for the Exploratory Factor Analyses with Geomin Rotation for the Whole Sample (n=411)

	One-Factor	Two-Factor
	1	1	2
Factor loadings
Flanker	0.83	0.85	−0.01
DCCS	0.81	0.81	0.02
Processing Speed	0.60	0.83	−0.08
Working Memory	0.79	0.71	0.13
Episodic Memory	0.76	0.51	0.14
Vocabulary	0.53	−0.01	0.93
Reading	0.55	0.10	0.77
χ2 test
χ2	255.255	12.945
df	14	8
p-value	<.0001	0.114
Model fit indices
CFI	0.787	0.996
RMSEA 90% CI	0.205 (0.183, 0.227)	0.039 (0.000, 0.076)
SRMR	0.086	0.015

Note. Insignificant factor loadings (p > .05) are underscored. Factor loadings > .50 are in boldface. CFI = comparative fit index; RMSEA = root mean squared error of approximation; SRMR = standardized root mean squared residual. Model fit is considered adequate by meeting the following criteria: CFI ≥ 0.95, RMSEA ≤ 0.08, SRMR ≤ 0.08. The three-factor solution is not reported, because standard errors could not be computed due to model identification issues.

Figure 1.

Factor structure of the whole sample and all groups except for the group with age < 65.

Table 7.

Standardized Parameter Estimates, χ² Test, and Model Fit Indices for Confirmatory Factor Analysis Final Models for the Whole Sample and Each Group

	The whole sample	Cognitively unimpaired	Dementia / MCI	Male	Female	URG	Non URG	< 65 years	≥ 65 years	Low education	High education
n	411	317	82	171	240	90	314	165	152	144	267
Factor loadings
Flanker (F1, FA)	0.85	0.70	0.87	0.87	0.83	0.83	0.86	0.67	0.63	0.80	0.87
DCCS (F1, FA)	0.82	0.78	0.53	0.80	0.82	0.80	0.82	0.82	0.69	0.78	0.84
Processing Speed (F1, FA)	0.78	0.62	0.81	0.70	0.83	0.57	0.81	0.52	0.54	0.78	0.76
Working Memory (F1, FB)	0.79	0.45 (0.24)a	0.69	0.82	0.77	0.74	0.68 (0.19)a	0.67	0.68	0.78	0.78
Episodic Memory (F1, FB)	0.60	0.36	0.41	0.68	0.55	0.42	0.63	0.42	0.27	0.66	0.55
Vocabulary (F2, FC)	0.85	0.79	0.65	0.85	0.85	0.85	0.81	0.78	0.91	0.87	0.81
Reading (F2, FC)	0.90	0.93	1.00	0.87	0.92	0.89	0.87	0.91	0.86	0.91	0.82
Test intercepts
Flanker	6.04	9.94	4.01	5.86	6.18	6.43	6.05	11.62	9.40	5.44	6.54
DCCS	4.74	8.20	2.98	4.44	5.02	4.33	4.89	10.96	7.26	3.90	5.55
Processing Speed	4.03	5.58	2.65	4.17	3.96	4.72	4.00	6.71	5.47	3.82	4.22
Working Memory	4.17	6.33	2.77	4.16	4.19	4.29	4.22	7.40	6.00	3.75	4.52
Episodic Memory	−0.98	−0.79	−4.57	−1.32	−0.80	−1.50	−0.88	−0.52	−1.19	−1.40	−0.82
Vocabulary	3.03	3.57	2.50	3.32	2.86	2.23	3.74	3.50	3.66	2.46	3.82
Reading	2.35	3.01	1.62	2.24	2.43	1.26	3.23	3.24	2.81	1.55	3.57
Test residual variances
Flanker	0.29	0.52	0.25	0.24	0.31	0.31	0.27	0.55	0.61	0.36	0.24
DCCS	0.34	0.39	0.73	0.36	0.33	0.35	0.32	0.33	0.52	0.39	0.30
Processing Speed	0.40	0.62	0.34	0.51	0.32	0.67	0.35	0.73	0.70	0.39	0.42
Working Memory	0.38	0.65	0.53	0.33	0.40	0.45	0.38	0.56	0.54	0.39	0.39
Episodic Memory	0.64	0.87	0.83	0.54	0.70	0.82	0.60	0.82	0.93	0.57	0.69
Vocabulary	0.28	0.38	0.58	0.28	0.28	0.28	0.34	0.40	0.18	0.25	0.35
Reading	0.19	0.13	0b	0.24	0.15	0.21	0.24	0.17	0.26	0.17	0.33
Factor covariance c
F1 with F2	0.56	0.42	0.22	0.53	0.57	0.72	0.51		0.61	0.63	0.44
FA with FB								0.40
FA with FC								0.34
FB with FC								0.57
χ2 test
χ2	29.014	16.945	10.452	26.686	17.082	23.978	18.566	26.796	22.133	20.249	27.342
df	13	12	14	13	13	13	12	11	13	13	13
p-value	0.007	0.152	0.729	0.014	0.196	0.031	0.100	0.005	0.053	0.089	0.011
Model fit indices
CFI	0.986	0.991	1.000	0.973	0.994	0.952	0.992	0.939	0.969	0.983	0.979
RMSEA (90% CI)	0.055 (0.028, 0.082)	0.036 (0.000, 0.073)	0.000 (0.000, 0.080)	0.078 (0.034, 0.121)	0.036 (0.000, 0.078)	0.097d (0.029, 0.157)	0.093d (0.000, 0.077)	0.093 (0.049, 0.139)	0.068 (0.000, 0.115)	0.062 (0.000, 0.112)	0.064 (0.030, 0.098)
SRMR	0.031	0.031	0.044	0.043	0.036	0.054	0.025	0.041	0.042	0.035	0.034

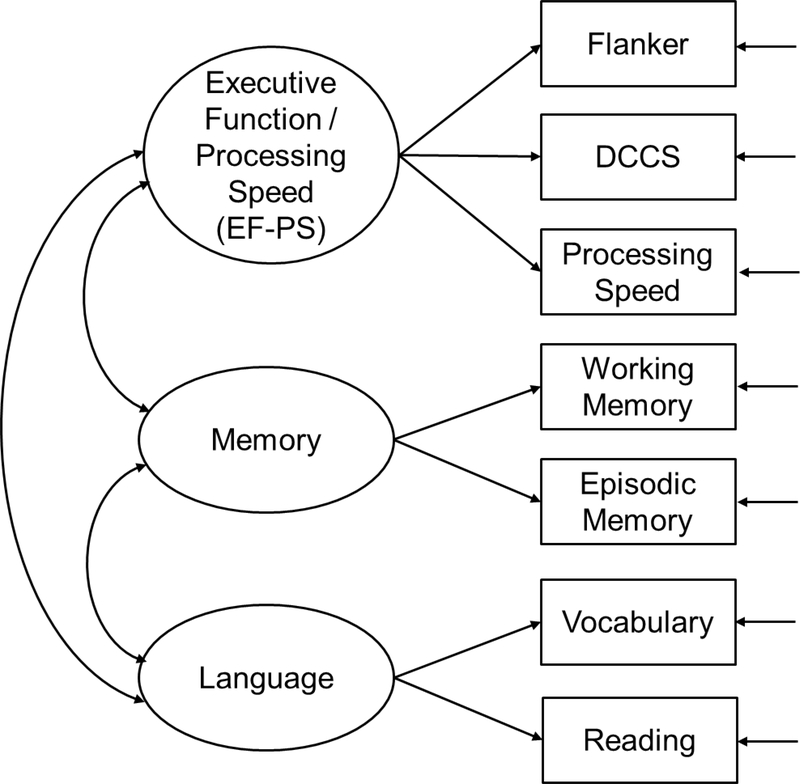
Note. For the whole sample and each group except for the group with age < 65, a two-factor model fit well, including (1) fluid cognition (F1) measured by Flanker, DCCS, Processing Speed, Working Memory, and Episodic Memory, and (2) crystalized cognition (F2) measured by Vocabulary and Reading. For the group with age < 65, the two-factor model did not fit well, χ2(df=13) = 52.761, p-value < 0.001, CFI = 0.846, RMSEA (90% CI) = 0.136 (0.099, 0.175), SRMR = 0.077. However, a three-factor model fit well, including (A) executive function / processing speed (FA) measured by Flanker, DCCS, and Processing Speed, (B) memory (FB) measured by Working Memory and Episodic Memory, and (C) language (FC) measured by Vocabulary and Reading. Factor variances are one under standardized solution. Factor means are fixed at zero to satisfy model identification. Insignificant parameter estimates (p > .05) are underscored. CFI = comparative fit index; RMSEA = root mean squared error of approximation; SRMR = standardized root mean squared residual. Model fit is considered adequate by meeting the following criteria: CFI ≥ 0.95, RMSEA ≤ 0.08, SRMR ≤ 0.08.

^aFactor loadings in “()” are crossloadings on the crystalized cognition factor (F2).

^bFixed at zero to satisfy model identification.

^cThe factor covariance equals correlation because factor variances are one under standardized solution.

^dRMSEA was slightly higher than the cutoff value. With small sample sizes (n < 200), RMSEA tends to be too high and over reject the true population model (Curran et al, 2003; Hu & Bentler, 1998). Given this limitation of RMSEA and the other model fit indices CFI and SRMR both being adequate, the factor model was still concluded to be acceptable.

CFA for Each Group

Except for the group with age < 65, the two-factor fluid-crystalized cognition CFA (Figure 1) fit well for all groups with a few minor variations: (1) Working Memory had small crossloadings on the crystalized cognition factor for the cognitively unimpaired (0.24) and non-URG (0.19) groups; and (2) the residual variance of Reading was fixed at zero for model identification needs for the dementia/MCI group. Differently, the group with age < 65 had three factors, including executive function / processing speed (EF-PS), memory, and language (Figure 2). More detailed results are summarized in Table 7.

Figure 2.

Factor structure of the group with age < 65.

Two-Group CFAs for Invariance Testing

Following the results of the single-group CFAs, two-group CFAs were next tested for factorial invariance across diagnosis, sex, race/ethnicity, and education, but not across age. Results are summarized in Table 8.

Table 8.

Summary of Factorial Invariance Testing Final Models with Two-Group Confirmatory Factor Analysis

Invariance level	m	χ2 test			Model fit			Model comparison	χ2 difference test			ΔCFI
		χ2	df	p-value	CFI	RMSEA (90% CI)	SRMR		Δχ2	Δdf	p-value
Diagnosis (n = 399)
1. Configural	1	27.290	26	0.394	0.998	0.016 (0.000,0.059)	0.034
2. Metric	1	43.001	31	0.074	0.983	0.044 (0.000,0.073)	0.076	1 vs. 2	15.984	5	0.007	0.015
3. Scalar	2	54.711	34	0.014	0.971	0.055 (0.025,0.081)	0.082	2 vs. 3	12.006	3	0.007	0.012
4. Residual variance	4	63.435	36	0.003	0.961	0.062 (0.036,0.086)	0.114	3 vs. 4	9.145	2	0.010	0.010
5. Factor variance-covariance	2	64.103	37	0.004	0.962	0.061 (0.034,0.085)	0.114	4 vs. 5	0.383	1	0.536	0.000
6. Factor mean	2	64.103	37	0.004	0.962	0.061 (0.034,0.085)	0.114	5 vs. 6a	-	-	-	-
Sex (n = 411)
1. Configural	0	43.323	26	0.018	0.985	0.057 (0.024,0.086)	0.039
2. Metric	0	53.196	31	0.008	0.981	0.059 (0.030,0.085)	0.071	1 vs. 2	9.948	5	0.077	0.004
3. Scalar	1	57.092	35	0.011	0.981	0.055 (0.027,0.081)	0.071	2 vs. 3	3.650	4	0.455	0.000
4. Residual variance	0	77.096	42	0.001	0.971	0.064 (0.041,0.086)	0.087	3 vs. 4	18.712	7	0.009	0.011
5. Factor variance-covariance	0	74.552	45	0.004	0.975	0.057 (0.032,0.079)	0.092	4 vs. 5	0.498	3	0.919	−0.005
6. Factor mean	0	76.458	47	0.004	0.975	0.055 (0.031,0.077)	0.097	5 vs. 6	1.723	2	0.423	0.000
Race/Ethinicity (n = 404)
1. Configural	1	42.337	25	0.017	0.984	0.059 (0.025,0.088)	0.034
2. Metric	1	53.200	29	0.004	0.978	0.064 (0.036,0.091)	0.062	1 vs. 2	10.402	4	0.034	0.006
3. Scalar	0	61.373	34	0.003	0.975	0.063 (0.037,0.088)	0.065	2 vs. 3	8.251	5	0.143	0.003
4. Residual variance	1	65.809	40	0.006	0.976	0.057 (0.030,0.080)	0.089	3 vs. 4	5.685	6	0.459	−0.001
5. Factor variance-covariance	0	77.352	43	0.001	0.968	0.063 (0.040,0.085)	0.111	4 vs. 5	11.701	3	0.008	0.008
6. Factor mean	1	80.958	44	0.001	0.966	0.064 (0.042,0.086)	0.123	5 vs. 6	3.701	1	0.054	0.002
Education (n = 411)
1. Configural	0	47.879	26	0.006	0.981	0.064 (0.034,0.092)	0.034
2. Metric	0	52.186	31	0.010	0.981	0.058 (0.028,0.084)	0.049	1 vs. 2	4.503	5	0.479	−0.001
3. Scalar	0	58.326	36	0.011	0.980	0.055 (0.027,0.080)	0.055	2 vs. 3	6.087	5	0.298	0.001
4. Residual variance	3	68.185	40	0.004	0.975	0.059 (0.033,0.082)	0.070	3 vs. 4	9.764	4	0.045	0.005
5. Factor variance-covariance	2	67.858	41	0.005	0.976	0.056 (0.031,0.080)	0.084	4 vs. 5	0.499	1	0.480	−0.001
6. Factor mean	2	67.858	41	0.005	0.976	0.056 (0.031,0.080)	0.084	5 vs. 6a	-	-	-	-

Note. m = number of parameters allowed to differ across groups; CFI = comparative fit index; RMSEA = root mean squared error of approximation; SRMR = standardized root mean squared residual; Δχ² = the Satorra-Bentler (SB) scaled correction χ² difference statistic; Δdf = change in df; ΔCFI = change in CFI. Model fit is considered adequate by meeting the following criteria: CFI ≥ 0.95, RMSEA ≤ 0.08, SRMR ≤ 0.08. Violation of invariance is considered under the following criteria: significant Δχ² (p <.01), ΔCFI > .01.

^aχ² difference test and ΔCFI are not applicable because the two models are identical.

Across diagnosis: cognitively unimpaired versus dementia/MCI

The results showed that (1) the configural invariance model fit well except that Working Memory was cross loaded on the crystalized cognition factor for the cognitively unimpaired group only. (2) The metric invariance model had a small deviation from meeting the criteria for similar model fit compared against the configural invariance model, p = 0.007 for χ² difference test and ΔCFI = 0.015. Given that the model had good overall fit and there were no large MIs to indicate misfit in individual parameters, the model was considered acceptable. Partial invariance was allowed such that Episodic Memory differed across diagnosis and yielded a greater loading for the cognitively unimpaired than dementia/MCI, which suggested that the test was more sensitive in detecting individual difference in the underlying latent fluid cognition construct for the unimpaired. (3) With similar justification, the scalar invariance model was considered acceptable with partial invariance. Working Memory and Episodic Memory yielded higher indicator intercepts for the cognitively unimpaired, which implied that these tests were more difficult and less favorable for individuals with dementia/MCI. (4) Four tests had residual variances different across diagnosis, including DCCS, Working Memory, Episodic Memory, and Vocabulary, which indicated that the group difference in some unique factors also contributed to the group difference in the observed scores of these tests in addition to the fluid and crystalized cognition constructs. (5) The two factors had greater variances and lower means for individuals with dementia/MCI than the cognitively unimpaired, which suggested greater individual variabilities and lower levels in the cognition constructs for this group.

Across sex: male versus female

(1) Testing across sex achieved configural, full metric, and close to full scalar invariance, except that Episodic Memory had a slightly higher intercept for females than males, which implied that the test was easier and more favorable for females. (2) All tests had residual variances invariant across sex, which suggested that sex similarity or difference in the test scores can be fully attributable to sex similarity or difference in the underlying fluid and crystalized cognition constructs. (3) The two sexes also had equal factor variances, covariance, and means, which indicated sex similarity in the variabilities, correlation, and average levels of the cognition constructs.

Across Race/Ethnicity: URG versus non-URG

(1) The two race/ethnicity groups generally had configural invariance, except that Working Memory was cross loaded on the crystalized cognition factor for non-URG only. (2) All tests had invariant factor loadings, except that Processing Speed had a greater loading for non-URG, which suggested that the test was more sensitive in detecting individual difference in the fluid cognition ability for non-URG. (3) All tests had invariant intercepts, which indicates that the tests had comparable difficulty levels across groups. (4) Invariant residual variances were observed for all tests, except for URG being larger in Reading, which implied that some unique factors contributed more to the Reading scores for URG, and thus contributed to group difference in the scores. (5) The two groups had equal factor variances and covariance, which indicates group similarity in the variabilities and correlation of the cognition constructs. (6) The two groups also had equal means in the fluid cognition factor, however, URG had a lower mean in the crystalized cognition factor.

Across Education: low versus high

(1) Testing across education achieved configural, full metric, and full scalar invariance, which implied that all tests had comparable discrimination abilities and difficulty levels for the two groups. (2) Three tests had unequal residual variances, including Flanker, DCCS, and Episodic Memory, which indicated that some unique factors contributed differently to the scores of these tests across education. (3) The two groups had equal variance in the fluid cognition, however, the low education group had a greater variance in the crystalized cognition and a higher correlation of the two factors. (4) The high education group had higher means for both factors.

Discussion

Factor Structure of the Whole Sample

The two-factor fluid-crystalized cognition structure was confirmed for the whole sample and for each group except for the group with age < 65. This factor structure was consistent with previous factor analyses on NIHTB-CB (Hackett et al., 2018; Mungas et al., 2014). These findings support using fluid and crystalized cognition composites for AD research. Fluid abilities are “used to solve problems, think and act quickly, and encode new episodic memories” (Heaton et al., 2014, p. 2), and are mostly influenced by biological processes. They grow rapidly through childhood, reach a peak at early adulthood, and decline afterward. These abilities tend to be more sensitive to changes in brain structure and functions associated with aging and neurological disorders. Thus, fluid cognition composite could be a sensitive measure to detect cognitive impairment associated with AD. Crystalized abilities “represent an accumulated store of verbal knowledge and skills” (Heaton et al., 2014, p. 3), and are influenced by experience, education, and cultural exposure. They develop rapidly during childhood, continue to improve slightly into middle adulthood, and remain stable at late adulthood. Thus, crystalized cognition composite may serve as an efficient measure for cognitive reserve (Hackett et al., 2018). A study (McDonough et al., 2016) found that cognitively unimpaired adults whose fluid cognitive ability was worse compared to crystalized cognitive ability measured using factor scores showed evidence of early AD neuropathology evaluated using structural MRI and PET imaging. Larger discrepancy in the fluid and crystalized cognitions was associated with greater beta-amyloid deposition and cortical thickness in AD-vulnerable brain regions. The finding suggested that this discrepancy may be a marker of preclinical AD, and highlighted the importance of the distinction between these two cognition constructs.

Different Factor Structure across Age

The two-factor fluid-crystalized cognition structure was held for individuals with age ≥ 65. However, for individuals with age < 65, the fluid cognition factor was separated into two factors: EF-PS and memory. This was aligned with the finding by Hackett et al. (2018) about the separation of EF-PS and memory into two factors when excluding AD participants, given that AD participants were much older than the rest of the sample on average. Previous research showed that age affects cognitive domains differently (Heaton, Ryan, & Grant, 2009; Tulsky et al, 2003). Therefore a possible reason is that memory may decline at a later age or at a different rate compared to EF-PS, and thus the two constructs may be more divergent during the transition period from middle to late adulthood. In addition, Flanker, DCCS, and Processing Speed tests all involve reaction time in scoring, whereas the other tests do not. This might have also contributed to age differences in the factor structure given that reaction speed might differ significantly between the two age groups. In total, researchers should exercise caution in the analysis and interpretation of longitudinal changes measured using the fluid cognition composite. Separate composites for EF-PS and memory could be considered for the age population under 65, and individual component tests might be preferred for longitudinal trajectories spanned across 65.

Partial Measurement Invariance across Diagnosis

Configural invariance across diagnosis was confirmed, such that the fluid and crystalized cognition factors were found for both cognitively unimpaired and impaired groups. Partial metric and scalar invariance was found: Episodic Memory was less sensitive in detecting individual difference for the group with dementia/MCI, and Episodic Memory and Working Memory were more difficult and less favorable for this group. Relatedly, higher missing rates were observed for these two tests, which was consistent with the low completion rates found on these tests by Hackett et al. (2018). Given that the majority of this group had AD as a cause, these findings highlight two things: (1) impairment in memory is a salient feature in AD dementia and, (2) the tests are too challenging for individuals with AD and insensitive at the lower end of memory function, suggesting potentially limited utility for this population. Additional factors could have also contributed to refusal or incompletion, including fatigue associated with immediately administering NIHTB-CB after completion of the NACC UDS 3 battery and unfamiliarity with electronic testing. Both cognition factors had greater variances for the dementia/MCI group than the cognitively unimpaired group, and the correlation of the two factors for the former (0.22) was only about half of the size for the latter (0.42). This suggested more heterogeneity in cognitive abilities for the impaired, which was likely due to the heterogeneity in their disease severity. Nonetheless, lower means for dementia/MCI than the unimpaired found on both factors supported the validity of these factors in distinguishing between clinical diagnoses.

Measurement Invariance across Sex, Race/Ethnicity, and Education

Measurement invariance was generally confirmed across sex, race/ethnicity, and education at the scalar invariance level, allowing meaningful comparisons of latent factor means, variances, and correlation and identification of demographic differences in these factors properties. URG had a lower mean level in crystalized cognition, which could have resulted from cultural differences and historical injustice in the exposure to the contents of test items. Moreover, these factors might have played different roles for each included URG subgroup. The high education group had higher mean levels in both cognition constructs, highlighting the positive influence of education on cognitive function and reserve.

Conclusions

To our knowledge, this is the first study that evaluated factor structure and tested measurement invariance of NIHTB-CB including all seven tests on an AD research sample. Its utility in AD research is supported by the confirmed fluid-crystalized cognition factor structure and its measurement invariance across sex, race/ethnicity, and education. Nonetheless, partial invariance was found across clinical diagnosis, highlighting the potential challenges in measuring memory of individuals with AD. Different factor structures were identified across age, suggesting the possible longitudinal variation in the underlying meaning of fluid cognition.

Limitations and Future Directions

Sample size

In this study, sample sizes (n) for individual impaired diagnoses and minority race/ethnicity groups were small. Small samples tend to have greater probability in model non-convergence and improper solutions, inflated type I error rates, and reduced statistical power for detecting the violation of invariance (Chen, 2007; Jorgensen, Kite, Chen, & Short, 2018; Marsh, Hau, & Wen, 2004; Meade, Johnson, & Braddy, 2008). Small ns in these groups also led to unbalanced ns in the two-group CFAs. Unbalanced ns are associated with reduced power, which becomes more severe as the ratio of group ns increases (Brace & Savalei, 2017; Chen, 2007; Yoon & Lai, 2018). To address these issues, we combined dementia and MCI, and combined more than one race/ethnicity into one group. Such grouping is admittedly problematic, because subgroups are not monolithic. If subgroups have different factor structures, the combined group would represent the largest membership, masking unique pattern(s) of the smaller subgroup(s). We recommend several strategies to address small or unbalanced ns for future invariance testing. (1) Increase efforts to recruit more participants with impaired diagnosis or from minority race/ethnicity groups. (2) The impact of limited ns can be alleviated with greater factor over-determination and higher communalities, which for example can be achieved by including more reliable indicators for each factor (MacCallum, Widaman, Zhang, & Hong, 1999; Meade & Lautenschlager, 2004; Meade & Bauer, 2007). (3) Two approaches adopted in this study may help yield more robust findings. One is to test CFA on each group separately to first ensure the same factor structure between groups before pooling them together for the two-group CFA. The other is to draw conclusions based on evaluating multiple test indices, including overall model fit indices, change in fit indices between nested models, and MI for individual parameters. (4) The subsampling method, which repeatedly samples a subset of the larger group to have the same n as the smaller group, may provide a solution to achieve adequate power under severe unbalanced ns (Yoon & Lai, 2018).

Missing data

The two memory tests were too challenging for participants with dementia or MCI and led to high missing rates. In addition, three unreliably extremely high scores on Vocabulary and Reading were excluded given lack of items to appropriately assess the highest functioning individuals. These findings implied limited utility of the battery for such populations. Logistic regression analyses showed that performance on other tests predicted missingness for each situation with high predictive power (c-statistic ranged from 0.87 to 0.97, Supplemental Table S3 and Figure S2). This supported that the data could be missing at random (MAR) if such prediction completely accounted for the missingness. However, if missingness was additionally related to the missing score itself, missing not at random (MNAR) could have occurred, which unfortunately was not testable. We used the FIML estimator to handle missing data. FIML provides unbiased parameter estimates under MAR, but biased estimates under MNAR, although the bias tends to be isolated to a subset of model parameters (Enders, 2010). The potential bias could possibly include omission of non-invariance or underestimation of difference in factor means across diagnosis.

Biomarker profile

Following the new NIA-AA research framework toward a biological definition of AD based on biomarkers (Jack et al., 2018), the next research steps could be the evaluation of factor structure and measurement invariance across different AT(N) biomarker profiles and brain changes. Findings would help further define the utility scope of NIHTB-CB in AD research.