Abstract
We develop a Bayesian group-based trajectory model (GBTM) and extend it to incorporate dual trajectories and Bayesian model averaging for model selection. Our framework lends itself to many of the standard distributions used in GBTMs, including normal, censored normal, binary, and ordered outcomes. On the model selection front, GBTMs require the researcher to specify a functional relationship between time and the outcome within each latent group. These relationships are generally polynomials with varying degrees in each group, but can also include additional covariates or other functions of time. When the number of groups is large, the model space can grow prohibitively complex, requiring a time-consuming brute-force search over potentially thousands of models. The approach developed in this paper requires just one model fit and has the additional advantage of accounting for uncertainty in model selection.
Keywords: Group-based Trajectory, Bayesian Estimation, Bayesian Model Averaging
1. Introduction
There has been a growing interest in examining trajectories of individual outcomes or developmental processes across a wide range of disciplines. The widespread interest and increasing availability of panel data with long time series creates a strong demand for methods that allow researchers to model trajectories and uncover the heterogeneity among them. Growth models (GMs) describe the process of development or growth in a hierarchical or random coefficient framework, by assuming that individual observations deviate around a single underlying population trajectory (Goldstein, 1987; Raudenbush and Bryk, 2002). By redefining certain random coefficients as latent factors, growth trajectories can also be estimated in a structural equation modeling (SEM) framework, which is referred to as the latent growth model (LGM) or the latent growth curve model (LGCM) (McArdle, 1988; Meredith and Tisak, 1990; McArdle and Epstein, 1987; Muthén, 2004). The LGM can be particularly appealing in psychology because many psychological variables have serious measurement errors and the latent variable approach can reduce bias in estimation (Curran et al., 2010).
The latent growth mixture model (LGMM) or the growth mixture model (GMM) is a recent development of LGMs. Repealing the assumption that the entire population is statistically homogeneous, it assumes that there are two or more latent subgroups of the population whose members appear to be more similar to each other than to the remaining individuals in a given dataset (Muthén and Shedden, 1999). Each individual belongs to one of a finite number of subgroups, each of which represents a component of a mixture distribution (McLachlan and Peel, 2004). Although appealing, the GMM can be quite complex to applied researchers (Jones et al., 2001; Jones and Nagin, 2007).
Enlightened by a nonparametric model developed by Heckman and Singer (1984), the group-based trajectory model (GBTM) provides an alternative and simplified approach to uncover hidden heterogeneity in outcome trajectories across individuals in the population (Nagin, 1999, 2005). Compared to the general GMM, the GBTM assumes homogeneity conditional on trajectory group membership. Moreover, rather than categorizing individuals into latent groups, the GBTM only assigns each individual a probability of belonging to each latent group (Nagin, 2005). The model has been applied in thousands of articles published in sociology (e.g. Hayford, 2009; Petts, 2009), psychology (e.g. Pepler et al., 2008; Li and Lerner, 2011), criminology (e.g. Nagin and Piquero, 2010; Block et al., 2010), economics and business (e.g. Day and Sin, 2011), public health and medicine (e.g. Gill et al., 2010; Fountain et al., 2012; Modi et al., 2011; Hsu and Jones, 2012), and many other fields.
One major drawback of the GBTM is its sensitivity to assumptions regarding the number of latent groups and shape of the trajectories within each group. The standard practice is to estimate many models differing across these two dimensions and to select the model which maximizes some measure of model fit, such as the Bayesian Information Criteria (BIC). This approach is subject to two criticisms. First, selecting one model over another based on a marginal improvement in model fit may be highly influenced by noise, particularly when multiple specifications yield similar model fit measures. Ideally, one would capture uncertainty in the model selection process. Second, optimizing over the entire model space requires a brute force search. For example, a researcher choosing the optimal polynomial specification for polynomials up to and including a third degree in a GBTM with five groups has at least 21 possible models to search through.1 If the researcher is also optimizing the number of groups, say by searching all specifications between two and five groups, this would increase to at least 52 possible models. Adding additional functions of age, adding other covariates, or extending to a dual trajectory model would quickly render the search unmanageable given that a single model on a moderately sized dataset often takes several minutes to fit using standard statistical software. This likely creates sub-optimal incentives for many researchers. For example, researchers may restrict the model space to simple functions such as polynomials whereas searching over a broader model space could yield richer insights. It also increases the burden of model checking and updating as the entire search would need to be redone with every alteration.
This paper addresses these issues by developing a Bayesian framework and Markov-chain Monte Carlo (MCMC) algorithms for estimation and model selection in GBTMs. Our primary contribution is a Bayesian model averaging procedure that can be used to select the functional forms of the trajectories. Bayesian model averaging serves several practical purposes in this context. First, it accounts for uncertainty in model selection by incorporating all of the best fitting models in the posterior predictive distribution of trajectories. Second, averaging over multiple plausible models (e.g. ensembling) typically yields more accurate predictions than selecting a single optimal model (Raftery et al., 1997). Third, model averaging can save researchers a considerable amount of time by relieving them of the need to fit dozens, or even hundreds, of models and compare their fits. We focus on several standard outcome types that are often used in the literature, including continuous, censored, binary, and ordered outcomes.
While selecting the number of latent groups is a key component in GBTMs, this paper instead focuses on selecting the functional forms within each group. There are several reasons for this choice. First, the optimal number of groups is a function of the chosen functional forms, and therefore it makes little sense to choose the number of groupings independently. Having settled on a functional form will therefore be complementary to the process of optimizing the number of groups. Second, the optimal number of groups typically depends on subjective factors such as model interpretability, whereas functional form selection may be more amenable to deterministic statistical criteria. Third, there have been several papers analyzing the optimal choice of groups in both GBTMs and the more general case of the finite mixture model (Biernacki et al., 2000; Brame et al., 2006; Klijn et al., 2017), whereas there has been little written about selecting functional forms.
Along the way to developing the model selection procedure, we first develop MCMC algorithms for estimating standard GBTMs in congruence with Nagin (2005) in the Bayesian framework. We hope this will provide a pedagogical contribution in clarifying how Bayesian estimation can proceed in this common context, and in demonstrating how various posterior quantities, such as trajectories and joint distributions of groups in dual trajectory models, can be analyzed in practice. Despite an growing interest in the Bayesian estimation of the GMM, no studies have focused on introducing Bayesian estimation for the standard GBTM that is already well known among many applied researchers. As we will demonstrate in the paper, the Bayesian approach has a number of features ideally suited for the GBTM independent of the model selection procedure. The first advantage is the ability to conduct finite sample inference of the model parameters without relying on asymptotic assumptions. Unlike approximation error due to invalid asymptotic assumptions, errors in the Monte Carlo approximations used in Bayesian estimation procedures can be made arbitrarily small by drawing more samples in the MCMC algorithm. Finite sample inference is particularly important in GBTM studies since the sample is partitioned into multiple subsets, each of which must be large enough to invoke asymptotic assumptions. This feature also plays a key role in dual trajectory models, in which there is typically some joint outcome that does not occur often enough to justify an asymptotic approximation.
A second advantage is the ability to conduct inference on arbitrary functions of model parameters. This is a crucial feature of GBTMs since many of the model’s key outputs are complicated functions of the estimated parameters. For example, the main object of interest is the trajectories themselves, which are typically nonlinear functions of the estimated parameters. A second example is the group membership probabilities. In the standard single trajectory model, these are often modeled using a generalized logit function of a subset of the model parameters. In the dual trajectory model, the problem is compounded since researchers may be interested in up to five distributions - the joint distribution of the group-membership probabilities, both conditional distributions of group memberships given the other pair member’s group membership, and both marginal group-membership distributions. Researchers typically only estimate either the joint distribution or one conditional and one marginal distribution, as the remaining distributions can be represented as functions of these distributions. However, using maximum likelihood methods, one has to resort to approximations to compute confidence intervals or standard errors for all five distributions. We demonstrate that MCMC methods provide exceedingly simple ways to examine the entire posterior distribution of each of these distributions’ parameters.
We focus our examples largely on the dual trajectory model for two reasons. First, the extant literature on Bayesian GMMs has focused on single trajectory models. Second, the model space is more likely to grow prohibitively large in dual models due to an increase in the number of groups, making it a natural point to apply the model averaging procedures. It should be noted that while estimation of multiple trajectories is possible (Nagin et al., 2018), we limit the scope of this paper to single and dual trajectory models used in the majority of applications.
The paper proceeds as follows. First, we review and discuss the relevant literature on group-based trajectory models. Next, we introduce the Bayesian models and present simple MCMC algorithms for sampling from the posterior distributions when the outcomes are normally distributed. Finally, we introduce the model averaging procedure and demonstrate its capabilities. The paper concludes with a discussion of the findings and a path for future research. The R code and data used in this paper are available in GitHub at https://github.com/jtm508/bayestraj. Vignettes are also provided to help users adapt the code to applications of their own interest.
2. Review of the Group-Based Trajectory Model
2.1. Model Specification
The GBTM requires longitudinal data which track some outcome for individuals i = 1, …, N over Ti periods. Following the notation in Nagin (2005), we denote individual i’s sequence of outcomes by yi = {yi1, …, yiTi}. Each individual i belongs to some latent group, ci ∈ {1, …, K} with respective probabilities π = {π1, …, πK}. Letting Pk(yi; θk) denote the likelihood of yi conditional on ci = k, we can write the likelihood for individual i as
where θ = {θ1, …, θK} parametrizes the model for each group. Throughout the paper, the likelihoods will implicitly be conditioning on the data as well. Because K is restricted to be a finite integer, this model falls into the general class of finite mixture models (McLachlan and Peel, 2004).
In order to simplify the model, it is assumed that the elements of yi are independent conditional on group memberships. That is, for each group k,
where pk(yit; θk) is the probability distribution function of yit conditional on ci = k. Under the standard assumption of independence across individuals, the complete likelihood of the data can be written as
| (1a) |
| (1b) |
Much of the applied literature using GBTMs has focused on the question of how trajectories can be related to a set of observed covariates. For such purposes, researchers often model the group membership probabilities for each individual using a logit formula:
| (2) |
where vi is a vector of time-invariant covariates associated with the individual and γ is a parameter to be estimated. As is the case in multinomial logit models, the researcher must fix γk = 0 for some baseline group k in order to identify the model because the resulting probabilities are only affected by differences in these parameters.
Researchers must make two important choices when fitting GBTMs. The first is the number of latent groups, K. While it is technically possible that subjects are truly clustered into K distinct groups, the reality is usually that the mixing distribution is continuous and requires infinite data to fully capture. The finite mixture model merely provides a flexible approximation to the more complex underlying reality (Nagin and Tremblay, 2005). The implication for researchers trying to maximize model fit is that the optimal number of latent groups can increase with sample size, provided that the additional data has sufficient variation. However, for a fixed sample, researchers must cope with the fact that the likelihood is guaranteed to increase with K, and therefore must settle on a criterion for balancing the better in-sample fit with the number of parameters in the model. Nagin (1999) suggests researchers can choose the number of groups which optimize some information criterion, such as BIC. Researchers using mixture models for cluster analysis may also want to consider more subjective criteria when choosing the number groups. It is often recommended to balance such metrics with considerations of interpretability and a reliance on subject matter expertise. A few interpretable clusters consistent with theory and previous research may be preferable compared with a large number of uninterpretable clusters which maximize BIC. Thus, even with arbitrarily large datasets, it will still always make sense to limit the number of groups.
The second consideration is the functional form of the outcomes. The functional form specifies the outcome’s probability distribution at each time period by relating the time variable to a parameter in the distribution. Common choices for the distribution include Poisson, Bernoulli, normal, and censored normal. For example, in the normal model, it is assumed that where xit is a vector of covariates. While the choice of distribution is usually obvious given the nature of the outcome variable, there is a considerable amount of freedom in choosing which variables to include xit. For example, in an age trajectory problem, the researcher could potentially include age, age2, age3, ln(age), spline terms, and so forth. The optimal functional forms ought to be flexible enough to capture nonlinearities in the trajectories, which naturally leads to a multitude of choices for model specification. This choice is further complicated by the fact that the optimal form will likely differ across the various latent groups. Like the choice of K, researchers often choose the functional forms by optimizing fit metrics like BIC. Unfortunately, this gives rise to an ugly combinatorial problem in which the number of possible combinations of K and the functional forms within each group becomes intractably large.2 Given the time-consuming nature of estimating each model and limited computational resources, researchers can only search a subset of the possible models before settling on an optimum.
An important extension of the group-based single trajectory model is the dual trajectory model (Nagin and Tremblay, 2001), which links two single trajectory models by a joint probability distribution over group memberships. The two series of measurements must share a common identity in order to link the outcomes. Formally, the dual trajectory model considers two series of outcomes for units i = 1, …, N. We refer to each unit i as a pair (though we note that in many application, i represents a single individual with two outcomes). For now we suppress the i subscripts and the parameter vector θ for notational simplicity. The measured outcomes for series 1 and series 2 are denoted by and respectively. We assume y1 ⊥ y2|c1 and y2 ⊥ y1|c2 where c1 ∈ {1, …, K1} and c2 ∈ {1, …, K2} denote the group memberships. Additionally, outcomes within each series of measurements are independent over time. That is, the likelihood of the outcomes in series 1 and 2, respectively, can be written as
and the joint likelihood as
| (3a) |
| (3b) |
| (3c) |
where and are probability distributions governing the outcome variables, and , , and are joint, conditional, and marginal probabilities of group membership, respectively. The joint distribution over latent groups ensures that one pair member’s group membership is informative about the other pair member’s group membership, and thus provides the crucial link between the two series of measurements.
The representation in equation 3c for the likelihood is the natural one for instances in which y1 temporally precedes y2, such as the intergenerational linkage model we estimate later in the paper. Note that we only need to estimate and in order to estimate the remaining probabilities of interest:
| (4a) |
| (4b) |
| (4c) |
We assume that each pair is independent. Thus if we denote yi1 and yi2 as the vectors of outcomes for pair i, then the likelihood of the entire data is
| (5) |
where π and θ represent the parameters of the model.
Like the standard group-based single trajectory model, an individual’s group membership probability can be modeled via a generalized logit function. It is common to estimate and for each c1 and c2. However, these equations are more difficult to estimate precisely due to the limited number of transitions between certain groups.
The same considerations discussed for the single trajectory model regarding choosing the optimal number of groups and the functional forms within each group apply to the dual trajectory model as well. However, the interaction between the two series causes a squared increase in the number of possibilities to consider. Nagin and Tremblay (2001) suggest choosing K1 and K2 in the dual trajectory model separately by fitting univariate trajectory models in order to simplify the choice set.
2.2. Frequentist Estimation and Challenges
Estimation of both the single and dual trajectory models are typically conducted using maximum likelihood methods. Jones et al. (2001) provide an efficient SAS procedure to estimate the model directly using quasi-Newton methods to maximize the likelihood. Similar packages have since been introduced in M-Plus (Muthén and Muthén, 2012) and Stata (Jones and Nagin, 2013). Thanks to canned software implementations, applications of the GBTM increased from 8 to 80 publications per year in major psychology journals in 2000–2010 (Nagin and Odgers, 2010). In psychology, GBTMs have been used to study disorders and depressions (e.g. Dekker et al., 2007; Mora et al., 2009; Côté et al., 2009; Odgers et al., 2008), inattention and hyperactivity (e.g. Jester et al., 2008), physical aggression (e.g. Brame et al., 2001), adherence (e.g. Li et al., 2014; Modi et al., 2010), risk involvement (e.g. Wang et al., 2014), and many other topics. Nagin and Odgers (2010), Frankfurt et al. (2016), and Piquero (2008) provide excellent review of GBTM applications for clinical research, counseling psychologists, and criminology, respectively.
While the existing packages provide unbiased point estimates of the model parameters, the standard errors are estimated by inverting the negative of the Hessian matrix evaluated at the maximum likelihood estimates to obtain estimates of the asymptotic covariance matrix. Though this is an asymptotically valid procedure, it may not yield valid inferences in finite samples. Acknowledging this problem, Loughran and Nagin (2006) conduct a resampling study where they estimate a GBTM on a sample of 13,000 individuals, and compare the estimates and standard errors with models fit to random subsets of the full dataset. They conclude that even for samples as small as 500 individuals, the estimates are comparable to that of the larger model. However, the biases tend to grow as the sample sizes decrease, particularly for groups with low membership probabilities. For example, in the 500-individual model, the mean absolute predictive error, defined as the absolute difference between the actual values and the predicted values, was over 10% for their “high-chronic” group, which is estimated to be only 3% of the population.
Since Loughran and Nagin (2006) use data which tracks cohort members from ages 10–26, tracking 500 individuals amounts to much more than 500 observations. When using data with shorter panels, asymptotic assumptions will require more individuals to justify. Moreover, while low-membership groups may not be a primary concern in single trajectory models, the imprecise estimates for such groups will be amplified in the dual trajectory model, where the researcher must estimate transition probabilities and joint distributions of group memberships. Even if the sample size within each group is large, there could be transitions or joint groups which occur with low probability. In such cases, asymptotic approximations may be difficult to defend.
Aside from computing standard errors for the model parameters, researchers also must calculate confidence intervals for the predicted trajectories. This presents a formidable challenge since trajectories are nonlinear transformations of the model parameters. Jones and Nagin (2007) suggest using either the bootstrap method or a first-order Taylor expansion to approximate the standard errors. They ultimately recommend the latter as the bootstrap can be quite time-consuming. An identical problem arises in computing standard errors for the group membership and transition probabilities.
2.3. Bayesian Approaches to Growth Mixture Models
While the majority of the GMM research has utilized maximum likelihood-based methods, a small body of research has used Bayesian estimation procedures, which can be relevant to the Bayesian estimation of GBTMs. Garrett and Zeger (2000) discuss issues regarding Bayesian estimation of latent class models, which provides the general framework for the GMM. More recent research has emphasized the advantages of Bayesian inference in the more general class of GMMs. In particular, Bayesian methods with accurate informative priors can recover parameters and class proportions more effectively than maximum-likelihood methods and Bayesian methods with diffuse priors (Depaoli, 2013). Researchers can directly incorporate background knowledge via the prior distribution, which is particularly valuable when some latent groups have small sizes due to limited data (van de Schoot et al., 2018).
The extant literature differs from this paper in a number of important ways. First, while most Bayesian GMMs are hierarchical generalizations of the single-trajectory GBTM specified in this paper, our proposed model averaging procedure does not directly apply to the more general GMMs aimed at modeling individual-level variation. Thus while the single-trajectory model in this paper can be thought of as a special case of extant work, its formalization is necessary as a stepping stone to the more complex model averaging framework we subsequently develop in Section 4. Additionally, the simpler GBTM model specification will be useful to researchers unsure how to reduce the GMM specification to the GBTM in the Bayesian framework.
Second, the extant literature has yet to tackle the dual trajectory model specified in Nagin and Tremblay (2001). A near-exception is Elliott et al. (2005) who formulate a Bayesian model and Gibbs sampling routine for dual trajectories. However, this particular model forces each unit into one group which determines both trajectories. This approach is less flexible than the model considered in this paper, which allows for separate groups in the two trajectories and a joint distribution over these two group-memberships.
Another stream of noteworthy contributions is the semiparametric Bayesian approaches used in Dunson and Herring (2006), Dunson et al. (2008), and Goldston et al. (2016) which use Dirichlet process priors to infer the number of latent groups. Dirichlet process priors have been the subject of considerable research in the machine learning and nonparametric Bayesian literature due to their ability to incorporate the optimal number of latent groups into a wide range of models. While we view the trend towards nonparametrics as exciting and important, many social scientists prefer to incorporate theory and subject matter expertise when selecting the number of groups, and the complexity of these models may prove to be prohibitive for many researchers.
3. Bayesian Group-Based Trajectory Models
In this section, we introduce a Bayesian approach to estimating the group-based single and dual trajectory models. First, we provide a brief overview of the Markov chain Monte Carlo (MCMC) methods which are used to estimate the models. We then develop the models, mirroring the frequentist version of the GBTM surveyed in Nagin (2005), which many applied researchers are already familiar with. We show how to construct a MCMC algorithm for the single trajectory model with continuous outcomes. We then discuss some common issues which researchers may come across, such as constructing trajectories from posterior samples and directly modeling group membership. Finally, we extend the model to incorporate dual trajectories. In Appendix 1, we also show how to extend the model to binary, ordered, and censored outcomes.
3.1. A Brief Overview of Markov Chain Monte Carlo
The goal of Bayesian inference is to obtain the posterior distribution of the model parameters by applying Bayes’ theorem:
where P(θ1, …, θP) is the prior distribution. However, since the posterior distribution is generally an intractable distribution with unknown properties, most Bayesian models rely on drawing samples and using Monte Carlo approximations to approximate various properties, such as posterior means, standard deviations and so forth. The challenge is devising an algorithm to obtain the samples. MCMC is a class of algorithms designed for this purpose. Q samples from the posterior distribution can be drawn by formulating a Markov chain:
where, by the Markov structure, each draw will depend on its predecessor.
The specific MCMC algorithm used throughout this paper is the Gibbs sampler Geman and Geman (1984). Via Gibbs sampling, the Markov chain will approximate the posterior distribution to arbitrary precision if each individual parameter is drawn conditional on the other parameters. That is, iteration q of the Markov chain consists of drawing from the following conditional distributions:
With carefully specified prior distributions, each of these conditional distributions can be shown via Bayes’ theorem to be a well-known distribution which can easily be sampled from. In this paper, we specify conjugate prior distributions, meaning the conditional distributions belongs to the same family as the prior (e.g. a normal prior will yield a normal conditional distribution).
Since successive samples are drawn conditional on the previous samples, it is clear that these samples are not independent. However, a version of the central limit theorem guarantees that Monte Carlo approximations based on these samples will correspond with the true distribution provided a sufficient number of samples are drawn. A more complete discussion on the MCMC can be found in various references, such as Brooks et al. (2011).
3.2. Single Trajectory Model
3.2.1. Model Specification
The Bayesian analysis retains the model specification used in the frequentist approach summarized in equation 1. We assume each outcome is independently and identically normally distributed conditional on the latent group membership and the remaining model parameters:
| (6) |
Although we will operate under the assumption of homoskedasticity to stay consistent with the literature, it is a simple extension to allow σ2 to vary across the groups.
Our prior distributions for the model parameters are standard independent conjugate priors often used in linear regression models - normal priors over the regression coefficients and an inverse-gamma prior over the variance. (Hoff, 2009). This prior specification enables posterior inference via Gibbs sampling. We also include a Dirichlet prior on the group membership probabilities, the standard conjugate prior used in finite mixture models (McLachlan and Peel, 2004).
| (7a) |
| (7b) |
| (7c) |
Diffuse prior settings which place roughly equal prior weight on all parameter values will yield results similar to the maximum likelihood estimates.3 For the Dirichlet distribution, setting αk = 1 for each k places a uniform prior over all group membership probabilities. For the inverse gamma prior, the standard interpretation is that the prior is based on a sample of size ν0 with a sample variance of . Setting ν0 = 0.001 and is considered a diffuse but proper prior (Hoff, 2009). Although inverse-gamma priors are subject to some criticism (Gelman, 2006), our experience is that they usually produce reasonable results and provide a useful starting point for Bayesian analysis.4 The priors on βk can be made diffuse by using a large covariance matrix for Σ. The notion of “large” depends on the scale of the data, but a common practice is to set μ = 0 and Σ = λI for some large constant λ, were I is the identity matrix. As λ approaches infinity, the distribution approaches an improper uniform prior. As with any Bayesian approach, there can be no prior specifications which are guaranteed to work well in any situation. The priors specified here can be considered as flexible default specifications, but researchers ought to validate their models through posterior predictive checks and be willing to alter priors when necessary.
Inference proceeds using a slight variation of the standard Gibbs sampler commonly used to estimate finite mixtures models. The Gibbs sampler exploits the independence of the outcome yi and the mixing distribution π conditional on the latent group membership, ci, by sampling ci in a data augmentation step of the MCMC algorithm. Specifically, the Gibbs sampling algorithm initializes the parameters randomly and then cycles through the following full conditional distributions:
The full conditional distributions are provided in Appendix 2. Readers may note that these distributions do not always condition on every single parameter in the model, as instructed in the section above. For example, π is only conditioned on c. The reason is simply that π is conditionally independent of the other parameters given c, and so P(π|c) = P(π|c, β, σ2, y). There is therefore no need to condition on the other parameters in this case. This concept will be applied in all of the Gibbs samplers discussed in this paper.
Researchers can estimate the model by iteratively drawing from these conditional distributions, Q times, forming a Markov chain consisting of Q samples from the joint posterior distribution of all of the model’s parameters. A potential problem which may arise in Gibbs Sampling is the label switching problem. We provide commentary on this issue in Appendix 3.
3.2.2. Estimating Trajectories
Once we have obtained samples from the posterior distribution of the model parameters, it is simple to use the estimates to obtain and plot the trajectories themselves. In the frequentist trajectory model, once one obtains the maximum likelihood estimate for for some group k, the predicted trajectory in the normal model can be obtained by multiplying for each t in the age range of the data, where xt is the vector of age variables for age t. For example, if our functional form includes age and age-squared, then x5 = (1, 5, 25) and is the predicted outcome at age 5 in group k. Calculating this for a range of t-values will yield the estimated trajectories. In the more general case, the prediction at age t can be written as f(xt; θ), where f is typically some inverse-link function and θ contains the model parameters. For example, in a logistic regression trajectory, f(xt; θ) would be the inverse-logit function which maps the linear predictor into a probability.
As discussed in the previous section, there is an added challenge of computing standard errors and confidence intervals when using maximum likelihood methods, since f can be a complicated nonlinear function. As a result, one has to resort to asymptotic approximations to compute confidence intervals. However, with Bayesian estimation, valid finite sample inference for these metrics essentially come free with the posterior samples. The distributions of the trajectories are the posterior predictive distributions of the outcomes. If we define to be a draw from the trajectory at time t, then the posterior predictive distribution of is
| (8) |
where p(θ|y) is the posterior distribution of θ.
In the normal model, is the normal distribution with parameters and σ2 for the corresponding group k. Once we have obtained samples from the posterior distribution of the model parameters, we can sample from the posterior predictive distribution using the following algorithm:
- For q = 1, …, Q:
- Sample , σ2,q from P(βk, σ2|y) (i.e. take a draw from the posterior distribution samples)
- Sample
The draws are samples from and can be used to conduct inference. For example, the expected outcome at time t is . Alternatively, the prediction can be summarized with the median of the draws. A 95% credible interval can be computed by taking the 0.025 and 0.975 quantiles from the distribution. Computing the same statistics for t = 1, …, T will yield the posterior predictive trajectories for group k with the associated confidence bands. While drawing these samples for each combination of t and k may seem time-consuming, it can actually be accomplished in a matter of seconds (after having obtained posterior samples) through matrix multiplication.
It is standard practice to ignore the contribution of σ2 in the trajectories and simply focus on the shape. The rationale is that shape of the trajectory is completely determined by βk, with σ2 only adding noise. In this case, one could ignore the σ2,q draw in step 1, and then calculate in step 2. This corresponds to integrating over βk but not σ2 in equation 8. However, while this method captures uncertainty regarding the mean trajectory within each group, it ignores individual variation around the mean.
3.2.3. Modeling Group Membership Probabilities
Just like in the frequentist GBTM model, researchers wishing to model the group membership probabilities as a function of covariates can use a generalized logit formula,
where vi is a vector of covariates. The γk parameters can be sampled in the MCMC algorithm in place of the πk’s. πi,k can then be computed deterministically conditional on vi and γk.
Note that this is equivalent to estimating a multinomial logit model using the latent group membership variables as the categorical outcomes. Once these latent variables are drawn in the Gibbs sampler, one can use any multinomial logit sampling routine to draw the γk’s conditional on the ci’s. A particularly convenient sampling routine to embed in a Gibbs sampler is the polya-gamma data augmentation scheme developed by Polson et al. (2013).
3.3. Dual Trajectory Model
Extending the Gibbs sampler to the dual trajectory model is straightforward, although the notation becomes much more burdensome. We use the superscripts 1 and 2 denote the two series, and assume likelihoods conditional on group membership of the following forms:
| (9a) |
| (9b) |
For the group membership probabilities, we must now define a prior on the joint distribution of group memberships for the two series of measurements. This can be done by placing priors on group memberships for the first series, and transition probabilities for the second series. Denote as the group membership probabilities for the first series. Then denote π2 as the K1 × K2 “transition” matrix with entry π2[j, k] ≡ πk|j. We refer to the kth row of π2 as . The priors are
| (10a) |
| (10b) |
| (10c) |
| (10d) |
| (10e) |
Inference is conducted by extending the Gibbs sampler developed for the single trajectory model. Recall that we introduced the group membership, ci, as a a model parameter by sampling ci in a data augmentation step of the MCMC algorithm. This reduced our model to a set of independent regressions by exploiting the conditional independence given group membership. The dual trajectory model extends this conditional independence insight further by noting that one pair member’s outcome is independent of the other pair member’s outcome conditional on its group membership. That is, by drawing both and for each pair i in the MCMC algorithm, we can perform inference for each group’s parameters as if the data were generated from independent normal models.
The Gibbs sampling algorithm cycles through the following full conditional distributions:
The full conditional distributions are mostly the same as in the single trajectory model, only now we need to incorporate each pair member’s group membership into the other member’s group membership probabilities. The altered full conditional distributions are provided in Appendix 2. Using equation 4, it is simple to sample the joint group membership probabilities, the marginal probabilities for series two, and the conditional probability for series one group membership given the series two group membership. The discussions of trajectory estimation, modeling group membership, and non-normal outcomes from the single trajectory section apply just the same to the dual trajectory model.
3.4. Demonstration on Simulated Data
Although the validity of our sampling algorithm can be justified on mathematical grounds (Geman and Geman, 1984), in this section we provide a simulation to further demonstrate the model performance and its ability to generate a rich set of output. Due to the page limit, we only present one simulation here. However, interested readers may follow our vignettes to set random parameters to generate simulated datasets and verify the model. We limit our simulations to the dual trajectory models since all single-trajectory model outputs can be discussed in the context of dual trajectory models, and because extant Bayesian GMMs can be viewed as a generalization of the single trajectory model.
We simulated data with known parameters from the dual trajectory data generating process for N = 1000 pairs and tested whether our algorithm could recover them. The outcomes were simulated for T = 9 periods for both series. We choose K1 = K2 = 3 as the number of latent groups for both outcomes. The data generating process is as follows. For each pair, a panel dataset was constructed using a second-degree polynomial. We then chose the parameter vector: , where each parameter is described in the previous subsection. Note that while π1 is the marginal probability of the first series’ group memberships, π2 is the K1 × K2 matrix of conditional probabilities for the second series’ group memberships. The values of the parameters can be seen in Table 1. Once the parameters were chosen, we drew each pair’s group membership for the first series as . Then we drew the second series’ group membership from . Outcomes were then generated for each observation in the panel as and .
Table 1.
Comparison of the Bayesian and Maximum Likelihood Estimation (MLE) of Simulated Dual Trajectory Data
| True Parameter | Estimate from MLE | SE from MLE | Estimated Median of the Posterior Distribution | Estimated SD of the Posterior Distribution | ||
|---|---|---|---|---|---|---|
| Panel A: Estimate from Series A | ||||||
| Latent Group 1 | Intercept | 118 | 117.94 | 0.09 | 117.93 | 0.09 |
| Age | 3 | 3.01 | 0.04 | 3.02 | 0.04 | |
| Age^2 | 0.1 | 0.10 | 0.00 | 0.10 | 0.00 | |
| Latent Group 2 | Intercept | 110 | 110.01 | 0.07 | 110.01 | 0.07 |
| Age | 5 | 5.01 | 0.03 | 5.01 | 0.03 | |
| Age^2 | −0.5 | −0.50 | 0.00 | −0.50 | 0.00 | |
| Latent Group 3 | Intercept | 111 | 110.95 | 0.10 | 110.93 | 0.10 |
| Age | −2 | −1.98 | 0.05 | −1.98 | 0.04 | |
| Age^2 | 0.1 | 0.10 | 0.00 | 0.10 | 0.00 | |
| Sigma | 1.414 | 1.19 | 0.01 | 1.19 | 0.01 | |
| Panel B: Estimate from Series B | ||||||
| Latent Group 1 | Intercept | 112 | 112.10 | 0.18 | 112.06 | 0.18 |
| Age | 2 | 1.90 | 0.08 | 1.91 | 0.08 | |
| Age^2 | 0.7 | 0.71 | 0.01 | 0.71 | 0.01 | |
| Latent Group 2 | Intercept | 111 | 111.02 | 0.14 | 110.99 | 0.14 |
| Age | −3 | −3.03 | 0.07 | −3.02 | 0.06 | |
| Age^2 | 0.1 | 0.10 | 0.01 | 0.10 | 0.01 | |
| Latent Group 3 | Intercept | 110 | 109.76 | 0.12 | 109.75 | 0.12 |
| Age | 6 | 6.13 | 0.06 | 6.14 | 0.06 | |
| Age^2 | −0.6 | −0.61 | 0.01 | −0.61 | 0.01 | |
| Sigma | 2 | 2.03 | 0.02 | 2.03 | 0.02 | |
Note: Maximum likelihood estimates are obtained from the package “traj” in Stata 16.
For illustrative purposes, we specified one transition probability which would be difficult to perform inference on using standard maximum likelihood methods with asymptotic assumptions. Group three was given a 20% membership probability for series one and the transition from group three to group one was specified as 1%. With 1000 pairs, this places 200 units in group three by expectation. With 200 units in group three, there is a roughly 13% chance that zero transitions between group three and group one would occur in the data. We simulated such a dataset to demonstrate the improved inference from using Bayesian methods on small or sparse datasets.
We first estimated model using the “traj” package in Stata 16 (Jones and Nagin, 2013) to form a baseline for comparison. We then ran the MCMC algorithm programmed in R for 10,000 draws, discarding the first 1000 as the burn-in period. Our hyper-parameters where chosen as follows: α1 = α2 = 1, ν0 = 0.001, , μ1 = μ2 = 0, and Σ1 = Σ2 = 100I, where I denotes the identity matrix. Judging by the trace plots, no label-switching occurred. Figure 1 plots the first 50 iterations from several trace plots to show that the Markov Chain quickly converges to a region surrounding the true parameter values. From Table 1, we can see that the MCMC algorithm is able to recover each of the regression parameters with reasonable precision. The medians of the posterior distributions are all very close to the true parameters, which generally fall within two standard deviations of the median. In the events where this is not the case, the maximum likelihood estimates displayed similar results, suggesting that any discrepancies between the estimated and true parameters arose from random variation in the data generating process rather than errors in the estimation routines.
Figure 1.
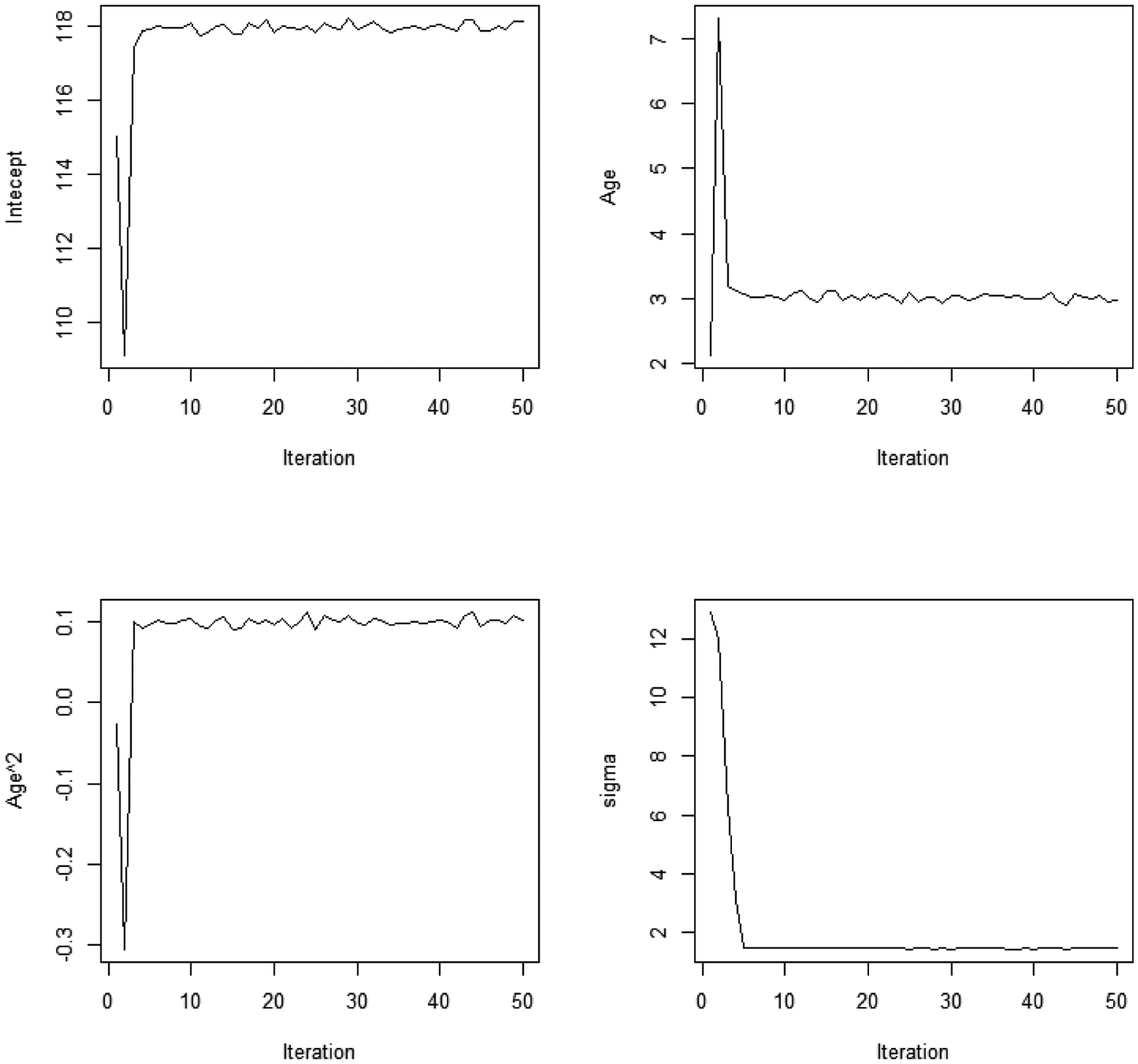
Trace Plots for the First Group for the First 50 Iterations, from Simulated Dual Trajectory Data
Note: The total number of iterations is 10,000. Here we only show the first 50 iterations for the first latent group to demonstrate the quick convergence of the Markov Chain Monte Carlo (MCMC).
Table 2 contains the maximum likelihood and Bayesian estimation results for the group membership and transition probabilities. Once again the true parameter values all fall within two standard deviations of the posterior medians. However, as expected, the maximum likelihood estimate is unable to obtain a good estimate of the transition from group three to group one. Since no such transition occurred in the data, the MLE is 0%. Further, due to an inappropriate application of asymptotics, the standard error is also roughly 0. By contrast, the Bayesian results produce a posterior distribution with the true value of 1% contained within the 95% credible interval. The full posterior distributions of the transition probabilities are shown in Figure 2.
Table 2.
Comparison of the Bayesian and Maximum Likelihood Estimation (MLE) of Group Probabilities
| True Parameter | Estimate from MLE | SE from MLE | Estimated Median of the Posterior Distribution | Estimated SD of the Posterior Distribution | 95% Credible Interval | |
|---|---|---|---|---|---|---|
| Panel A: Marginal Probabilities for Series A Latent Group | ||||||
| Group 1 | 30% | 30.5% | 1.5 | 30.5% | 1.5 | [27.7%, 33.5%] |
| Group 2 | 50% | 48.0% | 1.6 | 47.9% | 1.6 | [44.8%, 51.1%] |
| Group 3 | 20% | 21.5% | 1.3 | 21.5% | 1.3 | [19.1%, 24.1%] |
| Panel B: Marginal Probabilities for Series B Latent Group | ||||||
| Group 1 | 23.20% | 20.8% | -- | 20.9% | 1.3 | [18.5%, 23.5%] |
| Group 2 | 31% | 33.2% | -- | 33.2% | 1.5 | [30.3%, 36.0%] |
| Group 3 | 45.80% | 46.0% | -- | 45.9% | 1.6 | [42.8%, 49.0%] |
| Panel C: Transition Probabilities from Series A to Series B | ||||||
| 1|1 | 10% | 9.2% | 1.7 | 9.3% | 1.7 | [6.4%, 12.9%] |
| 2|1 | 20% | 20.7% | 2.3 | 20.7% | 2.3 | [16.5%, 25.5%] |
| 3|1 | 70% | 70.2% | 2.6 | 69.8% | 2.6 | [64.6%, 74.7%] |
| 1|2 | 40% | 37.5% | 2.2 | 37.4% | 2.2 | [33.2%, 41.9%] |
| 2|2 | 30% | 32.3% | 2.1 | 32.2% | 2.1 | [28.2%, 36.5%] |
| 3|2 | 30% | 30.2% | 2.1 | 30.2% | 2.1 | [26.2%, 34.5%] |
| 1|3 | 1% | 0.0% | 0.0 | 0.3% | 0.5 | [0.01%, 1.7%] |
| 2|3 | 50% | 53.0% | 3.4 | 52.7% | 3.4 | [46.3%, 59.4%] |
| 3|3 | 49% | 47.0% | 3.4 | 46.9% | 3.4 | [40.2%, 53.4%] |
| Panel D: Transition Probabilities from Series B to Series A | ||||||
| 1|1 | 12.9% | 13.5% | -- | 13.6% | 2.4 | [9.5%, 18.7%] |
| 2|1 | 86.2% | 86.5% | -- | 85.9% | 2.4 | [80.7%, 90.2%] |
| 3|1 | 0.8% | 0.0% | -- | 0.3% | 0.5 | [0.0%, 1.7%] |
| 1|2 | 19.4% | 19.0% | -- | 19.1% | 2.2 | [15.1%, 23.5%] |
| 2|2 | 48.4% | 46.7% | -- | 46.6% | 2.7 | [41.4%, 52.0%] |
| 3|2 | 32.3% | 34.3% | -- | 34.2% | 2.6 | [29.3%, 39.4%] |
| 1|3 | 45.9% | 46.5% | -- | 46.4% | 2.4 | [41.7%, 51.0%] |
| 2|3 | 32.8% | 31.5% | -- | 31.6% | 2.2 | [27.4%, 36.0%] |
| 3|3 | 21.4% | 22.0% | -- | 21.9% | 1.9 | [18.3%, 26.0%] |
Note: Maximum likelihood estimates are obtained from the package “traj” in Stata 16. i|j refers to the conditional probability of being in Group j in the Series B (A) conditional on being in Group i in the Series A (B). -- indicates that Traj does not compute standard errors for this paramater.
Figure 2.
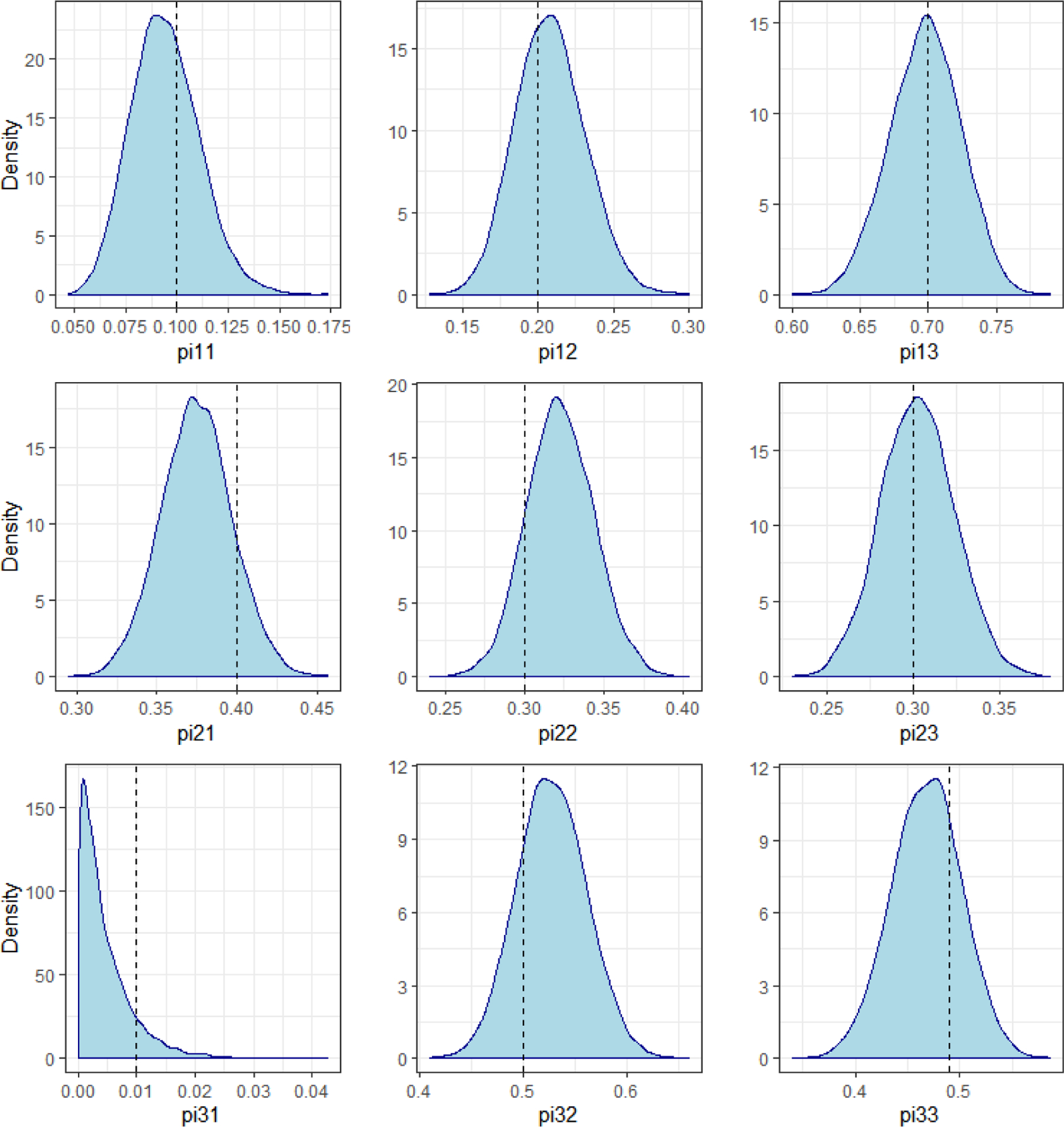
Marginal Distributions of Transition Probabilities, from Simulated Dual Trajectory Data
Note: pijk represents the transition probability from group j to group k.
Researchers may also be interested in recovering the joint probabilities of group membership, the marginal probabilities for the second trajectory, and the conditional probabilities of the first trajectory groups given the second trajectory group memberships. While these parameters were not used to generate the data, their true values can be computed using equation 4. As an example of our ability to recover these parameters, Figure 3 plots the posteriors of the joint distributions, with the true values being represented by the vertical lines. In each case, the true values lies inside the 95% credible interval. In the event that the probability was very close to 0, researchers can use these plots to examine the skewness of the posterior distribution. We note that using maximum likelihood methods, it would be difficult to calculate the standard error without asymptotic approximations, and examining the skewness of the distributions would require a time-consuming bootstrapping process after the model is fit. We report this result as a figure rather than a table in order to emphasize the ease and flexibility of examining the entire distribution of functions of the model parameters using MCMC methods.
Figure 3.
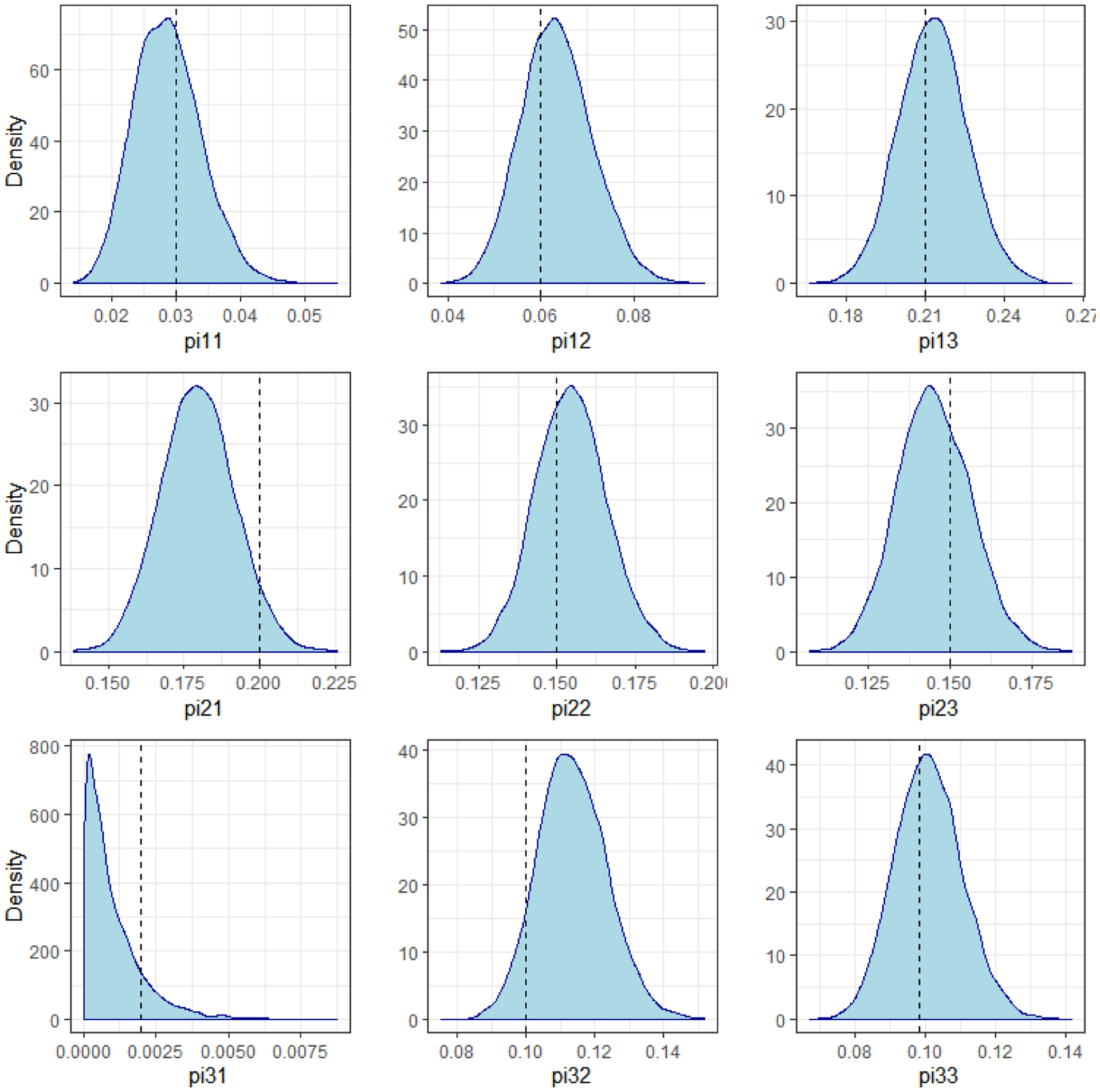
Joint Distribution of Group Membership Probabilities, from Simulated Dual Trajectory Data
Note: pijk represents the joint probability that the pair member from Series A belongs to group j and the corresponding pair member from Series B belongs to group k.
4. Bayesian Model Averaging
The main advantages of the Bayesian models introduced thus far are the ability to conduct finite sample inference without relying on asymptotic approximations for small samples or Taylor expansion approximations for functions of model parameters, including the trajectories. For some researchers, however, these advantages may seem more theoretical than practical. This section, by contrast, introduces a Bayesian procedure to automate model selection, which can save researchers dozens of hours of computing time while allowing for more flexible trajectory shapes.
As discussed earlier, the standard frequentist practice for functional form selection is to compare models with different degrees of polynomials and to select the model which maximizes BIC. This practice has two fundamental disadvantages. First, the number of possible models can become unmanageable, particularly in dual trajectory models. This can lead to unimaginative trajectories because the time-consuming nature of fitting the models leads researchers to exclude the majority of potential models from their tests. Second, when there are multiple models with comparable BIC, selecting a single model may not be sufficient. Ideally, a model selection technique would incorporate uncertainty in the model selection process. Our Bayesian procedure solves both of these problems and can be applied to both the single and dual trajectory models.
The model introduced in this section builds off of recent work from the statistics literature (Lee et al., 2016) that introduces a Bayesian model averaging method for the finite mixture model of linear regressions, of which the GBTM is a special case. The key insight is that the standard g-prior specification introduced by Zellner (1986), which is commonly used in applied Bayesian work for model selection in linear regression models, can easily be incorporated into the finite mixture model with similar results.
In practice, this works by introducing another data augmentation step into the Gibbs sampler. Consider the problem of selecting which of D functions of age, {f1(age), …, fD(age)} to include as variables in the trajectory model for each latent group k. For example, a simple variable selection problem may select for third-degree polynomials of age: {age0, age1, age2, age3}. For each group k we introduce an indicator vector where element takes on the value of 1 if fd(age) should be included in the model for group k. The solution to the variable selection problem is to sample each from its full conditional distribution in the Gibbs sampler, and impose whenever . Under this data augmentation scheme, each distinct value of zk represents a distinct model for group k. The posterior samples of βk, therefore, correspond to exactly one of these models in each sweep of the Markov chain. Continuing our example, suppose zk equals (1,1,0,0) in 50% of the sweeps,(1,1,1,0) in 30% of the sweeps, and (1,1,1,1) in 20% of the sweeps. The posterior distribution of βk will then consist of samples from a first-degree polynomial model 50% of the time, a second-degree polynomial model 30% of the time, and a third-degree polynomial model 20% of the time. Thus the full posterior distribution of βk and the resulting trajectories are weighted averages of these three model specifications, where the weights correspond to the inferred probabilities that each distinct model is the true model which generated the data.
4.1. The Gibbs Sampler
For notational simplicity, we only exposit the single trajectory model. The sampler can be extended to dual trajectories by applying the model selection equations to both series, and sampling the group-membership probabilities using the same equations specified in Section 3.3. We use the notation to denote the vector zk excluding the dth element. Using Bayes’ theorem, the conditional distribution of is Bernoulli where
| (11) |
where . Evaluating this function requires us to introduce priors for . It is convenient to assume uniform priors of in which case these terms cancel out in the fraction. The main challenge is then evaluating the marginal likelihood:
| (12) |
Clearly the solution to the integral will depend on our prior specification of θ. In the case of the normal latent trajectory model, θ = (β, σ2), so we must define a prior for which the marginal likelihood has an analytic solution. For this purpose, we switch the prior distributions to Zellner’s g-prior for the model parameters, which includes a heteroskedastic Jeffreys prior for σ2:
| (13a) |
| (13b) |
Some intuition for this choice of prior is as follows. In the classical maximum likelihood estimation of regression coefficients, the conditional covariance matrix of the estimator for β is . The g-prior sets the covariance term proportional to the frequentist estimator. The researcher, therefore, must only choose the gk term which determines the informativeness. Note that since Xk depends on the observations for which ci = k, this is a data-dependent prior which changes in each iteration of the Markov chain. Although this is somewhat controversial amongst traditional Bayesians (Berger, 2006), its practical advantages have distinguished the g-prior as the standard prior used in Bayesian model selection (Liang et al., 2008). Primarily, the marginal likelihood has a well-known closed form solution:
| (14) |
where Γ(·) is the gamma function, || · || is the Euclidean norm, is the number of observations in group k, is the number of variables selected by zk, π ≈ 3.14, and R2(zk) is the proportion of variance (R-squared) explained by the MLE:
where Xk(zk) contains the columns of Xk for which . Setting gk = nk will implement a ”unit-information prior“ which contains the informational equivalent of a single observation. This will retain the analytical benefits of efficient marginal likelihood evaluation while alleviating some of the concerns regarding the data-dependent prior. The full conditionals are provided in Appendix 2. We recommend setting βk,0 = βk,MLE in the prior distribution for βk as in Lee et al. (2016), as our own experience also suggests the estimates of are significantly more reliable when centering the prior around the MLE.5 Doing so simplifies the conditional distribution for βk to have a mean of βk,MLE in the Gibbs sampler.
The resulting Gibbs sampler will place a large mass at 0 on elements of the βk’s for which the associated variable has been effectively selected out of the model. The posterior predictive distributions used to plot the trajectories incorporate uncertainty over the possible models by integrating over z, for which each distinct value represents a distinct model. The Gibbs sampler allows researchers to integrate over a large number of models to perform efficient model selection while simultaneously accounting for model uncertainty.
4.2. Selecting Sets of Covariates
The approach outlined above selects each covariate individually. However, researchers may find it advantageous to select certain sets of covariates simultaneously. For example, by far the most common functional form in GBTMs is a polynomial of degree W. Yet the approach advocated above would likely contain samples from models which do not respect the full degree of the polynomial. For example, it may sample models where x3 is selected into the model while x2 is eliminated, contravening standard statistical practice.
This problem can be resolved by placing a prior over a set of covariates rather than its individual components. In the context of polynomials of degree W, one could put a prior over W rather than the individual terms. Suppose a researcher is considering polynomials of degree 0, 1, 2, and 3 in latent group k and has prior beliefs that Pr(Wk = w) = pw for w = 0, 1, 2, 3. Let denote the variables included in the model aside from the polynomial terms. Then
| (15) |
The terms are the marginal likelihoods given by equation 14 and can be computed analytically. Therefore Wk can be sampled from a categorical distribution with the corresponding posterior probabilities. Upon sampling Wk, the rest of zk can be filled in with 1’s and 0’s to reflect the selected model. Inference then proceeds according to the Gibbs sampler described above.
A default prior on Wk could be a uniform distribution. Researchers rarely consider terms degrees greater than 3 when searching manually, so one could set for w = 0, 1, 2, 3. Alternatively one could place informative priors which penalize higher degrees. However, the marginal likelihood already contains a term which penalizes additional covariates, thus imposing parsimony in the posterior distribution even with a uniform prior.
In practice, one may sample certain covariates as sets and others individually. For example, consider a model whose potential covariates include a polynomial of time up to degree 3, the logarithm of time, and an additional covariate x. Then x and the logarithm of time could both be sampled individually while the polynomial terms could be sampled as a set.
4.3. Demonstration on Simulated Data
To demonstrate the utility of the model averaging procedure, we simulated a second dataset from the dual trajectory model data generating process described earlier. The model includes 1000 pairs with three groups in each series. The first series contains simulations for 9 periods for each individual, while the second contains 8 periods. The covariates include an intercept and a third degree polynomial for age. We also fixed some of the second and third-degree coefficients to zero in order to verify that the model selection procedure removes these terms from the model. Our hyperparameters are chosen to be non-informative when possible. We set for each . For the g-priors, we set gk = nk for a unit-information prior and βk,0 = βk,MLE for each group. We retain the uniform prior over group memberships, with α1 = α2 = 1. The Gibbs sampler was run for 25,000 iterations, with the first 5,000 discarded as the burn-in period.
The results are reported in Table 3. The table includes an “Inclusion Probability,” defined as for variable d in group k, where Q is the number of posterior samples. If the procedure is working properly, the inclusion probabilities should be close to zero for terms where the coefficients were fixed to zero.
Table 3.
Group-Based Dual Trajectory Model Selection Coefficients from Simulated Data, with Three Latent Groups
| Series A | Series B | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| True Parameter | Estimated Median of the Posterior Distribution | 95% Credible Interval | Inclusion Probability | True Parameter | Estimated Median of the Posterior Distribution | 95% Credible Interval | Inclusion Probability | ||
| Panel A: Trajectory Coefficients | |||||||||
| Latent Group 1 | Intercept | 80 | 80.18 | [79.42, 80.93] | -- | 50 | 49.71 | [48.23, 50.60] | -- |
| Age | −1 | −1.04 | [−1.44, −0.65] | 100% | 1 | 1.20 | [0.79, 2.58] | 100% | |
| Age^2 | 0.5 | 0.50 | [0.45, 0.55] | 100% | −0.5 | −0.52 | [−0.85, −0.48] | 100% | |
| Age^3 | 0 | 0.00 | [0.00, 0.00] | 2% | 0 | 0.00 | [0.00, 0.02] | 9% | |
| Sigma | 4 | 3.97 | [3.96, 4.10] | -- | 6 | 6.16 | [5.99, 6.33] | -- | |
| Latent Group 2 | Intercept | 120 | 119.97 | [119.17, 120.66] | -- | 90 | 90.21 | [89.81, 90.65 | -- |
| Age | 20 | 19.90 | [19.55, 20.45] | 100% | 0.03 | 0.36 | [0.28, 0.44] | 100% | |
| Age^2 | −2 | −1.99 | [−2.13, −1.95] | 100% | 0 | 0.00 | [0.00, 0.00] | 2% | |
| Age^3 | 0 | 0.00 | [0.00, 0.01] | 4% | 0 | 0.00 | [0.00, 0.00] | 0% | |
| Sigma | 4 | 4.06 | [3.94, 4.18] | -- | 6 | 5.93 | [5.79, 6.06] | -- | |
| Latent Group 3 | Intercept | 100 | 100.43 | [99.55, 101.27] | -- | 100 | 101.40 | [99.84, 102.92] | -- |
| Age | 10 | 9.57 | [8.78, 10.37] | 100% | −30 | −31.00 | [−32.24, −29.75] | 100% | |
| Age^2 | −0.5 | −0.38 | [−0.59, −0.19] | 100% | 3 | 3.19 | [2.91, 3.47] | 100% | |
| Age^3 | 0.1 | 0.09 | [0.08, 0.11] | 100% | −0.3 | −0.31 | [−0.33, −0.29] | 100% | |
| Sigma | 4 | 3.99 | [3.91, 4.08] | -- | 6 | 6.08 | [5.92, 6.23] | -- | |
| Panel B: Group Probabilities | |||||||||
| 1 | 20% | 21.7% | [19.2%, 24.3%] | -- | 31% | 30.9% | [28.1%, 33.8%] | ||
| 2 | 30% | 28.0% | [25.2%, 30.8%] | -- | 40% | 40.5% | [37.5%, 43.6%] | ||
| 3 | 50% | 50.3% | [47.2$, 53.4%] | -- | 29% | 28.5% | [25.8%, 31.4%] | ||
| Panel C: Transition Probabilities | |||||||||
| 1 | 1 | 32.2% | 33.2% | [28.2%, 38.7%] | -- | 50% | 47.3% | [30.8%, 53.8%] | ||
| 2 | 1 | 19.4% | 17.8% | [13.8%, 22.3%] | -- | 20% | 25.3% | [19.8%, 31.5%] | ||
| 3 | 1 | 48.4% | 48.9% | [43.5%, 54.3%] | -- | 30% | 27.2% | [21.6%, 33.3%] | ||
| 1 | 2 | 10.0% | 13.6% | [10.4%, 17.1%] | -- | 20% | 19.7% | [15.4%, 24.6%] | ||
| 2 | 2 | 52.5% | 48.6% | [43.7%, 53.4%] | -- | 70% | 70.4% | [64.9%, 75.5%] | ||
| 3 | 2 | 37.5% | 37.8% | [33.2%, 42.6%] | -- | 10% | 9.8% | [6.7%, 13.6%] | ||
| 1 | 3 | 20.7% | 20.7% | [16.2%, 25.6%] | -- | 30% | 30.0% | [26.1%, 34.2%] | ||
| 2 | 3 | 10.3% | 9.6% | [6.5%, 13.3%] | -- | 30% | 30.4% | [26.5%, 34.6%] | ||
| 3 | 3 | 69.0% | 69.6% | [64.1%, 74.8%] | -- | 40% | 39.5% | [35.4%, 43.8%] | ||
Note: pi_k refers to the marginal probability of latent group k in Series A. pi_i_j refers to the conditional probability of being in latent group j in Series B conditional on being in latent group i in Series A. Sigma is the estimated standard deviation of the residual. Intercepts are forced into the model and not subject to model selection.
The results indicate that the method is efficiently selecting the correct variables. The inclusion probabilities are exactly one for each variable with a non-zero coefficient. Most of the variables with zero-valued coefficients had 95% credible intervals of [0,0] and all have inclusion probabilities under 4%, indicating that these variables have effectively been selected out of the model.
4.4. Application: Intergenerational Resemblance of Income Trajectories in the United States
Having demonstrated the approach using simulated data, we now turn to a use case involving observational data. The topic we choose is intergenerational resemblance of income trajectories, which is of interest to social scientists across disciplines but is understudied. Income changes and evolves over an individual’s life course. Most existing studies have only focused on income levels, whereas the shape of income trajectories is less studied. Two individuals with the same levels of lifetime income but different shapes of income trajectories may have different levels of well-being. For example, recent studies find that growing up in a family with decreasing or volatile household income trajectories is associated with a higher risk of psychiatric disorder for children (Björkenstam et al., 2017; Cheng et al., 2020). In this application, we look at income as another well-being outcome and examine the hypothesis that men’s income trajectories resemble both the level and the shape of their fathers’ income trajectories.
We apply our Bayesian model selection algorithm to data from the Panel Study of Income Dynamics (PSID), which reports longitudinal income data for fathers and sons from 1968–2017 (Johnson et al., 2020). We limit our sample to the 943 pairs of fathers and their first sons, with the goal of analyzing both inter- and intragenerational income resemblance. We fit models on log income and average over a model space consisting of up to third degree polynomials in order to emulate the typical model space a researcher may explore for such a scenario. As described above, we select the polynomial degree rather than individual polynomial terms in order to avoid averaging over models which include high degree terms while simultaneously selecting out lower degree terms.
We first attempted to optimize the number of latent groups using BIC, where the inclusion probabilities were used to determine the number of parameters in each model. However, BIC continued to increase until both fathers and sons had K = 9 latent groups, some with very low sample sizes and considerable uncertainty in the trajectory shapes. We ultimately settled on K = 5 groups for both fathers and sons, as adding additional groups beyond 5 created groups with either too much variability or not enough differentiation from the existing groups. Figure 5 includes the trajectories for our preferred specification. For transparency, we have also included the trajectories for K = 6 and K = 7 in Appendix Figures 1a and 1b.
Figure 5:
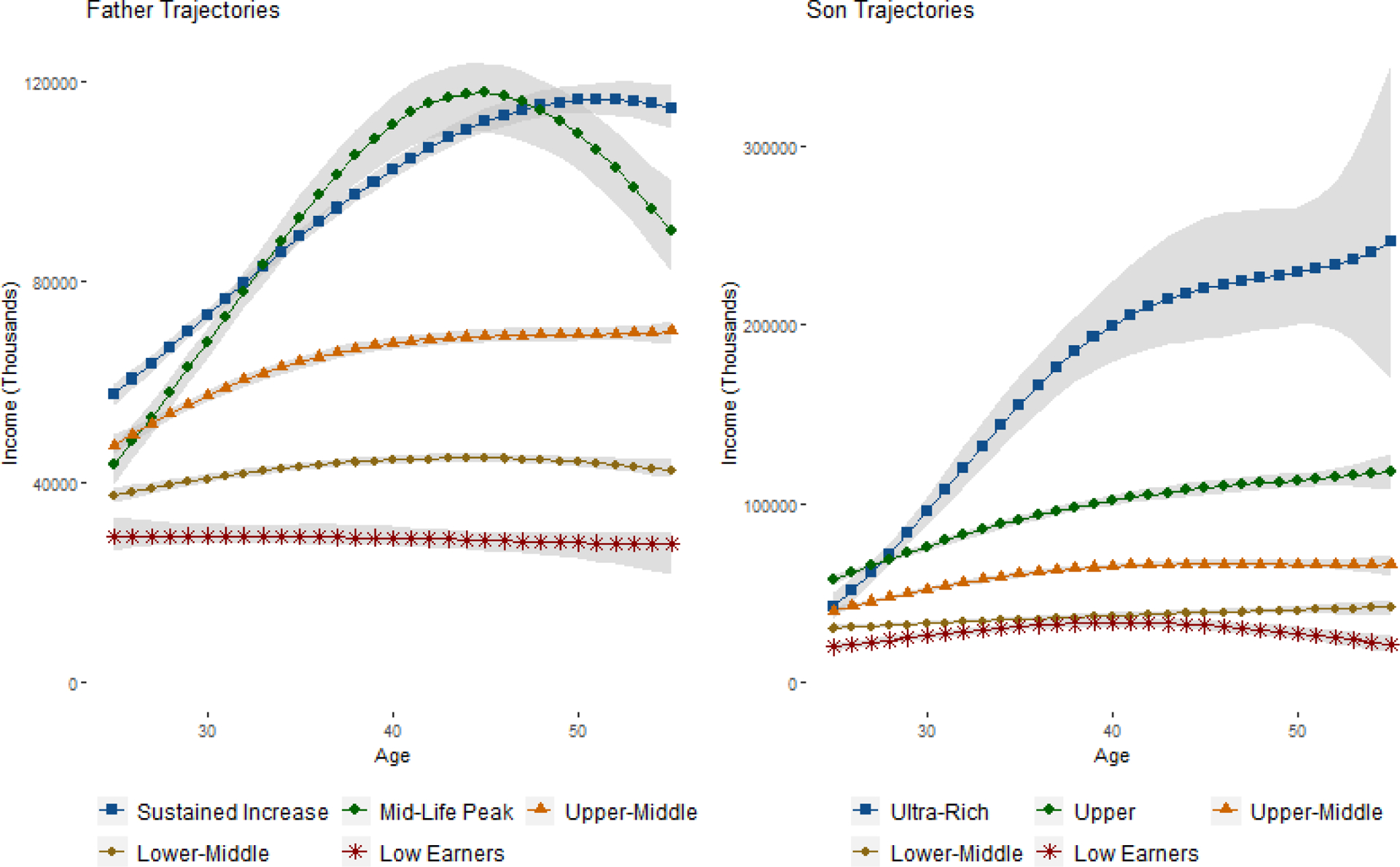
Trajectories for Fathers and Sons in Main Specification with 5 Groups
Note: In accordance with the GBTM literatures, predictive intervals correspond to the mean trajectories in the group. This incorporates uncertainty in the β parameters, but does not incorporate the variance from the σ2 parameters.
We use the same hyperparameters that we used in the simulation in order to be noninformative. Specifically, for each , gk = nk for each k, and βk,0 = βk,MLE for each k. In order to ensure that our MCMC algorithm did not converge to a local optimum, we ran multiple short chains using dispersed starting values and chose the initial settings which maximized the log-likelihood. We then ran the chain for 25,000 iterations and discarded the first 5,000 draws as the burn-in period. The total estimation time was 12 minutes.
Table 4 contains parameter estimates and inclusion probabilities for the linear, square, and cubic terms. Intercepts were forced into the model for each latent group. The model averaging procedure included the linear age term 100% of the time in each group with the exception of Low-Earning fathers. Here the linear term is only included in half of the models, indicating members of this group earn low wages consistently throughout their lives. Squared terms were included in nearly 100% of the iterations for eight of the ten groups. The other two groups contained squared terms in 18.9% and 47.6% of the iterations, respectively. The inclusion of cubic terms was more dispersed. Six of the ten groups included cubics in fewer than 11% of the iterations, while the remaining four groups included cubics in at least 77% of the iterations. It should be noted that due to the scale of the data, the cubic coefficients are sometimes indistinguishable from zero using three significant digits. Nonetheless, it is evident from Figure 5 they are sufficiently large to visibly alter several of the trajectories. To illustrate the mechanics of model averaging, the first 1000 samples from the posterior of the cubic coefficient for the sons’ “Upper” group are plotted in Figure 4. According to Table 4, this coefficient was selected out of 22% of models, which is illustrated by the cluster of zeros dispersed throughout the chain.
Table 4.
Group-Based Dual Trajectory Model Selection Coefficients from PSID Model
| Father | Son | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Posterior Median | 95% Credible Interval | Inclusion Probability | Posterior Median | 95% Credible Interval | Inclusion Probability | ||||
| Panel A: Trajectory Coefficients | |||||||||
| Sustained Increase | Intercept | 10.96 | [10.92, 10.99] | -- | Ultra-Rich | Intercept | 10.65 | [10.48, 10.84] | -- |
| Age | 0.05 | [0.05, 0.06] | 100.0% | Age | 0.21 | [0.14, 0.26] | 100.0% | ||
| Age^2 | 0.00 | [−0.00, −0.00] | 100.0% | Age^2 | −0.01 | [−0.01, −0.00] | 100.0% | ||
| Age^3 | 0.00 | [0.00, 0.00] | 3.2% | Age^3 | 0.00 | [0.00, 0.00] | 77.9% | ||
| Sigma | 0.25 | [0.24, 0.26] | -- | Sigma | 0.70 | [0.66, 0.74] | -- | ||
| Mid-Life Peak | Intercept | 10.68 | [10.58,10.76] | -- | Upper | Intercept | 10.96 | [10.91, 11.01] | -- |
| Age | 0.10 | [0.09,0.13] | 100.0% | Age | 0.07 | [0.05, 0.08] | 100.0% | ||
| Age^2 | 0.00 | [−0.00, −0.00] | 100.0% | Age^2 | 0.00 | [−0.00, −0.00] | 100.0% | ||
| Age^3 | 0.00 | [0.00, 0.00] | 9.6% | Age^3 | 0.00 | [0.00, 0.00] | 77.9% | ||
| Sigma | 0.68 | [0.65,0.71] | -- | Sigma | 0.28 | [0.27, 0.30] | -- | ||
| Upper Middle | Intercept | 10.76 | [10.73,10.81] | -- | Upper Middle | Intercept | 10.60 | [10.56, 10.65] | -- |
| Age | 0.05 | [0.03,0.06] | 100.0% | Age | 0.07 | [0.04, 0.08] | 100.0% | ||
| Age^2 | 0.00 | [−0.00, −0.00] | 100.0% | Age^2 | 0.00 | [−0.00, −0.00] | 100.0% | ||
| Age^3 | 0.00 | [0.00, 0.00] | 94.6% | Age^3 | 0.00 | [0.00, 0.00] | 86.7% | ||
| Sigma | 0.23 | [0.22,0.24] | -- | Sigma | 0.33 | [0.32, 0.34] | -- | ||
| Lower Middle | Intercept | 10.53 | [10.49,10.59] | -- | Lower-Middle | Intercept | 10.33 | [10.28,10.38] | |
| Age | 0.02 | [0.01,0.03] | 100.0% | Age | 0.01 | [0.01, 0.03] | 100.0% | ||
| Age^2 | 0.00 | [−0.00,−0.00] | 100.0% | Age^2 | 0.00 | [−0.00, 0.00] | 47.6% | ||
| Age^3 | 0.00 | [0.00, 0.00] | 10.2% | Age^3 | 0.00 | [0.00, 0.00] | 2.6% | ||
| Sigma | 0.37 | [0.36,0.38] | -- | Sigma | 0.39 | [0.38, 0.40] | -- | ||
| Low Earners | Intercept | 10.28 | [10.18, 10.40] | -- | Low Earners | Intercept | 9.90 | [9.77, 10.02] | -- |
| Age | 0.00 | [−0.01,0.03] | 50.0% | Age | 0.07 | [0.05, 0.09] | 100.0% | ||
| Age^2 | 0.00 | [−0.00,0.00] | 18.9% | Age^2 | 0.00 | [−0.00, −0.00] | 100.0% | ||
| Age^3 | 0.00 | [0.00, 0.00] | 0.0% | Age^3 | 0.00 | [0.00, 0.00] | 2.6% | ||
| Sigma | 1.06 | [1.03,1.08] | -- | Sigma | 1.17 | [1.13, 1.21] | -- | ||
| Panel B: Group Probabilities | |||||||||
| Sustained Increase | 15.1% | [12.8%, 17.7%] | -- | Ultra-Rich | 9.9% | [7.7%, 12.3%] | |||
| Mid-Life Peak | 15.0% | [12.6%, 17.7%] | -- | Upper | 16.4% | [13.9%, 19.2%] | |||
| Upper Middle | 21.8% | [19.0%, 24.7%] | -- | Upper Middle | 28.1% | [24.9%, 31.5%] | |||
| Lower Middle | 25.9% | [23.0%, 28.9%] | -- | Lower-Middle | 24.4% | [21.3%, 27.6%] | |||
| Low Earners | 22.0% | [19.2%, 24.9%] | -- | Low Earners | 21.1% | [18.4%, 24.0%] | |||
| Panel C: Transition Probabilities | |||||||||
| Sustained Increase | Ultra-Rich | 38.5% | [28.1%, 49.6%] | -- | Ultra-Rich | Sustained Increase | 25.1% | [17.7%, 33.6%] | |||
| Mid-Life Peak | Ultra-Rich | 25.0% | [15.4%, 35.9%] | -- | Upper | Sustained Increase | 26.6% | [19.2%, 35.1%] | |||
| Upper Middle | Ultra-Rich | 13.5% | [7.2%, 22.0%] | -- | Upper-Middle | Sustained Increase | 26.4% | [18.7%, 35.0%] | |||
| Lower Middle | Ultra-Rich | 14.4% | [7.6%, 23.2%] | -- | Lower-Middle | Sustained Increase | 9.3% | [4.2%, 16.0%] | |||
| Low Earners | Ultra-Rich | 7.5% | [2.3%, 15.4%] | -- | Low Earners | Sustained Increase | 11.7% | [6.6%, 18.4%] | |||
| Sustained Increase | Upper | 24.6% | [17.7%, 32.5%] | -- | Ultra-Rich | Mid-Life Peak | 16.4% | [9.4%, 25.0%] | |||
| Mid-Life Peak | Upper | 17.6% | [10.8%, 25.5%] | -- | Upper | Mid-Life Peak | 19.2% | [11.8%, 28.0%] | |||
| Upper Middle | Upper | 31.0% | [23.2%, 39.5%] | -- | Upper-Middle | Mid-Life Peak | 18.3% | [10.8%, 26.9%] | |||
| Lower Middle |Upper | 17.6% | [11.3%, 24.8%] | -- | Lower-Middle | Mid-Life Peak | 22.1% | [14.8%, 30.6%] | |||
| Low Earners | Upper | 8.5% | [4.2%, 14.4%] | -- | Low Earners | Mid-Life Peak | 23.1% | [16.0%, 31.2%] | |||
| Sustained Increase |Upper Middle | 14.2% | [9.8%, 19.5%] | -- | Ultra-Rich | Upper Middle | 6.1% | [3.2%, 10.2%] | |||
| Mid-Life Peak | Upper Middle | 9.8% | [5.7%, 14.8%] | -- | Upper | Upper Middle | 23.2% | [17.4%, 29.8%] | |||
| Upper Middle | Upper Middle | 25.6% | [20.0%, 31.8%] | -- | Upper-Middle | Upper Middle | 33.1% | [26.0%, 40.4%] | |||
| Lower Middle | Upper Middle | 27.7% | [22.0%, 34.1%] | -- | Lower-Middle | Upper Middle | 22.3% | [16.4%, 29.0%] | |||
| Low Earners | Upper Middle | 22.2% | [16.8%, 28.1%] | -- | Low Earners | Upper Middle | 14.8% | [10.1%, 20.4%] | |||
| Sustained Increase | Lower-Middle | 5.8% | [2.6%, 10.0%] | -- | Ultra-Rich | Lower Middle | 5.5% | [2.8%, 9.1%] | |||
| Mid-Life Peak | Lower-Middle | 13.6% | [9.1%, 19.1%] | -- | Upper | Lower Middle | 11.2% | [7.2%, 16.0%] | |||
| Upper Middle | Lower-Middle | 19.9% | [14.7%, 25.9%] | -- | Upper-Middle | Lower Middle | 30.2% | [23.9%, 37.0%] | |||
| Lower Middle | Lower-Middle | 33.6% | [27.1%, 40.6%] | -- | Lower-Middle | Lower Middle | 31.7% | [25.2%, 38.5%] | |||
| Low Earners | Lower-Middle | 26.5% | [20.4%, 33.2%] | -- | Low Earners | Lower Middle | 21.0% | [15.8%, 27.1%] | |||
| Sustained Increase | Low Earners | 8.4% | [4.7%, 13.3%] | -- | Ultra-Rich | Low Earners | 3.3% | [1.0%, 7.3%] | |||
| Mid-Life Peak | Low Earners | 16.5% | [11.3%, 22.6%] | -- | Upper | Low Earners | 6.3% | [3.1%, 10.9%] | |||
| Upper Middle | Low Earners | 15.3% | [10.4%, 21.2%] | -- | Upper-Middle | Low Earners | 28.3% | [21.5%, 35.7%] | |||
| Lower Middle | Low Earners | 25.7% | [19.6%, 32.9%] | -- | Lower-Middle | Low Earners | 29.4% | [22.6%, 36.8%] | |||
| Low Earners | Low Earners | 33.4% | [26.6%, 40.6%] | -- | Low Earners | Low Earners | 32.0% | [25.4%, 39.3%] | |||
Note: i|j refers to the conditional probability of the father (son) being in latent group j conditional on the son (father) being in latent group i. Sigma is the estimated standard deviation of the residuals. Intercepts are forced into the model and not subject to model selection.
Figure 4:
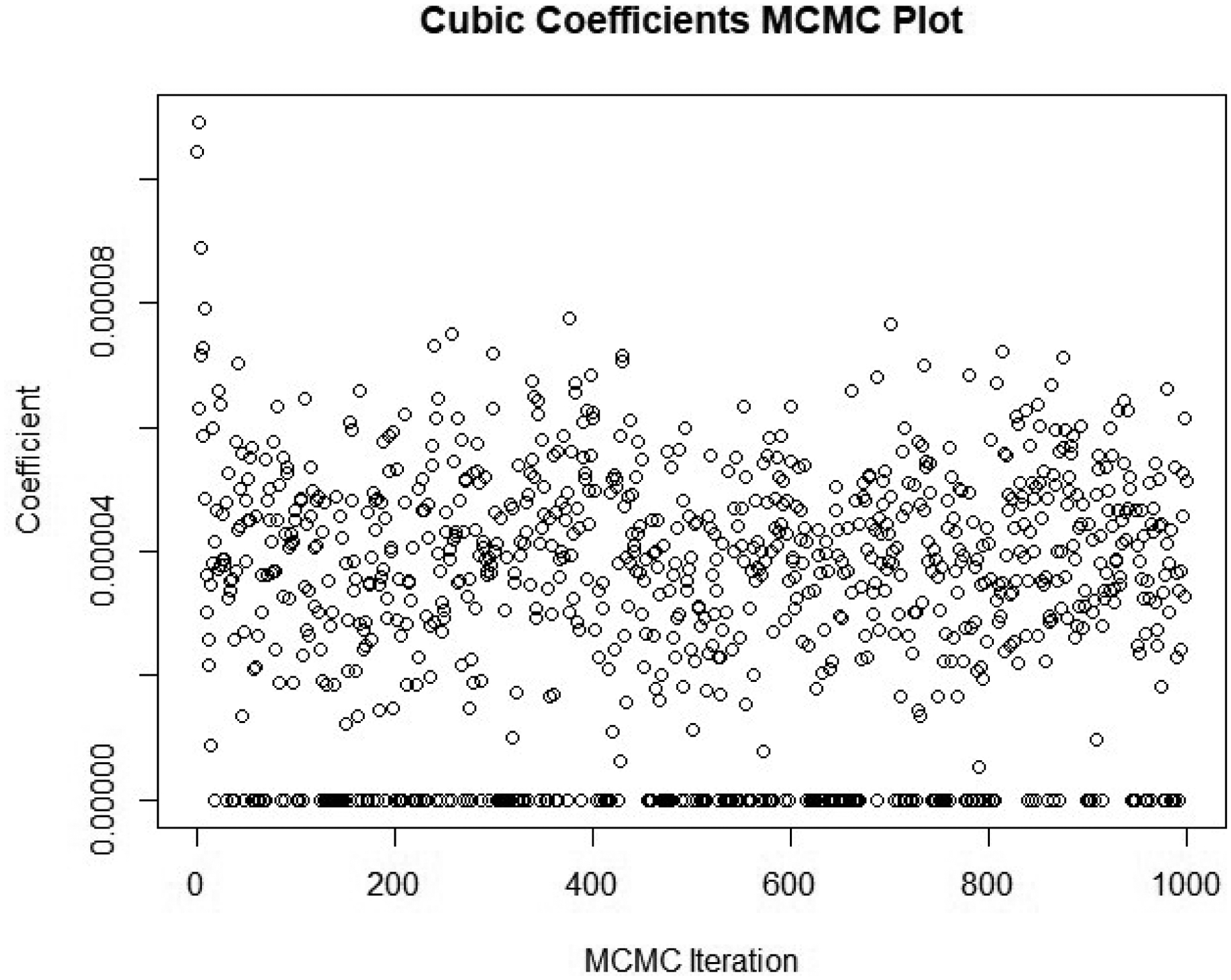
Example of MCMC Samples for Cubic Term with Model Selection
Note: This discretized version of a traceplot corresponds to the first 1,000 MCMC iterations for the cubic coefficient in the son’s “Upper” group. The cluster of zeros show the draws where the cubic term is selected out of the model.
Figure 5 plots the trajectories for both fathers and sons. The trajectories are ordered based on lifetime income, with the blue line group containing the highest lifetime income and the red line group containing the lowest lifetime income. We exponentiate the results in the posterior predictive distribution to transform the data from the log scale to dollars for easier interpretation, a task which would be considerably more difficult in the frequentist paradigm. There are five distinct groups in the fathers’ generation. Marginal probabilities in Table 4 Panel B represent the estimated percentages of fathers in each latent group. The group of “Low Earners” (22%) have both the lowest lifetime income and slightly decreasing income trajectories. The “Lower-Middle” group (25.9%) have the second lowest lifetime income and relatively stable income trajectories over time. The “Upper-Middle” group (21.8%) have higher lifetime income than the previous two groups and stably increasing income trajectories. The “Mid-Life Peak” group (15%) start with lower income than the “Upper-Middle” group, but have a dramatic increase in income in midlife before falling in the final years. The “Sustained Increase” group (15.1%) starts with the highest income and also have sustained increases into late adulthood.
In general, the income levels for sons’ generation are higher than those for the fathers. The shapes of sons’ income trajectories and the group sizes highly resemble those of their fathers’ trajectories for the groups of “Low Earners” (21.1%), “Lower-Middle” (24.4%), and “Upper-Middle” (28.1%). There is no “Mid-Life Peak” group in the sons’ generation, but instead there is a group of wealthy sons who start with the highest income and have stable increases in their income over the life course. There is also a “Ultra-Rich” group, with average annual income above $200,000. Despite the high average income, this group also has the largest estimated variance and the widest predictive intervals (which by convention does not include uncertainty associated with the variance term), suggesting this is somewhat of a catch-all group for varying levels of income above $100,000.
Transition probabilities for the sons in Table 4 Panel C provide the probabilities of sons being in group i conditional on fathers being in group j. We also report transition probabilities for the fathers, though these are less interesting from a theoretical standpoint due to the fathers preceding the sons. These transition probabilities give us clear information on the degree of “social fluidity” in the United States. For example, conditional on fathers being “Low Earners”, the probability of sons being “Low Earners” is 32.0%, whereas the probabilities of sons being “Upper” and “Ultra-Rich” are just 6.3% and 3.3%, respectively. By contract, conditional on fathers being in the “Sustained Increase” group, the probability of sons being “Low Earners” is just 11.7%, whereas the probabilities of sons being “Upper” and “Ultra-Rich” are 26.6% and 25.1%, respectively. We also examined plots of the group membership and posterior probabilities, as well as the transition probabilities, but the distributions were all nearly symmetric around the medians.
Figure 6 visualizes the group-membership probabilities discussed in the paragraph above using a Sankey diagram. The Sankey diagram visualizes the flow of groups from fathers to sons and has the advantage of including all information contained in the marginal, joint, and transition probabilities in a single figure. Starting at the bottom left, the “Low Earners” block takes up about 21% of the left y-axis, corresponding to the 21.1% group-membership probability recorded in Table 4. The five segments flowing out of the “Low Earners” block correspond to the transition probabilities in Table 4 when viewed as proportions of these five segments. The slim segments connecting “Low Earning” fathers to “Ultra Rich” and “Upper Class” sons highlight the dim prospects for upward mobility, as discussed in the preceding paragraph. Each segment can also be viewed as a joint probability of the two connected groups by considering the thickness as a proportion of the entire height of figure. Two joint probabilities can easily be compared through the thickness of the lines. For example, the segment connecting “Sustained Increase” and “Ultra Rich” is about twice as thick as the segment connecting “Sustained Increase” and “Low-Earners,” suggesting Pr(Father = Sustained Increase, Son = Ultra Rich) ≈ 2 × Pr(Father = Sustained Increase, Son = Low-Earners).
Figure 6:
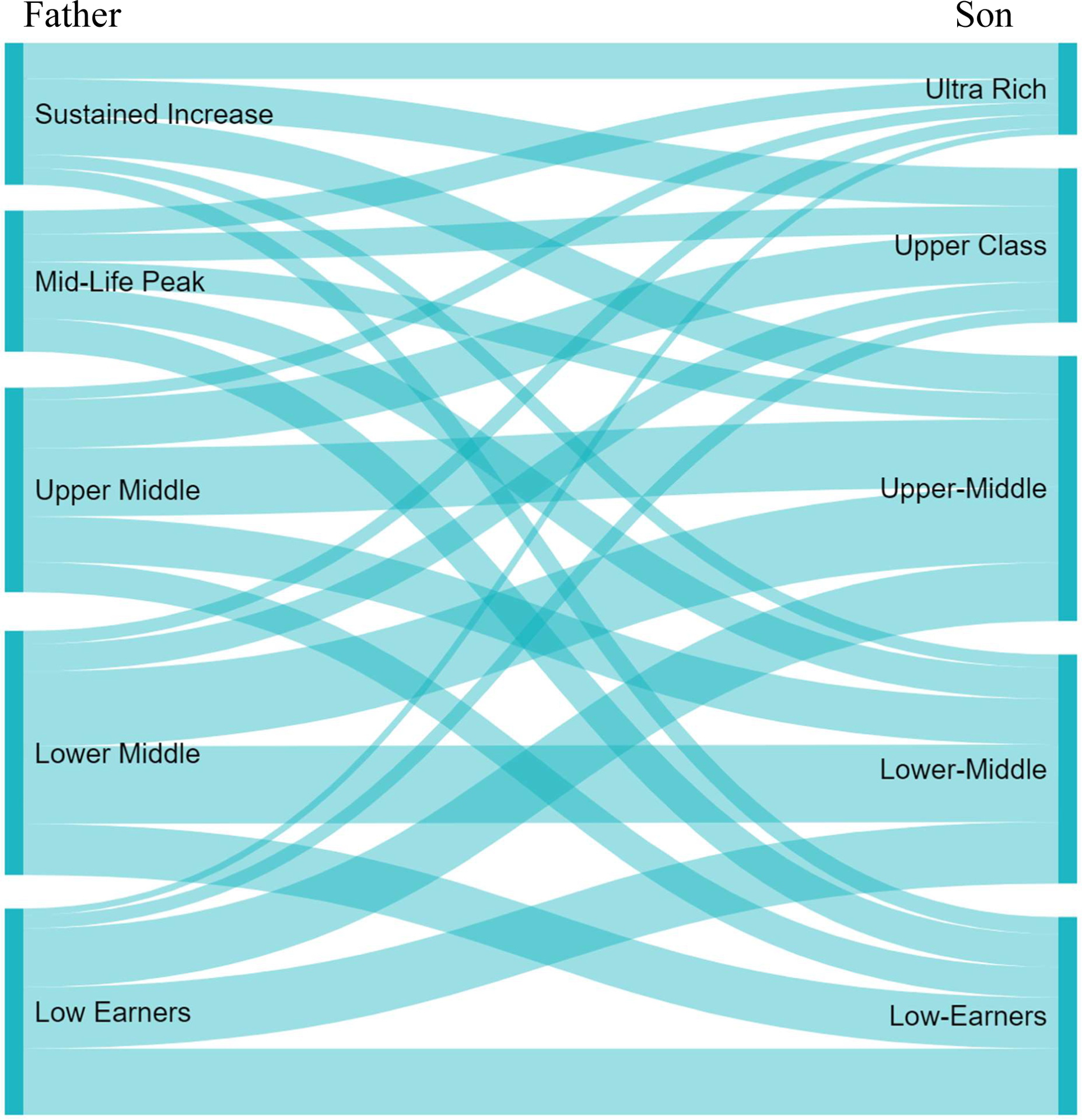
Sankey Diagram of Group Membership Transitions
Note: Groups are labeled in accordance with Table 4. The data used to make this figure come from the reported posterior medians of the group membership probabilities using data from the Panel Study of Income Dynamics 1968–2017. The width of the five blocks on the left correspond to fathers’ group membership probabilities. The width of the five blocks on the right correspond to sons’ group membership probabilities. The width of the five segments emanating out of each block correspond to transition probabilities. The width of a segment as a proportion of the total height of the figure corresponds to the joint probability.
The Sankey diagram convincingly demonstrates the existence of a substantial degree of persistence between the two generations. Children of the highest income fathers transition to the top three income groups for sons at a much higher rate than to the lowest two groups. Conversely, sons from low income fathers rarely attain high income status themselves, mostly topping out as middle income at best. Children of fathers in the middle income groups are more evenly dispersed across the distribution of sons’ incomes.
Overall, the model averaging procedure produced intuitive and rich results for income trajectories of fathers and sons. Moreover, we were able to produce a more robust model which accounted for uncertainty in polynomial degree in a fraction of the time it would have taken to exhaustively search across the model space using a sequence of frequentist models. We searched over a model space consisting of up to third-degree polynomials in order to emulate the typical model space which researchers would consider. However, the model space could be extended to include other transformations such as the logarithm of age with very little additional effort, which may allow researchers to dream up more imaginative trajectories.
5. Conclusion
This paper introduced MCMC algorithms to estimate Bayesian group-based single trajectory and dual trajectory models, and also proposed a Bayesian model averaging procedure for selecting the functional forms of the trajectories. The model averaging procedure has two key advantages over the standard model selection techniques. First, it automatically incorporates uncertainty in model selection. Second, it allows the researcher to forego the time-consuming process of searching over a high-dimensional model space. In addition to providing automatic model selection, Bayesian models also conduct finite sample inference for the posterior distribution without relying on asymptotics and have the ability to produce posterior samples for arbitrary functions of the parameters.
While we hope to have demonstrated the practical utility of the Bayesian approach, practitioners should be aware of the profound implications of the Bayesian approach to both inference and model selection. While the frequentist paradigm leads researchers to search for a single true model which generated the data, the Bayesian approach gives up on this goal entirely, in favor of an approach which embraces uncertainty in the data generation process by modeling the parameters themselves as random variables. In this sense, Bayesian inference should be viewed as an alternative to frequentist inference, rather than a solution to its problems. Future extensions of the frequentist approach are still needed to improve the efficiency of model selection in GBTMs. Although the Bayesian approach can get around this issue more easily, it does not solve the frequentist problem. Both approaches have their unique advantages, and the Bayesian approach introduced in this study is appealing particularly from a practical and computational perspective.
One potential limitation of our procedure, as in other models using the Gibbs sampler, is the tendency for the Markov chain to get stuck in a local optimum. This issue arises in all Bayesian mixture models and also in maximum likelihood estimation of GBTMs. In maximum likelihood estimation, it can potentially be overcome by using multiple starting values (McLachlan and Peel, 2000; Muthén and Muthén, 2012; Hipp and Bauer, 2006). In the Bayesian approach, we recommend the same solution. Researchers can begin the chain from multiple starting values and seeds and settle on the initial conditions which maximize some criterion such as the log-likelihood. However, future research may want to consider ways to reach the global optimum more efficiently.
Future research will also want to consider a broader set of distributions for the outcomes. We restrict our analysis in this paper to variants of normally distributed outcomes. While this encompasses a surprisingly broad class of models with continuous, censored, binary, and ordered outcomes, much of the applied literature has utilized other distributions such as the Poisson and zero-inflated Poisson distributions. The same basic approach used in this paper can apply to any distribution of the outcome, with the caveat that conjugate priors may not always be available. In such cases, parameters can be sampled using other MCMC algorithms such as Metropolis Hastings. Bayesian model averaging can also be performed using other distributions. However, priors will need to be specified such that the marginal likelihood can be efficiently computed in order the make the algorithms feasible. Li and Clyde (2018) provide an overview of g-priors in generalized linear models, which could potentially extend the model averaging framework to a wider class of models. For the time being, maximum likelihood approaches may be more easily applied to models outside the scope of this paper.
Future extensions of the Bayesian model can also look for model-based ways to select the number of latent groups. One potential method would be to place a prior on the number of groups. This can be done in a nonparametric fashion using Dirichlet process priors (Dunson and Herring, 2006; Dunson et al., 2008; Goldston et al., 2016). The main drawback of this approach is that the number of groups is not fixed throughout the MCMC iterations, which makes it difficult to interpret the results. For this reason, Goldston et al. (2016) adopt a multistage process where they fit a Dirichlet process model in stage one and then use the mean number of groups in stage two. Another drawback of a fully non-parametric approach is that it inhibits the researchers ability to guide the choice through subject matter expertise. However, Bayesian nonparametrics can sidestep this issue to some extent because the researcher can impose a strong prior to limit the number of groups in large datasets.
Finally, although the GBTM has many advantages, there are other methods that allow researchers to model trajectories. We see all these methods as complementary rather than competing. The choice of methods should depend on research questions and the plausibility of model assumptions in specific cases. Moreover, researchers are encouraged to verify their substantive results using multiple trajectory models to better understand the uncertainty (Warren et al., 2015; Feldman et al., 2009).
Acknowledgments
We are grateful to Kenneth C. Land, Scott M. Lynch, Xi Song. Xiang Zhou, Adrian Raftery, Andrew Gelman, and three anonymous reviewers for their helpful suggestions. We thank Anna Guo for her excellent research assistance. Send correspondence to Emma Zang, Department of Sociology, Yale University, 493 College Street, New Haven, CT 06511.
An earlier version of this paper was presented at the American Sociological Association annual meeting in Philadelphia, 2018. We posted a working paper Zang, E., & Max, J. (2019). Bayesian Estimation and Model Selection in Group-Based Trajectory Models. Available at Social Science Research Network 3315029.
The collection of the PSID data used in this study was partly supported by the National Institutes of Health under grant number R01 HD069609 and R01 AG040213, and the National Science Foundation under award numbers SES 1157698 and 1623684.
APPENDIX
Appendix 1: Extensions to Binary, Ordered, and Censored Normal Outcomes
The Gibbs sampler described for continuous outcomes can be extended to model trajectories for binary, ordered, and censored normal outcomes. This is accomplished by modeling each observed outcome yi as a function of a latent variable which is normally distributed conditional on the data and model parameters. Upon sampling this latent variable in the MCMC algorithm, each of these models can be reduced to the Gibbs sampler described above where is used in place of yi.
Frequentist GBTMs use logistic regression as the standard model for binary outcomes. For Bayesian inference, it will be more convenient to adopt the probit model,
where Φ(·) is the standard normal CDF. The probit model can be equivalently stated using latent variables:
| (16a) |
| (16b) |
where is not observed. Note that in a probit GBTM, the variance term is fixed to one and therefore does not need to be sampled in the Gibbs sampler.
The benefit of using probit regression rather than logistic regression is that probit regression reduces to linear regression on the latent variable. Therefore the Gibbs sampler derived in the previous section could be directly applied if was observed. While this is not the case, Albert and Chib (1993) point out that can be drawn from its conditional distribution in each iteration of the Gibbs sampler. Upon sampling each , the ci’s can be sampled conditional on rather than yi and the βk’s can be sampled conditional on rather than yk. The conditional distribution of is
| (17) |
where is a truncated normal distribution. The distribution is truncated above at 0 if yit = 0 and truncated below at 0 if yit = 1.
Albert and Chib (1993) also generalize their model to develop a Gibbs sampler for the ordered probit model which is appropriate when the outcome is discrete and ordered. Although not common in GBTM applications, it can sometimes be appropriate as a substitute for the commonly used Poisson-distributed GBTM for count data. Poisson regression requires more complex MCMC procedures and will be more difficult to integrate into the Bayesian model selection framework discussed later, leaving the ordered probit as a more tractable alternative.
Chib (1992) shows how to use essentially the same strategy when the outcome follows a censored normal distribution. If the outcome is bounded by Smin and Smax, then the latent variable representation is
| (18a) |
| (18b) |
where is once again not observed. Like the probit model, can be drawn in the Gibbs sampler which will reduce the problem to the linear regression case discussed earlier. If yit ∈ (Smin, Smax), then . Otherwise, it can be drawn from a truncated normal distribution:
| (19) |
Appendix 2: Full Conditionals
-
The full conditional distributions in the Bayesian single trajectory model can all be solved for by applying Bayes theorem. The results are:
(20a) (20b) (20c)
where Xk and yk are the design matrix and outcomes, respectively, for the data in group k, and is the sum of squared residuals. We use to denote the number of observations in the data.(20d) The conditional distributions described above are standard conjugate prior results, but still warrant some discussion. The conditional distribution of ci is a direct application of Bayes’ theorem for each group probability. The distribution for π highlights the interpretation of the α parameters as psuedo-counts, since each αi plays the same role in the conditional distribution as the number of units corresponding to group i. It αi = 1 for each i, the prior is as if the researcher had previously observed one unit belonging to each of the K categories. The full conditionals for βk and σ2 are standard results from Bayesian estimation of linear regression models (Hoff, 2009). ν0 plays the same role in the conditional as the sample size, and so can be thought of as a “prior sample size.” Similarly, corresponds to the prior variance of the outcome. The β, meanwhile, end up looking like the OLS estimate if Σ is sufficiently large.
- The full conditional distributions with the conditioning variables suppressed in the Bayesian dual trajectory model are:
(21a) (21b) (21c)
The full conditionals for the βk’s and σ’s are the same as in the single trajectory case, but using data restricted to their respective series of measurements. The explanations for these equations are largely the same as the single-trajectory case, only now the group membership conditional distributions require a more complicated application of Bayes’ rule in order to account for the dependence between the two series. Proofs for the full conditionals of and are below:(21d)
Similarly,
where we use that P(A|B, C) P(B|C) = P(A, B|C) = P(B|A, C) P(A|C). -
The Gibbs sampler for the Bayesian Model Averaging model is:
(22a) (22b) (22c) (22d) (22e) (22f) (22g) (22h)
where SSRk(zk) is the sum of squared residuals for group k in the maximum likelihood model restricted to the covariates selected by zk. Hoff (2009) suggests sampling in a random order over d.(22i) Most of these equations are similar to the models discussed above. However, the σ2 and β terms are slightly different. Compared with the previous models with proper priors on the variances, we see that the σ2 conditional corresponds to a prior sample size of zero. Meanwhile, the β has a conditional mean as a compromise between the prior mean and the MLE and a conditional variance proportional to the variance of the MLE.
Appendix 3: Label Switching
A potential problem of the Bayesian approach to mixture models is the so-called “label-switching problem” (Celeux et al., 2000; Frühwirth-Schnatter, 2006). Mixture models are not identified in the sense that the component labels have no inherent meaning. For example, suppose data is generated from a mixture of two normal distributions where the “first” mixture component is and the “second” mixture component is . This is equivalent to a model where the “first” mixture component is and the “second” mixture component is . The labels “first” and “second” are simply constructs to help researchers conceptualize and discuss the model. The implication is that a mixture model with K components will have K! symmetric posterior modes, one for every possible permutation of the group labels.
In practice, the Gibbs sampler may switch between these modes as it navigates the posterior, causing the draws from a given component’s parameter to switch to a different component’s parameter mid-chain and rendering the draws meaningless. In mixture model applications to density estimation, where the goal is to estimate the posterior predictive probability of a new observation conditional on the existing data, label switching can often be ignored as the predictive distribution is unaffected. However, in applications which require the researcher to attach meaning to the mixture components, as in GBTMs, this can potentially cause a problem. The typical solution is to “post process” the draws from the posterior distribution (Stephens, 2000; Papastamoulis, 2016).
Label-switching should tend to be less of an issue in the dual trajectory model relative to the single-trajectory model. The transition probabilities place so much structure on the data that navigating between posterior modes is only possible by navigating through a region of the posterior with extremely low density. Intuitively, if one group switched labels, it would make the labels in the other group extremely unlikely conditional on the group transition probabilities.
Researchers can easily detect label switching by examining the trace plots for sudden swaps of parameter values in two or more groups (Jasra et al., 2005). We did not experience any label switching for the models programmed in this paper even when running the chains for 200,000 iterations, and using both observational and simulated data. This suggests that the parameters associated with the different latent groups were sufficiently distinct from one another that label switching would have required the Gibbs sampler to traverse very sparse regions of the parameter space (De Haan-Rietdijk et al., 2017). However, researchers applying this method ought to be aware of the issue.
Appendix Figure 1a:
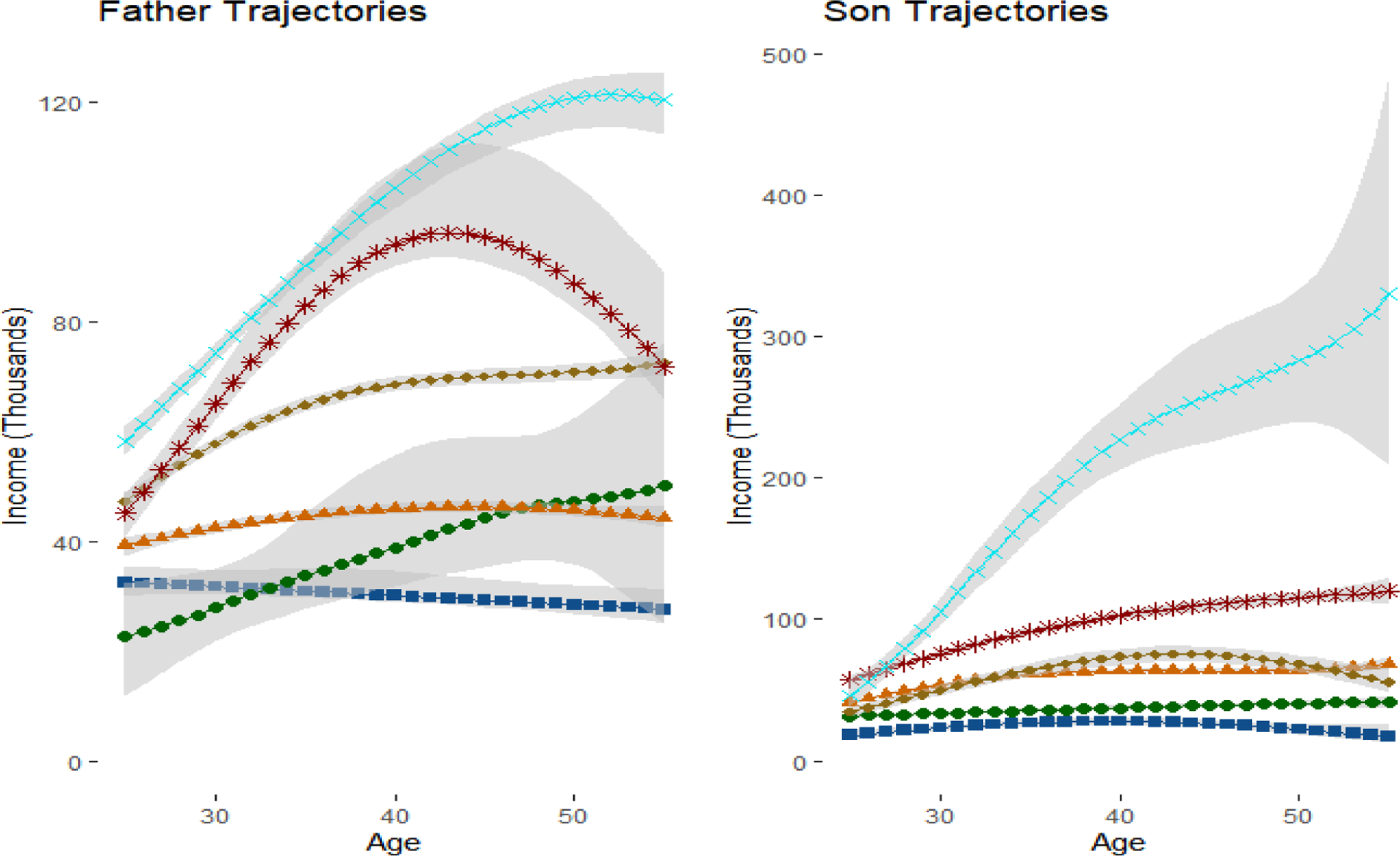
Trajectories for Fathers and Sons with 6 Groups
Appendix Figure 1b:
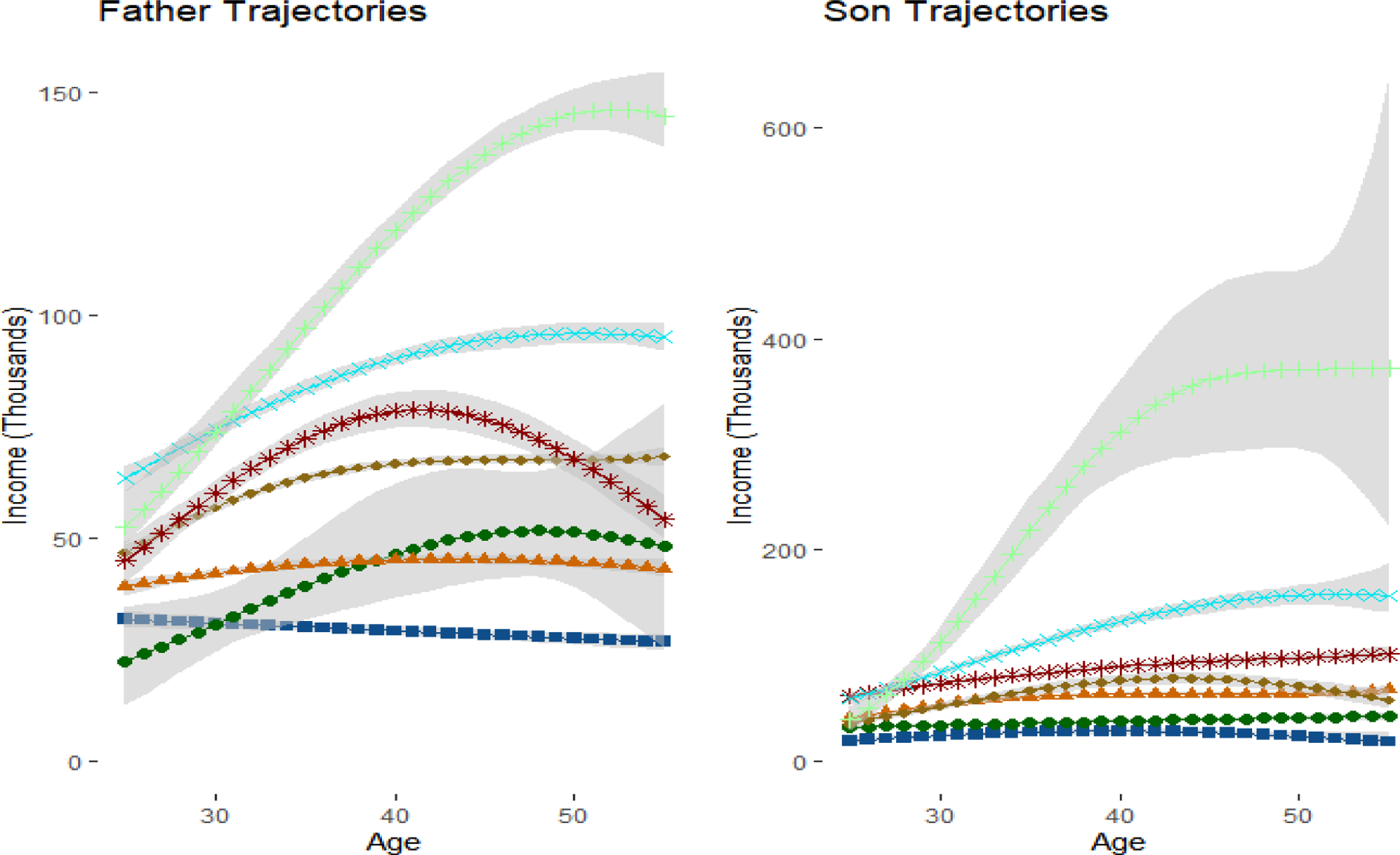
Trajectories for Fathers and Sons with 7 Groups
Footnotes
In single trajectory models where the researcher searches through polynomials up to degree d and the number of latent groups between 2 and K, there are possible models to choose, if the order of groups does not matter.
Functional forms may be additionally constrained by the nature of the data. In short panels, limited degrees of freedom will push researchers toward low-degree polynomials. In long panels, smooth functions may have difficulty adequately modeling the trajectories. In such situations, autoregressive models present a viable alternative. These methods are beyond the scope of this paper.
We have verified on both simulated and observational data that the maximum likelihood estimates and associated standard errors coincide with the posterior means and standard deviations, respectively, typically to several significant digits. Table 1 summarizes one such sample.
Researchers willing to break conjugacy may find improvements from other priors such as half-normal or half-Cauchy. This will require sampling the variance parameter using a more complex MCMC procedure. In our experience, the inverse-gamma prior work very well for the sample sizes and parameter values typical of GBTM models. Of course, we can make no guarantees under all circumstances. Researchers should validate their models and be willing to alter prior distributions if the resulting posteriors are problematic.
Note that this runs afoul of the standard practice for g-priors, as explained in Li and Clyde (2018). However, the standard practice involves standardizing X(zk) so that each column has mean zero and is orthogonal to a vector of 1’s. This would be difficult to do since we do not know which observations belong to group k a-priori. Without such standardization, our simulations suggested that groups with large intercepts tend to yield posterior distributions of centered well above the true values. As a result, we reluctantly favor using the MLE as the prior mean.
Contributor Information
Emma Zang, Department of Sociology, Yale University.
Justin T. Max, Capital One Financial Corporation
REFERENCES
- Albert James H and Chib Siddhartha. 1993. “Bayesian Analysis of Binary and Poly-chotomous Response Data.” Journal of the American Statistical Association 88:669–679. [Google Scholar]
- Berger James. 2006. “The Case for Objective Bayesian Analysis.” Bayesian Analysis 1:385–402. [Google Scholar]
- Biernacki Christophe, Celeux Gilles, and Govaert Gérard. 2000. “Assessing a Mixture Model for Clustering with the Integrated Completed Likelihood.” IEEE Transactions on Pattern Analysis and Machine Intelligence 22:719–725. [Google Scholar]
- Björkenstam Emma, Cheng Siwei, Burström Bo, Pebley Anne R, Björkenstam Charlotte, and Kosidou Kyriaki. 2017. “Association Between Income Trajectories in Childhood and Psychiatric Disorder: A Swedish Population-Based Study.” Journal of Epidemiology and Community Health 71:648–654. [DOI] [PubMed] [Google Scholar]
- Block Carolyn Rebecca, Blokland Arjan A. J., Van der Werff Cornelia, Van Os Rianne, and Nieuwbeerta Paul. 2010. “Long-Term Patterns of Offending in Women.” Feminist Criminology 5:73–107. [Google Scholar]
- Brame Bobby, Nagin Daniel S, and Tremblay Richard E. 2001. “Developmental Trajectories of Physical Aggression from School Entry to Late Adolescence.” The Journal of Child Psychology and Psychiatry and Allied Disciplines 42:503–512. [PubMed] [Google Scholar]
- Brame Robert, Nagin Daniel S, and Wasserman Larry. 2006. “Exploring Some Analytical Characteristics of Finite Mixture Models.” Journal of Quantitative Criminology 22:31–59. [Google Scholar]
- Brooks Steve, Gelman Andrew, Jones Galin, and Meng Xiao-Li. 2011. Handbook of Markov Chain Monte Carlo. CRC press. [Google Scholar]
- Celeux Gilles, Hurn Merrilee, and Robert Christian P. 2000. “Computational and Inferential Difficulties with Mixture Posterior Distributions.” Journal of the American Statistical Association 95:957–970. [Google Scholar]
- Cheng Siwei, Kosidou Kyriaki, Bo Burström Charlotte Björkenstam, Pebley Anne R, and Björkenstam Emma. 2020. “Precarious Childhoods: Childhood Family Income Volatility and Mental Health in Early Adulthood.” Social Forces, forthcoming. [Google Scholar]
- Chib Siddhartha. 1992. “Bayes inference in the Tobit censored regression model.” Journal of Econometrics 51:79–99. [Google Scholar]
- Côté Sylvana M, Boivin Michel, Liu Xuecheng, Nagin Daniel S, Zoccolillo Mark, and Tremblay Richard E. 2009. “Depression and Anxiety Symptoms: Onset, Developmental Course and Risk Factors During Early Childhood.” Journal of Child Psychology and Psychiatry 50:1201–1208. [DOI] [PubMed] [Google Scholar]
- Curran Patrick, Obeidat Khawla, and Losardo Diane. 2010. “Twelve Frequently Asked Questions About Growth Curve Modeling.” Journal of Cognition and Development 11:121–136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day David V and Sin Hock-Peng. 2011. “Longitudinal Tests of an Integrative Model of Leader Development: Charting and Understanding Developmental Trajectories.” The Leadership Quarterly 22:545–560. [Google Scholar]
- De Haan-Rietdijk S, Peter Kuppens C.S. Bergeman, Sheeber Lisa B., Allen Nicholas B., and Hamaker Ellen L.. 2017. “On the Use of Mixed Markov Models for Intensive Longitudinal Data.” Multivariate Behavioral Research 52:747–767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dekker Marielle C, Ferdinand Robert F, Van Lang Natasja DJ, Bongers Ilja L, Van Der Ende Jan, and Verhulst Frank C. 2007. “Developmental Trajectories of Depressive Symptoms from Early Childhood to Late Adolescence: Gender Differences and Adult Outcome.” Journal of Child Psychology and Psychiatry 48:657–666. [DOI] [PubMed] [Google Scholar]
- Depaoli Sarah. 2013. “Mixture Class Recovery in GMM Under Varying Degrees of Class Separation: Frequentist Versus Bayesian Estimation.” Psychological Methods 18:186. [DOI] [PubMed] [Google Scholar]
- Dunson David B and Herring Amy H. 2006. “Semiparametric Bayesian Latent Trajectory Models.” Proceedings ISDS Discussion Paper 16. [Google Scholar]
- Dunson David B, Herring Amy H, and Siega-Riz Anna Maria. 2008. “Bayesian Inference on Changes in Response Densities over Predictor Clusters.” Journal of the American Statistical Association 103:1508–1517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elliott Michael R., Gallo Joseph J., Ten Have Thomas R., Bogner Hillary R., and Katz Ira R.. 2005. “Using a Bayesian Latent Growth Curve Model to Identify Trajectories of Positive Affect and Negative Events Following Myocardial Infarction.” Biostatistics 6:119–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman Betsy J, Masyn Katherine E, and Conger Rand D. 2009. “New Approaches to Studying Problem Behaviors: A Comparison of Methods for Modeling Longitudinal, Categorical Adolescent Drinking Data.” Developmental Psychology 45:652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fountain Christine, Winter Alix S, and Bearman Peter S. 2012. “Six Developmental Trajectories Characterize Children with Autism.” Pediatrics 129:e1112–e1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frankfurt Sheila, Frazier Patricia, Syed Moin, and Jung Kyoung Rae. 2016. “Using Group-Based Trajectory and Growth Mixture Modeling to Identify Classes of Change Trajectories.” The Counseling Psychologist 44:622–660. [Google Scholar]
- Frühwirth-Schnatter Sylvia. 2006. Finite Mixture and Markov Switching Models. Springer Science & Business Media. [Google Scholar]
- Garrett Elizabeth S and Zeger Scott L. 2000. “Latent Class Model Diagnosis.” Biometrics 56:1055–1067. [DOI] [PubMed] [Google Scholar]
- Gelman Andrew. 2006. “Prior Distributions for Variance Parameters in Hierarchical Models (Comment on Article by Browne and Draper).” Bayesian Analysis 1:515–534. [Google Scholar]
- Geman Stuart and Geman Donald. 1984. “Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images.” IEEE Transactions on Pattern Analysis and Machine Intelligence PAMI-6:721–741. [DOI] [PubMed] [Google Scholar]
- Gill Thomas M, Gahbauer Evelyne A, Han Ling, and Allore Heather G. 2010. “Trajectories of Disability in the Last Year of Life.” New England Journal of Medicine 362:1173–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldstein Harvey. 1987. Multilevel Models in Education and Social Research. London: Oxford University Press. [Google Scholar]
- Goldston David B, Erkanli Alaattin, Daniel Stephanie S, Heilbron Nicole, Weller Bridget E, and Doyle Otima. 2016. “Developmental Trajectories of Suicidal Thoughts and Behaviors from Adolescence Through Adulthood.” Journal of the American Academy of Child & Adolescent Psychiatry 55:400–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayford Sarah R. 2009. “The Evolution of Fertility Expectations over the Life Course.” Demography 46:765–783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heckman James and Singer Burton. 1984. “A Method for Minimizing the Impact of Distributional Assumptions in Econometric Models for Duration Data.” Econometrica: Journal of the Econometric Society pp. 271–320. [Google Scholar]
- Hipp John R and Bauer Daniel J. 2006. “Local Solutions in the Estimation of Growth Mixture Models.” Psychological Methods 11:36. [DOI] [PubMed] [Google Scholar]
- Hoff Peter D. 2009. A First Course in Bayesian Statistical Methods. Springer Science & Business Media. [Google Scholar]
- Hsu Hui-Chuan and Jones Bobby L. 2012. “Multiple Trajectories of Successful Aging of Older and Younger Cohorts.” The Gerontologist 52:843–856. [DOI] [PubMed] [Google Scholar]
- Jasra Ajay, Holmes Chris C, and Stephens David A. 2005. “Markov Chain Monte Carlo Methods and the Label Switching Problem in Bayesian Mixture Modeling.” Statistical Science 20:50–67. [Google Scholar]
- Jester Jennifer M, Nigg Joel T, Buu Anne, Puttler Leon I, Glass Jennifer M, Heitzeg Mary M, Fitzgerald Hiram E, and Zucker Robert A. 2008. “Trajectories of Childhood Aggression and Inattention/Hyperactivity: Differential Effects on Substance Abuse in Adolescence.” Journal of the American Academy of Child & Adolescent Psychiatry 47:1158–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson David S., Freedman Vicki A., Sastry Narayan, McGonagle Katherine A, Brown Charles, Fomby Paula, Pfeffer Fabian R., Schoeni Robert F., and Stafford Frank P.. 2020. “Panel Study of Income Dynamics, public use dataset.” Produced and distributed by the Survey Research Center, Institute for Social Research, University of Michigan, Ann Arbor, MI: https://psidonline.isr.umich.edu/default.aspx. [Google Scholar]
- Jones Bobby L and Nagin Daniel S. 2007. “Advances in Group-Based Trajectory Modeling and an SAS Procedure for Estimating Them.” Sociological Methods & Research 35:542–571. [Google Scholar]
- Jones Bobby L and Nagin Daniel S. 2013. “A Note on a Stata Plugin for Estimating Group-Based Trajectory Models.” Sociological Methods & Research 42:608–613. [Google Scholar]
- Jones Bobby L, Nagin Daniel S, and Roeder Kathryn. 2001. “A SAS Procedure Based on Mixture Models for Estimating Developmental Trajectories.” Sociological Methods & Research 29:374–393. [Google Scholar]
- Klijn Sven L, Weijenberg Matty P, Lemmens Paul, van den Brandt Piet A, and Lima Passos Valéria. 2017. “Introducing the Fit-Criteria Assessment Plot–A Visualisation Tool to Assist Class Enumeration in Group-Based Trajectory Modelling.” Statistical Methods in Medical Research 26:2424–2436. [DOI] [PubMed] [Google Scholar]
- Lee Kuo-Jung, Chen Ray-Bing, and Wu Ying Nian. 2016. “Bayesian Variable Selection for Finite Mixture Model of Linear Regressions.” Computational Statistics & Data Analysis 95:1–16. [Google Scholar]
- Li Yingbo and Clyde Merlise A. 2018. “Mixtures of g-Priors in Generalized Linear Models.” Journal of the American Statistical Association 113:1828–1845. [Google Scholar]
- Li Yibing and Lerner Richard M. 2011. “Trajectories of School Engagement During Adolescence: Implications for Grades, Depression, Delinquency, and Substance Use.” Developmental Psychology 47:233. [DOI] [PubMed] [Google Scholar]
- Li Yunfeng, Zhou Huanxue, Cai Beilei, Kristijan H Kahler Haijun Tian, Gabriel Susan, and Arcona Steve. 2014. “Group-Based Trajectory Modeling to Assess Adherence to Biologics among Patients with Psoriasis.” ClinicoEconomics and Outcomes Research: CEOR 6:197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang Feng, Paulo Rui, Molina German, Clyde Merlise A, and Berger Jim O. 2008. “Mixtures of g Priors for Bayesian Variable Selection.” Journal of the American Statistical Association 103:410–423. [Google Scholar]
- Loughran Tom and Nagin Daniel S. 2006. “Finite Sample Effects in Group-Based Trajectory Models.” Sociological Methods & Research 35:250–278. [Google Scholar]
- McArdle John J. 1988. “Dynamic But Structural Equation Modeling of Repeated Measures Data.” In Handbook of Multivariate Experimental Psychology, pp. 561–614. Springer. [Google Scholar]
- McArdle John J and Epstein David. 1987. “Latent Growth Curves within Developmental Structural Equation Models.” Child Development 58:110–133. [PubMed] [Google Scholar]
- McLachlan Geoffrey and Peel David. 2004. Finite Mixture Models. John Wiley & Sons. [Google Scholar]
- McLachlan Geoffrey J and Peel David. 2000. Finite Mixture Models. New York: Wiley. [Google Scholar]
- Meredith William and Tisak John. 1990. “Latent Curve Analysis.” Psychometrika 55:107–122. [Google Scholar]
- Modi Avani C, Cassedy Amy E, Quittner Alexandra L, Accurso Frank, Sontag Marci, Koenig Joni M, and Ittenbach Richard F. 2010. “Trajectories of Adherence to Airway Clearance Therapy for Patients with Cystic Fibrosis.” Journal of Pediatric Psychology 35:1028–1037. [DOI] [PubMed] [Google Scholar]
- Modi Avani C, Rausch Joseph R, and Glauser Tracy A. 2011. “Patterns of Nonadherence to Antiepileptic Drug Therapy in Children with Newly Diagnosed Epilepsy.” The Journal of the American Medical Association 305:1669–1676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mora Pablo A, Bennett Ian M, Elo Irma T, Mathew Leny, Coyne James C, and Culhane Jennifer F. 2009. “Distinct Trajectories of Perinatal Depressive Symptomatology: Evidence from Growth Mixture Modeling.” American Journal of Epidemiology 169:24–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthén Bengt. 2004. “Latent Variable Analysis.” The Sage Handbook of Quantitative Methodology for the Social Sciences 345:106–109. [Google Scholar]
- Muthén Bengt and Shedden Kerby. 1999. “Finite Mixture Modeling with Mixture Outcomes Using the EM Algorithm.” Biometrics 55:463–469. [DOI] [PubMed] [Google Scholar]
- Muthén Linda K and Muthén Bengt O. 2012. MPlus: Statistical Analysis with Latent Variables–User’s Guide. Citeseer. [Google Scholar]
- Nagin Daniel. 2005. Group-Based Modeling of Development. Harvard University Press. [Google Scholar]
- Nagin Daniel S. 1999. “Analyzing Developmental Trajectories: A Semiparametric, Group-Based Approach.” Psychological Methods 4:139. [DOI] [PubMed] [Google Scholar]
- Nagin Daniel S, Jones Bobby L, Passos Valéria Lima, and Tremblay Richard E. 2018. “Group-Based Multi-Trajectory Modeling.” Statistical Methods in Medical Research 27:2015–2023. [DOI] [PubMed] [Google Scholar]
- Nagin Daniel S and Odgers Candice L. 2010. “Group-Based Trajectory Modeling in Clinical Research.” Annual Review of Clinical Psychology 6:109–138. [DOI] [PubMed] [Google Scholar]
- Nagin Daniel S and Piquero Alex R. 2010. “Using the Group-Based Trajectory Model to Study Crime Over the Life Course.” Journal of Criminal Justice Education 21:105–116. [Google Scholar]
- Nagin Daniel S and Tremblay Richard E. 2001. “Analyzing Developmental Trajectories of Distinct but Related Behaviors: A Group-Based Method.” Psychological Methods 6:18. [DOI] [PubMed] [Google Scholar]
- Nagin Daniel S and Tremblay Richard E. 2005. “Further Reflections on Modeling and Analyzing Developmental Trajectories: A Response to Maughan and Raudenbush.” The Annals of the American Academy of Political and Social Science 602:145–154. [Google Scholar]
- Odgers Candice L, Moffitt Terrie E, Broadbent Jonathan M, Dickson Nigel, Hancox Robert J, Harrington Honalee, Poulton Richie, Sears Malcolm R, Thomson W Murray, and Caspi Avshalom. 2008. “Female and Male Antisocial Trajectories: From Childhood Origins to Adult Outcomes.” Development and Psychopathology 20:673–716. [DOI] [PubMed] [Google Scholar]
- Papastamoulis Panagiotis. 2016. “label.switching: An R Package for Dealing with the Label Switching Problem in MCMC Outputs.” Journal of Statistical Software 69. [Google Scholar]
- Pepler Debra, Jiang Depeng, Craig Wendy, and Connolly Jennifer. 2008. “Developmental Trajectories of Bullying and Associated Factors.” Child Development 79:325–338. [DOI] [PubMed] [Google Scholar]
- Petts Richard J. 2009. “Trajectories of Religious Participation from Adolescence to Young Adulthood.” Journal for the Scientific Study of Religion 48:552–571. [Google Scholar]
- Piquero Alex R. 2008. “Taking Stock of Developmental Trajectories of Criminal Activity over the Life Course.” In The Long View of Crime: A Synthesis of Longitudinal Research, pp. 23–78. Springer. [Google Scholar]
- Polson Nicholas G, Scott James G, and Windle Jesse. 2013. “Bayesian Inference for Logistic Models Using Pólya–Gamma Latent Variables.” Journal of the American Statistical Association 108:1339–1349. [Google Scholar]
- Raftery Adrian E, Madigan David, and Hoeting Jennifer A. 1997. “Bayesian Model Averaging for Linear Regression Models.” Journal of the American Statistical Association 92:179–191. [Google Scholar]
- Raudenbush Stephen W and Bryk Anthony S. 2002. Hierarchical Linear Models: Applications and Data Analysis Methods. SAGE Publications. [Google Scholar]
- Stephens Matthew. 2000. “Dealing with Label Switching in Mixture Models.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 62:795–809. [Google Scholar]
- van de Schoot Rens, Sijbrandij Marit, Depaoli Sarah, Sonja D Winter Miranda Olff, and Van Loey Nancy E. 2018. “Bayesian PTSD-Trajectory Analysis with Informed Priors Based on a Systematic Literature Search and Expert Elicitation.” Multivariate Behavioral Research 53:267–291. [DOI] [PubMed] [Google Scholar]
- Wang Bo, Deveaux Lynette, Li Xiaoming, Marshall Sharon, Chen Xinguang, and Stanton Bonita. 2014. “The Impact of Youth, Family, Peer and Neighborhood Risk Factors on Developmental Trajectories of Risk Involvement from Early Through Middle Adolescence.” Social Science & Medicine 106:43–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren John Robert, Luo Liying, Halpern-Manners Andrew, Raymo James M, and Palloni Alberto. 2015. “Do Different Methods for Modeling Age-Graded Trajectories Yield Consistent and Valid Results?” American Journal of Sociology 120:1809–1856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zellner Arnold. 1986. “On Assessing Prior Distributions and Bayesian Regression Analysis with g-prior Distributions.” Bayesian Inference and Decision Techniques: Essays in Honor of Bruno De Finetti 6:233–243. [Google Scholar]


