Increased stem cell proliferation in atherosclerosis accelerates clonal hematopoiesis

Summary:

Clonal hematopoiesis, a condition in which individual hematopoietic stem cell clones generate a disproportionate fraction of blood leukocytes, correlates with higher risk for cardiovascular disease. The mechanisms behind this association are incompletely understood. Here we show that hematopoietic stem cell division rates are increased in mice and humans with atherosclerosis. We use mathematical modeling to demonstrate that increased stem cell proliferation expedites somatic evolution and expansion of clones with driver mutations. The experimentally determined division rate elevation in atherosclerosis patients is sufficient to produce a 3.5-fold increased risk of clonal hematopoiesis by age 70. We confirm the accuracy of our theoretical framework in mouse models of atherosclerosis and sleep fragmentation by showing that expansion of competitively transplanted Tet2^−/− cells is accelerated under conditions of chronically elevated hematopoietic activity. Hence, increased hematopoietic stem cell proliferation is an important factor contributing to the association between cardiovascular disease and clonal hematopoiesis.

eTOC/In brief:

Heyde et al. propose that clonal hematopoiesis can be a symptom rather than a cause of atherosclerosis, since this disease increases hematopoietic stem cell division which results in accelerated somatic evolution.

Graphical Abstract

INTRODUCTION

Normal peripheral blood is a polyclonal mixture descended from thousands of hematopoietic stem cells (HSCs). During aging, progeny of individual HSC clones can begin dominating considerable fractions of the blood, a phenomenon called clonal hematopoiesis (CH) (Genovese et al., 2014; Jaiswal et al., 2014; Xie et al., 2014). Hematopoietic clones often harbor recurrent driver mutations, principally in DNMT3A, TET2 and ASXL1, and copy number alterations (Loh et al., 2018). Furthermore, whole genome sequencing studies suggest that CH can also occur in the absence of known driver alterations in up to 59% of cases (Zink et al., 2017).

Individuals with CH have a higher incidence of hematological cancer, but surprisingly, CH also associates with coronary heart disease, ischemic stroke (Bick et al., 2020a; Jaiswal et al., 2014, 2017) and heart failure (Dorsheimer et al., 2019). Large meta-analyses indicate 1.3-fold to 2-fold increased risk of atherosclerotic disease in individuals with CH (Bick et al., 2020a; Jaiswal et al., 2014, 2017). Atherosclerosis is a systemic, multifactorial disorder characterized by atherosclerotic plaques in major arteries. When blood lipid levels are chronically elevated, lipoproteins may start forming deposits in vessel walls. Subsequent immune cell recruitment and failure to resolve local inflammation can result in complex, growing lesions that occlude vessels and lead to coronary heart disease, myocardial infarction, chronic heart failure, peripheral artery disease and stroke (Swirski and Nahrendorf, 2013).

A large body of prior work has established that the hematopoietic system is persistently activated in atherosclerosis. In the two most common mouse models of atherosclerosis (Ldlr^−/− and Apoe^−/− mice on an atherogenic diet), the percentage of hematopoietic stem and progenitor cells (HSPCs) is elevated and mice experience progressive monocytosis (Murphy et al., 2011; Swirski et al., 2007; Tacke et al., 2007). In both models, [³H] Thymidine incorporation is increased in whole bone marrow, indicating augmented hematopoietic cell proliferation (Murphy et al., 2011). Similarly, rabbits with atherosclerosis exhibit progressive leukocytosis (Feldman et al., 1991), and swine fed with a hyperlipidemic diet develop pronounced monocytosis (Averill et al., 1989). Human atherosclerosis patients also exhibit leukocytosis (Madjid et al., 2004) and elevated hematopoietic activity in the bone marrow (van der Valk et al., 2016). Furthermore, granulocyte/monocyte colony forming units (GM-CFU) are increased in bone marrow samples from mice (Murphy et al., 2011) and swine (Averill et al., 1989) with diet-induced atherosclerosis, and in HSPCs harvested from atherosclerosis patients (van der Valk et al., 2016).

The physiological mechanisms linking atherosclerosis and hematopoiesis are the subject of ongoing research. First, altered lipid levels can directly regulate HSPC proliferation. High HDL levels suppress HSPC proliferation, while impaired cholesterol efflux and high intracellular cholesterol levels instigate turnover, at least in part due to upregulation of the common β subunit of the IL-3/GM-CSF receptor and increased responsiveness to IL-3 and GM-CSF (Yvan-Charvet et al., 2010). Second, systemically increased cytokine levels – potentially fueled by immune cells in atheromata and other tissues responding to hyperlipidemia – may further drive hematopoietic activity (Murphy and Tall, 2016). We refer to the intricate interplay between hyperlipidemia, ensuing chronic inflammation and atherosclerotic plaque formation as the “atherosclerosis trait complex.”

Motivated by the association between CH and CVD, recent studies have explored a causal link from common CH driver mutations to atherosclerosis in murine models. TET2 and DNMT3A loss induce a pro-inflammatory phenotype in myeloid cells, lead to enhanced expression of inflammatory cytokines such as IL-6 and IL-1β and accelerates plaque formation (Fuster et al., 2017; Jaiswal et al., 2017; Sano et al., 2018b, 2018a). These data show that some CH driver genes can promote atherosclerosis by altering the behavior of myeloid cells. However, it is currently unknown whether mutant immune cell activity is the only factor driving the atherosclerosis risk increase in humans with CH. Given the interest in targeting mutant myeloid cells for therapeutic purposes (Hidalgo and Tall, 2019), further exploration of this question is warranted.

Here we evaluate the possible role of reverse causality by investigating whether the atherosclerosis trait complex can cause CH via chronic promotion of HSC proliferation. If proliferation of hematopoietic cells in general and HSCs in particular is augmented over long periods of time, fundamental evolutionary dynamics laws predict that the expansion rate of clones harboring both advantageous and neutral mutations will accelerate proportionally, leading to faster CH emergence. Most humans have small clones harboring driver mutations in their hematopoietic system (Young et al., 2016). In youth, driver clones occur at very low variant allele frequencies (VAFs) and can only be measured by deep error-corrected sequencing (Razavi et al., 2019; Young et al., 2016). The rate at which clones grow to reach a VAF of 2% (the currently agreed-upon threshold for diagnosing CH of indeterminate potential which has been linked to adverse outcomes (Steensma et al., 2015)) primarily depends on the selective advantage of the driver mutation and on the HSC proliferation rate. Therefore, if hyperlipidemia and atherosclerosis boost HSC proliferation, they will proportionately accelerate the emergence of CH.

Here, we measure HSC proliferation rates in mice and humans with atherosclerosis. We use the resulting data to parameterize a simple mathematical model of hematopoiesis and determine the effects of atherosclerosis-induced HSC proliferation on CH emergence. We find that the experimentally determined HSC proliferation increase in humans with CVD can explain the elevated incidence of CH in this patient group. We confirm our hypothesis in mouse models of atherosclerosis and sleep fragmentation by showing that Tet2^−/− bone marrow fractions expand significantly faster under conditions of increased HSC proliferation. Together, our data show that the atherosclerosis trait complex causally drives CH.

RESULTS

Competitive advantage and proliferation determine driver clone expansion rate

The logic underlying the reverse causality hypothesis is illustrated in Figure 1A. Consider an HSC pool that contains a small clone with a driver mutation. Once the mutant clone has reached a size that is large enough to make loss of the driver mutation through genetic drift unlikely, it will expand exponentially. Its expansion rate is determined by only two factors: the magnitude of the competitive advantage (a fixed value s associated with a particular genetic variant) and the average proliferation rate of HSCs in the pool. For example, if HSCs on average underwent four divisions per year and the driver advantage s was 15%, the mutant clone would on average expand from a size of 1% VAF to a size of 1.7% VAF (1% VAF * (1 + s)⁴ = 1.74% VAF) over one year. Now consider the same HSC pool but with a proliferation rate that is 2.25-fold elevated, for example due to inflammation and increased demand for peripheral blood cells. Such a pool would on average undergo nine divisions per year, and for the same driver advantage s of 15%, the mutant clone would on average expand to the considerably greater size of 3.5% VAF (1% VAF * (1 + s)⁹ = 3.52% VAF). Therefore, the central factor determining the expansion rate of mutant clones in the HSC pool is not chronological time, but cell division or generational time.

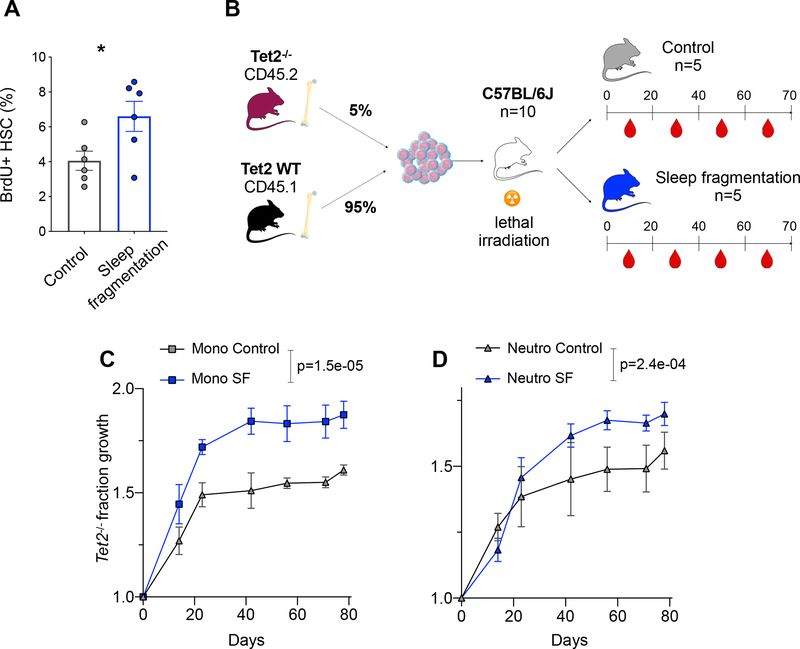
Figure 1. Apoe^−/− mice on an atherogenic diet exhibit increased HSC proliferation.

(A) Schematic illustrating hypothetical examples of driver clone growth. HSCs in one person (top row, grey boxes) undergo e.g. 4 symmetric self-renewal divisions per year. A driver that confers a fitness advantage s of 15% will on average expand from a VAF of 1% to 1.7%. HSCs in an person with a 2.25-fold elevated proliferation rate (bottom row, blue boxes) will undergo 9 self-renewal division in the same time, resulting in a driver VAF of 3.5%. (B) Experimental outline. Apoe^−/− mice are fed with atherogenic or control (chow) diets for 10 weeks. A BrdU pulse is administered and bone marrow cells are analyzed 12 hours later. (C) Representative flow cytometry plots and gating strategy for bone marrow HSCs. (D-F) Quantification of LSK percentage (D) HSC percentage (E) and BrdU⁺ HSCs (F) in bone marrow of Apoe^−/− mice on atherogenic (n=9) and control (n=9) diets. Data are represented as mean ± SEM. Mann-Whitney tests were used for statistical analysis in D-F. All tests were two-sided. * indicates p<0.05, n.s., not significant. See also Figure S1.

The atherosclerosis trait complex drives HSC proliferation

To determine whether the atherosclerosis trait complex leads to HSC proliferation, we studied hematopoiesis in atherosclerotic mice. Prior studies had shown that proliferation increases in whole bone marrow of Apoe^−/− mice fed with an atherogenic diet (Murphy et al., 2011), but it is not known whether DNA synthesis is elevated at the highest immunophenotypically defined level of the hematopoietic hierarchy in lineage^−/low Sca-1⁺ c-kit⁺ CD150⁺ CD48⁻ HSCs (Kiel et al., 2005). This is important because mutant clones must expand on the level of long-lived HSCs in order to grow progressively throughout an individual’s lifetime. We fed Apoe^−/− mice an atherogenic diet and after 10 weeks assessed bromodeoxyuridine (BrdU) incorporation in HSCs (Figure 1B and C). Apoe^−/− mice consuming regular chow diet served as a control group. Consistent with prior studies (Murphy et al., 2011), we saw an expansion of the lineage^−/lowSca-1⁺c-kit⁺ (LSK) HSPC population in Apoe^−/− fed with an atherogenic diet (2.1-fold increase, Figure 1D), accompanied by an increase in peripheral blood leukocytes, neutrophils and monocytes (Figure S1A–D). The relative abundance of HSCs did not change (Figure 1E). Twelve hours after administering BrdU, 8.5% (± 3.2% standard deviation) of HSCs in Apoe^−/− mice on atherogenic diet were positive, a 1.5-fold increase over 5.7% (± 2.2%) in chow-fed Apoe^−/− mice (Figures 1C and F). We note that there was no significant difference in BrdU incorporation in HSCs of control diet-fed Apoe^−/− mice and control diet-fed wild type C57BL/6J mice (Figure S1E), indicating that Apoe loss does not drive increased HSC proliferation in the steady state. These results suggest that HSCs increase their turnover after induction of the atherosclerosis trait complex.

Atherosclerotic patients exhibit increased HSC proliferation rates

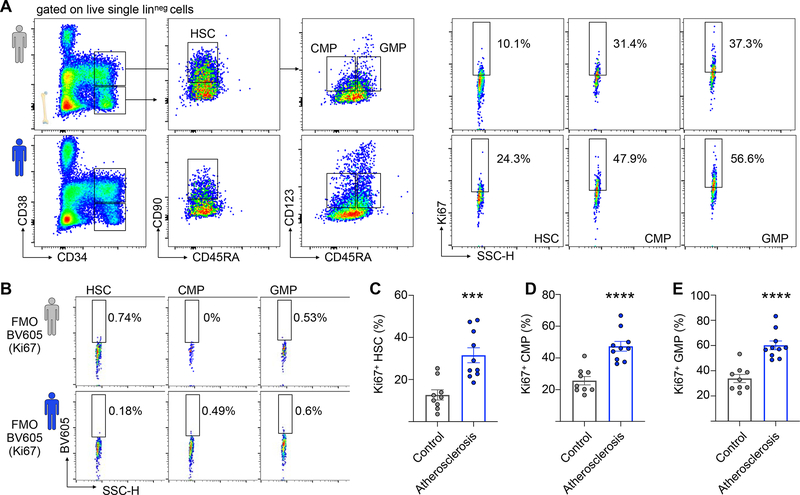
Studying hematopoiesis in atherosclerotic animals proves that the atherosclerosis trait complex leads to elevated HSC proliferation, but quantitatively estimating the impact of HSC proliferation on CH emergence requires human data. Therefore, we collected bone marrow from healthy controls and patients with atherosclerosis who had no history of ischemic events (STAR methods, Table S1). Groups were well-matched with respect to age and sex (Figure S1F–G). To assess cell division at different hematopoietic hierarchy levels, we measured proliferation marker Ki67 expression in lineage⁻ CD34⁺ CD38⁻ CD45RA^low CD90⁺ HSCs, lineage⁻ CD34⁺ CD38^int CD45RA⁻ CD123^int common myeloid progenitors (CMP) and lineage⁻ CD34⁺ CD38^int CD45RA⁺ CD123^int granulocyte-macrophage progenitors (GMP) (Dutta et al., 2015; Pang et al., 2011) (Figure 2A). Fluorescence-minus-one controls were used to determine gating (Figure 2B). Consistent with our results in the Apoe^−/− model, we observed an increased percentage of Ki67-positive HSCs in patients with atherosclerosis (Figure 2C, 12.7% ± 7.2% in healthy controls vs. 31% ± 11.2% in patients, corresponding to a 2.44-fold elevation). The relatively high baseline percentage of cycling HSCs may be due to the capture of symmetric differentiation divisions by this assay and/or due to some functional progenitor admixture in the immunophenotypically defined HSC gate. The increase observed in HSCs was mirrored at the CMP (25.7% ± 7.9% in healthy controls vs. 47.4% ± 9.7% in patients) and GMP (33.9% ± 9.7% in healthy controls vs. 60.2% ± 11.0% in patients) levels (Figures 2D and E). Interestingly, all atherosclerosis patients in our cohort had adequately managed cholesterol levels (90.5±23 mg/dl, Table S1), indicating that acute hyperlipidemia was not the reason for the elevated proliferation rates. We conclude that atherosclerosis associates with elevated proliferation across multiple hematopoietic hierarchy levels, including phenotypically defined HSCs.

Figure 2. Atherosclerosis associates with increased HSC proliferation in human patients.

(A) Representative flow cytometry plots and gating strategy for human bone marrow HSCs, CMPs and GMPs. The top row (grey human symbol) represents a healthy 72-year-old female (patient #9); the bottom row (blue human symbol) represents a 72-year-old male atherosclerosis patient (patient #18). (B) Fluorescence-minus-one (FMO) controls for patients #9 and #18. (C-E) Quantification of BrdU⁺ HSC (C) CMP (D) and GMPs (E) in controls (n=9) and patients with atherosclerosis (n=10). Data are represented as mean ± SEM. Unpaired t-tests with Welch’s correction were used for statistical analysis in (C-E). All tests were two-sided. *** indicates p=0.0005, **** indicates p<0.0001. See also Figure S1 and Table S1.

In atherosclerotic mice and rabbits, increased hematopoietic activity is chronic and progressive (Feldman et al., 1991; Swirski et al., 2007). Our human data suggest that the elevation is chronic in patients as well. Samples were collected across a range of ages and none of the patients experienced prior myocardial infarction, but in all of them, the HSC proliferation rates surpassed the mean of the control group. Furthermore, ¹⁸F-fluorodeoxyglucose (¹⁸F-FDG) positron emission tomography in patients with stable atherosclerotic disease has shown increased ¹⁸F-FDG in the bone marrow and increased progenitor potential of HSPCs (van der Valk et al., 2016), together suggesting chronically elevated proliferative activity of the hematopoietic system in atherosclerosis.

A stochastic model predicts accelerated CH emergence in atherosclerotic patients

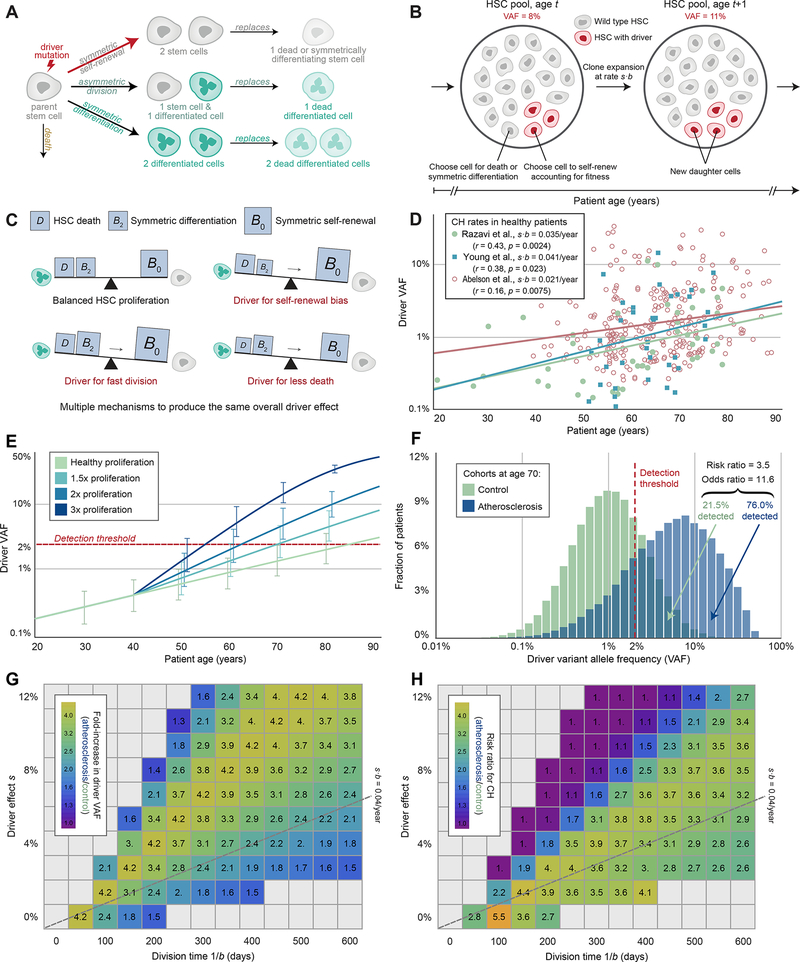
To understand the effects of chronically elevated HSC proliferation on CH emergence quantitatively, we formulated a stochastic model of HSC dynamics based on the Moran process of population genetics (Ashcroft et al., 2017; Moran, 1962; Nowak, 2006; Traulsen et al., 2013). In each individual, N diploid HSCs stochastically divide at a scale set by the baseline proliferation rate b, averaged across healthy subjects with no atherosclerosis. Cell divisions can result in three different outcomes (Figure 3A). Symmetric self-renewal divisions produce two HSCs which both remain in the pool; symmetric differentiation divisions produce two differentiated cells that both leave the HSC pool; and asymmetric divisions produce one HSC and one differentiated cell. An excess in the self-renewal rate relative to the symmetric differentiation rate compensates for any HSC death to ensure that the size of the pool remains constant over time. We furthermore model that the HSC pool contains a driver clone – a subpopulation of HSCs harboring a mutation which confers a fitness advantage of magnitude s and hence expands with age (Figure 3B). The driver mutation can exert its beneficial effects through several different biological mechanisms that lead to equivalent dynamics from a mathematical perspective: it can increase the odds of symmetric self-renewal relative to symmetric differentiation, it can cause faster division, or it can decrease the death rate (Figure 3C).

Figure 3. Elevated HSC proliferation expedites driver clone expansion.

(A) Schematic of stochastic HSC dynamics. Some genetic variants (“driver mutations”) result in an imbalance in cell fates in favor of self-renewal. (B) Moran model of driver VAF expansion. Each time an HSC is lost to death or symmetric differentiation and needs replacement via self-renewal, an HSC with a driver mutation (red) is more likely to self-renew than a baseline HSC (gray), resulting in expected growth of the driver clone size over time. (C), Imbalance in cell fates. Baseline HSCs (gray) balance their self-renewal rates (B₀) with the sum of their symmetric differentiation rates (B₂) and death rates (D), while any of three different driver mechanisms (self-renewal bias, fast division, or less death) all result in an imbalance towards self-renewal. (D) Observed driver clone sizes (VAFs) across patient ages from 3 published data sets. (E) Expected driver VAF expansion over time. The driver clone expands more rapidly in atherosclerosis patients with a higher proliferation rate at an onset of age 40 (blue curves with ±1 SD bars), such that these patients surpass a 2% detection threshold (red dotted line) at an earlier age. (F) Predicted driver VAF distributions at age 70 across two patient cohorts. Relative to the healthy cohort (green), patients in the atherosclerosis cohort (blue) have an elevated proliferation rate, corresponding to the Ki67⁺ HSC distributions measured in the two human cohorts as shown in Figure 2C scaled with a baseline rate of 1/(28 days). (G) Fold-increase in driver VAF at age 70. Across a wide range of potential division times 1/b and driver effect sizes s near our estimate from panel (D) (gray dotted line), our model predicts a consistently noticeable increase in driver clone size in atherosclerosis patients with a two-fold increase in proliferation. (H) Predicted risk ratios for CH associated with the atherosclerosis cohort relative to the healthy cohort in (F). Across a wide range of potential division times 1/b and driver effect sizes s near our estimate from panel (D), the model predicts a consistently greater risk of a detectable driver clone at age 70 in atherosclerosis patients. See also Figures S1–S4 and Table S2.

The Moran process provides an accurate description of the division and death events that affect the size of the driver clone over time, despite requiring few parameters. (See STAR methods and Table S2 for a list of relevant parameters and default values). The two most important parameters are the HSC proliferation rate b and the driver fitness advantage s, as their product sets the expected driver clone expansion rate. Less crucial is the HSC pool size N, which does not affect the average driver VAF (because we are measuring and modeling the driver clone as a fraction of the whole and not as an absolute number of cells) but can affect the consistency of these outcomes (i.e. the variance in driver VAF). To obtain estimates for these parameters of interest, we analyzed multiple datasets. Standard exome sequencing data would be insufficient for our use, as by the time a clone reached a detectable size (2% VAF), it would have already reached the CH stage and thus could not report on the rate of clone growth that unfolds throughout most of life. In order to get more accurate estimates, we instead relied on deep error-corrected sequencing that can detect very small clones relatively early in life. Specifically, we analyzed reported driver VAFs in white blood cells collected from healthy 20 to 87-year-old donors to the San Diego Blood Bank (Razavi et al., 2019), as well as from serially banked blood samples collected from healthy 50 to 76-year-old participants in the Nurses’ Health Study (Young et al., 2016) (STAR methods). We also included 39 to 88-year old healthy subjects from a recent study comparing benign CH to pre-acute myeloid leukemia samples (Abelson et al., 2018). We reasoned that the HSC pool’s genetic diversity is closely mirrored in circulating cells, as there is a strong correlation between VAFs in bone marrow and peripheral blood (Hwang et al., 2018). However, all conclusions described below also apply in scenarios where a driver mutation confers a strong increase or decrease in differentiation rate, thus leading to an over- or underrepresentation of the variant in peripheral blood cells (STAR methods, Figure S1H–I).

All datasets were well explained by our model (logit regression with p=0.0024, p=0.023 and p=0.0075, respectively) and produced consistent estimates for the average clone size in a healthy adult of age 50: VAF=0.51%, VAF=0.59% and VAF=1.16% from each dataset, respectively (Figure 3D, STAR methods). The three datasets also lead to similar estimates for the driver clone expansion rate during the lifetime: s·b=0.035 ± 0.022 per year, s·b=0.041 ± 0.023 per year and s·b=0.021 ± 0.008 per year, respectively. These values are consistent with many previously reported CH variants of low to moderate fitness, which tend to fall near s·b=0.04 per year (Watson et al., 2020). (Note that s as reported in Watson et al. 2020 is a fitness effect in % per year which corresponds to our s·b). Although decoupled values for the HSC proliferation rate b and the driver fitness advantage s are not needed for our modeling, orthogonal data constrain these possible values to a relatively small range. For example, s must be positive and is likely smaller than 25%, while an upper bound for b is approximately 1/(28 days). HSCs gain ~14 mutations per year (Osorio et al., 2018), and the mutation rate during early embryogenesis is approximately 1–1.2 mutations per division (Lee-Six et al., 2018). Assuming that the mutation rate does not change substantially in adulthood, this would imply that HSCs divide ~13 times per year, as has previously been pointed out (Watson et al., 2020). We consider 1/(28 days) an upper bound for b because not all divisions are self-renewal divisions. This is consistent with recent estimates by Lee-Six and colleagues who give an upper bound for the self-renewal rate in the range of 1/(2 months) (Lee-Six et al., 2018). If mutation rates instead go up in later development and adult life (Bae et al., 2018), it is possible that this proliferation rate could be substantially slower – some studies point to proliferation rates as low as b=1/(280 days) (Catlin et al., 2011). For the curves shown in Fig. 3D, a proliferation rate of b=1/(28 days) corresponds to an average driver fitness advantage in the range s=0.3% ± 0.2%. This value is consistent with the estimated average fitness effect of cancer drivers in solid tumors (approximately s=0.4%, (Bozic et al., 2010)).

Having calibrated our model to these data and taking s·b=0.041/year, we calculate the rate of driver clone expansion for healthy subjects and find that the driver VAF typically reaches the CH diagnosis threshold of 2% at a median age of 83.4 years (Figure 3E). This prediction is in agreement with an independent study that used deep sequencing to quantify CH in patients with non-hematological cancers and found that CH frequency is 50% when subjects reach their 80s (Coombs et al., 2017), further confirming that our model design appropriately maps the set of previously measured parameter values to realistic CH outcomes.

Next, we studied how increased HSC proliferation caused by the atherosclerosis trait complex affects CH emergence. Arterial fatty streaks, the first signs of atherosclerosis, begin developing in adolescence, but the incidence of clinically significant lesions rises considerably in the third decade of life (McGill et al., 2000). Therefore, we conservatively assume that atherosclerosis begins at age 40 (See Figures S2 and S3 and STAR methods for an extensive analysis of different ages of onset). At the age of 40, we model that HSC proliferation rates increase 1.5-fold, as we observed in Apoe^−/− mice after 10 weeks on an atherogenic diet, and then remain elevated throughout the rest of life, consistent with the chronic nature of the disease. Under these conditions, the age at which the mean driver VAF reaches a detection threshold of 2% drops from 83.4 to 68.9 years (Figure 3E). For patients with 2- and 3-fold elevated proliferation during atherosclerosis, CH emergence age drops further to 61.7 and 54.5 years, respectively (Figure 3E).

We sought to determine whether the observed HSC proliferation rates in atherosclerosis patients could explain the two-fold higher risk for coronary heart disease and four-fold higher risk for early-onset myocardial infarction in individuals with CH (Jaiswal et al., 2017). For this purpose, we must account for the inter-individual variation in HSC proliferation rate among both healthy individuals and atherosclerosis patients. We therefore simulated CH dynamics longitudinally across two cohorts, one with 500,000 healthy patients and one with 500,000 atherosclerotic patients, each harboring a driver clone of equal size and effect at the age of onset (40 years). Proliferation rates varied according to the distributions measured in human bone marrow samples. We evaluated the distribution of driver VAFs at age 70, corresponding to the median time of sample collection in the BioImage cohort (Jaiswal et al., 2017). To make the output of our mathematical model further comparable to previous results, we expressed the difference between healthy subjects and atherosclerosis patients in terms of risk and odds ratios. Specifically, we report the risk ratio (defined as $\frac{\text{Prob}(\text{CH|CVD})}{\mathrm{Prob}(\text{CH}\mid ~\text{CVD})}$) and the odds ratio (defined as $\frac{\text{Odds}(\text{CH|CVD})}{\mathrm{Odds}(\text{CH}\mid ~\text{CVD})}$). The two cohorts’ distributions overlapped only partially: the driver clone reached the 2% VAF limit that defines CH in 76.0% of patients with atherosclerosis, but in only 21.5% of the healthy control cohort (Figure 3F). This corresponds to a 3.5-fold elevated risk of CH in patients with atherosclerosis at the age of 70 (odds ratio = 11.6), qualitatively similar to results obtained by previous studies that quantified the converse risk of cardiovascular disease in patients with CH (Jaiswal et al., 2017).

We proceeded to perform a sensitivity analysis to explore a wide range of other plausible combinations of b and s, as well as alternative HSC pool sizes and atherosclerosis effects. For b and s pairs even relatively far from our estimate, we consistently observe at least a 1.5× expected fold-increase in driver VAF by age 70, assuming a two-fold elevation in the HSC proliferation rate onset at age 40 (Figure 3G). The same effect is visible for risk ratios (Figure 3H). Similar risk ratios of 2.6-fold to 4.6-fold were also obtained for alternative choices the age of onset, proliferation increase, and HSC pool size (Figures S2 and S3). We note if s·b were to be much larger than estimated, then the majority of cells would contain the driver in both healthy and atherosclerosis patients, slowing the rate of driver clone expansion as it approaches the largest possible size (50% VAF) and tapering the predicted increase in driver VAF. Critically, however, this predicted increase becomes more dramatic with greater increases to the HSC proliferation rate; with a more extreme elevation of 2.5×, we observe a 4.3× fold-increase in driver VAF (Figure S3D). We also confirmed that our model predictions for the fold-increase in driver VAF are fully independent of HSC pool size N. Finally, we explored the possibility of an HSC pool that is expanding over time, showing that the fraction of total cells which contain the driver variant and the driver VAF have the same dynamics regardless of whether the HSC pool is constant in size, expanding, or fluctuating (STAR methods and Figure S4A).

The effects of increased HSC proliferation on neutral evolution

Increased HSC proliferation accelerates not only driver clone expansion but also speeds up the effects of neutral drift. Drift refers to the stochastic changes in VAFs that arise over time because individual cells reproduce (and die) in a random fashion. Since the HSC population renews stochastically, some HSCs are randomly lost to symmetric differentiation or death. The genetic variants present in those cells are irretrievably lost. To compensate for cell loss, other cells randomly undergo symmetric self-renewal divisions, and their genetic variants increase in VAF. Over time, repetitions of this process result in a progressive remodeling of VAFs (Figure S4B). To determine whether higher proliferation rates in atherosclerosis patients could lead to CH emergence via drift, we implemented a modified version of our modeling framework. We initialize the process with a neutral VAF distribution at birth (STAR methods). The HSC pool then accrues additional neutral mutations as it undergoes turnover. At each cell division, u=1.5 new neutral mutations are acquired on average in each daughter cell (Lee-Six et al., 2018). Other choices of u would result in a different total number of neutral mutations but would not affect their VAFs or our main findings.

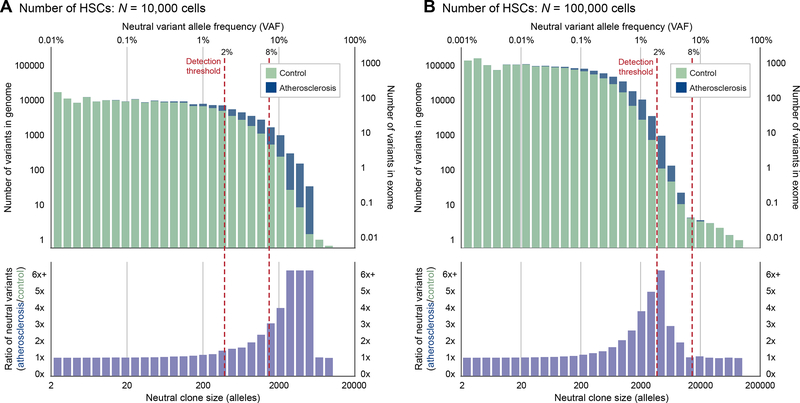
We studied the abundance of neutral mutations in healthy and atherosclerosis cohorts at age 70 for an HSC pool size of N = 10,000. This is the approximate HSC pool size that has historically been assumed in humans and other mammals (Abkowitz et al., 2002). We obtain the neutral VAF distributions by first simulating somatic evolution for 1,000 healthy individuals. For each healthy subject, a baseline mutation burden at birth is generated, and HSCs then divide at an average proliferation rate of b=1/(28 days), with variance equal to our human control data. At age 70, VAFs of all extant mutations are plotted (Figure 4A). In atherosclerosis patients, we assume that beginning at age 40, the turnover rate is chronically elevated according to the distribution of HSC proliferation rate increases in Figure 2C (Figure 4A). We provide two quantifications of the mutation burden: the number of mutations that would be present across different VAFs if the whole genome (left y-axis labels) or only the exome (right y-axis) was sequenced. We furthermore quantify the difference between healthy and atherosclerosis patients by calculating the ratio between the number of neutral variants present in the two populations across the full range of possible VAFs (Figure 4A, purple histogram).

Figure 4. Elevated HSC proliferation leads to excess neutral mutations.

(A-B), Distribution of variant allele frequency (VAF, top axis) and neutral clone size (total number of variant alleles out of 2N, bottom axis) of neutral somatic variants for an HSC pool size of either (A) N = 10,000 cells, or (B) N = 100,000 cells, averaged across patients with initial mutation burdens determined by simulated prenatal cell divisions. Patients in the atherosclerosis cohort (blue) have elevated proliferation rates consistent with Figures 2C and 3F that lead to more neutral variants at intermediate VAFs relative to patients in the healthy cohort (green). For N = 100,000 cells, the peak of this enrichment curve (purple) can be captured by sequencing with a 2% detection threshold but not an 8% threshold. For N = 10,000 cells, either a 2% or an 8% threshold are sufficient to detect enrichment. See also Figure S5.

Our results show a considerable excess of neutral mutations in atherosclerosis patients for nearly all VAFs exceeding 2%. HSCs in patients with elevated proliferation rates undergo more divisions, allowing them to accumulate additional variants and allowing extant variants to undergo larger changes in frequency, thereby increasing the number of variants that expand to large frequencies (Figure S5A–B). This excess accumulation falls within VAF ranges that are detectable by common sequencing studies. We also derive several analytic predictions for the expected number and frequency of neutral variants in the HSC population (Data S1) and find that this analysis also predicts a substantial accumulation of excess neutral mutations in the atherosclerosis cohort.

Next, we considered different HSC pool sizes. Recent evidence suggests that the HSC population may be substantially larger than previously estimated, on the order of 50,000–200,000 cells (Lee-Six et al., 2018; Watson et al., 2020). The analogous plot for a larger pool size of N = 100,000 (Figure 4B) shows that atherosclerosis will still cause neutral clones to expand more quickly, but at 70 years, they exist at relatively low VAFs (0.1%–5%). If a less sensitive detection threshold of 8% VAF instead were used, for example, the number of neutral variants detected in healthy and atherosclerosis patients would on average be virtually identical. To observe the effects of neutral drift at frequencies larger than 8% in an HSC pool of this size, at least part of the study population would need pathologically elevated HSC proliferation rates in the highest decile of the proliferation rates we measured in Figure 2C (Figure S5C).

Varying division times, mutation rate magnitudes, proliferation rates and HSC pool sizes, we consistently see a similar excess of neutral variants exceeding a 2% VAF detection threshold (Figure S5D). Because larger pool sizes tend to have fewer detectable variants, the fold-increase in the number of these variants is more sensitive to the same level of proliferation elevation. We further find that the observed excess of neutral variants is sensitive to the age of onset and the choice of detection threshold (Figure S5D). Finally, our findings also hold for an HSC pool that is expanding over time (Figure S5E). We conclude that the impact of drift is more pronounced in atherosclerosis patients experiencing augmented HSC proliferation. Many current study designs could readily detect this effect.

Experimental validation of accelerated CH emergence in CVD

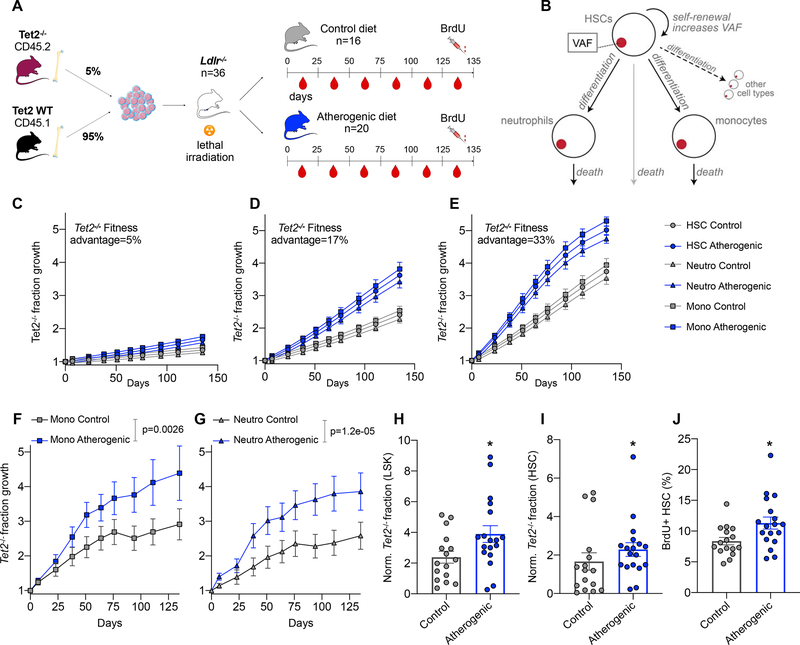
Our mathematical model makes testable predictions about the rate of driver mutation expansion under different HSC proliferation conditions. To test this model experimentally, we studied the evolution of Tet2^−/− cells in the Ldlr^−/− mouse model. Like Apoe^−/− animals, Ldlr^−/− mice develop hypercholesteremia, atherosclerosis and progressive monocytosis when fed an atherogenic diet, although the phenotype is more moderate than in Apoe^−/− mice (Murphy et al., 2011). We mixed bone marrow from Tet2^−/− mutant mice, marked by the cell surface marker CD45.2, with wild type bone marrow derived from mice expressing CD45.1 and transplanted the mixture into lethally irradiated Ldlr^−/− recipients (Figure 5A). Four weeks after transplantation, we collected baseline blood samples and then randomly assigned mice into chow vs. atherogenic diet groups. CD45.1 and CD45.2 fractions in the peripheral blood of these mice were then assessed biweekly over a period of 135 days.

Figure 5. Accelerated Tet2^−/− fraction growth in the Ldlr^−/− mouse model of atherosclerosis.

(A) Schematic overview of an experiment designed to track the evolution of Tet2^−/− cells in atherosclerotic mice. (B) A slightly modified version of the driver clone model (Figure 3) which explicitly incorporates monocytes and neutrophils (STAR methods) is used to predict the expected outcome of the experiment shown in (A). (C-E) Predictions of the model in (B) for s=5% (C), s=17% (D) and s=33% (E). We model a proliferation rate b = 1/(17.5 days) in the control group and a 75% elevation of b associated with the atherosclerosis trait complex. HSCs, neutrophils, monocytes are shown as circles, triangles and squares, respectively. The y-axis denotes fold change of the Tet2^−/− fraction with respect to the starting time point. Error bars indicate the SEM. (F-G), Results of the experiment shown in (A). The Tet2^−/− (CD45.2) fraction of monocytes (F) and neutrophils (G) is shown across all peripheral blood measurements in Ldlr^−/− mice receiving control or atherogenic diets. Error bars indicate the SEM, p-values are derived from linear regression of the logit-transformed baseline-normalized data. Y-axes as in (C-E). (H) Fraction of Tet2^−/− LSKs at the end of the experiment shown in (A), day 135. Since engraftment varies stochastically and every mouse has a different fraction of mutant cells at the outset of the experiment, the percentage of Tet2^−/− LSKs is normalized to baseline (divided by the CD45.2⁺ neutrophil percentage at day 0). P-values are calculated with a two-sided Mann-Whitney test. (I) as in (H) for HSCs. (J) Quantification of BrdU⁺ HSCs on day 135. P-values are calculated with a two-sided Mann-Whitney test. n=16 in the control group and n=18 in the atherosclerosis group in panels H-J (two mice died during the experiment in the atherosclerosis group). * indicates p<0.05. See also Figure S6–S7 and Table S3.

To define the expected outcome of this experiment,, we returned to our mathematical model. To predict the expected growth of the Tet2^−/− fraction, we expanded the model to explicitly include neutrophil and monocyte populations as they are replenished by HSC differentiation (Figure 5B, see Table S3 for a list of model parameters). We chose to focus on monocytes and neutrophils because these cells have a very short half-life (20 hours – 2.2 days (Yona et al., 2013) and 11 hours (Basu et al., 2002), respectively) relative to B and T lymphocytes (42 days (Fulcher and Basten, 1997) and 6–43 days (Gossel et al., 2017), respectively) and thus are the most accurate readout for the composition of the HSC pool at any given time in the experiment. The baseline HSC proliferation rate was assumed to be 17.5 days, a previously published estimate (Abkowitz et al., 2000) similar to the human rate. For illustrative purposes, we modeled a 75% elevation due to atherosclerosis. We plotted model predictions, expressed as a fold change (Tet2^−/− fraction at each time point divided by the value of the baseline measurement) for all three cell populations and a number of different possible s values (Figure 5C–E). As expected, across all three populations, chow control and atherosclerosis populations separated clearly and the overall rate of Tet2^−/− fraction growth accelerated with increasing values of s.

Analyzing flow cytometry data from the Ldlr^−/− experiment, we found that growth of the Tet2^−/− fraction in monocytes (Figure 5F) and neutrophils (Figure 5G) was consistent with these predictions. In both populations, Tet2^−/− fractions increased significantly more rapidly in mice fed with an atherogenic diet, with a 50.8% (95% confidence interval 33.9–62.9%) and 29.4% (95% confidence interval 12.1–42.4%) increase in the expansion rate in neutrophils and monocytes, respectively. Assuming b=1/(17.5 days), our model estimates s = 21.6% for neutrophils and s = 25.8% for monocytes. These estimates are significantly higher than s values inferred in the human setting under the assumption of a proliferation rate b = 1/28 days, potentially because the Tet2^−/− mouse does not just have a single heterozygous base pair substitution but homozygous loss of several crucial exons of Tet2 (Ko et al., 2011). Alternatively, proliferation rates exceed b=1/(17.5 days) after transplant.

At the end of the longitudinal experiment, we confirmed that mice fed with an atherogenic diet had higher cholesterol levels (Figure S6A). Then, we assessed Tet2^−/− fractions and BrdU incorporation in HSPCs. We found that as expected, accelerated mutant fraction growth in neutrophils and monocytes was accompanied by significantly larger Tet2^−/− fractions (normalized to baseline) in LSKs (Figure 5H) and HSCs (Figure 5I). We also compared BrdU incorporation in HSCs (Figure 5J) and LSKs (Figure S6B) between Ldlr^−/− on chow vs. atherogenic diets and found increased proliferation in the latter. Importantly, the experimentally observed HSC proliferation rate increase in the Ldlr^−/− model (35%) closely matched the proliferation acceleration inferred by our model from the separation of the mutant growth curves in Figures 5F/G, providing an important confirmation of the accuracy our theoretical framework. Furthermore, we were able to confirm our theoretical prediction that Tet2^−/− fractions in neutrophils and monocytes (but not B or T cells) are closely correlated with HSC Tet2^−/− fractions (Figure S6C).

To determine whether mild hypercholesterolemia in the absence of atherosclerosis is sufficient to increase HSC proliferation and mutant cell expansion, we repeated the same experiment in wild type mice. We lethally irradiated C57BL/6J animals and transplanted them with a mixture of Tet2^−/− and wild type bone marrow (Figure S7A), as we had done for Ldlr^−/− mice. In contrast to our results in Ldlr^−/− mice, we observed no significant difference in the mutant fraction growth rate between atherogenic diet and control groups (Figure S7B, p=0.75 for monocytes and p=0.67 for neutrophils), confirming that induction of the atherosclerosis trait complex is required to accelerate somatic evolution. At the end of the experiment, we measured cholesterol and confirmed that indeed wild type mice fed with an atherogenic diet had significantly higher levels (Figure S7C). However, HSC and LSK proliferation were not significantly affected, and mice did not exhibit any visible signs of atherosclerosis (Figure S7D–E). These results indicate that mild hypercholesterolemia in the absence of atherosclerosis does not trigger increased HSC proliferation and does not lead to an altered rate in the expansion of Tet2^−/− myeloid cells.

To assess further to what degree hyperlipidemia directly drives HSC proliferation, we next analyzed HSC BrdU incorporation in Ldlr^−/− mice after 3 weeks on atherogenic diet (Figure S7F). We found that cholesterol was already markedly increased and had almost reached the same levels as after 19 weeks on atherogenic diet (Figure S7G–H). At the time of sacrifice, we embedded aortic roots and confirmed by histology that no obvious atherosclerotic plaques were visible in atherogenic diet or control groups. At the same time point, BrdU incorporation analysis also showed no difference in HSC or LSK proliferation rates between groups (Figure S7I–J). We conclude that short term exposure to hyperlipidemia in the absence of atherosclerosis is not sufficient to increase BrdU incorporation in HSCs, indicating that systemic inflammatory changes and atherosclerosis developing as a result of hyperlipidemia are required to instigate hematopoiesis.

CH emergence is accelerated during sleep fragmentation

Finally, in order to establish that HSC proliferation was the driving factor behind accelerated Tet2^−/− fraction growth in Ldlr^−/− mice on an atherogenic diet (and not other, unknown changes associated with atherosclerosis), we set out to repeat the same experiment in an experimental setting in which HSC proliferation is chronically increased without accompanying atherosclerosis. In mice, sustained sleep fragmentation augments hematopoiesis and leads to systemic monocytosis and neutrophilia (McAlpine et al., 2019). These effects can be attributed to a colony stimulating factor-1(CSF1)-dependent enhancement of hematopoietic proliferation. We confirmed that proliferation of immunophenotypically defined HSCs is significantly increased as a consequence of sleep fragmentation (1.6× fold-increase) (Figure 6A). Then we again transplanted a mixture of Tet2^−/− and wild type bone marrow into lethally irradiated recipients and randomized them into control and sleep fragmentation groups (Figure 6B). We observed a highly significant acceleration of Tet2^−/− fraction growth in the setting of sleep fragmentation for both monocytes (49.2%, Figure 6C) and neutrophils (Figure 6D, 39.4%). This was matched by higher baseline-normalized Tet2^−/− fractions in the HSC and LSK (Figure S7K) populations of sleep-deprived mice, as assessed at the time of sacrifice. Assuming b=1/(17.5 days), our model estimates s = 23.4% for monocytes and s = 24.9% for neutrophils. These values do not significantly differ from our estimates in mice fed an atherogenic diet (p=0.71 and p=0.44, respectively).

Figure 6. Accelerated Tet2^−/− fraction growth in a sleep fragmentation mouse model.

(A) BrdU incorporation (after a 2-hour pulse) in HSCs of C57BL/6J mice exposed to sleep fragmentation (n=6) vs. control mice on a normal sleep schedule (n=6). Two-sided t-test with Welch’s correction. (B) Schematic of an experiment to track the evolution of Tet2^−/− cells in sleep-deprived mice, as in Figure 5A. (C-D) Tet2^−/− (CD45.2) fraction growth in monocytes (C) and neutrophils (D) is shown across all peripheral blood measurements in control mice or mice exposed to sleep fragmentation (SF). Error bars indicate the SEM; p-values are derived from linear regression of the logit-transformed baseline-normalized data. Axes as in Figure 5F–G. * indicates p<0.05. See also Figure S7.

DISCUSSION

The association between CH and CVD is one of the most surprising discoveries emerging from the analysis of thousands of normal blood exomes (Jaiswal et al., 2014, 2017). Subsequent work on the mechanistic basis of this association has shown that mutant myeloid cells exacerbate atherosclerosis through increased pro-inflammatory activity (Fuster et al., 2017; Jaiswal et al., 2017; Sano et al., 2018b). However, many questions remain. One unresolved puzzle is why driver mutations in distinct CH-associated genes appear to confer the same risk of coronary heart disease. In a meta-analysis of three patient cohorts, Jaiswal et al. found hazard ratios of 1.7, 1.9 and 2.0 associated with DNMT3A, TET2 and ASXL1 mutations, respectively. Furthermore, the hazard ratio for mutations in a large group of approximately 70 other genes was 2.2 (Jaiswal et al., 2017). The only appreciably different hazard ratio was found for mutant JAK2, which is strongly associated with myeloproliferative neoplasms that cause thrombosis and myocardial infarction (Tefferi and Pardanani, 2015). It is surprising that driver mutations in such a large number of distinct CH-associated genes have the same effect on the inflammatory activity of downstream myeloid cells and exacerbate atherosclerosis to the same degree, in particular because the molecular function of these genes differs, and selection happens for a different trait – competitive advantage on the level of hematopoietic stem cells.

Our mathematical model provides a simple explanation for the uniform hazard ratios. The magnitude of the risk is not determined by the specific mutations present in a driver clone, but by the average HSC proliferation rate difference between the healthy and atherosclerotic populations. This effect can be observed in Figures 3G and H: for a specific HSC baseline division rate and atherosclerosis-induced proliferation rate increase, the magnitude of the fitness effect s is relatively insignificant. For example, for an average baseline division time of 300 days, the fold increase in driver VAF is essentially the same for a driver with a fitness advantage of 1% or 12%. The fitness effect is comparatively unimportant because it does not differ between healthy and atherosclerotic populations. It determines how fast driver variant allele frequencies grow in the two populations (i.e. how fast the two distributions move to the right in the illustration in Figure 3F), but it does not determine to the same degree how much the distributions separate from each other. That separation is mainly determined by the proliferation rate difference between them, as seen in Figure S3D.

Beyond providing a simple and intuitive explanation for the surprisingly uniform hazard ratios associated with different CH driver mutations, our theory clarifies several other observations that have hitherto been poorly understood (Figure 7). For example, smoking has consistently been associated with CH across multiple studies (Genovese et al., 2014; Zink et al., 2017). This phenomenon has been attributed to DNA damage (Silver and Jaiswal, 2019). However, smoking also causes leukocytosis (Pedersen et al., 2019) and therefore likely chronic HSC proliferation elevation. Furthermore, CH has been associated with addiction and psychiatric disease even after correction for smoking (Zink et al., 2017). These conditions are linked with severe chronic stress and sleep disturbance (Kaskie and Ferrarelli, 2020). It is important to note that chronic psychosocial stress also causes increased HSC proliferation (Heidt et al., 2014). Many other chronic diseases with an inflammatory component that have been associated with CH (like type 2 diabetes (Jaiswal et al., 2014), chronic pulmonary disease (Zink et al., 2017) or HIV infection (Bick et al., 2020b)) may promote CH through elevated hematopoietic activity. For example, chronic heart failure, another disease that has been shown to significantly associate with CH (Dorsheimer et al., 2019), causes increased HSC division (Sager et al., 2016), as does myocardial infarction (Dutta et al., 2015). Our analysis of neutral evolution suggests that associations with inflammatory conditions may exist even in the special case of CH with no evident driver mutations (Zink et al., 2017).

Figure 7. Schematic summarizing the relationship between HSC proliferation and clonal hematopoiesis.

Factors that instigate HSC proliferation - for example the atherosclerosis trait complex, smoking, chronic psychosocial stress, heart failure or myocardial infarction - promote accelerated somatic evolution and CH emergence.

Finally, our model may explain why blood leukocytes in individuals with CH have shorter telomeres (Zink et al., 2017). Our results indicate that shorter telomeres may reflect a more proliferative history of the HSC compartment. Together with the observation that myeloid cells with some CH driver mutations can exacerbate atherosclerosis via pro-inflammatory actions in the plaque (Fuster et al., 2017; Jaiswal et al., 2017; Sano et al., 2018b, 2018a), our findings indicate that patients suffer from a vicious cycle in which atherosclerosis causes CH, which in turn drives further atherosclerosis development.

STAR+METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Kamila Naxerova (naxerova.kamila@mgh.harvard.edu).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

The code generated during this study is available at https://github.com/AlexHeyde/clonal-hematopoiesis.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Human subjects

Bone marrow samples from control donors and patients with atherosclerosis were obtained following written informed consent in accordance with the Declaration of Helsinki and after approval by the Institutional Review Boards (IRB) of University Hospital Germans Trias i Pujol and Massachusetts General Hospital. Bone marrow tissue was gathered from iliac crest under local anesthesia or sternum under general anesthesia. Atherosclerosis patients had previously diagnosed coronary artery disease, cerebrovascular disease and/or peripheral artery disease. Tissue samples were submerged in sterile phosphate buffered saline (PBS) with 0.5% bovine serum albumin (on ice) and passed through a 40μ m cell strainer. After centrifugation, the cell pellet was resuspended in 70% Dulbecco’s Modified Eagle’s Medium (D1145, Sigma-Aldrich, St. Louis, MO, USA), 20% fetal calf serum and 10% dimethyl sulfoxide, transferred to cryovials, cryopreserved, and stored in liquid nitrogen. Additional cryopreserved bone marrow samples from healthy donors, obtained from iliac crest puncture, were purchased from HemaCare BioResearch Products (Los Angeles, CA, USA) and AcceGen Biotech (Fairfield, NJ, USA).

Mouse models

Wild type C57BL/6J (#000664), Apoe^−/− (B6.129P2-Apoe^tm1Unc/J, #002052), Tet2^−/− (B6(Cg)-Tet2^tm1.2Rao/J, #023359), Ldlr^−/− (B6.129S7-Ldlr^tm1Her/J, #002207), and CD45.1 mice (B6.SJL-Ptprc^a Pepc^b/BoyJ, #002014) were purchased from The Jackson Laboratory (Bar Harbor, ME, USA). For all experiments, littermates of the same sex were randomly assigned to experimental groups. Mice were group-housed on a 12:12hrs light:dark cycle at 22°C with access to standard mouse chow or diet and water ad libitum. The study protocols were approved and reviewed by the Institutional Animal Care and Use Committee (IACUC) at Massachusetts General Hospital (Boston, MA, USA) and all animal experiments were performed in compliance with relevant regulatory standards.

METHOD DETAILS

Flow cytometry of human bone marrow

After thawing of cryovials at 37°C, cells were washed in sterile PBS and incubated with biotinylated anti-human lineage antibodies directed against CD2, CD3, CD4, CD7, CD8a, CD10, CD11b, CD14, CD19, CD20, CD56, CD235ab (all diluted 1:100) and LIVE/DEAD Fixable Aqua Dead Cell Stain (L-34957, Life Technologies, Carlsbad, CA, USA, 1:100). After washing, cell suspensions were stained with anti-human CD34-APC (1:100), CD38-PE/Cy7 (1:100), CD90-FITC (1:25), CD45RA-PB (1:25), CD123-PE (1:50) and streptavidin-APC/Cy7 (405208, BioLegend, San Diego, CA, USA, 1:50). Intracellular staining with anti-human Ki-67-BV605 (1:25) was performed using the BD Cytofix/Cytoperm Fixation/Permeabilization Kit (554714, BD Biosciences, San Jose, CA, USA). Samples were analyzed on an LSRII flow cytometer equipped with FACS Diva 6.1 software (BD Biosciences) and recorded events were analyzed with FlowJo 10 software (BD, Franklin Lakes, NJ, USA). For each sample, fluorescence minus one (FMO) controls were used to determine the gating. Hematopoietic stem cells (HSC) were identified as lineage^neg CD34⁺ CD38⁻ CD45RA^low CD90⁺, common myeloid progenitors (CMP) as lineage^neg CD34⁺ CD38^int CD45RA⁻ CD123^int and granulocyte-macrophage progenitors (GMP) as lineage^neg CD34⁺ CD38^int CD45RA⁺ CD123^int.

In vivo interventions

Sleep fragmentation

For sleep fragmentation experiments, female mice were placed in a sleep fragmentation chamber (Lafayette Instrument, Lafayette, IN, USA). The sweep bar moved along the bottom of the cage every 2 minutes during the light cycle (Zeitgeber time 0–12). The sweep bar automatically shut off and was stationary during the dark cycle (Zeitgeber time 12–24). Control mice receiving undisturbed sleep were placed in sleep fragmentation chambers with stationary sweep bars. For bone marrow transplantation experiments, mice were placed in sleep fragmentation cages 2–4 weeks after the transplant.

Atherosclerosis

For atherosclerosis induction in Apoe^−/− mice, 10-week-old male animals were kept on a Western-type diet (TD.88137, Envigo, Indianapolis, IN, USA) for 10 weeks. Control diet (chow)-fed Apoe^−/− male littermates were used as controls. For atherosclerosis induction in Ldlr^−/− mice, 12-week-old male animals were fed a high-cholesterol diet (D12108C, Research Diets, New Brunswick, NJ, USA). Chow-fed Ldlr^−/− male littermates were used as controls. For atherosclerosis control experiments in C57BL/6J wild type mice, male and female animals (with similar percentages in both groups) were fed a high-cholesterol diet (D12108C, Research Diets, New Brunswick, NJ, USA) or a control diet (chow), respectively. For bone marrow transplantation experiments, mice were put on respective diets 2–4 weeks after the transplant. We predominantly used male mice to avoid potential scatter related to estrous cycle effects.

Bone marrow transplantation

Recipient mice were lethally irradiated with 950cGy (single dose) and reconstituted with 5,000,000 bone marrow donor cells via retro-orbital injection the following day. Anesthetized donor mice were perfused with 20mL PBS. Bone marrow was flushed out of femora and tibiae with PBS and passed through a 40μm cell strainer. Single-cell suspensions were diluted in Trypan Blue and counted using a hemocytometer. Prior to transplantation, cells from different donor mouse strains were mixed as described for the respective experiments.

Flow cytometry of mouse blood and bone marrow

Sample preparation

Peripheral blood was collected via retro-orbital bleeding using Heparinized Capillary Tubes (420316, BD, Sparks, MD, USA). Red blood cell lysis was performed using 1× RBC lysis buffer (420301, BioLegend). For the isolation of bone marrow hematopoietic cells, mice were anesthetized and flushed with 20mL PBS in order to remove intravascular blood. Bones were dissected and the bone marrow was flushed out with PBS containing 0.5% bovine serum albumin (FACS buffer). A single-cell suspension was created by plunging the bone marrow through a 40μm cell strainer.

Flow cytometry

For blood leukocytes, samples were stained with Ly6G-FITC, CD11b-PE, CD3-PerCP/Cy5.5, CD115-BV421, Ly6C-BV605, CD8a-BV711, CD4-AF700, CD45.2-APC, CD45.1-PE/Cy7, CD19-APC/Cy7, B220-APC/Cy7, NK1.1-APC/Cy7 (all diluted 1:300) and LIVE/DEAD Fixable Aqua Dead Cell Stain (L-34957, Life Technologies, 1:300). For sleep fragmentation experiments, blood leukocytes were stained with Ly6G-FITC, CD8a-PE, CD45.1-PerCP/Cy5.5, B220-PE/Cy7, CD4-PacificBlue, CD115-BV605, CD11b-BV711, CD3-APC, CD90-APC, TCRβ-APC, CD19-APC, CD45.2-AF700 and Ly6C-APC/Cy7 (all diluted 1:300). For hematopoietic progenitor cells, isolated bone marrow cells were first stained with biotin-conjugated anti-mouse antibodies directed against CD3, CD4, CD8a, CD49b, CD90.2, CD19, B220, NK1.1, TER119, CD11b, CD11c, Gr-1 (all diluted 1:300) and LIVE/DEAD Fixable Aqua Dead Cell Stain (1:300). This was followed by one of the following secondary stainings: a) c-kit-PE/Cy7, Sca-1-BV605, CD16/32-BV711, CD34-FITC, CD150-PerCP/Cy5.5, and CD48-AF700 (all 1:150) and streptavidin-APC/Cy7 (405208, BioLegend); or b) CD34-FITC, CD45.2-PE, CD150-PerCP/Cy5.5, c-kit-PE/Cy7, CD48-AF700, BV421-CD45.1, Sca-1-BV605, CD16/32-BV711 (all 1:150) and streptavidin-APC/Cy7. For sleep fragmentation experiments, bone marrow cells were stained with CD34-FITC, B220-PE, CD19-PE, CD49b-PE, Ter119-PE, CD90.2-PE, CD11b-PE, CD11c-PE, Ly6G-PE, IL7Rα-PE, CD16/32-PerCP/Cy5.5, c-kit-PE/Cy7, CD115-BV421, CD150-BV605, CD45-BV711, CD48-AF700 and Sca-1-APC/Cy7 (all 1:150). Where applicable, cells were stained with APC BrdU Flow Kit (552598, BD Biosciences) following the manufacturer’s protocol. BrdU was administered via intraperitoneal injection 2 or 12hrs before sacrifice. Events were recorded on an LSRII flow cytometer and data were analyzed with FlowJo 10 software.

Gating strategy

All cell populations were pregated on single and viable cells. LSK were identified as lineage^neg c-kit⁺ Sca-1⁺ and hematopoietic stem cells (HSC) as lineage^neg c-kit⁺ Sca-1⁺ CD150⁺ CD48⁻. Blood monocytes were identified as lineage^neg CD11b⁺ SSC-A^low CD115⁺ Ly6G⁻ and neutrophils as lineage^neg CD11b⁺ SSC-A^low CD115⁻ Ly6G⁺. % CD45.2 was assessed by sub-gating each cell population on CD45.1⁻ CD45.2⁺.

Histology

Aortic roots were harvested from mice, embedded in O.C.T. Compound (4583, Sakura Finetek, Torrance, CA), and sectioned (6μm thickness). To investigate plaque presence, Hematoxylin and Eosin (H&E) (HHS32 and HT110132, Sigma-Aldrich, St. Louis, MO) staining was performed and the sections were scanned using a digital slide scanner, NanoZoomer 2.0RS (Hamamatsu, Japan).

Cholesterol measurement

Total plasma cholesterol levels of mice were assessed using the Wako Cholesterol E assay (999–02601, Fujifilm Wako Pure Chemical Corporation, Japan) according to the manufacturer’s instructions. In brief, 750μL of blood were obtained from cardiac puncture of terminally anaesthetized mice with an EDTA-coated syringe. Following centrifugation, 3μL of plasma or standard were pipetted into the assigned microplate wells. After addition of 300μL color reagent solution and incubation at 37° for 5 minutes, absorbance was measured at 600nm with 700nm set as reference wavelength using a microplate reader (Tecan Spark, Switzerland).

Statistical tests applied to experimental data

Throughout the manuscript, we used Welch’s t-tests to compare two groups if both passed the Shapiro-Wilk and Kolmogorov-Smirnov normality tests. Else we used Mann-Whitney tests. All tests were two-sided.

QUANTIFICATION AND STATISTICAL ANALYSIS

Mathematical model of HSC proliferation

We model cell turnover in a population of N hematopoietic stem cells (HSCs) using a Moran process, a frequently used stochastic framework in population genetics and evolutionary dynamics (Altrock et al., 2015; Ashcroft et al., 2017; Nowak, 2006; Traulsen et al., 2013). At each turnover event, one of the N HSCs is removed from the population by death or symmetric differentiation, and another HSC divides by self-renewal so that the number of HSCs remains constant. This process is repeated with proliferation rate b, such that the time between two turnover events along a cell lineage is distributed exponentially with mean 1/b. We note that b has two other equivalent interpretations – namely, (i) the self-renewal rate, or (ii) the sum of the death rate and symmetric differentiation rate. We note that b is not the total division rate – asymmetric divisions, in which an HSC divides into one HSC and one differentiated cell, can occur in between turnover events, but they do not alter extant variant frequencies in the HSC pool. However, in patients in which b is elevated, the total division rate is also elevated.

If a neutral variant is present in a fraction y of cells and absent in a fraction x of cells, such that x+y = 1, then the probability that a cell with the neutral variant dies or symmetrically differentiates is D_y = y/(x+y) = y, and the probability that a cell without it dies or symmetrically differentiates is D_x = x/(x+y) = x. Likewise, the probability that a cell with the neutral variant self-renews is B_y = y/(x+y) = y, and the probability that a cell without it self-renews is B_x = x/(x+y) = x. The neutral variant becomes more frequent if and only if a cell without it dies or symmetrically differentiates and a cell with it self-renews, and since these two choices are assumed to be independent, this has probability P⁺ = D_x B_y = x y. On the other hand, the neutral variant becomes less frequent if and only if a cell with it dies and a cell without it self-renews, which has probability P⁻ = D_y B_x = y x. It is possible for the neutral variant to grow in frequency multiple times in sequence, or repeatedly fall in frequency, until it either fixates in the population or goes extinct by random chance, but its mean growth rate is precisely zero, since P⁺ − P⁻ = 0.

If the variant instead confers a driver advantage, cells containing this driver variant are either less likely to die by a weight factor 1−s_d < 1 or more likely to self-renew by a weight factor 1+s_b > 1. For generality, here we consider a driver that confers both effects, though either s_d or s_b could be set to zero if only one effect is conferred. Then the death probability D_y for cells with the driver variant and D_x for cells without it are modified from the neutral case by these weight factors:

$$D_y=\frac{\left(1-s_d\right)y}{x+\left(1-s_d\right)y}\text{and}{D}_x=\frac{x}{x+\left(1-s_d\right)y}$$

where D_x + D_y = 1 as required. Likewise, the self-renewal probability B_y and B_x for cells with or without the driver variant, respectively, is given by replacing 1−s_d with 1+s_b to obtain

$$B_y=\frac{\left(1+s_b\right)y}{x+\left(1+s_b\right)y}\text{and}{B}_x=\frac{x}{x+\left(1+s_b\right)y}$$

such that B_x + B_y = 1. The driver variant increases in frequency with probability P⁺ = D_x B_y or decreases in frequency with P⁻ = D_y B_x, so that its mean growth rate per proliferation event is

$$P^{+}-P^{-}=D_x{B}_y-D_y{B}_x\approx \left(s_d+s_b\right)xy$$

where in the final step we assume that s_d and s_b are small (s_d, s_b ≪ 1). We define the total fitness effect to be s = s_d + s_b. Then, because x = 1−y and b gives the turnover rate, the average fraction $\overline{y}$ of cells containing the driver variant grows according to the dynamical growth law

$$\frac{\mathbf{\text{d}}\overline{\mathit{y}}}{\mathit{b}}=\left({\mathit{P}}^{+}-{\mathit{P}}^{-}\right)\mathbf{\text{d}}\mathit{t}=\mathit{s}\overline{\mathit{y}}(1-\overline{\mathit{y}})\mathbf{\text{d}}\mathit{t}.$$ (1)

where t measures patient age in years. This growth law for the mean driver clone size admits the logistic solution $\overline{y}={\left[1+\left(y_{50}^{-1}-1\right)e^{-bs(t-50)}\right]}^{-1}$, where y₅₀ denotes the fraction of cells with the driver variant at age t = 50 years. Because the model is stochastic, deviations about this mean behavior may be considerable; to quantify these, we solve for a realization of the driver size y at age t by numerical integration of the Langevin equation

$$\frac{\mathbf{\text{d}}\mathit{y}}{\mathit{b}}=\mathit{s}\mathit{y}(\mathbf{1}-\mathit{y})\mathbf{\text{d}}\mathit{t}+\sqrt{\frac{\mathit{y}(\mathbf{1}-\mathit{y})}{\mathit{N}}}\mathbf{\text{d}}\mathit{W},$$ (2)

where W denotes the Wiener process. Here the first term gives the effect of selection quantified by the mean growth law above, while the second term gives the effect of drift and contributes stochasticity to the process and, because random cells are chosen for division and death, is proportional to the marginal standard deviation in a binomial setting. For a heterozygous driver variant, the variant allele frequency f can then be calculated according to f = y/2.

Analysis of driver clone size

Our model of driver clone evolution is anchored in three sets of experimentally obtained data. First, we used mutation data from Razavi et al. (2019), a study which had conducted high-depth sequencing of white blood cells collected from 47 healthy 20- to 87-year-old donors to the San Diego Blood Bank; we did not include data from 124 patients with metastatic cancer as these patients would unlikely be representative of healthy hematopoiesis. To analyze these data, we made use of a property that our equation (1) predicts,

$$\mathbf{log}\frac{\mathit{y}}{\mathbf{1}-\mathit{y}}=\mathbf{log}\frac{{\mathit{y}}_{\mathbf{50}}}{\mathbf{1}-{\mathit{y}}_{\mathbf{50}}}+\mathit{b}\mathit{s}(\mathit{t}-\mathbf{50}),$$ (3)

where the left-hand side is the logit-transformed (base e) driver VAF. Correspondingly, we ran a linear regression for the logit-transformed VAF of the largest driver clone in each patient on the age t of each patient in years:

$$\log \frac{y}{1-y}=\alpha +\beta t.$$

Using the 95% confidence interval (CI) centered around the MLE for the slope and intercept of this regression, we obtained the following estimates: a typical driver clone size of 0.51% [95% CI: 0.35% to 0.74%] at age 50, and a typical driver clone expansion rate of β=b·s=0.035 ± 0.022 per year (Figure 3D, green curve).

Second, we used mutation data from Young et al. (2016), a study which had conducted error-corrected next-generation sequencing of 568 amplicons representing 54 acute myeloid leukemia driver genes in blood leukocytes from 20 healthy participants in the Nurse’s Health Study. We obtained each participant’s mutation data, consisting of all detected variants and their allele frequencies, from the supplement of Young et al. No mutations were listed for participant #3 in the supplementary information, although Young et al. reported that the range of detected variants was 1–17 across all participants. Participant #5 did not have a detectable variant at the first measurement time point. We therefore cautiously excluded this individual and proceeded with the remaining patients. Many participants had several detectable variants, potentially representing multiple co-existing or nested clones. To be consistent with our approach for Razavi et al., we first removed all variants that did not have measurable variant allele frequencies at both time points, and then chose the mutation with the largest average VAF across both measurement time points in each subject.

Using a paired version of the same linear regression analysis as for the Razavi et al. (2019) data, in which each pair of patient time points were coupled, we obtained the following estimates: a typical driver clone size of 0.36% [95% CI: 0.14% to 0.92%] at age 50, and a typical driver clone expansion rate of b·s=0.041 ± 0.023 per year (Figure 3D, blue curve).

Third, we used mutation data from Abelson et al. (2018), a study which compared benign CH to pre-AML samples from 39 to 88-year old healthy subjects. We obtained each participant’s age and AML driver gene mutation data from the supplement of Abelson et al. As with Young et al., many participants had several detectable variants, and we chose the mutation with the largest VAF. Using the same linear regression analysis, we inferred a typical driver clone size of 1.16% [95% CI: 0.89% to 1.52%] at age 50, and a typical driver clone expansion rate of b·s=0.021 ± 0.008 per year (Figure 3D, red curve).

At least two other studies have evaluated the selective advantage s conferred by mutations in clonal hematopoiesis driver genes. Buscarlet et al. (Buscarlet et al., 2017) measured how the mean VAF of driver variants changes with the age of mutated individuals and found that the estimated mean VAF of DNMT3A and TET2 variants increases by b·s=0.0395 and 0.0998 per year, respectively. Watson et al. (Watson et al., 2020) recently conducted a large meta-analysis of approximately 50,000 individuals, using variant allele frequencies in this large population to estimate the selective advantages conferred by specific variants, and concluded that the fitness effects of common mutations in DNMT3A range from b·s=0.112 to 0.187 per year. (To clarify, s as reported in Watson et al. 2020 corresponds to our b·s). The reason that the estimates of Buscarlet et al. are lower than those obtained by Watson et al. likely is that the former averaged the effects of many different mutations found in DNMT3A, while the latter calculated precise advantages for specific variants.

If the baseline proliferation rate were 28 days, then we can convert the driver expansion rate b·s per year into a fitness advantage per division by multiplying b·s by a factor of 1/b=0.077 (28 days ÷ 365 days). For the data in Watson et al., this corresponds to an advantage in the range s=0.086%−0.143%. Using our inferred b·s values from the data in Razavi et al. and Young et al., we obtain values of similar order of magnitude: s=0.270% ± 0.169% and s=0.316% ± 0.177%, respectively. For the data presented in the main figures, we use s=0.3% unless otherwise noted. Results for other s values are shown in Figure 3G.

Somatic evolution of a driver variant

We model the growth of a driver clone in each of M patients according to the HSC proliferation framework described above (Figure 3A–C). For each patient i, we track the dynamics of N HSCs that divide with a baseline proliferation rate b = b_i in the presence of a driver clone with fitness effect s and variant allele frequency f* at age t*. A fraction p of patients has an elevated proliferation rate b = B_i beginning at age T. Both b_i and B_i are drawn independently for each patient from the Ki67⁺ HSC distributions measured in the two human cohorts (Figure 2C) and scaled so that the mean baseline proliferation rate is $\overline{b}=1/(28\text{days})$ (Table S2). We solve for the mean growth and probability distribution of the driver frequency f at age t in each patient using the mean growth law (Eq. 1) and Langevin equation (Eq. 2), respectively.

Using the parameter values provided in Table S2, we plot the expected driver frequency $\overline{f}$ as solid curves, with ±1SD bars (Figure 3E). We then numerically simulate the Langevin equation by Monte Carlo across M = 500,000 independent patients and plot the distribution of driver frequencies f at age T* = 70 years (Figure 3F). From these distributions, we identify the fraction p of healthy individuals with driver clonal hematopoiesis (CH), defined as a driver mutation surpassing the detection frequency F, as well as the analogous fraction q of CH in individuals with cardiovascular disease (CVD). We compute the risk ratio RR and odds ratio OR for CH given CVD as follows:

$$\text{RR}=\frac{\mathrm{Prob}(CH\mid CVD)}{\mathrm{Prob}(CH\mid ~CVD)}=\frac{q}{p}.$$

$$\text{OR}=\frac{\mathrm{Odds}(CH\mid CVD)}{\mathrm{Odds}(CH\mid ~CVD)}=\frac{p^{-1}-1}{q^{-1}-1}.$$

To quantify the converse comparison, we can also compute the converse risk ratio CRR and converse odds ratio COR for CVD given CH by using the prevalence α of CVD, according to

$$\text{CRR}=\frac{\mathrm{P}(\mathit{CVD}\mid \mathit{CH})}{\mathrm{P}(\mathit{CVD}\mid ~\mathit{CH})}=\frac{q}{1-q}\frac{\alpha (1-q)+(1-\alpha )(1-p)}{\mathit{aq}+(1-\alpha )p}.$$

$$\mathrm{COR}=\frac{\mathrm{Odds}(CVD\mid CH)}{\mathrm{Odds}(CVD\mid ~CH)}=\frac{p^{-1}-1}{q^{-1}-1}.$$

We note that the odds ratio remains unchanged in the converse direction, since OR = COR.

Change in clonal hematopoiesis timing due to increased HSC proliferation

One of the key consequences of an increase to the HSC proliferation rate is that, by hastening the expansion of a driver clone, it on average leads to clonal hematopoiesis at a younger age. Here we compute this age difference between the timing of clonal hematopoiesis in a healthy individual and that in an individual with an elevated HSC proliferation rate.

The age t_healthy at which a patient with a baseline HSC proliferation rate b has a driver clone expand to reach detection VAF of F (or, equivalently, a detection cell fraction of Y = 2F) can be calculated by solving equation (3) for age:

$${\mathit{t}}_{\mathbf{\text{healthy}}}=\mathbf{50}+\frac{\mathbf{1}}{\mathit{b}\mathit{s}}\mathbf{log}\left(\frac{{\mathit{y}}_{\mathbf{50}}^{-\mathbf{1}}-\mathbf{1}}{{\mathit{Y}}^{-\mathbf{1}}-\mathbf{1}}\right)$$ (4)

To calculate the corresponding age t_athero for a patient with elevated HSC proliferation, we first note that the logistic property of our model gives the expected cell fraction $\overline{y}(T)$ at the age of onset T:

$$\overline{\mathit{y}}(\mathit{T})={\left[\mathbf{1}+\left({\mathit{y}}_{\mathbf{50}}^{-\mathbf{1}}-\mathbf{1}\right){\mathit{e}}^{-\mathit{b}\mathit{s}(\mathit{T}-\mathbf{50})}\right]}^{-\mathbf{1}}$$ (5)

Then, in analogy with equation (4),

$${\mathit{t}}_{\mathbf{\text{athero}}}=\mathit{T}+\frac{\mathbf{1}}{\mathit{R}\mathit{b}\mathit{s}}\mathbf{log}\left(\frac{\overline{\mathit{y}}{(\mathit{T})}^{-\mathbf{1}}-\mathbf{1}}{{\mathit{Y}}^{-\mathbf{1}}-\mathbf{1}}\right)$$ (6)

where R denotes the fold-change increase in the HSC proliferation rate b. Substitution of equation (5) into equation (6) gives

$${\mathit{t}}_{\mathbf{\text{athero}}}=\mathit{T}+\frac{\mathbf{50}-\mathit{T}}{\mathit{R}}+\frac{\mathbf{1}}{\mathit{R}\mathit{b}\mathit{s}}\mathbf{log}\left(\frac{{\mathit{y}}_{\mathbf{50}}^{-\mathbf{1}}-\mathbf{1}}{{\mathit{Y}}^{-\mathbf{1}}-\mathbf{1}}\right)$$ (7)

Finally, subtracting equation (7) from equation (4) gives the age difference for clonal hematopoiesis:

$$\mathbf{\Delta }\mathit{t}={\mathit{t}}_{\mathbf{\text{healthy}}}-{\mathit{t}}_{\mathbf{\text{athero}}}=\left(\mathbf{1}-{\mathit{R}}^{-\mathbf{1}}\right)\left(\mathbf{50}-\mathit{T}+\frac{\mathbf{1}}{\mathit{b}\mathit{s}}\mathbf{log}\frac{{\mathit{y}}_{\mathbf{50}}^{-\mathbf{1}}-\mathbf{1}}{{\mathit{Y}}^{-\mathbf{1}}-\mathbf{1}}\right)$$ (8)

In particular, we note that this age difference increases with the fold-increase R in the HSC proliferation rate, but that it decreases with the age of onset T. In other words, if the age at which the proliferation rate begins to be elevated is late, then the timing of clonal hematopoiesis will be less different than in a healthy individual that never experiences this elevated proliferation. We plot this effect in Figure S3A.

Somatic evolution of neutral variants

We study the distribution of neutral mutations in each patient at age T*, including mutations acquired both before and after patient birth. For mutations acquired before patient birth, we simulate a Yule process (Otto and Day, 2007) for the consecutive developmental divisions of a zygote into 10¹³ somatic cells, from which 100 lineages are chosen to give rise to the N HSCs at patient birth. For mutations acquired after patient birth, we use the standard coalescent associated with the Moran process (Lee-Six et al., 2018; Wakeley, 2008). For the set of all N HSCs present at age T* in each patient, we follow their ancestral lineages backwards in time to determine their phylogenetic structure. We determine the number of neutral mutations along each branch of the tree according to a Poisson process with a constant mutation rate u.

Excellent estimates for the embryonic mutation rate u are provided in a recent single HSC sequencing study (Lee-Six et al., 2018). The authors calculate that genome-wide mutation rates are approximately 1–2 per cell division in embryonic stages. An independent HSC sequencing study by Osorio et al. (Osorio et al., 2018) came to similar conclusions regarding the embryonic mutation rate and furthermore estimated that at patient birth, HSCs have undergone approximately 40 divisions, which is in excellent agreement with our embryogenesis model (see above). We therefore use u = 1.5 mutations during embryogenesis (Table S2).

We compute the number of descended cells with each mutation at age T* to obtain a VAF distribution for the neutral mutations in each patient. By integrating this VAF distribution over large frequencies, we can obtain the number of neutral mutations with a VAF that exceeds the detection threshold F.

We analyze this process in mathematical detail (Supplementary Analysis) as a stochastic population model of mutation (Karlin and McGregor, 1962) and simulate it independently in M patients, using the same procedure as described above for elevated proliferation rates beginning at age T in some patients. We calculate the relative increase in neutral variants at intermediate VAFs in patients with an elevated proliferation rate, relative to control patients with a baseline proliferation rate, for two different pool sizes N (Figure 4).

Prediction of Tet2^−/− growth in mouse model

To predict the expected growth of the Tet2^−/− fraction in Ldlr^−/− mice, we expanded our model to explicitly include neutrophil and monocyte populations as they are replenished by HSC differentiation (Figure 5B). In this formulation, differentiated cells die at rates given by the reciprocal of their mean lifespan. When a differentiated cell dies, it is replaced with a daughter cell produced by an asymmetric division of an HSC. However, with a probability described below, two differentiated cells can instead be simultaneously replaced by both daughter cells generated by the symmetric differentiation of an HSC. In this case, another HSC is selected to undergo a self-renewal division to ensure that the HSC pool size remains consistent, and HSCs with the Tet2^−/− mutation are (1+s) times as likely to be chosen for this self-renewal. It is this process that allows the Tet2^−/− mutation to expand in the HSC pool over time and thereby become increasingly represented also in the differentiated cell populations. We calibrate the probability of this simultaneous replacement to be the value needed to obtain the required proliferation rate b, defined in the same way as before to be the rate of cell turnover in the HSC pool.

Using this expanded model, we plot the expected cell fraction of Tet2^−/− as a mouse ages using the parameter values in Table S3 and a range of driver effect sizes s (Figure 5C–E). For mice with atherosclerosis, we increase b by 75% as an illustrative value. Average behavior is calculated via numerical integration of the system and quantified as a fold-change in Tet2^−/− fraction relative to the initial measurement. I

We also explore a modified version of this model in which HSCs with a driver variant are 25% less likely to be chosen than HSCs without the driver variant (Figure S1H). Because this change would reduce the total division rate of HSCs with the driver variant and increase that of HSCs without, we compensate by increasing the rate of self-renewal divisions for HSCs with the driver variant, on top of the already existing driver advantage, and decreasing that for HSCs without. The reverse scenario is explored for a 25% increase in differentiation likelihood associated with a driver variant (Figure S1I).

Analysis of Tet2^−/− growth in mouse model

We assessed whether mice in our experimental group (either atherosclerosis induced by atherogenic diet, see Fig. 5F–J, or sleep fragmentation, see Fig. 5L–M) showed evidence of a greater proliferation rate by means of a more rapid expansion in the fraction of Tet2^−/− cells over time when compared to mice in the control group. We again used the property given by equation (3), in which the logit-transformed Tet2^−/− fraction is predicted by our model to increase linearly with age, and we estimated this rate of increase b·s, allowing it to differ for each cohort.

Our data can be represented as the Tet2^−/− fraction y_iτ of each mouse i at timepoint τ, where tτ is the time in days since the first measurement. Then equation (3) can be rewritten as

$$\log \frac{y_{i\tau }}{1-y_{i\tau }}-\log \frac{y_{i1}}{1-y_{i1}}=bs\left(1+R{D}_i\right)t_{\tau },$$

where R denotes the relative increase (or decrease, if negative) in the proliferation rate associated with the experimental group relative to the control group, and D_i is an indicator variable such that D_i=0 for all mice in the control group, and D_i=1 for all mice in the experimental group. Expanding the right-hand side of the above equation then gives

$$bs\left(1+R{D}_i\right)t_{\tau }=\beta t_{\tau }+{\beta }^{\prime }{D}_i{t}_{\tau },$$

where the linear coefficients are the rate of Tet2^−/− fraction increase on a logit scale, β = b·s, and the additional rate of Tet2^−/− fraction increase on a logit scale associated with the experimental group, β′ = b·s·R.

We obtain estimates for these linear coefficients using standard linear regression on our data, and the null hypothesis that the experimental and control groups show no difference in proliferation rates is assessed by the p-value associated with β′ = 0. We further obtain a numerical estimate for the relative change in the proliferation rate associated with the experimental group by computing the quotient R = β′/β.

Comparison of inferred parameters between experiments

We statistically assessed whether our estimates for the Tet2^−/− expansion rate b·s and fold-increase in the HSC proliferation rate were consistent between our two experiments in mouse: atherogenic diet and sleep fragmentation. To evaluate the null hypothesis that each parameter x from the atherogenic diet experiment was equal to the corresponding parameter y from the sleep fragmentation experiment (or equivalently, that δ = x − y = 0), we computed the mean and standard error of δ from our previously described regressions, which we used to conduct a z-test.

We found no statistically significant difference between the scaled driver effect b·s in the atherogenic diet experiment with that in the sleep fragmentation experiment (neutrophils p = 0.44, monocytes p = 0.72). Similarly, we find no statistically significant difference in the proliferation fold-increase estimated for both experiments (neutrophils p = 0.55, monocytes p = 0.27).

The quantitative similarity of these two experimental conditions lends further support to our conceptual framework (Fig. 7), in which both conditions act to accelerate the clonal hematopoiesis of a driver clone by increasing the HSC proliferation rate.

Driver expansion in a growing HSC population

Our model considers somatic evolution in an HSC population of constant size, but it is easily adapted to an HSC population that is growing or fluctuating in size, and our key results remain unchanged even in this scenario.

For example, during driver clone expansion, we might consider the case in which the cells harboring a driver variant divide 1 + s_b times more often and die 1 − s_d times less often than the cells that are not, resulting in accelerating HSC population growth as the driver clone becomes more frequent. If the driver variant is present in Y cells and absent in X cells, where X+Y is no longer constant but instead growing, then we can write the following dynamic growth laws for these two subpopulations:

$$\begin{gathered} \frac{\text{d}X}{\text{d}t}=(b-d)X, \\ \frac{\text{d}Y}{\text{d}t}=\left[b\left(1+s_b\right)-d\left(1-s_d\right)\right]Y, \end{gathered}$$

which have the solutions X = X₅₀e^{(b−d)(t−50)} and Y = Y₅₀e^{[b(1+s)−d](t−50)}, where X₅₀ and Y₅₀ denote the number of HSCs without and with the driver variant at age 50, respectively. Then the expected driver frequency, denoted y as before, grows according to

$$\overline{y}=\frac{Y}{X+Y}={\left(1+\frac{X}{Y}\right)}^{-1}={\left(1+\frac{X_{50}{e}^{(b-d)(t-50)}}{Y_{50}{e}^{\left[b\left(1+s_b\right)-d\left(1-s_d\right)\right](t-50)}}\right)}^{-1}.$$

In terms of the driver frequency at age 50, y₅₀, this simplifies to the following result:

$$\overline{y}={\left[1+(y_{50}^{-1}-1)e^{-\left(b{s}_b+d{s}_d\right)(t-50)}\right]}^{-1},$$

which is the same logistic growth law as before, when we had assumed a constant population size. Moreover, in the special case in which the HSC would be constant over time if the driver never appeared, then we would have b = d, giving precisely the same result as our solution to equation (1), namely $\overline{y}={\left[1+(y_{50}^{-1}-1)e^{-bs(t-50)}\right]}^{-1}$. In patients with elevated proliferation rates b due to atherosclerosis or other conditions, the driver frequency would grow more quickly with age.

Hence a driver which causes the HSC population to expand (in addition to selectively promoting its own expansion within the HSC pool as before) will exhibit identical expected frequency growth as a driver which does not alter the size of the HSC population over time. In this paper, we choose to assume a constant HSC population size so that we can report the value we used in each simulation and study the effects of changing this value (see Fig. 3H), but even if we did not, we would observe the same relationship between elevated proliferation rates and accelerated driver clone expansion.

Supplementary Material

Figure S1

Figure S1. Characteristics of mice and humans with atherosclerosis and exploration of different driver effects on differentiation. Related to figures 1, 2 and 3. (A) Leukocytes, (B) neutrophils, (C) monocytes and (D) Ly6C^high monocytes in Apoe^−/− mice fed with chow (control) or atherogenic diets for 10 weeks. (E) BrdU incorporation in HSCs of Apoe^−/− and C57BL/6J mice fed with chow diets for 10 weeks. (F) Age and (G) sex in human control and atherosclerosis cohorts. Unpaired t-tests with Welch’s correction were used throughout. Fisher’s exact test was used in (G). Data are represented as mean ± SEM. All tests were two-sided. ** p<0.005; *** p<0.0005. (H, I) Predicted mutant expansion for a driver that inhibits (H) or facilitates (I) differentiation. We compare our model of a driver clone with elevated self-renewal proliferation to a similar model in which the driver clone has both elevated self-renewal and a 25% bias towards (H) or against (I) self-renewal cell fates rather than differentiation fates (STAR methods). Here, we plot the simulated driver clone size for s = 17%, with a proliferation rate b = 1/(17.5 days) in the control group and a 75% elevation of b associated with atherosclerosis in three cell types, although we note that conceptually equivalent results would be obtained for other choices of b and s. The y-axis denotes fold change of the Tet2^−/− fraction with respect to the starting time point.

3

Figure S2. Exploration of different ages of atherosclerotic disease age onset. Related to figure 3. (A) Expected driver VAF expansion over time for varying ages of onset. Relative to a healthy patient with a baseline proliferation rate (green curve), a patient with an elevated proliferation rate (blue curves) beginning at age 30, 40, 50, or 60, will have more rapid driver clone expansion. As a result, the age at which the driver clone becomes detectable (boxed values) is earlier than in healthy patients, and this difference is more pronounced when onset is at a young age. Parameter values are set as in Table S2. (B) Predicted driver VAF distributions at age 70 across two patient cohorts for varying ages of onset. Relative to the healthy cohort (green), patients in the atherosclerosis cohort (blue) have an elevated proliferation rate beginning at age 30, 40, 50, or 60, corresponding to the Ki67+ HSC distributions measured in the two human cohorts as shown in Figure 2C. The risk and odds ratios quantify the increased risk and odds for having a detectable driver clone associated with having atherosclerotic HSC proliferation elevation.

4

Figure S3. Sensitivity analysis for the driver clone model. Related to Figure 3. (A) Shift in CH timing as a function of the age of onset. Our model predicts that patients with various fold-increases in HSC proliferation (boxed values) that begin at some onset age T will on average have a detectable driver clone earlier than patients with a baseline HSC proliferation rate. This shift in timing, denoted Δt, is plotted here as a function of the onset age T, using s*b = 0.041/year (inferred from Young et al., Fig. 3D) and an R = 1.5-fold increased proliferation, alongside a frequency of f* = 0.51% at age t* = 50 years (Table S2) and a detection frequency F = 2%. (B) Fold-increase in driver VAF in a patient with twice the HSC proliferation rate as a healthy person, as a function of the age of onset and the age at sequencing. All other parameters are set as indicated in Table S2. When patient blood is sequenced after the age of onset, we find that patients with elevated HSC proliferation rates have larger driver clones, indicated by the values and colors in each grid box. (C) Predicted driver VAF distributions at age 70 across two patient cohorts for various model parameter choices. Relative to the healthy cohort (green), patients in the atherosclerosis cohort (blue) have an elevated proliferation rate (mean fold-increase = 1.25× in left column, 1.75× in right column), with a variance corresponding to the Ki67+ HSC distributions measured in the two human cohorts as shown in Figure 2C. The risk and odds ratios quantify the increased risk and odds for having a detectable driver clone associated with having atherosclerotic HSC proliferation elevation. These ratios are only very slightly sensitive to the HSC pool size (N = 10,000 cells in top column, N = 100,000 cells in bottom column). For all other parameters, we use the values provided in Table S2. (D) Sensitivity to two additional model parameters. Expected outcomes do not vary with HSC pool size but are primarily driven by atherosclerosis-driven proliferation increase.

5

Figure S4. Expanding HSC pool scenarios and genetic drift. Related to Figures 3 and 4. (A) Expected driver fraction growth is invariant to HSC pool size expansion or fluctuation. Left panel, the driver clone size (red) and non-driver clone size (gray) vary with patient age in one of four different scenarios: constant HSC pool size, HSC pool size expansion due to the driver clone only, HSC pool size expansion in both clones due to aging, and HSC pool size fluctuation. Left axis shows cell numbers for an HSC pool size of N=10,000, right axis for N=100,000. Right panel, the expected driver cell fraction (left axis) and expected driver VAF (right axis) are exactly the same at all ages, regardless of which of the four scenarios is modeled. (B) Schematic of genetic drift in a hypothetical cell population. Top row: Each cell, initially genetically distinct (different colors), can at random be chosen for death (cross) or symmetric differentiation (double arrow), events which must be compensated by a symmetric self-renewal division (rounded arrow). Over time, the population of cells loses genetic diversity. Bottom row: Beginning in middle age, the rate of cell turnover (proliferation) is increased in some patients, such that the genetic changes due to drift occur more rapidly.

6

Figure S5. Additional analyses of neutral evolution. Related to Figure 4. (A-B), Accumulation of neutral variants in the genome (left axis) and exome (right axis) during aging. The two overlaid curves depict the number of neutral variants across all HSCs that surpass a 2% (A) or 8% (B) VAF detection threshold (with ±1 SD bars), for both the healthy cohort (green) and the atherosclerosis cohort (blue) in simulations. (C), Neutral VAF distribution at age 70 with extreme atherosclerosis-driven effects. The proliferation rates in the atherosclerosis cohort were set to correspond to the highest proliferation rate observed in our human atherosclerosis data, giving rise to up to a 30-fold excess of neutral variants at detectable frequencies (bottom purple plot). For both panels, we used N = 30,000 HSCs and the parameters as listed in Table S2. (D) Sensitivity of neutral mutation accumulation to model parameters. Each box color corresponds to the fold-increase in the number of detected neutral variants surpassing a VAF detection threshold of 2% in a typical atherosclerosis patient relative to a control patient at age 70. Boxes with black outlines correspond to the assumed parameter pairs used elsewhere in the figure and this study. (E) Elevated HSC proliferation in a growing HSC pool leads to excess neutral mutations. Variant allele frequency (VAF) distribution of neutral somatic variants for an HSC pool size that grows exponentially from N = 10,000 cells at birth to N = 100,000 cells at age 70, averaged across patients at age 70 with initial mutation burdens determined by simulated prenatal cell divisions. Patients in the atherosclerosis cohort (blue) have elevated proliferation rates consistent with Figures 2C and 3F that lead to more neutral variants at intermediate VAFs relative to patients in the healthy cohort (green).

7

Figure S6. Tet2^−/− fraction growth in the Ldlr^−/− mouse model of atherosclerosis. Related to Figure 5. (A) Cholesterol levels and (B) BrdU⁺ LSKs in Ldlr^−/− mice fed with chow (control) or atherogenic diets at the end of the observation period. (C) Correlations between Tet2^−/− fractions in different cell types (HSCs, monocytes, neutrophils, B cells and T cells) at the end of the observation period. An unpaired t-test with Welch’s correction was used in (A), a Mann-Whitney test was used in (B). Data are represented as mean ± SEM. All tests were two-sided. Pearson correlation coefficients are shown in (C). ** p<0.005; **** p<0.0001.

8

Figure S7. Hyperlipidemia and HSC proliferation. Related to Figures 5 and 6. (A) HSC proliferation and Tet2^−/− fraction growth in wild type C57BL/6J mice. Experimental design. A mixture of Tet2^−/− and wild type bone marrow is transplanted into lethally irradiated wild type recipients. Mice are randomized to receive atherogenic or chow diet. Their blood is analyzed biweekly. At the end of the observation period (74 days), BrdU incorporation in HSCs is analyzed. (B) The Tet2^−/− (CD45.2) fraction of monocytes and neutrophils is shown across all peripheral blood measurements. Error bars indicate the SEM; p-values are derived from linear regression of the logit-transformed baseline-normalized data. (C) Plasma cholesterol levels in the two groups on day 74. P-value is calculated with a two-sided Mann-Whitney test. (D) BrdU incorporation in HSCs and LSKs after 74 days on control or atherogenic diets. Significance is assessed with a two-sided Welch’s t-test (E) Hematoxylin and eosin staining of aortic roots in representative mice from the control and atherogenic diet groups. (F) HSC proliferation in Ldlr^−/− mice after a 3-week exposure to atherogenic diet. Experimental design outline. Ldlr^−/− mice were randomized to atherogenic or control (chow) diet groups. After 21 days, BrdU incorporation in HSCs was assessed via flow cytometry. (G) Total plasma cholesterol levels in the two groups after 3 weeks. P-value is calculated with Welch’s t-test. (H), Comparison of total plasma cholesterol levels in Ldlr^−/− mice after 3 and 19 weeks on atherogenic or control diets. (I) Hematoxylin and eosin staining of aortic roots in representative Ldlr^−/− mice from the control and atherogenic diet groups. (J) BrdU incorporation in HSCs and LSKs after 3 weeks on control or atherogenic diets. (K) Fraction of Tet2^−/− HSCs and LSKs at the end of the sleep fragmentation experiment (Figure 6). Since engraftment varies stochastically and every mouse has a slightly different fraction of mutant cells at the outset of the experiment, the percentage of Tet2^−/− HSCs or LSKs is normalized to baseline (divided by the CD45.2⁺ monocyte percentage at day 0). Data are represented as mean ± SEM. P-values are calculated with a two-sided Welch’s test. * p<0.05; *** p<0.0005.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Biotin anti-human CD2	BioLegend	Cat# 300204, RRID:AB_314028
Biotin anti-human CD3	BioLegend	Cat# 300304, RRID:AB_314040
Biotin anti-human CD4	BioLegend	Cat# 300504, RRID:AB_314072
Biotin anti-human CD7	Thermo Fisher Scientific	Cat# 13-0079-82, RRID:AB_891490
Biotin anti-human CD8a	BioLegend	Cat# 301004, RRID:AB_314122
Biotin anti-human CD10	Thermo Fisher Scientific	Cat# 13-0108-82, RRID:AB_763433
Biotin anti-human CD11b	BioLegend	Cat# 301304, RRID:AB_314156
Biotin anti-human CD14	BioLegend	Cat# 325624, RRID:AB_2074052
Biotin anti-human CD19	BioLegend	Cat# 302204, RRID:AB_314234
Biotin anti-human CD20	Thermo Fisher Scientific	Cat# 13-0209-82, RRID:AB_657690
Biotin anti-human CD56	BioLegend	Cat# 318320, RRID:AB_893390
Biotin anti-human CD235ab	BioLegend	Cat# 306618, RRID:AB_2565773
APC anti-human CD34	BD Biosciences	Cat# 340667, RRID:AB_400531
PE/Cy7 anti-human CD38	BioLegend	Cat# 303516, RRID:AB_2072782
FITC anti-human CD90	BD Biosciences	Cat# 555595, RRID:AB_395969
PB anti-human CD45RA	Thermo Fisher Scientific	Cat# MHCD45RA28, RRID:AB_10371901
PE anti-human CD123	BD Biosciences	Cat# 554529, RRID:AB_395457
BV605 anti-human Ki-67	BioLegend	Cat# 350522, RRID:AB_2563863
FITC anti-mouse Ly-6G	BioLegend	Cat# 127606, RRID:AB_1236494
PE anti-mouse/human CD11b	BioLegend	Cat# 101208, RRID:AB_312791
PerCP/Cy5.5 anti-mouse CD3e	BD Biosciences	Cat# 551163, RRID:AB_394082
BV421 anti-mouse CD115	BioLegend	Cat# 135513, RRID:AB_2562667
BV605 anti-mouse Ly-6C	BioLegend	Cat# 128035, RRID:AB_2562352
BV711 anti-mouse CD8a	BioLegend	Cat# 100748, RRID:AB_2562100
AF700 anti-mouse CD4	BioLegend	Cat# 100430, RRID:AB_493699
APC anti-mouse CD45.2	BioLegend	Cat# 109814, RRID:AB_389211
PE/Cy7 anti-mouse CD45.1	BD Biosciences	Cat# 560578, RRID:AB_1727488
APC/Cy7 anti-mouse CD19	BioLegend	Cat# 115529, RRID:AB_830706
APC/Cy7 anti-mouse/human B220	BioLegend	Cat# 103224, RRID:AB_313007
APC/Cy7 anti-mouse NK1.1	BioLegend	Cat# 108724, RRID:AB_830871
Biotin anti-mouse CD3	BioLegend	Cat# 100304, RRID:AB_312669
Biotin anti-mouse CD4	BioLegend	Cat# 100404, RRID:AB_312689
Biotin anti-mouse CD8a	BioLegend	Cat# 100704, RRID:AB_312743
Biotin anti-mouse CD49b	BioLegend	Cat# 103522, RRID:AB_2566366
Biotin anti-mouse CD90.2	BioLegend	Cat# 105304, RRID:AB_313175
Biotin anti-mouse CD19	BioLegend	Cat# 115504, RRID:AB_313639
Biotin anti-mouse B220	BioLegend	Cat# 103204, RRID:AB_312989
Biotin anti-mouse NK1.1	BioLegend	Cat# 108704, RRID:AB_313391
Biotin anti-mouse TER119	BioLegend	Cat# 116204, RRID:AB_313705
Biotin anti-mouse CD11b	BioLegend	Cat# 101204, RRID:AB_312787
Biotin anti-mouse CD11c	BioLegend	Cat# 117304, RRID:AB_313773
Biotin anti-mouse Gr-1	BioLegend	Cat# 108404, RRID:AB_313369
FITC anti-mouse CD34	BD Biosciences	Cat# 553733, RRID:AB_395017
PE anti-mouse CD45.2	BioLegend	Cat# 109808, RRID:AB_313445
PerCP/Cy5.5 anti-mouse CD150	BioLegend	Cat# 115922, RRID:AB_2303663
PE/Cy7 anti-mouse c-kit	BioLegend	Cat# 105814, RRID:AB_313223
AF700 anti-mouse CD48	BioLegend	Cat# 103426, RRID:AB_10612755
BV421 anti-mouse CD45.1	BioLegend	Cat# 110732, RRID:AB_2562563
BV605 anti-mouse Sca-1	BioLegend	Cat# 103244, RRID:AB_2563312
BV711 anti-mouse CD16/32	BioLegend	Cat# 101337, RRID:AB_2565637
PE anti-mouse CD8a	BioLegend	Cat# 100708, RRID:AB_312747
PerCP/Cy5.5 anti-mouse CD45.1	BioLegend	Cat# 110726, RRID:AB_893345
PacificBlue anti-mouse CD4	BioLegend	Cat#100428, RRID:AB_493647
BV605 anti-mouse CD115	BioLegend	Cat#135517, RRID:AB_2562760
BV711 anti-mouse/human CD11b	BioLegend	Cat#101242, RRID:AB_2563310
APC anti-mouse CD3	BioLegend	Cat#100236, RRID:AB_2561456
APC anti-mouse CD90	BioLegend	Cat#140312, RRID:AB_10640728
APC anti-mouse TCRβ	BioLegend	Cat#109212, RRID:AB_3135435
APC anti-mouse CD19	BioLegend	Cat#152410, RRID:AB_2629839
AF700 anti-mouse CD45.2	BioLegend	Cat#109822, RRID:AB_493731
APC/Cy7 anti-mouse Ly6C	BioLegend	Cat#128026, RRID:AB_10640120
PE anti-mouse/human B220	BioLegend	Cat#103208, RRID:AB_312993
PE anti-mouse CD19	BioLegend	Cat#115508, RRID:AB_313643
PE anti-mouse CD49b	BioLegend	Cat#108908, RRID:AB_313415
PE anti-mouse Ter119	BioLegend	Cat#116208, RRID:AB_313709
PE anti-mouse CD90.2	BioLegend	Cat#105308, RRID:AB_313179
PE anti-mouse CD11b	BioLegend	Cat#101208, RRID:AB_312791
PE anti-mouse CD11c	BioLegend	Cat#117308, RRID:AB_313777
PE anti-mouse Ly6G	BioLegend	Cat#127608, RRID:AB_1186099
PE anti-mouse IL7Rα	BioLegend	Cat#135010, RRID:AB_1937251
PerCP/Cy5.5 anti-mouse CD16/32	BioLegend	Cat#101324, RRID:AB_1877267
BV421 anti-mouse CD115	BioLegend	Cat#135513, RRID:AB_2562667
BV605 anti-mouse CD150	BioLegend	Cat#115927, RRID:AB_11204248
BV711 anti-mouse CD45	BioLegend	Cat#103147, RRID:AB_2564383
APC/Cy7 anti-mouse Sca-1	BioLegend	Cat#108126, RRID:AB_10645327
Biological Samples
Healthy human bone marrow	HemaCare BioResearch Products	Cat# BM009C-2
Healthy human bone marrow	AcceGen Biotech	Cat# ABC-TC3122
Critical Commercial Assays
APC BrdU Flow Kit	BD Biosciences	Cat# 552598
Experimental Models: Organisms/Strains
C57BL/6J mice	The Jackson Laboratory	Cat# 000664
B6.129P2-Apoetm1Unc/J mice	The Jackson Laboratory	Cat# 002052
B6(Cg)-Tet2tm1.2Rao/J mice	The Jackson Laboratory	Cat# 023359
B6.129S7-Ldlrtm1Her/J mice	The Jackson Laboratory	Cat# 002207
B6.SJL-Ptprca Pepcb/BoyJ mice	The Jackson Laboratory	Cat# 002014
Software and Algorithms
FlowJo 10.6	BD	https://www.flowjo.com/
Prism 8	GraphPad Software	https://www.graphpad.com/
Mathematica, Matlab, R and Python code producing analyses in this paper	This paper	https://github.com/AlexHeyde/clonal-hematopoiesis

Highlights:

• HSC proliferation is elevated in mice and humans with atherosclerosis

• Increased proliferation accelerates somatic evolution and clonal hematopoiesis (CH)

• Measured rates imply several-fold increased risk of CH in atherosclerosis patients

• Mutant expansion is accelerated in mice with increased HSC proliferation