Correlation study to identify the factors affecting COVID-19 case fatality rates in India

Abstract

Background and aims

In India, COVID-19 case fatality rates (CFRs) have consistently been very high in states like Punjab and Maharashtra and very low in Kerala and Assam. To investigate the discrepancy in state-wise CFRs, datasets on various factors related to demography, socio-economy, public health, and healthcare capacity have been collected to study their association with CFR.

Methods

State-wise COVID-19 data was collected till April 22, 2021. The latest data on the various factors have been collected from reliable sources. Pearson correlation, two-tailed P test, Spearman rank correlation, and Artificial Neural Network (ANN) structures have been used to assess the association between various factors and CFR.

Results

Life expectancies, prevalence of overweight, COVID-19 test positive rates, and H1N1 fatality rates show a significant positive association with CFR. Human Development Index, per capita GDP, public affairs index, health expenditure per capita, availability of govt. doctors & hospital beds, prevalence of certain diseases, and comorbidities like diabetes and hypertension show insignificant association with CFR. Sex ratio, health expenditure as a percent of GSDP, and availability of govt. hospitals show a significant negative correlation with CFR.

Conclusion

The study indicates that older people, males of younger age groups, and overweight people are at more fatality risk from COVID-19. Certain diseases and common comorbidities like diabetes and hypertension do not seem to have any significant effect on CFR. States with better COVID-19 testing rates, health expenditure, and healthcare capacity seem to perform better with regard to COVID-19 fatality rates.

1. Introduction

In India, Kerala reported the first case of Coronavirus disease 2019 (COVID-19) on January 27, 2020 [1]. As per the data from the Ministry of Health and Family Welfare (MoHFW), Govt. of India, by April 22, 2021, more than 1.6 crore people have been infected with the COVID-19 in India, and more than 1.85 lakh people have lost their lives. India has been again witnessing a huge surge in COVID-19 cases and deaths from mid-February 2021. As of April 22, 2021, more than 3.3 lakh new cases and 2,200 deaths were being reported every day in India.

Since the beginning of the COVID-19 pandemic in India from late January 2020, some states like Punjab and Maharastra have consistently been showing very high COVID-19 deaths with respect to the confirmed cases. Whereas the number of deaths in states like Kerala and Assam has been low compared to the number of cases. So it becomes necessary to inspect for the factors that are impacting the varied COVID-19 death rates among Indian states and union territories (UTs). This will help the government and various agencies in framing proper policies and guidelines in curbing the number of deaths from COVID-19.

Sanyaolu et al. found that COVID-19 patients with pre-existing comorbidities such as hypertension and diabetes had more possibilities of developing serious disease symptoms. Also, the patients with comorbidities who are aged 65 years or more have more ICU admissions and COVID-19 fatality rates [2]. Elezkurtaj et al. performed autopsies on 26 patients who died from COVID-19 and also evaluated their clinical records to find that the most common causes of deaths were due to suppurative pulmonary infection, with multiple comorbidities such as obesity, heart diseases, and hypertension were present in most of the patients. Their research shows that the reasons for deaths were directly related to COVID-19 in most of the patients, with only contributory effects of pre-existing comorbidities [3]. Down et al. emphasized the significant role of demography, especially the population age structure in explaining the differences in the COVID-19 death rates across countries. They analyzed the age structure role in deaths in Italy and South Korea and showed that countries with older population had very high fatality rates compared to the countries with younger population [4]. Satyaki et al. used supervised machine learning techniques like Stochastic Gradient Descent (SGD), Support Vector Machine (SVM), Nearest Centroid (NC), Decision Trees (DTs), and Gaussian Naive Bayes (NB), and used COVID-19 data from the different states of US to suggest that the mortality rates tend to be driven by age, pre-existing conditions and not by ethnicity, gender or healthcare facilities [5]. Guan et al. analyzed data from 1590 hospitalized COVID-19 patients from across mainland China to assess the impact of comorbidities on them. They concluded that patients with any comorbidity (hypertension, diabetes, COPD, and malignancy) showed poorer clinical results than those without any comorbidities [6]. Shams et al. analyzed COVID-19 data from 18 worst affected countries to conclude that the fatality rate among people above the age of 60 increases exponentially with age [7]. Omori et al. concluded that even though there were large variations in the number of COVID-19 deaths in Japan, Spain, and Italy, the age distributions of deaths exhibit very little variations among these countries, suggesting that the COVID-19 mortality rate depends on age, irrespective of region or race [8]. Ghisolfi et al. estimated the COVID-19 infection fatality rates (IFR) for various low- and middle-income countries and suggested that IFR vary with age, gender, comorbidities, and health infrastructure. Lower fatality rates in low-income countries due to demographic factors were partially offset by their disadvantages in health infrastructure [9]. Khan et al. used the negative binomial regression model to assess the Covid-19 case fatality rate's association with healthcare capacity (number of midwives, physicians, nurses, and hospital beds per thousand people), Civil society index, and health expenditure as a percentage of GDP using the data from 86 countries. In the analysis, they found that the healthcare capacity was significantly negatively correlated with case fatalities, whereas civil society variables and health expenses were statistically insignificant but positively correlated with case fatalities [10]. Banik et al. analyzed various factors that affect the COVID-19 fatality rates using linear regression models across 29 countries. Their study revealed that BCG vaccination, poverty, age structure, and public health system were significantly affecting the fatality rates [11]. Alkhouli et al. in a study on 14,712 COVID-19 patients concluded that men had significantly higher mortality than women [12]. Lee et al. analyzed 800 COVID-19 symptomatic patients with cancer to find that fatality from COVID-19 among cancer patients were mainly affected by age, sex, and comorbidities. They were couldn't find any proof that cancer patients taking anticancer treatments had a different COVID-19 mortality rate than those cancer patients who are not on any treatment [13]. Mehta et al. identified 218 COVID-19 positive patients with cancer in Montefiore Health System (New York, NY). The age-adjusted COVID-19 case fatality rate (CFR) in cancer patients was found to be significantly higher than noncancer patients [14]. Arghadip et al. found that in India, the COVID-19 death rate was among the lowest in the world. They suggested that the current mutations in COVID-19 virus strains in circulation, genetic factors, innate immunity, and meteorological factors like humidity and temperature were some of the reasons behind the low fatality rates among Indians [15].

Several correlations and machine learning-based research have been done since the start of the COVID-19 pandemic to associate the disease features like virulence, severity, and fatality rates, etc. with factors related to demographics, socio-economic conditions of the population, comorbidities, and health infrastructure. Wang et al. in a study on COVID-19 patients from Hubei, China, performed Pearson correlation and Spearman Rank correlation analysis accompanied by a 2-tailed significance test (P test) to conclude that the severity of COVID-19 was associated with patient's age and comorbidities [16]. Liu et al. performed a correlation analysis along with a two-tailed P test on COVID-19 fatality rates with Human Development Index (HDI) in Italy. HDI is an index that depends on the life expectancy, education level, and living standard of a given population. Their analysis concluded that HDI is positively correlated with COVID-19 fatality rates [17]. Wei et al. in a study on 36 OECD countries and Taiwan used Spearman rank correlation to find that testing coverage was highly correlated with COVID-19 Case Fatality Rate as compared to just the testing numbers [18]. Mollalo et al. prepared a database of 57 variables and used Multi-layer Perceptron (MLP), also called Artificial Neural Network (ANN) to predict the COVID-19 case incidence across the United States. Their results indicated that an MLP with one hidden layer could explain about 65% of the association with the ground reality of COVID-19 [19]. Kumar et al. used Spearman rank correlation together with a 2-tailed significance test (P test) and Artificial Neural Network (ANN) technique to find the correlation between meteorological parameters and COVID-19 spread. It was found in this study that pressure and relative humidity had the strongest association with the number of active COVID-19 cases [20].

2. Data sources and methodology

2.1. Data sources

For this study, the state-wise cumulative data of COVID-19 testing numbers, number of cases, recovered patients, and deaths were taken from sources like COVID19-India API (http://api.covid19india.org) and the Ministry of Health and Family Welfare (MoHFW), Govt. of India (https://www.mohfw.gov.in/) till April 22, 2021.

Demographic factors such as state-wise sex ratios in different age groups are taken from 2011 census data (https://censusindia.gov.in/). State-wise life expectancies at different age levels are taken from SRS-based Abridged life Table 2014–18, Census India (https://censusindia.gov.in/Vital_Statistics/SRS_Life_Table).

Socio-economic factors like state-wise per capita GDP data are taken from the Ministry of Statistics and Program Implementation (MoSPI), Govt. of India (http://mospi.nic.in/). States and union territory-wise human development index (HDI) data is taken from Global Data Lab that translated data from UNDP HDI to the subnational level (https://globaldatalab.org/). Data on the performance of Indian states by governance is taken from scientifically rigorous ‘Public Affairs Index 2020’ published by Public Affairs Center (https://pacindia.org/).

Indian state-level datasets on the prevalence of diseases such as Diabetes, Overweight, Respiratory diseases like COPD and Asthma, and Cancer incidence are taken from research articles in reputable and reliable journals The Lancet Global Health and The Lancet Oncology [[21], [22], [23]]. Data on the prevalence of hypertension in the age group of 15–49 is taken from a reliable research article in the journal BMJ Open [24].

National Health Profile (NHP)-2019 published by Central Bureau of Health Intelligence, Ministry of Health and Family Welfare (MoHFW), Govt. of India (https://www.cbhidghs.nic.in/) is used for collecting data on the state-wise prevalence of disease like diabetes, hypertension in all age groups, common cancers, H1N1 (swine flu) fatality rates (2017), stroke and cardiovascular diseases (CVDs). NHP-2019 is also used for state-wise data on factors related to healthcare capacity such as the number of government allopathic doctors, health expenditure per capita, health expenditure as a percent of GSDP, number of govt. hospitals, and the number of beds available in govt. hospitals.

2.2. Case fatality rate (CFR) and test positive rate (TPR)

According to a scientific brief by World Health Organisation (WHO) [25], for an ongoing epidemic it would be more appropriate to use the following formula for COVID-19 Case Fatality Rate (CFR, in percentage):

$$CaseFatalityRatio\left(CFR,in\%\right)=\frac{NumberofDeaths}{Numberofdeaths+Numberofre\mathrm{cov}eredpatients}\times 100$$

Test Positive Rate (TPR) is the percentage of people who tested positive with respect to the total number of COVID-19 tests done in a given region.

$$TestPositiveRate\left(TPR,in\%\right)=\frac{TotalNumberofPositiveCases}{TotalNumberofTests}X100$$

High Test Positive Rate indicates a lower number of testing per positive case.

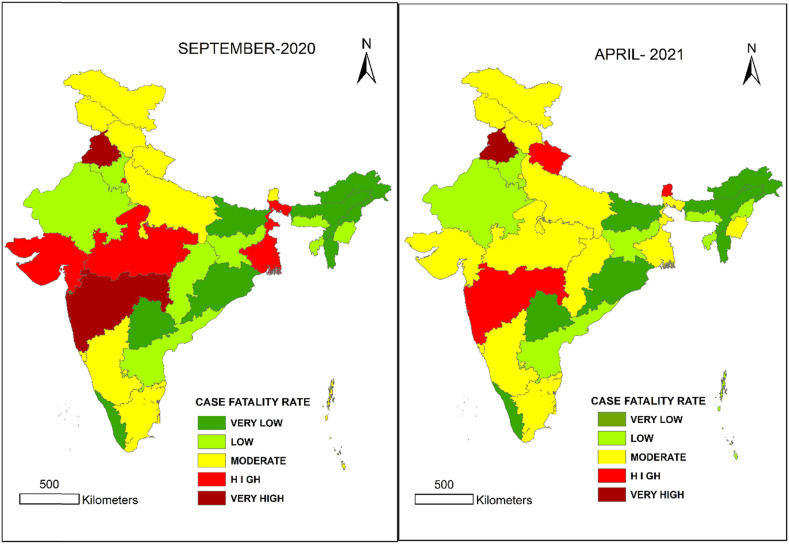
The COVID-19 data has been analyzed to calculate the CFRs. State-wise India maps, comparing states and union territories based on their COVID-19 CFR in September 2020 and in late April 2021 have been prepared using ArcGIS 10.5 software and shown in Fig. 1 .

Fig. 1.

The Indian States and UTs by comparative Covid-19 CFR in September 2020 and in late April 2021.

It is evident from the above maps that Punjab and Maharashtra consistently showed very high CFR whereas Kerala and Assam showed very low CFR.

2.3. Statistical techniques

The correlation analysis between state-wise CFRs and other variables has been done using Pearson product-moment correlation and Spearman Rank Correlation test. A two-tailed test (P test) is used for statistical significance testing.

Pearson correlation coefficient (ρ) measures the linear correlation between two variables. The formula for calculating the value of ρ is given below:

$$\rho =\frac{\sum \left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{\sum {\left(x_i-\overline{x}\right)}^2\sum {\left(y_i-\overline{y}\right)}^2}}$$

where x_i and y_i are the i_th value of variables x and y respectively. $\overline{x}$ and $\overline{y}$ are mean of the values of variables x and y. Pearson correlation coefficient (ρ) returns a value between +1 and −1 where a value near +1 represents a perfect positive association between the two variables x and y, whereas values near −1 represent a perfect negative association. A value of ρ near 0 implies that there is no association between the variables.

Spearman's rank correlation coefficient (r_s) measures the statistical association between the rankings of two variables. It is to assess the relationship between two datasets using the monotonic function. Spearman's rank correlation coefficient (r_s) can be calculated using the formula given below:

$${\text{r}}_{\text{s}}=1-\frac{6\sum d_i^2}{n\left(n^2-1\right)}$$

where d_i is the difference between the ranks of each observation in the two variables, number of observations in each variable is given by n. The value of r_s ranges from +1 to −1, where a value near +1 represents a perfect positive association and values near −1 represent a perfect negative association between the two variables. A value of r_s closer to 0 represents the weaker correlation between the ranks of the two variables.

Pearson product-moment correlation, Two-tailed P test, and Spearman Rank Correlation analysis have been done on Microsoft Excel.

2.4. Multilayer perceptron (MLP)

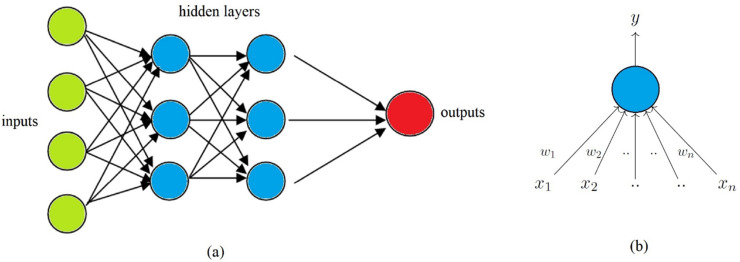
A multilayer perceptron (MLP) is a type of artificial neural network (ANN) consisting of an input layer, one or more hidden layers, and an output layer as shown in Fig. 2 (a). Each layer consists of one or more nodes called Perceptrons (artificial neurons) as shown in Fig. 2(b). Artificial neurons are the basic building block of an ANN structure and are based on the functioning of a biological neuron in a human brain. All the nodes in this network for our study are sigmoid, except the output node which is an unthresholded linear unit. The model uses backpropagation to learn the weights and biases (parameters of ANN). Weights of the connections between the nodes are initialized with random numbers and a momentum-based gradient descent algorithm is used to update the weights. A form of a sigmoid function called logistic function used in this model is given below.

$$\text{y}=\frac{1}{1+e^{-({\omega }_o+{\sum }_{i=1}^n{\omega }_i{x}_i)}}$$

Fig. 2.

(a) A typical feedforward artificial neural network (ANN) with two hidden layers, and (b) A single Perceptron (artificial neuron) with x₁ to x_n as inputs, w₁ to w_n as weights (parameters) and y as output.

here y is the output of a neuron, x_i is the input, ω_o and ω_i represents bias and weights (parameters of ANN) in the ANN structure. The update rule for momentum-based gradient descent is given below.

$${\text{update}}_{\text{t}}=\gamma {\text{.update}}_{\text{t}-1}+\eta \text{.}\nabla {\omega }_t$$

$${\omega }_{t+1}={\omega }_t-{\text{update}}_{\text{t}}$$

here ω_t is the values in the weights matrix at time t, γ is the momentum value and η is the learning rate. γ and η are also called hyperparameters of an ANN structure. The momentum value (γ) and the learning rate (η) are set at a value of 0.2 and 0.3 respectively for our analysis.

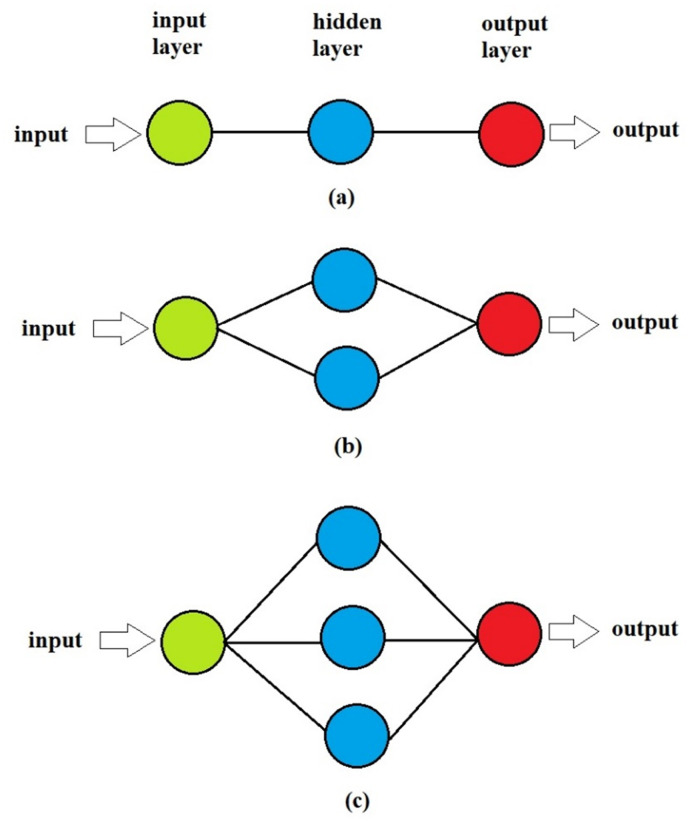
In this study, an MLP model consisting of one hidden layer is used. Three different ANN network structures (1-i-1, where i is the number of nodes in the hidden layer with values 1,2, and 3) are taken for analysis which is shown in Fig. 4. Several statistical performance measurement methods can be used in MLP such as MAPE, RMSE, MSE, R² and r [26]. In our study, we will use the correlation coefficient (r) to estimate the association between variables. The correlation analysis using MLP has been performed on the WEKA workbench for machine learning (ML) developed at the University of Waikato, New Zealand [27].

Fig. 4.

ANN structures: (a) 1-1-1, (b) 1-2-1, and (c) 1-3-1.

3. Results and discussion

3.1. State-wise CFRs

The COVID-19 CFR has been decreasing in the country from 1.82% on October 1, 2020, to 1.35% on April 22, 2021. Even though the CFRs have been falling in all the states and union territories, some states like Punjab and Maharashtra continue to show very high CFRs (2.93 and 1.84), whereas states like Kerala and Assam show very low (0.43 and 0.53) as compared to the national average. A state-wise comparative maps of CFRs in September 2020 and in late April 2021 are shown in Fig. 1. To investigate the causes responsible for CFR disparity among states, datasets for several factors related to state-wise demographics, socio-economic status, public health status, and healthcare capacity has been collected for correlation study.

3.2. Correlation of COVID-19 CFR with various factors

The state-wise data of cumulative number of COVID-19 cases, recoveries, and deaths have been collected till April 22, 2021. State-wise data of several factors related to demographics, socio-economics, public health status, and healthcare capacity have been collected from reliable data sources for correlation analysis. Table 1 shows the summary of results obtained from Pearson product-moment correlation analysis and a two-tailed significance test (P test).

Table 1.

Summary of Pearson correlation analysis between state-wise COVID-19 CFR and factors related to demographics, socio-economics, public health status, and healthcare capacity.

Factors	Pearson Correlation Coefficient (ρ)	Significance level of the two-tailed P test (α)
Life Expectancy at Birth	0.30	0.172
Life Expectancy at age 50	0.35	0.111
Life Expectancy at age 60c	0.39	0.069
Life Expectancy at age 70c	0.41	0.058
Overall Sex Ratio	−0.27	0.133
Child Sex Ratiob	−0.40	0.022
Age 0–6 Sex Ratiob	−0.40	0.022
Age 0–19 Sex Ratioa	−0.48	0.005
Age 15–59 Sex Ratio	−0.22	0.230
Sex Ratio at age 60	0.08	0.678
Per Capita GDP	0.29	0.118
HDI	0.19	0.288
Public Affairs Index 2020	0.14	0.431
Cancer Per Lakh	−0.13	0.498
Diabetes	0.20	0.293
Overweightb	0.41	0.025
Blood Pressure	0.11	0.547
Test Positive Ratec	0.29	0.092
COPDd DALYe	0.13	0.488
Asthma DALY	−0.03	0.885
Factors from NHP-2019
H1N1 (swine flu) Fatality Ratea	0.52	0.008
Hypertension (all age groups)	−0.01	0.942
Diabetes	−0.02	0.919
Both Hypertension & Diabetes	0.27	0.144
Cardio Vascular Diseases	0.10	0.595
Stroke	0.05	0.789
Common Cancer	−0.04	0.837
Doctors per thousand Cases	−0.25	0.147
Health Expenditure as % of GSDPc	−0.30	0.096
Health Expenditure Per Capita	−0.09	0.606
Govt. Hospitals per thousand Casesb	−0.40	0.018
Govt. Hospital Beds per thousand Cases	−0.27	0.117

^aStatistics at 99% significance level (α ≤ 0.01).

^bStatistics at 95% significance level (α ≤ 0.05).

^cStatistics at 90% significance level (α ≤ 0.10).

^dChronic obstructive pulmonary disease.

^eDisability-adjusted life year.

In the analysis, life expectancies at age levels 60 and 70 show a significant positive correlation with COVID-19 CFR. These results show stronger association of CFR with life expectancies at older age levels. Since states with better life expectancies at older age levels have a higher number of old age people, a positive correlation with CFR indicates towards the concentration of COVID-19 deaths at older ages. Sex ratio at younger age groups show significant negative correlation with CFR, indicating that CFR among males is higher than females in younger age groups. In old age groups, sex does not seem to affect the mortality rates of COVID-19. Socio-economic factors such as HDI, per capita GDP, and public affairs index show a weak positive association with CFR, and are statistically insignificant. Test positive rate shows a significant positive association with CFR indicating that states with lower COVID-19 testing rates (higher test positivity rate) exhibit higher CFR.

Prevalence of diseases like Cancer, COPD, Asthma, CVD, stroke, and common comorbidities like diabetes and hypertension do not show any significant association with COVID-19 CFR. However, the prevalence of overweight shows a statistically significant positive association with CFR, indicating that states with a greater proportion of overweight people have higher CFR. Interestingly, the COVID-19 CFR shows a strong positive correlation with H1N1 (swine flu) fatality rates of the year 2017, which shows that the fatality rate distribution of both the diseases has a lot of similarity in India.

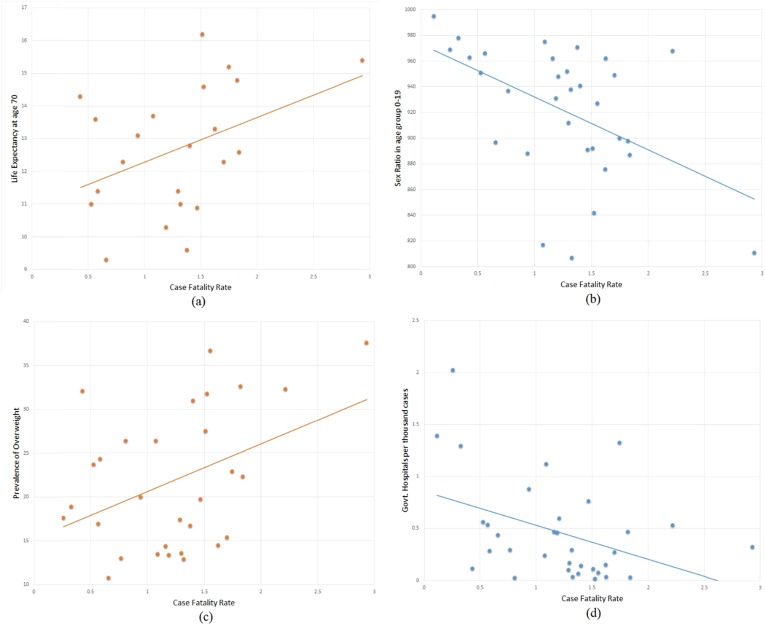
Although statistically insignificant, the number of govt. doctors per thousand COVID-19 cases, number of govt. hospital beds per thousand cases, and health expenditure per capita shows negative correlation with CFR. Health expenditure as a percentage of GSDP and number of govt. hospitals per thousand cases show significant negative correlation with CFR. These results indicate that the COVID-19 fatality rates are lesser in the states with better health spending and healthcare capacity. Fig. 3 graphically shows the association of CFR with the most significant factors ‘life expectancy at age 70’, ‘sex ratio in age group 0–19’, ‘prevalence of overweight’ and ‘govt. hospitals per thousand COVID-19 cases’.

Fig. 3.

Scatter chart with trendline showing association of CFR with (a) life expectancy at age 70 (b) Sex ratio in age group 0–19 (c) Prevalence of overweight and (d) Govt. hospitals per thousand COVID-19 cases.

3.3. Spearman Rank correlation and ANN structures analysis

Spearman Rank correlation test and Artificial Neural Network (ANN) structure analysis have only been done for the factors significant at a minimum 90% significance level (α ≤ 0.10). These tests have also been done for the statistically insignificant factor ‘sex ratio at 60+ age’ for the validity of results.

Artificial Neural Network (ANN) structures have been used in various studies related to the COVID-19 pandemic across the world [20,[28], [29], [30], [31], [32]]. For this study, an ANN model consisting of one hidden layer is used. Three different configurations (1-i-1, where i = 1, 2, and 3) of ANN structure are used based on the number of nodes in the hidden layer. These configurations are shown in Fig. 4.

The correlation coefficients obtained from Spearman rank correlation analysis and Artificial Neural Network (ANN) structures are summarized in Table 2 . From the three ‘r’ values from ANN structures, the highest value of ‘r’ (highlighted bold) is considered.

Table 2.

Correlation coefficient values obtained using Spearman Rank Correlation and Artificial Neural Network (ANN) for statistically significant factors.

Factor	Rank Correlation Coefficient (rs)	ANN Structures Correlation Coefficient (r)
		1-1-1	1-2-1	1-3-1
Life Expectancy at age 60	0.42	0.499	0.495	0.493
Life Expectancy at age 70	0.40	0.502	0.497	0.498
Child Sex Ratio	−0.37	0.374	0.372	0.444
0-6 Sex Ratio	−0.37	0.374	0.372	0.444
0-19 Sex Ratio	−0.46	0.466	0.474	0.564
Sex Ratio at 60+ age	0.19	0.036	0.030	0.023
Overweight	0.32	0.514	0.514	0.515
Test Positive Rate	0.33	0.319	0.259	0.262
H1N1 Fatality Rate 2017	0.33	0.531	0.611	0.611
Health Expenditure as % of GSDP	−0.27	0.266	0.267	0.269
Govt. Hospitals per thousand Cases	−0.37	0.655	0.653	0.349

It is evident from Table 2 that all the factors showing statistically significant associations with CFR in the Pearson correlation test and the two-tailed test (P test), exhibit significant associations with CFR in the Spearman rank correlation and ANN structures correlation tests. COVID-19 CFR increases with increase in life expectancy at older age levels, test positive rate, and prevalence of overweight. It decreases with increase in the sex ratio in younger age groups, health expenditure as percentage of GSDP and the availability of govt. doctors. The factor ‘Sex ratio at 60+ age’, found statistically insignificant in the Pearson correlation test and the two-tailed test, also shows no association with CFR in the ANN structures analysis.

4. Conclusion

This study aims to contribute to the ongoing research works related to the factors affecting COVID-19 CFR. This correlation study is done for finding the association of CFR with the various factors related to demographics, socio-economic condition, public health status, and healthcare capacity. States with higher life expectancies tend to show higher CFR. Life expectancy at older ages shows even stronger positive association with CFR, indicating a higher COVID-19 mortality rate in the old age population. Interestingly, H1N1 (swine flu) and COVID-19 found to have a lot of similarities in the fatality rate distribution in India. The results of this study establish and consolidate the facts that males in younger age groups, and overweight people are at a larger fatality risk from COVID-19. Sex does not seem to affect fatality rates in old age population. Diseases like cancer, chronic respiratory diseases (COPD and Asthma), CVD, stroke and common comorbidities like diabetes and hypertension do not show any significant effect on CFR. States with better COVID-19 testing rates, health expenditure, and healthcare capacity seem to have lesser death rates due to COVID-19. This study has been done with the most recent data available from the most reliable sources. However, availability of age-group and sex wise COVID-19 data would have significantly improved the accuracy of this work. This study is more or less consistent with the similar studies done across the world. Important measures such as increasing the number of COVID-19 testing, enhancing healthcare expenditure, and improving the overall healthcare capacity must be taken to curb this pandemic.

Declaration of competing interest

Declare that they have no known competing financial or non-financial interests or personal relationships that could have appeared to influence the work reported in this paper.