Abstract
Orange-Fleshed Sweet Potato (OFSP) is an important crop in Indonesia. Yield potential and genotypic adaptability are important factors in varietal development. The purpose of this study was to estimate the stability of yield and to select the best OFSP genotypes across three agroecosystems in West Java, Indonesia. The field trials used were augmented design with 50 F1 Orange-Fleshed Sweet Potato (OFSP) genotypes as treatment, and seven check varieties as controls. The experiments were conducted in three different agroecosystems in West Java (Sumedang, Bandung, and Karawang). Selection was based on physical characteristics of sweet potato tuber, yield and stability across three environments. Data analysis of the yield characters, yield component, and tuber quality were performed by combined variance analysis. Selected genotypes were analyzed for stability yield using the parametric, non-parametric, Additive Main effects and Multiplicative Interaction (AMMI), AMMI Stability Value (ASV), and Genotype and Genotype by Environment (GGE) biplot models. Results identified the top best ten F1 genotypes namely F1-38 (G1), F1-69 (G2), F1-71 (G3), F1-77 (G4), F1-127 (G5), F1-128 (G6), F1-135 (G7), F1-159 (G8), F1-191 (G9), and F1-226 (G10). Location showed a significant effect on yield. Genotypes F1-069, F1-077, F1-226, F1-038, and F1-128 have the lowest ASR based on non-parametric and parametric stability models and there were identified as the most stable. AMMI analysis identified F1-128, F1-135, F1-038, and F1-069 as the most stable genotypes. F1-38 (G1), F1-69 (G2), F1-128 (G6) were found to be the most stable genotypes based on ASV analysis, while GGE biplot identified F1-38 (G1) and F1-69 (G2) genotypes as the stable genotypes. Other genotypes were considered to as location-specific. Based on AMMI, ASV, and GGE Biplot models, F1-038, and F1-069 were identified as stable genotypes. They produced higher yields than other genotypes. Therefore, the F1-038 and F1-069 genotypes can be potentially recommended as superior varieties for West Java, Indonesia.
Keywords: ASV, Non-parametric, Orange-fleshed sweet potato, Parametric, Selection, Yield stability
ASV, Non-parametric, Orange-fleshed sweet potato, Parametric, Selection, Yield stability
1. Introduction
OFSP is a food crop that have complete nutrition. It has more nutrition content than vegetables, provides a lot of energy and contains large amounts of vitamin A. OFSP is a food plant that has primary food micronutrients status is enhanced through plant breeding (Laurie et al., 2015). OFSP has high carbohydrate content with low glycemic level and is a good vitamin A source and source of micronutrients including Zn, Fe, Ca, and K (Islam, 2006; Burri, 2011). OFSP contain significant amounts of carotenoids which are known as provitamins A and ß-carotene (Allen et al., 2012). Therefore, sweet potato is very useful to increase the nutritional intake of the community.
West Java is one of the major sweet potato production areas in Indonesia. Production of this commodity in West Java in 2015 reached 456.2 tons (Central Bureau of Statistics, 2016). These yields were the highest of all provinces in Indonesia, followed by Papua (446.9 tons) and East Java (350.5 tons). sweet potato planting area in West Java, Papua and East Java, respectively 23,514, 36,091, and 12,782 ha. Variability among sweet potato production areas inn West Java has an effect on sweet potato yield (Solihin et al., 2016). Soil biophysical factors affect yield (Solihin et al., 2018) and plant growth promoting rhizobacteria (PGPR) affect the sweetness quality of Cilembu sweet potatoes in West Java (Nasution et al., 2017). Since West Java possess the largest cultivation areas for sweet potato in Indonesia, hence West Java is considered as the most suitable location for yield trials.
Information about genotype and environmental interactions is very important to estimate the performance of varieties when grown across different environments. Andrade et al. (2016) and Mustamu et al. (2018) identified superior varieties of sweet potatoes across several environments in Mozambique and in West Java, Indonesia, respectively. Genotypic and environment interactions are important for selecting the suitable genotypes across three agroecosystems in West Java, Indonesia. Information about genotype and environment interactions of sweet potato varieties can help in the development on a large scale (Gruneberg et al., 2005; Adebola et al., 2013; Andrade et al., 2016). In addition, the genotypes and environment interactions are also an important consideration in plant breeding programs. Therefore, stability and adaptation studies to identify superior highly stable and adapted genotypes across diverse environments are imperative.
The current method widely used to estimate stability is AMMI and GGE biplot. Some researchers also evaluated stability and adaptability with the AMMI in some species. Mirosavljević et al. (2014) evaluated barley in Serbia and get two stable genotypes. Sweet potato was also evaluated in South Africa by Adebola et al. (2013) and obtained two specific genotypes and three stable genotypes. Andrade et al. (2016) evaluated sweet potato in Mozambique and get four genotypes stable, and Mustamu et al. (2018) evaluated sweet potato using AMMI and GGE biplot in Indonesia and get four stable genotypes, in which that superior genotypes were selected in specific environments. Kivuva et al. (2015) conveyed that in the AMMI analysis, the used of AMMI Biplot was needed to describe the performance of the genotypes and locations tested. Thus, using the AMMI models with Biplot can draw the distribution of genotypes tested across different environments.
The University of Padjadjaran (UNPAD) has developed 50 F1 OFSP lines. The goal of this research was to select new OFSP genotypes and identify their respective yield stability and adaptability. To accomplish this goal, it important to identify key morphological and yield traits to be used as references in order improve sweet potato production in Indonesia.
2. Materials and methods
2.1. Genetic materials
The plant materials used include 50 OFSP F1 lines and seven checks variety, i.e.: AC Putih, Rancing, Kokei, Ayamurasaki, Beniazuma, Kidal, and Narutokinotoki. The material used was the result of open crosses. These genotypes have been selected based on plants that produce tubers in the initial phase of growth.
2.2. Experimental design
Field experiments were conducted in three agroecosystems in West Java, Indonesia including Bandung, Sumedang, and Karawang. Bandung has an altitude of 900 m a.s.l., a latosols soil type with andesite tuff material, an average rainfall of 221 mm month−1, and air temperatures ranging from 23-29 °C. Sumedang at an altitude of 753 m a.s.l., an inceptisols soil type with andesite tuff material, an average rainfall of 241 mm month−1, and air temperatures ranging from 22-27 °C. The altitude of Karawang at an 24 m a.s.l., an inceptisols soil type, an average rainfall of 94,2 mm month−1, and air temperatures ranging from 23-36 °C. Because of limited seeds and large number of entries, experiments was laid out with an augmented design with 50 OFSP F1 lines as treatments and seven check varieties as controls. Fertilization was applied using chicken dung at the rate of 5 tons/ha and NPK at 200 kg/ha in each location.
2.3. Data collection
Traits observed include weight of tuber per plot (Kg) and converted to t/ha, number tuber per plot, level of sweetness (OBrix), tuber length (cm), and tuber diameter (cm) (Huaman, 1999). Level of sweetness was observed in fresh tubers using digital refractometer (Magwaza and Opara, 2015) brand ATAGO-Pal 1. Digital refractometer starts from the calibration of the tool with aquadest, then the liquid sample was dripped on the refractometer prism. The genotypes tested were selected based on the physical appearance of tubers according to consumer preference as reported by Maulana et al. (2016) and Andrade et al. (2016).
2.4. Data analysis
Variance component analysis used was conducted on check varieties to estimate standard errors. Adjustments for three block differences were based on the difference between the average value of checks in a given block and the average value of the entire experimental check (Federer et al., 2001). Genotypic by environment interactions was carried out on check varieties following You et al. (2013) with the equation number 1:
| (1) |
This linear model is an Modification Augmented Design (MAD) type 2, where : adjustment value of the genotype i at the location j; : the overall average; : genotype effect of the genotype i; : location influence of the location j; : effect of genotype i by location j interactions, and : estimation of the combined experimental error based on the analysis of the combined variance of the seven check varieties.
Non-parametric and parametric stability models used to identify stable genotypes. Linear regressions measure following Eberhart and Russell (1966). According this measurement, the genotypes are classified based on the size of two parameters, i.e. bi and S2di, with the formula in equations number 2 and 3:
| (2) |
| (3) |
Where, : grand yield in location j from genotype i, : overall average yield of genotype i in all locations, : average yield of the location j, : grand mean, N: number of locations. The genotypes that have bi > 1 would be more adapted to favorable locations, bi < 1 would be adapted to unfavorable growing locations, and bi = 1 would have an adapted to all locations. Genotypes with S2di > 0 indicated the lower stability across all locations, whereas a S2di = 0 indicate the most stable.
To estimated mean variance component (θi), following Plaisted and Peterson (1959) with the equation number 4:
| (4) |
The equation number 5 used to calculated the GE variance component (θ(i)) (Plaisted, 1960):
| (5) |
Estimation of the ecovalence value (Wi2) follows Wricke (1962), this measurement was estimated by equation number 6:
| (6) |
Shukla's stability variance (Shukla, 1972), for the genotype i was measures as follow the equation number 7:
| (7) |
Formula for Coefficient of variance (CVi) based on equation number 8 (Francis and Kannenberg, 1978):
| (8) |
For θi, θ(i), Wi2, , CVi measurements, were , , , : same with linear regressions; p and q is the numbers of genotypes and sites; SDg: the standard deviation of a genotype by location interactions.
Nassar and Huhn (1987) and Huehn (1990) proposed four non-parametric stability (S(i)) measures with the equations number 9, 10, 11, and 12:
| (9) |
| (10) |
| (11) |
| (12) |
Where rij is the rank of stability in the jth location from the ith genotype; : mean rank for each genotype in all locations; and N: number of location. Thennarasu (1995) proposed four parametric stability (NP(i)) measures. The equations of the four proposed measurements was the equations number 13, 14, 15, and 16:
| (13) |
| (14) |
| (15) |
| (16) |
where : rank of stability from genotype i in site j (adjusted data); : adjusted data from the median rank's; : unadjusted data from the median rank's (same parameters). N: number of location. The last, Kang (1988) proposed non-parametric stability measure (KR) based on yield rank from each genotype and Shukla's stability variance as selection index. The genotype with low stability variance and the highest average yield, were given a rank of 1. STABILITYSOFT (online software) was used to identify stable genotypes based on non-parametric and parametric stability measurements (Pour-aboughadareh et al., 2019).
AMMI model used to identify stable genotypes among the selected genotypes following the study of Gauch et al. (2008). ASV was calculated based on Purchase et al. (2000). The GGE biplot model following Yan et al. (2007).
3. Results and discussions
3.1. Selection of F1 orange fleshed sweet potato (OFSP) genotypes based on consumer preferences
Selection was based on consumer preferences in Indonesia. This is useful so that the new varieties produced can be readily accepted and immediately utilized by the community. Ten sweet potato genotypes were selected based on such consumer preferences. They are F1-38, F1-69, F1-71, F1-77, F1-127, F1-128, F1-135, F1-159, F1-191, and F1-226 genotypes. These selected genotypes have the tuber shape, color of skin and color of fleshed based on consumer preferences (Andrade et al., 2016; Maulana et al., 2016). The F1-38, F1-71, F1-77, F1-127, and F1-191 genotypes have creamy skin, yellow-fleshed color (without secondary color), and long elliptical shape. F1-69, F1-128, and F1-226 genotypes have red skin, orange-fleshed color (without secondary color), and long elliptical shape. F1-135 genotypes have red skin, yellow-fleshed color, and long elliptical shape, while F1-159 genotypes have creamy skin, orange-fleshed color, and long elliptic shape. Other genotypes were not selected because their shapes are not in accordance with consumer preferences. Therefore, selection based on consumer preferences is important to improve the competitiveness of new varieties.
Selection of sweet potato was done in the early generations. Sweet potatoes are considered as vegetatively propagated plants so that multiplication of varieties can be done through stem cuttings and or tubers. Propagation through the vegetative part allows the offsprings to be clone reproduction of the mother plant. In addition, self-incompatibility in sweet potato does not allow self-pollination (Vimala et al., 2012; Gurmu et al., 2013), resulting in heterozygous F1 seeds that are genetically different from one another. Self-incompatibility is a genetic system that can prevent the occurrence of self-fertilization in flowering plants and only allows outcrossing. Heterozygosity promotes increase genetic variation. Genetic variations that appear from new genotypes resulting from crosses facilitates individual selection of sweet potato plants (Bhandari et al., 2017). Outcrossing in sweet potatoes produces diversity among offspring for both qualitative and quantitative characters.
3.2. Genotype x environment interaction analysis for check varieties
Statistical analysis to estimate GxE in this experiment based on the combined variance analysis of the adjusted value from the check variety. This is due to the absence of repetition in the genotype tested, so that the combined experimental error is predicted based on the adjusted value (adj.) of the check variety. You et al. (2013) stated that in augmented design type 2 models, the heterogeneity of the soil from the control plot is eliminated by adjusting the data, so that the adjustment value of the check variety can be considered to represent the test environmental conditions. In addition, the combined value of the adjusted value from check variety can be used to test the yield stability and other properties of the test genotype in different environments. You et al. (2016) also added that the use of checks variety in estimating combined variance with MAD type 2 is efficient enough to repress test environment conditions. Therefore, the combined ANOVA from check varieties can be used to estimate experimental errors in several environments.
Combined analysis for all characters from the seven varieties used as checks across three different environments in West Java showed that the location had a significant effect (Table 1). The means square of environmental influences for the number of sweet potatoes, weight of sweet potato, sweet potato diameters, sweet potato length, and sweetness levels (p < 0.01) are 0.5025, 2.6188, 73.4295, 5.5731, 2.4276. These showed that the potential of each character tested were influenced by the location. Some researchers also stated that yield performance was strongly affected by the environment (Gruneberg et al., 2005; Solihin et al., 2016). Sholihin (2015) reported that environmental factors were important in determining stability. Similar results also occured in yellow passion fruit (de Oliveira et al., 2014), and grain (Coan et al., 2018), where environmental factors controlled yield variations.
Table 1.
Combined analysis of variance across genotypes, environment, and genotype x environment interactions for tuber number per plot, tuber weight per plot (kg), tuber diameter (cm), tuber length (cm), and tuber sweetness (Brix) traits for check varieties.
| Source of variation | df | Mean Square |
||||
|---|---|---|---|---|---|---|
| Number of Sweet Potato per Plot | Weight of Sweet Potato per Plot (kg) | Tuber Diameter (cm) | Tuber Length (cm) | Sweetness (Brix) | ||
| Block (loc.) | 6 | 0.2939 | 0.001 | 8.0761 | 0.3319 | 0.3662 |
| Genotype | 6 | 0.4219 | 0.0327 | 2.1708 | 1.449 | 0.7109 |
| Location | 2 | 0.5025∗∗ | 2.6188∗∗ | 73.4295∗∗ | 5.5731∗∗ | 2.4276∗ |
| Genotype x location | 12 | 0.4219 | 0.0506 | 3.7414 | 2.0506 | 0.8561 |
| Residual | 40 | 0.5025 | 0.0949 | 3.9648 | 1.5306 | 0.7465 |
| Total | 62 | 0.7222 | 0.1587 | 6.1214 | 1.7151 | 0.8062 |
∗Significant at P < 0.05; ∗∗Significant at P < 0.01.
Based on the results of the combined analysis, there is no significant genetic or genetic x environment (GxE) observed. The value of the influence of genetic factors for total number tubers, tuber weight, tuber diameter, tuber length, and sweetness (Brix) levels were 0.4219, 0.0327, 2.1708, 1.449, and 0.7109, respectively (Table 1). The GxE value for total number tubers, tuber weight, tuber diameter, tuber length, and sweetness (Brix) levels were 0.4219, 0.0506, 3.7414, 2.0506, 0.8561, respectively (Table 1). The absence of GxE effects means that selection across three agroecosystems will be effective. Andrade et al. (2016) also stated that the concept of Accelerated Breeding Scheme (ABS) in sweet potato would be effective if there were no or small GxE. The absence of GxE in this study indicated that the environmental conditions were relatively similar or the response of sweet potato genotypes was relatively uniform, thus the selection process would be easier.
3.3. Stability analysis of selected genotypes based on parametric and non-parametric stability models
Table 2 presented the results of the parametric stability analysis. According to Eberhart and Russell (1966) model, genotype stability was determined using regression coefficients (bi) and variance deviations (S2di), with estimates of bi = 1 and S2di being low. Genotypes F1-038, F1-069, F1-077, F1-128, F1-135, and F1-226 have bi = 1, where F1-077, F1-128, and F1-226 has lower yields than overall average yield. Therefore, the genotypes were less adaptable to all planting environments. Genotypes F1-071 and F1-191 with bi > 1 values has a low average level of stability, so they were specific and has high yields in certain environments. Genotypes F1-127 and F1-159 with bi < 1 and average yields which were lower than the average yields overall, so that the specifics in low production environments. Based on S2di measurements, the F1-226 genotype has the lowest value, followed by F1-077, F1-127, and F1-069, so declared the most stable genotypes according to this approach. Average yields for genotypes tested in three environments ranged from 2.467 to 15.167 tons/ha, with genotypes F1-071, F1-069 and F1-038 has the highest average yields, while F1-127, F1 -226, F1-077 and F1-159 has low yields (Table 3). Three parametric stability models: Wricke ekovalance (Wi2), Shukla stability variance () and GE variance component (θ(i)), showed that F1-069, F1-128, F1-135, and F1-038 as the most stable genotypes. The other genotypes that were selected the most stable were F1-071, F1-159, F1-191, and F1-127 by Plaisted and Peterson's ), and F1-077, F1-226, F1-069, and F1-038 by Francis and Kannenberg's (CVi). Table 3 presented the results of the non-parametric stability analysis for each genotype. According to S(1), S(2), S(3), and S(4) estimated the F1-226, F1-077, F1-071, and F1-068 genotypes have the smallest values and represent the most stable. NP(1) measurement identified the genotypes F1-069, F1-128, F1-038, F1-077, and F1-226 as stable genotypes. NP(2) identified genotypes F1-069, F1-071, F1-038, and F1-135 as stable genotypes. NP(3) identified the F1-069, F1-128, F1-038, and F1-077 genotypes as stable genotypes. NP(4) identified the F1-226, F1-071, F1-077, and F1-069 genotypes as the most stable. While the KR stability model predicted the F1-069, F1-038, F1-128, and F1-135 genotypes as stable genotypes. Many statistical methods were proposes for used as an index of selection of stable crops with high yields (Farshadfar et al., 2012; Ahmadi et al., 2015; Khalili and Pour-aboughadareh, 2016). However, Vaezi et al. (2019) reported that barley genotype selection with high yield and stable in Iran using parametric and non-parametric stability models is still quite difficult. Therefore, another approach is needed to determine the genotypes that was able to adapt to diverse environments and high yield.
Table 2.
Parametric stability models of the selected sweet potato genotypes.
| Genotype | Y | CVi | Wᵢ2 | σ2ᵢ | bᵢ | s2dᵢ | θᵢ | θ₍ᵢ₎ |
|---|---|---|---|---|---|---|---|---|
| F1-038 | 15.08 | 65.896 | 0.552 | 0.334 | 3.566 | 0.000 | 0.205 | 0.065 |
| F1-069 | 15.17 | 49.049 | 0.244 | 0.141 | 2.707 | 0.000 | 0.119 | 0.086 |
| F1-071 | 22.45 | 25.890 | 0.000 | -0.011 | 1.001 | 0.000 | 0.052 | 0.103 |
| F1-077 | 6.64 | 35.912 | 0.002 | -0.010 | 1.147 | 0.000 | 0.052 | 0.103 |
| F1-127 | 2.47 | 48.336 | 0.000 | -0.011 | 1.015 | 0.000 | 0.052 | 0.103 |
| F1-128 | 7.57 | 84.324 | 0.350 | 0.207 | -1.043 | 0.000 | 0.149 | 0.079 |
| F1-135 | 10.81 | 46.010 | 0.280 | 0.163 | -0.826 | 0.000 | 0.129 | 0.084 |
| F1-159 | 6.80 | 37.191 | 0.079 | 0.038 | 1.973 | 0.000 | 0.074 | 0.098 |
| F1-191 | 10.97 | 173.205 | 0.138 | 0.075 | -0.282 | 0.000 | 0.090 | 0.094 |
| F1-226 | 4.12 | 38.703 | 0.006 | -0.008 | 0.741 | 0.000 | 0.053 | 0.103 |
| Rank | |||||||
|---|---|---|---|---|---|---|---|
| Y | CVi | Wᵢ2 | σ2ᵢ | bᵢ | s2dᵢ | θᵢ | θ₍ᵢ₎ |
| 3 | 8 | 10 | 10 | 1 | 10 | 1 | 10 |
| 2 | 7 | 7 | 7 | 1 | 9 | 4 | 7 |
| 1 | 1 | 1 | 1 | 4 | 3 | 10 | 1 |
| 8 | 2 | 3 | 3 | 1 | 7 | 8 | 3 |
| 10 | 6 | 2 | 2 | 2 | 1 | 9 | 2 |
| 6 | 9 | 9 | 9 | 1 | 8 | 2 | 9 |
| 5 | 5 | 8 | 8 | 1 | 6 | 3 | 8 |
| 7 | 3 | 5 | 5 | 3 | 3 | 6 | 5 |
| 4 | 10 | 6 | 6 | 2 | 3 | 5 | 6 |
| 9 | 4 | 4 | 4 | 1 | 2 | 7 | 4 |
Table 3.
Non-parametric stability models of the selected sweet potato genotypes.
| Genotype | S⁽1⁾ | S⁽2⁾ | S⁽³⁾ | S⁽⁶⁾ | NP⁽1⁾ | NP⁽2⁾ | NP⁽³⁾ | NP⁽⁴⁾ | |
|---|---|---|---|---|---|---|---|---|---|
| F1-038 | 4.000 | 9.333 | 2.545 | 0.909 | 2.000 | 0.233 | 0.295 | 0.545 | 7.000 |
| F1-069 | 2.000 | 2.333 | 0.636 | 0.455 | 1.333 | 0.148 | 0.170 | 0.273 | 3.000 |
| F1-071 | 2.000 | 2.333 | 0.560 | 0.400 | 6.000 | 0.167 | 0.509 | 0.240 | 11.000 |
| F1-077 | 1.333 | 1.000 | 0.400 | 0.400 | 2.000 | 0.500 | 0.327 | 0.267 | 13.000 |
| F1-127 | 2.667 | 4.333 | 3.250 | 1.750 | 3.000 | 1.467 | 1.335 | 1.000 | 17.000 |
| F1-128 | 3.333 | 6.333 | 2.714 | 1.143 | 1.667 | 0.333 | 0.267 | 0.714 | 8.000 |
| F1-135 | 4.000 | 9.000 | 3.000 | 1.000 | 2.667 | 0.296 | 0.342 | 0.667 | 8.000 |
| F1-159 | 5.333 | 17.333 | 5.200 | 1.400 | 3.333 | 0.333 | 0.604 | 0.800 | 16.000 |
| F1-191 | 5.333 | 21.333 | 11.636 | 2.909 | 4.000 | 0.593 | 0.803 | 1.455 | 12.000 |
| F1-226 | 0.667 | 0.333 | 0.200 | 0.400 | 2.000 | 1.167 | 0.648 | 0.200 | 15.000 |
| Rank | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S⁽1⁾ | S⁽2⁾ | S⁽³⁾ | S⁽⁶⁾ | NP⁽1⁾ | NP⁽2⁾ | NP⁽³⁾ | NP⁽⁴⁾ | SR | ASR | SD | |
| 7 | 8 | 5 | 5 | 3 | 3 | 3 | 5 | 2 | 94 | 5.529 | 3.201 |
| 3 | 3 | 4 | 4 | 1 | 1 | 1 | 4 | 1 | 66 | 3.882 | 2.564 |
| 3 | 4 | 3 | 1 | 10 | 2 | 6 | 2 | 5 | 58 | 3.412 | 2.830 |
| 2 | 2 | 2 | 1 | 3 | 7 | 4 | 3 | 7 | 66 | 3.882 | 2.398 |
| 5 | 5 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 107 | 6.294 | 3.304 |
| 6 | 6 | 6 | 7 | 2 | 5 | 2 | 7 | 3 | 97 | 5.706 | 2.696 |
| 7 | 7 | 7 | 6 | 6 | 4 | 5 | 6 | 3 | 95 | 5.588 | 1.912 |
| 9 | 9 | 9 | 8 | 8 | 5 | 7 | 8 | 9 | 109 | 6.412 | 2.144 |
| 9 | 10 | 10 | 10 | 9 | 8 | 9 | 10 | 6 | 123 | 7.235 | 2.602 |
| 1 | 1 | 1 | 1 | 3 | 9 | 8 | 1 | 8 | 68 | 4.000 | 2.970 |
3.4. Spearman's rank correlation, stability models grouping, and selected genotype grouping
Based on Spearman's rank correlation coefficient, the average yield was positively and significantly correlated with NP(2) and KR (P < 0.05) (Table 4). Other positive and significant correlations were CVi with s2dᵢ, bi, S(2), S(3), S(6), NP(6) (P < 0.05), and NP(1) (p < 0.01). Wi2 with σ2ᵢ, bi, θ(i), NP(1), NP(3) and KR,. σ2ᵢ with bi, θ(i), NP(1), NP(3) and KR,. s2dᵢ with bi, S(1), S(2), S(3), and NP(1). Linear regression (bi) with θ(i), NP(1), and NP(3). θ(i) with NP(1), NP(3), and KR. S(1), S(2), S(3), S(6), and NP(4) were positively correlated and significant (P < 0.01). NP(1) with NP(3) (P < 0.01), and NP(2) with NP(3) and KR (p < 0.01). Overall, the results of Spearman's rank correlation analysis showed that the measures of stability NP(2) and KR were significantly correlated with average yields, thus provided a measure of stability in a dynamic sense. According to Akcura and Kaya (2008), a stability model that was positively correlated with yields can be used to recommend genotyping with a favorable growth environment. Ahmadi et al. (2015) and Vaezi et al. (2019) reported that CVi, bi, and TOP were significantly correlated with average yields, so the three were recommended as models to select genotypes with above average yields in locations with unfavorable growth conditions. Based on this, NP(2) and KR models can be used as a stability model to identify sweet potato yields in unfavorable environments.
Table 4.
Spearman's rank correlation of the parametric and non-parametric stability models.
| Yield | Cvi | Wᵢ2 | σ2ᵢ | s2dᵢ | bi | θᵢ | θ₍ᵢ₎ | S⁽1⁾ | S⁽2⁾ | S⁽³⁾ | S⁽⁶⁾ | NP⁽1⁾ | NP⁽2⁾ | NP⁽³⁾ | NP⁽⁴⁾ | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Yield | 1.000 | ||||||||||||||||
| Cvi | -0.285 | 1.000 | |||||||||||||||
| Wᵢ2 | 0.091 | 0.455 | 1.000 | ||||||||||||||
| σ2ᵢ | 0.091 | 0.455 | 1.000∗∗ | 1.000 | |||||||||||||
| s2dᵢ | -0.515 | 0.636∗ | 0.430 | 0.430 | 1.000 | ||||||||||||
| bi | -0.123 | 0.658∗ | 0.884∗∗ | 0.884∗∗ | 0.617∗ | 1.000 | |||||||||||
| θᵢ | -0.091 | -0.455 | -1.000∗∗ | -1.000∗∗ | -.430 | -0.884∗∗ | 1.000 | ||||||||||
| θ₍ᵢ₎ | 0.091 | 0.455 | 1.000∗∗ | 1.000∗∗ | 0.430 | 0.884∗∗ | -1.000∗∗ | 1.000 | |||||||||
| S⁽1⁾ | -0.202 | 0.544 | 0.159 | 0.159 | 0.826∗∗ | 0.318 | -0.159 | 0.159 | 1.000 | ||||||||
| S⁽2⁾ | -0.236 | 0.588∗ | 0.212 | 0.212 | 0.830∗∗ | 0.350 | -0.212 | 0.212 | 0.991∗∗ | 1.000 | |||||||
| S⁽³⁾ | 0.030 | 0.661∗ | 0.212 | 0.212 | 0.673∗ | 0.425 | -0.212 | 0.212 | 0.899∗∗ | 0.879∗∗ | 1.000 | ||||||
| S⁽⁶⁾ | 0.178 | 0.607∗ | 0.129 | 0.129 | 0.485 | 0.319 | -0.129 | 0.129 | 0.805∗∗ | 0.791∗∗ | 0.963∗∗ | 1.000 | |||||
| NP⁽1⁾ | -0.080 | 0.718∗∗ | 0.902∗∗ | 0.902∗∗ | 0.632∗ | 0.874∗∗ | -0.902∗∗ | 0.902∗∗ | 0.390 | 0.436 | 0.436 | 0.304 | 1.000 | ||||
| NP⁽2⁾ | 0.863∗∗ | 0.049 | 0.316 | 0.316 | -0.353 | 0.072 | -0.316 | 0.316 | -0.064 | -0.049 | 0.195 | 0.357 | 0.191 | 1.000 | |||
| NP⁽³⁾ | 0.491 | 0.467 | 0.758∗∗ | 0.758∗∗ | 0.115 | 0.596∗ | -0.758∗∗ | 0.758∗∗ | 0.147 | 0.176 | 0.370 | 0.399 | 0.730∗∗ | 0.742∗∗ | 1.000 | ||
| NP⁽⁴⁾ | 0.164 | 0.588∗ | 0.115 | 0.115 | 0.491 | 0.315 | -0.115 | 0.115 | 0.807∗∗ | 0.794∗∗ | 0.964∗∗ | 0.988∗∗ | 0.301 | 0.328 | 0.345 | 1.000 | |
| 0.778∗∗ | 0.085 | 0.681∗ | 0.681∗ | -0.103 | 0.495 | -0.681∗ | 0.681∗ | -0.058 | -0.061 | 0.182 | 0.234 | 0.498 | 0.808∗∗ | 0.827∗∗ | 0.219 | 1.000 |
∗Significant at P < 0.05; ∗∗Significant at P < 0.01.
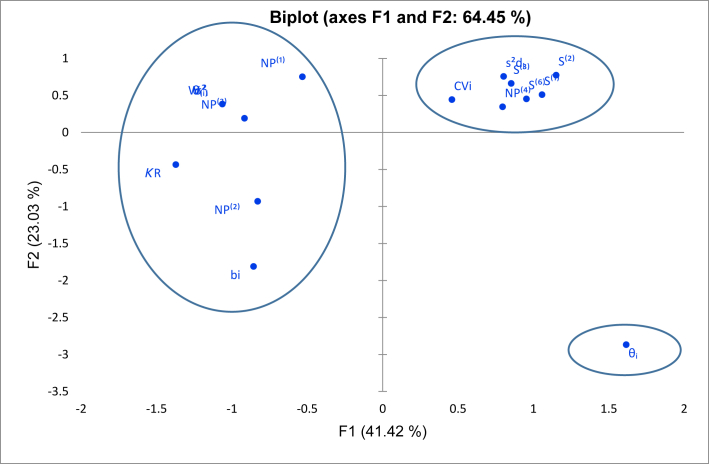
The Principal Component Analysis (PCA) of the stability model was used to determine the relationship between stability models and merge them into appropriate groups. The eigenvalue >1 were calculate the variations of 98.776% against the parametric and non-parametric models (data not shown). Because the first and second PCs have the highest variability values (51.56% and 27.77% respectively) and eigenvalue (8.25 and 4.44), biplot diagrams based on PC1 and PC2 were taken. Figure 1 showed the three groups of stability models: (1) K1, Wi2 models, σ2ᵢ, θ(i), bi, NP(1), NP(2), NP(3), and KR. K2, contains CVi, S2di, S(1), S(2), S(3), S(6), and NP(4) models, while K3 contains a stability model θᵢ.
Figure 1.
Principle component analysis of parametric and non-parametric models.
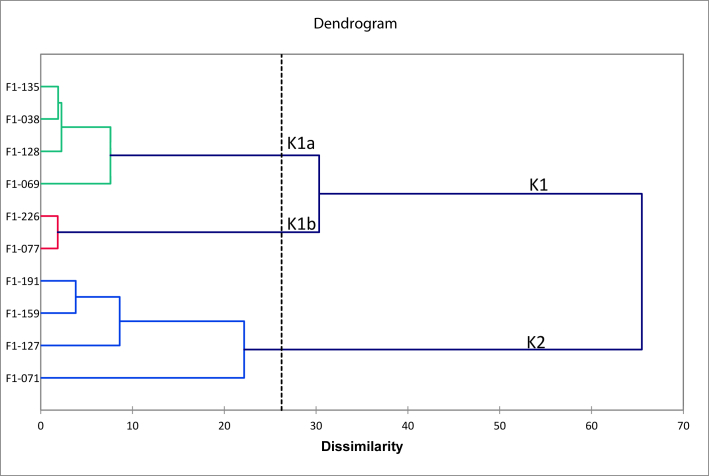
To classify selected sweet potato genotypes, cluster analysis (dendrogram) was performed. Sweet potato genotypes were classified into two main clusters (Figure 2). Two sub-clusters were produced in the first group (KI). (1) sub-cluster K1a consisted of genotypes F1-135, F1-038, F1-128, and F1-069, has high yields and average ranking lowest stability. (2) sub-cluster K1b consisted of F1-226 and F1-077 genotypes has smaller than average yields but has a low average stability rating. The second group (K2) consists of genotypes F1-191, F1-159, F1-127, and F1-071 with low yields and the highest average rating for stability models.
Figure 2.
Dendrogram of selected sweet potato genotypes.
3.5. Stability analysis of selected genotypes based on AMMI
Table 5 shows the average yield of each genotype across three different locations, IPCA 1 and IPCA 2 value for the across genotypes and locations, and ASV. For the test environment, the IPCA 1 and IPCA 2 relative values are small. From the data presented, it can be seen that Sumedang and Bandung have small values for IPCA 1 0.749 and 0.892, respectively. Likewise, small values were observed Sumedang and Bandung for IPCA 2, 0.761 and -0.718, respectively. This showed that the two locations were representative for testing, so the appearance of sweet potato yield is a representation of the genetic potential of each tested clone.
Table 5.
Yield Average. IPCA 1. IPCA 2. and AMMI Stability Value (ASV) of the ten best genotypes.
| No. | Genotypes | Yield Average (ton/ha) | IPCA 1 | IPCA 2 | ASV | Rank |
|---|---|---|---|---|---|---|
| 1 | F1-038 (G1) | 15.08 | -0.173 | -0.633 | 0.900 | 3 |
| 2 | F1-069 (G2) | 15.17 | -0.101 | -0.419 | 0.560 | 2 |
| 3 | F1-071 (G3) | 22.45 | -1.285 | -0.125 | 4.755 | 10 |
| 4 | F1-077 (G4) | 6.64 | 0.460 | 0.009 | 1.700 | 5 |
| 5 | F1-127 (G5) | 2.47 | 0.703 | 0.065 | 2.601 | 7 |
| 6 | F1-128 (G6) | 7.57 | 0.004 | 0.491 | 0.491 | 1 |
| 7 | F1-135 (G7) | 10.81 | -0.266 | 0.413 | 1.066 | 4 |
| 8 | F1-159 (G8) | 6.80 | 0.912 | -0.145 | 3.375 | 9 |
| 9 | F1-191 (G9) | 10.97 | -0.727 | 0.237 | 2.699 | 8 |
| 10 | F1-226 (G10) | 4.12 | 0.474 | 0.108 | 1.756 | 6 |
| Sumedang District (E1) | 0.749 | 0.761 | ||||
| Bandung District (E2) | 0.892 | -0.718 | ||||
| Karawang District (E3) | -1.641 | -0.043 |
Karawang has a larger IPCA 1 value (-1.641) and a relatively small IPCA 2 value (-0.043). These indicated that the genotypes planted at Karawang will have higher yields and reflect the true genetic ability of each clone tested due to the influence of small environmental factors. In addition, a high IPCA 1 score also indicated that environmental productivity was high. The results of AMMI analysis on selected genotypes showed that IPCA1 and IPCA2 produce relatively low values both positively and negatively. This showed that yield was influenced more by the environment than genetics. Thus, variation produced by the environment was greater than that of the genotype. This was also stated by de Oliveira et al. (2014) on passion fruit plants. This indicates that the test environment used has significant differences.
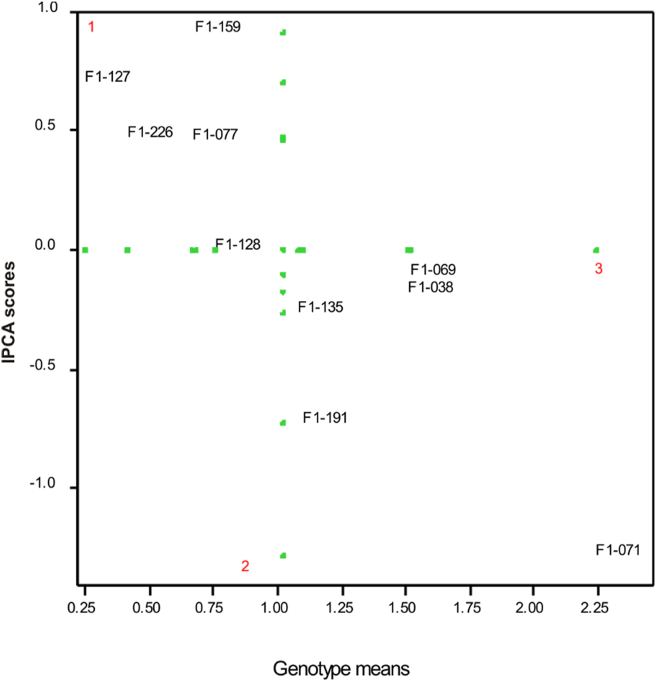
The graph of the distribution of sweet potato genotypes based on the yield character showed in Figure 3. Biplot in the AMMI analysis shows the genotype and environmental magnitude that contributed to the interaction. It shows the genotypes that were stable at specific locations. The horizontal green line shows the score of zero interaction and the vertical green line showed the average yield. The X-axis shows the main effect and the Y-axis shows the interaction effect (IPCA1). In the biplot, five sweet potato genotypes (F1-038, F1-069, F1-071, F1-135, and F1-191) and one environment (environment 3 Karawang) were located on the right side of the green vertical line (Figure 3). It is assumed that the genotypes and the environments performed higher-yield and appropriate condition. Values that are near to the zero axis (IPCA1) contribute to smaller interactions. Thus, the AMMI1 biplot shows that genotypes F1-128, F1-135, F1-038, and F1-069 have lower IPCA1 scores than other genotypes (Figure 3). This shows that the genotypes have smaller interaction with the environment, so they are stated to be the most stable according to this model. But F1-128 and F1-135 genotypes tend to have smaller yield. On the other hand, the F1-071 and F1-159 genotypes were the most unstable genotypes, but the F1-071 genotype had the highest average yield. Therefore, selected and ideal genotypes must be developed based on the adaptability of each genotype.
Figure 3.
AMMI biplot for selected sweet potato for yield.
The results of AMMI analysis on selected genotypes showed that IPCA1 and IPCA2 resulted relatively small values. This shows that the yield is more influenced by the environment than genetics. The higher positive or negative IPCA value means that genotypes adaptto specific locations (Adebola et al., 2013; Kivuva et al., 2015; Mustamu et al., 2018). The AMMI model is used to identify the main genotypic and environmental effects and to analyze the main components for identifying genotype by environment (GxE) interactions (IPCA) (Roostaei et al., 2014). This shows that the values of the genotypes can achieve high yield when planted in a productive locations.
Genotypes specific-adapt indicates differential response of the genotype depending on the environment. This means that they will produce a higher yield in environments that they are adapted but not in others. According to Thiyagu et al. (2013); Mirosavljević et al. (2014); and Gurmu (2017), stability analysis can selected the types of genotypes that are stable and those that are environment-specific and allows the identification of interaction between genotype with environment. Knowledge of the yield characteristics of each genotype makes it easy to carry out further genotyping.
Quantitatively, the results of the AMMI analysis did not showed a rank's of the exact stability of the genotypes tested (Figure 3). AMMI analysis only describes the distribution of genotypes visually. Therefore another approach is needed to determine stable genotypes. The ASV parameter was used to measure and classify stable genotypes from the smallest value range. This is also suggested by Purchase et al. (2000). Based on the ASV parameter (Table 5), all genotypes were sorted by stability rank. There were three genotypes that have values below 1 and were declared as stable genotypes, i.e., F1-038 (G1), F1-069 (G2), F1-128 (G6). The ASV has also been used as an additional analysis to select more stable sweet potato genotypes in Indonesia (Mustamu et al., 2018).
3.6. Stability analysis of selected genotypes based on GGE biplot
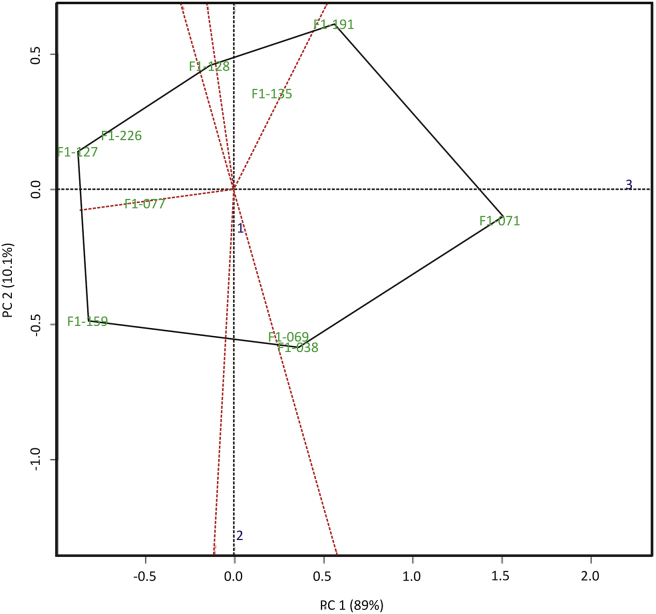
Figure 4 showed the average yield biplot of sweet potatoes. The length of the genotype vector, showed the difference of the genotypes to the average genotype in terms of the influence of genotype, location, and their interactions. Genotypes that located near the center of the biplot axis have small influences on genotype, and genotype x environment interactions. Genotypes that have a small vector distance from the centre of the biplot are considered as stable genotypes (Yan et al., 2007). The length of the environmental vector showed the magnitude of the influence of genotypic factors, the environments and their interactions. The longer environmental vector, the greater the genotype x environment interaction. The F1-077 and F1-135 genotypes are stable genotypes (Figure 4), but they have yield below the average overall yield. Genotype F1-071 has the longest vector which was the genotype with the highest yield, but genotype F1-127 with the lowest yield, and the most unstable genotypes were F1-191 and F1-127. Unstable genotypes can be put as adapted genotypes for specific location. The value and efficiency of yield genotypes were determined by their stability and adaptability (Zhang et al., 2016). Thus, the development of the genotypes must be in an appropriate environment.
Figure 4.
Biplot of selected sweet potato genotypes against average yields in three locations.
Figure 4 also showed that the F1-038 and F1-069 genotypes have close distances and small angles. This means that the two genotypes have almost similar potential yield. The average yield of the two genotypes was 15.08 t/ha and 15.17 t/ha, respectively. Genotype F1-191 showed well adapted to marginal environments, which shown by high yield in marginal environments. The distance and the angle formed by the two genotype vectors gave a picture of the differences between genotypes. The difference can be in the form of average yield or interactions with the environment. Li and Xu (2014) stated if two genotypes have large vector distance and angles, then the difference between two genotypes would be very large. This shows that genotypes which have close distances and small angles, have the same yield potential.
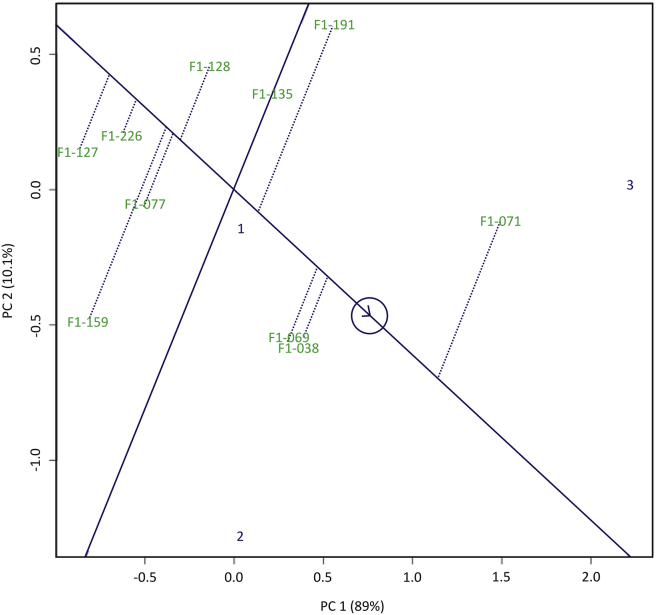
Figure 5 shows biplot of the average yield and its stability. Yan et al. (2007) stated that the X-axis shows the average yield of each genotype, and the Y-axis showed a picture of the yield stability of each genotype tested. The genotype to the right of the Y-axis has higher yields than the average overall yield. In contrast, the genotype to the left of the Y-axis has lower yield than the average overall yield. If the genotype was far from the X-axis, then the genotype was unstable. There were four genotypes that located on the right side of the Y- axis, namely F1-038,F1-069, F1-071, and F1-191. The yield of the four genotypes were above the overall average yield, while the other six genotypes have smaller yields. The F1-038 and F1-069 genotypes were the most agronomically stable (high yield), because they have the closest distance to the X-axis, while F1-071 and F1-191 genotypes were unstable because they have longer distance from the X-axis. Genotypes that have the closest distance to the ideal genotype values were F1-038 and F1-069 (Figure 5). Both genotypes were capable of high yield in both marginal and optimal environments (Figure 4). Ngailo et al. (2019) also reported the results of sweet potato selection in Tanzania using GGE Biplot. Both genotypes were also capable of producing maximum yield at all environments, so they can be recommended as new superior varieties.
Figure 5.
Biplot of average yield and stability of selected sweet potato genotypes in three locations.
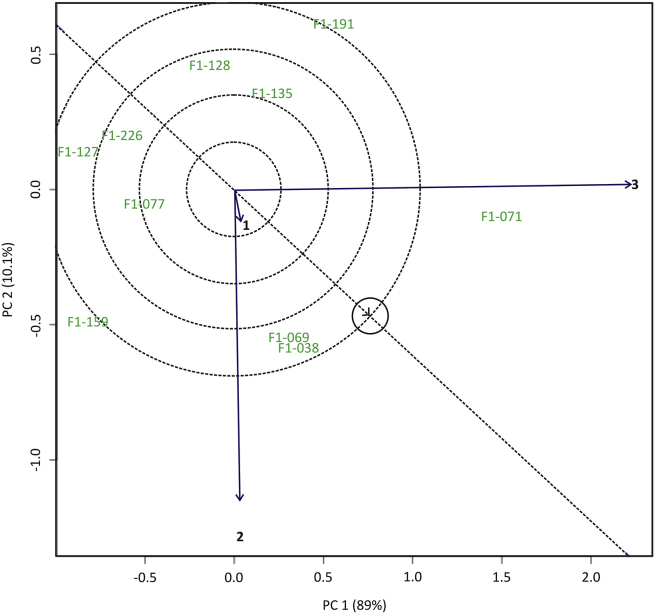
Figure 6 illustrated 99.1% of the total GGE variation, where PC1 explained 89% and PC2 10.1% of total variation. There were 6 sectors with F1-191, F1-071, F1-038, F1-159, F1-127, and F1-128 genotypes as the best genotype for each sector. The environment was divided into two sectors, namely sector 1 (environment 3) and sector 2 (environment 1 and 2). F1-071 genotype was well adapted to the environment 1. In sector 2 there was none well-adapted genotype. There were some superior genotypes in certain sectors but not in 3 test environments i.e. F1-159, F1-127, and F1-128. Environments in different sectors show that genotypes located in these location have unequal yields and that genotypes belong to region-specific genotypes.
Figure 6.
Mega environments biplots on selected sweet potato genotypes in three locations.
In general, this study used numerical stability measurements, AMMI and ASV, as well as a GGE biplot model to select stable sweet potato genotypes. Selection of stable sweet potato genotypes with high yields based on a single stability model is quite difficult. The average sum rank (ASR) used of all stability models to select a stable genotype that was superior with a low ASR value. F1-069, F1-077, F1-226, F1-038, and F1-128 have the smallest ASR and there were identified as the very stable genotypes (Table 3). AMMI models was able to describe stable genotypes in general, both low and high yields, so the determination of stable genotypes must be added to other analytical models such as ASV. However, GGE biplot described the stability of genotypes based on low and high yields, so GGE biplot was more informative. In general, based on parametric, non-parametric, AMMI, ASV and GGE biplots models, the F1-038 and F1-069 were declared as stable and higher yield genotypes. Hence, both genotypes can be declared as stable genotypes with high yields for West Java.
4. Conclusion
Ten sweet potato genotypes were selected that were in accordance with consumer preferences, i.e., F1-038 (G1), F1-069 (G2), F1-071 (G3), F1-077 (G4), F1-127 (G5), F1-128 (G6), F1-135 (G7), F1-159 (G8), F1-191 (G9), and F10226 (G10). Generally, Selection of stable sweet potato genotypes with high yields based on a single stability model is quite difficult. Parametric, non-parametric, AMMI, ASV, and GGE Biplot models identify F1-038, and F1-069 as stable genotypes. They produce higher yields than other genotype tested. Therefore, the F1-038 and F1-069 genotypes can be potentially recommended as superior varieties for West Java, Indonesia, while other genotypes were stated as environment-specific.
Declarations
Author contribution statement
Agung Karuniawan; Haris Maulana: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Sitaresmi Dewayani: Performed the experiments; Wrote the paper.
Eso Solihin; M. Amir Solihin: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.
Mahfud Arifin: Contributed reagents, materials, analysis tools or data; Wrote the paper.
Suseno Amien: Conceived and designed the experiments; Wrote the paper.
Funding statement
Dr. Sc.Agr.Agung Karuniawan from Faculty of Agriculture, University of Padjadjaran (UNPAD) was supported by Penelitian Unggulan Strategis Nasional (PUSNAS), Ministry of Research, Technology and Higher Education (Indonesia) years 2016/2017.
Data availability statement
Data will be made available on request.
Declaration of interests statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
Acknowledgements
Highly appreciation to mr. Koko Tjintokohadi M.Sc. and Dr. Sc.Agr. Wolfgang J. Gruneberg for Providing the seed materials from CIP.
References
- Adebola P.O., Shegro A., Laurie S.M., Zulu L.N., Pillay M. Genotype x environment interaction and yield stability estimate of some sweet potato [Ipomoea batatas (L.) Lam] breeding lines in South Africa. J. Plant Breed Crop Sci. 2013;5(9):182–186. [Google Scholar]
- Ahmadi J., Vaezi B., Shaabani A., Khademi K., Ourang S.F. Non-parametric measures for yield stability in grass pea (Lathyrus sativus l.) advanced lines in semi warm regions. J. Agric. Sci. Technol. 2015;17:1825–1838. [Google Scholar]
- Akcura M., Kaya Y. Nonparametric stability methods for interpreting genotype by environment interaction of bread wheat genotypes (Triticum aestivum L.) Genet. Mol. Biol. 2008;31(4):906–913. [Google Scholar]
- Allen J.C., Corbitt A.D., Maloney K.P., Butt M.S., Truong V.D. Glycemic index of sweet potato as affected by cooking methods. Open Nutr. J. 2012;6(1):1–11. [Google Scholar]
- Andrade M.I., Naico A., Ricardo J., Eyzaguirre R., Makunde G.S., Ortiz R., Gruneberg W.J. Genotype x environment interaction and selection for drought adaptation in sweetpotato (Ipomoea batatas [L.] Lam.) in Mozambique. Euphytica. 2016;209:261–280. [Google Scholar]
- Bhandari H.R., Bhanu A.N., Srivastava K., Singh M.N., Shreya, Hemantaranjan A. Assessment of genetic diversity in crop plants - an overview. Adv. Plants Agric. Res. 2017;7(3) [Google Scholar]
- Burri B.J. Evaluating sweet potato as an intervention food to prevent vitamin A deficiency. Compr. Rev. Food Sci. Food Saf. 2011;10(2):118–130. [Google Scholar]
- Central Bureau of Statistics . 2016. Produksi Ubi Jalar Menurut Provinsi, 1993-2015.https://www.bps.go.id/dynamictable/2015/09/09/883/produksi-ubi-jalar-menurut-provinsi-ton-1993-2015.html [Google Scholar]
- Coan M.M.D., Marchioro V.S., Pinto R.J.B., Scapim C.A., Baldissera J.N.C. Determination of genotypic stability and adaptability in wheat genotypes using mixed statistical models. J. Agri. Sci. Technol. 2018;20:1525–1540. [Google Scholar]
- Eberhart S.A., Russell W.A. Stability parameters for comparing varieties. Crop Sci. 1966;6(1):36–40. [Google Scholar]
- Farshadfar E., Sabaghpour S.H., Zali H. Comparison of parametric and non-parametric stability statistics for selecting stable chickpea (Cicer arietinum L.) genotypes under diverse environments. Aust. J. Crop. Sci. 2012;6(3):514–524. [Google Scholar]
- Federer W.T., Reynolds M., Crossa J. Combining results from augmented designs over sites. Agron. J. 2001;93(2):389–395. [Google Scholar]
- Francis T.R., Kannenberg L.W. Yield stability studies in short-season maize: I. A descriptive method for grouping genotypes. Can. J. Plant Sci. 1978;5:1029–1034. [Google Scholar]
- Gauch H.G., Piepho H.P., Annicchiarico P. Statistical analysis of yield trials by AMMI and GGE: further considerations. Crop Sci. 2008;48:866–889. [Google Scholar]
- Gruneberg W.J., Manrique K., Zang D., Herman M. Genotype x environment interactions for a diverse set of sweetpotato clones evaluated across varying ecogeographic conditions in Peru. Crop Sci. 2005;45(6):2160–2171. [Google Scholar]
- Gurmu F. Stability analysis of fresh root yield of sweetpotato in Southern Ethiopia using GGE biplot. Int. J. Pure Agric. Adv. 2017;1(1):1–9. [Google Scholar]
- Gurmu F., Hussein S., Laing M. Self- and cross-incompatibilities in sweetpotato and their implications on breeding. Aust. J. Crop. Sci. 2013;7(13):2074–2078. [Google Scholar]
- Huaman Z. Intrenational Potato Center (CIP); 1999. Sweetpotato Germplasm Management (Ipomoea Batatas) Training Manual. [Google Scholar]
- Huehn M. Nonparametric measures of phenotypic stability . Part 1: Theory. Euphytica. 1990;47:189–194. [Google Scholar]
- Islam S. Sweetpotato (Ipomoea batatas L.) leaf: its potential effect on human health and nutrition. J. Food Sci. 2006;71(2):R13–R121. [Google Scholar]
- Kang M.S. A rank-sum method for selecting high-yielding, stable corn genotypes. Cereal Res. Commun. 1988;16:113–115. [Google Scholar]
- Khalili M., Pour-aboughadareh A. Parametric and non-parametric measures for evaluation yield stability and adaptability in barley doubled haploid lines. J. Agric. Sci. Technol. 2016;18:789–803. [Google Scholar]
- Kivuva B.M., Githiri S.M., Yencho G.C., Sibiya J. Screening sweetpotato genotypes for tolerance to drought stress. Field Crop. Res. 2015;171:11–22. [Google Scholar]
- Laurie S., Faber M., Adebola P., Belete A. Biofortification of sweet potato for food and nutrition security in South Africa. Food Res. Int. 2015;76:962–970. [Google Scholar]
- Li J., Xu N. Cultivar selection and test site evaluation of cotton regional trials in Jiangsu Province based on GGE biplot. Agric. Sci. Technol. 2014;15(8):1277–1284. [Google Scholar]
- Magwaza L.S., Opara U.L. Analytical methods for determination of sugars and sweetness of horticultural products — a review. Sci. Hortic. (Amsterdam) 2015;184:179–192. [Google Scholar]
- Maulana H., Nugroho D.M., Trimo L., Karuniawan A. Proceedings of SABRAO 13th Congress and International Congress. IPB Press; Bogor: 2016. Participatory selection of sweet potato based on farmers preferences in banjar city. [Google Scholar]
- Mirosavljević M., Pržulj N., Boćanski J., Stanisavljević D., Mitrović B. The application of ammi model for barley cultivars evaluation in multi-year trials. Genetika. 2014;46(2):445–454. [Google Scholar]
- Mustamu Y.A., Tjintokohadi K., Gruneberg W.J., Karuniawan A., Ruswandi D. Selection of superior genotype of sweet-potato in Indonesia based on stability and adaptability. Chil. J. Agric. Res. 2018;78(4):461–469. [Google Scholar]
- Nassar R., Huhn M. Studies on Estimation of Phenotypic Stability: tests of significance for nonparametric measures of phenotypic stability. Biometrics. 1987;43(1):45–53. [Google Scholar]
- Nasution R.A., Tangapo A.M., Taufik I., Aditiawati P. Comparison of plant growth promoting rhizobacteria (PGPR) diversity and dynamics during growth of cilembu sweet potato (Ipomoea batatas L var. rancing) in Cilembu and Jatinangor Site, Indonesia. J. Pure Appl. Microbiol. 2017;11(2):837–845. [Google Scholar]
- Ngailo S., Shimelis H., Sibiya J., Mtunda K., Mashilo J. Genotype-by-environment interaction of newly-developed sweet potato genotypes for storage root yield , yield-related traits and resistance to sweet potato virus disease. Heliyon. 2019;5 doi: 10.1016/j.heliyon.2019.e01448. 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Oliveira E.J., de Freitas J.P.X., de Jesus O.N. AMMI analysis of the adaptability and yield stability of yellow passion fruit varieties. Sci. Agric. 2014;7(2):139–145. doi: 10.4238/2014.August.26.2. [DOI] [PubMed] [Google Scholar]
- Plaisted R.L. A shorter method for evaluating the ability of selections to yield consistently over locations. Am. Potato J. 1960;37:166–172. [Google Scholar]
- Plaisted R.L., Peterson L.C. A technique for evaluating the ability of selection to yield consistently in different locations or seasons. Am. Potato J. 1959;36:381–385. [Google Scholar]
- Pour-aboughadareh A., Yousefian M., Moradkhani H., Poczai P., Siddique K.H.M. STABILITYSOFT: a new online program to calculate parametric and non- parametric stability statistics for crop traits. Appl. Plant Sci. 2019;7(1):1–6. doi: 10.1002/aps3.1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purchase J.L., Hatting H., van Deventer C.S. Genotype × environment interaction of winter wheat (Triticum aestivum L .) in South Africa: II. Stability analysis of yield performance. S. Afr. J. Plant Soil. 2000;17:101–107. [Google Scholar]
- Roostaei M., Mohammadi R., Amri A. Rank correlation among different statistical models in ranking of winter wheat genotypes. Crop J. 2014;2(2–3):154–163. [Google Scholar]
- Sholihin Stability of cassava promising clones based on additive main effect and multiplicative interaction (AMMI) model. Energy Procedia. 2015;65:337–343. [Google Scholar]
- Shukla G.K. Some statistical aspects of partitioning genotype-environmental components of variability. Heredity (Edinb). 1972;29:237–245. doi: 10.1038/hdy.1972.87. [DOI] [PubMed] [Google Scholar]
- Solihin M.A., Santun R.P., Sitorus S.R.P., Sutandi A., Widiatmaka Discriminating land characteristics of yield and total sugar content classes of cilembu sweet potato (Ipomoea batatas L.) AGRIVITA J. Agric. Sci. 2018;40(1):15–24. [Google Scholar]
- Solihin M.A., Sitorus S.R.P., Sutandi A., Widiatmaka Biophysic factors related to a local famous sweet potato variety (Ipomoea batatas L.) production: a study based on local knowledge and field data in Indonesia. Am. J. Agric. Biol. Sci. 2016;11(3):164–174. [Google Scholar]
- Thennarasu K. Disertasi. PJ School, IARI; New Delhi, India: 1995. On Certain Non-parametric Procedures for Studying Genotype-Environment Interactions and Yield Stability. [Google Scholar]
- Thiyagu D., Rafii M.Y., Mahmud T.M.M., Latif M.A., Malek M.A., Sentoor G. Genotype by environment assessment in sweetpotato as leafy vegetable using AMMI model. Pakistan J. Bot. 2013;45(3):843–852. [Google Scholar]
- Vaezi B., Pour-Aboughadareh A., Mohammadi R., Mehraban A., Pour-Hossein T., Koohkan E., Ghasemi S., Moradkhani H., Siddique K.H.M. Integrating different stability models to investigate genotype x environment interactions and identify stable and high-yielding barley genotypes. Euphytica. 2019;5(63) [Google Scholar]
- Vimala B., Sreekanth A., Gruneberg W.J. Variation in morphological characters and storage root yield among exotic orange-fleshed sweet potato clones and their seedling population. J. Root Crops. 2012;38(1):32–37. [Google Scholar]
- Wricke G. Übereine methode zur erfassung der ökologischen streubreite in feldversuchen. Zeitschrift für Pflanzenzüchtung. 1962;47:92–96. [Google Scholar]
- Yan W., Kang M.S., Ma B., Woods S., Cornelius P.L. GGE Biplot vs . AMMI analysis of genotype-by-environment data. Crop Sci. 2007;47(2):641–653. [Google Scholar]
- You F.M., Duguid S.D., Thambugala D., Cloutier S. Statistical analysis and field evaluation of the type 2 modified augmented design (MAD) in phenotyping of flax (Linum usitatissimum) germplasms in multiple environments. Aust. J. Crop. Sci. 2013;7(11):1789–1800. [Google Scholar]
- You F.M., Song Q., Jia G., Cheng Y., Duguid S., Booker H., Cloutier S. Estimation of genetic parameters and their sampling variances for quantitative traits in the type 2 modified augmented design. Crop J. 2016;4(2):107–118. [Google Scholar]
- Zhang P.P., Song H., Ke X.W., Jin X.J., Yin L.H., Liu Y., Qu Y., Su W., Feng N.J., Zheng D.F., Feng B.L. GGE biplot analysis of yield stability and test location representativeness in proso millet (Panicum miliaceum L.) genotypes. J. Integr. Agric. 2016;15(6):1218–1227. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.