A sparse principal component analysis of Class III malocclusions

Abstract

Objectives:

To identify the most characteristic variables out of a large number of anatomic landmark variables on three-dimensional computed tomography (CT) images. A modified principal component analysis (PCA) was used to identify which anatomic structures would demonstrate the major variabilities that would most characterize the patient.

Materials and Methods:

Data were collected from 217 patients with severe skeletal Class III malocclusions who had undergone orthognathic surgery. The input variables were composed of a total of 740 variables consisting of three-dimensional Cartesian coordinates and their Euclidean distances of 104 soft tissue and 81 hard tissue landmarks identified on the CT images. A statistical method, a modified PCA based on the penalized matrix decomposition, was performed to extract the principal components.

Results:

The first 10 (8 soft tissue, 2 hard tissue) principal components from the 740 input variables explained 63% of the total variance. The most conspicuous principal components indicated that groups of soft tissue variables on the nose, lips, and eyes explained more variability than skeletal variables did. In other words, these soft tissue components were most representative of the differences among the Class III patients.

Conclusions:

On three-dimensional images, soft tissues had more variability than the skeletal anatomic structures. In the assessment of three-dimensional facial variability, a limited number of anatomic landmarks being used today did not seem sufficient. Nevertheless, this modified PCA may be used to analyze orthodontic three-dimensional images in the future, but it may not fully express the variability of the patients.

INTRODUCTION

When a data set has a large number of variables, principal component analysis (PCA) is a popular method of summarizing the information.1–8 PCA compresses original variables into several sets of linear combinations of variables. In theory, the reduced set of variables, known as the principal components (also called latent variables), enable focusing the information in a data set with a large number of variables into only a few underlying factors.9 In reality, however, complicated multivariate statistical methods such as PCA almost always have very complicated results to interpret. While the primary purpose of a PCA is to reduce the number of variables, a data set with a large number of measurement variables produces still a larger number of principal components, which entails difficulties in interpretation. For example, in theory, the data of the present study including 740 variables could produce 740 nonzero principal components. In this regard, a method that can simplify the resulting interpretation is necessary. The current study directed its attention to modification of the loading matrix via sparse PCA. If reducing the number of loading matrices in each principal component could be possible, this might help pinpoint which variables played a more important role than others in each principal component. This method could potentially be used by orthodontists to analyze more complex three-dimensional images, such as those obtained by computed tomography (CT).

The purpose of the present study was to identify the most characteristic variables out of a large number of anatomic landmark variables on three-dimensional CT images collected from 217 patients with severe skeletal Class III malocclusions. By applying a modified PCA, an attempt was made to identify which anatomic structures would demonstrate major variabilities characterizing the patients.

MATERIALS AND METHODS

Study Sample

As material of this study, three-dimensional CT images were chosen from a total of 217 patients (108 women and 109 men) with skeletal Class III malocclusions who had undergone orthognathic surgery. All were adult, nongrowing patients with an average age of 22.2 ± 3.7 years who demonstrated severe mandibular prognathism. On average, men had a greater degree of mandibular prognathism than women. For example, the mean overjet was −4.3 mm in women and −6.6 mm in men. A descriptive summary of the study sample is shown in Table 1. The exclusion criteria for this sample were cleft lip and palate, injury, or craniofacial syndrome.

Table 1.

Descriptive Summary of the Study Sample

Variable	Women (n = 108)		Men (n = 109)		Difference
	Mean	SD	Mean	SD	P Valuea
Age, y	23.6	5.0	23.8	4.2	.7574
SNA, °	80.2	3.2	80.5	3.8	.5908
SNB, °	82.1	3.5	84.3	4.4	.0001
ANB, °	−1.9	2.6	−3.8	3.4	<.0001
Nasion perpendicular to point A, mm	−3.8	3.7	−3.7	4.7	.9480
Nasion perpendicular to point B, mm	−2.4	6.8	1.9	9.2	.0001
Nasion perpendicular to Pogonion, mm	−1.1	7.9	3.9	10.5	.0001
Overjet, mm	−4.3	3.5	−6.6	4.2	<.0001
Overbite, mm	−0.2	1.5	−0.1	2.1	.7569
Molar relationship, mm	4.6	3.1	7.6	4.5	<.0001

^aResult of t-test to compare the mean values between the two groups.

The institutional review board for the protection of human subjects reviewed and approved the research protocol (IRB No. S-D20140025).

The three-dimensional CT images were obtained using multidetector spiral CT (Somatom Sensation 10, Siemens, Erlangen, Germany). These images were analyzed by Invivo 3D Imaging Software (Anatomage, San Jose, Calif). The reference-coordinate system used in this study was based on the framework developed by Muramatsu et al.,10 as follows: basion, a skull-base landmark, was set as the origin of the coordinate system (x, y, z) = (0, 0, 0); the X plane indicated the transverse (right or left) position of each landmark; Y indicated its sagittal (anterior or posterior) position; and Z indicated its vertical (upper or lower) position.10

Study Variables

Input variables.

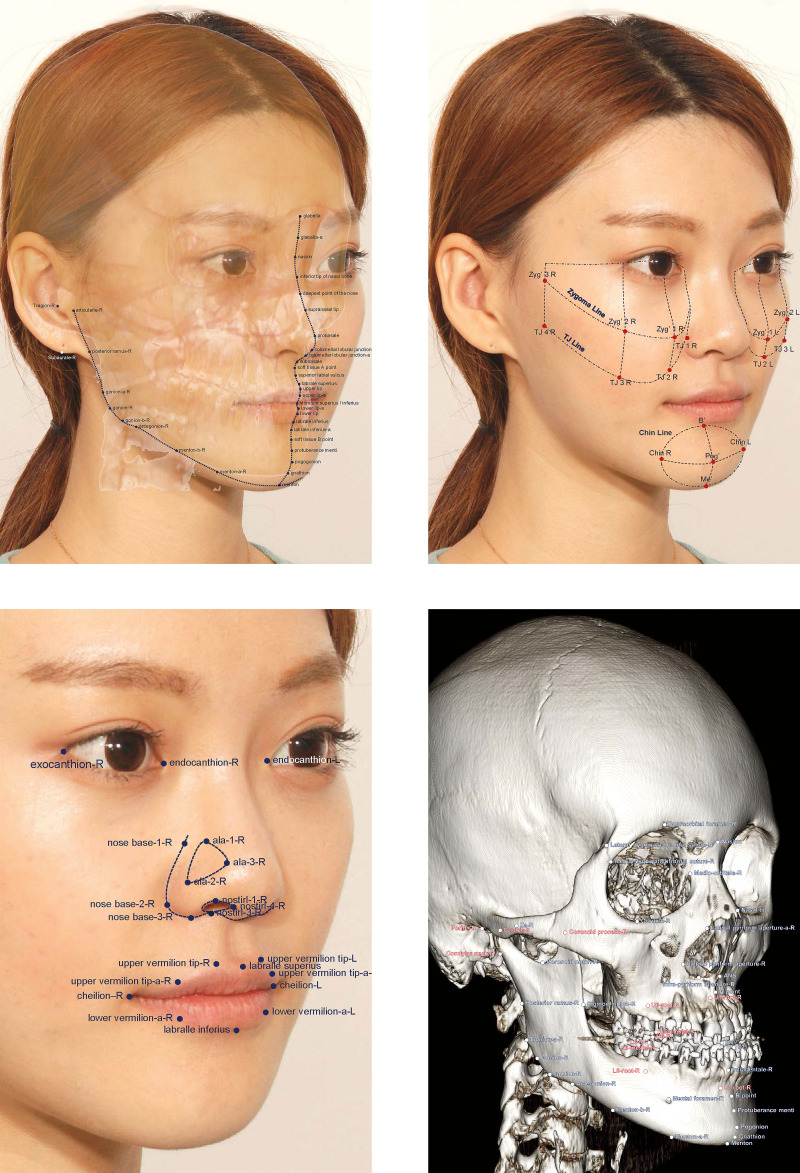
The input variables were composed of a total of 740 variables extracted from 185 anatomical landmarks identified on the CT images. To fully describe each anatomic position and to represent facial structures with as smooth as possible curves connecting the landmark points, 104 soft tissue and 81 hard tissue landmarks were identified (Figure 1). The three-dimensional Cartesian coordinates of the 185 facial landmarks (185 × 3 = 555 variables) and the Euclidean distance measures (185 variables) from the origin (0, 0, 0) that were obtained by calculating the square root of x² + y² + z² for each landmark were added to give a total of 740 variables and were entered into the sparse PCA.

Figure 1.

Landmarks identified in the present study: landmarks on soft-tissue outline (top left); cheek and chin area (top right); eyes, nose, and lips (bottom left); and hard tissue landmarks (bottom right).

Outcome variables.

The outcome variables were the first 10 principal components accounting for as much variability in the three-dimensional landmarks as possible. Having extracted the principal components, to identify which set of variables contributed to each principal component, the loading matrix of each principal component was analyzed and then interpreted as what the component represented (Figure 2).

Figure 2.

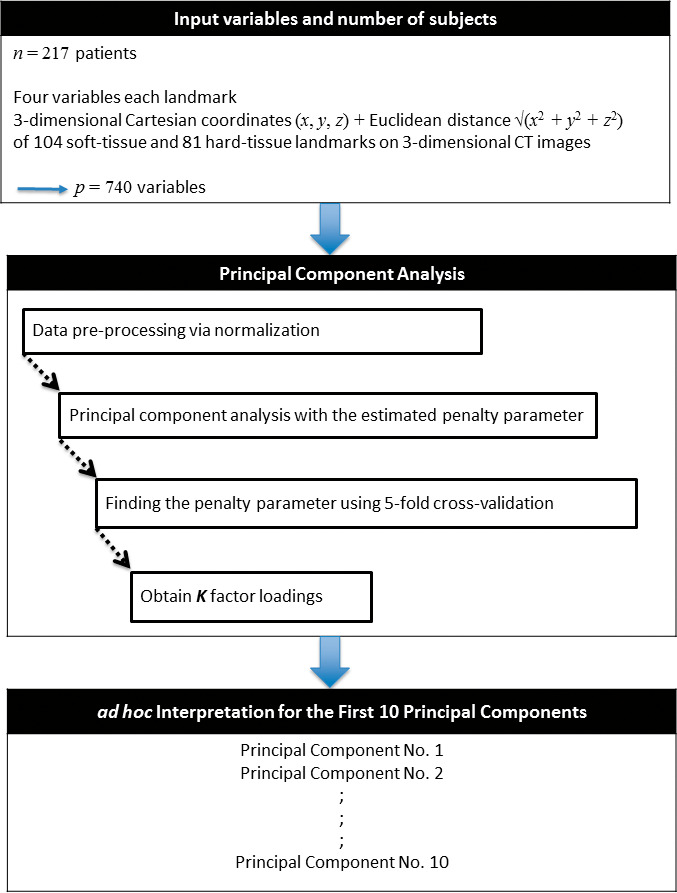
Flowchart illustrating the methods used in this study. Please refer to the text for the explanation.

Statistical Analysis

The sparse PCA was applied using the penalized multivariate analysis R package11 under version 3.5.1 of the R environment (Vienna, Austria).12 Although some mathematical details would have been needed, an attempt was made to focus on a qualitative interpretation and results. Instead, in the Appendix, technical details are briefly described as to how to determine the number of principal components, and the background of the sparse PCA is summarized. Further details of the statistical calculations may be obtained by contacting the authors.

RESULTS

Of the 740 input variables, the first 10 principal components are qualitatively described in Table 2. The first five principal components were interpreted as related to the soft tissue landmarks. The first and second principal components seemed to represent the anteroposterior and vertical positions of the base of the nose variables. The third and fourth principal components signified the upper lip and lower lip related variables, respectively. The fifth principal component was a latent variable that is related to the anteroposterior position of the eyes and nasal bridge (Table 2).

Table 2.

Variables That Contributed to Each Principal Component

Principal Component	Women	Men
1	Anteroposterior position of the nose base variables (soft tissue landmarks)	Anteroposterior position of the nose base variables (soft tissue landmarks)
2	Vertical position of the nose base variables (soft tissue landmarks)	Vertical position of the nose base variables (soft tissue landmarks)
3	Upper lip–related variables (soft tissue landmarks)	Upper lip–related variables (soft tissue landmarks)
4	Lower lip–related variables (soft tissue landmarks)	Lower lip–related variables (soft tissue landmarks)
5	Anteroposterior position of the eyes and nose bridge (soft tissue landmarks)	Anteroposterior position of the eyes and nose bridge (soft tissue landmarks)
6	Mandibular asymmetry–related variables (skeletal landmarks)	Mandibular asymmetry–related variables (skeletal landmarks)
7	Chin area–related variables (skeletal landmarks)	Vertical position of the eyes and nose bridge (soft tissue landmarks)
8	Vertical position of the eyes and nose bridge (soft tissue landmarks)	Chin area–related variables (skeletal landmarks)
9	Facial width–related variables (soft tissue and skeletal landmarks)	Anteroposterior position of the mandible (skeletal landmarks)
10	Facial height–related variables (soft tissue and skeletal landmarks)	Facial height–related variables (soft tissue and skeletal landmarks)

The first six principal components appeared to be similar between genders. From the seventh to the ninth principal component, for women and men, the principal components had a slightly different order. From the eighth onward, sexual dimorphism was noted, but the difference was not as evident. Specifically, the ninth component showed the most notable difference between the sexes. For women, the ninth component comprised variables relating to the width of the cheek area, whereas, for men, variables relating to the lower jaw border contributed to the ninth component. It may be conjectured that a prominent lower-jaw border might be a peculiar masculine characteristic of patients with mandibular prognathism, and a well-developed cheek area might be considered a common feature of women included in the present study. However, this explanation might be insignificant considering the ninth component had a proportion of variance explaining only approximately 4% (Table 3).

Table 3.

The First 10 Principal Components Extracted From the 740 Variables, Number of Nonzero Variables, and Their Cumulative Proportions of Variance Explained (%)

Principal Component	Number of Nonzero Variables in each Principal Component		Cumulative Proportion of Variance Explained by the Principal Components, %
	Women	Men	Women	Men
1	85	83	9.2	9.2
2	95	94	17.7	17.8
3	94	89	25.9	26.0
4	97	95	34.2	34.5
5	99	104	40.6	41.3
6	110	102	45.9	45.9
7	97	103	51.7	51.0
8	100	105	56.5	56.8
9	123	134	60.5	60.3
10	144	156	62.6	62.9

The number of nonzero variables that contributed to each principal component ranged from 83 to 156 for women and from 85 to 144 for men. The first 10 principal components explained 63% of the total variance for both women and men (Table 3).

DISCUSSION

At the beginning of this study's formulation, it was anticipated that skeletal landmarks related to mandibular anatomy would be found as the major principal components characterizing the patients because the study subjects were orthognathic surgery patients with mandibular prognathism. However, different from this expectation, groups of soft tissue landmarks on the nose, lips, and eyes showed greater variability than the skeletal variables did and were consequently more representative of the individual facial variabilities of those patients. A previous study using PCA on two-dimensional images (lateral cephalometric radiographs) showed that the first two principal components accounted for 84% of skeletal variation. Those two principal components were groups of cephalometric variables representing both anteroposterior and vertical skeletal relationships. In addition, two-dimensional skeletal configuration had been abstracted as a quadrangle that comprised point A, point B, gonion, and gnathion.13 The result of the two-dimensional PCA study motivated the current performance of a three-dimensional PCA study in the hopes of identifying a few number of principal components that might concisely explain major variabilities in skeletal Class III patients. However, unlike the PCA results of the two-dimensional study, the cumulative proportion of variance explained by the first 10 principal components reached only 63% in the present study. This was a smaller proportion than what was expected to be seen as a result of the previous two-dimensional PCA study. In the present study of three-dimensional images, contrary to the results on two-dimensional images, the principal components could not pinpoint important skeletal or soft tissue landmarks that could deliver a concise explanation for the variability characterizing the patients. That might be indicative of the inherent complexity of three-dimensional images.

Methods of interpreting three-dimensional images are currently at an early stage of development. With the advent of three-dimensional technology, orthodontic clinicians have access to an incredible amount of information to better analyze, diagnose, and treat patients.14,15 Consequently, modern orthodontists are becoming more acquainted with three-dimensional images. Using numerous cephalometric analyses, orthodontists have become very skilled at interpreting the variables within two-dimensional lateral cephalographs. However, unlike conventional two-dimensional cephalometric x-rays, there seems to be no accepted consensus yet upon which three-dimensional variables should be relied. This is likely partly because three-dimensional images have a greater number of anatomical landmarks and far more information than two-dimensional images have. For example, two-dimensional cephalographs may have 100 landmarks at the most.2,3,13,16,17 On three-dimensional images, however, additional landmarks are necessary to express three-dimensional curves as smoothly as possible. The number of variables can reach hundreds of landmarks. Furthermore, each three-dimensional landmark includes coordinate information of all three planes of space. Consequently, the number of variables triples.

Traditionally, principal components are computed mathematically via the singular-value decomposition of the data matrix. However, when the number of input variables and the number of significant principal components are increased, it is hard to interpret the resultant matrix loadings.18 In the present study, the number of input variables (p = 740) exceeded the number of subjects (n = 217), which was a typical “small n, large p” situation. A modification of conventional PCA was necessary to solve the “small n, large p” problem by shrinking the principal component loadings. A recently published sparsity algorithm was investigated in which an L₁ penalty is applied to the singular-value decomposition.19 This method, also known as the penalized matrix decomposition, was found to be computationally efficient and capable of preventing the misidentification of important variables during the selection process.20 The major advantages of the sparse PCA are the following: First, it facilitates the interpretation of data. Traditional methods yield an extremely large number of nonzero loadings, which makes it difficult to interpret what the extracted principal components represent. Second, artificially setting threshold values and treating loadings below a given threshold as null might be arbitrary and potentially misleading. Third, the “small n, large p” problem may be increasingly prevalent in the future, particularly when obtaining a large number of subjects, which will be difficult for ethical and funding reasons. The number of research variables will probably grow because of the advancement in three-dimensional technology and digital data acquisition devices. Applying the sparse PCA might be an objective tool for reducing the complexity while ensuring that the information within the data are as intact as possible.

The results of the present study might imply that when a commonly accepted and used three-dimensional analysis similar to the two-dimensional cephalometric analysis method is to be developed, unlike the relatively limited number of landmarks used in two-dimensional cephalometrics, a fairly large number of three-dimensional landmarks or groups of variables might be necessary. Limited numbers of simple cephalometric measurements being used today might not fully express and assess the facial variability in all three planes of space. With the advantages of three-dimensional imaging becoming available, more complex measurements and better analyses are needed to more thoroughly describe and consequently customize orthodontic treatment planning. It is hoped that the method proposed in this study may be helpful in handling complicated three-dimensional image data.

This study seems to be the first application of the sparse PCA on a large number of variables found on three-dimensional CT images. Consequently, it was not possible to compare this study's results with those of other studies published on the topic. A limitation of the study was that the subjects were not representative of the general population but were patients with severe skeletal Class III malocclusions who received orthognathic surgery. This was because CT images from all types of patients have not yet been obtained. Another limitation is that one understanding of facial variability might not accurately be applied to other ethnic populations.

CONCLUSIONS

• On three-dimensional images, soft tissues had more variability than skeletal anatomic structures.

• In the assessment of three-dimensional facial variability, the limited number of anatomic landmarks being used today did not seem sufficient.

APPENDIX

We considered a data set comprising information on the three-dimensional coordinates and Euclidean distances of n samples, denoted as data matrix X with dimensions n by p. We assumed that the data were centered. Matrix X was decomposed by singular-value decomposition, as follows:

The method of penalized matrix decomposition proposed by Witten et al.19 was constructed by imposing additional constraints on the singular-value decomposition, as follows¹:

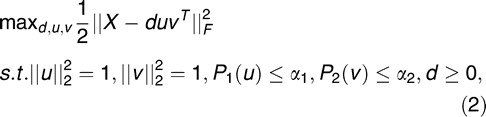where u is a column of U, v is a column of V, d is a diagonal element of D, || || is the Frobenious norm, and P₁ and P₂ are penalty functions. A reasonable value of α gives a sparse loading matrix, V, with many zero entries. The parameter for the penalty function is determined by fivefold cross-validation.

To find the first K sparse principal components, the penalized matrix decomposition was applied to a covariance matrix with symmetrical L₁ penalties, as follows:

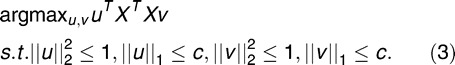where the vector u_k denotes the sparse principal components for k = 1, 2, … K. This problem was solved by biconvexity optimization using an iterative algorithm. For more details, please refer to Witten et al.19