Reliability of 3D dental and skeletal landmarks on CBCT images

Abstract

Objectives:

To quantify reliability of three-dimensional skeletal landmarks and a comprehensive set of dental landmarks in cone-beam computed tomography (CBCT) and to determine the shapes of envelope of error.

Materials and Methods:

Three judges located 31 skeletal landmarks and 60 dental landmarks on the pre- and posttreatment CBCT images of 22 patients. Landmark error was determined by calculating the distance of deviation of landmark locations around their average. Standard deviation and mean radial spherical error were calculated. Scatterplots were constructed to characterize envelope of error.

Results:

The midline landmarks of the cranial base were highly reliable. Bilateral skeletal landmarks tended to have larger error than midline landmarks. Among the nonconventional landmarks, fronto-zygomatic suture, condyle, and mental foramen showed relatively high reliability. However, foramen spinosum and temporal fossa showed larger errors. Gonion was the least reliable landmark. Most dental landmarks were located more reliably than skeletal landmarks. The highest reliability was found at incisal edges. Mesiobuccal cusp of first molars also showed high reliability.

Conclusions:

There were differences in the size and shape of the distributions of errors of different landmarks. Most landmarks showed elongated envelopes. Bilateral structures tended to show greater errors than midline structures. Most dental landmarks were more reliable than skeletal landmarks.

INTRODUCTION

The long search for a valid three-dimensional (3D) representation of the skull has achieved success with the development of cone beam computed tomography (CBCT).1–4 One of the advantages of CBCT is that it permits clinicians to accurately determine 3D positions of individual teeth and their displacement relative to the skull, which has been a challenging problem for two-dimensional (2D) cephalograms. Typically, study casts have been used to record relative positions of individual teeth, such as molar and canine relationships, while lateral cephalograms were used separately to locate the positions of incisors and molars relative to the skull.

As the specialty's experience with CBCT images increases, diagnostic techniques that make fuller use of its capabilities are being devised. In time, the full capabilities of CBCT will be better understood, but discovering them will involve a trial-and-error process that can be expected to take time. Part of the learning process will involve characterizing the 3D reliability of landmark location.

Baumrind and Frantz's5 work on 2D landmark reliability presented characteristic envelopes of error for landmarks on lateral cephalograms. It could be anticipated that the 3D envelope of error may be different for landmarks located on CBCT images both in shape and magnitude. Previous studies on 3D landmark reliability showed improved reliability for many conventional cephalometric landmarks and introduced some nontraditional cephalometric landmarks.6–11 However, there is little information on landmark-specific envelopes of error in three dimensions and reliability of various dental landmarks. This study sought to quantify the 3D reliability of skeletal landmarks and a comprehensive set of dental landmarks and to determine the shapes of their envelope of error.

MATERIALS AND METHODS

This retrospective study was approved by the Institutional Review Board of the University of the Pacific (#14-49). The data reported were derived from records of 22 growing patients with Class II malocclusion who were treated in the practice of a single orthodontist (Dr. Carlson). This study was part of a study designed to evaluate 3D changes of skeletal and dental structures in Class II treatment. At the time the study started, records of 148 patients for whom both pre- and posttreatment CBCT images were available. Of these, 22 subjects were identified as the Class II adolescent sample who started treatment before their 16th birthday and presented greater than half-cusp bilateral Class II molar relationship.

The sample included 8 boys and 14 girls. At the beginning of treatment, mean age was 12.5 years, (range = 10.8 to 15.2 years); at the end of treatment, mean age was 14.2 years (range = 12.4 to 17.0 years). The CBCT images were generated using the Next Generation iCAT (Imaging Sciences, Hatfield, Pa). The image acquisition protocol included a scan time of 8.9 seconds, 16 × 13 cm field of view, and 0.4 mm³ voxel size. The DICOM (Digital Imaging and Communications in Medicine) files from the iCAT were processed using InVivo 5.3 software (Anatomage, San Jose, Calif).

The CBCT images were oriented to an anatomic frame of reference (AFOR). The axial plane was determined by right porion, left porion, and the midpoint between right and left orbitale. The sagittal plane was made perpendicular to the axial plane and contained nasion and basion. The coronal plane was set perpendicular to the other two planes and passed through sella.

Thirty-one skeletal landmarks and 60 dental landmarks (Table 1) were located on both pre- and posttreatment CBCT images by three members of a team of four second-year orthodontic residents who had regularly used the InVivo software. Prior to this study, judges were provided with more specific 3D definitions for each landmark and were calibrated using 10 cases. All judges located landmarks for each subject on the same AFOR previously set by the author (Dr. Park). Pre- and posttreatment CBCT images of the sample were regarded as separate and independent images. Landmarks were first located on the volumetric CBCT images. After the landmark's location had been approximated, its location was refined in the axial, sagittal, and coronal cross-sections (Figure 1).

Table 1.

Landmark Definition^a

Landmark	Variable Name	Skeletal Landmark Definition
Sella	Sella	The midpoint of the pituitary fossa as determined by inspection
Nasion	Nasion	The most antero-inferior point on the frontal bone at the middle of fronto-nasal suture
Basion	Basion	The inferior-most point on the anterior margin of the foramen magnum in the middle
Porion	Porion_R; Porion_L	The most superior and lateral point at the external enterance to the auditory meatus
Orbitale	Orbitale_R; Orbitale_L	The most inferior point of the lower border of the bony orbit
Crista galli	CristaG	The most superior and anterior point on the median ridge of bone that projects upward from the cribriform plate of the ethmoid bone
Nasal bone	NasBone	The middle of the nasal bone tip at its most inferior end
Fronto-zygomatic suture	FroZyg_R; FroZyg_L	The most anterior point at the intersection of the frontozygomatic suture on the inner rim of orbit
Foramen spinosum	ForSpin_R; ForSpin_L	The center of the opening of foramen spinosum in the greater wing of the sphenoid bone, situated lateral to the foramen ovale
Temporal fossa	TempFos_R; TempFos_L	The most superior and lateral point of inferior zygomatic arch border, above condylar head as seen from the sagittal perspective
ANS	ANS	The anterior-most point of the anatomic anterior nasal spine
PNS	PNS	The posterior-most point of the anatomic posterior nasal spine
Point A	Point A	The deepest point on the curvature of the surface of the maxillary bone between ANS and the alveolar crest in the middle of maxilla
Key ridge	KeyRig_R; KeyRig_L	The most inferior point of the zygomaticomaxillary ridge along the suture between the zygomatic bone and the maxillary bone
Jugale	Jug_R; Jug_L	The intersection of the outline of the maxillary tuberosity and the zygomatic buttress
Pogonion	Pogonion	The anterior-most point on the chin in the midline of the mandibular symphysis
Menton	Menton	The inferior-most point on the chin at the midline of the mandibular symphysis
Point B	Point B	The deepest point on the curvature of the anterior border of the mandible between pogonion and the alveolar crest of the lower incisors at the middle of mandible
Condyle	Condyle_R; Condyle_L	The most superior (sagittal perspective) and the middle (frontal perspective) point on the contour of the condyle head
Gonion	Gonion_R; Gonion_L	The most inferior point on the curvature of the angle of the jaw where the body of the mandible meets the ramus
Mental foramen	MentFor_R; MentFor_L	The center of mental foramen located on the external surface of the mandible
Central incisor	UR1_MInc; UL1_Minc;	The most inferior and mesial point along the incisal edge of central incisor
Mesio-incisal edge	LR1_MInc; LL1_Minc
Central incisor	UR1_DInc; UL1_Dinc;	The most inferior and distal point along the incisal edge of central incisor
Disto-incisal edge	LR1_DInc; LL1_DInc
Central incisor	UR1_Apex; UL1_Apex;	The most apical point on the root of central incisor
Root apex	LR1_Apex; LL1_Apex
Canine	UR3_MCon; UL3_Mcon;	The most lateral point on the mesial contact point of canine
Mesial contact point	LR3_MCon; LL3_MCon
Canine	UR3_DCon; UL3_Dcon;	The most lateral point on the distal contact point of canine
Distal contact ooint	LR3_DCon; LL3_DCon
Canine cusp	UR3_Cusp; UL3_Cusp;	The most occlusal point on the cusp of canine
	LR3_Cusp; LL3_Cusp
Canine root apex	UR3_Apex; UL3_Apex;	The most apical point on the root of canine
	LR3_Apex; LL3_Apex
First premolar	UR4_BCusp; UL4_Bcusp;	The most occlusal point on the buccal cusp of first premolar
Buccal cusp	LR4_BCusp; LL4_BCusp
First molar	UR6_MBCusp; UL6_MBCusp;	The most occlusal point on the mesiobuccal cusp of first molar
Mesiobuccal cusp	LR6_MBCusp; LL6_MBCusp
First molar	UR6_DBCusp; UL6_DBCusp;	The most occlusal point on the distobuccal cusp of first molar
Distobuccal cusp	LR6_DBCusp; LL6_DBCusp
First molar	UR6_MLCusp; UL6_MLCusp;	The most occlusal point on the mesiolingual cusp of first molar
Mesiolingual cusp	LR6_MLCusp; LL6_MLCusp
First molar	UR6_DLCusp; UL6_DLCusp;	The most occlusal point on the distolingual cusp of first molar
Distolingual cusp	LR6_DLCusp; LL6_DLCusp
Upper first molar	UR6_MBApex; UL6_MBApex	The most apical point on the mesiobuccal root of upper first molar
Mesiobuccal root apex
Upper first molar	UR6_DBApex; UL6_DBApex	The most apical point on the distobuccal root of upper first molar
Distobuccal root apex
Upper first molar	UR6_PApex; UL6_PApex	The most apical point on the palatal root of upper first molar
Palatal root apex
Lower first molar	LR6_MApex; LL6_MApex	The most apical point on the mesial root of lower first molar (if there is bifurcation, then mesiobuccal root)
Mesial root apex
Lower first molar	LR6_DApex; LL6_DApex	The most apical point on the distal root of lower first molar
Distal root apex
Lower first molar	LR6_MBGroove;	The point at the height of counter of the buccal groove of lower first molar
Buccal groove	LL6_MBGroove

^aL indicates left; LL, lower left; LR, lower right; R, right; UL, upper left; UR, upper right.

Figure 1.

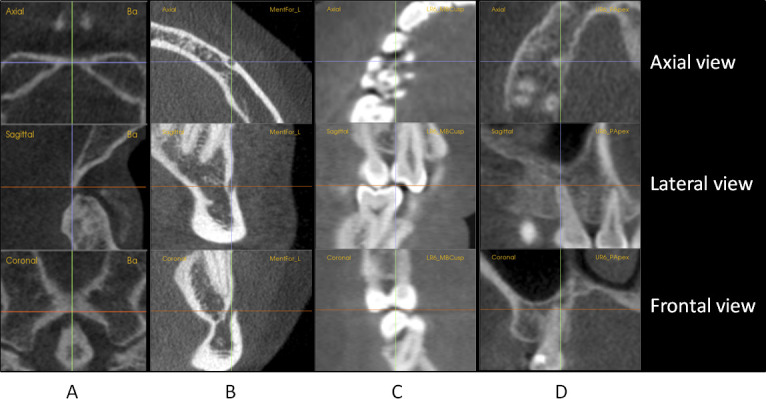
Axial, sagittal, and coronal sectional views used for locating landmarks. (A) Basion. (B) Mental foramen_left. (C) Lower right first molar mesiobuccal cusp. (D) Upper right first molar palatal root apex

The method for calculating landmark reliability is illustrated in Figure 2. It is difficult to illustrate the process in 3D, so it is done in 2D plots. For each landmark of each case, three judges' landmark locations were averaged, and the average represented the best estimate of the landmark location. Error was determined in the X, Y, and Z dimensions by calculating deviations of each judge's estimate from the average. A gross outlier was identified and deleted when an estimate of landmark location deviated more than 5 mm from the average.12 The two remaining estimates were then averaged. A total of 115 outliers were identified out of 12,012 estimates (0.96%).

Figure 2.

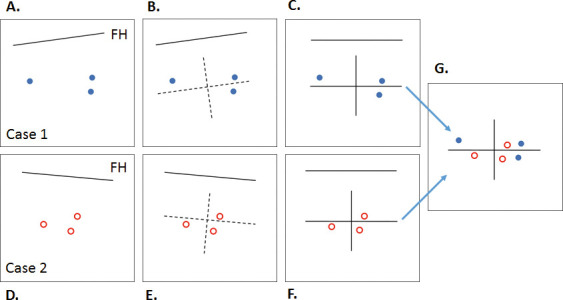
The method for constructing scatterplots. (A) Each judge located the landmark independently. The individual images of three judges were registered with their coordinates expressed in terms of the image AFOR. (B) The estimates of the three judges were averaged. The average was taken as the origin of a local AFOR for that landmark on that image with coordinates parallel and perpendicular to the image's Frankfort plane. (C) The local landmark's data were rotated and translated such that the axes became horizontal and vertical. (D–F) For the same landmark from another case, Steps A through C were repeated. (G) The plot of the second case was translated and registered on the plot of the first case. In a similar manner, the estimates for the same landmark on the remaining 20 cases were registered on the plot from G, yielding the final plot for all 22 cases.

Scatterplots were generated for all landmarks to determine the shape of envelope of error. All the averages for each landmark were plotted on the origin with the individual estimates of four judges for all cases arrayed around them (Figure 2).

Statistical Analysis

The distance that each judge's estimate was from the average for each landmark was determined. Errors of landmark location are reported in terms of standard deviations (SDs) of these distances, which were calculated with respect to the transverse axis (SD_X), the anterior-posterior (AP) axis (SD_Y), and the vertical axis (SD_Z).

The mean radial spherical error (MRSE) was also calculated for each landmark. The MRSE provides an estimate of the radius of a sphere around the origin, which contains approximately 61% of the values of all judges.13 The MRSE was used to report overall 3D reliability and was directly computed from the variances in X, Y, and Z as follows:

RESULTS

Tables 2 and 3 show average error for each landmark in terms of SD in each dimension and MRSE. The midline landmarks of the cranial base: nasion, sella, and basion, were highly reliable. Their scatterplots showed circular shapes of error distribution (Figure 3). Bilateral skeletal landmarks tended to have larger error than midline landmarks. Among the nonconventional skeletal landmarks, fronto-zygomatic suture, condyle, and mental foramen showed relatively high reliability and appeared to be promising. However, other landmarks, such as foramen spinosum, and temporal fossa, showed larger errors. Foramen spinosum was the most error prone among the landmarks on the cranial base. Gonion was the least reliable landmark; it showed MRSE in excess of 2 mm.

Table 2.

Skeletal Landmarks^a

Anatomic Region	Landmark		Error in Each Dimension (mm)			MRSE (mm)
	Midline	Bilateral	SD_X	SD_Y	SD_Z
Cranial base	Sella		0.39	0.23	0.30	0.54
	Nasion		0.32	0.26	0.47	0.62
	Basion		0.52	0.26	0.23	0.63
		FroZyg_R	0.28	0.41	0.46	0.67
		FroZyg_L	0.34	0.62	0.39	0.81
	NasBone		0.29	0.55	0.57	0.85
	CristaG		0.25	0.87	0.92	1.29
		Orbitale_L	1.14	0.68	0.28	1.36
		TempFos_R	1.15	0.64	0.44	1.39
		Porion_L	1.01	0.73	0.60	1.39
		Porion_R	1.26	0.57	0.51	1.48
		Orbitale_R	1.39	0.98	0.30	1.73
		ForSpin_L	0.89	1.14	1.00	1.76
		ForSpin_R	0.96	0.98	1.24	1.85
		TempFos_L	1.35	1.16	0.56	1.87
Maxilla	ANS		0.35	0.51	0.49	0.79
	Point A		0.22	0.20	0.84	0.90
	PNS		0.25	1.01	0.55	1.18
		KeyRig_L	1.09	0.69	0.70	1.47
		Jug_L	0.84	1.11	0.96	1.69
		KeyRig_R	1.31	0.76	0.80	1.71
		Jug_R	1.00	1.02	0.98	1.74
Mandible	Menton		0.37	0.43	0.14	0.59
		MentFor_L	0.47	0.49	0.44	0.81
	Pogonion		0.65	0.20	0.59	0.89
		Condyle_L	0.77	0.48	0.23	0.94
		Condyle_R	0.81	0.48	0.24	0.97
		MentFor_R	0.54	0.63	0.51	0.98
	Point B		0.31	0.17	0.97	1.03
		Gonion_L	0.77	1.87	1.45	2.49
		Gonion_R	0.85	2.06	1.73	2.82

^aLandmarks are listed by the order of size of MRSE within each group of anatomical region. MRSE indictes mean radial spherical error.

Table 3.

Dental Landmarks^a

Landmark	Error in Each Dimension (mm)			MRSE (mm)
	SD_X	SD_Y	SD_Z
UR1_MInc	0.30	0.17	0.24	0.42
UR1_DInc	0.37	0.27	0.41	0.61
UR1_Apex	0.24	0.24	0.31	0.46
UR3_MCon	0.33	0.29	0.47	0.65
UR3_DCon	0.47	0.38	0.38	0.72
UR3_Cusp	0.25	0.37	0.52	0.69
UR3_Apex	0.35	0.33	0.57	0.74
UR4_BCusp	0.29	0.17	0.22	0.40
UR6_MBCusp	0.39	0.28	0.23	0.53
UR6_DBCusp	0.55	0.29	0.18	0.65
UR6_MLCusp	0.78	0.84	0.28	1.18
UR6_DLCusp	0.74	0.81	0.35	1.15
UR6_MBApex	0.40	0.32	0.33	0.61
UR6_DBApex	0.34	0.26	0.35	0.55
UR6_PApex	0.32	0.26	0.73	0.83
LR1_MInc	0.31	0.15	0.34	0.48
LR1_DInc	0.24	0.22	0.18	0.37
LR1_Apex	0.44	0.29	0.48	0.71
LR3_MCon	0.29	0.35	0.57	0.73
LR3_DCon	0.40	0.36	0.51	0.75
LR3_Cusp	0.36	0.34	0.28	0.57
LR3_Apex	0.51	0.38	0.68	0.94
LR4_BCusp	0.39	0.57	0.28	0.74
LR6_MBCusp	0.32	0.28	0.28	0.51
LR6_DBCusp	0.30	0.58	0.26	0.70
LR6_MLCusp	0.59	0.32	0.23	0.71
LR6_DLCusp	0.43	0.34	0.27	0.61
LR6_MApex	0.66	0.52	0.35	0.91
LR6_DApex	0.56	0.27	0.43	0.76
LR6_MBGroove	1.19	0.70	0.63	1.52
UL1_MInc	0.26	0.15	0.16	0.33
UL1_DInc	0.38	0.35	0.41	0.66
UL1_Apex	0.20	0.23	0.30	0.43
UL3_MCon	0.45	0.43	0.54	0.82
UL3_DCon	0.43	0.36	0.40	0.69
UL3_Cusp	0.24	0.21	0.17	0.36
UL3_Apex	0.31	0.39	0.69	0.85
UL4_BCusp	0.42	0.87	0.18	0.99
UL6_MBCusp	0.21	0.49	0.39	0.66
UL6_DBCusp	0.52	0.46	0.20	0.72
UL6_MLCusp	0.62	0.84	0.28	1.08
UL6_DLCusp	0.79	0.86	0.39	1.23
UL6_MBApex	0.44	0.26	0.28	0.59
UL6_DBApex	0.47	0.45	0.65	0.92
UL6_PApex	0.46	0.37	0.49	0.77
LL1_MInc	0.21	0.17	0.15	0.31
LL1_DInc	0.66	0.25	0.21	0.74
LL1_Apex	0.27	0.34	0.40	0.59
LL3_MCon	0.49	0.58	0.68	1.02
LL3_DCon	0.37	0.44	0.62	0.85
LL3_Cusp	0.41	0.49	0.30	0.70
LL3_Apex	0.39	0.41	0.63	0.84
LL4_BCusp	0.65	0.61	0.45	1.00
LL6_MBCusp	0.32	0.34	0.20	0.51
LL6_DBCusp	0.32	0.54	0.21	0.66
LL6_MLCusp	0.44	0.40	0.22	0.64
LL6_DLCusp	0.42	0.39	0.18	0.60
LL6_MApex	0.54	0.59	0.32	0.86
LL6_DApex	0.59	0.30	0.38	0.77
LL6_MBGroove	1.05	0.62	0.65	1.38

^aMRSE indictes mean radial spherical error.

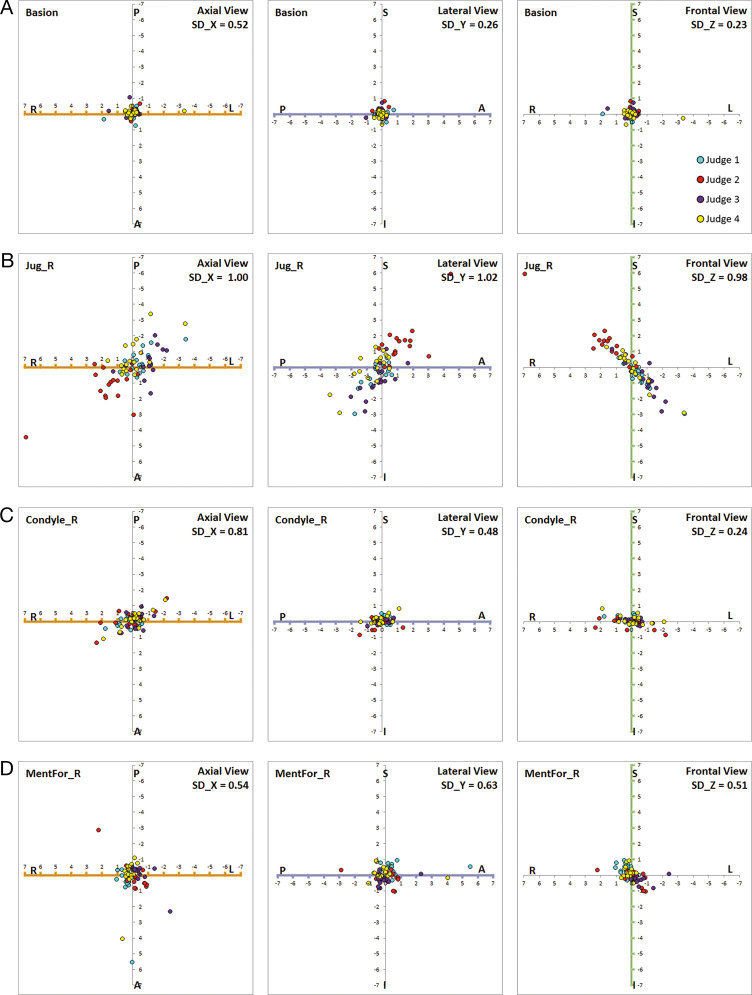
Figure 3.

Scatterplots of skeletal landmarks. (A) Basion. (B) Jugale_R. (C) Condyle_R. (D) Mental foramen_R

Most dental landmarks were located more reliably than skeletal landmarks and had MRSE values <1 mm, except for the lingual cusps of the maxillary first molars (U6) and the buccal grooves of the mandibular first molars (L6). The highest reliability was observed for mesial and distal incisal edges. Mesiobuccal cusp (MBCusp) of U6 and L6 also showed high reliability (Figure 4). The reliability of root apices was not as high as crowns, yet the highest MRSE value was still <1 mm. The buccal grooves of L6 showed the largest errors among the dental landmarks.

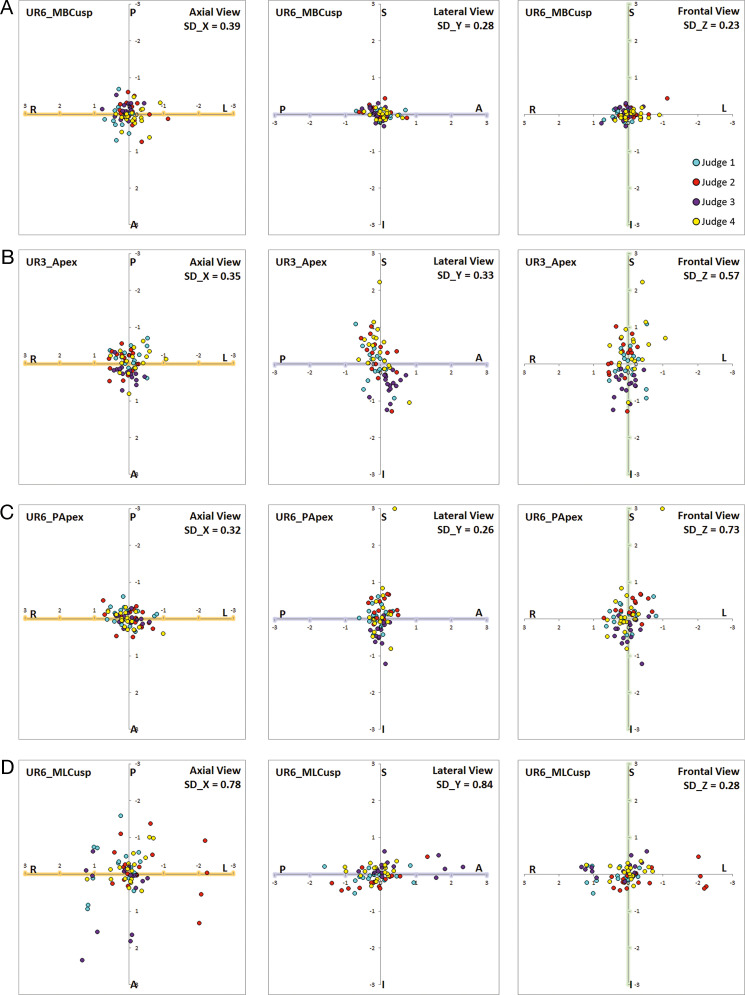
Figure 4.

Scatterplots of dental landmarks. (A) UR6_MBCusp. (B) UR3_Apex. (C) UR6_PApex. (D) UR6_MLCusp.

DISCUSSION

The landmarks conventionally used for defining the midsagittal plane (MSP) of the AFOR, nasion, sella, and basion, were shown to be highly reliable. Their scatterplots showed that the shape of error distribution was circular (Figure 3A). The 3D estimates of nasion were more reliable than the 2D estimates, in which errors in the vertical direction were much larger than the AP direction. As noted in the scatterplot for basion, the occasional outliers in the transverse axis can result in an exaggerated rotational effect around the vertical axis when it is used to define the MSP (Figure 3A).

Porion presented relatively large error, but its practical importance for defining the Frankfort horizontal (FH) plane dictates its continued use. Fortunately, its vertical component of error was relatively small, SD_Z approximating 0.6 mm. Its scatterplot sloped superiorly from the medial to lateral direction, which followed the shape of the auditory meatus in the coronal view. Orbitale also presented relatively large errors and its vertical error was less than half that of porion. Relatively small vertical errors for porion and orbitale supported the inference that it serves its function in the orientation of the FH plane quite well. Therefore, the proposed AFOR may be used in comparing two data sets of before and after treatment.

Other cranial base landmarks were also evaluated as possible alternatives for defining the AFOR. Crista-galli can be used to evaluate symmetry of the skull and to mark the anterior limit of the cranial base. While it was located reliably in the transverse dimension (SD_X = 0.25 mm), it was less well located in other dimensions. Its MRSE was 1.29 mm, implying that it should be used with caution. Although nasal bone showed less error than crista-galli, its variable shape has caused it to be studied much less frequently.

Foramen spinosum and temporal fossa were also evaluated, but they were even less reproducible than porion and orbitale. Foramen spinosum was the most error prone among the landmarks on the cranial base with its MRSE in excess of 1.5 mm. This was in contrast with other studies that found satisfactory reliability for cranial base landmarks, most likely because of different software and methods used to locate the landmarks.7,9 The judges in this study found that clear visualization of foramen spinosum in the volume render mode was difficult for some subjects.

The fronto-zygomatic suture has been used on occasion to define an AFOR. Such an AFOR might have certain advantages, since fronto-zygomatic suture was much more reliably located than either orbitale or porion. However, it was uncertain that its actual vertical position is the same bilaterally or that it maintains its location sufficiently well through growth. For superimposition purposes, however, this landmark should not continue to be overlooked.

In the maxilla, bilateral landmarks also had more errors than midline landmarks. Frontal scatterplots for jugale displayed a systematic error.14 The judge of the red points located it more superiorly and laterally, whereas the judge of the purple points located it more inferiorly and mesially (Figure 3C). The dispersion of errors in the frontal view was spread along the slope of the maxillary process.

Among the mandibular landmarks, menton demonstrated the highest reliability. The MRSE of 0.59 seemed small, and the error distribution along the AP and the vertical dimensions seemed more favorable than it did in earlier 2D studies.5 Pogonion is used to locate the most anterior point in the mandible. Pogonion seemed to serve this function well since the error in the AP dimension was small (SD_Y = 0.2 mm). Point B performed satisfactorily in the AP and the transverse dimensions but less well in the vertical dimension.

Gonion was the most unreliable landmark. It showed a strong propensity for a systematic error which was most likely due to the difference in interpretation of the location of gonion among the judges. Such differences warrant more explicit landmark definitions and rigorous calibration of judges. Condyle was more reliable than expected. The smallest error was found in the vertical dimension, and therefore, condyle can be used to determine the vertical positions of the condylar heads (Figure 3D). Mental foramina were examined as potential reference landmarks for regional superimposition and their reliability was found to be satisfactory.

Most dental landmarks were located more reliably than skeletal landmarks and performed better than in 2D cephalograms except for incisal edge points. In the 2D lateral cephalograms, the mean estimating errors for U1 and L1 edges were reported to be 0.37 ± 0.11 mm and 0.44 ± 0.19 mm, respectively, which were close to the MRSE values found in this study for the same landmarks.5

In this study, the highest reliability was found at incisal edges. MBCusp of first molars also showed high reliability (Figure 4A). Lower reliability was expected for MBCusp of L6 because the maxillary teeth usually overlie the buccal cusps of L6. However, the protocol to utilize both the volumetric image and the sectional images appeared to have helped in reliable location of the MBCusp of L6 (Figure 1). The remaining cusps of L6 also showed relatively high landmark reliability. In general, higher reliability of locating cusps of the first molars was found for the 3D CBCT images than for the 2D lateral cephalograms.

The reliability of root apices was not as high as crowns (Figure 4B and 4C). Equally high reliability had been expected because of the presumption that apices have a pointy shape similar to cusps. However, it was observed that some apices were rounded, dilacerated, or open for young patients. Nonetheless, the highest MRSE value was <1 mm, which was better than the 2D lateral cephalograms,5 most likely because superimposing bone over the root apex can be clipped off in 3D imaging software.

The buccal grooves of L6 had the largest errors among dental landmarks. Unlike other dental landmarks, which were located on pointy edges, the buccal groove was located on the broad surface of a crown. It was apparent that ease of defining or visualizing an anatomic feature was an important factor affecting the reliability of landmark location in 3D images.

In a CBCT image, it is possible to measure the degree of molar rotation during treatment. For example, it can be measured by the angle formed by the distobuccal cusp, mesiolingual cusp, and midline of the palate (Figure 5). However, it was found that the lingual cusps were located with much higher error than the buccal cusps (Figure 4D). It may be desirable to place more weight on the buccal cusp than on the lingual cusp in the calculation of molar rotation or, alternatively, to use two buccal cusps.

Figure 5.

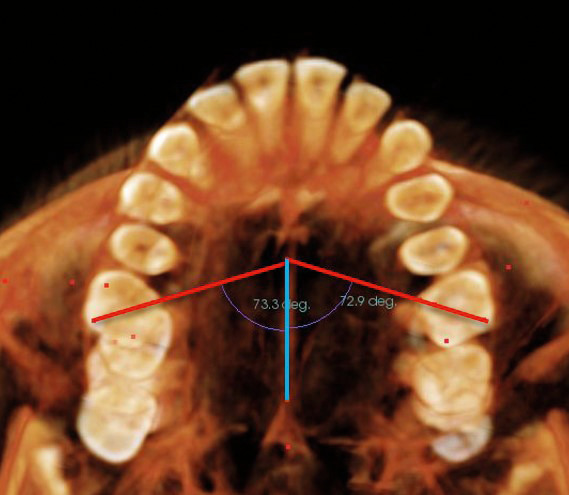
Molar rotation can be measured by the angle formed by the distobuccal cusp, mesiolingual cusp, and midline of the palate (the line connecting ANS and PNS).

Similar to the findings of the 2D reliability study, 3D scatterplots demonstrated that the error distributions for different landmarks varied in size and shape, which was only rarely spherical. However, reduced errors in both AP and vertical dimensions were observed for most landmarks located on 3D images in comparison to those located on 2D lateral cephalograms. For example, the vertical error (SD_Z) for orbitale in this study was approximately 0.3 mm in comparison to 1.61 mm for the same landmark in the 2D head film.5

The results of this study showed similar magnitude of error as the previous studies on 3D landmark reliability.6–11 In this study, the smallest error was found for menton in the vertical direction (SD_Z = 0.14 mm) and the largest error was found at gonion_R in the AP direction (SD_Y = 2.06 mm). The MRSE values ranged from 0.31 mm to 2.82 mm. This comparison should be interpreted with caution due to the difference in the landmarks tested, the CBCT machine used, the CBCT image quality, 3D imaging software, methods of locating landmarks, landmark definition, and degree of experience of examiners.

Although this study was conducted carefully, there were limitations. Among the reservations was the small sample size from a single practice and only a single kind of patient (young adolescents with Class II malocclusion). Landmark locations were obtained from three judges, yet adding more judges might have strengthened defining the envelope of error for the landmarks. The judges were orthodontic residents who may not have been the true experts.

The MRSE is a novel way to estimate 3D reliability of landmark location since its value is directly computed from the variances in X, Y, and Z, and the measure of reliability can be described with a single value. Yet, one must be cautious when interpreting the MRSE values because it assumes that 61% of the landmark locations are included within a sphere with the radius of the MRSE value. However, the results of this study demonstrated that many landmarks had a nonspherical nature of error distribution. Therefore, it is important to interpret MRSE values with errors in each dimension in X, Y, and Z.

CONCLUSIONS

• In general, the envelopes of error for most landmarks were elongated rather than spherical. The distributions for landmarks located on curved surfaces tended to resemble the curve of the surface on which they lie.

• The 3D error distributions for most landmarks were similar to the distributions of the same landmarks in two dimensions but were generally smaller.

• Bilateral structures in general tended to be located with greater errors than midline structures.

• Nonconventional landmarks—fronto-zygomatic suture, condyle, and mental foramen—had relatively high reliability and are promising for 3D cephalometric measurements.

• Most dental landmarks were located reliably expect for lingual cusps of maxillary first molars and the buccal groove of the mandibular first molar.