Correcting an estimator of a multivariate monotone function with isotonic regression

Abstract

In many problems, a sensible estimator of a possibly multivariate monotone function may fail to be monotone. We study the correction of such an estimator obtained via projection onto the space of functions monotone over a finite grid in the domain. We demonstrate that this corrected estimator has no worse supremal estimation error than the initial estimator, and that analogously corrected confidence bands contain the true function whenever the initial bands do, at no loss to band width. Additionally, we demonstrate that the corrected estimator is asymptotically equivalent to the initial estimator if the initial estimator satisfies a stochastic equicontinuity condition and the true function is Lipschitz and strictly monotone. We provide simple sufficient conditions in the special case that the initial estimator is asymptotically linear, and illustrate the use of these results for estimation of a G-computed distribution function. Our stochastic equicontinuity condition is weaker than standard uniform stochastic equicontinuity, which has been required for alternative correction procedures. This allows us to apply our results to the bivariate correction of the local linear estimator of a conditional distribution function known to be monotone in its conditioning argument. Our experiments suggest that the projection step can yield significant practical improvements.

1. Introduction

1.1. Background

In many scientific problems, the parameter of interest is a component-wise monotone function. In practice, an estimator of this function may have several desirable statistical properties, yet fail to be monotone. This often occurs when the estimator is obtained through the pointwise application of a statistical procedure over the domain of the function. For instance, we may be interested in estimating a conditional cumulative distribution function θ₀, defined pointwise as θ₀(a, y) = P₀(Y ≤ y ∣ A = a), over its domain $\mathcal{D}\subset {\mathbb{R}}^2$. Here, Y may represent an outcome and A an exposure. The map y ↦ θ₀(a, y) is necessarily monotone for each fixed a. In some scientific contexts, it may be known that a ↦ θ₀(a, y) is also monotone for each y, in which case θ₀ is a bivariate component-wise monotone function. An estimator of θ₀ can be constructed by estimating the regression function (a, y) ↦ E_P0 [I(Y ≤ y) ∣ A = a] for each (a, y) on a finite grid using kernel smoothing, and performing suitable interpolation elsewhere. For some types of kernel smoothing, including the Nadaraya-Watson estimator, the resulting estimator is necessarily monotone as a function of y for each value of a, but not necessarily monotone as a function of a for each value of y. For other types of kernel smoothing, including the local linear estimator, which often has smaller asymptotic bias than the Nadaraya-Watson estimator, the resulting estimator need not be monotone in either component.

Whenever the function of interest is component-wise monotone, failure of an estimator to itself be monotone can be problematic. This is most apparent if the monotonicity constraint is probabilistic in nature – that is, the parameter mapping is monotone under all possible probability distributions. This is the case, for instance, if θ₀ is a distribution function. In such settings, returning a function estimate that fails to be monotone is nonsensical, like reporting a probability estimate outside the interval [0, 1]. However, even if the monotonicity constraint is based on scientific knowledge rather than probabilistic constraints, failure of an estimator to be monotone can be an issue. For example, if the parameter of interest represents average height or weight among children as a function of age, scientific collaborators would likely be unsatisfied if presented with an estimated curve that were not monotone. Finally, as we will see, there are often finite-sample performance benefits to ensuring that the monotonicity constraint is respected.

Whenever this phenomenon occurs, it is natural to seek an estimator that respects the monotonicity constraint but nevertheless remains close to the initial estimator, which may otherwise have good statistical properties. A monotone estimator can be naturally constructed by projecting the initial estimator onto the space of monotone functions with respect to some norm. A common choice is the L₂-norm, which amounts to using multivariate isotonic regression to correct the initial estimator.

1.2. Contribution and organization of the article

In this article, we discuss correcting an initial estimator of a multivariate monotone function by computing the isotonic regression of the estimator over a finite grid in the domain, and interpolating between grid points. We also consider correcting an initial confidence band by using the same procedure applied to the upper and lower limits of the band. We provide three general results regarding this simple procedure.

1. Building on the results of Robertson, Wright and Dykstra (1988) and Chernozhukov, Fernández-Val and Galichon (2009), we demonstrate that the corrected estimator is at least as good as the initial estimator, meaning:

   1. its uniform error over the grid used in defining the projection is less than or equal to that of the initial estimator for every sample;
   2. its uniform error over the entire domain is less than or equal to that of the initial estimator asymptotically;
   3. the corrected confidence band contains the true function on the projection grid whenever the initial band does, at no cost in terms of average or uniform band width.

2. We provide high-level sufficient conditions under which the uniform difference between the initial and corrected estimators is $O_P(r_n^{-1})$ for a generic sequence r_n → ∞.

3. We provide simpler lower-level sufficient conditions in two special cases:

   1. when the initial estimator is uniformly asymptotically linear, in which case the appropriate rate is r_n = n^1/2;
   2. when the initial estimator is kernel-smoothed with bandwidth h_n, in which case the appropriate rate is r_n = (nh_n)^1/2 for univariate kernel smoothing.

We apply our theoretical results to two sets of examples: nonparametric efficient estimation of a G-computed distribution function for a binary exposure, and local linear estimation of a conditional distribution function with a continuous exposure.

Other authors have considered the correction of an initial estimator using isotonic regression. To name a few, Mukarjee and Stern (1994) used a projectionlike procedure applied to a kernel smoothing estimator of a regression function, whereas Patra and Sen (2016) used the projection procedure applied to a univariate cumulative distribution function in the context of a mixture model. These articles addressed the properties of the projection procedure in their specific applications. In contrast, we provide general results that are applicable broadly.

1.3. Alternative projection procedures

The projection approach is not the only possible correction procedure. Dette, Neumeyer and Pilz (2006), Chernozhukov, Fernández-Val and Galichon (2009), and Chernozhukov, Fernández-Val and Galichon (2010) studied a correction based on monotone rearrangements. However, monotone rearrangements do not generalize to the multivariate setting as naturally as projections — for example, Chernozhukov, Fernández-Val and Galichon (2009) proposed averaging a variety of possible multivariate monotone rearrangements to obtain a final monotone estimator. In contrast, the L₂ projection of an initial estimator onto the space of component-wise monotone functions is uniquely defined, even in the context of multivariate functions.

Daouia and Park (2013) proposed an alternative correction procedure that consists of taking a convex combination of upper and lower monotone envelope functions, and they demonstrated conditions under which their estimator is asymptotically equivalent in supremum norm to the initial estimator. There are several differences between our contributions and those of Daouia and Park (2013). For instance, Daouia and Park (2013) did not study correction of confidence bands, which we consider in Section 2.3, or the important special case of asymptotically linear estimators, which we consider in Section 3.1. Our results in these two sections apply equally well to our correction procedure and to the correction procedure considered by Daouia and Park (2013).

Perhaps the most important theoretical contribution of our work beyond that of existing research is the weaker form of stochastic equicontinuity that we require for establishing asymptotic equivalence of the initial and projected estimators. In contrast, Daouia and Park (2013) explicitly required the usual uniform asymptotic equicontinuity, while application of the Hadamard differentiability results of Chernozhukov, Fernández-Val and Galichon (2010) requires weak convergence to a tight limit, which is stronger than uniform asymptotic equicontinuity. Our weaker condition allows us to use our general results to tackle a broader range of initial estimators, including kernel smoothed estimators, which are typically not uniformly asymptotically equicontinuous at useful rates, but nevertheless can frequently be shown to satisfy our condition. We discuss this in detail in Section 3.2. We illustrate this general contribution in Section 4.2 by studying the bivariate correction of a conditional distribution function estimated using local linear regression, which would not be possible using the stronger asymptotic equicontinuity condition. In numerical studies, we find that the projected estimator and confidence bands can offer substantial finite-sample improvements over the initial estimator and bands in this example.

2. Main results

2.1. Definitions and statistical setup

Let $\mathcal{M}$ be a statistical model of probability measures on a probability space ($\mathcal{X}$, $\mathcal{B}$). Let $\theta :\mathcal{M}\to {\ell }^{\infty }(\mathcal{T})$ be a parameter of interest on $\mathcal{M}$, where $\mathcal{T}≔[0,1{]}^d$ and ${\ell }^{\infty }(\mathcal{T})$ is the Banach space of bounded functions from $\mathcal{T}$ to $\mathbb{R}$ equipped with supremum norm $\Vert \cdot {\Vert }_{\mathcal{T}}$. We have specified this particular $\mathcal{T}$ for simplicity, but the results established here apply to any bounded rectangular domain $\mathcal{T}\subset {\mathbb{R}}^d$. For each $P\in \mathcal{M}$, denote by θ_P the evaluation of θ at P and note that θ_P is a bounded real-valued function on $\mathcal{T}$. For any $t\in \mathcal{T}$, denote by ${\theta }_P(t)\in \mathbb{R}$ the evaluation of θ_P at t.

For any vector $t\in {\mathbb{R}}^d$ and 1 ≤ j ≤ d, denote by t_j the j^th component of t. Define the partial order ≤ on ${\mathbb{R}}^d$ by setting t ≤ t′ if and only if $t_j\le t_j^{\prime }$ for each 1 ≤ j ≤ d. A function $f:{\mathbb{R}}^d\to \mathbb{R}$ is called (component-wise) monotone non-decreasing if t ≤ t′ implies that f(t) ≤ f(t′). Denote ∥t∥ = max_1≤j≤d ∣t_j∣ for any vector $t\in {\mathbb{R}}^d$. Additionally, denote by $\Theta \subset {\ell }^{\infty }(\mathcal{T})$ the convex set of bounded monotone non-decreasing functions from $\mathcal{T}$ to $\mathcal{R}$. For concreteness, we focus on non-decreasing functions, but all results established here apply equally to non-increasing functions.

Let ${\mathcal{M}}_0≔\{P\in \mathcal{M}:{\theta }_P\in \Theta \}\subseteq \mathcal{M}$ and suppose that ${\mathcal{M}}_0$ is nonempty. Generally, this inclusion is strict only if, rather than being implied by the rules of probability, the monotonicity constraint stems at least in part from prior scientific knowledge. Also, define Θ₀ := {θ ∈ Θ : θ = θ_P for some $P\in \mathcal{M}$} ⊆ Θ. We are primarily interested in settings where Θ₀ = Θ, since in this case there is no additional knowledge about θ encoded by $\mathcal{M}$, and in particular there is no danger of yielding a corrected estimator that is compatible with no $P\in \mathcal{M}$.

Suppose that observations X₁, X₂, … , X_n are sampled independently from an unknown distribution $P_0\in {\mathcal{M}}_0$, and that we wish to estimate θ₀ := θ_P0 based on these observations. Suppose that, for each $t\in \mathcal{T}$, we have access to an estimator θ_n(t) of θ₀(t) based on X₁, X₂, … , X_n. We note that the assumption that the data are independent and identically distributed is not necessary for Theorems 1 and 2 below. For any suitable $f:\mathcal{X}\to \mathbb{R}$, we define Pf := ʃ f(x) P(dx) and ${\mathbb{G}}_{n}f≔n^{1∕2}\int f(x)({\mathbb{P}}_n-P_0)(dx)$, where ${\mathbb{P}}_n$ is the empirical distribution based on X₁, X₂, … , X_n.

The central premise of this article is that θ_n(t) may have desirable statistical properties for each t or even uniformly in t, but that θ_n as an element of ${\ell }^{\infty (\mathcal{T})}$ may not fall in Θ for any finite n or even with probability tending to one. Our goal is to provide a corrected estimator ${\theta }_n^{\ast }$ that necessarily falls in Θ, and yet retains the statistical properties of θ_n. A natural way to accomplish this is to define ${\theta }_n^{\ast }$ as the closest element of Θ to θ_n in some norm on $\mathcal{T}$. Ideally, we would prefer to take ${\theta }_n^{\ast }$ to minimize $\Vert \theta -{\theta }_n{\Vert }_{\mathcal{T}}$ over θ ∈ Θ. However, this is not tractable for two reasons. First, optimization over the entirety of $\mathcal{T}$ is an infinite-dimensional optimization problem, and is hence frequently computationally intractable. To resolve this issue, for each n, we let ${\mathcal{T}}_n=\{t_1,t_2,\dots ,t_{m_n}\}\subseteq \mathcal{T}$ be a finite rectangular lattice in $\mathcal{T}$ over which we will perform the optimization, and define and consider $\Vert \cdot {\Vert }_{{\mathcal{T}}_n}$. as the supremum norm over ${\mathcal{T}}_n$. While it is now computationally feasible to define ${\theta }_{n,\infty }^{\ast }$ as a minimizer over θ ∈ Θ of the finite-dimensional objective function $\Vert \theta -{\theta }_n{\Vert }_{{\mathcal{T}}_n}$, this objective function is challenging due to its non-differentiability. Instead, we define

$${\theta }_n^{\ast }\in \underset{\theta \in \Theta }{\text{argmin}}\sum _{t\in {\mathcal{T}}_n}[\theta (t)-{\theta }_n(t){]}^2.$$ (2.1)

The squared-error objective function is smooth in its arguments. In dimension d = 1, ${\theta }_n^{\ast }$ thus defined is simply the isotonic regression of θ_n on the grid ${\mathcal{T}}_n$, which has a closed-form representation as the greatest convex minorant of the so-called cumulative sum diagram. Furthermore, since $\Vert {\theta }_n^{\ast }-{\theta }_n{\Vert }_{{\mathcal{T}}_n}\ge \Vert {\theta }_{n,\infty }^{\ast }-{\theta }_n{\Vert }_{{\mathcal{T}}_n}$, many of our results also apply to ${\theta }_{n,\infty }^{\ast }$.

We note that ${\theta }_n^{\ast }$ is only uniquely defined on ${\mathcal{T}}_n$. To completely characterize ${\theta }_n^{\ast }$, we must monotonically interpolate function values between elements of ${\mathcal{T}}_n$. We will permit any monotonic interpolation that satisfies a weak condition. By the definition of a rectangular lattice, every $t\in \mathcal{T}$ can be assigned a hyper-rectangle whose vertices {s₁, s₂ … , s₂d} are elements of ${\mathcal{T}}_n$ and whose interior has empty intersection with ${\mathcal{T}}_n$. If multiple such hyper-rectangles exist for t, such as when t lies on the boundary of two or more such hyper-rectangles, one can be assigned arbitrarily. We will assume that, for $t\notin {\mathcal{T}}_n$,

$${\theta }_n^{\ast }(t)=\sum _k{\lambda }_{k,n}(t){\theta }_n^{\ast }(s_k)$$

for weights λ_1,n(t), λ_2,n(t), … , λ_2^d,n(t) ∈ (0, 1) such that Σ_k λ_k,n(t) = 1. In words, we assume that ${\theta }_n^{\ast }(t)$ is a convex combination of the values of ${\theta }_n^{\ast }$ on the vertices of the hyper-rectangle containing t. A simple interpolation approach consists of setting ${\theta }_n^{\ast }(t)={\theta }_n^{\ast }(t^{\prime })$ with t′ the element of ${\mathcal{T}}_n$ closest to t, and choosing any such element if there are multiple elements of ${\mathcal{T}}_n$ equally close to t. This particular scheme satisfies our requirement.

Finally, for each n, we let ℓ_n(t) ≤ u_n(t) denote lower and upper endpoints of a confidence band for θ₀(t). We then define ${\ell }_n^{\ast }$ and $u_n^{\ast }$ as the corrected versions of ℓ_n and u_n using the same projection and interpolation procedure defined above for obtaining ${\theta }_n^{\ast }$ from ${\theta }_n$.

In dimension d = 1, ${\theta }_n^{\ast }(t)$, ${\ell }_n^{\ast }(t)$, and $u_n^{\ast }(t)$ can be obtained for $t\in {\mathcal{T}}_n$ via the Pool Adjacent Violators Algorithm (Ayer et al., 1955), as implemented in the R command isoreg (R Core Team, 2018). In dimension d = 2, the corrections can be obtained using the algorithm described in Bril et al. (1984), which is implemented in the R command biviso in the package Iso (Turner, 2015). In dimension d ≥ 3, Kyng, Rao and Sachdeva (2015) provides algorithms for computing the isotonic regression based on embedding the points in a directed acyclic graph. Alternatively, general-purpose algorithms for minimization of quadratic criteria over convex cones have been developed and implemented in the R package coneproj and may be used in this case (Meyer, 1999; Liao and Meyer, 2014).

2.2. Properties of the projected estimator

The projected estimator ${\theta }_n^{\ast }$ is the isotonic regression of θ_n over the grid ${\mathcal{T}}_n$. Hence, many existing finite-sample results on isotonic regression can be used to deduce properties of ${\theta }_n^{\ast }$. Theorem 1 below collects a few of these properties, building upon the results of Barlow et al. (1972) and Chernozhukov, Fernández-Val and Galichon (2009). We denote ${\omega }_n≔{\text{sup}}_{t\in \mathcal{T}}{\text{min}}_{s\in {\mathcal{T}}_n}\Vert t-s\Vert$ as the mesh of ${\mathcal{T}}_n$ in $\mathcal{T}$.

Theorem 1. (i) It holds that $\Vert {\theta }_n^{\ast }-{\theta }_0{\Vert }_{{\mathcal{T}}_n}\le \Vert {\theta }_n-{\theta }_0{\Vert }_{{\mathcal{T}}_n}$.

(ii) If ω_n = o_P(1) and θ₀ is continuous on $\mathcal{T}$, then

$$\Vert {\theta }_n^{\ast }-{\theta }_0{\Vert }_{\mathcal{T}}\le \Vert {\theta }_n-{\theta }_0{\Vert }_{{\mathcal{T}}_n}+o_P(1).$$

(iii) If there exists some α > 0 for which ${\text{sup}}_{s,t\in \mathcal{T}:\Vert t-s\Vert \le \delta }\mid {\theta }_0(t)-{\theta }_0(s)\mid =O({\delta }^{\alpha })$ as δ → 0, then

$$\Vert {\theta }_n^{\ast }-{\theta }_0{\Vert }_{\mathcal{T}}\le \Vert {\theta }_n-{\theta }_0{\Vert }_{{\mathcal{T}}_n}+o_P({\omega }_n^{\alpha }).$$

(iv) If θ₀(t) ∈ [ℓ_n(t), u_n(t)] for all $t\in {\mathcal{T}}_n$, then ${\theta }_0(t)\in [{\ell }_n^{\ast }(t),u_n^{\ast }(t)]$ for all $t\in {\mathcal{T}}_n$.

(v) It holds that $\Vert u_n^{\ast }-{\ell }_n^{\ast }{\Vert }_{{\mathcal{T}}_n}\le \Vert u_n-{\ell }_n{\Vert }_{{\mathcal{T}}_n}$ and

$$\sum _{t\in {\mathcal{T}}_n}[u_n^{\ast }(t)-{\ell }_n^{\ast }(t)]=\sum _{t\in {\mathcal{T}}_n}[u_n(t)-{\ell }_n(t)].$$

Theorem 1 is proved in Appendix A.1. We remark briefly on the implications of Theorem 1. Part (i) says that the estimation error of ${\theta }_n^{\ast }$ over the grid ${\mathcal{T}}_n$ is never worse than that of θ_n, whereas parts (ii) and (iii) provide bounds on the estimation error of ${\theta }_n^{\ast }$ on all of $\mathcal{T}$ in supremum norm. In particular, part (ii) indicates that ${\theta }_n^{\ast }$ is uniformly consistent on $\mathcal{T}$ as long as θ_n is uniformly consistent on $\mathcal{T}$, θ₀ is continuous on $\mathcal{T}$, and ω_n = o_P(1). Part (iii) provides an upper bound on the uniform rate of convergence of ${\theta }_n^{\ast }$ − θ₀, and indicates that if θ₀ is known to lie in a Hölder class, then ω_n can be chosen in such a way as to guarantee that the estimation error of ${\theta }_n^{\ast }$ on all of $\mathcal{T}$ is asymptotically no worse than the estimation error of θ_n on ${\mathcal{T}}_n$ in supremum norm. We note that parts (i)–(iii) also hold for the L_p norm with respect to uniform measure on $\mathcal{T}$ for any p ∈ [1, ∞). Part (iv) guarantees that the isotonized band [${\ell }_n^{\ast }$, $u_n^{\ast }$] never has worse coverage than the original band over ${\mathcal{T}}_n$. Finally, part (v) states that the potential increase in coverage comes at no cost to the average or supremum width of the bands over ${\mathcal{T}}_n$. We note that parts (i), (iv) and (v) hold true for each n.

While comprehensive in scope, Theorem 1 does not rule out the possibility that ${\theta }_n^{\ast }$ performs strictly better, even asymptotically, than θ_n, or that the band [${\ell }_n^{\ast }$, $u_n^{\ast }$] is asymptotically strictly more conservative than [ℓ_n, u_n]. In order to construct confidence intervals or bands with correct asymptotic coverage, a stronger result is needed: it must be that $\Vert {\theta }_n^{\ast }-{\theta }_n{\Vert }_{\mathcal{T}}=O_P(r_n^{-1})$, where r_n is a diverging sequence such that $r_n\Vert {\theta }_n-{\theta }_0{\Vert }_{\mathcal{T}}$ converges in distribution to a non-degenerate limit distribution. Then, we would have that $r_n\Vert {\theta }_n^{\ast }-{\theta }_0{\Vert }_{\mathcal{T}}$ converges in distribution to this same limit, and hence confidence bands constructed using approximations of this limit distribution would have correct coverage when centered around ${\theta }_n^{\ast }$, as we discuss more below.

We consider the following conditions on θ₀ and the initial estimator θ_n:

1. there exists a deterministic sequence r_n tending to infinity such that, for all δ > 0,

   $$\underset{\Vert t-s\Vert <\delta ∕r_n}{\text{sup}}\mid r_n[{\theta }_n(t)-{\theta }_0(t)]-r_n[{\theta }_n(s)-{\theta }_0(s)]\mid =o_P(1);$$

2. there exists K₁ < ∞ such that ∣θ₀(t) − θ₀(s)∣ ≤ K₁∥t − s∥ for all t, $s\in \mathcal{T}$;

3. there exists K₀ > 0 such that K₀∥t − s∥ ≤ ∣θ₀(t) − θ₀(s)∣ for all t, $s\in \mathcal{T}$.

Based on these conditions, we have the following result.

Theorem 2. If (A)–(C) hold and ${\omega }_n=O_P(r_n^{-1})$, then $\Vert {\theta }_n^{\ast }-{\theta }_n{\Vert }_{\mathcal{T}}=O_P(r_n^{-1})$.

The proof of Theorem 2 is presented in Appendix A.2. This result indicates that the projected estimator is uniformly asymptotically equivalent to the original estimator in supremum norm at the rate r_n.

Condition (A) is related to, but notably weaker than, uniform stochastic equicontinuity (van der Vaart and Wellner, 1996, p. 37). (A) follows if, in particular, the process $\{r_n[{\theta }_n(t)-{\theta }_0(t)]:t\in \mathcal{T}\}$ converges weakly to a tight limit in the space ${\ell }^{\infty }(\mathcal{T})$. However, the latter condition is sufficient but not necessary for (A) to hold. This is important for application of our results to kernel smoothing estimators, which typically do not converge weakly to a tight limit, but for which condition (A) nevertheless often holds. We discuss this at length in Section 4.2. The results of Daouia and Park (2013) (see in particular condition (C3) therein) and Chernozhukov, Fernández-Val and Galichon (2010) rely on uniform stochastic equicontinuity in demonstrating asymptotic equivalence of their correction procedures, which essentially limits the applicability of their procedures to estimators that converge weakly to a tight limit in ${\ell }^{\infty }(\mathcal{T})$.

Condition (B) constrains θ₀ to be Lipschitz. Condition (C) constrains the variation of θ₀ from below, and is slightly more restrictive than a requirement for strict monotonicity. If, for instance, θ₀ is differentiable, then (C) is satisfied if all first-order partial derivatives of θ₀ are bounded away from zero. Condition (C) excludes, for instance, situations in which θ₀ is differentiable with null derivative over an interval. In such cases, ${\theta }_n^{\ast }$ may have strictly smaller variance on these intervals than θ_n because ${\theta }_n^{\ast }$ will pool estimates across the flat region while θ_n may not. Hence, in such cases, ${\theta }_n^{\ast }$ may potentially asymptotically improve on θ_n, so that ${\theta }_n^{\ast }$ and θ_n are not asymptotically equivalent at the rate r_n. Theoretical results in these cases would be of interest, but are beyond the scope of this article.

In addition to conditions (A)–(C), Theorem 2 requires that the mesh ω_n of ${\mathcal{T}}_n$ tend to zero in probability faster than $r_n^{-1}$. Since ${\mathcal{T}}_n$ is chosen by the user, as long as r_n (or an upper bound thereof) is known, this is not a problem in practice. Furthermore, except in irregular problems, the rate of convergence is typically not faster than n^−1/2, and hence it is typically sufficient to set ω_n = c_nn^−1/2 for some c_n = o(1). We note, however, that the computational complexity of obtaining the isotonic regression of θ_n over ${\mathcal{T}}_n$ increases as ω_n decreases. Hence, in cases where the rate of convergence of the initial estimator is strictly slower than n^−1/2, it may be preferable to choose ω_n more carefully based on a precise determination of r_n. We expect this to be especially true in the context of large d and n.

We note that conditions (A)–(C) and ${\omega }_n=O_P(r_n^{-1})$ also imply that $\Vert {\theta }_n^{\ast }-{\theta }_n{\Vert }_{L_p(\mathcal{T})}=O_P(r_n^{-1})$ for any p ∈ [1, ∞), where $L_p(\mathcal{T})$ is the L_p norm on $\mathcal{T}$ with respect to uniform measure on $\mathcal{T}$. However, it may be possible to relax conditions (A)–(C) for the purpose of demonstrating L_p asymptotic equivalence of ${\theta }_n^{\ast }$ and θ_n for p < ∞. It is not clear whether our method of proof of Theorem 2 is amenable to such weakening. We have chosen to focus on uniform asymptotic equivalence in part for its use in constructing uniform confidence bands for θ₀, as we discuss in the next section.

2.3. Construction of confidence bands

Suppose there exists a fixed function ${\gamma }_{\alpha }:\mathcal{T}\to \mathbb{R}$ such that ℓ_n and u_n satisfy:

1. $\Vert r_n({\theta }_n-{\ell }_n)-{\gamma }_{\alpha }{\Vert }_{\mathcal{T}}{\to }_{\mathrm{P}}0$;

2. $\Vert r_n(u_n-{\theta }_n)-{\gamma }_{\alpha }{\Vert }_{\mathcal{T}}{\to }_{\mathrm{P}}0$;

3. P₀ [r_n∣θ_n(t) − θ₀(t)∣ ≥ γ_α(t) for all $t\in \mathcal{T}$] → 1 − α.

As an example of a confidence band that satisfies conditions (a)–(c), suppose that ${\sigma }_0:\mathcal{T}\to (0,+\infty )$ is a scaling function and c_α is a fixed constant such that, as n tends to infinity,

$$P_0\left(r_n{\Vert \frac{{\theta }_n-{\theta }_0}{{\sigma }_0}\Vert }_{\mathcal{T}}\ge c_{\alpha }\right)\to 1-\alpha .$$

If σ_n is an estimator of σ₀ satisfying $\Vert {\sigma }_n-{\sigma }_0{\Vert }_{\mathcal{T}}{\to }_{\mathrm{P}}$ 0 and c_α,n is an estimator of c_α such that c_α,n →_P c_α, then the Wald-type band defined by lower and upper endpoints ${\ell }_n(t)≔{\theta }_n(t)-c_{\alpha ,n}{r}_n^{-1}{\sigma }_n(t)$ and $u_n(t)≔{\theta }_n(t)+c_{\alpha }{r}_n^{-1}{\sigma }_n(t)$ satisfies (a)–(c) with γ_α = c_ασ₀. However, the latter conditions can also be satisfied by other types of bands, such as those constructed with a consistent bootstrap procedure.

Under conditions (a)–(c), the confidence band [ℓ_n, u_n] has asymptotic coverage 1 − α. When conditions (A) and (B) also hold, the corrected band [${\ell }_n^{\ast }$, $u_n^{\ast }$] has the same asymptotic coverage as the original band [ℓ_n, u_n], as stated in the following result.

Corollary 1. If (A)–(B) and (a)–(c) hold, γ_α is uniformly continuous on $\mathcal{T}$, and ${\omega }_n=O_P(r_n^{-1})$, then the band [${\ell }_n^{\ast }$, $u_n^{\ast }$] has asymptotic coverage 1 − α.

The proof of Corollary 1 is presented in Appendix A.3. We also note that Theorem 2 implies that Wald-type confidence bands constructed around θ_n have the same asymptotic coverage if they are constructed around ${\theta }_n^{\ast }$ instead.

3. Refined results under additional structure

In this section, we provide more detailed conditions that imply condition (A) in two special cases: when θ_n is asymptotically linear, and when θ_n is a kernel smoothing-type estimator.

3.1. Special case I: asymptotically linear estimators

Suppose that the initial estimator θ_n is uniformly asymptotically linear (UAL): for each $t\in \mathcal{T}$, there exists ${\varphi }_{0,t}:\mathcal{X}\mapsto \mathbb{R}$ depending on P₀ such that ʃ ϕ_0,t dP₀ = 0, $\int {\varphi }_{0,t}^{2}d{P}_0<\infty$ and

$${\theta }_n(t)={\theta }_0(t)+\frac{1}{n}\sum _{i=1}^n{\varphi }_{0,t}(X_i)+R_{n,t}$$ (3.1)

for a remainder term R_n,t with n^1/2 ${\text{sup}}_{t\in \mathcal{T}}\mid R_{n,t}\mid =O_P(1)$. The function ϕ_0,t is the influence function of θ_n(t) under sampling from P₀. It is desirable for θ_n to have representation (3.1) because this implies its uniform weak consistency as well as the pointwise asymptotic normality of n^1/2 [θ_n(t) − θ₀(t)] for each $t\in \mathcal{T}$. If in addition the collection {${\varphi }_{0,t}:t\in \mathcal{T}$} of influence functions forms a P₀-Donsker class, then {$n^{1∕2}[{\theta }_n(t)-{\theta }_0(t)]:t\in \mathcal{T}$} converges weakly in ${\ell }^{\infty }(\mathcal{T})$ to a Gaussian process with covariance function Σ₀ : (t, s) ↦ ʃ ϕ_0,t(x)ϕ_0,s(x)dP₀(x). Uniform asymptotic confidence bands based on θ_n can then be formed by using appropriate quantiles from any suitable approximation of the distribution of the supremum of the limiting Gaussian process.

We introduce two additional conditions:

(A1) the collection {${\varphi }_{0,t}:t\in \mathcal{T}$} of influence curves is a P₀-Donsker class;

(A2) Σ₀ is uniformly continuous in the sense that

$$\underset{\Vert t-s\Vert \to 0}{\text{lim sup}}\mid {\Sigma }_0(s,t)-{\Sigma }_0(t,t)\mid =0.$$

Whenever θ_n is uniformly asymptotically linear, Theorem 2 can be shown to hold under (A1), (A2) and (B), as implied by the theorem below. The validity of (A1) and (A2) can be assessed by scrutinizing the influence function ϕ_0,t of θ_n(t) for each $t\in \mathcal{T}$. This fact renders the verification of these conditions very simple once uniform asymptotic linearity has been established.

Theorem 3. For any UAL estimator θ_n, (A1)–(A2) together imply (A).

The proof of Theorem 3 is provided in Appendix A.4. In Section 4.1, we illustrate the use of Theorem 3 for the estimation of a G-computed distribution function.

We note that conditions (A1)–(A2) are actually sufficient to establish uniform asymptotic equicontinuity, which as discussed above is stronger than (A). Therefore, Theorem 3 can also be used to prove asymptotic equivalence of the majorization/minorization correction procedure studied in Daouia and Park (2013).

3.2. Special case II: kernel smoothed estimators

For certain parameters, asymptotically linear estimators are not available. In particular, this is the case when the parameter of interest is not sufficiently smooth as a mapping of P₀. For example, density functions, regression functions, and conditional quantile functions do not permit asymptotically linear estimators in a nonparametric model when the exposure is continuous. In these settings, a common approach to nonparametric estimation is kernel smoothing.

Recent results suggest that, as a process, the only possible weak limit of {$r_n[{\theta }_n-{\theta }_0(t)]:t\in \mathcal{T}$} in ${\ell }^{\infty }(\mathcal{T})$ is zero when θ_n is a kernel smoothed estimator. For example, in the case of the Parzen-Rosenblatt density estimator with bandwidth h_n, Theorem 3 of Stupfler (2016) implies that if

$$c_n≔r_n(n{h}_n∕\mid \log h_n\mid {)}^{-1∕2}\to 0,$$

then {$r_n[{\theta }_n(t)-{\theta }_0(t)]:t\in \mathcal{T}$} converges weakly to zero in ${\ell }^{\infty }(\mathcal{T})$, whereas if c_n → c ∈ (0, ∞], then it does not converge weakly to a tight limit in ${\ell }^{\infty }(\mathcal{T})$. As a result, {$r_n[{\theta }_n(t)-{\theta }_0(t)]:t\in \mathcal{T}$} only satisfies uniform stochastic equicontinuity for r_n such that c_n → 0. However, for any such rate r_n, $r_n^{-1}$ is slower than the pointwise and uniform rates of convergence of θ_n − θ₀. As a result, θ_n and ${\theta }_n^{\ast }$ may not be asymptotically equivalent at the uniform rate of convergence of θ_n − θ₀, so that confidence intervals and regions based on the limit distribution of θ_n − θ₀, but centered around ${\theta }_n^{\ast }$, may not have correct coverage. We note that, while Stupfler (2016) establishes formal results for the Parzen-Rosenblatt estimator, we expect that the results therein extend to a variety of kernel smoothed estimators.

As a result of the lack of uniform stochastic equicontinuity of r_n(θ_n − θ₀) for useful rates r_n, establishing (A) is much more difficult for kernel smoothed estimators than for asymptotically linear estimators. However, since (A) is weaker than uniform stochastic equicontinuity, it may still be possible. Here, we provide alternative sufficient conditions that imply condition (A) and that we have found useful for studying a kernel smoothed estimator θ_n.

When the initial estimator θ_n is kernel smoothed, we can often show that

$$\underset{t\in \mathcal{T}}{\text{sup}}\mid r_n[{\theta }_n(t)-{\theta }_0(t)]-a_n{b}_0(t)-R_n(t)\mid \stackrel{\mathrm{P}}{\to }0,$$ (3.2)

where $b_0:\mathcal{T}\to \mathbb{R}$ is a deterministic bias, a_n is sequences of positive constants, and $R_n:\mathcal{T}\to \mathbb{R}$ is a random remainder term. We then have that

$$\begin{gathered} \underset{\Vert t-s\Vert <\delta ∕r_n}{\text{sup}}\mid r_n[{\theta }_n(t)-{\theta }_0(t)]-r_n[{\theta }_n(s)-{\theta }_0(s)]\mid \\ =\underset{\Vert t-s\Vert <\delta ∕r_n}{\text{sup}}{a}_n\mid b_0(t)-b_0(s)\mid +\underset{\Vert t-s\Vert <\delta ∕r_n}{\text{sup}}\mid R_n(t)-R_n(s)\mid +o_P(1). \end{gathered}$$

If b₀ is uniformly continuous on $\mathcal{T}$ and a_n = O(1), or b₀ is uniformly α-Hölder on $\mathcal{T}$ and $a_n=O(r_n^{\alpha })$, then the first term on the right-hand side tends to zero in probability. Attention may then be turned to demonstrating that the second term vanishes in probability. It appears difficult to provide a general characterization of the form of R_n that encompasses kernel smoothed estimators. However, in our experience, it is frequently the case that R_n(t) involves terms of the form ${\mathbb{G}}_n{\nu }_{n,t}$, where ${\nu }_{n,t}:\mathcal{X}\to \mathbb{R}$ is a deterministic function for each n ∈ {1, 2, …} and $t\in \mathcal{T}$. In the course of demonstrating that

$$\underset{\Vert t-s\Vert <\delta ∕r_n}{\text{sup}}\mid R_n(t)-R_n(s)\mid \stackrel{\mathrm{P}}{\to }0,$$

a rate of convergence for

$$\underset{\Vert t-s\Vert <\delta ∕r_n}{\text{sup}}\mid {\mathbb{G}}_n({\nu }_{n,t}-{\nu }_{n,s})\mid$$

is then required. Defining ${\mathcal{F}}_{n,\eta }≔\{{\nu }_{n,t}-{\nu }_{n,s}:\Vert t-s\Vert <\eta \}$ for each η > 0, this is equivalent to establishing a rate of convergence for the local empirical process $\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{T}}_{n,\delta ∕r_n}}≔{\text{sup}}_{\xi \in {\mathcal{F}}_{n,\delta ∕r_n}}\mid {\mathbb{G}}_n\xi \mid$. Such rates can be established using tail bounds for empirical processes. We briefly comment on two approaches to obtaining such tail bounds.

We first define bracketing and covering numbers of a class of functions $\mathcal{F}$ — see van der Vaart and Wellner (1996) for a comprehensive treatment. We denote by ∥F∥_P,2 = [P(F²)]^1/2 the L₂(P) norm of a given P-square-integrable function $F:\mathcal{X}\to \mathbb{R}$. The bracketing number $N_{[]}(\epsilon ,\mathcal{F},L_2(P))$ of a class of functions $\mathcal{F}$ with respect to the L₂(P) norm is the smallest number of ε-brackets needed to cover $\mathcal{F}$, where an ε-bracket is any set of functions {f : ℓ ≤ f ≤ u} with ℓ and u such that ∥ℓ − u∥_P,2 < ε. The covering number $N(\epsilon ,\mathcal{F},L_2(Q))$ of $\mathcal{F}$ with respect to the L₂(Q) norm is the smallest number of ε-balls in L₂(Q) required to cover $\mathcal{F}$. The uniform covering number is the supremum of $N(\epsilon \Vert F{\Vert }_{2,Q},\mathcal{F},L_2(Q))$ over all discrete probability measures Q such that ∥F∥_Q,2 > 0, where F is an envelope function for $\mathcal{F}$. The bracketing and uniform entropy integrals for $\mathcal{F}$ with respect to F are then defined as

$$\begin{gathered} J_{[]}(\delta ,\mathcal{F})≔{\int }_0^{\delta }[1+\log N_{[]}(\epsilon \Vert F{\Vert }_{P_0,2},\mathcal{F},L_2(P_0)){]}^{1∕2}d\epsilon \\ J(\delta ,\mathcal{F})≔\underset{Q}{\text{sup}}{\int }_0^{\delta }[1+\log N(\epsilon \Vert F{\Vert }_{Q,2},\mathcal{F},L_2(Q)){]}^{1∕2}d\epsilon . \end{gathered}$$

We discuss two approaches to controlling $\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{F}}_{n,\delta ∕r_n}}$ using these integrals. Suppose that ${\mathcal{F}}_{n,\eta }$ has envelope function F_n,η in the sense that ∣ξ(x)∣ ≤ F_n,η for all $\xi \in {\mathcal{F}}_{n,\eta }$ and $x\in \mathcal{X}$. The first approach is useful when ∥F_n,δ/rn∥_P0,2 can be adequately controlled. Specifically, if either $J(1,{\mathcal{F}}_{n,\delta ∕r_n})$ or $J_{[]}(1,{\mathcal{F}}_{n,\delta ∕r_n})$ is O(1), then $\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{F}}_{n,{\delta }_n}}\le M_{\delta }\Vert F_{n,\delta ∕r_n}{\Vert }_{P_{0,}2}$ for all n and some constant M_δ ∈ (0, ∞) not depending on n by Theorems 2.14.1 and 2.14.2 of van der Vaart and Wellner (1996).

The second approach we consider is useful when the envelope functions do not shrink in expectation, but the functions in ${\mathcal{F}}_{n,\eta }$ still get smaller in the sense that ${\gamma }_{n,\delta }≔{\text{sup}}_{\xi \in {\mathcal{F}}_{n,\delta ∕r_n}}\Vert \xi {\Vert }_{P_0,2}$ tends to zero. For example, if ν_n,t is defined as ν_n,t(x) := I(0 ≤ x ≤ t) for each $x\in \mathcal{X}\subseteq \mathbb{R}$, t ∈ [0, 1], and n, then F_n,η : x ↦ I(0 ≤ x ≤ 1) is the natural envelope function for ${\mathcal{F}}_{n,\eta }$ for all n and η, so that ∥F_n,δ/rn∥_P0,2 does not tend to zero. However, if the density p₀ corresponding to P₀ is bounded above by ${\overline{p}}_0$, then ${\gamma }_{n,\delta }^2\le {\overline{p}}_0\delta ∕r_n$, which does tend to zero. In these cases, the basic tail bounds in Theorem 2.14.1 and 2.14.2 of van der Vaart and Wellner (1996) are too weak. Sharper, but slightly more complicated, bounds may be used instead. Specifically, if F_n,δ/rn ≤ C < ∞ for all n large enough and either

$$J({\gamma }_{n,\delta },{\mathcal{F}}_{n,\delta ∕r_n})+\frac{J({\gamma }_{n,\delta },{\mathcal{F}}_{n,\delta ∕r_n}{)}^2}{{\gamma }_{n,\delta }^2{n}^{1∕2}}\text{or}{J}_{[]}({\gamma }_{n,\delta },{\mathcal{F}}_{n,\delta ∕r_n})+\frac{J_{[]}({\gamma }_{n,\delta },{\mathcal{F}}_{n,\delta ∕r_n}{)}^2}{{\gamma }_{n,\delta }^2{n}^{1∕2}}$$

are $o(z_n^{-1})$, then $\Vert {\mathbb{G}}_n{\Vert }_{{\mathcal{F}}_{n,\delta ∕r_n}}=o_P(z_n^{-1})$ by Lemma 3.4.2 of van der Vaart and Wellner (1996) and Theorem 2.1 of van der Vaart and Wellner (2011). Analogous statements hold if these expressions are $O(z_n^{-1})$.

In some cases, both of these approaches must be used to control different terms arising within R_n(t), as for the conditional distribution function discussed in Section 4.2.

4. Illustrative examples

4.1. Example 1: Estimation of a G-computed distribution function

We first demonstrate the use of Theorem 3 in the particular problem in which we wish to draw inference on a G-computed distribution function. Suppose that the data unit is the vector X = (Y, A, W), where Y is an outcome, A ∈ {0, 1} is an exposure, and W is a vector of baseline covariates. The observed data consist of independent draws X₁, X₂, … , X_n from $P_0\in \mathcal{M}$, where $\mathcal{M}$ is a nonparametric model.

For $P\in \mathcal{M}$ and a₀ ∈ {0, 1}, we define the parameter value θ_P,a0 pointwise as θ_P,a0(t) := E_P {P (Y ≤ t ∣ A = a₀, W)} the G-computed distribution function of Y evaluated at t, where the outer expectation is over the marginal distribution of W under P. We are interested in estimating θ_0,a0 := θ_P0,a0. This parameter is often of interest as an interpretable marginal summary of the relationship between Y and A accounting for the potential confounding induced by W. Under certain causal identification conditions, θ_0,a0 is the distribution function of the counterfactual outcome Y(a₀) defined by the intervention that deterministically sets exposure to A = a₀ (Robins, 1986; Gill and Robins, 2001).

For each t, the parameter P ↦ θ_P,a0 (t) is pathwise differentiable in a nonparametric model, and its nonparametric efficient influence function φ_P,a0,t at $P\in \mathcal{M}$ is given by

$$(y,a,w)\mapsto \frac{I(a=a_0)}{g_P(a_0\mid w)}[I(y\le t)-{\overline{Q}}_P(t\mid a_0,w)]+{\overline{Q}}_P(t\mid a_0,w)-{\theta }_{P,a_0}(t),$$

where g_P(a₀ ∣ w) := P(A = a₀ ∣ W = w) is the propensity score and ${\overline{Q}}_P(t\mid a_0,w)≔P(Y\le t\mid A=a_0,W=w)$ is the conditional exposure-specific distribution function, as implied by P (van der Laan and Robins, 2003). Given estimators g_n and ${\overline{Q}}_n$ of g₀ := g_P0 and ${\overline{Q}}_0≔{\overline{Q}}_{P_0}$, respectively, several approaches can be used to construct, for each t, an asymptotically linear estimator of θ₀(t) with influence function ϕ_0,a0,t = φ_P0,a0,t. For example, the use of either optimal estimating equations or the one-step correction procedure leads to the doubly-robust augmented inverse-probability-of-weighting estimator

$${\theta }_{n,a_0}(t)≔\frac{1}{n}\sum _{i=1}^n\left\{\frac{I(A_i=a_0)}{g_n(a_0\mid W_i)}[I(Y_i\le t)-{\overline{Q}}_n(t\mid a_0,W_i)]+{\overline{Q}}_n(t\mid a_0,W_i)\right\},$$

as discussed in detail in van der Laan and Robins (2003). Under conditions on g_n and ${\overline{Q}}_n$, including consistency at fast enough rates, θ_n,a0(t) is asymptotically efficient relative to $\mathcal{M}$. In this case, θ_n,a0(t) satisfies (3.1) with influence function ϕ_0,a0,t. However, there is no guarantee that θ_n,a0 is monotone.

In the context of this example, we can identify simple sufficient conditions under which conditions (A)–(B), and hence the asymptotic equivalence of the initial and isotonized estimators of the G-computed distribution function, are guaranteed. Specifically, we find this to be the case when both:

1. there exists η > 0 such that g₀(a₀ ∣ W) ≥ η almost surely under P₀;

2. there exist non-negative real-valued functions K₁, K₂ such that

$$\begin{gathered} K_1(w)\mid t-s\mid \le \mid {\overline{Q}}_0(t\mid a_0,w)-{\overline{Q}}_0(s\mid a_0,w)\mid \\ \le K_2(w)\mid t-s\mid \end{gathered}$$

for all t, $s\in \mathcal{T}$, and such that, under P₀, K₁(W) is strictly positive with non-zero probability and K₂(W) has finite second moment.

We conducted a simulation study to validate our theoretical results in the context of this particular example. For samples sizes 100, 250, 500, 750, and 1000, we generated 1000 random datasets as follows. We first simulated a bivariate covariate W with independent components W₁ and W₂, respectively distributed as a Bernoulli variate with success probability 0.5 and a uniform variate on (−1, 1). Given W = (w₁, w₂), exposure A was simulated from a logistic regression model with

$$P_0(A=1\mid W_1=w_1,W_2=w_2)=\text{expit}(0.5+w_1-2w_2).$$

Given W = (w₁, w₂) and A = a, Y was simulated as the inverse-logistic transformation of a normal variate with mean 0.2 − 0.3a − 4w₂ and variance 0.3.

For each simulated dataset, we estimated θ_0,0(t) and θ_0,1(t) for t equal to each outcome value observed between 0.1 and 0.9. To do so, we used the estimator described above, with propensity score and conditional exposure-specific distribution function estimated using correctly-specified parametric models. We employed two correction procedures for the estimators θ_n,0 and θ_n,1. First, we projected θ_n,0 and θ_n,1 onto the space of monotone functions separately. Second, noting that θ_0,0(t) ≤ θ_0,1(t) for all t, so that (a, t) ↦ θ_0,a(t) is component-wise monotone for this particular data-generating distribution, we considered the projection of (a, t) ↦ θ_n,a(t) onto the space of bivariate monotone functions on $\{0,1\}\times \mathcal{T}$. For each simulation and each projection procedure, we recorded the maximal absolute differences between (i) the initial and and projected estimates, (ii) the initial estimate and the truth, and (iii) the projected estimate and the truth. We also recorded the maximal widths of the initial and projected confidence bands.

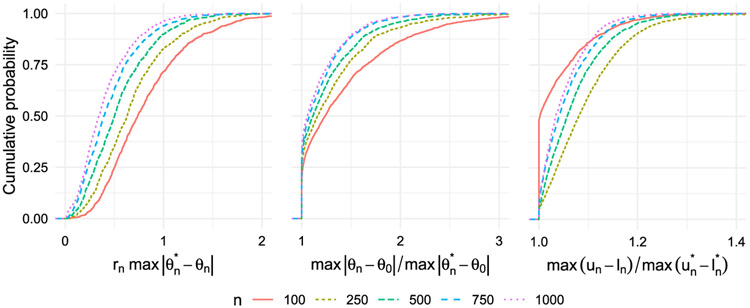
Figure 1 displays the results of this simulation study, with output from the univariate and bivariate projection approaches summarized in the top and bottom rows, respectively. The left column displays the empirical distribution of the scaled maximum absolute discrepancy between θ_n and ${\theta }_n^{\ast }$ for all sample sizes studied. This plot confirms that the discrepancy between these two estimators indeed decreases faster than n^−1/2, as our theory suggests. Furthermore, for each n, the discrepancy is larger for the two-dimensional projection.

Fig 1.

Summary of simulation results for G-computed distribution function. Each plot shows cumulative distributions of a particular discrepancy over 1000 simulated datasets for different values of n. Left panel: maximal absolute difference between the initial and isotonic estimators over the grid used for projecting, scaled up by root-n. Middle panel: ratio of the maximal absolute difference between the initial estimator and the truth and the maximal absolute difference between the isotonic estimator and the truth. Right panel: ratio of the maximal width of the initial confidence band and the maximal width of the isotonic confidence band. The top row shows the results for the univariate projection, and the bottom row shows the results for the bivariate projection.

The middle column of Figure 1 displays the empirical distribution function of the ratio between the maximum discrepancy between θ_n and θ₀ and that of ${\theta }_n^{\ast }$ and θ₀. This plot confirms that ${\theta }_n^{\ast }$ is always at least as close to θ₀ than is θ_n over ${\mathcal{T}}_n$. The maximum discrepancy between θ_n and θ₀ can be more than 25% larger than that between ${\theta }_n^{\ast }$ and θ₀ in the univariate case, and up to 50% larger in the bivariate case.

The right column of Figure 1 displays the empirical distribution function of the ratio between the maximum size of the initial uniform 95% influence function-based confidence band and that of the isotonic band. For large samples, the maximal widths are often close, but for smaller samples, the initial confidence bands can be up to 50% larger than the isotonic bands, especially for the bivariate case. The empirical coverage of both bands is provided in Table 1. The coverage of the isotonic band is essentially the same as the initial band for the univariate case, whereas it is slightly larger than that of the initial band in the bivariate case.

Table 1.

Coverage of 95% confidence bands for the true counterfactual distribution function.

	n	100	250	500	750	1000
d=1	Initial band	92.5	94.1	96.0	94.5	95.5
	Monotone band	92.5	94.1	96.0	94.5	95.5
d=2	Initial band	93.9	94.0	95.0	94.6	94.9
	Monotone band	95.7	95.9	95.5	95.3	95.1

4.2. Example 2: Estimation of a conditional distribution function

We next demonstrate the use of Theorem 2 with dimension d = 2 for drawing inference on a conditional distribution function. Suppose that the data unit is the vector X = (A, Y), where Y is an outcome and A is now a continuous exposure. The observed data consist of independent draws (A₁, Y₁), (A₂, Y₂), … , (A_n, Y_n), from $P_0\in \mathcal{M}$, where $\mathcal{M}$ is a nonparametric model. We define the parameter value θ_P pointwise as θ_P(t₁, t₂) := P (Y ≤ t₁ ∣ A = t₂). Thus, θ_P is the conditional distribution function of Y at t₁ given A = t₂. The map (t₁, t₂) ↦ θ_P(t₁, t₂) is necessarily monotone in t₁ for each fixed t₂, and in some settings, it may be known that it is also monotone in t₂ for each fixed t₁. This parameter completely describes the conditional distribution of Y given A, and can be used to obtain the conditional mean, conditional quantiles, or any other conditional parameter of interest.

For each t₁, the true function θ₀(t₁, t₂) = θ_P0 (t₁, t₂) may be written as the conditional mean of I(Y ≤ t₁) given A = t₂. Hence, any method of nonparametric regression can be used to estimate t₂ ↦ θ₀(t₁, t₂) for fixed t₁, and repeating such a method over a grid of values of t₁ yields an estimator of the entire function. We expect that our results would apply to many of these methods. Here, we consider the local linear estimator (Fan and Gijbels, 1996), which may be expressed as

$${\theta }_n(t_1,t_2)≔\frac{1}{n{h}_n}\sum _{i=1}^{n}I(Y_i\le t_1)\left[\frac{s_{2,n}(t_2)-s_{1,n}(t_2)(A_i-t_2)}{s_{0,n}(t_2)s_{2,n}(t_2)-s_{1,n}(t_2{)}^2}\right]K\left(\frac{A_i-t_2}{h_n}\right),$$

where $K:\mathbb{R}\to \mathbb{R}$ is a symmetric and bounded kernel function, h_n → 0 is a sequence of bandwidths, and

$$s_{j,n}(t_2)≔\frac{1}{n{h}_n}\sum _{i=1}^n(A_i-t_2{)}^{j}K\left(\frac{A_i-t_2}{h_n}\right)$$

for j ∈ {0, 1, 2}. Under regularity conditions on the true distribution function θ₀, the marginal density f₀ of A, the bandwidth sequence h_n, and the kernel function K, for any fixed (t₁, t₂), θ_n satisfies

$$\begin{gathered} (n{h}_n{)}^{1∕2}[{\theta }_n(t_1,t_2)-{\theta }_0(t_1,t_2)-h_n^2{V}_K{b}_0(t_1,t_2)] \\ \stackrel{\mathrm{d}}{\to }N(0,S_K{v}_0(t_1,t_2)), \end{gathered}$$

where V_K := ʃ x²K(x)dx is the variance of K, S_K := ʃ K(x)²dx, and b₀(t₁, t₂) and v₀(t₁, t₂) depend on the derivatives of θ₀ and on f₀. If h_n is chosen to be of order n^−1/5, the rate that minimizes the asymptotic mean integrated squared error of θ_n relative to θ₀, then n^2/5 [θ_n(t₁, t₂) − θ₀(t₁, t₂)] converges in law to a normal random variate with mean V_Kb₀(t₁, t₂) and variance S_Kv₀(t₁, t₂). Under stronger regularity conditions, the rate of convergence of the uniform norm $\Vert {\theta }_n-{\theta }_0{\Vert }_{\mathcal{T}}$ can be shown to be (nh_n/ log n)^1/2 (Hardle, Janssen and Serfling, 1988).

Theorem 3 cannot be used to establish (A) in this problem, since θ_n is not an asymptotically linear estimator. Furthermore, as discussed above, recent results suggest that {$\{r_n[{\theta }_n(t)-{\theta }_0(t)]:t\in \mathcal{T}\}$} does not converge weakly to a tight limit in ${\ell }^{\infty }(\mathcal{T})$ for any useful rate r_n. Despite this lack of weak convergence, condition (A) can be verified directly in the context of this example under smoothness conditions on θ₀ and f₀ using the tail bounds for empirical processes outlined in Section 3.2. Denoting by ${\theta }_{0,t_2}^{\prime }$ and ${\theta }_{0,t_2}^{″}$ the first and second derivatives of θ₀ with respect to its second argument, we define

$$R_{\theta }^{(2)}(t,\delta )≔{\theta }_0(t_1,t_2+\delta )-{\theta }_0(t_1,t_2)-\delta {\theta }_{0,t_2}^{\prime }(t_1,t_2)-\frac{1}{2}{\delta }^2{\theta }_{0,t_2}^{″}(t_1,t_2)$$

and $R_f^{(1)}(t,\delta )≔f_0(t_2+\delta )-f_0(t_2)-\delta f_0^{\prime }(t_2)$, where $f_0^{\prime }$ is the derivative of f₀. We then introduce the following conditions on θ₀, f₀, and K:

(d) ${\theta }_{0,t_2}^{″}$ exists and is continuous on $\mathcal{T}$, and as δ → 0, ${\text{sup}}_{t\in \mathcal{T}}\mid R_{\theta }^{(2)}(t,\delta )\mid =o({\delta }^2)$;

(e) ${\text{inf}}_{t\in \mathcal{T}}{f}_0(t)>0$, $f_0^{\prime }$ exists and is continuous on $\mathcal{T}$, and ${\text{sup}}_{t\in \mathcal{T}}\mid R_f^{(1)}(t,\delta )\mid =o(\delta )$;

(f) K is a Lipschitz function supported on [−1, 1] satisfying condition (M) of Stupfler (2016).

We also define

$$\begin{gathered} {\nu }_{n,t}(y,a)≔[I(y\le t_1)-{\theta }_0(t_1,a)]K\left(\frac{a-t_2}{h_n}\right); \\ {g}_n(t_2)≔s_{0,n}(t_2)s_{2,n}(t_2)-s_{1,n}(t_2{)}^2; \\ {R}_n(t)≔h_n^{-1∕2}\left[\frac{s_{2,n}(t_2)}{g_n(t_2)}{\mathbb{G}}_n{\nu }_{n,t}-\frac{s_{1,n}(t_2)}{g_n(t_2)}{\mathbb{G}}_n({\ell }_t{\nu }_{n,t})\right]. \end{gathered}$$

We then have the following result.

Proposition 1. If (d)–(f) hold, $n{h}_n^4∕\log h_n^{-1}\to \infty$ and $n{h}_n^5=O(1)$, then

$$\underset{t\in \mathcal{T}}{\text{sup}}\mid (n{h}_n{)}^{1∕2}[{\theta }_n(t_1,t_2)-{\theta }_0(t_1,t_2)]-(n{h}_n^5{)}^{1∕2}\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)K_2-R_n(t)\mid \stackrel{\mathrm{P}}{\to }0.$$

Proposition 1 aids in establishing the following result, which formally establishes asymptotic equivalence of the local linear estimator of a conditional distribution function and its correction obtained via isotonic regression at the rate r_n = (nh_n)^1/2.

Proposition 2. If (d)–(f) hold and $n{h}_n^5\to c\in (0,\infty )$, then (A) holds for the local linear estimator with r_n = (nh_n)^1/2.

The proofs of Propositions 1 and 2 are provided in Appendix A.5. These results may also be of interest in their own right for establishing other properties of the local linear estimator.

As with the first example, we conducted a simulation study to validate our theoretical results. For samples sizes n ∈ {100, 250, 500, 750, 1000}, we generated 1000 random datasets as follows. We first simulated A as a Beta(2, 3) variate. Given A = a, Y was simulated as the inverse-logistic transformation of a normal variate with mean 0.5 × [1 + (a − 1.2)²] and variance one.

For each simulated dataset, we estimated θ₀(y, a) for each (y, a) in an equally spaced square grid of mesh ω_n = n^−4/5. For each unique y in this grid, we estimated the function a ↦ θ₀(y, a) using the local linear estimator, as implemented in the R package KernSmooth (Wand, 2015; Wand and Jones, 1995). For each value of y in the grid, we computed the optimal bandwidth based on the direct plug-in methodology of Ruppert, Sheather and Wand (1995) as implemented by the dpill function, and we then set our bandwidth as the average of these y-specific bandwidths. We constructed initial confidence bands using a variable-width nonparametric bootstrap (Hall and Kang, 2001).

We first note that, for all sample sizes considered, over 99% of simulations had monotonicity violations in both the y- and a-directions. Figure 2 displays the results of this simulation study. The left exhibit of Figure 2 confirms that the discrepancy between θ_n and ${\theta }_n^{\ast }$ decreases faster than $r_n^{-1}=n^{-2∕5}$, as our theory suggests. The middle exhibit indicates that in roughly 50% of simulations, there is less than 5% difference between $\Vert {\theta }_n^{\ast }-{\theta }_0{\Vert }_{{\mathcal{T}}_n}$ and $\Vert {\theta }_n-{\theta }_0{\Vert }_{{\mathcal{T}}_n}$, but even for n = 1000, in roughly 25% of simulations, ${\theta }_n^{\ast }$ offers at least a 25% improvement in estimation error. In smaller samples, the estimation error of ${\theta }_n^{\ast }$ is less than half that of θ_n in 5–10% of simulations. The rightmost exhibit indicates that the projected confidence bands regularly reduce the uniform size of the initial bands by 10–20%. Finally, the empirical coverage of uniform 95% bootstrap-based bands and their projected versions is provided in Table 2. As before, the projected band is always more conservative than the initial band, and the difference in coverage diminishes as n grows. However, the initial bands in this example are anti-conservative, even at n = 1000, likely due to the slower rate of convergence, and the corrected bands offer a much more substantial improvement in this example than in the first.

Fig 2.

Summary of simulation results for conditional distribution function. The three columns display the same results as those in Figure 1.

Table 2.

Coverage of 95% confidence bands for the true conditional distribution function.

n	100	250	500	750	1000
Initial band	37.6	64.9	83.2	86.3	89.7
Monotone band	60.8	80.4	90.3	92.3	93.9

5. Discussion

Many estimators of function-valued parameters in nonparametric and semiparametric models are not guaranteed to respect shape constraints on the true function. A simple and general solution to this problem is to project the initial estimator onto the constrained parameter space over a grid whose mesh goes to zero fast enough with sample size. However, this introduces the possibility that the projected estimator has different properties than the original estimator. In this paper, we studied the important shape constraint of multivariate component-wise monotonicity. We provided results indicating that the projected estimator is generically no worse than the initial estimator, and that if the true function is strictly increasing and the initial estimator possesses a relatively weak type of stochastic equicontinuity, the projected estimator is uniformly asymptotically equivalent to the initial estimator. We provided especially simple sufficient conditions for this latter result when the initial estimator is uniformly asymptotically linear, and provided guidance on establishing the key condition for kernel smoothed estimators.

We studied the application of our results in two examples: estimation of a G-computed distribution function, for use in understanding the effect of a binary exposure on an outcome when the exposure-outcome relationship is confounded by recorded covariates, and of a conditional distribution function, for use in characterizing the marginal dependence of an outcome on a continuous exposure. In numerical studies, we found that the projected estimator yielded improvements over the initial estimator. The improvements were especially strong in the latter example.

In our examples, we only studied corrections in dimensions d = 1 and d = 2. In future work, it would be interesting to consider corrections in dimensions higher than 2. For example, for the conditional distribution function, it would be of interest to study multivariate local linear estimators for a continuous exposure A taking values in ${\mathbb{R}}^{d-1}$ for d > 2. Since tailored algorithms for computing the isotonic regression do not yet exist for d > 2, it would also be of interest to determine whether a version of Theorem 2 could be established for the relaxed isotonic estimator proposed by Fokianos, Leucht and Neumann (2017). Alternatively, it is possible that the uniform stochastic equicontinuity currently required by Chernozhukov, Fernández-Val and Galichon (2010) and Daouia and Park (2013) for asymptotic equivalence of the rearrangement- and envelope-based corrections, respectively, could be relaxed along the lines of our condition (A). Finally, our theoretical results do not give the exact asymptotic behavior of the projected estimator or projected confidence band when the true function possesses flat regions. This is also an interesting topic for future research.

Appendix A: Technical proofs

A.1. Proof of Theorem 1

Part (i) follows from Corollary B to Theorem 1.6.1 of Robertson, Wright and Dykstra (1988). For parts (ii) and (iii), we note that by assumption

$$\mid {\theta }_n^{\ast }(t)-{\theta }_0(t)\mid \le \sum _k{\lambda }_{k,n}(t)\mid {\theta }_n^{\ast }(s_k)-{\theta }_0(s_k)\mid +\sum _k{\lambda }_{k,n}(t)\mid {\theta }_0(s_k)-{\theta }_0(t)\mid$$

for every $t\in \mathcal{T}$, where Σ_k λ_k,n(t) = 1, and for each k, $s_k\in {\mathcal{T}}_n$ and ∥s_k − t∥ ≤ 2ω_n. By part (i), the first term is bounded above by ${\text{sup}}_{s\in {\mathcal{T}}_n}\mid {\theta }_n(s)-{\theta }_0(s)\mid$. The second term is bounded above by γ(2ω_n), where we define

$$\gamma (\delta )≔\text{sup}\{\mid {\theta }_0(t)-{\theta }_0(s)\mid :t,s\in \mathcal{T},\Vert t-s\Vert \le \delta \}.$$

If θ₀ is continuous on $\mathcal{T}$, then it is also uniformly continuous since $\mathcal{T}$ is compact. Therefore, γ(δ) → γ(0) = 0 as δ → 0, so that γ(2ω_n) →_P 0 if ω_n →_P 0. If γ(δ) = o(δ^α) as δ → 0, then $\gamma (2{\omega }_n)=o_P({\omega }_n^{\alpha })$.

Part (iv) follows from the proof of Proposition 3 of Chernozhukov, Fernández-Val and Galichon (2009), which applies to any order-preserving monotonization procedure. For the first statement of (v), by their definition as minimizers of the least-squares criterion function, we note that ${\sum }_{t\in {\mathcal{T}}_n}{u}_n^{\ast }(t)={\sum }_{t\in {\mathcal{T}}_n}{u}_n(t)$, and similarly for ${\ell }_n^{\ast }$. The second statement of (v) follows from a slight modification of Theorem 1.6.1 of Robertson, Wright and Dykstra (1988). As stated, the result says that ${\sum }_{t\in {\mathcal{T}}_n}G({\theta }^{\ast }(t)-\theta (t))\le {\sum }_{t\in {\mathcal{T}}_n}G(\theta (t)-\psi (t))$ for any convex function $G:\mathbb{R}\to \mathbb{R}$ and monotone function ψ, where θ* is the isotonic regression of θ over ${\mathcal{T}}_n$. A straightforward adaptation of the proof indicates that ${\sum }_{t\in {\mathcal{T}}_n}G({\theta }_1^{\ast }(t)-{\theta }_2^{\ast }(t))\le {\sum }_{t\in {\mathcal{T}}_n}G({\theta }_1(t)-{\theta }_2(t))$, where now ${\theta }_1^{\ast }$ and ${\theta }_2^{\ast }$ are the isotonic regressions of θ₁ and θ₂ over ${\mathcal{T}}_n$, respectively. As in Corollary B, taking G(x) = ∣x∣^p and letting p → ∞ yields that $\Vert {\theta }_1^{\ast }-{\theta }_2^{\ast }{\Vert }_{{\mathcal{T}}_n}\le \Vert {\theta }_1-{\theta }_2{\Vert }_{{\mathcal{T}}_n}$. Applying this with θ₁ = u_n and θ₂ = ℓ_n establishes the second portion of (v). □

A.2. Proof of Theorem 2

We prove Theorem 2 via three lemmas, which may be of interest in their own right. The first lemma controls the size of deviations in θ_n over small neighborhoods, and does not hinge on condition (C) holding.

Lemma 1. If (A)–(B) hold and $b_n=o_P(r_n^{-1})$, then

$$\underset{\Vert t-s\Vert \le b_n}{\text{sup}}\mid {\theta }_n(t)-{\theta }_0(s)\mid =o_P(r_n^{-1}).$$

Proof of Lemma 1. In view of the triangle inequality,

$$\mid {\theta }_n(t)-{\theta }_n(s)\mid \le \mid \{{\theta }_n(t)-{\theta }_0(t)\}-\{{\theta }_n(s)-{\theta }_0(s)\}\mid +\mid {\theta }_0(t)-{\theta }_0(s)\mid .$$

The first term is $o_P(r_n^{-1})$ by (A), whereas the second term is $o_P(r_n^{-1})$ by (B). □

The second lemma controls the size of neighborhoods over which violations in monotonicity can occur. Henceforth, we define

$${\kappa }_n≔\text{sup}\{\Vert t-s\Vert :s,t\in \mathcal{T},s\le t,{\theta }_n(t)\le {\theta }_n(s)\}.$$

In this lemma we again require (A) but now require (C) rather than (B).

Lemma 2. If (A) and (C) hold, then ${\kappa }_n=o_P(r_n^{-1})$.

Proof of Lemma 2. Let ϵ > 0 and η_n := ϵ/r_n. Suppose that κ_n > η_n. Then, there exist s, $t\in \mathcal{T}$ with s < t and ∥t − s∥ > η_n such that θ_n(s) ≥ θ_n(t). We claim that there must also exist s*, $t^{\ast }\in \mathcal{T}$ with s* < t* and ∥t* − s*∥ ∈ [η_n/2, η_n] such that θ_n(s*) ≥ θ_n(t*). To see this, let J = ⌊∥t − s∥/(η_n/2)⌋ − 1, and note that J ≥ 1. Define t_j := s+(jη_n/2)(t − s)/∥t − s∥ for j = 0, 1, … , J, and set t_J+1 := t. Thus, t_j < t_j+1 and ∥t_j+1 − t_j∥ ∈ [η_n/2, η_n] for each j = 0, 1, … , J. Since then ${\sum }_{j=0}^J[{\theta }_n(t_{j+1})-{\theta }_n(t_j)]={\theta }_n(t)-{\theta }_n(s)\le 0$, it must be that θ_n(t_j+1) ≤ θ_n (t_j) for at least one j. This proves the claim.

We now have that κ_n > η_n implies that there exist s, $t\in \mathcal{T}$ with s < t and ∥t − s∥ ∈ [η_n/2, η_n] such that θ_n(s) ≥ θ_n(t). This further implies that

$$\{{\theta }_n(t)-{\theta }_0(t)\}-\{{\theta }_n(s)-{\theta }_0(s)\}\le -\{{\theta }_0(t)-{\theta }_0(s)\}\le -K_0\Vert t-s\Vert \le -K_0{\eta }_n∕2$$

by condition (B). Finally, this allows us to write

$$P_0\left({\kappa }_n>\frac{ϵ}{r_n}\right)\le P_0\left\{\underset{\Vert t-s\Vert \le ϵ∕r_n}{\text{sup}}{r}_n\mid [{\theta }_n(t)-{\theta }_0(t)]-[{\theta }_n(s)-{\theta }_0(s)]\mid \ge \frac{K_0ϵ}{2}\right\}.$$

By condition (A), this probability tends to zero for every ϵ > 0, which completes the proof. □

Our final lemma bounds the maximal absolute deviation between ${\theta }_n^{\ast }$ and θ_n over the grid ${\mathcal{T}}_n$ in terms of the supremal deviations of θ_n over neighborhoods smaller than κ_n. This lemma does not depend on any of the conditions (A)–(C).

Lemma 3. It holds that ${\max }_{t\in {\mathcal{T}}_n}\mid {\theta }_n^{\ast }(t)-{\theta }_n(t)\mid \le {\text{sup}}_{\Vert s-t\Vert \le {\kappa }_n}\mid {\theta }_n(s)-{\theta }_n(t)\mid$.

Proof of Lemma 3. By Theorem 1.4.4 of Robertson, Wright and Dykstra (1988), for any $t\in {\mathcal{T}}_n$,

$${\theta }_n^{\ast }(t)=\underset{U\in {\mathcal{U}}_t}{\max }\underset{L\in {\mathcal{L}}_t}{\text{min}}{\theta }_n(U\cap L)=\underset{L\in {\mathcal{L}}_t}{\text{min}}\underset{U\in {\mathcal{U}}_t}{\max }{\theta }_n(U\cap L),$$

where, for any finite set $S\subseteq {\mathcal{T}}_n$, θ_n(S) is defined as ∣S∣⁻¹ Σ_s∈S θ_n(s). The sets U range over the collection ${\mathcal{U}}_n$ of upper sets of ${\mathcal{T}}_n$ containing t, where $U\subseteq {\mathcal{T}}_n$ is called an upper set if t₁ ∈ U, $t_2\in {\mathcal{T}}_n$ and t₁ ≤ t₂ implies t₂ ∈ U. The sets L range over the collection ${\mathcal{L}}_t$ of lower sets of ${\mathcal{T}}_n$ containing t, where $L\subseteq {\mathcal{T}}_n$ is called a lower set if t₁ ∈ L, $t_2\in {\mathcal{T}}_n$ and t₂ ≤ t₁ implies t₂ ∈ L.

Let U_t := {s : s ≥ t} and L_t := {s : s ≤ t}. First, suppose there exists $L_0\in {\mathcal{L}}_t$ and s₀ ∈ L₀ with s₀ > t and ∥t − s₀∥ > κ_n. Then, we claim that there exists another lower set $L_0^{\prime }\in {\mathcal{L}}_t$ such that θ_n(U_t ∩ L₀) > θ_n $(U_t\cap L_0^{\prime })$. If θ_n(U_t ∩ L₀) > θ_n(t) = θ_n(U_t ∩ L_t), then $L_0^{\prime }=L_t$ satisfies the claim. Otherwise, if θ_n(U_t ∩ L₀) ≤ θ_n(t), let

$$L_0^{\prime }≔L_0\setminus \{s:s>t,\Vert t-s\Vert >{\kappa }_n\}.$$

One can verify that $L_0^{\prime }\in {\mathcal{L}}_t$, and since s₀ ∈ L₀ \ $L_0^{\prime }$, $L_0^{\prime }$ is a strict subset of L₀. Furthermore, by definition of κ_n, θ_n(s) > θ_n(t) for all s > t such that ∥t − s∥ > κ_n, and since θ_n(U_t ∩ L₀) ≤ θ_n(t), removing these elements from L₀ can only reduce the average, so that ${\theta }_n(U_t\cap L_0^{\prime })$ < θ_n(U_t ∩ L₀). This establishes the claim. By an analogous argument, we can show that if there exists $U_0\in {\mathcal{U}}_t$ and s₀ ∈ U₀ with s₀ < t and ∥t − s₀∥ > κ_n, then there exists another upper set $U_0^{\prime }\in {\mathcal{U}}_t$ such that θ_n(U₀ ∩ L_t) < ${\theta }_n(U_0^{\prime }\cap L_t)$.

Let $L^{\ast }\in {\text{argmin}}_{L\in {\mathcal{L}}_t}{\theta }_n(U_t\cap L)$ and $U^{\ast }\in {\text{argmax}}_{U\in {\mathcal{U}}_t}{\theta }_n(U\cap L_t)$. Then,

$$\begin{gathered} {\theta }_n^{\ast }(t)=\underset{U\in {\mathcal{U}}_t}{\max }\underset{L\in {\mathcal{L}}_t}{\text{min}}{\theta }_n(U\cap L)\ge \underset{L\in {\mathcal{L}}_t}{\text{min}}{\theta }_n(U_t\cap L)={\theta }_n(U_t\cap L^{\ast })\text{and} \\ {\theta }_n^{\ast }(t)=\underset{L\in {\mathcal{L}}_t}{\text{min}}\underset{U\in {\mathcal{U}}_t}{\max }{\theta }_n(U\cap L)\le \underset{U\in {\mathcal{U}}_t}{\max }{\theta }_n(U\cap L_t)={\theta }_n(U^{\ast }\cap L_t). \end{gathered}$$

Hence, ${\theta }_n(U_t\cap L^{\ast })\le {\theta }_n^{\ast }(t)\le {\theta }_n(U^{\ast }\cap L_t)$. By the above argument, we have that both

$$\begin{gathered} {\theta }_n(U_t\cap L^{\ast })\ge \text{inf}\{{\theta }_n(s):s\ge t,\Vert t-s\Vert \le {\kappa }_n\}\text{and} \\ {\theta }_n(U^{\ast }\cap L_t)\le \text{sup}\{{\theta }_n(s):s\le t,\Vert t-s\Vert \le {\kappa }_n\}. \end{gathered}$$

Therefore, we find that

$$\begin{gathered} \text{inf}\{{\theta }_n(s)-{\theta }_n(t):\Vert t-s\Vert \le {\kappa }_n\}\le {\theta }_n^{\ast }(t)-{\theta }_n(t) \\ \le \text{sup}\{{\theta }_n(s)-{\theta }_n(t):\Vert t-s\Vert \le {\kappa }_n\}, \end{gathered}$$

and thus, $\mid {\theta }_n^{\ast }(t)-{\theta }_n(t)\mid \le \text{sup}\{\mid {\theta }_n(s)-{\theta }_n(t)\mid :\Vert t-s\Vert \le {\kappa }_n\}$. Taking the maximum over $t\in {\mathcal{T}}_n$ yields the claim. □

The proof of Theorem 2 follows easily from Lemmas 1, 2 and 3.

Proof of Theorem 2. By construction, for each $t\in \mathcal{T}$, we can write

$$\mid {\theta }_n^{\ast }(t)-{\theta }_n(t)\mid \le {\Sigma }_{j=1}^{2^d}{\lambda }_{j,n}(t)\mid {\theta }_n^{\ast }(s_j)-{\theta }_n(s_j)\mid +{\Sigma }_{j=1}^{2^d}{\lambda }_{j,n}(t)\mid {\theta }_n(s_j)-{\theta }_n(t)\mid ,$$

where $s_j\in {\mathcal{T}}_n$ and ∥s_j − t∥ ≤ 2ω_n for all t, s_j by definition. Thus, since Σ_j λ_j,n(t) = 1, it follows that

$$\underset{t\in \mathcal{T}}{\text{sup}}\mid {\theta }_n^{\ast }(t)-{\theta }_n(t)\mid \le \underset{t\in {\mathcal{T}}_n}{\max }\mid {\theta }_n^{\ast }(t)-{\theta }_n(t)\mid +\underset{\Vert s-t\Vert \le 2{\omega }_n}{\text{sup}}\mid {\theta }_n(s)-{\theta }_n(t)\mid .$$

By Lemma 3, the first summand is bounded above by sup_{∥s−t∥≤κn} ∣θ_n(s) − θ_n(t)∣, which is $o_P(r_n^{-1})$ by Lemmas 1 and 2. The second summand is $o_P(r_n^{-1})$ by Lemma 1. □

A.3. Proof of Corollary 1

We note that ℓ_n(t) ≤ θ₀(t) ≤ u_n (t) if and only if

$$\begin{gathered} \{r_n[{\theta }_n(t)-{\ell }_n(t)]-{\gamma }_{\alpha }(t)\}+{\gamma }_{\alpha }(t)\ge r_n[{\theta }_n(t)-{\theta }_0(t)] \\ \ge -{\gamma }_{\alpha }(t)-\{r_n[u_n(t)-{\theta }_n(t)]-{\gamma }_{\alpha }(t)\}. \end{gathered}$$

Therefore, by conditions (a)–(c), $P_0[{\ell }_n(t)\le {\theta }_0(t)\le u_n(t)\text{for all}t\in \mathcal{T}]\to 1-\alpha$. Next, we let δ > 0 and note that

$$\begin{gathered} \underset{\Vert t-s\Vert \le \delta ∕r_n}{\text{sup}}\mid r_n\{{\ell }_n(t)-{\theta }_n(t)\}-r_n\{{\ell }_n(s)-{\theta }_0(s)\}\mid \\ \le \underset{\Vert t-s\Vert \le \delta ∕r_n}{\text{sup}}\mid r_n\{{\theta }_n(t)-{\theta }_0(t)\}-r_n\{{\theta }_n(s)-{\theta }_0(s)\}\mid \\ +\underset{\Vert t-s\Vert \le \delta ∕r_n}{\text{sup}}\mid {\gamma }_{\alpha }(t)-{\gamma }_{\alpha }(s)\mid +2\Vert r_n({\theta }_n-{\ell }_n)-{\gamma }_{\alpha }{\Vert }_{\mathcal{T}}. \end{gathered}$$

The first term tends to zero in probability by (A), the second by conditions (a)–(c), and the third by the assumed uniform continuity of γ_α. An analogous decomposition holds for u_n. Therefore, we can apply Theorem 2 with u_n and ℓ_n in place of θ_n to find that $\Vert {\ell }_n^{\ast }-{\ell }_n{\Vert }_{\mathcal{T}}=o_P(r_n^{-1})$ and $\Vert u_n^{\ast }-u_n{\Vert }_{\mathcal{T}}=o_P(r_n^{-1})$. Finally, applying an analogous argument to the event ${\ell }_n^{\ast }$ ≤ θ₀ ≤ $u_n^{\ast }$ as we applied to ℓ_n ≤ θ₀ ≤ u_n above yields the result. □

A.4. Proof of Theorem 3

Let ϵ, δ, η > 0. By (3.1) and since ${\text{sup}}_{t\in \mathcal{T}}\mid R_{n,t}\mid =o_P(n^{-1∕2})$,

$$n^{1∕2}\mid \{{\theta }_n(t)-{\theta }_0(t)\}-\{{\theta }_n(s)-{\theta }_0(s)\}\mid \le \mid {\mathbb{G}}_n({\varphi }_{0,t}-{\varphi }_{0,s})\mid +o_P(1).$$

Condition (A2) implies that {${\varphi }_{0,t}:t\in \mathcal{T}$} is uniformly mean-square continuous, in the sense that

$$\underset{h\to 0}{\text{lim}}\underset{\Vert t-s\Vert \le h}{\text{sup}}\int \{{\varphi }_{0,s}(x)-{\varphi }_{0,t}(x){\}}^{2}d{P}_0(x)=0.$$

Since $\mathcal{T}$ is totally bounded in ∥ · ∥, this also implies that {${\varphi }_{0,t}:t\in \mathcal{T}$} is totally bounded in the L₂(P₀) metric. This, in addition to (A1), implies that : {${\mathbb{G}}_n{\varphi }_{0,t}:t\in \mathcal{T}$} converges weakly in ${\ell }^{\infty }(\mathcal{T})$ to a Gaussian process $\mathbb{G}$ with covariance function Σ₀. Furthermore, (A2) implies that this limit process is a tight element of ${\ell }^{\infty }(\mathcal{T})$. By Theorem 1.5.4 of van der Vaart and Wellner (1996), {${\mathbb{G}}_n{\varphi }_{0,t}:t\in \mathcal{T}$} is asymptotically tight. By Theorem 1.5.7 of van der Vaart and Wellner (1996), {${\mathbb{G}}_n{\varphi }_{0,t}:t\in \mathcal{T}$} is thus asymptotically uniformly mean-square equicontinuous in probability, in the sense that there exists some δ₀ = δ₀(ϵ, η) > 0 such that

$$\underset{n\to \infty }{\text{lim sup}}{P}_0\left[\underset{\rho (s,t)<{\delta }_0}{\text{sup}}\mid {\mathbb{G}}_n({\varphi }_{0,t}-{\varphi }_{0,s})\mid >ϵ\right]<\eta$$

with ρ(s, t) := [ʃ{ϕ_0,t(x) − ϕ_0,s(x)}²dP₀(x)]^1/2. By (A2), sup_{∥t−s∥≤h} ρ(t, s) < δ₀ for some h > 0. Hence, for all n large, both δn^−1/2 ≤ h and

$$P_0\left[\underset{\rho (s,t)<{\delta }_0}{\text{sup}}\mid {\mathbb{G}}_n({\varphi }_{0,t}-{\varphi }_{0,s})\mid >ϵ\right]<\eta ,$$

so that

$$P_0\left[\underset{\Vert t-s\Vert \le \delta ∕n^{1∕2}}{\text{sup}}\mid {\mathbb{G}}_n({\varphi }_{0,t}-{\varphi }_{0,s})\mid >ϵ\right]\le P_0\left[\underset{\rho (s,t)<{\delta }_0}{\text{sup}}\mid {\mathbb{G}}_n({\varphi }_{0,t}-{\varphi }_{0,s})\mid >ϵ\right]<\eta$$

and the proof is complete. □

A.5. Proof of Propositions 1 and 2

Below, we refer to van der Vaart and Wellner (1996) as VW. Throughout, the symbol ≲ should be interpreted to mean ‘bounded above, up to a multiplicative constant not depending on n, t, y or a.’

We first note that condition (M) of Stupfler (2016) guarantees that the class

$$\left\{x\mapsto K\left(\frac{x-t}{h}\right):h>0,t\in \mathbb{R}\right\}$$

is Vapnik–Chervonenkis (henceforth VC) with index 2. In addition, we define K_j := ʃ u^jK(u) du and

$$\begin{gathered} w_n(a,t_2)≔s_{2,n}(t_2)-s_{1,n}(t_2)(a-t_2), \\ {w}_0(a,t_2)≔f_0(t_2)-f_0^{\prime }(t_2)(a-t_2). \end{gathered}$$

Before proving Propositions 1 and 2, we state and prove a lemma we will use.

Lemma 4. If (d)–(f) hold, $n{h}_n^4\to \infty$ and $n{h}_n^5=O(1)$, then

$$\begin{gathered} (n{h}_n^5{)}^{1∕2}\underset{t\in \mathcal{T}}{\text{sup}}\mid \frac{s_{1,n}(t_2)}{g_n(t_2)}-\frac{f_0^{\prime }(t_2)}{f_0(t_2{)}^2}\mid \stackrel{\mathrm{P}}{\to }0, \\ (n{h}_n^5{)}^{1∕2}\underset{t\in \mathcal{T}}{\text{sup}}\mid \frac{s_{2,n}(t_2)}{g_n(t_2)}-\frac{1}{f_0(t_2)}\mid \stackrel{\mathrm{P}}{\to }0, \\ (n{h}_n^5{)}^{1∕2}\underset{t\in \mathcal{T}}{\text{sup}}\underset{\mid a-t_2\mid \le h_n}{\text{sup}}\mid \frac{w_n(a,t_2)}{g_n(t_2)}-\frac{w_0(a,t_2)}{f_0(t_2{)}^2}\mid \stackrel{\mathrm{P}}{\to }0, \end{gathered}$$

and for any δ > 0,

$$\begin{gathered} (n{h}_n^5{)}^{1∕2}\underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{1∕2}}{\text{sup}}\mid \frac{s_{1,n}(t_2)}{g_n(t_2)}-\frac{s_{1,n}(s_2)}{g_n(s_2)}\mid \stackrel{\mathrm{P}}{\to }0, \\ (n{h}_n^5{)}^{1∕2}\underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{1∕2}}{\text{sup}}\mid \frac{s_{2,n}(t_2)}{g_n(t_2)}-\frac{s_{2,n}(s_2)}{g_n(s_2)}\mid \stackrel{\mathrm{P}}{\to }0. \end{gathered}$$

Proof of Lemma 4. We first show that ${\text{sup}}_{t\in \mathcal{T}}\mid s_{0,n}(t_2)-f_0(t_2)\mid =o_P(h_n)$. We have that

$$\begin{gathered} s_{0,n}(t_2)-f_0(t_2)=h_n^{-1}\int K\left(\frac{a-t_2}{h_n}\right)f_0(a)da-f_0(t_2) \\ +n^{-1∕2}{h}_n^{-1}{\mathbb{G}}_{n}K\left(\frac{\cdot -t_2}{h_n}\right). \end{gathered}$$

By the change of variables u = (a − t₂)/h_n, we have that

$$\begin{gathered} h_n^{-1}\int K\left(\frac{a-t_2}{h_n}\right)f_0(a)da-f_0(t_2) \\ =\int K(u)[f_0(t_2)+h_{n}u)-f_0(t_2)]du \\ =h_n\int uK(u)(h_{n}u{)}^{-1}{R}_f^{(1)}((t_1,t_2),h_{n}u)du, \end{gathered}$$

which, in view of the assumed uniform negligibility of $R_f^{(1)}$, tends to zero uniformly over t₂ faster than h_n. For the second term, since K is uniformly bounded and the class

$$\left\{a\mapsto K\left(\frac{a-t_2}{h_n}\right):t_2\in [0,1]\right\}$$

is P₀-Donsker, as implied by condition (M) of Stupfler (2016), Theorem 2.14.1 of VW implies that

$$\underset{t_2}{\text{sup}}\mid {\mathbb{G}}_{n}K\left(\frac{\cdot -t_2}{h_n}\right)\mid =O_P(1).$$

Then, since $n^{-1∕2}{h}_n^{-1}=h_n(n{h}_n^4{)}^{-1∕2}=o_P(h_n)$, this term is also o_P(h_n).

We next show that ($(n{h}_n^5{)}^{1∕2}{\text{sup}}_{t\in \mathcal{T}}\mid h_n^{-2}{s}_{1,n}(t_2)-f_0^{\prime }(t_2)K_2\mid =o_P(1)$). We have that

$$\begin{gathered} (n{h}_n{)}^{1∕2}{s}_{1,n}(t_2)=(n{h}_n^{-1}{)}^{1∕2}\int (a-t_2)K\left(\frac{a-t_2}{h_n}\right)f_0(a)da \\ +h_n^{-1∕2}\iint (a-t_2)K\left(\frac{a-t_2}{h_n}\right){\mathbb{G}}_n(dy,da). \end{gathered}$$

By the change of variables u = (a − t₂)/h_n, the first term equals

$$\begin{gathered} (n{h}_n^3{)}^{1∕2}\int uK(u)f_0(t_2+h_{n}u)du \\ =(n{h}_n^3{)}^{1∕2}\int uK(u)[f_0(t_2+h_{n}u)-f_0(t)-(h_{n}u)f_0^{\prime }(t_2)]du \\ +(n{h}_n^5{)}^{1∕2}{f}_0^{\prime }(t_2)K_2 \\ =(n{h}_n^5{)}^{1∕2}\int uK(u)h_n^{-1}{R}_f^{(1)}((t_1,t_2),h_{n}u)du+(n{h}_n^5{)}^{1∕2}{f}_0^{\prime }(t_2)K_2. \end{gathered}$$

By the assumed uniform negligibility of $R_f^{(1)}$ and since h_n = O(n^−1/5), the first term tends to zero in probability uniformly over $t\in \mathcal{T}$.

Turning to the second term in s_1,n(t₂), we will apply Theorem 2.14.1 of VW to obtain a tail bound for the supremum of this empirical process over the onedimensional class indexed by t₂. We note that, since K is bounded by some $\overline{K}$ and supported on [−1, 1],

$$\mid (a-t_2)K\left(\frac{a-t_2}{h_n}\right)\mid \le \overline{K}\mid a-t_2\mid I(\mid a-t_2\mid \le h_n)\le \overline{K}{h}_n.$$

Therefore, the class of functions

$$\left\{(y,a)\mapsto (a-t_2)K\left(\frac{a-t_2}{h_n}\right):(t_1,t_2)\in \mathcal{T}\right\}$$

has envelope $\overline{K}{h}_n$. Furthermore, since (y, a) ↦ (a − t₂) and K are both uniformly bounded VC classes of functions, and K is bounded, the class of functions possesses finite entropy integral. Hence, we have that

$$E_0\left[\underset{(t_1,t_2)\in \mathcal{T}}{\text{sup}}\mid h_n^{-1∕2}\iint (a-t_2)K\left(\frac{a-t_2}{h_n}\right){\mathbb{G}}_n(dy,da)\mid \right]\le C^{\prime }{h}_n^{1∕2}\stackrel{}{\to }0.$$

We now have that $(n{h}_n{)}^{1∕2}{\text{sup}}_{t\in \mathcal{T}}\mid s_{1,n}(t_2)-h_n^2{f}_0^{\prime }(t_2)K_2\mid =o_P(1)$, which implies in particular that

$$\underset{t\in \mathcal{T}}{\text{sup}}\mid s_{1,n}(t_2)\mid =(n{h}_n{)}^{-1∕2}{o}_P(1)+h_n^2{O}_P(1)=O_P\left((n{h}_n{)}^{-1∕2}\right).$$

Next, we show that $(n{h}_n^5{)}^{1∕2}{\text{sup}}_{t\in \mathcal{T}}\mid h_n^{-2}{s}_{2,n}(t_2)-f_0(t_2)K_2\mid =o_P(h_n)$. The proof of this is nearly identical to the preceding proof. We have that

$$\begin{gathered} (n{h}_n{)}^{1∕2}{s}_{2,n}(t_2)=(n{h}_n^{-1}{)}^{1∕2}\int (a-t_2{)}^{2}K\left(\frac{a-t_2}{h_n}\right)f_0(a)da \\ +h_n^{-1∕2}\iint (a-t_2{)}^{2}K\left(\frac{a-t_2}{h_n}\right){\mathbb{G}}_n(dy,da). \end{gathered}$$

By the change of variables u = (a − t₂)/h_n, the first term equals

$$\begin{gathered} (n{h}_n^5{)}^{1∕2}\int u^{2}K(u)f_0(t_2+h_{n}u)du=(n{h}_n^5{)}^{1∕2}{h}_n\int u^{3}K(u)\frac{R_f^{(1)}(t,h_{n}u)}{h_{n}u}du \\ +(n{h}_n^5{)}^{1∕2}{f}_0(t_2)K_2. \end{gathered}$$

By the uniform negligibility of $R_f^{(1)}$, the first term is o_P(h_n) uniformly in t.

Analysis of the second term in s_2,n is analogous to that of s_1,n, except that the envelope function is now $\overline{K}{h}_n^2$, so that the empirical process term is $O_P(h_n^{3∕2})$. We also note that sup_t2 ∣s_2,n(t₂)∣ = O_P ((nh_n)^−1/2).

The above derivations imply that

$$\begin{gathered} (n{h}_n^5{)}^{1∕2}\underset{t\in \mathcal{T}}{\text{sup}}\mid h_n^{-2}{g}_n(t_2)-f_0(t_2{)}^2{K}_2\mid \\ \le (n{h}_n^5{)}^{1∕2}\underset{t\in \mathcal{T}}{\text{sup}}\mid [h_n^{-2}{s}_{2,n}(t_2)-f_0(t_2)K_2]s_{0,n}(t_2)\mid +(n{h}_n{)}^{1∕2}{\left[\underset{t\in \mathcal{T}}{\text{sup}}\mid s_{1,n}(t_2)\mid \right]}^2 \\ +(n{h}_n^5{)}^{1∕2}\underset{t\in \mathcal{T}}{\text{sup}}\mid s_{0,n}(t_2)-f_0(t_2)]f_0(t_2)K_2\mid \\ =o_P(1)O_P(1)+(n{h}_n^5{)}^{1∕2}{o}_P(h_n)+(n{h}_n{)}^{1∕2}{O}_P\left((n{h}_n{)}^{-1}\right)=o_P(1). \end{gathered}$$

We now proceed to the statements in the lemma. We write that

$$\begin{gathered} \mid \frac{s_{n,1}(t_2)}{g_n(t_2)}-\frac{f_0^{\prime }(t_2)}{f_0(t_2{)}^2}\mid =\mid \frac{h_n^{-2}{s}_{n,1}(t_2)}{h_n^{-2}{g}_n(t_2)}-\frac{f_0^{\prime }(t_2)K_2}{f_0(t_2{)}^2{K}_2}\mid \\ =\mid \frac{h_n^{-2}{s}_{n,1}(t_2)-f_0^{\prime }(t_2)K_2}{h_n^{-2}{g}_n(t_2)}-f_0^{\prime }(t_2)K_2\frac{h_n^{-2}{g}_n(t_2)-f_0(t_2{)}^2{K}_2}{h_n^{-2}{g}_n(t_2)f_0(t_2{)}^2{K}_2}\mid \\ \le \frac{\mid h_n^{-2}{s}_{n,1}(t_2)-f_0^{\prime }(t_2)K_2\mid }{h_n^{-2}{g}_n(t_2)}+f_0^{\prime }(t_2)K_2\frac{\mid h_n^{-2}{g}_n(t_2)-f_0(t_2{)}^2{K}_2\mid }{h_n^{-2}{g}_n(t_2)f_0(t_2{)}^2{K}_2}. \end{gathered}$$

Since ${\text{inf}}_{t\in \mathcal{T}}\mid f_0(t_2)\mid >0$, we have that

$$\underset{t\in \mathcal{T}}{\text{sup}}[h_n^{-2}{g}_n(t_2){]}^{-1}=O_P(1)\text{and}\underset{t\in \mathcal{T}}{\text{sup}}[h_n^{-2}{g}_n(t_2)f_0(t_2{)}^2{]}^{-1}=O_P(1),$$

and the result follows.

We omit the proof of the statement about s_n,2, since it is almost identical to the above. For the statement about w_n, by the above calculations, we have that

$$(n{h}_n^5{)}^{1∕2}\underset{(t_1,t_2)\in \mathcal{T}}{\text{sup}}\underset{\mid a-t_2\mid \le h_n}{\text{sup}}\mid h_n^{-2}{w}_n(a,t_2)-w_0(a,t_2)K_2\mid \stackrel{\mathrm{P}}{\to }0.$$

We write that

$$\begin{gathered} \mid \frac{w_n(a,t_2)}{g_n(t_2)}-\frac{w_0(a,t_2)}{f_0(t_2{)}^2}\mid =\mid \frac{h_n^{-2}{w}_n(a,t_2)}{h_n^{-2}{g}_n(t_2)}-\frac{w_0(a,t_2)K_2}{f_0(t_2{)}^2{K}_2}\mid \\ =\mid \frac{h_n^{-2}{w}_n(a,t_2)-w_0(a,t_2)K_2}{h_n^{-2}{g}_n(t_2)}-w_0(a,t_2)\frac{h_n^{-2}{g}_n(t_2)-f_0(t_2{)}^2{K}_2}{h_n^{-2}{g}_n(t_2)f_0(t_2{)}^2}\mid \\ \le [h_n^{-2}{g}_n(t_2){]}^{-1}\mid h_n^{-2}{w}_n(a,t_2)-w_0(a,t_2)K_2\mid \\ +\mid w_0(a,t_2)\mid [h_n^{-2}{g}_n(t_2)f_0(t_2{)}^2{]}^{-1}\mid h_n^{-2}{g}_n(t_2)-f_0(t_2{)}^2{K}_2\mid \end{gathered}$$

and the result follows.

We note that the above implies that

$$\begin{gathered} \underset{\mid t_2-s_2\mid \le \eta }{\text{sup}}\mid s_{1,n}(t_2)-s_{1,n}(s_2)\mid \\ \le 2\underset{t_2}{\text{sup}}\mid s_{1,n}(t_2)-h_n^2{f}_0^{\prime }(t_2)K_2\mid +h_n^2\underset{\mid t_2-s_2\mid \le \eta }{\text{sup}}\mid f_0^{\prime }(t_2)-f_0^{\prime }(s_2)\mid K_2 \\ \le o_P\left((n{h}_n{)}^{-1∕2}\right)+h_n^2\eta , \end{gathered}$$

so that

$$\underset{\mid t_2-s_2\mid \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid s_{1,n}(t_2)-s_{1,n}(s_2)\mid =o_p\left((n{h}_n{)}^{-1∕2}\right).$$

Similarly, we have that sup_{∣t2−s2∣≤η} ∣s_0,n(t₂) − s_0,n(s₂)∣ = o_P (h_n) and

$$\underset{\mid t_2-s_2\mid \le \eta }{\text{sup}}\mid s_{2,n}(t_2)-s_{2,n}(s_2)\mid =o_p\left(h_n(n{h}_n{)}^{-1∕2}\right).$$

Therefore, we find that

$$\begin{gathered} \underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid g_n(t_2)-g_n(s_2)\mid \\ \le \underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid [s_{0,n}(t_2)-s_{0,n}(s_2)]s_{2,n}(s_2)\mid \\ +\underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid s_{0,n}(t_2)[s_{2,n}(t_2)-s_{2,n}(s_2)]\mid \\ +\underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid [s_{1,n}(t_2)-s_{2,n}(s_2)][s_{1,n}(t_2)-s_{1,n}(s_2)]\mid \\ \lesssim o_P(h_n)O_P\left((n{h}_n{)}^{-1∕2}\right)+O_P(1)o_P\left(h_n(n{h}_n{)}^{-1∕2}\right) \\ =o_P\left(h_n(n{h}_n{)}^{-1∕2}\right). \end{gathered}$$

We can now write that

$$\begin{gathered} \underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid \frac{s_{1,n}(t_2)}{g_n(t_2)}-\frac{s_{1,n}(s_2)}{g_n(s_2)}\mid \\ \le h_n^{-2}\underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid \frac{s_{1,n}(t_2)-s_{1,n}(s_2)}{h_n^{-2}{g}_n(t_2)}\mid \\ +h_n^{-4}\underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid s_{1,n}(s_2)\frac{g_n(t_2)-g_n(s_2)}{h_n^{-2}{g}_n(t_2)h_n^{-2}{g}_n(s_2)}\mid \\ =h_n^{-2}{o}_P\left((n{h}_n{)}^{-1∕2}\right)+h_n^{-4}{O}_P\left((n{h}_n{)}^{-1∕2}\right)o_P\left(h_n(n{h}_n{)}^{-1∕2}\right) \\ =o_P\left((n_n^5{)}^{-1∕2}\right) \end{gathered}$$

and

$$\begin{gathered} \underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid \frac{s_{2,n}(t_2)}{g_n(t_2)}-\frac{s_{2,n}(s_2)}{g_n(s_2)}\mid \\ \le h_n^{-2}\underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid \frac{s_{2,n}(t_2)-s_{2,n}(s_2)}{h_n^{-2}{g}_n(t_2)}\mid \\ +h_n^{-4}\underset{\Vert t-s\Vert \le \delta ∕(n{h}_n{)}^{-1∕2}}{\text{sup}}\mid s_{2,n}(s_2)\frac{g_n(t_2)-g_n(s_2)}{h_n^{-2}{g}_n(t_2)h_n^{-2}{g}_n(s_2)}\mid \\ =h_n^{-2}{o}_P\left(h_n(n{h}_n{)}^{-1∕2}\right)+h_n^{-4}{O}_P\left((n{h}_n{)}^{-1∕2}\right)o_P\left(h_n(n{h}_n{)}^{-1∕2}\right) \\ =o_P\left((n_n^4{)}^{-1}\right). \end{gathered}$$

We can now prove Proposition 1.

Proof of Proposition 1. We define

$$\begin{gathered} m_{1,n}(t_1,t_2)≔h_n^{-1}\iint [{\theta }_0(t_1,a)-{\theta }_0(t_1,t_2)]\frac{w_n(a,t_2)}{g_n(t_2)}K\left(\frac{a-t_2}{h_n}\right){\mathbb{P}}_n(dy,da) \\ {m}_{2,n}(t_1,t_2)≔h_n^{-1}\iint [I(y\le t_1)-{\theta }_0(t_1,a)]\frac{w_n(a,t_2)}{g_n(t_2)}K\left(\frac{a-t_2}{h_n}\right){\mathbb{P}}_n(dy,da). \end{gathered}$$

Then, we have that θ_n(t₁, t₂) − θ₀(t₁, t₂) = m_1,n(t₁, t₂) + m_2,n(t₁, t₂). We note that, since E₀ [I(Y ≤ t₁) ∣ A = a] = θ₀(t₁, a), (nh_n)^1/2m_2,n(t₁, t₂) equals

$$\begin{gathered} h_n^{-1∕2}\iint [I(y\le t_1)-{\theta }_0(t_1,a)]\frac{w_n(a,t_2)}{g_n(t_2)}K\left(\frac{a-t_2}{h_n}\right){\mathbb{G}}_n(dy,da) \\ =h_n^{-1∕2}\left[\frac{s_{2,n}(t_2)}{g_n(t_2)}{\mathbb{G}}_n{v}_{n,t}-\frac{s_{1,n}(t_2)}{g_n(t_2)}{\mathbb{G}}_n({\ell }_t{v}_{n,t})\right]. \end{gathered}$$

Therefore, we can write that

$$\begin{gathered} (n{h}_n{)}^{1∕2}[{\theta }_n(t_1,t_2)-{\theta }_0(t_1,t_2)]-(n{h}_n^5{)}^{1∕2}\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)K_2-R_n(t_1,t_2) \\ =(n{h}_n{)}^{1∕2}{m}_{1,n}(t_1,t_2)-(n{h}_n^5{)}^{1∕2}\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)K_2. \end{gathered}$$

We now proceed to analyze m_1,n. We have that (nh_n)^1/2 m_1,n(t₁, t₂) equals

$$\begin{gathered} (n{h}_n^{-1}{)}^{1∕2}\int [{\theta }_0(t_1,a)-{\theta }_0(t_1,t_2)]\frac{w_n(a,t_2)}{g_n(t_2)}K\left(\frac{a-t_2}{h_n}\right)f_0(a)da \\ +h_n^{-1∕2}\iint [{\theta }_0(t_1,a)-{\theta }_0(t_1,t_2)]\frac{w_n(a,t_2)}{g_n(t_2)}K\left(\frac{a-t_2}{h_n}\right){\mathbb{G}}_n(dy,da). \end{gathered}$$

The second term in m_1,n may be further decomposed as

$$h_n^{-1∕2}\frac{s_{2,n}(t_2)}{g_n(t_2)}{\mathbb{G}}_n{\gamma }_{t,n}-h_n^{-1∕2}\frac{s_{1,n}(t_2)}{g_n(t_2)}{\mathbb{G}}_n({\ell }_t{\gamma }_{t,n})$$

with ${\gamma }_{t,n}(y,a)≔[{\theta }_0(t_1,a)-{\theta }_0(t_1,t_2)]K\left(\frac{a-t_2}{h_n}\right)$ and ℓ_t(y, a) := a − t₂. By Lemma 4, we have that

$$\underset{t\in \mathcal{T}}{\text{sup}}\mid \frac{s_{2,n}(t_2)}{g_n(t_2)}\mid =O_p\left((n{h}_n^5{)}^{-1∕2}\right),$$

and similarly for s_1,n. We will use Theorem 2.14.2 of VW to obtain bounds for ${\text{sup}}_{t\in \mathcal{T}}\mid {\mathbb{G}}_n{\gamma }_{t,n}\mid$ and ${\text{sup}}_{t\in \mathcal{T}}\mid {\mathbb{G}}_n({\ell }_t{\gamma }_{t,n})\mid$. We first note that, since K is bounded and supported on [−1, 1] and θ₀ is Lipschitz on $\mathcal{T}$, ${\text{sup}}_{t\in \mathcal{T}}\mid {\gamma }_{t,n}\mid \lesssim h_n$ and ${\text{sup}}_{t\in \mathcal{T}}\mid {\ell }_t{\gamma }_{t,n}\mid \lesssim h_n^2$. These will be our envelope functions for these classes. Next, since K is Lipschitz, we have that

$$\begin{gathered} \mid {\gamma }_{t,n}-{\gamma }_{s,n}\mid \le \mid [{\theta }_0(t_1,a)-{\theta }_0(s_1,a)]-[{\theta }_0(t_1,t_2)-{\theta }_0(s_1,s_2)]\mid K\left(\frac{a-s_2}{h_n}\right) \\ +\mid {\theta }_0(t_1,a)-{\theta }_0(t_1,t_2)\mid \mid K\left(\frac{a-t_2}{h_n}\right)-K\left(\frac{a-s_2}{h_n}\right)\mid \\ \lesssim \mid t_1-s_1\mid +\Vert t-s\Vert +\mid t_2-s_2\mid h_n^{-1}\lesssim \Vert t-s\Vert h_n^{-1}. \end{gathered}$$

Therefore, by VW Theorem 2.7.11, we have

$$N_{[]}(2\epsilon h_n^{-1},{\mathcal{G}}_n,L_2(P_0))\lesssim N(\epsilon ,\mathcal{T},\Vert \cdot \Vert )\lesssim {\epsilon }^{-2},$$

where ${\mathcal{G}}_n≔\{{\gamma }_{n,t}:t\in \mathcal{T}\}$. Thus, by Theorem 2.14.2 of VW,

$$\begin{gathered} \underset{t\in \mathcal{T}}{\text{sup}}\mid {\mathbb{G}}_n{\gamma }_{n,t}\mid \lesssim {\int }_0^1[N_{[]}(\epsilon h_n,{\mathcal{G}}_n,L_2(P_0)){]}^{1∕2}d\epsilon h_n\lesssim {\int }_0^1[-\log (\epsilon h_n^2){]}^{1∕2}d\epsilon h_n \\ =h_n^{-1}{\int }_0^{h_n^2}(-\log \epsilon {)}^{1∕2}d\epsilon \lesssim h_n^{-1}\{h_n^2[\log (h_n^{-2}){]}^{1∕2}\}\lesssim h_n(\log h_n^{-1}), \end{gathered}$$

where we have used the fact that ${\int }_0^z(\log x^{-1}{)}^{1∕2}dx\lesssim z(\log z^{-1}{)}^{1∕2}$ for all z small enough. A similar argument applies to ${\text{sup}}_{t\in \mathcal{T}}\mid {\mathbb{G}}_n({\ell }_t{\gamma }_{n,t})\mid$. We thus have that the second summand in m_1,n is bounded above up to a constant not depending on n and uniformly in t by

$$h_n^{-1∕2}{O}_P\left((n{h}_n^5{)}^{-1∕2}\right)h_n(\log h_n^{-1}{)}^{1∕2}=O_P\left({\left(\frac{n{h}_n^4}{\log h_n^{-1}}\right)}^{-1∕2}\right),$$

which is o_P (1) since $n{h}_n^4∕(\log h_n^{-1})\to \infty$.

By the change of variables u = (a − t₂)/h_n, the first term in m_1,n equals

$$\begin{gathered} (n{h}_n{)}^{1∕2}\int [{\theta }_0(t_1,t_2+h_{n}u)-{\theta }_0(t_1,t_2)]\frac{w_n(t_2+h_{n}u,t_2)}{g_n(t_2)}K(u)f_0(t_2+h_{n}u)du \\ =(n{h}_n{)}^{1∕2}\int \left[R_{\theta }^{(2)}(t,h_{n}u)+{\theta }_{0,t_2}^{\prime }(t_1,t_2)(h_{n}u)+\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)(h_{n}u{)}^2\right] \\ \cdot \left[R_f^{(1)}(t_2,h_{n}u)+f_0(t_2)+f_0^{\prime }(t_2)(h_{n}u)\right]\frac{w_n(t_2+h_{n}u,t_2)}{g_n(t_2)}K(u)du. \end{gathered}$$

Expanding the product, this is equal to

$$\begin{gathered} (n{h}_n{)}^{1∕2}\int (h_{n}u)[{\theta }_{0,t_2}^{\prime }(t_1,t_2+\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)(h_{n}u)][f_0(t_2)+f_0^{\prime }(t_2)h_{n}u] \\ \cdot \frac{w_n(t_2+h_{n}u,t_2)}{g_n(t_2)}K(u)du \\ +(n{h}_n{)}^{1∕2}\int R_{\theta }^{(2)}(t,h_{n}u)[f_0(t_2)+f_0^{\prime }(t_2)h_{n}u]\frac{w_n(t_2+h_{n}u,t_2)}{g_n(t_2)}K(u)du \\ +(n{h}_n{)}^{1∕2}\int R_f^{(1)}(t_2,h_{n}u)(h_{n}u)[{\theta }_{0,t_2}^{\prime }(t_1,t_2)+\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)h_{n}u] \\ \cdot \frac{w_n(t_2+h_{n}u,t_2)}{g_n(t_2)}K(u)du \\ +(n{h}_n{)}^{1∕2}\int R_{\theta }^{(2)}(t,h_{n}u)R_f^{(1)}(t_2,h_{n}u)\frac{w_n(t_2+h_{n}u,t_2)}{g_n(t_2)}K(u)du. \end{gathered}$$

By the assumed negligibility of $R_{\theta }^{(2)}$ and $R_f^{(1)}$ as well as Lemma 4, the second through fourth summands tend to zero in probability uniformly over $\mathcal{T}$. The first term equals

$$\begin{gathered} \int f_0^{\prime }(t_2)[{\theta }_{0,t_2}^{\prime }(t_1,t_2)+\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)(h_{n}u)] \\ \cdot (n{h}_n^5{)}^{1∕2}\left[\frac{w_n(t_2+h_{n}u,t_2)}{g_n(t_2)}-\frac{w_0(t_2+h_{n}u,t_2)}{f_0(t_2{)}^2}\right]u^{2}K(u)du \\ +(n{h}_n^5{)}^{1∕2}\int f_0^{\prime }(t_2)[{\theta }_{0,t_2}^{\prime }(t_1,t_2)+\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)(h_{n}u)] \\ \cdot \frac{w_0(t_2+h_{n}u,t_2)}{f_0(t_2{)}^2}{u}^{2}K(u)du \\ +(n{h}_n^3{)}^{1∕2}\int f_0^{\prime }(t_2)[{\theta }_{0,t_2}^{\prime }(t_1,t_2)+\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)(h_{n}u)] \\ \cdot \frac{w_n(t_2+h_{n}u,t_2)}{g_n(t_2)}uK(u)du. \end{gathered}$$

By Lemma 4, the first summand tends to zero uniformly over $\mathcal{T}$. By symmetry of K, the second plus third summands simplifies to

$$\begin{gathered} (n{h}_n^5{)}^{1∕2}\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)K_2+(n{h}_n^5{)}^{1∕2}\left[\frac{s_{2,n}(t_2)}{g_n(t_2)}-\frac{1}{f_0(t_2)}\right]f_0(t_2)\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)K_2 \\ -(n{h}_n^5{)}^{1∕2}\left[\frac{s_{1,n}(t_2)}{g_n(t_2)}-\frac{f_0^{\prime }(t_2)}{f_0(t_2{)}^2}\right]{\theta }_{0,t_2}^{\prime }(t_1,t_2)f_0(t_2)K_2. \end{gathered}$$

Once again, the second and third summands tend to zero uniformly over $\mathcal{T}$ by Lemma 4. We have now shown that

$$\underset{t\in \mathcal{T}}{\text{sup}}\mid (n{h}_n{)}^{1∕2}{m}_{1,n}(t_1,t_2)-(n{h}_n^5{)}^{1∕2}\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)K_2\mid \stackrel{\mathrm{P}}{\to }0,$$

which completes the proof. □

Finally, we prove Proposition 2.

Proof of Proposition 2. Since ${\theta }_{0,t_2}^{″}$ is uniformly continuous and $n{h}_n^5=O(1)$,

$$\underset{\Vert t-s\Vert \le \delta ∕r_n}{\text{sup}}\mid (n{h}_n^5{)}^{1∕2}\frac{1}{2}{\theta }_{0,t_2}^{″}(t_1,t_2)K_2-(n{h}_n^5{)}^{1∕2}\frac{1}{2}{\theta }_{0,t_2}^{″}(s_1,s_2)K_2\mid \stackrel{\mathrm{P}}{\to }0.$$

Therefore, it only remains to show that ${\text{sup}}_{\Vert t-s\Vert \le \delta ∕r_n}\mid R_n(t)-R_n(s)\mid \stackrel{\mathrm{P}}{\to }0$. Recalling that ℓ_t(y, a) := a − t₂ and

$${\nu }_{n,t}(y,a)≔[I(y\le t_1)-{\theta }_0(t_1,a)]K\left(\frac{a-t_2}{h_n}\right),$$

we have that R_n(t) − R_n(s) equals

$$\begin{gathered} \left[\frac{s_{2,n}(t_2)}{g_n(t_2)}-\frac{s_{2,n}(s_2)}{g_n(s_2)}\right]{\mathbb{G}}_n{\nu }_{n,t}-\left[\frac{s_{1,n}(t_2)}{g_n(t_2)}-\frac{s_{1,n}(s_2)}{g_n(s_2)}\right]{\mathbb{G}}_n({\ell }_t{\nu }_{n,t}) \\ +\frac{s_{2,n}(s_2)}{g_n(s_2)}{\mathbb{G}}_n({\nu }_{n,t}-{\nu }_{n,s})-\frac{s_{1,n}(s_2)}{g_n(s_2)}{\mathbb{G}}_n({\ell }_t{\nu }_{n,t}-{\ell }_s{\nu }_{n,s}). \end{gathered}$$

Focusing first on ${\mathbb{G}}_n{\nu }_{n,t}$, we have ${\mathbb{G}}_n{\nu }_{n,t}={\mathbb{G}}_n{\nu }_{n,t,1}-{\mathbb{G}}_n{\nu }_{n,t,2}$ for

$${\nu }_{n,t,1}(y,a)=I(y\le t_1)K\left(\frac{a-t_2}{h_n}\right)\text{and}{\nu }_{n,t,2}(y,a)={\theta }_0(t_1,a)\left(\frac{a-t_2}{h_n}\right).$$

The classes

$$\{I(y\le t_1):t\in \mathcal{T}\}\text{and}\left\{K\left(\frac{a-t_2}{h_n}\right):t\in \mathcal{T}\right\}$$

are both uniformly bounded above and VC. Therefore, the uniform covering numbers of the class

$$\left\{I(y\le t_1)K\left(\frac{a-t_2}{h_n}\right):t\in \mathcal{T}\right\}$$

are bounded up to a constant by ε^−V for some V < ∞, so that the uniform entropy integral satisfies

$$J(\eta ,{\mathcal{G}}_{n,1})\lesssim \eta {\left(\log {\eta }^{-1}\right)}^{1∕2}$$

for all η small enough, where ${\mathcal{G}}_{n,1}≔\{{\nu }_{n,t,1}:t\in \mathcal{T}\}$. We also have P₀ (ν_n,t,1)² ≲ h_n for all $t\in \mathcal{T}$ and all n large enough. Thus, Theorem 2.1 of van der Vaart and Wellner (2011) implies that

$$\underset{t\in \mathcal{T}}{\text{sup}}\mid {\mathbb{G}}_n{\nu }_{n,t,1}\mid \lesssim h_n^{1∕2}{\left(\log h_n^{-1}\right)}^{1∕2}+n^{-1∕2}\log h_n^{-1}.$$

For ${\mathbb{G}}_n{\nu }_{n,t,2}$, we have that

$$\mid {\nu }_{n,t,2}(y,a)-{\nu }_{n,s,2}(y,a)\mid \lesssim \Vert t-s\Vert (1+h_n^{-1})\le h_n^{-1}\Vert t-s\Vert$$

for all n large enough and all (y, a). We can therefore apply Theorem 2.7.11 of VW to conclude that $N_{[]}(2\epsilon h_n^{-1},{\mathcal{G}}_{n,2},L_2(P_0))\lesssim {\epsilon }^{-2}$ for all ε small enough, where ${\mathcal{G}}_{n,2}=\{{\nu }_{n,t,2}:t\in \mathcal{T}\}$}, which implies that $N_{[]}(\epsilon ,{\mathcal{G}}_{n,2},L_2(P_0))\lesssim (\epsilon h_n{)}^{-2}$. Thus, we have that

$$J_{[]}(\eta ,{\mathcal{G}}_{n,2})\lesssim \eta {\left[\log (\eta h_n{)}^{-1}\right]}^{1∕2}.$$

Since P₀ (ν_n,t,2)² ≲ h_n as well, by Lemma 3.4.2 of VW, we then have

$$E_{P_0}\underset{t\in \mathcal{T}}{\text{sup}}\mid {\mathbb{G}}_n{\nu }_{n,t,2}\mid \lesssim h_n^{1∕2}{\left(\log h_n^{-1}\right)}^{1∕2}+n^{-1∕2}\log h_n^{-1}.$$

Combining these two bounds with the last statement of Lemma 4 yields

$$\begin{gathered} h_n^{-1∕2}\underset{t\in \mathcal{T}}{\text{sup}}\mid \left[\frac{s_{2,n}(t_2)}{g_n(t_2)}-\frac{s_{2,n}(s_2)}{g_n(s_2)}\right]{\mathbb{G}}_n{\nu }_{n,t}\mid \\ \lesssim h_n^{-1∕2}{o}_P\left((n{h}_n^4{)}^{-1}\right)O_P\left(h_n^{1∕2}(\log h_n^{-1}{)}^{1∕2}+n^{-1∕2}\log h_n^{-1}\right) \\ =o_P(1){\left[\frac{n{h}_n^4}{(\log h_n^{-1}{)}^{1∕2}}\right]}^{-1}+o_P(1){\left(n{h}_n^{11∕3}\right)}^{-3∕2}{h}_n\log h_n^{-1}. \end{gathered}$$

Both terms tend to zero.

The analysis for ${\mathbb{G}}_n({\ell }_t{\nu }_{n,t})$ is very similar. In this case, we have $P_0({\ell }_t{\nu }_{n,t}{)}^2\lesssim h_n^3$, so that, using the same approach as above, we get

$$E_{P_0}\underset{t\in \mathcal{T}}{\text{sup}}\mid {\mathbb{G}}_n({\ell }_t{\nu }_{n,t})\mid \lesssim h_n^{3∕2}{\left(\log h_n^{-1}\right)}^{1∕2}+n^{-1∕2}(\log h_n^{-1}{)}^{1∕2}$$

and therefore, in view of Lemma 4,

$$\begin{gathered} h_n^{-1∕2}\underset{t\in \mathcal{T}}{\text{sup}}\mid \left[\frac{s_{1,n}(t_2)}{g_n(t_2)}-\frac{s_{1,n}(s_2)}{g_n(s_2)}\right]{\mathbb{G}}_n({\ell }_t{\nu }_{n,t})\mid \\ \lesssim h_n^{-1∕2}{o}_P\left((n{h}_n^5{)}^{-1∕2}\right)O_P\left(h_n^{3∕2}(\log h_n^{-1}{)}^{1∕2}+n^{-1∕2}\log h_n^{-1}{)}^{1∕2}\right) \\ =o_P(1)(n{h}_n^4{)}^{-1∕2}(h_n\log h_n^{-1}{)}^{1∕2}+o_P(1)(n{h}_n^3{)}^{-1∕2}(h_n\log h_n^{-1}{)}^{1∕2}, \end{gathered}$$

which goes to zero in probability.

It remains to bound

$$\underset{\Vert t-s\Vert <\delta ∕r_n}{\text{sup}}\mid {\mathbb{G}}_n({\nu }_{n,t}-{\nu }_{n,s})\mid \text{and}\underset{\Vert t-s\Vert <\delta ∕r_n}{\text{sup}}\mid {\mathbb{G}}_n({\ell }_t{\nu }_{n,t}-{\ell }_s{\nu }_{n,s})\mid .$$

For the former, we work on the terms ${\mathbb{G}}_n({\nu }_{n,t,1}-{\nu }_{n,s,1})$ and ${\mathbb{G}}_n({\nu }_{n,t,2}-{\nu }_{n,s,2})$ separately. For the first of these, we let ${\mathcal{F}}_{n,\delta ,2}≔\{{\nu }_{n,t,1}-{\nu }_{n,s,1}:\Vert t-s\Vert \le \delta ∕r_n\}$. We have that ∥ν_n,t,1 − ν_n,s,1∥_P0,2 is bounded above by

$$\begin{gathered} {\left[E_{P_0}\left\{[I(Y\le t_1)-I(Y\le s_1){]}^{2}K{\left(\frac{A-s_2}{h_n}\right)}^2\right\}\right]}^{1∕2} \\ +{\left[E_{P_0}\left\{[I(Y\le t_1){\left[K\left(\frac{A-t_2}{h_n}\right)-K\left(\frac{A-s_2}{h_n}\right)\right]}^2\right\}\right]}^{1∕2} \\ \lesssim (E_{P_0}\{I(s_1<Y\le t_1)I(\mid A-s_2\mid \le h_n)\}{)}^{1∕2}+h_n^{-1}\mid t_2-s_2\mid \\ \lesssim h_n^{1∕2}\mid t_1-s_1{\mid }^{1∕2}+h_n^{-1}\mid t_2-s_2\mid . \end{gathered}$$

Therefore, it follows that

$$\underset{f\in {\mathcal{F}}_{n,\delta ,1}}{\text{sup}}(P_0{f}^2{)}^{1∕2}\lesssim (n{h}_n^{-1}{)}^{-1∕4}+(n{h}_n^3{)}^{-1∕2}\lesssim (n{h}_n^3{)}^{-1∕2}$$

for all n large enough. In addition, ${\mathcal{F}}_{n,\delta ,1}$ has uniform covering numbers bounded up to a constant by ε^−V for all n and δ because the classes {$I(y\le t_1):t\in \mathcal{T}$} and

$$\left\{K\left(\frac{a-t_2}{h_n}\right):t\in \mathcal{T}\right\}$$

are VC. Therefore, $J(\eta ,{\mathcal{F}}_{n,\delta ,1})\lesssim \eta (\log {\eta }^{-1}{)}^{1∕2}$ for all η small enough. Thus, Theorem 2.1 of VW implies that

$$E_{P_0}\underset{\Vert t-s\Vert \le \delta ∕r_n}{\text{sup}}\mid {\mathbb{G}}_n({\nu }_{n,t,1}-{\nu }_{n,s,1})\mid \lesssim {\left[\frac{\log (n{h}_n^3)}{n{h}_n^3}\right]}^{1∕2}+\frac{\log (n{h}_n^3)}{n^{1∕2}}.$$

Turning to ${\mathbb{G}}_n({\nu }_{n,t,2}-{\nu }_{n,s,2})$, we analogously define

$${\mathcal{F}}_{n,\delta ,2}≔\{{\nu }_{n,t,2}-{\nu }_{n,s,2}:\Vert t-s\Vert \le \delta ∕r_n\}.$$

By the Lipschitz property of θ₀ and K, we have that

$$\mid {\theta }_0(t_1,a)K\left(\frac{a-t_2}{h_n}\right)-{\theta }_0(s_1,a)K\left(\frac{a-s_2}{h_n}\right)\mid \lesssim h_n^{-1}\Vert t-s\Vert .$$

Therefore, up to a constant, an envelope function F_n,δ,2 for ${\mathcal{F}}_{n,\delta ,2}$ is given by $h_n^{-1}\delta ∕r_n\lesssim (n{h}_n^3{)}^{-1∕2}$. Next, we have, for any (t, s) and (t′, s′) in ${\mathcal{T}}^2$,

$$\begin{gathered} \mid \left[{\theta }_0(t_1,a)K\left(\frac{a-t_2)}{h_n}\right)-{\theta }_0(s_1,a)K\left(\frac{a-s_2}{h_n}\right)\right]\phantom{\mid } \\ -\phantom{\mid }\left[{\theta }_0(t_1^{\prime },a)K\left(\frac{a-t_2^{\prime }}{h_n}\right)-{\theta }_0(s_1^{\prime },a)K\left(\frac{a-s_2^{\prime }}{h_n}\right)\right]\mid \\ \le \mid {\theta }_0(t_1,a)-{\theta }_0(t_1^{\prime },a)\mid K\left(\frac{a-t_2^{\prime }}{h_n}\right) \\ +\mid {\theta }_0(t_1,a)\mid \mid K\left(\frac{a-t_2}{h_n}\right)-K\left(\frac{a-t_2^{\prime }}{h_n}\right)\mid \\ +\mid {\theta }_0(s_1,a)-{\theta }_0(s_1^{\prime },a)\mid K\left(\frac{a-s_2^{\prime }}{h_n}\right)+\mid {\theta }_0(s_1,a)\mid K\left(\frac{a-s_2}{h_n}\right)-K\left(\frac{a-s_2^{\prime }}{h_n}\right)\mid \\ \lesssim \mid t_1-t_1^{\prime }\mid +h_n^{-1}\mid t_2-t_2^{\prime }\mid +\mid s_1-s_1^{\prime }\mid +h_n^{-1}\mid s_2-s_2^{\prime }\mid \lesssim h_n^{-1}\Vert (t,s)-(t^{\prime },s^{\prime }){\Vert }_{{\mathcal{T}}^2} \end{gathered}$$

with $\Vert (t,s)-(t^{\prime },s^{\prime }){\Vert }_{{\mathcal{T}}^2}≔\max \{\Vert t-s\Vert ,\Vert t^{\prime }-s^{\prime }\Vert \}$. Therefore, by Theorem 2.7.11 of VW, we have that

$$N_{[]}(2\epsilon h_n^{-1},{\mathcal{F}}_{n,\delta ,2},L_2(P_0))\le N(\epsilon ,{\mathcal{U}}_{\delta ∕r_n},\Vert \cdot {\Vert }_{{\mathcal{T}}^2}),$$

where ${\mathcal{U}}_{\delta ∕r_n}≔\{(t,s)\in {\mathcal{T}}^2:\Vert t-s\Vert \le \delta ∕r_n\}$. Since ${\mathcal{U}}_{\delta ∕r_n}\subseteq {\mathcal{T}}^2$, we trivially have that $N(\epsilon ,{\mathcal{U}}_{\delta ∕r_n},\Vert \cdot {\Vert }_{{\mathcal{T}}^2})\lesssim {\epsilon }^{-4}$. Thus, it follows that

$$N_{[]}\left(\epsilon (n{h}_n^3{)}^{-1∕2},{\mathcal{F}}_{n,\delta ,2},L_2(P_0)\right)\lesssim {\left[\epsilon (n{h}_n{)}^{-1∕2}\right]}^{-4}.$$

Therefore, Theorem 2.14.2 of VW implies that

$$\begin{gathered} E_{P_0}\underset{\Vert t-s\Vert \le \delta ∕r_n}{\text{sup}}\mid {\mathbb{G}}_n({\nu }_{n,t,2}-{\nu }_{n,s,2})\mid \\ \lesssim (n{h}_n^3{)}^{-1∕2}{\int }_0^1{\left\{\log {\left[\epsilon (n{h}_n{)}^{-1∕2}\right]}^{-1}\right\}}^{1∕2}d\epsilon \\ =(n{h}_n^3{)}^{-1∕2}(n{h}_n{)}^{1∕2}{\int }_0^{(n{h}_n{)}^{-1∕2}}(\log u^{-1}{)}^{1∕2}du\lesssim (n{h}_n^3{)}^{-1∕2}[\log (n{h}_n){]}^{1∕2}. \end{gathered}$$

We now have that

$$\begin{gathered} h_n^{-1∕2}\underset{\Vert t-s\Vert \le \delta ∕r_n}{\text{sup}}\mid \frac{s_{2,n}(s_2)}{g_n(s_2)}{\mathbb{G}}_n({\nu }_{n,t}-{\nu }_{n,s})\mid \lesssim h_n^{-1∕2}{O}_P\left((n{h}_n^5{)}^{-1∕2}\right)O_P\left((n{h}_n^3{)}^{-1∕2}\right)[\log (n{h}_n^3){]}^{1∕2}+n^{-1∕2}\log \left(n{h}_n^3)\right) \\ =O_P(1)\left\{(n{h}_n^{9∕2}{)}^{-1}[\log (n{h}_n^3){]}^{1∕2}+(n{h}_n^3{)}^{-1}\log (n{h}_n^3)\right\}. \end{gathered}$$

Both terms tend to zero in probability.

We can address ${\text{sup}}_{\Vert t-s\Vert <\delta ∕r_n}\mid {\mathbb{G}}_n({\ell }_t{\nu }_{n,t}-{\ell }_s{\nu }_{n,s})\mid$ in a very similar manner. As before, we work on terms ${\mathbb{G}}_n({\ell }_t{\nu }_{n,t,1}-{\ell }_s{\nu }_{n,s,1})$ and ${\mathbb{G}}_n({\ell }_t{\nu }_{n,t,2}-{\ell }_s{\nu }_{n,s,2})$ separately. It is straightforward to see that the same line of reasoning as used above applies to each of these terms as well, yielding the same negligibility. □