Causal Isotonic Regression

Abstract

In observational studies, potential confounders may distort the causal relationship between an exposure and an outcome. However, under some conditions, a causal dose-response curve can be recovered using the G-computation formula. Most classical methods for estimating such curves when the exposure is continuous rely on restrictive parametric assumptions, which carry significant risk of model misspecification. Nonparametric estimation in this context is challenging because in a nonparametric model these curves cannot be estimated at regular rates. Many available nonparametric estimators are sensitive to the selection of certain tuning parameters, and performing valid inference with such estimators can be difficult. In this work, we propose a nonparametric estimator of a causal dose-response curve known to be monotone. We show that our proposed estimation procedure generalizes the classical least-squares isotonic regression estimator of a monotone regression function. Specifically, it does not involve tuning parameters, and is invariant to strictly monotone transformations of the exposure variable. We describe theoretical properties of our proposed estimator, including its irregular limit distribution and the potential for doubly-robust inference. Furthermore, we illustrate its performance via numerical studies, and use it to assess the relationship between BMI and immune response in HIV vaccine trials.

1. Introduction

1.1. Motivation and literature review

Questions regarding the causal effect of an exposure on an outcome are ubiquitous in science. If investigators are able to carry out an experimental study in which they randomly assign a level of exposure to each participant and then measure the outcome of interest, estimating a causal effect is generally straightforward. However, such studies are often not feasible, and data from observational studies must be relied upon instead. Assessing causality is then more difficult, in large part because of potential confounding of the relationship between exposure and outcome. Many nonparametric methods have been proposed for drawing inference about a causal effect using observational data when the exposure of interest is either binary or categorical – these include, among others, inverse probability weighted (IPW) estimators (Horvitz and Thompson, 1952), augmented IPW estimators (Scharfstein et al., 1999; Bang and Robins, 2005), and targeted minimum loss-based estimators (TMLE) (van der Laan and Rose, 2011).

In practice, many exposures are continuous, in the sense that they may take any value in an interval. A common approach to dealing with such exposures is to simply discretize the interval into two or more regions, thus returning to the categorical exposure setting. However, it is frequently of scientific interest to learn the causal dose-response curve, which describes the causal relationship between the exposure and outcome across a continuum of the exposure. Much less attention has been paid to continuous exposures. Robins (2000) and Zhang et al. (2016) studied this problem using parametric models, and Neugebauer and van der Laan (2007) considered inference on parameters obtained by projecting a causal dose-response curve onto a parametric working model. Other authors have taken a nonparametric approach instead. Rubin and van der Laan (2006) and Díaz and van der Laan (2011) discussed nonparametric estimation using flexible data-adaptive algorithms. Kennedy et al. (2017) proposed an estimator based on local linear smoothing. Finally, van der Laan et al. (2018) recently presented a general framework for inference on parameters that fail to be smooth enough as a function of the data-generating distribution and for which regular root-n estimation theory is therefore not available. This is indeed the case for the causal dose-response curve, and van der Laan et al. (2018) discussed inference on such a parameter as a particular example.

Despite a growing body of literature on nonparametric estimation of causal dose-response curves, to the best of our knowledge, existing methods do not permit valid large-sample inference and may be sensitive to the selection of certain tuning parameters. For instance, smoothing-based methods are often sensitive to the choice of a kernel function and bandwidth, and these estimators typically possess non-negligible asymptotic bias, which complicates the task of performing valid inference.

In many settings, it may be known that the causal dose-response curve is monotone in the exposure. For instance, exposures such as daily exercise performed, cigarettes smoked per week, and air pollutant levels are all known to have monotone relationships with various health outcomes. In such cases, an extensive literature suggests that monotonicity may be leveraged to derive estimators with desirable properties – the monograph of Groeneboom and Jongbloed (2014) provides a comprehensive overview. For example, in the absence of confounding, isotonic regression may be employed to estimate the causal dose-response curve (Barlow et al., 1972). The isotonic regression estimator does not require selection of a kernel function or bandwidth, is invariant to strictly increasing transformations of the exposure, and upon centering and scaling by n^−1/3, converges in law pointwise to a symmetric limit distribution with mean zero (Brunk, 1970). The latter property is useful since it facilitates asymptotically valid pointwise inference.

Nonparametric inference on a monotone dose-response curve when the exposure-outcome relationship is confounded is more difficult to tackle and is the focus of this manuscript. To the best of our knowledge, this problem has not been comprehensively studied before.

1.2. Parameter of interest and its causal interpretation

The prototypical data unit we consider is O = (Y, A, W), where Y is a response, A a continuous exposure, and W a vector of covariates. The support of the true data-generating distribution P₀ is denoted by $\mathcal{O}=\mathcal{Y}\times \mathcal{A}\times \mathcal{W}$, where $\mathcal{Y}\subseteq \mathbb{R}$, $\mathcal{A}\subseteq \mathbb{R}$ is an interval, and $\mathcal{W}\subseteq {\mathbb{R}}^p$. Throughout, the use of subscript 0 refers to evaluation at or under P₀. For example, we write θ₀ and F_P0 to denote θ_P0 and F_P0, respectively, and E₀ to denote expectation under P₀.

Our parameter of interest is the so-called G-computed regression function from $\mathcal{A}$ to $\mathbb{R}$, defined as

$$a\mapsto {\theta }_0(a)≔E_0[E_0(Y\mid A=a,W)],$$

where the outer expectation is with respect to the marginal distribution Q₀ of W. In some scientific contexts, θ₀(a) may have a causal interpretation. Adopting the Neyman-Rubin potential outcomes framework, for each a ∈ $\mathcal{A}$, we denote by Y(a) a unit’s potential outcome under exposure level A = a. The causal parameter m₀(a) := E₀ [Y (a)] corresponds to the average outcome under assignment of the entire population to exposure level A = a. The resulting curve m₀ : $\mathcal{A}$ → $\mathbb{R}$ is what we formally define as the causal dose-response curve. Under varying sets of causal conditions, m₀(a) may be identified with functionals of the observed data distribution, such as the unadjusted regression function r₀(a) := E₀ (Y ∣ A = a) or the G-computed regression function θ₀(a).

Suppose that (i) each unit’s potential outcomes are independent of all other units’ exposures; and (ii) the observed outcome Y equals the potential outcome Y(A) corresponding to the exposure level A actually received. Identification of m₀(a) further depends on the relationship between A and Y(a). If (i) and (ii) hold, and in addition, (iii) A and Y (a) are independent, and (iv) the marginal density of A is positive at a, then m₀(a) = r₀(a). Condition (iii) typically only holds in experimental studies (e.g., randomized trials). In observational studies, there are often common causes of A and Y(a) – so-called confounders of the exposure-outcome relationship – that induce dependence. In such cases, m₀(a) and r₀(a) do not generally coincide. However, if W contains a sufficiently rich collection of confounders, it may still be possible to identify m₀(a) from the observed data. If (i) and (ii) hold, and in addition, (v) A and Y(a) are conditionally independent given W, and (vi) the conditional density of A given W is almost surely positive at A = a, then m₀(a) = θ₀(a). This is a fundamental result in causal inference (Robins, 1986; Gill and Robins, 2001). Whenever m₀(a) = θ₀(a), our methods can be interpreted as drawing inference on the causal dose-response parameter m₀(a).

We note that the definition of the counterfactual outcome Y(a) presupposes that the intervention setting A = a is uniquely defined. In many situations, this stipulation requires careful thought. For example, in Section 6 we consider an application in which body mass index (BMI) is the exposure of interest. There is an ongoing scientific debate about whether such an exposure leads to a meaningful causal interpretation, since it is not clear what it means to intervene on BMI.

Even if the identifiability conditions stipulated above do not strictly hold or the scientific question is not causal in nature, when W is associated with both A and Y, θ₀(a) often has a more appealing interpretation than the unadjusted regression function r₀(a). Specifically, θ₀(a) may be interpreted as the average value of Y in a population with exposure fixed at A = a but otherwise characteristic of the study population with respect to W. Because θ₀(a) involves both adjustment for W and marginalization with respect to a single reference population that does not depend on the value a, the comparison of θ₀(a) over different values of a is generally more meaningful than for r₀(a).

When P₀(A = a) = 0, the parameter P ↦ θ_P(a) is not pathwise differentiable at P₀ with respect to the nonparametric model (Díaz and van der Laan, 2011). Heuristically, due to the continuous nature of A, θ_P(a) corresponds to a local feature of P. As a result, regular root-n rate estimators cannot be expected, and standard methods for constructing efficient estimators of pathwise differentiable parameters in nonparametric and semiparametric models (e.g., estimating equations, one-step estimation, targeted minimum loss-based estimation) cannot be used directly to target and obtain inference on θ₀(a).

1.3. Contribution and organization of the article

We denote by F_P : $\mathcal{A}\to \mathbb{R}$ the distribution function of A under P, by ${\mathcal{F}}_{\theta }$ the class of non-decreasing real-valued functions on $\mathcal{A}$, and by ${\mathcal{F}}_F$ the class of strictly increasing and continuous distribution functions supported on $\mathcal{A}$. The statistical model we will work in is $\mathcal{M}≔\{P:{\theta }_P\in {\mathcal{F}}_{\theta },F_P\in {\mathcal{F}}_F\}$, which consists of the collection of distributions for which θ_P is non-decreasing over $\mathcal{A}$ and the marginal distribution of A is continuous with positive Lebesgue density over $\mathcal{A}$.

In this article, we study nonparametric estimation and inference on the G-computed regression function a ↦ θ₀(a) = E₀ [E₀ (Y ∣ A = a, W)] for use when A is a continuous exposure and θ₀ is known to be monotone. Specifically, our goal is to make inference about θ₀(a) for a ∈ $\mathcal{A}$ using independent observations O₁, O₂, … ,O_n drawn from P₀ ∈ $\mathcal{M}$. This problem is an extension of classical isotonic regression to the setting in which the exposure-outcome relationship is confounded by recorded covariates – this is why we refer to the method proposed as causal isotonic regression. As mentioned above, to the best of our knowledge, nonparametric estimation and inference on a monotone G-computed regression function has not been comprehensively studied before. In what follows, we:

1. show that our proposed estimator generalizes the unadjusted isotonic regression estimator to the more realistic scenario in which there is confounding by recorded covariates;

2. investigate finite-sample and asymptotic properties of the proposed estimator, including invariance to strictly increasing transformations of the exposure, doubly-robust consistency, and doubly-robust convergence in distribution to a non-degenerate limit;

3. derive practical methods for constructing pointwise confidence intervals, including intervals that have valid doubly-robust calibration;

4. illustrate numerically the practical performance of the proposed estimator.

We note that in Westling and Carone (2019), we studied estimation of θ₀ as one of several examples of a general approach to monotonicity-constrained inference. Here, we provide a comprehensive examination of estimation of a monotone dose-response curve. In particular, we establish novel theory and methods that have important practical implications. First, we provide conditions under which the estimator converges in distribution even when one of the nuisance estimators involved in the problem is inconsistent. This contrasts with the results in Westling and Carone (2019), which required that both nuisance parameters be estimated consistently. We also propose two estimators of the scale parameter arising in the limit distribution, one of which requires both nuisance estimators to be consistent, and the other of which does not. Second, we demonstrate that our estimator is invariant to strictly monotone transformations of the exposure. Third, we study the joint convergence of our proposed estimator at two points, and use this result to construct confidence intervals for causal effects. Fourth, we study the behavior of our estimator in the context of discrete exposures. Fifth, we propose an alternative estimator based on cross-fitting of the nuisance estimators, and demonstrate that this strategy removes the need for empirical process conditions required in Westling and Carone (2019). Finally, we investigate the behavior of our estimator in comprehensive numerical studies, and compare its behavior to that of the local linear estimator of Kennedy et al. (2017).

The remainder of the article is organized as follows. In Section 2, we concretely define the proposed estimator. In Section 3, we study theoretical properties of the proposed estimator. In Section 4, we propose methods for pointwise inference. In Section 5, we perform numerical studies to assess the performance of the proposed estimator, and in Section 6, we use this procedure to investigate the relationship between BMI and immune response to HIV vaccines using data from several randomized trials. Finally, we provide concluding remarks in Section 7. Proofs of all theorems are provided in Supplementary Material.

2. Proposed approach

2.1. Review of isotonic regression

Since the proposed estimator of θ₀(a) builds upon isotonic regression, we briefly review the classical least-squares isotonic regression estimator of r₀(a). The isotonic regression r_n of Y₁, Y_n, … , Y_n on A₁, A₂, …, A_n is the minimizer in r of ${\sum }_{i=1}^n[Y_i-r(A_i){]}^2$ over all monotone non-decreasing functions. This minimizer can be obtained via the Pool Adjacent Violators Algorithm (Ayer et al., 1955; Barlow et al., 1972), and can also be represented in terms of greatest convex minorants (GCMs). The GCM of a bounded function f on an interval [a, b] is defined as the supremum over all convex functions g such that g ≤ f. Letting F_n be the empirical distribution function of A₁, A₂, … , A_n, r_n(a) can be shown to equal the left derivative, evaluated at F_n(a), of the GCM over the interval [0,1] of the linear interpolation of the so-called cusum diagram

$$\left\{\frac{1}{n}\left(i,\sum _{j=0}^i{Y}_{(i)}^{\ast }\right):i=0,1,\dots ,n\right\},$$

where $Y_{(0)}^{\ast }$ := 0 and $Y_{(i)}^{\ast }$ is the value of Y corresponding to the observation with i^th smallest value of A.

The isotonic regression estimator r_n has many attractive properties. First, unlike smoothing-based estimators, isotonic regression does not require the choice of a kernel function, bandwidth, or any other tuning parameter. Second, it is invariant to strictly increasing transformations of A. Specifically, if H : $\mathcal{A}$ → $\mathbb{R}$ is a strictly increasing function, and $r_n^{\ast }$ is the isotonic regression of Y₁, Y₂, … , Y_n on H(A₁), H(A₂), …, H(A_n), it follows that $r_n^{\ast }=r_n\circ H^{-1}$. Third, r_n is uniformly consistent on any strict subinterval of $\mathcal{A}$. Fourth, n^1/3[r_n(a) – r₀(a)] converges in distribution to [$4r_0^{\prime }(a){\sigma }_0^2(a)∕f_0(a)$]^1/3 $\mathbb{W}$ for any interior point a of $\mathcal{A}$ at which $r_0^{\prime }(a)$, $f_0(a)≔F_0^{\prime }(a)$ and ${\sigma }_0^2(a)≔E_0\{[Y-r_0(a){]}^2\mid A=a\}$ exist, and are positive and continuous in a neighborhood of a. Here, $\mathbb{W}≔{\text{argmax}}_{u\in \mathbb{R}}\{Z_0(u)-u^2\}$, where Z₀ denotes a two-sided Brownian motion originating from zero, and is said to follow Chernoff’s distribution. Chernoff’s distribution has been extensively studied: among other properties, it is a log-concave and symmetric law centered at zero, has moments of all orders, and can be approximated by a N(0, 0.52) distribution (Chernoff, 1964; Groeneboom and Wellner, 2001). It appears often in the limit distribution of monotonicity-constrained estimators.

2.2. Definition of proposed estimator

For any given P ∈ $\mathcal{M}$, we define the outcome regression pointwise as μ_P(a, ω) := E_P (Y ∣ A = a, W = ω), and the normalized exposure density as $g_P(a,w)≔{\pi }_P(a\mid w)∕f_P(a)$, where π_P(a ∣ ω) is the evaluation at a of the conditional density function of A given W = ω and $f_P$ is the marginal density function of A under P. Additionally, we define the pseudo-outcome ξ_μ,g,Q(y, a, ω) as

$${\xi }_{\mu ,g,Q}(y,a,w)≔\frac{y-\mu (a,w)}{g(a,w)}+\int \mu (a,z)Q(dz).$$

As noted by Kennedy et al. (2017), E₀ [ξ_μ,g,Q0 (Y, A, W) ∣ A = a] = θ₀(a) if either μ = μ₀ or g = g₀. They used this fact to motivate an estimator θ_n,h(a) of θ₀(a), defined as the local linear regression with band-width h > 0 of the pseudo-outcomes ξ_μn,gn,Qn (Y₁, A₁, W₁), ξ_μn,gn,Qn(_Y2,A2,W2), …, ξμn,g_n,Q_n(Y_n, A_n, W_n)on A₁, A₂, …, A_n, where μ_n is an estimator of μ₀, g_n is an estimator of g₀, and Q_n is the empirical distribution function based on W₁, W₂, …, W_n. The study of this nonparametric regression problem is not standard because these pseudo-outcomes are dependent when the nuisance function estimators μ_n and g_n are estimated from the data. Nevertheless, Kennedy et al. (2017) showed that their estimator is consistent if either μ_n or g_n is consistent. Additionally, under regularity conditions, they showed that if both nuisance estimators converge fast enough and the bandwidth $h_n^{\ast }$ tends to zero at rate n^−1/5, then n^2/5 $[{\theta }_{n,h_n^{\ast }}(a)-{\theta }_0(a)]\stackrel{\mathrm{d}}{\to }N(b_0(a),v_0(a))$ where b₀(a) is an asymptotic bias depending on the second derivative of θ₀, and ν₀(a) is an asymptotic variance.

In our setting, θ₀ is known to be monotone. Therefore, instead of using a local linear regression to estimate the conditional mean of the pseudo-outcomes, it is natural to consider as an estimator the isotonic regression of the pseudo-outcomes on A₁, A₂, … , A_n. Using the GCM representation of isotonic regression stated in the previous section, we can summarize our estimation procedure as follows:

1. Construct estimators μ_n and g_n of μ₀ and g₀, respectively.

2. For each a in the unique values of A₁, A₂, …, A_n, compute and set

$${\Gamma }_n(a)≔\frac{1}{n}\sum _{i=1}^n{I}_{(-\infty ,a]}(A_i)\left[\frac{Y_i-{\mu }_n(A_i,W_i)}{g_n(A_i,W_i)}\right]+\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{I}_{(-\infty ,a]}(A_i){\mu }_n(A_i,W_j).$$ (1)

1. Compute the GCM ${\overline{\Psi }}_n$ of the set of points {(0,0)} ∪ {(F_n(A_i), Γ_n(A_i)) : i = 1, 2, … , n} over [0,1].

2. Define θ_n(a) as the left derivative of ${\overline{\Psi }}_n$ evaluated at F_n(a).

As in the work of Kennedy et al. (2017), while the proposed estimator θ_n can be defined as an isotonic regression, the asymptotic properties of our estimator do not appear to simply follow from classical results for isotonic regression because the pseudo-outcomes depend on the estimators μ_n, g_n and Q_n, which themselves depend on all the observations. However, θ_n is of generalized Grenander-type, and thus the asymptotic results of Westling and Carone (2019) can be used to study its asymptotic properties. To see that θ_n is a generalized Grenander-type estimator, we define ψP := θ_P o $F_P^{-1}$ and note that since θ_P and $F_P^{-1}$ are increasing, so is ψ_P. Therefore, the primitive function ${\Psi }_P(t)≔{\int }_0^t{\psi }_P(u)du={\int }_{-\infty }^{F_P^{-1}(t)}{\theta }_P(v)F_P(dv)$ is convex. Next, we define Γ_P := Ψ_P o F_P, so that ${\Gamma }_P(a)={\int }_{-\infty }^a{\theta }_P(u)F_P(du)=\int {\int }_{-\infty }^a{\mu }_P(u,w)F_P(du)Q_P(dw)$. The parameter Γ_P(a₀) is pathwise differentiable at P in $\mathcal{M}$ for each a₀, and its nonparametric efficient influence function

$$(y,a,w)\mapsto I_{(-\infty ,a_0]}(a)\left[\frac{y-{\mu }_P(a,w)}{g_P(a,w)}\right]+{\int }_{-\infty }^{a_0}{\mu }_P(u,w)F_P(du)+I_{(-\infty ,a_0]}(a){\theta }_P(a)-2{\Gamma }_P(a_0).$$

Denoting by P_n any estimator of P₀ compatible with estimators μ_n, g_n, F_n and Q_n of μ₀, g₀, F₀ and Q₀, respectively the one-step estimator of Γ₀(a) is given by Γ_n(a) := Γ_μn,Fn,Qn(a) + $\frac{1}{n}{\sum }_{i=1}^n{\varphi }_{{\mu }_n,g_n,F_n,Q_n,a}^{\ast }(O_i)$ where we define ${\Gamma }_{{\mu }_n,F_n,Q_n}(a)≔\int {\int }_{-\infty }^a{\mu }_n(u,w)F_n(du)Q_n(dw)$. This one-step estimator is equivalent to that defined in (1). We then define ${\Psi }_n≔{\Gamma }_n\circ F_n^{-}\text{for}{F}_n^{-}$ the empirical quantile function of A as our estimator of Ψ₀, and ψ_n as the left derivative of the GCM of Ψ_n. Thus, we find that θ_n = ψ_n o F_n is the estimator defined in steps 1–4. This form of the estimator was described in Westling and Carone (2019), where it was briefly discussed as one of several examples of a general strategy for nonparametric monotone inference.

If θ₀(a) were only known to be monotone on a fixed sub-interval ${\mathcal{A}}_0\subseteq \mathcal{A}$, we would define F_P(a) := P(A ≤ a ∣ A ∈ ${\mathcal{A}}_0$) as the marginal distribution function restricted to ${\mathcal{A}}_0$, and F_n as its empirical counterpart. Similarly, I_(−∞,a](A_i) in (1) would be replaced with $I_{(-\infty ,a]\cap {\mathcal{A}}_0}$ (A_i). In all other respects, our estimation procedure would remain the same.

Finally, as alluded to earlier, we observe that the proposed estimator generalizes classical isotonic regression in a way we now make precise. If it is known that A is independent of W (Condition 1), so that g₀(a, ω) = 1 for all supported (a, ω), we may take g_n = 1. If, furthermore, it is known that Y is independent of W given A (Condition 2), then we may construct μ_n such that μ_n(a, ω) = μ_n(a) for all supported (a, ω). Inserting g_n = 1 and any such μ_n into (1), we obtain that ${\Gamma }_n(a)=\frac{1}{n}{\sum }_{i=1}^n{I}_{(-\infty ,a]}(A_i)Y_i$ and thus that θ_n(a) = r_n(a) for each a. Hence, in this case, our estimator reduces to least-squares isotonic regression.

3. Theoretical properties

3.1. Invariance to strictly increasing exposure transformations

An important feature of the proposed estimator is that, as with the isotonic regression estimator, it is invariant to any strictly increasing transformation of A. This is a desirable property because the scale of a continuous exposure is often arbitrary from a statistical perspective. For instance, if A is temperature, whether A is measured in degrees Fahrenheit, Celsius or Kelvin does not change the information available. In particular, if the parameters θ₀ and ${\theta }_0^{\ast }$ correspond to using as exposure A and H(A), respectively, for H some strictly increasing transformation, then θ₀ and ${\theta }_0^{\ast }$ encode exactly the same information about the effect of A on Y after adjusting for W. It is therefore natural to expect any sensible estimator to be invariant to the scale on which the exposure is measured.

Setting X := H(A) for a strictly increasing function $H:\mathcal{A}\to \mathbb{R}$, we first note that the function ${\theta }_0^{\ast }$ : x ↦ E₀ [E₀ (Y ∣ X = x, W)] = θ₀ o H⁻¹(x) is non-decreasing. Next, we define ${\mu }_0^{\ast }(x,w)≔E_0(Y\mid X=x,W=w)$ and $g_0^{\ast }(x,w)={\pi }_0^{\ast }(x\mid w)∕f_0^{\ast }(x)$, ${\pi }_0^{\ast }(x\mid w)$ is the evaluation at x of the conditional density function of X given $W=w\text{and}{f}_0^{\ast }$ is the marginal density function of X under P₀, and we denote by ${\mu }_n^{\ast }$ and $g_n^{\ast }$ estimators of ${\mu }_0^{\ast }$ and $g_0^{\ast }$, respectively. The estimation procedure defined in the previous section but using exposure X instead of A then leads to estimator ${\theta }_n^{\ast }(x)≔{\psi }_n^{\ast }\circ F_n^{\ast }(x)$, where $F_n^{\ast }≔F_n\circ H^{-1}$ is the empirical distribution function based on X₁, X₂, …, X_n, and ${\psi }_n^{\ast }$ is the left derivative of the GCM of ${\Psi }_n^{\ast }≔{\Gamma }_n^{\ast }\circ F_n^{\ast -}$ for

$$\begin{gathered} {\Gamma }_n^{\ast }(x)≔\frac{1}{n}\sum _{i=1}^n\left\{I_{(-\infty ,x]}(X_i)\left[\frac{Y_i-{\mu }_n^{\ast }(X_i,W_i)}{g_n^{\ast }(X_i,W_i)}\right]+{\int }_{-\infty }^x{\mu }_n^{\ast }(x,W_i)F_n^{\ast }(dx)\right\} \\ =\frac{1}{n}\sum _{i=1}^n\left\{I_{(-\infty ,H^{-1}(x)]}(A_i)\left[\frac{Y_i-{\mu }_n^{\ast }(H(A_i),W_i)}{g_n^{\ast }(H(A_i),W_i)}\right]+{\int }_{-\infty }^{H^{-1}(x)}{\mu }_n^{\ast }(H(a),W_i)F_n^{\ast }(da)\right\}. \end{gathered}$$

If it is the case that ${\mu }_n^{\ast }(H(a),w)={\mu }_n(a,w)$ and $g_n^{\ast }(H(a),w)=g_n(a,w)$, implying that nuisance estimators μ_n and g_n are themselves invariant to strictly increasing transformation of A, then we have that ${\Gamma }_n^{\ast }={\Gamma }_n\circ H^{-1}$, and so, ${\Psi }_n^{\ast }={\Gamma }_n\circ H^{-1}\circ H\circ F_n=\Psi$. It follows then that ${\theta }_n^{\ast }={\theta }_n\circ H^{-1}$. In other words, the proposed estimator θ_n of θ₀ is invariant to any strictly increasing transformation of the exposure variable.

We note that it is easy to ensure that ${\mu }_n^{\ast }(H(a),w)={\mu }_n(a,w)$ and $g_n^{\ast }(H(a),w)=g_n(a,w)$. Set U := F_n(A), which is also equal to $F_n^{\ast }(X)$, and let ${\overline{\mu }}_n(u,w)$ be an estimator of the conditional mean of Y given (U, W) = (u,w). Then, taking ${\mu }_n(a,w)≔{\overline{\mu }}_n(F_n(a),w)$, we have that ${\mu }_n^{\ast }(x,w)≔{\overline{\mu }}_n(F_n^{\ast }(x),w)$ satisfies the desired property. Similarly, letting ${\overline{g}}_n(u,w)$ be an estimator of the conditional density of U = u given W = ω, and setting $g_n(a,w)≔{\overline{g}}_n(F_n(a),w)$, we may take $g_n^{\ast }(x,w)≔{\overline{g}}_n(F_n^{\ast }(x),w)$.

3.2. Consistency

We now provide sufficient conditions under which consistency of θ_n is guaranteed. Our conditions require controlling the uniform entropy of certain classes of functions. For a uniformly bounded class of functions $\mathcal{F}$, a finite discrete probability measure Q, and any ε > 0, the ε-covering number N(ε,$\mathcal{F}$,L₂(Q)) of $\mathcal{F}$ relative to the L₂(Q) metric is the smallest number of L₂(Q)-balls of radius less than or equal to e needed to cover $\mathcal{F}$. The uniform ε-entropy of $\mathcal{F}$ is then defined as logsup_Q N(ε, $\mathcal{F}$, L₂(Q)), where the supremum is taken over all finite discrete probability measures. For a thorough treatment of covering numbers and their role in empirical process theory, we refer readers to van der Vaart and Wellner (1996).

Below, we state three sufficient conditions we will refer to in the following theorem.

(A1) There exist constants C, δ, K₀, K₁, K₂ ∈ (0, +∞) and V ∈ [0, 2) such that, almost surely as n → ∞, μ_n and g_n are contained in classes of functions ${\mathcal{F}}_0$ and ${\mathcal{F}}_1$, respectively, satisfying:

1. ∣μ∣ ≤ K₀ for all μ ∈ ${\mathcal{F}}_0$, and K₁ ≤ g ≤ K₂ for all g ∈ ${\mathcal{F}}_1$;

2. logsup_Q N(ε, ${\mathcal{F}}_0$, L₂(Q)) ≤ Cε^−V/2 and logsup_Q N(ε, ${\mathcal{F}}_1$, L₂(Q)) ≤ Cε^−V for all ε ≤ δ.

(A2) There exist μ_∞ ∈ ${\mathcal{F}}_0$ and g_∞ ∈ ${\mathcal{F}}_1$ such that $P_0({\mu }_n-{\mu }_{\infty }{)}^2\stackrel{\mathrm{P}}{\to }0$ and $P_0(g_n-g_{\infty }{)}^2\stackrel{\mathrm{P}}{\to }0$.

(A3) There exist subsets S₁, S₂ and S₃ of $\mathcal{A}\times \mathcal{W}$ such that P₀(S₁ ∪ S₂ ∪ S₃) = 1 and:

1. μ_∞(a, ω) = μ0(a, ω) for all (a, ω) ∈ S₁;

2. g_∞(a, ω) = g0 (a, ω) for all (a, ω) ∈ S₂;

3. μ_∞(a,ω) = μ0(a,w) and g₀(a, ω) = g₀(a,ω) for all (a, ω) ∈ S₃.

Under these three conditions, we have the following result.

Theorem 1 (Consistency). If conditions (A1)-(A3) hold, then ${\theta }_n(a)\stackrel{\mathrm{P}}{\to }{\theta }_0(a)$ for any value a ∈ $\mathcal{A}$ that F₀(a) ∈ (0,1), θ₀ is continuous at a, and F₀ is strictly increasing in a neighborhood of a. uniformly continuous and F₀ is strictly increasing on $\mathcal{A}$, then ${\text{sup}}_{a\in {\mathcal{A}}_0}\mid {\theta }_n(a)-{\theta }_0(a)\mid \stackrel{\mathrm{P}}{\to }0$ for any bounded strict subinterval ${\mathcal{A}}_0⊊\mathcal{A}$.

We note that in the pointwise statement of Theorem 1, F₀(a) is required to be in the interior of [0, 1], and similarly, the uniform statement of Theorem 1 only covers strict subintervals of $\mathcal{A}$. This is due to the well-known boundary issues with Grenander-type estimators. Various remedies have been proposed in particular settings, and it would be interesting to consider these in future work (see, e.g., Woodroofe and Sun, 1993; Balabdaoui et al., 2011; Kulikov and Lopuhaä, 2006).

Condition (A1) requires that μ_n and g_n eventually be contained in uniformly bounded function classes that are small enough for certain empirical process terms to be controlled. This condition is easily satisfied if, for instance, ${\mathcal{F}}_0$ and ${\mathcal{F}}_1$ are parametric classes. It is also satisfied for many infinite-dimensional function classes. Uniform entropy bounds for many such classes may be found in Chapter 2.6 of van der Vaart and Wellner (1996). We note that there is an asymmetry between the entropy requirements for ${\mathcal{F}}_0$ and ${\mathcal{F}}_1$ in part (b) of (A1). This is due to the term ∫$\int {\int }_{-\infty }^a{\mu }_n(u,w)F_n(du)Q_n(dw)$ appearing in Γ_n(a). To control this term, we use an upper bound of the form ${\int }_0^1\log {\text{sup}}_{Q}N(\epsilon ,{\mathcal{F}}_0,L_2(Q))d\epsilon$ from the theory of empirical U-processes (Nolan and Pollard, 1987) – this contrasts with the uniform entropy integral ${\int }_0^1[\log {\text{sup}}_{Q}N(\epsilon ,\mathcal{F},L_2(Q))]$^1/2dε that bounds ordinary empirical processes indexed by a uniformly bounded class $\mathcal{F}$. In Section 3.7, we consider the use of cross-fitting to avoid the entropy conditions in (A1).

Condition (A2) requires that μ_n and g_n tend to limit functions μ_∞ and g_∞, and condition (A3) requires that either μ_∞(a, ω) = μ₀(a, ω) or g_∞(a, ω) = g₀(a, ω) for (F₀ × Q₀)-almost every (a, ω). If either (i) S₁ and S₃ are null sets or (ii) S₂ and S₃ are null sets, then condition (A3) is known simply as double-robustness of the estimator θ_n relative to the nuisance functions μ₀ and g₀: θ_n is consistent as long as μ_∞ = μ₀ or g_∞ = g₀. Doubly-robust estimators are at this point a mainstay of causal inference and have been studied for over two decades (see, e.g., Robins et al., 1994; Rotnitzky et al., 1998; Scharfstein et al., 1999; van der Laan and Robins, 2003; Neugebauer and van der Laan, 2005; Bang and Robins, 2005). However, (A3) is more general than classical double-robustness, as it allows neither μ_n nor g_n to tend to their true counterparts over the whole domain, as long as at least one of μ_n or g_n tends to the truth for almost every point in the domain.

3.3. Convergence in distribution

We now study the convergence in distribution of n^1/3[θ_n(a) – θ₀(a)] for fixed a. We first define for any square-integrable functions h₁, h₂ : $\mathcal{A}$ × $\mathcal{W}$ → $\mathbb{R}$, ε > 0 and S ⊆ $\mathcal{A}$ × $\mathcal{W}$ the pseudo-distance

$$d(h_1,h_2;a,\epsilon ,\mathcal{S})≔{\left[\underset{\mid u-a\mid \le \epsilon }{\text{sup}}{E}_0\left\{I_{\mathcal{S}}(u,W)[h_1(u,W)-h_2(u,W){]}^2\right\}\right]}^{1∕2}.$$ (2)

We also denote by ${\sigma }_0^2(a,w)$ the conditional variance E₀ {[Y – μ₀(A,W)]² ∣A = a, W = ω} of Y given A = a and W = ω under P₀. Below, we will refer to these two additional conditions:

(A4) There exists ε₀ > 0 such that:

1. max{d(μ_n, μ_∞; a, ε₀, S₁), d(g_n, g_∞; a, ε₀, S₂)} = o_P(n^−1/3);

2. max{d(μ_n, μ_∞; a, ε₀, S₂), d(g_n; g,_∞; a, ε₀, S₁)} = o_P(1);

3. d(μ_n, μ_∞; a, ε₀, S₃)d(g_n, g_∞; a, ε₀, S₃) = o_p(n^−1/3).

(A5) F₀, μ₀, μ_∞, g₀, g_∞ and ${\sigma }_0^2$ are continuously differentiable in a neighborhood of a uniformly over ω ∈ $\mathcal{W}$. Under conditions introduced so far, we have the following distributional result.

Theorem 2 (Convergence in distribution). If conditions (A1)–(A5) hold, then

$$n^{1∕3}[{\theta }_n(a)-{\theta }_0(a)]\stackrel{\mathrm{d}}{\to }{\left[\frac{4{\theta }_0^{\prime }(a){\kappa }_0(a)}{f_0(a)}\right]}^{1∕3}\mathbb{W},$$

for any a ∈ $\mathcal{A}$ such that F₀(a) ∈ (0,1), where $\mathbb{W}$ follows the standard Chernoff distribution and

$${\kappa }_0(a)≔E_0\left\{\phantom{[}{E}_0[{\left\{\left[\frac{Y-{\mu }_{\infty }(a,W)}{g_{\infty }(a,W)}\right]+{\theta }_{\infty }(a)-{\theta }_0(a)\right\}}^2\mid A=a,W]g_0(a,W)\right\}$$

with θ_∞(a) denoting ∫ μ_∞(a,ω)Q₀(dω).

We note that the limit distribution in Theorem 2 is the same as that of the standard isotonic regression estimator up to a scale factor. As noted above, when either (i) Y and W are independent given A or (ii) A is independent of W, the functions θ₀ and r₀ coincide. As such, we can directly compare the respective limit distributions of n^1/3 [θ_n(a) – θ₀(a)] and n^1/3 [r_n(a) – r₀(a)] under these conditions. When both μ_∞ = μ₀ and g_∞ = g₀, r_n(a) is asymptotically more concentrated than θ_n(a) in scenario (i), and less concentrated in scenario (ii). This is analogous to findings in linear regression, where including a covariate uncorrelated with the outcome inflates the standard error of the estimator of the coefficient corresponding to the exposure, while including a covariate correlated with the outcome but uncorrelated with the exposure deflates its standard error.

Condition (A4) requires that, on the set S₁ where μ_n is consistent but g_n is not, μ_n converges faster than n^−1/3 uniformly in a neighborhood of a, and similarly for g_n on the set S₂. On the set S₃ where both μ_n and g_n are consistent, only the product of their rates of convergence must be faster than n^−1/3. Hence, a non-degenerate limit theory is available as long as at least one of the nuisance estimators is consistent at a rate faster than n^−1/3, even if the other nuisance estimator is inconsistent. This suggests the possibility of performing doubly-robust inference for θ₀(a), that is, of constructing confidence intervals and tests based on θ_n (a) with valid calibration even when one of μ₀ and g₀ is inconsistently estimated. This is explored in Section 4. Finally, as in Theorem 1, we allow that neither μ_n nor g_n be consistent everywhere, as long as for (F₀ × Q₀)-almost every (a,ω) at least one of μ_n or g_n is consistent.

We remark that if it is known that μ_n (a, ·) is consistent for μ₀(a, ·) in an L₂(Q₀) sense at rate faster than n^−1/3, the isotonic regression of the plug-in estimator θ_μn(a) := ∫ μ_n(a,ω)Q_n(dω) – which can be equivalently obtained by setting g_n(a, ·) = +∞ in the construction of θ_n(a) – achieves a faster rate of convergence to θ₀(a) than does θ_n(a). This might motivate an analyst to use θ_μn (a) rather than θ_n(a) in such a scenario. However, the consistency of θ_μn(a) hinges entirely on the fact that μ_∞ = μ₀, and in particular, θ_μn (a) will be inconsistent if μ_∞ ≠ μ₀, even if g_∞ = g₀. Additionally, the estimator θ_μn (a) may not generally admit a tractable limit theory upon which to base the construction of valid confidence intervals, particularly when machine learning methods are used to build μ_n.

3.4. Grenander-type estimation without domain transformation

As indicated earlier, the isotonic regression estimator based on estimated pseudo-outcomes coincides with a generalized Grenander-type estimator for which the marginal exposure empirical distribution function is used as domain transformation. An alternative estimator could be constructed via Grenander-type estimation without the use of any domain transformation. Specifically, we let a₋,a₊ ∈ $\mathbb{R}$ be fixed, and we define ${\Theta }_0(a)={\int }_{a_{-}}^a{\theta }_0(u)du$. Under regularity conditions, for a ≤ a₊, the one-step estimator of Θ₀(a) given by

$${\Theta }_n(a)≔\frac{1}{n}\sum _{i=1}^n\left\{I_{(a_{-},a]}(A_i)\left[\frac{Y_i-{\mu }_n(A_i,W_i)}{{\pi }_n(A_i,W_i)}\right]+{\int }_{a_{-}}^a{\mu }_n(u,W_i)du\right\}$$

is asymptotically efficient, where π_n is an estimator of π₀, the conditional density of A given W under P₀. The left derivative of the GCM of Θ_n over [a₋,a₊] defines an alternative estimator ${\overline{\theta }}_n$(a).

It is natural to ask how ${\overline{\theta }}_n$ compares to the estimator θ_n we have studied thus far. First, we note that, unlike θ_n, ${\overline{\theta }}_n$ neither generalizes the classical isotonic regression estimator nor is invariant to strictly increasing transformations of A. Additionally, utilizing the transformation F₀ fixes [0, 1] as the interval over which the GCM should be performed. If $\mathcal{A}$ is known to be a bounded set, [a₋,a₊] can be taken as the endpoints of $\mathcal{A}$, but otherwise the domain [a₋, a₊] must be chosen in defining ${\overline{\theta }}_n$. Turning to an asymptotic analysis, using the results of Westling and Carone (2019), it is possible to establish conditions akin to (A1)–(A5) under which n^1/3 $[{\overline{\theta }}_n(a)-{\theta }_0(a)]\stackrel{\mathrm{d}}{\to }[4{\theta }_0^{\prime }(a){\overline{\kappa }}_0(a){]}^{1∕3}\mathbb{W}$ with scale parameter

$${\overline{\kappa }}_0(a)≔\phantom{[}{E}_0\left[E_0\{{\left[\frac{Y-{\mu }_{\infty }(A,W)}{{\pi }_{\infty }(A\mid W)}\right]}^2\mid A=a,W\right\}{\pi }_0(a\mid W)],$$

where π_∞ is the limit of π_n in probability. We denote by [4τ₀(a)]^1/3 and [$[4{\overline{\tau }}_0(a){]}^{1∕3}$]^1/3 the limit scaling factors of n^1/3 [θ_n(a) – θ₀(a)] and n^1/3 [${\overline{\theta }}_n(a)$ – θ₀(a)], respectively. If g_∞ = π_∞/f₀ and μ_∞ = μ₀, then ${\tau }_0(a)={\overline{\tau }}_0(a)$, and n^1/3 [θ_n(a) – θ₀(a)] and n^1/3 [${\overline{\theta }}_n(a)-{\theta }_0(a)$] have the same limit distribution. If instead g_∞ = π_∞/f₀ = g₀ but μ_∞ ≠ μ₀, this is no longer the case. In fact, we can show that

$$\begin{gathered} {\tau }_0(a)={\theta }_0^{\prime }(a)E_0\left[\frac{E_0\{[Y-{\mu }_{\infty }(a,W){]}^2\mid A=a,W\}}{{\pi }_0(a\mid W)}\right]-{\theta }_0^{\prime }(a)\frac{\{{\theta }_{\infty }(a)-{\theta }_0(a){\}}^2}{f_0(a)} \\ \le {\theta }_0^{\prime }(a)E_0\left[\frac{E_0\{[Y-{\mu }_{\infty }(a,W){]}^2\mid A=a,W\}}{{\pi }_0(a\mid W)}\right]=\overline{\tau }(a). \end{gathered}$$

Hence, when the outcome regression estimator μ_n is inconsistent, gains in efficiency are achieved by utilizing the transformation, and the relative gain in efficiency is directly related to the amount of asymptotic bias in the estimation of μ₀.

3.5. Discrete domains

In some circumstances, the exposure A is discrete rather than continuous. Our estimator works equally well in these cases, since, as we highlight below, it turns out to then be asymptotically equivalent to the well-studied augmented IPW (AIPW) estimator. As a result, the large-sample properties of our estimator can be derived from the large-sample properties of the AIPW estimator, and asymptotically valid inference can be obtained using standard influence function-based techniques.

Suppose that $\mathcal{A}=\{a_1<a_2<\cdots <a_m\}$ and f_0,j := P₀(A = a_j) > 0 for all j ∈ {1, 2,…, m} and ${\sum }_{j=1}^m{f}_{0,j}=1$. Our estimation procedure remains the same with one exception: in defining g₀ := π₀/f₀, we now take π₀ to be the conditional probability π₀(a_j ∣ ω) := P₀(A = a_j ∣ W = ω) rather than the corresponding conditional density, and we take f₀ as the marginal probability f₀(a_j) := P₀(A = a_j) = f_0,j rather than the corresponding marginal density. We then set g_n := π_n/f_n, as the estimator of g₀, where π_n is any estimator of π₀ and $f_n(a_j)≔n_j∕n\text{for}{n}_j≔{\sum }_{i=1}^{n}I(A_i=a_j)$. In all other respects, our estimation procedure is identical to that defined previously. With these definitions, we denote by ξ_n,i the estimated pseudo-outcome for observation i. Our estimator is then the isotonic regression of ξ_n,1, ξ_n,2, …, ξ_n,n on A₁, A₂, …, A_n. However, since for each i there is a unique j such that A_i = a_j, this is equivalent to performing isotonic regression of ${\theta }_n^{†}(a_1)$, ${\theta }_n^{†}(a_2)$, …, ${\theta }_n^{†}(a_m)$ on a₁, a₂, … , a_m, where ${\theta }_n^{†}(a_j)≔n_j^{-1}{\sum }_{i=1}^n{I}_{\{a_j\}}(A_i){\xi }_{n,i}$. It is straightforward to see that

$${\theta }_n^{†}(a_j)=\frac{1}{n}\sum _{i=1}^n\left\{I_{\{a_j\}}(A_i)\left[\frac{Y_i-{\mu }_n(a_j,W_i)}{{\pi }_n(a_j\mid W_i)}\right]+{\mu }_n(a_j,W_i)\right\},$$

which is exactly the AIPW estimator of θ₀(a_j). Therefore, in this case, our estimator reduces to the isotonic regression of the classical AIPW estimator constructed separately for each element of the exposure domain.

The large-sample properties of ${\theta }_n^{†}$, including doubly-robust consistency and convergence in distribution at the regular parametric rate n^−1/2, are well-established (Robins et al., 1994). Therefore, many properties of θ_n in this case can be determined using the results of Westling et al. (2018), which studied the behavior of the isotonic correction of an initial estimator. In particular, ${\max }_{a\in \mathcal{A}}\mid {\theta }_n(a)-{\theta }_0(a)\mid \le {\mathrm{maxc}}_{a\in \mathcal{A}}\mid {\theta }_n^{†}(a)-{\theta }_0(a)\mid$ as long as θ₀ is non-decreasing on $\mathcal{A}$. Uniform consistency of ${\theta }_n^{†}$ over $\mathcal{A}$ thus implies uniform consistency of θ_n. Furthermore, if θ₀ is strictly increasing on $\mathcal{A}$ and {n^1/2 [${\theta }_n^{†}(a)-{\theta }_0(a)$] : a ∈ $\mathcal{A}$} converges in distribution, then ${\max }_{a\in \mathcal{A}}\mid {\theta }_n(a)-{\theta }_n^{†}(a)\mid =\text{op}\left(n^{1∕2}\right)$, so that large-sample standard errors for ${\theta }_n^{†}$, are also valid for θ_n. If θ₀ is not strictly increasing on $\mathcal{A}$ but instead has flat regions, then θ_n is more efficient than θ₀ on these regions, and confidence intervals centered around θ_n but based upon the limit theory for ${\theta }_n^{†}$ will be conservative.

3.6. Large-sample results for causal effects

In many applications, in addition to the causal dose response curve a ↦ m₀(a) itself, causal effects of the form (a₁, a₂) ↦ m₀(a₁) – m₀(a₂) are of scientific interest as well. Under the identification conditions discussed in Section 1.2 applied to each of a₁ and a₂, such causal effects are identified with the observed-data parameter θ₀(a₁) – θ₀(a₂). A natural estimator for such a causal effect in our setting is θ_n(a₁) – θ_n(a₂). If the conditions of Theorem 1 hold for both a₁ and a₂, then the continuous mapping theorem implies that ${\theta }_n(a_1)-{\theta }_n(a_2)\stackrel{\mathrm{P}}{\to }{\theta }_0(a_1)-{\theta }_0(a_2)$. However, since Theorem 2 only provides marginal distributional results, and thus does not describe the joint convergence of Z_n(a₁, a₂) := (n^1/3[θ_n(a₁)–θ(a₁)],n^1/3[θ_n(a₂)–θ₀(a₂)–θ₀(a₂)], it cannot be used to determine the large-sample behavior of n^1/3 {[θ_n(a₁) – θ_n(a₂)] – [θ₀(a₁) – θ₀(a₂)]}. The following result demonstrates that such joint convergence can be expected under the aforementioned conditions, and that the bivariate limit distribution of Z_n(a₁, a₂) has independent components.

Theorem 3 (Joint convergence in distribution). If conditions (A1)–(A5) hold for a ∈ {a₁,a₂} ⊂ $\mathcal{A}$ and F₀(a₁), F₀(a₂) ∈ (0,1), then Z_n(a₁, a₂) converges in distribution to ($[4{\tau }_0(a_1){]}^{1∕3}{\mathbb{W}}_1$, $[4{\tau }_0(a_2){]}^{1∕3}{\mathbb{W}}_2$), where ${\mathbb{W}}_1$ and ${\mathbb{W}}_2$ are independent standard Chernoff distributions and the scale parameter τ₀ is as defined in Theorem 2.

Theorem 3 implies that, under the stated conditions, n^1/3 {θ_n(a₁) – θ_n(a₂)] – [θ₀(a₁) – θ₀(a₂)]} converges in distribution to $[4{\tau }_0(a_1){]}^{1∕3}{\mathbb{W}}_1$ – $[4{\tau }_0(a_2){]}^{1∕3}{\mathbb{W}}_2$.

3.7. Use of cross-fitting to avoid empirical process conditions

Theorems 1 and 2 reveal that the statistical properties of θ_n depend on the nuisance estimators μ_n and g_n in two important ways. First, we require in condition (A1) that μ_n or g_n fall in small enough classes of functions, as measured by metric entropy, in order to control certain empirical process remainder terms. Second, we require in conditions (A2)–(A3) that at least one of μ_n or g_n be consistent almost everywhere (for consistency), and in condition (A4) that the product of their rates of convergence be faster than n^−1/3 (for convergence in distribution). In observational studies, researchers can rarely specify a priori correct parametric models for μ₀ and g₀. This motivates use of data-adaptive estimators of these nuisance functions in order to meet the second requirement. However, such estimators often lead to violations of the first requirement, or it may be onerous to determine that they do not. Thus, because it may be difficult to find nuisance estimators that are both data-adaptive enough to meet required rates of convergence and fall in small enough function classes to make empirical process terms negligible, simultaneously satisfying these two requirements can be challenging in practice.

In the context of asymptotically linear estimators, it has been noted that cross-fitting nuisance estimators can resolve this challenge by eliminating empirical process conditions (Zheng and van der Laan, 2011; Belloni et al., 2018; Kennedy, 2019). We therefore propose employing cross-fitting of μ_n and g_n in the estimation of Γ₀ in order to avoid entropy conditions in Theorems 1 and 2. Specifically, we fix V ∈ {2, 3, …, n/2} and suppose that the indices {1, 2, … , n} are randomly partitioned into V sets ${\mathcal{V}}_{n,1}$, ${\mathcal{V}}_{n,2}$, …, ${\mathcal{V}}_{n,V}$. We assume for convenience that N := n/V is an integer and that ∣$\mid {\mathcal{V}}_{n,v}\mid$∣ = N for each ν, but all of our results hold as long as ${\max }_{v}n∕\mid {\mathcal{V}}_{n,v}\mid =\text{op}(1)$. For each ν ∈ {1, 2, … , V}, we define ${\mathcal{T}}_{n,v}≔\{O_i:i\notin {\mathcal{V}}_{n,v}\}$ as the training set for fold ν, and denote by μ_n,ν and g_n,ν the nuisance estimators constructed using only the observations from ${\mathcal{T}}_{n,v}$. We then define pointwise the cross-fitted estimator ${\Gamma }_n^{\circ }$ of Γ₀ as

$${\Gamma }_n^{\circ }(a)≔\frac{1}{V}\sum _{v=1}^V\left\{\frac{1}{N}\sum _{i\in {\mathcal{V}}_{n,v}}{I}_{(-\infty ,a]}(A_i)\left[\frac{Y_i-{\mu }_{n,v}(A_i,W_i)}{g_{n,v}(A_i,W_i)}\right]+\frac{1}{N^2}\sum _{i\in {\mathcal{V}}_{n,v}}{I}_{(-\infty ,a]}(A_i){\mu }_{n,v}(A_i,W_j)\right\}.$$ (3)

Finally, the cross-fitted estimator ${\theta }_n^{\circ }$ of θ₀ is constructed using steps 1–4 outlined in Section 2.2, with Γ_n replaced by ${\Gamma }_n^{\circ }$.

As we now demonstrate, utilizing the cross-fitted estimator ${\theta }_n^{\circ }$ allows us to avoid the empirical process condition (A1b). We first introduce the following two conditions, which are analogues of conditions (A1) and (A2).

(B1) There exist constants C′, δ′, $K_0^{\prime }$, $K_1^{\prime }$, $K_2^{\prime }$, $K_3^{\prime }$ ∈ (0, +∞) such that, almost surely as n → ∞ and for all ν, μ_n,ν and g_n,ν, are contained in classes of functions ${\mathcal{F}}_0^{\prime }$ and ${\mathcal{F}}_1^{\prime }$, respectively, satisfying:

1. $\mid \mu \mid \le K_0^{\prime }$ for all $\mu \in {\mathcal{F}}_0^{\prime }$, and $K_1^{\prime }$ ≤ g ≤ $K_2^{\prime }$ for all g ∈${\mathcal{F}}_1^{\prime }$; and ${\sigma }_0^2(a,w)\le K_3^{\prime }$ for almost all a, ω.

(B2) There exist ${\mu }_{\infty }\in {\mathcal{F}}_0^{\prime }$ and $g_{\infty }\in {\mathcal{F}}_1^{\prime }$ such that max_ν $P_0({\mu }_{n,v}-{\mu }_{\infty }{)}^2\stackrel{\mathrm{P}}{\to }0$ and ${\max }_v{P}_0(g_{n,v}-g_{\infty }{)}^2\stackrel{\mathrm{P}}{\to }0$.

We then have the following analogue of Theorem 1 establishing consistency of the cross-fitted estimator ${\theta }_n^{\circ }$.

Theorem 4 (Consistency of the cross-fitted estimator). If conditions (B1)–(B2) and (A3) hold, then ${\theta }_n^{\circ }(a)\stackrel{\mathrm{P}}{\to }{\theta }_0(a)$ for any a ∈ $\mathcal{A}$ such that F₀(a) ∈ (0,1), θ₀ is continuous at a, and F₀ is strictly increasing in a neighborhood of a. If θ₀ is uniformly continuous and F₀ is strictly increasing on $\mathcal{A}$, then ${\text{sup}}_{a\in {\mathcal{A}}_0}\mid {\theta }_n^{\circ }(a)-{\theta }_0(a)\mid \stackrel{\mathrm{P}}{\to }0$ for any bounded strict subinterval ${\mathcal{A}}_0⊊\mathcal{A}$.

For convergence in distribution, we introduce the following analogue of condition (A4).

(B4) There exists ε₀ > 0 such that:

1. (a) max_ν max{d(μ_n,ν, μ_∞; a, ε₀, S₁), d(g_n,ν, g_∞; a, ε₀, S₂)} = o_P(n^−1/3);

2. (b) max_ν max{d(μ_n,ν, μ_∞; a, ε₀, S₂), d(g_n,ν, g_∞; a, ε₀, S₁)} = o_P(1);

3. (c) max_ν d(μ_n,ν, μ_∞; a, ε₀, S₃)d(g_n,ν, g_∞; a, ε₀, S₃) = o_P(n^−1/3).

We then have the following analogue of Theorem 2 for the cross-fitted estimator ${\theta }_n^{\circ }$.

Theorem 5 (Convergence in distribution for the cross-fitted estimator). If conditions (B1), (B2), (A3), (B4), and (A5) hold, then n^1/3 $[{\theta }_n^{\circ }(a)-{\theta }_0(a)]\stackrel{\mathrm{d}}{\to }[4{\tau }_0(a){]}^{1∕3}\mathbb{W}$ for any a ∈ $\mathcal{A}$ such that F₀(a) ∈ (0,1).

The conditions of Theorems 4 and 5 are analogous to those of Theorems 1 and 2, with the important exception that the entropy condition (A1b) is no longer required. Therefore, the estimators μ_n,ν and g_n,ν may be as data-adaptive as one desires without concern for empirical process terms, as long as they satisfy the boundedness conditions stated in (B1).

4. Construction of confidence intervals

4.1. Wald-type confidence intervals

The distributional results of Theorem 2 can be used to construct a confidence interval for θ₀(a). Since the limit distribution of n^1/3 [θ_n(a) – θ₀(a)] is symmetric around zero, a Wald-type construction seems appropriate. Specifically, writing ${\tau }_0(a)≔{\theta }_0^{\prime }(a){\kappa }_0(a)∕f_0(a)$ and denoting by τ_n(a) any consistent estimator of τ₀(a), a Wald-type 1 – α level asymptotic confidence interval for θ₀(a) is given by

$$\left[{\theta }_n(a)-{\left[\frac{4{\tau }_n(a)}{n}\right]}^{1∕3}{q}_{1-\alpha ∕2},{\theta }_n(a)+{\left[\frac{4{\tau }_n(a)}{n}\right]}^{1∕3}{q}_{1-\alpha ∕2}\right],$$

where q_p denotes the p^th quantile of $\mathbb{W}$. Quantiles of the standard Chernoff distribution have been numerically computed and tabulated on a fine grid (Groeneboom and Wellner, 2001), and are readily available in the statistical programming language R. Estimation of τ₀(a) involves, either directly or indirectly, estimation of ${\theta }_0^{\prime }(a)∕f_0(a)$ and ${\kappa }_0(a)$. We focus first on the former.

We note that ${\theta }_0^{\prime }(a)∕f_0(a)={\psi }_0^{\prime }(F_0(a))$ with ${\psi }_0≔{\theta }_0\circ F_0^{-1}$. This suggests that we could either estimate ${\theta }_0^{\prime }$ and f₀ separately and consider the ratio of these estimators, or that we could instead estimate ${\psi }_0^{\prime }$ directly and compose it with the estimator of F₀ already available. The latter approach has the desirable property that the resulting scale estimator is invariant to strictly monotone transformations of the exposure. As such, this is the strategy we favor. To estimate ${\psi }_0^{\prime }$, we recall that the estimator ψ_n from Section 2 is a step function and is therefore not differentiable. A natural solution consists of computing the derivative of a smoothed version of ψ_n. We have found local quadratic kernel smoothing of points {(u_j, ψ_n (u_j)) : j = 1, 2, … K}, for u_j the midpoints of the jump points of ψ_n, to work well in practice.

Theorem 3 can be used to construct Wald-type confidence intervals for causal effects of the form θ₀(a₁) – θ₀(a₂). We first construct estimates τ_n(a₁) and τ_n(a₂) of the scale parameters τ₀(a₁) and τ₀(a₂), respectively, and then compute an approximation ${\overline{q}}_{n,1-\alpha ∕2}$ of the (1 – α/2)-quantile of $[4{\tau }_n(a_1){]}^{1∕3}{\mathbb{W}}_1$ – $[4{\tau }_n(a_2){]}^{1∕3}{\mathbb{W}}_2$, where ${\mathbb{W}}_1$ and ${\mathbb{W}}_2$ are independent Chernoff distributions, using Monte Carlo simulations, for example. An asymptotic 1 – α level Wald-type confidence interval for ${\theta }_0(a_1)-{\theta }_0(a_2)\text{is then}{\theta }_n(a_1)-{\theta }_n(a_2)\pm {\overline{q}}_{n,1-\alpha ∕2}{n}^{-1∕3}$.

In the next two subsections, we discuss different strategies for estimating the scale factor κ₀(a).

4.2. Scale estimation relying on consistent nuisance estimation

We first consider settings in which both μ_n and g_n are consistent estimators, that is, g_∞ = g₀ and μ_∞ = μ₀. In such cases, we have that ${\kappa }_0(a)=E_0\left[{\sigma }_0^2(a,W)∕g_0(a,W)\right]$ with ${\sigma }_0^2(a,w)$ denoting the conditional variance E₀{[Y – μ₀(a, W)]² ∣ A = a, W = ω}. Any regression technique could be used to estimate the conditional expectation of Z_n := [Y – μ_n(A,W)]² given A and W, yielding an estimator ${\sigma }_n^2(a,w)$ of ${\sigma }_0^2(a,w)$. A plug-in estimator of κ₀(a) is then given by

$${\kappa }_n(a)≔\frac{1}{n}\sum _{i=1}^n\frac{{\sigma }_n^2(a,W_i)}{g_n(a,W_i)}.$$

Provided μ_n, g_n and ${\sigma }_n^2$ are consistent estimators of μ₀, g₀ and ${\sigma }_0^2$, respectively, κ_n(a) is a consistent estimator of κ₀(a). We note that in the special case of a binary outcome, the fact that ${\sigma }_0^2(a,w)={\mu }_0(a,w)[1-{\mu }_0(a,w)]$ motivates the use of μ_n(a, ω)[1 – μ_n(a, ω)] as estimator ${\sigma }_n^2(a,w)$, and thus eliminates the need for further regression beyond the construction of μ_n and g_n. In practice, we typically recommend the use of an ensemble method – for example, the SuperLearner (van der Laan et al., 2007) – to combine a variety of regression techniques, including machine learning techniques, to minimize the risk of inconsistency of μ_n, g_n and ${\sigma }_n^2$.

4.3. Doubly-robust scale estimation

As noted above, Theorem 2 provides the limit distribution of n^1/3 [θ_n(a) – θ₀(a)] even if one of the nuisance estimators is inconsistent, as long as the consistent nuisance estimator converges fast enough. We now show how we may capitalize on this result to provide a doubly-robust estimator of κ₀(a). Since ψ_n is itself a doubly-robust estimator of ψ₀, so will be the proposed estimator ${\psi }_n^{\prime }$ of ${\psi }_0^{\prime }$ and hence also of the resulting estimator τ_n(a) of τ₀(a). This contrasts with the estimator of κ₀(a) described in the previous section, which required the consistency of both μ_n and g_n.

To construct an estimator of κ₀(a) consistent even if either μ_∞ ≠ μ₀ or g_∞ ≠ g₀, we begin by noting that κ₀(a) = lim_h↓0 E₀ [K_h (F₀(A) – F₀(a)) η_∞(Y, A, W)], where K_h : u ↦ h⁻¹ K(uh⁻¹) for some bounded density function K with bounded support, and we have defined

$${\eta }_{\infty }:(y,a,w)\mapsto {\left[\frac{y-{\mu }_{\infty }(a,w)}{g_{\infty }(a,w)}+{\theta }_{\infty }(a)-{\theta }_0(a)\right]}^2.$$

Setting θ_μn := ∫ μ_n(a, ω)Q_n(dω) with Q_n the empirical distribution based on W₁, W₂, …, W_n, we define ${\kappa }_{n,h}^{\ast }(a)≔\frac{1}{n}{\sum }_{i=1}^n{K}_h(F_n(A_i)-F_n(a)){\eta }_n(Y_i,A_i,W_i)$ with η_n obtained by substituting μ_∞, g_∞, and μ_∞ by θ_n, g_n, and θ_μn, respectively, in the definition of η_∞. Under conditions (A1)–(A5), it can be shown that ${\kappa }_{n,h_n}^{\ast }(a)\stackrel{\mathrm{P}}{\to }{\kappa }_0(a)$ by standard kernel smoothing arguments for any sequence h_n → 0. In particular, ${\kappa }_{n,h_n}^{\ast }(a)$ is consistent under the general form of doubly-robustness specified by condition (A3).

To determine an appropriate value of the bandwidth h in practice, we propose the following empirical criterion. We first define the integrated scale γ₀ := ∫ κ₀(a)F₀(da), and construct the estimator γ_n(h) := ∫ κ_n,h(a)F_n(da) for any candidate h > 0. Furthermore, we observe that γ₀ = E₀ [η_∞(Y, A, W)], which suggests the use of the empirical estimator ${\overline{\eta }}_n≔\frac{1}{n}{\sum }_{i=1}^n{\eta }_n(Y_i,A_i,W_i)$. This motivates us to define $h_n^{\ast }≔{\text{argmin}}_h[{\gamma }_n(h)-{\overline{\eta }}_n{]}^2$, that is, the value of h that makes γ_n(h) and ${\overline{\eta }}_n$ closest. The proposed doubly-robust estimator of κ₀(a) is thus ${\kappa }_{n,\text{DR}}(a)≔{\kappa }_{n,h_n^{\ast }}(a)$.

We make two final remarks regarding this doubly-robust estimator of κ₀(a). First, we note that this estimator only depends on A and a through the ranks F_n(A) and F_n(a). Hence, as before, our estimator is invariant to strictly monotone transformations of the exposure A. Second, we note that if μ_n(a, ω) = μ_n(a) does not depend on ω and g_n = 1, κ_n,dr(a) tends to the conditional variance Var₀(Y ∣ A = a), which is precisely the scale parameter appearing in standard isotonic regression.

4.4. Confidence intervals via sample splitting

As an alternative, we note here that the sample-splitting method recently proposed by Banerjee et al. (2019) could also be used to perform inference. Specifically, to implement their approach in our context, we randomly split the sample into m subsets of roughly equal size, perform our estimation procedure on each subset to form subset-specific estimates θ_n,1, θ_n,2, …, θ_n,m, and then define ${\overline{\theta }}_{n,m}(a)≔\frac{1}{n}{\sum }_{j=1}^m{\theta }_{n,j}(a)$. Banerjee et al. (2019) demonstrated that if m > 1 is fixed, then under mild conditions ${\overline{\theta }}_{n,m}$ has strictly better asymptotic mean squared error than θ_n(a), and that for moderate m,

$$\left[{\overline{\theta }}_{n,m}(a)-\frac{{\sigma }_{n,m}(a)}{\sqrt{m}{n}^{1∕3}}{t}_{1-\alpha ∕2,m-1},{\overline{\theta }}_{n,m}(a)+\frac{{\sigma }_{n,m}(z)}{\sqrt{m}{n}^{1∕3}}{t}_{1-\alpha ∕2,m-1}\right]$$ (4)

forms an asymptotic 1 – α level confidence interval for θ₀(a), where ${\sigma }_{n,m}^2(a)≔\frac{1}{m-1}{\sum }_{j=1}^m[{\theta }_{n,j}(a)-{\overline{\theta }}_{n,m}(a){]}^2$ and t_1-α/2,m-1 is the (1 – α/2)-quantile of the t-distribution with m – 1 degrees of freedom.

5. Numerical studies

In this section, we perform numerical experiments to assess the performance of the proposed estimators of θ₀(a) and of the three approaches for constructing confidence intervals, which we also compare to that of the local linear estimator and associated confidence intervals proposed in Kennedy et al. (2017).

In our experiments, we simulate data as follows. First, we generate W ∈ ${\mathbb{R}}^4$ as a vector of four independent standard normal variates. A natural next step would be to generate A given W. However, since our estimation procedures requires estimating the conditional density of U := F₀(A) given W, we instead generate U given W, and then transform U to obtain A. This strategy makes it easier to construct correctly-specified parametric nuisance estimators in the context of these simulations. Given W = ω, we generate U from the distribution with conditional density function ${\overline{g}}_0(u\mid w)=I_{[0,1]}(u)\{\lambda (w)+2u[1-\lambda (w)]\}$ for $\lambda (w)≔0.1+1.8\text{expit}({\beta }^{\mathsf{T}}w)$. We note that ${\overline{g}}_0(u\mid w)\ge 0.1$ for all u ∈ [0,1] and ω ∈ ${\mathbb{R}}^4$, and also, that $\int {\overline{g}}_0(u\mid w)Q_0(dw)=I_{[0,1]}(u)$, so that U is marginally uniform. We then take A to be the evaluation at U of the quantile function of an equal-weight mixture of two normal distributions with means −2 and 2 and standard deviation 1, which implies that A is marginally distributed according to this bimodal normal mixture. Finally, conditionally upon A = a and W = ω, we simulate Y as a Bernoulli random variate with conditional mean function given by μ₀(a, ω) := expit (${\gamma }_1^{\mathsf{T}}\underset{¯}{\mathrm{w}}+{\gamma }_2^{\mathsf{T}}\underset{¯}{\mathrm{w}}a+{\gamma }_3{a}^2$), where w denotes (1,ω). We set $\beta =(-1,-1,1,1{)}^{\mathsf{T}}$, ${\gamma }_1=(-1,-1,-1,1,1{)}^{\mathsf{T}}$, ${\gamma }_2=(3,-1,-1,1,1{)}^{\mathsf{T}}$ and γ₃ = 3 in the experiments we report on.

We estimate the true confounder-adjusted dose-response curve θ₀ using the causal isotonic regression estimator θ_n, the local linear estimator of Kennedy et al. (2017), and the sample-splitting version of θ_n proposed by Banerjee et al. (2019) with m = 5 splits. For the local linear estimator, we use the data-driven bandwidth selection procedure proposed in Section 3.5 of Kennedy et al. (2017). We consider three settings in which either both μ_n and g_n are consistent; only μ_n consistent; and only g_n consistent. To construct a consistent estimator μ_n, we use a correctly specified logistic regression model, whereas to construct a consistent estimator g_n, we use a maximum likelihood estimator based on a correctly specified parametric model. To construct an inconsistent estimator μ_n, we still use a logistic regression model but omit covariates W₃, W₄ and all interactions. To construct an inconsistent estimator g_n, we posit the same parametric model as before but omit W₃ and W₄. We construct pointwise confidence intervals for θ₀ in each setting using the Wald-type construction described in Section 4 using both the plug-in and doubly-robust estimators of κ₀(a). We expect intervals based on the doubly-robust estimator of κ₀(a) to provide asymptotically correct coverage rates for θ₀(a) for each of the three settings, but only expect asymptotically correct coverage rates in the first setting when the plug-in estimator of κ₀(a) is used. We construct pointwise confidence intervals for the local linear estimator using the procedure proposed in Kennedy et al. (2017), and for the sample splitting procedure using the procedure discussed in Section 4.4. We consider the performance of these inferential procedures for values of a between −3 and 3.

The left panel of Figure 1 shows a single sample path of the causal isotonic regression estimator based on a sample of size n = 5000 and consistent estimators μ_n and g_n. Also included in that panel are asymptotic 95% pointwise confidence intervals constructed using the doubly-robust estimator of κ₀(a). The right panel shows the unadjusted isotonic regression estimate based on the same data and corresponding 95% asymptotic confidence intervals. The true causal and unadjusted regression curves are shown in red. We note that θ₀(a) ≠ r₀(a) for a ≠ 0, since the relationship between Y and A is confounded by W, and indeed the unadjusted regression curve does not have a causal interpretation. Therefore, the marginal isotonic regression estimator will not be consistent for the true causal parameter. In this data-generating setting, the causal effect of A on Y is larger in magnitude than the marginal effect of A on Y in the sense that θ₀(a) has greater variation over values of a than does r₀(a).

Figure 1:

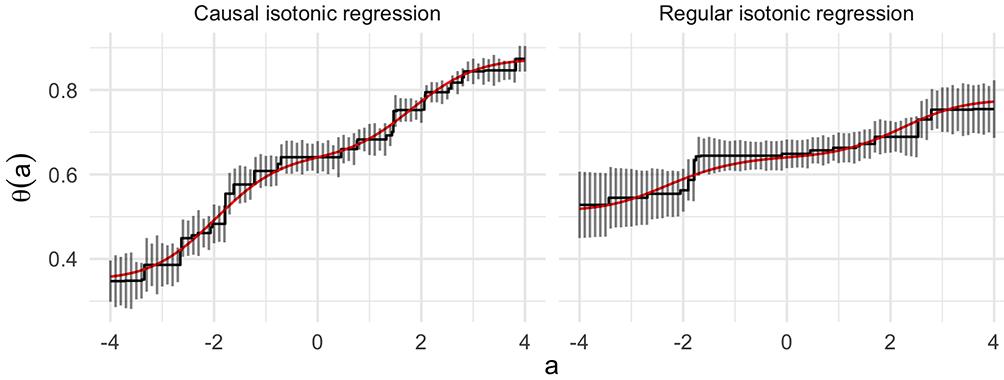
Causal isotonic regression estimate using consistent nuisance estimators μ_n and g_n (left), and regular isotonic regression estimate (right). Pointwise 95% confidence intervals constructed using the doubly-robust estimator are shown as vertical bars. The true functions are shown in red.

We perform 1000 simulations, each with n ∈ {500,1000, 2500, 5000} observations. Figure 2 displays the empirical standard error of the three considered estimators over these 1000 simulated datasets as a function of a and for each value of n. We first note that the standard error of the local linear estimator is smaller than that of θ_n, which is expected due to the faster rate of convergence of the local linear estimator. The sample splitting procedure also reduces the standard error of θ_n. Furthermore, the standard deviation of the local linear estimator appears to decrease faster than n^−1/3, whereas the standard deviation of the estimators based on θ_n do not, in line with the theoretical rates of convergence of these estimators. We also note that inconsistent estimation of the propensity has little impact on the standard errors of any of the estimators, but inconsistent estimation of the outcome regression results in slightly larger standard errors.

Figure 2:

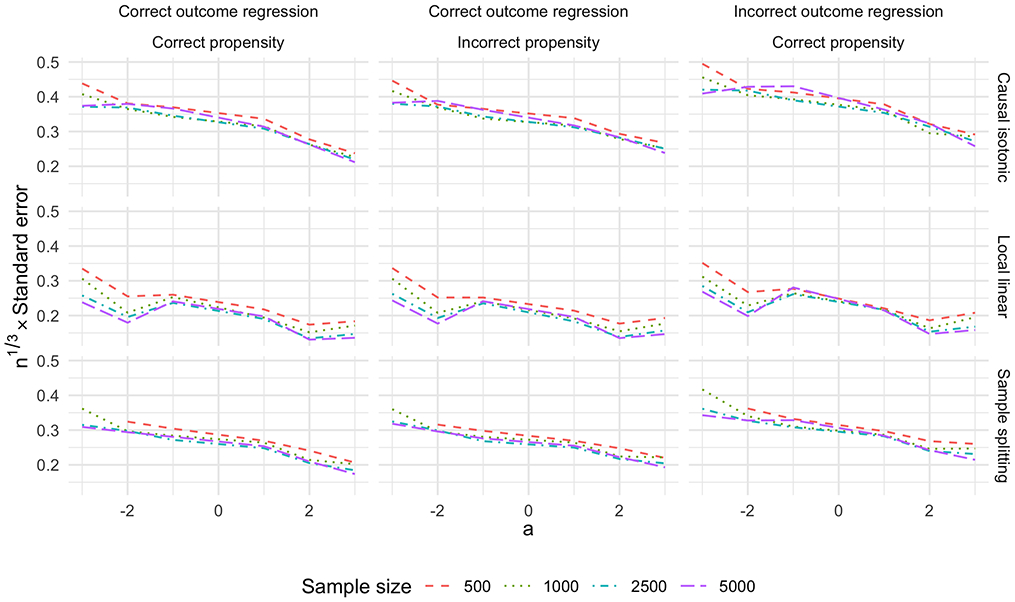
Standard error of the three estimators scaled by n^1/3 as a function of n for different values of a and in contexts in which μ_n and g_n are either consistent or inconsistent, computed empirically over 1000 simulated datasets of different sizes.

Figure 3 displays the absolute bias of the three estimators. For most values of a, the estimator θ_n proposed here has smaller absolute bias than the local linear estimator, and its absolute bias decreases faster than n^−1/3. The absolute bias of the local linear estimator depends strongly on a, and in particular is largest where the second derivative of θ₀ is large in absolute value, agreeing with the large-sample theory described in Kennedy et al. (2017). The sample splitting estimator has larger absolute bias than θ_n because it inherits the bias of θ_n/m. The bias is especially large for values of a in the tails of the marginal distribution of A.

Figure 3:

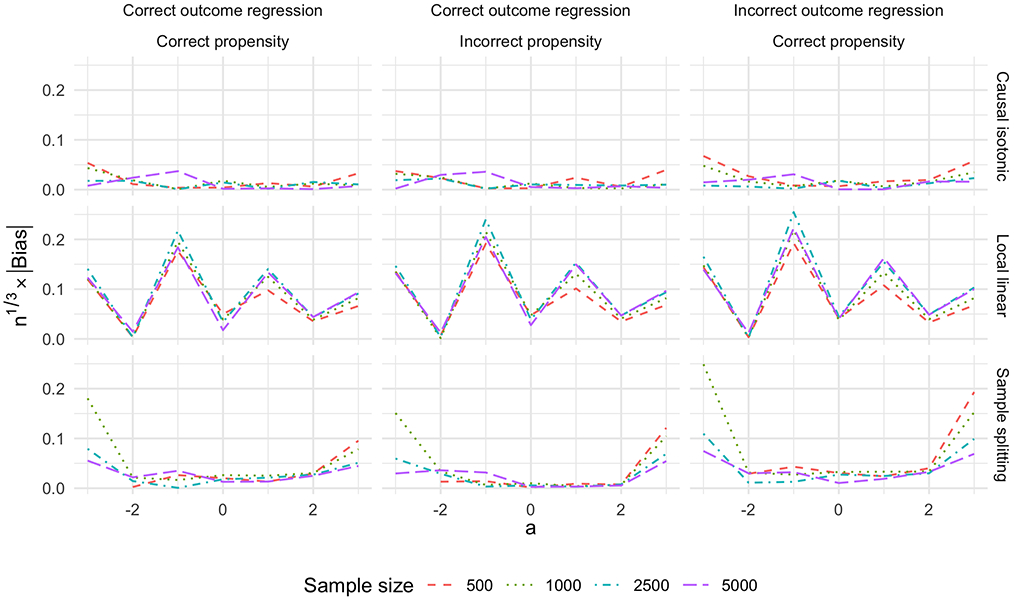
Absolute bias of the three estimators scaled by n^1/3 as a function of n for different values of a and in contexts in which μ_n and g_n are either consistent or inconsistent, computed empirically over 1000 simulated datasets of different sizes.

Figure 4 shows the empirical coverage of nominal 95% pointwise confidence intervals for a range of values of a for the four methods considered. For both the plug-in and doubly-robust intervals centered around θ_n, the coverage improves as n grows, especially for values of a in the tails of the marginal distribution of A. Under correct specification of outcome and propensity regression models, the plug-in method attains close to nominal coverage rates for a between −3 and 3 by n = 1000. When the propensity estimator is inconsistent, the plug-in method still performs well in this example, although we do not expect this to always be the case. However, when μ_n is inconsistent, the plug-in method is very conservative for positive values of a. The doubly-robust method attains close to nominal coverage for large samples as long as one of g_n or μ_n is consistent. Compared to the plug-in method, the doubly-robust method requires larger sample sizes to achieve good coverage, especially for extreme values of a. This is because the doubly-robust estimator of κ₀(a) has a slower rate of convergence than does the plug-in estimator, as demonstrated by box plots of these estimators provided in Supplementary Material.

Figure 4:

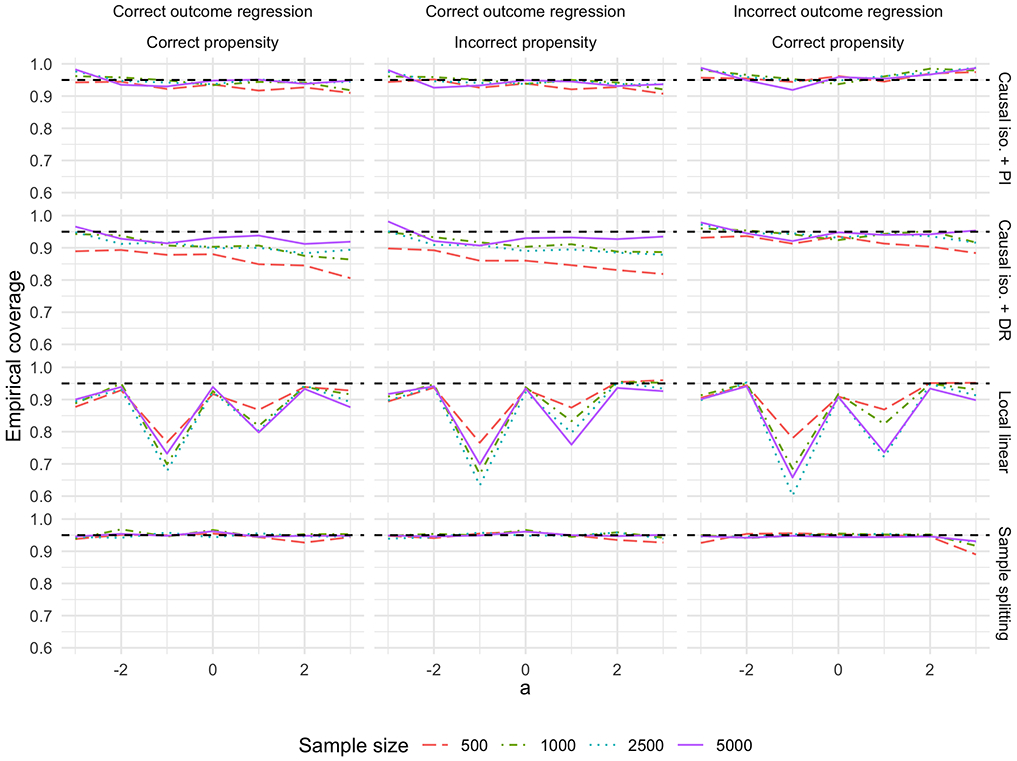
Observed coverage of pointwise 95% confidence intervals using θ_n and the plug-in method (top row), θ_n and eht doubly-robust method (second row), the local linear estimator and associated intervals (third row), and the sample splitting estimator (bottom row), considered for different values of a and computed empirically over 1000 simulated datasets of different sizes. Columns indicate whether μ_n and g_n is consistent or not. Black dashed lines indicate the nominal coverage rate.

The confidence intervals associated with the local linear estimator have poor coverage for values of a where the bias of the estimator is large, which, as mentioned above, occurs when the second derivative of θ₀ is large in absolute value. Overall, the sample splitting estimator has excellent coverage, except perhaps for values of a in the tails of the marginal distribution of A when n is small or moderate, in which case the coverage is near 90%.

We also conducted a small simulation study to illustrate the performance of the proposed procedures when machine learning techniques are used to construct μ_n and g_n. To consistently estimate μ₀, we used a Super Learner (van der Laan et al., 2007) with a library consisting of generalized linear models, multivariate adaptive regression splines, and generalized additive models. To consistently estimate g₀, we used the method proposed by Díaz and van der Laan (2011) with covariate vector (W₁, W₂, W₃, W₄). To produce inconsistent estimators μ_n or g_n, we used the same estimators but omitted covariates W₁ and W₂. We also considered the estimator ${\theta }_n^{\circ }$ obtained via cross-fitting these nuisance parameters, as discussed in Section 3.7, as well as the local linear estimator. Due to computational limitations, we performed 1000 simulations at sample size n = 1000 only. Figure 5 shows the coverage of nominal 95% confidence intervals. The plug-in intervals achieve very close to nominal coverage under consistent estimation of both nuisances, and also achieve surprisingly good coverage rates when the propensity is inconsistently estimated. The plug-in intervals are somewhat conservative when the outcome regression is inconsistently estimated. The doubly-robust method is anti-conservative under inconsistent estimation of both nuisances and also when the propensity is inconsistently estimated, with coverage rates mostly between 90 and 95%. Good coverage rates are also achieved when the outcome regression is inconsistently estimated. These results suggest that the doubly-robust intervals may require larger sample sizes to achieve good coverage, particularly when machine learning estimators are used for μ_n and g_n. The plug-in intervals appear to be relatively robust to moderate misspecification of models for the nuisance parameters in smaller samples. Histograms of the estimators of κ₀(a) and ${\psi }_0^{\prime }$(a) are provided in the Supplementary Material. Confidence intervals based on the local linear estimator show a similar pattern as in the previous simulation study, undercovering where the second derivative of the true function is large in absolute value. Cross-fitting had little impact on coverage.

Figure 5:

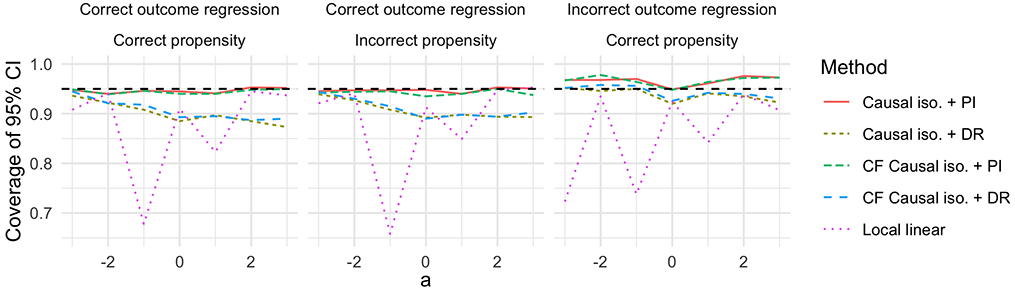
Observed coverage of pointwise 95% doubly-robust and plug-in confidence intervals using machine learning estimators based on simulated data including n = 1000 observations. Columns indicate whether μ_n and g_n are consistent or not. Black dashed lines indicate the nominal coverage rate. CF stands for cross-fitted; PI for plug-in; DR for doubly-robust.

As noted above, we found in our numerical experiments that the plug-in estimator of the scale parameter was surprisingly robust to inconsistent estimation of the nuisance parameters, while its doubly-robust estimator was anti-conservative even when the nuisance parameters were estimated consistently. This phenomenon can be explained in terms of the bias and variance of the two proposed scale estimators. On one hand, under inconsistent estimation of any nuisance function, the plug-in estimator of the scale parameter is biased, even in large samples. However, its variance decreases relatively quickly with sample size, since it is a simple empirical average of estimated functions. On the other hand, the doubly-robust estimator is asymptotically unbiased, but its variance decreases much slower with sample size. These trends can be observed in the figures provided in the Supplementary Material. In sufficiently large samples, the doubly-robust estimator is expected to outperform the plug-in estimator in terms of mean squared error when one of the nuisances is inconsistently estimated. However, the sample size required for this trade-off to significantly affect confidence interval coverage depends on the degree of inconsistency. While we did not see this tradeoff occur at the sample sizes used in our numerical experiments, we expect the benefits of the doubly-robust confidence interval construction to become apparent in smaller samples in other settings.

6. BMI and T-cell response in HIV vaccine studies

The scientific literature indicates that, for several vaccines, obesity or BMI is inversely associated with immune responses to vaccination (see, e.g. Sheridan et al., 2012; Young et al., 2013; Jin et al., 2015; Painter et al., 2015; Liu et al., 2017). Some of this literature has investigated potential mechanisms of how obesity or higher BMI might lead to impaired immune responses. For example, Painter et al. (2015) concluded that obesity may alter cellular immune responses, especially in adipose tissue, which varies with BMI. Sheridan et al. (2012) found that obesity is associated with decreased CD8+ T-cell activation and decreased expression of functional proteins in the context of influenza vaccines. Liu et al. (2017) found that obesity reduced Hepatitis B immune responses through “leptin-induced systemic and B cell intrinsic inflammation, impaired T cell responses and lymphocyte division and proliferation.” Given this evidence of a monotone effect of BMI on immune responses, we used the methods presented in this paper to assess the covariate-adjusted relationship between BMI and CD4+ T-cell responses using data from a collection of clinical trials of candidate HIV vaccines. We present the results of our analyses here.

In Jin et al. (2015), the authors compared the compared the rate of CD4+ T cell response to HIV peptide pools among low (BMI < 25) medium (25 ≤ BMI < 30) and high (BMI ≥ 30) BMI participants, and they found that low BMI participants had a statistically significantly greater response rate than high BMI participants using Fisher’s exact test. However, such a marginal assessment of the relationship between BMI and immune response can be misleading because there are known common causes, such as age and sex, of both BMI and immune response. For this reason, Jin et al. (2015) also performed a logistic regression of the binary CD4+ responses against sex, age, BMI (not discretized), vaccination dose, and number of vaccinations. In this adjusted analysis, they found a significant association between BMI and CD4+ response rate after adjusting for all other covariates (OR: 0.92; 95% CI: 0.86, 0.98; p=0.007). However, such an adjusted odds-ratio only has a formal causal interpretation under strong parametric assumptions. As discussed in Section 1.2, the covariate-adjusted dose-response function θ₀ is identified with the causal dose-response curve without making parametric assumptions, and is therefore of interest for understanding the continuous covariate-adjusted relationship between BMI and immune responses.

We note that there is some debate in the causal inference literature about whether exposures such as BMI have a meaningful interpretation in formal causal modeling. In particular, some researchers suggest that causal models should always be tied to hypothetical randomized experiments (see, e.g., Bind and Rubin, 2019), and it is difficult to imagine a hypothetical randomized experiment that would assign participants to levels of BMI. From this perspective, it may therefore not be sensible to interpret θ₀(a) in a causal manner in the context of this example. Nevertheless, as discussed in the introduction, we contend that θ₀(a) is still of interest. In particular, it provides a meaningful summary of the relationship between BMI and immune response accounting for measured potential confounders. In this case, we interpret θ0(a) as the probability of immune response in a population of participants with BMI value a but sex, age, vaccination dose, number of vaccinations, and study with a similar distribution to that of the entire study population.

We pooled data from the vaccine arms of 11 phase I/II clinical trials, all conducted through the HIV Vaccine Trials Network (HVTN). Ten of these trials were previously studied in the analysis presented in Jin et al. (2015), and a detailed description of the trials are contained therein. The final trial in our pooled analysis is HVTN 100, in which 210 participants were randomized to receive four doses of the ALVAC-HIV vaccine (vCP1521). The ALVAC-HIV vaccine, in combination with an AIDSVAX boost, was found to have statistically significant vaccine efficacy against HIV-1 in the RV-144 trial conducted in Thailand (Rerks-Ngarm et al., 2009). CD4+ and CD8+ T-cell responses to HIV peptide pools were measured in all 11 trials using validated intracellular cytokine staining at HVTN laboratories. These continuous responses were converted to binary indicators of whether there was a significant change from baseline using the method described in Jin et al. (2015). We analyzed these binary responses at the first visit following administration of the last vaccine dose-either two or four weeks after the final vaccination depending on the trial. After accounting for missing responses from a small number of participants, our analysis datasets consisted of a total of n = 439 participants for the analysis of CD4+ responses and n = 462 participants for CD8+ responses. Here, we focus on analyzing CD4+ responses; we present the analysis of CD8+ responses in Supplementary Material.

We assessed the relationship between BMI and T-cell response by estimating the covariate-adjusted dose-response function θ₀ using our cross-fitted estimator ${\theta }_n^{\circ }$, the local linear estimator, and the sample-splitting version of our estimator with m = 5 splits. We adjusted for sex, age, vaccination dose, number of vaccinations, and study. We estimated μ₀ and g₀ as in the machine learning-based simulation study described in Section 5, and constructed confidence intervals for our estimator using both the plug-in and doubly-robust estimators described above.

Figure 6 presents the estimated probability of a positive CD4+ T-cell response as a function of BMI for BMI values between the 0.05 and 0.95 quantile of the marginal empirical distribution of BMI using our estimator (left panel), the local linear estimator (middle panel), and the sample-splitting estimator (right panel). Pointwise 95% confidence intervals are shown as dashed/dotted lines. The three methods found qualitatively similar results. We found that the change in probability of CD4+ response appears to be largest for BMI < 20 and BMI > 30. We estimated the probability of having a positive CD4+ T-cell response, after adjusting for potential confounders, to be 0.52 (95% doubly-robust CI: 0.44–0.59) for a BMI of 20, 0.47 (0.42–0.52) for a BMI of 25, 0.47 (0.32–0.62) for a BMI of 30, and 0.29 (0.12–0.47) for a BMI of 35. We estimated the difference between these probabilities for BMIs of 20 and 35 to be 0.22 (0.03{0.41).

Figure 6:

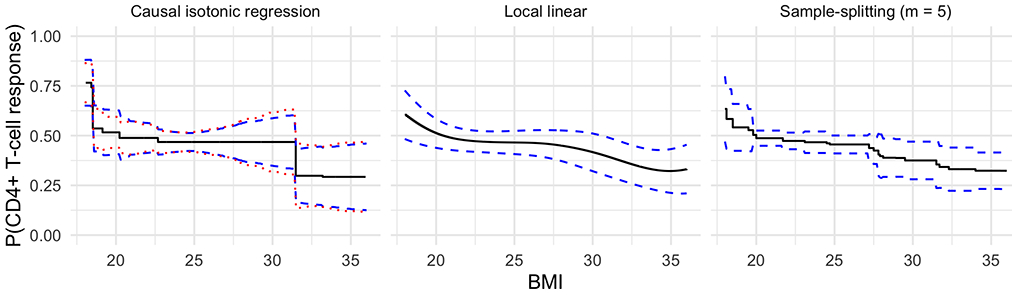
Estimated probabilities of CD4+ T-cell response and 95% pointwise confidence intervals as a function of BMI, adjusted for sex, age, number of vaccinations received, vaccine dose, and study. The left panel displays the estimator proposed here, the middle panel the local linear estimator of Kennedy et al. (2017), and the right panel the sample-splitting version of our estimator with m = 5 splits. In the left panel, the blue dashed lines are confidence intervals based on the plug-in estimator of the scale parameter, and the dotted lines are based on the doubly-robust estimator of the scale parameter.

7. Concluding remarks

The work we have presented in this paper lies at the interface of causal inference and shape-constrained nonparametric inference, and there are natural future directions building on developments in either of these areas. Inference on a monotone causal dose-response curve when outcome data are only observed subject to potential coarsening, such as censoring, truncation, or missingness, is needed to increase the applicability of our proposed method. To tackle such cases, it appears most fruitful to follow the general primitive strategy described in Westling and Carone (2019) based on a revised causal identification formula allowing such coarsening.

It would be useful to develop tests of the monotonicity assumption, as Durot (2003) did for regression functions. Such a test could likely be developed by studying the large-sample behavior of $\Vert {\overline{\Psi }}_n-{\Psi }_n{\Vert }_p$ under the null hypothesis that θ₀ is monotone, where Ψ_n and ${\overline{\Psi }}_n$ are the primitive estimator and its greatest convex minorant as defined in Section 2.2. Such a result would likely permit testing with a given asymptotic size when θ₀ is strictly increasing, and asymptotically conservative inference otherwise. It would also be useful to develop methods for uniform inference. Uniform inference is difficult in this setting due to the fact that {n^1/3 [θ_n(a) – θ₀(a)] : a ∈ $\mathcal{A}$} does not convergence weakly as a process in the space ${\ell }^{\infty }(\mathcal{A})$ of bounded functions on $\mathcal{A}$ to a tight limit process. Indeed, Theorem 3 indicates that {n^1/3[θ_n(a) – θ₀(a)] : a ∈ $\mathcal{A}$} converges to an independent white noise process, which is not tight, so that this convergence is not useful for constructing uniform confidence bands. Instead, it may be possible to extend the work of Durot et al. (2012) to our setting (and other generalized Grenander-type estimators) by demonstrating that log n [$[(n∕\log n{)}^{1∕3}{\text{sup}}_{a\in {\mathcal{A}}_n}\mid {\theta }_n(a)-{\theta }_0(a)\mid ∕{\alpha }_0-c_n]$] converges in distribution to a non-degenerate limit for some constant α₀ depending upon P₀, a deterministic sequence c_n, and a suitable sequence of subsets ${\mathcal{A}}_n$ increasing to $\mathcal{A}$. Developing procedures for uniform inference and tests of the monotonicity assumption are important areas for future research.

An alternative approach to estimating a causal dose-response curve is to use local linear regression, as Kennedy et al. (2017) did. As is true in the context of estimating classical univariate functions such as density, hazard, and regression functions, there are certain trade-offs between local linear smoothing and monotonicity-based methods. On the one hand, local linear regression estimators exhibit a faster n^−2/5 rate of convergence whenever optimal tuning rates are used and the true function possesses two continuous derivatives. However, the limit distribution involves an asymptotic bias term depending on the second derivative of the true function, so that confidence intervals based on optimally-chosen tuning parameters provide asymptotically correct coverage only for a smoothed parameter rather than the true parameter of interest. In contrast, monotonicity-constrained estimators such as the estimator proposed here exhibit an n^−1/3 rate of convergence whenever the true function is strictly monotone and possesses one continuous derivative, do not require choosing a tuning parameter, are invariant to strictly increasing transformations of the exposure, and their limit theory does not include any asymptotic bias (as illustrated by Theorem 2). We note that both estimators achieve the optimal rate of convergence for pointwise estimation of a univariate function under their respective smoothness constraints. In our view, the ability to perform asymptotically valid inference using a monotonicity-constrained estimator is one of the most important benefits of leveraging the monotonicity assumption rather than using smoothing methods. This advantage was evident in our numerical studies when comparing the isotonic estimator proposed here and the local linear method of Kennedy et al. (2017). Under-smoothing can be used to construct calibrated confidence intervals using kernel-smoothing estimators, but performing adequate under-smoothing in practice is challenging.

The two methods for pointwise asymptotic inference we presented require estimation of the derivative ${\theta }_0^{\prime }(a)$ and the scale parameter κ₀(a). We found that the plug-in estimator of κ₀(a) had low variance but possibly large bias depending on the levels of inconsistency of μ_n and g_n, and that its doubly-robust estimator instead had high variance but low bias as long as either μ_n or g_n is consistent. In practice, we found the low variance of the plug-in estimator to often outweigh its bias, resulting in better coverage rates for intervals based on the plug-in estimator of κ₀(a), especially in samples of small and moderate sizes. Whether a doubly-robust estimator of κ₀(a) with smaller variance can be constructed is an important question to be addressed in future work. We found that sample splitting with as few as m = 5 splits provided doubly-robust coverage, and the sample splitting estimator also had smaller variance than the original estimator, at the expense of some additional bias.

It would be even more desirable to have inferential methods that do not require estimation of additional nuisance parameters or sample splitting. Unfortunately, the standard nonparametric bootstrap is not generally consistent in Grenander-type estimation settings, and although alternative bootstrap methods have been proposed, to our knowledge, all such proposals require the selection of critical tuning parameters (Kosorok, 2008; Sen et al., 2010). Likelihood ratio-based inference for Grenander-type estimators has proven fruitful in a variety of contexts (see, e.g. Banerjee and Wellner, 2001; Groeneboom and Jongbloed, 2015), and extending such methods to our context is also an area of significant interest in future work.