Structural, Spectroscopic, Electrochemical, and Magnetic Properties for Manganese(II) Triazamacrocyclic Complexes

Abstract

We report the synthesis of [Mn(tacud)₂](OTf)₂ (1) (tacud = 1,4,8-triazacycloundecane), [Mn(tacd)₂](OTf)₂ (2) (tacd = 1,4,7-triazacyclodecane), and [Mn(tacn)₂](OTf)₂ (3) (tacn = 1,4,7-triazacyclononane). Electrochemical measurements on the Mn^III/II redox couple show that complex 1 has the largest anodic potential of the set (E_1/2 = 1.16 V vs NHE, ΔE_p = 106 mV) compared to 2 (E_1/2 = 0.95 V, ΔE_p = 108 mV) and 3 (E_1/2 = 0.93 V, ΔE_p = 96 mV). This is due to the fact that 1 has the fewest 5-membered chelate rings and thus is least stabilized. Magnetic studies of 1−3 revealed that all complexes remain high spin throughout the temperature range investigated (2 – 300 K). X-band EPR investigations in methanol glass indicated that the manganese(II) centers for 2 and 3 resided in a more distorted octahedral geometric configuration compared to 1. To ease spectral interpretation and extract ZFS parameters, we performed high-frequency high-field EPR (HFEPR) at frequencies above 200 GHz and a field of 7.5 T. Simulation of the spectral data yielded g = 2.0013 and D = −0.031 cm⁻¹ for 1, g = 2.0008, D = −0.0824 cm⁻¹, |E/D| = 0.12 for 2, and g = 2.00028, D = −0.0884 cm⁻¹ for 3. These results are consistent with 3 possessing the most distorted geometry. Calculations (PBE0/6–31G(d)) were performed on 1−3. Results show that 1 has the largest HOMO-LUMO gap energy (6.37 eV) compared to 2 (6.12 eV) and 3 (6.26 eV). Complex 1 also has the lowest HOMO energies indicating higher stability.

1. Introduction

Mononuclear manganese(II) centers are found in many biological systems. They include superoxide dismutase (MnSOD) [1,2], oxalate oxidase (OxOx) [3,4], oxalate decarboxylase (OxDC) [5–7], quercetin 2,3-dioxygenase (Mn-QDO) [8–10] lipoxygenase (Mn-LOX) [11,12] and galactotransferase [13]. In the majority of cases, ligand donor sets are comprised of oxygen and/or nitrogen atoms. Understanding how the ligand environment influences the reactivities of the manganese centers can be explored through synthetic model studies. Cyclic triamines such as 1,4,7-triazacyclononane (tacn) are well established building blocks for the construction of active site models for metalloenzymes [4,14–26]. Complexes of manganese tacn complexes have been explored [27–36]. The properties of these complexes is compared with their geometry and thus with their electronic structure. Hence, a precise understanding of the coordination environment of the central metal ion is required. X-band EPR spectroscopy (9.4 GHz) has been used to study several biological manganese(II) sites [37–40]. A high spin Mn(II) ion (3d⁵) is characterized by the electronic spin S = 5/2 and a nuclear spin I = 5/2. A typical manganese(II) EPR spectrum for mononuclear complexes at high temperature under very dilute condition with small zero field splitting (ZFS) parameters shows a characteristic sextuplet near g ≈ 2.0. With increasing ZFS the X-band spectrum becomes broader and more complicated and the low-field conditions make straightforward interpretation difficult. To simplify and better understand the spectra, one can record the spectra at higher microwave frequencies such as 35 GHz (Q-band) [41,42], 95 GHz (W-band) or even higher, up to THz which is commonly known as high-field EPR (HFEPR) [37,41,43–52].

In this study we present the synthesis, structure and characterization of three manganese(II) complexes supported by 1,4,8-triazacycloundecane (tacud), 1,4,7-triazacyclodecane (tacd), and 1,4,7-triazacyclononane (tacn) (Scheme 1). The complexes are [Mn(tacud)₂](OTf)₂ (1), [Mn(tacd)₂](OTf)₂ (2), and [Mn(tacn)₂](OTf)₂ (3). Complexes 1−3 have been characterized by X-ray crystallography, variable temperature magnetic susceptibility, cyclic voltammetry, as well as X-band and high-frequency high-field EPR. Calculations (DFT) have also been performed on these complexes. The relationship between structural, magnetic, spectroscopic, and calculated properties for 1−3 are discussed.

Scheme 1.

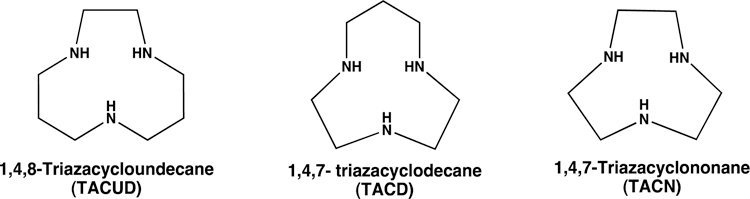
Triaza macrocyclic ligands.

2. Experimental section

2.1. Materials and methods

Mn(OTf)₂∙2CH₃CN was prepared according to a literature procedure [53]. 1,4,8-Triazacycloundecane trihydrobromide [54] and the free-base form (tacud) [55] were prepared according to literature procedures. The ligands tacn and tacd were synthesized according to published methods [56]. Air sensitive manipulations were performed using an Innovative Technologies, Inc. nitrogen-filled glovebox or standard Schlenk techniques. Pure dry solvents were obtained using a solvent purification system (Innovative Technologies, Inc.). Samples were heated in vacuum prior to submission for elemental analysis (Atlantic Microlab, Inc., Norcross, GA).

2.2. Synthesis

2.2.1. [Mn(tacud)₂](OTf)₂ (1)

To a stirring solution of Mn(OTf)₂∙2CH₃CN (123 mg, 0.283 mmol) in 2 mL DMF was added freshly distilled tacud (89 mg, 0.566 mmol) dissolved in 1 mL DMF. After 1 h of stirring, the solution was filtered and placed in an ether diffusion chamber. After 24 h, colorless crystals were deposited. The crystals were collected and washed with ether. Yield: 124.7 mg (65.9%). Anal. Calcd for C₁₈H₃₈F₆MnN₆O₆S₂ (2): C, 32.38; H, 5.74; N, 12.59. Found: C, 32.37; H, 5.64; N, 12.39. FTIR (cm⁻¹, KBr, intensive bands only): 3270 (s), 2937 (s), 2889 (s), 1469 (m), 1434 (m), 1381 (m), 1291 (s), 1169 (s), 1120 (s), 1098 (s), 1028 (s), 988 (s), 918 (m), 867 (s), 818 (w) cm⁻¹.

2.2.2. [Mn(tacd)₂](OTf)₂ (2)

To a stirring solution of Mn(OTf)₂∙2CH₃CN (122 mg, 0.280 mmol) in 2 mL DMF was added tacd (81.1 mg, 0.5612 mmol) dissolved in 1 mL DMF. After 1 h of stirring, the solution was filtered and placed in an ether diffusion chamber. After 24 h, colorless crystals were deposited. The crystals were collected and washed with ether. Yield: 114.6 mg (64%). Anal. Calcd for C₁₆H₃₄F₆MnN₆O₆S₂ (2): C, 30.05; H, 5.36; N, 13.14. Found: C, 30.21; H, 5.32; N, 12.92. FTIR (cm⁻¹, KBr, intensive bands only): 3264 (s), 2955 (s), 1671 (w), 1466 (s), 1383 (s), 1291 (s), 1170 (s), 1059 (s), 978 (s), 877 (s), 825 (s), 628 (s), 574 (s), 521 (s), 438 (m) cm⁻¹.

2.2.3. [Mn(tacn)₂](OTf)₂ (3)

To a stirring solution of Mn(OTf)₂∙2CH₃CN (123 mg, 0.283 mmol) in 2 mL DMF was added tacn (73.1 mg, 0.566 mmol) dissolved in 1 mL DMF. After 1 h of stirring, the solution was filtered and placed in an ether diffusion chamber. After 24 h, clear crystals were deposited. The crystals were collected and washed with ether. Yield: 148.9 mg (86%). Anal. Calcd for C₁₄H₃₀F₆MnN₆O₆S₂ (3): C, 27.50; H, 4.95; N, 13.74. Found: C, 27.52; H, 4.90; N, 13.48. FTIR (cm⁻¹, KBr, intensive bands only): 3297 (s), 2925 (m), 1461 (m), 1261 (s), 1103 (m), 1028 (s), 914 (s), 864 (m), 808 (w), 637 (s), 573 (m), 517 (s) cm⁻¹.

2.3. Physical Measurements

FT-IR spectra were measured on a BioRad FTS 175C instrument. Magnetic susceptibilities were measured using a Quantum Design MPMS SQUID susceptometer calibrated with a 765-Palladium standard purchased from NIST (formally NSB). Measurements on polycrystalline samples were taken in the temperature range 2–300 K with H = 0.1 T. Samples were loaded into plastic containers under nitrogen. The very small diamagnetic contribution of the sealed plastic container had a negligible effect on the overall magnetization, which was dominated by the sample. For the electrochemical measurements, a Pt electrode was used as the working electrode. Pt wire and Ag/AgCl (in saturated KCl) were used as counter electrode and reference electrode, respectively. Potentials were converted to NHE (the normal hydrogen electrode) by adding 0.200 V to the measured potential and all measurements were performed at 23 °C. Cyclic voltammograms were obtained with a Bioanalytical Systems, Inc. potentiostat controlled by Epsilon Electrochemical Workstation software. The supporting electrolyte was 0.1 M TBAPF₆. Measurements were externally referenced to ferrocene and all electrochemical measurements were performed under dry dinitrogen. X-Band EPR spectra were recorded at 77 K on a Varian Century Series X-band (9.3 GHz) EPR spectrometer with an E-4531 dual cavity, 9 in. magnet and a 200 mW klystron. Data recording was carried out employing ESRTAK software and ‘ferman.scn” program. HFEPR (>100 GHz) spectra were collected on the 7.5 T transmission EPR spectrometer at the National High Magnetic Field Laboratory in Tallahassee/FL [57]. Samples were prepared in dry methanol in a glovebox under nitrogen atmosphere and flame sealed. To facilitate the HFEPR measurements the sample tubes had to be broken while the content was frozen at liquid nitrogen temperatures. The frozen samples were then loaded into the pre-cooled probe and re-immersed in liquid nitrogen, following which the probe was loaded into the precooled helium cryostat. Due to hysteresis in the magnet used at high field all spectra had to be field corrected. This was done by introducing a high field standard (in our case atomic hydrogen trapped in an octaisobutylsilsesquioxane cage) [58]. Sweeps were performed in both directions at each frequency with the field standard and the experimental signal adjusted to the simulated hydrogen radical position. Experimental spectra without the field standard were then adjusted to the position of the same spectrum collected with the field standard.

2.4. X-ray crystallography

Complexes 1–3 were obtained by diffusing diethyl ether into a solution of these complexes in DMF. All complexes formed as colorless needles. The crystals were placed onto the tip of a 0.1 mm diameter glass capillary tube or fiber and mounted on a Bruker SMART APEX II CCD Platform diffractometer for data collection at 100.0(1) K [59]. The full data collection was carried out using MoKα radiation (graphite monochromator). The intensity data were corrected for absorption and decay (SADABS) [60]. Final cell constants were calculated from the xyz centroids of 4034 reflection after integration (SAINT) [61]. The structures were solved using SIR-97 [62] and refined using SHELXL-97 [63]. Direct-methods provided most non-hydrogen atoms from the E-map. Full-matrix least squares/difference Fourier cycles were performed which located the remaining non-hydrogen atoms. All non-hydrogen atoms were refined with anisotropic displacement parameters. All hydrogen atoms were placed in ideal positions and refined as riding atoms with relative isotropic displacement parameters. Refer to Table 1 for additional crystal and refinement information.

Table 1.

Crystallographic data and refinement parameters for [Mn(tacud)₂](OTf)₂ (1), [Mn(tacd)₂](OTf)₂ (2) and [Mn(tacn)₂](OTf)₂ (3)

	1	2	3
formula	C18H38MnF6N6O6S2	C16H34MnF6N6O6S2	C14H30MnF6N6O6S2
form. wt.(g/mol)	667.60	639.55	611.50
T (K)	100.0(1)	100.0(1)	100.0(1)
λ (Å)	0.71073	0.71073	0.71073
cryst. system	Triclinic	Monoclinic	Orthorhombic
space group	$P\overline{1}$	P21/c	Pbca
a (Å)	8.2285(7)	7.7340(6)	12.4706(12)
b (Å)	12.8318(10)	15.9119(12)	14.0519(13)
c (Å)	14.1406(12)	10.4714(8)	27.491(3)
α (deg)	87.615(2)	90	90
β(deg)	76.990(2)	98.749(2)	90
γ(deg)	73.671(2)	90	90
Volume (Å3)	1395.7(4)	1273.64(17)	4817.5(8)
Z	2	2	8
ρcalc. (Mg/m3)	1.589	1.668	1.686
R1[I>2σ(I)]	0.0367	0.0449	0.0379
wR2	0.0892	0.0934	0.0873

2.5. Computational details

Quantum chemical calculations providing energy minimized molecular geometries, molecular orbitals (HOMO-LUMO), and vibrational spectra for complexes 1−3 were carried out using density functional theory (DFT) as implemented in the GAUSSIAN09 (Rev. C.01) program package [64]. We employed the hybrid functional PBE0 [65] containing 25% of exact exchange and the basis set 6–31G(d) [66]. Full ground state geometry optimization was carried out without any symmetry constraints. Only the default convergence criteria were used during the geometry optimizations. The initial geometry was taken from the crystal structure coordinates in the sextet state. Optimized structures were confirmed to be local minima (no imaginary frequencies for both cases). Experimental and computational geometric parameters are summarized in Table 2. Molecular Orbitals were generated using Avogadro [67] (an open-source molecular builder and visualization tool, Version1.1.0. http://avogadro.openmolecules.net/).

Table 2.

Selected bond distances (Å) and angles (°) for [Mn(tacud)₂](OTf)₂ (1), [Mn(tacd)₂](OTf)₂ (2), and [Mn(tacn)₂](OTf)₂ (3). Calculated values are in brackets

Bond Lengths
	1	2	3
Mn(1)−N(1)	2.2894(10) [2.319]	2.2626(12) [2.301]	2.2771(11) [2.295]
Mn(1)−N(2)	2.2846(10) [2.300]	2.2744(12) [2.301]	2.2701(10) [2.293]
Mn(1)−N(3)	2.3011(13) [2.333]	2.2336(12) [2.271]	2.2485(11) [2.293]
Mn(1)−N(4)			2.2556(11) [2.293]
Mn(1)−N(5)			2.2636(10) [2.295]
Mn(1)−N(6)			2.2662(11) [2.293]

Bond Angles
	1	2	3
N(1)−Mn(1)−N(2)	85.93(4) [85.043]	83.74(4) [83.504]	77.64(4) [77.058]
N(1)−Mn(1)−N(2A)	94.07(4) [94.989]	96.26(4) [96.496]
N(1)−Mn(1)−N(3)	78.48(5) [78.087]	80.04(4) [78.447]	77.76(4) [77.093]
N(1)−Mn(1)−N(3A)	101.52(5) [101.826]	99.96(4) [101.553]
N(1)−Mn(1)−N(4)			173.63(4) [177.539]
N(1)−Mn(1)−N(5)			95.54(4) [104.428]
N(1)−Mn(1)−N(6)			103.88(4) [101.230]
N(2)−Mn(1)−N(3)	92.95(4) [90.110]	79.03(4) [78.447]	78.75(4) [77.099]
N(2A)−Mn(1)−N(3)	87.05(4) [89.910]	100.97(4) [101.553]
N(2)−Mn(1)−N(4)			108.38(4) [101.515]
N(2)−Mn(1)−N(5)			172.89(4) [177.594]
N(2)−Mn(1)−N(6)			101.12(4) [104.526]
N(3)−Mn(1)−N(4)			101.18(4) [104.618]
N(3)−Mn(1)−N(5)			101.96(4) [101.312]
N(3)−Mn(1) −N(6)			178.41(4) [177.382]
N(4)−Mn(1)−N(5)			78.52(4) [77.067]
N(4)−Mn(1)−N(6)			77.34(4) [77.123]
N(5)−Mn(1)−N(6)			78.37(4) [77.085]

3. Result and discussion

3.1. Synthesis

Three macrocyclic ligands of the type, eleven membered 1,4,8-triazacycloundecane (tacud), ten membered 1,4,7-triazacyclodecane (tacd), and nine membered 1,4,7-triazacyclononane (tacn) were used in the present work. The stoichiometric reaction of Mn(OTf)₂∙2CH₃CN with the respective ligand in the ratio of (1:2) in DMF followed by ether diffusion afforded colorless crystals of [Mn(tacud)₂](OTf)₂ (1), [Mn(tacd)₂](OTf)₂ (2), and [Mn(tacn)₂](OTf)₂ (3) in very good yield.

3.2. Crystal structure

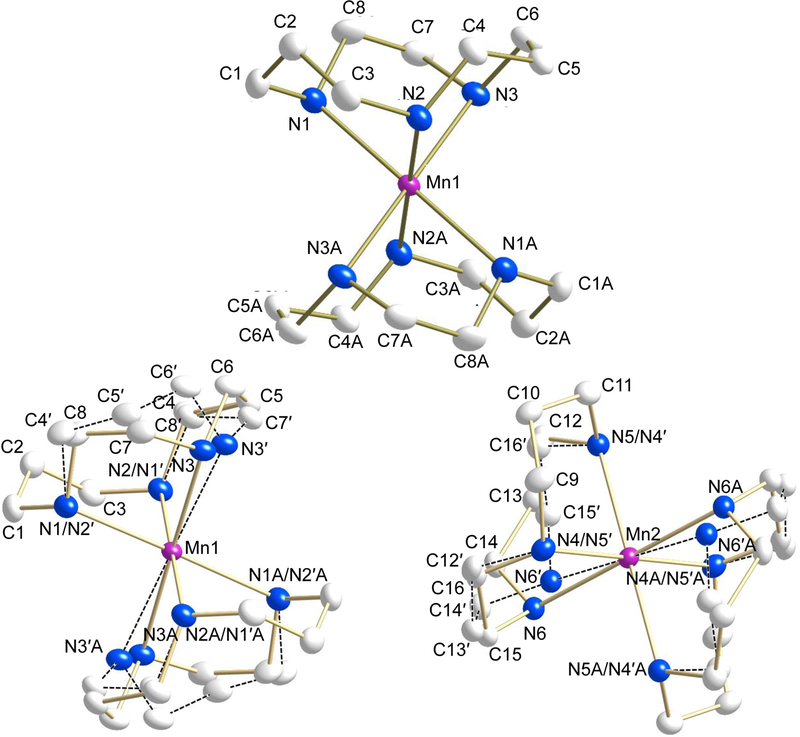
Structural determinations were undertaken on single crystals of complexes 1−3. In each complex the central manganese atom shows distorted octahedral coordination geometry coordinated by six nitrogen atoms. Selected crystallographic and geometric parameters for complexes 1−3 are presented in Tables 1 and 2 and the molecular structures of the cations are shown in Figs. 1–3, respectively.

Fig. 1.

ORTEP plot of [Mn(tacud)₂](OTf)₂ (1) (50% probability) showing one independent cation without disorder (top) and both the independent cations with disordered ligand (bottom). Dashed line indicate connectivity of the disordered atoms. Hydrogen atoms and anions have been removed for the sake of clarity.

Fig. 3.

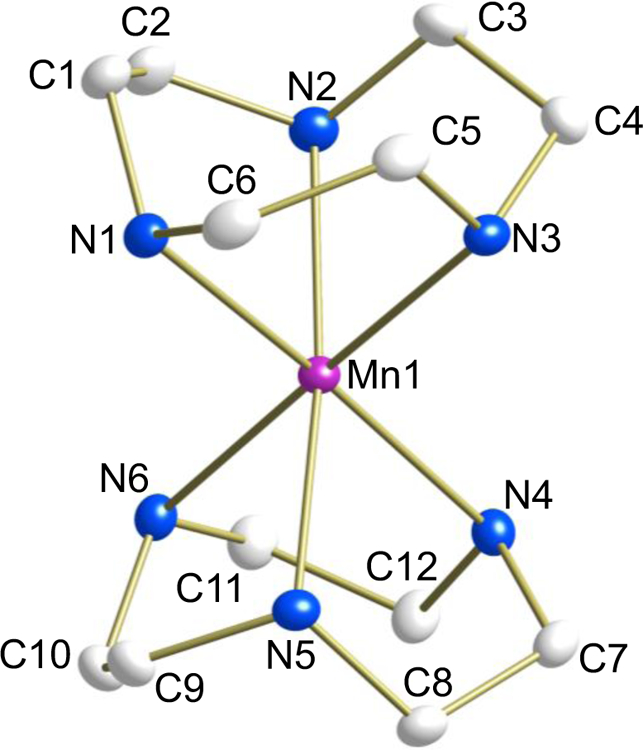
ORTEP plot of [Mn(tacn)₂](OTf)₂ (3) (50% probability). Hydrogen atoms and anions have been removed for the sake of clarity.

For complex 1 (Fig. 1), the tacud-ligand is disordered with the two-carbon linkage (67.7(2) : 32.3(2) and 60.6(2) : 39.4(2), respectively, for cations containing atoms Mn(1) and Mn(2)). In both cases one three carbon linkage is ordered, while the other is disordered with a two-carbon linkage in a pseudo-mirror fashion that comprises a similar volume (Fig. S1). Since the manganese atoms coincide with crystallographic inversion centers, the disorder is that of two trans configurations. For the disordered parts of the cyclic ligands, analogous bond lengths and angles, including those for atom pairs Mn(1)−N(3)/Mn(1)−N(3’) and Mn(2)−N(6)/Mn(2)−N(6’) were restrained to be similar, respectively. Anisotropic displacement parameters for proximal atoms from the different components of disorder and positional parameters for atom pairs N(1)/N(2’), N(2)/N(1’), N(4)/N(5’), N(5)/N(4’) were constrained to be equivalent, respectively. For additional tests, the structure was modelled in chiral space group P1 with the disorder ratio of each ligand refined independently from all others. This resulted in essentially equal disorder ratios between the two ligands attached to each metal center and an inversion twinning mass ratio of 50:50. This confirmed that the best structural model is centrosymmetric space group $P\overline{1}$.

For 2 (Fig. 2), the asymmetric unit contains the metal center and one tacd ligand of the cation, located on a crystallographic inversion center. All the atoms of complex 3 (Fig. 3) lie on general positions.

Fig. 2.

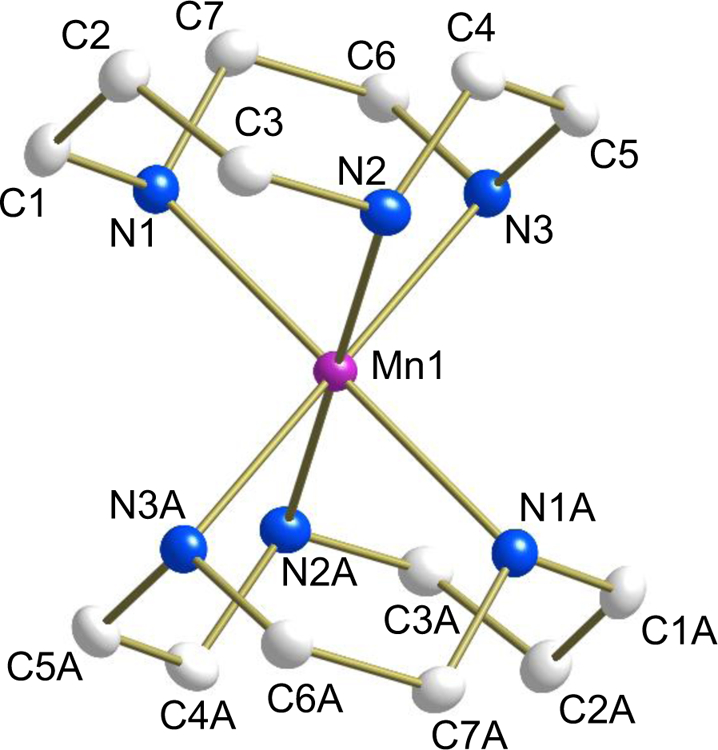
ORTEP plot of [Mn(tacd)₂](OTf)₂ (2) (50% probability). Hydrogen atoms and anions have been removed for the sake of clarity.

The average Mn‒N bond lengths for complexes 1−3 are 2.292, 2.257 and 2.264 Å, respectively and are characteristic for high spin Manganese(II) octahedral complexes coordinated to aliphatic secondary amines (2.214‒2.369 Å) [68–83]. Complex 1 exhibits the longest Mn‒N bond lengths while 2 and 3 are more similar.

As expected in 1, the N‒Mn‒N bond angles associated with the propylene group have larger values (N(2)−Mn(1)−N(3): 92.95(4)° and N(1)−Mn(1)−N(2): 85.93(4)°) compared to the ethylene linkage (N(1)−Mn(1)−N(3): 78.48(5)°), A similar phenomenon is observed in complex 2 where the N‒Mn‒N bond angle for the propylene group (N(1)−Mn(1)−N(2): 83.74(5)°) is larger than the bond angles associated with the ethylene linkers (N(1)−Mn(1)−N(3): 80.04(4)° and N(2)−Mn(1)−N(3): 79.03(4)°). In complex 3, the average N‒Mn‒N bond angle is 78.04° establishing the ethylene attachment in the complex. Three dimensional weak hydrogen bonding is present for all of the complexes via ligand NH and triflate oxygen groups (See Tables S7, S14, S21 for complexes 1, 2 and 3, respectively).

3.3. Electrochemistry

The electrochemical properties of complexes 1−3 were investigated by cyclic voltammetry. All the measurements were carried out in dry CH₃CN under dry nitrogen and referenced to the normal hydrogen electrode (NHE). Complexes 2 and 3 exhibit a quasi-reversible wave (Fig. 4) at E_1/2 = 0.95 V (ΔE_p = 108 mV) and E_1/2 = 0.93 V (ΔE_p = 96 mV), respectively. On the other hand complex 1 shows a quasi-reversible oxidative redox process at E_1/2 = 1.16 V (ΔE_p = 106 mV). To assign our results we ran the cyclic voltammetry on the free ligands and found that they irreversibly oxidized at much higher potentials. Oxidation of secondary amines at potentials higher than 1.3 V has been established in the literature [84–86]. From this we can unambiguously state that the observed quasi-reversible peaks arise from metal centered Mn^III/II redox processes. These results also confirm that the increase in redox potentials destabilized the Mn(III) state in 1 with respect to 2 and 3 and supports the weaker donating ability of tacud relative to tacn and tacd [15]. These results are in line with the redox properties of other Mn(II) complexes supported by amine ligands [87].

Fig. 4.

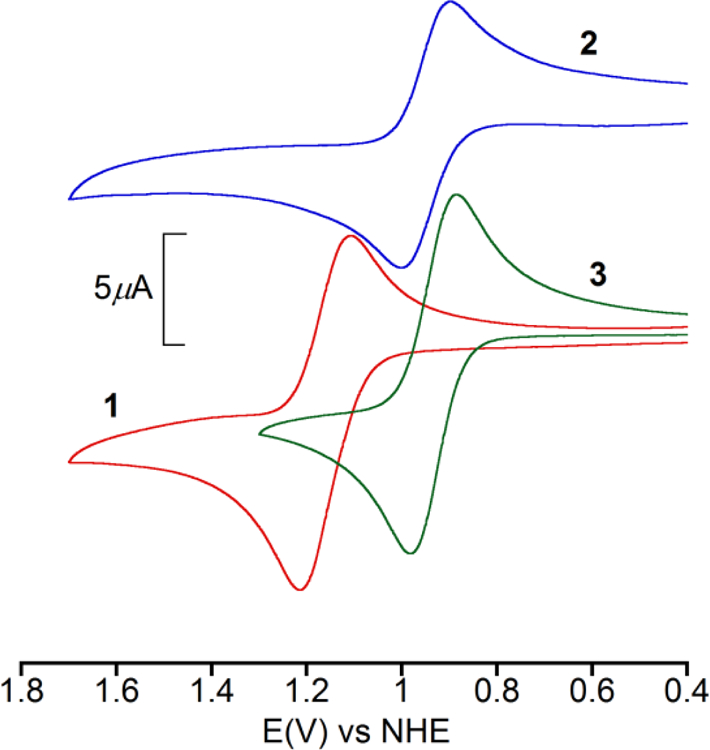
Cyclic voltammograms for 1 (red), 2 (blue) and 3 (green) in dry CH₃CN. Supporting electrolyte: TBAPF₆ (0.1 M); working electrode: Pt; reference electrode: Ag/AgCl; auxiliary electrode: Pt wire; scan rate: 100 mV s⁻¹. [complex] ~ 1 mM.

3.4. Magnetic Studies

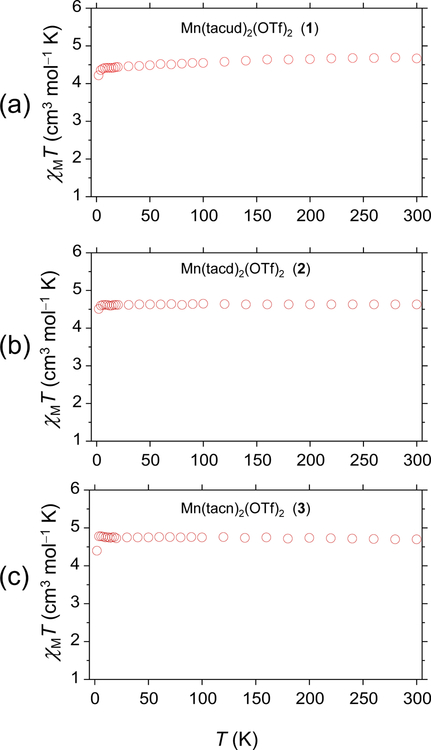
Variable temperature magnetic susceptibility measurements were performed on complexes 1−3 in powder form in the temperature range 2−300 K under an applied field of 0.1 T. The plots of _χMT versus T for 1−3 are shown in Fig. 5. The variable temperature data confirm that the complexes are high spin (S = 5/2) over the entire temperature range studied. The _χMT values for 1−3 are 4.68, 4.63, and 4.70 cm³ mol⁻¹ K at 300 K and remain almost constant down to 10 K and then decrease to 4.20, 4.51, and 4.39 cm³ mol⁻¹ K, respectively at 2 K. The SQUID results are consistent with the EPR results and can be simulated with the same parameters.

Fig. 5.

Plot of _χMT vs T for [Mn(tacud)₂](OTf)₂ (1, a), [Mn(tacd)₂](OTf)₂ (2, b), and [Mn(tacn)₂](OTf)₂ (3, c) along with fits and simulated parameters. H = 0.1 T.

3.5. EPR Spectroscopy

EPR spectra were acquired for the three complexes in neat methanol glass under low field conditions (X-band) at liquid nitrogen temperature and at high magnetic field between 5 and 20 K. The latter experiments were performed to obtain unambiguous results for the spin Hamiltonian parameters g and A and the ZFS parameters D and E. High-spin (S = 5/2) manganese(II) is found in the ⁶S electronic ground state and has a nuclear spin of I = 5/2 due to the 100% natural abundance of ⁵⁵Mn. It has been well studied and its magnetic parameters, particularly the zero field splitting constants as well as computational approaches to calculate them have been reviewed [88,89]. The g-factor and hyperfine anisotropy of high spin Mn(II) is usually small and may not easily be observed or used to correlate structure and magnetic parameters.

X-band EPR spectra of complexes 1−3 acquired at 9.3 GHz in frozen methanol glass are shown in Fig. 6. There is similarity between the EPR signals of complex 2 and 3 with multiple broad signals across the scan range from zero field to ca. 4000 G, yet complex 1 is much different showing primarily one broad EPR signal with the characteristic Mn sextet hyperfine splitting near g ≈ 2 with a low-field shoulder near 2500 G. Such spectra are commonly observed for Mn(II) in octahedral environments with minimal distortion and small magnitudes of D and E. On the other hand, broad spectra such as those observed for complex 2 and 3 point to a much larger ZFS constant which is indicative of a more distorted octahedral environment. This qualitative observation from low-field EPR spectra is supported by the crystallographic studies, with 2 and 3 showing shorter bond distances and angles and more overall structural similarity as compared to 1. D and E parameters extracted from the SQUID data indicate that these values are similar for complexes 1−3, despite the fact that EPR spectra suggest larger disparity. To probe this issue further, we conducted high field EPR studies.

Fig. 6.

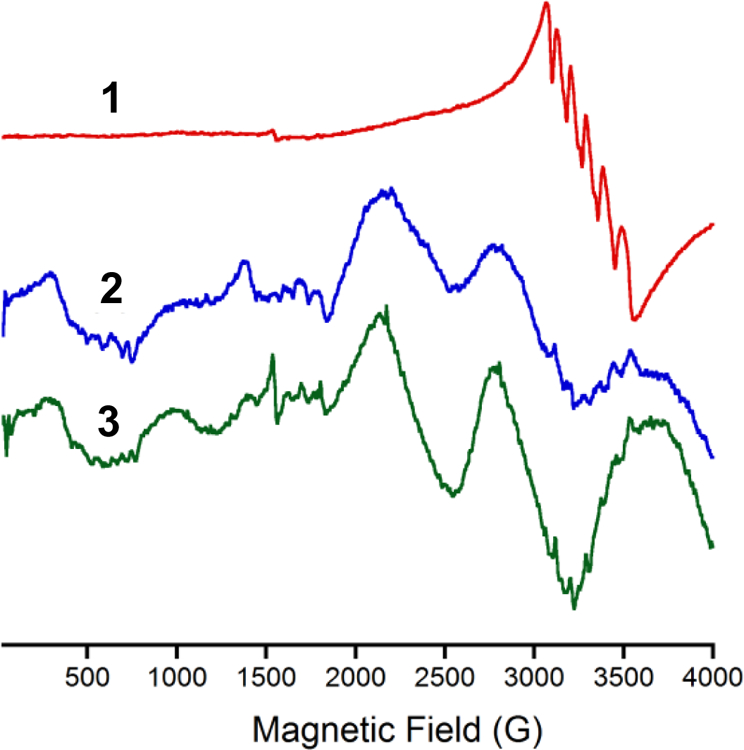
X-band EPR spectrum (77 K) of 1 (red), 2 (blue) and 3 (green) in methanol glass. Spectrometer settings microwave frequency 9.3 GHz; microwave power, 0.22 mW (30dB); modulation frequency, 100 kHz; modulation amplitude, 6.3 G; gain, 8 × 10³. [Complex] = 1 mM.

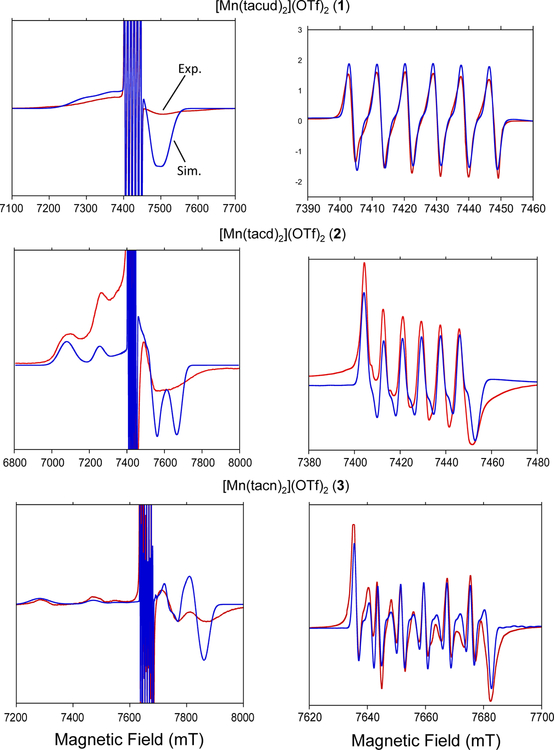
The full set of magnetic parameters for complexes 1−3 were obtained using high frequency high field EPR at 208 and 214.4 GHz (HFEPR) and 5 to 20 K (see Fig. 7). Spectral simulations were performed using the Easyspin toolbox for Matlab [90] and yielded the ZFS parameters, hyperfine interactions, and g-values listed in Table 3. It should be noted that the sign of the D-parameter is unequivocally negative based on the asymmetry visible in the high-field spectra. All spectra were well simulated with a unique set of magnetic parameters that fall well within the range of expectations. This points to the presence of a single Mn(II) complex in each of these samples.

Fig. 7.

High field EPR (red) with simulation (blue) for each complex. Full spectrum with g = 2 region clipped is shown on the left; g = 2 region exclusively is shown on the right. Simulation parameters are as follows: 1, g = 2.0013, A = 244 MHz, D = −930 MHz, Dstrain = 600 MHz; 2, g = 2.0008, A = 233 MHz, D = −2470 MHz, E = 300 MHz, Dstrain = 600 MHz; 3, g = 2.00028, A = 223 MHz, D = −2650 MHz, Dstrain = 500 MHz. Data for complexes 1 and 2 were collected at 208 GHz. Data for complex 3 was collected at 214.4 GHz. Spectra presented were recorded at 5K.

Table 3.

Magnetic parameters of complexes 1 – 3 from simulations of HFEPR experiments

Complex	D [cm−1]	|E/D|	g	|A| [MHz]
1	−0.031	<0.06	2.0013	244
2	−0.0824	0.12	2.00080	233
3	−0.0884	<0.06	2.00028	223

The high field spectra of complexes 1 and 3 showed an axial fine structure tensor (E = 0). Simulations with a small amount of rhombicity were also performed and compared with the experimental spectra. The rhombicity becomes noticeable in the simulation at a level of ca 6% for |E/D| which was considered to yield an upper limit for the magnitude of E. The spectra of 2 were well simulated with a non-zero but small amount of rhombicity of |E/D| ≈ 12%. Please note that the m_s = −1/2 ↔ +1/2 transitions are usually well resolved and may be used to further refine the spectral determination of the ZFS parameters since the lineshapes of the sextet are related to |D|/gβB₀ in second order of perturbation theory. The resulting spectral broadening and splitting is clearly visible in Fig. 7 for complexes 2 and 3 which show larger magnitudes for D compared to 1.

It is interesting to note that the HFEPR simulated D values are close to those obtained in the SQUID simulations. One could argue that differences could arise from the fact that the SQUID experiments were performed in powder form (with crystallographic lattice forces present) versus methanolic solutions with possible H-bonding interactions between methanol and the NH groups. Nonetheless, the ZFS parameters of all complexes remain close.

The g-factor of high spin Mn(II) is usually isotropic and found in a narrow range between 1.97 and 2.03 around that of the free electron which is certainly true for the three complexes studied here. Similarly, the hyperfine coupling constant |A| is usually found to be isotropic and for a first coordination shell with six N-ligands (MnN₆) observed in the range between 215 and 300 MHz, again consistent with our results. Zero field splitting parameters D and E can be correlated with the structure of the complex. For tri-dentate N-ligands leading to a MnN₆ cluster the axial ZFS parameter |D| ranges between 0.04 and 0.2 cm⁻¹ [89]. Our values fall toward and slightly beyond the lower end of that range. The sign of D is negative for all three complexes. The most flexible ligand (and weakest electron donor), tacud, shows the least amount of distortion and hence the smallest magnitude of D. The rhombicity factor E/D is small in the tacd complex and undetectable in the tacn and tacud complexes consistent with their smaller deviations from axial symmetry. Based on symmetry considerations alone tacn is expected to have the closest agreement with axial symmetry and hence E ≈ 0. On the other hand the crystal structure of the tacud complex (1) should show a clear deviation based on the presence of both a 2-carbon and two 3-carbon loops but it does not. However, one should bear in mind that Mn-N bonds are weaker in 1 compared to 2 (See Table 2) and in solution 1 may adopt a more symmetrical ligand field due to greater flexibility accounting for greater axial symmetry compared to 2. Previous X-band EPR work using [Mn(tacn)₂](ClO₄)₂ [91] and a related complex [92] revealed ZFS parameters similar to those found in our variable temperature magnetic studies, however the HFEPR studies in this work is expected to afford the most accurate results.

Mn(tacud)₂ has the highest degree of flexibility, correspondingly, the smallest zero field splitting value of the series investigated. This complex also exhibits perfect 180° bond angles across the metal. The g = 2 region of the spectrum shows no distortion from anisotropic components within the resolution of the experiment. When the entire spectrum is considered, the impact of the zero field splitting is readily observed. A small ZFS exists in the complex with a magnitude of −930 MHz (−0.03 cm⁻¹). The negative sign of this parameter indicates axial elongation on the bonds aligned with the D tensor.

In order of decreasing ring size, the second complex in the series is 2. The ring in this complex involves one less carbon atom compared to 1, but the impact of this change is readily visible in the EPR spectrum. The magnitude of the zero-field splitting increases drastically to 2470 MHz (0.082 cm⁻¹). The central g = 2 sextet begins to show the effects of a moderate Mn(II) ZFS. Splitting of the peaks is observed, but this splitting is not a result of any anisotropy in the system. The central g value of the complex differs slightly from that of 1, showing a decrease from 2.0013 to 2.0008. The hyperfine also decreases from 244 MHz to 233 MHz for 2, which suggests that electrons are more delocalized for as would be expected from the presence of two more chelate rings compared to 1. The space group of 2 is P2₁/c, but the mirror plane is retained, resulting in preservation of the 180° angles across the metal ion. When observing the entire field range it is readily apparent that this spectrum is significantly different compared to 1. While that spectrum had strong overlap between the ZFS-influenced high spin manifolds, in this complex the peaks are well separated. The simulation predicts two high field peaks, which match well with the inflection points of the highly broadened high field peak observed in the experimental spectrum.

The final complex in this series, and the most geometrically strained is 3. It represents the minimum number of carbon atoms between each nitrogen that will still take on a tridentate chelating mode. In the solid state this complex becomes strained enough that the 180° angles across the metal ion are distorted and the mirror plane that was inherent in the other two complexes is lost. The increased complexity of the g = 2 region is, again, a result of the slightly larger ZFS, increasing from −2470 MHz for 2 to −2650 MHz for 3. The field range is higher on this complex but this is not due to a large g factor shift. Instead, data collection gave better line shapes and less dispersion at 214.4 GHz compared to 208 GHz. The g factor decreases slightly for 2 (2.0008 → 2.0003). This is still within the generally observed range for manganese(II) complexes. The hyperfine coupling, again, sees a small decrease from the previous complex from 233 MHz to 223 MHz. This change is on the order of 3.5 G.

The high field spectrum shows the stronger effect of the constrained geometry on the ZFS of the tacn complex. The separation between the observed high field peaks increases even further, resulting in a total field range of 800 mT. High spin manifolds are resolved in terms of location, but the hyperfine interaction is still broadened out, as previously observed in the other two complexes in the series.

When comparing the parameters side-by-side, a clear trend emerges. The g-factor and hyperfine coupling constants decrease as the strain in the system increases. The zero-field splitting increases in magnitude but retains the same sign as the rest of the series. A decrease in the hyperfine coupling indicates less delocalization between the electrons on Mn(II) and the nitrogen atoms, which makes logical sense with the greater elongation of the orbitals aligned with the D tensor. The D strain parameter is relatively consistent across all of the samples and represents a Gaussian distribution about the principal ZFS value in order to simulate broadening in liquid samples, as simple peak-to-peak Gaussian broadening is insufficient to describe higher spin species (S > 1/2). The upper limit before spectral distortion is observed in the simulation is less than 100 MHz in the E parameter for both the undecane and cyclononane macrocycle, however the cyclodecane warrants a higher E term to obtain a good fit. This indicates that the undecane and cyclononane are truly axial, as introduction of a meaningful E results in a worse fit. The relationship between the zero-field parameters D and E with chemical and physical properties of Mn²⁺ is poorly understood [93]. The development of such correlations have to be based on the correlations between the ZFS parameters and the complex structure and would be very helpful to understand the properties of Mn-containing enzymes [43]. Gätjens et al. observed a strong correlation between the Mn^III/II redox potential and the Mn²⁺ zero-field interaction parameter D for a series of Mn(II) terpyridine complexes [50,94]. Complexes wth a larger magnitude of the (negative) D parameter showed smaller reduction potentials. Our complexes show the same trend, perhaps hinting at a more general relationship between D and the redox potentials. No relationship between the standard potentials and the ZFS parameter E were observed.

3.6. Computational studies

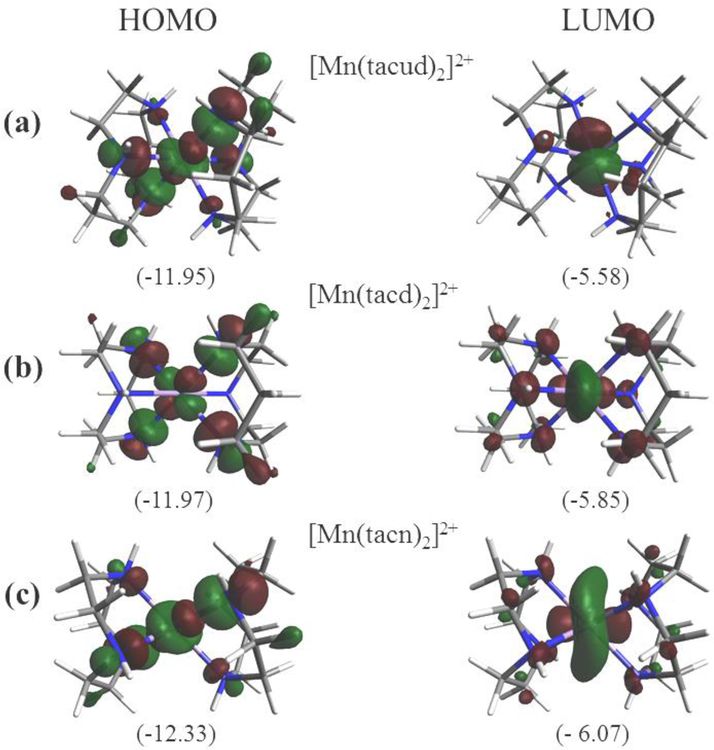
Calculations were carried out on complexes 1−3 using DFT. Ground state geometries were fully optimized in the gas phase. Orbital energies were calculated using PBE0/6–31G(d) unrestricted methods. A comparison between the experimental and computational metric parameters revealed that experimental bond lengths (Table 2) are very close to optimized values. The greatest difference between the experimental and calculated Mn−N bond lengths are 0.03, 0.04, and 0.04 Å for 1−3, respectively. The experimental and calculated bond angles are also in good agreement. Given the close accordance, the calculated values represent good approximations and therefore the electronic properties can be confidently inferred. Fig. 8 illustrate the highest occupied molecular orbital (HOMO) and lowest occupied molecular orbital (LUMO) for complexes 1−3.

Fig. 8.

Plots of Molecular orbitals: HOMO and LUMO (a) [Mn(tacud)₂]²⁺ (cation of 1), (b) [Mn(tacd)₂]²⁺ (cation of 2), (c) [Mn(tacn)₂]²⁺ (cation of 3). Oribital energies (eV) are indicated.

For 1 (Fig. 8(a)) it is seen that the HOMO (α−102) is largely distributed over nitrogen p orbitals and the Mn $d_{z^2}$ orbital in an anti-bonding configuration whereas the LUMO (β−98) is primarily distributed over the Mn d_xz/d_yz and s oribtals with very little contribution from the ligands. The HOMO (α−94) of 2 (Fig. 8(b)) is mainly distributed over the nitrogen p orbitals and the Mn $d_{x^2-y^2}$ and the LUMO (β−90) is likewise composed of the Mn d_xz/d_yz and s oribtals. For complex 3 (Fig. 8(c)), The HOMO (α−85) which make up the anti-bonding orbitals constructed from Mn $d_{z^2}$ and nitrogen p orbitals. The LUMO (β−82) is distributed over the Mn d_xz/d_yz and s oribtals as seen for 1 and 2.

The HOMO energy for the set display the order 3 < 2 < 1 and indicates that 3 is the most stable which can be attributed to the presence of six 5-membered chelate rings compared to two 5-memberd chelate rings in 1. The influence of 5-membered chelate rings on the redox potential has been documented in the literature [94].

4. Conclusions

This investigation focused on the synthesis and characterization of a series of bis(triazamacrocycle)manganese(II) complexes. The ligands employed were 1,4,8-triazacycloundecane (tacud), 1,4,7-triazacyclodecane (tacud), and 1,4,7-triazacyclononane (tacn). With these ligands, the synthesis and structural characterization of [Mn(tacud)₂](OTf)₂ (1), [Mn(tacd)₂](OTf)₂ (2), and [Mn(tacn)₂](OTf)₂ (3) was achieved. The structures revealed that 1 was less constrained compared to 2 and 3. This structural difference was manifested in the electrochemical, magnetic, and spectroscopic properties of this set. Electrochemical studies using cyclic voltammetry indicate that quasi-reversible Mn^III/II couples for all complexes. Complex 1 requires a much higher potential for oxidation (E_1/2 = 1.16 V) when compared to 2 (E_1/2 = 0.75 V) and 3 (E_1/2 = 0.73 V) which are close in redox properties. The higher redox potential for 1 is likely due to the fact that 5-membered chelate rings assist in stabilizing higher oxidation states. 1 possesses 2 such rings while 2 has 4 rings and 3 has 6 rings. The larger bond distances in 1 (compared to 2 and 3) is consistent with a more Lewis acidic manganese center for 1 compared to 2 and 3. Magnetic studies were consistent with high spin (S = 5/2) in the temperature range 2−300 K and the data was to extract the g vales and ZFS parameters. High-frequency high-field EPR studies helped to simplify spectra and allowed simulation of data to also extract ZFS parameters and their signs yielding more reliable data. Results were consistent with structural studies and indicated an increase in distortion from octahedral geometry when going from 1 to 3. Calculations revealed that complex 1 possessed the greatest amount of charge on the manganese center consistent with this complex being the most Lewis acid in the series. Complex 3, on the other hand, displayed the least amount of Lewis acidic and the most amount of covalency in bonding. The metric parameters from the X-ray data corroborate this. In addition, the HOMO energy for 3 was the lowest which is also supported by the existence of six 5-member chelate rings. The prediction from these properties would be that 3 should possess the lowest oxidation potential and this is again supported by the experimental data. These results are valuable as a reference for Mn(II) in proteins since it is often difficult to directly measure all of these properties for enzymatic systems. Thus the information garnered from these studies is useful to manganese biochemical investigations and adds to a growing body of knowledge for manganese biosites.