Optoelectronic mixing with high-frequency graphene transistors

Abstract

Graphene is ideally suited for optoelectronics. It offers absorption at telecom wavelengths, high-frequency operation and CMOS-compatibility. We show how high speed optoelectronic mixing can be achieved with high frequency (~20 GHz bandwidth) graphene field effect transistors (GFETs). These devices mix an electrical signal injected into the GFET gate and a modulated optical signal onto a single layer graphene (SLG) channel. The photodetection mechanism and the resulting photocurrent sign depend on the SLG Fermi level (E_F). At low E_F (<130 meV), a positive photocurrent is generated, while at large E_F (>130 meV), a negative photobolometric current appears. This allows our devices to operate up to at least 67 GHz. Our results pave the way for GFETs optoelectronic mixers for mm-wave applications, such as telecommunications and radio/light detection and ranging (RADAR/LIDARs.)

Here, the authors report optoelectronic mixing up to 67 GHz using high-frequency back-gated graphene field effect transistors (GFETs). These devices mix an electrical signal injected into the GFET gate and a modulated optical signal onto a single layer graphene channel.

Introduction

Mixers are a key component of modern communication modules¹. In telecommunications and in radio detection and ranging (RADAR) systems², the receiver analyzes the modulation of a carrier wave (or waveform) with frequencies in the microwave (3–30 GHz) or mm-wave (30–300 GHz) range, to extract information^3,4. As signal processing is performed at near-zero frequencies (baseband^3,4), frequency downconversion is required^3,4. Downconversion is performed by mixing the modulated high-frequency signal centered around the radio frequency (RF) carrier frequency, f_RF, with a local oscillator signal at frequency f_LO. This translates the modulation centered around f_RF to f_IF = f_LO − f_RF. The local oscillator frequency is typically set near f_RF, so that f_IF is close to zero^3,4. Superheterodyne receivers are a common type of radio receivers using frequency downconversion to process the original signal⁵. For multi-antenna systems, it is preferable to use a single optical signal as a local oscillator and distribute it to each antenna⁶, decreasing the receiver complexity and noise. For this purpose, one option is to use photodetectors (PDs) to transfer the local oscillator signal from the optical to the electrical domain⁶. After that, an electrical mixer is used⁵. A second option is to employ optoelectronic mixers (OEMs)⁷, i.e., PDs capable of mixing optical local oscillator with an electrical signal⁷. OEMs are particularly convenient in RADAR and light detection and ranging (LIDAR) applications^7–10. State-of-the-art OEMs at 1.55 μm are based on III–V semiconductors epitaxially grown on InP^11,12. These are efficient, but expensive, and can only be heterogeneously integrated in an Si platform^11,12. Low cost and complementary metal-oxide-semiconductor (CMOS) compatible OEMs require CMOS-compatible materials absorbing light at 1.55 μm¹³.

Graphene is promising for optoelectronics^14–18, with mobilities up to ~150,000 cm² V⁻¹ s⁻¹ at room temperature (RT)¹⁹, a short (~1 ps) photocarrier lifetime^20–22, and a 2.3% broadband light absorption (including telecom wavelengths)²³. Graphene-based optoelectronic devices are compatible with Si platforms^16,24–27. Therefore, graphene-based OEMs could combine telecom operation and CMOS compatibility.

Low frequency (2MHz) optoelectronic mixing in single-layer graphene (SLG) was studied in ref. ²⁸ using a transistor structure with an on-chip bias resistor. This reported upconversion of a 2MHz signal, and downconversion of a 0.45 MHz one, in two types of OEMs consisting of a SLG field-effect transistor (GFET) and a bias resistor. For the first, the oscillating electrical signal was applied to the GFET drain (the optical signal illuminated the GFET channel), whereas in the second the signal was applied to the gate, and the mixing was proportional to the on-chip resistance. A 30 GHz bandwidth (BW) OEM based on SLG was reported in ref. ²⁹, based on an SLG coplanar waveguide (GCPW) integrating a SLG channel grown by chemical vapor deposition (CVD). The RF signal was injected into the GCPW, whereas a 1.55 μm laser illuminated the channel. Optoelectronic mixing was based on the linear dependence of the photocurrent on both optical incident power (P_opt) and voltage drop (V_bias) along the channel. As the photocurrent is proportional to P_optV_bias³⁰, upconverted and downconverted signals were generated. This GCPW operated up to 30 GHz, with a conversion efficiency, (i.e., ratio of output power at f_IF and input power at f_RF), of −85 dB for a 10 GHz modulated signal. The results in ref. ²⁹ are far from state-of-the-art OEM performances achieved with III–V semiconductor-based uni-traveling carrier photodiodes: −22 dB conversion efficiency at 35 GHz³¹, and −40 dB at 100 GHz¹². However, the CMOS integration of III–V semiconductors is challenging¹³. SLG is CMOS-compatible¹⁶ but, to technologically bridge the gap with III–V-based OEMs, BW, and conversion efficiency need to be improved²⁹. Furthermore, the OEM in ref. ²⁹ was a two-contact device operating only in the photoconductive regime, at a fixed Fermi level (E_F).

Here, we present a 67 GHz GFET-OEM (three-contact device), exploiting the modulation of E_F, that controls the photoconductivity. At low (equilibrium) E_F (<130 meV) the laser power induces interband transitions³², thus the charge carrier density, n, and the channel conductance increase (positive photoconductivity). At high E_F (>130 meV), the laser heating induces intraband transitions³². In this case, the hot carrier distribution reduces the effectiveness of the electronic screening³² which, in turn, leads to a higher scattering rate (e.g., owing to Coulomb impurities³² or strain disorder³³). The increased scattering decreases the carrier mobility³² and the resulting photoconductivity is negative^32,34–36. In our OEMs, an intensity-modulated (up to 67 GHz) laser beam illuminates part of the SLG channel, generating an AC photocurrent, proportional to the product of optical power and photoresponsivity. An RF signal applied to the gate of 20 GHz-BW GFETs modulates the photoresponsivity, mixing optical and electrical signals. The performance far exceeds that in ref. ²⁹. The conversion efficiency (−67 dB) for a 67 GHz modulated optical signal (f_opt) is 21 dB higher than ref. ²⁹ at f_opt = 10 GHz, thanks to the use of an RF GFET with a strong coupling between the input RF signal and SLG (a 0.8 V signal induces E_F ~ 0.2 eV). Our results pave the way for the use of graphene in CMOS-compatible OEMs.

Results

Graphene growth and characterization

SLG is grown via CVD on 35 μm-thick Cu foil, following ref. ³⁷. The temperature, T, is raised to 1000 ^∘C in an H₂ atmosphere (~200 mTorr), and kept constant for 30 mins. In all, 5 sccm CH₄ are then added to the 20 sccm H₂ flow to start growth, for additional 30 mins at 300 mTorr. The sample is then cooled at ~1 mTorr to RT. We use Raman spectroscopy at 514nm to characterize the material. Figure 1a shows the Raman spectrum on Cu (red line), after Cu photoluminescence removal³⁸. The D peak is absent, indicating negligible defects^39,40. The 2D peak at ~2705 cm⁻¹ is a single Lorentzian with full width at half maximum (FWHM) ~31 cm⁻¹, a fingerprint of SLG⁴¹. The position of the G peak, Pos(G), is ~1593 cm⁻¹, with FWHM(G) ~12 cm⁻¹. The 2D to G intensity and area ratios are I(2D)/I(G) ~ 2.4, A(2D)/A(G) ~ 6.3.

Fig. 1. SLG Raman characterization and device description.

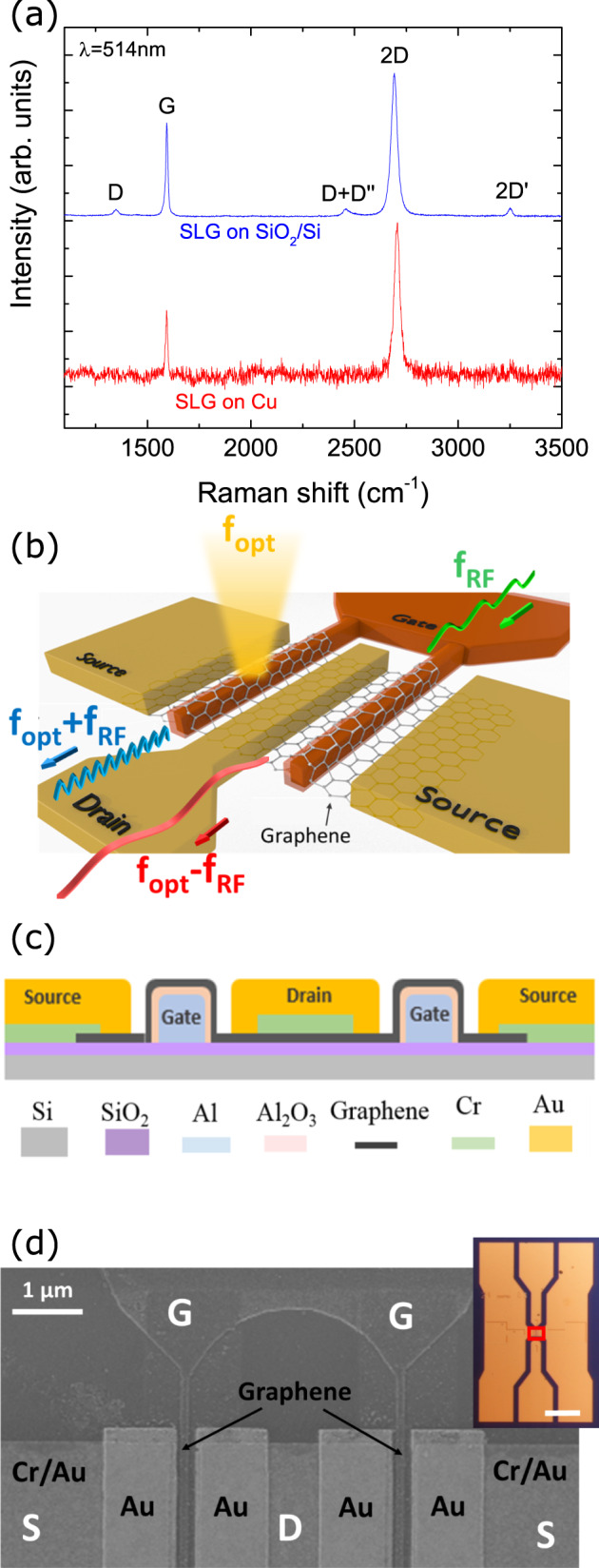
a Representative Raman spectra at 514 nm of SLG as-grown on Cu (red), and after transfer on SiO₂/Si (blue). b Principle of operation of our OEM. The mixing of the electrical signal at f_RF with the photodetected signal at f_opt generates two signals at the output (drain): f_opt + f_RF and f_opt − f_RF. c Schematic GFET cross-section. The two Al gates (pale blue) are covered by a thin Al₂O₃ oxide (pink). SLG (black) is placed on the two gates. The drain and source contacts are Au (yellow) and Cr (green). d SEM image of GFET with dual-bottom gate finger covered by SLG. The metal in contact with SLG is Au. The inset shows the GFET (red rectangle) integrated into a coplanar waveguide (CPW) (scale bar: 100 μm).

To prevent ohmic losses at microwave frequencies, a high resistivity Si wafer (> 8000Ωcm) covered with  285nm SiO₂ is used. SLG is wet transferred^42,43 on it as follows. A poly(methyl methacrylate) (PMMA) layer is spin-coated on the surface of SLG/Cu and then placed in a solution of ammonium persulfate (APS) and deionized (DI) water for Cu etching⁴². The PMMA membrane with attached SLG is then immersed into a beaker filled with DI water for cleaning APS residuals. After, the PMMA/SLG stack is transferred onto the target substrate and the PMMA layer is removed. SLG is then ion etched to define the channel.

We then characterize via Raman spectroscopy the transferred SLG (blue curve, Fig. 1a). Both measurements on Cu and Si+SiO₂ are performed under the same conditions of laser power, objective, wavelength, and accumulation time. The Raman signal of SLG on Cu is more noisy than on Si+SiO₂ due to interference enhancement by the 300 nm SiO₂ layer on Si^44,45. For SLG on Si+SiO₂ we have Pos(G) ~1594 cm⁻¹, FWHM(G) ~11, Pos(2D) ~2691 cm⁻¹, FWHM(2D) ~34 cm⁻¹, I(2D)/I(G) ~1.6, A(2D)/A(G) ~4.5. This indicates p-doping ~300 meV^46,47. I(D)/I(G) ~0.09 corresponds to a defect density ~4 × 10¹⁰ cm^−240,48, consistent with what is commonly observed in CVD-SLG⁴⁹. It is possible to improve the process to get a smaller D peak⁵⁰.

Operational principle and device fabrication

Figure 1b is a sketch of our SLG OEM and illustrates its operational principle. It consists of a GFET with a symmetric dual-bottom gate finger. This layout is commonly used for RF applications⁵¹ and GFETs⁵², and is well suited for GCPWs⁵³. Dual-gate finger FETs have a more compact design and a reduced small-signal gate resistance compared with single-gate configurations, for a given equivalent channel width, resulting in a higher voltage gain⁵⁴. A laser beam is modulated at f_opt and focused on the GFET channel. As a result, a photocurrent that contains an AC component at f_opt flows through the SLG channel. If a RF signal f_RF is applied to the gate, the output current presents a term at f_RF. When both optical and electric signals are applied, the device acts as an OEM: the output contains the product of the two signals, and two AC components at f_opt + f_RF and f_opt − f_RF appear.

A schematic cross-section of the bottom gate GFET is in Fig. 1c. The fabrication starts by patterning the dual-bottom gate finger by e-beam lithography (EBPG 5000 Plus). The gates are made of a 40 nm-thick Al layer deposited by evaporation. A 4 nm Al₂O₃ layer is formed on top of the gates by exposing the substrate to pure oxygen for 30 mins⁵⁵ with an Oxford Plasmalab80Plus at ~100 mTorr. This thin oxide acts as gate dielectric. The source and drain contacts are made in a two-steps process. First, Cr/Au (5/50 nm) pre-contacts are deposited on SLG. Then, ohmic contacts are obtained by placing 30 nm Au on the Cr/Au-SLG junction. Finally, a CPW is built with a Ni/Au film (50/300 nm). Figure 1d is a scanning electron microscopy (SEM) image of the bottom gates covered by SLG. The inset shows a GFET integrated into the CPW. The red square indicates the area occupied by the GFET. The bottom gate GFET design is suitable for OEMs since (1) the SLG channel is on the gate and can be directly illuminated; (2) the use of a thin (4 nm) Al₂O₃ dielectric and short gate (<0.4 μm or less) ensures high-frequency operation^5,56,57.

The device has a cutoff frequency (not de-embedded) f_t ~ 25 GHz, and a maximum oscillating frequency f_max ~ 14GHz, as deduced from the S-parameters measured with a Vector Network Analyzer (VNA, Agilent, E8361A). To calibrate the VNA, we use the Line-Reflect-Reflect-Match approach⁵⁸. This allows us to eliminate errors in S-measurements introduced by the environment, such as cables and probe tips used to contact the device under test, and the VNA non-idealities.

Electrical and optoelectronic measurements

The setup in Fig. 2a is used to measure photocurrent and optoelectronic mixing. The output of a 1.55 μm distributed feedback laser is modulated by a Mach Zehnder modulator in the double sideband suppression carrier mode⁵⁹, to obtain a modulated beam at f_opt. This is then amplified with an Erbium-doped fiber amplifier. The maximum f_opt that our setup can probe is 67 GHz. The diameter of the focused laser spot is ~2 μm (inset of Fig. 2a). The maximum power impinging on the sample is ~60 mW, which corresponds to ~20 mW/μm². The gate and drain are connected to a VNA with two high-frequency (67 GHz) air coplanar probes. Bias tees are used to add a DC bias to channel and gate electrodes, and to measure the DC currents and voltages with a Source-Measure-Unit (Keithley 2636B). After illuminating the device, we verify the stability of the signal before measuring the RF photocurrent, whereas monitoring the DC value of the channel resistance, to ensure that no damage nor significant modification is induced by the laser power or DC bias. We do not observe any degradation or time-dependent drift in the DC or RF currents over a period of at least 3 h, the typical measurement time.

Fig. 2. Measurement setup and device characteristics.

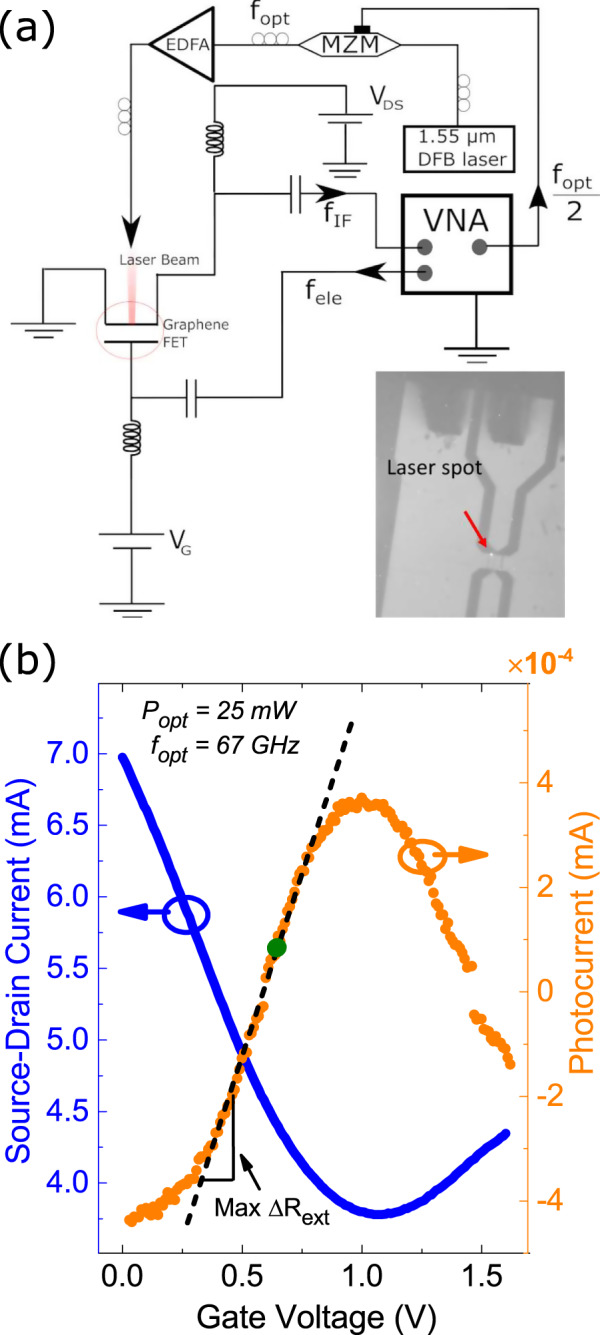
a Experimental setup: a CW laser is modulated via a MZM. It is then amplified with an EDFA and focused on the GFET. An AC signal is applied to the gate. The output f_IF is measured on a VNA. Inset: optical image of device with laser focused on the channel. b Blue curve: source-drain current versus gate voltage, for V_DS = 200 mV. Orange curve: photocurrent versus gate voltage, generated by a 25 mW beam focused on the SLG channel.

We now present the results for a representative OEM with SLG channel width W = 24 μm, length L = 400 nm, and gate length L_G = 200 nm. The blue curve in Fig. 2b is the source-drain current, I_DS, as a function of gate voltage, V_GS, at V_DS = 200 mV, which shows the typical ambipolar conduction behavior of a GFET (i.e, electrical conductivity due to electrons/holes (e/h), depending on the position of E_F with respect to the charge neutrality point, CNP)⁶⁰. The minimum conductance is reached at V_GS = 1.1 V, which corresponds to the CNP voltage (V_CNP). When V_GS increases (decreases) with respect to V_CNP, the e(h) density increases, leading to a reduction of channel resistivity, so an increase of the current flowing in the channel⁶⁰. μ is calculated as μ = Lg_m/(W ⋅ C_GV_DS)⁶¹. The transconductance g_m = dI_DS/dV_GS¹³ is obtained from the transfer characteristic I_DS(V_GS) at V_DS = 10 mV. The gate capacitance is C_ox is ~5 fF/μm, obtained from S parameters measurements on 60 devices of the same kind⁵⁵. We get μ ~ 2500 cm² V⁻¹ s⁻¹, consistent with that of non-encapsulated CVD-SLG³⁷.

We now consider the photoresponse. The OEM is biased at V_DS = 200 mV and illuminated with a laser modulated at f_opt = 67 GHz. The electrical power P_RF measured by the VNA is used to derive the photocurrent I_ph. From Joule’s law¹³ $I_{\mathrm{ph}}=\sqrt{\frac{P_{\mathrm{RF}}}{Z_{\mathrm{VNA}}}}$, with Z_VNA = 50 Ω the VNA input impedance. The use of bias tees allows us to simultaneously measure the DC component, i.e., the dark current (blue curve in Fig. 2b) and the AC component, i.e., the photocurrent (orange curve in Fig. 2b) as a function of V_GS, for a 25 mW incident optical power. The photocurrent, I_ph, sign depends on V_GS. I_ph is positive and has a local maximum close to the CNP. At low (equilibrium) E_F (<130 meV), the laser power induces interband heating³², thus an increase of n (positive photoconductivity). Therefore, the photocurrent has the same sign as the DC current in the channel, owing to the DC bias. At high E_F > 130 meV, the sign of the photocurrent is opposite to the DC current (negative photoconductivity). In this case, laser heating induces intraband transitions, which lead to a reduction of electronic screening of the long-range Coulomb interaction between SLG’s carriers and charged impurities in the substrate^22,32. The E_F at which the transition between positive and negative photocurrent takes place is ~0.1–0.2 eV^32,34. The value depends on the charge transport scattering rate in SLG, i.e., the mean time interval between two collisions in the diffusive transport picture⁶², and on the charge neutrality region width⁶³ (see Methods). In our experiment, we observe this transition at ~130 meV.

The external photoresponsivity, R_ext, is defined as^15,64 R_ext = $\frac{\mid I_{\mathrm{ph}}\mid }{P_{\mathrm{c}}{\mathrm{w}}_{\mathrm{eff}}}$, with $P_{\mathrm{c}}{\mathrm{w}}_{\mathrm{eff}}$ = 31%P_cw the fraction of the optical power coupled to the SLG channel. We get R_ext ~ 0.22 mA/W. For V_GS = 0V, the device reaches its maximum I_ph ~ −4.2 × 10⁻⁴ mA and the photocurrent generated by a 67 GHz laser modulation is measured as a function of DC bias and optical power.

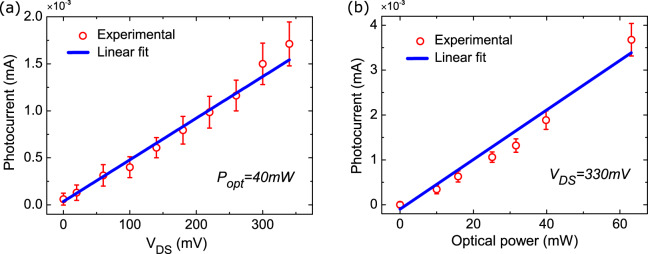
Figures 3a, b plot the photocurrent as a function of DC bias at P_opt = 40 mW and as a function of the optical power for V_DS = 330 mV. The response is linear in both cases, as expected for a photoconductor³⁴. The frequency response of the photodetected power is then measured as a function of f_opt, Fig. 4a. We get a flat response over the whole band that can be investigated by our VNA, showing that the intrinsic photodetection BW is >67 GHz. The photocurrent can originate from the SLG channel located above the gate, or from the SLG-metal contacts that are not gated (see Fig. 1c). As the photoresponse strongly depends on V_GS, as shown in Fig. 2b, we ascribe it to the illuminated part of the SLG channel located above the gate. If both contacts are illuminated, the photocurrents are opposite and cancel out. If the photocurrent originates mainly from one SLG-metal contact, the photocurrent at V_DS = 0V should be significant. R_ext ~ 0.8 mA/W was reported in ref. ⁶⁵ for a detector exploiting the metal-SLG contacts, at V_DS = 0V. As seen in Fig. 3, at V_DS = 0V the photocurrent is negligible. We also rule out possible asymmetric heating effects on the channel, owing to beam location, by performing a photocurrent measurement as a function of laser spot position. We observe a very weak response at V_DS = 0V, regardless of laser spot position, as shown in Methods, Fig. 10. Thus, the role of contacts can be neglected.

Fig. 3. Photocurrent measurements.

a Photocurrent as a function of V_DS at 40 mW optical power, b photocurrent as a function of the optical power, at V_DS = 330 mV. Error bars are obtained from the VNA measurement noise standard deviation.

Fig. 4. RF Optoelectronic characterization.

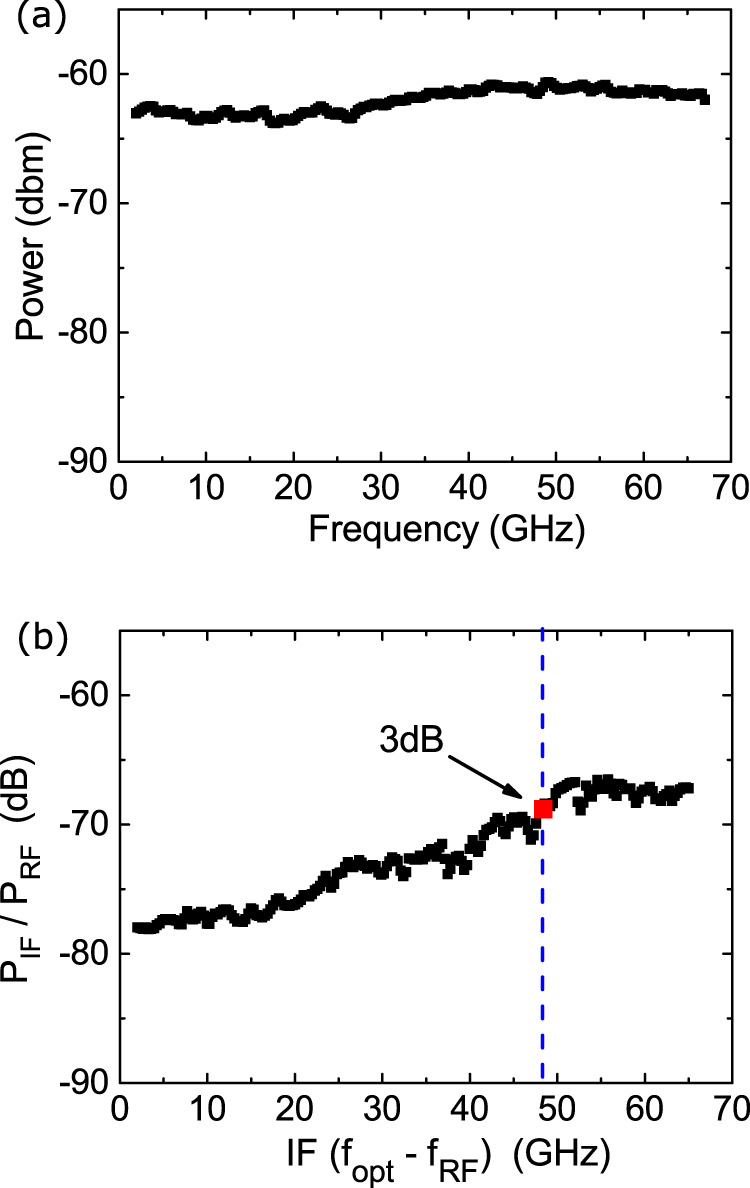
a Maximum photodetected power at V_GS = 0V, V_DS = 330 mV, as a function of f_opt. b P_IF/P_RF at V_GS = 0.6V, V_DS = 330 mV. Optical power in a, b is 60 mW.

Fig. 10. Photoresponse as a function of laser spot position.

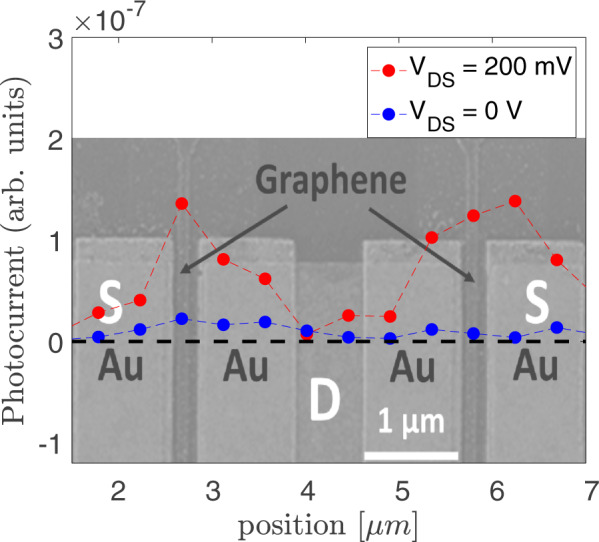
The red and blue curves show the measured photoresponse as a function of laser spot position along the black dashed cut line, at 200 mV and 0 V, respectively.

In order to operate the device as an OEM (instead of a PD), an RF signal f_RF is added to the DC gate, Fig. 1b. f_opt is maintained at 67 GHz, whereas f_RF is swept between 2 and 65 GHz. A VNA is used to record P_IF and the transistor power at the intermediate frequency f_IF = f_opt−f_RF.

An important parameter for OEMs is the downconversion efficiency⁵: P_IF/P_RF, with P_RF the power at the source and P_IF that measured at the VNA. For our device, the maximum P_IF/P_RF is −67 dB at V_GS = 0.6 V. For this V_GS, Fig. 4b plots P_IF/P_RF as a function of f_IF. The BW and P_IF/P_RF of our OEMs far exceed (+37 GHz in BW and 2 orders of magnitude in P_IF/P_RF) those of ref. ²⁹, where the input RF signal modulates the SLG bias (resistive coupling), thus the photocurrent amplitude. In our OEMs, the input RF signal is coupled to SLG via the gate oxide (capacitive coupling), which results in a modulation of E_F and, consequently, in a change of the photocurrent mechanism and sign. These high BW and P_IF/P_RF come from the strong coupling (i.e., strong electric field for a small applied voltage, 0.25 V/nm) between the input RF signal (applied to the Al back-gate) and the SLG channel, thanks to the use of a ~4 nm oxide. As a consequence, an efficient field effect is achieved⁶⁰. A signal with an amplitude ~0.8 V induces a E_F modulation ~0.2 eV. Thus, a small signal (0.8 V) is needed to obtain optoelectronic mixing. The high-frequency operation of the GFET (~20 GHz, 3 dB BW, Fig. 4b) comes from the short channel length (400 nm) and the small gate capacitance C_ox ~ 60 fF⁶⁶.

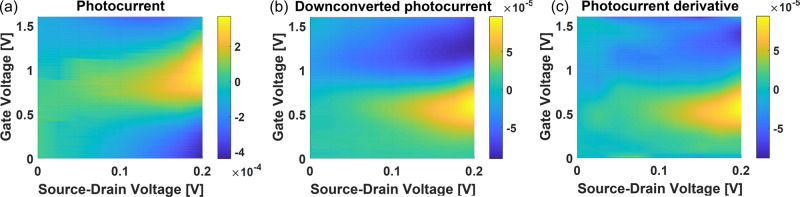
Figure 5a is a color map of the 67 GHz photocurrent as a function of V_GS, V_DS. We then add to the DC gate bias an electrical signal at 10 GHz. The resulting downconverted photocurrent at f_IF = 57 GHz is plotted as a function of V_DS, V_GS in Fig. 5b. By differentiating the map in Fig. 5a with respect to V_GS, we obtain Fig. 5c, which resembles Fig. 5b. This is best seen in Fig. 6, which plots both values as a function of V_GS for V_DS = 200 mV. The curves of the downconverted photocurrent and of the derivative of the photocurrent can be superposed. This result is valid regardless of frequency, see Methods Fig. 9.

Fig. 5. V_GS–V_DS maps.

a Photocurrent map as a function of V_GS, V_DS. b Downconverted photocurrent map as a function of V_GS, V_DS. c Derivative of a with respect to V_GS. The photocurrent values are in mA.

Fig. 6. Downconversion efficiency vs V_GS.

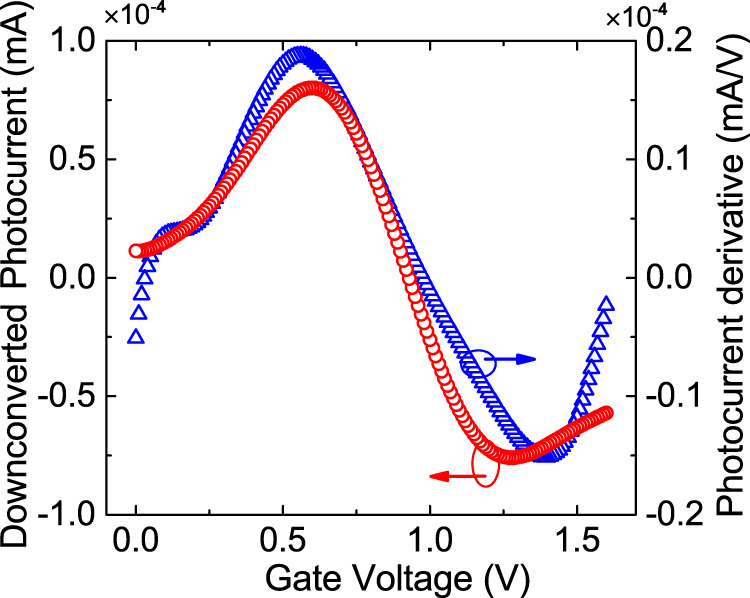
Red curve: cut of Fig. 5c for V_DS = 200 mV. Blue curve: cut of Fig. 5b for V_DS = 200 mV.

Fig. 9. Downconverted photocurrent versus gate voltage at different frequencies.

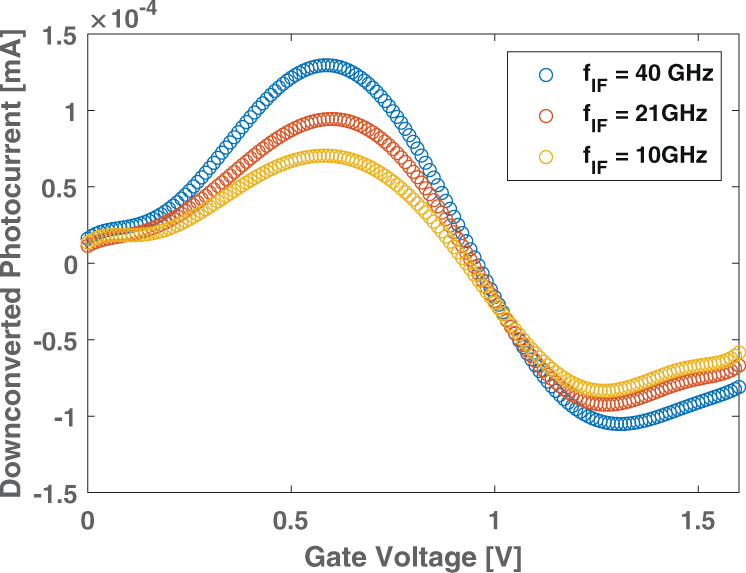
The three curves show the downconverted photocurrent at 10, 21, 40 GHz. The same behavior shown in Fig. 6 is observed, regardless of the operating frequency.

Discussion

This behavior can be explained by a small-signal analysis.

Let us consider the modulated optical power impinging on the PD, P_opt = P_cw + P_modsin(2πf_optt), with P_mod the amplitude of the varying part of the optical power. The photocurrent is proportional to P_opt through the factor R_ext. This depends on V_GS, as for Fig. 2b, and is almost independent on f_opt, Fig. 4a. Therefore, the photocurrent can be written as:

$$I_{\mathrm{ph}}\left(V_{\mathrm{GS}}\right)=R_{\mathrm{ext}}\left(V_{\mathrm{GS}}\right)\left[P_{\mathrm{cw}}+P_{\mathrm{mod}}sin\left(2\pi f_{\mathrm{opt}}t\right)\right]$$ 1

By applying to the gate a DC bias ${\overline{V}}_{\mathrm{GS}}$ and a small signal ${\delta }_{V_{\mathrm{GS}}}sin\left(2\pi f_{\mathrm{RF}}t\right)$, we get:

$$R_{\mathrm{ext}}\left(V_{\mathrm{GS}}\right)=R_{{\mathrm{ext}}_{\mathrm{DC}}}\left({\overline{V}}_{\mathrm{GS}}\right)+{\delta }_{V_{\mathrm{GS}}}{\mathrm{\Delta }}_{R_{\mathrm{ext}}}sin\left(2\pi f_{\mathrm{RF}}t\right)$$ 2

where

$${\mathrm{\Delta }}_{R_{\mathrm{ext}}}=\beta \left(f_{\mathrm{RF}}\right)\frac{d{R}_{\mathrm{ext}}\left(V_{\mathrm{GS}}\right)}{d{V}_{\mathrm{GS}}}{\mid }_{V_{\mathrm{GS}}={\overline{V}}_{\mathrm{GS}}}$$ 3

We include dependence on injected electrical frequency through a frequency-dependent proportionality constant β(f_RF). The total photocurrent has four terms:

$$I_{\mathrm{ph}}=R_{{\mathrm{ext}}_{\mathrm{DC}}}\left({\overline{V}}_{\mathrm{GS}}\right)P_{\mathrm{cw}}+{\delta }_{V_{\mathrm{GS}}}{\mathrm{\Delta }}_{R_{\mathrm{ext}}}{P}_{\mathrm{cw}}sin\left(2\pi f_{\mathrm{RF}}t\right)+R_{{\mathrm{ext}}_{\mathrm{DC}}}\left({\overline{V}}_{\mathrm{GS}}\right)P_{\mathrm{mod}}sin\left(2\pi f_{\mathrm{opt}}t\right)+{\delta }_{V_{\mathrm{GS}}}{\mathrm{\Delta }}_{R_{\mathrm{ext}}}{P}_{\mathrm{mod}}sin\left(2\pi f_{\mathrm{RF}}t\right)sin\left(2\pi f_{\mathrm{opt}}t\right)$$ 4

The first is the DC photocurrent. The second describes the DC photocurrent modulated by the electrical signal. The third represents the photocurrent modulated at f_opt, Fig. 2b. The fourth describes the optoelectronic mixing and can be rewritten as:

$${\delta }_{V_{\mathrm{GS}}}{\mathrm{\Delta }}_{R_{\mathrm{ext}}}{P}_{\mathrm{mod}}sin\left(2\pi f_{\mathrm{RF}}t\right)sin\left(2\pi f_{\mathrm{opt}}t\right)=\frac{1}{2}{\delta }_{V_{\mathrm{GS}}}{\mathrm{\Delta }}_{R_{\mathrm{ext}}}{P}_{\mathrm{mod}}\left\{cos\left[2\pi \left(f_{\mathrm{RF}}-f_{\mathrm{opt}}\right)t\right]\right)+\left(-cos\left[2\pi \left(f_{\mathrm{RF}}+f_{\mathrm{opt}}\right)t\right)\right\}$$ 5

Equation (5) has two components at f_opt + f_RF and f_IF = f_opt − f_RF. It shows that the mixed signal depends exclusively on ${\mathrm{\Delta }}_{R_{\mathrm{ext}}}$, i.e., on the derivative of R_ext with respect to V_GS, not on R_ext itself, in accordance with Fig. 5. ${\mathrm{\Delta }}_{R_{\mathrm{ext}}}$ is maximum for V_GS ~ 0.6 V, Fig. 6, i.e., in a region where the photocurrent changes sign, indicated in Fig. 2b with a green dot. The sharper is the transition between the two competing phenomena (photoconductive and bolometric) generating the photocurrent, the higher is ${\mathrm{\Delta }}_{R_{\mathrm{ext}}}$ and the optoelectronic-mixing efficiency.

Since R_ext is proportional to the photoconductivity σ_ph(V_GS)³⁰, the optimization of the mixing efficiency (${\mathrm{\Delta }}_{R_{\mathrm{ext}}}$) requires $\frac{d{\sigma }_{\mathrm{ph}}}{d{V}_{\mathrm{GS}}}$ to be maximized. σ_ph(V_GS) depends on several factors, such as the residual charge carrier density, n₀⁶³, and the dominating scattering mechanisms^63,67. So, it depends on SLG quality and its dielectric environment. We compute σ_ph(V_GS) from the Drude model for free carrier conductivity in SLG⁶³:

$$\sigma \left(T_e,{\mu }_c\right)=\frac{D\left(T_e,{\mu }_c\right)}{\pi \mathrm{\Gamma }\left(T_e,{\mu }_c\right)}$$ 6

where T_e is the electron temperature, Γ is the scattering rate, D is the Drude weight^63,67, and μ_c is the chemical potential. We calculate μ_c (see Methods for details), and then the effect of e-h puddles by replacing μ_c with ${\mu }_c\to \sqrt[4]{{\mu }_c^4+\mathrm{\Delta }{{\mu }_{\mathrm{puddles}}}^4}$⁶³, where ${\mathrm{\Delta }}_{{\mu }_{\mathrm{puddles}}}$ is the energy width of the puddles region⁶³. The photoconductivity due to illumination of the SLG channel at a given μ_c is then given by⁶³:

$${\sigma }_{\mathrm{ph}}=\sigma \left(T_{\mathrm{light}}\right)-\sigma \left(T_{\mathrm{dark}}\right)=\frac{D\left(T_{\mathrm{light}}\right)}{\pi \mathrm{\Gamma }\left(T_{\mathrm{light}}\right)}-\frac{D\left(T_{\mathrm{dark}}\right)}{\pi \mathrm{\Gamma }\left(T_{\mathrm{dark}}\right)}$$ 7

where T_light is the hot-electron temperature of the illuminated SLG and T_dark is the electron temperature in dark, see Methods for details. Figure 7 plots the measured photoconductivity (blue) and the computed one (red) using Eq. (7). We calculate Δμ_puddles from n₀, extracted from the experimental DC measurement of the conductivity (see Methods). We calculate Γ from the measured μ (see Methods). We get Γ ~ 50 meV, which corresponds to a scattering time τ ~ 80 fs at E_F ~ 200 meV, at the maximum V_GS, in agreement with experiments.

Fig. 7. Comparison between measured and calculated photoconductivity.

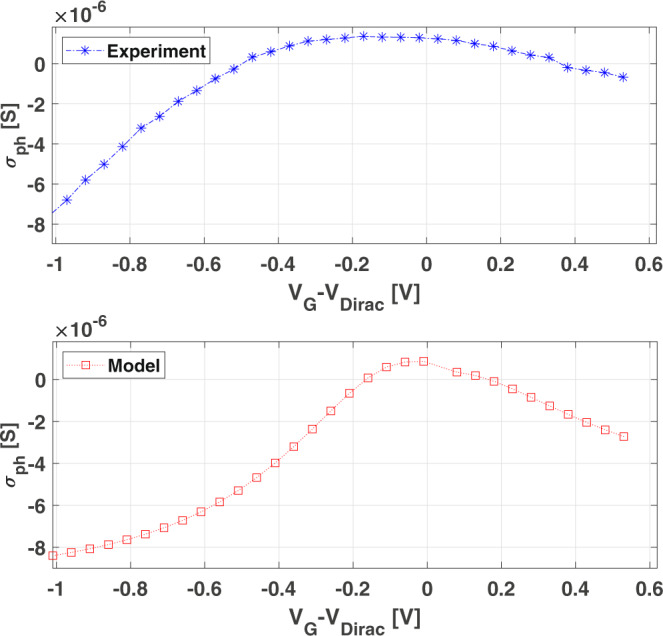
a Measured and b calculated photoconductivity of illuminated SLG channel.

We then calculate $\frac{d{\sigma }_{\mathrm{ph}}}{d{V}_{\mathrm{GS}}}$ to find the maximum downconversion efficiency. This can be increased by ~27 dB (power unit) for SLG with μ_fe ~30,000 cm² V⁻¹ s⁻¹ (τ = 1/Γ ~ 0.6 ps) and n₀ ~ 10¹¹ cm⁻², see Methods. Thus, the control of the transition between the two different photocurrent mechanisms could lead to a maximization of ${\mathrm{\Delta }}_{R_{\mathrm{ext}}}$ and, in turn, a maximization of downconversion efficiency.

The 3 dB BW is ~19.7 GHz when operated as OEM, Fig. 4. This behavior is modeled in Eq. (3) by including the factor β(f_RF). To understand the optoelectronic-mixing dependence on f_RF and, thus, on f_IF (f_opt being fixed), we consider a typical figure of merit of high-frequency transistors: the transducer power gain⁵, defined as: G_T = $\frac{P_{\mathrm{load}}}{P_{\mathrm{avs}}}$, where P_load is the power delivered to the load and P_avs is the source power. G_T coincides with the modulus of the S₂₁ parameter when source and load are matched⁵. This is the case in our measurements, where the power is delivered from the VNA 50Ω-source and measured on a 50Ω receiver. G_T is close to the S₂₁ parameters. An external impedance matching could increase the downconversion efficiency by maximizing the power delivered by the GFET, other than increasing BW. We do not observe saturation in the photodetected signal at the highest optical power available in our setup (60 mW). Thus, illuminating a wider channel surface, while maintaining the same optical power density, should increase the downconversion efficiency. An enhancement of SLG-light interaction can also improve the downconversion efficiency. In all, ~70% absorption could be achieved by integrating SLG on a waveguide⁶⁸. This could enhance the downconversion efficiency by ~30 dB, compared with the normal incidence case (~2.3% absorption²³).

In summary, we reported high-frequency graphene transistors operating as OEMs for frequencies up to at least 67 GHz. The photodetection BW exceeds 67 GHz. The BW of the devices operated as OEMs is 19.7 GHz. The conversion efficiency is at least two orders of magnitude higher than previous graphene OEMs²⁹. It can be further increased using high-quality samples with μ ~ 10,000–100,000 cm² V⁻¹ s⁻¹ and increasing light-matter interaction. This can increase the downconversion efficiency >50 dB, overcoming state-of the-art performances of OEMs based on any other technology³¹. Our frequency operation is already comparable with state-of-the-art performance of OEMs based on any other technology³¹. Thus, our work paves the way for the use of graphene-based transistors as OEMs in applications exploiting mm-waves, such as telecommunications and RADAR/LIDAR.

Methods

Photocurrent modeling

Equations 1–5 show that the optoelectronic-mixing efficiency is proportional to ${\mathrm{\Delta }}_{R_{\mathrm{ext}}}$, which can be expressed as:

$${\mathrm{\Delta }}_{R_{\mathrm{ext}}}=\beta \left(f_{\mathrm{RF}}\right)\frac{d{R}_{\mathrm{ext}}\left(V_{\mathrm{GS}}\right)}{d{V}_{\mathrm{GS}}}{\mid }_{V_{\mathrm{GS}}={\overline{V}}_{\mathrm{GS}}}$$ 8

Since R_ext is proportional to σ_ph(V_GS)³⁰, the optimization of the mixing efficiency requires $\frac{d{\sigma }_{\mathrm{ph}}}{d{V}_{\mathrm{GS}}}$ to be maximized. The mixing efficiency can be related via ${\mathrm{\Delta }}_{R_{\mathrm{ext}}}$ to SLG’s μ and n^63,67. The Drude model for free carrier conductivity in SLG gives⁶³:

$$\sigma \left(\omega ,T_e\right)=\frac{D\left(T_e\right)}{\pi \left[\mathrm{\Gamma }\left(T_e\right)-i\omega \right]}$$ 9

In the case of Dirac Fermions the Drude weight is⁶³:

$$D\left(T_e\right)=\frac{2e^2}{{\hslash }^2}{k}_B{T}_{e}ln\left[2cosh\left(\frac{{\mu }_c\left(T_e\right)}{2k_B{T}_e}\right)\right]$$ 10

with k_B the Boltzmann constant. In the GHz range, ω ~ 10⁹−10¹⁰ rad/s. This value is negligible compared to our Γ, which lies in the range 10¹²−10¹³ rad/s³². The photoconductivity owing to the illumination of the SLG channel is then ⁶³:

$${\sigma }_{\mathrm{ph}}=\sigma \left(T_{\mathrm{light}}\right)-\sigma \left(T_{\mathrm{dark}}\right)=\frac{D\left(T_{\mathrm{light}}\right)}{\pi \mathrm{\Gamma }\left(T_{\mathrm{light}}\right)}-\frac{D\left(T_{\mathrm{dark}}\right)}{\pi \mathrm{\Gamma }\left(T_{\mathrm{dark}}\right)}$$ 11

This depends on T, as experimentally shown in ref. ³⁴. Increasing T decreases the photodetection efficiency³⁴. This is consistent with the screening reduction of the scattering mechanism while increasing T_e³², since a smaller T change between dark and illumination conditions takes place.

μ_c is T-dependent. It decreases while increasing T to keep the number of conduction band carriers constant⁶⁹. So, it is lower in illumination conditions with respect to dark. To account for this, we compute μ_c by numerical inversion of the following T-dependent formula^60,63:

$$\frac{2}{\pi }\frac{{\left(k_{B}T\right)}^2}{{\left(\hslash v_0\right)}^2}\left[L{i}_2\left(-e^{\frac{-{\mu }_c}{k_{B}T}}\right)-L{i}_2\left(-e^{\frac{{\mu }_c}{k_{B}T}}\right)\right]=\frac{C_{\mathrm{ox}}{V}_{\mathrm{GS}}}{e}-\frac{{\mu }_c{C}_{\mathrm{ox}}}{e^2}$$ 12

In Eq. (12), C_ox is the geometrical gate capacitance per unit area, v₀ is the Fermi velocity and Li₂ is the dilogarithm function. This is valid in low and high doping and also includes the effects of quantum capacitance. Γ is calculated from μ_fe ~ 2500 cm²/(Vs) using¹⁶:

$$\mathrm{\Gamma }=\frac{1}{\tau }=\frac{e{v}_F^2}{{\mu }_c\left(T_e\right){\mu }_{\mathrm{fe}}}$$ 13

We get Γ ~ 80 meV, i.e. τ ~ 50 fs for μ_c ~ 0.2 eV. Charge puddles are taken into account by replacing μ_c with⁶³:

$${\mu }_c\to \sqrt[4]{{\mu }_c^4+\mathrm{\Delta }{{\mu }_{\mathrm{puddles}}}^4}$$ 14

Δμ_puddles is calculated as⁶⁰:

$$\mathrm{\Delta }{\mu }_{\mathrm{puddles}}=\sqrt{n_0\pi }\hslash v_F~120\mathrm{meV}$$ 15

Here, n₀ ~ 5 ⋅ 10¹¹ cm⁻² extracted from the measured DC minimum of conductivity σ_min⁶⁰:

$$n_0=\frac{{\sigma }_{\min }}{e{\mu }_{\mathrm{fe}}}$$ 16

From the DC measurements, we get C_ox ~ 4fF/μm². The experimental curve in Fig. 7 uses T_e as a fitting parameter, getting T_e ~ 320 K in the laser spot region.

Optoelectronic mixing efficiency

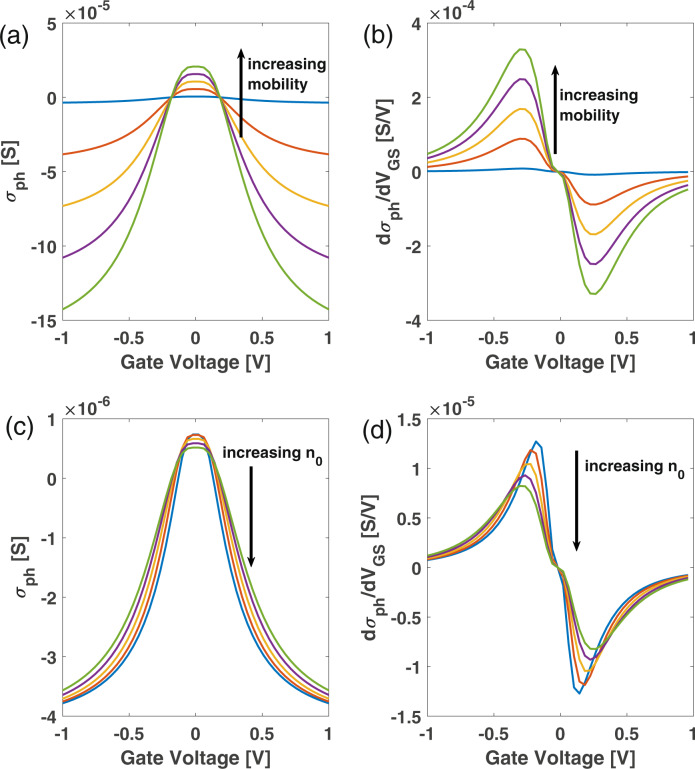
We now evaluate the effects of μ and n₀ on mixing efficiency. Since our SLG is substrate-supported and not encapsulated in hBN, long-range scattering limits conductivity³², more specifically Coulomb scattering^32,70,71. In this regime, the typical τ is in the range of hundreds of fs³². High-quality SLG can have low n₀ (<10¹² cm⁻²) and high μ > 100,000 cm² V⁻¹ s⁻¹)⁵⁰. In high-quality SLG encapsulated with hBN, as in ref. ⁵⁰, transport is dominated by random-strain fluctuations^33,72. For such SLG, a change in μ < 20% was measured as a function of n⁵⁰. In order to estimate the performance in such SLG, we assume no dependence of μ o n. Within this assumption, τ ∝ μ for μ >> K_BT⁶⁰, so Eq. (13) is still valid. For μ ~ 100,000 cm² V⁻¹ s⁻¹, τ can be up to 2ps for E_F ~ 0.2 eV¹⁶. We thus calculate σ_ph for μ up to 100,000 cm² V⁻¹ s⁻¹ and n₀ ~ 5 ⋅ 10¹¹ cm⁻², Fig. 8a. By comparing the green and the blue curves, which show the photoconductivity for μ ~ 100,000 and 2.500 cm² V⁻¹ s⁻¹, we predict an increase ~40 times at both low (i.e. V_GS = 0) and high electrostatic doping (i.e., for V_GS = 1 V). We then differentiate the curves in Fig. 8a. Figure 8b shows an increase in dσ_ph/dV_GS, (i.e. an increase of ${\mathrm{\Delta }}_{R_{\mathrm{ext}}}$) of a factor ~40.

Fig. 8. Optoelectronic-mixing performance.

a Calculated photoconductivity and b photoconductivity derivative for μ_fe varying from 3800 to 100,000 cm² V⁻¹ s⁻¹. c Calculated photoconductivity and d photoconductivity derivative for n₀ varying from 10¹¹ to 4.5^.10¹¹ cm⁻².

Another parameter that can be improved by employing high-quality SLG is n₀. Fig. 8c plots the photoconductivity for n₀ between 10¹¹ cm⁻² (corresponding to high-quality SLG⁵⁰) and 5 × 10¹¹ cm⁻² (our case), while keeping μ_fe = 2500 cm² V⁻¹ s⁻¹. In this case, the photoconductivity increases by a factor ~1.4 near the CNP, as well as at high doping (V_GS = 1 V), with dσ_ph/dV_GS almost doubled, Fig. 8d. This means that the voltage operating point of the device can be decreased.

Our prediction is based on the model presented in ref. ³², which indicates the screening reduction of the Coulomb impurity scattering mechanism while increasing T³². For Coulomb scattering in samples with μ_fe up to 1000 cm² V⁻¹ s⁻¹⁷¹, this is supported by several experimental and theoretical works^32,63,67. For samples with ultra-high μ_fe up to 100,000 cm² V⁻¹ s⁻¹⁵⁰), the dominant mechanism limiting μ_fe is strain disorder³³, with two contributions: (i) random scalar potential and (ii) random gauge potential³³. The first is sensitive to T increase owing to screening reduction³³, similar to what happens for Coulomb scattering³², while the second is not³³. Thus, for ultra-high-quality μ_fe samples, the “screening reduction” picture may not be accurate. Therefore, we use an intermediate value μ_fe = 30,000 cm² V⁻¹ s⁻¹, between 10,000 cm² V⁻¹ s⁻¹ (i.e., Coulomb scattering regime⁷¹) and 100,000 cm² V⁻¹ s⁻¹ (i.e., random-strain fluctuations-induced scattering regime³³) to infer the performance boost of OEMs based on SLG FET owing to μ_fe increase. In this case, for n₀ = 10¹¹ cm⁻², we predict an increase of dσ_ph/dV_GS by a factor ~23 dB. Thus, the downcoversion efficiency in power units can increase ~27dB, overcoming the OEMs state-of-the-art performance^12,31. Fig. 9 plots the downconverted photocurrent at three frequencies as a function of V_GS. This shows Fig. 6 is valid regardless of operating frequency.

Dependence of the laser spot position on photoresponse

Figure 10 shows the photoresponse as a function of laser spot position over the device, along the dashed black line. The photocurrent is measured with the VNA used for the RF measurements in Fig. 2a. The optical beam intensity is modulated at 10 GHz and the optical power impinging the sample is ~10 mW. The beam scan step is ~300 nm, smaller than the spot size of the laser ~2 μm, as defined by the FWHM of the intensity of the Gaussian laser profile. The red dots represent the measured photocurrent at V_DS = 0.2 V, whereas the blue ones are for V_DS = 0 V. The maximum photocurrent is registered when V_DS = 0.2 V and the laser spot is over the GFET channel. We observe very low photocurrent, comparable with the instrument noise floor (~−90 dBm electrical power detected over the internal 50Ω impedance of the instrument) at V_DS = 0. At V_DS = 0.2 V, we do not observe a change of the photocurrent sign (due to, e.g., asymmetrical heating effect⁷³) when the laser spot is scanned from the source to the drain contact. Thus, the role of contacts in the photocurrent generation can be neglected.

Author contributions

A.M. and W.W. performed the optoelectronic, DC, and RF characterization. A.M. and P.A. carried out the device simulations, W.W. fabricated the device, D.D.F., U.S., G.S., A.C.F. grew, transferred, and characterized the graphene samples. A.C.F., P.L., H.H. supervised the work. A.M., P.L., E.P. conceived the idea. A.M. wrote the paper, with contributions from all authors.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Competing interests

The authors declare no competing interests.