A fast MR-thermometry method for quantitative assessment of temperature increase near an implanted wire

Marylène Delcey; Pierre Bour; Valéry Ozenne; Wadie Ben Hassen; Bruno Quesson

doi:10.1371/journal.pone.0250636

. 2021 May 13;16(5):e0250636. doi: 10.1371/journal.pone.0250636

A fast MR-thermometry method for quantitative assessment of temperature increase near an implanted wire

Marylène Delcey ^1,^2,^3,^4,^*, Pierre Bour ^1,^2,³, Valéry Ozenne ^1,^2,³, Wadie Ben Hassen ⁴, Bruno Quesson ^1,^2,³

Editor: Nick Todd⁵

PMCID: PMC8118538 PMID: 33983935

Abstract

Purpose

To propose a MR-thermometry method and associated data processing technique to predict the maximal RF-induced temperature increase near an implanted wire for any other MRI sequence.

Methods

A dynamic single shot echo planar imaging sequence was implemented that interleaves acquisition of several slices every second and an energy deposition module with adjustable parameters. Temperature images were processed in real time and compared to invasive fiber-optic measurements to assess accuracy of the method. The standard deviation of temperature was measured in gel and in vivo in the human brain of a volunteer. Temperature increases were measured for different RF exposure levels in a phantom containing an inserted wire and then a MR-conditional pacemaker lead. These calibration data set were fitted to a semi-empirical model allowing estimation of temperature increase of other acquisition sequences.

Results

The precision of the measurement obtained after filtering with a 1.6x1.6 mm² in plane resolution was 0.2°C in gel, as well as in the human brain. A high correspondence was observed with invasive temperature measurements during RF-induced heating (0.5°C RMSE for a 11.5°C temperature increase). Temperature rises of 32.4°C and 6.5°C were reached at the tip of a wire and of a pacemaker lead, respectively. After successful fitting of temperature curves of the calibration data set, temperature rise predicted by the model was in good agreement (around 5% difference) with measured temperature by a fiber optic probe, for three other MRI sequences.

Conclusion

This method proposes a rapid and reliable quantification of the temperature rise near an implanted wire. Calibration data set and resulting fitting coefficients can be used to estimate temperature increase for any MRI sequence as function of its power and duration.

Introduction

Magnetic resonance imaging (MRI) is increasingly performed in the presence of cardiac electronic implantable devices (CEIDs) [1, 2], or deep brain stimulation (DBS) electrodes [3], together with interventional devices such as for MRI-guided catheterization [4]. In these situations, radiofrequency pulses of the MRI sequence are considered as a principal risk since energy deposition in the patient may induce currents along the device’s conductive part and result in local hotspots at its interface with the surrounding tissue [5]. Several theoretical [6–8] and experimental studies [9–12] have shown that tissue temperature increase can easily reach several tens of degrees Celsius, potentially leading to severe burn injuries [13, 14].

Standards were imposed by the U.S Food and Drug Administration (FDA) and the International Electrotechnical Commission (IEC) [15] both for maximum tissue temperature and RF exposure conditions. Various methods have been proposed to evaluate device safety [16]. Numerical simulations of electromagnetic fields, induced currents and resulting temperature evolution (using the bio-heat transfer equation) [17–19] require precise knowledge of the device’s 3D geometrical arrangements, its composition, size and its position relative to the MRI scanner’s excitation coil, together with electrical and thermal tissue properties, making personalized simulation for each patient unpractical. To overcome this limitation, in vivo assessments are preferred. One solution is to integrate temperature sensors in the device, located where hot spots are likely to occur [11]. However, these methods require transmission of temperature readings during MRI scanning which complicates the design of the device itself, particularly for DBS and CEIDs where no percutaneous access to the device is available. Moreover, in cases of disconnection or rupture of the device lead [20], the location of the sensor may no longer correspond to the anticipated hot spot location in surrounding tissue. Other approaches based on MRI measurements were proposed to quantify induced currents into the device through B₁₊ mapping, using either magnitude [21] or phase images [22]. However, these methods still require some assumptions (homogeneous or known B1 transmit and/or receive fields) to work efficiently. Moreover, they suffer from being simple surrogates of the relevant quantity of interest which is tissue temperature. In the context of measuring small temperature changes near devices, MRI-thermometry should be rapid with a sufficiently large spatial coverage around the implanted wire and provide a spatial resolution in the range of a few millimeters. The thermometry method should also be dynamic to monitor temperature evolution, while being precise enough to map small temperature changes with degree of uncertainty below 1°C. MRI-Temperature imaging methods based on Proton Resonance Frequency Shift (PRFS) [23, 24], T1-measurements [25–27] and using paramagnetic lanthanide complex [28] have been proposed. However, they do not fulfil all requirements in terms of spatial resolution, rapidity, spatial coverage and precision of temperature measurements specified above. The temperature rise near the tip of an implanted wire depends on the local absorbed power by the tissue and its conversion into heat. The maximal temperature reached at the end of a MRI sequence varies depending on tissue thermal diffusivity and perfusion. Thus, time-average values such as SAR or B_1+rms and total energy emitted by the sequence may be insufficient to predict maximal temperature rise near an implanted wire for any MRI sequence.

In this study, we propose a method to address these points in the context of implanted wires. A sub-second dynamic MRI-thermometry method based on the PRFS technique was implemented, including a module for energy deposition interleaved between successive rapid temperature measurements. We measured the local temperature increase with this sequence near the tip of an implanted wire into a gel for various acquisition conditions, to create a calibration data set. We also propose a model for fitting temperature evolution of this calibration data set together with an associated processing method to predict the maximal temperature rise for other MRI sequences.

Materials and methods

Set-up for ex vivo experiments

A Plexiglas box filled with agar (2% with 0.9% NaCl to match tissue electrical conductivity) was used for experiments. The container was designed to position a copper wire vertically and to hold a fluoroptic probe perpendicular to the wire.

MRI-thermometry sequence

All measurements were performed on a 1.5T clinical imaging system (MAGNETOM Avanto-fit, Siemens Healthcare Erlangen, Germany) equipped with a maximum gradient strength of 45 mT/m and a maximum slew rate of 200 T/m/s. A circular loop of 11 cm in diameter and two spine elements (4 elements each) were used for imaging (for a total of 9 receiver coils). The acquisition sequence (Fig 1) was a modified single-shot gradient echo planar imaging (EPI) sequence, with the following parameters: FOV = 120 mm, Repetition Time(TR)/Echo Time(TE) = 1000/18 ms, matrix size = 74x74 pixels (zero filled to 148x148 pixels), slice thickness = 2.4 mm, bandwidth = 1648 Hz/pixel, FA = 53°, GRAPPA acceleration factor of 2, 7/8 Partial Fourier. Between each EPI acquisition (62 ms per slice, including fat saturation pulses), a train of RF-pulses (called “heating module” in the remaining text) was applied between dynamic acquisitions #10 and #90 with adjustable parameters: flip angle, inter-pulse delay and number of pulses. In the remaining text, the flip angle of the heating module RF pulses is called FA_HM. Each RF pulse had a sinc shape of 1 ms duration (with an inter-pulse delay of 2 ms) and was emitted with a tunable frequency offset (typically 100 kHz) to avoid direct proton signal saturation [24, 26]. For 3 EPI slices and a TR of 1 s, 242 pulses were played between each stack of slices, resulting in a duty cycle of the heating module of 72% per TR.

Fig 1 — Single shot gradient echo EPI acquisition interleaved with a train of RF pulses (heating module) with adjustable flip angle, inter-pulse delay and number of pulses.

Thermometry pipeline

Temperature evolution was computed and visualized in real time during experiments using an MRI-thermometry pipeline similar to one proposed for monitoring cardiac radiofrequency ablations [29, 30]. The MRI raw data were streamed through TCP/IP to the Gadgetron framework for online image reconstruction [31], including EPI ghost-correction followed by GRAPPA reconstruction [32]. Prior to Fourier transform of the data, zero filling was applied resulting in a matrix size of 148x148 pixels and a reconstructed pixel spacing of 0.8x0.8mm². Temperature images were then computed from phase images using the PRFS method (with a constant of − 0.0094 ppm/°C) [33, 34]. The first 10 acquired slice stacks in the time series were averaged together to create reference phase images for each slice. Potential spatio-temporal phase-drifts were corrected using the method proposed by Ozenne et al. [29], using a temporal sliding window over the last 10 acquired stacks. Finally, a low pass temporal filter (first order Butterworth with 0.04 Hz cutoff frequency) was applied on a pixel-by-pixel basis on temperature curves to reduce uncertainty. Resulting temperature maps were sent online to a remote computer for display (Thermoguide, Image Guided Therapy, Pessac, France).

B_1+rms measurements

B_1+rms values were dynamically retrieved from the MRI scanner interface during acquisition at dynamic #90 (end of heating module). The total energy emitted by the sequence was computed and displayed in the user interface of the MRI console. A minimum delay of 6 minutes was observed between consecutive measurements with a different FA_HM to reset B_1+rms values by the MRI console. This delay also ensured proper cooling of the gel between consecutive experiments.

Validation of the MRI-thermometry method

For validation purposes, a test experiment was performed in a gel containing a copper wire (0.4 mm diameter, 1.2m length). One end of the wire was inserted vertically into the Plexiglas tank filled with agar gel. The remaining part of the wire was positioned in contact with the tunnel bore to favor RF-induced heating (highest electric field emitted by the transmit coil [6]). A fluoroptic temperature fiber (Luxtron® Fiber Optic, STF probe, LumaSense Technologies, Santa Clara, CA, USA) was inserted in the gel perpendicularly to the copper wire. The distance between the wire tip and the optical sensor was approximately 1 mm. A 3D balanced-SSFP sequence was acquired to locate the fiber optic temperature probe within the gel, using the following acquisition parameters: bandwidth = 250 Hz/pixel, TR/TE = 666/2.43 ms, 0.8 mm isotropic resolution, FOV = 130 mm, Flip Angle = 90°. The position of the optical fiber tip was identified and the slice stacks of the thermometry sequence were positioned at this reference location.

Potential RF-induced heating near the implanted wire measurement

In a second batch of experiments, another gel of identical content was used and the optical fiber temperature sensor was not inserted to obtain temperature maps devoid of any signal drop close to the wire. The same imaging sequence was repeated while varying the FA_HM from 0° to 90° by steps of 10° in order to create a calibration dataset. For each acquisition, the temperature evolution in the same pixel was analyzed, selecting the pixel with the maximal temperature increase at the end of the energy deposition (acquisition #90) from the temperature data corresponding to the largest FA_HM. To verify absence of temperature drift during experiment, temperature evolution in a pixel located outside the heating zone was also plotted.

Potential RF-induced heating near a pacemaker lead

We evaluated our method on a commercial MR conditional pacemaker lead (CapSureFix Novus MRI Surescan, 65-cm length, Medtronic). The latter was inserted vertically (perpendicular to B₀) into a gel and not connected to its generator to simulate an abandoned lead scenario. The tip of the lead that is normally screwed into the myocardium was inserted into the gel while the other extremity was left in the air. A 3D gradient echo (TE/TR = 3.9/8 ms, isotropic resolution of 0.8 mm) was acquired to locate the lead and position the central slice (stack of 3 slices) of the proposed sequence (with acquisition parameters identical to those mentioned above) at the lead tip.

Statistical analyses

To assess the thermometry precision, a first acquisition with FA_HM = 0° of the heating module was performed in gel. The same scan parameters as described in section MRI-thermometry sequence were used. The temporal average of temperature (μ_T) and the temporal standard deviation of temperature (σ_T) were computed for each pixel in a region of interest around the wire over the 120 dynamic acquisitions. The same analysis was repeated after temporal filtering.

MRI-thermometry assessment in volunteer

A healthy volunteer was informed about the protocol and consented to be included in the study (the institution review board "Commité de protection des personnes îles de France IV" #IRB0003835 approved this study under the approval number 2017-A03313-50) in order to measure the mean temporal standard deviation of the temperature in the brain with the proposed method, without energy deposition (FA_HM = 0°). Image acquisition parameters were 40° FA, 149*149 mm FOV, 92x92 matrix (zero filled to 184x184), 1510 Hz/px bandwidth, 70 repetitions, 1s repetition time. Measurements were repeated with different TE values of 22, 30, 40, 50, 60 and 70 ms. The standard 16-elements head coil provided by the manufacturer was used. A ROI was manually drawn to cover most of the brain over the 3 slices. The temporal standard deviation (σ_T) was computed over the 3 slices and analyzed with a Box-and-Whisker plot (selected values: lower value, first quartile, median value, third quartile and 95% of the distribution) to characterize precision of the method.

Temperature dependence on flip angle, B_1+rms and energy emitted by the MRI sequence

For each experiment of the calibration dataset, a temporal window of 5 dynamic acquisitions was used to compute the mean temperature and the temporal standard deviation at the end of energy deposition (between acquisitions #86 and #90). The μ_T ± σ_T temperature values were plotted as a function of the flip angle, B_1+rms and energy emitted (i.e. sum of the energies of each individual RF pulse, including pulses for imaging and pulses of the heating module). A quadratic fit was performed on the resulting first two curves and a linear fit on the last one. Coefficients (namely, β₁, β₂ and β₃) and R² of the fit were retrieved.

Prediction of temperature increase for other MRI sequences

In this section, we propose a semi-empirical approach to exploit temperature data obtained from a calibration dataset to predict the maximal temperature rise for any other MRI sequence. Considering that heating induced near an implanted wire is localized around its tip, we chose to approximate this heating source by a Gaussian function with isotropic dimensions. Under this assumption, temperature evolution at the hottest point resulting from energy deposition at constant power (P₀) applied between t₀ and t₁ can be analytically described by the following equation [35]:

T (t) = {\begin{cases} 0 f o r t \leq t_{0} \\ α P_{0} τ l n \frac{t - t_{0} + τ}{τ} f o r t_{0} \leq t \leq t_{1} \\ α P_{0} τ l n \frac{t - t_{0} + τ}{t - t_{1} + τ} f o r t \geq t_{1} \end{cases}

[1]

Where α is the absorption coefficient and τ is a time constant. Temperature evolution at the hottest point for each temperature curve of the calibration data set acquired at different powers P_i (i.e. for each flip angle of the SAR module) was fit using equation [1] to retrieve α and τ. Then, we plot α_i and τ_i as a function of P_i and fit these two curves with a second order polynomial function. The resulting functions allow then to compute α and τ values corresponding to the power of any other MRI sequence. Thus, temperature evolution for the selected sequence can then be simulated by taking its effective emitted power (total energy divided by acquisition duration) and its acquisition duration. In a third batch of experiments, we included the tip of the wire already described above together with the optical fiber into a gel (wire perpendicular to B₀ and identical gel preparation as described above). After the calibration data set was created, temperature curves for each flip angle were processed as indicated above. Then, three other acquisition sequences typically used in clinic were launched and temperature was recorded by the fiber optic probe:

A 2D Turbo spin echo sequence, emitting 11.093 W power during 38 s
A 3D gradient echo sequence, emitting 2.522 W during 2 min 15 s
A 2D cine true-fisp sequence, emitting 43.590 W during 9s

Temperature evolution simulated for these 3 sequences using equation [1] and parameters derived from the proposed method were compared to fiber optic readings.

Results

Precision of the MRI-thermometry method

Fig 2A shows the temporal average of temperature (μ_T) and the temporal standard deviation of temperature (σ_T) in the gel over the 120 dynamic acquisitions for the first slice, when no energy is deposited (FA_HM = 0° for the heating module). μ_T and σ_T values were (mean ± std) 0.00±0.20°C and 0.65±0.05°C without filtering, and 0.00±0.20°C and 0.21±0.04°C after filtering, respectively. Fig 2B shows the three slices acquired on a volunteer with the proposed method (TE = 30 ms) together with the map of temporal standard deviation in an ROI covering most of the brain. Box-and-whisker plots of σ_T show that median values decreased from 0.2°C for a TE of 22 ms to 0.12°C for a TE ranging 40–70 ms. Moreover, at least 75% of the pixels included in the ROI remained below 0.25°C, irrespective of the echo time (90% or more for TE ranging 40–70 ms).

Accuracy of the MRI-thermometry method during heating

Fig 3A shows the magnitude image of the gel sample with the optical fiber inserted near the wire tip. Fig 3B displays the temperature distribution at the end of the energy deposition (dynamic acquisition #90) within the blue square shown in Fig 3A. Local heating can be observed around the tip of the copper wire. Evolution of the temperature over the 120 dynamic acquisitions is plotted in Fig 3C for a single pixel located near the fiber optic sensor, together with temperature evolution in another pixel located away from the heated region. Overlaid dashed lines correspond to the MRI-temperature data in the same pixels after low-pass filtering. A strong correspondence is observed between temperature evolution measured by the fiber optic sensor (green curve) and filtered MRI-temperature data (dashed black curve). The maximal temperature value computed over 5 dynamic acquisitions around #90 for filtered MRI-thermometry data and fluoroptic probe were 11.5°C and 11.7°C, respectively. To compensate the latency induced by the filter (delay of three repetition times) and compute correct root mean squared error (RMSE) values, the filtered curve was shifted left by three dynamic acquisitions in post processing before subtraction to temperature readings from the optical thermometer. The resulting RMSE were 1.2°C and 0.5°C for unfiltered and filtered MR temperature values, respectively.

Phantom experiments with varying flip angles

Fig 4A displays the MRI-temperature maps at the dynamic acquisition #90 for each flip angle of the heating module. No artifact related to the presence of the wire was observed on the magnitude image of the thermometry sequence. A temperature increase was observed close to the tip of the wire, with an increasing maximal value with the flip angle. In the present configuration, the maximal temperature increase was 32.4°C for a 90° flip angle. Temperature evolution is plotted in Fig 4B (red curves) for each flip angle in the same pixel (intersection of the dashed red lines) and in a pixel located outside the heated region (blue curves). Table 1 reports the measured B_1+rms, total emitted energy and maximal temperature increases for flip angles of the heating module ranging from 0 to 90°. Maximal B_1+rms values were 4.1 μT for a 90° FA_HM. The maximal temperature as a function of the FA_HM, B_1+rms and energy is displayed in Fig 5, together with the fits. Coefficients resulting from the fits were β₁ = 4.3 ± 0.1.10⁻³°C/°², β₂ = 2.0 ± 0.05°C/(μT)² and β₃ = 2.3 ± 0.1 10⁻³°C/J, respectively. A strong correspondence was found between experimental data and fits (R² = 0.98 for each fit).

Table 1. Summary of experimental conditions and temperature increase as a function of the flip angle of the heating module.

FA (°) (heating module)	B_1+rms (μT) (EPI + heating module)	Energy (J) (heating module)	Max temperature increase (°C)
0	0.6	0	0.2
10	0.8	150	0.7
20	1.1	602	1.4
30	1.4	1354	2.6
40	1.9	2407	6.7
50	2.3	3761	9
60	2.8	5415	15.7
70	3.2	7371	24
80	3.8	9627	29
90	4.1	12185	32.4

Open in a new tab

Measured B_1+rms are those provided by the scanner at the end of heating (dynamic acquisition #90). Energy values of the heating module are computed from the sequence. The last column reports the maximal temperature values measured by the proposed MRI thermometry method.

Fig 5 — Each point corresponds to the mean of the temperature over 5 dynamic acquisitions at the end of the energy deposition (acquisition #90) obtained for FA_HM ranging from 0° to 90°. The same pixel was selected for each experiment. Error bars correspond to the σ_T over the same 5 dynamic acquisitions. A quadratic curve fit was performed for the two first curves and a linear fit for the last one. Coefficients resulting from the fits were β₁ = 4.3 ± 0.1.10⁻³°C/°², β₂ = 2.0 ± 0.05°C/(μT)² and β₃ = 2.3 ± 0.1 10⁻³°C/J, respectively.

Applicability of the method on a pacemaker lead

A local temperature rise up to 6.5°C was observed near the tip of the device (Fig 6A right) for a 90° flip angle. A small (2x2 pixels) hypo intense (less than 20% reduction in intensity) region was observed in the central slice of the magnitude image of the thermometry sequence near the tip of the wire. However, temperature SD measured in these pixels was identical to values measured everywhere else into the gel. Calibration curves are displayed in Fig 6B, with β₁, β₂ and β₃ values of 8.8±0.5.10⁻⁴°C/°² (R² = 0.96), 0.40±0.02°C/μT² (R² = 0.97) and 5.8±0.3.10⁻⁴°C/J (R² = 0.96), respectively.

Prediction of temperature rise for three MRI sequences

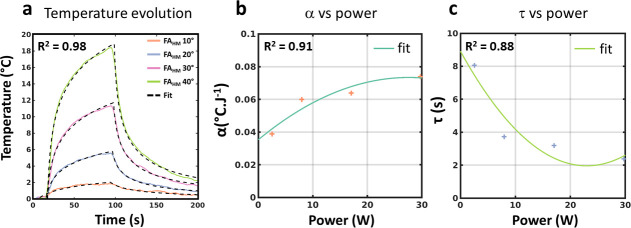
Fig 7 presents results from an additional experiment performed in a gel to evaluate the proposed model and processing technique. The temperature curves of the calibration data set (Fig 7A) were fit with Eq [1] for each flip angle of the FA_HM. The resulting α and τ values derived from these fits are plotted as a function of the corresponding powers in Fig 7B and 7C, together with the results of the polynomial fits. Fig 8A displays the temperature values measured by the optic fiber during a 2D cine, a 2D turbo spin-echo and a 3D gradient echo, emitting 43.59 W during 9 s, 11.09 W during 38 s and 2.52 W during 135 s, respectively. For each sequence, the temperature curves were simulated using Eq [1], after calculating α and τ from the polynomial fits shown in Fig 7B and 7C. A good correspondence can be observed between experimental and simulated curves, with maximal values of 11.19°C (Cine) 5.62°C (2D TSE) and 2.32°C (3D GRE) for experimental values and predicted values of 11.88°C, 5.85°C and 2.33°C, respectively. On the contrary, using the calibration curves (namely coefficient β₃) from Fig 5C to estimate the maximal temperature increase from the total energy of each sequence leads to 2.78°C, 2.96°C and 2.42°C, respectively. Such an approach is thus irrelevant for predicting maximal temperature rise in the context of an implanted wire.

Fig 8B shows contour plots of the predicted maximal temperature increases for a range of power and duration using the fitting method and for this experimental configuration. Isotherms can then be used to define acceptable exposure conditions for any sequence.

Discussion

Sequence implementation

The hybrid sequence proposed in this study interleaves adjustable RF energy deposition with multi-slice EPI acquisitions to provide sufficient spatial (1.6 mm in-plane interpolated to 0.8 mm) and temporal resolution (1s refresh rate with a 3 s temporal footprint in our setting) for real-time visualization of the potential temperature increase in-situ. Similar approach was already proposed in Gensler et al., using T1 measurements to assess temperature evolution near a copper wire inserted into a gel. In plane spatial resolution was 2.3 mm with slice thickness of 5 mm, leading to an elementary voxel size of 26.5 mm³, much larger (factor 4) than in the present study (6.1 mm³). Ehses et al. proposed a PRF-based MR-thermometry method with similar in-plane spatial resolution (1.6 mm) but a slice thickness of 5 mm. Moreover, temporal resolution was 3.9 s per slice, making rapid and multi-slice monitoring of temperature evolution near the wire more difficult than in the present study. Here, the achieved spatial resolution was considered sufficient for observing local temperature hot spots near the wire tip, since the heating region observed in Fig 4A had a dimension ranging from 2.4 to 5.6 mm (full width at half maximum of temperature profile for FA_HM ≥ 20°). The proposed implementation provides flexibility between the number of slices to acquire volumetric temperature data and energy deposition duty cycle (72% in our experiment). Higher acceleration factors, partial Fourier sampling [36] and/or simultaneous multi-slice techniques [37] may be implemented to increase volume coverage at constant acquisition time.

Precision of the MRI-thermometry

In our implementation, a temperature uncertainty of ~0.2°C was obtained on a clinical 1.5T MRI scanner (both on phantom and in vivo in the human brain). Such a precision was better than those previously reported [24, 26] and was considered sufficient in the context of MR safety evaluation of devices, where maximum temperature should not exceed 39°C for the brain (IEC-60601 and FDA regulation). Although optimal value for PRFS thermometry is achieved when TE equals T2*, the uncertainty in the human brain was found good enough for TE values ranging from 22 ms to 50 ms since they remained below 0.25°C for at least 75% of the pixels located in the brain irrespective of echo time.

In a previous study, a similar thermometry technique without the heating module showed a good precision (around 1°C) in vivo in mobile organs such as the heart [29, 30] and the liver at 1.5T [38] including real time motion compensation and correction of the potential temporal drift of the magnet (also implemented in the present work). In the context of monitoring small temperature increases near implanted wires in mobile organs, more sophisticated filtering techniques could be used to further improve the precision of thermometry as proposed by Roujol et al. [39] for example. Despite the proposed implementation creates a latency of 3 s, the risk of reaching a lethal thermal dose within this time scale (according to the CEM43 [40] model) which is unlikely to occur with optimized clinical devices.

Calibration technique

In the experiments with the copper wire, we observed an important temperature increase when the flip angle of the heating module was higher than 30°, although B_1+rms values provided by the scanner interface remained within regulatory limit (maximal B_1+rms of 3.2 μT, as indicated in the fixed‐parameter option of IEC 60601–2‐33) for most of the experimental conditions (FA_HM up to 70°, see Table 1). As expected from the theory [6], the maximal experimental temperature showed a quadratic variation (β₁ and β₂ coefficients) with the flip angle and B_1+rms, together with a linear dependence (β₃ coefficient) with the emitted energy. In the experiment with the MR conditional pacemaker lead, we were able to perform identical experiments and obtain different calibration curves, with maximal temperature increase of 6.5°C.

Prediction of temperature increase from the model

In the last experiment (Figs 7 and 8), we illustrate that the proposed model can correctly fit the temperature curves of the calibration dataset. From these fits, we show that temperature evolution of other acquisition sequences can be reasonably estimated. An exponential fitting function was proposed in the literature to model temperature increase during the heating phase. However, experimental results reported in Ehses et al. [24] and Gensler et al. [26] did not perfectly fit the MR-temperature curves and diverged from fiber optic measurements using this model. Here, we chose a more physically-realistic model of temperature evolution (derived from a Gaussian-shaped heating source), although this shape is an approximation for RF-induced heating. This model fits both the heating and cooling phases of the temperature curve. Whatever the model, indeed, the two parameters resulting from the fit (here α and τ) are directly linked to tissue absorption and thermal diffusivity, and are thus not expected to vary with the emitted power, at least for moderate temperature increases (i.e. remaining below the lethal thermal dose). However, parameters α and τ (Fig 7B and 7C) derived from the fit of temperature curves (Fig 7A) show a strong variation when varying FA_HM from 10° to 20° and lower changes for higher FA_HM (30° and 40°). For these reasons, we introduced a polynomial fitting function in Fig 7B and 7C. Variation of α and τ as a function of the power was attributed to the relative small dimensions of the heating spot for low FA_MH values, where partial volume effect of the thermometry sequence may play a role, although an effort was made to provide high resolution temperature images with the proposed sequence. This semi-empirical model allowed to predict the maximal temperature increase for three other MRI sequences. However, a key point of the calibration step is to avoid creating excessive temperature increase, since protein denaturation can occur when absolute temperature reaches 43°C (i.e. 6°C temperature rise above physiological body temperature). In our results, we reached much higher maximal temperature rises when wires were included in the gel. However, in our implementation, we chose a long duration of the heating module (80 s) to validate the acquisition method and the associated processing. Shorter duration of the heating module may be considered to reduce the temperature rise, taking advantage of the 1 s temporal resolution of our thermometry sequence to sample the temperature curve and thus derive α and τ, without inducing excessive temperature increase. Moreover, sampling the flip angles from 0 to 90° by 10° steps is probably not mandatory since risks are mainly associated with high power deposition, which correspond to large flip angles. This was observed on the pacemaker lead where significant heating was only observed for large flip angles (FA_MH of 70° and higher in see Fig 6B). Such an optimization of the calibration process was considered out of the scope of the present work, whose objective was to present the acquisition sequence and processing method and to evaluate them under well controlled experimental conditions, as a proof of concept.

The resulting temperature increases may differ in vivo since absorption, thermal diffusivity and perfusion (not present here) are tissue-specific, resulting in different calibration data sets. However, the method is expected to remain valid since perfusion acts as a scaling factor in temperature evolution. Thus, by generating calibration data set at the beginning of the MRI session, it should be possible to determine personalized RF exposure conditions for each patient with an implanted wire. In this objective, real-time MRI-thermometry as proposed here is of central interest to avoid creating excessive temperature rise during the calibration process.

Study limitations

This study has some limitations. First, PRFS technique is not applicable in fatty tissue. Second, our method may be dependent on size and magnetic susceptibility, limiting its applicability, since local image distortion and signal losses can be particularly severe with echo planar imaging. In our experiments, although the implanted wire was systematically positioned orthogonally to B₀, we were able to obtain temperature curves of sufficient quality to successfully process the data. For tissue with long T2* such as in the brain, echo time can be reduced in the presence of an implanted wire to balance the effect of local susceptibility artifacts, while keeping acceptable temperature accuracy (see Fig 2B). Moreover, shortening the echo train duration of the EPI by parallel imaging contributes to reducing susceptibility artifacts. Although EPI suffers from known limitations, this technique was preferred for the aforementioned advantages (rapid and multi slice imaging, high duty cycle), especially given that this technique is available on any scanner and that MRI compatibility of medical devices having implanted wires is under constant improvement by manufacturers [41]. In the present work however, no in vivo data with implanted wires could be produced to assess the method in real conditions, justifying further studies.

Conclusion

We propose here a practical MRI-based method to monitor the risk of heating during RF deposition by a MRI sequence through direct measurement of local temperature increase. This method may be combined with other MR-based approaches [21, 22] that aim to measure effective current induced in the device. The proposed method could be used at preliminary stage of the design of new devices with implanted wires to quantify the risk of heating depending on the exposure conditions, using phantoms with tissue-mimicking absorption and thermal diffusivity for example. In patients having devices with implanted wires, this method might be used at the beginning of the MRI session to assess acceptable exposure conditions. This will however require optimization of the calibration process and further in vivo evaluation.

Data Availability

Data has been uploaded to Zenodo: https://zenodo.org/record/4735614 (DOI: 10.5281/zenodo.4735614).

Funding Statement

This work received the financial support from the French National Investments for the Future Programs ANR-10-IAHU-04 (IHU Liryc), the Laboratory of Excellence ANR-10-LABX-57 (TRAIL, BQ), the French National Investment: ANR-17-CE19-0007(CARTLOVE, VO), and the French National Investment: ANR-19-CE19-0008-01(CARCOI, BQ). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. The funder provided support in the form of salaries for authors [MD and WBH], but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript.The specific roles of these authors are articulated in the ‘author contributions’ section.

References

1.Dacher J-N, Gandjbakhch E, Taieb J, Chauvin M, Anselme F, Bartoli A, et al. Joint Position Paper of the Working Group of Pacing and Electrophysiology of the French Society of Cardiology (SFC) and the Société française d’imagerie cardiaque et vasculaire diagnostique et interventionnelle (SFICV) on magnetic resonance imaging in patients with cardiac electronic implantable devices. Diagnostic and Interventional Imaging. 2020. February; 101(9):507–517 10.1016/j.diii.2020.02.003 [DOI] [PubMed] [Google Scholar]
2.Jabehdar Maralani P, Schieda N, Hecht EM, Litt H, Hindman N, Heyn C, et al. MRI safety and devices: An update and expert consensus. J Magn Reson Imaging. 2020. March;51(3):657–74. 10.1002/jmri.26909 [DOI] [PubMed] [Google Scholar]
3.Erhardt JB, Fuhrer E, Gruschke OG, Leupold J, Wapler MC, Hennig J, et al. Should patients with brain implants undergo MRI? J Neural Eng. 2018. August;15(4):041002. 10.1088/1741-2552/aab4e4 [DOI] [PubMed] [Google Scholar]
4.Campbell-Washburn AE, Tavallaei MA, Pop M, Grant EK, Chubb H, Rhode K, et al. Real-time MRI guidance of cardiac interventions: Real-Time Cardiac MRI Interventions. J Magn Reson Imaging. 2017. October;46(4):935–50. 10.1002/jmri.25749 [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Murbach M, Zastrow E, Neufeld E, Cabot E, Kainz W, Kuster N. Heating and Safety Concerns of the Radio-Frequency Field in MRI. Curr Radiol Rep. 2015. December;3(12):45. [Google Scholar]
6.Nitz WR, Oppelt A, Renz W, Manke C, Lenhart M, Link J. On the heating of linear conductive structures as guide wires and catheters in interventional MRI. J Magn Reson Imaging. 2001. January;13(1):105–14. [DOI] [PubMed] [Google Scholar]
7.Park S-M, Kamondetdacha R, Nyenhuis JA. Calculation of MRI-induced heating of an implanted medical lead wire with an electric field transfer function. J Magn Reson Imaging. 2007. November;26(5):1278–85. 10.1002/jmri.21159 [DOI] [PubMed] [Google Scholar]
8.Achenbach S, Moshage W, Diem B, Bieberlea T, Schibgilla V, Bachmann K. Effects of magnetic resonance imaging on cardiac pacemakers and electrodes. American Heart Journal. 1997. September;134(3):467–73. 10.1016/s0002-8703(97)70083-8 [DOI] [PubMed] [Google Scholar]
9.Konings MK, Bartels LW, Smits HFM, Bakker CJG. Heating Around Intravascular Guidewires by Resonating RF Waves. J Magn Reson Imaging. 2000. July;12(1):79–85. [DOI] [PubMed] [Google Scholar]
10.Rezai AR, Finelli D, Nyenhuis JA, Hrdlicka G, Tkach J, Sharan A, et al. Neurostimulation systems for deep brain stimulation: In vitro evaluation of magnetic resonance imaging-related heating at 1.5 tesla. J Magn Reson Imaging. 2002. March;15(3):241–50. 10.1002/jmri.10069 [DOI] [PubMed] [Google Scholar]
11.Luechinger R, Zeijlemaker VA, Pedersen EM, Mortensen P, Falk E, Duru F, et al. In vivo heating of pacemaker leads during magnetic resonance imaging. European Heart Journal. 2005. February 1;26(4):376–83. 10.1093/eurheartj/ehi009 [DOI] [PubMed] [Google Scholar]
12.Mattei E, Triventi M, Calcagnini G, Censi F, Kainz W, Mendoza G, et al. Complexity of MRI induced heating on metallic leads: Experimental measurements of 374 configurations. BioMed Eng OnLine. March 2008;7(1):11. 10.1186/1475-925X-7-11 [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Spiegel J, Fuss G, Backens M, Reith W, Magnus T, Becker G, et al. Transient dystonia following magnetic resonance imaging in a patient with deep brain stimulation electrodes for the treatment of Parkinson disease. Journal of Neurosurgery. 2003. October;99(4):772–4. 10.3171/jns.2003.99.4.0772 [DOI] [PubMed] [Google Scholar]
14.Henderson JM, Tkach J, Phillips M, Baker K, Shellock FG, Rezai AR. Permanent Neurological Deficit Related to Magnetic Resonance Imaging in a Patient with Implanted Deep Brain Stimulation Electrodes for Parkinson’s Disease: Case Report. Neurosurgery. 2005. November 1;57(5):E1063–E1063. 10.1227/01.neu.0000180810.16964.3e [DOI] [PubMed] [Google Scholar]
15.Woods TO. Standards for medical devices in MRI: Present and future. J Magn Reson Imaging. 2007. November;26(5):1186–9. 10.1002/jmri.21140 [DOI] [PubMed] [Google Scholar]
16.Winter L, Seifert F, Zilberti L, Murbach M, Ittermann B. MRI‐Related Heating of Implants and Devices: A Review. J Magn Reson Imaging. 2020. May 26;jmri.27194. 10.1002/jmri.27194 [DOI] [PubMed] [Google Scholar]
17.Collins CM. Numerical field calculations considering the human subject for engineering and safety assurance in MRI. NMR in Biomedicine. 2009. November;22(9):919–26. 10.1002/nbm.1251 [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Fiedler TM, Ladd ME, Bitz AK. SAR Simulations & Safety. NeuroImage. 2018. March;168:33–58. 10.1016/j.neuroimage.2017.03.035 [DOI] [PubMed] [Google Scholar]
19.Bottauscio O, Cassarà AM, Hand JW, Giordano D, Zilberti L, Borsero M, et al. Assessment of computational tools for MRI RF dosimetry by comparison with measurements on a laboratory phantom. Phys Med Biol. 2015. July;60(14):5655–80. 10.1088/0031-9155/60/14/5655 [DOI] [PubMed] [Google Scholar]
20.Langman DA, Goldberg IB, Finn JP, Ennis DB. Pacemaker lead tip heating in abandoned and pacemaker-attached leads at 1.5 tesla MRI. J Magn Reson Imaging. 2011. February;33(2):426–31. 10.1002/jmri.22463 [DOI] [PubMed] [Google Scholar]
21.Etezadi-Amoli M, Stang P, Kerr A, Pauly J, Scott G. Controlling radiofrequency-induced currents in guidewires using parallel transmit: Controlling RF Current Using Parallel Transmit. Magn Reson Med. 2015. December;74(6):1790–802. 10.1002/mrm.25543 [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Griffin GH, Anderson KJT, Celik H, Wright GA. Safely assessing radiofrequency heating potential of conductive devices using image-based current measurements: Images to Predict RF Heating Behavior. Magn Reson Med. 2015. January;73(1):427–41. 10.1002/mrm.25103 [DOI] [PubMed] [Google Scholar]
23.Pfeil A, Drobnik S, Rzanny R, Aboud A, Böttcher J, Schmidt P, et al. Compatibility of temporary pacemaker myocardial pacing leads with magnetic resonance imaging: an ex vivo tissue study. The International Journal of Cardiovascular Imaging. 2012. February;28(2):317–26. 10.1007/s10554-011-9800-y [DOI] [PubMed] [Google Scholar]
24.Ehses P, Fidler F, Nordbeck P, Pracht ED, Warmuth M, Jakob PM, et al. MRI thermometry: Fast mapping of RF-induced heating along conductive wires. Magn Reson Med. 2008. August;60(2):457–61. 10.1002/mrm.21417 [DOI] [PubMed] [Google Scholar]
25.Detti V, Grenier D, Perrin E, Beuf O. Assessment of radiofrequency self-heating around a metallic wire with MR T1-based thermometry. Magn Reson Med. 2011. August;66(2):448–55. 10.1002/mrm.22834 [DOI] [PubMed] [Google Scholar]
26.Gensler D, Fidler F, Ehses P, Warmuth M, Reiter T, Düring M, et al. MR safety: Fast T1 thermometry of the RF-induced heating of medical devices. Magn Reson Medicine. 2012. November 1;68(5):1593–9. [DOI] [PubMed] [Google Scholar]
27.Weber H, Taviani V, Yoon D, Ghanouni P, Pauly KB, Hargreaves BA. MR thermometry near metallic devices using multispectral imaging: MSI Thermometry. Magn Reson Med. 2017. March;77(3):1162–9. 10.1002/mrm.26203 [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Dharmadhikari S, James JR, Nyenhuis J, Bansal N. Evaluation of radiofrequency safety by high temperature resolution MR thermometry using a paramagnetic lanthanide complex: Evaluation of Specific Absorption Rate by MR Thermometry. Magn Reson Med. 2016. May;75(5):2121–9. 10.1002/mrm.25792 [DOI] [PubMed] [Google Scholar]
29.Ozenne V, Toupin S, Bour P, Senneville BD de, Lepetit‐Coiffé M, Boissenin M, et al. Improved cardiac magnetic resonance thermometry and dosimetry for monitoring lesion formation during catheter ablation. Magn Reson Med. 2017. January; 77(2):673–83. 10.1002/mrm.26158 [DOI] [PubMed] [Google Scholar]
30.Toupin S, Bour P, Lepetit-Coiffé M, Ozenne V, Denis de Senneville B, Schneider R, et al. Feasibility of real-time MR thermal dose mapping for predicting radiofrequency ablation outcome in the myocardium in vivo. Journal of Cardiovascular Magnetic Resonance. 2017. December;19(1):1–12. 10.1186/s12968-016-0318-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Hansen MS, Sørensen TS. Gadgetron: An open source framework for medical image reconstruction: Gadgetron. Magn Reson Med. 2013. June;69(6):1768–76. 10.1002/mrm.24389 [DOI] [PubMed] [Google Scholar]
32.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002. June;47(6):1202–10. 10.1002/mrm.10171 [DOI] [PubMed] [Google Scholar]
33.Ishihara Y, Calderon A, Watanabe H, Okamoto K, Suzuki Y, Kuroda K, et al. A precise and fast temperature mapping using water proton chemical shift. Magn Reson Med. 1995. December;34(6):814–23. 10.1002/mrm.1910340606 [DOI] [PubMed] [Google Scholar]
34.Poorter JD. Noninvasive MRI thermometry with the proton resonance frequency method: Study of susceptibility effects. Magn Reson Med. 1995. September;34(3):359–67. 10.1002/mrm.1910340313 [DOI] [PubMed] [Google Scholar]
35.Quesson B, Vimeux F, Salomir R, de Zwart JA, Moonen CTW. Automatic Control of Hyperthermic Therapy Based on Real-Time Fourier Analysis of MR Temperature Maps. 2002. June;47(6):1065–1072 [DOI] [PubMed] [Google Scholar]
36.Haacke EM, Lindskogj ED, Lin W. A fast, iterative, partial-fourier technique capable of local phase recovery. J Magn Reson (1969). 1991. March;92(1):126–45. [Google Scholar]
37.Borman PTS, Bos C, de Boorder T, Raaymakers BW, Moonen CTW, Crijns SPM. Towards real-time thermometry using simultaneous multislice MRI. Phys Med Biol. 2016. September 7;61(17):N461–77. 10.1088/0031-9155/61/17/N461 [DOI] [PubMed] [Google Scholar]
38.Bour P, Marquet F, Ozenne V, Toupin S, Dumont E, Aubry J-F, et al. Real-time monitoring of tissue displacement and temperature changes during MR-guided high intensity focused ultrasound: Monitoring of Changes During MRgHIFU. Magn Reson Med. 2017. November;78(5):1911–21. 10.1002/mrm.26588 [DOI] [PubMed] [Google Scholar]
39.Roujol S, de Senneville BD, Hey S, Moonen C, Ries M. Robust Adaptive Extended Kalman Filtering for Real Time MR-Thermometry Guided HIFU Interventions. IEEE Trans Med Imaging. 2012. March;31(3):533–42. 10.1109/TMI.2011.2171772 [DOI] [PubMed] [Google Scholar]
40.Sapareto SA, Dewey WC. Thermal dose determination in cancer therapy. International Journal of Radiation Oncology*Biology*Physics. 1984. April;10(6):787–800. 10.1016/0360-3016(84)90379-1 [DOI] [PubMed] [Google Scholar]
41.Sethi K, Chutani S. Magnetic resonance imaging-conditional devices: Where have we reached today? Int J Heart Rhythm. 2018;3(1):16. [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0250636.r001

Decision Letter 0

Nick Todd

24 Nov 2020

PONE-D-20-32401

A fast MR-thermometry method for quantitative assessment of temperature increase near an implanted wire

PLOS ONE

Dear Dr. Delcey,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

The manuscript has been reviewed by two reviewers with significant experience in MR thermometry. Both feel that a major revision is necessary to clarify the methods, motivate the application of the technique and potentially expand the scope of work. Please provide a detailed response to all comments made.

Please submit your revised manuscript by Jan 08 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

We look forward to receiving your revised manuscript.

Kind regards,

Nick Todd, PhD

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. Thank you for including your ethics statement: "Institution of review board "Commité de protection des personnes îles de France IV", #IRB 0003835

approval number: 2017-A03313-50

written consent ".

Please amend your current ethics statement to confirm that your named institutional review board or ethics committee specifically approved this study.

Once you have amended this/these statement(s) in the Methods section of the manuscript, please add the same text to the “Ethics Statement” field of the submission form (via “Edit Submission”).

For additional information about PLOS ONE ethical requirements for human subjects research, please refer to http://journals.plos.org/plosone/s/submission-guidelines#loc-human-subjects-research.

3. Thank you for stating the following in the Competing Interests section:

"I have read the journal's policy and the authors of this manuscript have the following competing interests: Marylene Delcey and Wadie Ben Hassen are employees of Siemens Healthcare."

We note that one or more of the authors are employed by a commercial company: Siemens Healthcare.

3.1. Please provide an amended Funding Statement declaring this commercial affiliation, as well as a statement regarding the Role of Funders in your study. If the funding organization did not play a role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript and only provided financial support in the form of authors' salaries and/or research materials, please review your statements relating to the author contributions, and ensure you have specifically and accurately indicated the role(s) that these authors had in your study. You can update author roles in the Author Contributions section of the online submission form.

Please also include the following statement within your amended Funding Statement.

“The funder provided support in the form of salaries for authors [insert relevant initials], but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The specific roles of these authors are articulated in the ‘author contributions’ section.”

If your commercial affiliation did play a role in your study, please state and explain this role within your updated Funding Statement.

3.2. Please also provide an updated Competing Interests Statement declaring this commercial affiliation along with any other relevant declarations relating to employment, consultancy, patents, products in development, or marketed products, etc.

Within your Competing Interests Statement, please confirm that this commercial affiliation does not alter your adherence to all PLOS ONE policies on sharing data and materials by including the following statement: "This does not alter our adherence to PLOS ONE policies on sharing data and materials.” (as detailed online in our guide for authors http://journals.plos.org/plosone/s/competing-interests) . If this adherence statement is not accurate and there are restrictions on sharing of data and/or materials, please state these. Please note that we cannot proceed with consideration of your article until this information has been declared.

Please include both an updated Funding Statement and Competing Interests Statement in your cover letter. We will change the online submission form on your behalf.

Please know it is PLOS ONE policy for corresponding authors to declare, on behalf of all authors, all potential competing interests for the purposes of transparency. PLOS defines a competing interest as anything that interferes with, or could reasonably be perceived as interfering with, the full and objective presentation, peer review, editorial decision-making, or publication of research or non-research articles submitted to one of the journals. Competing interests can be financial or non-financial, professional, or personal. Competing interests can arise in relationship to an organization or another person. Please follow this link to our website for more details on competing interests: http://journals.plos.org/plosone/s/competing-interests

4. We note that you have stated that you will provide repository information for your data at acceptance. Should your manuscript be accepted for publication, we will hold it until you provide the relevant accession numbers or DOIs necessary to access your data. If you wish to make changes to your Data Availability statement, please describe these changes in your cover letter and we will update your Data Availability statement to reflect the information you provide.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Partly

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: This work presents a method to assess heating near implanted wires during an MRI scan due to RF

deposition and induced currents. It uses fast measurements of temperature using PRFS MR

Thermometry interleaved with an RF heating module. The method was shown to be precise and

accurate in a variety of ex vivo heating scenarios and an in vivo no-heat scenario. Experiments and

analysis are scientifically sound. I appreciated the inclusion of the limitations and comparison to existing

methods in the discussion. Clarification of the scope, methods, and figures are needed.

After these adjustments, I believe the article is suitable for publication.

Specific comments:

1) The title implies the work is for measurement near implanted wires, but the intro (page 5, line

99), methods (page 8 line 172), and others refer to "implants” or “devices." This terminology

should be clarified throughout, as no evidence is presented to discuss how the work would be

applicable to other types of implanted devices.

2) The use case for the work should be made clear. How do you see the method being used in

practice? Is the method intended to be used during real-time monitoring, as a one-time

phantom calibration that exists in look-up-table form for each wire type, or something else?

How would this be used safely at the beginning of each MRI session (page 19, line 384) without

applying heating to the patient? Clarifying this in the abstract, introduction, and discussion will

help clearly define the impact of the work.

3) How much artifact was seen around the tips of the lead wires tested? Did it interfere with

maximum heat voxel selection/voxel near thermocouple selection? How would the method

perform if the lead wire were oriented differently with respect to B0, thus potentially having a

larger artifact?

4) Is the low-pass filtering necessary for generating the calibration curves, or would the original

data be precise enough? Would the filter latency (page 12, line 246) be an issue for clinical

implementation?

5) Figure 1 could be expanded to include which dynamics were averaged together. Add a label the

thermometry module.

6) Add titles to all sub-parts of Figures 2 and 3, and 6a.

7) Scale bar in Fig 2A blends in, consider a different color and moving outside the phantom into the

black area and adding the value to the image.

8) Figures 3c, 4b, 5, 6b need plot legends.

9) Page 6 line 127: How long was each dynamic (with and without interleaving the heating

module)?

10) Page 9 line 175: How was the voxel of interest chosen?

11) Page 9 line 179: add scan parameters to statistics section

12) Page 9 line 189: is this FA for the thermometry imaging module or the RF heating module?

13) Page 10 line 199: Was there any appreciable cooling during the 5 dynamics that were averaged?

Since this depends on # of slices, how many slices were used in each of the experiments?

14) Page 10 line 202: Explain how energy emitted was computed.

15) Page 16 lines 307-314 should be in the methods section.

16) Page 18 line 373: What is the regulatory limit?

Reviewer #2: This manuscript describes a method to run an MRI pulse sequence with an added “Heating module” to induce heating in implanted wires. The pulse sequence is a single-shot EPI pulse sequence for PRF MR thermometry, previously described in multiple papers by the same group. If the sequence is run multiple times with different parameters for the “Heating module”, the flip angle, B1+, and Energy can be plotted as functions of the temperature increase measured (with PRF MR thermometry) at the tip of a wire/lead. This creates what the authors call calibration curves, and which they claim can then be used to be sure temperature increases stay below regulatory limits even when other pulse sequences are used. Experiments were performed in agar gel phantoms to investigate accuracy (as compared to fiber optic temperature measurements) and precision of the MR thermometry, and in one healthy volunteer to investigate precision in vivo in brain.

Over all the approach is interesting and probably worth investigating. It is however not clearly described in the manuscript how the authors envision the approach being used, and the reader has to “read between the lines” to really understand the point of the “calibration curves”. This should be made clearer and described more straight forward in the introduction.

Secondly, it’s not clear why the authors went through the trouble of doing all these experiments and stopped short of actually evaluating the method for its intended purpose. The whole point of getting the calibration curves are so you can predict how much heating other (more clinically relevant) pulse sequence will induce. So, when doing the phantom experiment with the fiber optic probe, why didn’t the authors derive the calibration curves and then used them to predict how much heating a set of clinically relevant pulse sequences would induce, and then compare to what the probe actually measured? Without this experiment, the paper will be of very limited impact as it is not clear if the described method will actually work as intended. In my opinion this experiment (at the very least in phantom or maybe better in ex vivo tissue, but ideally in vivo in an animal model) must be included before the manuscript can be published. When doing this experiment the maximum temperature rise when getting the calibration curves should ideally be kept below 6 °C as this is generally when thermal dose starts to accumulate in vivo (i.e., at 43 °C assuming 37 °C starting temperature). Without this experiment the authors can probably not make statements/claims such as “Calibration curves derived from temperature measurements under different RF exposure levels were fit to predict temperature increase for any MR-acquisition sequence”.

Lastly, the orientation of leads/wires inside the bore can affect how much heating and artifacts are created, and it is not clear how well the single-shot EPI sequence handles this. This is another straight forward experiment to perform that would improve the readers excitement about the paper.

Minor comments:

Abstract

“...compared to invasive fiber-optic measurements to assess precision…“ this would assess accuracy and not precision?

“In gel, as well as in the human brain, temperature measurements within ± 0.2 °C

certainty” Please reformulate this. I assume this is from the SD through time, so maybe say something like “the precision of the measurement was 0.2 °C…”. Also mention that this is after temporal filtering.

Ln 117: The Introduction discusses the importance of a large enough FOV – why was such a small FOV (only 12 cm) chosen? That’s not practical for anything but maybe imaging extremities – certainly too small for head and body imaging.

Ln 118: How many slices were interleaved in the 1000 ms TR?

Ln 124: Change KHz to kHz

Ln 125: TR is used above – define when it’s first used (and define other parameters above, too).

Ln 136: What algorithm was used for EPI ghost correction?

Ln 138: Please change “pixel size” to “pixel spacing” (the size doesn’t change with zero filling, but spacing does)

Ln 152-154: This sentence is not clear. Did it take 6 minutes before you could run the sequence again? Why was that?

Ln 171-172: When removing probes from gel phantoms an air-filled “track” is often left behind, resulting in susceptibility artifacts – did you observe this? Or did you use a new/separate phantom for this experiment?

Ln 174: Doing 10 heatings in a single location can seem like quite a lot – did you somehow check/control that the heatings were repeatable, by, e.g., repeating the same heating at the beginning, middle and end?

Ln 211-212: Please use same number of significant figures for all numbers

Ln 252: Suggest change “given” to “measured”

Ln 306: Most (all?) of this paragraph seems to belong better in the Materials section. This whole experiment wasn’t mention in the Materials at all.

Ln 339: Again, interpolation doesn’t change the size of the voxel, just the spacing. So, the voxel size is 6.3 mm3 both before and after zero filled interpolation.

Ln 348-350: Changing the TR will change the duty cycle no matter if the heating is fast or slow, so why do you say “since the temperature evolution is relatively slow”? Even if it was fast the duty cycle would change with changing TR? Or do you mean something else?

Ln 354-356: This was, however, after temporal filtering. Please add if references 24 and 26 also used temporal filtering. If they didn’t, how did your unfiltered values compare to theirs?

Ln 386-388: “In this objective, real-time MRI-thermometry as proposed here is of central interest to avoid creating excessive temperature rise during the calibration process.” Well, yes, but you need the MR thermometry to create the curves in the first place.

Ln 396: Do you mean Figure 2b?

References

Please check all references. They seem to contain months (and other things?) in French rather than English, etc.

Figures

The Figures are overall fairly low quality (at least in the provided pdf), so it’s hard to see any details. Please include higher resolution figures.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2021 May 13;16(5):e0250636. doi: 10.1371/journal.pone.0250636.r002

Author response to Decision Letter 0

5 Feb 2021

Response to Reviewers

We thank both reviewers for their overall positive evaluation of our work and suggestions for improving the manuscript. We understand that the main criticisms were:

Clarify how calibration curves can be used to actually evaluate the temperature rise of any MRI sequence

How can this technique be used practically

In our initial manuscript, we wrote that calibration curves can be used to predict maximal temperature rise for any other MRI sequence. The idea of these calibration curves was to provide quantitative estimate of maximal temperature rise near the tip of the wire as a function of the total energy (through the fits of maximal �T vs flip angle, B1+rms or Energy, providing �1, �2 and �3 coefficients). From these fits, one would then be able to estimate the temperature rise of any other MRI sequence based on energy of the sequence only. This idea was driven by the current safety approach in MRI, where SAR and B1+rms are commonly accepted quantities to assess safety, both being time-averaged values.

When reading comments from the reviewers (and particularly those from reviewer #2), we realized that this idea is in fact incorrect in the context of an implanted wire, since temperature rise effectively depends on the emitted power and duration (thus is energy dependent) of a given MRI sequence, but that the most relevant parameter is the power since it is linked to the temperature rise. As an example, 100 W applied during 10s will produce a much higher heating than 1 W applied during 1000 s, although energy is identical. We thus worked to solve this issue and to improve the manuscript by providing a method that takes into account the power emitted by the sequence instead of its cumulative energy or B1+rms.

We introduced in the revised manuscript a temperature model derived from previously published work on high intensity focused ultrasound. Using this approach, we can exploit the temperature curves obtained from the SAR module sequence in a different manner. First, we approximated the nearly punctual heating source (tip of the wire) as a Gaussian shape. This assumption offers the advantage of allowing to use an analytical function of temperature evolution at the hottest point, already referenced in the literature for HIFU heating (where a Gaussian function is considered as a realistic model).

Then, we fit temperature evolution for each flip angle of the SAR module with this function to derive two parameters (α and �) linked to tissue characteristics (absorption and thermal diffusivity).

For a MRI sequence depositing a power P0 over a duration D, one can then simulate temperature evolution and predict maximal temperature rise, which is the relevant parameter for safety consideration regarding IEC standards. This semi-empirical model is presented together with an additional data set, comparing temperature rises measured by an optical fiber with those predicted by the model for three MRI sequences having different duration and emitted power. We show that the method is accurate for predicting the maximal temperature rise within 5% error.

We believe these amendments clarifies the focus of the paper and provide more evidence of the interest and potential of the proposed method. We also discuss the potential operating modes in perspective of future use.

We unfortunately could not implement an in vivo experiments to evaluate this method due to several practical constraints. However, we think this paper is a proof of concept and we hope this new manuscript will receive a positive evaluation.

We again thank both reviewers for their comments that helped us to improve the manuscript and avoid publishing incorrect conclusions.

Reviewer #1: This work presents a method to assess heating near implanted wires during an MRI scan due to RF deposition and induced currents. It uses fast measurements of temperature using PRFS MR Thermometry interleaved with an RF heating module. The method was shown to be precise and accurate in a variety of ex vivo heating scenarios and an in vivo no-heat scenario. Experiments and analysis are scientifically sound. I appreciated the inclusion of the limitations and comparison to existing methods in the discussion. Clarification of the scope, methods, and figures are needed. After these adjustments, I believe the article is suitable for publication.

Introduction was amended to clarify the scope. The method section now includes a processing technique to predict temperature evolution for other MRI sequence from temperature data obtained during the calibration phase. New results have been added to illustrate this technique using 3 different MRI sequences with different power and duration. The discussion has also been amended accordingly.

Specific comments:

R1.1) The title implies the work is for measurement near implanted wires, but the intro (page 5, line 99), methods (page 8 line 172), and others refer to "implants” or “devices." This terminology should be clarified throughout, as no evidence is presented to discuss how the work would be applicable to other types of implanted devices.

We modified the text to remove any ambiguity since the method is effectively intended to assess temperature increase near an implanted wire.

R1.2) The use case for the work should be made clear. How do you see the method being used in practice? Is the method intended to be used during real-time monitoring, as a one-time

phantom calibration that exists in look-up-table form for each wire type, or something else?

How would this be used safely at the beginning of each MRI session (page 19, line 384) without applying heating to the patient? Clarifying this in the abstract, introduction, and discussion will help clearly define the impact of the work.

We addressed this question in the introduction, discussion and conclusion of the revised manuscript. Objectives of the method is three fold: 1) to present a real time and precise temperature monitoring technique with adequate spatial and temporal resolutions for the targeted application, 2) to create a calibration data set by exploiting this sequence using interleaved heating module with frequent (1s update rate) temperature estimates, and 3) propose a model for predicting the maximal temperature increase for other MRI acquisition sequences from this calibration dataset, without requiring sophisticated modelling or using surrogates of temperature measurements.

This manuscript aims at presenting the proof of concept and potential optimizations are proposed in the discussion section to avoid inducing excessive heating (as pointed out by reviewer #2 also) in the patient.

We propose typical use cases in the conclusion of the manuscript.

R1.3) How much artifact was seen around the tips of the lead wires tested? Did it interfere with

maximum heat voxel selection/voxel near thermocouple selection? How would the method

perform if the lead wire were oriented differently with respect to B0, thus potentially having a

larger artifact?

We are aware that this could be a limitation of the imaging sequence. However, in each experiment presented in this manuscript, the implanted wire was systematically positioned vertically into the gel, thus orthogonally to B0. This is now indicated in the material and method section for each experiment. No visible artifact could be identified in the thermometry slice crossing the tip of the implanted wire when no fiber-optic probe was present. For the pacemaker lead a small reduction in signal intensity was observed in 4 pixels but without impacting significantly the thermometry precision (also indicated into the revised manuscript).

R1.4) Is the low-pass filtering necessary for generating the calibration curves, or would the original data be precise enough? Would the filter latency (page 12, line 246) be an issue for clinical implementation?

The low-pass filter was introduced to reduce noise on temperature images. Whether this is necessary or not is directly related to the standard deviation of the thermometry. In our implementation at 1.5T, with the selected coils on these gels with the selected spatial resolution and echo time, we decided to include it to reach good temperature precision. The latency induced by this filter is acceptable (3 seconds) since in case an important temperature increase is observed, the sequence can be immediately stopped, without creating risks for the patient. In 3 s, a temperature of 55°C (+18°C above body temperature) is necessary to reach the lethal thermal dose (taking the CEM43 metric). Other types of filters may be included in the thermometry pipeline such as Kalman filters (as already stated in the discussion section of the original manuscript). However, we do not consider the current implementation is an issue for clinical application.

A sentence has been added in the discussion section:

“However, despite the proposed implementation creates a latency of 3 s, a temperature increase of 18°C is necessary to reach a lethal thermal dose within this time scale (according to the CEM43 model) which is unlikely to occur with optimized clinical devices.”

R1.5) Figure 1 could be expanded to include which dynamics were averaged together. Add a label the thermometry module.

Done

R1.6) Add titles to all sub-parts of Figures 2 and 3, and 6a.

Done

R1.7) Scale bar in Fig 2A blends in, consider a different color and moving outside the phantom into the black area and adding the value to the image.

We changed the bar color and location to avoid such a blend.

R1.8) Figures 3c, 4b, 5, 6b need plot legends.

Done

R1.9) Page 6 line 127: How long was each dynamic (with and without interleaving the heating

module)?

Each dynamic was 1 sec long and maintained constant during the acquisition. When heating module is played, the remaining “empty” delay before the following acquisition of slices is filled with pulses (see figure 1 and M&M section for details)

“TR/TE = 1000/18 ms” was already indicated in the original manuscript

We kept the original text unchanged.

R1.10) Page 9 line 175: How was the voxel of interest chosen?

The sentence was amended as follow:

“For each acquisition, the temperature evolution in the same pixel was analyzed, selecting the pixel with the maximal temperature increase at the end of the energy deposition (acquisition #90) from the temperature data corresponding to the largest FAHM”

R1.11) Page 9 line 179: add scan parameters to statistics section

The following sentence was added. ” The same scan parameters as described in section MRI-thermometry sequence were used”

R1.12) Page 9 line 189: is this FA for the thermometry imaging module or the RF heating module?

This FA is the flip angle of the thermometry sequence, since here the heating module emitted no energy (FAHM=0°)

R1.13) Page 10 line 199: Was there any appreciable cooling during the 5 dynamics that were averaged? Since this depends on # of slices, how many slices were used in each of the experiments?

No cooling was observed during the 5 successive acquisitions (see temperature curves in Fig 4b). Three slices were used in each of the experiments (already indicated in the original manuscript). The text in the manuscript was not modified, but we added a mark in Fig 4b (FAHM=40°) showing the temporal window corresponding to this averaging.

This will help the reader to see that temperature can be considered nearly constant over this temporal window.

R1.14) Page 10 line 202: Explain how energy emitted was computed.

The sentence was modified as follow:

“ The µT ± σT temperature values were plotted as a function of the flip angle, B1+rms and energy emitted (i.e. sum of the energies of each individual RF pulse, including pulses for imaging and pulses of the heating module) “

R1.15) Page 16 lines 307-314 should be in the methods section.

We moved this section to Methods section.

R1.16) Page 18 line 373: What is the regulatory limit?

In the latest version of IEC 60601–2‐33, the so‐called fixed‐parameter option (FPO) was introduced for 1.5T systems (FPO:B), which specifically addresses the scanning of implant carriers and fixed limit value of B_(1,rms)^+ = 3.2 µT. In Table 1, this correspond to FAHM of 70° .

The sentence was amended as follow:

“In the experiments with the copper wire, we observed an important temperature increase when the flip angle of the heating module was higher than 30°, although B1+rms values provided by the scanner interface remained within regulatory limit (maximal B1+rms of 3.2 µT, as indicated in the fixed‐parameter option of IEC 60601 –2‐33) for most of the experimental conditions (FAHM up to 70 °, see Table 1).”

R2.1 Over all the approach is interesting and probably worth investigating. It is however not clearly described in the manuscript how the authors envision the approach being used, and the reader has to “read between the lines” to really understand the point of the “calibration curves”. This should be made clearer and described more straightforward in the introduction.

We agree that this was unclear in the original manuscript. We have thoroughly modified the manuscript to explain this in the introduction, added a section in material and methods, include new results and discuss them in the revised manuscript.

We hope these modifications bring clarity and a more precise focus to the manuscript.

R 2.2 Secondly, it’s not clear why the authors went through the trouble of doing all these experiments and stopped short of actually evaluating the method for its intended purpose. The whole point of getting the calibration curves are so you can predict how much heating other (more clinically relevant) pulse sequence will induce. So, when doing the phantom experiment with the fiber optic probe, why didn’t the authors derive the calibration curves and then used them to predict how much heating a set of clinically relevant pulse sequences would induce, and then compare to what the probe actually measured? Without this experiment, the paper will be of very limited impact as it is not clear if the described method will actually work as intended. In my opinion this experiment (at the very least in phantom or maybe better in ex vivo tissue, but ideally in vivo in an animal model) must be included before the manuscript can be published.

Thank you very much for this criticism of the original manuscript. We have amended the method to introduce a heating model and propose a method to compute temperature evolution of other sequences from calibration data set using our proposed MR-thermometry sequence. We included an additional experiment to evaluate this method and discuss these points. Unfortunately, we could not organize an in vivo experiment for various practical reasons. This is clearly stated in the revised manuscript and we believe this new version brings enough new material to be considered for publication as a proof of concept. In the discussion, we propose potential improvements of the method and conclude with potential use-case scenarios.

We hope all these improvements will convince the reviewer.

R 2.3 When doing this experiment the maximum temperature rise when getting the calibration curves should ideally be kept below 6 °C as this is generally when thermal dose starts to accumulate in vivo (i.e., at 43 °C assuming 37 °C starting temperature). Without this experiment the authors can probably not make statements/claims such as “Calibration curves derived from temperature measurements under different RF exposure levels were fit to predict temperature increase for any MR-acquisition sequence”.

We totally agree with the reviewer. In the revised version of the manuscript we added a paragraph to the discussion section to address this comment.

R2.4 Lastly, the orientation of leads/wires inside the bore can affect how much heating and artifacts are created, and it is not clear how well the single-shot EPI sequence handles this. This is another straight forward experiment to perform that would improve the readers excitement about the paper.

Each experiment presented here was performed with the wire tip positioned vertically into the gel (thus perpendicular to B0). This was thus the worst case configurations. Please see answer to R1.3 for more details.

Minor comments:

R2.5 Abstract

“...compared to invasive fiber-optic measurements to assess precision…“ this would assess accuracy and not precision?

We corrected this in the text.

R2.6 “In gel, as well as in the human brain, temperature measurements within ± 0.2 °C

We reformulated the sentence as suggested

R2.7 Ln 117: The Introduction discusses the importance of a large enough FOV – why was such a small FOV (only 12 cm) chosen? That’s not practical for anything but maybe imaging extremities – certainly too small for head and body imaging.

We initially chose a small FOV to concentrate on only a local heating at the wire and pacemaker lead tips. However, as depicted in the human volunteer, it is possible to adjust the FOV depending on the region of interest and thus, acquiring with a larger FOV. The meaning of the sequence was that FOV must be large enough to cover regions around the implanted wire, while being rapid, precise and spatially resolved.

The sentence was modified as follow: “In the context of measuring small temperature changes near devices, MRI-thermometry should be rapid with a sufficiently large spatial coverage around the implanted wire and provide a spatial resolution in the range of a few millimeters.”

R2.8 Ln 118: How many slices were interleaved in the 1000 ms TR?

3 slices were acquired every second. This was already indicated in the original text.

R2.9 Ln 124: Change KHz to kHz

Corrected

R2.10 Ln 125: TR is used above – define when it’s first used (and define other parameters above, too).

Corrected

R2.11 Ln 136: What algorithm was used for EPI ghost correction?

Reconstruction pipeline included EPI ghost correction using three central line of k-space. We refer the reader to the paper by Ozenne et al for implementation details (reference #29 in the manuscript).

R 2.12 Ln 138: Please change “pixel size” to “pixel spacing” (the size doesn’t change with zero filling, but spacing does)

We proceeded to change

R2.13 Ln 152-154: This sentence is not clear. Did it take 6 minutes before you could run the sequence again? Why was that?

On the MR scanner, it takes 6 minutes to reset the B1+rms value to zero. As we wanted to consider the B1+rms emitted by one sequence only we had to wait this delay. Acquiring before this delay would have result in a mix of B1+rms emitted by several sequences. Moreover, this 6 minute delay ensured proper cooling of the gel before the following experiment with a different FAHM.

The text was amended accordingly.

R 2.14 Ln 171-172: When removing probes from gel phantoms an air-filled “track” is often left behind, resulting in susceptibility artifacts – did you observe this? Or did you use a new/separate phantom for this experiment?

A new phantom was use for each separate experiment to avoid the mentioned issue of susceptibility artifacts induced by air-filled track of previous experiments. This mentioned in the revised manuscript.

R2.15 Ln 174: Doing 10 heatings in a single location can seem like quite a lot – did you somehow check/control that the heatings were repeatable, by, e.g., repeating the same heating at the beginning, middle and end?

After the last heating was performed (largest FAHM value), a delay was observed for cooling down. Then another sequence with FAHM of 30° was acquired again to ensure same value of maximal temperature increase was obtained as for the previous experiment performed with identical FAHM. This was the case, demonstrating repeatability of the heating.

The text was not modified, since we believe this does not bring major added value to the manuscript.

R2.16 Ln 211-212: Please use same number of significant figures for all numbers

This was corrected in the text.

R2.17 Ln 252: Suggest change “given” to “measured”

Done

R2.18 Ln 306: Most (all?) of this paragraph seems to belong better in the Materials section. This whole experiment wasn’t mention in the Materials at all.

We moved this paragraph in the method section, as suggested.

R2.19 Ln 339: Again, interpolation doesn’t change the size of the voxel, just the spacing. So, the voxel size is 6.3 mm3 both before and after zero filled interpolation.

We removed “before interpolation” in the text.

R2.20 Ln 348-350: Changing the TR will change the duty cycle no matter if the heating is fast or slow, so why do you say “since the temperature evolution is relatively slow”? Even if it was fast the duty cycle would change with changing TR? Or do you mean something else?

Of course, changing the TR results in a different duty cycle. This sentence suggested that considering the relative slow evolution of the temperature, the update time of temperature measurement could be increased (eg ever 2 seconds). This increase in TR might be invested in acquiring more EPI slices to increase the spatial coverage of the temperature measurement, if desired. However, this sentence does not appear essential and we prefer to remove it if it is unclear.

R2.21 Ln 354-356: This was, however, after temporal filtering. Please add if references 24 and 26 also used temporal filtering. If they didn’t, how did your unfiltered values compare to theirs?

Comparing temperature SD results with those from Refs 24 and 26 is not straightforward since it depends on several parameters such as the SNR, which is linked to the voxel size and receiver coil performance. Ehses et al used a PRF thermometry technique with a larger voxel size of 1.56x1.56x5mm (12.168 mm3 vs 6.1 mm3 in our study) with an update time of 3.9 s (versus 1 s in our implementation). They spatially averaged temperature data in 2 adjacent pixels that resulted in 0.5°C standard deviation. Gensler used a T1-based thermometry and reported a temperature standard deviation of 1.37°C. However, their update time was 6.4 s for an elementary voxel size of 26.5 mm3.

In both cases, a precise comparison of their achievements with the standard deviation reported with our method appears hardly feasible, except using the raw values provided in their studies (0.5°C and 1.37°C) and compare them to our 0.2°C after temporal filtering, without taking into account the different voxel dimensions and update times.

Thus, we prefer to keep the original text unchanged.

R2.22 Ln 386-388: “In this objective, real-time MRI-thermometry as proposed here is of central interest to avoid creating excessive temperature rise during the calibration process.” Well, yes, but you need the MR thermometry to create the curves in the first place.

In this study, we first propose a fast MR-thermometry method. Then, this is used to create a calibration data set from which one can derive maximal temperature increase using a model to fit temperature curves of the calibration data set. We report an example of our method using a medical device where small heating was observed (<6°C).

As pointed out in the discussion section, the model allows to fit temperature data during heating and cooling. Thus optimization of the calibration process can be envisioned, with the idea of reducing the duration of the heating module (here 80 s). This paper is thus a proof of concept of the method with a lot of potential improvement in perspective of clinical use and will require further studies, including in vivo application.

Please see the discussion section that covers these points.

R2.23 Of course, but having thermometry does not mean that you need to heat excessively. The use of thermometry in real-time avoids reaching excessive temperature (eg no larger than 43°C).

This is now discussed in the revised manuscript.

R2.24 Ln 396: Do you mean Figure 2b?

Yes, thank you for having noticed.

R2.25 References

Please check all references. They seem to contain months (and other things?) in French rather than English, etc.

Corrected

R2.26 Figures

The Figures are overall fairly low quality (at least in the provided pdf), so it’s hard to see any details. Please include higher resolution figures.

This is due to the conversion process.

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(35.2KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0250636.r003

Decision Letter 1

Nick Todd

17 Mar 2021

PONE-D-20-32401R1

A fast MR-thermometry method for quantitative assessment of temperature increase near an implanted wire

PLOS ONE

Dear Dr. DELCEY,

Both reviewers feel that the manuscript is much improved due to the revisions made and that their major concerns have all been addressed. They also both had a few minor points that would be worth addressing before publication, some about the new material that was added. Please include a formal response to the points raised and make revisions as necessary. If all points are addressed, this round of revision can be taken care of at the editorial level without having to go back out to the reviewers.

Please submit your revised manuscript by May 01 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

We look forward to receiving your revised manuscript.

Kind regards,

Nick Todd, PhD

Academic Editor

PLOS ONE

Journal Requirements:

Please review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the rebuttal letter that accompanies your revised manuscript. If you need to cite a retracted article, indicate the article’s retracted status in the References list and also include a citation and full reference for the retraction notice.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: (No Response)

Reviewer #2: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: N/A

Reviewer #2: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: Yes

**********

6. Review Comments to the Author

Reviewer #1: The manuscript has been greatly improved this round. All previous comments have been addressed. A new set of analysis and figures have been added to address previous concerns around how the work is to be used/calibration curves. These were effective additions. I also appreciate the text that was added to the conclusion discussing how the work can be used. Given the substantial additions to the text and figures, all comments below relate to the added work. Once addressed I believe the article is suitable for publication.

Figure 7 (and associated results/methods text) - Report the goodness of fit. Add text justifying why a second order polynomial should be used. Based on the figure I don't think there is enough data to justify a second order polynomial. Add subfigure labels a and b to the figure itself.

Figure 8 - Add units to the temperature isotherm lines (or indicate in caption). Add subfigure labels a and b to the figure itself.

Page 9 ~line 200 and Page 12 ~line 260 (in tracked changes version) - indicate wire direction relative to scanner B0, not relative to the gel.

Page 12 (in tracked changes version) - Make sure all symbols used in eqn 1 are explicitly defined (I couldn't find T, t, alpha, and tau)

Page 23 line 504 (in tracked changes version) - clarify whether the alpha and tau were allowed to vary in the data shown in the figures. I'm not convinced they should be allowed to vary unless you're seeing temperature rises above coagulations thresholds.

Reviewer #2: Thank you for answering my previous questions and updating the manuscript, which now is clearer and easier to follow. I just have a few minor suggestions on this latest version.

Abstract, Purpose; Suggest adding that you use scans from one sequence to predict heating for other sequences.

Ln 51: Is 0.5 °C maximum error, RMSE etc.? Please clarify.

Ln 204-205: Please reformulate “The tip of the lead screwed into the myocardium was inserted…”

Ln 225-227: What was the TR for these scans? Was it the same for all TEs (if not, compare the precision later on gets challenging)?

Ln 249-250: Does the Gaussian have the same width in all three dimensions (what was it?)? Or is it elongated like most focused ultrasound focal spots?

Ln 350: This reviewer can’t seem to find any blue line (showing “baseline”)? Also, consider calling it “background” rather than “baseline”.

Ln 408-410: It’s a bit unclear what you mean with this sentence - simply that you can use the plot in 5c to estimate the maximum temperature rise?

Ln 436: “(1 s refresh rate in our setting)” please add “with a 5 s temporal foot print”. This is important as you had to shift the temporal curve to align it with the probe measurements. Hence, it is not optimally suited for real-time applications (similar to using a sliding window reconstruction for undersampled k-space data).

Ln 448: Change “FA ≥ 20°” to “FAHM ≥ 20°”, right?

Ln 472: This doesn’t quite tell the full story, right? This assumes a “step function” going straight to 18 °C and holding it there for 3 s. In reality you will start accumulating dose as soon as your increase is 6 °C so with the fairly slow heatings shown in Fig 4 you’ll have a substantial dose before getting to 18 °C.

Figure 8: Both the CINE and TSE predict the heating and start of cooling pretty well, but starts to deviate substantially at the end of the cooling period – can the authors speculate why this is?

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

PLoS One. 2021 May 13;16(5):e0250636. doi: 10.1371/journal.pone.0250636.r004

Author response to Decision Letter 1

7 Apr 2021

Answer to comments

We thank both reviewers for their positive evaluation of the revised manuscript.

Please find below our point-by-point response to their comments.

R1.1: Figure 7 (and associated results/methods text) –

Report the goodness of fit: We reported the goodness of fit within the figure.

Add text justifying why a second order polynomial should be used. Based on the figure I don't think there is enough data to justify a second order polynomial:

Please see answer to comment R1.5 below

Add subfigure labels a and b to the figure itself: done

R1.2: Figure 8 –

Add units to the temperature isotherm lines (or indicate in caption): we added the unit (°C) in the subfigure label for fig b

Add subfigure labels a and b to the figure itself:

Done

R1.3: Page 9 ~line 200 and Page 12 ~line 260 (in tracked changes version) - indicate wire direction relative to scanner B0, not relative to the gel.

Done at both places.

R1.4: Page 12 (in tracked changes version) - Make sure all symbols used in eqn 1 are explicitly defined (I couldn't find T, t, alpha, and tau)

This is now detailed. There were also typo errors in the equation that are now corrected.

R1.5: Page 23 line 504 (in tracked changes version) - clarify whether the alpha and tau were allowed to vary in the data shown in the figures. I'm not convinced they should be allowed to vary unless you're seeing temperature rises above coagulations thresholds.

Alpha and tau were allowed to vary in the data shown in the figures. In the discussion section we already mentioned this explicitly and discussed that point:

“the two parameters resulting from the fit (here � and �) are directly linked to tissue absorption and thermal diffusivity, and are thus not expected to vary with the emitted power. However, allowing � and � to vary in our processing improved the fitting quality on each temperature curve of the calibration dataset. This was attributed to the relative small dimensions of the heating spot for low FAHM values, where partial volume effect of the thermometry sequence may play a role, although an effort was made to provide high resolution temperature images with the proposed sequence. This semi-empirical model allowed to predict the maximal temperature increase for three other MRI sequences.”

Of course, alpha and tau may vary with coagulation but this is not the use case of the method since the plan is to create a moderate heating and use temperature curves to predict the maximal temperature rise for any other sequence.

Moreover, if you compare the values of alpha and tau derived from the fits for the two first experiments (FAHM =10° and 20°) in Fig 7b and 7c, they appear different although there is no expected change in gel composition with temperature increases below 2°C (FAHM=10°) and 6°C (FAHM = 20°) starting from room temperature (~20°C). Thus, we attributed these changes to partial volume effect of the thermometry sequence that is more pronounced for very low temperature increase, despite we tried to use a high resolution thermometry sequence.

The text was modified as follow:

“Whatever the model, indeed, the two parameters resulting from the fit (here ��and �) are directly linked to tissue absorption and thermal diffusivity, and are thus not expected to vary with the emitted power, at least for moderate temperature increases (i.e. remaining below the lethal thermal dose). However, parameters � and � (Fig 7b and 7c) derived from the fit of temperature curves (Fig 7a) show a strong variation when varying FAHM from 10° to 20° and lower changes for higher FAHM (30° and 40°). For these reasons, we introduced a polynomial fitting function in Fig. 7b and 7c. Variation of � and � as a function of the power was attributed to the relative small dimensions…”

The following sentence was removed:

“However, allowing � and � to vary in our processing improved the fitting quality on each temperature curve of the calibration dataset.”

Reviewer #2: Thank you for answering my previous questions and updating the manuscript, which now is clearer and easier to follow. I just have a few minor suggestions on this latest version.

R2.1: Abstract, Purpose; Suggest adding that you use scans from one sequence to predict heating for other sequences.

The sentence now reads: “To propose a MR-thermometry method and associated data processing technique to predict the maximal RF-induced temperature increase near an implanted wire for any other MRI sequence”

R2.2: Ln 51: Is 0.5 °C maximum error, RMSE etc.? Please clarify.

Thank you for this remark. The difference between maximal predicted and measured temperature increases was around 5% for the three tested sequences.

Therefore, we corrected the sentence as follow:

“After successful fitting of temperature curves of the calibration data set, temperature rise predicted by the model was in good agreement (around 5% difference) with measured temperature by a fiber optic probe, for three other MRI sequences. “

R2.3: Ln 204-205: Please reformulate “The tip of the lead screwed into the myocardium was inserted…”

We reformulated the sentence as follow:

“The tip of the lead that is normally screwed into the myocardium was inserted into the gel while the other extremity was left in the air”

R2.4: Ln 225-227: What was the TR for these scans? Was it the same for all TEs (if not, compare the precision later on gets challenging)?

Repetition time was identical for each measurement and set to 1s. This is now indicated in the text.

R2.5: Ln 249-250: Does the Gaussian have the same width in all three dimensions (what was it?)? Or is it elongated like most focused ultrasound focal spots?

Yes, we assume a Gaussian source with isotropic dimensions. In our model, we do not need to explicitly provide a width for the Gaussian function, since this is included in the parameter “tau”. The idea here is that if you have a Gaussian source of heating, then you can use Eq 1 to fit the temperature curve vs time at the hottest point to derive alpha and tau (see ref 35 for details).

In order to avoid any confusion, we removed « as for high intensity focused ultrasound » from the sentence that now reads:”

“Considering that heating induced near an implanted wire is localized around its tip, we chose to approximate this heating source by a Gaussian function with isotropic dimensions.”

R2.6: Ln 350: This reviewer can’t seem to find any blue line (showing “baseline”)? Also, consider calling it “background” rather than “baseline”.

Effectively, we forgot to include these blue lines in the figure. Instead, we added a blue arrow (as in Figure 3) in Figure 4 to show the pixel selected for background temperature evolution. We also changed “baseline” into “background” as suggested.

R2.7: Ln 408-410: It’s a bit unclear what you mean with this sentence - simply that you can use the plot in 5c to estimate the maximum temperature rise?

What is meant here is that the method relying on time-averaged power deposition are irrelevant to predict the maximal temperature rise.

The sentence has been modified as follow to clarify this point:

“On the contrary, using the calibration curves (namely coefficient �3) from Fig 5c to estimate the maximal temperature increase from the total energy of each sequence leads to 2.78°C, 2.96°C and 2.42°C, respectively. Such an approach is thus irrelevant for predicting maximal temperature rise in the context of an implanted wire.”

R2.8: Ln 436: “(1 s refresh rate in our setting)” please add “with a 5 s temporal foot print”. This is important, as you had to shift the temporal curve to align it with the probe measurements. Hence, it is not optimally suited for real-time applications (similar to using a sliding window reconstruction for undersampled k-space data).

We added “with a 3 s temporal footprint”, not 5 s, since this is the time shift we needed to align MR-temperature curve and probe measurements.

R2.9: Ln 448: Change “FA ≥ 20°” to “FAHM ≥ 20°”, right?

Changed

R2.10: Ln 472: This doesn’t quite tell the full story, right? This assumes a “step function” going straight to 18 °C and holding it there for 3 s. In reality you will start accumulating dose as soon as your increase is 6 °C so with the fairly slow heatings shown in Fig 4 you’ll have a substantial dose before getting to 18 °C.

These numbers were introduced in the revised manuscript to illustrate that having a 3 s latency is not considered problematic, since a substantial heating (18°C) is required to reach a lethal thermal dose within this time scale. In the discussion section, we already explained that the sequence may be used with shorter duration of the heating module, which will also reduce the risk of accumulating excessive thermal dose. Altogether, we believe that this 3 s latency is not an issue. In order to simplify the text, we propose to modify the sentence as follow:

“Despite the proposed implementation creates a latency of 3 s, the risk of reaching a lethal thermal dose within this time scale (according to the CEM43 (40) model) is unlikely to occur with optimized clinical devices.”

R2.11: Figure 8: Both the CINE and TSE predict the heating and start of cooling pretty well, but starts to deviate substantially at the end of the cooling period – can the authors speculate why this is?

This deviation can result from uncertainty in estimation of alpha and tau parameters that are used to simulate the heating. In this case, deviation may accumulate and become more visible at the end of the cooling. However, as stated in the discussion section, the relevant parameter from the IEC is the maximal temperature rise, which is predicted within 5% error with our method. Since this point is already indicated in the previous revised manuscript, we prefer to keep the text unchanged.

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(24.4KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0250636.r005

Decision Letter 2

Nick Todd

12 Apr 2021

A fast MR-thermometry method for quantitative assessment of temperature increase near an implanted wire

PONE-D-20-32401R2

Dear Dr. DELCEY,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Nick Todd, PhD

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

PLoS One. doi: 10.1371/journal.pone.0250636.r006

Acceptance letter

Nick Todd

5 May 2021

PONE-D-20-32401R2

A fast MR-thermometry method for quantitative assessment of temperature increase near an implanted wire

Dear Dr. Delcey:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Nick Todd

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(35.2KB, docx)}

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file.^{(24.4KB, docx)}

Data Availability Statement

Data has been uploaded to Zenodo: https://zenodo.org/record/4735614 (DOI: 10.5281/zenodo.4735614).

[pone.0250636.ref001] 1.Dacher J-N, Gandjbakhch E, Taieb J, Chauvin M, Anselme F, Bartoli A, et al. Joint Position Paper of the Working Group of Pacing and Electrophysiology of the French Society of Cardiology (SFC) and the Société française d’imagerie cardiaque et vasculaire diagnostique et interventionnelle (SFICV) on magnetic resonance imaging in patients with cardiac electronic implantable devices. Diagnostic and Interventional Imaging. 2020. February; 101(9):507–517 10.1016/j.diii.2020.02.003 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref002] 2.Jabehdar Maralani P, Schieda N, Hecht EM, Litt H, Hindman N, Heyn C, et al. MRI safety and devices: An update and expert consensus. J Magn Reson Imaging. 2020. March;51(3):657–74. 10.1002/jmri.26909 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref003] 3.Erhardt JB, Fuhrer E, Gruschke OG, Leupold J, Wapler MC, Hennig J, et al. Should patients with brain implants undergo MRI? J Neural Eng. 2018. August;15(4):041002. 10.1088/1741-2552/aab4e4 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref004] 4.Campbell-Washburn AE, Tavallaei MA, Pop M, Grant EK, Chubb H, Rhode K, et al. Real-time MRI guidance of cardiac interventions: Real-Time Cardiac MRI Interventions. J Magn Reson Imaging. 2017. October;46(4):935–50. 10.1002/jmri.25749 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0250636.ref005] 5.Murbach M, Zastrow E, Neufeld E, Cabot E, Kainz W, Kuster N. Heating and Safety Concerns of the Radio-Frequency Field in MRI. Curr Radiol Rep. 2015. December;3(12):45. [Google Scholar]

[pone.0250636.ref006] 6.Nitz WR, Oppelt A, Renz W, Manke C, Lenhart M, Link J. On the heating of linear conductive structures as guide wires and catheters in interventional MRI. J Magn Reson Imaging. 2001. January;13(1):105–14. [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref007] 7.Park S-M, Kamondetdacha R, Nyenhuis JA. Calculation of MRI-induced heating of an implanted medical lead wire with an electric field transfer function. J Magn Reson Imaging. 2007. November;26(5):1278–85. 10.1002/jmri.21159 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref008] 8.Achenbach S, Moshage W, Diem B, Bieberlea T, Schibgilla V, Bachmann K. Effects of magnetic resonance imaging on cardiac pacemakers and electrodes. American Heart Journal. 1997. September;134(3):467–73. 10.1016/s0002-8703(97)70083-8 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref009] 9.Konings MK, Bartels LW, Smits HFM, Bakker CJG. Heating Around Intravascular Guidewires by Resonating RF Waves. J Magn Reson Imaging. 2000. July;12(1):79–85. [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref010] 10.Rezai AR, Finelli D, Nyenhuis JA, Hrdlicka G, Tkach J, Sharan A, et al. Neurostimulation systems for deep brain stimulation: In vitro evaluation of magnetic resonance imaging-related heating at 1.5 tesla. J Magn Reson Imaging. 2002. March;15(3):241–50. 10.1002/jmri.10069 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref011] 11.Luechinger R, Zeijlemaker VA, Pedersen EM, Mortensen P, Falk E, Duru F, et al. In vivo heating of pacemaker leads during magnetic resonance imaging. European Heart Journal. 2005. February 1;26(4):376–83. 10.1093/eurheartj/ehi009 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref012] 12.Mattei E, Triventi M, Calcagnini G, Censi F, Kainz W, Mendoza G, et al. Complexity of MRI induced heating on metallic leads: Experimental measurements of 374 configurations. BioMed Eng OnLine. March 2008;7(1):11. 10.1186/1475-925X-7-11 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0250636.ref013] 13.Spiegel J, Fuss G, Backens M, Reith W, Magnus T, Becker G, et al. Transient dystonia following magnetic resonance imaging in a patient with deep brain stimulation electrodes for the treatment of Parkinson disease. Journal of Neurosurgery. 2003. October;99(4):772–4. 10.3171/jns.2003.99.4.0772 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref014] 14.Henderson JM, Tkach J, Phillips M, Baker K, Shellock FG, Rezai AR. Permanent Neurological Deficit Related to Magnetic Resonance Imaging in a Patient with Implanted Deep Brain Stimulation Electrodes for Parkinson’s Disease: Case Report. Neurosurgery. 2005. November 1;57(5):E1063–E1063. 10.1227/01.neu.0000180810.16964.3e [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref015] 15.Woods TO. Standards for medical devices in MRI: Present and future. J Magn Reson Imaging. 2007. November;26(5):1186–9. 10.1002/jmri.21140 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref016] 16.Winter L, Seifert F, Zilberti L, Murbach M, Ittermann B. MRI‐Related Heating of Implants and Devices: A Review. J Magn Reson Imaging. 2020. May 26;jmri.27194. 10.1002/jmri.27194 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref017] 17.Collins CM. Numerical field calculations considering the human subject for engineering and safety assurance in MRI. NMR in Biomedicine. 2009. November;22(9):919–26. 10.1002/nbm.1251 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0250636.ref018] 18.Fiedler TM, Ladd ME, Bitz AK. SAR Simulations & Safety. NeuroImage. 2018. March;168:33–58. 10.1016/j.neuroimage.2017.03.035 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref019] 19.Bottauscio O, Cassarà AM, Hand JW, Giordano D, Zilberti L, Borsero M, et al. Assessment of computational tools for MRI RF dosimetry by comparison with measurements on a laboratory phantom. Phys Med Biol. 2015. July;60(14):5655–80. 10.1088/0031-9155/60/14/5655 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref020] 20.Langman DA, Goldberg IB, Finn JP, Ennis DB. Pacemaker lead tip heating in abandoned and pacemaker-attached leads at 1.5 tesla MRI. J Magn Reson Imaging. 2011. February;33(2):426–31. 10.1002/jmri.22463 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref021] 21.Etezadi-Amoli M, Stang P, Kerr A, Pauly J, Scott G. Controlling radiofrequency-induced currents in guidewires using parallel transmit: Controlling RF Current Using Parallel Transmit. Magn Reson Med. 2015. December;74(6):1790–802. 10.1002/mrm.25543 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0250636.ref022] 22.Griffin GH, Anderson KJT, Celik H, Wright GA. Safely assessing radiofrequency heating potential of conductive devices using image-based current measurements: Images to Predict RF Heating Behavior. Magn Reson Med. 2015. January;73(1):427–41. 10.1002/mrm.25103 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref023] 23.Pfeil A, Drobnik S, Rzanny R, Aboud A, Böttcher J, Schmidt P, et al. Compatibility of temporary pacemaker myocardial pacing leads with magnetic resonance imaging: an ex vivo tissue study. The International Journal of Cardiovascular Imaging. 2012. February;28(2):317–26. 10.1007/s10554-011-9800-y [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref024] 24.Ehses P, Fidler F, Nordbeck P, Pracht ED, Warmuth M, Jakob PM, et al. MRI thermometry: Fast mapping of RF-induced heating along conductive wires. Magn Reson Med. 2008. August;60(2):457–61. 10.1002/mrm.21417 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref025] 25.Detti V, Grenier D, Perrin E, Beuf O. Assessment of radiofrequency self-heating around a metallic wire with MR T1-based thermometry. Magn Reson Med. 2011. August;66(2):448–55. 10.1002/mrm.22834 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref026] 26.Gensler D, Fidler F, Ehses P, Warmuth M, Reiter T, Düring M, et al. MR safety: Fast T1 thermometry of the RF-induced heating of medical devices. Magn Reson Medicine. 2012. November 1;68(5):1593–9. [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref027] 27.Weber H, Taviani V, Yoon D, Ghanouni P, Pauly KB, Hargreaves BA. MR thermometry near metallic devices using multispectral imaging: MSI Thermometry. Magn Reson Med. 2017. March;77(3):1162–9. 10.1002/mrm.26203 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0250636.ref028] 28.Dharmadhikari S, James JR, Nyenhuis J, Bansal N. Evaluation of radiofrequency safety by high temperature resolution MR thermometry using a paramagnetic lanthanide complex: Evaluation of Specific Absorption Rate by MR Thermometry. Magn Reson Med. 2016. May;75(5):2121–9. 10.1002/mrm.25792 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref029] 29.Ozenne V, Toupin S, Bour P, Senneville BD de, Lepetit‐Coiffé M, Boissenin M, et al. Improved cardiac magnetic resonance thermometry and dosimetry for monitoring lesion formation during catheter ablation. Magn Reson Med. 2017. January; 77(2):673–83. 10.1002/mrm.26158 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref030] 30.Toupin S, Bour P, Lepetit-Coiffé M, Ozenne V, Denis de Senneville B, Schneider R, et al. Feasibility of real-time MR thermal dose mapping for predicting radiofrequency ablation outcome in the myocardium in vivo. Journal of Cardiovascular Magnetic Resonance. 2017. December;19(1):1–12. 10.1186/s12968-016-0318-2 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0250636.ref031] 31.Hansen MS, Sørensen TS. Gadgetron: An open source framework for medical image reconstruction: Gadgetron. Magn Reson Med. 2013. June;69(6):1768–76. 10.1002/mrm.24389 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref032] 32.Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002. June;47(6):1202–10. 10.1002/mrm.10171 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref033] 33.Ishihara Y, Calderon A, Watanabe H, Okamoto K, Suzuki Y, Kuroda K, et al. A precise and fast temperature mapping using water proton chemical shift. Magn Reson Med. 1995. December;34(6):814–23. 10.1002/mrm.1910340606 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref034] 34.Poorter JD. Noninvasive MRI thermometry with the proton resonance frequency method: Study of susceptibility effects. Magn Reson Med. 1995. September;34(3):359–67. 10.1002/mrm.1910340313 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref035] 35.Quesson B, Vimeux F, Salomir R, de Zwart JA, Moonen CTW. Automatic Control of Hyperthermic Therapy Based on Real-Time Fourier Analysis of MR Temperature Maps. 2002. June;47(6):1065–1072 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref036] 36.Haacke EM, Lindskogj ED, Lin W. A fast, iterative, partial-fourier technique capable of local phase recovery. J Magn Reson (1969). 1991. March;92(1):126–45. [Google Scholar]

[pone.0250636.ref037] 37.Borman PTS, Bos C, de Boorder T, Raaymakers BW, Moonen CTW, Crijns SPM. Towards real-time thermometry using simultaneous multislice MRI. Phys Med Biol. 2016. September 7;61(17):N461–77. 10.1088/0031-9155/61/17/N461 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref038] 38.Bour P, Marquet F, Ozenne V, Toupin S, Dumont E, Aubry J-F, et al. Real-time monitoring of tissue displacement and temperature changes during MR-guided high intensity focused ultrasound: Monitoring of Changes During MRgHIFU. Magn Reson Med. 2017. November;78(5):1911–21. 10.1002/mrm.26588 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref039] 39.Roujol S, de Senneville BD, Hey S, Moonen C, Ries M. Robust Adaptive Extended Kalman Filtering for Real Time MR-Thermometry Guided HIFU Interventions. IEEE Trans Med Imaging. 2012. March;31(3):533–42. 10.1109/TMI.2011.2171772 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref040] 40.Sapareto SA, Dewey WC. Thermal dose determination in cancer therapy. International Journal of Radiation Oncology*Biology*Physics. 1984. April;10(6):787–800. 10.1016/0360-3016(84)90379-1 [DOI] [PubMed] [Google Scholar]

[pone.0250636.ref041] 41.Sethi K, Chutani S. Magnetic resonance imaging-conditional devices: Where have we reached today? Int J Heart Rhythm. 2018;3(1):16. [Google Scholar]

PERMALINK

A fast MR-thermometry method for quantitative assessment of temperature increase near an implanted wire

Marylène Delcey

Pierre Bour

Valéry Ozenne

Wadie Ben Hassen

Bruno Quesson

Roles

Abstract

Purpose

Methods

Results

Conclusion

Introduction

Materials and methods

Set-up for ex vivo experiments

MRI-thermometry sequence

Fig 1. Schematic of the MRI-thermometry technique.

Thermometry pipeline

B1+rms measurements

Validation of the MRI-thermometry method

Potential RF-induced heating near the implanted wire measurement

Potential RF-induced heating near a pacemaker lead

Statistical analyses

MRI-thermometry assessment in volunteer

Temperature dependence on flip angle, B1+rms and energy emitted by the MRI sequence

Prediction of temperature increase for other MRI sequences

Results

Precision of the MRI-thermometry method

Fig 2. Temperature precision in gel and in human brain.

Accuracy of the MRI-thermometry method during heating

Fig 3. Comparison between temperature values measured by the optical fiber and the proposed imaging method.

Phantom experiments with varying flip angles

Fig 4.

Table 1. Summary of experimental conditions and temperature increase as a function of the flip angle of the heating module.

Fig 5. Dependence of temperature increase in a single pixel on flip angle, B1+rms and deposited energy by the MRI sequence.

Applicability of the method on a pacemaker lead

Fig 6. Application of the proposed method on a pacemaker lead.

Prediction of temperature rise for three MRI sequences

Fig 7. Temperature data for 4 different FAHM.

Fig 8. Prediction of maximal temperature rise for other acquisition sequences.

Discussion

Sequence implementation

Precision of the MRI-thermometry

Calibration technique

Prediction of temperature increase from the model

Study limitations

Conclusion

Data Availability

Funding Statement

References

Decision Letter 0

Nick Todd

Roles

Author response to Decision Letter 0

Decision Letter 1

Nick Todd

Roles

Author response to Decision Letter 1

Decision Letter 2

Nick Todd

Roles

Acceptance letter

Nick Todd

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

B_1+rms measurements

Temperature dependence on flip angle, B_1+rms and energy emitted by the MRI sequence

Fig 5. Dependence of temperature increase in a single pixel on flip angle, B_1+rms and deposited energy by the MRI sequence.

Fig 7. Temperature data for 4 different FA_HM.