Abstract
Purpose of Review
Negative controls are a powerful tool to detect and adjust for bias in epidemiological research. This paper introduces negative controls to a broader audience and provides guidance on principled design and causal analysis based on a formal negative control framework.
Recent Findings
We review and summarize causal and statistical assumptions, practical strategies, and validation criteria that can be combined with subject-matter knowledge to perform negative control analyses. We also review existing statistical methodologies for the detection, reduction, and correction of confounding bias, and briefly discuss recent advances towards nonparametric identification of causal effects in a double-negative control design.
Summary
There is great potential for valid and accurate causal inference leveraging contemporary healthcare data in which negative controls are routinely available. Design and analysis of observational data leveraging negative controls is an area of growing interest in health and social sciences. Despite these developments, further effort is needed to disseminate these novel methods to ensure they are adopted by practicing epidemiologists.
Keywords: Bias correction, Bias detection, Bias reduction, Negative control, Unmeasured confounding
Introduction
Despite ongoing efforts to improve study design and statistical analysis of epidemiological research, failure to rule out non-causal explanation of empirical findings has prompted substantial discussions in health science [1, 2]. A powerful tool increasingly recognized to mitigate bias is negative control study design and analysis [3••, 4, 5]. Negative controls have a long history in laboratory experiments and epidemiology [3••, 6–8]. However, they have mainly been used to detect bias rather than to remove bias. More recent methodological advances that enable both bias detection and bias removal have not been fully recognized. As a result, the potential for valid and accurate causal inference leveraging contemporary healthcare data with abundant negative controls has to date not been fully realized. This paper aims to introduce negative controls to a broader audience and provide guidance on principled design and causal analysis based on a formal negative control framework. We focus on resolving bias due to unmeasured confounding in observational studies, although negative controls have recently also been used to tackle a variety of biases such as selection bias [3••, 4, 9], measurement bias [3••, 4], and homophily bias [10, 11] in both observational studies and randomized trials [5].
Definition and Notation
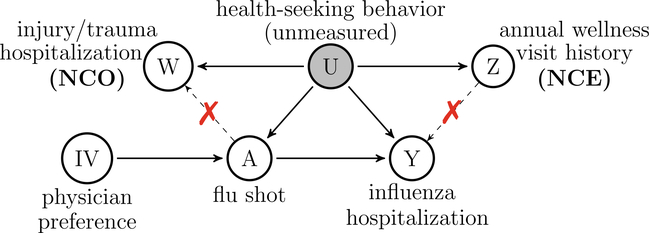
A negative control outcome (NCO) is a variable known not to be causally affected by the treatment of interest. Likewise, a negative control exposure (NCE) is a variable known not to causally affect the outcome of interest. To the extent possible, both NCO and NCE should be selected such that they share a common confounding mechanism as the exposure and outcome variables of primary interest, although this is not always necessary [12•, 13]. These known-null effects have been used to detect residual confounding bias: the presence of an association between the NCE and the outcome (or between the NCO and the exposure) constitutes compelling evidence of residual confounding bias, while the absence of such association implies no empirical evidence of such bias. For example, in a study about the effects of influenza vaccination on influenza hospitalization in the elderly (Fig. 1), injury/trauma hospitalization was considered an NCO as it cannot be causally affected by influenza vaccination, but may be subject to the same confounding mechanism mainly driven by health-seeking behavior [14]. The authors found that despite efforts to control for confounding, influenza vaccination not only appeared to reduce the risk of influenza hospitalization after influenza season (risk ratio 0.82, 95% CI 0.73–0.92) but also appeared to reduce the risk of injury/trauma hospitalization (risk ratio 0.83, 95% CI 0.75–0.91). This was interpreted as evidence of bias due to inadequately controlled confounding. Likewise, annual wellness visit history can be considered an NCE as it is unlikely to cause flu-related hospitalization. In the following, we adopt the potential outcome framework which we use to formally define causal effects as well as to articulate sufficient identification conditions to perform valid causal inferences from observational data. We proceed under the fundamental assumption that for each subject in the target population, there exists a potential outcome variable Y(a) that would be observed if possibly contrary to fact, the subject were exposed to treatment value a, for all possible treatment values of a in a set . In the common setting where the treatment is dichotomous , the assumption states that each subject has a well-defined pair of potential outcomes (Y(0), Y(1)) corresponding to their outcome under active treatment a = 1 and control treatment a = 0, respectively [15, 16]. In such a setting, our goal is to make inferences about the population average treatment effect (ATE) defined as ATE = E [Y(1)-Y(0)]. Now, consider an observational study in which one observes independent and identically distributed samples on (Y, A, X), where A is a subject’s observed binary treatment assignment, Y is his/her observed outcome, and X is the observed confounders of the association between A and Y. We sometimes refer to A as primary treatment and Y as the primary outcome. We assume that the treatment is defined with enough specificity such that among subjects with A = a, the observed outcome Y is a realization of the potential outcome value Y(a), that is.
Fig. 1.
An example of different types of negative controls: consider studying the causal effect of flu shot (A) on influenza hospitalization (Y), subject to confounding by unmeasured health-seeking behavior (U). Annual wellness visit history (Z) is an NCE which does not causally affect Y. Injury/trauma hospitalization (W) is an NCO which is not causally affected by A. Both Z and W are proxies of health-seeking behavior. Physician’s prescribing preference (IV) is an instrumental variable which likely induces variation in the choice of treatment and may not affect the outcome other than through its influence on the treatment. As discussed in “Definition and Notation” and “Bias detection” sections, both a valid instrumental variable and an invalid instrumental variable associated with U are valid NCE. All arguments are made implicitly conditional on measured covariates X. Independence between A and Z (or Y and W) conditional on U is not necessary. See more examples in Table 3 of the Appendix.
Assumption 1 (Consistency).
Y(a)= Y when A = a.
Much of the literature on causal inference in observational studies relies on the strong assumption of no unmeasured confounding for the purpose of identification, i.e., A ⊥ Y(a) | X, which is sometimes referred to as the ignorability assumption. This assumption essentially rules out the existence of unmeasured common causes, denoted as U, of the treatment and outcome variables—an untestable assumption which is often at the source of much skepticism about causal interpretation of associations found in observational data. We do not make such ignorability assumption to establish causation. Instead, we invoke the following assumption that describes the relationship between treatment and outcome in the presence of both measured and unmeasured confounding.
Assumption 2 (latent ignorability).
A ⊥ Y(a) | U, X
In addition to (A, Y, X), suppose that one has also observed a secondary outcome W and/or a secondary exposure Z, and let Y(a, z) and W(a, z) denote the corresponding counterfactual values that would be observed had the primary treatment and secondary exposure taken value (a, z). W and Z are formally defined as negative control outcome and exposure variables provided that the following assumptions hold
Assumption 3 (negative control outcome).
W(a, z)= W and W ⊥ A | U, X
Assumption 4 (negative control exposure).
Y(a, z)= Y (a) and Z ⊥ (Y (a), W) | U, X
Assumptions 3 and 4 entail the following: (1) there is no remaining unmeasured common cause between (A, Z) and (Y, W) conditional on (U, X); (2) there is no causal effect of Z on Y conditional on U, A, and X, and there is no causal effect of A and Z on W conditional on U and X, which are referred to as the exclusion restrictions. We refer to a pair of W and Z as the double negative control. It is not necessary to have both NCO and NCE, although the double-negative control will be sufficient for nonparametric identification of the ATE as detailed in the “Bias Reduction and Bias Correction” section.
Figure 1 illustrates a directed acyclic graph (DAG) encoding the above assumptions. Consider a study of the effectiveness of flu shot (A) on influenza-related hospitalization (Y). A major concern in such studies is potential hidden bias due to unmeasured health-seeking behavior (U), a well-known common cause of flu shot status and influenza hospitalization. In such a study, routinely captured information on a person’s annual wellness visit history entails a good candidate NCE (Z) satisfying Assumption 4, as it reflects a person’ s tendency to engage in healthy behavior, and is unlikely to cause influenza hospitalization. Similarly, recorded data on a person’s injury/trauma hospitalization provides compelling candidate NCO (W) satisfying Assumption 3, as it is likely associated with health-seeking behavior and unaffected by flu shot. In addition, we can view an instrumental variable (IV) as an NCE [12•, 17•]. An IV is a pre-treatment variable satisfying the following three core assumptions: (IV relevance) the IV must be associated with the treatment; (exclusion restriction) the IV must not have a direct effect on the outcome that is not mediated by the treatment; and (IV independence) the IV must be independent of unmeasured confounders. For example, physician’s prescribing preference is often taken as an IV in comparative effectiveness studies, because it likely induces variation in the choice of treatment, and may not affect the outcome other than through its influence on the treatment [18]. A valid IV satisfies Assumption 4 and hence is a valid NCE, which is further explained in the “Bias Detection” section. Besides the above three IV conditions, a fourth condition is necessary to identify a causal effect, such as the monotonicity assumption or the no current treatment interaction assumption [19–22]. Alternatively, causal effect identification using IV is also made possible by further incorporating an NCO under a double negative control framework introduced in the “Bias Reduction and Bias Correction” section. It is important to note that Fig. 1 is not the only DAG satisfying the negativecontrol assumptions. For example, a more general DAG would allow Z to affect A, corresponding to the case where an annual wellness visit could result in flu vaccination during flu season. Moreover, physician preferences are not randomized and may be associated with U via physician-patient interactions, potentially violating the IV independence assumption. Such an invalid IV violating the IV independence assumption is still a valid NCE as long as the exclusion restriction holds, regardless of whether the IV relevance assumption holds. In this case, an NCO can be used to repair an invalid IV for causal effect identification under a double-negative control framework [12•, 17•]. Additional DAGs illustrating settings in which Assumptions 2 and 3 hold are provided in Table 3 of the Appendix. As demonstrated in [12•, 17•], an NCE can be either pre- or post-treatment variable. Unmeasured common causes of the Z–A association and Y–W association can also be present without necessarily invalidating Assumptions 3–4. A key insight is that a valid NCO does not necessarily need to be an outcome variable and may in fact precede the treatment in view, while a valid NCE need not necessarily be a treatment and may in fact be ascertained either together with primary outcome of interest or subsequently.
Inconsistent Terminology in Literature
In prior literature, NCO has been referred to as falsification outcome/endpoint [23–26], control outcome [14, 27, 28], secondary outcome [29, 30], supplementary response [6], and unaffected outcome [31]. NCE has been referred to as control exposure [27] and residual confounding indicator [32, 33•]. Both NCO and NCE have been referred to as proxies of unmeasured confounder [34, 35, 36••]. In addition, an exposure- outcome pair known a priori to be unrelated has also been referred to as a negative control pair [37•, 38–41].
The literature reviewed in the current paper is largely limited to papers that use the aforementioned nomenclature. Although [3••, 27] review negative control literature, to the best of our knowledge, this paper is the first to systematically summarize both formal causal and statistical methodology together with applications of negative controls. The rest of the paper is organized as follows. The design and validation of negative controls are discussed in the “Review of Applications” section. We then review both assumptions and methods for using negative controls to detect, reduce, and remove unmeasured confounding bias in the “Review of Applications” section. We use a simple example to illustrate double negative control adjustment (i.e., leveraging NCE and NCO when both are available) of confounding bias in the “Bias Reduction and Bias Correction” section. We close with a summary in the “Conclusions” section.
Review of Applications
Existing applications of negative controls mainly focus on the detection of uncontrolled confounding bias. We list in Table 1 selected studies that employed negative controls to detect residual confounding and to strengthen causal conclusions. Among these studies, eight used NCEs and nine used NCOs. Table 1 is by no means comprehensive, as hundreds of studies have leveraged negative control variables as evidenced by the number of recent articles that have cited [3••] as the foundational paper on the use of negative control exposures and outcomes in epidemiology, but rather a representative set of examples that help illustrate strategies for identifying compelling candidate negative controls.
Table 1.
Summary of selected applications using negative controls for detection of confounding bias
| Reference | Exposure | Outcome | Negative control exposure | Negative control outcome |
|---|---|---|---|---|
| [42] | Maternal smoking | Low birth weight | Paternal smoking | |
| [43] | Maternal smoking | Sudden infant death syndrome | Paternal smoking | |
| [44] | Maternal smoking | Offspring height, ponderal index, body mass index | Paternal smoking | |
| [45] | Maternal smoking | Offspring blood pressure | Paternal smoking | |
| [47] | Maternal distress | Offspring asthma | Paternal distress | |
| [46, 48]: | Maternal smoking, alcohol use or dietary patterns | Offspring development | Paternal smoking, alcohol use, or dietary patterns | |
| [51] | Air pollutant | Asthma | Future air pollutant, air pollutant elsewhere | |
| [54•] | Mammography-screening participation | Death from breast cancer | Dental care participation | Death from causes other than breast cancer and from external causes such as accidents, intentional self-harm, and assaults |
| [14] | Influenza vaccination | Mortality and pneumonia/influenza hospitalization | Outcome before and after influenza season; injury/trauma hospitalization | |
| [55] | Air pollutant | Asthma hospitalization | Appendicitis hospitalization | |
| [56–59] | Smoking | Mortality from lung cancer | Other causes of death | |
| [60] | Psychological stress post earthquake | Deaths from cardiac events | Other causes of death, e.g. cancer | |
| [52, 53] | Screening sigmoidoscopy | Mortality from distal colon tumor | Mortality from proximal colon tumor (above the reach of the sigmoidoscopy) | |
Examples of Negative Control Designs
Effect of Influenza Vaccination on Influenza Hospitalization: Using Injury/Trauma Hospitalization as an NCO
As detailed in the “Definition and Notation” section, to study the effects of influenza vaccination on influenza hospitalization in the elderly, injury/trauma hospitalization was taken as an NCO to detect confounding by unmeasured health-seeking behavior [14]. Influenza hospitalization before the flu season was also used as an NCO, because flu vaccine cannot protect against influenza hospitalization when there is little flu virus circulation.
Effect of Maternal Exposure on Offspring Outcomes: Using Paternal Exposure as an NCE
A number of publications have used paternal exposure as an NCE to study the intrauterine effect of maternal exposure on offspring outcome. Specifically, [42–46] studied the association between maternal smoking and offspring outcomes and compared paternal and maternal associations to detect potential bias due to unmeasured confounding by family-level confounding factors or parental phenotypes. Similarly, [47] compared maternal and paternal distress and their associations with offspring asthma. The evaluation of the validity of paternal exposure as an NCE has also been considered in [48]. They found that the cotinine level from exposure to partner smoking was low in non-smoking pregnant women, which suggests that using paternal smoking as an NCE for investigating intrauterine effects is valid.
Effect of Air Pollution on Health Outcomes: Using Future Air Pollution as an NCE
Besides the use of paternal exposures, NCEs are also used in air pollution studies. For example, [32,33•, 49,50] studied statistical methods that utilize future air pollution as an NCE for bias detection and bias reduction, because the future is not expected to causally affect the past. In addition, [51] studied the effect of air pollutants on asthma and leveraged two different NCEs: air pollutant level in the future and air pollutant level in a distant city.
Summary of Negative Control Designs
In addition to the above examples, various negative control designs are also summarized in Table 1. Rather than detailing each study in Table 1, we summarize these studies in terms of their respective strategy to identify negative control variables below. A commonly used strategy to select negative controls leverages temporal and spatial constraints that essentially guarantee the exclusion restrictions in Assumptions 3 and 4. Temporal ordering leverages the universal truth that the future cannot causally affect the past. For example, as detailed above, [32, 33•, 49–51] specify future measurements of air pollution as an NCE to study the effect of current air pollution on health outcomes. Similarly, [46] proposed to look at maternal exposure before and after pregnancy in studying the intrauterine effect of maternal exposure on offspring outcome. An essential prerequisite for this design is that primary outcome does not cause subsequent exposure (at least in the short term), certainly a reasonable assumption in air pollution settings. Prior information about timing of exposure also sometimes allows one to leave out an essential ingredient [3••]. For instance, [14] defined NCO as the number of hospitalizations prior to the influenza season in order to estimate the effect of influenza vaccination on influenza hospitalization, as little to no flu circulates prior to flu season for influenza vaccination to be protective against. Spatial distancing has also been considered an effective means to enforce exclusion restrictions in Assumptions 3 and 4. For instance, [51] took air pollutant level in a distant city as an NCE to study the effect of air pollutants on asthma. Others [52, 53] studied screening sigmoidoscopy and mortality from colon tumor and selected tumor from the proximal colon that is beyond the reach of the sigmoidoscopy as an NCO.
Another strategy is to select as NCO an outcome analogous to the primary outcome however resulting from mechanism a priori known to be unrelated to the primary treatment. As an illustration of this approach, consider [14] which took hospitalization due to injury/trauma as an NCO for the primary outcome, hospitalization due to influenza. Similarly, to evaluate the effect of air pollution on hospitalization due to asthma, [55] defined hospitalization due to appendicitis as an NCO. In addition, several studies routinely use death from other causes as NCO: [56–59] studied the effect of smoking on lung cancer with mortality from other causes as an NCO, [60] studied the effect of psychological stress on deaths from cardiac events after an earthquake with death from other causes as an NCO, and [54•] selected death from causes other than breast cancer and from external causes such as accidents, intentional self-harm, and assaults as NCO to estimate the effect of mammography screening participation on breast cancer mortality.
Validation of Negative Controls by Subject Matter Knowledge
Despite the various strategies in the literature to find candidate negative controls, researchers should rigorously validate the choice of negative controls and be aware of possible violations of negative control assumptions. Similar to the assumptions of no unmeasured confounding, negative control assumptions (Assumptions 3 and 4) are causal assumptions that can only be established by subject matter considerations and not by empirical tests without additional assumptions. In practice, we recommend checking the following criteria in finding a candidate negative control.
“Irrelevant to Y (or A)”: The NCE should not cause the outcome of interest, while the NCO should not be caused by the treatment of interest nor the NCE. These conditions are formally implied by Assumptions 3 and 4.
“Comparable to A (or Y)”: In most cases, it is important to have the source of bias in mind before designing a negative control study although this is not always necessary [12•, 13]. Unmeasured confounding mechanism of negative controls should be comparable to that of A and Y in the following sense: the NCE must be associated with unmeasured confounders conditional on measured confounders and primary treatment; the NCO must be associated with unmeasured confounders conditional on measured confounders. Hence, the negative control variable is often viewed as a proxy of the unmeasured confounders. A variable completely irrelevant to all mechanisms under consideration would not provide any useful information. These conditions are formally required by Assumptions 5 and 7 in the “Review of Methods” section.
“Adequate Negative Control Power”: The NCE and NCO are not exceedingly rare relative to primary treatment and outcome variables, respectively. For example, in the event that the negative control variable is a rare binary variable, or if the association between unmeasured confounder and negative control variable is weak, then, large sample may be necessary to achieve sufficient power for detecting confounding bias.
We list examples of possible violations of negative control assumptions in the Appendix.
Review of Methods
Bias Detection
Key Assumption and Rationale for Bias Detection
Assumptions 3 and 4 give rise to formal statistical tests of the null hypothesis that adjustment for observed covariates suffices to control for confounding bias, rejection of which indicates the presence of an unmeasured confounder U. A key assumption for this bias detection strategy is that the negative control exposure or outcome is U-comparable to the primary exposure or outcome:
Assumption 5 (U-comparable).
W⊥ f ⊥ U | X and Z⊥ f ⊥ U | A, X
The U-comparability assumption requires that unmeasured confounders U of A–Y association are identical to those of the A–W association and Z–Y association, such that a non-null A–W or Z–Y association can be attributed to U. Therefore, the presence of an association between primary and negative control variables implies residual confounding bias, while the absence of such associations implies no empirical evidence of unmeasured confounding. It is important to note that when evaluating Z–Y association, one must also adjust for A to rule out the potential association between Z and Y due to the pathway Z–A→Y (the arrow between Z and A could either be Z→A or Z←A). Examples of such relationships are listed in Table 3 of the Appendix. Notably, conditional on X, a valid IV independent of U and associated with A satisfies Assumption 5 because of conditioning on a collider A on the IV→A←U pathway [12•, 17•]; likewise, an invalid IV that violates the IV independence assumption defined in the “Definition and Notation” section woud also satisfy Assumption 5 regardless of whether IV and A are associated, as mentioned in the “Definition and Notation” section.
Methods
As detailed in the “Review of Application” section, the majority of existing applications used negative controls for bias detection, by testing for an association between primary and negative control variables. A review of bias detection methods is presented in Table 2. For example, [32] formalized bias detection as a Wald test of the coefficient of NCE in a regression model of the outcome on the primary and negative control exposures. Moreover, [61, 62] noted that an invalid NCE that violates the exclusion restriction but satisfies the U-comparable assumption can nevertheless validate a causal interpretation when it does not appear to be associated with the outcome adjusting for the treatment of interest.
Table 2.
Summary of published methodologies using negative controls for detection (D), reduction (R), and correction (C) of confounding bias
| Reference and Setting | Main Assumptions Besides Assumptions 2–5 | Methods | |
|---|---|---|---|
| D | [32]: Time-series study. Z = future air pollution At+1. | (1) At+1 ⟂ Yt | At, Ut, Xt. (2) log[E(Yt)] = α + βAt + γXt + βfAt+1. |
Bias detection by Wald-test on βf. |
| [60, 61]: invalid NCE Z. | (1) Violation of exclusion restriction Y(a, z) ≠ Y(a). (2) Z is U-comparable with . |
No evidence of Z-Y association adjusting for A implies no residual confounding of A-Y association. | |
| R | [33, 49]: Time-series study. Z = future air pollution At+1. | (1) At+1 ⟂ Yt | At, Ut, Xt; . (2) Yt(at, xt, ut) = β0 + β1αt + β2xt + β3ut + ϵt; E[ϵt | At = at, Ut = ut, Xt = xt] = 0. (3) ; sign(α1) = sign(α3). (4) E[At+1 | At = at, Xt = xt] = γ0 + γ1at + γ2xt; γ1 > 0. |
Bias reduction by fitting E[Yt | At, Xt, At+1] instead of fitting E[Yt | At, Xt]. Further bias reduction considered in [49] by incorporating Xt+1 or At−1. Identification of β1 is possible with multiple future exposures under autoregressive model for exposure time series. |
| [62]: Standardized mortality ratio in occupational cohort study. | (1) E[Y(1) | X = k]/E[Yref | X = k] = exp(αk − δk) E[W | X = k]/E[Wref | X = k] = exp(−ϵk). (2) sign(ϵk) = sign(δk) and 0 < |ϵk| < 2|δk|. |
Adjust for bias δk via E[Y(1) | X = k]E[Wref | X = k]/E[Yref | X = k]E[W | X = k]. | |
| [38, 40]: Define negative controls as drug–outcome pairs where one believes no causal effect exists. | (1) For a negative control drug-outcome pair, the effect estimate , i = 1,..., n, where θi ∼ N(μ, σ2) is the true bias. (2) Under the null of no treatment effect, the effect estimate . |
Estimate μ, σ by MLE with . Calibrated p-value computed via Wald-test of βn+1. Confidence interval calibrated similarly using distribution generated by positive controls. | |
| C | [63, 64]: W, Y = Time-to-event outcome. | (1) There exist monotonic functions that describe U-Y and U-W associations: Y(0) = hy(U, X), W = hw(U, X). (2) Cox models for Y and W w/ hazard ratio and . |
The hazard ratio measuring the causal effect of treatment is . |
| [13, 65]: Generalized difference-in-differences using NCO. | (1) There exist monotonic functions that describe U-Y and U-W associations: Y(0) = hy(U, X), W = hw(U, X). (2) Positivity: if 0 < fW|A=1,X(W*) then 0 < fW|A=0,X(W*) < 1, where W* = (W | A = 1, X) is distributed as W in the exposed group. |
The average treatment effect on the treated is . Generalized the difference-in-differences approach to the broader context of NCO. | |
| [66]: Calibration using NCO. | (1) W ⟂ A | X, Y(1), Y(0). (2) Rank preservation: Y = Y(0) + ΨA, and hence W ⟂ A | X, Y(0) by (1). (3) E[W | A, Y(0) = Y − ΨA, X] = β1 + β2X + β3Y(Ψ) + β4A, where β4 = 0 by (1). | The 95% CI for any Ψ0 consists of all Ψ for which contains 0; Under (1)–(3), fit E[W | A, Y, X] = β1 + β2X + β3Y + βΨA, then the causal effect Ψ = −βΨ/β3. | |
| [67–69]: Removing unwanted variation in gene-expression analysis. | (1) Y1×p = X1×qβq×p + U1×rΓr×p + ϵ1×p, p ≥ r + 1. (2) , s ≥ r, . (3) . (4) . |
[67, 68]: Estimate U by factor analysis of (2), then estimate β from (1). [69]: Estimate ΓW and Γ by factor analysis of Y = X(β + αΓ) + (ϵUΓ + ϵ) (5) and W = XαΓW + (ϵUΓW + ϵW) (6). Then estimate α from (6), and estimate β from (5). | |
| [12, 17, 36]: Nonparametric identification. | Assumption 7 | Identify h in E[Y | A, Z, X] = E[h(W, A, X) | A, Z, X], then ATE = E[h(W, A = 1, X)] − E[h(W, A = 0, X)]. |
Bias Reduction and Bias Correction
Summary of Literature
Beyond bias detection, recent developments have made it possible to reduce and sometimes completely remove unmeasured confounding bias using negative controls. In air pollution studies, current and future pollutant levels are often positively correlated and are associated with unmeasured con- founders in the same direction. In this setting, [33•] showed that incorporating future air pollution, an NCE, in the outcome model can reduce confounding bias. Further bias attenuation was proposed in [49] by incorporating both past and future exposures. Bias reduction using an NCO was considered by [63] in the estimation of standardized mortality ratio, where the standardized mortality ratio of the NCO was used to reduce bias in that of the primary outcome. In addition, [38, 40] considered calibrating p value and confidence intervals by deriving an empirical null distribution from the association between primary and negative control variables.
Several methods were developed to achieve full bias removal, under certain assumptions such as monotonicity [13, 64–66], rank preservation [67], and linear model for unmeasured confounding. Specifically, [64, 65] considered bias correction by using a negative control time-to-event outcome under a monotonicity assumption that describes the U – Y and U – W association. Under a similar monotonicity assumption, [13] generalized the difference-in-difference method to the NCO method, which is further extended by [66]. In addition, [67] developed an outcome calibration approach with a rank preservation assumption under which the counterfactual primary outcome can account for the unmeasured confounding between the A–W associations. Lastly, [68, 69, 70•] assumed a linear model for the unmeasured confounder and proposed to estimate U by factor analysis.
Nonparametric Identification in a Double-Negative Control Design
The above methods remove unmeasured confounding bias under relatively stringent assumptions. Sufficient conditions are established by [36••] under which the ATE can be nonparametrically identified leveraging an NCE and an NCO, i.e., via a double-negative control design [17•]. That is, the ATE can be uniquely expressed as a function of the observed data distribution without imposing any restriction on the observed data distribution, such that distinct data-generating mechanisms are guaranteed to lead to distinct ATE values. Further method developments include semiparametric estimation under categorical negative controls and unmeasured confounding [17•] and alternative strategies to identify the ATE via a so-called confounding bridge function [12•].
Double-negative controls are widely available in health sciences. For example, in air pollution studies, [12•] used future air pollution level and past health outcome as negative control exposure and outcome, respectively. Two routinely monitored control outcomes are taken by [17•] from administrative healthcare data in vaccine safety studies as double-negative control, in the setting where both control outcomes are independent of the primary outcome and satisfy both Assumption 3 and Assumption 4. In influenza vaccine effectiveness research presented in Fig. 1, annual wellness visit and injury/trauma hospitalization can serve as double-negative control. In addition, when IV is available, identification is made possible by further incorporating an NCO such as a pretreatment measurement of the outcome.
Below, we will first detail the identification conditions established in [36••] and then introduce the identification methods proposed in [12•, 36••].
Assumption 6 (positivity).
0< P (A = a, Z = z | X) < 1 for all a, z.
Assumption 7 (completeness).
(a) For all a, W ∦ Z | A = a, X. (b) For any square integrable function g, if E [g(W)| Z = z, A = a, X] = 0 for almost all z, a, then g(W ) = 0.
Assumption 6 is a regular positivity assumption ensuring that in all strata of X, there are always some individuals with A = a, Z = z for all a, z. Assumption 7 is a commonly used completeness condition for identification [71]. Specifically, Assumption 7(a) essentially requires U-comparability. That is, both Z and W should be associated with U such that variation in U can be recovered from variation in Z and W. Assumption 7(b) aims to ensure that the underlying unmeasured confounding mechanism in E [Y | A, U ] can be identified using Z and W. For example, suppose U is a binary variable. Then, Assumption 7 further requires that Z and W have at least two categories, and E [W | A = a, Z =1, X = x] - E [W | A=a, Z =0, X = x].
Rationale
In the presence of unmeasured confounding by a latent variable U, an observed difference in the outcome between the treatment and control groups is a combination of the underlying causal effect and confounding bias. One cannot directly disentangle the variation in the outcome due to the treatment from the unwanted variation due to U, as U is not measured. We seek to indirectly remove such unwanted variation, i.e., unmeasured confounding bias, by leveraging available proxies of U. An important example of such proxy is an NCO chosen to be associated with U but not causally affected by the treatment (Figure 1), such that any difference in the NCO, W, between the treatment and control groups can only be attributed to U. Such a difference can uncover the unwanted variation due to U assuming that U–Y and U–W associations are the same, and there is no U–A additive interaction on Y. An example of such W is the pre-exposure baseline measure of the outcome, in which case, bias adjustment reduces to the well-known difference-in-difference approach [13]. The above describes the identification of the ATE under assumptions that are generally untenable, because the U–Y and U–W associations will often be on different scales, and there may be U–A interactions in the model for Y. In order to nonparametrically identify unmeasured confounding bias, we make use of the NCE Z. Because Z is associated with Y or W only through U, the ratio of Z–Y and Z–W associations captures the ratio of U–Y and U–W associations, allowing for U–A interactions. In summary, leveraging a double-negative control design one can nonparametrically identify the magnitude of unmeasured confounding bias via the following mechanism: The NCO uncovers the confounding bias up to a scale that reflects the difference between U–Y and U–W associations, while the NCE recovers the scale leveraging Z–Y and Z–W associations. This mechanism is further illustrated in an example below.
Example
To further illustrate the idea of identification using a double-negative control, consider a simple example where we assume the following linear structural equation models involving unmeasured confounding U, although the nonparametric identification proposed in [36••] does not rely on any restriction about the data generating models. We suppress measured confounders X to ease notation—all arguments are made implicitly conditional on X.
Had U been measured, we could fit (1) and obtain the true causal effect which is βYA. When in fact U is not measured, to leverage double-negative control, we additionally assume the U–W relationship in (2) and U–Z relationship in (3).
| (1) |
| (2) |
| (3) |
Models (1)–(3) indicate the following models that one could actually fit using the observed data (Y, A, W, Z). These models are obtained by replacing U with E [U| A, Z] in the primary and negative control outcome models (1) and (2).
| (4) |
| (5) |
| (6) |
| (7) |
From (1), we know that the true causal effect is βYA. However, if one were to regress Y on A and Z without accounting for U such as in [33•], then the coefficient of A would be equal to βYA + βYUβUA. Here, βYUβYA is confounding bias, which arises when there exists a U that is associated with both Y and A. One cannot directly separate the confounding bias from the true causal effect because U is not observed. Nevertheless, the coefficients in the observed models (5) and (7) allow us to infer βYUβYA. To facilitate discussion, we introduce notation for the coefficients in models (5) and (7). and denote the coefficients of A and Z in the primary outcome model (5), respectively, and let and denote the coefficients of A and Z in the negative control outcome model (7), respectively.
We detail three strategies to identify the unmeasured confounding bias βYUβYA leveraging a single NCO, a single NCE, or the double-negative control. First, we note that coefficient of A in the primary outcome model, , is a combination of both true causal effect and confounding bias, whereas the coefficient of A in the negative control outcome model, , reflects pure confounding bias because A does not causally affect W. In fact, if U–Y and U–W associations are equal on the additive scale, i.e., βWU = βYU, then matches the confounding bias βYUβUA. That is, under the assumption of equal U–Y and U–W additive association, a form of “additive outcome equi-confounding” [13], the treatment effect on NCO is equal to the unmeasured confounding bias. Hence, the causal effect can be recovered by backing out the association of the treatment with the NCO from the association of the treatment with the primary outcome. Note that in this scenario, it is not necessary to have an NCE: one can fit the primary and negative control outcome on treatment without adjusting for the NCE, and then take the difference in treatment effects. When NCO is the baseline outcome, the above reduces to the difference-in-difference method [13].
Second, the coefficient of Z in the primary outcome model, , would be zero if there was no unmeasured confounding because Z does not causally affect Y. Therefore, the coefficient of Z in the outcome model reflects pure confounding bias. In fact, if U–A and U–Z associations are equal on the additive scale, i.e., βUA = βUZ, then captures the bias βYUβYA due to unmeasured confounding. That is, under the assumption of equal U–A and U–Z additive association, a form of “additive treatment equi-confounding,” the NCE effect on the primary outcome is equal to the unmeasured confounding bias. Hence, the causal effect is given by the difference in coefficients of treatment and NCE in the primary outcome model. Note that in this scenario, it is not necessary to have an NCO: one can fit the primary outcome on treatment and NCE and then take the difference in the effects of treatment and NCE on Y.
In both scenarios described above, the “additive outcome equi-confounding” or “additive treatment equi-confounding” is a rather strong assumption, as it requires Y and W or Z and A, to operate on the same scale. To relax these assumptions, we can leverage the double-negative control. Specifically, if U–Y and U–W associations are unequal, then reflects pure confounding bias up to a scale which is equal to βYU/βWU. Because Z–Y (Z–W) association is a product of U–Z and U – Y (U – W ) associations, the ratio of Z–Y and Z–W associations is equal to the ratio of U–Y and U–W associations. That is, . The confounding bias is thus equal to scaled by , and the true causal effect is given by . It is important to note that the first two adjustment methods are a special case of the general adjustment method in that the confounding bias is always equal to across all three scenarios.
To summarize, the confounding bias
| (8a, b, c) |
Hence, the true causal effect is identified as.
| (9) |
It is important to note that Eq. (9) is only meaningful when is not equal to zero. If , then either there is no evidence of the presence of U and βyuβya = 0 or a selected negative control variable is not sufficiently associated with U, violating Assumption 7. Similar arguments apply to and . In fact, as summarized in Table 2, many negative control methods detect, reduce, and remove unmeasured confounding bias using analogies of scenario (8a) [13, 63–65] and scenario (8b) [32, 33•, 49].
In practice, identification via (9) relies on fitting the primary and negative control outcome models E [Y | A, Z] and E [W | A, Z]. Alternatively, one could directly make an assumption about the underlying unmeasured confounding mechanism E [Y | A, U] which is proposed in [12•]. To illustrate, consider again the example above. Let then by (2) is a good proxy of U in the sense that . In particular, let , then by (1), we have
| (10) |
| (11) |
where (11) is obtained by taking expectations on both sides of (10). The above equations indicate that h captures the relationship between U–Y and U–W associations via (10), which can be identified by the relationship between Z–Y and Z–W associations via (11). Because of this key observation, h is referred to as the confounding bridge function in [12•]. The functional form of h is implied by (1) and (2). Once h is identified, we have that . In practice, one may assume a familiar linear model about the functional form of h that satisfies (10), such as
| (12) |
Then, under Assumption 7, θ can be identified by the population moment equation E [g(A, Z){Y-h(A, W; θ)}] = 0 using the generalized method of moments (GMM) method [72]. With θ identified, the ATE is given by
| (13) |
A simple version of the above GMM procedure can be realized via a simple two-stage least squares procedure as follows [12•]:
Stage I: regress W on A and Z and obtain the fitted value as a proxy of U; Stage II: regress Y on A adjusting for , then, the coefficient of A is the true causal effect βYA assuming (1) and (2). The two-stage least squares approach given above provides a simple implementation of the NC method using existing and widely disseminated IV software packages such as the ivregress, ivreg, or ivreg2 command in Stata; the gmm, sem, ivpack, or AER package in R; and the SYSLIN procedure in SAS.
Conclusions
Negative controls are innovative and important tools in observational studies. The development of negative control methods will encourage researchers to routinely check for evidence of confounding bias and rigorously adjust for residual confounding bias. Negative control variables are widely available in routinely collected healthcare data such as administrative claims and electronic health records data, because information on secondary treatments and outcomes beyond the primary treatment and outcome of interest is often recorded and such secondary treatments and outcomes can potentially serve as negative controls. Therefore, the development of negative control methods is critical to unlocking the full potential of contemporary healthcare data and ultimately improve the validity of research findings. It is important to note that other sources of bias, such as selection bias and misclassification bias, are typical in routinely collected healthcare data. Developing negative control methods accounting for bias beyond residual confounding is thus an important area of future research. We have specified statistical assumptions, practical strategies, and validation criteria that can be combined with subject-matter knowledge to design negative control studies in the “Review of Applications” section. We also illustrated identification of the ATE by either fitting the observed primary and negative control outcome models or through assumption on the unmeasured confounding mechanism followed by a simple two-stage least squares procedure in the “Review of Methods” section. We believe that these examples can provide practical guidance on the use of negative control methods to a broader audience.
Appendix 1. Examples of invalid negative controls that violates some assumption
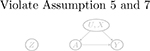
Violation 1: no arrow between U and W. There must be an arrow between U and W, because an NCO is a proxy of unmeasured confounder. It recovers the confounding bias by reflecting variation due to U.
Violation 2: no arrow between U and Z and Z↛A. The only scenario that Z does not need to be associated with U is when Z is an instrumental variable (see first cell of Table 3 of the Appendix). In this case, A is a collider between Z and U, such that Z and U are marginally independent. Conditioning on a collider will create collider bias such that Z and U become conditionally dependent. The requirements about Z in Assumptions 5 and 7 are all made conditioning on A. Therefore, an instrumental variable is a valid NCE.
Violation 3: Y → W. If the outcome causes the NCO, then the treatment directly causes the NCO via the path A→Y→W, which violates Assumption 3.
Violation 4: Z→U⟵W. The direction of the arrow between U and the negative control does not always matter. For example, we can have Z→U, U→Z, W→U, or U→W. However, if both Z and W cause U, then U is a collider in the path Z→U⟵W. In this case, conditional on U, Z and W will become associated. This violates Assumption 2.
Appendix 2. Example of causal graphs encoding the negative control assumptions
Below, we enumerate the possible relationships among Z, A, U and among Y, W, U in Appendix Table 3. These partial graphs can be combined into a directed acyclic graph that encodes the negative control assumptions. Grey-colored graphs are invalid because of violation of key assumptions.
Table 3.
Examples of graphs for Z, A, U relationships and for W, Y, U relationships. The two pieces of graphs can be combined in to a directed acyclic graph that encodes the negative control assumptions. Gray-colored graphs are invalid because of violation of key assumptions
| Examples of graphs for Z, A, U relationships | |||
| Z → A (pre-treatment) | A → Z (post-treatment) | Z ⫫ A | |
| No arrow between U and Z (may violate Assumption 5 and 7) | 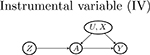 |
 |
 |
| U → Z | 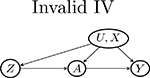 |
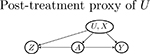 |
 |
| Z → U | May violate Assumption 4 if there is W → U | ||
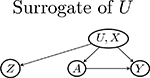
| Examples of graphs for W, Y, U relationships | |||
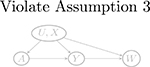
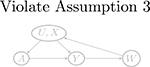
| W → Y (a) | Y (a) → W (violate Assumptions 3 and 4) | Y (a) ⫫ W | (U, X) | |
| No arrow between U and W (violate Assumption 5 and 7) | 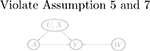 |
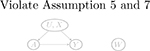 |
|
| U → W | 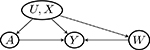 |
 |
|
| May violate Assumption 4 if there is Z → U | |||
| W → U | 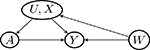 |
 |
|
Footnotes
Compliance with Ethical Standards
Conflict of Interest The authors declare that they have no conflicts of interest.
Human and Animal Rights This article does not contain any studies with human or animal subjects performed by any of the authors.
References
Papers of particular interest, published recently, have been highlighted as:
• Of importance
•• Of major importance
- 1.Ioannidis John PA. “Why most published research findings are false”. In: PLOS Medicine 2.8 (2005), pp. 696–701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hernán MA, Robins JM. Using big data to emulate a target trial when a randomized trial is not available. In: Am J Epidemiol. 2016;183(8):758–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lipsitch M, Tchetgen Tchetgen EJ, Cohen T. Negative controls: a tool for detecting confounding and bias in observational studies. In: Epidemiology. 2010;21.3:383–8•• This paper is the first to formally define negative control exposure and outcome with conditions for bias detection as well as examples in epidemiology.
- 4.Arnold BF, Ercumen A, Benjamin-Chung J, Colford JM Jr. Brief report: negative controls to detect selection bias and measurement bias in epidemiologic studies. In: Epidemiology. 2016;27.5:637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Arnold B, Ercumen A. Negative control outcomes: a tool to detect bias in randomized trials. In: J Am Med Assoc. 2016;316(24): 2597–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rosenbaum PR. The role of known effects in observational studies. In: Biometrics. 1989;45(2):557–69. [Google Scholar]
- 7.Weiss NS. Can the “specificity” of an association be rehabilitated as a basis for supporting a causal hypothesis? In: Epidemiology. 2002;13(1):6–8. [DOI] [PubMed] [Google Scholar]
- 8.Glass DJ. Experimental Design for Biologists. Cold Spring Harbor Laboratory Press, 2014. [Google Scholar]
- 9.Cai Z and Kuroki M. “On identifying total effects in the presence of latent variables and selection bias”. In: Proceedings of the Twenty-Fourth Conference on Uncertainty in Artificial Intelligence. 2008, pp. 62–69. [Google Scholar]
- 10.Liu Lan and Tchetgen Eric Tchetgen. “Regression-based negative control of homophily in dyadic peer effect analysis”. In: arXiv preprint arXiv:2002.06521 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Egami N “Identification of Causal Diffusion Effects Under Structural Stationarity”. In: arXiv preprint arXiv:1810.07858 (2018). [Google Scholar]
- 12.Miao W, Shi X, and Tchetgen Tchetgen EJ. “A Confounding Bridge Approach for Double Negative Control Inference on Causal Effects”. In: (2020). In progress, a prior version can be found at https://arxiv.org/abs/1808.04945.• This paper introduces the confounding bridge function that links primary and negative control outcome distributions for identification of the average treatment effect leveraging a negative control exposure.
- 13.Sofer T, Richardson DB, Colicino E, Schwartz J, Tchetgen Tchetgen EJ. On negative outcome control of unobserved confounding as a generalization of difference-in-differences. In: Stat Sci. 2016;31(3):348–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jackson LA, Jackson ML, Nelson JC, Neuzil KM, Weiss NS. Evidence of bias in estimates of influenza vaccine effectiveness in seniors. In: Int J Epidemiol. 2006;35(2):337–44. [DOI] [PubMed] [Google Scholar]
- 15.Splawa-Neyman J, Dabrowska DM, Speed TP. On the application of probability theory to agricultural experiments. Essay on principles. Section 9. In: Stat Sci. 1990:465–72. [Google Scholar]
- 16.Rubin DB. Estimating causal effects of treatments in randomized and nonrandomized studies. In: Journal of Educational Psychology. 1974;66.5:688. [Google Scholar]
- 17.Shi X, Miao W, Tchetgen Tchetgen EJ. Multiply robust causal inference with double negative control adjustment for categorical unmeasured confounding. In: J Royal Stat Soc: Series B (Statistical Methodology). 2020;82.2:521–40• This paper provides a general semiparametric framework for obtaining inferences about the average treatment effect under categorical unmeasured confounding and negative controls.
- 18.Alan Brookhart M, Rassen JA, Schneeweiss S. Instrumental variable methods in comparative safety and effectiveness research. In: Pharmacoepidemi- ology and Drug Safety. 2010;19(6):537–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Angrist JD, Imbens GW, Rubin DB. Identification of causal effects using instrumental variables. In: J Am Stat Assoc. 1996;91 (434): 444–55. [Google Scholar]
- 20.Hernán MA and Robins JM. “Instruments for causal inference: an epidemiologist’s dream?” In: Epidemiology (2006), pp. 360–372. [DOI] [PubMed] [Google Scholar]
- 21.Robins JM. Correcting for non-compliance in randomized trials using structural nested mean models. In: Commun Stat-Theory and methods. 1994;23(8):2379–412. [Google Scholar]
- 22.Wang L, Tchetgen Tchetgen EJ. Bounded, efficient and multiply robust estimation of average treatment effects using instrumental variables. In: J Royal Stat Soc: Series B (Statistical Methodology). 2018;80.3:531–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Prasad V, Jena AB. Prespecified falsification end points: can they validate true observational associations? In: J Am Med Assoc. 2013;309(3):241–2. [DOI] [PubMed] [Google Scholar]
- 24.Markovitz AA, Hollingsworth JM, Ayanian JZ, Norton EC, Yan PL, Ryan AM. Performance in the Medicare shared savings program after accounting for nonrandom exit: an instrumental variable analysis. In: Ann Int Med. 2019;171(1):27–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bijlsma MJ, Vansteelandt S, Janssen F, Hak E. The effect of adherence to statin therapy on cardiovascular mortality: quantification of unmeasured bias using falsification end-points. In: BMC Public Health. 2016;16.1:303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lin C-K, Lin R-T, Chen P-C, Wang P, De Marcellis-Warin N, Zigler C, et al. A global perspective on sulfur oxide controls in coal-fired power plants and cardiovascular disease. In: Sci Rep. 2018;8(1): 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Dusetzina SB, Brookhart MA, Maciejewski ML. Control outcomes and exposures for improving internal validity of nonrandomized studies. In: Health Serv Res. 2015;50(5):1432–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rosenbaum PR. Design of observational studies. New York, NY: Springer-Verlag, 2010. [Google Scholar]
- 29.Munafo MR, Tilling K, Taylor AE, Evans DM, Smith GD. Collider scope: when selection bias can substantially influence observed associations. In: Int J Epidemiol. 2018;47(1):226–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mealli F, Pacini B. Using secondary outcomes to sharpen inference in randomized experiments with noncompliance. In: J Am Stat Assoc. 2013;108(503):1120–31. [Google Scholar]
- 31.Rosenbaum PR. Detecting bias with confidence in observational studies. In: Biometrika. 1992;79(2):367–74. [Google Scholar]
- 32.Flanders WD, Klein M, Darrow LA, Strickland MJ, Sarnat SE, Sarnat JA, et al. A method for detection of residual confounding in time-series and other observational studies. In: Epidemiology. 2011;22.1:59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Flanders WD, Strickland MJ, Klein M. A new method for partial correction of residual confounding in time-series and other observational studies. In: Am J Epidemiol. 2017;185.10:941–9• This paper develops a regression-based method taking future air pollution as a negative control exposure to reduce residual confounding bias in a time-series study on air pollution effects.
- 34.de Luna X, Fowler P, Johansson P. Proxy variables and nonparametric identification of causal effects. In: Econ Lett. 2017;150:152–4. [Google Scholar]
- 35.Kuroki M, Pearl J. Measurement bias and effect restoration in causal inference. In: Biometrika. 2014;101(2):423–37. [Google Scholar]
- 36.Miao W, Geng Z, Tchetgen Tchetgen EJ. Identifying causal effects with proxy variables of an unmeasured confounder. In: Biometrika. 2018;105.4:987–93•• This paper establishes sufficient conditions for nonparametric identification of the average treatment effect using double negative control.
- 37.Madigan D, Stang PE, Berlin JA, Schuemie M, Overhage JM, Suchard MA, et al. A systematic statistical approach to evaluating evidence from observational studies. In: Annu Rev Stat Appl. 2014;1:11–39• This paper provides a systematic review of challenges in observational studies and describes a data-driven approach to calculating calibrated p values leveraging negative controls.
- 38.Schuemie MJ, Ryan PB, DuMouchel W, Suchard MA, Madigan D. Interpreting observational studies: why empirical calibration is needed to correct p-values. In: Stat Med. 2014;33(2):209–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Schuemie MJ, Hripcsak G, Ryan PB, Madigan D, Suchard MA. Robust empirical calibration of p-values using observational data. In: Statistics in Medicine. 2016;35.22:3883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Schuemie MJ, Hripcsak G, Ryan PB, Madigan D, Suchard MA. Empirical confidence interval calibration for population-level effect estimation studies in observational healthcare data. In: Proc Natl AcadSci. 2018;115(11):2571–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Schuemie MJ, Ryan PB, Hripcsak G, Madigan D, Suchard MA. Improving reproducibility by using high-throughput observational studies with empirical calibration. In: Philos Trans Royal Soc A: Math Phys Eng Sci. 2018;376.2128:20170356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Yerushalmy J The relationship of parents’ cigarette smoking to outcome of pregnancy- implications as to the problem of inferring causation from observed associations. In: Am J Epidemiol. 1971;93(6):443–56. [DOI] [PubMed] [Google Scholar]
- 43.Mitchell EA, Ford RPK, Stewart AW, Taylor BJ, Becroft DMO, Thompson JMD, et al. Smoking and the sudden infant death syndrome. In: Pediatrics. 1993;91(5):893–6. [PubMed] [Google Scholar]
- 44.Howe LD, Matijasevich A, Tilling K, Brion M-J, Leary SD, Smith GD, et al. Maternal smoking during pregnancy and off- spring trajectories of height and adiposity: comparing maternal and paternal associations. In: Int J Epidemiol. 2012;41(3):722–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Brion M-JA, Leary SD, Smith GD, Ness AR. Similar associations of parental prenatal smoking suggest child blood pressure is not influenced by intrauterine effects. In: Hypertension. 2007;49(6): 1422–8. [DOI] [PubMed] [Google Scholar]
- 46.Smith GD. Assessing intrauterine influences on offspring health outcomes: can epidemiological studies yield robust findings? In: Basic Clin Pharmacol Toxicol. 2008;102(2):245–56. [DOI] [PubMed] [Google Scholar]
- 47.Brew BK, Gong T, Williams DM, Larsson H, Almqvist C. Using fathers as a negative control exposure to test the developmental origins of health and disease hypothesis: a case study on maternal distress and off- spring asthma using Swedish register data. In: Scand J Public Health. 2017;45.17(suppl):36–40. [DOI] [PubMed] [Google Scholar]
- 48.Taylor AE, Smith GD, Bares CB, Edwards AC, Munafo MR. Partner smoking and maternal cotinine during pregnancy: implications for negative control methods. In: Drug Alcohol Depend. 2014;139:159–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang M, Tchetgen Tchetgen EJ. Invited commentary: bias attenuation and identification of causal effects with multiple negative controls. In: Am J Epidemiol. 2017;185(10):950–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Yu Y, Li H, Sun X, Liu X, Yang F, Hou L, et al. Identification and estimation of causal effects using a negative control exposure in time-series studies with applications to environmental epidemiology. Am J Epidemiol. kwaa172. 10.1093/aje/kwaa172. [DOI] [PubMed] [Google Scholar]
- 51.Lumley T, Sheppard L. Assessing seasonal confounding and model selection bias in air pollution epidemiology using positive and negative control analyses. In: Environmetrics. 2000;11(6):705–17. [Google Scholar]
- 52.Selby JV, Friedman GD, Quesenberry CP Jr, Weiss NS. A case- control study of screening sigmoidoscopy and mortality from colorectal cancer. In: N Engl J Med. 1992;326(10):653–7. [DOI] [PubMed] [Google Scholar]
- 53.Zauber AG. The impact of screening on colorectal cancer mortality and incidence: has it really made a difference? In: Digest Dis Sci. 2015;60(3):681–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lousdal ML, Lash TL, Flanders WD, Brookhart MA, Kristiansen IS, Kalager M, et al. Negative controls to detect uncontrolled confounding in observational studies of mammographic screening com- paring participants and non-participants. In: Int J Epidemiol. 2020;• This paper uses both negative control exposure and negative control outcome to detect residual confounding in an observational study of mammographic screening comparing participants and non-participants.
- 55.Sheppard L, Levy D, Norris G, Larson TV, Koenig JQ. Effects of ambient air pollution on nonelderly asthma hospital admissions in Seattle, Washington, 1987–1994. In: Epidemiology. 1999:23–30. [PubMed] [Google Scholar]
- 56.Cuyler Hammond E, Horn D. The relationship between human smoking habits and death rates: a follow-up study of 187,766 men. In: J Am Med Assoc. 1954;155(15):1316–28. [DOI] [PubMed] [Google Scholar]
- 57.Doll R, Bradford Hill A. The mortality of doctors in relation to their smoking habits. In: Br Med J. 1954;1(4877):1451–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Doll R, Bradford Hill A. Lung cancer and other causes of death in relation to smoking. In: BrMed J. 1956;2(5001):1071–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Cornfield J, William H, Cuyler Hammond E, Lilienfeld AM, Shimkin MB, Wynder EL. Smoking and lung cancer: recent evidence and a discussion of some questions. In: J Natl Cancer Inst. 1959;22(1):173–203. [PubMed] [Google Scholar]
- 60.Trichopoulos D, Zavitsanos X, Katsouyanni K, Tzonou A, Dalla-Vorgia P. Psychological stress and fatal heart attack: the Athens (1981) earthquake natural experiment. In: Lancet. 1983;321 (8322):441–4. [DOI] [PubMed] [Google Scholar]
- 61.Smith GD. Negative control exposures in epidemiologic studies. Comments on “Negative controls: a tool for detecting confounding and bias in observational studies”. In: Epidemiology. 2012;23(2): 350–1. [DOI] [PubMed] [Google Scholar]
- 62.Weisskopf MG, Tchetgen Tchetgen EJ, Raz R. Commentary: on the use of imperfect negative control exposures in epidemiologic studies. In: Epidemiology. 2016;27(3):365–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Richardson DB, Keil A, Tchetgen Tchetgen EJ, Cooper GS. Negative control outcomes and the analysis of standardized mortality ratios. In: Epidemiology. 2015;26(5):727–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Richardson DB, Laurier D, Schubauer-Berigan MK, Tchetgen Tchetgen EJ, Cole SR. Assessment and indirect adjustment for confounding by smoking in cohort studies using relative hazards models. In: Am J Epidemiol. 2014;180(9):933–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Tchetgen Tchetgen EJ, Sofer T, and Richardson D. “Negative outcome control for unobserved confounding under a Cox proportional hazards model”. In: (2015). Available at https://biostats.bepress.com/harvardbiostat/paper192/. [Google Scholar]
- 66.Glynn A, Ichino N. “Generalized nonlinear difference-in-difference-in-differences”. In: V-Dem Working Paper 90 (2019). Available at https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3410888. [Google Scholar]
- 67.Tchetgen ET. The control outcome calibration approach for causal inference with unobserved confounding. In: Am J Epidemiol. 2014;179(5):633–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Gagnon-Bartsch JA, Speed TP. Using control genes to correct for unwanted variation in microarray data. In: Biostatistics. 2012;13(3): 539–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Jacob L, Gagnon-Bartsch JA, Speed TP. Correcting gene expression data when neither the unwanted variation nor the factor of interest are observed. In: Biostatistics. 2016;17(1): 16–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Wang J, Zhao Q, Hastie T, Owen AB. Confounder adjust- ment in multiple hypothesis testing. In: Ann Stat. 2017;45.5:1863–94• This paper unifies unmeasured confounding adjustment methods in multiple hypothesis testing and provides theoretical guarantees for these methods.
- 71.Newey WK, Powell JL. Instrumental variable estimation of nonpara- metric models. In: Econometrica. 2003;71(5):1565–78. [Google Scholar]
- 72.Hansen LP. Large sample properties of generalized method of moments estimators. In: Econometrica. 1982:1029–54. [Google Scholar]