Abstract
BACKGROUND AND PURPOSE: Hemodynamics is often recognized as one of the major factors in aneurysm rupture. Flow impingement, greater pressure, and abnormal wall shear stress are all indications for aneurysm rupture. Characterizing wall shear stress for intracranial aneurysms at similar anatomic locations may help in understanding its role.
MATERIALS AND METHODS: Twenty-six intracranial aneurysms at the paraclinoid and superclinoid segments of the internal carotid artery from 25 patients between July 2006 and July 2007 were studied retrospectively. Among them, 8 aneurysms were ruptured and 18 were unruptured. Computational fluid dynamics was used to determine the wall shear distribution. Morphologic and hemodynamic variables was analyzed by using the Mann-Whitney rank sum test.
RESULTS: Wall shear stress was qualitatively the same throughout the cardiac cycle; thus, only wall shear stress at the end of diastole was compared. Both ruptured and unruptured aneurysms have similar maximal wall shear stress (26 versus 23 N/m2), and mean wall shear stress is shown to be a function of the aneurysm area. Ruptured aneurysms also have a greater portion of aneurysm under low wall shear stress (27% versus 11% for unruptured aneurysms, P = .03).
CONCLUSION: For intracranial aneurysms at the internal carotid artery, an area of low wall shear is associated with aneurysm rupture.
Hemodynamics is recognized as one of the many factors responsible for aneurysm rupture.1 Many hemodynamic variables, including flow pattern and wall shear stress, are hypothesized to be the causes.2,3 Intra-aneurysmal flow results in complex flow structure and different flow impinging sites, some at the ostium and some at the dome.3,4 This complex flow yields a variable wall shear stress distribution on the aneurysm wall. Because wall shear stress regulates endothelial functions,5,6 understanding of wall shear distribution on the aneurysm wall becomes very important.
Recent development of numerical tools has enabled us to study hemodynamics in realistic patient aneurysm geometries.3,7 Studies based on patient-specific aneurysm models are benefited greatly by advanced 3D angiography because 3D images capture detailed anatomic features that are often neglected in idealized geometry.7-9 Fine anatomic details render a different flow structure, and these studies have improved our knowledge of the influence of aneurysm morphology on intra-aneurysmal flow.10 Studying aneurysms at similar anatomic locations allows us to focus on intra-aneurysmal flow, wall shear stress, and aneurysm behaviors. Therefore, we studied the wall shear stress distribution on 26 intracranial aneurysms at the paraclinoid and superclinoid segments of the internal carotid artery and examined the role of hemodynamic variables.
Materials and Methods
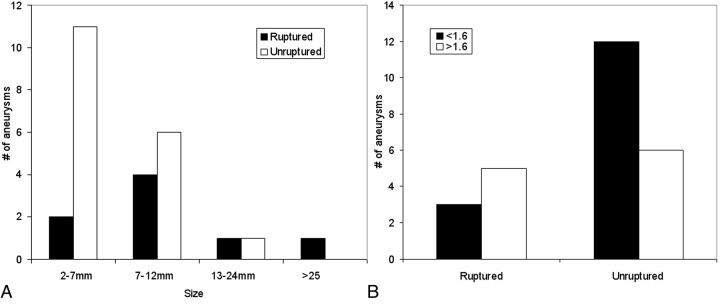
All intracranial aneurysms at the paraclinoid and superclinoid segments of the internal carotid artery available on our archived data base, dated between July 2006 and July 2007, were reviewed. Because of the requirement of 3D images, 26 aneurysms from 25 patients were identified after review. Patients whose 3D digital subtraction angiography images were available were studied retrospectively. Of these aneurysms, 8 were ruptured and 18 were unruptured, with their sizes ranging from 5 to 25 mm for ruptured and from 3 to 11 mm for unruptured aneurysms. Distributions of their sizes and aspect ratios are shown in Fig 1. These patients were examined at our hospital for possible neurovascular diseases or were imaged during endovascular treatment. One of them had bilateral aneurysms. All patients were imaged with 3D rotational angiography (Axiom Artis dBA; Siemens Medical Solutions, Erlangen, Germany) at a 0.4-mm isotropic resolution.11 Inclusion of these patients was based solely on the location of aneurysms and the availability of 3D images. Nevertheless, only 1 patient was male.
Fig 1.
Size (A) and aspect ratio (B) distributions of aneurysms
Image segmentation and construction of an aneurysm model were based on the technique that was reported previously.12 Computational meshes defining vessel boundary were generated from 3D rotational angiography, and flow field within the lumen was solved by using a commercial computational fluid-dynamics package (FLUENT 6.2; ANSYS, Lebanon, NH). The solution was tested for grid independence, and an average final mesh for an aneurysm model had 4 million cells. The inlet flow rate was specified at the cervical segment of the internal carotid artery, far away from the aneurysm, so the flow within the aneurysm was not sensitive to the inflow boundary condition.13,14 The same cardiac waveform was applied at the entrance of the internal carotid artery for every aneurysm case, but only the results at the end of diastole were used for comparisons. These results represented the hemodynamic behaviors of these aneurysms at the same physiologic flow condition (2.6 mL/s).15 Analyses were done blindly, without knowing the outcome of aneurysms until all analyses were completed.
The wall shear at each branch was assumed to be the same on the basis of the principle of optimal work,16 so the mass flow rate through each artery was proportional to the cube of its diameter. The mass flow rate at each branch could then be determined from its size. In simulations, flow-rate ratios (percentage of total mass flow rate) were given as the boundary conditions. Depending on the number and size of the branches that were constructed, different flow-rate ratios were used for each case. These flow-rate ratios were enforced throughout the cardiac cycle. The flow rates at these vessels were varied to test further the sensitivity of intra-aneurysmal flow to these branches.
Including all small branches presented a technical challenge because of their small size, image resolution, and the limitations of computer hardware. Most branches were removed from the aneurysm model unless they were close to the ostium or came out from the aneurysm directly. On average, the middle cerebral artery in our study was 2.7 mm in diameter, the anterior cerebral artery, 2.3 mm; and the ophthalmic artery, 1.1 mm. The diameter of the posterior communicating artery was 1.0 mm, and the superior hypophyseal and anterior choroidal arteries were even smaller. If there was an equal wall shear at these vessels, the middle cerebral artery would receive approximately 56% of the total flow rate; the anterior cerebral artery, 35%; the ophthalmic artery, 4%; and other small branches, <1%–3%. Seven of these aneurysms were selected to study the influence of these small branches.
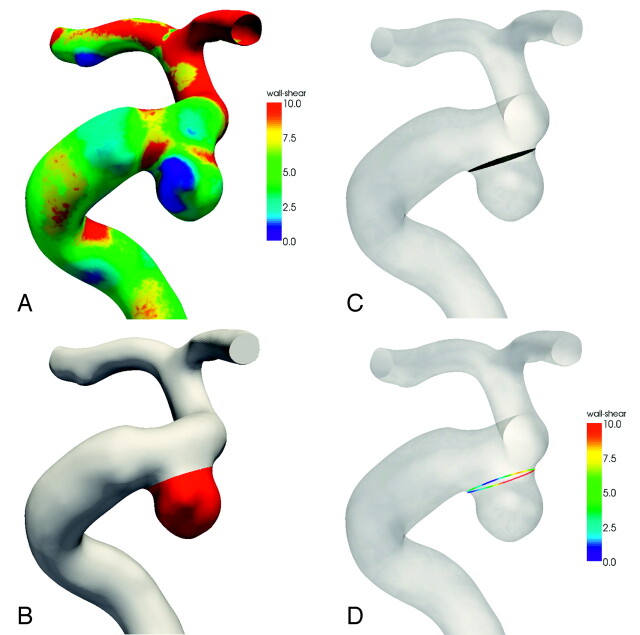
Morphologic and hemodynamic variables were measured on the images and on the aneurysm models. Because these models are 3D, areas of the aneurysm and ostium were also measured. An example of how these variables were calculated is shown in Fig 2.
Fig 2.
An example of how hemodynamic parameters are computed. A, Wall shear stress distribution. Wall shear stress is in newtons per square meter. Maximum wall shear is determined from the entire aneurysm region and is not limited to the ostium. B, Aneurysm surface is defined, and mean wall shear stress is the average of the wall shear over the entire aneurysm surface. C, The ostium is determined by a plane between the aneurysm and the parent artery, and the ostium area is calculated from the shaded region. D, The mean ostium shear is calculated from the average of wall shear around the circumference of the ostium. A similar procedure is used to determine the average wall shear for the parent artery. A variable wall shear stress is often found at the ostium.
Variations in the wall shear at the artery and aneurysm might arise from the differences in artery and aneurysm sizes. Thus, the mean wall shear at the anterior genu of the carotid siphon (averaged over the entire circumference of the carotid artery) was used as a reference. This wall shear value defined the normal level of wall shear and is reported as arterial wall shear in Table 1. Wall shear at the aneurysm was compared against this reference to determine whether the wall shear was normal. Abnormal wall shear was defined as <10% of this reference wall shear. The area of the aneurysm that had abnormal wall shear is reported as the low wall shear area in Table 1. The Mann-Whitney rank sum test was used to evaluate the statistical significance of each variable. A P value < .05 was considered significant.
Table 1:
Morphologic and hemodynamic variables for the ruptured and unruptured aneurysms*
| Ruptured (n = 8) | Unruptured (n = 18) | P Value | |
|---|---|---|---|
| Age (yr) | 60 ± 17 | 55 ± 12 | .31 |
| Artery size (mm) | 4.7 ± 0.7 | 4.7 ± 0.4 | .60 |
| Aneurysm size (mm) | 11.0 ± 6.9 | 6.9 ± 3.3 | .09 |
| Ostium size (mm) | 4.1 ± 1.1 | 4.1 ± 1.2 | .60 |
| Aspect ratio | 2.0 ± 0.9 | 1.5 ± 0.8 | .19 |
| Area at aneurysm (mm2) | 256 ± 351 | 124 ± 110 | .37 |
| Ostium area (mm2) | 18 ± 8 | 19 ± 11 | .85 |
| Mean shear at artery (N/m2) | 4.0 ± 1.8 | 4.5 ± 2.1 | .57 |
| Mean shear at aneurysm (N/m2) | 1.9 ± 1.1 | 2.6 ± 1.9 | .50 |
| Mean shear at ostium (N/m2) | 5.7 ± 4.3 | 5.5 ± 3.2 | .99 |
| Aneurysm shear/arterial shear (%) | 48 ± 33 | 59 ± 33 | .26 |
| Maximal wall shear (N/m2) | 26 ± 15 | 23 ± 12 | .80 |
| Low wall shear area (mm2) | 128 ± 290 | 22 ± 44 | .04 |
| Ratio of low shear area (%) (low shear area/dome area) | 27 ± 25 | 11 ± 17 | .03 |
Numbers are presented as mean ± SD. The Mann-Whitney rank sum test is used for statistical analysis. A P value < .05 is deemed statistically significant.
Results
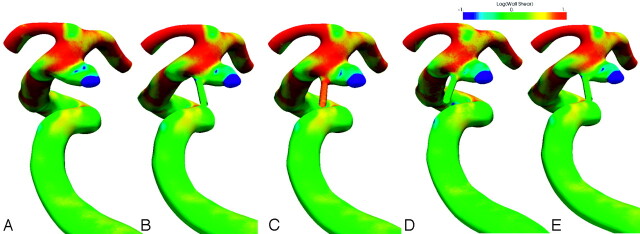
Seven aneurysms with small arteries were first studied to justify the validity of exclusion of small branches and the choice of diastolic shear for wall shear comparison. Figure 3 shows the wall shear distribution for a ruptured anterior choroidal aneurysm under various conditions. The anterior choroidal artery can be seen at the proximal ostium of the aneurysm and is extended further for simulation. Figure 3A shows the wall shear distribution for the case with the anterior choroidal artery excluded. In Fig 3B, the anterior choroidal artery receives 1% of the total flow rate from the internal carotid artery. The flow-rate ratio is increased to 5% in Fig 3C. Figure 3D and E show the wall shear distributions at systole and diastole, respectively. All the wall shear stresses were scaled so that the arterial wall shears were the same. A logarithmic scale was used to demonstrate the level of wall shear changes at these conditions. Despite their subtle differences, the wall shear distribution after scaling varies little in these conditions. The low wall shear area remains at the dome and does not change significantly in size, even though the flow rate increases 3 times from diastole to systole.
Fig 3.
Wall shear distribution for a ruptured anterior choroidal aneurysm. A, Exclusion of the anterior choroidal artery. B, One percent of the flow rate through the anterior choroidal artery. C–E, Five percent of the flow rate through the anterior choroidal artery (C), at systole (D) and at diastole (E). All wall shears are scaled so that the mean arterial wall shears are the same for all cases. Wall shear is on a logarithmic scale.
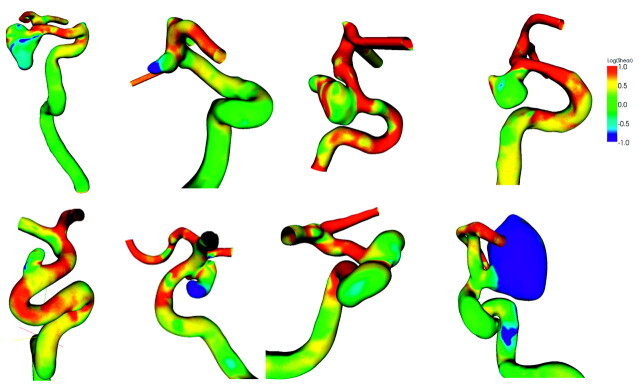
Distributions of wall shear at diastole for ruptured and unruptured aneurysms are shown in Figs 4 and 5, respectively. Wall shear stresses at these aneurysms are shown in a logarithmic scale. Green indicates a normal level of wall shear stress at 1 Pa or 1 N/m2, whereas red is for shear stress >10 N/m2 and blue is for <0.1 N/m2. Most unruptured aneurysms have regular shapes, whereas the shapes of ruptured aneurysms tend to be irregular. The branches distal to the aneurysms, the anterior and middle cerebral arteries, often have higher wall shear stresses than the aneurysms, mostly because of their smaller size. The low wall shear stress region occurs at the proximal aneurysm wall, locates at the dome, or occupies the entire aneurysm; the high wall shear stress region often, but not always, occurs at the distal ostium.
Fig 4.
The wall shear stress distribution for 8 ruptured intracranial carotid aneurysms. The color is coded on a logarithmic scale.
Fig 5.
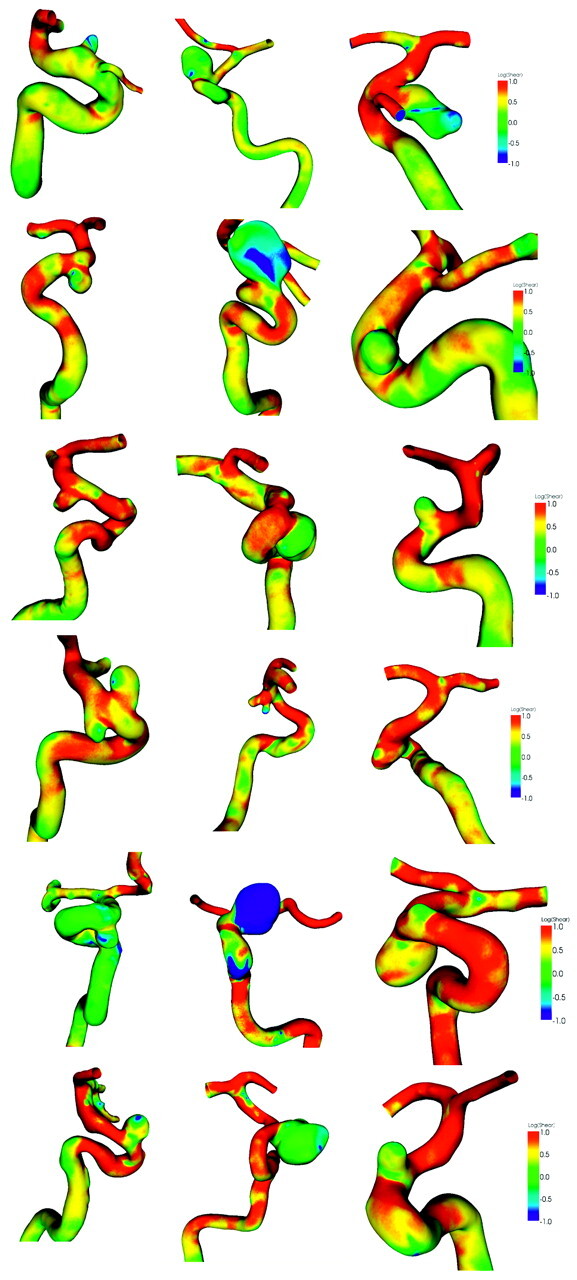
The wall shear stress distribution for 18 unruptured intracranial carotid aneurysms. The color is coded on a logarithmic scale.
Table 1 is a comparison of morphologic and hemodynamic variables between ruptured and unruptured aneurysms. These 2 groups have very similar age distributions (60 versus 55 years) and the same artery size near the aneurysm (4.7 mm). In addition, the wall shear stresses at the artery are also comparable: 4.0 N/m2 for the ruptured and 4.5 N/m2 for the unruptured aneurysms at diastole. The mean wall shear on the aneurysm is 1.9 N/m2 for ruptured aneurysms and 2.6 N/m2 for unruptured aneurysms, but their difference is not statistically significant.
The maximal wall shear stress is 26 N/m2 for ruptured aneurysms and 23 N/m2 for unruptured aneurysms. Because low wall shear cannot be quantified by its magnitude, the area of aneurysm surface subject to low wall shear stress is used. A threshold (0.4 N/m2) is chosen as 10% of the mean arterial shear, which is 4 N/m2 from Table 1. The difference in the low wall shear area between ruptured and unruptured aneurysms is statistically significant (128 mm2 versus 22 mm2, P = .04), and so is the percentage of aneurysm under this low wall shear (27% versus 11%, P = .03).
Comparisons between aneurysms originating from the ophthalmic and posterior communicating arteries are shown in Table 2. There is no statistical difference between aneurysms originating from these 2 arteries. Aneurysms originating from arteries other than these 2 arteries also do not show any difference.
Table 2:
Morphologic and hemodynamic variables and the origin of aneurysms*
| Oph (n = 9) | PcomA (n = 8) | P Value | |
|---|---|---|---|
| Age (yr) | 56 ± 18 | 63 ± 14 | .98 |
| Artery size (mm) | 4.4 ± 0.7 | 4.2 ± 0.8 | .56 |
| Aneurysm size (mm) | 8.0 ± 3.3 | 10.2 ± 7.3 | .74 |
| Ostium size (mm) | 4.4 ± 1.5 | 3.6 ± 1.1 | .32 |
| Aspect ratio | 1.7 ± 1.0 | 2.1 ± 0.9 | .94 |
| Dome area at aneurysm (mm2) | 133 ± 125 | 259 ± 350 | .96 |
| Ostium area (mm2) | 21 ± 14 | 17 ± 9 | .84 |
| Mean shear at artery (N/m2) | 4.0 ± 1.3 | 4.3 ± 2.1 | .81 |
| Mean shear at aneurysm (N/m2) | 2.2 ± 1.9 | 2.2 ± 1.4 | .99 |
| Mean shear at ostium (N/m2) | 4.7 ± 2.3 | 6.7 ± 4.8 | .89 |
| Aneurysm shear/arterial shear (%) | 49 ± 30 | 61 ± 21 | .89 |
| Maximal wall shear (N/m2) | 25 ± 10 | 25 ± 16 | .89 |
| Low wall shear area (mm2) | 30 ± 55 | 133 ± 288 | .61 |
| Ratio of low shear area (%) (low shear area/dome area) | 14 ± 20 | 30 ± 24 | .32 |
Note:—Oph indicates ophthalmic artery; PcomA, posterior communicating artery.
Numbers are presented as mean ± SD. The Mann-Whitney rank sum test is used for statistical analysis. A P value < .05 is deemed statistically significant.
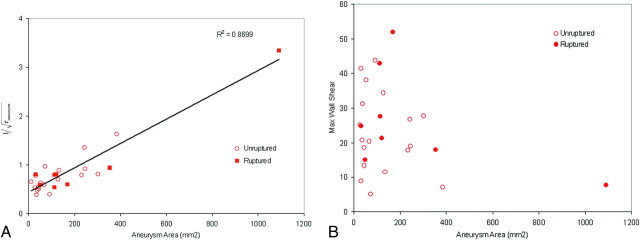
Figure 6A, -B show the mean and maximal aneurysmal wall shear at diastole versus the aneurysm area, respectively. The mean aneurysmal wall shear appears to be a function of the aneurysm area. In Fig 6A,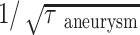 
is used for the y-axis where τ is the mean wall shear for the aneurysm. Use of this new variable allows better appreciation of a linear relationship between the mean wall shear and the aneurysm area in the figure. The mean wall shear decreases with an increase of aneurysm area, implying that larger aneurysms have lower mean wall shear stresses; however, the maximal wall shear is not related to the size of the aneurysm in Fig 6B. From the figure, we find that when there are no aneurysms, τ = 5.27 N/m2, which is the average shear at the ostium. When the aneurysm area equals to the size of ostium, τ = 4.32 N/m2, the arterial wall shear stress.
Fig 6.
Mean wall shear (A) and maximal wall shear (B) at diastole versus the aneurysm surface area. The wall shear stress is in newtons per square meter. τ indicates wall shear; Max, maximal.
Discussion
Twenty-six intracranial aneurysms at the internal carotid artery were examined retrospectively in this study. Several morphologic and hemodynamic variables were compared. No morphologic variables reached a level of statistical significance (P < .05), but ruptured aneurysms were found to have greater aneurysm areas under low wall shear (128 versus 22 mm2) and higher percentages of aneurysm area under low wall shear (27% versus 11%) than unruptured aneurysms. Both results are statistically significant.
Ruptured aneurysms are larger than unruptured aneurysms (11 versus 7 mm),17,18 but their average sizes are comparable when the giant aneurysm is excluded. There is a large overlap in the size distribution between the ruptured and unruptured aneurysms, and characterizing rupture risk poses a great challenge for clinicians, especially for aneurysms falling into this overlapped region. This gray area includes aneurysm size between 4 and 10 mm, which amounts to 60% of unruptured aneurysms in 1 study.19
Aneurysm size influences the wall shear stress on the aneurysm. Our results show that the mean wall shear stress is related to the aneurysm area, and both ruptured and unruptured aneurysms have similar maximal wall shears at the same flow rate. Larger aneurysms have lower mean wall shears, but the maximal wall shear stress is independent of the aneurysm size. Average maximal wall shears at the ostium are comparable for ruptured and unruptured aneurysms (26 versus 23 N/m2).
The size and tapering of the internal carotid artery may influence the wall shear stress, rendering greater wall shear for small arteries and lower wall shear for large arteries. Thus, a reference wall shear stress at the internal carotid artery is needed so that wall shears at different aneurysms can be compared. The anterior genu of the carotid siphon is selected for easy identification of its location and close proximity to these aneurysms. Wall shear stress at this location is independent of the size of the carotid artery and conditions of the aneurysm (4.0 N/m2 for the ruptured and 4.5 N/m2 for the unruptured aneurysms). The mean wall shear on the aneurysm is smaller than the wall shear at the parent artery: 48% of arterial shear on ruptured aneurysms and 59% for unruptured aneurysms. A previous study has shown that the wall shear stress was 3.6 N/m2 at the middle cerebral artery and 1.6 N/m2 for the middle cerebral artery aneurysms.9 Both studies show that the mean aneurysmal shear is approximately half of the mean wall shear at neighboring arteries.
High wall shear stress is often localized at the region where the blood enters an aneurysm, whereas the remaining aneurysm area has relatively lower wall shear stress. Maximal wall shear is also sensitive to the flow rate, waveform, heart rate, and the ostium geometry and curvature. Because resolving ostium geometry fully requires high image resolution, an analysis based solely on the level of maximal wall shear may suffer from insufficient image resolution or unresolved aneurysm ostium. In addition, a theory based on local high wall shear stress ignores aneurysm morphology away from the ostium, and the location of high wall shear is often different from the place where most aneurysms rupture. In our study, ruptured and unruptured aneurysms had similar maximal wall shears, so hemodynamic factors other than the maximal shear stress play an equally important role in aneurysm rupture.
This is a retrospective study on the wall shear stress distribution of ruptured and unruptured intracranial aneurysms at the internal carotid artery. Intra-aneurysmal flow and wall shear stress are dependent on the aneurysm geometry and neighboring vessels.10 This is why only aneurysms within a short section of the internal carotid artery are studied. A small sample size is a limitation of our study, and bias in patient selection might exist. Because of a lower rupture risk for intracranial aneurysms at the internal carotid artery,20 only a small number of aneurysms ruptured; however, these ruptured aneurysms had a reasonable size distribution.
Giant aneurysms at this location are uncommon; thus, they are not well represented in our cohort. There was only 1 aneurysm >25 mm, and this may have influenced the trend between the mean wall shear and aneurysm area in Fig 6A. Nevertheless, most aneurysms are in a small size range except the giant aneurysm, making the linear relationship harder to appreciate. The Mann-Whitney test is a rank sum test, not a median test; therefore, the statistical test was not biased by a single giant aneurysm. The ratio of low wall shear area to the total aneurysm area is a measure of the extent of the aneurysm under low wall shear stress and is also not influenced by the aneurysm size. The difference between ruptured and unruptured aneurysms is still significant, even if the giant aneurysm is excluded.
We have assumed in our hemodynamic analysis that the flow is laminar; the blood, Newtonian; and the vessel wall, rigid. Realistic conditions may differ from these assumptions; however, they provide a reasonable estimate of the hemodynamic conditions within aneurysms. Every hemodynamic variable in this study was evaluated at diastole, including the low wall shear area, mean wall shear, and maximal wall shear. The flow rate of the internal carotid artery at that instant was 2.6 mL/s, comparable to the end-diastolic flow rate of Marshall et al.15 There is a large variation in the flow rate at the internal carotid artery,21 but the older and female populations, the prevalent population for intracranial aneurysms, have lower flow rates.22 Pulsatility may play a role in aneurysm development, but it is unclear how the pulsatility should be evaluated. There is also a wide variation in flow waveform and heart rate among individuals21; thus, diastole was selected for its relatively constant flow rate and longer duration in the cardiac cycle.12 Figure 3 shows the difference in wall shear at various conditions. The area exposed to low wall shear remains similar in size at all times. Subtle differences can still be observed in Fig 3, but these differences are much smaller than the differences exhibited among the aneurysms in Figs 4 and 5. The morphology of an aneurysm apparently dictates the characteristics of wall shear distribution, but physiologic conditions, such as flow rate and waveform, determine the level of wall shear to which an aneurysm is exposed. Therefore, if the low wall shear area is measured in a consistent way, the choice of a single time point will not limit the application of our results.
One can gain more knowledge by studying a group of aneurysms at similar anatomic locations. Orientation of an aneurysm subjects the aneurysm to different hemodynamics. Ophthalmic aneurysms have smaller low wall shear areas than the posterior communicating aneurysms in Table 2; however, no significant difference was found between aneurysms at these 2 different anatomic locations. We have also simplified our models by trimming small branches near the aneurysm. These small arteries introduce higher wall shear locally and divert part of flow rate through these branches. Seven of these aneurysm models were studied for this effect. Their effects are shown to be localized and do not affect the wall shear at the aneurysm.
The results of our study apply only to intracranial aneurysms at specific segments of the internal carotid artery. Aneurysms at other anatomic locations may have a different natural history and rupture risk19,23 and behave differently.24,25 However, the trend shown in the current study may shed light on how other aneurysms behave.
Conclusions
For intracranial aneurysms at the internal carotid artery under the same flow rate, mean wall shear stress is determined by the aneurysm size. Ruptured aneurysms have a greater area under low wall shear stress than unruptured aneurysms, and their difference is statistically significant.
References
- 1.Hashimoto T, Meng H, Young WL. Intracranial aneurysm: link among inflammation, hemodynamics and vascular remodeling. Neurol Res 2006;28:372–80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ma B, Harbaugh RE, Raghavan ML. Three-dimensional geometrical characterization of cerebral aneurysms. Ann Biomed Eng 2004;32:264–73 [DOI] [PubMed] [Google Scholar]
- 3.Cebral JR, Castro MA, Burgess JE, et al. Characterization of cerebral aneurysms for assessing risk of rupture by using patient-specific computational hemodynamics models. AJNR Am J Neuroradiol 2005;26:2550–59 [PMC free article] [PubMed] [Google Scholar]
- 4.Shojima M, Oshima M, Takagi K, et al. Role of the bloodstream impacting force and the local pressure elevation in the rupture of cerebral aneurysms. Stroke 2005;36:1933–38. Epub 2005 Aug 4 [DOI] [PubMed] [Google Scholar]
- 5.Davis PF, Tripathi SC. Mechanical stress mechanisms and the cell: an endothelial paradigm. Circ Res 1993;72:239–45 [DOI] [PubMed] [Google Scholar]
- 6.Li Y-SJ, Gaga JH, Chien S. Molecular basis of the effects of shear stress on vascular endothelial cells. J Biomech 2005;38:1949–71 [DOI] [PubMed] [Google Scholar]
- 7.Steinman D, Miller J, Norley C, et al. Image-based computational simulation of flow dynamics in a giant intracranial aneurysm. AJNR Am J Neuroradiol 2003;24:559–64 [PMC free article] [PubMed] [Google Scholar]
- 8.Jou L, Quick C, Young W, et al. Computational approach to quantifying hemodynamic forces in giant cerebral aneurysms. AJNR Am J Neuroradiol 2003;24:1804–10 [PMC free article] [PubMed] [Google Scholar]
- 9.Shojima M, Oshima M, takagi K, et al. Magnitude and role of wall shear stress on cerebral aneurysm: computational fluid dynamics study of 20 middle cerebral artery aneurysms. Stroke 2004;35:2500–05 [DOI] [PubMed] [Google Scholar]
- 10.Castro MA, Putman CM, Cebral JR. Patient-specific computational fluid dynamics modeling of anterior communicating artery aneurysms: a study of the sensitivity of intra-aneurysmal flow patterns to flow conditions in the carotid arteries. AJNR Am J Neuroradiol 2006;27:2061–68 [PMC free article] [PubMed] [Google Scholar]
- 11.Heran NS, Song JK, Namba K, et al. The utility of DynaCT in neuroendovascular procedures. AJNR Am J Neuroradiol 2006;27:330–32 [PMC free article] [PubMed] [Google Scholar]
- 12.Jou LD, Wong G, Dispensa B, et al. Correlation between lumenal geometry changes and hemodynamics in fusiform intracranial aneurysms. AJNR Am J Neuroradiol 2005;26:2357–63 [PMC free article] [PubMed] [Google Scholar]
- 13.Venugopal P, Valentino D, Schmitt H, et al. Sensitivity of patient-specific numerical simulation of cerebral aneurysm hemodynamics to inflow boundary conditions. J Neurosurg 2007;106:1051–60 [DOI] [PubMed] [Google Scholar]
- 14.Moyle KR, Antiga L, Steinman DA. Inlet conditions for image-based CFD models of the carotid bifurcation: is it reasonable to assume fully developed flow? J Biomech Eng 2006;128:371–79 [DOI] [PubMed] [Google Scholar]
- 15.Marshall I, Papathanasopoulou P, Wartolowska K. Carotid flow rates and flow division at the bifurcation in healthy volunteers. Physiol Meas 2004;25:691–97 [DOI] [PubMed] [Google Scholar]
- 16.Oka S, Nakai M. Optimality principle in vascular bifurcation. Biorheology 1987;24:737–51 [DOI] [PubMed] [Google Scholar]
- 17.McCormick WF, Acosta-Rua GJ. The size of intrancranial aneurysms: an autopsy study. J Neurosurg 1970;33:422–27 [DOI] [PubMed] [Google Scholar]
- 18.Beck J, Rohde S, Berkefeld J, et al. Size and location of ruptured and unruptured intracranial aneurysms measured by 3-dimensional rotational angiography. Surg Neurol 2006;65:18–25 [DOI] [PubMed] [Google Scholar]
- 19.Weir B, Disney L, Karrison T. Sizes of ruptured and unruptured aneurysms in relation to their sites and the ages of patients. J Neurosurg 2002;96:64–70 [DOI] [PubMed] [Google Scholar]
- 20.Clarke G, Mendelow AD, Mitchell P. Predicting the risk of rupture of intracranial aneurysms based on anatomical location. Acta Neurochir (Wien) 2005;147:259–63 [DOI] [PubMed] [Google Scholar]
- 21.Ford MD, Alperin N, Lee SH, et al. Characterization of volumetric flow rate waveforms in the normal internal carotid and vertebral arteries. Physiol Meas 2005;26:477–88 [DOI] [PubMed] [Google Scholar]
- 22.Zhao M, Amin-Hanjani S, Ruland S, et al. Regional cerebral blood flow using quantitative MR angiography. AJNR Am J Neuroradiol 2007;28:1470–73 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mira JMS, Costa FA, Horta BL, et al. Risk of rupture in unruptured anterior communicating artery aneurysms: meta-analysis of natural history studies. Surg Neurol 2006;66 (suppl 3):S12–19 [DOI] [PubMed] [Google Scholar]
- 24.Kerber CW, Imbesi SG, Knox K. Fluid dynamics in a lethal anterior communicating artery aneurysm. AJNR Am J Neuroradiol 1999;20:2000–03 [PMC free article] [PubMed] [Google Scholar]
- 25.Forget TR, Benitez R, Veznedaroglu E, et al. A review of size and location of ruptured intracranial aneurysms. Neurosurgery 2001;49:1322–26 [DOI] [PubMed] [Google Scholar]