Diffusion Tensor MR Imaging of the Neurologically Intact Human Spinal Cord

Abstract

BACKGROUND AND PURPOSE: The aim of this study was to characterize the diffusion properties of the entire human spinal cord in vivo. These data are essential for comparisons to pathologic conditions as well as for comparisons of different pulse sequence design parameters aimed to reduce scan time and more accurately determine diffusion coefficients.

MATERIALS AND METHODS: A total of 13 neurologically intact subjects were enrolled in this study. A single-shot, twice-refocused, spin-echo, diffusion-weighted, echo-planar imaging (EPI) pulse sequence was used to obtain axial images throughout the entire spinal cord (C1–L1) in 45 minutes.

RESULTS: Diffusion images indicated slight geometric distortions; however, gray and white matter contrast was observed. All measurements varied across the length of the cord. Whole cord diffusion coefficients averaged 0.5–1.3 × 10⁻³ mm²/s depending on orientation, mean diffusivity (MD) averaged 0.83 ± 0.06 × 10⁻³ mm²/s, fractional anisotropy (FA) averaged 0.49 ± 0.05, and volume ratio (VR) averaged 0.73 ± 0.05.

CONCLUSION: This study provided normative diffusion values for the entire spinal cord for use in comparisons with pathologic conditions as well as improvements in pulse sequence design.

Despite the potential of diffusion tensor imaging (DTI) for providing anatomic and histologic information about the spinal cord, DTI is not yet routinely performed for identifying and characterizing pathologic changes. One important limitation to the application of DTI to spinal cord pathologic disorders is the absence of normative data for comparison. For example, diffusion changes in the spinal cord have been reported after spinal artery stroke,¹ multiple sclerosis,² cervical spondylotic myelopathy,³ spinal cord compression,⁴ acute spinal cord injury,⁵ and chronic spinal cord injury,^6,7 yet detailed baseline data with use of common imaging sequences are lacking for comparison. Some diffusion measurements have been documented in targeted regions of the neurologically intact human spinal cord,^8–12 and these values have been used for comparison to pathologic conditions; however, a comprehensive study of diffusion parameters throughout the entire spinal cord has not been reported. As a result, the primary purpose of this study was to characterize the normative diffusion values of the entire human spinal cord with use of a clinically available pulse sequence for comparison with pathologic conditions and new pulse sequence designs.

Current DTI research in the human spinal cord is primarily devoted to the development of pulse sequences aimed at obtaining artifact-free diffusion measurements. Single-shot echo-planar imaging (EPI) is relatively fast but is typically not used in the spinal cord because of the small size of the cord and the perceived risk for susceptibility-related distortions. Unfortunately, the main alternative to EPI, pulsed-gradient, spin-echo DTI, is highly sensitive to motion and has very long imaging times, requiring approximately 15 minutes to image a single diffusion axis.⁹ A few pulse sequences focus on a compromise between these 2 methods, including line scan diffusion imaging,¹³ multishot echo-planar imaging,¹⁰ and fast single-shot EPI with use of sensitivitiy encoding (SENSE).¹⁴ Although these new techniques have established a reputation for accurate diffusion measurements with minimal artifacts, they typically have low signal-to-noise ratio (SNR). A novel technique, presented by Bammer et al,^12,15 uses a phase-navigated interleaved EPI method to overcome SNR challenges; however, the technique is currently not available on MR scanners and thus has limited clinical usefulness.

In contrast to recently developed DTI pulse sequences, single-shot EPI is widely available on clinical MR scanners; thus, diffusion-tensor (DT) EPI could serve as a standard for comparison of new pulse sequences. Previous studies involving single-shot DT EPI of the spinal cord have demonstrated its usefulness in estimating diffusion parameters within the spinal cord,^1,4,11,16 though a systematic study of the entire spinal cord has not been conducted. To establish baseline diffusion parameters for comparing new DTI sequences, we aimed to measure the DTI parameters and SNR of the entire spinal cord by using a single-shot, twice-refocused, spin-echo EPI diffusion sequence¹⁷ in the axial plane, with no respiratory or cardiac gating to image the entire spinal cord (C1–L1). We then compared the diffusion parameters from this DT EPI sequence with reported diffusion measurements that were obtained with a variety of recently developed pulse sequences to determine the agreement in diffusion parameters.

Thus, the primary aim of this study was to characterize the diffusion properties of the human spinal cord in vivo with a single-shot DT EPI sequence to establish a baseline for clinicians to compare with measurements made in pathologic conditions. The secondary goal was to characterize the diffusion measurements from the current literature and determine if differences exist in mean diffusion characteristics across various pulse sequences and imaging platforms.

Materials and Methods

Subjects

Thirteen neurologically intact subjects (6 men and 7 women) between the ages of 19 and 40 years old (median age, 25 years) participated in the study. The number of subjects was chosen on the basis of a power analysis¹⁸ of average fractional anisotropy (FA) values with use of β = 0.9, α = 0.05, SD in FA of 0.1, and an effect size of 0.1 for comparisons. Subjects had no history of neurologic illness and were free from medical implants. We obtained informed consent before enrolling subjects. All procedures complied with the principles of the Declaration of Helsinki and were approved by the Institutional Review Boards of Marquette University and the Medical College of Wisconsin.

MR Imaging

We obtained axial DTI throughout the entire spinal cord (C1–L1) by using a standard single-shot, twice-refocused, spin-echo EPI pulse sequence.¹⁷ A CTL spine coil (GE Medical Systems, Milwaukee, Wis) and 1.5T clinical MR scanner (Signa Excite; GE Medical Systems) were used for all image acquisitions. We determined spinal levels using anatomic landmarks from sagittal fast low-angle shot (FLASH) locator MR images. DT images were acquired nonsequentially with TR, 6000 ms; TE, 96.3 ms; matrix size, 128 × 128; NEX, 1; FOV, 200 mm; section thickness, 5 mm; and no intersection gap (ie, contiguous). After reconstruction, images were zero-padded and interpolated to 256 × 256. Diffusion-weighted images (DWIs) were collected with b = 1500 s/mm², in 25 equidistant directions, and a single T2-weighted image (b = 0) was collected for each axial section.

After imaging, we calculated diffusion parameters and SNR from axial DT images of the spinal cord to identify normative diffusion values. Initially, the Analysis of Functional Neuroimages software (AFNI; available at http://afni.nimh.nih.gov/) was used to perform a Fourier transform-based affine registration of the 25 DWIs to the T2-weighted reference image to correct for bulk motion, eddy current, and susceptibility-related image distortions. AFNI was also used to calculate the 3 × 3 diffusion tensor from the 25 DWIs, and the eigenvalues of the tensor (λ₁, λ₂, λ₃) were identified for each voxel. The mean diffusivity (MD, or average of all 3 eigenvalues) was calculated to characterize the overall diffusion, and fractional anisotropy (FA) and volume ratio (VR)¹⁹ were calculated off-line as measures of diffusion anisotropy for each voxel with use of in-house MATLAB (Mathworks, Natick, Mass) algorithms. In addition, the transverse apparent diffusion coefficient (tADC, or average of the smallest 2 eigenvalues, λ₂ and λ₃) and longitudinal apparent diffusion coefficient (lADC, or largest eigenvalue, λ₁) were calculated to compare with literature values (see below). A total of 108 to 126 axial sections were obtained throughout the entire spinal cord, resulting in a total scan time of approximately 45 ± 10 SD minutes, depending on the height of the subject. Individual subject scan times were determined from the start of the first FLASH locator image to the last DWI image. We calculated T2-weighted SNR for every section in every subject and then averaged across spinal levels for each subject by using the method outlined by Kaufman et al.²⁰ This resulted in 1 SNR distribution per subject per level.

Data Description for Regions of Interest

Manual segmentation of spinal cord regions of interest (ROIs) was performed for the whole cord and for separate identification of gray and white matter regions. First, we manually segmented the spinal cord from the CSF by using the T2-weighted images for a whole cord analysis (ie, no gray and white matter segmentation). ROIs for the whole cord analysis were placed within the spinal cord such that at least 2 voxels around the edge of the cord were excluded to assure no partial volume contamination from the surrounding CSF. Whole cord segmentation may benefit future studies conducted in imaging planes or with use of pulse sequences where gray and white matter differentiation is not possible or may be particularly difficult. For example, gray and white matter differentiation in images collected within the sagittal plane is not typically feasible. Thus, these studies will benefit from diffusion values related to the whole cord instead of diffusion characteristics related to individual ROIs within the cord. In addition, diffusion values and anisotropy indices from the CSF surrounding the cord were collected from each image section.

Manual identification of targeted ROIs within the spinal cord were selected from FA color images of the spinal cord to identify white matter (WM) and gray matter (GM) regions. For GM and WM ROIs, regions were selected within the spinal cord such that at least 2 voxels around the edge of the tissue of interest were excluded to assure no partial volume contamination. This method of segmentation may benefit future studies aimed at characterizing changes in diffusion characteristics within particular regions of the spinal cord. For example, investigators studying motor neuron plasticity after injury to the spinal cord may be interested in changes in GM diffusion properties that result from specific treatments or rehabilitation strategies. Although more targeted ROIs could have been created to represent individual WM spinal tracts, image resolution at 1.5T restricts these tracts to only a few voxels per image and thus are susceptible to partial volume contamination. Also, we did not control for the motion of the spinal cord; therefore, confident estimates of diffusion values within smaller spinal tracts were not feasible.

For the whole cord analysis, histograms of the diffusion characteristics for each spinal level were created to represent the results. Sections in the same transverse plane as intervertebral disks were excluded from analysis to decrease the effects of susceptibility-related distortions.²¹ The remaining sections were pooled to create a single distribution per spinal segment for each subject (approximately 3–5 sections per segment per subject, or a total of approximately 200–600 voxels per segment per subject). Finally, distributions for all subjects were pooled across respective spinal levels. The total number of voxels represented in each diffusion distribution for a particular spinal level reported in this study ranged from approximately 2500 to 5000 voxels.

Group statistics (mean and SD) were then calculated for the diffusion parameters. For each subject, the mean eigenvalues, FA, and VR were calculated for each segment and each ROI (whole cord, WM, GM, and CSF). Then, we calculated the group means and SDs by using the subject means. The data were represented by plotting the values against segmental level.

There is currently no criterion standard for spinal cord segmentation in MR imaging. In our study, we have chosen to use manually defined ROIs, which is the method of choice in most DTI studies of the spinal cord.^{3,8,10,12,14,22} Other methods of segmentation used in DTI analysis of the human spinal cord include thresholding the diffusion or anisotropy images²³ and fuzzy-logic–based tissue classification.^6,24 These methods seem to be sufficient; however, they may differ in their performance if diffusion characteristics change throughout the length of the cord.

To validate the manual segmentation technique, we calculated the percentage of agreement between manual segmentation and the 2 other segmentation techniques. We calculated the percentage agreement for each section by first manually cropping the 256 × 256 images to 128 × 128. Then, segmentation was implemented, and the number of similarly labeled voxels from the 2 techniques was found. The total percentage of agreement was calculated by dividing the number of similarly labeled voxels by the total number of voxels in the cropped image (128 × 128 image = 16,384 voxels). First, we compared manual segmentation of the spinal cord from the CSF with segmentation by using an FA threshold of 0.3, resulting in an average 78% agreement (median, 81%). Second, manual segmentation of the entire spinal cord from the CSF was compared with a fuzzy-logic–based segmentation described elsewhere.²⁴ This comparison resulted in an average of 81% agreement (median, 85%). To compare ROIs within the spinal cord (GM, WM), we compared manual segmentation with fuzzy-logic–based segmentation.²⁴ The percent agreement between these techniques for GM, WM, and CSF averaged 61%, 72%, and 91%, respectively. Because manual segmentation produced agreement in most scenarios, values obtained from manually selected ROIs were used in the statistical analysis.

Statistics

To determine if SNR varied across the length of the spinal cord, we used a one-way repeated-measures analysis of variance (ANOVA) to evaluate differences in SNR across spinal levels (fixed factor: spinal level; random factor: subject). In a similar fashion, each eigenvalue (λ₁, λ₂, λ₃), MD, FA, and VR were evaluated across the length of the spinal cord with use of a one-way repeated-measures ANOVA if the data were normally distributed. If the dataset failed the normality test, a Friedman repeated measures nonparametric ANOVA on ranks was performed. We conducted multiple post hoc comparisons between spinal levels for all measurements by using Tukey tests for multiple comparisons, either in nonparametric or parametric form depending on the ANOVA performed. We conducted post hoc comparisons by using Tukey tests. The level of significance used for all statistical tests was α = 0.05. Minitab 14 software (Minitab, State College, Pa) was used for the statistical analyses.

Comparison With Published Diffusion Characteristics

To address the fundamental question as to whether diffusion characteristics can be generalized across imaging platforms, pulse sequences, and postprocessing algorithms, we identified an estimate of MD across multiple published studies of spinal cord diffusion imaging (see Table for summary). Using data from 13 studies, we estimated signal intensity attenuation by using the diffusion equation:

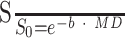Here, (S/S₀) is signal intensity attenuation, b is the diffusion weighting in s/mm², and MD is mean diffusivity in mm²/s. Once an estimate of signal intensity attenuation was calculated from each study, data were plotted as a function of b-value and a regression was used to estimate MD across studies. Many of the diffusion values used in this calculation were averages across the spinal cord, and differences across segmental levels were not reported. Therefore, we did not distinguish between segments when performing the regression analysis, assuming MD is relatively consistent throughout the length of the spinal cord.

Identification numbers (ID), study name/date, and pulse sequence used for studies included in regression analysis (Fig. 4)

ID	Study	Pulse Sequence
1	Ellingson et al, 20067	SS-EPI + Fuzzy logic
2	Robertson et al, 200026	LSDI
3	Cercignani et al, 200314	SENSE-EPI
4	Clark et al, 19999	Nav. echo - SE
5	Murphy et al, 200127	LSDI
6	Mamata et al, 20053	LSDI
7	Holder et al, 200010	Multishot SE-EPI
8	Bammer et al, 200012	Phase nav., IEPI
9	Wheeler-Kingshott et al, 200223	ZOOM-EPI
10	Maier and Mamata, 200528	LSDI
11	Ries et al, 20008	Multishot SE-EPI
12	Bammer et al, 200229	FSE & IEPI
13	Clark et al, 20002	Nav. echo - SE

Note:—SS-EPI indicates single-shot, echo-planar imaging; LSDI, line-scan diffusion imaging; IEPI, interleaved echo-planar imaging; SENSE, sensitivity encoding; SE, spin-echo; FSE, fast spin-echo; ZOOM-EPI, zonally magnified oblique multisection echo-planar imaging; nav., navigator.

Results

FA images of the entire spinal cord showed reasonable gray and white matter contrast and only slight geometric distortion after Fourier transform-based image registration (Fig 1). Voxels on the contour of the spinal cord appeared to be slightly blurred, particularly in the midthoracic regions where the spinal cord has the smallest cross-sectional area.

Fig 1.

FA images across the spinal cord for a representative subject.

The SNR of the T2-weighted images from the 13 subjects varied along the length of the spinal cord with a range of approximately 3 to 9 (mean, 5.7). ANOVA results indicated significant differences between levels (ANOVA: F = 5.723, P < .001). Tukey test for multiple comparisons indicated that the upper cervical segments (C1–C4) had significantly higher SNR (Tukey Test: P < .05) compared with that of the the midthoracic regions (T2–T5).

The diffusion tensor eigenvalues (λ₁, λ₂, λ₃) varied along the length of the spinal cord (Fig 2A–C). Because all 3 eigenvalues failed normality (Anderson-Darling Normality Test; P < .004 for all 3 eigenvalues), the Friedman repeated-measures nonparametric ANOVA on ranks was performed. Results indicated significant differences between spinal levels for all 3 eigenvalues (Friedman ANOVA: P < .001). Multiple comparison tests indicated that the primary eigenvalue, λ₁, was significantly larger (Tukey Test; P < .05) in the cervical regions (C2–C7) compared with the lower thoracolumbar regions (T10–L1). The secondary and tertiary eigenvalues (λ₂ and λ₃), which together make up the transverse apparent diffusion coefficient, were statistically similar across all spinal levels besides L1. The FA magnitude of the whole cord decreased in the rostral to caudal direction, with a range of approximately 0.95 to 0.2 throughout the length of the cord (Fig 2D). The VR demonstrated an inverse relationship to FA, the magnitude of which increased rostral to caudal. Both FA and VR indicated significant differences in anisotropy across spinal level (ANOVA: P < .001), with a significant reduction in anisotropy in the lower thoracolumbar regions (T11–L1) compared with that of the cervical levels (C2–C6) (Tukey Test: P < .05). The MD was relatively consistent throughout the spinal cord with a mean of approximately 0.83 × 10⁻³ mm²/s. Similar to the eigenvalues, MD was significantly higher at L1 compared with the rest of the spinal cord (Tukey Test: P < .05).

Fig 2.

Eigenvalue and anisotropy distributions for the entire spinal cord. A, Primary eigenvalue (λ₁) histogram for control group. Bin frequency is shown as gray-scale level across the entire spinal cord (bin size = 1 × 10⁻⁵ mm²/s). Superimposed on the gray-scale histogram is the group mean and SD (solid black line and error bars). B, Secondary eigenvalue (λ₂) histogram for control group. Bin frequency is shown as a gray-scale level across the entire spinal cord (bin size = 1 × 10⁻⁵ mm²/s). Superimposed on the gray-scale histogram is the group mean and SD (solid black line and error bars). C, Tertiary eigenvalue (λ₃) histogram for the control group. Bin frequency is shown as a gray-scale level across the spinal cord (bin size = 1 × 10⁻⁵ mm²/s). Superimposed on the gray-scale histogram is the group mean and SD (solid black line and error bars). D, Fractional anisotropy histogram for control group. Bin frequency is shown as a gray-scale level across the spinal cord (bin size = 0.01). Superimposed on the gray-scale histogram is the group mean and SD (solid black line and error bars).

Two-way repeated-measures ANOVA results for individual ROIs within the spinal cord indicated significant differences among WM, GM, and CSF for all 3 eigenvalues (ANOVA: P < .001). These data are summarized in Fig 3 for the entire length of the spinal cord. As expected, the eigenvalues of the CSF were larger than those of both spinal WM and GM. Also, secondary and tertiary eigenvalues were significantly larger for GM compared with WM (ANOVA; P < .001), and the primary eigenvalue was significantly smaller for GM compared with WM (ANOVA; P < .001). Measurements of FA in individual ROIs were significantly higher in magnitude for spinal WM (mean, 0.68) compared with spinal GM (mean, 0.47) (ANOVA: P < .001), illustrating the well-documented anisotropic property of WM. The FA of CSF was consistent at approximately 0.15 throughout the length of the spinal cord (Fig 3D).

Fig 3.

Primary eigenvalue, λ₁; secondary eigenvalue, λ₂; and tertiary eigenvalue, λ₃, across the spinal cord for WM regions (A), ventral GM (B), and CSF (C). FA across the spinal cord (D) for individual WM regions, ventral GM, and CSF. Mean values are shown as solid black lines. Error bars indicate SD across subjects.

Comparison With Published Diffusion Characteristics

The estimated signal intensity attenuation was plotted versus diffusion weighting (b-value) for the published values (Fig 4), with results consistent with the expected exponential relationship, despite differences in imaging platform and pulse sequence. The subsequent logarithmic regression resulted in a diffusivity of 0.997 × 10⁻³ mm²/s with R² = 0.842 and P < .001. This value was slightly higher than the MD measured in our study (0.83 × 10⁻³ mm²/s) but within 1 SD of the mean. (The SD of MD in our study was 0.2 × 10⁻³ mm²/s, measured across subjects and across spinal levels.)

Fig 4.

Regression analysis of mean apparent diffusion coefficients from DTI studies of the human spinal cord with use of a variety of pulse sequences. Numbers represent identification numbers and are located in the accompanying table. Results of logarithmic regression are also shown. Solid circle indicates average signal intensity attenuation for this study.

Discussion

The objective of this study was to characterize diffusion properties of the entire noninjured human spinal cord in vivo so that these measurements can be used as a baseline for clinical comparisons with pathologic conditions and new pulse sequence designs. Although previous studies have documented diffusion characteristics of the spinal cord, there has been no comprehensive study, to date, that examines diffusion characteristics throughout the entire spinal cord through sequential axial sections. Furthermore, there has been no known study of SNR across segments of the spinal cord.

According to our results, the SNR was significantly lower in the midthoracic regions compared with that of the cervical segments. The higher SNR in the cervical regions may have been an effect of the anterior part of the CTL spine coil, which only covers the cervical spine and functions specifically to increase the SNR in these regions. Also, the cervical spinal cord contains a larger cross-sectional area of GM compared with thoracic regions; thus, T2-weighted image intensity may have been higher in cervical regions because of a higher T2 of the GM, leading to a higher measure of SNR. This may also be the case in the thoracolumbar regions where SNR was slightly elevated compared with the high thoracic levels.

Results of our study demonstrated that diffusion characteristics are not consistent throughout the spinal cord and are dependent on specific segmental level. Of particular interest is the significant dependence of the λ₁ value and FA on segmental level. The primary eigenvalue (λ₁) represents the longitudinal component of diffusion (rostral-caudal), which we observed to be higher in the cervical segments compared with that of the thoracolumbar regions. Although the precise mechanisms responsible for determining λ₁ are still controversial, Schwartz et al²⁵ demonstrated a high correlation between diameter of the axons and the magnitude of λ₁. Thus, the elevated λ₁ observed in the cervical spinal cord may reflect a higher percentage of large-diameter axons present in the cervical spinal cord compared with that of the thoracolumbar regions.

Similar to the increase in λ₁, we also observed an increase in FA in cervical segments compared with that of the thoracolumbar regions. This increase may have been directly related to the increase in λ₁ observed in almost the same regions. An increase in λ₁ increases FA if the secondary and tertiary eigenvalues are relatively constant, which is consistent with observations in our study. Because FA showed level dependence throughout the length of the spinal cord, thresholding techniques for GM and WM segmentation involving the FA should be avoided unless adjusted to the specific segments or if only used in a few segments.

Diffusion characteristics in targeted regions of the noninjured human spinal cord have been documented with use of several pulse sequences, including line scan diffusion imaging,^3,13,26–28 phase-navigated corrections,^2,9,12,29 multi-shot echo-planar techniques,^8,10 targeted excitation,²³ and parallel imaging.¹⁴ Despite the specific pulse sequence used, mean diffusion measurements are generally similar across studies and to the measurements of MD in our study (Fig 4). Although these reported pulse sequence techniques vary in SNR, scan time, and acquisition methods, they seem to be in general agreement when the overall mean measured diffusion coefficient of the intact human spinal cord are compared. Despite this agreement, however, none of the previous studies have addressed how specific diffusion characteristics in both the whole cord and in ROIs within the spinal cord vary across spinal segments. Also, none of these studies have documented level-dependent SNR within the spinal cord, which may play an important role in determining the best pulse sequence for certain applications or imaging orientations, or both. In summary, our study used a relatively “primitive” pulse sequence (single-shot EPI) that was easily used clinically and obtained adequate axial DT images in a clinically realizable timeframe.

Limitations

Despite obtaining similar average diffusion measurements to those reported in the current literature, many potential limitations to our study remained. The use of manual ROI selection may have introduced partial volume contamination, primarily in regions where the spinal cord cross-sectional area was smallest and in the lower thoracic regions where spinal nerves may run along the spinal cord. Despite a high percentage agreement between manual ROI selection and other techniques (see Methods section), a need for more precise segmentation is necessary. The use of fuzzy-logic–based tissue classification has recently been proposed as a method for delineating GM and WM in the spinal cord^6,24; however, its usefulness in pathologic conditions still requires validation.⁷

Another limitation to our study was the lack of cardiac and respiratory gating during image acquisition. Cardiac and respiratory gating during DT image acquisition substantially reduces errors related to diffusion measurements^30,31 because the spinal cord moves in the craniocaudal direction synchronously with the cardiac cycle. This is of particular interest when sagittal images of the spinal cord are obtained. Although motion of the spinal cord is lower in the transverse plane, the lack of cardiac and respiratory gating in our study was a possible limitation.

Susceptibility-related image artifacts have limited the clinical use of DTI in the spinal cord. These artifacts arise from magnetic susceptibility differences between the spinal cord and the surrounding bony vertebral column. Although we did observe slight geometric distortions (Fig 1), we were careful not to use sections that may have been strongly affected. In particular, the regions of the spinal cord most sensitive to changes in B0 from susceptibility inhomogeneity are located proximal to the vertebral disk (because of the spinous process from the rostral vertebral level).²¹ Furthermore, we used a Fourier-transform–based image registration algorithm to correct geometric distortions between the T2-weighted and DWIs. Regardless, the lack of B0 correction for susceptibility artifacts for both T2-weighted and DWIs may have distorted the images of our study.

A final limitation to our study was the age range represented by this normative dataset. MD increases and FA decreases with increasing age, though the magnitude of the changes is minimal. Between ages 25 and 85 years, the average MD increases 0.1 × 10⁻³ mm²/s, and mean FA decreases approximately 0.04,³ well within the ranges represented in our dataset. Although the magnitude of changes in diffusion characteristics is expected to change only slightly during normal aging, discretion should be used when comparing our data with older populations.

Conclusion

Our study characterized the diffusion properties of the entire neurologically intact human spinal cord with use of a single-shot EPI pulse sequence. Data from this study will be useful for clinical comparisons of DTI parameters measured with pathologic conditions of the spine as well as for comparisons with different pulse sequence design parameters aimed to reduce scan time, increase SNR, and decrease variance of diffusion coefficients.