Local accumulation of extracellular matrix regulates global morphogenetic patterning in the developing mammary gland

Summary

The tree-like pattern of the mammary epithelium is formed during puberty through a process known as branching morphogenesis. While mammary epithelial branching is stochastic and generates an epithelial tree with a random pattern of branches, the global orientation of the developing epithelium is predictably biased along the long axis of the gland. Here, we combine analysis of pubertal mouse mammary glands, a 3D-printed engineered tissue model, and computational models of morphogenesis to investigate the origin and the dynamics of the global bias in epithelial orientation during pubertal mammary development. Confocal microscopy analysis revealed that a global bias emerges in the absence of pre-aligned networks of type I collagen in the fat pad and is maintained throughout pubertal development until the widespread formation of lateral branches. Using branching and annihilating random walk simulations, we found that the angle of bifurcation of terminal end buds (TEBs) dictates both the dynamics and the extent of the global bias in epithelial orientation. Our experimental and computational data demonstrate that a local increase in stiffness from the accumulation of extracellular matrix, which constrains the angle of bifurcation of TEBs, is sufficient to pattern the global orientation of the developing mammary epithelium. These data reveal that local mechanical properties regulate the global pattern of mammary epithelial branching and may provide new insight into the global patterning of other branched epithelia.

eTOC blurb

The orientation of the developing mammary epithelium is generally thought to result from global signals within the fat pad. Nerger at al. find that the local accumulation of extracellular matrix along the flanks and at the cleft site of bifurcating terminal end buds is sufficient to regulate the global orientation of the mammary epithelium.

Introduction

The murine mammary gland consists of epithelial tubes embedded in an adipose-rich stroma called the fat pad. During puberty, the mammary epithelium undergoes recursive rounds of bifurcation and extension within the fat pad to generate a branched ductal network. Lateral branches then arise from primary ducts to further elaborate the epithelial tree.¹ In contrast to the stereotyped branching that drives embryonic development of the lung², postnatal branching of the mammary epithelium is stochastic and generates a random geometry.³ Nonetheless, the developing epithelium has a global orientation bias along the long axis of the fat pad.⁴ This orientation bias likely enables the branching epithelium to efficiently fill available space within the fat pad, which is important for maximizing the subsequent synthesis of milk. The origin and dynamics of the epithelial orientation bias remain unclear, and it is unknown if global chemical or physical signals are required to pattern ductal extension.⁵

In the pubertal mouse mammary gland, bulbous multicellular structures called terminal end buds (TEBs) collectively extend into the fat pad at an average rate of ~0.5 mm/day.⁶ TEBs consist of an outer layer of cap cells—covered by a continuous basement membrane—and several inner layers of highly proliferative body cells.^{7, 8} Although the exact mechanism of TEB extension is unknown⁹, the lack of protrusions from the basal surface suggests that the structure is pushed through the fat pad.^{8, 10} Previous studies have used mammary gland whole mounts, explants, and organoids to identify both physical and chemical signals that regulate TEB extension.^{5, 11–16} Seminal work postulated that collagen fiber alignment may direct mammary ductal extension,¹⁷ and pre-patterned networks of type I collagen in the fat pad were subsequently hypothesized to bias ductal growth along the long axis of the developing gland.⁴ Nevertheless, it remains unclear how and when networks of type I collagen are aligned in the fat pad and how topographical signals from aligned collagen fibers might direct TEB extension.¹² In addition to the extracellular matrix (ECM), recent studies using engineered epithelial tissues have shown that mechanical stresses affect the local pattern of branching.¹⁸ Transforming growth factor-β (TGFβ), an autocrine inhibitory morphogen¹⁹, is also important for local self-avoidance of developing mammary epithelial branches.²⁰ Nonetheless, a connection between these local signals and the global orientation of the epithelium has not been identified. Furthermore, experimental evidence of a global signaling gradient that might guide TEBs along the long axis of the fat pad has remained elusive.²¹

To complement experimental studies, mathematical models have been used to investigate pubertal development of the mammary epithelium.^{6, 22, 23} Building on the experimental observation that TEBs bifurcate and terminate with equal probability²², a branching and annihilating random walk (BARW) model revealed that a bias in the direction of epithelial extension could emerge in the absence of long-range guidance cues.²² However, the extent to which the BARW model captures the dynamics of epithelial morphogenesis during pubertal development remains unclear.

Here, we set out to define both the timing of the mammary epithelial orientation bias as well as its underlying physical mechanisms. We found that the orientation bias consistently emerges in 4-week-old thoracic and inguinal mouse mammary glands. This bias is maintained throughout pubertal development until the widespread formation of lateral branches. In contrast to existing hypotheses, we found that the orientation bias emerges in the absence of pre-aligned networks of type I collagen fibers in the fat pad. Using experimental and computational approaches, we reveal that local ECM accumulation constrains the bifurcation angle of TEBs and drives the global bias in epithelial orientation along the long axis of the fat pad. Our observations challenge the conventional view that the orientation of the mammary epithelium is regulated by global signals that guide TEB extension. Instead, we demonstrate that local stiffness resulting from ECM accumulation regulates the relative positioning of daughter branches, which is sufficient to dictate the global orientation of the mammary epithelium. Our data reconcile the stochastic nature of mammary epithelial branching with the local patterns of ECM and the global bias in epithelial orientation observed during pubertal development. These findings demonstrate that long-range tissue patterning can emerge from local patterns of stiffness, which might play a role in the morphogenesis of other branched epithelial tissues.

Results

The mammary epithelial orientation bias changes over developmental time

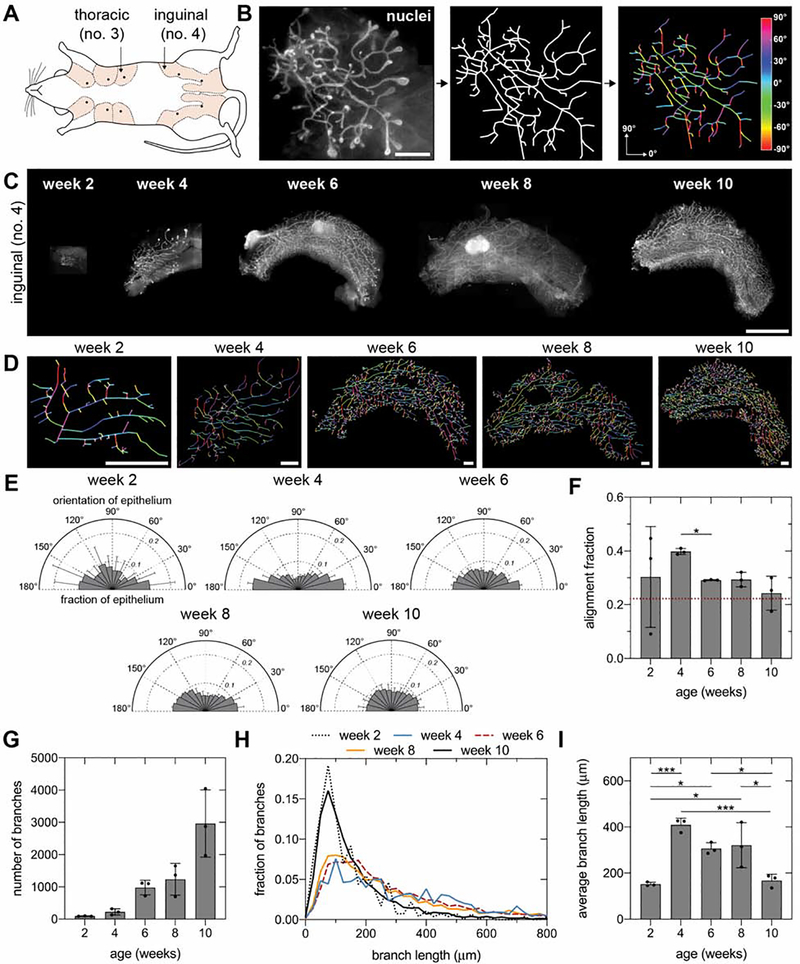
To visualize the orientation of the mammary epithelium, we began by dissecting whole no. 4 inguinal mammary glands (Figure 1A), which were selected due to their large size, accessibility, and prevalent use in previous investigations of mammary morphogenesis. We labeled the glands using a nuclear stain and acquired and stitched together fluorescent images of the epithelium (Figure 1B and C). Epithelial orientation was quantified using a skeleton structure that we generated by manually tracing fluorescent images (Figure 1D).

Figure 1. A bias in epithelial orientation emerges along the long axis of 4-week-old inguinal mammary glands.

A) Schematic of mouse mammary glands (inspired by57). B) Representative fluorescent image of a mammary gland labeled with Hoechst 33342 (left; scale bar represents 1 mm), skeleton of epithelium (middle), and visualization of branch orientation (right). C) Representative fluorescent images of no. 4 inguinal mammary glands at different stages of pubertal development labeled with Hoechst 33342 (scale bar represents 5 mm) and D) corresponding skeletons (scale bars represent 1 mm). E) Orientation and F) alignment fraction of epithelium at different stages of pubertal development. The dashed red line represents the alignment fraction corresponding to an epithelium without an orientation bias. G) Number of epithelial branches, H) distribution of branch length, and I) average branch length at different stages of pubertal development. Data are represented as mean ± SD. *p ≤ 0.05 and ***p ≤ 0.001. See also Figure S1.

To investigate the dynamics of the orientation bias, we measured epithelial orientation in glands from pubertal CD-1 mice ranging from 2 to 10 weeks of age (Figure 1E and F). These measurements revealed a consistent bias in epithelial orientation along the long axis of the fat pad in 4-, 6-, and 8-week-old glands, which is absent from 2- and 10-week-old glands. Quantification of the alignment fraction, which represents the fraction of the epithelium oriented within 20° of the long axis, revealed that the average orientation bias decreases significantly after week 4 (Figure 1F). The epithelial orientation in 2-week-old glands is highly variable owing to the small number of branches present at this early stage of development (Figure 1G). In contrast, the heterogenous orientation of the epithelium in 10-week-old glands can be attributed to the large number of relatively short lateral branches (Figure 1H and I). We found that the epithelium is also biased along the long axis of no. 3 thoracic mammary glands (Figure S1A and B). These data reveal that a consistent bias in epithelial orientation first arises in 4-week-old mammary glands and is maintained throughout pubertal development until the widespread formation of lateral branches. In contrast to extending TEBs, lateral branches extend perpendicular to the duct through a dense network of collagen in the periductal matrix.⁵

Epithelial orientation bias emerges in the absence of pre-aligned networks of type I collagen in the fat pad

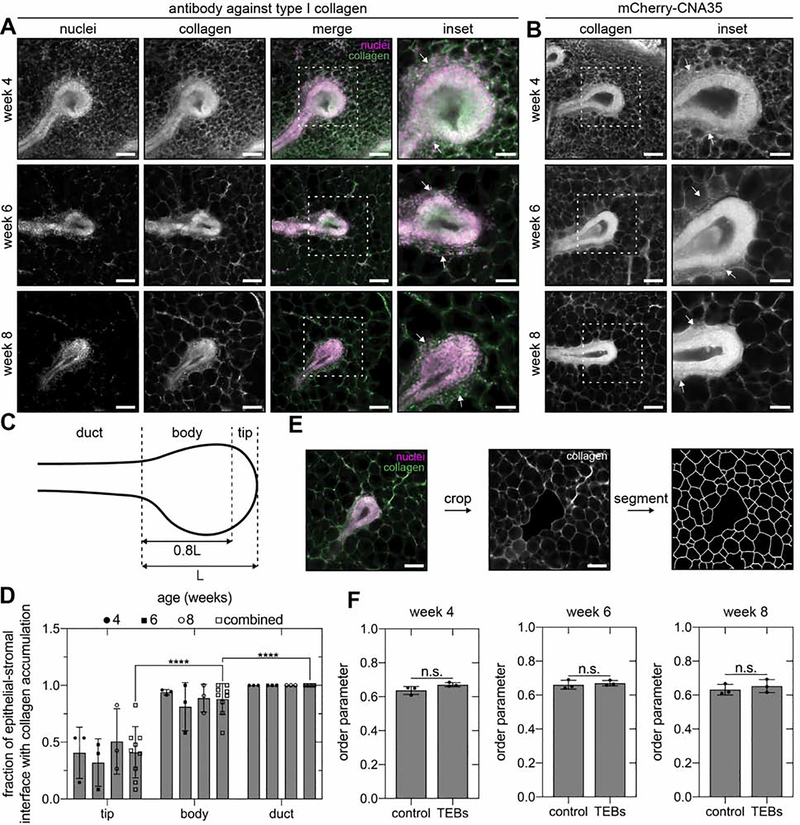
We hypothesized that physical signals from aligned fibers of type I collagen in the fat pad could explain the dynamic changes in epithelial orientation during pubertal development. Daniel and colleagues first posited that collagen fibers affect local mammary epithelial orientation when they observed that TEBs embedded in type I collagen gels branch in the direction of fiber alignment.¹⁷ Consistent with this hypothesis, Bissell and colleagues subsequently postulated that pre-aligned networks of type I collagen located at the leading edge of TEBs and emanating throughout the fat pad serve as a template to orient the mammary epithelium along the long axis of the gland.⁴ To determine whether a collagen template is consistent with the dynamics of epithelial orientation during pubertal morphogenesis, we next mapped the distribution of type I collagen fibers in the fat pad at different stages of development using immunofluorescence staining. Surprisingly⁴, confocal microscopy analysis revealed that aligned fibers of type I collagen are absent from the fat pad at the leading edge of extending TEBs (Figure 2A). Instead, we observed that the leading edge of extending TEBs remains apposed to adipocytes throughout puberty (Figure 2A). Collagen accumulates along the flanks of extending TEBs and surrounds each adipocyte in the fat pad (Figure 2A). These observations are consistent with reports of mammary TEB sections^{7, 24}, which show cap cells in direct contact with adipocytes, and the lack of type I collagen gene expression at the tip of extending TEBs²⁴, as well as with observations of collagen and stromal cell accumulation along the flanks of TEBs in the periductal sheath.²⁵

Figure 2. Type I collagen accumulates along the flanks of extending TEBs.

Representative fluorescent images of TEBs in 4-, 6-, and 8-week-old no. 4 inguinal mammary glands labeled with an A) antibody against type I collagen or B) the collagen-binding protein mCherry-CNA35. White arrows denote collagen accumulation. C) Schematic of the tip, body, and duct regions of a TEB and D) quantification of collagen accumulation in each region. E) Representative segmentation of adipocyte cell borders surrounding a TEB and F) order parameter describing the orientation of epithelial extension with respect to adipocyte packing in a randomly selected region of the fat pad (control) or around TEBs. Scale bars represent 100 μm or 50 μm for insets. Data are represented as mean ± SD. ****p ≤ 0.0001 and n.s., not significant. See also Figure S2.

To verify our immunofluorescence staining, we used two additional approaches to image collagen fibers. We labeled type I collagen with the fluorescently tagged collagen-binding protein mCherry-CNA35, which was previously used to investigate collagen fiber alignment in the developing mammary gland.⁴ We confirmed that mCherry-CNA35 binds to networks of type I collagen (Figure S2A), used the fusion protein to label mammary glands, and acquired images of TEBs at different stages of pubertal development (Figure 2B). These data revealed that collagen accumulates along the flanks of TEBs and that aligned collagen fibers are absent from the fat pad, consistent with our immunofluorescence analysis. Quantitative image analysis (Figure 2C) revealed a significant reduction in the accumulation of collagen at the tips of TEBs as compared to the body and duct regions (Figure 2D). We further confirmed this distribution of collagen using a label-free imaging technique called confocal reflection microscopy (Figure S2B). Aligned networks of collagen are also absent from the leading edge of extending TEBs in whole mounts (Figure S2C) or 150-μm-thick sections (Figure S2D) of no. 3 thoracic mammary glands from CD-1 mice or in mammary glands from C57BL/6J mice or CUBIC-cleared mammary glands (Figure S2D). These data reveal that the leading edge of extending TEBs does not contact aligned fibers of type I collagen.

The only collagen located near the leading edge of extending TEBs is the network that surrounds individual adipocytes. To determine whether this collagen network is oriented in the direction of TEB extension, we measured adipocyte packing (Figure 2E) and quantified an order parameter describing the correlation between adipocyte packing and the direction of epithelial extension. As a control, we quantified the order parameter for adipocytes from random regions of the fat pad. This analysis revealed that adipocytes are not packed preferentially in the direction of branching (Figure 2F). We thus conclude that the network of collagen surrounding adipocytes is also not preferentially oriented in the direction of TEB extension.

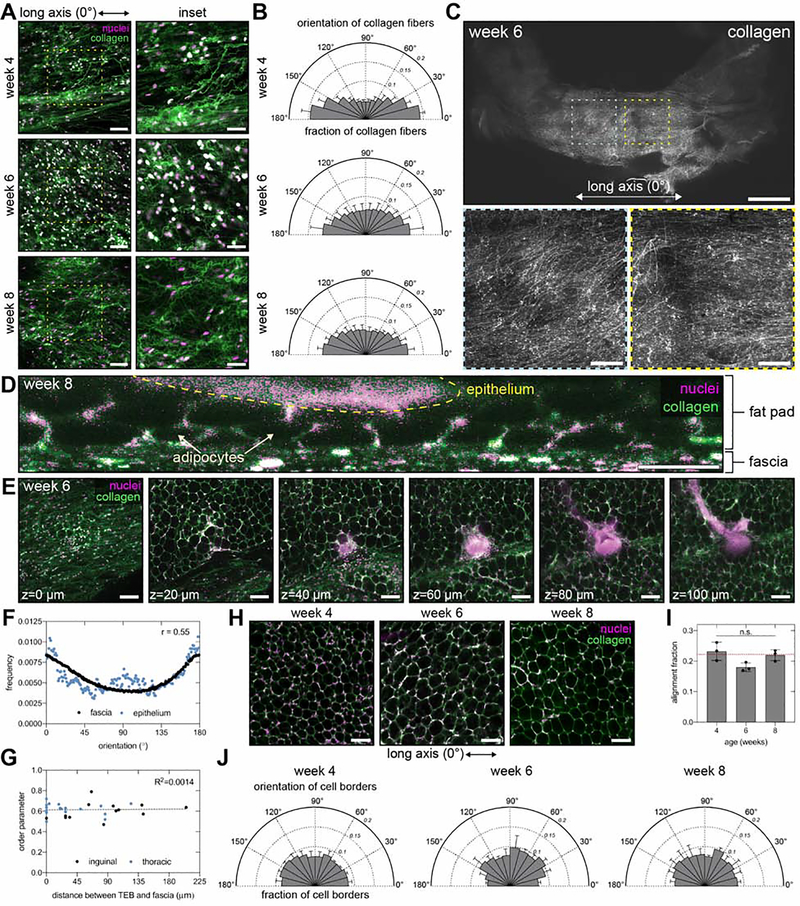
We next investigated whether aligned collagen fibers are present outside of the fat pad in regions that might be physically accessible to extending TEBs. We observed aligned collagen networks immediately adjacent to the fat pad in the connective tissue layer that envelops the mammary gland, known as the superficial fascia. Local (Figure 3A and B) and global (Figure 3C) confocal microscopy analysis revealed that collagen fibers in the fascia are largely aligned along the long axis of the gland. We hypothesized that aligned collagen in the fascia might provide a guidance signal that biases the direction of TEB extension. However, optical cross-sections revealed that the majority of TEBs are physically separated from the fascia by at least one layer of adipocytes (Figure 3D and E). On a global scale, epithelial orientation only weakly correlates with collagen fiber orientation in the fascia, as indicated by a Spearman correlation coefficient of 0.55 (Figure 3F). On a local scale, these two orientations are not consistently correlated, as indicated by the large range of order parameters (Figure 3G). Moreover, the distance of separation between TEBs and the fascia does not correlate with the magnitude of the order parameter, as indicated by a coefficient of determination of 0.0014 (Figure 3G). Therefore, the alignment of collagen fibers in the fascia does not correlate with that of the mammary epithelium, which suggests another cue is responsible for long-range patterning in the gland.

Figure 3. Aligned networks of collagen are observed in the superficial fascia adjacent to the mammary gland.

A) Representative fluorescent images of fascia and B) orientation of collagen fibers in the fascia in 4-, 6-, and 8-week-old no. 4 inguinal mammary glands; n=5 replicates. Scale bars represent 100 μm or 50 μm for insets. C) Low-magnification fluorescent images of collagen in the fascia of a 6-week-old no. 4 inguinal mammary gland. Scale bars represent 2 mm (top) or 500 μm (insets). Representative fluorescent images of a D) cross-section (scale bar 50 μm) and E) different z slices (scale bar 100 μm) through a no. 4 inguinal mammary gland. F) Spearman correlation between global orientation of collagen fibers in the fascia and the mammary epithelium for the same gland; n=1 gland. G) Pearson correlation between the order parameter describing the local orientation of TEBs with respect to collagen fiber orientation in the fascia and the distance of separation between the fascia and the TEB; n=18 and 13 TEBs from thoracic and inguinal glands, respectively. H) Representative fluorescent images of adipocytes in the fat pad of no. 4 inguinal mammary glands. Scale bars represent 100 μm. I) Alignment fraction and J) orientation of adipocyte cell borders. For all fluorescent images in the figure, tissues are stained with Hoechst 33342 to label nuclei (magenta) and an antibody against type I collagen (green). Data are represented as mean ± SD. n.s., not significant. See also Figure S3.

The above analysis could not rule out the possibility that the fascia might indirectly influence TEB extension by affecting the orientation of the collagen network around adipocytes in the fat pad. However, confocal microscopy analysis revealed that the collagen network around adipocytes has a random orientation (Figure 3H–J) distinct from that of collagen fibers within the adjacent fascia (Figure S3). Therefore, the mammary epithelial orientation bias develops in the absence of pre-aligned networks of type I collagen fibers in the fat pad.

Direct contact with aligned collagen fibers guides branch extension in culture

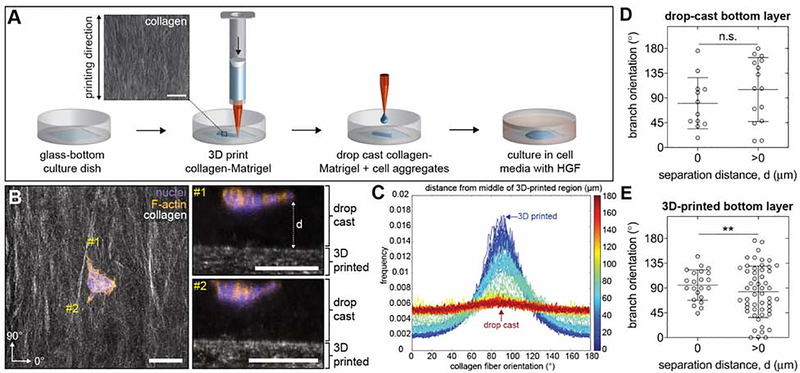
Our imaging data revealed that the only aligned collagen fibers present in the vicinity of the mammary epithelium are those in the superficial fascia, located several micrometers away from TEBs. To directly test whether aligned collagen fibers can guide mammary epithelial branching when separated by the distances observed in the fascia, we engineered a 3D-printed tissue model to reproduce the distribution of collagen fibers in and around the developing mammary gland. Collagen-Matrigel hydrogels were 3D printed onto a glass surface to generate aligned networks that mimic the orientation of collagen within the superficial fascia (Figure 4A). Aggregates of normal mammary epithelial cells were then mixed with collagen-Matrigel and drop cast on top of the 3D-printed networks to reproduce the separation distances observed in vivo. We treated samples with HGF to induce branching²⁶ and then measured the resulting orientation and distance of separation between epithelial branches and 3D-printed collagen-Matrigel. We defined branches as actin-rich extensions containing at least one cell nucleus. Confocal microscopy analysis revealed branching epithelial aggregates separated from aligned collagen fibers by distances comparable to our in vivo observations (Figure 4B). Quantitative image analysis confirmed that collagen fibers are aligned in the printing direction in the 3D-printed layer and not in the drop-cast layer of the engineered tissues (Figure 4C). As a control, we engineered tissues in which the epithelial aggregates were drop-cast above heterogeneous networks of collagen-Matrigel. In these control samples, epithelial aggregates branch in random directions irrespective of their distance from the bottom layer (Figure 4D). In contrast, epithelial aggregates that were drop cast on top of 3D-printed networks of collagen branch in the direction of fiber alignment if, and only if, they directly contact the aligned collagen fibers (Figure 4E). These data reveal that aligned collagen fibers only influence branching when in direct contact with the epithelial cells themselves. These results are consistent with our conclusion that, because of their distance from the mammary epithelium, the aligned collagen fibers that are present in the fascia do not directly guide TEB extension.

Figure 4. Aligned networks of collagen fibers only influence branch orientation when in direct contact with mammary epithelial cell aggregates in culture.

A) Schematic depicting fabrication of the multilayered engineered tissue model using sequential 3D printing and drop casting. Scale bar represents 100 μm. B) Representative confocal microscopy images showing a mammary epithelial cell aggregate seeded within drop-cast collagen-Matrigel on top of 3D-printed collagen-Matrigel. Left image represents a maximum-intensity z-projection (scale bar represents 100 μm) and right images represent optical cross-sections along lines labeled #1 and #2 (scale bars represent 100 μm). C) Representative distribution of collagen fiber orientation throughout the z-axis of the engineered tissue model starting in the 3D-printed region and ending in the drop-cast region; n=1. D) Branch orientation in control engineered tissues that consist of mammary epithelial cell aggregates cultured within drop-cast collagen-Matrigel on top of a layer of drop-cast collagen-Matrigel; n=12 and 15 cell aggregates with a separation distance of 0 and >0, respectively. E) Branch orientation in mammary epithelial cell aggregates cultured within drop-cast collagen-Matrigel on top of 3D-printed collagen-Matrigel; n=22 and 53 cell aggregates with a separation distance of 0 and >0, respectively. Data are represented as mean ± SD. **p ≤ 0.01 and n.s., not significant. See also Figure S4.

We also used our 3D-printed tissues to determine whether contact with aligned collagen fibers polarizes adipocyte packing. We seeded 3T3-L1 preadipocytes onto 3D-printed networks of collagen, differentiated the cells, and quantified the orientation of intercellular borders between adipocytes (Figure S4). Concordant with our in vivo observations, we found that the orientation of intercellular borders is not polarized in the direction of collagen fiber alignment in the adjacent 3D-printed network of collagen. These findings are consistent with our conclusion that aligned collagen fibers in the fascia do not influence the orientation of the network of collagen in between adipocytes in the fat pad.

Bifurcation angle regulates the global orientation of the mammary epithelium

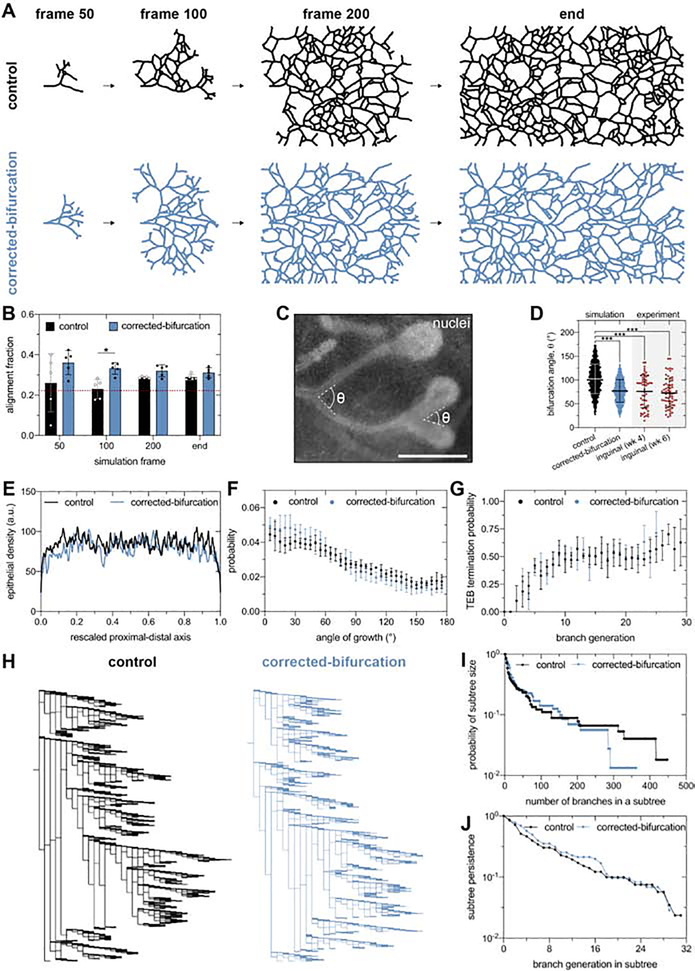
To investigate how a bias in epithelial orientation can arise in the absence of a directional template from aligned collagen fibers, we simulated mammary epithelial morphogenesis as a branching and annihilating random walk (BARW).^{22, 27} In this simulation, TEBs randomly explore space, bifurcate stochastically with a constant probability, and terminate when they reach a specified distance from neighboring epithelium. BARW simulations can reproduce the directional bias of the mammary epithelium without external signaling gradients.²² However, previous studies did not test whether these simulations also reproduce the dynamics of epithelial orientation observed developmental time in vivo. We therefore repeated the BARW simulations using the same parameters reported previously²², and quantified the alignment fraction of the simulated epithelial tree as a function of simulation time (Figure 5A and B). These “control” simulations show a gradual increase in alignment fraction (Figure 5B), indicating that the published BARW parameters do not predict the dynamic changes in epithelial orientation bias observed in vivo (Figure 1F).

Figure 5. The angle of bifurcation of TEBs dictates the global alignment of simulated mammary epithelium.

A) Representative control and corrected-bifurcation BARW simulations and B) corresponding quantification of alignment fraction as a function of simulation time. The dashed red line represents the alignment fraction corresponding to an epithelium without an orientation bias. C) Representative bifurcation angles measured from a fluorescent image of a bifurcating mammary epithelium labeled with Hoechst 33342. Scale bar represents 500 μm. D) Distribution of bifurcation angles quantified in control and corrected-bifurcation simulations and 4- and 6-week-old inguinal mammary glands; n=54 and 65 measurements for 4- and 6-week-old glands, respectively. Quantification of E) epithelial density, F) angle of growth probability, and G) TEB annihilation probability for control and corrected-bifurcation BARW simulations. H) Representative lineage tree for control and corrected-bifurcation BARW simulations as well as quantification of I) subtree size and J) subtree persistence. Data are represented as mean ± SD in panels b, d, f, and g or as the mean in panels e, i, and j. *p ≤ 0.05 and ***p ≤ 0.001. See also Figure S5.

In order to identify the parameters that affect the global orientation of the epithelium, we further compared the simulated and in vivo epithelial trees. In the BARW simulations, we measured that each TEB bifurcates at an average angle of ~100°. However, in intact inguinal glands in vivo, we measured an average bifurcation angle of ~75° (Figure 5C and D). Our measurements of inguinal glands are consistent those of 4-week-old thoracic glands (Figure S1C) as well as with previous reports.⁶ Based on these measurements, we hypothesized that correcting the average bifurcation angle to 75° would alter the alignment fraction in the BARW simulations. Consistent with this hypothesis, corrected-bifurcation simulations have a significantly higher alignment fraction than control simulations (Figure 5A and B). The corrected-bifurcation simulations also demonstrate alignment dynamics similar to that of the mammary gland in vivo, wherein the average alignment fraction starts at ~0.4 and decreases to ~0.3 (Figure 1F and 5B), and reproduce the distribution of bifurcation angles observed in our in vivo data (Figure 5D). Reducing the average bifurcation angle in BARW simulations to 50° leads to further increases in the final alignment fraction of the epithelium (Figure S5A), suggesting that alignment increases as bifurcation angle decreases. Consistently, in 6-week-old thoracic glands, which have an average bifurcation angle of ~90°, we observed decreased alignment as compared to 4-week-old thoracic glands (Figure S1). Finally, to determine whether bifurcation angle is sufficient to regulate alignment fraction, we conducted BARW simulations with varying levels of TEB persistence. These simulations revealed that TEB persistence does not affect alignment (Figure S5B). We therefore predict that the magnitude and dynamics of the global orientation of the mammary epithelium are explained by the bifurcation angle of TEBs.

To determine whether correcting the bifurcation angle affects other morphological features of simulated mammary epithelium, we compared macroscopic features of the final epithelial trees generated by corrected-bifurcation and control simulations. Given that the final epithelial tree generated by control simulations reproduces many macroscopic features of mammary glands in vivo22, this comparison reveals differences specifically between the corrected-bifurcation model and mammary epithelial trees in vivo. Control and corrected-bifurcation simulations generate similar epithelial density (Figure 5E), angle-of-growth distribution (Figure 5F), and TEB annihilation probability (Figure 5G). However, lineage tree analysis revealed a reduction in the number of branches in epithelial subtrees in the corrected-bifurcation simulations and a similar subtree persistence for both simulations (Figure 5H–J). The addition of lateral branching, an aspect of mammary development that is not included in the BARW simulation framework, might correct for the difference in the number of branches in subtrees without affecting subtree persistence.

Collagen accumulation around bifurcating TEBs varies with bifurcation angle

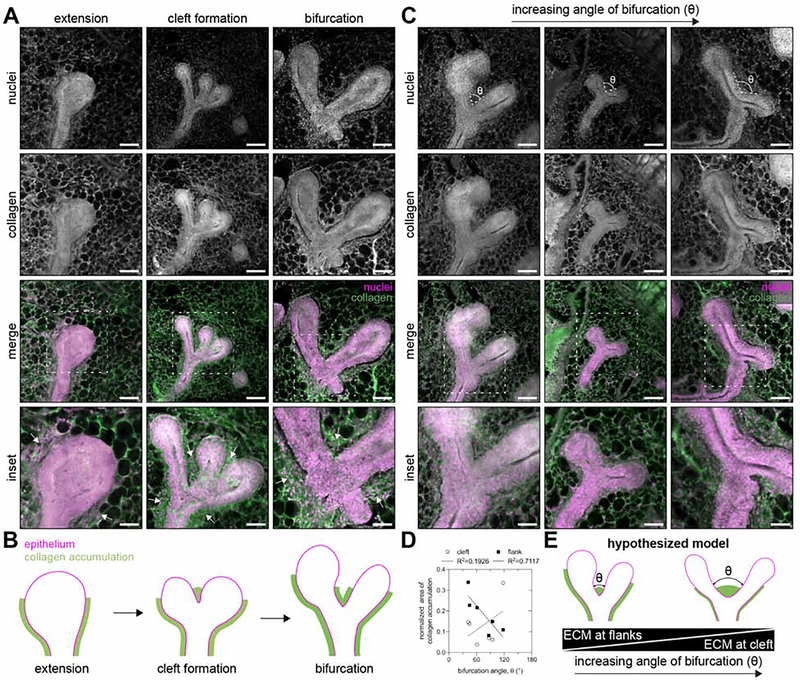
Given our prediction that the bifurcation angle is a key parameter that regulates the global orientation bias of the mouse mammary gland, we next focused on the physical signals that orchestrate TEB bifurcation in vivo. Previous studies have reported dense regions of type I collagen and sulfated glycosaminoglycans located at the cleft site and along the flanks of bifurcating TEBs^{7, 10}. We observed similar patterns of collagen accumulation around bifurcating TEBs (Figure 6A and B). These ECM-rich regions have been hypothesized to direct local epithelial growth¹⁰, although this hypothesis has not been tested experimentally or computationally. To determine if local collagen accumulation correlates with bifurcation angle, we acquired images of TEBs and measured both their bifurcation angles (Figure 6C) as well as the length of collagen at the cleft site and along the flanks (Figure 6D). As the bifurcation angle decreased, we observed increasing collagen accumulation along the flanks and decreasing collagen accumulation at the cleft (Figure 6D). Based on these data, we hypothesize that local collagen accumulation regulates TEB bifurcation angle (Figure 6E).

Figure 6. Collagen-rich ECM is deposited along the flanks and at the cleft site of bifurcating TEBs.

A) Representative fluorescent images of 150-μm-thick sections of TEBs during extension, cleft formation, and bifurcation and B) corresponding schematic of the pattern of collagen accumulation. C) Representative fluorescent images of 150-μm-thick sections of bifurcating TEBs with different angles of bifurcation. D) Area of collagen accumulation along the flanks and at the cleft site as a function of the angle of bifurcation; n=6 bifurcations. E) Schematic of hypothesized model in which the local extent of collagen accumulation regulates the angle of TEB bifurcation. Tissues are stained with Hoechst 33342 to label nuclei (magenta) and an antibody against type I collagen (green). Scale bars represent 100 μm or 50 μm for insets.

Local collagen accumulation is sufficient to regulate bifurcation angle of simulated TEBs

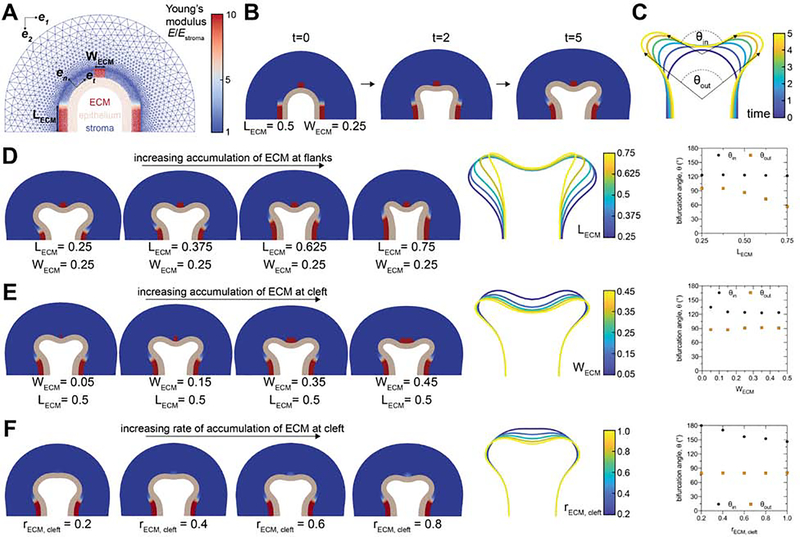
To test our hypothesis, we used the finite element method (FEM) to solve a computational model of the physical process of mammary epithelial branching²⁸. To simulate TEB bifurcation in vivo, the model includes epithelial, adipose, and ECM-rich compartments (Figure 7A). We set the stiffness of the ECM-rich compartment to be higher than that of the epithelial and adipose compartments based on atomic force microscopy measurements of mouse mammary glands^{29, 30}. Under these conditions, we observed that stiff regions of ECM are sufficient to drive bifurcation of a growing epithelium (Figure 7B).

Figure 7. Local accumulation of stiff ECM constrains the angle of bifurcation of simulated TEBs.

A) Geometry and mesh of FEM-based model of bifurcating TEB. B) Different time steps during a simulated bifurcation of a TEB. C) Traces of the epithelial geometry as a function of simulation time. The final time point of simulations, traces of the final epithelial geometry, and bifurcation angles for simulations with D) varying ECM accumulation on the flanks of the TEB, E) varying ECM accumulation at the leading edge of the TEB, and F) varying rates of ECM accumulation at the leading edge of the TEB. See also Figure S6 and Videos S1–S8.

We next tested whether changing the geometry of the ECM-rich compartment affects the inner (θ_in) and outer (θ_out) angles of epithelial bifurcation in our computational model (Figure 7C). Consistent with our in vivo observations (Figure 6D), we found that increasing the length of the ECM deposits around the flanks of the TEB decreases θ_out (Figure 7D). In contrast, increasing ECM accumulation at the cleft site results in a modest decrease in θ_in (Figure 7E). However, we found that altering the rate of ECM accumulation at the cleft site has a substantial effect on θ_in. As expected, removing the ECM compartment or completely surrounding the epithelium in ECM prevents epithelial bifurcation (Figure S6). Furthermore, we observed modest changes in bifurcation angle when we varied the stiffness of the epithelial and adipose compartments (Figure S6). These data reveal that both the pattern and rate of collagen accumulation are sufficient to regulate the bifurcation angle of simulated TEBs. These results also suggest that changes in tissue stiffness and geometry might account for the different bifurcation angles that we observe at different stages of thoracic mammary gland development (Figure S1C). Together, our experimental and computational data are consistent with a conceptual model in which the local mechanical microenvironment regulates the bifurcation angle of TEBs. This bifurcation angle sets the orientation of daughter branches, which drives the global bias in orientation of the epithelial tree observed during pubertal development of the mammary gland.

Discussion

The mouse mammary gland is widely appreciated as a model of branching morphogenesis, but how the pattern of the mammary epithelial tree is specified during puberty has remained a longstanding question. The random geometry of the mammary epithelium suggests that TEB is regulated by signals within the surrounding microenvironment.^{3, 5} Although there is no evidence of long-range guidance cues in the fat pad²¹, local patterns of MMPs¹³, TGFβ³¹, stromal and immune cells^32–34, type I collagen^{4, 35}, sulfated glycosaminoglycans⁷, hyaluronate⁷, and tenascin C³⁶, among others, as well as local patterns of gene expression^{24, 37, 38} have been reported. A connection between these local signals and the global orientation of the epithelium has not been confirmed, in part because it remains unclear how local signals influence the bifurcation and extension of TEBs. Nevertheless, the orientation bias of the developing epithelium was thought to be a consequence of guidance cues from the ECM⁴, although the mechanism by which the ECM might orient TEB extension was never identified in vivo12. In contrast, recently published simulations suggested that mammary epithelial branching is purely stochastic and occurs in the absence of long-range guidance cues.²²

Here, we propose that the local accumulation of collagen-rich ECM adjacent to bifurcating TEBs is sufficient to generate the global pattern of the developing mammary epithelium. Based on results from experimental and computational analyses, we posit that local ECM accumulation constrains the bifurcation angle of TEBs, which regulates the dynamics and bias of epithelial orientation during pubertal development. Our data suggest that an orientation bias can arise from the relative positioning of daughter branches during bifurcation rather than local alterations in the direction of TEB extension during ductal elongation.

In contrast to the prevailing hypothesis, we found that a bias in epithelial orientation emerges in the absence of local alignment of type I collagen fibers at the leading edge of extending TEBs or global alignment of type I collagen fibers within the fat pad. Others have reported various patterns of collagen fiber alignment around extending TEBs^{4, 30, 35} and globally throughout the fat pad⁴, but our data show that the leading edge of extending TEBs is adjacent to adipocytes and that globally aligned networks of collagen are instead located outside of the fat pad within the superficial fascia. The pattern of collagen around extending TEBs is distinct from that surrounding bifurcating TEBs, where we and others observe collagen accumulation along the flanks of the epithelium and at the cleft site^{7, 10}. Previous reports of collagen fibers aligned in front of extending TEBs may be an artifact of alternative processing techniques, which can cause contraction or expansion of mammary tissue³⁹ and thereby alter the distance between the epithelium and the fascia. Although our imaging data show no aligned collagen fibers in the fat pad, we acknowledge that absence of evidence is not evidence of absence. Challenges with epitope preservation due to the partial denaturation of collagen can affect the affinity of antibodies for type I collagen fibers⁴⁰. Imaging techniques such as second harmonic generation might be capable of detecting smaller diameter collagen fibrils than the three orthogonal approaches that we used here⁴¹. Nevertheless, physical signals from aligned networks of collagen would be hypothesized to direct the persistence of TEB extension, which is not responsible for generating the orientation bias of simulated epithelium. Thus, if there are aligned collagen fibers in front of TEBs that we failed to detect, this still would not explain the global bias in epithelial orientation. Our conclusions are further corroborated by recently published computational analysis²², which revealed that long-range guidance cues, such as those that might arise from the aforementioned hypothetical collagen fibers, cannot reproduce the architecture of the mammary gland in vivo.

Although previous studies have alluded to close contact between TEBs and fascia¹⁰, this observation has not been supported by quantitative image analysis. Our data show that TEBs are separated from aligned collagen fibers within the superficial fascia by at least one layer of adipocytes. While we found occasional examples of TEBs in direct contact with the fascia in inguinal and thoracic glands, the orientation of these TEBs did not correlate with that of the collagen fibers in the adjacent fascia. Moreover, it has been widely observed that TEBs regress upon reaching the limit of the fat pad⁴², which suggests that close contact between TEBs and the fascia may inhibit rather than direct extension. While our data reveal that collagen fibers in the fascia do not provide direct physical signals to orient TEB extension, the alignment of these fibers might indicate the presence of alternative cues, such as global tension gradients along the long axis of the developing gland, which may influence the direction of extension.

BARW simulations of branching morphogenesis can describe many macroscopic features of the developing mammary gland²². However, we found that the parameters used in the original simulations fail to predict the dynamic changes in the global epithelial orientation bias that we observed in vivo. This discrepancy might be attributed to the specific mammary glands that were used to inform the original model parameters, the developmental stages at which these parameters were measured, or the mouse strain, which can affect the extent of lateral branching.⁴³ Nonetheless, we found that correcting the average bifurcation angle to 75° is sufficient to correct for the differences in epithelial orientation bias between the simulations and our experimental data.

Using an FEM-based approach to model the physical process of epithelial branching, we found local patterns of stiffness and the rate of ECM accumulation tune the bifurcation angle of TEBs. However, one fundamental limitation of this model is the lack of experimental measurements of the mechanical properties in and around extending and bifurcating TEBs. In future work, local measurements of stiffness in different regions of the developing gland may permit the generation of epithelial geometries that more closely match bifurcating TEBs in vivo. Our computational model could also be expanded to account for the effects of molecular signals and cell-cell interactions within the TEB, which may provide further insight into why we observe distinct bifurcation angles at different stages of development in thoracic mammary glands.

Our data challenge the conventional view that patterning of the mouse mammary epithelium is templated by long-range signals that guide TEB extension. Instead, we find that local physical signals are sufficient to tune bifurcation angle and thereby control the global orientation of the mammary epithelium. While the physical mechanisms that orchestrate bifurcation in vivo remain unclear, ECM accumulation has been previously proposed to drive TEB bifurcation.^{10, 44–47} The ECM that accumulates in the cleft and along the flank of the bifurcating TEB contains type I collagen¹⁰, which is synthesized in the stroma, as well as sulfated glycosaminoglycans, which are synthesized in both the epithelium and stroma.⁷ The composition of this matrix is similar to that near TEBs in glands in which exogenous TGFβ1²⁴, TGFβ2³¹, or TGFβ3³¹ is released from implants, which suggests that TGFβ-family members may regulate ECM accumulation around bifurcating TEBs.⁴⁸ Beyond regulating ECM accumulation, TGFβ-induced autocrine inhibition could affect the angle of branching, similar to the effect of bone morphogenetic protein 7 during patterning of the collecting duct in the developing mouse kidney.⁴⁹ Moreover, a partial reduction in insulin-like growth factor 1 has been shown to decrease the frequency of bifurcation during pubertal mammary epithelial development.⁵⁰ How these and other signals might orchestrate bifurcation and how ECM accumulation affects the collective migratory behavior of cap and body cells within the TEB remain open questions. It also remains unclear from tissue sections of bifurcating TEBs whether the deposition of collagen-rich ECM occurs before, during, or after the initiation of clefting.

Similar patterns of type I collagen deposition have been observed in the embryonic mouse salivary gland.⁵¹ Collagen deposition may stabilize adjacent epithelial cells through interactions with a heparan sulphate-rich proteoglycan.⁵¹ A similar concept might provide insight into the role of ECM accumulation during TEB bifurcation, but this possibility remains challenging to test given that type I collagen-deficient mice are embryonic lethal.⁵² In addition, local fibronectin accumulation in the embryonic mouse salivary gland drives cleft formation by decreasing cell-cell adhesions and increasing cell-matrix adhesions.⁵³ Interactions between cap cells and accumulated ECM might have a similar role in regulating TEB bifurcation.

Advances in imaging whole-mount mammary glands will help further elucidate what signals regulate bifurcation in vivo.⁵⁴ Specifically, live imaging with a fluorescent collagen probe could reveal whether collagen-rich ECM is deposited before, during, or after the initiation of TEB bifurcation and may provide further insight into the physical and cellular mechanisms that drive this process. While the pubertal mammary gland is particularly challenging to image due to the presence of adipocytes, new methods for fluorescence imaging in scattering media might address this challenge.⁵⁵ Alternatively, culture models that contain adipocytes⁵⁶ could allow for live imaging in microenvironments that are optically accessible and more physiologically representative than the collagen-Matrigel hydrogels used here. Looking forward, a deeper understanding of TEB bifurcation may provide new insight into how the local mechanical microenvironment regulates the global patterning of other branched epithelia.

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Celeste Nelson (celesten@princeton.edu)

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

The code supporting the current study is available from the corresponding author on request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Animal husbandry

Experiments were performed using CD-1 (Charles River Laboratories, Wilmington, MA) or C57BL/6J (The Jackson Laboratory, Bar Harbor, ME) mice. All experiments involving animals were conducted using protocols approved by the Princeton University Institutional Animal Care and Use Committee.

Cell culture

Functionally normal EpH4 mouse mammary epithelial cells (gift from Mina Bissell, Lawrence Berkeley National Laboratory) were cultured in 1:1 DMEM:F12 medium (Life Technologies, Carlsbad, CA) supplemented with 2% fetal bovine serum (FBS) (Gemini Bioproducts, West Sacramento, CA), 50 μg/mL gentamicin (Sigma-Aldrich), and 5 μg/mL insulin (Sigma-Aldrich). To generate mammary epithelial cell aggregates, EpH4 cells were suspended in culture medium supplemented with 0.1% (w/v) Pluronic F108 (BASF, Ludwigshafen, Germany) overnight in an incubator at 37°C and 5% CO₂. Branching of epithelial cell aggregates was promoted by supplementing culture medium with 5 ng/mL hepatocyte growth factor (HGF) (Sigma-Aldrich). As described previously⁵⁶, 3T3-L1 preadipocytes (ATCC) were cultured in DMEM (ATCC 30–2002) supplemented with 10% calf serum (R&D Systems, Minneapolis, MN) and 50 μg/mL gentamicin. Differentiation of 3T3-L1 preadipocytes was induced at 100% confluency using differentiation medium containing DMEM supplemented with 10% FBS, 50 μg/mL gentamicin, 1 μg/mL insulin, 115 μg/mL 3- isobutyl-1-methylxanthine (Sigma-Aldrich), and 1 μM dexamethasone (Sigma-Aldrich) for 48 h. Cells were subsequently cultured in DMEM supplemented with 10% FBS, 50 μg/mL gentamicin, and 1 μg/mL insulin for 8 days, and the medium was replaced every 48 h. 3T3-L1 preadipocytes were not used after passage 6 because of increased failure to differentiate at later passages⁵⁶. Cells were maintained in an incubator at 37°C and 5% CO₂.

METHOD DETAILS

Collagen-Matrigel preparation

Acid-solubilized bovine type I collagen (Advanced Biomatrix, Carlsbad, CA) and growth factor-reduced Matrigel (Corning, Corning, NY) were used for all cell-culture experiments. Collagen and Matrigel were mixed in a volumetric ratio of 7:3 (collagen:Matrigel) in order to promote epithelial branching⁵⁸. The final concentrations of collagen and Matrigel were 2.14 mg/ml and 2.34 mg/ml, respectively, and the pH of the resulting mixture was adjusted to ~8 using the collagen neutralizing solution provided by the manufacturer (Advanced Biomatrix). All components were stored on ice during mixing to prevent gelation of the collagen-Matrigel mixture.

3D printing

Collagen-Matrigel inks were incubated on ice for 1 h and then 3D printed at room temperature (~20°C) as described previously^{59, 60}. 3D-printing experiments were completed using a microextrusion bioprinter (Inkredible+, CELLINK, Sweden) and conical polyethylene nozzles with a diameter of 254 μm (Nordson EFD, Robbinsville, NJ). The printing pressure and speed were ~30 kPa and 80 mm/s, respectively, and the distance of separation between the printing nozzle and the substratum was ~0.1 mm. Samples were 3D printed onto no. 1 glass coverslips and gelled in an incubator at 37°C and 5% CO₂. To prevent alignment of collagen fibers due to evaporation⁶¹, ~300 μL of sterile phosphate-buffered saline (PBS) was added around the construct before incubation. Prior to printing, glass coverslips were treated in a UV/ozone (UVO) cleaner (Jelight Company, Irvine, CA) for 7 min and then silanized by exposure to 3,3,3-trifluoropropyl-trichlorosilane (Alfa Aesar, Haverhill, MA) under vacuum for 20 min.

Processing mammary glands

After dissection, whole mammary glands were placed onto an untreated glass slide and immediately immersed in PBS stored on ice. Glands were subsequently fixed by immersion in a 4% (w/v) solution of paraformaldehyde (PFA) (Alfa Aesar) in PBS at 4°C overnight. Next, glands were washed with PBS and dehydrated by immersion in 70%, 80%, and 90% ethanol for 1 h each and 100% ethanol overnight. After dehydration, glands were defatted by immersion in acetone for 48 h at room temperature. The acetone was replaced with fresh acetone after 24 h. A magnetic stir bar at 200 rpm was used to mix the acetone and mammary glands throughout the defatting process. Glands were then washed with PBS before immunofluorescence analysis. Unless stated otherwise, stained mammary glands were cleared by immersion in 25%, 50%, and 75% glycerol (Sigma-Aldrich) in PBS for 3 h each and 100% glycerol overnight. After clearing, mammary glands were stored in glycerol at 4°C.

Alternatively, whole mammary glands were cleared using the clear, unobstructed brain imaging cocktails and computational analysis (CUBIC) protocol^{62, 63}. After immunofluorescence staining, mammary glands were washed in PBS overnight at 4°C and then immersed in a 1:1 (v:v) solution of water and reagent 1 [12.5 g urea (Sigma-Aldrich), 15.6 g 80% (w/w) Quadrol (Sigma-Aldrich) in water, 14.4 g water, and 7.5 g Triton X-100 (Sigma-Aldrich)] for a minimum of 3 h at room temperature. Glands were then immersed in pure reagent 1 for 48 h at room temperature. Reagent 1 was replaced after 24 h with fresh reagent 1. Next, glands were washed with PBS overnight at 4°C. After washing, glands were immersed in a 1:1 solution of reagent 2 [12.5 g urea, 25 g sucrose (Sigma-Aldrich), 7.5 g water, and 5 g triethanolamine (Sigma-Aldrich)] and PBS at room temperature for a minimum of 6 h. Glands were then immersed in pure reagent 2 for 48 h at room temperature. Reagent 2 was replaced after 24 h with fresh reagent 2 and samples were stored in reagent 2 at room temperature.

Mammary glands labeled with the mCherry-CNA35 fusion protein were treated as described previously⁴. Briefly, whole mammary glands were fixed overnight in a solution containing ethanol (75%) and glacial acetic acid (25%), rinsed in PBS, and immersed in a 1:100, 1:500, or 1:1000 solution of mCherry-CNA35 fusion protein in PBS overnight at 4°C. Glands were then washed with PBS and dehydrated in 70%, 80%, 90%, 95%, and 100% ethanol for 30 min each. After dehydration, glands were defatted by immersion in xylene for 48 h at room temperature, mounted using Permount (Fisher Scientific, Hampton, NH), and dried overnight before imaging.

Immunofluorescence analysis

To label type I collagen, whole mammary glands were first permeabilized in a 0.3% (v/v) solution of Triton X-100 in PBS (PBST) for 15 min. Glands were then immersed in blocking buffer [10% (v/v) goat serum (Sigma-Aldrich) in PBST] for 4 h. After blocking, glands were immersed in a 1:4000 (v/v) solution of primary antibody [monoclonal (MA1–26771; Thermo Fisher Scientific)] against type I collagen at 4°C overnight and then washed in PBST. Unless stated otherwise, glands were then incubated in a 1:1000 (v/v) solution of Alexa Fluor 488 goat anti-mouse secondary antibody (Thermo Fisher Scientific) at 4°C overnight and washed in PBST. To label nuclei, samples were immersed in a 1:5000 (v/v) solution of Hoechst 33342 (Invitrogen, Carlsbad, CA) in PBS for 20 min and washed with PBS. To label F-actin, blocked samples were incubated in a 1:200 (v/v) solution of Alexa Fluor 594 phalloidin (Thermo Fisher Scientific) in blocking buffer for 2 h at room temperature.

mCherry-CNA35 fusion protein

pET28a-mCherry-CNA35 was a gift from Maarten Merkx (Addgene plasmid # 61607)⁶⁴. Protein expression was induced in BL21(DE3) E. coli at OD₆₀₀=0.6 with 1 mM isopropyl β-D-1-thiogalactopyranoside (Gold Biotechnology, St. Louis, MO) and cultures were grown at 25°C and 250 rpm for ~20 h. The cultures were centrifuged at 4000 × g for 15 min at 4°C. Next, the cell pellet was resuspended in 20 mL of lysis buffer [pH~7.9; 20 mM Tris-HCl (Sigma-Aldrich), 0.5 M NaCl (Sigma-Aldrich), and 10 mM imidazole (Sigma-Aldrich)] on ice. 1 mg/mL lysozyme (Sigma-Aldrich) was added to the cell-lysis mixture and incubated on ice for 25 min. Next, the cell mixture was sonicated on ice for 12 intervals (10 s each) and then centrifuged for 15 min at 4000 × g at 4°C. Clarified lysate was then centrifuged for 10 min at 8000 × g and 4°C, incubated with 1 mL of Ni-NTA resin (Qiagen, Hilden, Germany) while rotating for 1 h at 4°C, and emptied into a gravity column. From this point on, the procedure was carried out in the dark to protect the fluorescent protein. The resin was washed once with 10 mL of wash buffer 1 (pH~7.9; 20 mM Tris-HCl, 0.5 M NaCl, and 30 mM imidazole) and twice with 10 mL of wash buffer 2 (pH~7.9; 20 mM Tris-HCl, 0.5 M NaCl, and 50 mM imidazole). Next, 8 mL of elution buffer (pH~7.9; 20 mM Tris-HCl, 0.5 M NaCl, and 500 mM imidazole) were added to the column. Collected fractions were run on an SDS-PAGE gel, and concentrated fractions were combined. Finally, the combined fractions were buffer-exchanged into 10% (v/v) glycerol in PBS and further concentrated to ~60 mg/ml using a 30 kDa Amicon concentrator. The mCherry-CNA35 fusion protein was stored at −80°C.

Mammary gland sectioning and embedding

After fixation in 4% PFA, whole mouse mammary glands were washed overnight in PBS at 4°C. Glands were then immersed overnight at 4°C in a 20% (w/v) solution of sucrose in PBS followed by overnight immersion at 4°C in a 30% (w/v) solution of sucrose in PBS and a 1:1 solution of 30% sucrose and OCT compound (Sakura, Torrance, CA). Glands were then embedded in OCT, frozen on dry ice, and stored at −80°C until they were sectioned. 150-μm-thick sections were cut using a Leica CM3050S cryostat at a temperature of −17°C. Mammary gland sections were placed onto Superfrost Plus glass slides (Thermo Fisher Scientific), stained using the protocol described in the immunofluorescence section, and mounted under a no. 1.5 glass coverslip using Fluoromount-G mounting medium (Thermo Fisher Scientific).

Microscopy

Hoechst 33342 staining in whole mouse mammary glands was visualized using a 2× objective and an ORCA-03G digital CCD camera (Hamamatsu Photonics, Japan). Images of terminal end buds (TEBs) were acquired using a Nikon A1 laser-scanning microscope and 10×/0.3 NA air, 20×/0.75 NA air, or 40×/1.3 NA oil-immersion objective. Collagen fibers in collagen-Matrigel hydrogels were visualized in reflection mode using a Nikon A1 laser-scanning confocal microscope with a 488 nm argon laser and GaAsP detector and 20×/0.75 NA air objective.

Quantification of epithelial orientation

Alignment of the mammary epithelium was determined using a skeleton structure that was generated by manually tracing the epithelial tree for each mammary gland labeled with Hoechst 33342. Glands with global curvature were straightened in ImageJ before analysis to ensure that the long axis was oriented along the x axis (0°). The orientation of the resulting skeleton was quantified using the directionality plug-in (Fourier components analysis) in ImageJ. These directionality data were used to quantify the alignment fraction, which represents the fraction of the epithelium oriented within 20° of the long axis. Color-coded orientation plots of mammary epithelial skeletons were generated using the OrientationJ plug-in in ImageJ⁶⁵. Rose plots of the epithelial orientation were generated in MATLAB (R2015b; MathWorks, Natick, MA).

Quantification of collagen fiber orientation

Collagen fiber orientation in 3D-printed constructs and in the fascia was quantified using the directionality plug-in (local gradient orientation method) in ImageJ. Rose plots of collagen fiber orientation were generated in MATLAB.

Quantification of type I collagen around TEBs

TEBs were divided into three regions of interest denoted as tip, body, and duct (Figure 2C). The tip region was defined as 20% of the total length of the TEB measured from the leading edge, and the body region was defined as the remaining 80% of the TEB. Next, the fraction of the epithelial-stromal interface with accumulated type I collagen was measured in each region using ImageJ.

Quantification of adipocyte boundaries

Adipocyte cell-cell boundaries in the mammary fat pad and on 3D-printed networks of collagen were segmented using Imaris (9.5.1; Bitplane, Switzerland). The segmented image was converted to a binary image and the orientation of the cell-cell boundaries was quantified using the directionality plug-in (Fourier components analysis) in ImageJ.

Order parameter

The correlation between the orientation of a TEB and the orientation of collagen fibers in the fascia beneath that TEB was quantified using an order parameter (ϕ, Eq. 1), where α_i represents the fraction of collagen fibers in the fascia with a particular orientation (θ_i), and θ_epithelium represents the orientation of TEB extension. The same approach was used to determine the correlation between the direction of epithelial growth and the orientation of adipocyte packing.

$$\varphi =\sum _i{\alpha }_i\left|\cos \left({\theta }_{epithelium}-{\theta }_i\right)\right|$$ (1)

Quantification of branch number and length

The average branch length and number of branches in vivo was measured using the analyze skeleton plug-in in ImageJ.⁶⁶

BARW model and analysis

Mammary epithelial branching morphogenesis was simulated using a previously published BARW model.²² In this model, ductal extension is simulated as a persistent random walk. The active tips that drive ductal extension bifurcate stochastically with a constant probability and terminate when they are within a defined annihilation radius of neighboring epithelium.²² Simulated mammary epithelial trees were visualized using gnuplot (version 5.2) and lineage trees were generated using the ETE3 Python toolkit (version 3.1.1).⁶⁷ The alignment fraction of simulated structures was quantified using the same approach for pubertal mammary glands. The epithelial density of simulated structures was quantified using profile plot analysis in ImageJ. TEB termination probability as well as the probability of subtree size and persistence were calculated using MATLAB.

FEM-based model of TEB bifurcation

To investigate how collagen accumulation along the flanks and at the cleft site of a TEB affects the angle of TEB bifurcation, we constructed a 2D computational model of a growing epithelium constricted by a stiff extracellular matrix (ECM), based on our previous work.²⁸

Geometry

The model geometry comprises 3 layers representing the epithelium, ECM, and surrounding stroma all around a central lumen (Figure 7A). At the start of the simulation, each layer consists of a semi-circular region at the end of a rectangular region to emulate the geometry of an un-bifurcated TEB (Figure 7A). The layer of ECM contains gaps on either flank of the TEB where the epithelium may elongate through. The length of the ECM at the flanks of the bud is denoted as L_ECM and the width of the ECM accumulation at the tip of the TEB is denoted as W_ECM.

Mechanical model

In order to allow the tissues in our model to both grow and deform, we decomposed the total deformation into components due to growth and deformation following Rodriguez, et al.⁶⁸ such that the deformation gradient F = F^eF^g, where the growth tensor F^g represents the deformation due to tissue growth and the elastic deformation tensor F^e represents the elastic deformation of the structure.

The total deformation gradient F follows finite deformation theory ⁶⁹ such that

$$\mathit{F}=\mathit{I}+\frac{\mathit{\partial }\mathit{u}}{\mathit{\partial }\mathit{X}}$$ (2)

where u is the displacement field: u = x − X, where X are the coordinates of a material point in the reference configuration and x are the corresponding coordinates of that point in the deformed configuration. All three layers were modeled as purely hyperelastic solids with a stored energy function ψ such that⁶⁹:

$$\psi ({\mathit{F}}^e=\mathit{F}{({\mathit{F}}^g)}^{-1})=\frac{\mu }{2}(I_{\mathit{C}}^e-2)-\mu \ln (J^e)+\frac{\lambda }{2}\ln {(J^e)}^2.$$ (3)

Here, the right Cauchy-Green deformation tensor C is

$$\mathit{C}={({\mathit{F}}^e)}^T{\mathit{F}}^e,$$ (4)

and

$$J^e=\det ({\mathit{F}}^e),I_{\mathit{C}}^e=\mathrm{trace}(\mathit{C}),$$ (5a, b)

where J denotes the Jacobian, and with Lamé parameters:

$$\lambda =\frac{Ev}{(1+v)(1-2v)},\mu =\frac{E}{2(1+v)}.$$ (6a, b)

Figure 7A shows the relative Young’s moduli E of the tissue layers and v = 0.4. A linear, triangular mesh of the geometry was created using Gmsh (version 4.5.6.).⁷⁰

Growth tensor

We considered the epithelium to grow in a direction tangent to its geometry at every point so that

$${\mathit{F}}_{ep}^g={\mathit{e}}_n\otimes {\mathit{e}}_n+g{\mathit{e}}_t\otimes {\mathit{e}}_t\equiv \left[\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & g\hfill \end{array}\right],$$ (7a)

where e_n is the unit normal vector of the epithelium and e_t is the unit tangent vector to the epithelium. At the vertical sides of the epithelium reduces to

$${\mathit{F}}_{ep}^g=\left[\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & g\hfill \end{array}\right],$$ (7b)

and at all points

$${\mathit{F}}_{stroma}^g={\mathit{F}}_{ECM}^g=\left[\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right].$$ (8)

g = 1 at the beginning of the simulation and increases linearly for five timesteps until g = 2.

Boundary conditions

The bottom surface of the model, Γ_b, has displacement u₂ = 0. To prevent translation in the u₁-direction, the displacement of the point in the stroma at the minimum u₂ position is u₁ = 0.

The outside stromal surface is traction-free, but the inner surface of the epithelium, Γ_lumen, has a positive pressure opposite to the unit normal vector n at every point such that the traction force

$$\mathit{t}=-p\mathit{n}$$ (9)

where p = 0.1E_stroma.

To simulate the ECM being strongly tethered in place, we applied a restoring body force on the ECM layer wherever it was stiffer than the stroma (red regions in Figure 7A) proportional to the negative of its displacement vector such that body force

$$\mathit{B}=-b\mathit{u}$$ (10)

where b = 80E_stroma wherever E_ecm is nonzero. We set the magnitude of b much higher than the stiffness of all three tissue layers to ensure that the simulated ECM would not be moved by tissue growth. This reflects the fact that, in vivo, accumulated collagen at TEB tips would be tethered to the surrounding matrix.

Finite element method

We solved the for the energy-minimizing displacement at every timestep numerically using the finite element method.⁷¹ We calculated the displacement u: Ω → R², at each timestep by minimizing the total potential energy of the system⁷²

$$\Pi ={\int }_{\Omega }{J}^g\psi ({\mathit{F}}^e)dX-{\int }_{{\Omega }^{ECM}}\mathit{B}\cdot \mathit{u}d\text{X}-{\int }_{\partial {\Omega }_t^{in}}\mathit{t}\cdot \mathit{u}d\text{s,}$$ (11)

which is equivalent to solving the following system:

$$\begin{gathered} 0=\delta \Pi =\delta {\int }_{\Omega }{J}^g\psi ({\mathit{F}}^e)dX-{\int }_{{\Omega }^{ECM}}\mathit{B}\cdot \delta \mathit{u}dX+{\int }_{\partial {\Omega }_t^{in}}p\mathit{n}\cdot \delta \mathit{u}ds \\ ={\int }_{\Omega }{J}^g\frac{\partial \psi ({\mathit{F}}^e)}{\partial \mathit{u}}\delta \mathit{u}dX+{\int }_{{\Omega }^{ECM}}b\mathit{u}\cdot \delta \mathit{u}d\text{X}+{\int }_{\partial {\Omega }^{in}}p(J{\mathit{F}}^{-T}\mathit{N})\cdot \delta \mathit{u}dS, \end{gathered}$$ (12)

where Eq. 12 corresponds to the balance of the work done by the external forces (pressure p, body force b) with the internal work (stress) written in the reference configuration. In Eq. 12, Ω is the whole domain of the model (reference configuration), Ω^ECM is the ECM domain (Figure 7A), dX is an infinitesimal element of the reference domain, $\partial {\Omega }_t^{in}={\mathrm{\Gamma }}_{\mathit{lumen}}$ is the inner surface of the deformed epithelial domain, ds are the infinitesimal surface elements of the deformed epithelial inner surface, and ∂Ωⁱⁿ and dS are the corresponding domain and elements of the undeformed epithelial inner surface. Note that the test function δu is an arbitrary function, such that δu = 0 on the part of the boundary domain Γ where displacements are prescribed.

The domain Ω was discretized using the triangular mesh generated by Gmsh. We used the open-source FEniCS software (version 2019.1.0)⁷³ to apply the Newton-Raphson algorithm⁷⁴ in each mesh element. Where the Newton-Raphson algorithm failed to converge, we applied the dynamic relaxation method⁷⁵ to find the minimizing u. We used the open-source visualization software ParaView (version 5.7.0)⁷⁶ to plot the resulting displacements. The solution was tested for robustness against mesh refinements. Outlines of simulated epithelial geometry were generated using MATLAB.

QUANTIFICATION AND STATISTICAL ANALYSIS

Unless stated otherwise, experimental and computational data represent the average of 3 and 5 replicates, respectively, and error bars represent the standard deviation of the mean. All statistical analysis was performed using GraphPad Prism (8.0; GraphPad Software, San Diego, CA) and the recommendations in the Prism statistics guide. Statistical comparison of means for normally distributed data was conducted using an unpaired parametric Student’s t test (equal variance; Figure 2F, 4D, S1C, and S2B), Welch’s t test (unequal variance; Figure 4E), one-way ANOVA with Tukey-Kramer multiple comparisons test (Figure 1I and 3I), or two-way ANOVA with Sidak’s (Figure 5B) or Tukey-Kramer multiple comparisons test (Figure 2D, S2C, S5A, and S5B). Sphericity was not assumed for two-way ANOVA analysis, so the Geisser-Greenhouse correction was used. The means of non-normally distributed data were compared using Welch’s one-way ANOVA with Dunnett’s T3 multiple comparisons test (Figure 1F) or the Kruskal-Wallis test with Dunn’s multiple comparisons test (Figure 5D). For sufficiently large samples, normality was determined using the D’Agostino-Pearson test; otherwise, the Shapiro-Wilk test was used. Statistical comparison of variance was conducted using an F test (Figure 4E). P-values less than 0.05 were considered statistically significant. Spearman nonparametric correlation (Figure 3F), Pearson correlation (Figure 3G), or simple linear regression analysis (Figure 6D) was used.

Supplementary Material

3

Video S1. Simulations of epithelial branching with different patterns of ECM. Related to Figure 7 and Figure S6.

4

Video S2. Simulations of epithelial branching with varying extents of ECM accumulation along the flanks of the epithelium. Related to Figure 7 and Figure S6.

5

Video S3. Simulations of epithelial branching with varying extents of ECM accumulation at the leading edge of the epithelium. Related to Figure 7 and Figure S6.

6

Video S4. Simulations of epithelial branching with varying rates of ECM accumulation at the leading edge of the epithelium. Related to Figure 7 and Figure S6.

7

Video S5. Simulations of epithelial branching with varying epithelial stiffness. Related to Figure 7 and Figure S6.

8

Video S6. Simulations of epithelial branching with varying ECM stiffness. Related to Figure 7 and Figure S6.

9

Video S7. Simulations of epithelial branching with varying stromal stiffness. Related to Figure 7 and Figure S6.

10

Video S8. Simulations of epithelial branching with varying epithelial thickness. Related to Figure 7 and Figure S6.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Mouse monoclonal anti-collagen 1	Thermo Fisher Scientific	Cat#MA1–26771 RRID:AB_2081889
Alexa Fluor 488 goat anti-mouse secondary antibody	Thermo Fisher Scientific	Cat#A-11001
Bacterial and Virus Strains
BL21(DE3)	Addgene	N/A
Biological Samples
Chemicals, Peptides, and Recombinant Proteins
Matrigel (growth factor reduced; protein concentration 8.4 mg/ml)	Corning	Cat#354230
Bovine, Type I collagen with intact telopeptide	Advanced BioMatrix	Cat#5026
Hepatocyte growth factor	Sigma-Aldrich	Cat#H9661
Fetal bovine serum	Gemini Bioproducts	Cat#100–106
Calf serum	R&D Systems	Cat#S11450
Dexamethasone	Sigma-Aldrich	Cat#D2915
3- isobutyl-1-methylxanthine	Sigma-Aldrich	Cat#I7018
Ni-NTA resin	Qiagen	Cat#30230
Imidazole	Sigma-Aldrich	Cat#I2399
Lysozyme	Sigma-Aldrich	Cat#L6876
TRIS HCl	Sigma-Aldrich	Cat#T5941
Triethanolamine	Sigma-Aldrich	Cat#90278
Quadrol®	Sigma-Aldrich	Cat#122262
Tissue-Tek® O.C.T. compound	Sakura	Cat#4583
Permount™ mounting medium	Fisher Scientific	Cat#SP15–100
(3,3,3-Trifluoropropyl)trichlorosilane, 97%	Alfa Aesar	Cat#L16670
Critical Commercial Assays
Deposited Data
Experimental Models: Cell Lines
Normal EpH4 mouse mammary epithelial cells	ATCC
3T3-L1 preadipocytes	ATCC	CL-173 RRID:CVCL_0123
Experimental Models: Organisms/Strains
Mouse: CD-1	Charles River Laboratories	Strain code: 022
Mouse: C57BL/6J	The Jackson Laboratory	Jax: 000664
Oligonucleotides
Recombinant DNA
pET28a-mCherry-CNA35	64	Addgene Plasmid #61607 RRID:Addgene_61607
Software and Algorithms
Imaris v9.5.1	Bitplane	https://imaris.oxinst.com/
GraphPad Prism v8.0 and 9.0	GraphPad	https://www.graphpad.com/
MATLAB vR2015b and vR2019a	MathWorks	https://www.mathworks.com/products/matlab.html
Mechanical model of epithelial branching	28	N/A
Branching and annihilating random walk model	22	N/A
ETE3 Python toolkit v 3.1.1	67	http://etetoolkit.org/
gnuplot v5.2	N/A	http://www.gnuplot.info/
Gmsh v4.5.6	70	https://gmsh.info/
ParaView v5.7.0	76	https://www.paraview.org/
FEniCS v2019.1.0	73	https://fenicsproject.org/book/
Other

Highlights.

• Epithelial orientation bias emerges without aligned collagen fibers in the fat pad

• The bifurcation angle of terminal end buds regulates global epithelial orientation

• Local accumulation of extracellular matrix constrains the angle of bifurcation

• The pattern and rate of extracellular matrix accumulation affect bifurcation angle

Abbreviations:

3D

three-dimensional

BARW

branching and annihilating random walk

ECM

extracellular matrix

FEM

finite element method

HGF

hepatocyte growth factor

TEB

terminal end bud

TGF

transforming growth factor