Abstract
Entropy optimization in convective viscous fluids flow due to a rotating cone is explored. Heat expression with heat source/sink and dissipation is considered. Irreversibility with binary chemical reaction is also deliberated. Nonlinear system is reduced to ODEs by suitable variables. Newton built in shooting procedure is adopted for numerical solution. Salient features velocity filed, Bejan number, entropy rate, concentration and temperature are deliberated. Numerical outcomes for velocity gradient and mass and heat transfer rates are displayed through tables. Assessments between the current and previous published outcomes are in an excellent agreement. It is noted that velocity and temperature show contrasting behavior for larger variable viscosity parameter. Entropy rate and Bejan number have reverse effect against viscosity variable. For rising values of thermal conductivity variable both Bejan number and entropy optimization have similar effect.
Subject terms: Engineering, Mathematics and computing
Introduction
Influence of variable viscosity (temperature dependent viscosity) for flow of fluids is more realistic. Augmentation in temperature leads to decay of viscosity of liquids while gases viscosity enhances. In oiling liquids the enhancement in heat creates inner resistance which distresses the fluid viscosity, and therefore viscosity of liquid does not remain constant. Thus it is described to scrutinize the impact of different temperature variable viscosity. Mukhopadhyay and Layek1 studied the radiative convective flow by a porous stretchable surface with temperature dependant viscosity. Impact of variable viscosity in an unsteady magnetohydrodynamic convection flow is investigated by Seddeek2. Salient features of variable properties for thin film flow is explored by Khan et al.3. Hayat et al.4 studied unsteady convective viscous liquids flow. Effect of heat flux on unsteady magnetohydrodynamic viscous liquids flow over a rotating disk is discoursed by Turkyilmazoglu5. Hayat et al.6 scrutinized the behavior of chemical reaction in Jeffrey liquid flow with variable thermal conductivity. Some relevant attempts about variable properties made in Refs.7–10.
The ability of noteworthy improvement apparatus such as spinning cone columns, centrifugal disc atomizers, fluid degausser, rotating packed-bed reactors and centrifugal film evaporators etc. depends upon the nature of motion of liquid and pressure distributions. Rotating cone has utilizations in engineering field, advanced nanotechnology and industrial sites including nuclear reactor, liquid film evaporators and cooling system etc. Shevchuk11 successfully presented the novel numerical and analytical simulations for the various rotating flows like system rotation, swirl flows associated with the swirl generators and surface curvature in bends as well as turns. The impact of centrifugal and Coriolis forces on the distinct flow pattern due to rotating flows was also successfully presented in this scientific continuation. The work of Shevchuk12 visualized the impact of wall temperature in order to inspect the heat transfer characteristics in the laminar flow confined by rotating disk. The analytical solutions for the formulated rotating disk problems were also successfully addressed. In interesting another continuation, Shevchuk13 modeled the turbulent flow problem in presence of heat transfer phenomenon due to rotating disk. The applications of heat and mass transfer pattern in rotating flow of cone and plate devices has been pointed out by Shevchuk14. Turkyilmazoglu15 presented the analytical solutions for a rotating cone problem for viscous fluid. In another continuation, Turkyilmazoglu16 inspected the heat transfer pattern in viscous fluid confined by a rotating cone. Behaviors of variable properties on mixed convection viscous liquid flow with dissipation over a rotating cone are deliberated by Malik et al.17. Turkyilmazoglu18 analyzed the fluctuation in heat transfer mechanism for viscous fluid flow configured by rotating disk in with porous space. Impact of variable viscosity in magnetohydrodynamic flow of Carreau nanofluid by a rotating cone is illustrated by Ghadikolaei et al.19. Sulochana et al.20 studied radiative magnetohydrodynamic flow of laminar liquid with Soret effect over a rotating cone. Salient behaviors of thermal flux in unsteady MHD convective flow due to a rotating cone are presented by Osalusi et al.21. Turkyilmazoglu22 addressed the radially impacted flow of viscous fluid accounted by rotating disk. Asghar et al.23 used Lie group approach to simulate the solution for a rotating flow problem in presence of heat transfer. Turkyilmazoglu24 visualized the flow pattern of triggered fluid due to rotating stretchable disk. The fluid flow due to stationary and moving rotating cone subject to the magnetic force impact has been depicted by Turkyilmazoglu25.
With excellent thermal effectiveness and multidisciplinary applications, the study of nanoparticles becomes the dynamic objective of scientists. The valuable importance of nano-materials in distinct processes includes solar systems, technological processes, engineering devices, nuclear reactors, cooling phenomenon etc. With less than 100 nm size and structure, the nanoparticles are famous due to extra-ordinary thermal performances in contrast to base liquids. In modern medical sciences, the nanoparticles are used to demolish the precarious cancerous tissues. Choi26 presents the novel investigation on nanofluids and examined the extra-ordinary thermal activities of such materials. Later on, many investigations are claimed in the literature to analyze the thermal assessment of nano-materials. For example, Chu27 explained the thermal aspects of third grade nanofluid with significances of activation energy and microorganisms. Majeed et al.28 inspected the improvement in thermal properties of conventional base fluids with interaction of magnetic nano-fluid subject to the dipole effects. Hassan et al.29 visualized the shape factor in ferrofluid with dynamic of oscillating magnetic force. The thermal inspection in Maxwell nanofluid with external impact of heat generation was directed numerically by Majeed et al.30. Khan31 discussed the entropy optimized flow of hybrid nanofluid over a stretched surface of rotating disk. The enhanced features of metallic nanoparticles subject to the magnetic dipole phenomenon were addressed by Majeed et al.32.
In microscopic level the entropy rate is caused due to heat transfer, molecular vibration, dissipation, spin movement, molecular friction, kinetic energy Joule heating etc. and heat loss occurs. For improvement the productivity of numerous thermal schemes, it is necessary to optimize the irreversibility. Thermodynamic second law redirects more significant behaviors in comparison to thermodynamic first law. Thermodynamics second law gives the entropy optimization and scientific tools for decrease of confrontation. It helps us to develop the ability of various engineering improvements. These processes encompass heat conduction and furthermore to calculate the entropy generation rate. Primary attention of entropy generation problems is done by Bejan33. Zhou et al.34 discussed irreversibility analysis about convective flow of nanoliquids in a cavity. Salient characteristics of thermophoretic and Brownian diffusion in flow of Prandtl-Eyring liquids with entropy optimization are exemplified by Khan et al.35. Irreversibility analysis in magnetohydrodynamic flow of Carreau nanofluids through Buongiorno nanofluid model is validated by Khan et al.36. Jiang and Zhou37 studied viscous nanoliquid flow with irreversibility. Some advancement about irreversibility analysis is given in Refs.38–45.
The above presented research work, it is observed that no determination has been completed to investigate the irreversibility consideration for convective viscous fluid flow over a rotating cone. Therefore intension in this paper is to scrutinize the irreversibility for mixed convection reactive flow of viscous fluid by a rotating cone. Heat transfer is demonstrated with heat generation/absorption and dissipation. Furthermore a physical characteristic of entropy is considered. Nonlinear governing system is altered to ODEs. The given system is than tackled through NDSolve procedure. Prominent characteristics of different engineering variable on velocity field, entropy rate, Bejan number, concentration and temperature are realistically examined. The computational outcomes of surface drag force, heat transfer rate and gradient of concentration are scrutinized via different remarkable parameters.
Formulation
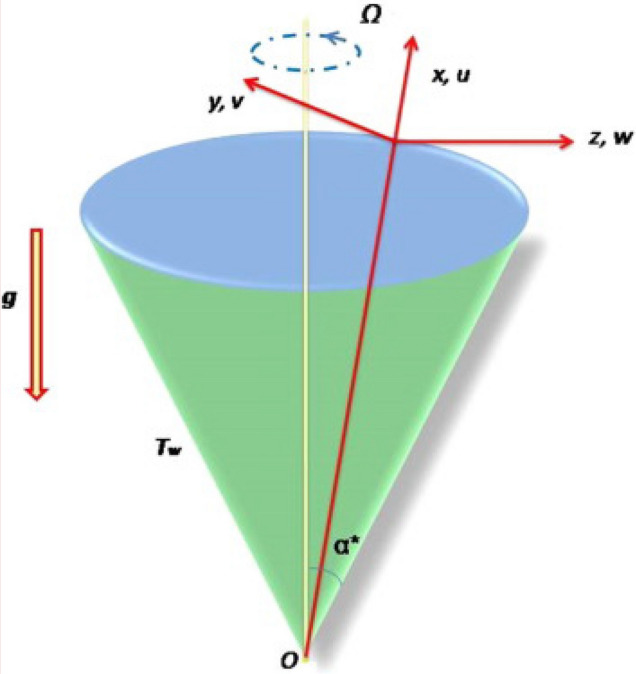
We examine mixed convective flow of incompressible laminar fluid over a rotating cone. Angular velocity is denoted by . Energy expression with heat source/sink and dissipation is considered. Innovative behaviors regarding entropy optimization is accounted. First order chemical reaction is deliberated. The resistive force arises owing to variation in concentration and temperature in the liquid and flow is axi-symmetric. The acceleration associated with gravitational force are assumed along the downward direction. Figure 1 describes the physical model9,10.
Figure 1.
The related expressions are15,16:
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
with
| 6 |
here viscosity and conductivity are employed in the forms44
| 7 |
| 8 |
| 9 |
| 10 |
here denotes the density, the constant viscosity, and the velocity components, the semi-vertical angle, the coefficient of solutal expansion, the variable viscosity parameter, the thermal coefficient expansion, , the temperature, the constant thermal conductivity, the specific heat, the wall temperature, the variable thermal conductivity parameter, the ambient temperature, the heat generation/absorption coefficient, the concentration, the dimensionless angular velocity, the ambient concentration the mass diffusivity, the wall concentration and the chemical reaction rate.
Letting
| 11 |
one has
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
where shows the mixed convection parameter, the Reynold number, the Grashoff number, the buoyancy ratio variable, the Eckert number, the Prandtl number, the heat generation variable, the chemical reaction variable and the Schmidt number.
Entropy modeling
Mathematically entropy optimization is given by41–43:
| 17 |
while after utilization of Eq. (11) yields41–43:
| 18 |
Bejan number is given as41–43:
| 19 |
or
| 20 |
in which signifies the entropy rate, the Brinkman number, the concentration ratio parameter, the temperature difference variable, dimensionless parameter and the diffusion variable.
Physical quantities
Velocity gradient
Surface drag forces are given as
| 21 |
with and as shear stresses are given by
| 22 |
Finally we can write
| 23 |
Nusselt number
It is expressed as
| 24 |
with heat flux represented by
| 25 |
now
| 26 |
Mass transfer rate
Sherwood number is
| 27 |
with as mass flux through following expression
| 28 |
Finally we have
| 29 |
Validation of results
Tables 1 and 2 are provided to authenticate the precision of current outcome with aforementioned published outcomes in literature. These tables deliberated the evaluation of velocity gradient and Nusselt number versus increasing values of with those of Saleem and Nadeem34 and Chamka et al.35. These outcomes are established in good agreement.
Table 1.
| Saleem and Nadeem44 | Chamka et al.45 | Recent results | |||||
|---|---|---|---|---|---|---|---|
| 0.7 | 0.0 | 1.0255 | 0.6154 | 1.0255 | 0.6158 | 1.0255 | 0.6156 |
| 1.0 | 2.2010 | 0.8493 | 2.2012 | 0.8496 | 2.2010 | 0.8494 | |
| 10.0 | 8.5042 | 1.3992 | 8.5041 | 1.3995 | 8.5043 | 1.3992 | |
| 10.0 | 0.0 | 1.0255 | 0.6158 | 1.0256 | 0.6158 | 1.0256 | 0.6158 |
| 1.0 | 1.5630 | 0.6835 | 1.5636 | 0.6837 | 1.5631 | 0.6835 | |
| 10.0 | 5.0820 | 0.9845 | 5.0821 | 0.9840 | 5.0822 | 0.9842 | |
Table 2.
Physical description
Noticeable performances of various sundry variables about entropy rate, temperature, velocity field, Bejan number and concentration and are deliberated through graphs. Velocity gradient and Nusselt and Sherwood numbers are numerically computed against various parameters. The analysis is performed for flow parameters with specified numerical values range like and
Velocity
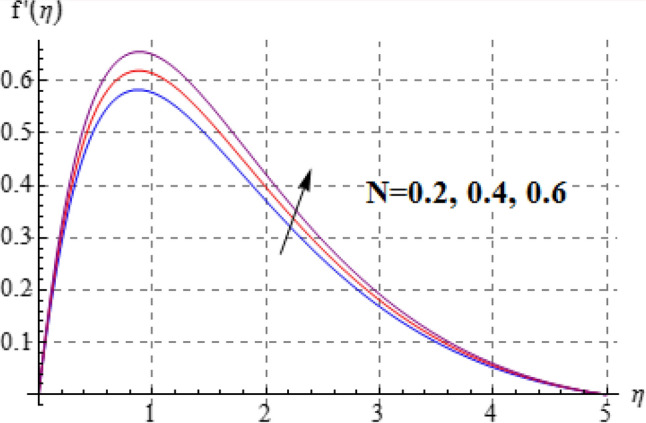
Salient effects of , and on (tangential velocity) and (azimuthal velocity) are examined in Figs. 2, 3, 4, 5, 6 and 7. Figure 2 depicts characteristics of tangential velocity for viscosity parameter . For increasing values of an enhancement occurs in . Characteristic of on is exposed in Fig. 3. Clearly is a decaying function of viscosity parameter . In fact increments in leads to reduction in temperature difference (convective potential) between ambient fluid heated surface and as a result azimuthal velocity decays. Figures 4 and 5 scrutinize the behaviors of on (tangential velocity) and (azimuthal velocity). One can find that and have reverse effects via larger . In fact augmentation in makes the fluid viscous and consequently decreases. Characteristics of on and are demonstrated in Figs. 6 and 7. These figures demonstrates that higher estimation of improves the tangential velocity , while reverse effect holds for azimuthal velocity .
Figure 2.

against A.
Figure 3.
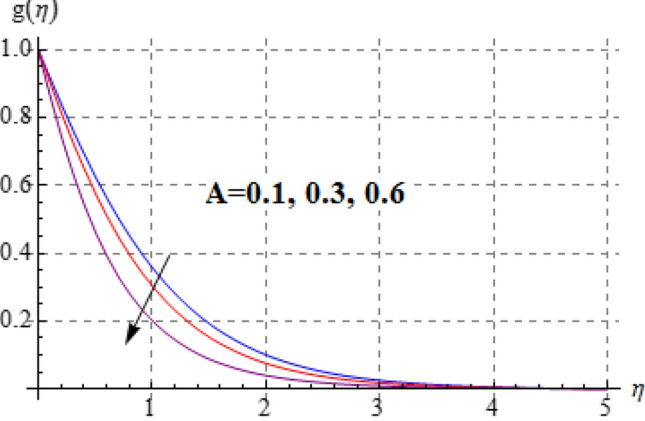
against A.
Figure 4.
against N.
Figure 5.
against N.
Figure 6.
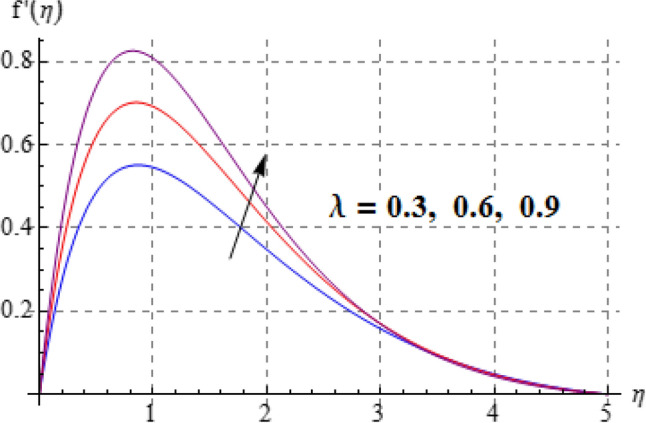
against .
Figure 7.
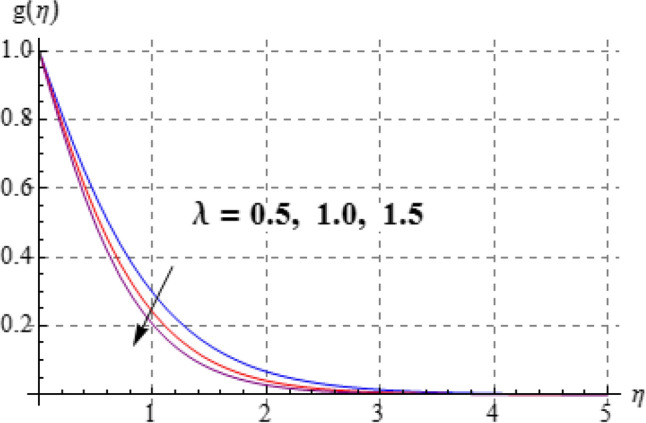
against .
Temperature
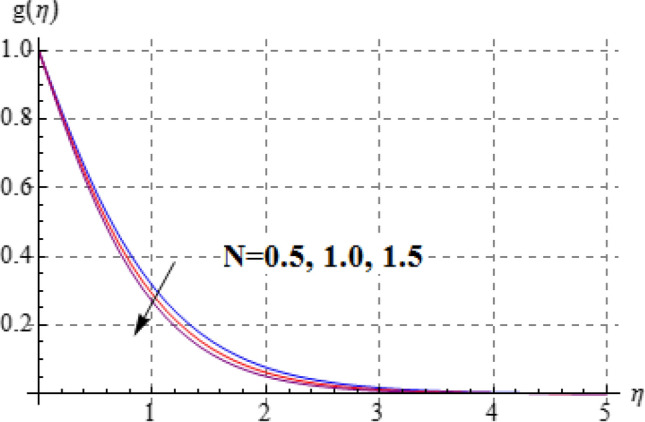
Figures 8, 9, 10, 11 and 12 have been displayed to explore behavior of pertinent variables like , , , and on . Figure 8 studied effect of viscosity variable on . Clearly temperature is a decreasing function of . Outcome of (Br) on temperature is sketched in Fig. 9. Here the increasing values of corresponds to an augmentation in . For larger Brinkman number the slower heat transmission is produced by viscous force and therefore boosts up. Figure 10 interprets the behaviors of on temperature. We noted that temperature improves through . Variation of on is interpreted in Fig. 11. Temperature against rises. Figure 12 is devoted to see the outcome of on . Clearly larger the thermal layer reduces which improves and heat transfer rate improves. Therefore decays.
Figure 8.
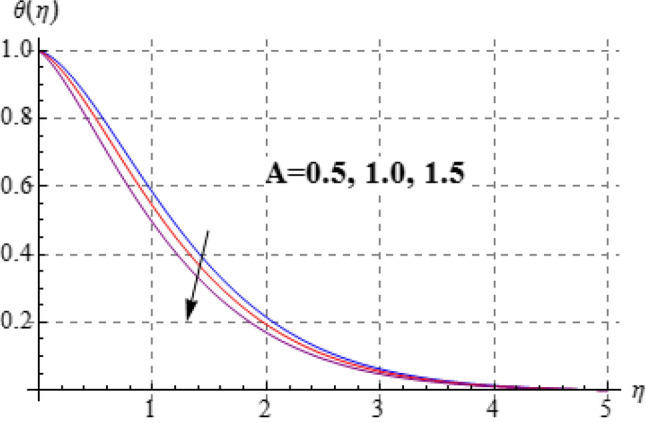
against A.
Figure 9.

against Br.
Figure 10.
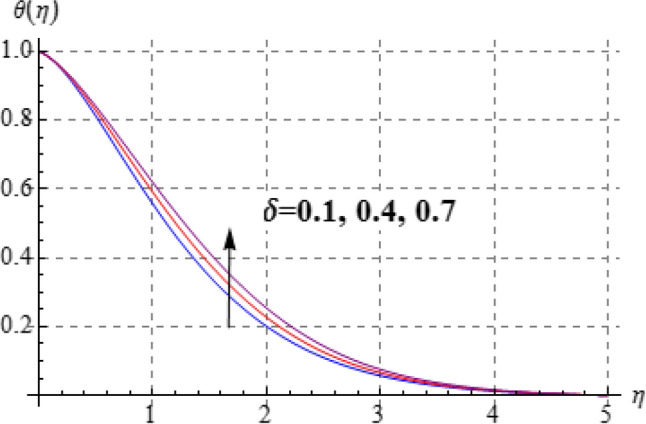
against .
Figure 11.
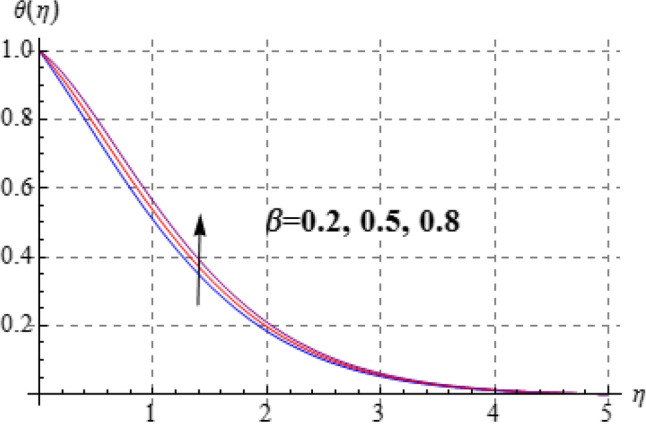
against .
Figure 12.
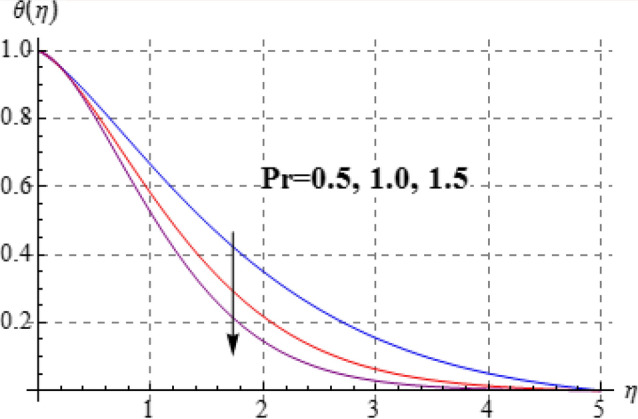
against .
Concentration
Impact of on is plotted in Fig. 13. Through Schmidth number, the concentration decays. Figure 14 is depicts the characteristics of on concentration . Clearly is diminished for higher estimation of . The fluid acts thick for higher and so reduction in occurs.
Figure 13.
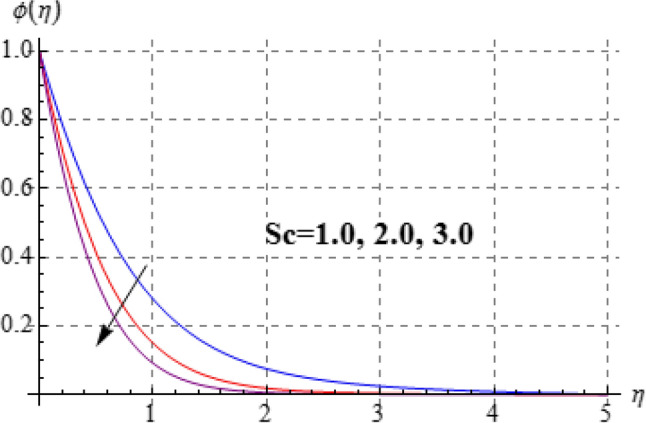
against .
Figure 14.
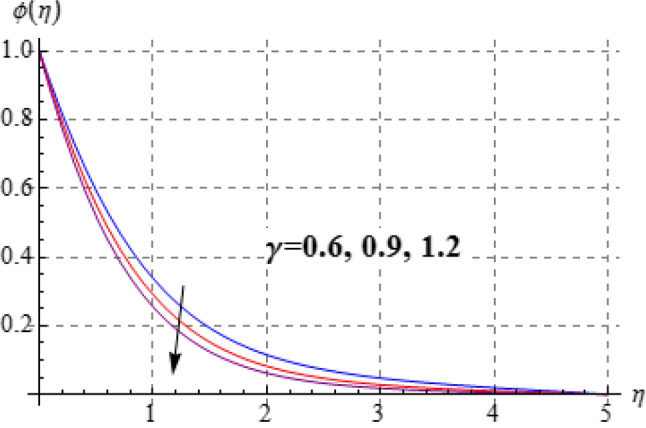
against .
Entropy and Bejan number
Figures 15, 16, 17, 18, 19, 20, 21 and 22 are devoted to scrutinize the behaviors of various interesting parameter like viscosity parameter , thermal conductivity parameter , diffusion parameter and Brinkman number on and . Figures 15 and 16 are depicted to explore the effect of on and . Here and have opposite impact for increasing values of . Variation of on and is shown in Figs. 17 and 18. Clearly increasing values of give rise to both the and . Figures 19 and 20 are devoted to see the behavior of on and . Clearly for larger both and have increasing behaviors. Figures 21 and 22 display impact of and for Brinkman number . Larger Brinkman number rises the entropy generation. Figure 22 shows that for rising values of the decays.
Figure 15.
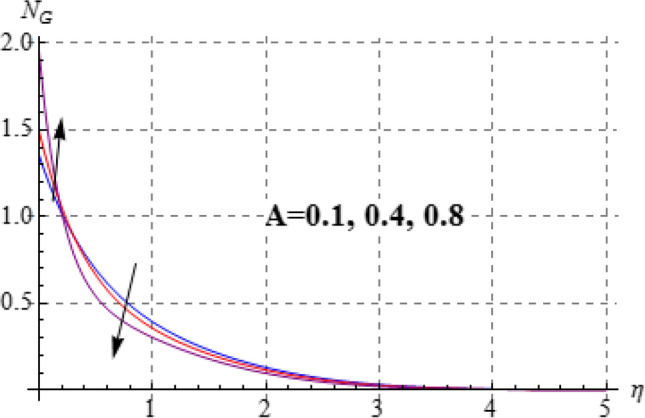
against A.
Figure 16.
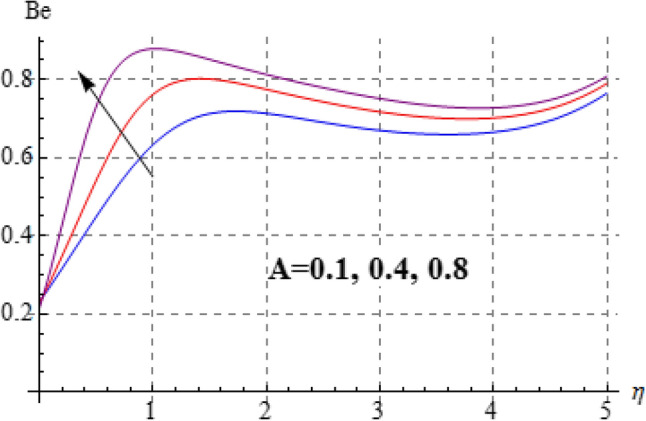
against A.
Figure 17.
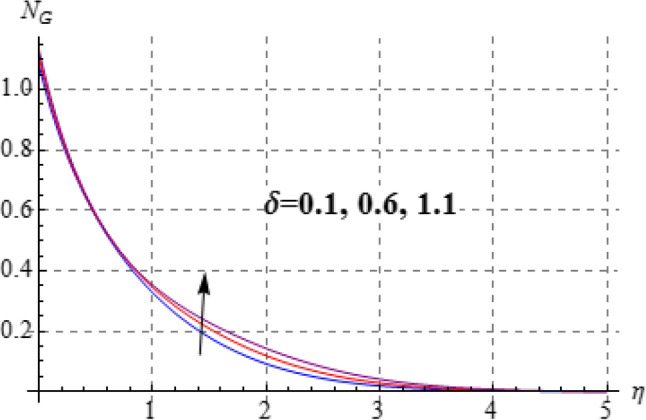
against .
Figure 18.
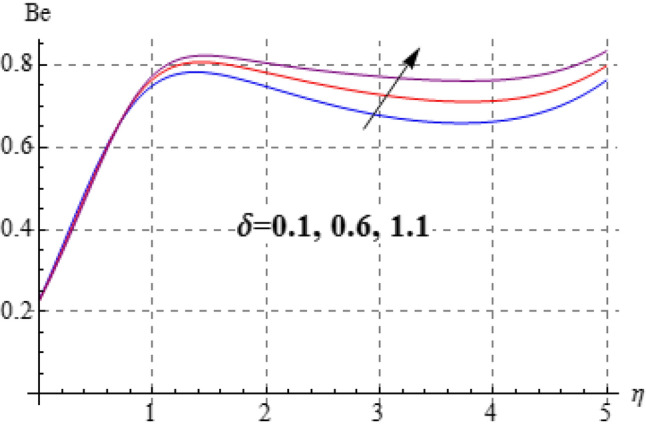
against .
Figure 19.
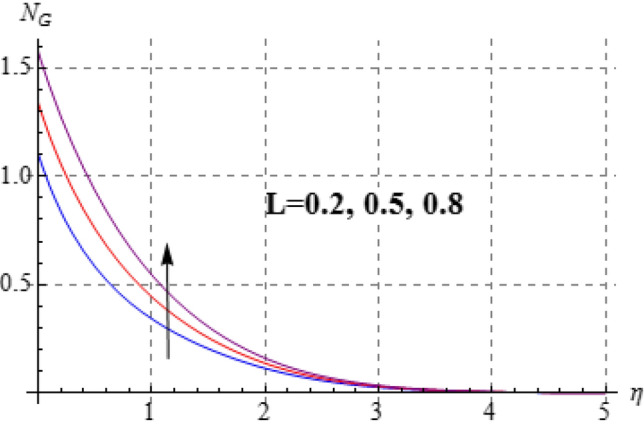
against L.
Figure 20.

against L.
Figure 21.
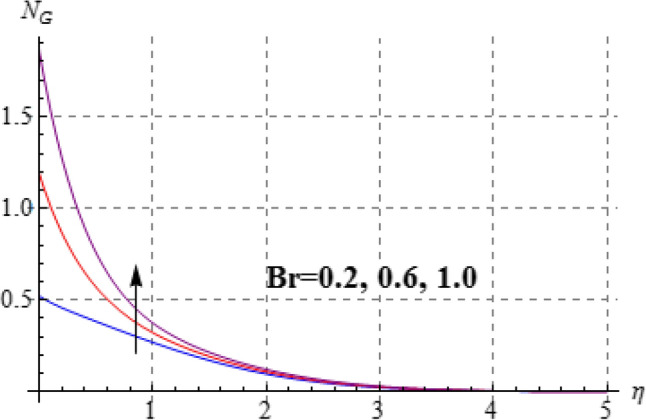
against Br.
Figure 22.
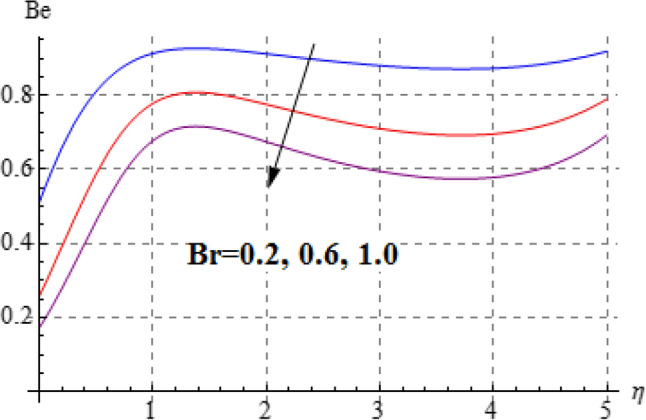
against Br.
Analysis for engineering quantities
Here impacts of various influencing variables on gradient of velocity ( and ) along azimuthal and tangential direction respectively, mass transfer rate and gradient of temperature are discussed in Tables 3, 4, and 5.
Table 3.
Computational outcomes of .
| Surface drag force | |||
|---|---|---|---|
| 1 | 0.2 | 1.1345 | 0.46536 |
| 3 | 2.02356 | 0.76543 | |
| 5 | 3.0145 | 1.45362 | |
| 2 | 0.2 | 0.89654 | 0.80983 |
| 0.4 | 0.75643 | 0.69954 | |
| 0.6 | 0.65874 | 0.56432 | |
Table 4.
Computational outcomes of .
| 0.0 | 0.7 | 2.0 | 0.2 | 0.6126 |
| 0.5 | 0.5325 | |||
| 1.0 | 0.4765 | |||
| 1.0 | 1.0 | 2.0 | 0.2 | 1.6875 |
| 3.0 | 1.7894 | |||
| 5.0 | 1.9283 | |||
| 1.0 | 0.7 | 1.0 | 0.2 | 0.7865 |
| 2.0 | 0.6923 | |||
| 3.0 | 0.6198 | |||
| 1.0 | 0.7 | 2.0 | 0.2 | 0.7967 |
| 0.4 | 0.6987 | |||
| 0.6 | 0.6089 |
Table 5.
Numerical value of .
| 0.0 | 0.4 | 0.1 | 0.56796 |
| 0.5 | 0.60289 | ||
| 1.0 | 0.64156 | ||
| 0.5 | 0.1 | 0.1 | 0.45342 |
| 0.3 | 0.49786 | ||
| 0.5 | 0.53675 | ||
| 0.5 | 0.4 | 0.2 | 0.5745 |
| 0.5 | 0.6745 | ||
| 0.8 | 0.7981 |
Velocity gradient
The numerical results of via various interesting parameters like viscosity parameter and mixed convection parameter are analyzed in Table 3. Clearly one can find that an increment occurs in via increasing values of . From this table it is noted that for larger estimation of viscosity variable the are decreased.
Temperature gradient
Influences of different sundry variables like , , and on is scrutinized in Table 4. Nusselt number in enhanced for larger and . Further is decreased for higher viscosity parameter and thermal conductivity parameter .
Sherwood number
The computational outcomes of via various flow variables are studied in Table 5. Here has similar characteristics for larger and . We noticed that rises via .
Conclusions
The applications of entropy generation phenomenon in the convective transport of viscous nanofluid due to rotating cone have been addressed in presence of viscous dissipation and heat generation. The analysis is performed in presence of variable thermal conductivity and fluid viscosity. The key observations are given below.
The tangential velocity and azimuthal velocity have contradictory behavior for mixed convection parameters.
The applications of viscosity parameter show increasing effects on tangential velocity.
The tangential velocity boosts up via buoyancy ratio variable.
The nanofluid temperature is enhanced for larger heat generation variable it decreased for viscosity parameter.
The nanofluid concentration is decreased for higher values of chemical reaction variable and Schmidt number.
The entropy rate and Bejan number are enhanced for diffusion variable.
The entropy rate upsurges versus Brinkman number.
The entropy rate and Bejan number have reverse effects for viscosity parameter.
The wall shear force increase via higher mixed convection parameter.
The surface drag force is diminished against viscosity parameter as it is reversely related to the magnitude of drag force per unit area.
The Nusselt number is increased for larger Prandtl number.
Gradient of temperature versus Brinkman number decreases.
Acknowledgements
“The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT”. Moreover, this research project is supported by Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2021 under project number 64A306000005.
Author contributions
All authors are equally contributed in the manuscript.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Zahir Shah, Email: zahir@ulm.edu.pk.
Poom Kumam, Email: poom.kum@kmutt.ac.th.
References
- 1.Mukhopadhyay S, Layek GC. Effects of thermal radiation and variable fluid viscosity on free convective flow and heat transfer past a porous stretching surface. Int. J. Heat Mass Tranf. 2008;51:2167–2178. doi: 10.1016/j.ijheatmasstransfer.2007.11.038. [DOI] [Google Scholar]
- 2.Seddeek MA. Effects of radiation and variable viscosity on a MHD free convection flow past a semi-infinite flat plate with an aligned magnetic field in the case of unsteady flow. Int. J. Heat Mass Tranf. 2002;45:931–935. doi: 10.1016/S0017-9310(01)00189-2. [DOI] [Google Scholar]
- 3.Khan Y, Wu Q, Faraz N, Yildirim A. The effects of variable viscosity and thermal conductivity on a thin film flow over a shrinking/stretching sheet. Comput. Math. Appl. 2011;61:3391–3399. doi: 10.1016/j.camwa.2011.04.053. [DOI] [Google Scholar]
- 4.Hayat T, Khan MI, Farooq M, Gull N, Alsaedi A. Unsteady three-dimensional mixed convection flow with variable viscosity and thermal conductivity. J. Mol. Liq. 2016;223:1297–1310. doi: 10.1016/j.molliq.2016.09.069. [DOI] [Google Scholar]
- 5.Turkyilmazoglu M. Thermal radiation effects on the time-dependent MHD permeable flow having variable viscosity. Int. J. Ther. Sci. 2011;50:88–96. doi: 10.1016/j.ijthermalsci.2010.08.016. [DOI] [Google Scholar]
- 6.Hayat T, Khan MI, Farooq M, Alsaedi A, Waqas M, Yasmeen T. Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Tranf. 2016;99:702–710. doi: 10.1016/j.ijheatmasstransfer.2016.04.016. [DOI] [Google Scholar]
- 7.Waqas H, Imran M, Khan SU, Shehzad SA, Meraj MA. Slip flow of Maxwell viscoelasticity-based micropolar nanoparticles with porous medium: A numerical study. Appl. Math. Mech. (English Edition) 2019;40:1255–1268. doi: 10.1007/s10483-019-2518-9. [DOI] [Google Scholar]
- 8.Sun X, Wang S, Zhao M. Numerical solution of oscillatory flow of Maxwell fluid in a rectangular straight duct. Appl. Math. Mech. (English Edition) 2019;40:1647–1656. doi: 10.1007/s10483-019-2535-6. [DOI] [Google Scholar]
- 9.Khan SA, Hayat T, Khan MI, Alseadi A. Salient features of Dufour and Soret effect in radiative MHD flow of viscous fluid by a rotating cone with entropy generation. Int. J. Hydrogen Energy. 2020;45:14552–14564. doi: 10.1016/j.ijhydene.2020.03.123. [DOI] [Google Scholar]
- 10.Hayat T, Khan SA, Khan MI, Alseadi A. Irreversibility characterization and investigation of mixed convective reactive flow over a rotating cone. Comput. Meth. Prog. Biomed. 2020;185:105168. doi: 10.1016/j.cmpb.2019.105168. [DOI] [PubMed] [Google Scholar]
- 11.Shevchuk IV. Modelling of Convective Heat and Mass Transfer in Rotating Flow. Springer; 2016. [Google Scholar]
- 12.Shevchuk IV. Effect of the wall temperature on laminar heat transfer in a rotating disk: An approximate analytical solution. TVT. 2001;39(4):682–685. [Google Scholar]
- 13.Shevchuk IV. Turbulent heat transfer of rotating disk at constant temperature or density of heat flux to the wall. High Temp. 2000;38:499–501. doi: 10.1007/BF02756017. [DOI] [Google Scholar]
- 14.Shevchuk IV. Laminar heat and mass transfer in rotating cone-and-plate devices. J. Heat Transfer. 2011;133(2):024502. doi: 10.1115/1.4002606. [DOI] [Google Scholar]
- 15.Turkyilmazoglu M. On the purely analytic computation of laminar boundary layer flow over a rotating cone. Int. J. Eng. Sci. 2009;47(9):875–882. doi: 10.1016/j.ijengsci.2009.05.008. [DOI] [Google Scholar]
- 16.Turkyilmazoglu M. A note on the induced flow and heat transfer due to a deforming cone rotating in a quiescent fluid. J. Heat Transfer. 2018;140(12):124502. doi: 10.1115/1.4041184. [DOI] [Google Scholar]
- 17.Malik MY, Jamil H, Salahuddin T, Bilal S, Rehman KU, Mustafa Z. Mixed convection dissipative viscous fluid flow over a rotating cone by way of variable viscosity and thermal conductivity. Results Phy. 2016;6:1126–1135. doi: 10.1016/j.rinp.2016.11.027. [DOI] [Google Scholar]
- 18.Turkyilmazoglu M. Purely analytic solutions of the compressible boundary layer flow due to a porous rotating disk with heat transfer. Phys. Fluids. 2009;21:106104. doi: 10.1063/1.3249752. [DOI] [Google Scholar]
- 19.Ghadikolaei SS, Hosseinzadeh K, Ganji DD. Investigation on ethylene glycol-water mixture fluid suspend by hybrid nanoparticles (TiO2–CuO) over rotating cone with considering nanoparticles shape factor. J. Mol. Liq. 2018;272:226–236. doi: 10.1016/j.molliq.2018.09.084. [DOI] [Google Scholar]
- 20.Sulochana C, Samrat SP, Sandeep N. Numerical investigation of magnetohydrodynamic (MHD) radiative flow over a rotating cone in the presence of Soret and chemical reaction. Propul. Power Resear. 2018;7:91–101. doi: 10.1016/j.jppr.2018.01.001. [DOI] [Google Scholar]
- 21.Bejan A. Method of entropy generation minimization, or modeling and optimization based on combined heat transfer and thermodynamics. Rev. Generale de Thermique. 1996;35:637–646. doi: 10.1016/S0035-3159(96)80059-6. [DOI] [Google Scholar]
- 22.Turkyilmazoglu M. Effects of uniform radial electric field on the MHD heat and fluid flow due to a rotating disk. Int. J. Eng. Sci. 2012;51:233–240. doi: 10.1016/j.ijengsci.2011.09.011. [DOI] [Google Scholar]
- 23.Asghar S, Jalil M, Hussan M, Turkyilmazoglu M. Lie group analysis of flow and heat transfer over a stretching rotating disk. Int. J. Heat Mass Transf. 2014;69:140–146. doi: 10.1016/j.ijheatmasstransfer.2013.09.061. [DOI] [Google Scholar]
- 24.Turkyilmazoglu M. Latitudinally deforming rotating sphere. Appl. Math. Model. 2019;71:1–11. doi: 10.1016/j.apm.2019.01.016. [DOI] [Google Scholar]
- 25.Turkyilmazoglu M. On the fluid flow and heat transfer between a cone and a disk both stationary or rotating. Math. Comput. Simulat. 2020;177:329–340. doi: 10.1016/j.matcom.2020.04.004. [DOI] [Google Scholar]
- 26.Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995;231:99–106. [Google Scholar]
- 27.Chu Y, Khan MI, Khan NB, Kadry S, Khan SU, Tlili I, Nayak MK. Significance of activation energy, bio-convection and magnetohydrodynamic in flow of third grade fluid (non-Newtonian) towards stretched surface: A Buongiorno model analysis. Int. Commun. Heat Mass Transfer. 2020;118:104893. doi: 10.1016/j.icheatmasstransfer.2020.104893. [DOI] [Google Scholar]
- 28.Majeed A, Zeeshan A, Bhatti MM, Ellahi R. heat transfer in magnetite (Fe3O4) nanoparticles suspended in conventional fluids: Refrigerant-134a (C2H2F4), kerosene (C10H22), and water (H2o) under the impact of dipole. Heat Transf. Res. 2020;51(3):217–232. doi: 10.1615/HeatTransRes.2019029919. [DOI] [Google Scholar]
- 29.Hassan, M., Fetecau, C., Majeed, A., Zeeshan, A. Effects of iron nanoparticles’ shape on convective flow of ferrofluid under highly oscillating magnetic field over stretchable rotating disk. J. MagN. Mag. Mater.465, 531–539 (2018).
- 30.Majeed A, Zeeshan A, Noori FM, Masud U. Influence of rotating magnetic field on Maxwell saturated ferrofluid flow over a heated stretching sheet with heat generation/absorption. Mech. Ind. 2019;20(5):502. doi: 10.1051/meca/2019022. [DOI] [Google Scholar]
- 31.Khan MI. Transportation of hybrid nanoparticles in forced convective Darcy-Forchheimer flow by a rotating disk. Int. Commu. Heat Mass Transf. 2021;122:105177. doi: 10.1016/j.icheatmasstransfer.2021.105177. [DOI] [Google Scholar]
- 32.Majeed A, Zeeshan A, Hayat T. Analysis of magnetic properties of nanoparticles due to applied magnetic dipole in aqueous medium with momentum slip condition. Neural Comput. Appl. 2019;31:189–197. doi: 10.1007/s00521-017-2989-5. [DOI] [Google Scholar]
- 33.Bejan A. A study of entropy generation in fundamentsl convective heat transfer. J. Heat Transf. 1979;101:718–725. doi: 10.1115/1.3451063. [DOI] [Google Scholar]
- 34.Zhou X, Jiang Y, Li X, Cheng K, Huai X, Zhang X, Huang H. Numerical investigation of heat transfer enhancement and entropy generation of natural convection in a cavity containing nano liquid-metal fluid. Int. Commun. Heat Mass Tranf. 2019;106:46–54. doi: 10.1016/j.icheatmasstransfer.2019.05.003. [DOI] [Google Scholar]
- 35.Khan MI, Khan SA, Hayat T, Khan MI, Alsaedi A. Nanomaterial based flow of Prandtl-Eyring (non-Newtonian) fluid using Brownian and thermophoretic diffusion with entropy generation. Comput. Meth. Prog. Biomed. 2019;180:105017. doi: 10.1016/j.cmpb.2019.105017. [DOI] [PubMed] [Google Scholar]
- 36.Khan MI, Kumar A, Hayat T, Waqas M, Singh R. Entropy generation in flow of Carreau nanofluid. J. Mol. Liq. 2019;278:677–687. doi: 10.1016/j.molliq.2018.12.109. [DOI] [Google Scholar]
- 37.Jiang Y, Zhou X. Heat transfer and entropy generation analysis of nanofluids thermocapillary convection around a bubble in a cavity. Int. Commun. Heat Mass Transf. 2019;105:37–45. doi: 10.1016/j.icheatmasstransfer.2019.03.013. [DOI] [Google Scholar]
- 38.Khan SA, Khan MI, Hayat T, Alsaedi A. Physical aspects of entropy optimization in mixed convective MHD flow of carbon nanotubes (CNTs) in a rotating frame. Phys. Script. 2019;94:125009. doi: 10.1088/1402-4896/ab36cd. [DOI] [Google Scholar]
- 39.Parveen R, Mahapatra TR. Numerical simulation of MHD double diffusive natural convection and entropy generation in a wavy enclosure filled with nanofluid with discrete heating. Heliyon. 2019;5:e02496. doi: 10.1016/j.heliyon.2019.e02496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Alsaadi FE, Hayat T, Khan MI, Alsaadi FE. Heat transport and entropy optimization in flow of magneto-Williamson nanomaterial with Arrhenius activation energy. Comput. Meth. Prog. Biomed. 2020;183:105051. doi: 10.1016/j.cmpb.2019.105051. [DOI] [PubMed] [Google Scholar]
- 41.Khan MI, Hayat T, Khan MI, Waqas M, Alsaedi A. Numerical simulation of hydromagnetic mixed convective radiative slip flow with variable fluid properties: A mathematical model for entropy generation. J. Phy. Chem. Solid. 2019;125:153–164. doi: 10.1016/j.jpcs.2018.10.015. [DOI] [Google Scholar]
- 42.Alsaadi FE, Hayat T, Khan SA, Alsaadi FE, Khan MI. Investigation of physical aspects of cubic autocatalytic chemically reactive flow of second grade nanomaterial with entropy optimization. Comput. Meth. Prog. Biomed. 2020;183:105061. doi: 10.1016/j.cmpb.2019.105061. [DOI] [PubMed] [Google Scholar]
- 43.Ganesh NV, Mdallal QMA, Chamkha AJ. A numerical investigation of Newtonian fluid flow with buoyancy, thermal slip of order two and entropy generation. Case Stud. Ther. Eng. 2019;13:100376. doi: 10.1016/j.csite.2018.100376. [DOI] [Google Scholar]
- 44.Saleem S, Nadeem S. Theoretical analysis of slip flow on a rotating cone with viscous dissipation effects. J. Hydrodyn. 2015;27:616–623. doi: 10.1016/S1001-6058(15)60523-6. [DOI] [Google Scholar]
- 45.Chamkha AJ, Al-Mudhaf A. Unsteady heat and mass transfer from a rotating vertical cone with a magnetic field and heat generation or absorption effects. Int. J. Therm. Sci. 2005;44:267–276. doi: 10.1016/j.ijthermalsci.2004.06.005. [DOI] [Google Scholar]


