Summary
A frequent assumption in value-based decision-making tasks is that agents make decisions based on the feature dimension that reward probabilities vary on. However, in complex, multidimensional environments, stimuli can vary on multiple dimensions at once, meaning that the feature deserving the most credit for outcomes is not always obvious. As a result, individuals may vary in the strategies used to sample stimuli across dimensions, and these strategies may have an unrecognized influence on decision-making. Sex is a proxy for multiple genetic and endocrine influences on decision-making strategies, including how environments are sampled. In this study, we examined the strategies adopted by female and male mice as they learned the value of stimuli that varied in both image and location in a visually-cued two-armed bandit, allowing two possible dimensions to learn about. Female mice acquired the correct image-value associations more quickly than male mice, and they used a fundamentally different strategy to do so. Female mice were more likely to adopt a strategy of constraining their decision-space early in learning by preferentially sampling one location over which images varied. Conversely, male mice tended to be inconsistent - changing their choice frequently and responding to the immediate experience of stochastic rewards. Individual strategies were related to sex-biased changes in neuronal activation in early learning. Together, we find that in mice, sex is linked with divergent strategies for sampling and learning about the world, revealing substantial unrecognized variability in the approaches implemented during value-based decision-making.
Introduction
Value-based decision-making tasks are used to determine the cognitive and neural mechanisms for reward learning and choice [1–4]. One frequent assumption is that agents make their decisions based on the feature dimension that the experimenter has designed the reward probabilities to vary on. However, in complex, multidimensional environments, stimuli can vary on multiple feature dimensions such as identity and location simultaneously, and the features that predict reward outcomes are not always obvious [5]. As a result of this complexity, differences in learning and decision-making within and between individuals could result as much from differences in the strategies employed to learn, as they could from the capacity to learn. Understanding the diversity of strategies employed during multidimensional decision-making, and the factors that influence strategy selection, is not only essential for understanding typical decision-making, but also vulnerability to neuropsychiatric disease [6–9].
Rodents, particularly mice, are increasingly used to probe the neural mechanisms of value-based decision-making [3,10–14], and can be tested in large numbers to allow the analysis of individual differences in decision strategies, including the influence of sex differences. Sex is a proxy for multiple genetic, developmental, and endocrine mechanisms that vary across individuals [15–17] and could be a source of diversity in learning strategies [18–20]. Indeed, sex differences in rodents (and gender differences in humans) appear in a variety of value-based decision-making tasks, but these effects are frequently inconsistent with a simple difference in learning rates [21–23], suggesting sex influences on latent strategies as an alternative hypothesis. However, much of this literature has used tasks with low trial counts and/or choices that vary on only one dimension, which are not well-suited to elucidating the strategies employed during decision-making in higher dimensional environments.
To determine whether there are sex differences in the strategies employed during value-based decision-making, we trained male and female mice on a two-dimensional decision-making task: a visual bandit [1,2,4,24–28]. While all animals eventually reached the same performance level, female mice learned more rapidly than males on average. Because choice could vary in two dimensions [29,30], we asked whether individual animals were adopting different strategies during learning. Sex explained a substantial fraction of individual variability in strategy. Female mice were more likely to systematically confine their choices to one spatial location, accelerating their learning about image values by constraining the decision-space. Conversely, males used a combination of image and spatial dimensions, were sensitive to the stochastic experience of reward, and changed choice strategies frequently. During early learning, gene expression for the neuronal activation marker c-fos in the nucleus accumbens and prefrontal cortex significantly correlated with the female-biased strategy. These results show that individuals adopt widely divergent strategies for interacting with the same uncertain world, and that sex is a factor in guiding these strategies.
Results
Age-matched male and female wildtype mice (n=32, 16 per sex) were trained to perform a visually-cued two-armed bandit task (Figure 1a). This visually-cued task design was similar to those employed in humans and nonhuman primates [1,2,4,24–28,31,32], in contrast to the spatial bandit designs frequently employed with rodents [33–36]. Animals were presented with a repeating set of two different image cues which were each associated with different probabilistic reward outcomes (80%/20%) (Figure 1b). Reward contingencies were yoked to image identity, which was randomized with respect to location on each trial. This means that the sides (left/right) where image cues appeared were not informative of the reward contingencies. We repeated the task with six different sets of image pairs. Two out of six image pairs were excluded before analysis due to extremely high initial preference (>70%) for one image. We included four image pairs with equal initial preference for each image and quantified behavioral data in bins of 150 trials for each animal.
Figure 1. Females showed accelerated acquisition of the high reward probability image in a stochastic two-armed visual bandit task.
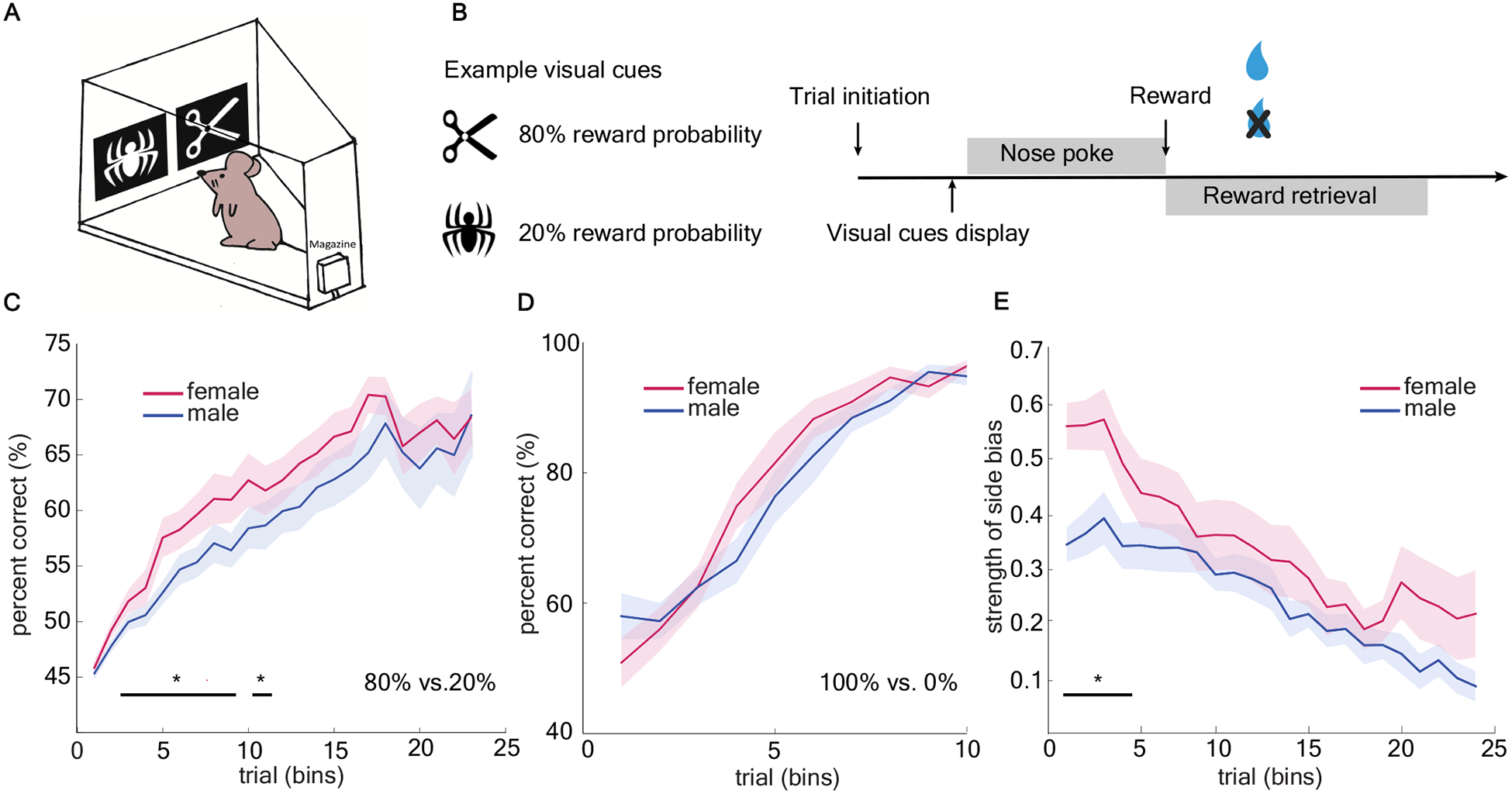
A) Schematic of the mouse touch-screen operant chamber. B) Schematic of two-armed visual bandit task. Images varied between the two locations across trials. C) Average learning performance (percent correct) across four repetitions of the task in males and females. D) No sex difference in learning performance was observed in deterministic reward schedule. Data shown as bins of 50 trials. E) Females displayed stronger side bias early on in learning. Data shown as bins of 150 trials unless specified otherwise. * indicates p < 0.05. Graphs depict mean ± SEM.
Females showed accelerated learning, but males and females reached equivalent final performance
To examine learning, we first calculated the average probability of choosing the high-value image (23 bins in total). Regardless of sex, mice eventually learned which image was associated with the higher reward probability (Figure 1c, GLM, main effect of sex, p = 0.51, β1 = - 0.05; main effect of number of trials, p < 0.0001, β2 = 0.10, see equation 1 in Methods). However, females repeatedly learned the image pair discrimination significantly faster than did males (GLM, interaction term, p < 0.05, β3 = −0.02). We compared these results to a deterministic version of the task in the same animals, in which one image was always rewarded (100%) and the other was never rewarded (0%). We did not find any significant sex difference in rate of learning across trials in the deterministic task (Figure 1d), suggesting the difference was revealed by the stochastic experience of reward.
Females systematically reduced the dimensions of the task by strongly preferring one side
Since rodents are generally highly spatial, we hypothesized that mice might have a bias towards using spatial information earlier in the task before they learned the reward contingency. Consistent with our hypothesis, we observed a short period of heightened side bias [37] (either left or right in females early in learning (Figure 1e) which seemed to precede the acquisition of the reward contingency. Following this period, female mice improved their percentage of choosing high-value image more rapidly than males (GLM, main effect of sex, p < 0.001, β1= −0.129; main effect of number of trials, p < 0.001, β2 = −0.017).
An outcome-insensitive side bias is only one of several “local strategies” that mice could have been using as they learned the reward contingencies. For example, mice could have been using an outcome-sensitive win-stay strategy based on spatial or image dimension, where the side or image is repeated if it was rewarded. Likewise, animals could use an outcome-sensitive image win-stay strategy, or an outcome-insensitive image bias. To understand how these different local strategies were employed by mice over time, we constructed a generalized linear model (GLM) to predict each choice based on a weighted combination of local strategies. The model had a term to account for two classes of basic strategies: outcome-independent (bias) strategies and outcome-dependent (win-stay) strategies (Figure 2a, see Equation 4 in Methods). Fitting the GLM allowed us to estimate how much each of these four strategies was employed within each animal in each bin of 150 trials. We will call this set of beta weights -- the precise pattern of local strategies employed over time -- the “global strategy” employed by each individual animal.
Figure 2. Female mice use a procession of strategies, initially using a spatial bias followed by a switch to responding based on image domain.
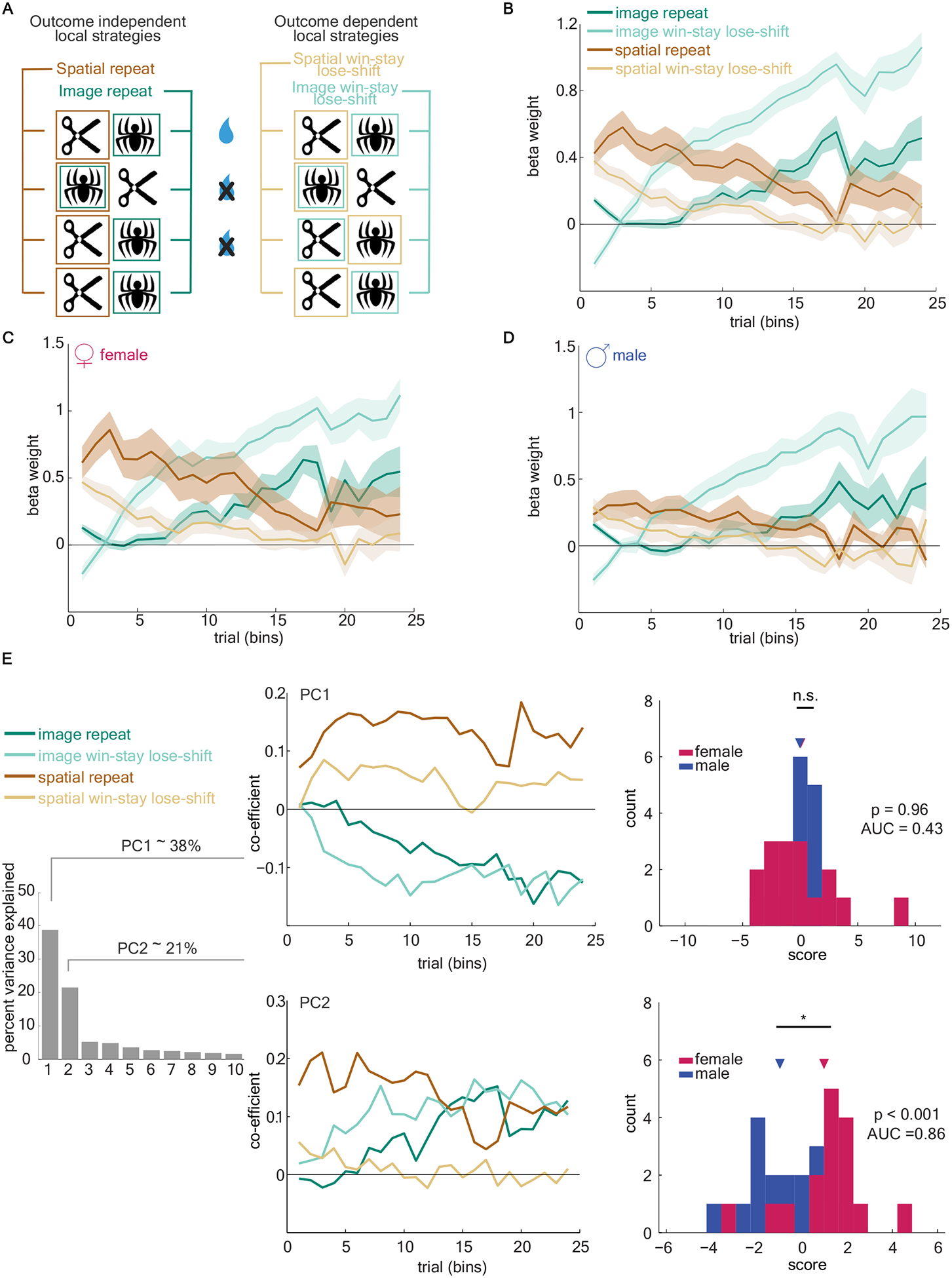
A) Schematic of four basic local strategies based on choice and reward history of image and spatial dimensions of the task. B) The GLM beta weights of the four local strategies, averaged across all animals. C and D) Same as B, for female mice and male mice, respectively. E) A principal component analysis (PCA) was conducted on the estimates of global strategy strength over time across all animals regardless of sex. Left) Variance explained by each principal component (PC). Middle) The coefficients of the first two PCs. Right) PC scores for individual male (blue) and female (pink) animals, for PC1 (top) and PC2 (bottom). See also Figure S1. Data shown as bins of 150 trials. Graphs depict mean ± SEM.
Across all animals, we found that a specific pattern of local strategies was used when learning image pairs (Figure 2b). Animals showed an early tendency towards repeating one side, giving way to an image win-stay, and finally repeating an image (the optimal strategy) late in learning. To examine whether sex influenced the strength of this global strategy, we compared the global strategy beta weights used by male and female animals. We observed this consistent and pronounced pattern of strategy procession only in females (Figure 2c). In contrast, in males we found a markedly reduced influence of either spatial strategy, while the weight of both image-based strategies increased slowly over time (Figure 2d).
To examine how individuals varied in their use of local strategies, regardless of sex, we used an unsupervised method: principle component analysis (PCA). We represented each animal’s behavior as the set of beta weights for the four local strategies identified above, in each trial bin and for each image pair. The principal components of the set of individual strategy vectors then reflect the axes that explain the most inter-individual variability in these beta weights, meaning that combinations of local strategies over time that differ the most between individuals. Principal components (PC) 1 and 2 captured the majority of the interindividual variance: 59% of the variability between animals (Figure 2e). PC1 reflected a global preference for side- or image-based responding and did not significantly differ between sexes (receiver operating characteristic analysis, AUC = 0.43; females = 0.03, males = −0.03; mean(F-M)0.07, 95% CI = [−1.70, 1.80], t(30) = 0.08, p > 0.9). PC2, however, mirrored the spatial-to-image pattern of local strategies observed primarily in female mice (Figure 2c–d). This principal component explained a large fraction (22%) of the interindividual variability in our animals. Principal component 2 was identified as a pattern of strategies across individuals without regard to sex; however, females and males were highly discriminable in terms of their PC2 scores (AUC = 0.86, females = 0.98, males = −0.98; mean(F-M) = 1.96, 95% CI = [0.87, 3.05], t(30) = 3.67, p < 0.001). Though the sexes were not categorically distinct along this axis, they were highly discriminable and most males had negative PC2 scores (Figure S1). No other PCs differed between sexes (all AUC < 0.6, all p > 0.4). There were no significant differences in PC2 score of each image pair within each animal (main effect of image pair: F(3,90)= 0, p>0.99; subject matching (F(30,90) = 5.724, p <0.0001). Thus, the PC2 score of each animal was stable across all four image pairs, suggesting that PC2 score reflects a property of an individual animal, but not of the immediate task or a specific image pair. Together, these results demonstrated substantial inter-individual variability in strategy selection in the same multidimensional decision-making task and suggest that one major axis of strategic variability is sex.
Female-biased early side preference did not speed decision making
The global strategy pattern identified by our GLM and principal components analysis was preferentially employed by females as they learned the task, suggesting that this strategy might be responsible for faster acquisition of image-value responding in females. However, it remained unclear why this might be the case. One possibility is that the early side preference strategy was a fast and frugal heuristic for decision-making. Studies show decision-makers use simplifying heuristics to minimize cognitive demands [38–41]. Since heuristics are simplifying mental shortcuts [38] and choice response time is proportional to the computational complexity of the strategy used to make choices [42–44], the use of heuristics should speed decision-making. Therefore, to determine whether the early side-bias was a kind of simplifying heuristic, we asked whether it sped reaction time for decisions. Specifically, we asked whether (1) females responded faster across all trials, and (2) whether females were fastest when the side preference was the strongest. We computed average RTs across 23 bins of 150 trials for males and females. Contrary to our hypothesis, female reaction times were slower during early learning (bin 1–15) (GLM, interaction term, β3 = 0.03, p = 0.0007, see equation 1 in Methods) and significantly slower than males across all trials (GLM, main effect of sex, β1 = −0.62, p < 0.0001; males = 1.89, SD = 0.13; females = 2.04, SD = 0.21). The reaction time decreased as the animals ran more trials in both males and females (Figure 3a, GLM, main effect of number of trials, β2 = −0.04, p<0.0001). Critically, this was not due to sex differences in motor performance as there was no difference between response time in males and females in the deterministic schedule (Figure S2).We conclude that early side preference in females did not speed their decision-making, and thus was unlikely to be a simplifying heuristic.
Figure 3. Female-biased early side preference did not speed decision making.
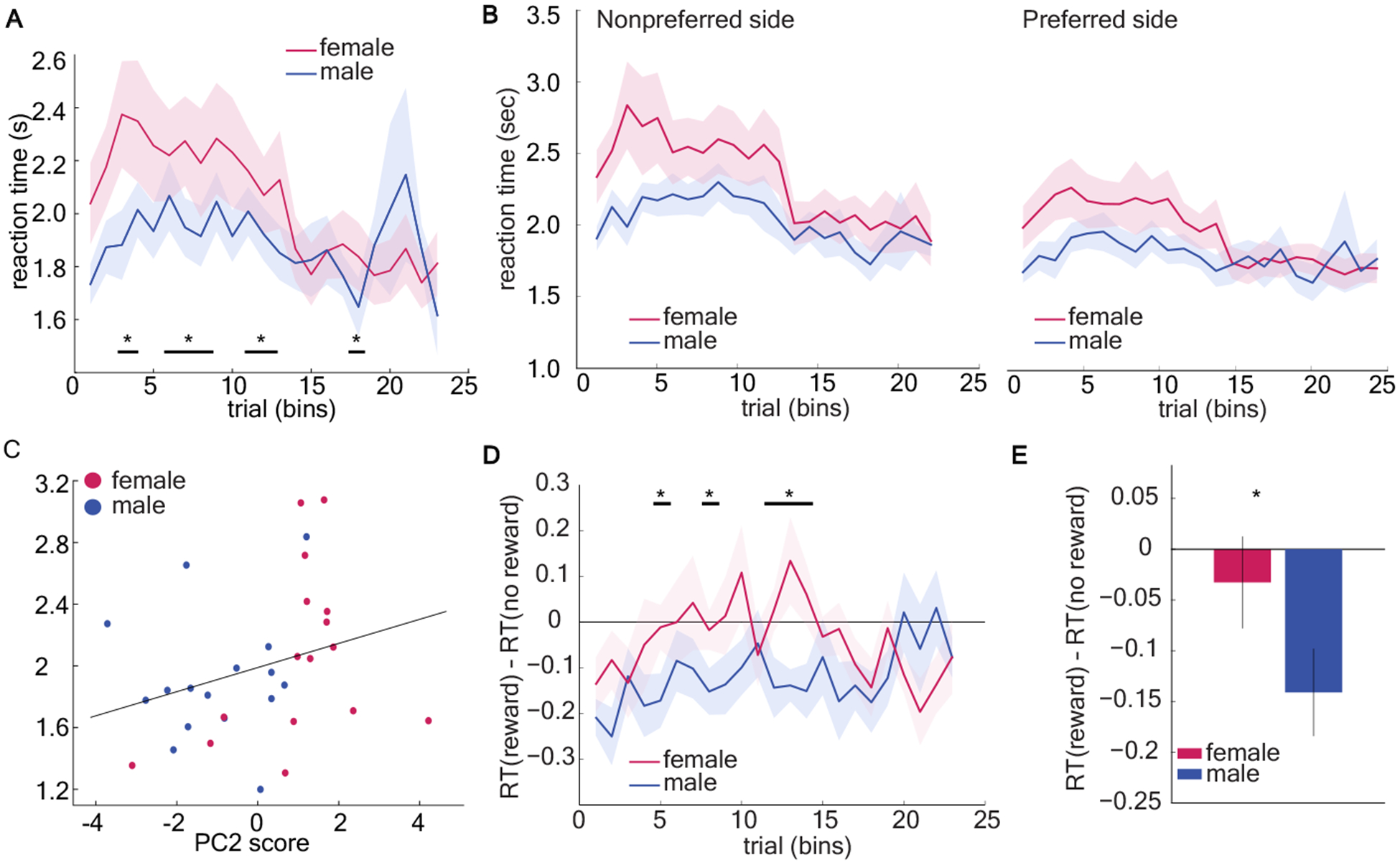
A) Predominantly using the early side preference, females responded slower during early learning. See also Figure S2. B) Average reaction time of both sexes when choosing a preferred side and a nonpreferred side across bins of 150 trials. C) Correlation analyses revealed a significant positive correlation between PC2 scores and reaction time. D) One-sample t-test was conducted across bins to compare the difference in reaction time (RT) between rewarded and unrewarded trials to 0 (when there is no effect of past outcome on the reaction time). Male mice have significant RT effects on the last reward. There was no difference in reaction time between rewarded and unrewarded trials in female mice. E) Average RT difference following a rewarded vs. an unrewarded trial across all trials. Overall, male responded faster when the last trial was rewarded than unrewarded. Data shown as bins of 150 trials. * indicates p < 0.05. Graphs depict mean ± SEM.
We next considered two additional hypotheses. Slow response times in females could reflect increased conflict between intrinsic side preference and value-based choice compared to males. If this is true, then females would only be slower than males when conflict is present: when they choose a non-preferred side. When choosing the preferred side, they may even be faster than males. However, we found that the response time of females was significantly longer than that of males both when choosing a non-preferred side (Figure 3b, GLM, main effect of sex, β1 = −0.58, p < 0.0001) and when choosing a preferred side (GLM, main effect of sex, β1 = −0.42, p < 0.0001). This effect was strongest in the earliest stages of training (GLM, preferred side: main effect of number of trials, β2 = −0.04, p < 0.0001, interaction term, β3 = 0.02, p = 0.001; nonpreferred side: main effect of number of trials, β2 = −0.03, p < 0.0001, interaction term, β3 = 0.02, p = 0.007). Therefore, slower response times in females were not driven solely by those trials with a conflict between preferred side and value, but did seem to be enhanced in the earliest stages of training when it was least clear what the optimal choice was, and decisions might be more demanding as a result.
This led to a third hypothesis: that female response times were slower because this global strategy pattern was more computationally demanding. If so, females would have slower response times during both preferred and non-preferred side choices, as observed. If the female-biased global strategy procession was computationally expensive or time consuming to execute, then individual variability in the use of this strategy should predict variability in response time. We quantified individual variability in strategy with PC2 scores and asked whether there was a direct correlation between PC2 score and reaction time across individuals, regardless of sex. PC2 scores were positively correlated with reaction time (Figure 3c, Spearman’s correlation, rs = 0.452, p = 0.009; Pearson’s correlation, r = 0.347, p = 0.051), suggesting that the animals using the early side bias strategy tended to make slower decisions. The fact that the nonparametric Spearman correlation was significant but the Pearson correlation was not implied that the relationship between these variables was probably nonlinear. However, this analysis cannot rule out the possibility that this relationship between PC2 and RT is mediated by some nonlinear effect of sex on both PC2 and RT. Regardless, although we tend to think of a side-bias as not cognitively demanding, here, the animals that were slowest to make decisions were those who used this strategy. This is difficult to reconcile with the idea that the females used this strategy as a fast and frugal heuristic.
Male strategies were not more random
Although our regression analyses captured the procession of strategies typically employed as female mice that learned the task, they provided little insight into what the males were doing during early learning. Substantial prior research has found higher impulsive and exploratory behavior in males compared to females [21,45–48], so perhaps males, as a group, lacked a coherent strategy because they simply chose randomly before the reward contingencies were learned. Instead, across several analyses, we found that males’ choices depended more on both past outcomes and past choice history than females’.
One classic, agnostic measure of outcome sensitivity is response time speeding. Males responded significantly faster when they had just received a reward (Figure 3d and 3e, one-sample t-test, mean RTreward – RTno reward = −0.14, 95% CI = [−0.23, −0.05], t(15) = −3.38, p = 0.004). Conversely, the reaction times of females were not systematically affected by the outcome of the last trial (mean RT effect = −0.03, 95% CI = [−0.13, 0.06], t(15) = −0.75, p = 0.47). These results reinforce the idea that females were following a global strategy, but not the idea that males lacked evidence of a global strategy because they were more random. Instead, males were more sensitive to reward outcomes than females in terms of response time.
We next examined whether males’ choices, in addition to their response times to make those choices, was also more outcome sensitive than females. Although our regression results did not suggest that males were more likely to follow a classic win-stay/lose-shift policy than females (see also Figure S3), win-stay/lose-shift could not capture all possible reward-dependent behaviors in this two-dimensional task. For example, rather than always repeating a side or an image after reward, animals could have different policies for different combinations of sides or images, or follow outcome-based alternation rules. To account for the breadth of ways that animals could be responding to reward, we compared the pattern of choices following rewards with the pattern following no-reward, allowing us to estimate how much animals adapted their choices in responses to rewards without assuming what those choices were. We found that males’ choices were much more outcome sensitive. Male’s choices after a reward, compared to females’, diverged more from their behavior after non-reward (Figure 4a, GLM, main effect of sex, β1 = 4.55, p < 0.0001). Note that the optimal strategy in this task is to consistently choose the high reward image regardless of outcome. Consistent with this, both males and females learned to become less reward sensitive over time (Figure 4a, main effect of number of trials, β2 = −0.99, p < 0.0001). Thus, males were more outcome sensitive than females when measured either by response time or by choice, again suggesting that males were not more random.
Figure 4. Male mice were more likely to differ from themselves over time, with choice patterns dependent on past outcomes.

A) Comparing choice strategies as vector angles. Left) We calculate the joint probability distribution of all possible choices at time t (image x side) and all previous choices at t-1. This probability distribution can be thought of as a vector on the probability = 1 simplex (middle). We then compare choice strategies by measuring the angle between choice strategy vectors, here between strategy vectors following a reward and following no reward. Right) Average angle between choice strategy vectors following reward and no reward, plotted separately for males (blue) and females (pink). See also Figure S3. B. Left) If choice on trial t is independent of choice on the previous trial (t-1), mutual information will be low. Conversely, if choice t depends on t-1, mutual information will be high. Right) Conditional mutual information is higher in males, indicating that responses are more dependent on the previous trial variables than they are in females. C). Average angle between choice strategy vectors between animals within sex. D) Average angle between choice strategy vectors within animals across trial bins See also Figure S4. E) Average angle between choice strategy vectors within animals across repetitions of the task. F) Multidimensional scaling (MDS) was used to reduce the dimensionality of the strategy space in order to visualize each animal’s strategy paths. Each graph is a different animal, with the colors representing repetitions of the task. The star represents the optimal strategy for each projection (i.e. the choice pattern that only repeats high value image). Note that the strategy paths of both sexes are approaching the optimal strategy point. See also Figure S5. Data shown as bins of 150 trials. * indicates p < 0.05. Graphs depict mean ± SEM.
The males’ choices were more organized with respect to past reward than females, but were they also more organized with respect to their previous choices? Within each block of trials in each animal, we calculated conditional mutual information for each bin [49,50], which quantifies the dependence of current choices (side, image) on the previous choice given the outcome of the previous trial (Figure 4b). Note that this is related to our previous regression results in Figure 2b–d, but allows us to quantify structure in a model-free way. The result suggested that mutual information decreased over time in both sexes, reflecting the gradual acquisition of the optimal strategy for this task (repeat high-value image no matter the previous trial) (Figure 4b, GLM, main effect of number of trials, β2 = −0.001, p =0.0002, see equation 1&5 in Methods). However, the mutual information of male mice was higher than that of females (main effect of sex, β1 = 0.043, p < 0.0001), particularly early in learning (interaction term, β3 = - 0.002, p < 0.0001). This suggests that male strategies were not only more outcome-sensitive but also more dependent on their past choices, again indicating that the strategy employed by males was not a random one.
Males changed their strategies more over time
Although males were more outcome and choice sensitive than females, our regression analysis did not show a pronounced or unified strategy pattern preferred by males. This could suggest that males were less consistent in their choice of strategy across individuals and/or across time (i.e. within the same individual). To test these hypotheses, we used a model-free analysis to compare how similar one set of choices was to another (similar to our approach in Figure 4a). We expressed the choices in each bin as a probability vector, with each element of the vector reflecting the probability of that unique combination of behaviors {last choice, last outcome, current choice}. The average angle between any two of probability vectors reflects the variability in choices across conditions. Males were not more idiosyncratic than females on a population level; the choices of any given male were not more variable from other males than any given female’s choices were from other females (Figure 4c, GLM, main effect of sex, β1 = −1.47, p = 0.11). However, a given male was more variable within himself, both across trial bins within one image pair (Figure 4d, GLM, main effect of sex, β1 = 4.24, p < 0.0001; Figure S4 for the same analysis across non-adjacent blocks) and across multiple image pairs (Figure 4e, GLM, main effect of sex, β1 = 4.54, p = 0.047). Overall, the variability in choices captured by these analyses decreased across time as the divergent strategies used by individual animals started to converge to the optimal strategy (GLM, main effect of number of trials, within sex between subject: β2 = −0.78, p < 0.0001; within subject across bins: β2 = −0.359, p < 0.0001). Together, these results suggest that individual males tended to change their strategies over days and repetitions of the same task, while females employed a systematic strategy to each repetition.
Choice patterns are high dimensional, so to visualize the change or stability in strategies in two dimensions we used multidimensional scaling [51–53] to visualize “strategy paths” throughout learning. This allows us to see the similarity between patterns of choice across animals over time and across repetitions (Figure 4f). Both representative male and female “strategy paths” approached the optimal strategy over time. Consistent with the quantification described above, the strategy path of males are visibly more variable and different across repetitions of the task, whereas the strategy path of a given female tends to be more consistent across repetitions.
Sex mediated the ability of neuronal activity to explain strategy selection
Learning and decision-making is highly sensitive to alterations in corticolimbic structures. However, it remains unclear how alterations in these structures predict choice strategy, much less sex differences in strategy. To address this question, we examined neuronal activity in several corticolimbic brain regions through the expression of c-fos, an immediate early gene that is a marker of neuronal activation. The animals were sacrificed after the second day of a new, final image-reward pair (after 400–500 trials), corresponding to when the female side bias was greatest. We compared mRNA expression level for c-fos in homogenized pieces of tissue from five brain regions, including nucleus accumbens (NAc), dorsal medial striatum (DMS), amygdala (AMY), hippocampus (HPC), and prefrontal cortex (PFC), using quantitative real-time PCR (Figure 5a). In each region, females had a higher c-fos expression than males (unpaired t-test, NAc: t(30) = 2.41, p = 0.02; DMS: t(30) = 2.31, p = 0.03; AMY: t(30) = 4.05, p < 0.001; HPC: t(30) = 2.74, p = 0.01; PFC: t(29) = 3.163, p = 0.003).
Figure 5. Both sex and neuronal activity can account for strategy selection, but sex mediated the ability of neural activity to explain strategy selection.
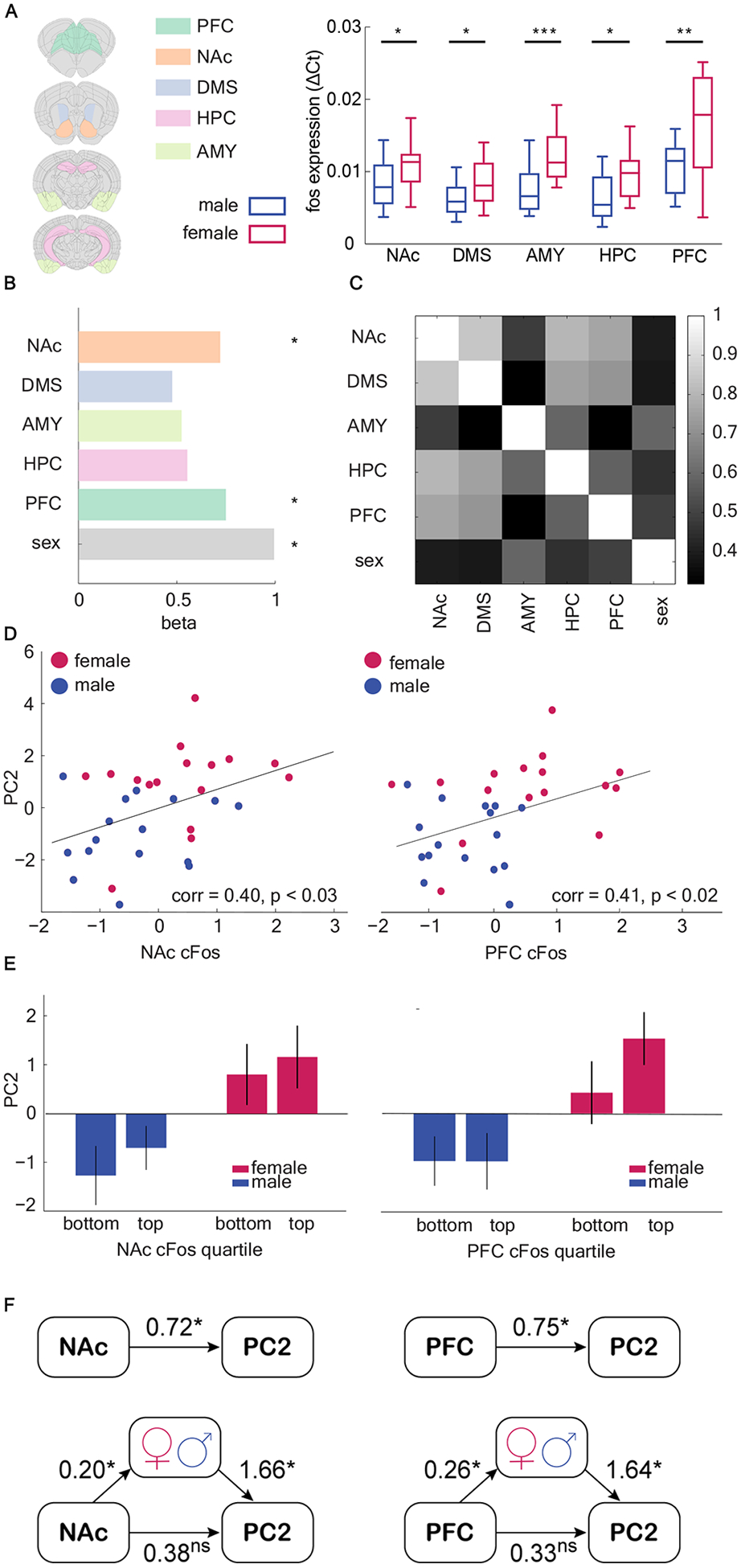
A) cFos gene expression (qRT-PCR) in five brain regions: nucleus accumbens (NAc), dorsal medial striatum (DMS), amygdala (AMY), hippocampus (HPC), and prefrontal cortex (PFC). Female mice showed elevated c-fos expression across all five brain regions. Extracted brain sections for each brain region are shown in the altas. B) regression coefficient of c-fos expression in NAc and PFC, and sex in predicting the use of PC2 strategy C) Heatmap of correlation matrix of c-fos expression level among five brain regions. Colorbar = Pearson’s r. D) cFos gene expression in NAc and PFC is significantly correlated with the weight of PC2. E) Median split of c-fos expression in NAc and PFC and PC2 scores within each sex. F) Sex mediated the relationship between c-fos expression in NAc and PFC and PC2 scores.The top models demonstrate thedirect effect and the bottom models demonstrate the mediated effect. Effects are labeled with estimated coefficients. The strength of the direct model is greatly reduced after mediation, suggesting that sex mediated neural measures in explaining strategy selection. See also Table S1. Graphs depict mean ± SEM. Asterisks marked significant effects (*: p < 0.05 **: p < 0.01 ***: p<0.001).
To understand whether activation of any of these brain regions correlated with the side bias strategy, we constructed a GLM to predict PC2 from c-fos levels in each brain region. The results suggested that only two regions, the NAc and PFC predicted strategy use, as indexed by PC2 score (Figure 5b, GLM, NAc: β1 = 0.72, p = 0.02; DMS: β2 = 0.48, p = 0.14; AMY: β3 = 0.52, p = 0.10; HPC: β4 = 0.55, p = 0.08; PFC: β5 = 0.75, p = 0.02; sex was included as a variable in the model and was also significant: β6 = 0.99, p = 0.0009, equation 2 in Methods). Correlations between c-fos expression in NAc/PFC and PC2 scores were further confirmed with a Pearson product-moment correlation (Figure 5d–e, NAc: r = 0.40, n = 32, p < 0.03; PFC: r = 0.41, n = 32, p < 0.02). No region predicted PC1 scores in an identical analysis. Because each region was also correlated with sex (and sex independently predicted PC2), NAc and PFC could have been the best predictors of PC2 because these regions were the most strongly correlated with sex (Figure 5c). However, sex was most strongly correlated with AMY, which was not a significant predictor of PC2. This evidence is circumstantial, however, and with 16 subjects per sex we lacked the power to measure the correlation between cfos and PC2 within each sex. To understand if sex mediated the relationship between NAc and PFC c-fos activity and PC2 scores, we used a structural equation modeling (SEM) approach [54,55] to analyze the relationship between sex, gene expression, and PC2 and latent constructs (Figure 5f; Table S1). The results suggested that sex was a significant mediator of the relationship between neural activation and PC2 in both NAc and PFC, highlighting these regions as promising targets for future studies looking at the effects of sex on the neural circuits responsible for implementing strategic learning.
Discussion
Male and female mice used a range of problem solving strategies in a stochastic two-dimensional decision-making task. In the task, each cue had two dimensions - the identity of the image and the location of the image - but animals did not appear to know which was most predictive of reward. Although both male and female mice eventually learned to choose the high-value image, female mice learned faster. The dimensionality of the task allowed us to uncover sex differences in how the animals achieved the associations across time. We discovered that female mice were more likely to adopt a consistent and systematic strategy procession over time that constrained the search space early in learning by preferentially sampling the outcomes of images on one side (left or right). This approach, which occurred when animals were most uncertain about the best choice, may have permitted more rapid acquisition of the image-value association. In contrast, males were less likely to employ this systematic approach, and instead responded to a combination of visual and spatial dimensions, changed their approach frequently, and were strongly influenced by the immediate prior experience of reinforcement. While animals of both sexes reached equivalent levels of performance, the strategic paths individuals took to get there varied dramatically.
Sequential decision-making and learning in rodents is often studied with spatial bandit tasks, in which reward probabilities are linked to sides that are visually identical [1,4,11,13,33,56]. In these spatial bandit tasks, side bias in choice has sometimes been equated with inflexible, automatized habitual behaviors and animals displaying such bias were often excluded from experiments [57–59]. However, the slower choice response time in side-biased females suggests that the early side preference was more likely to be cognitively demanding than a heuristic. The animals that used this approach appeared to “jump start” their learning, suggesting that side-biased animals may covertly learn about the correct dimension while behaviorally selecting the wrong item, and were able to convert this to successful learning due to the stability of the task structure.
Traditional reinforcement learning (RL) models often employ simplifying assumptions that agents select actions 1) based only on reward-associated dimensions and 2) in a consistent manner across learning. Our findings indicate that naturalistic learning can violate both of these assumptions, yet be successful. Analyses like the ones we perform here could help inform the design of RL models in future work. For example, hierarchical RL models [60] can deal with changes in strategies over time, and multidimensional RL models can incorporate feature-based and higher dimensional learning [61].
Our data implicate the prefrontal cortex (PFC) and nucleus accumbens (NAc) in the differences in strategy between males and females. These regions have been widely implicated in reward-guided decision-making, but so have the other regions we tested for which we didn’t find a significant relationship to these strategies [2,29,62]. One possibility is that the PFC and accumbens are particularly engaged in strategic decision-making. This resonates with previous studies that have implicated the PFC in implementing strategies and rule-guided behaviors [56,63–68] and the NAc in selecting and implementing learning strategies [29,30]. Implementing different strategies produces changes in how different choice dimensions are represented in the PFC and NAc [41], and lesions in the NAc can drive animals towards a low-dimensional action-based strategy or prevent animals from switching between strategies [2,30]. These signals could be sex-biased: the PFC is sensitive to gonadal hormones during risky decision-making [69], and dopaminergic function in the accumbens has sex-specific effects on risky decision-making[70], perhaps due to sex differences in dopamine neurons [71]. Our result, that the relationship between neural activity and strategy was mediated by sex, is broadly consistent with this growing literature.
One fundamental unanswered question is why females tended to employ a shared and systematic strategy. Zador (2019) recently proposed that much of animal behavior is not dictated by supervised or unsupervised learning algorithms, but instead by biological constraints [72]. “Habitual” or repetitive choice behaviors tend to be enhanced in females [21,22,73] hinting at a shared mechanism. Sexual differentiation involves multiple mechanisms, many of which influence reward-guided decision-making circuits [71,74]. For example, while testosterone increases effort expenditure and impulsive behavior [65–67], estradiol limits high-effort choices [16,69,75]. Sex chromosomes also independently influence such behaviors [15] with elevated habit in XX carriers and increased effort in XY carriers [76,77]. It is important to note that such influences of sexual differentiation are graded, rather than dichotomous, and can interact with non-sex biological mechanisms in complex ways. Indeed, here we found that a small number of males adopted a similar approach to most females, implicating the graded engagement of both sex difference and non-sex difference mechanisms in the degree of adoption of sex-biased exploratory strategies we observed here. An intriguing possibility is that the spectrum of behaviors we observed across animals, from systematic to volatile, may emerge from sex-biased tuning of learning strategies that were critical to survival for the species as a whole.
STAR METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Nicola Grissom (ngrissom@umn.edu)
Materials Availability
This study did not generate new unique reagents.
Data and Code Availability
Data and software are available upon request to the Lead Contact, Nicola Grissom (ngrissom@umn.edu)
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Thirty-two BL6129SF1/J mice (16 males and 16 females) were obtained from Jackson Laboratories (stock #101043). Mice arrived at the lab at 7 weeks of age, and were housed in groups of four with ad libitum access to water while being mildly food restricted (85–95% of free feeding weight) for the experiment. Animals engaging in operant testing were housed in a 0900–2100 hours reversed light cycle to permit testing during the dark period, between 09:00 am and 5:00 pm. Before operant chamber training, animals were food restricted to 85%−90% of free feeding body weight and had been pre-exposed to the reinforcer (Ensure). Pre-exposure to the reinforcer occurred by providing an additional water bottle containing Ensure for 24 hours in the home cage and verifying consumption by all cagemates. Operant testing occurred five days per week (Monday-Friday), and the animals were fed after training with ad lib food access provided on Fridays. All animals were cared for according to the guidelines of the National Institution of Health and the University of Minnesota.
METHOD DETAILS
Apparatus.
Sixteen identical triangular touchscreen operant chambers (Lafayette Instrument Co., Lafayette, IN) were used for training and testing. Two walls black were acrylic plastic. The third wall housed the touchscreen and was positioned directly opposite the magazine. The magazine provided liquid reinforcer (Ensure) delivered by a peristaltic pump, typically 7ul (280 ms pump duration). ABET-II software (Lafayette Instrument Co., Lafayette, IN) was used to program operant schedules and to analyze all data from training and testing.
Operant Training and tasks
Pretraining.
Animals were exposed daily to a 30-min session of initial touch training, during which a blank white square (cue) was presented on one side of the touchscreen, counterbalancing left and right between trials. This schedule provided free reinforcement every 30 seconds, during which the cue was on. If animals touched the cue during this period, a reward three times the size of the regular reward was dispensed (840 ms). This led to rapid acquisition. Following this, animals were exposed daily to a 30-min session of must touch training. This schedule followed the same procedure as the initial touch training, but free reinforcers were terminated and animals were required to nose poke the image in order to obtain a regular reward (7-uL, 280 ms).
Deterministic pairwise discrimination training.
Animals were exposed to 10 days of pairwise discrimination training, during which animals were presented with two highly discriminable image cues (“marbles” and “fan”). One image was always rewarded and the other one was not. Within each session, animals completed either 250 trials or spent a maximum of two hours in the operant chamber (typically these mice completed ~200 trials/day).
Two-armed bandit task.
Animals were trained to perform a two-arm visual bandit task in the touchscreen operant chamber. On eEach trial, animals were presented with a repeating set of two different images on the left and right side of the screen, counterbalancing left and right across the session. Responses were registered by nose poking to one of the displayed images on the touchscreen. Nose poke on one image triggered a reward 80% of the time (high payoff image), whereas the other image was only reinforced 20% of the time (low payoff image). Following the reward collection, which was registered as entry and exit of the feeder hole, the magazine would illuminate again and the mouse must re-enter and exit the feeder hole to initiate the next image trial. If the previous trial was unrewarded, a 3-second time-out was triggered, during which no action could be taken. Following the timeout, the magazine would illuminate and the mouse must enter and exit the feeder hole to initiate the next image trial. The ABET II system recorded trial to trial image chosen history, reward history, grid position of the images with time-stamp. Within each day, animals completed either 250 trials or spent a maximum of two hours in the operant chamber. Animals were given 14 days to learn about the probabilistic reward schedule of one image pair, before moving onto the next image pair. A total of six image pairs were trained, but two image pairs were eliminated from analyses due to very high initial preference (>70%) for one novel image over another, indicating that (to the mice) these images appeared unexpectedly similar to previously experienced images with learned reward values.
RNA quantification.
At the end of training, animals were sacrificed after the second day of learning a new image pair (around 400–500 trials of experience per mouse), when we expected to see the biggest difference in learning performance and strength of lateralization. Animal brains were extracted and targeted brain regions were dissected. We extracted RNA from targeted brain areas and assessed gene expression for the fos genes in the nucleus accumbens (NAc), dorsal medial striatum (DMS), amygdala (AMY), and hippocampus (HPC), using quantitative Real Time PCR system (BioRad, USA). Fos expression normalized to the housekeeper gene glyceraldehyde 3-phosphate dehydrogenase (gapdh) was calculated using the comparative delta Ct method.
QUANTIFICATION AND STATISTICAL ANALYSIS
General analysis techniques
Data was analyzed with custom PYTHON, MATLAB, and RStudio scripts. Generalized linear models were used to determine sex differences over time, unless otherwise specified. P values were compared against the standard ɑ = 0.05 threshold. The sample size is n=16 for both males and females for all statistical tests. No animal was excluded from the experiment. All statistical tests used and statistical details were reported in the results or the supplemental table. All figures depict mean ± SEM.
Data analyses
Generalized Linear Models (GLMs).
In order to determine whether sex and number of trials (bins) predicts the accuracy of the task, strength of lateralization, reaction time, mutual information (MI), or angle between probability vectors, we fit a series of generalized linear models of the following form:
| [1] |
where Y is the dependent variable (accuracy, laterality, reaction time, MI, or angle). In this model, β1 described the main effect of sex and β2 described the main effect of number of trials (bins). β3 captures any interaction effect between sex and number of trials (bins).
To determine whether c-fos expression in NAc, DMS, AMY, HPC, PFC, and sex predicted the weights of Principal Component (PC) 2, we fit the following generalized linear model:
| [2] |
In this model, β1- β5 captures the predictive effect of gene expression in five regions on the use of PC2 strategy. β6 described the effect of sex on the weights of PC2.
Degree of lateralization.
As a measure of the strength of side bias, we used the absolute percentage of laterality [37], calculated for each mouse according to the following formula:
| [3] |
Generalized Logistic Regression Model.
Mice could base their decisions on reward history in the spatial or image domains or on choice history in the spatial or image domains. To determine how these four aspects of previous experience affected choice and how these effects changed over time, we estimated the effect of the last trials’ reward outcome (O), image choice (I), and chosen side (S) using logistic regression. If image (image 1) was on the left side of the screen, we could predict the probability of choosing that image as a linear combination of the following four terms:
| [4] |
where each term (O, I, and S) is a logical, indicating whether or not that event occurred on the last trial. As a result, the term (I1,t-1- I2,t-1) is 1 if image 1 was chosen on the last trial, and −1 otherwise. The term β1 thus captures the tendency to either repeat the previous image (when positive) or choose the other image (when negative). The term β2 * Ot-1 accounts for any additional effect of the previous image on choice, when that previous choice was rewarded.. If image 1 was on the left side, SL,t-1 denotes the probability of repeating the left side where image 1 appeared. However, because image 1 could be either on the left or the right side of the screen (which allowed us to dissociably estimate the probability of choosing it based on side bias or image bias), we expanded the (SL,t-1- SR, t-1) term to account for the current position of image 1 as follows:
meaning that the current position of image 1 determined the sign of the side bias term. This model was fit individually to each bin of 150 trials, within each animal and image pair, via cross-entropy minimization with a regularization term (L2/ridge regression).
Principal component analysis.
In order to determine how decision-making strategies differed across animals and bins, we looked for the major axes of inter-individual variability in decision-making strategies. To do this, we took advantage of the fact that the coefficients of the generalized linear model provided a simplified description of how decision-making depended on image, side, and outcome for each subject within each image pair. Because the generalized logistic regression model estimated 4 terms per image pair and there were 23 independent bins per image pair, we described this meant that each animals’ behavior for each given image pair could be described as 4*23 92*1 dimensional vectors. Because 32 animals completed 4 image pairs, this gave us a total of 128 total strategy vectors, or a 92×128 dimensional strategy matrix, with each column corresponding to one animal’s strategy in one image pair. We then used principal component analysis to identify the linear combinations of model parameters that explained the most variance across these strategy matrix. The first two principal components, which explained the majority of the variance (59%), are illustrated in Figure 2e.
Conditional mutual information and model-free analyses.
To account for idiosyncratic strategies, which could vary across animals or image pairs, we used a model-free approach to quantify the extent to which behavior was structured without making strong assumptions about what form this structure might take. We quantified the extent to which choice history was informative about current choices as the conditional mutual information between the current choice (C) and the last choice (Ct-1), conditioned on the reward outcome of the last trial (R):
| [5] |
where the set of choice options (C) represented the unique combinations of each of the 2 images and 2 sides (4 combinations). To account for observed differences in overall probability of reward for male and female animals, the mutual information was calculated independently for trials following reward delivery and omission, and then summed across these two conditions.
We used a similar approach to provide a modrel-free description of the animals’ choice patterns. Briefly, instead of finding the set of beta weights that best described reliance on various history-dependent strategies over time, we directly calculated the joint probability of each possibility combination of last choice (image and side), last outcome (reward and unrewarded), and current choice (image and side). This means that we represented the animals’ history-dependent choice pattern for each image pair as an 32-dimensional vector (4 (last choice) x 2 (last outcome) x 4 (current choice) = 32) of joint probabilities. Via a geometric interpretation of a multinomial distribution, we considered the animal’s pattern of behavior within any bin of trials as a point on the 32–1 dimensional simplex formed by length-1 vectors. This geometric approach allowed us to map strategies over time or across bins as a diffusion process across this simplex, where the angle between two vectors (between animals/between bins/between repetitions) is proportional to step between them on a strategy simplex. The bigger the step between two vectors, the more variable the behavior pattern is.
Multidimensional Scaling (MDS).
MDS allows the visualization of complex strategies and choice behaviors. Since the choice behaviors across both spatial and image dimensions are high-dimensional, we had to plot in a lower dimensional space in order to visualize them. MDS is a means of visualizing similarity and variability of choices across trial bins within individuals. Choice patterns within a trial bin (150 trials) that are more similar are closer together (shorter distance) on the graphs than patterns that are less similar. The star represents the optimal strategy, which in this task, is to consistently choose the high reward image. In MDS graphs allow visualization of how choice behaviors in one trial bin differ the next trial bin and how choice behaviors vary across image pairs. For example, in the MDS graph of the second female animal (Figure S5), this animal only learned one image pair as only one path approached the optimal strategy (marked by the star). In most males’ graphs, the distance between each step, which represents the choice pattern in one trial bin, is longer than most females. This suggests that choice behavior of males are more variable and heterogeneous compared to that of females.
Mediation Analysis.
First we used a direct model and regressed c-fos expression of either NAc or PFC on weights of PC2. When assessing a mediation effect, three regression models are examined:
Model 1 (direct):
| [6] |
Model 2 (mediation):
| [7] |
Model 3 (indirect):
| [8] |
In these models, γ1, γ2, and γ3 represent the intercepts for each model, while ε1, ε2, and ε3 represent the error term. β denotes the relationship between dependent variable (PC2 weights) and independent variable (NAc c-fos expression) in the first model, and β’denotes the same relationship in the third model. α represents the relationship between independent variable (NAc c-fos expression) and mediator (sex) in the second model. The mediation effect is calculated using the product of coefficients (αβ1). The Sobel test is used to determine whether the mediation effect is statistically significant [45].
Supplementary Material
Acknowledgements
The authors would like to thank Sarah Heilbronner and Vincent Costa for helpful comments on the manuscript. This work was supported by NIMH R01 MH123661, NIMH P50 MH119569, and NIMH T32 training grant MH115886, startup funds from the University of Minnesota (N.M.G.), a Young Investigator Grant from the Brain and Behavior Foundation (R.B.E.), and an Unfettered Research Grant from the Mistletoe Foundation (R.B.E.).
Footnotes
Declaration of Interests
The authors declare no competing interests.
References
- 1.Ebitz RB, Albarran E, and Moore T (2018). Exploration Disrupts Choice-Predictive Signals and Alters Dynamics in Prefrontal Cortex. Neuron 97, 475. Available at: 10.1016/j.neuron.2018.01.011. [DOI] [PubMed] [Google Scholar]
- 2.Averbeck BB, and Costa VD (2017). Motivational neural circuits underlying reinforcement learning. Nat. Neurosci 20, 505–512. Available at: 10.1038/nn.4506. [DOI] [PubMed] [Google Scholar]
- 3.Parker NF, Cameron CM, Taliaferro JP, Lee J, Choi JY, Davidson TJ, Daw ND, and Witten IB (2016). Reward and choice encoding in terminals of midbrain dopamine neurons depends on striatal target. Nat. Neurosci 19, 845–854. Available at: 10.1038/nn.4287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pearson JM, Hayden BY, Raghavachari S, and Platt ML (2009). Neurons in posterior cingulate cortex signal exploratory decisions in a dynamic multioption choice task. Curr. Biol 19, 1532–1537. Available at: 10.1016/j.cub.2009.07.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bartolo R, Saunders RC, Mitz A, and Averbeck BB (2019). Dimensionality, information and learning in prefrontal cortex. bioRxiv, 823377. Available at: https://www.biorxiv.org/content/10.1101/823377v1 [Accessed July 5, 2020]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Grissom NM, McKee SE, Schoch H, Bowman N, Havekes R, O’Brien WT, Mahrt E, Siegel S, Commons K, Portfors C, et al. (2018). Male-specific deficits in natural reward learning in a mouse model of neurodevelopmental disorders. Mol. Psychiatry 23, 544–555. Available at: 10.1038/mp.2017.184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Solomon M, Smith AC, Frank MJ, Ly S, and Carter CS (2011). Probabilistic reinforcement learning in adults with autism spectrum disorders. Autism Res. 4, 109–120. Available at: 10.1002/aur.177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Grissom N, McKee S, Schoch H, Bowman N, Havekes R, Nickl-Jockschat T, Reyes T, and Abel T (2015). Male-Specific Reward Learning Deficits in a Mouse Model of Autism. In NEUROPSYCHOPHARMACOLOGY (NATURE PUBLISHING GROUP MACMILLAN BUILDING, 4 CRINAN ST, LONDON N1 9XW, ENGLAND), pp. S293–S293. [Google Scholar]
- 9.Kim H, Lee D, Shin Y-M, and Chey J (2007). Impaired strategic decision making in schizophrenia. Brain Res. 1180, 90–100. Available at: 10.1016/j.brainres.2007.08.049. [DOI] [PubMed] [Google Scholar]
- 10.Engelhard B, Finkelstein J, Cox J, Fleming W, Jang HJ, Ornelas S, Koay SA, Thiberge SY, Daw ND, Tank DW, et al. (2019). Specialized coding of sensory, motor and cognitive variables in VTA dopamine neurons. Nature 570, 509–513. Available at: 10.1038/s41586-019-1261-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mohebi A, Pettibone JR, Hamid AA, Wong J-MT, Vinson LT, Patriarchi T, Tian L, Kennedy RT, and Berke JD (2019). Dissociable dopamine dynamics for learning and motivation. Nature 570, 65–70. Available at: 10.1038/s41586-019-1235-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alabi OO, Fortunato MP, and Fuccillo MV (2019). Behavioral Paradigms to Probe Individual Mouse Differences in Value-Based Decision Making. Front. Neurosci 13, 50. Available at: 10.3389/fnins.2019.00050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bari BA, Grossman CD, Lubin EE, Rajagopalan AE, Cressy JI, and Cohen JY (2019). Stable Representations of Decision Variables for Flexible Behavior. Neuron 103, 922–933.e7. Available at: 10.1016/j.neuron.2019.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cohen JY (2015). Dopamine and serotonin signals for reward across time scales. Science 350, 47. Available at: 10.1126/science.aad3003. [DOI] [PubMed] [Google Scholar]
- 15.McCarthy MM, and Arnold AP (2011). Reframing sexual differentiation of the brain. Nat. Neurosci 14, 677–683. Available at: 10.1038/nn.2834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Becker JB, and Chartoff E (2019). Sex differences in neural mechanisms mediating reward and addiction. Neuropsychopharmacology 44, 166–183. Available at: 10.1038/s41386-018-0125-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shansky RM (2019). Are hormones a “female problem” for animal research? Science 364, 825–826. Available at: 10.1126/science.aaw7570. [DOI] [PubMed] [Google Scholar]
- 18.Shansky RM (2018). Sex differences in behavioral strategies: avoiding interpretational pitfalls. Curr. Opin. Neurobiol 49, 95–98. Available at: 10.1016/j.conb.2018.01.007. [DOI] [PubMed] [Google Scholar]
- 19.Gruene TM, Flick K, Stefano A, Shea SD, and Shansky RM (2015). Sexually divergent expression of active and passive conditioned fear responses in rats. Elife 4. Available at: 10.7554/eLife.11352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.McCarthy MM, Arnold AP, Ball GF, Blaustein JD, and De Vries GJ (2012). Sex differences in the brain: the not so inconvenient truth. J. Neurosci 32, 2241–2247. Available at: 10.1523/JNEUROSCI.5372-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Grissom NM, and Reyes TM (2018). Let’s call the whole thing off: evaluating gender and sex differences in executive function. Neuropsychopharmacology. Available at: 10.1038/s41386-018-0179-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Orsini CA, and Setlow B (2017). Sex differences in animal models of decision making. J. Neurosci. Res 95, 260–269. Available at: 10.1002/jnr.23810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.van den Bos R, Homberg J, and de Visser L (2013). A critical review of sex differences in decision-making tasks: Focus on the Iowa Gambling Task. Behavioural Brain Research 238, 95–108. Available at: 10.1016/j.bbr.2012.10.002. [DOI] [PubMed] [Google Scholar]
- 24.Izquierdo A, Aguirre C, Hart EE, and Stolyarova A (2019). Rodent Models of Adaptive Value Learning and Decision-Making. In Psychiatric Disorders: Methods and Protocols, Kobeissy FH, ed. (New York, NY: Springer New York; ), pp. 105–119. Available at: 10.1007/978-1-4939-9554-7_7. [DOI] [PubMed] [Google Scholar]
- 25.Rudebeck PH, and Murray EA (2011). Balkanizing the primate orbitofrontal cortex: distinct subregions for comparing and contrasting values. Ann. N. Y. Acad. Sci 1239, 1–13. Available at: 10.1111/j.1749-6632.2011.06267.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Morris G, Nevet A, Arkadir D, Vaadia E, and Bergman H (2006). Midbrain dopamine neurons encode decisions for future action. Nat. Neurosci 9, 1057–1063. Available at: 10.1038/nn1743. [DOI] [PubMed] [Google Scholar]
- 27.Pearson JM, Heilbronner SR, Barack DL, Hayden BY, and Platt ML (2011). Posterior cingulate cortex: adapting behavior to a changing world. Trends Cogn. Sci 15, 143–151. Available at: 10.1016/j.tics.2011.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pessiglione M, Seymour B, Flandin G, Dolan RJ, and Frith CD (2006). Dopamine-dependent prediction errors underpin reward-seeking behaviour in humans. Nature 442, 1042–1045. Available at: 10.1038/nature05051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Costa VD, Dal Monte O, Lucas DR, Murray EA, and Averbeck BB (2016). Amygdala and Ventral Striatum Make Distinct Contributions to Reinforcement Learning. Neuron 92, 505–517. Available at: 10.1016/j.neuron.2016.09.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Rothenhoefer KM, Costa VD, Bartolo R, Vicario-Feliciano R, Murray EA, and Averbeck BB (2017). Effects of Ventral Striatum Lesions on Stimulus-Based versus Action-Based Reinforcement Learning. J. Neurosci 37, 6902–6914. Available at: 10.1523/JNEUROSCI.0631-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Steyvers M, Lee MD, and Wagenmakers E-J (2009). A Bayesian analysis of human decision-making on bandit problems. J. Math. Psychol 53, 168–179. Available at: http://www.sciencedirect.com/science/article/pii/S0022249608001090. [Google Scholar]
- 32.Zhang S, and Yu AJ (2013). Forgetful Bayes and myopic planning: Human learning and decision-making in a bandit setting. In Advances in Neural Information Processing Systems 26, Burges CJC, Bottou L, Welling M, Ghahramani Z, and Weinberger KQ, eds. (Curran Associates, Inc.), pp. 2607–2615. [Google Scholar]
- 33.Daw ND, O’Doherty JP, Dayan P, Seymour B, and Dolan RJ (2006). Cortical substrates for exploratory decisions in humans. Nature 441, 876–879. Available at: 10.1038/nature04766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kim H, Sul JH, Huh N, Lee D, and Jung MW (2009). Role of striatum in updating values of chosen actions. J. Neurosci 29, 14701–14712. Available at: 10.1523/JNEUROSCI.2728-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ito M, and Doya K (2009). Validation of decision-making models and analysis of decision variables in the rat basal ganglia. J. Neurosci 29, 9861–9874. Available at: 10.1523/JNEUROSCI.6157-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sul JH, Kim H, Huh N, Lee D, and Jung MW (2010). Distinct roles of rodent orbitofrontal and medial prefrontal cortex in decision making. Neuron 66, 449–460. Available at: 10.1016/j.neuron.2010.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Castellano MA, Diaz-Palarea MD, Rodriguez M, and Barroso J (1987). Lateralization in male rats and dopaminergic system: evidence of right-side population bias. Physiol. Behav 40, 607–612. Available at: 10.1016/0031-9384(87)90105-3. [DOI] [PubMed] [Google Scholar]
- 38.Gigerenzer G, and Goldstein DG (1996). Reasoning the fast and frugal way: models of bounded rationality. Psychol. Rev 103, 650–669. Available at: 10.1037/0033-295x.103.4.650. [DOI] [PubMed] [Google Scholar]
- 39.Bossaerts P, and Murawski C (2017). Computational Complexity and Human Decision-Making. Trends Cogn. Sci 21, 917–929. Available at: 10.1016/j.tics.2017.09.005. [DOI] [PubMed] [Google Scholar]
- 40.Tversky A, and Kahneman D (1974). Judgment under Uncertainty: Heuristics and Biases. Science 185, 1124–1131. Available at: 10.1126/science.185.4157.1124. [DOI] [PubMed] [Google Scholar]
- 41.Ebitz RB, Tu JC, Hayden BY Rule adherence warps choice representations and increases decision-making efficiency. under review. [Google Scholar]
- 42.Kurdi B, Gershman SJ, and Banaji MR (2019). Model-free and model-based learning processes in the updating of explicit and implicit evaluations. Proc. Natl. Acad. Sci. U. S. A 116, 6035–6044. Available at: 10.1073/pnas.1820238116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Filipowicz ALS, Levine J, Piasini E, Tavoni G, Kable JW, and Gold JI (2019). The complexity of model-free and model-based learning strategies. Available at: 10.1101/2019.12.28.879965. [DOI] [Google Scholar]
- 44.Kool W, and Botvinick M (2014). A labor/leisure tradeoff in cognitive control. J. Exp. Psychol. Gen 143, 131–141. Available at: 10.1037/a0031048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lynn DA, and Brown GR (2009). The ontogeny of exploratory behavior in male and female adolescent rats (Rattus norvegicus). Dev. Psychobiol 51, 513–520. Available at: 10.1002/dev.20386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gagnon KT, Thomas BJ, Munion A, Creem-Regehr SH, Cashdan EA, and Stefanucci JK (2018). Not all those who wander are lost: Spatial exploration patterns and their relationship to gender and spatial memory. Cognition 180, 108–117. Available at: 10.1016/j.cognition.2018.06.020. [DOI] [PubMed] [Google Scholar]
- 47.Gagnon KT, Cashdan EA, Stefanucci JK, and Creem-Regehr SH (2016). Sex Differences in Exploration Behavior and the Relationship to Harm Avoidance. Hum. Nat 27, 82–97. Available at: 10.1007/s12110-015-9248-1. [DOI] [PubMed] [Google Scholar]
- 48.Chowdhury TG, Wallin-Miller KG, Rear AA, Park J, Diaz V, Simon NW, and Moghaddam B (2019). Sex differences in reward- and punishment-guided actions. Cogn. Affect. Behav. Neurosci 19, 1404–1417. Available at: 10.3758/s13415-019-00736-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Leao D Jr, Fragoso M, and Ruffino P (2004). Regular conditional probability, disintegration of probability and Radon spaces. Proyecciones 23, 15–29. Available at: https://scielo.conicyt.cl/pdf/proy/v23n1/art02.pdf. [Google Scholar]
- 50.Wyner AD (1978). A definition of conditional mutual information for arbitrary ensembles. Information and Control 38, 51–59. Available at: http://www.sciencedirect.com/science/article/pii/S0019995878900268. [Google Scholar]
- 51.Nadel L ed. (2006). Multidimensional Scaling. In Encyclopedia of Cognitive Science (Chichester: John Wiley & Sons, Ltd), p. 516. Available at: http://doi.wiley.com/10.1002/0470018860.s00585.
- 52.Jaworska N, and Chupetlovska-Anastasova A (2009). A Review of Multidimensional Scaling (MDS) and its Utility in Various Psychological Domains. TQMP 5, 1–10. Available at: http://www.tqmp.org/RegularArticles/vol05-1/p001. [Google Scholar]
- 53.Buja A, Swayne DF, Littman ML, Dean N, Hofmann H, and Chen L (2008). Data Visualization With Multidimensional Scaling. J. Comput. Graph. Stat 17, 444–472. Available at: 10.1198/106186008X318440. [DOI] [Google Scholar]
- 54.Preacher KJ, Rucker DD, and Hayes AF (2007). Addressing Moderated Mediation Hypotheses: Theory, Methods, and Prescriptions. Multivariate Behav. Res 42, 185–227. Available at: 10.1080/00273170701341316. [DOI] [PubMed] [Google Scholar]
- 55.Sobel ME (1986). Some New Results on Indirect Effects and Their Standard Errors in Covariance Structure Models. Sociol. Methodol 16, 159–186. Available at: http://www.jstor.org/stable/270922. [Google Scholar]
- 56.Johnson CM, Peckler H, Tai L-H, and Wilbrecht L (2016). Rule learning enhances structural plasticity of long-range axons in frontal cortex. Nat. Commun 7, 10785. Available at: 10.1038/ncomms10785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Treviño M, Frey S, and Köhr G (2012). Alpha-1 adrenergic receptors gate rapid orientation-specific reduction in visual discrimination. Cereb. Cortex 22, 2529–2541. Available at: 10.1093/cercor/bhr333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Prusky GT, West PW, and Douglas RM (2000). Behavioral assessment of visual acuity in mice and rats. Vision Res. 40, 2201–2209. Available at: 10.1016/s0042-6989(00)00081-x. [DOI] [PubMed] [Google Scholar]
- 59.Vallortigara G, and Rogers LJ (2005). Survival with an asymmetrical brain: advantages and disadvantages of cerebral lateralization. Behav. Brain Sci 28, 575–89; discussion 589–633. Available at: 10.1017/S0140525X05000105. [DOI] [PubMed] [Google Scholar]
- 60.Botvinick MM (2012). Hierarchical reinforcement learning and decision making. Curr. Opin. Neurobiol 22, 956–962. Available at: 10.1016/j.conb.2012.05.008. [DOI] [PubMed] [Google Scholar]
- 61.Farashahi S, Rowe K, Aslami Z, Lee D, and Soltani A (2017). Feature-based learning improves adaptability without compromising precision. Nat. Commun 8, 1768. Available at: 10.1038/s41467-017-01874-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Soltani A, and Izquierdo A (2019). Adaptive learning under expected and unexpected uncertainty. Nat. Rev. Neurosci 20, 635–644. Available at: 10.1038/s41583-019-0180-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Miller EK, and Cohen JD (2001). An integrative theory of prefrontal cortex function. Annu. Rev. Neurosci 24, 167–202. Available at: 10.1146/annurev.neuro.24.1.167. [DOI] [PubMed] [Google Scholar]
- 64.Wallis JD, Anderson KC, and Miller EK (2001). Single neurons in prefrontal cortex encode abstract rules. Nature 411, 953–956. Available at: 10.1038/35082081. [DOI] [PubMed] [Google Scholar]
- 65.Buckley MJ, Mansouri FA, Hoda H, Mahboubi M, Browning PGF, Kwok SC, Phillips A, and Tanaka K (2009). Dissociable components of rule-guided behavior depend on distinct medial and prefrontal regions. Science 325, 52–58. Available at: 10.1126/science.1172377. [DOI] [PubMed] [Google Scholar]
- 66.Barraclough DJ, Conroy ML, and Lee D (2004). Prefrontal cortex and decision making in a mixed-strategy game. Nat. Neurosci 7, 404–410. Available at: 10.1038/nn1209. [DOI] [PubMed] [Google Scholar]
- 67.Bussey TJ, Wise SP, and Murray EA (2001). The role of ventral and orbital prefrontal cortex in conditional visuomotor learning and strategy use in rhesus monkeys (Macaca mulatta). Behav. Neurosci 115, 971–982. Available at: 10.1037//0735-7044.115.5.971. [DOI] [PubMed] [Google Scholar]
- 68.Genovesio A, Brasted PJ, Mitz AR, and Wise SP (2005). Prefrontal cortex activity related to abstract response strategies. Neuron 47, 307–320. Available at: 10.1016/j.neuron.2005.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Uban KA, Rummel J, Floresco SB, and Galea LAM (2012). Estradiol modulates effort-based decision making in female rats. Neuropsychopharmacology 37, 390–401. Available at: 10.1038/npp.2011.176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Georgiou P, Zanos P, Bhat S, Tracy JK, Merchenthaler IJ, McCarthy MM, and Gould TD (2018). Dopamine and Stress System Modulation of Sex Differences in Decision Making. Neuropsychopharmacology 43, 313–324. Available at: 10.1038/npp.2017.161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Calipari ES, Juarez B, Morel C, Walker DM, Cahill ME, Ribeiro E, Roman-Ortiz C, Ramakrishnan C, Deisseroth K, Han M-H, et al. (2017). Dopaminergic dynamics underlying sex-specific cocaine reward. Nat. Commun 8, 13877. Available at: 10.1038/ncomms13877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Zador AM (2019). A critique of pure learning and what artificial neural networks can learn from animal brains. Nat. Commun 10, 3770. Available at: 10.1038/s41467-019-11786-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Kie JG (1999). Optimal Foraging and Risk of Predation: Effects on Behavior and Social Structure in Ungulates. J. Mammal 80, 1114–1129. Available at: https://academic.oup.com/jmammal/article-abstract/80/4/1114/851833 [Accessed September 26, 2019]. [Google Scholar]
- 74.Arnold AP, and Chen X (2009). What does the “four core genotypes” mouse model tell us about sex differences in the brain and other tissues? Front. Neuroendocrinol 30, 1–9. Available at: 10.1016/j.yfrne.2008.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Song Z, Kalyani M, and Becker JB (2018). Sex differences in motivated behaviors in animal models. Curr Opin Behav Sci 23, 98–102. Available at: 10.1016/j.cobeha.2018.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Seu E, Groman SM, Arnold AP, and Jentsch JD (2014). Sex chromosome complement influences operant responding for a palatable food in mice. Genes Brain Behav. 13, 527–534. Available at: 10.1111/gbb.12143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Quinn JJ, Hitchcott PK, Umeda EA, Arnold AP, and Taylor JR (2007). Sex chromosome complement regulates habit formation. Nat. Neurosci 10, 1398–1400. Available at: 10.1038/nn1994. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data and software are available upon request to the Lead Contact, Nicola Grissom (ngrissom@umn.edu)


