The relationship between 3D dentofacial photogrammetry measurements and traditional cephalometric measurements

Abstract

Objectives:

To determine the relationship between traditional cephalometric measurements and corresponding nonradiographic three-dimensional (3D) photogrammetry measurements.

Materials and Methods:

This was a cross-sectional study of 20 orthodontic patients (10 male and 10 female) who received lateral cephalometric radiographs and 3D dentofacial photogrammetric records with each subject serving as his or her own control for a total sample size of 40 images (20 per method). A 3D analysis that resembled a traditional cephalometric analysis was established using the eyes and natural head orientation as substitutes for the cranial base. Pearson correlation coefficients and multivariable linear regression plots were calculated to evaluate the relationship between the photogrammetry measurements and the cephalometric measurements.

Results:

The ANB angle, mandibular plane angle, lower anterior face height, upper incisor angle to SN, upper incisor angle to NA, and all measurements of lower incisor position and inclination had strong positive Pearson correlation coefficients with the corresponding 3D photogrammetry measurements (P < .004). Statistically significant regression plots demonstrated that cephalometric relationships between the jaws and incisor orientation can be predicted from corresponding 3D photogrammetry measurements.

Conclusions:

3D photogrammetry measurements relating the jaws to each other and incisor orientation has a strong positive correlation with corresponding traditional cephalometric measurements and can serve as cephalometric predictors. Capturing the eyes using 3D photogrammetry can obviate the need to expose the cranial base and allow limiting the radiographic field to the area of interest.

INTRODUCTION

In 1931, Broadbent1 standardized cephalometric radiography and proposed the use of sella and nasion as references for measuring the position and orientation of the jaws and teeth due to their relative stability,2 Since then, the cranial base has been widely used as a reference for orthodontic diagnosis.3 However, sella and nasion exhibit high individual positional variation that can result in misleading cephalometric interpretation. This has led to the development of cephalometric analyses that depend on extracranial references like the occlusal plane and true horizontal, which is based on natural head position.4–6 This brings into question the need to expose the upper half of the face radiographically since orthodontists lack the ability to affect that area.

Several studies have reported no significant difference in the consistency of orthodontic treatment planning, regardless of whether or not cephalometrics were used.7–10 Others have noted that cephalograms may not be routinely needed but that the indication may depend on a patient's individual needs rather than general conditions.11–14

Unlike medical computed tomography, to which patients are seldom exposed, the public health concerns related to orthodontics stem from repeated exposure of a large population to small doses of radiation. Regulating bodies have provided guidelines for prescribing dental radiographs to promote the principle of “as low as reasonably achievable” (ALARA). Recognizing that there is no safe dose of radiation and that radiation exposure is cumulative, they concluded that there should not be a set of routine radiographs for all orthodontic patients and that the risk involved is only justified when there is a health benefit to the patient (justification) from a minimum dose (optimization).15–17 As a result of these guidelines, many countries have made it illegal to take cephalometric radiographs after the completion of orthodontic treatment without further justification.

The necessity for noninvasive diagnostic imaging systems that focus on soft tissues led to the development of a variety of two-dimensional (2D) and three-dimensional (3D) soft tissue analyses.18–21 Plooij et al.22 demonstrated the accuracy and reliability of bone-related soft tissue 3D photograph-based soft tissue analysis and concluded that hard tissue data were not necessary to perform an accurate soft tissue analysis. Kochel et al. 20,21 demonstrated that 3D photogrammetry measurements were significantly correlated to cephalometric measurements in both sagittal and vertical dimensions. One of the greatest obstacles to the mainstream use of 3D photogrammetry has been the absence of reference values for a system that allows registration of the teeth to the soft tissue. Rosati et al.23 demonstrated that a digital dental model can be accurately registered to a 3D soft tissue reconstruction. In 2017, a 3D dentofacial photogrammetry method that allowed measurement of the position of orientation of the teeth and surrounding soft tissue using the eyes and natural head position as a reference instead of the cranial base was introduced along with reference values for adult men and women. The eyes have been shown to undergo a limited amount of change after the age of 5 years,24,25 and using them as references instead of the cranial base makes it possible to limit radiographic exposure to the lower half of the face. The aim of the present study was to correlate measurements from 3D constructed dentofacial surface images to measurements from traditional cephalometric radiographs on the same individuals.

MATERIALS AND METHODS

The protocol for this study was approved by the institutional review board (#IRB14-1347 and #H-31863). This study was a cross-sectional analysis of 20 consecutive orthodontic patients (10 female and 10 male) who had traditional orthodontic records and 3D dentofacial photogrammetry records taken between March 2013 and January 2015. Since each subject served as his or her own control, subjects were not excluded due to variations in type of malocclusion or ethnicity. The sample size for the present study was based on previously published work comparing standard records and nonradiographic 3D dentofacial photogrammetry records for orthodontic diagnosis and treatment planning.26 A sample size of 20 was necessary to detect correlations in regression models at an alpha of 0.05 of power of 80% with all statistical tests being two-sided.

Each patient was asked to sign a consent (assent for minors) form to participate in the study. In addition to standard orthodontic records, which included photographs, study models, and panoramic and cephalometric radiographs, all subjects had extraoral 3D facial and dental images taken using the Vectra M3 imaging system (Canfield Imaging Systems, Fairfield, NJ) and the Ortho Insight scanner (Motion View Software, Chattanooga, Tenn), respectively.

The 3D facial images were taken in natural head orientation (determined by having the patients look straight at their eyes in a mirror at eye level²⁷) with the lips at rest and with a full smile, both with the teeth together. The patient's maxillary and mandibular dental casts and bite registrations were scanned with the Ortho Insight scanner. The mandibular teeth were registered to the maxillary teeth using the bite registration. The maxillary teeth were registered to the smiling 3D facial image using at least 6 common landmarks, including the incisal and gingival embrasures.28 The smiling and nonsmiling images were registered using the centers of the pupils, the endocanthal points, the highest points on the brow lines, and the mesial and lateral limits of the eyebrows as documented by Masoud et al.28 Figure 1 shows the registration process described previously. The 3D dental casts were digitized with landmarks described by Huanca Ghislanzoni et al.29 The facial landmarks were identified according to Plooij et al.22 and Farkas et al.30

Figure 1.

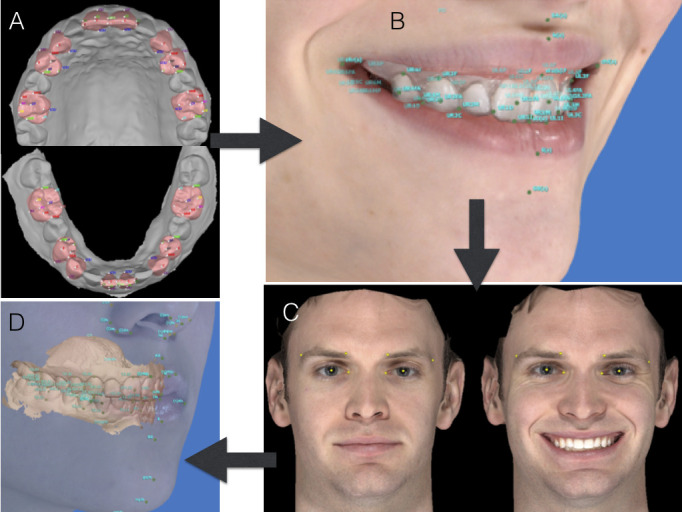
Steps for registering the dental and facial images. From Masoud et al.28

After registration and digitization using a custom version of Facial Insight 3D (Motion View Software), measurements were generated using the eyes and the natural head position as references. Figure 2 shows the three reference planes based on the eyes and natural head position intersecting midway between the two pupils at M point as described by Masoud et al.28 Figure 3 displays the sagittal and vertical photogrammetry measurements used in the study. The long axes of the uppermost and lowermost labial incisors were determined by connecting a line from the midpoint of the incisal edges to a point midway between the labial and palatal/lingual height of contour of the gingival margin as described by Carlsson and Ronnerman.31 The lateral cephalometric radiographs were digitized and analyzed using Steiner's analysis and components from other cephalometric analyses (Figure 4).3,4,32 Table 1 describes the cephalometric and photogrammetric variables used in the study.

Figure 2.

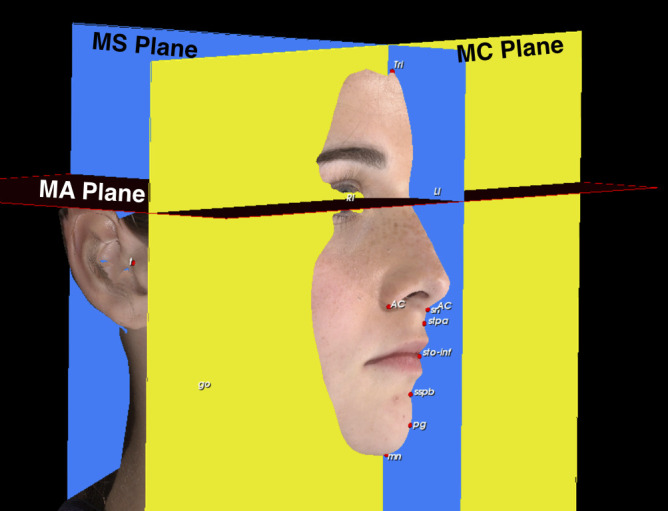
MC plane: A coronal plane perpendicular to the true horizontal and touching pupil points. MA plane: An axial plane parallel to the natural head position passing through the pupils. MS plane: A plane perpendicular to the true horizontal passing through a point midway between the pupils.

Figure 3.

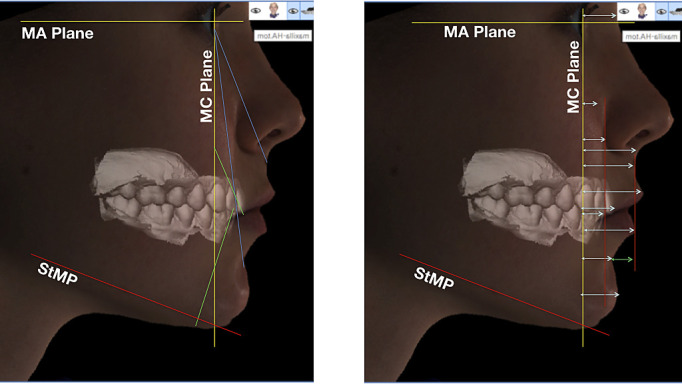
Lateral and vertical components of the 3D photogrammetry analysis correlated to cephalometric measurements.

Figure 4.

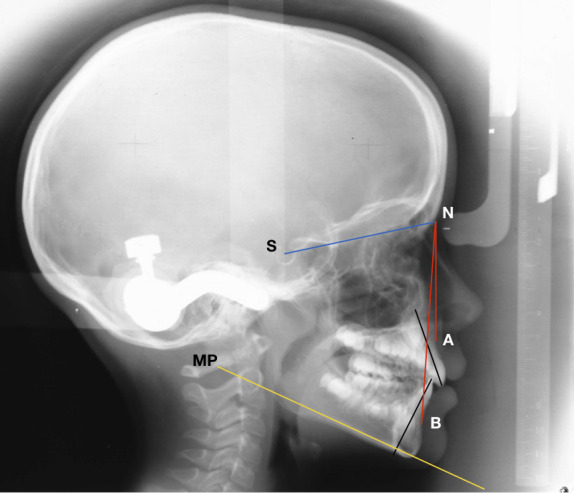
Some of the cephalometric measurements correlated to the 3D photogrammetry measurements.

Table 1.

Demographics and Baseline Data

	N	%
Sex
Female	10	50%
Male	10	50%
Age
Adolescents (<]18 years)	9	45%
Adults (≥18 years)	11	55%
Ethnicity
Caucasian	10	50%
African American	5	25%
Hispanic	5	25%
Angle classification
Class I	6	30%
Class II (division 1 and division 2)	8	40%
Class III	6	30%

All examiners were calibrated before landmarking. Two examiners blinded to the 3D photogrammetry records landmarked all 20 lateral cephalograms twice, 3 weeks apart. Two different examiners, who were both blinded to the cephalometric results, conducted the photogrammetric analysis and established inter- and intraexaminer reliability. The cephalometric measurements were then correlated with their corresponding 3D photogrammetry measurements and to different cephalometric measurements designed to measure the same parameters.

Statistical Analysis

Intraclass correlation coefficients (Cronbach alpha) were used to assess consistency of landmarking and reliability between examiners. The descriptive data were analyzed in two ways. First, all patients were compiled together, and the paired cephalometric vs photogrammetric measurements were analyzed. Multiple 3D measurements were paired for every standard 2D measurement. For each dentofacial measurement, the paired data were cross-tabulated and a Pearson correlation (R) was calculated as shown in Table 2 (R² is also included). Additionally, nine pairs of cephalometric measurements were correlated to each other and their Pearson correlation coefficients (R) are shown in Table 3 along with R², two-tailed P values, and those correlations that were significant are highlighted.

Table 2.

Description of Lateral Cephalometric and 3D Photogrammetry Measurements and Planes

Measurement Name	Measurement Description	Unit
Lateral cephalometric measurements
SNA	Angle between Sella, Nasion, and A point	°
SNB	Angle between Sella, Nasion, and B point	°
ANB	Angle between A point, Nasion, and B point	°
Mandibular length	Distance from Condylion to Gnathion	mm
Maxillary length	Distance from Condylion to A point	mm
LAFH (lower anterior face height)	Distance from Anterior Nasal Spine to Menton	mm
TAFH (total anterior face height)	Distance from Nasion to Menton	mm
U1-NA	Angle between most proclined upper central incisor long axis to Nasion-A point line	°
U1-NA	Distance between most protruded upper central incisor cusp tip to Nasion-A point line	mm
U1-SN	Angle between most proclined upper central incisor long axis to Sella-Nasion line	°
L1-MP	Angle between most proclined lower central incisor long axis to Mandibular plane	°
L1-NB	Angle between most proclined lower central incisor long axis to Nasion-B point line	°
L1-NB	Distance between most protruded lower central incisor tip to Nasion-B point line	mm
MP-SN	Angle between mandibular plane to Sella-Nasion line	°
MP-FH	Angle between mandibular plane to Frankfurt horizontal line (Porion to Orbitale)	°
Wits	Difference in distance between the perpendicular lines from A and B points onto the occlusal plane	mm
Harvold	Difference in distance between Condylion-Gnathion and Condylion-A point	mm
3D photogrammetry measurements
StAM-MC	Angle formed between soft tissue A plane to irises and coronal plane through the Irises	°
StBM-MC	Angle formed between soft tissue B plane to the irises and coronal plane through the irises	°
(StA-MC) - (StB-MC)	Distance between soft tissue A point and soft tissue B point relative to coronal plane through the irises	mm
StAM-StBM	Angle formed between soft tissue A plane to irises and soft tissue B plane to the irises	°
StMP-MA (mandibular plane angle)	Angle formed between soft tissue mandibular plane and axial plane through the irises	°
3DLAFH (lower anterior face height)	Distance between soft tissue menton and subnasale	mm
3DTAFH (total anterior face height)	Distance between soft tissue menton and trichion	mm
U1-MC (maxillary incisors)	Angle formed between the most proclined upper Incisor long axis and coronal plane through the Irises	°
U1-MC	Distance between the most protruded upper incisor tip to coronal plane through the irises	mm
L1-MC (mandibular incisors)	Angle formed between the most proclined lower incisor long axis and coronal plane through the irises	°
L1-MC	Distance between the most protruded lower incisal tip to coronal plane through the irises	mm
L1-MP	Angle formed between the most proclined lower incisor long axis and the soft tissue mandibular plane	°
Planes used in the 3D photogrammetry measurements
MC plane	Coronal plane passing through the irises perpendicular to the true horizontal (determined by the patient's NHP)
MA plane	Axial plane passing through the irises to the true horizontal (determined by the patient's NHP)
MS plane	Sagittal plane passing through M point (midpoint between the irises perpendicular to the true horizontal (determined by the patient's NHP)
StAM	Plane formed between soft tissue A point and R/L irises
StBM	Plane formed between soft tissue B point and R/L irises
StMP	Plane formed between soft tissue Menton and R/L soft tissue Gonion Inferior

Table 3.

Pearson Correlation Between Lateral Cephalometric Measurements and Corresponding 3D Photogrammetry Measurements^a

Measurement	P Value	R Value	R2 Value	Statistical Significance	Correlation Strength
AP
SNA (°) vs StAM-MC (°)	.857	0.043	0.00185
SNB (°) vs StBM-MC (°)	.518	−0.153	0.02341
Wits (mm) vs SA-MC - SB-MC (mm)	.021	0.511	0.26112
ANB (°) vs StAM-StBM (°)	<.0001	0.771	0.59444	**	Strong
Vertical
LAFH (mm) vs 3DLAFH (mm)	<.0001	0.888	0.78854	**	Very strong
TAFH (mm) vs 3DTAFH (mm)	<.0001	0.758	0.57456	**	Strong
MP-SN (°) vs StMP-MA (°)	.005	0.601	0.3612
MP-FH (°) vs StMP-MA (°)	.002	0.643	0.41345	**	Strong
Dental
U1-NA (°) vs U1-MC (°)	.001	0.671	0.45024	**	Strong
U1-SN (°) vs U1-MC (°)	<.0001	0.726	0.52708	**	Strong
L1-MP (°) vs L1-MC (°)	<.0001	0.715	0.51123	**	Strong
L1-NB (°) vs L1-MC (°)	<.0001	0.818	0.66912	**	Very strong
L1-NB (mm) vs L1-MC (mm)	<.0001	0.73	0.5329	**	Strong
U1-NA (mm) vs U1-MC (mm)	.092	0.386	0.149

^aStrength of correlation coefficient (R) is estimated as follows: 0.8–1 (very strong), 0.6–0.79 (strong), 0.4–0.59 (moderate), 0.2–0.39 (weak), and 0–0.19 (very weak).

^**Correlation is significant at P < .004 for 15 distinct 2D measurements.

Overall, 14 primary outcomes were examined when comparing the cephalometric measurements to the photogrammetry measurements, and nine primary outcomes examined when correlating the different cephalometric measurements to each other. To adjust for Type 1 errors attributed to multiple outcomes, P values were adjusted to determine statistical significance. Since 14 outcomes were evaluated when comparing traditional cephalometric measurements to 3D photogrammetry measurements, a P value <.004 was deemed to be statistically significant. When comparing different cephalometric measurements to each other, nine outcomes were examined and a P value <.005 was deemed statistically significant. Multivariable linear regression models were used to examine the association between 3D photogrammetry measurements (modeled as the outcome variable) and 2D cephalometric measurements (primary predictor variable). Fourteen different models were used for the 14 different 3D and 2D measurements. In all the regression models, the effect of age (adult or adolescent), sex, and race were adjusted. The parameter estimates for each unit change in 3D photogrammetry measurements and its impact on 2D cephalometric measurements were computed. For these models, a P value <.004 was deemed to be statistically significant. All statistical tests were two-sided. All statistical analyses were performed using SPSS software version 25.0 (IBM Corp, Armonk, NY).

RESULTS

The average interexaminer correlation coefficient was 0.96. The lowest intraexaminer correlation coefficients were for SNA (°) at 0.86. The rest of the cephalometric measurements had intra- and interexaminer correlation coefficients of 0.9 and above. Inter- and intraexaminer reliability for the 3D photogrammetry method averaged 0.94 and 0.92, respectively.

Table 3 shows the correlation between the traditional cephalometric measurements and the corresponding 3D photogrammetry measurements using Pearson correlation coefficients. The ANB angle, LAFH, TAFH, MPFH, U1-SN (°) U1-NA (°), L1-MP, L1-NB (°), and L1-NB (mm) all had strong or very strong correlations with their corresponding 3D dentofacial measurements (P < .004).33

Table 4 shows the results of the multivariable linear regression models for predicting traditional cephalometric measurements from 3D dentofacial measurements after adjusting for the effects of age (adult vs adolescent), sex, and race. The model was statistically significant for predicting ANB, LAFH, TAFH, and upper and lower incisor inclinations (P < .004). For example, a soft tissue intermaxillary angle (StAM-StBM) of 12° would predict an ANB angle of the following:

Table 4.

Summary of Estimates From Multivariable Linear Regression Model

Predictor Variable (Photogrammetry)a	Outcome Variable (Cephalometric)b	Constant	Parameter Estimate	95% Confidence Interval		R2	P Value
				Lower Bound	Upper Bound
StAM-MC (°)	SNA (°)	81.561	–0.092	–0.635	0.451	0.126	.723
StBM-MC (°)	SNB (°)	79.576	–0.81	–0.575	0.413	0.278	.73
StAM-StBM (°)	ANB (°)	–11.49	1.074	0.792	1.357	0.865	<.0001**
(SA-MCP) - (SB-MCP)	Witts (mm)	–4.794	0.689	0.239	1.138	0.56	.005
3DLAFH (mm)	DLAFH (mm)	–30.765	1.398	0.881	1.915	0.844	<.0001**
3DTAFH (mm)	TAFH (mm)	–6.278	0.982	0.393	1.57	0.705	.003**
StMP-MA (°)	MPSN (°)	12.789	0.58	0.211	0.95	0.698	.005
StMP-MA (°)	MPFH (°)	2.055	0.625	0.22	1.031	0.522	.005
U1-MC (°)	U1-NA (°)	11.517	0.651	0.33	0.972	0.626	.001**
U1-MC (°)	U1-SN (°)	93.166	0.513	0.258	0.767	0.672	.001**
U1-MC (mm)	U1-NA (mm)	3.419	0.18	–0.256	0.616	0.436	.39
L1-MC (°)	L1-NB (°)	5.738	0.678	0.456	0.9	0.872	<.0001**
L1-MC (°)	L1-MP (°)	79.5	0.761	0.328	1.194	0.548	.002**
L1-MC (mm)	L1-NB (mm)	1.596	0.297	–0.044	0.637	0.649	.083

^aRegression model is adjusted for the effects of age (adult vs adolescent), sex, and race.

^bOutcome = Constant + Parameter estimate of predictor variable.

^**Statistically significance for regression set at P < .004.

Table 5 shows correlations between pairs of traditional cephalometric measurements using Pearson correlation coefficients. Wits vs Harvold, Wits vs ANB, ANB vs Harvold, MP-SN vs MP-FH, U1-NA (°) vs U1-SN (°), and IMPA vs L1-NB (°) all had strong or very strong correlations.

Table 5.

Pearson Correlation Between Different Lateral Cephalometric Measurements Evaluating the Similar Parameters^a

Measurement	P Value	R Value	R2 Value	Statistical Significance	Correlation Strength
AP
Wits (mm) vs Harvold (mm)	<.0001	–0.733	0.537	**	Strong
Wits (mm) vs ANB (°)	.025	0.5	0.25	*	Strong
ANB (°) vs Harvold (mm)	<.0001	–0.775	0.601	**	Strong
SNA (°) vs Harvold Max Length (mm)	.175	0.316	0.1
SNB (°) vs Harvold Mand Length (mm)	.143	0.34	0.116
Vertical
MP-SN (°) vs MP-FH (°)	<.0001	0.784	0.615	**	Strong
Dental
U1-NA (°) vs U1-SN (°)	<.0001	0.89	0.792	**	Very strong
IMPA (°) vs L1-NB (°)	<.0001	0.772	0.596	**	Strong

^aStrength of correlation coefficient (R) is estimated as follows: 0.8–1 (very strong), 0.6–0.79 (strong), 0.4–0.59 (moderate), 0.2–0.39 (weak), and 0–0.19 (very weak).

^**Correlation is significant at P < .005 level for nine distinct cephalometric measurements.

Neither SNA nor SNB had significant correlations with any traditional cephalometric or photogrammetry measurements.

DISCUSSION

This study demonstrated high inter- and intraexaminer reliability for cephalometric and photogrammetric measurements which was consistent with results from earlier reliability studies.22,34 The 3D photogrammetry measurements evaluating the sagittal relationship between the upper and lower jaws and the orientation of the upper and lower incisors were strongly correlated with the corresponding cephalometric measurements and were shown to be predictive of them. However, there was a nonstatistically significant correlation between SNA and SNB measurements and their corresponding photogrammetry counterparts as well as traditional cephalometric measurements. This could be related to SNA and SNB being dependent on Sella. which has been shown to have significant individual variation. Further research is necessary to evaluate the viability of 3D photogrammetry for determining the sagittal position of the individual jaws.

The 3D photogrammetry measurements of the upper incisors had a stronger correlation to the cephalometric upper incisor measurement to SN than the upper incisors to NA. This could potentially be related to the difficulty in locating A point on cephalometric radiographs, which was the point associated with the least examiner agreement. It was unlikely related to the methodologic limitation of the photogrammetry records using estimated root positions since the same estimations resulted in other dental measurements being highly correlated to their cephalometric counterparts. Even though 3D photogrammetry and cephalometric measurements were performed on two completely different types of records, the correlation coefficients of their corresponding measurements were comparable to those of different cephalometric measurements designed to measure the same parameter using the same cephalometric record.

An obvious shortcoming of this study was related to the inherent limitations of the cephalometric “gold standard” to which 3D photogrammetry measurements were correlated. In addition to the 2D limitations of traditional cephalometrics, many studies have discussed problems with using S-N as a cranial reference and have proposed using true horizontal or the occlusal plane as alternatives.4–6 The short-term and long-term reproducibility and reliability of NHP were tested, with the conclusion that NHP was reproducible to within 1°to 2°.35,36 The 3D photogrammetry measurements relied on NHP and could potentially be better than the “gold standard” to which they were correlated.

The findings were consistent with those of Manosudprasit et al.26 in supporting the use of 3D dentofacial photogrammetry in routine orthodontic diagnosis. Nevertheless, orthodontic diagnosis still needs to be supplemented with radiographic information. Among the benefits of 3D dentofacial photogrammetry is that it allows the eyes to be used as a reference, thus permitting a custom radiographic field of view based on the patient's individual needs. For limited tooth movement cases, this may involve periapical radiographs, a panoramic radiograph, or cone beam computed tomography (CBCT) limited to the teeth being moved and taken at an appropriate resolution depending on the patient. For more complex cases with skeletal problems, a CBCT or a cephalometric radiograph limited to the upper and lower jaws can be taken. The radiographs can be registered to the 3D dentofacial photogrammetry records to address the shortcomings shown by the present study at estimating the position of the apical bases and root positions. Newer CBCT units and software allow the resolution to be lowered to the point where a field of view limited to the maxilla and mandible can be taken with an effective dose comparable to that of a panoramic radiograph and still provide more information.37 A limited field CBCT also offers the potential for using thyroid and eye shielding,38 which are not compatible with panoramic radiographs.

CONCLUSIONS

• 3D photogrammetry measurements relating the jaws to each other and incisor orientation had a strong positive correlation with corresponding traditional cephalometric measurements and could serve as cephalometric predictors.

• Capturing the eyes using 3D photogrammetry can obviate the need to expose the cranial base and allow the radiographic field to be limited to the area of interest.