Graphical abstract

Keywords: Hi-C, Normalization, Matrix balancing, Doubly stochastic matrix, Sparsity
Abstract
The high-throughput genome-wide chromosome conformation capture (Hi-C) method has recently become an important tool to study chromosomal interactions where one can extract meaningful biological information including P(s) curve, topologically associated domains, A/B compartments, and other biologically relevant signals. Normalization is a critical pre-processing step of downstream analyses for the elimination of systematic and technical biases from chromatin contact matrices due to different mappability, GC content, and restriction fragment lengths. Especially, the problem of high sparsity puts forward a huge challenge on the correction, indicating the urgent need for a stable and efficient method for Hi-C data normalization. Recently, some matrix balancing methods have been developed to normalize Hi-C data, such as the Knight-Ruiz (KR) algorithm, but it failed to normalize contact matrices with high sparsity. Here, we presented an algorithm, Hi-C Matrix Balancing (HCMB), based on an iterative solution of equations, combining with linear search and projection strategy to normalize the Hi-C original interaction data. Both the simulated and experimental data demonstrated that HCMB is robust and efficient in normalizing Hi-C data and preserving the biologically relevant Hi-C features even facing very high sparsity. HCMB is implemented in Python and is freely accessible to non-commercial users at GitHub: https://github.com/HUST-DataMan/HCMB.
1. Introduction
The high-throughput genome-wide chromosome conformation capture (Hi-C) method has been widely adopted to measure pairwise contacts between pairs of genomic loci that are distant in the linear genome and significantly facilitated the study of spatial genomics [1], [2]. Researches in recent years have certificated how this technology plays an important role in various biological fields ranging from genome assembly and haplotyping [3], [4], [5] to discovering the potential associations between changes in chromatin hierarchical organization and genome function [6], [7], [8], [9]. In order to comprehensively and correctly interpret the results and in-depth understand the chromatin structure and the genetic significance behind it, complete workflows and sophisticated algorithms are required, and it is necessary to ensure the accuracy of each step in Hi-C data processing.
The main processing procedure of raw Hi-C data consists of four steps: alignment, filtering, binning and normalization [10], [11]. The first step is the alignment of the raw reads on a reference genome, and then proceed with the detection and filtering of valid interaction products, so that the analysis carries on the retained high-quality sequences [12]. In the third step, the whole genome is partitioned into small equal-sized regions (usually called bins), inside which the counting number of paired-end reads was reserved to evaluate the observed interactions between genomic loci, thereby transforming the dataset into a square symmetric matrix that also known as raw contact matrix. Specifically, each bin corresponds to each row or each column in the matrix, and the size of each bin measured by the unit kilobase (kb) is called the resolution of Hi-C contact matrix.
Subsequently, the contact matrix needs to be normalized for the purpose of removing experimental and technical biases that affect downstream analysis including P(s) estimation, topologically associated domains (TADs) calling, compartments annotation, and detection of other biologically relevant signals [13], [14]. It is regarded as a crucial step that can have a strong impact on the results [15], cause it was reported as a major caveat call for special attention that the incorrect normalization of sequencing data may bring about the risk of artifacts in data interpretation especially in Hi-C type of approaches [16]. Although the entries of the raw chromatin interaction data matrices in the Hi-C data would be proportional to the true contact frequency ideally, systematic and experiment biases due to different mappability, GC content and restriction fragment lengths of these data can strongly affect the prior probability of generating and sequencing Hi-C ligation products and may result in more reads regardless of actual interaction frequency [13], [17]. These biases could strongly affect the measurement of both interchromosomal (trans) and intrachromosomal (cis) contact probabilities between different chromosomal loci, reducing the correlation between replicate experiments and the comparability between Hi-C datasets [18]. The normalization is an important preprocessing step that aims to address this issue by somehow mitigate and eliminate these biases, and thus facilitating Hi-C data analysis which could characterize chromosome structure at a higher resolution and provides reproducible global insights into chromosome architecture. Previous studies have demonstrated that the normalization significantly increases the correspondence between contact maps and improves the consistency of coverage curves [13], [18].
Several normalization software packages are available for Hi-C data process and are discussed in multiple reviews [13], [17], [18], [19]. Commonly used normalization methods can be divided into two main categories: explicit factors correction and matrix balancing (implicit). Explicit methods such as Yaffy and Tanay’s integrated probabilistic background multiplicative model that considers three major factors [18], and HiCNorm based on the Poisson regression distribution [17]. This type method requires a large number of explicit parameters to be estimated or make appropriate statistical distribution assumptions on the data to be processed in advance. The implicit method is built on the assumption that all loci on the genome should have equal visibility [13]. It does not require consideration of the specific sources of system biases, but correct collectively for all factors affecting experimental visibility. Here, the normalization of Hi-C contact maps can be transformed into a matrix balancing problem of rescaling a given square nonnegative matrix to a doubly stochastic matrix, where every row and column sums to one, by multiplying two diagonal matrices [10], [20], [21]. Examples include Knight-Ruiz (KR) algorithm, Sinkhorn & Knopp (SK) algorithm, iterative Correction (IC) algorithm and Vanilla-Coverage (VC) algorithm, etc., in which the KR algorithm [20] was widely used because of its high convergence rate and numerical stability [22], [23], [24]. However, it was observed that the KR algorithm may fail to result in a balanced matrix when the original matrix shows high sparsity at high resolutions [21] and we also verified this issue on high-performance computing clusters.
To fill in this gap, we proposed a novel algorithm named Hi-C Matrix Balancing (HCMB) to tackle matrix balancing and bias correction task of raw large-scale Hi-C contact data. This algorithm HCMB is architected on an iterative solution of equations combining with a linear search and projection strategy to normalize the Hi-C original interaction data. It can be seen as a variant of the Levenberg-Marquardt-type method, of which one salient characteristic is that the coefficient matrix of linear equations will usually be dense during the iterative process [25]. The experiments we performed showed that our HCMB method is efficient for normalizing Hi-C contact map data as well as the KR method, and also is able to preserve the biologically relevant Hi-C features including P(s) curve, A/B compartments and TADs. Furthermore, the HCMB algorithm outperforms the KR algorithm in terms of fewer number iterations and a more robust practical behavior on highly sparse matrices.
2. Materials and methods
In this section, we first provided the technicalities about the implementation of the HCMB algorithm, and then illustrated how to generate the simulated and real biological datasets for verification and comparison of algorithms. Finally, we described the evaluative dimension of the display results.
2.1. Algorithms and implementation
To handle the normalization of Hi-C contact maps, the HCMB algorithm applies the same matrix balancing model as the KR method [20]. The matrix balancing can be defined as the problem of rescaling a given square nonnegative matrix to a doubly stochastic matrix P, where every row and column sums to one, by multiplying two diagonal matrices and . For symmetric matrices, . Because of the symmetric characteristic of the Hi-C raw contact matrix, we consider that M is a symmetric matrix. So, for balancing symmetric matrices, we need to solve the following transformed system of nonlinear equations [20] The Jacobian matrix of the at is
The following mathematical notations will be used. The subscript T denotes transposed of a matrix, denotes the set of n-dimensional real column vectors. denotes the set of n-by-n dimensional real matrix. represents the diagonal matrix with the vector on its diagonal. stands for the Euclidean projection of the vector on the nonnegative orthant of , i.e., the plus operator is applied component wise . Let represent a vector of ones. The stands for an identity matrix that is a square n-by-n matrix with ones along the diagonal from the upper left to the bottom right and zeros elsewhere. The symbol stands for the Euclidean norm of the vector.
The HCMB algorithm uses Levenberg-Marquardt-type (LMT) as a method for solving the balancing problem of symmetric matrices. Levenberg-Marquardt-type (LMT) method is a classical and widely used method for solving the system of nonlinear equations and has locally fast convergent rates [26], [27]. The main principle of LMT is to solve the approximate linear equations and take the solution of this system of linear equations as a search direction in each iteration step, where is a sequence of positive parameters. The coefficient matrix of the iterative linear equations is always symmetric and positive definite, which makes the iterative linearized equations always have solutions. Based on LMT method, HCMB solves only one system of linearized equations per iteration and combines with a linear search and Euclidean projection strategy to solve transformed nonlinear equation and normalize the Hi-C original interaction data.
Let be the natural merit function corresponding to the mapping , and its gradient is . The HCMB algorithm is described in details for matrix balancing as follows:
Step 0 Initialization: Choose constants . Let be an arbitrary point and set .
Step 1 If , STOP
Step 2 Set and find a solution of the following linear system
| (1) |
Set .
Step 3 If
| (2) |
Then set and perform Step 6.Otherwise go to Step 4.
Step 4 If (2) is not satisfied but the condition
| (3) |
is satisfied, then compute a stepsize such that
| (4) |
Set and perform Step 6.Otherwise go to Step 5.
Step 5 If none of the above conditions (2), (3) is met, then set and compute a stepsize such that
| (5) |
Set and go to Step 6.
Step 6 Set , and . Return to Step 1.
2.2. Hi-C contact datasets
The contact matrix datasets used for experimental verification are divided into two parts: computer simulated datasets and real experimental datasets.
2.2.1. Simulated datasets
In our simulations, to approximate the characteristics of real raw Hi-C contact maps as possible, we produced symmetric nonnegative matrices randomly with two dimensions of 100-by-100 and 1000-by-1000 respectively, each matrix sampled from Poisson distributions entries. We repeated the experiment test with two different random seeds. For follow-up investigation, we removed a certain fraction of the total values for each dataset to create a certain coverage of sparsity, which was defined as the proportion of zero elements. In order to test the performance of the algorithms under different sparsity levels, we simulated matrices with sparsity levels from 0% to 100% as test data sets.
2.2.2. Real Hi-C datasets
This paper uses Hi-C datasets from different studies to conduct the evaluation experiments, all of which are available for download from public websites.
(1) Bulk Hi-C dataset [21]: This dataset contains Hi-C maps of eight diverse human cell lines and one mouse cell line. The raw observed contact matrices at different base pair delimited resolutions from human mammary epithelial cells with strain ID CC2551 (HMEC) and normal human epidermal keratinocytes cells with strain ID 192,627 (NHEK) were selected for this study. The dataset is available under NCBI Gene Expression Omnibus (GEO) GSE63525.
(2) Single-cell Hi-C (scHi-C) dataset [28]: This dataset contains single-cell Hi-C data of CD4 + T cells from male mouse spleen. We randomly select raw contact map data of GSM1173502_cell-10 for the study. It can be downloaded from NCBI GEO GSE48262.
(3) Capture Hi-C (CHi-C) dataset [29]: This dataset contains capture Hi-C data for the long-range interactions of all promoters in 2 human blood cell types. The data from CD34 + is selected for this study. The interaction data of TS5_CD34 is available in the ArrayExpress database under accession E-MTAB-2323. (https://www.ebi.ac.uk/arrayexpress/experiments/E-MTAB-2323/).
In general, the sparsity of the Hi-C matrix is dependent on the data resolution and the depth of coverage. There exist three cases of the extremely sparse interactome data including 5 kb resolution bulk Hi-C data [30], scHi-C dataset [28] and Capture Hi-C dataset [29]. For the two bulk datasets, the sparsity is obviously correlated with resolution: the smaller the resolution, the higher the sparsity. At the tested highest resolution of 5 kb, the sparsity levels for the HMEC and NHEK datasets ranged between 98.04% and 99.41%, and between 97.39% and 99.23%, respectively. When the resolution reaches 50 kb, the sparsity of bulk Hi-C data is generally below 80%, while the sparsity levels of scHi-C data range from 99.41% to 99.99%, and those of CHi-C map data range from 98.35% to 99.99% (Supplementary Table S1).
With the express purpose of detecting the operation of the algorithm for the case of very high matrix sparsity, the raw Hi-C contact maps for HMEC at the highest resolution 5 kb were chosen. In terms of chromosome selection, we divided all 23 chromosomes into three groups according to their size (The chromosome X is placed between chromosomes 6 and 7). The first group contained chromosomes 1–6 and X and the latter groups each contained 8 chromosomes, from which chromosome 10, 22 and X were randomly selected for comparison of algorithms at different sparsity levels under real-world scenarios. By plotting heatmaps of 5 kb resolution raw contact map data of chromosome 10, 22 and X, we identified chromosomal intervals of low read coverage as the chromosomal regions chosen for the verification experiments. Considering to set up matrices with extensive and continuous sparsity, we intercepted the chromosome regions using a sliding window with a distance of 100 bins per move (Supplementary Table S2). The selected chromosome regions for verification was detailed in Supplementary Figure S1.
2.3. Evaluation dimensions
We evaluated the HCMB algorithm from different dimensions in this paper. We first assessed the efficiency of the HCMB algorithm generated normalized contact matrices for all intrachromosomal raw maps at different resolutions on real datasets. The stratum adjusted correlation coefficient (SCC) [31] and the root-mean-square deviation (RMSD) were used for quantifying the similarity and consistency between normalized Hi-C contact matrices generated by the HCMB algorithm and the KR algorithm. Furthermore, we quantitatively evaluated the performance represented by the number of iterations and the processing running time of both algorithms at different contact matrix sparsity levels. The faster convergence means reaching the solution's approximation after a smaller number of iterations. Moreover, we discussed the robustness of the HCMB method under diverse distribution characteristics of matrix entries. At last, we demonstrated the efficacy of the proposed HCMB for P(s) curve estimation, TAD calls and A/B compartments annotation. We confirmed the presence of TADs in the dataset HMEC near the DXZ4 region on Chromosome X [21], and normalized the raw contact map matrices of chromosome X using both algorithms at 5 kb and 250 kb resolution, respectively. After that, FAN-C [32] toolkit was used for the analysis of the above chromosomes hierarchical structures. We compared the consistency between the called TADs (measured by BPscore), A/B compartments (measured by Jaccard index) and P(s) curves of the normalized matrices generated by the HCMB algorithm and the KR algorithm.
3. Results
3.1. The efficiency of HCMB
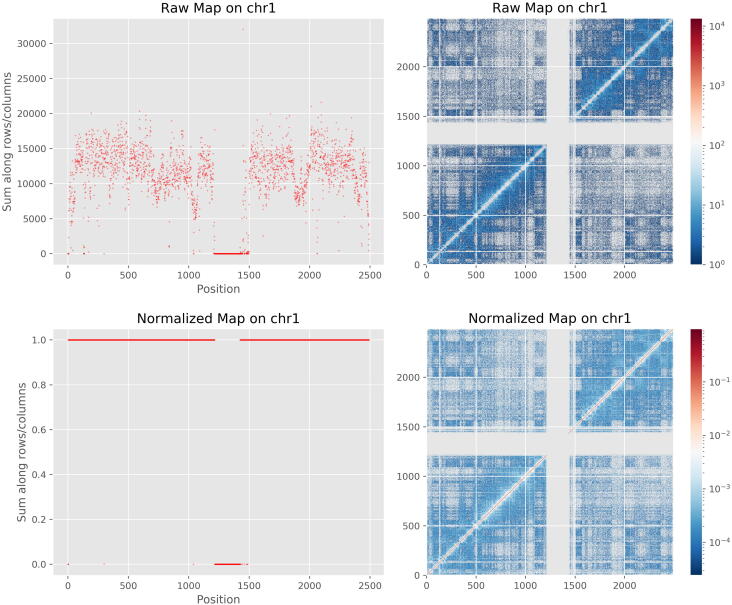
The availability of the HCMB algorithm was validated on four real Hi-C datasets including two bulk datasets, one scHi-C dataset and one CHi-C dataset. We compared all intrachromosomal raw maps and normalized contact matrices generated by the HCMB algorithm at 50 kb, 100 kb, and 250 kb resolutions. Seen from a chromosome example at 100 kb resolution in Fig. 1 (Examples from the other three datasets and at different resolutions in Supplementary Figure S2-S4), the HCMB matrix balancing analyses were all done and achieved well. The raw maps were successfully converted to doubly stochastic matrices, where every sum of rows and columns are equal to one.
Fig. 1.
Comparison of Hi-C contact maps before and after normalized by the HCMB algorithm on Chr1 of HMEC at 100 kb resolution. After normalization, the sum of rows and columns are equal to one.
Besides, to quantitatively evaluate the performance of the HCMB algorithm, we further compared the normalized maps created by the HCMB algorithm with the current mainstream KR algorithm by calculating the SCCs and RMSDs. We found out that the RMSDs between the normalized contact maps are close to zero, and the SCCs are 1.0 with statistical significance at all taken experimental conditions (Supplementary Table S3), which exhibited that both methods implemented normalization yield the almost exactly same results. These results illustrated the high consistency between the HCMB method and the KR method mathematically, and also indicated that the results of the HCMB are available and credible.
In summary, the HCMB algorithm achieves comparable computational efficiency in matrix balancing as well as the KR method.
3.2. HCMB normalized matrices with high sparsity
We delved into the performance of these two methods by recording the number of iterations and processing running time on simulated and real Hi-C contact matrices with different sparsity (Fig. 2, Fig. 3 and Supplementary Figure S5). We first conducted a simulation study in computer-generated matrices with two dimensions of 100-by-100 and 1000-by-1000 respectively.
Fig. 2.
Performance comparison on the number of iterations and the runtime of the HCMB algorithm and the KR algorithm on the simulated datasets. (A) The number of iterations on 100-by-100 simulated sparse contact matrices. (B) The runtime on 100-by-100 simulated sparse contact matrices. (C) The number of iterations on 1000-by-1000 simulated sparse contact matrices. (D) The runtime on 1000-by-1000 simulated sparse contact matrices. Note: When KR failed to convergence, the running time was shown under the zero line.
Fig. 3.
Performance comparison on the number of iterations and the runtime of the HCMB algorithm and the KR algorithm on the real Hi-C dataset HMEC. (A) The number of iterations on 1000-by-1000 Hi-C data matrices from Chr10. (B) The runtime on 1000-by-1000 Hi-C data matrices from Chr10. (C) The number of iterations on 1000-by-1000 Hi-C data matrices from Chr22. (D) The runtime on 1000-by-1000 Hi-C data matrices from Chr22. (E) The number of iterations on 1000-by-1000 Hi-C data matrices from ChrX. (F) The runtime on 1000-by-1000 Hi-C data matrices from ChrX. Note: When KR failed to convergence, the running time was shown under the zero line.
As shown on 100-by-100 simulated sparse contact matrices, the number of iterations of the HCMB method is smaller, the performance of HCMB is more stable than that of KR, and the HCMB method ran faster than the KR method when sparsity ranges from 95% to 97% approximately(Fig. 2A and Fig. 2B). More importantly, the HCMB algorithm succeeded in normalizing contact matrices with sparsity up to 97% or more while the KR method failed to solve. Similar results came out when the dimension was expanded to 1000-by-1000 (Fig. 2C and Fig. 2D), the HCMB method successfully normalized contact matrix with more than 99.55% sparsity which contrasted with KR and had fewer iterations at all sparse levels. Besides, to increase the confidence of the simulation, the experiment was repeated using matrices generated by another different random seed, and the results were similar (Supplementary Figure S5).
Furthermore, we examined whether the HCMB method can be directly used to analyze real Hi-C datasets and whether the above-mentioned tendency still holds by verifying on the real 1000-by-1000 Hi-C datasets from human cell type HMEC (Supplementary Table S2). Observing the results on all three chromosomes as a whole, the numbers of iterations of the HCMB algorithm were relatively constant 5 ± 0 and the runtime lifts with the decreasing sparsity, while both two properties of the KR algorithm varied drastically with sparsity and showed an inconspicuous trend of being superior with increasing sparsity(Fig. 3). Further specifying the details, it is worth noting on data matrices from Chromosome 10, the HCMB algorithm achieved normalization under different sparsity, and the runtime of the HCMB method had an approximately linear relationship with matrix sparsity. Contrary to this phenomenon, when the sparsity was about 91% or more, the KR algorithm showed unstable performance, including four failures and dramatic fluctuations in processing iterations and runtime (Fig. 3A and Fig. 3B). Experiments on chromosome 22 yielded a clear result that the HCMB method implemented faster than KR with matrix sparsity more than about 88% (Fig. 3C and Fig. 3D). As seen from results on Chromosome X, there was a distinct boundary at the sparsity approximation of 92.5%. When the sparsity was below the boundary, the overall trend of the performance curves of the two algorithms was trend-approximate as the sparsity decreases; However, on the other side of the boundary, the HCMB method still maintained a steady performance while the KR method had sharply fluctuating iterations and overall slower runtime (Fig. 3E and Fig. 3F). These results demonstrated that the HCMB algorithm performs a robust practical behavior on the normalization of Hi-C data with very high sparsity.
It is worth mentioning that previous studies have addressed this disadvantage of the KR method by adopting the protocol to remove the low-coverage bins. This traditional way (hereinafter referred to as the Traditional Approach) worked with Hi-C data at relatively high resolutions by throwing out the sparsest rows and columns with sparsity up to 95% in the original matrix and then renormalize it still using the KR algorithm [21]. We used the same datasets as in Fig. 3 to compare among the HCMB algorithm, the KR algorithm and the Traditional Approach, and the results demonstrated that the Traditional Approach has notably fewer iterations than using the KR algorithm directly, and can guarantee the success rate of normalization without failures due to the high sparsity (Supplementary Table S4). Even with this in mind, the HCMB algorithm still exhibits superior performance: it requires fewer iterations even comparing with the Traditional Approach. To sum up the above, the comparison with the direct KR algorithm and the Traditional Approach once again confirms the advantage of the HCMB algorithm in normalizing highly sparse Hi-C interaction matrices.
3.3. HCMB performs robustly on matrices with diverse distribution characteristics
Subsequently, we discussed the robustness of the HCMB method and the KR method on matrices with diverse distribution characteristics. To avoid the biases caused by sparsity and other influence factors, we deliberately selected several regions on the same chromosome with almost the same sparsity for comparison and analysis.
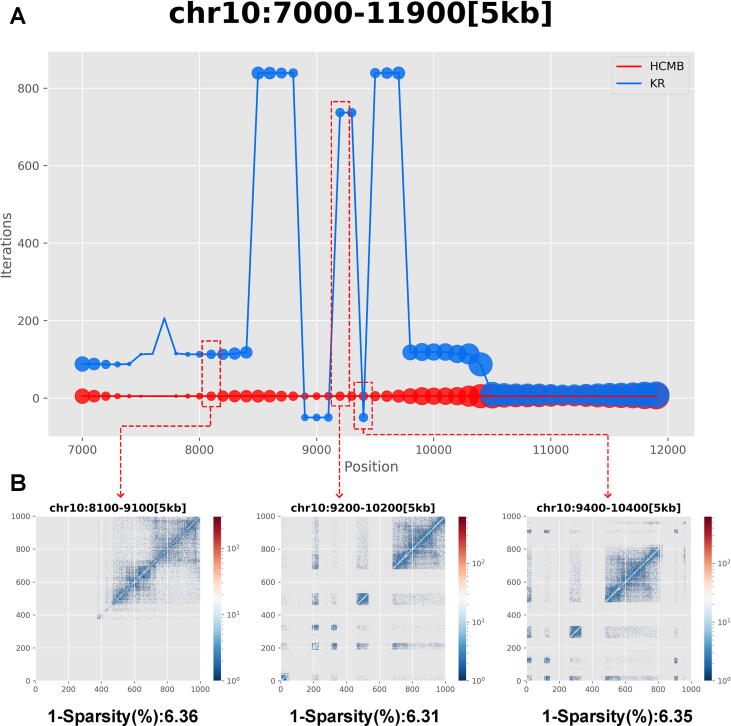
The three examples on chromosome 10 suggested that in the case of roughly equal sparsity (around 93.65%), the HCMB algorithm had a consistently robust performance even when handling with different matrix distribution characteristics of Hi-C data (Fig. 4 and Supplementary Figure S6). In contrast to this, the KR algorithm was strongly affected by the distribution characteristics of matrix entries which leads to its seemingly erratic success rate and undulating iterations and runtime. We also picked up regions of similar sparsity on chromosome X and the results implied the above conclusion once again (Supplementary Figure S7 and Figure S8). However, we did not replicate this procedure on chromosome 22, because the overall degree of sparsity on chromosome 22 varied greatly and we were unsuccessful to locate typical cases with close sparsity and distinct matrix characteristics.
Fig. 4.
(A)Performance comparison on the number of iterations of the HCMB algorithm and the KR algorithm with but different chromosomal intervals on Chr10 from HMEC. The radius of bubble represents the sparsity of raw contact maps. The smaller the radius, the higher the sparsity. (B) Heatmaps of raw contact maps with similar sparsity but different chromosomal intervals on Chr10 from HMEC. Three chromosomal intervals were chosen due to the approximately equal sparsity and different distribution characteristics of matrix entries.
3.4. HCMB preserves the biologically relevant Hi-C features
As previously stated, the purpose of the Hi-C data normalization is to remove experimental and technical biases that affect the downstream biological analysis, such as P(s) curve plotting, TADs and A/B compartments calling, etc. To justify the efficacy of the HCMB algorithm to accomplish these biological tasks, we compared the consistency between the TADs, A/B compartments and P(s) curves of the normalized matrices.
The result showed that at different sparsity, the BPscores are 0.00, Jaccard indexes are 1.00, and the P(s) curves are also completely overlapping (Supplementary Table S5 and Figure S9), which demonstrated that the TADs, A/B compartments and P(s) curve called using the Hi-C matrices normalized by the HCMB algorithm are similar to those that obtained by the KR algorithm. The HCMB algorithm is able to preserve the biological features and pave the way to investigate the biological mechanism of spatial genomics.
4. Discussions
With the continuous development of Hi-C technology, mass and growing Hi-C raw datasets with diverse characteristics need to be processed accurately to fulfill the increasing requirements. In multiple steps of data preprocessing, normalization is an essential procedure because of its effectiveness in reducing biases. As of now, several relatively mature normalization algorithms have been progressed to normalize Hi-C interaction data, each of which is not perfect and has its own shortcomings. The limitations of the explicit balancing method have been briefly introduced, and as for the implicit matrix balancing methods to which the HCMB algorithm belongs, it can also be broadly classified into two groups. The HCMB algorithm and the KR algorithm belong to the same group which is based on the principle of transforming the matrix balancing problem into solving a system of nonlinear equations to get normalized factor vectors, thus normalizing the Hi-C matrix.
The IC and VC methods belong to another different class of methods and are all derived from the SK algorithm with some improvements. From the principle of achieving matrix normalization, these SK type methods are an iterative method for matrix balancing by alternately normalizing columns and rows in a sequence of iterative matrices using some eigenvalue until convergence is achieved, and the convergence rate is linear. Some numerical experiments have shown that the KR algorithm converges two orders of magnitude faster than the SK type algorithm[20]. However, the KR algorithm also induced a new problem about handling the high sparsity [21]. Inspired by this, our proposed new HCMB algorithm hopes to solve the normalization problem of highly sparse matrices without discarding the original information, and at the same time achieve better performance.
In this work, we have developed HCMB, a stable and efficient algorithm for processing the normalization of raw Hi-C contact maps, especially with high sparsity. The HCMB algorithm is a kind of implicit method based on an iterative solution of equations, combining with linear search and projection strategy. The efficiency and robustness of the HCMB method has been certificated by the comparison with the mainstream KR method. HCMB is implemented in Python and is freely accessible to non-commercial users at GitHub: https://github.com/HUST-DataMan/HCMB
Conducted experiments have revealed that our HCMB method is as efficient as the KR method for normalizing Hi-C contact map data, both mathematically and biologically. Notably, biological features such as compartments and P(s) curve are dependent on the probabilities of long-range interactions that are typically very small and might be affected by differences between very similar balancing techniques. Therefore, it is particularly vital to guarantee that the HCMB algorithm can accurately preserve of biological relevant characteristics which reflect the cells' regulatory and cell cycle state in the Hi-C experiments. Based on this study, we consider that the HCMB algorithm and the KR algorithm indeed can be used interchangeably for routine Hi-C analysis when both algorithms can successfully normalize the raw Hi-C contact matrix.
The core concern of HCMB in this study is the high sparsity degree of the matrix. According to our survey, since the KR algorithm may fail to handle highly sparse matrices, some packaged Hi-C data processing software formulate accompanying solutions, such as setting different cut-off schemes for different resolutions to discard very sparse rows and columns during normalizations [24]. It is noteworthy that while our study provided an indirect verification of traditional approach’s ability to solve the problem of highly sparse matrices and relatively robust and efficient performance compare with the simple KR method, it has been suggested that sparse rows and columns in the Hi-C interaction matrix are also biologically significant and relevant to the detection of small differences at high resolution [33]. Therefore, the direct discarding of these sparse rows and columns will inevitably lead to the loss of information and may even miss meaningful biological discoveries. Back to HCMB, as a Levenberg-Marquardt-type variant method, it is characterized by maintaining matrix density during the convergence process [25]. By the way, this is the first time that Levenberg-Marquardt-type methods were proposed to solve matrix balancing directly to our knowledge. As explained in the above results, both simulated and experimental data confirmed that the HCMB method with fewer number of iterations and shorter runtime performs better and remains steadier than the KR methods in highly sparse matrices.
This advantage of the HCMB method in dealing with high sparsity matrices can bring it many application scenarios. One of the most probably frequent application is small-resolution bulk Hi-C data. Hi-C data at high resolution can offer deep insights into more elaborate chromatin 3D structures like chromatin loop, but at the same time, a typical drawback of the finer resolution is that the high proportion of zero-contact counts between loci (especially long-range contacts) in the matrix [34]. Besides, the paradoxical combination of deep sequencing depth resolution and lower sequencing costs (which also may lead to high sparsity) is always encountered in practical research. Hence, the HCMB method may help researchers acquire a smooth and reliable analysis result of Hi-C data with less sequencing cost. In addition, there are two other popular types of data that use unique C-technologies, scHi-C data and CHi-C data. The scHi-C technique is designed to capture the unique DNA proximities of individual cells and eliminate noises caused by the variability of each cell [28], [35], [36], and the CHi-C enables deep sequencing of specific loci like examining the long-range interactions promoters [29]. As expected and calculated, both techniques acquire sparser genomic interaction data than multi-cell Hi-C datasets [29], [34]. However, although some researchers have proposed workflow using algorithms based on similar iterative correction method [37], [38], the analysis for scHi-C data is not yet standardized and raises novel bioinformatic challenges. It’s necessary to state in particular that currently there are no studies explicitly demonstrated that scHi-C data follow the assumptions of the implicit normalization method (i.e. matrix-balancing normalization method, based on the assumption that each genomic locus should have “equal visibility” instead of relying on any specific assumptions on the sources of biases in Hi-C read counts [11]). On the other side, the normalization of Chi-C data may also require additional background correction after balancing the matrix [39], [40]. Consequently, the HCMB methods may be a choice to be considered for normalization to satisfy the multi-zero nature of scHi-C and Chi-C data, but its applicability also needs to be explored in greater depth.
Finally, there is still room for further advancement in the implementation of the HCMB method in the future. For instance, we observed that HCMB requires a larger demand of computer memory and takes a longer runtime per iteration step, especially at high resolution. With the current hardware, each iteration may occupy about 50 GB to 100 GB of memory when the resolution reaches 1 kb to 5 kb. In subsequent research, improvements can be made in various ways to reduce memory and speed up each iteration, such as using matrix chunking parallelly distributed computation and lower-level programming language implementations such as C/C++. In fact, although multiple algorithms have been developed for the same normalization function, each algorithm has its corresponding assumptions and priorities. In further studies, we researchers need to enhance the understanding of the performance and influencing factors of the algorithms to clarify the adaptable circumstances for suitable selection.
CRediT authorship contribution statement
Honglong Wu: Conceptualization, Methodology, Data curation, Computational analyses, Writing - review & editing. Xuebin Wang: Conceptualization, Investigation, Methodology, Computational analyses, Software, Data curation, Validation, Visualization, Writing - original draft, Writing - review & editing. Mengtian Chu: Writing - review & editing, Investigation. Dongfang Li: Investigation. Lixin Cheng: Supervision, Writing - review & editing. Ke Zhou: Conceptualization, Supervision.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Thanks to all our friends that give us suggestions on the project. The authors would like to thank all anonymous reviewers for carefully reading the paper and helpful comments.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.csbj.2021.04.064.
Contributor Information
Lixin Cheng, Email: easonlcheng@gmail.com.
Ke Zhou, Email: zhke@hust.edu.cn.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome Science. 2009. 326(5950): 289-93. https://doi.org/10.1126/science.1181369 [DOI] [PMC free article] [PubMed]
- 2.Jin F., Li Y., Dixon J.R., Selvaraj S., Ye Z. A high-resolution map of the three-dimensional chromatin interactome in human cells. Nature. 2013;503(7475):290–294. doi: 10.1038/nature12644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Burton J.N., Adey A., Patwardhan R.P., Qiu R., Kitzman J.O. Chromosome-scale scaffolding of de novo genome assemblies based on chromatin interactions. Nat Biotechnol. 2013;31(12):1119–1125. doi: 10.1038/nbt.2727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kaplan N., Dekker J. High-throughput genome scaffolding from in vivo DNA interaction frequency. Nat Biotechnol. 2013;31(12):1143–1147. doi: 10.1038/nbt.2768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Selvaraj S, J RD, Bansal V, and Ren B. Whole-genome haplotype reconstruction using proximity-ligation and shotgun sequencing Nat Biotechnol. 2013. 31(12): 1111-8. https://doi.org/10.1038/nbt.2728 [DOI] [PMC free article] [PubMed]
- 6.Bonev B., Mendelson Cohen N., Szabo Q., Fritsch L., Papadopoulos G.L. Multiscale 3D Genome Rewiring during Mouse Neural Development. Cell. 2017;171(3):557–572 e24. doi: 10.1016/j.cell.2017.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chandra T., Ewels P.A., Schoenfelder S., Furlan-Magaril M., Wingett S.W. Global reorganization of the nuclear landscape in senescent cells. Cell Rep. 2015;10(4):471–483. doi: 10.1016/j.celrep.2014.12.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Du Z., Zheng H., Huang B., Ma R., Wu J. Allelic reprogramming of 3D chromatin architecture during early mammalian development. Nature. 2017;547(7662):232–235. doi: 10.1038/nature23263. [DOI] [PubMed] [Google Scholar]
- 9.Kong S., Zhang Y. Deciphering Hi-C: from 3D genome to function. Cell Biology and Toxicology. 2019;35(1):15–32. doi: 10.1007/s10565-018-09456-2. [DOI] [PubMed] [Google Scholar]
- 10.Lajoie BR, Dekker J, and Kaplan N. The Hitchhiker's guide to Hi-C analysis: practical guidelines Methods. 2015. 72: 65-75. https://doi.org/10.1016/j.ymeth.2014.10.031 [DOI] [PMC free article] [PubMed]
- 11.Pal K., Forcato M., Ferrari F. Hi-C analysis: from data generation to integration. Biophys Rev. 2019;11(1):67–78. doi: 10.1007/s12551-018-0489-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Di Filippo L., Righelli D., Gagliardi M., Matarazzo M.R., HiCeekR A.C. A Novel Shiny App for Hi-C. Data Analysis Front Genet. 2019;10:1079. doi: 10.3389/fgene.2019.01079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Imakaev M., Fudenberg G., McCord R.P., Naumova N., Goloborodko A. Iterative correction of Hi-C data reveals hallmarks of chromosome organization. Nat Methods. 2012;9(10):999–1003. doi: 10.1038/nmeth.2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Samborskaia M.D., Galitsyna A., Pletenev I., Trofimova A., Mironov A.A. Cumulative contact frequency of a chromatin region is an intrinsic property linked to its function. PeerJ. 2020;8 doi: 10.7717/peerj.9566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ay F., Noble W.S. Analysis methods for studying the 3D architecture of the genome. Genome Biol. 2015;16:183. doi: 10.1186/s13059-015-0745-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sati S and Cavalli G. Chromosome conformation capture technologies and their impact in understanding genome function Chromosoma. 2017. 126(1): 33-44. https://doi.org/10.1007/s00412-016-0593-6 [DOI] [PubMed]
- 17.Hu M., Deng K., Selvaraj S., Qin Z., Ren B. HiCNorm: removing biases in Hi-C data via Poisson regression. Bioinformatics. 2012;28(23):3131–3133. doi: 10.1093/bioinformatics/bts570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yaffe E., Tanay A. Probabilistic modeling of Hi-C contact maps eliminates systematic biases to characterize global chromosomal architecture. Nat Genet. 2011;43(11):1059–1065. doi: 10.1038/ng.947. [DOI] [PubMed] [Google Scholar]
- 19.Hansen P., Gargano M., Hecht J., Ibn-Salem J., Karlebach G. Computational Processing and Quality Control of Hi-C. Capture Hi-C and Capture-C Data Genes. 2019;10(7):548. doi: 10.3390/genes10070548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Knight P.A., Ruiz D. A fast algorithm for matrix balancing IMA. Journal of Numerical Analysis. 2012;33(3):1029–1047. doi: 10.1093/imanum/drs019. [DOI] [Google Scholar]
- 21.Rao S.S., Huntley M.H., Durand N.C., Stamenova E.K., Bochkov I.D. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell. 2014;159(7):1665–1680. doi: 10.1016/j.cell.2014.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Durand N.C., Shamim M.S., Machol I., Rao S.S., Huntley M.H. Juicer Provides a One-Click System for Analyzing Loop-Resolution Hi-C Experiments Cell Syst. 2016;3(1):95–98. doi: 10.1016/j.cels.2016.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kumar R, Sobhy H, Stenberg P, and Lizana L. Genome contact map explorer: a platform for the comparison, interactive visualization and analysis of genome contact maps Nucleic Acids Res. 2017. 45(17): e152. https://doi.org/10.1093/nar/gkx644 [DOI] [PMC free article] [PubMed]
- 24.T. Liu Z. Wang normGAM: an R package to remove systematic biases in genome architecture mapping data BMC genomics. 20 Suppl 12 2019 1006 1006 10.1186/s12864-019-6331-8 [DOI] [PMC free article] [PubMed]
- 25.A.W. Westerberg S.W. Director A modified least squares algorithm for solving sparse n × n sets of nonlinear equations Computers & Chemical Engineering. 2 2 1978 77 81 https://doi.org/https://doi.org/10.1016/0098-1354(78)80011-8.
- 26.Yamashita N and Fukushima M, On the Rate of Convergence of the Levenberg-Marquardt Method. 2001: Topics in Numerical Analysis.
- 27.Dan H, Yamashita N, and Fukushima M. Convergence Properties of the Inexact Levenberg-Marquardt Method under Local Error Bound Conditions Optimization Methods and Software. 2002. 17(4): 605-626
- 28.Nagano T., Lubling Y., Stevens T.J., Schoenfelder S., Yaffe E. Single-cell Hi-C reveals cell-to-cell variability in chromosome structure. Nature. 2013;502(7469):59–64. doi: 10.1038/nature12593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mifsud B, Tavares-Cadete F, Young AN, Sugar R, Schoenfelder S, et al. Mapping long-range promoter contacts in human cells with high-resolution capture Hi-C Nature Genetics. 2015. 47(6): 598-606. https://doi.org/10.1038/ng.3286 [DOI] [PubMed]
- 30.Servant N., Varoquaux N., Lajoie B.R., Viara E., Chen C.J. HiC-Pro: an optimized and flexible pipeline for Hi-C data processing. Genome Biol. 2015;16:259. doi: 10.1186/s13059-015-0831-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yang T., Zhang F., Yardımcı G.G., Song F., Hardison R.C. HiCRep: assessing the reproducibility of Hi-C data using a stratum-adjusted correlation coefficient. Genome Res. 2017;27(11):1939–1949. doi: 10.1101/gr.220640.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kruse K., Hug C.B., Vaquerizas J.M. FAN-C: a feature-rich framework for the analysis and visualisation of chromosome conformation capture data. Genome Biol. 2020;21(1):303. doi: 10.1186/s13059-020-02215-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.J.C. Stansfield K.G. Cresswell V.I. Vladimirov M.G. Dozmorov HiCcompare: an R-package for joint normalization and comparison of HI-C datasets BMC bioinformatics. 19 1 2018 279 279 10.1186/s12859-018-2288-x [DOI] [PMC free article] [PubMed]
- 34.O. Oluwadare M. Highsmith J. Cheng An Overview of Methods for Reconstructing 3-D Chromosome and Genome Structures from Hi-C Data Biological procedures online. 21 2019 7 7 10.1186/s12575-019-0094-0 [DOI] [PMC free article] [PubMed]
- 35.Ramani V., Deng X., Qiu R., Gunderson K.L., Steemers F.J. Massively multiplex single-cell Hi-C. Nat Methods. 2017;14(3):263–266. doi: 10.1038/nmeth.4155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhu H., Wang Z.S.C.L. a lattice-based approach to infer 3D chromosome structures from single-cell Hi-C data Bioinformatics (Oxford. England) 2019;35(20):3981–3988. doi: 10.1093/bioinformatics/btz181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Collombet S., Pérez-Rico Y.A., Ancelin K., Servant N., Heard E., Analysis B. NY, US; New York: 2021. Springer; pp. 295–316. [DOI] [PubMed] [Google Scholar]
- 38.Servant N., Varoquaux N., Lajoie B.R., Viara E., Chen C.-J. HiC-Pro: an optimized and flexible pipeline for Hi-C data processing. Genome Biol. 2015;16(1):259. doi: 10.1186/s13059-015-0831-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cairns J., Freire-Pritchett P., Wingett S.W., Várnai C., Dimond A. CHiCAGO: robust detection of DNA looping interactions in Capture Hi-C data. Genome Biol. 2016;17(1):127. doi: 10.1186/s13059-016-0992-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Cairns J., Orchard W.R., Malysheva V., Spivakov M. Chicdiff: a computational pipeline for detecting differential chromosomal interactions in Capture Hi-C data. Bioinformatics. 2019;35(22):4764–4766. doi: 10.1093/bioinformatics/btz450. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.