Multimodal brain-age prediction and cardiovascular risk: The Whitehall II MRI sub-study

Highlights

• •Cardiovascular risk factors are associated with older brain age.
• •Blood pressure is more strongly associated with white matter compared to gray matter.
• •Resting state functional connectivity provides lower brain-age prediction accuracy.
• •Brain-age prediction accuracy depends on sample size and age range.

Abstract

Brain age is becoming a widely applied imaging-based biomarker of neural aging and potential proxy for brain integrity and health. We estimated multimodal and modality-specific brain age in the Whitehall II (WHII) MRI cohort using machine learning and imaging-derived measures of gray matter (GM) morphology, white matter microstructure (WM), and resting state functional connectivity (FC). The results showed that the prediction accuracy improved when multiple imaging modalities were included in the model (R² = 0.30, 95% CI [0.24, 0.36]). The modality-specific GM and WM models showed similar performance (R² = 0.22 [0.16, 0.27] and R² = 0.24 [0.18, 0.30], respectively), while the FC model showed the lowest prediction accuracy (R² = 0.002 [-0.005, 0.008]), indicating that the FC features were less related to chronological age compared to structural measures. Follow-up analyses showed that FC predictions were similarly low in a matched sub-sample from UK Biobank, and although FC predictions were consistently lower than GM predictions, the accuracy improved with increasing sample size and age range. Cardiovascular risk factors, including high blood pressure, alcohol intake, and stroke risk score, were each associated with brain aging in the WHII cohort. Blood pressure showed a stronger association with white matter compared to gray matter, while no differences in the associations of alcohol intake and stroke risk with these modalities were observed. In conclusion, machine-learning based brain age prediction can reduce the dimensionality of neuroimaging data to provide meaningful biomarkers of individual brain aging. However, model performance depends on study-specific characteristics including sample size and age range, which may cause discrepancies in findings across studies.

1. Introduction

In older age, the human brain undergoes structural changes including reductions in brain volume, cortical thinning, and decline in white-matter microstructure (Fjell et al., 2014), and large-scale resting-state networks become less segregated (Mowinckel, Espeseth, Westlye, 2012, Sala-Llonch, Bartrés-Faz, Junqué, 2015). Age-related changes in brain structure and functional connectivity are associated with decreased cognitive performance in domains including memory and processing speed (Cabeza, Albert, Belleville, Craik, Duarte, Grady, Lindenberger, Nyberg, Park, Reuter-Lorenz, et al., 2018, Grady, 2012, Sala-Llonch, Bartrés-Faz, Junqué, 2015), and comprise an increased risk for neurodegenerative disorders such as dementia (Vos et al., 2012). Although the senescent deterioration of the brain is well-known, older populations are characterised by substantial variation in neurobiological aging trajectories (Fjell et al., 2014), and recent neuroimaging studies have focused on developing potential markers for brain aging (Brown, Kuperman, Chung, Erhart, McCabe, Hagler Jr, Venkatraman, Akshoomoff, Amaral, Bloss, et al., 2012, Cole, Poudel, Tsagkrasoulis, Caan, Steves, Spector, Montana, 2017). Brain-age prediction based on machine-learning algorithms estimates an individual's ‘brain age’ using structural and functional brain characteristics derived from magnetic resonance imaging (MRI) (Cole, Franke, 2017, Cole, Poudel, Tsagkrasoulis, Caan, Steves, Spector, Montana, 2017, Franke, Gaser, 2019, Franke, Ziegler, Klöppel, Gaser, Initiative, et al., 2010). Subtracting chronological age from estimated brain age provides an estimate of brain aging, the brain-age delta. For instance, if a 70 year old individual exhibits a brain age delta of +5 years, their typical aging pattern resembles the brain structure of a 75 year old, i.e. their estimated brain age is older than what is expected for their chronological age (Franke and Gaser, 2019). Individual variation in delta estimations are associated with a range of cognitive and biological measures (Cole, 2020, Cole, Ritchie, Bastin, Hernández, Maniega, Royle, Corley, Pattie, Harris, Zhang, et al., 2018, Cole, Marioni, Harris, Deary, 2019a, Cole, Franke, 2017, de Lange et al., 2019, Franke, Gaser, 2019, Smith, Vidaurre, Alfaro-Almagro, Nichols, Miller, 2019, de Lange et al., 2020a), including cardiovascular health (Cole, 2020), and differences in brain age delta have been established between patient groups and healthy controls: individuals with conditions such as Alzheimer’s disease, multiple sclerosis, epilepsy, and psychiatric disorders show on average older brain age relative to their chronological age (Franke, Ziegler, Klöppel, Gaser, Initiative, et al., 2010, Franke, Gaser, 2012, Kaufmann et al., 2019, Koutsouleris, Davatzikos, Borgwardt, Gaser, Bottlender, Frodl, Falkai, Riecher-Rössler, Möller, Reiser, et al., 2013, Pardoe, Cole, Blackmon, Thesen, Kuzniecky, Investigators, et al., 2017, Schnack, Van Haren, Nieuwenhuis, Hulshoff Pol, Cahn, Kahn, 2016). Longitudinal studies have documented highly reliable brain age prediction in stroke patients (Richard et al., 2019), and accelerated brain aging in patients with schizophrenia and multiple sclerosis (Cole, Raffel, Friede, Eshaghi, Brownlee, Chard, De Stefano, Enzinger, Pirpamer, Filippi, et al., Høgestøl, Kaufmann, Nygaard, Beyer, Sowa, Nordvik, Kolskår, Richard, Andreassen, Harbo, et al., 2019, Koutsouleris, Davatzikos, Borgwardt, Gaser, Bottlender, Frodl, Falkai, Riecher-Rössler, Möller, Reiser, et al., 2013). Combined with studies on the association between brain age delta and biomedical factors in healthy population cohorts (Cole, Marioni, Harris, Deary, 2019a, Smith, Vidaurre, Alfaro-Almagro, Nichols, Miller, 2019), the documented reliability and clinical sensitivity supports the utility of brain-age estimation as a candidate biomarker for neurological senescence and disease (Cole et al., 2017).

Modality-specific brain age models (based on e.g. gray and white matter separately) provide information about tissue-specific aging processes (Richard, Kolskår, Sanders, Kaufmann, Petersen, Doan, Sanchez, Alnæs, Ulrichsen, Dørum, et al., 2018, Smith, Elliott, Alfaro-Almagro, McCarthy, Nichols, Douaud, Miller, 2020). For instance, imaging-derived measures of gray matter are known to detect cortical atrophy in older age-groups (Fjell and Walhovd, 2010), while changes in diffusion MRI measures reflect age-related decline in white matter microstructure, as well as white matter lesions, which are more prevalent in aging, relative to young, populations  (Debette and Markus, 2010). Functional MRI (fMRI) measures are indicative of brain network connectivity, which may change with advancing age (Mowinckel, Espeseth, Westlye, 2012, Sala-Llonch, Bartrés-Faz, Junqué, 2015). Cardiovascular risk factors may influence these neural aging processes differently (Niu, Zhang, Kounios, Liang, 2019, Richard, Kolskår, Sanders, Kaufmann, Petersen, Doan, Sanchez, Alnæs, Ulrichsen, Dørum, et al., 2018, Smith, Elliott, Alfaro-Almagro, McCarthy, Nichols, Douaud, Miller, 2020), and in a recent Whitehall II (WHII) MRI study using voxelwise analyses, allostatic load, metabolic syndrome, and multifactorial stroke risk predicted gray matter density measured decades later, while only cumulative stroke risk measured by the Framingham stroke risk score (D’Agostino et al., 1994) predicted white matter integrity in terms of fractional anisotropy and mean diffusivity (Zsoldos et al., 2018).

In this study of the WHII MRI cohort (N = 610), we investigated whether machine learning using neuroimaging data could produce reliable biomarkers of brain aging, and whether cardiovascular risk factors including blood pressure, alcohol intake, and cumulative risk as indicated by the Framingham stroke risk score were associated with modality-specific brain-age markers. We estimated brain age using 10-fold cross validation in separate models based on I) gray matter (GM) measures, II) white matter (WM) metrics derived from diffusion tensor imaging (DTI) and white matter hyperintensites (WMH), III) functional connectivity measures derived from resting state fMRI (rs-fMRI), and IV) a multimodal model that included all of the brain measures. A detailed description of the methodology is provided below.

2. Materials and methods

2.1. Sample

The WHII study was established in London in 1985, and included an initial cohort of 10,308 civil servants. Between 2012 and 2013, 6035 individuals participated in the Phase 11 assessment, from which a random sample of 800 participants was enrolled in an MRI sub-study including brain scans and biomedical assessments (Filippini et al., 2014) (www.psych.ox.ac.uk/research/neurobiology-of-ageing/research-projects-1/whitehall-oxford). The study received ethical approval from the University of Oxford Central University Research Ethics Committee, as well as the University College London Medical School Committee on the Ethics of Human Research. Written informed consent was obtained from all participants enrolled in this study. The current sample was drawn from the WHII MRI sub-study, and included 715 participants with multimodal MRI data. Forty-four participants were excluded based on self-reported neurological disease and incidental MRI findings, 23 were excluded based on depressive symptoms reported from previous WHII clinical examinations (Filippini et al., 2014), and 38 were excluded based on mood disorder assessed at the time of scan using Structured Clinical Interview for DSM-IV Axis I Disorders (SCID-I), yielding a final MRI sample of 610 participants. Sample demographics are provided in Table 1.

Table 1.

Sample demographics. Age range (mean age  ±  standard deviation = 69.71  ±  5.07), percentage male (M) and female (F) participants, percentage with white (W) and non-white (NW) ethnic background, and percentage with educational qualifications U = university degree, PG = post-graduate / masters / PhD, Pr = Professional qualifications, A = A levels or equivalent, O = O levels or equivalent, N = No qualifications.

N	Age range	Sex %	Ethnicity %	Educational qualification %
610	60.34 - 84.58	M81 | F19	W94 | NW6	U27 | PG22 | Pr12 | A18 | O14 | C5 | N3

2.2. MRI data acquisition and processing

MRI data were acquired using a 3 Tesla Siemens Magnetom Verio (n. of participants = 473) with a 32-channel receive head coil (between April 2012 Dec 2014). T1-weighted structural images were acquired using a gradient echo sequence (TR = 2530ms, TE = 1.79/3.65/5.51/7.37 ms, flip angle = 7∘, FOV = 256mm, voxel dimension = 1.0 mm isotropic, acquisition time = 6m12s). Diffusion-weighted images were acquired using an echoplanar sequence, with 60 diffusion-weighted directions (b-value = 1500 s/mm2), 5 non-diffusion weighted images (b-value = 0s/mm2) and one b0 volume in the reversed phase-encoded direction (TR = 8900ms, TE = 91.2ms, FOV= 192 mm, voxel dimension = 2.0mm isotropic). FLAIR images were acquired with TR = 9000ms, TE = 73, voxel dimension = 0.9x0.9x3mm, FOV = 220, and acquisition time = 4m14s. rs fMRI data were acquired using multiband echo-planar imaging (voxel = 2 mm isotropic, TR = 1.3 s, TE = 40 ms, acquisition time = 10 min 10 s, multi-slice acceleration factor = 6, number of volumes = 460). Following a scanner update, a 3 Tesla Siemens Magnetom Prisma with a 64-channel head-neck coil was used for the rest of the participants (n = 198; June 2015 Dec 2016). T1-weighted structural images were acquired using a gradient echo sequence (TR = 1900ms, TE= 3.97ms, flip angle = 8∘, FOV = 192mm, voxel dimension = 1.0 mm isotropic, acquisition time = 5m31s). FLAIR (TR = 9000ms, TE = 73, voxel dimension=0.4x0.4x3mm, FOV = 220, acquisition time = 4m14s). rs-fMRI and diffusion-weighted images were acquired with a matched protocol except for a change in echo time for the diffusion-weighted sequence (TE = 91ms). MRI images for all participants were processed using the analysis pipeline described in Filippini et al. (2014), including automated surface-based morphometry and subcortical segmentation as implemented in FreeSurfer 6.0 (Fischl et al., 2002).

2.2.1. Gray matter

In line with recent large-scale implementations (de Lange et al., 2019, Kaufmann et al., 2019), we utilized a fine-grained cortical parcellation scheme (Glasser et al., 2016) to extract cortical thickness, area, and volume for 180 regions of interest per hemisphere, in addition to the classic set of subcortical and cortical summary statistics from FreeSurfer (Fischl et al., 2002). This yielded a total set of 1118 structural brain imaging features (360/360/360/38 for cortical thickness/area/volume, as well as cerebellar/subcortical and cortical summary statistics, respectively). The gray matter variables were residualized with respect to scanner, relative head motion during the acquisition of rs-fMRI images (Miller, Alfaro-Almagro, Bangerter, Thomas, Yacoub, Xu, Bartsch, Jbabdi, Sotiropoulos, Andersson, et al., 2016, Smith, Nichols, Vidaurre, Winkler, Behrens, Glasser, Ugurbil, Barch, Van Essen, Miller, 2015), intracranial volume (ICV Voevodskaya et al., 2014), sex, and ethnic background using linear models.

2.2.2. White matter microstructure

Global and tract-specific estimates of fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (AD), radial diffusivity (RD) and mode of anisotropy (MO) were calculated for each individual. In accordance with established methods (Alfaro-Almagro et al., 2018), tract-specific estimates of each DTI metric were derived using 48 standard-space masks available from the ICBM-DTI-81 White-Matter Labels Atlas (Mori, Wakana, Van Zijl, Nagae-Poetscher, 2005, Wakana, Caprihan, Panzenboeck, Fallon, Perry, Gollub, Hua, Zhang, Jiang, Dubey, et al., 2007), producing a total of 245 DTI features. Global WMH volumes were automatically extracted from FLAIR images with Brain Intensity AbNormality Classification Algorithm (BIANCA) (Griffanti et al., 2016). To avoid scanner-specific biases in these estimates, BIANCA was initially trained with WMH masks manually delineated in a sub-sample of individuals scanned on the Prisma (n = 24) and Verio (n = 24) scanners and an independent sample from the UK Biobank study (n = 12). The white matter variables were residualized with respect to scanner, relative head motion, sex, and ethnic background using linear models.

2.2.3. Functional connectivity

Spatial maps of large-scale resting state networks were derived by applying MELODIC group Independent Component Analysis (group-ICA) to the rs-fMRI images of 671 individuals of the Whitehall II MRI sub-study, using 100 of components in line with recent studies (Beckmann, Smith, 2004, Miller, Alfaro-Almagro, Bangerter, Thomas, Yacoub, Xu, Bartsch, Jbabdi, Sotiropoulos, Andersson, et al., 2016, Smith, Vidaurre, Beckmann, Glasser, Jenkinson, Miller, Nichols, Robinson, Salimi-Khorshidi, Woolrich, et al., 2013). All non-artefactual group-ICA components (n = 86) and subject-specific rs-fMRI timeseries (extracted with dual regression (Beckmann, Mackay, Filippini, Smith, 2009, Filippini, MacIntosh, Hough, Goodwin, Frisoni, Smith, Matthews, Beckmann, Mackay, 2009)) were used in FSLNets (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FSLNets) in order to generate a 86x86 matrix representing subject-specific correlations between each pair of networks. Partial correlations (derived using L2 Regularization, setting rho = 0.01 in Ridge Regression option in FSLNets) were examined in the present study, as these estimates allow for a more direct estimate of the connectivity between each pair of nodes (Suri et al., 2017). These partial correlations were then z-transformed using Fisher’s transformation. The functional connectivity matrix produced by FSLNets is shown in Supplementary Information (SI) Figs. 1 and 2. Subsequently, the upper triangle of the matrix was converted into a row vector, producing a total of 3655 inter-node connectivity features for each participant. The fMRI variables were residualized with respect to scanner, relative head motion, sex, and ethnic background using linear models.

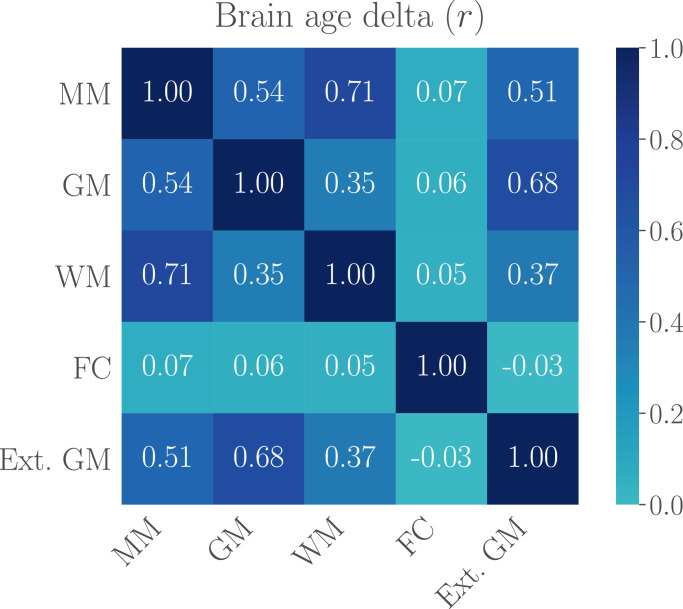
Fig. 1.

The correlations (Pearson’s r) between brain age deltas of the multimodal model (MM), the gray matter (GM), white matter (WM), and functional connectivity (FC) models, and the external gray matter model (Ext. GM) based on a separate training sample, indicating the amount of shared variance explained by the models. The delta values were first corrected for age-bias as described in Section 2.3.5, and the corrected deltas were used in the correlation analysis.

2.3. Brain age prediction

2.3.1. Regression model

The XGBoost python package (https://xgboost.readthedocs.io/en/latest/python) was used to run the brain age prediction. XGBoost uses a gradient boosting framework designed for speed and performance, where the final model is based on a collection of individual models (https://github.com/dmlc/xgboost). As compared to regular gradient boosting, which uses the loss function of the base model as a proxy for minimizing the error, XGBoost computes second-order derivatives to provide information about the direction of gradients and how to obtain the minimum loss function. It also includes advanced regularization to reduce overfitting (Chen and Guestrin, 2016). For the current study, we used the XGBoostregressor model, which is based on a decision-tree-based ensemble algorithm that has been used in recent large-scale brain age studies (de Lange et al., 2019, de Lange et al., 2020b, Kaufmann et al., 2019). The first step included parameter optimization based on cross-validation grid search with ten folds and two repeats per fold, using the complete set of multimodal features as input. The scanned parameter ranges were set to maximum depth = [2, 10, 1], number of estimators = [60, 220, 40], and learning rate = [0.1, 0.01, 0.05]. The optimized parameters were maximum depth = 2, number of estimators = 180, and learning rate = 0.05, which were used for all subsequent models.

2.3.2. Dimensionality reduction

To reduce multicollinear features in the input data, we trained each model on 70% of the data, applied them to 100 bootstrapped test sets generated from the remaining 30%, and performed hierarchical clustering on the Spearman rank-order correlations. A 70/30 test-train split was selected to ensure sufficient training statistics and limit potential overfitting. To select a cluster threshold, the models were run with a series of thresholds starting from the first full-number threshold value removing any features. SI Fig. 3 shows the brain age model predictions with different thresholds based on the dimensionality reduction procedure. Dendrograms showing the hierarchical relationship between features are shown in SI Figure 4. The selected thresholds, corresponding number of features, and the average R² values from the reduced models versus the models using the full set of features are provided in Table 2.

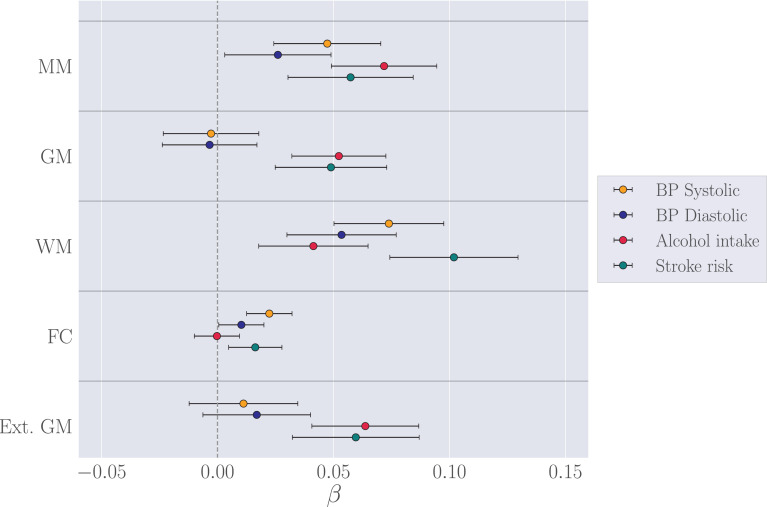
Fig. 3.

The associations (β ±  standard error) between standardized measures of brain age delta and blood pressure, alcohol intake, and Framingham stroke risk score for each of the brain-age models. The analyses included age as a covariate. The vertical gray line indicates β = 0. MM = multimodal, GM = gray matter, WM = white matter, FC = functional connectivity, Ext. GM = external gray matter model (gray matter predictions based on the external UK Biobank training set (Section 2.3.5).

Table 2.

Selected thresholds (TH) based on hierarchical clustering on the Spearman rank-order correlation. The models were trained on 70% of the data and applied to 100 bootstrapped test sets generated from the remaining 30%. Number (N) of features and average R² ±  SD are shown before and after the feature reduction; full = all imaging features included, reduced = selected features included based on cluster threshold. MM = multimodal, GM = gray matter, WM = white matter, FC = functional connectivity.

Model	N featuresfull	${\mathrm{R}}_{full}^2$	TH	N featuresreduced	${\mathrm{R}}_{reduced}^2$
MM	5019	0.40  ±  0.05	9	97	0.34  ±  0.05
GM	1118	0.32  ±  0.05	4	156	0.27  ±  0.05
WM	246	0.31  ±  0.05	5	19	0.31  ±  0.05
FC	3655	-0.03  ±  0.04	7	25	-0.03  ±  0.03

The relative contribution of the top 20 features in the multimodal model was measured with permutation feature importance, which defines the decrease in model performance when a single feature value is randomly shuffled (Breiman, 2001). SI Figure 5 shows the relative contribution of the top 20 features in the multimodal model measured by permutation feature importance, and SI Figure 6 shows partial dependence plots for the highest-ranked feature from each modality. As the clustering procedure eliminates features if they do not provide any additional information about the dataset, features that are redundant due to strong correlation with another feature could be excluded from the model input, but still be equally age-dependent. The feature ranking is thus model specific, and should not be interpreted as a ranking of all the imaging-derived variables used in the study.

To ensure that results were consistent across dimensionality reduction methods, the models were re-run using principal component analyses (PCA), which combines all features into new components. The results showed similar prediction patterns, as shown in SI Table 1.

2.3.3. Brain age estimation

The features extracted based on hierarchical clustering were used as input to cross-validation models with ten folds, yielding multimodal and modality-specific brain age estimates for each individual. To investigate the prediction accuracy, correlation analyses were run for predicted versus chronological age, and R², root mean square error (RMSE), and mean absolute error (MAE) were calculated for each model. For the multimodal model, an average R² value was calculated from a cross validation with ten splits and ten repetitions, and compared to a null distribution calculated from 1000 permutations.

2.3.4. Data quality analyses

To test whether excluding low-quality imaging data had an effect on prediction accuracy, we trained models for each modality based on (a) 70% of the data including the full sample (N = 427; 70% of 610) and (b) 70% of the data for a sub-sample including only data that was categorized as “high quality” based on manual quality assessment (N for each modality is provided in Table 3). Images were manually inspected and classified as “low quality” if they contained evidence of excessive motion and/or scanner-related artefacts. Each scan was checked for motion and other artefacts by two independent analysts, and where there was disagreement, classification was decided through discussion. For diffusion weighted images, images with > 5 volumes missing from their scans (which were excluded due to containing 10 or more outlier slices) were also labelled as “low quality”. The percentage of identified low-quality data in the training sets was 6.32% for the gray matter model, 7.26% for the white matter model, 7.96% for the RS functional connectivity model, and 8.90% for the multimodal model. The number of subjects and the age range for each of the high-quality training sub-samples are shown in Table 3. The models with and without low-quality data were then applied to 100 bootstrapped test sets generated from 30% of the full sample (N = 183). To test for differences in model performance, the distribution of R² values for each model were compared using a Z test for correlated samples (Zimmerman, 2012)

$$Z=(r_{\text{All}}-r_{\text{QC}})/\sqrt{{\sigma }_{\text{All}}^2+{\sigma }_{\text{QC}}^2-2\rho {\sigma }_{\text{All}}{\sigma }_{\text{QC}}}$$ (1)

where “All” represents the full sample, “QC” represents the sample with low-quality data removed, the r terms represent the Pearson’s correlation coefficients of predicted versus chronological age, the σ terms represent their errors, and ρ represents the correlation between the two sets of model predictions.

Table 3.

Age distribution for the high-quality training sub-samples for each modality.

Model	N	Mean age  ±  SD	Age range
Multimodal	389	69.71  ±  5.13	60.56 - 84.58
Gray matter	400	69.76  ±  4.97	60.56 - 84.58
White matter	396	69.78  ±  5.17	61.56 - 84.58
F. connectivity	393	69.69  ±  5.12	60.56 - 84.58

2.3.5. External training set

To test whether brain age estimation based on a separate training sample showed results corresponding to the within-sample approach described in Section 2.3.3, we estimated gray matter based brain age in the current sample using an external model trained on a 27,200 subjects from UK Biobank, with a mean age  ±  SD of 55.40  ±  7.46 and 48% vs 52% male/female subjects. The MRI data were residualized with respect to scanning site, data quality and motion using Euler numbers (Rosen et al., 2018) extracted from FreeSurfer, ICV, sex, and ethnic background using linear models. Subjects with known brain disorders were excluded based on ICD10 diagnosis (chapter V and VI, field F and G, except G50-G59 “Nerve, nerve root and plexus disorders” (http://biobank.ndph.ox.ac.uk/showcase/field.cgi?id=41270), yielding a total of 27,157 subjects.

The model contained the same 286 gray matter features as those included in the reduced WHII k-folding model (see Section 2.2.1), and was run with the same algorithm and parameter specifications as described in Section 2.3.1. To adjust for age-bias (de Lange and Cole, 2020c, Le, Kuplicki, McKinney, Yeh, Thompson, Paulus, Investigators, et al., 2018, Smith, Elliott, Alfaro-Almagro, McCarthy, Nichols, Douaud, Miller, 2020), we applied a statistical correction by first fitting Y = $\alpha \times \Omega +\beta$ in the UK Biobank training set, where Y is the modelled predicted age as a function of chronological age (Ω), and α and β represent the slope and intercept. We then used the derived values of α and β to correct predicted age in the WHII sample with Corrected Predicted Age = Predicted Age + $[\Omega -(\alpha \times \Omega +\beta \left)\right]$ before re-calculating RMSE and MAE. The result of the correction is shown in SI Fig. 7.

2.4. Brain age delta and cardiovascular risk factors

To investigate associations with cardiovascular risk factors, the brain age delta (predicted age – chronological age) was used as a measure of apparent brain aging. Clinical measures included systolic and diastolic blood pressure, alcohol intake measured by units per week (see Topiwala et al., 2017 for details), and the Framingham stroke risk score (D’Agostino et al., 1994), which includes cardio-metabolic measures, smoking habits, diabetes, sex, and age (see Zsoldos et al., 2018 for full description). Blood pressure and alcohol intake were corrected for sex, ethnic background, and educational level using linear models. Stroke risk score was corrected for ethnic background and educational level, as sex was already accounted for in the score. 589 subjects had data on all clinical variables as well as demographic variables. To remove outliers, subjects with values  ±  4 SD away from the average on any of the clinical variables were excluded from the analyses, yielding 582 subjects in total. The mean  ±  SD for each measure is shown in Table 4.

Table 4.

Mean  ±  standard deviation of each of the clinical variables.

N	Systolic BP	Diastolic BP	Alcohol intake	Stroke Risk score
582	140.43  ±  16.61	77.14  ±  10.54	14.82  ±  13.54	11.04  ±  6.53

Regression analyses were run for each of the brain age delta estimations and the clinical variables. Chronological age was included as a covariate in order to adjust for age-bias in the brain age predictions as well as age-dependence in the clinical variables (de Lange and Cole, 2020c). To obtain a direct comparison of β values, the brain age deltas and the clinical variables were standardized (subtracting the mean and dividing by the SD) before they were entered into the regression analyses. Correction for multiple comparisons was performed using false discovery rate correction (FDR) (Benjamini and Hochberg, 1995). The statistical analyses were conducted using Python 3.7.0.

2.5. Data availability

The study follows MRC data sharing policies (https://www.mrc.ac.uk/research/policies-and-guidance-forresearchers/data-sharing). In accordance with these guidelines, data from the Whitehall II Imaging Sub-study will be accessible via the Dementias Platform UK (https://portal.dementiasplatform.uk) 430 after 2019. Data from the Whitehall II Study is available through formal request to the data sharing committee (https://www.ucl.ac.uk/iehc/research/epidemiology-public-health/research/whitehallII/data-sharing) The UK Biobank data are available through the UK Biobank data access procedures (https://www.ukbiobank.ac.uk/researchers). For researchers with access to the WHII dataset, code for pre-processing streams and analyses will be made available following the open-access database procedures. Code is also available for researchers without access to the WHII database, currently upon request.

3. Results

3.1. Multimodal brain age model

The multimodal model that was run on the full sample using ten-fold cross-validation (described in Section 2.3.3) showed a prediction accuracy of R² = 0.30 [0.24, 0.36] (95% confidence interval), as shown in Table 5. Based on the additional run with ten splits and ten repetitions, the mean R²  ±  SD was 0.29  ±  0.10, while the null distribution calculated from 1000 permutations showed mean R²  ±  SD = -0.08  ±  0.03, as shown in SI Fig. 8. The number of permuted results from the null distribution that exceeded the mean from the cross validation was 0 (p < 0.001). Due to the low prediction accuracy of the functional connectivity data (see Table 2), we repeated the multimodal model without the rs-fMRI data to test for prediction improvements. The clustering and dimension reduction plots for this model are shown in SI Fig. 9. The results showed similar model performance with and without the rs-fMRI data (R² = 0.30 [0.24, 0.36] versus 0.31 [0.25, 0.37], z = 0.84, p = 0.40).

Table 5.

The correlations (r) between predicted age and chronological age, R², root mean square error (RMSE), and mean absolute error (MAE) for each of the brain age models. 95% confidence intervals are indicated in square brackets. MM = multimodal, GM = gray matter, WM = white matter, FC = functional connectivity, Ext. GM = external gray matter model, which represents the gray matter model trained on the external UK Biobank training set (Section 2.3.5). RMSE and MAE are reported in years, and represent the values estimated before and after age-bias correction as described in 2.3.5 and shown in SI Fig. 7.

Model	r	R2	RMSE	MAE	RMSEcorr	MAEcorr
MM	0.55 [0.49, 0.60]	0.30 [0.24, 0.36]	4.25	3.37	2.32	1.85
GM	0.46 [0.40, 0.52]	0.22 [0.16, 0.27]	4.49	3.60	2.18	1.73
WM	0.49 [0.43, 0.55]	0.24 [0.18, 0.30]	4.43	3.51	2.49	1.95
FC	0.04 [-0.04, 0.12]	0.002 [-0.005, 0.008]	5.16	4.18	1.19	0.90
Ext. GM	0.45 [0.38, 0.51]	0.20 [0.14, 0.26]	11.61	10.69	2.51	2.07

3.2. Modality-specific brain age models

The prediction accuracy of each of the modality-specific models run on the full sample using ten-fold cross-validation are shown in Table 5. The gray and white matter models showed similar performance with R² = 0.22 [0.16, 0.27] and 0.24 [0.18, 0.30], respectively. The functional connectivity model showed the lowest prediction accuracy with R² = 0.002 [-0.005, 0.008]. Plots showing the correlations between all the MRI features and chronological age are provided in SI Figure 10. The prediction accuracy of the external gray matter model (R² = 0.20 [0.14, 0.25]) was similar to the prediction accuracy of the within-sample gray matter model (R² = 0.22 [0.16, 0.27]).

Fig. 1 shows the correlations between the brain age deltas, indicating the amount of shared variance explained by the models. As seen in the figure, the correlation between the gray and white matter deltas (corrected for chronological age) was r = 0.35, while the functional connectivity delta correlated on average 0.05 with the gray and white matter deltas. The moderate correlations between the gray and white matter deltas may indicate that the model features are sensitive to different aspects of aging. However, they could also partly reflect measurement error in one or both models, considering the correlation of 0.68 between the gray matter (GM) deltas based on the external versus the within-sample GM models. The low correlations between the functional connectivity model and the other models was likely driven by the lack of age-sensitivity of the fMRI-based features, as indicated by the low model prediction accuracy.

3.3. Data quality analyses

Comparisons of models trained with and without low-quality data showed that the model trained without low-quality data improved the gray matter prediction with an increase in R² from 0.224  ±  0.060 (SD) to 0.271  ±  0.065 (z = –2.586, p = .009). None of the other models improved statistically, as shown in Table 6.

Table 6.

The R² values  ±  standard deviation based on training sets with and without low-quality data applied to 100 bootstrapped test sets generated from 30% of the full sample. 95% confidence intervals are indicated in square brackets. Z represents the difference in r values expressed in standard deviations, accounting for the correlated samples (Eq. (1)). MM = multimodal, GM = gray matter, WM = white matter, FC = functional connectivity.

Model	${\mathrm{R}}_{full}^2$	${\mathrm{R}}_{LQD-excluded}^2$	Z	p	% LQD removed
MM	0.228  ±  0.060	0.250  ±  0.063	-1.416	0.157	8.90
GM	0.224  ±  0.065	0.271  ±  0.065	-2.586	0.009	6.32
WM	0.203  ±  0.066	0.184  ±  0.062	1.097	0.273	7.26
FC	-0.011  ±  0.040	-0.019  ±  0.039	0.299	0.765	7.96

3.4. Additional resting state fMRI analyses

To investigate potential causes for the low prediction accuracy of the functional connectivity (FC) model, we performed additional analyses as described below.

3.4.1. FC prediction in a matched UK Biobank sub-sample

To test the FC prediction accuracy in a different dataset, we utilized UK Biobank FC data which was available for 4114 participants through our current data access. The ICA and partical correlations were performed by UK Biobank researchers (see page 16 in https://biobank.ctsu.ox.ac.uk/crystal/crystal/docs/brain_mri.pdf), following the same procedure as the current study (described in Section 2.2.3). We first residualized the data with respect to scanner, relative head motion, sex, and ethnic background using linear models. Next, we identified the overlapping age range between the WHII and UK biobank samples, and generated matching sub-samples that included 567 subjects between 60 and 79 years from each of the datasets. Brain age prediction models were run for each of the datasets using ten-fold cross-validation, as described in Section 2.3.3. The results showed a prediction accuracy of R² = 0.002 [-0.005,0.008] for the UK biobank sub-sample, indicating a similarly low age-sensitivity of the fMRI-based features to that observed in the WHII sample. The results from both sub-samples are shown in Table 7.

Table 7.

The correlations (r) between predicted age and chronological age, R², root mean square error (RMSE), and mean absolute error (MAE) for the brain age models based on WHII and UK Biobank (UKB) sub-samples matched on sample size (N) and age range. 95% confidence intervals are indicated in square brackets. RMSE and MAE are reported in years. SD = standard deviation.

Model	N	Mean age ± SD	r	R2	RMSE	MAE
WHII	567	68.88  ±  4.22	0.06 [-0.02, 0.14]	0.004 [-0.006, 0.014]	4.27	3.48
UKB	567	67.07  ±  4.61	0.04 [-0.04, 0.12]	0.002 [-0.005, 0.008]	4.69	3.85

3.4.2. FC predictions for different sample sizes and age ranges

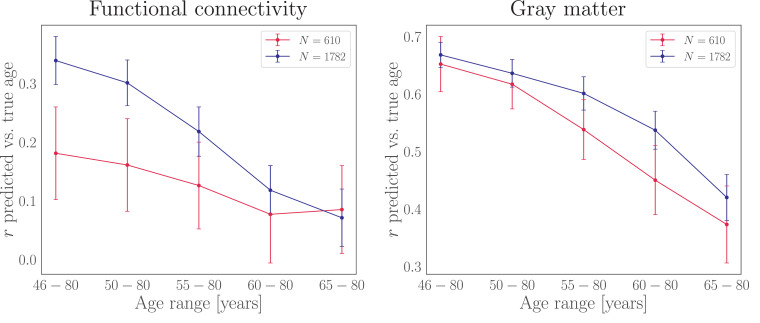
To test whether the FC prediction accuracy changed depending on (a) sample size and (b) age range, we ran a series of prediction models on two UK Biobank sub-samples of 610 and 1782 participants across five age ranges, as shown in Fig. 2. The sample size of 1782 represented the maximum number of participants available with the smallest age range, and was used in order to keep N stable across age ranges. The sample size of 610 was chosen to resemble the size of the WHII sample. For the sub-sample of 1782 participants, the prediction accuracy measured by the correlation between predicted and chronological age was r = 0.34 [0.30, 0.38] for the largest age range, decreasing to r = 0.07 [0.02, 0.12] for the smallest age range. For the sub-sample of 610 participants, the prediction accuracy was r = 0.18 [0.10, 0.26] for the largest age range, decreasing to r = 0.09 [0.01, 0.16] for the smallest age range. For the full sub-sample of 4114 participants with the full age range (46 - 80), the FC prediction accuracy was r = 0.42 [0.40, 0.45]. To test whether the effects of sample size and age range also applied to gray-matter based models, the analysis was repeated using the gray matter features described in Section 2.2.1. For the sub-sample of 1782 participants, the prediction accuracy was r = 0.67 [0.64, 0.69] for the largest age range, decreasing to r = 0.42 [0.38, 0.46] for the smallest age range. For the sub-sample of 610 participants, the prediction accuracy was r = 0.65 [0.60, 0.70] for the largest age range, decreasing to r = 0.37 [0.30, 0.44] for the smallest age range. For the sub-sample of 4114 participants with the full age range, the GM prediction accuracy was r = 0.66 [0.64, 0.68].

Fig. 2.

Prediction accuracy (y-axis) for functional connectivity (left plot) and gray matter (right plot) for two different sample sizes (N) across five different age ranges. The sample of 610 (red) resembles the size of the WHII dataset, while the sample of 1782 represents the maximum number of participants available with the smallest age range, keeping N stable across age ranges.

3.5. Cardiovascular risk factors

The associations between clinical variables and brain age deltas are shown in Fig. 3 and Table 8. After correcting for multiple comparisons, white matter based brain age delta was significantly associated with systolic blood pressure and stroke risk score, while multimodal and gray matter based deltas were associated with alcohol intake. To test whether the gray and white matter models showed differential associations with the clinical variables, Z tests for correlated samples (Eq. (1)) were run for each of the variables. The results showed stronger associations between blood pressure and white matter compared to gray matter, as shown in Table 9. No differences in the associations of alcohol intake and stroke risk with these modalities were observed. As visible from Fig. 3, associations with clinical variables were similar across the gray matter predictions based on the within-sample k-folding model and the external gray matter model.

Table 8.

Relationships between (standardized) clinical variables and brain age delta for each modality. p-values are reported before and after FDR correction. Corrected p-values below 0.05 are marked with an asterisk. MM = multimodal, GM = gray matter, WM = white matter, FC = functional connectivity, Ext. GM = external gray matter model gray matter predictions based on the external UK Biobank training set (Section 2.3.5).

Model	β	SE	t	p	pcorr
BP Systolic
MM	0.047	0.023	2.053	0.041	0.077
GM	-0.003	0.021	-0.135	0.892	0.940
WM	0.074	0.024	3.121	0.002	0.013*
FC	0.022	0.010	2.282	0.023	0.067
Ext.GM	0.011	0.023	0.478	0.633	0.744
BP Diastolic
MM	0.026	0.023	1.137	0.256	0.366
GM	-0.003	0.020	-0.166	0.868	0.940
WM	0.053	0.024	2.271	0.024	0.067
FC	0.010	0.010	1.058	0.291	0.388
Ext. GM	0.017	0.023	0.729	0.466	0.583
Alcohol intake
MM	0.072	0.023	3.163	0.002	0.013*
GM	0.052	0.020	2.582	0.010	0.040*
WM	0.041	0.024	1.754	0.080	0.133
FC	$-0.2\times {10}^{-3}$	0.010	-0.025	0.980	0.980
Ext. GM	0.064	0.023	2.766	0.006	0.029*
Stroke risk score
MM	0.057	0.027	2.126	0.034	0.075
GM	0.049	0.024	2.036	0.042	0.077
WM	0.102	0.028	3.688	$0.2\times {10}^{-3}$	0.005*
FC	0.016	0.011	1.417	0.157	0.242
Ext. GM	0.060	0.027	2.181	0.030	0.074

Table 9.

Differences between the gray matter (GM) and white matter (WM) associations with clinical variables. P-values are reported before and after FDR correction. BP = blood pressure.

	GM β ± SE	WM β ± SE	Z	p	pcorr
BP systolic	-0.003  ±  0.021	0.074  ±  0.024	2.988	0.003	0.011
BP diastolic	-0.003  ±  0.020	0.053  ±  0.020	2.214	0.027	0.054
Alcohol intake	0.052  ±  0.020	0.052  ±  0.020	-0.435	0.664	0.664
Stroke risk score	0.049  ±  0.024	0.102  ±  0.028	1.778	0.076	0.100

4. Discussion

Our findings demonstrate that machine learning models can provide meaningful imaging-based biomarkers for brain aging in healthy population cohorts (Cole, Marioni, Harris, Deary, 2019a, Smith, Vidaurre, Alfaro-Almagro, Nichols, Miller, 2019). In line with previous studies (Cole, 2020, Cole, Marioni, Harris, Deary, 2019a, Liem, Varoquaux, Kynast, Beyer, Masouleh, Huntenburg, Lampe, Rahim, Abraham, Craddock, et al., 2017, Niu, Zhang, Kounios, Liang, 2019), the prediction accuracy improved when multiple imaging modalities were included in the model. The modality-specific gray and white matter models showed similar performance, while the rs-fMRI model showed low prediction accuracy, indicating that the functional connectivity measures were less related to chronological age compared to structural measures. Follow-up analyses showed that rs-fMRI predictions were similarly low in a matched sample from the UK Biobank, and that the prediction accuracy increased with (a) sample size and (b) larger age range. However, the rs-fMRI predictions were consistently lower than the predictions based on gray-matter features. Although it is possible that voxel-wise functional connectivity measures could improve the model performance (Li et al., 2018), the lower age-sensitivity of rs-fMRI measurements may be explained by these metrics reflecting a state, rather than trait based, assessment (Blautzik, Vetter, Peres, Gutyrchik, Keeser, Berman, Kirsch, Mueller, Pöppel, Reiser, et al., 2013, Harrison, Pujol, Ortiz, Fornito, Pantelis, Yücel, 2008, Waites, Stanislavsky, Abbott, Jackson, 2005). While resting-state networks, including the default mode network, are characterized as highly replicable both within-participants and across studies (Beckmann, Mackay, Filippini, Smith, 2009, Damoiseaux, Rombouts, Barkhof, Scheltens, Stam, Smith, Beckmann, 2006, Fox, Greicius, 2010), investigations employing dynamic rs-fMRI conversely suggest that the connectivity between these networks may vary even within a single session of scanning (Allen et al., 2014). Alternatively, resting-state networks and their connectivity to other networks may be preserved though plasticity despite age-related structural changes (Benson et al., 2018). Another potential explanation is that age-related changes to network connectivity occur in a modular, rather than gradual manner (Betzel, Byrge, He, Goñi, Zuo, Sporns, 2014, Song, Birn, Boly, Meier, Nair, Meyerand, Prabhakaran, 2014). While gray and white matter based brain-age models provide relatively accurate predictions across studies (Cole, Marioni, Harris, Deary, 2019a, Kaufmann et al., 2019, Richard, Kolskår, Sanders, Kaufmann, Petersen, Doan, Sanchez, Alnæs, Ulrichsen, Dørum, et al., 2018, Smith, Vidaurre, Alfaro-Almagro, Nichols, Miller, 2019, de Lange et al., 2020a), a recent application of brain-age estimation in the UK Biobank cohort similarly highlights fMRI-based brain-age prediction as a weaker correlate of chronological age (r = 0.43), relative to gray matter (r = 0.69) and DTI-based white matter (r = 0.67) predictions (Cole, 2020). However, other studies have shown reliable age predictions based on resting-state functional connectivity patterns using convolutional (Li et al., 2018) and deep (He et al., 2020) neural networks, as well as connections across multiple functional systems (Nielsen et al., 2019). Our results indicate that such discrepancies between studies may be related to variations in sample size and age range; two factors that influence model performance substantially.

The external gray matter model trained on an independent sample from the UK Biobank showed consistent predictions with the k-folding based gray matter model. Hence, the application of brain-age models trained on independent samples can provide equivalent prediction accuracy to within-sample approaches when confounding factors including scanner site and age-bias are carefully controlled for (Madan, 2017). The exclusion of low-quality data improved the performance of the gray matter model, suggesting that established procedures for data quality control may have implications for model performance (Alfaro-Almagro, Jenkinson, Bangerter, Andersson, Griffanti, Douaud, Sotiropoulos, Jbabdi, Hernandez-Fernandez, Vallee, et al., 2018, Graham, Drobnjak, Zhang, 2018). However, while there was a tendency for the multimodal model to also improve with the exclusion of low-quality data, discarding such data did not affect the performance of the white matter and functional connectivity models. Future studies investigating the effect of data quality on model performance in larger samples are needed to establish the importance of data quality procedures in brain-age prediction studies.

In line with recent findings from UK Biobank (Cole, 2020, Smith, Vidaurre, Alfaro-Almagro, Nichols, Miller, 2019), the results showed positive associations between brain age deltas and diastolic blood pressure, alcohol intake, and stroke risk, concurring with previous WHII studies (Topiwala, Allan, Valkanova, Zsoldos, Filippini, Sexton, Mahmood, Fooks, Singh-Manoux, Mackay, et al., 2017, Zsoldos, Filippini, Mahmood, Mackay, Singh-Manoux, Kivimäki, Jenkinson, Ebmeier, 2018), and demonstrating that brain age delta reflects individual variation in neural aging processes (Niu et al., 2019). However, in light of our results showing significant impact of age range on model performance, future brain-age studies could benefit from assessing associations with risk factors across different age ranges. While modality-specific models are informative in patient groups where tissue types are differentially affected by disease (Cherubini, Caligiuri, Péran, Sabatini, Cosentino, Amato, 2016, Groves, Smith, Fjell, Tamnes, Walhovd, Douaud, Woolrich, Westlye, 2012, Liem, Varoquaux, Kynast, Beyer, Masouleh, Huntenburg, Lampe, Rahim, Abraham, Craddock, et al., 2017, Richard, Kolskår, Sanders, Kaufmann, Petersen, Doan, Sanchez, Alnæs, Ulrichsen, Dørum, et al., 2018, Smith, Elliott, Alfaro-Almagro, McCarthy, Nichols, Douaud, Miller, 2020), individual estimations from such models may to a large extent overlap in healthy cohorts (Cole, 2020). Our results suggest that modality-specific models may provide information beyond multimodal models, as indicated by the diverging gray and white matter associations with blood pressure which are not reflected in the multimodal association (Fig. 3). However, associations with other clinical predictors, including alcohol intake and stroke risk, were similar across modalities (as visible by the overlapping error bars in Fig. 3), and regional modelling of tissue-specific brain aging patterns may be more suitable to detect specific associations with biomedical and clinical measures (Kaufmann et al., 2019), which could get lost in machine learning models that summarize aging across the whole brain to produce a single global prediction (Eavani, Habes, Satterthwaite, An, Hsieh, Honnorat, Erus, Doshi, Ferrucci, Beason-Held, et al., 2018, Smith, Elliott, Alfaro-Almagro, McCarthy, Nichols, Douaud, Miller, 2020).

In conclusion, machine-learning based brain age prediction can reduce the dimensionality of neuroimaging data to provide meaningful biomarkers of individual brain aging. However, model performance depends on study-specific characteristics including sample size and age range, which may cause discrepancies in findings across studies. While the presented imaging-derived markers can help to assess general effects of clinical risk factors on the brain, models of distinct and regional neural aging patterns may result in more refined biomarkers that can capture additional biological detail (Kaufmann et al., 2019, Richard, Kolskår, Sanders, Kaufmann, Petersen, Doan, Sanchez, Alnæs, Ulrichsen, Dørum, et al., 2018, Smith, Elliott, Alfaro-Almagro, McCarthy, Nichols, Douaud, Miller, 2020).

CRediT authorship contribution statement

Ann-Marie G. de Lange: Visualization, Conceptualization, Methodology, Software, Formal analysis, Project administration, Writing - original draft, Writing - review & editing. Melis Anatürk: Conceptualization, Methodology, Resources, Software, Formal analysis, Writing - original draft, Writing - review & editing. Sana Suri: Resources, Investigation, Methodology, Writing - review & editing. Tobias Kaufmann: Conceptualization, Methodology, Resources, Writing - review & editing. James H. Cole: Methodology, Writing - review & editing. Ludovica Griffanti: Methodology, Resources, Writing - review & editing. Enikő Zsoldos: Resources, Investigation, Writing - review & editing. Daria E.A. Jensen: Resources, Writing - review & editing. Nicola Filippini: Investigation, Writing - review & editing. Archana Singh-Manoux: Investigation, Writing - review & editing. Mika Kivimäki: Investigation, Writing - review & editing. Lars T. Westlye: Conceptualization, Methodology, Writing - review & editing. Klaus P. Ebmeier: Conceptualization, Methodology, Investigation, Project administration, Writing - review & editing.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/