Evidence inconsistency degrees of freedom in Bayesian network meta-analysis

Abstract

Network meta-analysis (NMA) is a popular tool to synthesize direct and indirect evidence for simultaneously comparing multiple treatments, while evidence inconsistency greatly threatens its validity. One may use the inconsistency degrees of freedom (ICDF) to assess the potential that an NMA might suffer from inconsistency. Multi-arm studies provide intrinsically consistent evidence and complicate the ICDF’s calculation; they commonly appear in NMAs. The existing ICDF measure may not feasibly handle multi-arm studies. Motivated from the effective numbers of parameters of Bayesian hierarchical models, we propose new ICDF measures in generic NMAs that may contain multi-arm studies. Under the fixed- or random-effects setting, the new ICDF measure is the difference between the effective numbers of parameters of the consistency and inconsistency NMA models. We used artificial NMAs created based on an illustrative example and 39 empirical NMAs to evaluate the performance of the existing and new measures. In NMAs with two-arm studies only, the proposed ICDF measure under the fixed-effects setting was nearly the same with the existing measure. Among the empirical NMAs, 27 (69%) contained at least one multi-arm study. The existing measure was not applicable to them, while the proposed measures led to interpretable ICDFs in all NMAs.

1. Introduction

Meta-analysis is an important tool to integrate and contrast findings from various independent studies on common topics. It has been widely used to produce high-quality overall evidence for treatment comparisons that can help underpin guidelines and make decisions (Gurevitch et al. 2018; Niforatos, Weaver, and Johansen 2019). For a certain disease condition, multiple treatments are often available, and clinicians aim at choosing optimal treatment options for patients. In recent years, network meta-analysis (NMA), also known as multiple-treatment meta-analysis or mixed treatment comparison, has been rapidly developed to inform the benefits and harms of all available treatments (Lumley 2002; Lu and Ades 2004; Salanti 2012; Cipriani et al. 2013; Nikolakopoulou et al. 2018). The fundamental idea is to simultaneously synthesize both direct and indirect evidence for treatment comparisons, and thus to provide more precise treatment effect estimates than conventional pairwise meta-analysis that separately and directly compares each pair of treatments (Caldwell, Ades, and Higgins 2005; Riley et al. 2017).

An NMA often relies on a critical assumption that the direct and indirect evidence is consistent for all treatment comparisons (Donegan et al. 2013; Jansen and Naci 2013). Such consistency is sometimes termed coherence (Ioannidis 2009; Mills, Thorlund, and Ioannidis 2013; Brignardello-Petersen et al. 2019). Consider that the comparison between treatments A and B is of interest; the studies that include both treatment groups provide the direct evidence for this comparison. However, such evidence may be sparse (e.g., when no financial incentive supports conducting head-to-head trials of A vs. B). Alternatively, many studies may compare A or B with another common comparator such as placebo, denoted by C. These studies of A vs. C and B vs. C provide the indirect evidence for comparing A and B. The three treatments A, B, and C form an evidence loop in the treatment network; such a loop is critical for an NMA to outperform the conventional pairwise meta-analyses (Salanti, Kavvoura, and Ioannidis 2008; Mills, Thorlund, and Ioannidis 2013; Lin et al. 2019; Lin, Chu, and Hodges 2020; Papakonstantinou et al. 2020).

The evidence consistency assumption may not hold in some NMAs; violating this important assumption may lead to biased treatment effect estimates (Song et al. 2011). The inconsistency may be caused by many factors, such as imbalanced distributions of effect modifiers between different types of comparisons, outlying treatment effects, treatment intransitivity, and publication and related bias (Jansen and Naci 2013; Brignardello-Petersen et al. 2019). Higgins et al. (2012) introduced the concepts of loop inconsistency and design inconsistency. The loop inconsistency is relevant to the scenario of three treatments A, B, and C illustrated above; that is, the underlying overall effect sizes of A vs. C and C vs. B may not add up to that of A vs. B. This article is primarily concerned with such inconsistency. On the other hand, the design inconsistency refers to differences in underlying overall effect sizes in different study designs (i.e., sets of treatments compared within studies).

Each NMA should rigorously evaluate the evidence consistency assumption for rating evidence quality and validating its conclusions (Mills et al. 2012; Puhan et al. 2014; Hutton et al. 2015), whereas empirical studies have found that many published NMAs did not carefully check this assumption (Veroniki et al. 2013; Nikolakopoulou et al. 2014; Petropoulou et al. 2017). Most existing approaches focus on testing for the presence of evidence inconsistency and modeling treatment comparisons with such inconsistency; they include the node-splitting approach, the model with inconsistency factors, the design-by-treatment interaction model, etc. (Lu and Ades 2006; Dias et al. 2010; Higgins et al. 2012; van Valkenhoef et al. 2012; Jackson et al. 2014; Tu 2016; Donegan, Dias, and Welton 2019). These approaches typically specify additional parameters in NMA models to permit evidence inconsistency.

Before using statistical methods to test and adjust for evidence inconsistency, it is also critical to assess the potential that an NMA might suffer from such inconsistency. Lu and Ades (2006) referred to such potential as inconsistency degrees of freedom (ICDF), and they proposed a measure to quantify it. This ICDF measure is interpreted as the number of independent evidence loops in an NMA. For example, in a star-shaped NMA with all active treatments compared with a common placebo, no evidence loop exists and thus its ICDF is 0. As such, the ICDF is a characteristic about the treatment comparison structure; it does not draw conclusions about whether evidence inconsistency is actually present.

In addition, the ICDF relates closely to the benefit of performing an NMA compared with performing separate pairwise meta-analyses; to gain more power from an NMA, researchers need to accept a greater risk of evidence inconsistency. For example, although a star-shaped NMA does not suffer from evidence inconsistency with ICDF = 0, the absence of evidence loops implies no synthesis of direct and indirect evidence. Such evidence synthesis is the primary reason that an NMA could outperform separate pairwise meta-analyses (Lu and Ades 2004).

The explicit calculation of the ICDF proposed by Lu and Ades (2006) is restricted to special cases, i.e., when all studies in an NMA are two-armed. Multi-arm studies, however, are common in practice (Chan and Altman 2005). Because the evidence from multi-arm studies is intrinsically consistent, the presence of multi-arm studies complicates the calculation of the ICDF (Lu and Ades 2006; Dias et al. 2010; Higgins et al. 2012; Dias, Welton, et al. 2013). For example, if an evidence loop is formed by two-arm studies only, then the ICDF is clearly 1. On the other hand, if this loop is formed by a multi-arm study only, it is not subject to evidence inconsistency and thus does not contribute to the ICDF. When the evidence loop is mixed by both two- and multi-arm studies, the calculation of the ICDF needs a tradeoff between the two types of studies. Because of such complication, the ICDF is rarely reported in the current literature, although it provides important information about NMAs.

Based on the effective number of parameters (ENP) of Bayesian hierarchical models (Spiegelhalter et al. 2002), this article proposes alternative methods to calculate the ICDF in generic NMAs that may or may not include multi-arm studies. The ICDF can be expressed as the difference between the ENPs in NMA models with and without the evidence consistency assumption. It can be feasibly calculated in all NMAs, because the ENP can be obtained in various software packages for Bayesian analyses.

The rest of this article is organized as follows. We first present an illustrative example of comparisons among multiple antidepressants, and review the commonly-used Bayesian hierarchical models to implement NMAs. Based on these setups, we demonstrate the problem of evidence inconsistency and the difficulty in deriving the ICDF in the presence of multi-arm studies. Then, we introduce the proposed methods to calculate the ICDF in generic NMAs under both the fixed-effects (FE) and random-effects (RE) settings. The performance of the proposed methods is assessed using both artificial and empirical datasets. We conclude this article with a brief discussion.

2. Methods

2.1. Illustrative example and model of network meta-analysis

We consider an illustrative example of NMA reported by Cipriani et al. (2009) that investigated the efficacy of 12 antidepressants. Figure 1 presents its treatment network, and the treatment names are in the figure legend. This NMA includes a total of 111 studies, among which 109 are two-armed and two are three-armed, both comparing treatments 5, 9, and 11.

Figure 1.

Treatment network plot of the NMA by Cipriani et al. (2009). The 12 treatments are sorted in alphabetical order: 1) bupropion; 2) citalopram; 3) duloxetine; 4) escitalopram; 5) fluoxetine; 6) fluvoxamine; 7) milnacipran; 8) mirtazapine; 9) paroxetine; 10) reboxetine; 11) sertraline; and 12) venlafaxine. Each node denotes a treatment; each edge represents a direct comparison between the corresponding two treatments. The node size is proportional to the total sample size in the corresponding treatment groups across studies; the edge width is proportional to the number of studies that directly compare the corresponding treatments. The shaded loop indicates that it contains evidence contributed by multi-arm studies.

We consider Bayesian hierarchical models for implementing NMAs. Suppose that an NMA collects $N$ studies and compares a total of $K$ (>2) treatments. Each study compares a subset of the $K$ treatments; denote the treatment set of study $i$ by ${\mathcal{T}}_i$. Let $y_{ik}$ be the observed outcome measure in study $i$’s treatment group $k$. It follows a distribution with the probability density/mass function $f\left(\cdot |{\mathrm{\Delta }}_{ik},{\mathcal{D}}_{ik}\right)$, which depends on an unknown parameter ${\mathrm{\Delta }}_{ik}$, representing treatment $k$’s effect in study $i$, and some known data ${\mathcal{D}}_{ik}$. For example, in the illustrative NMA, $K$ = 12 and $N$ = 111. For binary outcomes, $y_{ik}$ represents event counts and follows a binomial distribution, with ${\mathrm{\Delta }}_{ik}$ being the true event rate and ${\mathcal{D}}_{ik}$ being the sample size.

An NMA typically focuses on estimating relative effects between treatments. A baseline treatment, denoted by $b_i$, needs to be specified for each study. The treatment sets ${\mathcal{T}}_i$ of different studies need not intersect, so different studies may have different baseline treatments. When it does not lead to confusion, $b_i$ is simply denoted by $b$. The Bayesian hierarchical RE model for the NMA is (Lu and Ades 2004, 2009):

$$\begin{gathered} y_{ik}\sim f\left(y|{\mathrm{\Delta }}_{ik},{\mathcal{D}}_{ik}\right),\mathrm{ }\mathrm{ }i=1,\dots ,N,\mathrm{ }k\in {\mathcal{T}}_i; \\ g\left({\mathrm{\Delta }}_{ik}\right)={\mu }_i+{\delta }_{ibk}I\left(k\ne b\right); \\ {\delta }_{ibk}\sim N\left(d_{bk},{\tau }_{bk}^2\right); \\ \mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\left({\delta }_{ibh},{\delta }_{ibk}\right)={\gamma }_{bhk},\mathrm{ }\mathrm{ }b\ne h\ne k\in {\mathcal{T}}_i; \\ {\mu }_i,d_{bk},{\tau }_{bk},\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }{\gamma }_{bhk}\sim \mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}\mathrm{s}. \end{gathered}$$ (1)

The link function $g\left(\cdot \right)$ transforms ${\mathrm{\Delta }}_{ik}$ to be in a linear form; it is usually the logit link $g\left(t\right)=\log \left[t/\left(1-t\right)\right]$ for binary outcomes. The indicator function $I\left(\cdot \right)$ returns 0 if treatment $k$ is study $i$’s baseline ($k=b$); otherwise, it returns 1 ($k\ne b$). The parameters ${\mu }_i$ represent the studies’ baseline effects; they are usually of less interest and modeled as nuisances, because the studies’ baselines may dramatically differ in terms of their patients’ characteristics, etc. Moreover, ${\delta }_{ibk}$ are study-specific relative effects between treatments; they represent log odds ratios when using the logit link.

This model assumes the study-specific relative effects are random effects, following normal distributions, whose means are the overall relative effects $d_{bk}$ and variances are ${\tau }_{bk}^2$ across studies due to heterogeneity. Within multi-arm studies, the relative effects are correlated with correlation coefficients ${\gamma }_{bhk}$. To reduce model complexity and computational difficulty, the between-study variances of all treatment comparisons are frequently assumed equal, i.e., ${\tau }_{bk}^2={\tau }^2$, and all within-study correlation coefficients ${\gamma }_{bhk}$ are 0.5 (Higgins and Whitehead 1996; Lu and Ades 2004). We will make the above assumptions in the following data analyses.

Besides this RE model, the FE model may be also used. The FE model assumes homogeneity across studies; that is, all between-study variances ${\tau }_{bk}^2$ are 0, so the study-specific underlying relative effects ${\delta }_{ibk}$ shrink to the common overall relative effect $d_{bk}$ for each treatment comparison. Specifically, the FE model for NMA is:

$$\begin{gathered} y_{ik}\sim f\left(y|{\mathrm{\Delta }}_{ik},{\mathcal{D}}_{ik}\right),\mathrm{ }\mathrm{ }i=1,\dots ,N,\mathrm{ }k\in {\mathcal{T}}_i; \\ g\left({\mathrm{\Delta }}_{ik}\right)={\mu }_i+d_{bk}I\left(k\ne b\right); \\ {\mu }_i\mathrm{ }\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }{d}_{bk}\sim \mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}\mathrm{s}. \end{gathered}$$ (2)

Because the FE model has much fewer parameters than the RE model, its implementation is easier. However, the studies in an NMA are likely heterogeneous in practice (Higgins 2008), so the FE model may produce too narrow credible intervals with low coverage probabilities (Mills, Thorlund, and Ioannidis 2013).

2.2. Evidence inconsistency

The overall relative effects of different treatment comparisons in Equation (1) or (2) are of primary interest. For the comparison of $k$ vs. $h\mathrm{ }(h\ne k$), its overall direct evidence is quantified by $d_{hk}$; the evidence consistency assumes that the direct evidence is identical to the evidence provided by indirect comparisons via any other treatment $c$. Formally, the evidence consistency implies that $d_{hk}=d_{ck}-d_{ch}$ for any trio of treatments $c,\mathrm{ }h$, and $k$. Consequently, under this assumption, a certain treatment, say treatment 1, can be selected as a reference, and the overall relative effect of any treatment comparison is determined by comparisons vs. the reference: $d_{hk}=d_{1k}-d_{1h}$. The evidence consistency reduces the set of all $K\left(K-1\right)/2$ possible treatment comparisons to the set of $K-1$ “basic” parameters (i.e., $d_{12},\mathrm{ }...,\mathrm{ }{d}_{1K}$).

However, treatment effects based on direct evidence may not always agree with those based on indirect evidence, leading to evidence inconsistency. The inconsistency is a sort of discrepancy that lies between treatment comparisons, which differs from the heterogeneity between individual studies (Lu and Ades 2006; Salanti 2012). Several methods have been proposed to account for evidence inconsistency. For example, Dias, Welton, et al. (2013) proposed the unrelated-mean-effects (UME) model, which treats all direct treatment comparisons as separate, unrelated parameters $d_{hk}$ to be estimated, so this model does not require the consistency assumption.

Lu and Ades (2006) proposed the ICDF to quantify the potential that an NMA might suffer from evidence inconsistency; we denote it by ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$. It is interpreted as the number of independent evidence loops, where the independence means that evidence consistency within a certain loop does not rely on evidence consistency within other loops. For example, in an NMA with four treatments A, B, C, and D, suppose that A, B, C form a loop and B, C, D form another loop, and denote these loops by A-B-C and B-C-D, respectively. Then, the loop A-B-C-D depends on A-B-C and B-C-D, and thus these three loops are not independent.

For an NMA with two-arm studies only, Lu and Ades (2006) calculated the ICDF as

$${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}=T-K+1$$ (3)

where $T$ is the total number of treatment pairs that are directly compared. For example, in a simple NMA with only three mutually compared treatments A, B, and C, $T$ = 3 and $K$ = 3, so the ICDF = 1, coinciding with the fact that this NMA has one evidence loop. If the two three-arm studies are removed from the NMA by Cipriani et al. (2009), all remaining studies are two-armed. The network structure in Figure 1 remains unchanged, with $T$ = 42 and $K$ = 12, so the ICDF = 31.

Equation (3), however, is not directly applicable to NMAs with multi-arm studies. In an effort to account for such studies, Lu and Ades (2006) also suggested calculating the ICDF as $T-K+1-S$, where $S$ denotes the number of loops in which direct treatment comparisons are only present in multi-arm studies. However, when an NMA contains many multi-arm studies, this calculation becomes fairly difficult, and it has been concluded that the ICDF may have to be counted “by hand.” For example, recall that the original NMA by Cipriani et al. (2009) contains two three-arm studies, comparing treatments 5, 9, and 11. The evidence loop of 5-9-11 is intrinsically consistent within each three-arm study. Meanwhile, ten two-arm studies of treatment comparison 9 vs. 5, six of 11 vs. 5, and two of 11 vs. 9 also contribute evidence to this loop; their evidence is subject to inconsistency. Such mixtures of evidence from these two- and multi-arm studies complicate the concept of the ICDF (Lu and Ades 2006; Dias, Welton, et al. 2013). To facilitate calculating the ICDF in generic NMAs, we propose new methods based on the ENPs of Bayesian hierarchical models.

2.3. Effective number of parameters

The ENP is frequently used to assess the complexity of Bayesian hierarchical models; it is an important part for deriving the deviance information criterion (DIC) for Bayesian model selection. The DIC is the sum of a deviance term, representing the goodness-of-fit, and a penalty term, representing the model complexity (Spiegelhalter et al. 2002); that is,

$$\mathrm{D}\mathrm{I}\mathrm{C}=\stackrel{-}{D}+p_D$$

where $\stackrel{-}{D}$ is the deviance term, and $p_D$ penalizes the model complexity and is interpreted as the ENP. A complex model with many parameters generally fits the data well, but it may be bad for prediction, producing estimates with large variances. On the other hand, a simple model with few parameters may fit the data poorly. Therefore, the DIC is a useful tool for trading off the goodness-of-fit and the model complexity.

In NMAs, the calculation of the deviance $\stackrel{-}{D}$ depends on the outcome measures (Dias, Sutton, et al. 2013). Each treatment group in each study contributes an expected value 1 to $\stackrel{-}{D}$, so the deviance is expected to be around ${\sum }_{i=1}^N\left|{\mathcal{T}}_i\right|$ (i.e., the total number of treatment groups in the NMA), where $\left|\cdot \right|$ denotes a set’s size.

The $p_D$ describes the number of parameters that effectively model the NMA data. For example, under the evidence consistency assumption, the ENP of the FE model in Equation (2) is expected to be

$$p_D^{\mathrm{F}\mathrm{E},\mathrm{c}\mathrm{o}\mathrm{n}}=N+K-1$$ (4)

which is contributed by the baseline effects ${\mu }_i$ of all $N$ studies and the $K-1$ “basic” parameters of relative effects $d_{1k}\mathrm{ }(k=2,\dots ,K$). On the other hand, using the UME model by Dias, Welton, et al. (2013) to permit evidence inconsistency and assuming that all studies are two-armed, the ENP is expected to be

$$p_D^{\mathrm{F}\mathrm{E},\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}}=N+T$$ (5)

because this model treats the $T$ relative effects as separate, unrelated parameters. Of note, in the presence of multi-arm studies, Equation (4) for the consistency model is valid because such studies intrinsically satisfy the consistency assumption. However, Equation (5) for the inconsistency model may not hold, because it treats all comparisons as entirely separate parameters and does not account for the intrinsic consistency within multi-arm studies. For example, consider a three-arm study comparing treatments A, B, and C. The inconsistency UME model assigns 3 parameters, $d_{\mathrm{A}\mathrm{B}},\mathrm{ }{d}_{\mathrm{B}\mathrm{C}}$, and $d_{\mathrm{A}\mathrm{C}}$, to estimate the relative effects; however, within this three-arm study, $d_{\mathrm{A}\mathrm{C}}$ is actually determined by $d_{\mathrm{A}\mathrm{B}}$ and $d_{\mathrm{B}\mathrm{C}}$, so the ENP is 2, rather than 3. The exact form of $p_D^{\mathrm{F}\mathrm{E},\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}}$ may not be explicitly derived when two-arm studies are mixed with this three-arm study.

It is also not straightforward to derive the exact form of the ENP of the RE model. Although the study-specific relative effects ${\delta }_{ibk}$ are different, they cannot be counted as separate effective parameters because they are assumed as random effects: ${\delta }_{ibk}\sim N\left(d_{bk},{\tau }_{bk}^2\right)$. If the between-study variance ${\tau }_{bk}^2$ is zero, then all ${\delta }_{ibk}$ equal to $d_{bk}$, effectively leading to a single parameter; if ${\tau }_{bk}^2$ approaches infinity, then all ${\delta }_{ibk}$ are essentially separate parameters. The ENP of the RE model lies between the two extreme cases above.

Despite of the difficulty in theoretically deriving the ENPs’ explicit forms in generic cases, they can be numerically calculated by many software packages via rigorous Bayesian methods (Plummer 2002; Spiegelhalter et al. 2002; Gelman et al. 2014).

2.4. Proposed methods

Based on the ENP, we propose new methods to calculate the ICDF in generic NMAs, regardless of the presence of multi-arm studies. Recall that Lu and Ades (2006) calculated the ICDF as $T-\left(K-1\right)$ in an NMA with two-arm studies only; this turns out to be the difference between the ENPs $p_D^{\mathrm{F}\mathrm{E},\mathrm{c}\mathrm{o}\mathrm{n}}$ and $p_D^{\mathrm{F}\mathrm{E},\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}}$ under the FE setting with and without the evidence consistency assumption in Equations (4) and (5). Motivated by this observation, the ICDF’s definition can be naturally generalized to handle NMAs with multi-arm studies: for the FE setting, we define

$${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}=p_D^{\mathrm{F}\mathrm{E},\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}}-p_D^{\mathrm{F}\mathrm{E},\mathrm{c}\mathrm{o}\mathrm{n}}$$ (6)

In NMAs with two-arm studies only, ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ is expected to be identical to ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$. In practice, ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ is numerically calculated by Bayesian methods via the Markov chain Monte Carlo (MCMC) algorithm, while ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ is given by an explicit form in Equation (3); therefore, they may be slightly different owing to computing errors. This difference may also relate to Markov chains’ stabilization and convergence.

The ICDF’s alternative definition in Equation (6) is valid for generic NMAs, even in the presence of multi-arm studies, because the ENPs can be readily obtained in all Bayesian hierarchical models. In addition, this definition is intuitive because the difference in the ENPs naturally represents the change of the degrees of freedom of treatment comparisons caused by making the evidence consistency/inconsistency assumption.

The ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ is derived under the FE setting, which is inappropriate if substantial heterogeneity appears. We may define the ICDF similarly under the RE setting:

$${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}=p_D^{\mathrm{R}\mathrm{E},\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}}-p_D^{\mathrm{R}\mathrm{E},\mathrm{c}\mathrm{o}\mathrm{n}}$$ (7)

where $p_D^{\mathrm{R}\mathrm{E},\mathrm{c}\mathrm{o}\mathrm{n}}$ and $p_D^{\mathrm{R}\mathrm{E},\mathrm{i}\mathrm{n}\mathrm{c}\mathrm{o}\mathrm{n}}$ are the ENPs of the consistency and inconsistency RE models, respectively.

2.5. Analyses of artificial and empirical data

We constructed artificial data based on the illustrative NMA by Cipriani et al. (2009) to assess the proposed ICDFs’ performance; Figure 2 shows the process. Specifically, we first reduced the original data (Data O) to be star-shaped (Data S) with the center at treatment 5 (fluoxetine), because it had been conventionally used as the reference antidepressant. As the star-shaped NMA contained no loop, its ICDF is 0 in theory. On the one hand, by iteratively adding two-arm studies of different direct comparisons to Data S, we created Data T1 to T3. Here, we use “T” to indicate that these artificial data contained two-arm studies only, so that ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ could be calculated and thus be compared with our proposed ICDFs. On the other hand, by iteratively adding three-arm studies with different treatment sets to Data S, we created Data M1 to M3, where “M” indicates the existence of multi-arm studies. These three artificial datasets contained different numbers of multi-arm studies comparing different sets of treatments, so that we could explore their impact on the ICDF.

Figure 2.

Flow chart of constructing artificial NMA datasets.

We also assessed ICDFs in empirical NMA datasets with binary outcomes. They were extracted from a total of 58 NMAs investigated by Bafeta et al. (2013, 2014), Veroniki et al. (2013), and Trinquart et al. (2016). After excluding datasets that were originally devoted to extensions of the classic NMA model (e.g., models for competing risks) or those containing overlapping studies, we obtained 40 NMAs with various disease outcomes, including cancer, depressive disorder, major cardiovascular events, rheumatoid arthritis, stroke, etc. These 40 NMAs included our illustrative example. We calculated ICDFs of the remaining 39 NMAs; each NMA will be denoted by the first author’s surname with the publication year. The Supplemental Material (Appendix A) presents the full references of these 39 NMAs.

We used the MCMC algorithm to implement the Bayesian analyses in both artificial and empirical NMA data with R (version 4.0.2) via the package “rjags” (version 4–10) and JAGS (version 4.3.0). The results were based on three Markov chains; each chain contained 200,000 iterations after a burn-in period with 50,000 iterations, and the thinning rate was 2 for reducing posterior sample autocorrelations. The vague normal prior $N\left(0, {100}^2\right)$ was used for the baseline effects and the overall log odds ratios. Under the RE setting, the uniform prior $U\left(0, 5\right)$ was used for the heterogeneity standard deviation. We examined the Markov chains’ convergence based on their traceplots. The Supplemental Material (Appendix B) includes the code for all analyses.

3. Results

3.1. Artificial data

Table 1 shows the ICDFs in the various artificial NMA datasets. Each Markov chain for each NMA converged well. Because Data O and M1 to M3 contained multi-arm studies, the ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ was not applicable to them. When ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ could be calculated, it was close to ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$. Moreover, ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ was generally smaller than ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$.

Table 1.

Inconsistency degrees of freedom in artificial data based on the network meta-analysis by Cipriani et al. (2009).

Data	No. of studies (no. of multi-arm studies)	${\mathbf{I}\mathbf{C}\mathbf{D}\mathbf{F}}^{\mathbf{L}\mathbf{A}}$	${\mathbf{I}\mathbf{C}\mathbf{D}\mathbf{F}}^{\mathbf{F}\mathbf{E}}$	${\mathbf{I}\mathbf{C}\mathbf{D}\mathbf{F}}^{\mathbf{R}\mathbf{E}}$
Data O	111 (2)	NA	31.05	26.99
Data S	50 (0)	0	$-$0.02	$-$0.24
Data T1	58 (0)	2	2.04	1.21
Data T2	68 (0)	5	4.88	2.62
Data T3	109 (0)	31	31.02	26.52
Data M1	52 (2)	NA	$-$0.06	$-$0.13
Data M2	60 (10)	NA	0.01	$-$0.26
Data M3	68 (18)	NA	1.92	1.32

NA, not applicable; the ICDF proposed by Lu and Ades (2006) is applicable to network meta-analyses with two-arm studies only.

Recall that Data S was star-shaped, so it contained no evidence loop; consequently, ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ = 0 and ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ was almost 0. Both ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ and ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ were slightly negative; they were possibly subject to Monte Carlo errors. Data T1 added more studies that directly compared two treatment pairs to Data S, creating two independent loops; thus, ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ = 2, which approximately equaled to ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ = 2.04. These two ICDF measures also had similar values for Data T2.

In addition, Data T3 and O differed by only two three-arm studies of 5 vs. 9 vs. 11. Data T3 had ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ = 31 and ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ = 31.02, which were fairly close to ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ = 31.05 in Data O. The two three-arm studies did not have much impact on the ICDF, likely because the NMA contained much more two-arm studies. Similarly, the ICDF of Data M1 was close to that of Data S; they also only differed by the two three-arm studies. Increasing the number of such three-arm studies as in Data M2 did not dramatically change the ICDF; both ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ and ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ were close to 0 because the loop of 5-9-11 was contributed mostly by the three-arm studies and thus tended to be consistent. However, after adding eight three-arm studies of 9 vs. 10 vs. 11 to Data M2, ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ and ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ increased to 1.92 and 1.32, respectively. Although the added studies were three-armed and the evidence was consistent within them, they contributed comparisons to form evidence loops with other two-arm studies. For example, the comparisons of 9 vs. 10 from the three-arm studies formed an evidence loop with the two-arm studies of 5 vs. 9 and 5 vs. 10. Therefore, the ICDF was no longer 0 in Data M3.

3.2. Empirical data

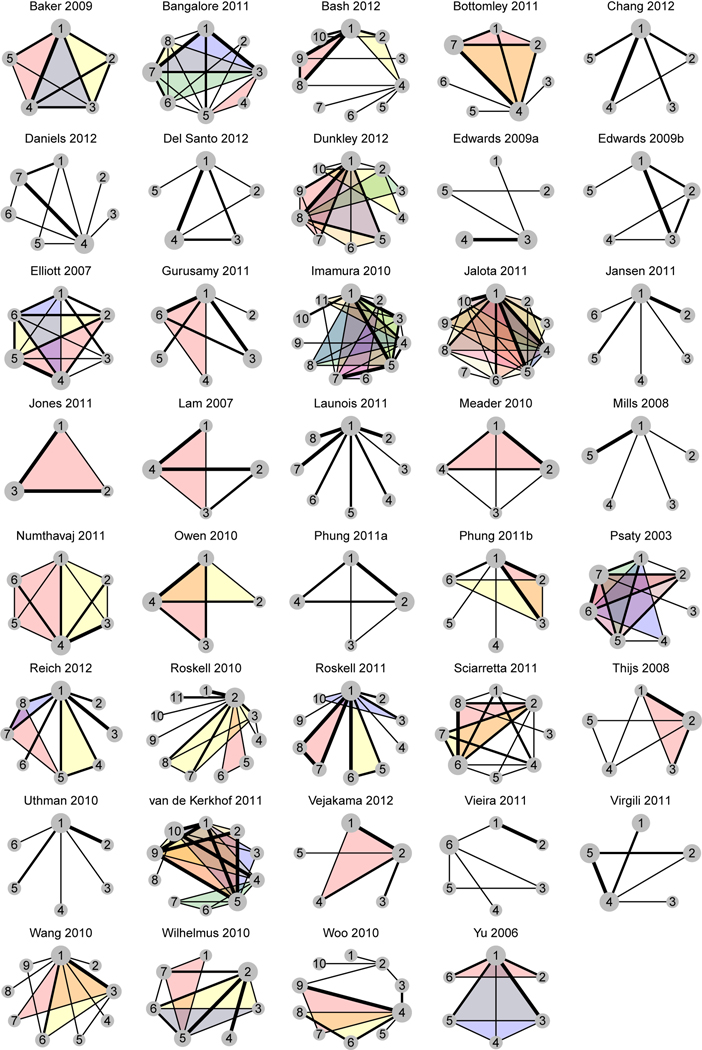
Figure 3 shows the treatment networks of 39 empirical NMA datasets, and Table 2 presents their ICDFs. Among the 39 NMAs, 27 (69%) contained at least one multi-arm study, so the ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ was not applicable to them. For each of the remaining 12 NMAs, ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ was fairly close to ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$; their difference was up to 0.04. Also, ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ was generally smaller than ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$.

Figure 3.

Treatment network plots of 39 empirical NMA datasets. Shaded loops in different colors indicate multi-arm studies with different treatment sets.

Table 2.

Characteristics and inconsistency degrees of freedom in the 39 empirical network meta-analyses.

Network meta-analysis	No. of studies (no. of multi-arm studies)	No. of treatments	${\mathbf{I}\mathbf{C}\mathbf{D}\mathbf{F}}^{\mathbf{L}\mathbf{A}}$	${\mathbf{I}\mathbf{C}\mathbf{D}\mathbf{F}}^{\mathbf{F}\mathbf{E}}$	${\mathbf{I}\mathbf{C}\mathbf{D}\mathbf{F}}^{\mathbf{R}\mathbf{E}}$	Poor MCMC convergence
Baker 2009	38 (9)	5	NA	3.00	2.18	No
Bangalore 2011	49 (4)	8	NA	9.83	8.89	$d_{68}$ (IC, BE)
Bash 2012	20 (3)	10	NA	3.03	1.37	No
Bottomley 2011	10 (2)	7	NA	3.01	1.05	No
Chang 2012	12 (0)	5	1	1.03	0.23	No
Daniels 2012	18 (0)	7	3	2.99	0.41	No
Del Santo 2012	10 (0)	5	2	2.03	1.14	No
Dunkley 2012	13 (5)	10	NA	2.03	0.79	No
Edwards 2009a	34 (0)	5	0	$-$0.03	0.01	No
Edwards 2009b	10 (0)	5	2	2.03	1.47	No
Elliott 2007	22 (4)	6	NA	9.00	4.84	No
Gurusamy 2011	11 (1)	6	NA	1.04	0.49	$d_{2*}$ (C, RE); $d_{12}$ (IC, RE)
Imamura 2010	36 (7)	11	NA	11.72	2.87	$d_{14}$ (IC, BE)
Jalota 2011	99 (19)	10	NA	0.03	0.09	No
Jansen 2011	8 (0)	6	0	$-$0.01	0.01	No
Jones 2011	19 (1)	3	NA	1.01	0.86	No
Lam 2007	11 (1)	4	NA	1.01	1.01	No
Launois 2011	19 (0)	8	0	$-$0.01	0.06	No
Meader 2010	20 (1)	4	NA	2.99	1.36	No
Mills 2008	19 (0)	5	0	$-$0.02	$-$0.05	No
Numthavaj 2011	6 (2)	6	NA	3.00	1.11	No
Owen 2010	14 (2)	4	NA	1.97	2.84	No
Phung 2011a	13 (0)	4	2	1.99	0.24	No
Phung 2011b	20 (2)	6	NA	0.65	0.66	$d_{23},\mathrm{ }{d}_{26}$ (IC, RE)
Psaty 2003	30 (7)	7	NA	7.02	$-$1.17	No
Reich 2012	18 (5)	8	NA	2.05	1.65	No
Roskell 2010	17 (2)	11	NA	1.00	$-$0.20	No
Roskell 2011	12 (6)	10	NA	0.01	0.05	No
Sciarretta 2011	26 (2)	8	NA	9.08	1.92	No
Thijs 2008	25 (3)	5	NA	3.00	1.33	No
Uthman 2010	14 (0)	6	0	0.02	0.00	No
van de Kerkhof 2011	7 (5)	10	NA	3.94	3.36	No
Vejakama 2012	9 (1)	5	NA	1.07	0.55	$d_{5*}$ (C, BE); $d_{25}$ (IC, BE)
Vieira 2011	7 (0)	6	1	0.99	0.55	No
Virgili 2011	10 (0)	5	1	1.04	1.17	No
Wang 2010	43 (2)	9	NA	3.02	0.78	No
Wilhelmus 2010	43 (3)	7	NA	5.98	4.65	No
Woo 2010	13 (2)	10	NA	0.66	1.01	$d_{1*}$ (C, BE); $d_{12}$ (IC, BE)
Yu 2006	14 (3)	6	NA	0.04	0.11	No

ICDF represents inconsistency degrees of freedom.

MCMC represents Markov chain Monte Carlo algorithm.

NA, not applicable; the ICDF proposed by Lu and Ades (2006) is applicable to network meta-analyses with two-arm studies only.

C, IC, RE, and BE represent the consistency model, the inconsistency model, the random-effects setting, and both the fixed- and random-effects settings, respectively; $d$ represents a comparison between treatments specified in its subscript; an asterisk ($*$) in the subscript indicates any other treatment in the network.

The proposed measures were consistent with the intuition that better-connected NMAs generally have larger ICDFs; for example, Bangalore 2011 had relatively large ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ and ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$. Some NMAs seemed well-connected, but most treatment loops were actually formed by multi-arm studies, which were not subject to inconsistency. The proposed methods accurately yielded ICDFs in such situations. For example, both ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ and ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ of Jalota 2011 were nearly 0; although this NMA seemed to contain many loops, they were mostly formed by multi-arm studies. Specifically, this NMA contained 99 studies; except one study of 6 vs. 7, all remaining studies contained treatment 1. If multi-arm studies were removed, this NMA would be nearly star-shaped. Additionally, the ICDFs under the FE and RE settings dramatically differed in some NMAs; for example, Sciarretta 2011 had ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ = 9.08 and ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ = 1.92. On the other hand, ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ was noticeably larger than ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ in a few NMAs, such as Owen 2010.

Of note, computational issues occurred in three NMAs, i.e., Edwards 2009a, Jones 2011, and Wilhelmus 2010. Specifically, Edwards 2009a contained a two-arm study with event counts equaling to the corresponding sample sizes in both arms. Jones 2011 similarly contained two such studies. In addition, Wilhelmus 2010 contained a four-arm study of 2 vs. 3 vs. 5 vs. 6; treatments 2 and 3 were directly compared by only this study in the whole network, while the event count in treatment group 3 equaled to its sample size. These cases were counterparts of the problem of zero-count studies, leading to potential estimation issues; see, e.g., Chapter 10.4.4 in Higgins et al. (2019). To successfully produce the ICDFs in these three NMAs, we reduced event counts by one in each treatment group in the aforementioned studies. Their results in Table 2 were based on the adjusted event counts. Another computational problem was related to the MCMC convergence. Table 2 indicates that six NMAs contained comparisons with poor MCMC convergence. They had relatively rare outcomes with low or zero event counts. Some adjustment for the zero events might help improve the convergence.

4. Discussion

As its name suggests, the ICDF describes the degrees of freedom that an NMA could suffer from evidence inconsistency. It is not designed to test for the evidence consistency assumption; a large ICDF value indicates the potential, but not the presence, of evidence inconsistency. As such, the ICDF relates closely to the possible ways of effectively mixing the direct and indirect evidence, and thus implies the benefit of an NMA over separate pairwise meta-analyses that cannot synthesize these two types of evidence.

This article has proposed new measures to assess the ICDF. The existing measure can be feasibly applicable to NMAs with two-arm studies only, because multi-arm studies form intrinsically consistent evidence loops and complicate the calculation. Due to this limitation, the current literature seldom reports this measure. Based on the ENPs of Bayesian hierarchical models, the proposed measures can be naturally applied to generic NMAs that may contain multi-arm studies under both the FE and RE settings. The data analyses have shown that the new measure under the FE setting produced essentially the same values with the existing measure in NMAs with two-arm studies only. In addition, although we have focused on NMAs with binary outcomes, the proposed measures can be similarly obtained for those with other outcomes. In summary, the ICDF is an important characteristic of an NMA; the proposed methods enable its calculation in generic NMAs, and it may be routinely reported in practice.

The ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ by Lu and Ades (2006) is arguably a geometry-based measure, because it is driven by the concept of “number of independent loops in a network.” This nature makes it difficult to handle multi-arm studies when they are mixed with the inconsistency loops. On the other hand, the ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ and ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ may be considered as model-based measures, because they are driven by Bayesian models. Their interpretations as differences in the ENPs of consistency and inconsistency models may be more intuitive than the ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$ from the statistical perspective; the latter is interpreted purely from the geometric perspective. For example, suppose a simple network contains three treatments A, B, and C, and 10 studies directly compare each pair of treatments. If only one three-arm study of A vs. B vs. C is added to this network, its impact on the ICDF is expected to be small. However, if 100 three-arm studies are added, their intrinsically consistent evidence would dominate the network and the ICDF would decrease. Therefore, it may be more sensible to use the model-based, rather than the geometry-based, measures of ICDF to make a tradeoff between the two- and multi-arm studies.

The data analyses indicated that the ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{F}\mathrm{E}}$ was slightly less than 0 in some NMAs due to Monte Carlo errors. It is expected to be nonnegative in theory, because the inconsistency FE model should contain more effective parameters than the consistency FE model. On the other hand, the ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ was noticeably negative in a few NMAs; this seems counterintuitive as the inconsistency model appears to have more parameters than the consistency model. Nevertheless, this intuition is based on the conventional counting of parameters in a model, rather than the ENP used for calculating the ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$. Under the RE setting, the consistency and inconsistency models may produce fairly different estimates of heterogeneity variances, which have great impact on the ENPs. The ENP of the inconsistency model is not necessarily larger than that of the consistency model, possibly yielding a negative value of ICDF. Indeed, the ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{R}\mathrm{E}}$ is not proposed in an effort to mimic the ${\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{F}}^{\mathrm{L}\mathrm{A}}$; it aims to provide new insights for understanding the evidence inconsistency under the RE setting. We will further explore the properties of these ICDF measures in future studies.