Abstract
Current methods for comparing single-cell RNA sequencing datasets collected in multiple conditions focus on discrete regions of the transcriptional state space, such as clusters of cells. Here we quantify the effects of perturbations at the single-cell level using a continuous measure of the effect of a perturbation across the transcriptomic space. We describe this space as a manifold and develop a relative likelihood estimate of observing each cell in each of the experimental conditions using graph signal processing. This likelihood estimate can be used to identify cell populations specifically affected by a perturbation. We also develop vertex frequency clustering to extract populations of affected cells at the level of granularity that matches the perturbation response. The accuracy of our algorithm at identifying clusters of cells that are enriched or depleted in each condition is, on average, 57% higher than the next-best-performing algorithm tested. Gene signatures derived from these clusters are more accurate than those of six alternative algorithms in ground truth comparisons.
As single-cell RNA sequencing (scRNA-seq) has become more accessible, the design of single-cell experiments has become increasingly complex. Researchers regularly use scRNA-seq to quantify the effect of a drug, gene knockout or other experimental perturbation on a biological system. However, quantifying the differences between single-cell datasets collected from multiple experimental conditions remains an analytical challenge1. This task is hindered by biological heterogeneity, technical noise and uneven exposure to a perturbation. Furthermore, each single-cell dataset comprises several intrinsic structures of heterogeneous cells, and the effect of the treatment condition could be diffuse across all cells or isolated to particular populations. To address this, we developed a method that quantifies the probability that each cell state would be observed in a given sample condition.
Our goal is to quantify the effect of an experimental perturbation on every cell observed in matched treatment and control scRNA-seq samples of the same biological system. We begin by modeling the cellular transcriptomic state space as a smooth, low-dimensional manifold or set of manifolds. This approach has been previously applied to characterize cellular heterogeneity and dynamic biological processes in single-cell data2–8. We then define and calculate a sample-associated density estimate, which quantifies the density of each sample over the manifold of cell states. We then consider differences in the sample-associated density estimates for each cell to calculate a sample-associated relative likelihood, which quantifies the effect of an experimental perturbation as the likelihood of observing each cell in each experimental condition (Fig. 1).
Fig. 1 |. Illustrative description of perturbation analysis using MELD and VFC.
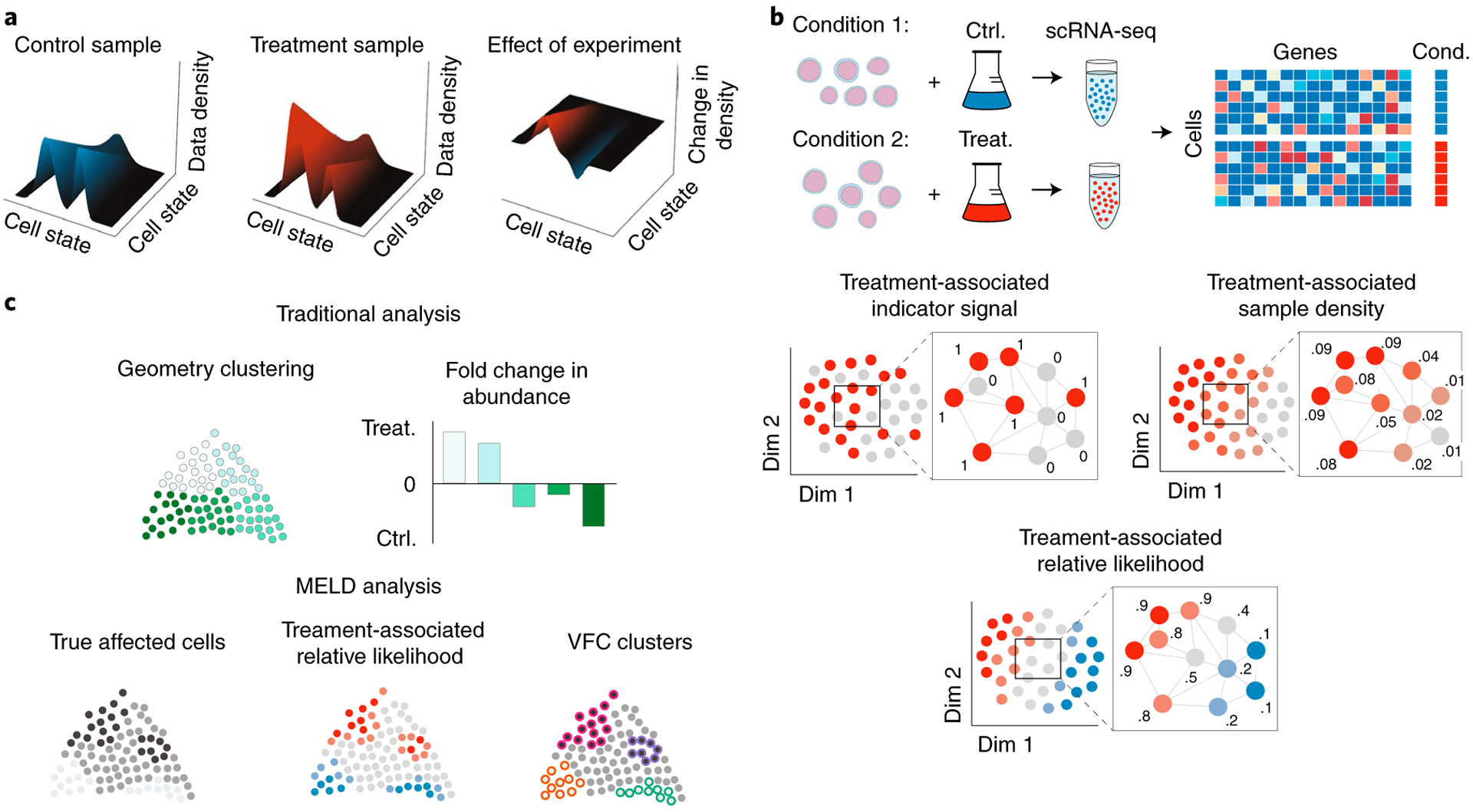
a, To quantify the effect of an experiment, we model single-cell experiments as samples from a probability density function (pdf) over the underlying transcriptomic cell state space manifold. The pdf for the control sample is the frequency with which cell states are observed in the control sample compared to the overall frequency of the cell state in both samples combined. In this context, the effect of an experimental perturbation is to alter this probability density and, thus, the data density in the treatment sample relative to the control. Therefore, the effect of an experimental perturbation can be quantified as the change in the probability density in the experiment condition relative to the control. b, The sample-associated relative likelihood quantifies this effect by computing a kernel density estimate (KDE) over the cell similarity graph using graph signals representing indicator vectors for each sample. The sample-associated relative likelihood indicates the likelihood that a particular cell is from the treatment or control conditions. c, In traditional analysis of scRNA-seq datasets, the clusters are based solely on the data geometry, and changes in abundance between conditions might not align with the true affected populations. Using the sample-associated relative likelihood and VFC, we can identify the correct cluster resolution for downstream analysis.
Almost all previous work quantifying differences between single-cell datasets relies on discrete partitioning of the data before downstream analysis9–16. First, datasets are merged, applying either batch normalization15,16 or a simple concatenation of data matrices9–14. Next, clusters are identified by grouping either sets of cells or modules of genes. Finally, within each cluster, the cells from each condition are used to calculate statistical measures, such as fold change between samples. Even recently described methods for identifying cell composition changes between scRNA-seq datasets such as MILO17 and scCODA18 limit the resolution of their analysis to graph neighborhoods or discrete cluster labels, respectively. However, reducing experimental analysis to the level of clusters sacrifices the power of single-cell data. We demonstrate cases where subsets of a cluster exhibit divergent responses to a perturbation that were missed in published analysis that was limited to clusters derived using data geometry alone. Instead of quantifying the effect of a perturbation within clusters, we focus on the level of single cells.
In the sections that follow, we show that the sample-associated relative likelihood has useful information for the analysis of experimental conditions in scRNA-seq. First, the relative likelihoods of each condition can be used to identify the cell states most and least affected by an experimental treatment. Second, we show that the frequency composition of the sample label and the relative likelihood scores can be used as the basis for a clustering algorithm that we call vertex frequency clustering (VFC). VFC identifies populations of cells that are similarly affected (enriched, depleted or unchanged) between conditions at the level of granularity of the perturbation response. Third, we obtain gene signatures of a perturbation by performing differential expression between VFCs.
We call the algorithm to calculate the sample-associated density estimate and relative likelihood the MELD algorithm, so named for its utility in joint analysis of single-cell datasets. The MELD and VFC algorithms are provided in an open-source Python package available on GitHub at https://github.com/KrishnaswamyLab/MELD.
Results
Overview of the MELD algorithm.
We propose a framework for quantifying differences in cell states observed across single-cell samples. The power of scRNA-seq as a measure of an experimental treatment is that it provides samples of cell state at thousands to millions of points across the transcriptomic space in varying experimental conditions. Our approach is inspired by recent successes in applying manifold learning to scRNA-seq analysis19. The manifold model is a useful approximation for the transcriptomic space because biologically valid cellular states are intrinsically low dimensional with smooth transitions between similar states. In this context, our goal is to quantify the change in enrichment of cell states along the underlying cellular manifold as a result of an experimental treatment (Fig. 1).
For an intuitive understanding, we first consider a simple experiment with one sample from a treatment condition and one sample from a control condition. Here, sample refers to a library of scRNA-seq profiles, and condition refers to a particular configuration of experimental variables. In this simple experiment, our goal is to calculate the relative likelihood that each cell would be observed in either the treatment or control condition over a manifold approximated from all cells from both conditions. This relative likelihood can be used as a measure of the effect of the experimental perturbation because it indicates, for each cell, how much more likely we are to observe that cell state in the treatment condition relative to the control condition (Fig. 1). We refer to this ratio as the sample-associated relative likelihood. The steps to calculate the sample-associated relative likelihood are given in Algorithm 1, and a visual depiction can be found in Suppplementary Fig. 1.
As has been done previously, we first approximate the cellular manifold by constructing an affinity graph between cells from all samples2–8. In this graph, each node corresponds to a cell, and the edges between nodes describe the transcriptional similarity between the cells. We then estimate the density of each sample over the graph using graph signal processing (GSP)20. A graph signal is any function that has a defined value for each node in a graph. Here, we use labels indicating the sample origin of each cell to develop a collection of one-hot indicator signals over the graph, with one signal per sample. Each indicator signal has value 1 associated with each cell from the corresponding sample and value 0 elsewhere. In a simple two-sample experiment, the sample indicator signals would comprise two one-hot signals—one for the control sample and one for the treatment sample. These one-hot signals are column-wise L1 normalized to account for different numbers of cells sequenced in each sample. After normalization, each indicator signal represents an empirical probability density over the graph for the corresponding sample. We next use these normalized indicator signals to calculate a kernel density estimate (KDE) of each sample over the graph.
Algorithm 1. The MELD algorithm.
Input:
Dataset X = {x1, x2, …, xn}, ; Condition labels y s.t. yi indicates the condition in which observation xi was sampled.
Output:
Sample-associated relative likelihood where d is the number of unique conditions in y.
Build graph G = {V, E} by applying anisotropic or other kernel function on X;
Instantiate one-hot Indicator Y, with one column for each unique condition in y;
Column-wise L1 normalize Y to yield Ynorm;
Apply manifold heat filter over (G, Ynorm) to calculate Ỹ, the KDE of the data in each condition, also referred to as the sample-associated density estimates;
Row-wise L1 normalize Ỹ to yield Ỹnorm also referred to as the sample-associated relative likelihoods. If the dataset comprises multiple experimental replicates, L1 normalization is applied to each replicate independently.
Calculating sample-associated density estimates.
A popular non-parametric approach to estimating data density is using a KDE, which relies on an affinity kernel function. To estimate the density of single-cell samples over a graph, we turn to the heat kernel. This kernel uses diffusion to provide local adaptivity in regions of varying data density21, such as is observed in single-cell data. Here, we extend this kernel as a low-pass filter over a graph to estimate the density of a sample represented by the sample indicator signals defined above. To begin, we take the Gaussian KDE, which is a well-known tool for density estimation, in . We then generalize this form to smooth manifolds. The full construction of this generalization is described in detail in the Methods, and a high-level overview is provided here.
A kernel density estimator with bandwidth t > 0 and kernel function K(x, y, t) is defined as
| (1) |
where X is the observed data, x is some point in (that is, is defined as ) and is endowed with the Gaussian kernel is defined as
| (2) |
Thus, Equation (2) defines the Gaussian KDE in . However, this function relies on the Euclidean distance , which is derived from the kernel space in . Because manifolds are only locally Euclidean, we cannot apply this KDE directly to a general manifold.
To generalize the Gaussian KDE to a manifold, we need to define a kernel space (that is, the range of a kernel operator) over a manifold. In , the kernel space is often defined via infinite weighted sums of sines and cosines, also known as the Fourier series. However, this basis is not well defined for a Riemannian manifold, so we, instead, use the eigenbasis of the Laplace operator as our kernel basis. The derivation and implication of this extension is formally explored in the Methods. The key insight is that, using this kernel space, the Gaussian KDE can be defined as a filter constructed from the eigenvectors and eigenvalues of the Laplace operator on a manifold. When this manifold is approximated using a graph, we define this KDE as a graph filter over the graph Laplacian given by the following equation:
| (3) |
where t is the kernel bandwidth, is the graph Laplacian, x is the empirical density, Ψ and Λ are the eigenvectors and corresponding eigenvalues of and is the matrix exponential. This signal processing formulation can alternatively be formulated as an optimization with Tikhonov regularization, which seeks to reconstruct the original signal while penalizing differences along edges of the graph. This connection is further explored in the Methods.
To achieve an efficient implementation of the filter in Equation (3), the MELD algorithm considers the spectral representation of the sample indicator signals and uses a Chebyshev polynomial approximation22 to efficiently compute the sample-associated density estimate (Methods). The result is a highly scalable implementation. The sample-associated density estimate for two conditions can be calculated on a dataset of 50,000 cells in less than 8 min in a free Google Colaboratory notebook (freely available at colab.research.google.com; most instances provide a 4-core 2-GHz CPU and 20 GB of RAM), with more than 7 min of that time spent constructing a graph that can be reused for visualization3 or imputation4. With the sample-associated density estimates, it is now possible to identify the cells that are most and least affected by an experimental perturbation.
Using sample-associated relative likelihood to quantify differences between experimental conditions.
Each sample-associated density estimate over the graph indicates the probability of observing each cell within a given experimental sample. For example, in a healthy peripheral blood sample, we would expect high-density estimates associated with abundant blood cells, such as neutrophils and T cells, and low-density estimates associated with less abundant cell types, such as basophils and eosinophils. When considering the effect of an experimental perturbation, we are not only interested in these density estimates directly; we also want to quantify the change in density associated with a change in an experimental variable. For example, one might want to know if a drug treatment causes a change in probability of observing some kinds of blood cells in peripheral blood.
When examining the rows of the sample-associated density estimates for a single cell, the values represent the likelihood of observing that cell in each experimental condition. To quantify the change in likelihood across conditions, we apply a normalization across the likelihoods for each cell to calculate sample-associated relative likelihoods. These relative likelihoods sum to 1 for each cell and provide a basis for quantifying the change in likelihood of observing a cell in each condition. We then use these relative likelihoods to identify cell states that are enriched, depleted or unaffected by the perturbation.
The sample-associated relative likelihoods can be used to analyze scRNA-seq perturbation studies of varying experimental designs. For cases with only one experimental condition and one control condition, we typically refer only to the sample-associated relative likelihood of the treatment condition for downstream analysis. For more complicated experiments comprising replicates, we normalize matched treatment and control conditions individually and then average the relative likelihood of the each condition across replicates, as in the analysis of the zebrafish and pancreatic datasets below. With datasets comprising three or more experimental conditions, each sample-associated relative likelihood may be used individually to analyze cells that are enriched, depleted or unaffected in the corresponding condition. We expect that this flexibility will enable the use of sample-associated density estimates and relative likelihoods across a wide range of single-cell studies.
VFC identifies cell populations affected by a perturbation.
A common goal for analysis of experimental scRNA-seq data is to identify subpopulations of cells that are responsive to the experimental treatment. Existing methods cluster cells by transcriptome alone and then attempt to quantify the degree to which these clusters are differentially represented in the two conditions. However, this is problematic because the granularity, or sizes, of these clusters might not correspond to the sizes of the cell populations that respond similarly to experimental treatment. Additionally, when partitioning data along a continuum, cluster boundaries are somewhat arbitrary and might not correspond to populations with distinct differences between conditions. Our goal is to identify clusters that are not only transcriptionally similar but also respond similarly to an experimental perturbation (Fig. 2).
Fig. 2 |. Vertex frequency analysis using the sample-associated indicator signals and relative likelihood.
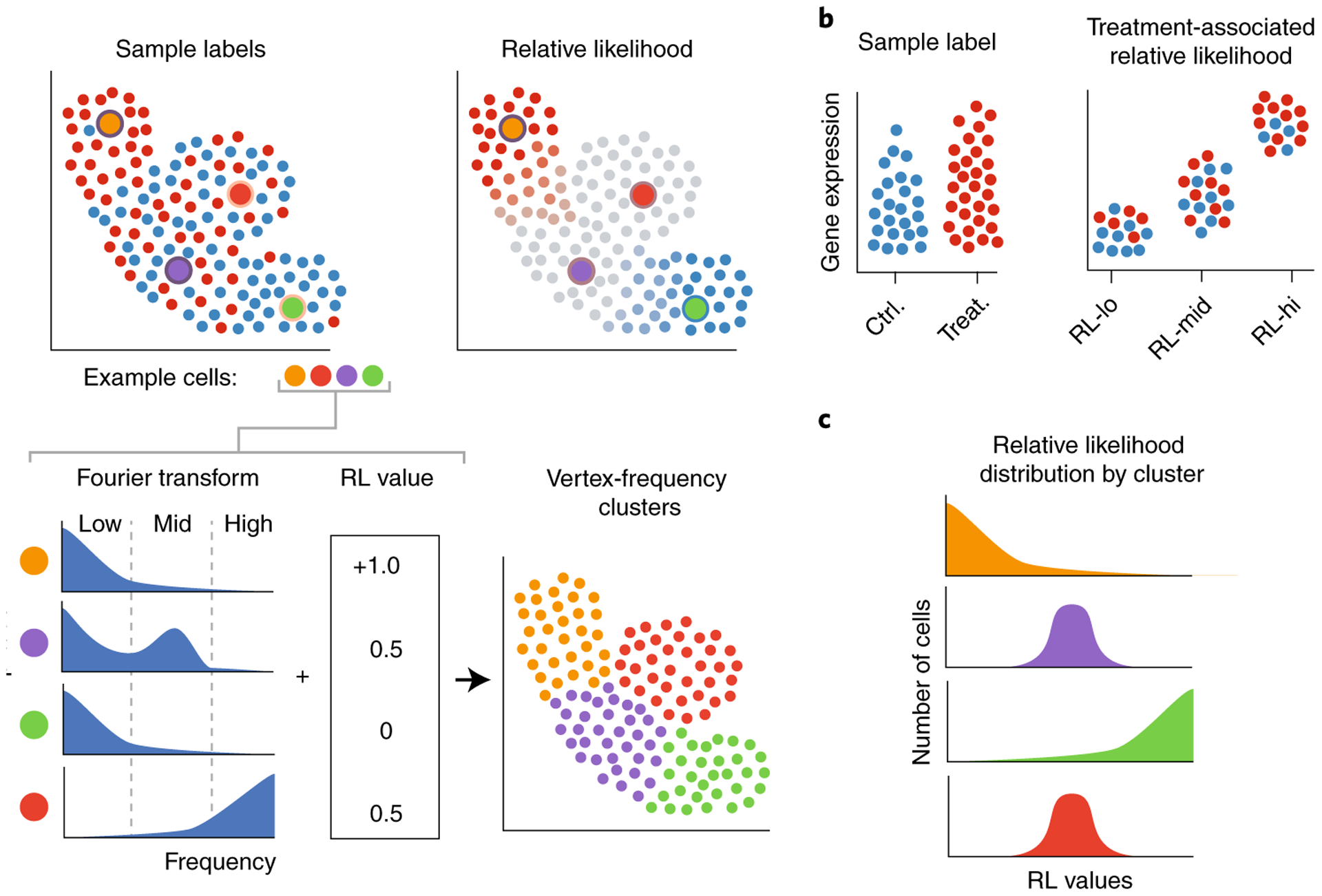
a, The WGFT of the sample-associated indicator signals and values of sample-associated relative likelihood (RL) values at four example points shows distinct patterns between a transitional (blue) and unaffected (red) cell. This information is used in spectral clustering, resulting in VFC. b, Characterizing VFCs with the highest and lowest sample-associated relative likelihood values elucidates gene expression changes associated with experimental perturbations. c, Examining the distribution of sample-associated relative likelihood scores in VFCs identifies cell populations most affected by a perturbation.
A naive approach to identify such clusters would be to simply concatenate the sample-associated relative likelihood to the gene expression data as an additional feature and cluster on these combined features. However, the magnitude of the relative likelihood does not give a complete picture of differences in response to a perturbation. For example, even in a two-sample experiment, there are multiple ways for a cell to have a sample-associated relative likelihood of 0.5. In one case, it might be that there is a continuum of cells one end of which is enriched in the treatment condition, and the other end is enriched in the control condition. In this case, transitional cells halfway through this continuum will have a sample-associated relative likelihood of 0.5 (we show an example of this in the analysis of the T cell dataset below). Another scenario that would result in a relative likelihood of 0.5 is even mixing of a population of cells between control and treatment conditions with no transition—that is, cells that are part of a non-responsive cell subtype that is unchanged between conditions (we show an example of this in the analysis of the pancreatic dataset below and Suppplementary Fig. 2). To differentiate between such scenarios, we must consider not only the magnitude of the sample-associated relative likelihood but also the frequency of the input sample indicator signals over the manifold. Indeed, in the transitional case, the input sample labels change gradually or have low frequency over the manifold, and, in the even-mixture case, they change frequently between closely connected cells or have high frequency over the manifold.
As no contemporary method is suitable for resolving these cases, we developed an algorithm that integrates gene expression, the magnitude of sample-associated relative likelihoods and the frequency response of the input sample labels over the cellular manifold (Suppplementary Fig. 2). In particular, we cluster using local frequency profiles of the sample indicator signal around each cell. This method, which we call VFC, is an adaptation of the signal-biased spectral clustering proposed in ref.23. The VFC algorithm provides a feature basis for clustering based on the spectrogram23 of the sample indicator signals, which can be thought of as a histogram of frequency components of graph signals. We observe that we can distinguish between non-responsive populations of cells with high-frequency sample indicator signal components and transitional populations with lower-frequency indicator signal components. The VFC feature basis combines this frequency information with the magnitude of the sample-associated relative likelihood and the cell similarity graph to identify phenotypically similar populations of cells with uniform response to a perturbation. The algorithm is discussed in further detail in the Methods.
With VFC, it is possible to define a new paradigm for recovering the gene signature of a perturbation. In traditional analysis, where clusters are calculating data geometry alone, gene signatures are often calculated using differential expression analysis between experimental conditions within each cluster (Suppplementary Fig. 3a). The theory of the traditional framework is that these expression differences reflect the change in cell states observed as a result of the perturbation. However, if the cluster contains multiple subpopulations that each contain different responses to the perturbation, we can first separate these populations using VFC and then compare each subpopulation individually (Suppplementary Fig. 3b). Not only does this allow for more finely resolved comparisons, we show in the following section that this approach is capable of recovering gene signatures more accurately than directly comparing two samples.
We describe a full pipeline for analysis of scRNA-seq datasets with MELD and VFC in Supplementary Note 1 and Fig. S4.
Quantitative validation of the MELD and VFC algorithms.
No previous benchmarks exist to quantify the ability of an algorithm to capture changes in density between scRNA-seq samples. To validate the sample-associated relative likelihood and VFC algorithms, we used a combination of simulated scRNA-seq data and synthetic experiments using previously published datasets. To create simulated scRNA-seq data, we used Splatter24. To ensure that the algorithms worked on real scRNA-seq datasets, we also used two previously published datasets of Jurkat T cells13 and cells from whole zebrafish embryos15. In each dataset, we created a ground truth relative likelihood distribution over all cells that determines the relative likelihood that each cell would be observed in one of two simulated conditions. In each simulation, different populations of cells of varying sizes were depleted or enriched. Cells were then randomly split into two samples according to this ground truth relative likelihood and used as input to each algorithm. More detail on the comparison experiments is provided in the Methods.
We performed three sets of quantitative comparisons. First, we calculated the degree to which the MELD algorithm captured the ground truth relative likelihood distribution in each simulation. We found that MELD outperformed other graph-smoothing algorithms by 10–52% on simulated data and 36–51% on real datasets (Fig. 3 and Suppplementary Table 1). We also determined that the MELD algorithm is robust to the number of cells captured in the experiment, with only a 10% decrease in performance when 65% of the cells in the T cell dataset were removed (Supplementary Fig. 5). We used results from these simulations to determine the optimal parameters for the MELD algorithm (Supplementary Note 3). Next, we quantified the accuracy of the VFC algorithm to identify clusters of cells that were enriched or depleted in each condition. When compared to six common clustering algorithms, including Leiden25 and CellHarmony26, VFC was the top performing algorithm on every simulation on the T cell data and best performing, on average, on the zebrafish dataset, with a 57% increase in average performance over Louvain, which was the next best algorithm (Suppplementary Figs. 6a–c and 7 and Suppplementary Table 2). Finally, we calculated how well VFC clusters could be used to calculate the gene signature of a perturbation. Gene signatures obtained using VFC were compared to signatures obtained using direct comparison of two conditions—the current standard—and those obtained using other clustering algorithms (Supplementary Fig. 6d). These results confirm that MELD and VFC outperform existing methods for analyzing multiple scRNA-seq datasets from different experimental conditions.
Fig. 3 |. Quantitative comparison of the sample-associated relative likelihood and VFC.
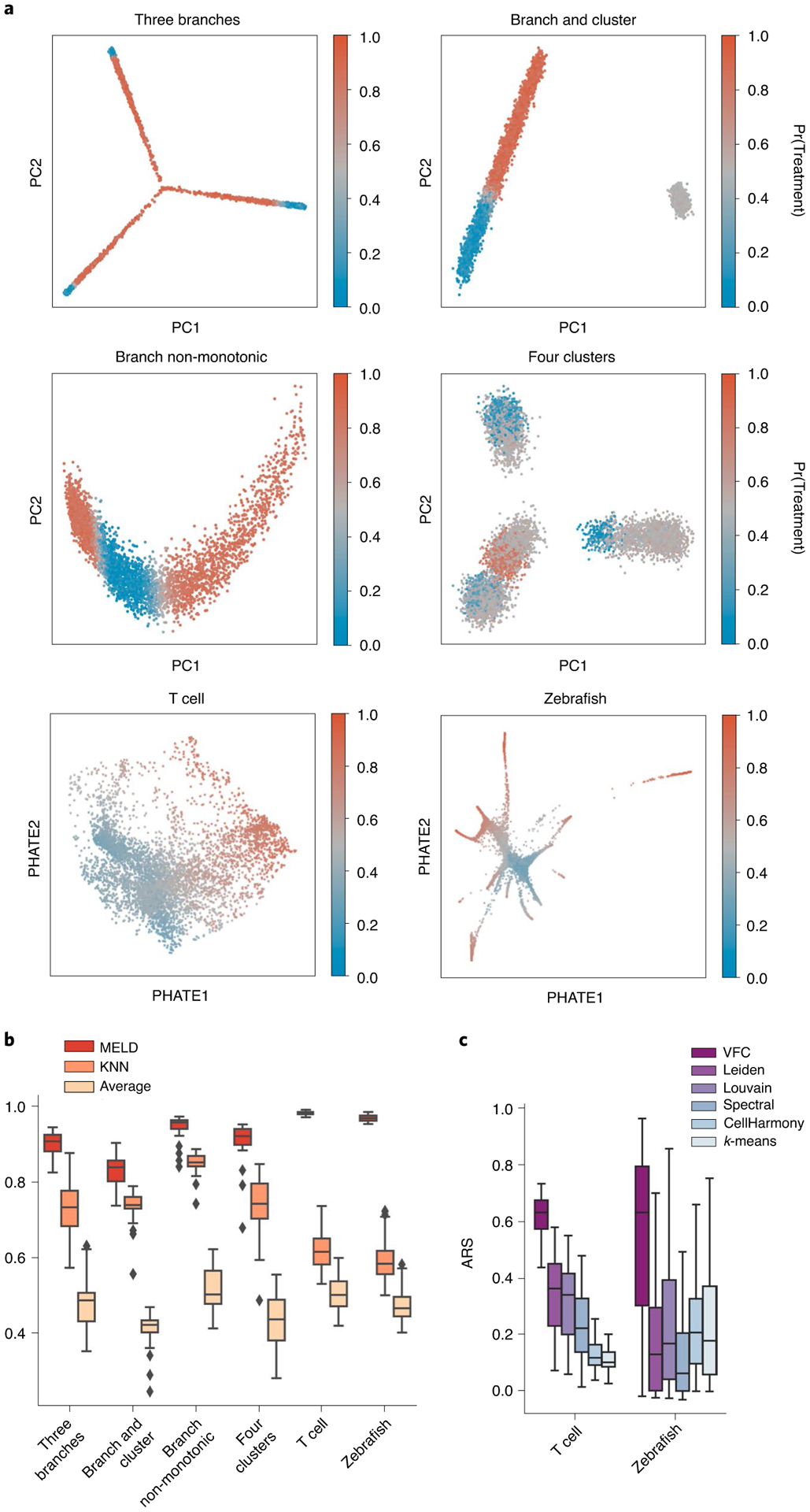
a, Single-cell datasets were generated using Splatter24 or taken from previously published experiments13,15. Ground truth sample assignment probabilities with each of two conditions were randomly generated 20 times with varying noise and regions of enrichment for the simulated data, and 100 random sample assignments were generated for the real-world datasets. Each cell is colored by the probability of being assigned to the treatment sample. b, Pearson correlation comparison of the sample-associated relative likelihood algorithm to KNN averaging of the sample labels and graph averaging of the sample labels. Higher values are better. c, Comparison of VFC to popular clustering algorithms. Adjusted Rand score (ARS) quantifies how accurately each method detects regions that were enriched, depleted or unchanged in the experimental condition relative to the control. Higher values are better.
The sample-associated relative likelihood identifies a biologically relevant signature of T cell activation.
To demonstrate the biological relevance of the MELD algorithm, we analyze Jurkat T cells cultured for 10 d with and without anti-CD3/anti-CD28 antibodies as part of a Cas9 knockout screen published in ref.13 (Fig. 4a). The goal of this experiment was to characterize the transcriptional signature of T cell receptor (TCR) activation and determine the effect of gene knockouts in the TCR pathway. First, we visualized cells using PHATE, a visualization and dimensionality reduction tool for scRNA-seq data (Fig. 4b)3. We observed a large degree of overlap in cell states between the stimulated and control conditions, as noted in the original study13.
Fig. 4 |. MELD recovers signature of TCR activation.
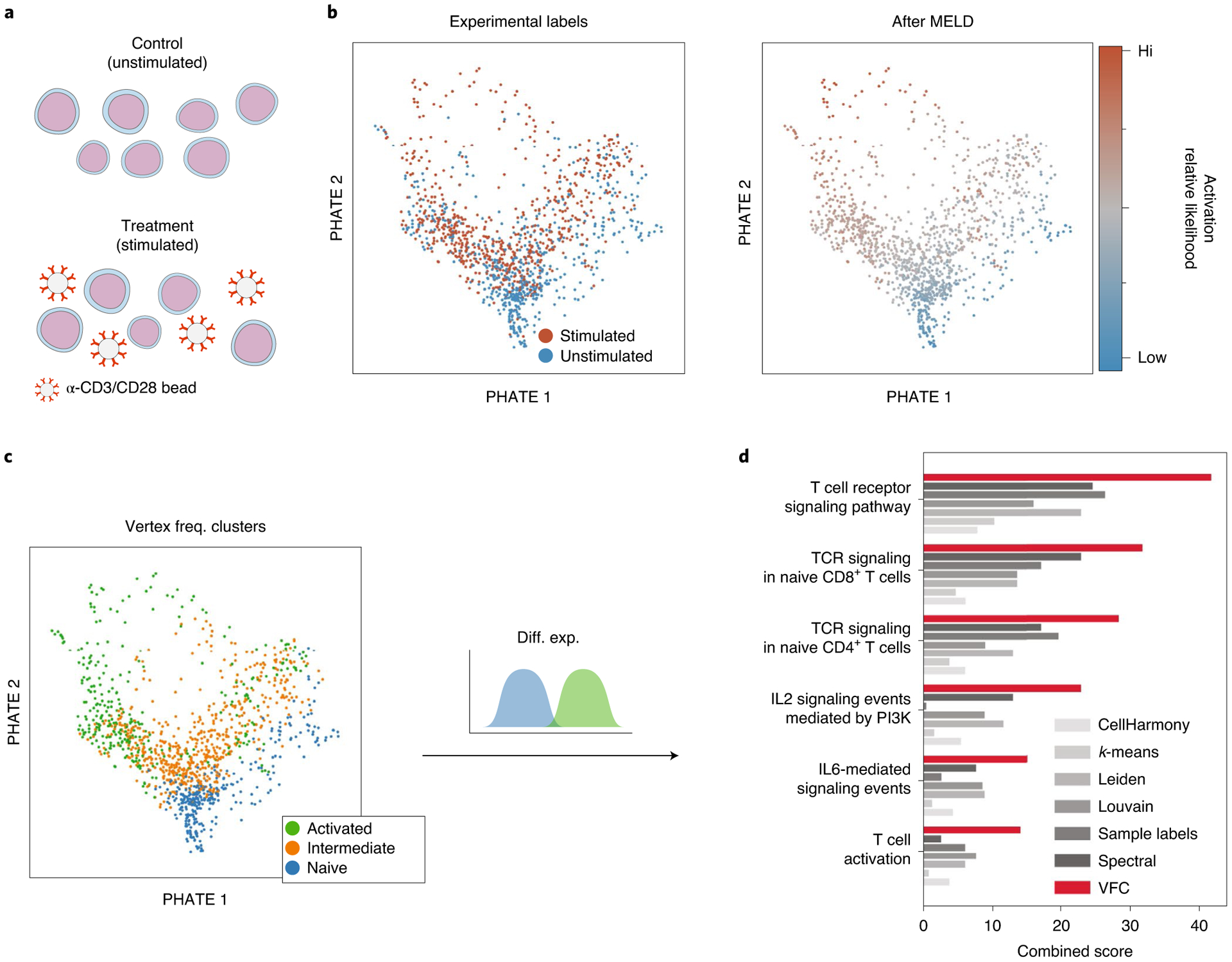
a, Jurkat T cells were stimulated with α-CD3/CD28-coated beads for 10 d before collection for scRNA-seq. b, Examining a PHATE plot, there is a large degree of overlap in cell state between experimental conditions. However, after MELD, it is clear which cell states are prototypical of each experimental condition. c, VFC identifies an activated, a naive and an intermediate population of cells. d, Signature genes identified by comparing the activated to naive cells are enriched for annotations related to TCR activation using EnrichR analysis. Combined scores for the MELD gene signature are shown in red, and scores for a gene signature obtained using the sample labels only are shown in gray. IL, interleukin.
To determine a gene signature of the TCR activation, we considered cells with no CRISPR perturbation. First, we computed sample-associated relative likelihood and VFC clusters on these samples. Then, we derived a gene signature by performing differential expression analysis between VFC clusters with the highest and lowest relative likelihood values. We identified 2,335 genes with a q value < 0.05 as measured by a rank sum test with a Benjamini–Hochberg false discovery rate correction27. We then compared this signature to those obtained using the same methods from our simulation experiments. To determine the biological relevance of these signature genes, we performed gene set enrichment analysis on both gene sets using EnrichR28. Considering the Gene Ontology (GO) terms highlighted in ref.13, we found that the MELD gene list has the highest combined score in all of the gene terms we examined (Fig. 4d). These results show that the sample-associated relative likelihood and VFC are capable of identifying a biologically relevant dimension of T cell activation at the resolution of single cells. Furthermore, the gene signature identified using the MELD and VFC outperformed standard differential expression analyses to identify the signature of a real-world experimental perturbation.
Finally, to quantitatively rank the effect of each Cas9 gene knockout on TCR activation, we examined the distribution of sample-associated relative likelihood values for all stimulated cells transfected with guide RNAs (gRNAs) targeting a given gene (Suppplementary Fig. 8). We observed a large variation in the effect of each gene knockout consistent with the published results in ref.13. Encouragingly, our results agree with the bulk RNA sequencing validation experiment in ref.13, showing strongest depletion of TCR response with knockout of kinases LCK and ZAP70 and adaptor protein LAT. We also found a slight increase in relative likelihood of the stimulation condition in cells in which negative regulators of TCR activation are knocked out, including PTPN6, PTPN11 and EGR3. Together, these results show that the MELD and VFC algorithms are suitable for characterizing a biological process, such as TCR activation in the context of a complex Cas9 knockout screen.
VFC improves characterization of subpopulation response to chordin loss of function.
To demonstrate the utility of sample-associated relative likelihood analysis applied to datasets composed of multiple cell types, we analyzed a chordin loss-of-function experiment in zebrafish using CRISPR–Cas9 (Suppplementary Fig. 9)15. In the experiment published in ref.15, zebrafish embryos were injected at the one-cell stage with Cas9 and gRNAs targeting either chordin (chd), a BMP antagonist required for developmental patterning, or tyrosinase (tyr), a control gene. Embryos were collected for scRNA-seq at 14–16 h after fertilization. We expect incomplete penetrance of the perturbation in this dataset because of the mosaic nature of Cas9 mutagenesis29.
First, we calculate the sample-associated relative likelihood between the chd and tyr conditions. Because the experiment was performed in triplicate with three paired chd and tyr samples, we first calculated the sample-associated density estimates for each of the six samples. We then normalized the density estimated across the paired chd and tyr conditions. Finally, we averaged the replicate-specific relative likelihoods of the chd condition for downstream analysis. We refer to this averaged likelihood simply as the chordin-relative likelihood (Suppplementary Fig. 9).
To characterize the effect of mutagenesis on various cell populations, we first examined the distribution of chordin-relative likelihood values across the 28 cell state clusters generated in ref.15 (Fig. 5b). We found that, overall, the most enriched clusters contain mesodermal cells, and the most depleted clusters contain dorsally derived neural cells matching the ventralization phenotype previously reported with chd loss of function30–32. However, we observed that several clusters had a wide range of chordin-relative likelihood values, suggesting that there are cells in these clusters with different perturbation responses. Using VFC analysis, we found that several of these clusters contained biologically distinct subpopulations of cells with divergent responses to chd knockout.
Fig. 5 |. Characterizing chordin Cas9 mutagenesis with MELD.

a, PHATE shows a high degree of overlap of sample labels across cell types. Applying MELD to the mutagenesis vector reveals regions of cell states enriched in the chd or tyr conditions. b, Using published cluster assignments, we show that the chd-associated relative likelihood quantifies the effect of the experimental perturbation on each cell, providing more information than calculating fold change in the number of cells between conditions in each cluster (gray dot), as was done in the published analysis. The color of each point corresponds to the sample labels in a. Generally, average relative likelihood within each cluster aligns with the fold change metric. However, we can identify clusters, such as the TPM or TSC, with large ranges of relative likelihoods, indicating non-uniform response to the perturbation. c, Visualizing the TPM cluster using PHATE, we observe several cell states with mostly non-overlapping relative likelihood values. d, VFC identifies four cell types in the TPM. e, We see that the range of relative likelihood values in the TPM cluster is due to subpopulations with divergent responses to the chd perturbation. f, We observe that changes in gene expression between the tyr (blue) and chd (red) conditions is driven mostly by changes in abundance of subpopulations with the TPM cluster. PSM, presomitic mesoderm.
An advantage of using MELD and VFC is the ability to characterize the response to the perturbation at the resolution corresponding to the perturbation response (Fig. 2c). We infer that the resolution of the published clusters is too coarse because the distribution of chordin-relative likelihood values is very large for several of the clusters. For example, the chordin-relative likelihoods within the tailbud, presomitic mesoderm (TPM) range from 0.29 to 0.94, indicating that some cells are strongly enriched, whereas others are depleted. To disentangle these effects, we performed VFC subclustering for all clusters using the strategy proposed in Supplementary Note 1. We found that 12 of the 28 published clusters warranted further subclustering with VFC, resulting in a total of 50 final cluster labels (Suppplementary Fig. 10j). To determine the biological relevance of the VFC clusters, we manually annotated each of the three largest clusters subdivided by VFC, revealing previously unreported effects of chd loss of function within this dataset. A full exploration can be found in Supplementary Note 2, with the results of TPM cluster shown in Fig. 5c–f.
Identifying the effect of interferon-gamma stimulation on pancreatic islet cells.
To determine the ability of the MELD and VFC to uncover biological insights, we generated and characterized a dataset of human pancreatic islet cells cultured for 24 h with and without interferon-gamma (IFN-γ), a system with considerable clinical relevance to auto-immune diseases of the pancreas, such as type I diabetes mellitus and islet allograft rejection33. Previous studies characterized the effect of these cytokines on pancreatic beta cells using bulk RNA sequencing34, but no studies have addressed this system at single-cell resolution.
To better understand the effect of immune cytokines on islet cells, we cultured islet cells from three donors for 24 h with and without IFN-γ and collected cells for scRNA-seq. After filtering, we obtained 5,708 cells for further analysis. Examining the expression of marker genes for major cell types of the pancreas, we observed a noticeable batch effect associated with the donor ID, driven by the maximum expression of glucagon, insulin and somatostatin in alpha, beta and delta cells, respectively (Supplementary Fig. 11a). To correct for this difference while preserving the relevant differences between donors, we applied the mutual nearest neighbors (MNN) kernel correction described in the Methods. Note that, here, the MNN correction was only applied across donors, not across the IFN-γ treatment. We developed guidelines for applying batch correction before running MELD, as shown in Supplementary Note 3.
To quantify the effect of IFN-γ treatment across these cell types, we calculated the sample-associated relative likelihood of IFN-γ stimulation using the same strategy to handle matched replicates as was done for the zebrafish data (Fig. 6a). We then used established marker genes of islet cells35 to identify three major populations of cells corresponding to alpha, beta and delta cells (Suppplementary Figs. 6a,b and 11b). We next applied VFC to each of the three endocrine cell types and identified a total of nine clusters. Notably, we found two clusters of beta cells with intermediate IFN-γ relative likelihood values. These clusters are cleanly separated on the PHATE plot of all islet cells (Fig. 6a), and, together, the beta cells represent the largest range of IFN-γ relative likelihood scores in the dataset.
Fig. 6 |. MELD characterizes the response to IFN-γ in pancreatic islet cells.
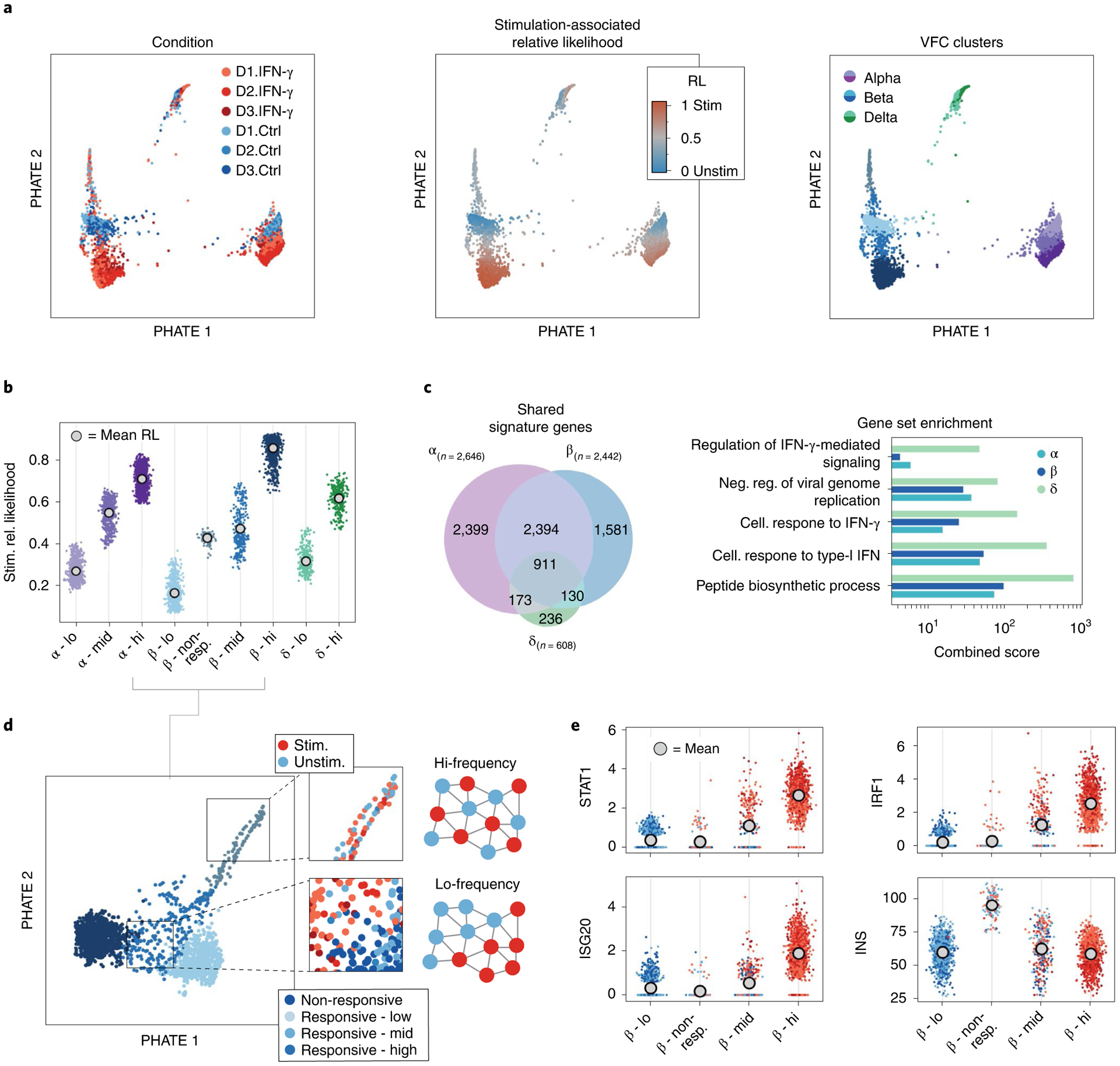
a, PHATE visualization of pancreatic islet cells cultured for 24 h with or without IFN-γ. VFC identifies nine clusters corresponding to alpha, beta and delta cells. b, Examining the stimulation-associated relative likelihood in each cluster, we observe that beta cells have a wider range of responses than alpha or delta cells. c, We identify the signature of IFN-γ stimulation by calculating differential expression between the VFC clusters with the highest and lowest stimulation likelihood values for each cell type. We find a high degree of overlap of the significantly differentially expressed genes between alpha and beta cells. d, Results of gene set enrichment analysis for signature genes in each cell type. Beta cells have the strongest enrichment for IFN response pathway genes. e, Examining the four beta cell clusters more closely, we observe two populations with intermediate relative likelihood values. These populations are differentiated by the structure of the sample label in each cluster (outset). In the non-responsive cluster, the sample label has very high frequency, unlike the low-frequency pattern in the transitional mid-responsive cluster. f, We find that the non-responsive cluster has low expression of IFN-γ-regulated genes, such as STAT1, despite containing roughly equal numbers of unstimulated and stimulated cells. This cluster is marked by approximately 40% higher expression of insulin. RL, relative likelihood.
To further inspect these beta cell clusters, we consider a separate PHATE plot of the cells in the four beta cell clusters (Fig. 6e). Examining the distribution of input sample signals values in these intermediate cell types, we find that one cluster, which we label as non-responsive, exhibits high-frequency input sample signals indicative of a population of cells that does not respond to an experimental treatment. The responsive–mid cluster matches our characterization of a transitional population with a structured distribution of input sample signals. Supporting this characterization, we find a lack of upregulation in IFN-γ-regulated genes, such as STAT1, in the non-responsive cluster, similarly to the cluster of beta cells with the lowest IFN-γ relative likelihood values (Fig. 6f).
To understand the difference between the non-responsive beta cells and the responsive populations, we calculated differential expression of genes in the non-responsive clusters and all others. The gene with the greatest difference in expression was insulin, the major hormone produced by beta cells, which is approximately 2.5-fold increased in the non-responsive cells (Fig. 6f). This cluster of cells bears resemblance to a recently described ‘extreme’ population of beta cells that exhibit elevated insulin messenger RNA (mRNA) levels and are found to be more abundant in diabetic mice36,37. That these cells appear non-responsive to IFN-γ stimulation and exhibit extreme expression of insulin suggests that the presence of extreme high insulin in a beta cell before IFN-γ exposure might inhibit the IFN-γ response pathway through an unknown mechanism.
We next characterized the gene expression signature of IFN-γ treatment across all three endocrine cell types (Fig. 6c,d). Using a rank sum test to identify genes that change the most between the clusters with highest and lowest IFN-γ relative likelihood values within each endocrine population, we identified 911 genes differentially expressed in all three cell types. This consensus signature includes activation of genes in the JAK-STAT pathway, including STAT1 and IRF1 (ref.38), and in the IFN-mediated antiviral response, including MX1, OAS3, ISG20 and RSAD2 (refs.39–41). The activation of both of these pathways was previously reported in beta cells in response to IFN-γ42,43. To confirm the validity of our gene signatures, we use EnrichR28 to perform gene set enrichment analysis on the signature genes and found strong enrichment for terms associated with IFN signaling pathways (Supplementary Fig. 11d). From these results, we conclude that, although IFN-γ leads to upregulation of the canonical signaling pathways in all three cell types, the response to stimulation in delta cells is subtly different to that of alpha or beta cells.
Here, we applied MELD analysis to identify the signature of IFN-γ stimulation across alpha, beta and delta cells, and we identified a population of beta cells with high insulin expression that appears unaffected by IFN-γ stimulation. Together, these results demonstrate the utility of MELD analysis to reveal biological insights in a clinically relevant biological experiment.
Analysis of donor-specific composition.
Although most of the analysis here focuses on two-condition experiments, we show that it is possible to use the sample-associated relative likelihood to quantify the differences between more than two conditions. In the islet dataset, we have samples of treatment and control scRNA-seq data from three different donors. To quantify the differences in cell profiles between donors, we first created a one-hot vector for each donor label and normalized across all three smoothed vectors. This produces a measure of how likely each transcriptional profile is to be observed in donor 1, 2 or 3. We then analyzed each of these signals for each cluster identified during the IFN-γ stimulation analysis (Suppplementary Fig. 12). We found that all of the alpha cell and delta cell clusters are depleted in donor 3, and the non-responsive beta cell cluster is enriched primarily in donor 1. Furthermore, the most highly activated alpha cell cluster is enriched in donor 2. As with the sample-associated relative likelihood derived for the IFN-γ response, it is also possible to identify donor-specific changes in gene expression or clusters of cells differentially abundant between each donor. We propose that this strategy could be used to extend MELD analysis to experiments with multiple categorical experimental conditions, such as data collected from different tissues or stimulus conditions.
Discussion
When performing multiple scRNA-seq experiments in various experimental and control conditions, researchers often seek to characterize the cell types or sets of genes that change from one condition to another. However, quantifying these differences is challenging owing to the subtlety of most biological effects relative to the biological and technical noise inherent to single-cell data. To overcome this hurdle, we designed the MELD and VFC algorithms to quantify compositional differences between samples. The key innovation in the sample-associated relative likelihood algorithm is quantifying the effect of a perturbation at the resolution of single cells using theory from manifold learning.
We have shown that our analysis framework improves over the current best practice of clustering cells based on gene expression and calculating differential abundance and differential expression within clusters. Clustering before quantifying compositional differences can fail to identify the divergent responses of subpopulations of cells within a cluster. Using the sample labels and sample-associated relative likelihood, we apply VFC to derive clusters of cells to identify cells that are most enriched in either condition and cells that are unaffected by an experimental perturbation. We show that gene signatures extracted using these clusters outperform those derived from direct comparison of two samples or traditional clustering approaches.
We demonstrated the application of MELD analysis on single-cell datasets from three different biological systems and experimental designs. We provided a framework for handling matched treatment and control replicates and guidance on analysis of complex experimental designs with more than two conditions and in the context of a single-cell Cas9 knockout screen. In our analysis of the zebrafish dataset, we showed that the published clusters contained biologically relevant subpopulations of cells with divergent responses to the experimental perturbation. We also described a previously unpublished dataset of pancreatic islet cells stimulated with IFN-γ and characterized a previously unreported subpopulation of beta cells that appeared unresponsive to stimulation. We related this to emerging research describing a beta cell subtype marked by high insulin mRNA expression and unique biological responses.
We anticipate MELD to have widespread use in many contexts because experimental labels can arise in many contexts. As we showed, if we have sets of single-cell data from healthy individuals versus sick individuals, the sample-associated relative likelihood could indicate cell types specific to disease. This framework could potentially be extended to patient-level measurements where patients’ phenotypes, as measured with clinical variables and laboratory values, can be associated with enriched states in disease or treatment conditions. Indeed, MELD has already seen use in several contexts44–48.
Methods
In this section, we will provide details about our computational methods for computing the sample-associated density estimate and relative likelihood as well as extracting information from the sample label and sample-associated relative likelihood by way of a method we call VFC. We will outline the mathematical foundations for each algorithm, explain how they relate to previous works in manifold learning and GSP and provide details of the implementations of each algorithm.
Computation of the sample-associated density estimate.
Computing the sample-associated density estimate and relative likelihood involves the following steps, each of which we will describe in detail.
A cell similarity graph is built over the combined data from all samples where each node or vertex in the graph is a cell and edges in the graph connect cells with similar gene expression values.
The sample label for each cell is used to create the sample-associated indicator signal.
Each indicator signal is then smoothed over the graph to estimate the density of each sample using the manifold heat filter.
Sample-associated density estimates for paired treatment and control samples are normalized to calculate the sample-associated relative likelihood.
Graph construction.
The first step in the MELD algorithm is to create a cell similarity graph. In scRNA-seq, each cell is measured as a vector of gene expression counts measured as unique molecules of mRNA. Following best practices for scRNA-seq analysis1, we normalize these counts by the total number of unique molecular identifiers (UMIs) per cell to give relative abundance of each gene and apply a square root transform. Next, we compute the similarity of all pairs of cells by using their Euclidean distances as an input to a kernel function. More formally, we compute a similarity matrix W such that each entry Wij encodes the similarity between cell gene expression vectors xi and xj from the dataset X.
In our implementation, we use α-decaying kernel proposed in ref.3 because, in practice, it provides an effective graph construction for scRNA-seq analysis. However, in cases where batch, density and technical artifacts confound graph construction, we also use an MNN kernel, as proposed in ref.49.
The α-decaying kernel3 is defined as
| (4) |
where x, y are data points, εk(x), εk(y) are the distance from x, y to their k-th nearest neighbors, respectively, and α is a parameter that controls the decay rate (that is, heaviness of the tails) of the kernel. This construction generalizes the popular Gaussian kernel, which is typically used in manifold learning but also has some disadvantages alleviated by the α-decaying kernel, as explained in ref.3.
The similarity matrix effectively defines a weighted and fully connected graph between cells such that every two cells are connected and the connection between cells x and y is given by K(x, y). To allow for computational efficiency, we sparsify the graph by setting very small edge weights to 0.
Although the kernel in Equation (4) provides an effective way of capturing neighborhood structure in data, it is susceptible to batch effects. For example, when data are collected from multiple patients, subjects or environments (generally referred to as ‘batches’), such batch effects can cause affinities within each batch and are often much higher than between batches, thus creating separation between batches rather than following the underlying biological state. To alleviate such effects, we adjust the kernel construction using an approach inspired by recent work in ref.49 on the MNN kernel. We extend the standard MNN approach, which was previously applied to the KNN kernel, to the α-decay kernel as follows. First, within each batch, the affinities are computed using Equation (4). Then, across batches, we compute slightly modified affinities as
where are now computed via the k-th nearest neighbor of x in the batch containing y (and vice versa for ). Next, a rescaling factor γxy is computed such that
for every x and y, where β > 0 is a user-configurable parameter. This factor gives rise to the rescaled kernel
Finally, the full symmetric kernel is then computed as
and used to set the weight matrix for the constructed graph over the data. Note that this construction is a well-defined extension of Equation (4), as it reduces back to that kernel when only a single batch exists in the data.
We also perform an anisotropic density normalization transformation so that the kernel reflects the underlying geometry normalized by density, as in ref.50. The density-normalized kernel deivides out by density, estimated by the sum of outgoing edge weights for each node as follows:
where
We use this density-normalized kernel in all experiments. When the data are uniformly sampled from the manifold, then the density around each point is constant, and this normalization has no effect. When the density is non-uniformly sampled from the manifold, this allows an estimation of the underlying geometry unbiased by density. This is especially important when performing density estimation from empirical distributions with different underlying densities. By normalizing by density, we allow for construction of the manifold geometry from multiple differently distributed samples and individual density estimation for each of these densities on the same support. This normalization is further discussed below in the discussion of the relation between MELD and Gaussian KDE.
Estimating sample-associated density and relative likelihood on a graph.
Density estimation is difficult in high dimensions because the number of samples needed to accurately reconstruct density with bounded error is exponential in the number of dimensions. Because general high-dimensional density estimation is an intrinsically difficult problem, additional assumptions must be made. A common assumption is that the data exist on a manifold of low intrinsic dimensionality in ambient space. Under this assumption, several works on graphs addressed density estimation limited to the support of the graph nodes51–55. Instead of estimating kernel density or histograms in D dimensions where D could be large, these methods render the data as a graph, and density is estimated at each point on the graph (each data point) as some variant counting the number of points, which lie within a radius of each point on the graph.
The MELD algorithm also estimates density of a signal on a graph. In the following sections, we use a generalization of the standard heat kernel on the graph to estimate signal density. We then draw analogs between the resulting sample-associated density estimate and Gaussian kernel density estimation on the manifold, showing that our density estimate with a specific parameter set is equivalent to the Gaussian density estimate on the graph.
GSP.
The MELD algorithm leverages recent advances in GSP20, which aim to extend traditional signal processing tools from the spatiotemporal domain to the graph domain. Such extensions include, for example, wavelet transforms56, windowed Fourier transforms23 and uncertainty principles57. All of these extensions rely heavily on the fundamental analogy between classical Fourier transform and graph Fourier transform (GFT) (described in the next section) derived from eigenfunctions of the graph Laplacian, which are defined as
| (5) |
where D is the degree matrix, which is a diagonal matrix with Dii = d(i) = ΣjWij containing the degrees of the vertices of the graph defined by W.
The GFT.
One of the fundamental tools in traditional signal processing is the Fourier transform, which extracts the frequency content of spatiotemporal signals58. Frequency information enables various insights into important characteristics of analyzed signals, such as pitch in audio signals or edges and textures in images. Common to all of these is the relation between frequency and notions of smoothness. Intuitively, a function is smooth if one is unlikely to encounter a dramatic change in value across neighboring points. A simple way to imagine this is to look at the zero-crossings of a function. Consider, for example, sine waves sin ax of various frequencies a = 2k, . For k = 0, the wave crosses the x axis (a zero-crossing) when x = π. When we double the frequency at k = 1, our wave is now twice as likely to cross the zero and is, thus, less smooth than k = 0. This simple zero-crossing intuition for smoothness is relatively powerful, as we will see shortly.
Next, we show that our notions of smoothness and frequency are readily applicable to data that are not regularly structured, such as single-cell data. The graph Laplacian can be considered as a graph analog of the Laplace (second derivative) operator ∇2 from multivariate calculus. This relation can be verified by deriving the graph Laplacian from first principles.
For a graph on N vertices, its graph Laplacian and an arbitrary graph signal , we use Equation (5) to write
| (6) |
As the graph Laplacian is a weighted sum of differences of a function around a vertex, we may interpret it analogously to its continuous counterpart as the curvature of a graph signal. Another common interpretation made explicit by the derivation in Equation (6) is that measures the local variation of a function at vertex i.
Local variation naturally leads to the notion of total variation,
which is effectively a sum of all local variations. TV(f) describes the global smoothness of the graph signal f. In this setting, the more smooth a function is, the lower the value of the variation. This quantity is more fundamentally known as the Laplacian quadratic form,
| (7) |
Thus, the graph Laplacian can be used as an operator and in a quadratic form to measure the smoothness of a function defined over a graph. One effective tool for analyzing such operators is to examine their eigensystems. In our case, we consider the eigendecomposition , with eigenvalues. (Note that, in this discussion, we abuse notation by treating Λ as an ordered set of Laplacian eigenvalues and as the diagonal matrix with entries from the elements of this set. Similarly, Ψ is both the set of column eigenvectors as well as the N × N matrix [ψ1ψ2 · · · ψN] with eigenvector as a column.) Λ: = {0 = λ1≤λ2≤ ⋯ ≤λN} and corresponding eigenvectors . As the Laplacian is a square and symmetric matrix, the spectral theorem tells us that its eigenvectors in Ψ form an orthonormal basis for . Furthermore, the Courant–Fischer theorem establishes that the eigenvalues in Λ are local minima of when fTf = 1 and f ∈ U as dim(U) = i = 1, 2, …, N. At each eigenvalue λi, this function has f = ψi. In summary, the eigenvectors of the graph Laplacian (1) are an orthonormal basis and (2) minimize the Laplacian quadratic form for a given dimension.
Henceforth, we use the term ‘graph Fourier basis’ interchangeably with graph Laplacian eigenvectors, as this basis can be thought of as an extension of the classical Fourier modes to irregular domains20. In particular, the ring graph eigenbasis is composed of sinusoidal eigenvectors, as they converge to discrete Fourier modes in one dimension. The graph Fourier basis, thus, allows one to define the GFT by direct analogy to the classical Fourier transform.
The GFT of a signal f is given by , which can also be written as the matrix–vector product
| (8) |
As this transformation is unitary, the inverse graph Fourier transform (IGFT) is . Although the graph setting presents a new set of challenges for signal processing, many classical signal processing notions, such as filterbanks and wavelets, have been extended to graphs using the GFT. We use the GFT to process, analyze and cluster experimental signals from single-cell data using a novel graph filter construction and a new harmonic clustering method.
The manifold heat filter.
In the MELD algorithm, we seek to estimate the change in sample density between experimental labels along a manifold represented by a cell similarity graph. To estimate sample density along the graph, we employ a novel graph filter construction, which we explain in the following sections. To begin, we review the notion of filtering with focus on graphs and demonstrate manifold heat filter in a low-pass setting. Next, we demonstrate the expanded version of the manifold heat filter and provide an analysis of its parameters. Finally, we provide a simple solution to the manifold heat filter that allows fast computation.
Filters on graphs.
Filters can be thought of as devices that alter the spectrum of their input. Filters can be used as bases, as is the case with wavelets, and they can be used to directly manipulate signals by changing the frequency response of the filter. For example, many audio devices contain an equalizer that allows one to change the amplitude of bass and treble frequencies. Simple equalizers can be built simply by using a set of filters called a filterbank. In the MELD algorithm, we use a tunable filter to estimate density of a sample indicator signal on a single-cell graph.
Mathematically, graph filters work analogously to classical filters. Specifically, a filter takes in a signal and attenuates it according to a frequency response function. This function accepts frequencies and returns a response coefficient. This is then multiplied by the input Fourier coefficient at the corresponding frequency. The entire filter operation is, thus, a reweighting of the input Fourier coefficients. In low-pass filters, the function only preserves frequency components below a threshold. Conversely, high-pass filters work by removing frequencies below a threshold. Band-pass filters transfer frequency components that are within a certain range of a central frequency. The tunable filter in the MELD algorithm is capable of producing any of these responses.
As graph harmonics are defined on the set Λ, it is common to define them as functions of the form h: [0, max(Λ)] ↦ [0, 1]. For example, a low-pass filter with cutoff at λk would have h(x) > 0 for x < λk and h(x) = 0 otherwise. By abuse of notation, we will refer to the diagonal matrix with the filter h applied to each Laplacian eigenvalue as h(Λ), although h is not a set-valued or matrix-valued function. Filtering a signal f is clearest in the spectral domain, where one simply takes the multiplication .
Finally, it is worth using the above definitions to define a vertex-valued operator to perform filtering. As a graph filter is merely a reweighting of the graph Fourier basis, one can construct the filter matrix
| (9) |
A manipulation using Equation (8) will verify that Hf is the windowed graph Fourier transform (WGFT) of . This filter matrix will be used to solve the manifold heat filter in approximate form for computational efficiency.
Laplacian regularization.
A simple assumption for density estimation is smoothness. In this model, the density estimate is assumed to have a low amount of neighbor-to-neighbor variation. Laplacian regularization59–67 is a simple technique that targets signal smoothness via the optimization
| (10) |
Note that this optimization has two terms. The first term (a), called a reconstruction penalty, aims to keep the density estimate similar to the input sample information. The second term (b) ensures smoothness of the signal. Balancing these terms adjusts the amount of smoothness performed by the filter.
Laplacian regularization is a sub-problem of the manifold heat filter that we will discuss for low-pass filtering. In the above, a reconstruction penalty (a) is considered alongside the Laplacian quadratic form (b), which is weighted by the parameter β. The Laplacian quadratic form may also be considered as the norm of the graph gradient—that is,
Thus, one may view Laplacian regularization as a minimization of the edge derivatives of a function while preserving a reconstruction. Because of this form, this technique has been cast as Tikhonov regularization61,68, which is a common regularization to enforce a low-pass filter to solve inverse problems in regression. In our results, we demonstrate a manifold heat filter that may be reduced to Laplacian regularization using a squared Laplacian.
Above, we introduced filters as functions defined over the Laplacian eigenvalues (h(Λ)) or as vertex operators in Equation (9). Minimizing optimization in Equation (10) reveals a similar form for Laplacian regularization. Although Laplacian regularization filter is presented as an optimization, it also has a closed-form solution. We derive this solution here as it is a useful building block for understanding the sample-associated density estimate. To begin,
Substituting y = z, we next differentiate with respect to y and set this to 0:
so the global minima of (10) can be expressed in closed form as
| (11) |
As the input x is a graph signal in the vertex domain, the least squares solution (11) is a filter matrix as discussed above. The spectral properties of Laplacian regularization immediately follow as
| (12) |
Thus, Laplacian regularization is a graph filter with frequency response hreg(λ) = (1+βλ)−1. Supplementary Fig. 13 shows that this function is a low-pass filter on the Laplacian eigenvalues with cutoff parameterized by β.
Tunable filtering.
Although simple low-pass filtering with Laplacian regularization is a powerful tool for many machine learning tasks, we sought to develop a filter that is flexible and capable of filtering the signal at any frequency. To accomplish these goals, we introduce the manifold heat filter:
| (13) |
This filter expands upon Laplacian regularization by the addition of a new smoothness structure. Early and related work proposed the use of a power Laplacian smoothness matrix S in a similar manner as we apply here61, but little work has since proven its utility. In our construction, α is referred to as modulation, β acts as a reconstruction penalty and ρ is filter order. These parameters add a great deal of versatility to the manifold heat filter, and we demonstrate their spectral and vertex effects in Supplementary Fig. 13, as well as provide mathematical analysis of the MELD algorithm parameters in the following section.
A similar derivation as in Equation (11) reveals the filter matrix
| (14) |
which has the frequency response
| (15) |
Thus, the value of the MELD algorithm parameters in the vertex optimization (Equation (13)) has a direct effect on the graph Fourier domain.
Parameter analysis.
β steepens the cutoff of the filter and shifts it more toward its central frequency (Supplementary Fig. 13). In the case of α = 0, this frequency is λ1 = 0. This is done by scaling all frequencies by a factor of β. For stability reasons, we choose β > 0, as a negative choice of β yields a high-frequency amplifier.
The parameters α and ρ change the filter from low pass to band pass or high pass. Supplementary Fig. 13 highlights the effect on frequency response of the filters and showcases their vertex effects in simple examples. We begin our mathematical analysis with the effects of ρ.
ρ powers the Laplacian harmonics. This steepens the frequency response around the central frequency of the manifold heat filter. Higher values of ρ lead to sharper tails (Supplementary Fig. 13d,e), limiting the frequency response outside of the target band but with increased response within the band. Finally, ρ can be used to make a high-pass filter by setting it to negative values (Supplementary Fig. 13f).
For the integer powers, a basic vertex interpretation of ρ is available. Each column of is k − hoplocalized, meaning that is non-zero if and only if the there exists a path length k between vertex i and vertex j (for a detailed discussion of this property, see ref.56, Section 5.2.) Thus, for , the operator considers variation over a hop distance of ρ. This naturally leads to the spectral behavior that we demonstrate in Supplementary Fig. 13d, as signals are required to be smooth over longer hop distances when α = 0 and ρ > 1.
The parameter α removes values from the diagonal of . This results in a modulation of frequency response by translating the Laplacian harmonic that yields the minimal value for the problem (Equation (13)). This allows one to change the central frequency, as α effectively modulates a band-pass filter. As graph frequencies are positive, we do not consider α < 0. In the vertex domain, the effect of α is more nuanced. We study this parameter for α > 0 by considering a modified Laplacian with ρ = 1.
To conclude, we propose a filter parameterized by reconstruction β (Supplementary Fig. 13), order ρ and modulation α. The parameters α and β are limited to be strictly greater than or equal to 0. When α = 0, ρ may be any integer, and it adds more low frequencies to the frequency response as it becomes more positive. On the other hand, if ρ is negative and α = 0, ρ controls a high-pass filter. When α > 0, the manifold heat filter becomes a band-pass filter. In standard use cases, we propose to use the parameters α = 0, β = 60 and ρ = 1. Other parameter values are explored further in Supplementary Fig. 13. We note that the results are relatively robust to parameter values around this default setting. All of our biological results were obtained using this parameter set, which gives a square-integrable low-pass filter. As these parameters have direct spectral effects, their implementation in an efficient graph filter is straightforward and presented below.
In contrast to previous works using Laplacian filters, our parameters allow analysis of signals that are combinations of several underlying changes occurring at various frequencies. For an intuitive example, consider that the frequency of various Google searches will vary from winter to summer (low-frequency variation), Saturday to Monday (medium-frequency variation) or morning to night (high-frequency variation). In the biological context, such changes could manifest as differences in cell type abundance (low-frequency variation) and cell cycle (medium-frequency variation)69. We illustrate such an example in Supplementary Fig. 13 by blindly separating a medium-frequency signal from a low-frequency contaminating signal over simulated data. Such a technique could be used to separate low- and medium-frequency components so that they can be analyzed independently.
Relation between MELD and the Gaussian KDE through the heat kernel.
KDEs are widely used as estimating density is one of the fundamental tasks in many data applications. The density estimate is normally done in ambient space, and there are many methods to do so with a variety of advantages and disadvantages depending on the application. We, instead, assume that the data are sampled from some low-dimensional subspace of the ambient space—for example, that the data lie along a manifold. The MELD algorithm can be thought of as a Gaussian KDE over the discrete manifold formed by the data. This gives a density estimate at every sampled point for a number of distributions. This density estimate, as the number of samples goes to infinity, should converge to the density estimate along a continuous manifold formed by the data. The case of data uniformly sampled on the manifold was explored in ref.70, proving convergence of the eigenvectors and eigenvalues of the discrete Laplacian to the eigenfunctions of the continuous manifold. Reference71 explored when the data are non-uniformly sampled from the manifold and provided a kernel that can normalize out this density that results in a Laplacian modeling the underlying manifold geometry, irrespective of data density. Building on these two works, MELD allows us to estimate the manifold geometry using multiple samples with unknown distribution along it and estimate density and conditional density for each distribution on this shared manifold.
A general KDE f(x, t) with bandwidth t > 0 and kernel function K(x, y, t) is defined as
| (16) |
With , and endowed with the Gaussian kernel
| (17) |
we have the Gaussian KDE in .
This kernel is of particular interest for its thermodynamic interpretation. Namely, the Gaussian KDE is a space discretization of the unique solution to the heat diffusion partial differential equation (PDE)21,72:
| (18) |
with where δx is the Dirac measure at x. This is sometimes called Green’s function for the diffusion equation. Intuitively, can be thought of as measuring the heat after time t after placing units of heat on the data points at t = 0.
In fact, the Gaussian kernel can be represented, instead, in terms of the eigenfunctions of the ambient space. With eigenfunctions ϕ and eigenvalues λ, the Gaussian kernel can be alternative expressed as
| (19) |
Of course, for computational reasons, we often prefer the closed-form solution in (17). We now consider the case when instead consists of uniform samples from a Riemannian manifold embedded in , such that . An analog to the Gaussian KDE in on a manifold is then the solution to the heat PDE restricted to the manifold, and, again, we can use the eigenfunction interpretation of the Green’s function in (19), except replacing the eigenfunctions of the manifold.
The eigenfunctions of the manifold can be approximated through the eigenvectors of the discrete Laplacian. The solution of the heat equation on a graph is defined in terms of the discrete Laplacian as
| (20) |
where δx, δy are Dirac functions at x and y, respectively. This is equivalent to MELD when β = tλmax, α = 0 and ϕ = 1.
When data are sampled uniformly from the manifold and the standard Gaussian kernel is used to construct the graph, then Theorem 2.1 of ref.70, which proves the convergence of the eigenvalues of the discrete graph Laplacian to the continuous Laplacian and implies (20), converges to the Gaussian KDE on the manifold.
However, real data are rarely uniformly sampled from a manifold. When the data are, instead, sampled from a smooth density over the manifold, then the density must be normalized out to recover the geometry of the manifold. This problem was first tackled in ref.50 by constructing an anisotropic kernel that divides out the density at every point. This correction allows us to estimate density over the underlying geometry of the manifold even in the case where data are not uniformly sampled. This allows us to use samples from multiple distributions, in our case distributions over cellular states, which allows a better estimate of underlying manifold using all available data.
In practice, we combine two methods to construct a discrete Laplacian that reflects the underlying data geometry over which we estimate heat propagation and perform density estimation, as explained above in the discussion of graph construction.
Implementation.
A naive implementation of the MELD algorithm would apply the matrix inversion presented in Equation (14). This approach is untenable for the large single-cell graphs that the MELD algorithm is designed for, as will have many elements and, for high powers of ρ or non-sparse graphs, be extremely dense. A second approach to solving Equation (13) would diagonalize such that the filter function in Equation (15) could be applied directly to the Fourier transform of input raw experimental signals. This approach has similar shortcomings as eigendecomposition is substantively similar to inversion. Finally, a speedier approach might be to use conjugate gradient or proximal methods. In practice, we found that these methods are not well suited for estimating sample-associated density.
Instead of gradient methods, we use Chebyshev polynomial approximations of hMELD(λ) to rapidly approximate and apply the manifold heat filter. These approximations, proposed in ref.56 and ref.22, have gained traction in the GSP community for their efficiency and simplicity. Briefly, a truncated and shifted Chebyshev polynomial approximation is fit to the frequency response of a graph filter. For analysis, the approximating polynomials are applied as polynomials of the Laplacian multiplied by the signal to be filtered. As Chebyshev polynomials are given by a recurrence relation, the approximation procedure reduces to a computationally efficient series of matrix–vector multiplications. For a more detailed treatment, one may refer to ref.56 where the polynomials are proposed for graph filters. For application of the manifold heat filter to a small set of input sample indicator signals, Chebyshev approximations offer the simplest and most efficient implementation of our proposed algorithm. For sufficiently large sets of samples, such as when considering hundreds of conditions, the computational cost of obtaining the Fourier basis directly might be less than repeated application of the approximation operator; in these cases, we diagonalize the Laplacian either approximately through randomized singular value decomposition or exactly using eigendecomposition, depending on user preference. Then, one simply constructs HMELD = ΨhMELD(Λ)ΨT to calculate the sample-associated density estimate from the input sample indicator signals.
Summary of the MELD algorithm.
In summary, we have proposed a family of graph filters based on a generalization of Laplacian regularization framework to implement the computation of sample-associated density estimates on a graph. This optimization, which can be solved analytically, allows us to derive the relative likelihood of each sample in a dataset as a smooth and de-noised signal, while also respecting multi-resolution changes in the likelihood landscape. As we show in our quantitative comparisons, this formulation performs better at deriving the true conditional likelihood in quantitative comparisons than simpler label-smoothing algorithms. Furthermore, the MELD algorithm is efficient to compute.
The MELD algorithm is implemented in Python 3 as part of the MELD package and is built atop the scprep, graphtools and pygsp packages. We developed scprep to efficiently process single-cell data, and graphtools was developed for construction and manipulation of graphs built on data. Fourier analysis and Chebyshev approximations are implemented using functions from the pygsp toolbox73.
VFC.
Next, we will describe the VFC algorithm for partitioning the cellular manifold into regions of similar response to experimental perturbation. For this purpose, we use a technique proposed in ref.23 based on a graph generalization of the classical short-time Fourier transform. This generalization will allow us to simultaneously localize signals in both frequency and vertex domains. The output of this transform will be a spectrogram Q, where the value in each entry Qi,j indicates the degree to which each sample indicator signal in the neighborhood around vertex i is composed of frequency j. We then concatenate the sample-associated relative likelihood and perform k-means clustering. The resultant clusters will have similar transcriptomic profiles, similar likelihood estimates and similar frequency trends of the sample indicator signals. The frequency trends of the sample indicator signals are important because they allow us to infer movements in the cellular state space that occur during experimental perturbation.
We derive VFCs in the following steps:
We create the cell graph in the same way as is done for the MELD algorithm.
For each vertex in the graph (corresponding to a cell in the data), we create a series of localized windowed signals by masking the sample indicator signal using a series of heat kernels centered at the vertex. Graph Fourier decomposition of these localized windows capture frequency of the sample indicator signal at different scales around each vertex.
The graph Fourier representation of the localized windowed signals is thresholded using a tanh activation function to produce pseudo-binary signals.
These pseudo-binarized signals are summed across windows of various scales to produce a single N × N spectrogram Q. Principal component analysis (PCA) is performed on the spectrogram for dimensionality reduction.
The sample-associated relative likelihood is concatenated to the reduced spectrogram weighted by the L2-norm of PC1 to produce , which captures both local sample indicator frequency trends and changes in conditional density around each cell in both datasets.
k-means is performed on the concatenated matrix to produce VFCs.
Analyzing frequency content of the sample indicator signal.
Before we go into further detail about the algorithm, it might be useful to provide some intuitive explanations for why the frequency content of the sample indicator signal provides a useful basis for identifying clusters of cells affected by an experimental perturbation. Because the low-frequency eigenvectors of the graph Laplacian identify smoothly varying axes of variance through a graph, we associate trends in the sample indicator signal associated with these low-frequency eigenvectors as biological transitions between cell states. This might correspond to the shift in T cells from naive to activated, for example. We note that, at intermediate cell transcriptomic states between the extreme states that are most enriched in either condition, we observe both low- and middle-frequency sample indicator signal components; see the blue cell in the cartoon in Fig. 2a. This is because, locally, the sample indicator signal varies from cell to cell but, on a large scale, is varying from enriched in one condition to being enriched in the other. This is distinct from what we observe in our model when a group of cells is completely unaffected by an experimental perturbation. Here, we expect to find only high-frequency variations in the sample indicator signal and no underlying transition or low-frequency component. The goal of VFC is to distinguish between these four cases: enriched in the experiment, enriched in the control, intermediate transitional states and unaffected populations of cells. We also want these clusters to have variable size so that even small groups of cells that might be differentially abundant are captured in our clusters.
Using the WGFT to identify local changes in sample indicator signal frequency.
Although the GFT is useful for exploring the frequency content of a signal, it is unable to identify how the frequency content of graph signals change locally over different regions of the graph. In VFC, we are interested in understanding how the frequency content of the sample indicator signal changes in neighborhoods around each cell. In the time domain, the windowed Fourier transform (WFT) identifies changing frequency composition of a signal over time by taking slices of the signal (for example, a sliding window of 10 s) and applying a Fourier decomposition to each window independently58. The result is a spectrogram Q, where the value in each cell Qi,j indicates the degree to which time slice i is composed of frequency j. Recent works in GSP have generalized the construction of WFT to graph signals23. To extend the notion of a sliding window to the graph domain,23 write the operation of translation in terms of convolution as follows.
The generalized translation operator of signal f to vertex i ∈ {1, 2, …, N} is given by
| (21) |
which convolves the signal f, in our case the sample indicator signal, with a Dirac at vertex i. Reference23 demonstrates that this operator inherits various properties of its classical counterpart; however, the operator is not isometric and is affected by the graph that it is built on. Furthermore, for signals that are not tightly localized in the vertex domain and on graphs that are not directly related to Fourier harmonics (for example, the circle graph), it is not clear what graph translation implies.
In addition to translation, a generalized modulation operator is defined in ref.23 as for frequencies k ∈ {0, 1, …, N − 1} as
| (22) |
This formulation is analogous in construction to classical modulation, defined by point-wise multiplication with a pure harmonic—a Laplacian eigenvector in our case. Classical modulation translates signals in the Fourier domain; because of the discrete nature of the graph Fourier domain, this property is only weakly shared between the two operators. Instead, the generalized modulation Mk translates the DC component of f, , to λk—that is, . Furthermore, for any function f whose frequency content is localized around λ0, (Mkf) is localized in frequency around λk. Reference23 details this construction and provides bounds on spectral localization and other properties.
With these two operators, a graph windowed Fourier atom is constructed23 for any window function :
| (23) |
We can then build a spectrogram by taking the inner product of each gi,k ∀ i ∈ {1, 2, …, N} ∧ ∀ k ∈ {0, …, N − 1} with the target signal f:
| (24) |
As with the classical WFT, one could interpret this as segmenting the signal by windows and then taking the Fourier transform of each segment:
| (25) |
where ⊙ is the element-wise product.
Using heat kernels of increasing scales to produce the WGFT of the sample indicator signal.
To generate the spectrogram for clustering, we first need a suitable window function. We use the normalized heat kernel as proposed in ref.23:
| (26) |
| (27) |
By translating this kernel, element-wise multiplying it with our target signal f and taking the Fourier transform of the result, we obtain a WGFT of f that is localized based on the diffusion distance23,57 from each vertex to every other vertex in the graph.
For an input sample indicator signal f, signal-biased spectral clustering as proposed in ref.23 proceeds as follows:
Generate the window matrix Pt, which contains, as its columns, translated and normalized heat kernels at the scale t.
Column-wise multiply Ft = P ⊙ f; the i-th column of Ft is an entry-wise product of the i-th window and f.
Take the Fourier transform of each column of Ft. This matrix, Ĉt is the normalized WGFT matrix.
This produces a single WGFT for the scale t. At this stage, ref.23 proposed to saturate the elements of Ĉt using the activation function tanh (|Ĉt|) (where ∣ . ∣ is an element-wise absolute value). Then, k-means is performed on this saturated output to yield clusters. This operation has connections to spectral clustering as the features that k-means is run on are coefficients of graph harmonics.
We build upon this approach to add robustness, sensitivity to sign changes and scalability. Particularly, VFC builds a set of activated spectrograms at different window scales. These scales are given by simulated heat diffusion over the graph by adjusting the time scale t in Equation (26). Then, the entire set is combined through summation.
Combining the sample-associated relative likelihood and WGFT of the sample indicator signal.
As discussed in the introduction of VFC in the Results, it is useful to consider the value of the sample likelihood in addition to the frequency content of the sample indicator. This is because, if we consider two populations of cells, one of which is highly enriched in the experimental condition and another that is enriched in the control, we expect to find similar frequency content of the sample indicator signal. Namely, both should have very low-frequency content, as indicated in the cartoon in Fig. 2a. However, we expect these two populations to have very different sample likelihood values. To allow us to distinguish between these populations, we also include the sample-associated relative likelihood in the matrix used for clustering.
We concatenate the sample-associated relative likelihood as an additional column to the multi-resolution spectrogram Q. However, we want to be able to tune the clustering with respect to how much the likelihood affects the result compared to the frequency information in Q. Therefore, inspired by spectral clustering as proposed in ref.74, we first perform PCA on Q to get k + 1 principle components and then normalize the likelihood by the L2-norm of the first principle component. We then add the likelihood as an additional column to the PCA-reduced Q to produce the matrix . The weight of the likelihood can be modulated by a user-adjustable parameter w, but, for all experiments in this paper, we leave w = 1. Finally, is used as input for k-means clustering.
The multi-scale approach that we have proposed has several benefits. Foremost, it removes the complexity of picking a window size. Second, using the actual input signal as a feature allows the clustering to consider both frequency and sign information in the raw experimental signal. For scalability, we leverage the fact that Pt is effectively a diffusion operator and, thus, can be built efficiently by treating it as a Markov matrix and normalizing the graph adjacency by the degree.
Summary of the VFC algorithm.
To identify clusters of cells that are transcriptionally similar and also affected by an experimental perturbation in the same way, we introduced an algorithm called VFC. Our approach builds upon previous work23 analyzing the local frequency content of the sample indicator vector as defined over the vertices of a graph. Here, we introduce two novel adaptations of the algorithm. First, we take a multi-resolution approach to quantifying frequency trends in the neighborhoods around each node. By considering windowed signals that are large (that is, contain many neighboring points) and small (that is, very proximal on the graph), we can identify clusters both large and small that are similarly affected by an experimental perturbation. Our second contribution is the inclusion of the relative likelihood of each sample in our basis for clustering. This allows VFC to take into account the degree of enrichment of each group of cells between condition.
Parameter search for the MELD algorithm.
To determine the optimal set of parameters for the MELD algorithm, we performed a parameter search using Splatter-generated datasets. For each of the four dataset structures, we generated ten datasets with different random seeds and ten random ground truth probability densities per dataset, for a total of 400 datasets per combination of parameters. A coarse-grained grid search revealed that setting α = 0 and ρ = 1 performed best regardless of the β parameter. This is expected because, with these settings, the MELD filter is the standard heat kernel. A fine-grained search over parameters for β showed that optimal values were between 50 and 75 (Supplementary Fig. 14). We chose a value of 60 as the default in the MELD toolkit, and this was used for all experiments. We note that the optimal β parameter will vary with dataset structure and the number of cells. Supplementary Fig. 14b shows how the optimal β values vary as a function of the number of cells generated using Splatter while keeping the underlying geometry the same.
Processing and analysis of the T cell datasets.
Gene expression counts matrices prepared in ref.13 were accessed from the National Center for Biotechnology Information (NCBI) Gene Expression Omnibus (GEO) database accession GSE92872. In total, 3,143 stimulated and 2,597 unstimulated T cells were processed in a pipeline derived from the published supplementary software. First, artificial genes corresponding to gRNAs were removed from the counts matrix. Genes observed in fewer than five cells were removed. Cells with a library size higher than 35,000 UMIs per cell were removed. To filter dead or dying cells, expression of all mitochondrial genes was Z-scored, and cells with an average Z-score expression greater than 1 were removed. As in the published analysis, all mitochondrial and ribosomal genes were excluded. Filtered cells and genes were library size normalized and square root transformed. To build a cell state graph, 100 PCA dimensions were calculated, and edge weights between cells were calculated using an alpha decay kernel as implemented in the graphtools library (www.github.com/KrishnaswamyLab/graphtools) using default parameters. MELD was run on the cell state graph using the stimulated/unstimulated labels as input with the smoothing parameter β = 60. To identify a signature, the top and bottom VFC clusters by sample-associated relative likelihood were used for differential expression using a rank test as implemented in diffxpy27 and a q-value cutoff of 0.05. GO term enrichment was performed using EnrichR using the gseapy Python package (https://pypi.org/project/gseapy/).
Processing and analysis of the zebrafish dataset.
Gene expression counts matrices prepared in ref.15 (the chordin dataset) were downloaded from NCBI GEO (GSE112294). In total, 16,079 cells from chd embryos injected with gRNAs targeting chordin and 10,782 cells from tyr embryos injected with gRNAs targeting tyrosinase were accessed. Lowly expressed genes detected in fewer than five cells were removed. Cells with library sizes larger than 15,000 UMIs per cell were removed. Counts were library size normalized and square root transformed. Cluster labels included with the counts matrices were used for cell type identification.
During preliminary analysis, a group of 24 cells were identified originating exclusively from the chd embryos. Despite an average library size in the bottom 12% of cells, these cells exhibited 546-fold, 246-fold and 1,210-fold increased expression of Sh3Tc1, LOC101882117 and LOC101885394, respectively, relative to other cells. To our knowledge, the function of these genes in development is not described. These cells were annotated in ref.15 as belonging to seven cell types, including the Tailbud–Spinal Cord and Neural–Midbrain. These cells were excluded from further analysis.
To generate a cell state graph, 100 PCA dimensions were calculated from the square root-transformed filtered gene expression matrix of both datasets. Edge weights between cells on the graph were calculated using an alpha decay kernel with parameters KNN = 20 and decay = 40. MAGIC was used to impute gene expression values using default parameters. MELD was run using the tyr or chd labels as input. The sample-associated density estimate was calculated for each of the six samples independently and normalized per replicate to generate three chordin-relative likelihood estimates. The average likelihood for the chordin condition was calculated and used for downstream analysis. To identify subpopulations within the published clusters, we manually examined a PHATE embedding of each subcluster, the distribution of chordin likelihood values in each cluster and the results of VFC subclustering with varying numbers of clusters. The decision to apply VFC was done on a per-cluster basis with the goal of identifying cell subpopulations with transcriptional similarity (as assessed by visualization) and uniform response to perturbation (as assessed by likelihood values). Cell types were annotated using sets of marker genes curated in ref.16. Changes in gene expression between VFC clusters were assessed using a rank sum test as implemented by diffxpy.
Generation, processing and analysis of the pancreatic islet datasets.
scRNA-seq was performed on human islet cells from three different islet donors in the presence and absence of IFN-γ. The islets were received on three different days. Cells were cultured for 24 h with 25 ng ml−1 of IFN-γ (R&D Systems) in CMRL 1066 medium (Gibco) and subsequently dissociated into single cells with 0.05% Trypsin EDTA (Gibco). Cells were then stained with FluoZin-3 (Invitrogen) and TMRE (Life Technologies) and sorted using an FACS Aria II (BD). The three samples were pooled for the sequencing. Cells were immediately processed using the 10× Genomics Chromium 3′ Single Cell RNA sequencing kit at the Yale Center for Genome Analysis. The raw sequencing data were processed using the 10× Genomics Cell Ranger Pipeline. Raw data will be made available before publication.
Data from all three donors were concatenated into a single matrix for analysis. First, cells not expressing insulin, somatostatin or glucagon were excluded from analysis using donor-specific thresholds. The data were square root transformed and reduced to 100 PCA dimensions. Next, we applied an MNN kernel to create a graph across all three donors with parameters KNN = 5 and decay = 30. This graph was then used for PHATE. MELD was run on the sample labels using default parameters. To identify coarse-grained cell types, we used previously published markers of islet cells35. We then used VFC to identify subpopulations of stimulated and unstimulated islet cells. To identify signature genes of IFN-γ stimulation, we calculated differential expression between the clusters with the highest and lowest treatment likelihood values within each cell type using a rank sum test as implemented in diffxpy. A consensus signature was then obtained by taking the intersection genes with q values < 0.05. Gene set enrichment was then calculated using gseapy.
Quantitative comparisons.
To generate single-cell data for the quantitative comparisons, we used Splatter. Datasets were all generated using the ‘Paths’ mode so that a latent dimension in the data could be used to create the ground truth likelihood that each cell would be observed in the ‘experimental’ condition relative to the ‘control’. We focused on four data geometries: a tree with three branches, a branch and cluster with either end of the branch enriched or depleted and the cluster unaffected, a single branch with a middle section either enriched or depleted and four clusters with random segments enriched or depleted. To create clusters, a multi-branched tree was created, and all but the tips of the branches were removed. The ground truth experimental signal was created using custom Python scripts, taking the ‘Steps’ latent variable from Splatter and randomly selecting a proportion of each branch or cluster between 10% and 80% of the data to be enriched or depleted by 25%. These regions were divided into thirds to create a smooth transition between the unaffected regions and the differentially abundant regions. This likelihood ratio was then centered so that, on average, half the cells would be assigned to each condition. The centered ground truth signal was used to parameterize a Bernoulli random variable and assign each cell to the experimental or control conditions. The data and sample labels were used as input to the respective algorithms.
To quantify the accuracy of MELD to approximate the ground truth likelihood ratio, we compared MELD, a KNN-smoothed signal or a graph averaged signal to the ground truth likelihood of observing each cell in either of the two conditions. We used the Pearson’s R statistic to calculate the degree to which these estimates approximate the likelihood ratio. Each of the four data geometries was tested 30 times with different random seeds.
We also performed MELD comparisons using the T cell and zebrafish datasets described above. The pre-processed data were used to generate a three-dimensional PHATE embedding that was Z-score normalized. We then used a combination of PHATE dimensions to create a ground truth probability that each cell would be observed in the experimental or control condition. Cells were then assigned to either condition based on this probability as described above. We ran the same comparisons as on the simulated data with 100 random seeds per dataset.
To quantify the accuracy of VFC to detect the regions of the dataset that were enriched, depleted or unaffected between conditions, we calculated the adjusted Rand score (ARS) between the ground truth regions with enriched, depleted or unchanged likelihood ratios between conditions. VFC was compared to k-means, spectral clustering, Louvain, Leiden and CellHarmony. As Leiden and Louvain do not provide a method to control the number of clusters, we implemented a binary search to identify a resolution parameter that provides the target number of clusters. Although CellHarmony relies on an initial Louvain clustering, the tool does not implement Louvain with a tuneable resolution. It is also not possible to provide an initial clustering to CellHarmony, so we resorted to cutting Louvain at the level closest to our target number of clusters. Finally, because CellHarmony does not reconcile the disparate cluster assignments in the reference and query datasets, and because not all cells in the query dataset may be aligned to the reference, we needed to generate manually new cluster labels for cells in the query dataset so that the method could be compared to other clustering tools.
To characterize the ability of MELD to characterize gene signatures of a perturbation dataset, we returned to the T cell dataset. We, again, used the same setup to create synthetically three regions with different sampling probabilities in the dataset using PHATE clusters as above. Because one of these clusters has no differential abundance between conditions, we calculated the ground truth gene expression signature between the enriched and depleted clusters only using diffxpy27. To calculate the gene signature for each clustering method, we performed differential expression between the most enriched cluster in the experimental condition and the most depleted cluster in the experimental condition (or highest and lowest treatment likelihood for MELD). We also considered directly performing two-sample comparison using the sample labels. To quantify the performance of each method, we used the area under the receiving operating characteristic curve (AUC-ROC) to compare the q values produced using each method to the ground truth q values. This process was repeated over 100 random seeds. The AUC-ROCs and performance of each method relative to VFC are displayed in Supplementary Fig. 6d,e.
Reporting Summary.
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
Gene expression counts matrices prepared in ref.13 were accessed from NCBI GEO database accession GSE92872. Gene expression counts matrices prepared in ref.15 were downloaded from NCBI GEO accession GSE112294. The pancreatic islets datasets are available on NCBI GEO at accession GSE161465.
Code availability
Code for the MELD and VFC algorithms implemented in Python is available as part of the MELD package on GitHub (https://github.com/KrishnaswamyLab/MELD) and on the Python Package Index. The GitHub repository also contains tutorials, code to reproduce the analysis of the zebrafish dataset and code associated with several of the quantitative comparisons.
Supplementary Material
Acknowledgements
The authors would like to thank C. Vejnar, R. Coifman, J. Noonan, V. Tornini and C. Kontur for fruitful discussions. We would also like to thank G. Wang of the Yale Center for Genome Analysis for help in preparing the pancreatic islet data. This research was supported, in part, by the Eunice Kennedy Shriver National Institute of Child Health & Human Development of the National Institues of Health (NIH) (award no. F31HD097958) (to D.B.); the Gruber Foundation (to S.G.); IVADO Professor startup and operational funds, IVADO Fundamental Research Project grant PRF-2019-3583139727 (to G.W.); NIH grants R01GM135929 and R01GM130847 (to G.W. and S.K.); and Chan-Zuckerberg Initiative grants 182702 and CZF2019-002440 (to S.K.). The content provided here is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.
Footnotes
Online content
Any methods, additional references, Nature Research reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41587-020-00803-5.
Competing interests
The authors declare the following competing interest: S.K. is a paid scientific advisor to AI Therapeutics.
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1038/s41587-020-00803-5.
References
- 1.Luecken MD & Theis FJ Current best practices in single-cell RNA-seq analysis: a tutorial. Mol. Syst. Biol 15, e8746 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Weinreb C, Wolock S, Klein AM & Berger B SPRING: a kinetic interface for visualizing high dimensional single-cell expression data. Bioinformatics 34, 1246–1248 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Moon KR et al. Visualizing structure and transitions in high-dimensional biological data. Nat. Biotechnol 37, 1482–1492 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.van Dijk D et al. Recovering gene interactions from single-cell data using data diffusion. Cell 174, 716–729 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shekhar K et al. Comprehensive classification of retinal bipolar neurons by single-cell transcriptomics. Cell 166, 1308–1323 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Levine JH et al. Data-driven phenotypic dissection of AML reveals progenitor-like cells that correlate with prognosis. Cell 162, 184–197 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xu C & Su Z Identification of cell types from single-cell transcriptomes using a novel clustering method. Bioinformatics 31, 1974–1980 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Becht E et al. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol 37, 38–44 (2019). [DOI] [PubMed] [Google Scholar]
- 9.Patel AP et al. Single-cell RNA-seq highlights intratumoral heterogeneity in primary glioblastoma. Science 344, 1396–1401 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Finak G et al. MAST: a flexible statistical framework for assessing transcriptional changes and characterizing heterogeneity in single-cell RNA sequencing data. Genome Biol. 16, 278 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tirosh I et al. Dissecting the multicellular ecosystem of metastatic melanoma by single-cell RNA-seq. Science 352, 189–196 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jaitin DA et al. Dissecting immune circuits by linking CRISPR-pooled screens with single-cell RNA-seq. Cell 167, 1883–1896 (2016). [DOI] [PubMed] [Google Scholar]
- 13.Datlinger P et al. Pooled CRISPR screening with single-cell transcriptome readout. Nat. Methods 14, 297–301 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gao X, Hu D, Gogol M & Li H ClusterMap: comparing analyses across multiple single cell RNA-seq profiles. Bioinformatics 35, 3038–3045 (2018). [DOI] [PubMed] [Google Scholar]
- 15.Wagner DE et al. Single-cell mapping of gene expression landscapes and lineage in the zebrafish embryo. Science 360, 981–987 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Farrell JA et al. Single-cell reconstruction of developmental trajectories during zebrafish embryogenesis. Science 360, eaar3131 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dann E, Henderson NC, Teichmann SA, Morgan MD & Marioni JC Milo: differential abundance testing on single-cell data using k-NN graphs | Preprint at bioRxiv 10.1101/2020.11.23.393769 (2020). [DOI] [PMC free article] [PubMed]
- 18.Büttner M, Ostner J, Müller C, Theis F & Schubert B scCODA: a Bayesian model for compositional single-cell data analysis. Preprint at bioRxiv 10.1101/2020.12.14.422688 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Moon KR et al. Manifold learning-based methods for analyzing single-cell RNA-sequencing data. Curr. Opin. Syst. Biol 7, 36–46 (2018). [Google Scholar]
- 20.Shuman DI, Narang SK, Frossard P, Ortega A & Vandergheynst P The emerging field of signal processing on graphs: extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag 30, 83–98 (2013). [Google Scholar]
- 21.Botev ZI, Grotowski JF & Kroese DP Kernel density estimation via diffusion. Ann. Stat 38, 2916–2957 (2010). [Google Scholar]
- 22.Shuman DI, Vandergheynst P & Frossard P Chebyshev polynomial approximation for distributed signal processing. In: Distributed Computing in Sensor Systems and Workshops (DCOSS). 2011 International Conference on Distributed Computing in Sensor Systems, 1–8 (IEEE, 2011). [Google Scholar]
- 23.Shuman DI, Ricaud B & Vandergheynst P Vertex-frequency analysis on graphs. Applied Comput. Harmon. Anal 40, 260–291 (2016). [Google Scholar]
- 24.Zappia L, Phipson B & Oshlack A Splatter: simulation of single-cell RNA sequencing data. Genome Biol. 18, 174 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Traag VA, Waltman L & van Eck NJ From Louvain to Leiden: guaranteeing well-connected communities. Sci. Rep 9, 5233 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.DePasquale EAK et al. CellHarmony: cell-level matching and holistic comparison of single-cell transcriptomes. Nucleic Acids Res. 47, e138–e138 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fischer D Theislab/diffxpy. Theis Lab https://github.com/theislab/diffxpy (2020). [Google Scholar]
- 28.Kuleshov MV et al. Enrichr: a comprehensive gene set enrichment analysis web server 2016 update. Nucleic Acids Res. 44, W90–W97 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yen S-T et al. Somatic mosaicism and allele complexity induced by CRISPR/Cas9 RNA injections in mouse zygotes. Dev. Biol 393, 3–9 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hammerschmidt M et al. Dino and mercedes, two genes regulating dorsal development in the zebrafish embryo. Development 123, 95–102 (1996). [DOI] [PubMed] [Google Scholar]
- 31.Schulte-Merker S, Lee KJ, McMahon AP & Hammerschmidt M The zebrafish organizer requires chordino. Nature 387, 862–863 (1997). [DOI] [PubMed] [Google Scholar]
- 32.Fisher S & Halpern ME Patterning the zebrafish axial skeleton requires early chordin function. Nat. Genet 23, 442–446 (1999). [DOI] [PubMed] [Google Scholar]
- 33.Ablamunits V, Elias D, Reshef T & Cohen IR Islet T cells secreting IFN-γ in NOD mouse diabetes: arrest by p277 peptide treatment. J. Autoimmun 11, 73–81 (1998). [DOI] [PubMed] [Google Scholar]
- 34.Lopes M et al. Temporal profiling of cytokine-induced genes in pancreatic β-cells by meta-analysis and network inference. Genomics 103, 264–275 (2014). [DOI] [PubMed] [Google Scholar]
- 35.Muraro MJ et al. A single-cell transcriptome atlas of the human pancreas. Cell Syst. 3, 385–394 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Xin Y et al. Pseudotime ordering of single human β-cells reveals states of insulin production and unfolded protein response. Diabetes 67, 1783–1794 (2018). [DOI] [PubMed] [Google Scholar]
- 37.Farack L et al. Transcriptional heterogeneity of beta cells in the intact pancreas. Dev. Cell 48, 115–125 (2019). [DOI] [PubMed] [Google Scholar]
- 38.Ramana CV, Gil MP, Schreiber RD & Stark GR Stat1-dependent and -independent pathways in IFN-γ-dependent signaling. Trends Immunol. 23, 96–101 (2002). [DOI] [PubMed] [Google Scholar]
- 39.Sadler AJ & Williams BRG Interferon-inducible antiviral effectors. Nat. Rev. Immunol 8, 559–568 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fitzgerald KA The interferon inducible gene: viperin. J. Interferon Cytokine Res 31, 131–135 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Zheng Z, Wang L & Pan J Interferon-stimulated gene 20-kDa protein (ISG20) in infection and disease: review and outlook. Intractable Rare Dis. Res 6, 35–40 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hultcrantz M et al. Interferons induce an antiviral state in human pancreatic islet cells. Virology 367, 92–101 (2007). [DOI] [PubMed] [Google Scholar]
- 43.Stewart AF et al. Human β-cell proliferation and intracellular signaling: part 3. Diabetes 64, 1872–1885 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chen X et al. MLL-AF9 initiates transformation from fast-proliferating myeloid progenitors. Nat. Commun 10, 5767 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Dutrow EV et al. The human accelerated region HACNS1 modifies developmental gene expression in humanized mice. Preprint at https://www.biorxiv.org/content/10.1101/2019.12.11.873075v1 (2019).
- 46.Savell KE et al. A dopamine-induced gene expression signature regulates neuronal function and cocaine response. Sci. Adv 6, eaba4221 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chung KM et al. Endocrine–exocrine signaling drives obesity-associated pancreatic ductal adenocarcinoma. Cell 181, 832–847 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ravindra NG et al. Single-cell longitudinal analysis of SARS-CoV-2 infection in human airway epithelium. Preprint at https://www.biorxiv.org/content/10.1101/2020.05.06.081695v2 (2020). [DOI] [PMC free article] [PubMed]
- 49.Haghverdi L, Lun ATL, Morgan MD & Marioni JC Batch effects in single-cell RNA-sequencing data are corrected by matching mutual nearest neighbors. Nat. Biotechnol 36, 421–427 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Coifman RR & Lafon S Diffusion maps. Applied Comput. Harmon. Anal 21, 5–30 (2006). [Google Scholar]
- 51.Mack YP & Rosenblatt M Multivariate k-nearest neighbor density estimates. J. Multivar. Anal 9, 1–15 (1979). [Google Scholar]
- 52.Biau G, Chazal F, Cohen-Steiner D, Devroye L & Rodríguez C A weighted k-nearest neighbor density estimate for geometric inference. Electron. J. Stat 5, 204–237 (2011). [Google Scholar]
- 53.Kung Y-H, Lin P-S & Kao C-H An optimal k-nearest neighbor for density estimation. Stat. Probabil. Lett 82, 1786–1791 (2012). [Google Scholar]
- 54.Von Luxburg U & Alamgir M Density estimation from unweighted k-nearest neighbor graphs: a roadmap. In: Burges CJC, Bottou L, Welling M, Ghahramani Z & Weinberger KQ (eds.) Advances in Neural Information Processing Systems 26, 225–233 (Curran Associates, 2013). [Google Scholar]
- 55.Silverman BW Density Estimation for Statistics and Data Analysis (Routledge, 2018). [Google Scholar]
- 56.Hammond DK, Vandergheynst P & Gribonval R Wavelets on graphs via spectral graph theory. Applied Comput. Harmon. Anal 30, 129–150 (2011). [Google Scholar]
- 57.Perraudin N, Ricaud B, Shuman D & Vandergheynst P Global and local uncertainty principles for signals on graphs. APSIPA Trans. Signal Inform. Process 7, E3 (2018); 10.1017/ATSIP.2018.2 [DOI] [Google Scholar]
- 58.Mallat SA Wavelet Tour of Signal Processing: The Sparse Way (Academic Press, 2008). [Google Scholar]
- 59.Zhou D & Schölkopf B A regularization framework for learning from graph data. In: ICML Workshop on Statistical Relational Learning and Its Connections to Other Fields 15, 67–68 (2004). [Google Scholar]
- 60.Ham J, Lee DD & Saul LK Semisupervised alignment of manifolds. Proc. Annu. Conf. Uncertainty in Artificial Intelligence (eds Ghahramani Z & Cowell R) (AUAI Press, 2005). [Google Scholar]
- 61.Belkin M, Matveeva I & Niyogi P Regularization and semi-supervised learning on large graphs. In: International Conference on Computational Learning Theory, 624–638 (Springer, 2004). [Google Scholar]
- 62.Ando RK & Zhang T Learning on graph with Laplacian regularization. In: Schölkopf B, Platt JC & Hoffman T (eds.) Advances in Neural Information Processing Systems 19, 25–32 (MIT Press, 2007). [Google Scholar]
- 63.Weinberger KQ, Sha F, Zhu Q & Saul LK Graph Laplacian regularization for large-scale semidefinite programming. In: Schölkopf B, Platt JC & Hoffman T (eds.) Advances in Neural Information Processing Systems 19, 1489–1496 (MIT Press, 2007). [Google Scholar]
- 64.He X, Ji M, Zhang C & Bao H A variance minimization criterion to feature selection using Laplacian regularization. IEEE Trans. Pattern Anal. Mach. Intell 33, 2013–2025 (2011). [DOI] [PubMed] [Google Scholar]
- 65.Liu X, Zhai D, Zhao D, Zhai G & Gao W Progressive image denoising through hybrid graph Laplacian regularization: a unified framework. IEEE Trans. Image Process 23, 1491–1503 (2014). [DOI] [PubMed] [Google Scholar]
- 66.Pang J, Cheung G, Ortega A & Au OC Optimal graph Laplacian regularization for natural image denoising. In: 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2294–2298 (IEEE, 2015). [Google Scholar]
- 67.Pang J & Cheung G Graph Laplacian regularization for image denoising: analysis in the continuous domain. IEEE Trans. Image Process 26, 1770–1785 (2017). [DOI] [PubMed] [Google Scholar]
- 68.Perraudin N et al. GSPBOX: a toolbox for signal processing on graphs. Preprint at https://arxiv.org/abs/1408.5781 (2016).
- 69.Barron M & Li J Identifying and removing the cell-cycle effect from single-cell RNA-sequencing data. Sci. Rep 6, 33892 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Belkin M & Niyogi P Convergence of Laplacian eigenmaps. In: Schölkopf B, Platt JC & Hoffman T (eds.) Advances in Neural Information Processing Systems 19, 129–136 (MIT Press, 2006). [Google Scholar]
- 71.Coifman RR & Maggioni M Diffusion wavelets. Applied Comput. Harmon. Anal 21, 53–94 (2006). [Google Scholar]
- 72.Chaudhuri P & Marron JS Scale space view of curve estimation. Ann. Stat 28, 408–428 (2000). [Google Scholar]
- 73.Perraudin N, Holighaus N, Søndergaard PL & Balazs P Designing Gabor windows using convex optimization. Appl. Math. Comput 330, 266–287 (2018). [Google Scholar]
- 74.Ng AY, Jordan MI & Weiss Y On spectral clustering: analysis and an algorithm. In: Advances in Neural Information Processing Systems 849–856 (NIPS, 2001). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Gene expression counts matrices prepared in ref.13 were accessed from NCBI GEO database accession GSE92872. Gene expression counts matrices prepared in ref.15 were downloaded from NCBI GEO accession GSE112294. The pancreatic islets datasets are available on NCBI GEO at accession GSE161465.


