Abstract
The aim of the work is to identify a clustering structure for the 20 Italian regions according to the main variables related to COVID-19 pandemic. Data are observed over time, spanning from the last week of February 2020 to the first week of February 2021. Dealing with geographical units observed at several time occasions, the proposed fuzzy clustering model embedded both space and time information. Properly, an Exponential distance-based Fuzzy Partitioning Around Medoids algorithm with spatial penalty term has been proposed to classify the spline representation of the time trajectories. The results show that the heterogeneity among regions along with the spatial contiguity is essential to understand the spread of the pandemic and to design effective policies to mitigate the effects.
Keywords: Fuzzy Partitioning Around Medoids, Robust clustering, Time series clustering, Spatial clustering, COVID-19
1. Introduction
Severe acute respiratory syndrome Coronavirus-2 (SARS-CoV-2) is the name given to the new 2019 coronavirus while COVID-19 is that given to the disease associated with the virus. This new strain of coronavirus, not previously identified in humans, has exponentially spread out from the capital of the Chinese province of Hubei, Wuhan, the epicentre of the contagion, worldwide causing a pandemic with serious effects on national health systems (Li et al., 2020).
In Italy the outbreak of COVID-19 started at the end of February in Lombardy and then hit Northern Italy. As a consequence the Italian government imposed a nationwide lockdown (on 9 March 2020) in order to mitigate the disease and avoid further spreading of the virus. Flows of people travelled from North to South when the national lockdown measures were first announced on 8 March 2020.
The lockdown was gradually suspended at the beginning of May 2020 as the number of new daily active cases and the number of deaths due to COVID-19 steadily declined, also considering its economic cost. People could gather provided they maintained social distancing. Nonetheless, it was not possible to move freely between regions until 3 June 2020. The count of the new daily infections remained stable until August 2020, when the number of new daily cases, on a national level, increased to over 1200.
In October, with an average of 10 000 new daily cases and the exponential growth of the incidence rate, Italy faced its second pandemic wave involving all territories, from the North to the South. It is worth noting that the higher number of new daily infections in the second wave was also strictly related to the considerably higher number of tested people by day.
New restrictive measures were introduced by the Italian authorities that varied based on the classification of Italian provinces into three areas – red, orange and yellow – corresponding to three risk profiles on the basis of the value of 21 indicators. The 21 indicators are divided into three different categories: process indicators on monitoring capacity; process indicators on the ability to diagnose, investigate and manage contacts; result indicators relating to transmission stability and the resilience of health services. The red colour corresponds to higher risk. They contributed to control the pandemic spread in Italy and are still adopted to this day.
On 2 December 2020, Health Minister presented the guidelines of the Strategic Plan for anti-SARS-CoV-2/COVID-19 vaccination (Decree 2 January 2021) to Parliament, produced by the Ministry of Health, Extraordinary Commissioner for the Emergency, Higher Institute of Health, Agenas and Aifa. As foreseen by the Plan itself, on 8 February 2021, the document was published that updates the categories and the order of priority for the second phase of the vaccination campaign against Covid-19 based on the evolution of knowledge and information on vaccines.
The official data for the COVID-19 pandemic are collected, daily, by the Italian Civil Protection Department. The GitHub repository1 contains multiple counts, such as the new incident cases, the total cases, the currently positives, the number of hospitalized patients, the number of patients in Intensive Care Units, the deaths. They are available at regional level and, in such cases, at provincial level.
Nonetheless the new starting vaccination campaign, on 27 January 2021, the Italian Civil Protection Department recorded total cases and deaths due to COVID-19.
We argue that the lack of uniformity in reporting and signalling the COVID-19 new infections and deaths, the latter due above all to the presence of comorbidities, affects the reliability of the estimates of the incidence and mortality/fatality rates; in particular for the latter, the under-estimation is also related to the certification of the “COVID-19” victims that could be done only among swabbed individuals.
According to the last bulletin provided by the Italian National Institute of Health (ISS) (Iss, 2021), the mean age of died patients positive to SARS-CoV-2 infection was 81 years, with women having an older age than men (median age 86 years for women versus median age for men). Moreover, it is worth noting that the median age of patients dying for COVID-19 was years while that of infected people was years.
Taking into account gender, out of the 85418 patients died for SARS-CoV-2, 43.7% was female. Based on an opportunistic sample of only 6381 patients died in hospital, the average number of diseases was 3.6 and the 84.9% of the sample had 2 or more comorbidities.
In this study, we focused on the daily time-series of the cumulative cases over population (per 10,000 inhabitants), of the cumulative cases over monitored cases and of the cumulative deaths over population (per 10 000 inhabitants), spanning from 2020-02-24 to 2021-02-08.
From a methodological point of view, one deals with spatial units observed at several time occasions. The corresponding spatial time data array is a two-way data array, therefore an array of the type: spatial objects occasions.
Several space–time series clustering techniques have been proposed in the literature: some of them take into account the spatial dependence in the non-spatial time series clustering models by defining a suitable spatial dissimilarity measure (Izakian et al., 2013), while others are density-based (Ester et al., 1996, Wang et al., 2006, Birant and Kut, 2007, Ienco and Bordogna, 2016, Xie et al., 2016) or model-based (Basford and McLachlan, 1985, Viroli, 2011, Torabi, 2014, Torabi, 2016, Disegna et al., 2017) clustering techniques.
The approach followed in this work belongs to the broad group of the spatially constrained time series clustering techniques (Hu and Sung, 2006, Coppi et al., 2010, Gao and Yu, 2016). More specifically, it is based on the fuzzy clustering algorithm for spatial-time data proposed by D’Urso et al. (2019) that, in turn, is an extension of the fuzzy C-Means algorithm for time series with spatial information developed in Coppi et al. (2010). Both fuzzy algorithms proposed in Coppi et al. (2010) and D’Urso et al. (2019) include a spatial penalization term in the objective function. The role of this term and of the related tuning parameter is to smooth the membership degrees of all units contiguous to the generic th unit in all clusters to which th unit does not belong.
The time series are transformed onto (finite dimensional) vectors of coefficients for dimension reduction purposes. This is obtained by projecting each time series onto a finite dimensional functional basis. Afterwards, robust clustering is applied to the resulting basis coefficients. Projection onto a suitable functional basis is considered, in particular the cubic B-spline basis.
The need for robust clustering methods is naturally justified by the possible and frequent presence of outlier time series. Notice that outliers are likely to occur in large, and sometimes fully automatized, data sets. Part of the variability of data can be removed by the regularization or smoothing procedure considered, but other sources of variability could be due to particularities of the data themselves. To achieve robustness, in the paper the Exponential distance is considered (Wu and Yang, 2002, D’Urso and De Giovanni, 2014).
In this study, the Exponential distance-based Fuzzy -Medoids clustering algorithm based on B-splines with spatial penalty term (BS-Exp-FCMd-S) is applied to clustering of time series related to COVID-19 pandemic.
Summing up the proposed clustering method used for analysing the Covid time series presents different benefits inherited by its structural features. In particular:
Clustering procedure: adopting the PAM (Partitioning Around Medoids) approach, the cluster prototypes (i.e., medoids) are units actually observed and not “virtual” units like the “centroids” derived with a fuzzy c-means (Bezdek, 1981). Overall, having non-fictitious representative units available makes interpreting the obtained clusters easier (Kaufman and Rousseeuw, 2005a). In addition, PAM procedure provides a “timid robustification” of the c-means clustering (García-Escudero and Gordaliza, 1999, García-Escudero et al., 2010). Robustness: we consider in the clustering process a suitable transformation (exponential transformation) of the distance measure (exponential distance) capable to smooth the effect of the outliers and to tune their influence properly. In particular, the exponential distance gives less importance to outliers and more importance to those data points laying close to the bulk of the data set (for more details see Wu and Yang, 2002, D’Urso et al., 2015). Fuzziness: fuzzy clustering appears more attractive than the traditional clustering methods when it is difficult to identify a clear boundary among clusters (McBratney and Moore, 1985, Wedel and Kamakura, 2000). In addition, the memberships indicate whether there is a second-best cluster almost as good as the best cluster, a scenario which standard clustering methods cannot uncover (Everitt et al., 2011). Furthermore, fuzzy clustering is attractive because it is easily compatible with distribution free methods (Hwang et al., 2007) and it is computationally efficient (McBratney and Moore, 1985, Heiser and Groenen, 1997). For more details, see D’Urso (2015). Temporal information: the time series are “re-parametrized” by means of the B-splines; in this manner, the temporal information of the time series is preserved considering a reduced number of values (the estimates of the splines coefficients) instead of the numerous actual observations of the time series. In this way we are able to preserve time information in the clustering process in a more parsimonious way from a computational point of view. Furthermore, our method inherits all the theoretical benefits of the B-splines in the time series clustering process (de Boor, 2001). Spatial information: our clustering method is capable to take into account the spatial information by means of a spatial penalty term defined on the basis of the following assumption: “...when a spatial unit belongs to a cluster with a high membership degree, then the penalty term forces the neighbouring spatial units to have high membership degrees in the cluster, as much as possible. In other words, it is expected that a spatial unit with high (low) membership degree in a cluster, will have neighbouring areas with low (high) membership degrees in the remaining clusters. It follows that the spatial penalty term attempts to determine a spatially smoothed membership degrees under the empirical evidence that neighbouring spatial units are often characterized by approximately similar features. Nonetheless, it may also occur that neighbouring spatial units are described by pretty diverse profiles. In this respect, there is a parameter which plays the role of increasing or decreasing the emphasis of the spatial penalty term in the clustering process” (Coppi et al., 2010). For this purpose, the parameter is chosen on the basis of an appropriate spatial autocorrelation measure.
The paper is structured as follows. Section 2 describes data formalization and processing, Section 3 the proposed BS-Exp-FCMd-S clustering model while Section 4 the application of the model to COVID-19 data. The last section addresses some conclusions.
2. Data formalization and B-spline modelling
A two-way data array of type “same objects same quantitative variable occasions”, in which the objects are spatial units (geographical areas, pixels, etc.) and the occasions are times, is called spatial-time data array.
In this study, the Italian regions are analysed with respect to variables related to COVID-19 pandemic, collected daily over one year. Therefore, the corresponding objects of the spatial-time data array are represented by the Italian regions, the corresponding variable by a COVID-19 variable and the occasions by the days under consideration.
In a formal way, a spatial-time data matrix can be algebraically formalized as (D’Urso, 2000, D’Urso, 2004, D’Urso, 2005):
| (1) |
where indicates the generic spatial unit and the generic time; is the value of the variable observed for the th unit at time . The time data matrix can be conveniently represented as the set of vectors:
| (2) |
The spatial proximity between the objects is described by means of the contiguity matrix . It is a symmetric matrix with zero diagonal elements and with off-diagonal elements given by ():
Contiguity, on its turn, can be specified in several ways, for instance, two spatial units can be contiguous: if they are adjacent (neighbours); if they belong to the same macro-area, even if they are not adjacent. In both cases, a binary index can be created where 1 is assigned to contiguous spatial units, 0 otherwise. Different definitions of connectivity and contiguity can be embedded in the clustering procedure.
2.1. B-splines
A time series is the result of collecting a variable on unit at the times . Given a -dimensional functional basis , we can model that time series by a simple linear least-squares fit as:
Thus, for time series , , we will obtain vectors of fitted coefficients , . Notice that these parameters can be determined by using ordinary least squares regression. We consider the cubic B-spline bases. Notice that, considering interior knots , a cubic B-spline basis will be made up of basis elements. To fit a cubic spline to a data set with knots we perform least square regression with an intercept and predictors, of the form and truncated cubic functions (one per knot).
Other functional bases may be used, Fourier basis when the data curves exhibit periodical nature, wavelets basis that allows multiresolution analysis (in time and frequency scale). Cubic B-spline bases have good mathematical properties and are easy to implement (de Boor, 2001). Notice also that cubic B-spline bases have an attractive property in that they are locally sensitive to data (each parameter is nonzero over a span of at most five distinct nodes).
One option for the choice of the number of knots is to try out different numbers of knots and see which produces the best looking curve. A more objective approach is to assess the accuracy of the model using the Residual Sum of Squares (RSS) between observed values and predicted values. A portion of the data is removed, a spline with a certain number of knots is fitted to the remaining data, and then the splines are used to make predictions for the held-out portion. The process is repeated multiple times until each observation has been left out once, and then RSS is computed. The procedure is repeated for different number of knots and the value corresponding to the smallest RSS is chosen.
2.2. Exponential distance
Let and be the vectors of fitted spline coefficients of time series and . In order to deal with outlier time series the complementary exponential distance is introduced. The exponential distance between two vectors of coefficients is defined as (Wu and Yang, 2002, Zhang and Chen, 2004):
| (3) |
The exponential distance gives a small weight to those noisy points or outliers and a large weight to those compact points in the data set. First, it should be noted that the exponential distance is bounded by 1. Second, as the value of increases, the distance tends more rapidly to its maximum value.
The parameter plays an important role in the distance. Hence, if is too high, in the classification process each time series is a singleton, since it has no neighbours. Fig. 1 shows the effect of increasing values of on the exponential distance. Following Wu and Yang (2002), is set as the inverse of the variability of the data:
| (4) |
where , i.e. the vector of coefficients closest to all other vectors.
Fig. 1.
Effect of the parameter on the exponential distance (3).
The value of appropriately tunes the distance according to the variability of the data so that in the presence of low variability moderate distances are heavily magnified.
See Wu and Yang (2002) for further insights on the robustness of the exponential distance.
3. The BS-Exp-FCMd-S clustering model with spatial penalty term
In this study, a suitable version of the well-known fuzzy -Medoids (FCMd) algorithm is proposed. More specifically, the FCMd with spatial penalty term and squared Exponential distance is adopted, after transforming the times series onto the coefficients of the projection on a B-splines functional basis. As known, the FCMd technique allows to identify non-fictitious representative time series, the so called “medoids” favouring the interpretation of the final partition (Kaufman and Rousseeuw, 2005b).
Its main advantage is related to a series of computational aspects: it is more efficient since the distance matrix needs to be computed once at the beginning of the iterative process and it is less affected by getting stuck in a local optima or by convergence problems (Everitt et al., 2001, Hwang et al., 2007).
The BS-Exp-FCMd-S clustering model can be defined as follows:
| (5) |
where and are the vectors of coefficients of the B-spline representation of the th spatial time series and of the th spatial medoid (c 1,…,C) respectively, while is well-known fuzziness parameter.
As far as the spatial penalty term is concerned:
it is worth noting that has to be seen as the tuning parameter of spatial information; is the generic element of the “contiguity” matrix while is the set of the clusters but cluster .
The is the membership degree of the unit belonging to the cluster , that is equal to:
| (6) |
We argue again that the role of the spatial penalty term is of increasing, for all spatial units contiguous to th unit, their final membership degrees to the cluster to which belongs.
In the next paragraph, we introduce the validity measure used in the application to choose the best partition.
3.1. Validity measure
In order to choose the best solution in terms of number of groups, in this study we adopt the Fuzzy Silhouette () index (Campello and Hruschka, 2006), one of the most known cluster internal validity criteria based on the weighted average of the individual silhouettes width, , as follows:
| (7) |
where is the average distance of object to all other objects belonging to the same cluster (, …, ) and is the minimum (over clusters) average distance of the th unit to all units belonging to the cluster with . is the weight of each , where and correspond to the first and the second largest element of the th column of the fuzzy partition matrix , respectively; is an optional user defined weighting coefficient. Setting , it reduces to the crisp Silhouette measure.
A higher value of means a better assignment of the units to the clusters implying that, simultaneously, the intra-cluster distance is minimized while the intercluster distance is maximized.
3.2. Spatial autocorrelation
As deeply analyzed in Coppi et al. (2010), the optimal choice of the value of the parameter is a very complex issue. It has to be set exogenously by means of a heuristic procedure based on the spatial autocorrelation measure introduced in Coppi et al. (2010), that could be seen as a generalization of the Moran’s index (Moran, 1950a). For a chosen value of and , the algorithm is run for increasing values of (chosen in a suitable interval): the optimal value is that maximizes the within cluster spatial autocorrelation. Properly, it maximizes the Global Moran overall spatial autocorrelation measure that, for a given partition, is computed as follows:
| (8) |
where .
The , the spatial autocorrelation measure for the th cluster, is computed as:
| (9) |
where is the centred “compromise” vector (mean of the vectors ); is the square diagonal matrix (of order ) of the membership degrees of cluster , and is the spatial contiguity matrix. The operator creates a diagonal matrix whose elements in the main diagonal are the same as those of the square matrix in the argument. If is a contiguity matrix with 0/1 values, every diagonal element contains the number of neighbouring units for the associated spatial unit. It is important to observe that (9) is very similar to the measure proposed by Moran (1950b). The main difference concerns the matrix , which tunes the contribution of the neighbours.
The vector (mean of the vectors ) was also used to compute (9) with the same results.
As for Moran’s index, also for , a value of () identifies a perfect positive (negative) autocorrelation, while indicates the absence of autocorrelation. Therefore, to higher values of the corresponds a better spatial assignment of the units to the clusters.
3.3. The BS-Exp-FCMd clustering model
With the choice the spatial regularization term is not taken into account. In this case only the temporal information is taken into account in the clustering process. Then, we obtain the BS-Exp-FCMd clustering model formalized as follows:
| (10) |
The membership degree of the unit belonging to the cluster , is equal to:
| (11) |
4. Clustering of Italian regions — COVID-19 data
In this study, we proposed the BS-Exp-FCMd clustering model with spatial penalty term (BS-Exp-FCMd-S) to COVID-19 data collected during the pandemic in order to cluster Italian regions. Specifically, the data refer to variables observed on 20 Italian regions2 during 351 times represented by the days from 2020-02-24 to 2021-02-08. Dealing with Italian regions, we expect that there would be a strong highly positive spatial autocorrelation between units, that motivates the use and application of a space–time series clustering model.
To apply the proposed BS-Exp-FCMd-S clustering model the following procedure has been taken into account (Coppi et al., 2010). The optimal number of clusters has been identified running the model, with and , and choosing the number of groups that maximizes the Fuzzy Silhouette index described in Section 3.1. The optimal value of the tuning parameter is chosen according to the procedure described in Section 3.2; in detail, we ran the algorithm, with fixed number of groups selected by the Fuzzy Silhouette index and , for all values of in the range with increasing steps equal to 0.01. To assign each region to a specific cluster we have set cut-off values. In two (three) cluster partitions the th time series is assigned to the th cluster if its fuzzy membership degree was (). Notice that the chosen cut-off point for the membership degrees is compatible with the indications suggested in literature; see, e.g., D’Urso and Maharaj, 2009, Maharaj et al., 2010, Maharaj and D’Urso, 2011, Dembélé and Kastner, 2003 and Lafuente-Rego et al. (2018). Time series membership degrees in the interval () define fuzzy time series. One notices that, in the contiguity matrix, Calabria and Sicily have been considered contiguous since they are separated only by the Strait of Messina and the coasts are very close, with very frequent ferry connections. Moreover, the number of knots has been set to 50 according to the number of weeks in the reference period of time.
In the following sections, the clustering results will be described in detail with reference to the total cases over population (per 10 000 inhabitants), the total deaths over population (per 10 000 inhabitants) and the total cases over swabs, respectively, spanning from 2020-02-24 to 2021-02-08. One notices that total cases include active cases (infected patients) and closed cases (deaths and recovery/discharged). As far as the cumulative cases over monitored cases (over swabs) are concerned, we argue that the quality of clustering results is strictly related to the strategies of contact tracing and to the number of available daily swabs that are variable among regions and over time making this kind of data much less reliable.
4.1. Total cases over population
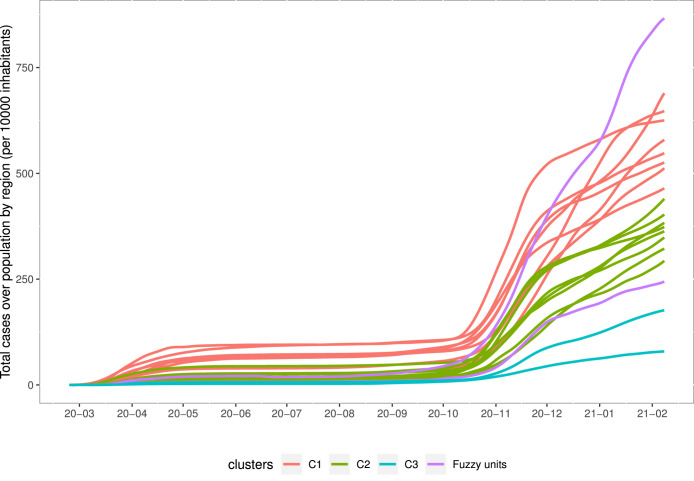
The total number of cases over population (per 10 000 inhabitants), by region, is shown in Fig. 2 while the daily number of new infections over population (per 10 000 inhabitants), by region, is shown in Fig. 3, spanning from 2020-02-24 to 2021-02-08. Both graphs well highlight regional heterogeneity and, looking at the second graph, in particular, we can clearly distinguish two peaks in correspondence of the first and second wave; the latter have soon surpassed the incidence rate of the former essentially because contact tracing has been more accurate and faster, carrying out more swab tests daily.
Fig. 2.
Total cases over population by region (per 10 000 inhabitants).
Fig. 3.
New infections over population (per 10 000 inhabitants).
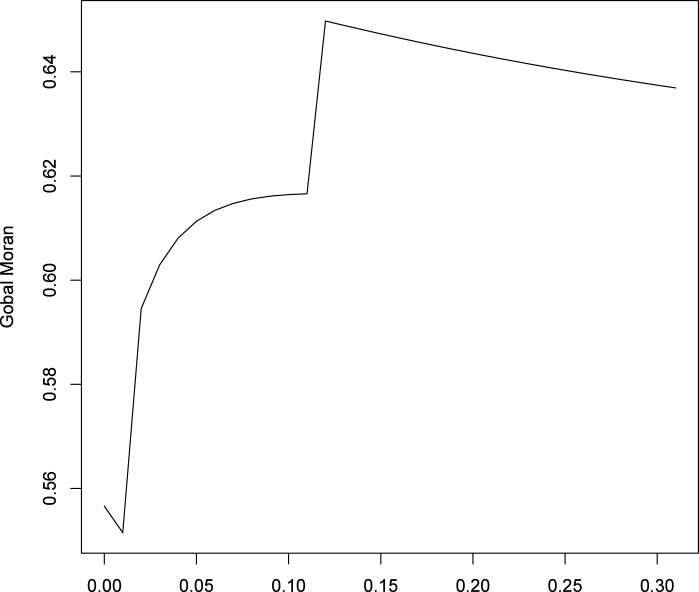
The BS-Exp-FCMd-S clustering model with spatial penalty term has been applied with reference to the total number of cases over population (per 10 000 inhabitants). The Fuzzy Silhouette index selected three groups showing a value of 0.52. Fig. 4 shows the values of the spatial correlation index (9) over . The optimum value of is 0.12 related to a value of Global Moran index . The membership degrees for the partition without and with penalty term are shown in Table 1; the latter is also reported in the ternary plot of Fig. 5. The corresponding partition is plotted in both Fig. 6, Fig. 7 to emphasize the clustering results in time and space, respectively.
Fig. 4.
Spatial correlation over .
Table 1.
Total cases over population (per 10 000 inhabitants) — 3 clusters memberships.
| Region | Model with no spatial penalty () |
Model with spatial penalty () |
|||||
|---|---|---|---|---|---|---|---|
| Cluster 1 | Cluster 2 | Cluster 3 | Cluster 1 | Cluster 2 | Cluster 3 | ||
| Piedmont | Lazio | Basilicata | Piedmont | Lazio | Calabria | ||
| 1 | Piedmont | 1.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| 2 | Aosta Valley | 0.646 | 0.179 | 0.174 | 0.697 | 0.154 | 0.150 |
| 3 | Lombardy | 0.989 | 0.006 | 0.005 | 0.992 | 0.004 | 0.003 |
| 4 | Trentino–South Tyrol | 0.910 | 0.049 | 0.041 | 0.936 | 0.035 | 0.029 |
| 5 | Veneto | 0.759 | 0.134 | 0.106 | 0.849 | 0.083 | 0.068 |
| 6 | Friuli-Venezia Giulia | 0.622 | 0.266 | 0.112 | 0.688 | 0.222 | 0.089 |
| 7 | Liguria | 0.923 | 0.055 | 0.023 | 0.881 | 0.087 | 0.032 |
| 8 | Emilia-Romagna | 0.814 | 0.137 | 0.049 | 0.784 | 0.160 | 0.056 |
| 9 | Tuscany | 0.042 | 0.911 | 0.047 | 0.095 | 0.860 | 0.045 |
| 10 | Umbria | 0.070 | 0.878 | 0.052 | 0.031 | 0.953 | 0.016 |
| 11 | Marche | 0.010 | 0.957 | 0.034 | 0.019 | 0.964 | 0.017 |
| 12 | Lazio | 0.000 | 1.000 | 0.000 | 0.000 | 1.000 | 0.000 |
| 13 | Abruzzo | 0.001 | 0.995 | 0.005 | 0.000 | 0.999 | 0.000 |
| 14 | Molise | 0.001 | 0.044 | 0.955 | 0.013 | 0.943 | 0.044 |
| 15 | Campania | 0.025 | 0.943 | 0.032 | 0.020 | 0.964 | 0.015 |
| 16 | Apulia | 0.005 | 0.289 | 0.706 | 0.018 | 0.910 | 0.072 |
| 17 | Basilicata | 0.000 | 0.000 | 1.000 | 0.044 | 0.433 | 0.523 |
| 18 | Calabria | 0.024 | 0.059 | 0.918 | 0.000 | 0.000 | 1.000 |
| 19 | Sicily | 0.414 | 0.295 | 0.291 | 0.376 | 0.279 | 0.345 |
| 20 | Sardinia | 0.160 | 0.213 | 0.627 | 0.027 | 0.036 | 0.937 |
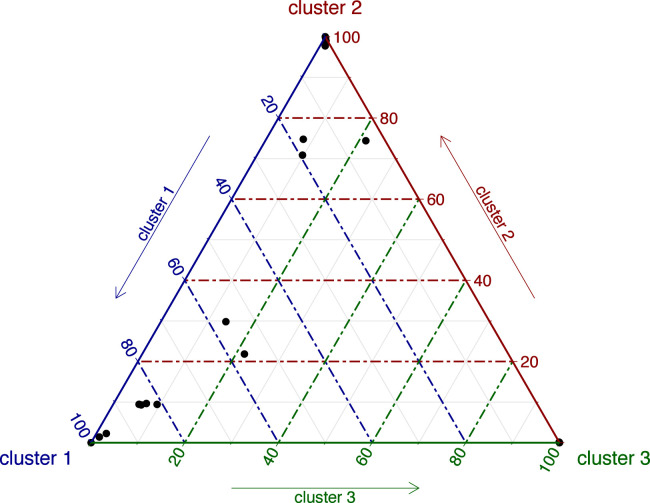
Fig. 5.
Total cases over population (per 10 000 inhabitants) — ternary plot.
Fig. 6.
Total cases over population (per 10 000 inhabitants) — partition of the daily time-series.
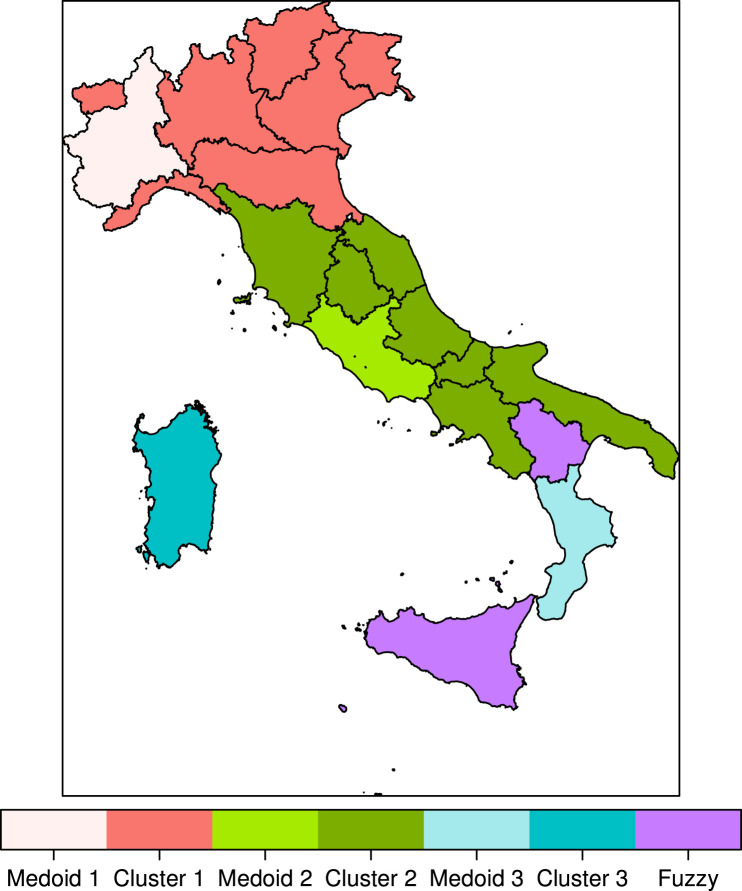
Fig. 7.
Total cases over population (per 10 000 inhabitants) — partition map.
Focusing on the partition with spatial penalty term, three clusters are clearly identified. The first cluster, with medoid Piedmont, also includes Aosta Valley, Lombardy, Trentino–South Tyrol, Veneto, Friuli-Venezia Giulia, Liguria and Emilia-Romagna, all the Northern regions characterized by a higher number of total infections over time that firstly faced the second wave too. The second cluster, with medoid Lazio, also collects Tuscany, Umbria, Marche, Abruzzo, Molise, Campania and Apulia; they are central-southern regions for which the number of total infections over time was, however, lower and that faced the second wave later than the first group. The third cluster, with medoid Calabria, also includes Sardinia with a high membership degree, Sicily and Basilicata, that can be classified as fuzzy being their membership degree less than 0.6. Calabria and Sardinia are characterized by the lowest number of total cases over time that also faced the second wave later with respect to all other Italian regions. It is worth noticing that while Basilicata is clearly a fuzzy unit sharing features belonging to the clusters 2 and 3, the low membership of Sicily is due to an anomalous increase of infections during the second wave, as we can see by looking at Fig. 3 showing the twofold sharp increase of new infections in Sicily, that exhibits amongst the highest values.
With respect to the partition without spatial penalty term, the Molise region moves from the cluster with medoid Basilicata, not contiguous with the former, to the cluster with medoid Lazio, contiguous instead. As far as Sicily is concerned, with the spatial penalty term, its membership in cluster 1 is fuzzier than it was without penalty term (0.376 versus 0.414) and it is also comparable to that of the cluster 3, whose medoid is Calabria, its contiguous region. The memberships of the regions considering the spatial penalty term are improved.
4.2. Total deaths over population
The total deaths over population due to COVID-19 disease, by region, is shown in Fig. 8, spanning from 2020-02-24 to 2021-02-08. The trends are comparable with those referred, in the previous section, to the number of infections. Even if they are cumulative values, the time series give fair evidence of the effects of two pandemic waves, with the Northern regions more hit by the outbreak, especially in the first phase. Sicily deserves attention being the only Southern region with a worrying upward trend of deaths in the last period, similar to that of the Northern areas.
Fig. 8.
Total deaths over population by region (per 10 000 inhabitants).
To this purpose, a little focus on the main results presented in the last available official report jointly produced by the Italian National Institute of Statistics (Istat) and the Italian National Institute of Health (ISS) (Istat and Iss, 2020) about total excess mortality during the period January–November 2020, is particularly useful.
In the report, one has been confirmed that the fatality rate for people aged under 50 was about 1% for both males and females while people aged over 80 were the most hit, males more than females, representing the 60% of all COVID-19 deaths.
In general, COVID-19 deaths weighted the 13% out of the total mortality, in the first wave (February–May 2020), to rise to 16% in the second wave (end of September–November 2020).
During the first pandemic wave, from March to May , the number of total deaths was more than , more than the average recorded in the same period with reference to the years 2015–2019. Moreover, of these were residents in the Northern regions; in particular, the same areas recorded an increase of deaths equal to in March 2020 and to in April 2020, if compared to the average value recorded in the same month of the years 2015–2019.
The highest price has been paid by Lombardy () while the other Northern regions recorded a rate between the 28% and 38%: only Veneto and Friuli-Venezia Giulia recorded lower rates, and , respectively. Among Central regions, it is worth noting the case of Marche with an increment of , considerably higher if compared with the same average increment recorded by the geographic partition to which it belongs .
The number of total deaths, for all regions, became comparable with those of the reference period 2015–2019 only during the summer increasing, once again, in correspondence on the second pandemic wave, beginning at the end of September 2020. The excess mortality, in November 2020, was in the North, in the Centre, and in the South. Many Northern regions exceeded the peak recorded in March–April 2020: Aosta Valley ( versus in April 2020), Piedmont ( versus in April 2020), Veneto ( versus in April 2020) and Friuli-Venezia Giulia ( versus in April 2020).
In countertrend there were only Lombardy ( versus in March 2020 and in April 2020) and Emilia-Romagna ( versus in March 2020).
Moreover, in the summer and in the second wave, the median age class of deaths rose both for male and females (85–89 years for females versus 80–84 years in the first wave; 80–84 years for males versus 75–79 years in the first wave); moreover, the higher age of deaths was also accompanied by a higher severity of comorbidities in the population of deaths.
In this second outbreak wave, many regions belonging to the Centre and South of Italy experienced, for the first time, an increase of mortality for all causes. Even if the excess mortality by age was similar to that of the Northern regions, their increments were however considerably lower than those recorded by Northern regions in March and April 2020 with reference to the same age classes. The Fuzzy Silhouette index identified three groups showing a value of 0.63 while the optimum value of is 0.5 related to a value of the Global Moran index . The membership degrees for the partition without and with penalty term are shown in Table 2; the latter is also reported in the ternary plot of Fig. 9. The corresponding partition is plotted in both Fig. 10, Fig. 11 to emphasize the clustering results in time and space, respectively.
Table 2.
Total deaths over population (per 10 000 inhabitants) — 3 clusters memberships.
| Region | Model with no spatial penalty () |
Model with spatial penalty () |
|||||
|---|---|---|---|---|---|---|---|
| Piedmont | Veneto | Campania | Trentino–South Tyrol | Lazio | Calabria | ||
| 1 | Piedmont | 1.000 | 0.000 | 0.000 | 0.956 | 0.023 | 0.021 |
| 2 | Aosta Valley | 0.452 | 0.280 | 0.267 | 0.563 | 0.218 | 0.218 |
| 3 | Lombardy | 0.433 | 0.287 | 0.281 | 0.812 | 0.094 | 0.094 |
| 4 | Trentino–South Tyrol | 0.496 | 0.480 | 0.024 | 1.000 | 0.000 | 0.000 |
| 5 | Veneto | 0.000 | 1.000 | 0.000 | 0.975 | 0.014 | 0.011 |
| 6 | Friuli-Venezia Giulia | 0.005 | 0.988 | 0.006 | 0.850 | 0.095 | 0.055 |
| 7 | Liguria | 0.997 | 0.002 | 0.001 | 0.834 | 0.097 | 0.070 |
| 8 | Emilia-Romagna | 0.997 | 0.002 | 0.001 | 0.846 | 0.093 | 0.061 |
| 9 | Tuscany | 0.042 | 0.606 | 0.352 | 0.194 | 0.708 | 0.097 |
| 10 | Umbria | 0.002 | 0.008 | 0.990 | 0.004 | 0.990 | 0.007 |
| 11 | Marche | 0.165 | 0.744 | 0.091 | 0.173 | 0.748 | 0.079 |
| 12 | Lazio | 0.001 | 0.005 | 0.994 | 0.000 | 1.000 | 0.000 |
| 13 | Abruzzo | 0.046 | 0.621 | 0.333 | 0.011 | 0.978 | 0.011 |
| 14 | Molise | 0.001 | 0.003 | 0.997 | 0.000 | 1.000 | 0.000 |
| 15 | Campania | 0.000 | 0.000 | 1.000 | 0.001 | 0.997 | 0.002 |
| 16 | Apulia | 0.001 | 0.002 | 0.998 | 0.001 | 0.998 | 0.001 |
| 17 | Basilicata | 0.000 | 0.000 | 1.000 | 0.042 | 0.744 | 0.215 |
| 18 | Calabria | 0.004 | 0.007 | 0.989 | 0.000 | 0.000 | 1.000 |
| 19 | Sicily | 0.037 | 0.923 | 0.040 | 0.563 | 0.298 | 0.139 |
| 20 | Sardinia | 0.013 | 0.018 | 0.969 | 0.000 | 0.001 | 0.999 |
Fig. 9.
Total deaths over population (per 10 000 inhabitants) — ternary plot.
Fig. 10.
Total deaths over population (per 10 000 inhabitants) — partition of the daily time-series.
Fig. 11.
Total deaths over population (per 10 000 inhabitants) — partition map.
Focusing on the partition based on spatial penalty, the first cluster, with medoid Trentino–South Tyrol, includes all Northern regions while the second cluster, with medoid Lazio, all its neighbour Central regions (Tuscany, Marche and Umbria) and all the Southern regions but Calabria, Sicily and Sardinia. It is worth noting that Tuscany, Marche and Basilicata belong to the second cluster with a membership degree considerably lower if compared with the other units of the same cluster. The membership of Marche could be explained taking into account that it was the only region, in the first wave, with an excess of deaths considerably higher if compared to that of its neighbour regions.
The third group is a nich cluster composed only by Calabria, the medoid, and Sardinia, both characterized by the lowest values of mortality rates.
Two fuzzy units have been identified, that are Aosta Valley and Sicily; the former is a clear global outlier, as one can see by inspecting its trend with an abnormal upward step in the last period; the latter is a clear local outlier since its upward trend, in the second pandemic wave, does not match with those of the other Southern regions. The anomalous trend of Aosta Valley had been already observed in the last November whose excess of total mortality went up to , if compared with the average value recorded in the same month of period 2015–2019, as already mentioned.
The three clusters identified three profile, from that which paid the highest price in terms of deaths to that which paid the least price; indeed, the first cluster included all regions with the highest number, and also the highest increase in time, of the mortality due COVID-19 pandemic.
The model with the spatial penalty had a substantially different partition from that for the model without the spatial penalty; all fuzzy units in the latter with the exception of Aosta Valley became non-fuzzy in the former, and they were assigned to the groups of its own geographically nearest units.
Furthermore, not all units belonging to the second group in the model with no spatial penalty, with medoid Veneto, were assigned to the same group in the model with spatial penalty. Indeed, the Veneto region was included in the cluster 1, whose new medoid was the contiguous region Trentino–South Tyrol, together with Friuli-Venezia Giulia, that is contiguous with Veneto. Tuscany, Marche and Abruzzo, instead, were assigned to the group of its contiguous regions (cluster 2 of the model with spatial penalty). Abruzzo, in particular, moved to the cluster with medoid Lazio with a high membership degree.
The added value produced by the robust spatial model is evident when we consider Sicily. Its membership degree (0.923), associated to the first cluster with medoid Veneto, had been considerably reduced so that it became a fuzzy unit in the spatial model. In other words, the model with penalty term and squared exponential distance is able to detect the presence of local outliers of particular interest in spatial statistics.
4.3. Total cases over swabs
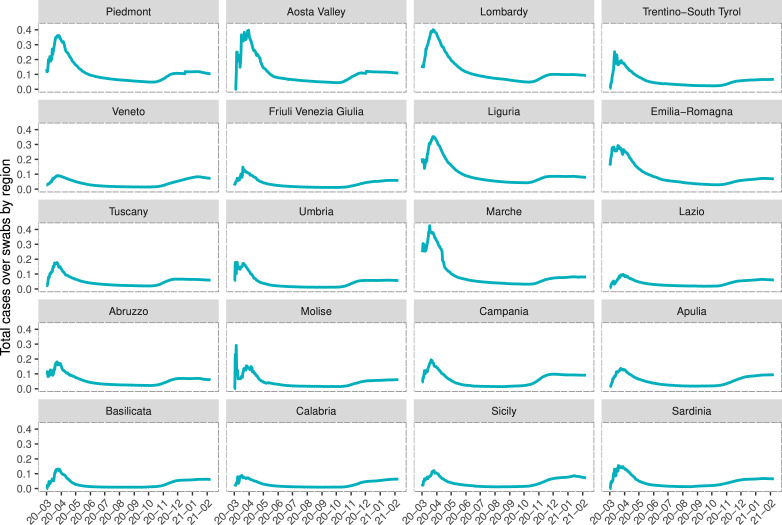
In October 2020 Health Minister announced quick swabs in pharmacy as already carried out in some regions and an agreement with general practitioners to carry out the rapid swabs. The total cases over swabs are presented by region in Fig. 12 spanning from 2020-02-24 to 2021-02-08. The regional heterogeneity on the onset of an epidemic outbreak, the occurrence of possible recurrent epidemic waves and the policy about swabs can be analysed in terms of the range of the variable and the time of occurrence of changes.
Fig. 12.
Total cases over swabs by region.
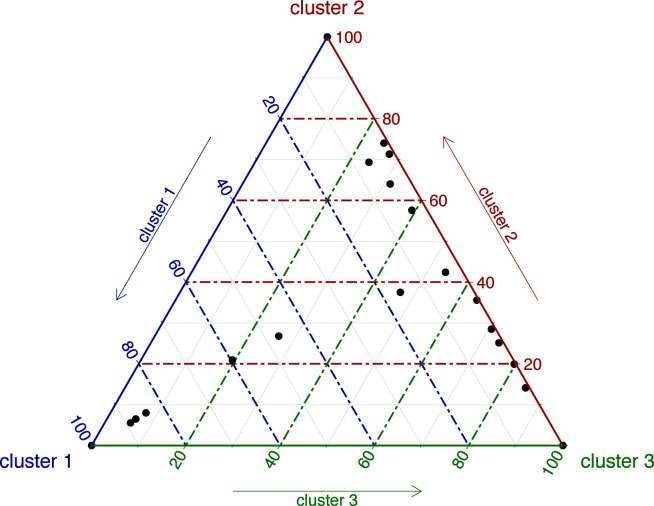
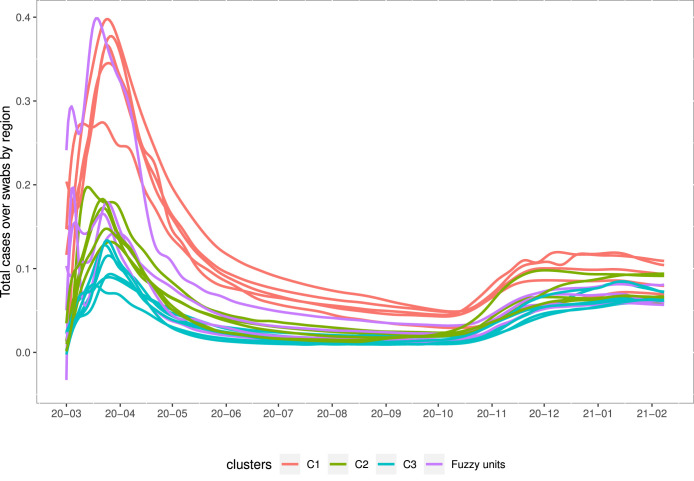
The Fuzzy Silhouette index selected three groups showing a value of 0.42. The optimum value of the spatial correlation index (9) over is 0.10 related to a value of Global Moran index . The membership degrees for the partition without and with penalty term are shown in Table 3; the latter is also reported in the ternary plot of Fig. 13. The corresponding partition is plotted in both Fig. 14, Fig. 15 to emphasize the clustering results in time and space, respectively.
Table 3.
Total cases over swabs by region — 3 clusters memberships.
| Region | Model with no spatial penalty () |
Model with spatial penalty () |
|||||
|---|---|---|---|---|---|---|---|
| Piedmont | Tuscany | Friuli-Venezia Giulia | Piedmont | Sardinia | Friuli-Venezia Giulia | ||
| 1 | Piedmont | 1.000 | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 |
| 2 | Aosta Valley | 0.836 | 0.086 | 0.078 | 0.845 | 0.080 | 0.075 |
| 3 | Lombardy | 0.905 | 0.048 | 0.047 | 0.890 | 0.055 | 0.055 |
| 4 | Trentino–South Tyrol | 0.046 | 0.773 | 0.181 | 0.065 | 0.693 | 0.242 |
| 5 | Veneto | 0.006 | 0.107 | 0.887 | 0.010 | 0.251 | 0.739 |
| 6 | Friuli-Venezia Giulia | 0.000 | 0.000 | 1.000 | 0.000 | 0.000 | 1.000 |
| 7 | Liguria | 0.877 | 0.065 | 0.058 | 0.874 | 0.065 | 0.061 |
| 8 | Emilia-Romagna | 0.572 | 0.237 | 0.191 | 0.600 | 0.206 | 0.194 |
| 9 | Tuscany | 0.000 | 1.000 | 0.000 | 0.012 | 0.713 | 0.275 |
| 10 | Umbria | 0.028 | 0.512 | 0.460 | 0.037 | 0.424 | 0.539 |
| 11 | Marche | 0.486 | 0.263 | 0.251 | 0.469 | 0.268 | 0.263 |
| 12 | Lazio | 0.005 | 0.085 | 0.911 | 0.009 | 0.285 | 0.706 |
| 13 | Abruzzo | 0.016 | 0.778 | 0.206 | 0.033 | 0.576 | 0.392 |
| 14 | Molise | 0.153 | 0.389 | 0.458 | 0.158 | 0.375 | 0.467 |
| 15 | Campania | 0.028 | 0.784 | 0.188 | 0.046 | 0.640 | 0.313 |
| 16 | Apulia | 0.011 | 0.664 | 0.324 | 0.010 | 0.740 | 0.250 |
| 17 | Basilicata | 0.002 | 0.040 | 0.957 | 0.004 | 0.199 | 0.797 |
| 18 | Calabria | 0.009 | 0.081 | 0.910 | 0.009 | 0.141 | 0.850 |
| 19 | Sicily | 0.006 | 0.167 | 0.827 | 0.005 | 0.356 | 0.640 |
| 20 | Sardinia | 0.003 | 0.658 | 0.338 | 0.000 | 1.000 | 0.000 |
Fig. 13.
Total cases over swabs — ternary plot.
Fig. 14.
Total cases over swabs — partition of the daily time-series.
Fig. 15.
Total cases over swabs — partition map.
Focusing on the partition with spatial penalty, three clusters are clearly identified. The first cluster, with medoid Piedmont, collects the Northern regions Aosta Valley, Lombardy, Liguria, Emilia-Romagna. With respect to the other regions, they show higher values of the variable total cases over swabs, that stand in the second wave. The second cluster, with medoid Sardinia, collects the Central and Southern regions of Tuscany, Campania, Apulia and the northern region of Trentino–South Tyrol. The values of the variable total cases over swabs are lower and stand lower with respect to cluster 1. The third cluster, with medoid Friuli-Venezia Giulia, collects Northern, Central and Southern regions: Veneto, Lazio, Basilicata, Calabria, Sicily. The values of the variable total cases over swabs are the lowest. Four regions, Umbria, Marche, Abruzzo and Molise are classified as fuzzy as their membership to the cluster is less than 0.6. They share the characteristics of two clusters. The interpretation is facilitated by considering the variable cumulative swabs, showing the policies of monitored cases and swabs (Fig. 16).
Fig. 16.
Cumulative swabs.
With respect to the partition without spatial penalty term, the membership of Lazio and Sicily to the cluster with medoid the non contiguous region Friuli-Venezia Giulia decreases.
5. Conclusions
In this study, the Exponential distance-based Fuzzy -Medoids clustering algorithm based on B-splines with spatial penalty term (BS-Exp-FCMd-S) is applied to clustering of time series related to COVID-19 pandemic.
Data reduction is obtained by the use of B-splines, robustness is obtained by the use of the exponential distance while spatial information is taken into account by the use of a penalty term in the objective function.
We obtain on the entire period almost the same partition into yellow, orange and red area obtained on the basis of the 21 indicators considered by the Ministry of Health.
The results show that the heterogeneity among regions along with the spatial contiguity is essential to understand the spread of the pandemic and to design effective policies to mitigate the effects. In particular the clustering of the regions taking into account the spatial proximity along with socio-demographic profiling of the clusters might lead to similar data driven policies of prevention for regions sharing the same cluster.
Footnotes
Trentino–South Tyrol has recently been split into two different and autonomous provinces for administrative purposes (Provincia Autonoma di Trento and Provincia Autonoma di Bolzano). Here, the data of the two provinces have been summed up to recover data at a regional level.
References
- Basford K., McLachlan G. The mixture method of clustering applied to three-way data. J. Classification. 1985;2:109–125. [Google Scholar]
- Bezdek J. Kluwer Academic; Norwell, MA, USA: 1981. Pattern Recognition with Fuzzy Objective Function Algorithms. [Google Scholar]
- Birant D., Kut A. ST-DBSCAN: An algorithm for clustering spatial-temporal data. Data Knowl. Eng. 2007;60:208–221. [Google Scholar]
- de Boor C. Springer; 2001. A Practical Guide to Splines. [Google Scholar]
- Campello R., Hruschka E. A fuzzy extension of the silhouette width criterion for cluster analysis. Fuzzy Sets and Systems. 2006;157:2858–2875. [Google Scholar]
- Coppi R., D’Urso P., Giordani P. A fuzzy clustering model for multivariate spatial time series. J. Classification. 2010;27(1):54–88. [Google Scholar]
- Dembélé D., Kastner P. Fuzzy C-means method for clustering microarray data. Bioinformatics. 2003;19:973–980. doi: 10.1093/bioinformatics/btg119. [DOI] [PubMed] [Google Scholar]
- Disegna M., D’Urso P., Durante F. Copula-based fuzzy clustering of spatial time series. Spat. Statist. 2017;21:209–225. [Google Scholar]
- D’Urso P. Dissimilarity measures for time trajectories. Stat. Methods Appl. 2000;9(1–3):53–83. [Google Scholar]
- D’Urso P. Fuzzy C-means clustering models for multivariate time-varying data: Different approaches. Internat. J. Uncertain. Fuzziness Knowledge-Based Systems. 2004;12(3):287–326. [Google Scholar]
- D’Urso P. Fuzzy clustering for data time arrays with inlier and outlier time trajectories. IEEE Trans. Fuzzy Syst. 2005;13(5):583–604. [Google Scholar]
- D’Urso P. In: Handbook of Cluster Analysis. Hennig C., Meila M., Murtagh F., Rocci R., editors. Chapman and Hall; 2015. Fuzzy clustering; pp. 545–573. [Google Scholar]
- D’Urso P., De Giovanni L. Robust clustering of imprecise data. Chemometr. Intell. Lab. Syst. 2014;136:58–80. [Google Scholar]
- D’Urso P., De Giovanni L., Disegna M., Massari R. Fuzzy clustering with spatial–temporal information. Spat. Statist. 2019;30:71–102. [Google Scholar]
- D’Urso P., De Giovanni L., Massari R. Time series clustering by a robust autoregressive metric with application to air pollution. Chemometr. Intell. Lab. Syst. 2015;141:107–124. [Google Scholar]
- D’Urso P., Maharaj E.A. Autocorrelation-based fuzzy clustering of time series. Fuzzy Sets and Systems. 2009;160(24):3565–3589. [Google Scholar]
- Ester M., Kriegel H.-P., Sander J., Xu X. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining. AAAI Press; 1996. A density-based algorithm for discovering clusters in large spatial databases with noise; pp. 226–231. (KDD’96). [Google Scholar]
- Everitt B., Landau S., Leese M. forth ed. Arnold Press; London: 2001. Cluster Analysis. [Google Scholar]
- Everitt B., Landau S., Leese M., Stahl D. fifth ed. John Wiley & Sons, Ltd; London: 2011. Cluster Analysis. [Google Scholar]
- Gao, X., Yu, F., 2016. Fuzzy C-means with spatiotemporal constraints. In: Proceedings - 2016 IEEE International Symposium on Computer, Consumer and Control, IS3C 2016. pp. 337–340.
- García-Escudero L.Á., Gordaliza A. Robustness properties of k means and trimmed k means. J. Amer. Statist. Assoc. 1999;94:956–969. [Google Scholar]
- García-Escudero L.A., Gordaliza A., Matrán C., Mayo-Iscar A. A review of robust clustering methods. Adv. Data Anal. Classif. 2010;4:89–109. [Google Scholar]
- Heiser W., Groenen P. Cluster differences scaling with a within-clusters loss component and a fuzzy successive approximation strategy to avoid local minima. Psychometrika. 1997;62(1):63–83. [Google Scholar]
- Hu T., Sung S. A hybrid EM approach to spatial clustering. Comput. Statist. Data Anal. 2006;50(5):1188–1205. [Google Scholar]
- Hwang H., Desarbo W., Takane Y. Fuzzy clusterwise generalized structured component analysis. Psychometrika. 2007;72(2):181–198. [Google Scholar]
- Ienco D., Bordogna G. Fuzzy extensions of the DBScan clustering algorithm. Soft Comput. 2016:1–12. [Google Scholar]
- Iss, 2021. Characteristics of SARS-CoV-2 Patients Dying in Italy Report Based on Available Data on January 27th, 2021. Tech. rep., URL https://www.epicentro.iss.it/en/coronavirus/bollettino/Report-COVID-2019_27_january_2021.pdf.
- Istat, Iss, 2020. Impatto Dell’Epidemia COVID-19 Sulla Mortalità Totale della Popolazione Residente Periodo Gennaio-Novembre 2020. Tech. rep., URL https://www.istat.it/it/files//2020/12/Rapp_Istat_Iss.pdf.
- Izakian H., Pedrycz W., Jamal I. Clustering spatiotemporal data: An augmented fuzzy C-means. IEEE Trans. Fuzzy Syst. 2013;21(5):855–868. [Google Scholar]
- Kaufman L., Rousseeuw P. WileyBlackwell; 2005. Finding Groups in Data: An Introduction to Cluster Analysis. [Google Scholar]
- Kaufman L., Rousseeuw P. John Wiley & Sons; 2005. Finding Groups in Data: An Introduction to Cluster Analysis. [Google Scholar]
- Lafuente-Rego B., D’Urso P., Vilar J. Robust fuzzy clustering based on quantile autocovariances. Statist. Papers. 2018:1–56. [Google Scholar]
- Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., Ren R., Leung K.S., Lau E.H., Wong J.Y., Xing X., Xiang N., Wu Y., Li C., Chen Q., Li D., Liu T., Zhao J., Liu M., Tu W., Chen C., Jin L., Yang R., Wang Q., Zhou S., Wang R., Liu H., Luo Y., Liu Y., Shao G., Li H., Tao Z., Yang Y., Deng Z., Liu B., Ma Z., Zhang Y., Shi G., Lam T.T., Wu J.T., Gao G.F., Cowling B.J., Yang B., Leung G.M., Feng Z. Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N. Engl. J. Med. 2020;382(13):1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maharaj E.A., D’Urso P. Fuzzy clustering of time series in the frequency domain. Inform. Sci. 2011;181(7):1187–1211. [Google Scholar]
- Maharaj E., D’Urso P., Galagedera D. Wavelet-based fuzzy clustering of time series. J. Classification. 2010;27:231–275. [Google Scholar]
- McBratney A., Moore A. Application of fuzzy sets to climatic classification. Agricult. Forest Meteorol. 1985;35(1–4):165–185. [Google Scholar]
- Moran P. A test for the serial independence of residuals. Biometrika. 1950;37:178–181. [PubMed] [Google Scholar]
- Moran P. A test for the serial independence of residuals. Biometrika. 1950;37(1-2):178–181. [PubMed] [Google Scholar]
- Torabi M. Spatial generalized linear mixed models with multivariate CAR models for areal data. Spat. Statist. 2014;10:12–26. [Google Scholar]
- Torabi M. Hierarchical multivariate mixture generalized linear models for the analysis of spatial data: An application to disease mapping. Biom. J. 2016;58(5):1138–1150. doi: 10.1002/bimj.201500248. [DOI] [PubMed] [Google Scholar]
- Viroli C. Finite mixtures of matrix normal distributions for classifying three-way data. Stat. Comput. 2011;21(4):511–522. [Google Scholar]
- Wang M., Wang A., Li A. In: Advanced Data Mining and Applications: Second International Conference, ADMA 2006, Xi’an, China, August 14-16, 2006 Proceedings. Li X., Zaïane O.R., Li Z., editors. Springer; Berlin, Germany: 2006. Mining spatial-temporal clusters from geo-databases; pp. 263–270. (Advanced Data Mining and Applications). [Google Scholar]
- Wedel M., Kamakura W. Springer; 2000. Market Segmentation: Conceptual and Methodological Foundations, Vol. 8. [Google Scholar]
- Wu K.-L., Yang M.-S. Alternative c-means clustering algorithms. Pattern Recognit. 2002;35(10):2267–2278. [Google Scholar]
- Xie J., Gao H., Xie W., Liu X., Grant P. Robust clustering by detecting density peaks and assigning points based on fuzzy weighted -nearest neighbors. Inform. Sci. 2016;354:19–40. [Google Scholar]
- Zhang D.-Q., Chen S.-C. A comment on “Alternative c-means clustering algorithm”. Pattern Recognit. 2004;37(2):173–174. [Google Scholar]