Cytokine-mediated communications: a quantitative appraisal of immune complexity

Abstract

Intercellular communication mediated by cytokines is the main mechanism by which cells of the immune system ‘talk’ to each other. Many aspects of cytokine signaling in the immune system have been explored in great detail at the structural, biophysical, biochemical and cellular levels. However, a systematic understanding of the quantitative rules that govern cytokine-mediated cell-to-cell communication is still lacking. Here, we discuss recent efforts in the field of systems immunology to bring about a quantitative understanding of cytokine-mediated communication between leukocytes and to provide novel insights into the orchestration of immune responses and inflammation.

Table of Contents

Recent advances in systems immunology are beginning to elucidate the quantitative rules that govern cytokine-mediated cell-to-cell communication. This Review describes how combining theoretical analysis with experimental validation can lead to a better understanding of cytokine-mediated communication between cells of the immune system.

Introduction

Recent developments in systems immunology are starting to unravel the combinatorial complexity of cellular phenotypes during an immune response¹. With the advent of high-dimensional single-cell methodologies, such as single-cell RNA sequencing (RNA-seq) and mass cytometry^2,3, there has been an explosion of data in the past few years aimed at delivering a more global view of immune cell phenotypes. Together with a large number of machine learning packages that can analyse large quantities of data⁴, such studies have been extremely efficient in finding patterns of cell types or secreted molecules that are associated with disease-specific immune responses^1,4,5. However, these studies have been largely phenomenological and often fail to provide mechanistic and functional insights about the physiology of tissues beyond the cataloguing of the immunological eco-systems. An alternative approach has been the construction of dynamic models derived from explicit physico-chemistry^6–8. Although such models have been more useful for obtaining mechanistic insights into the collective behaviour of heterogeneous populations of cells, one shortcoming of such approaches is often a lack of experimental validation. Here, we review how taking a more quantitative and integrated approach, combining theoretical analysis with experimental validation, can lead to a better understanding of cytokine-mediated communication between cells of the immune system.

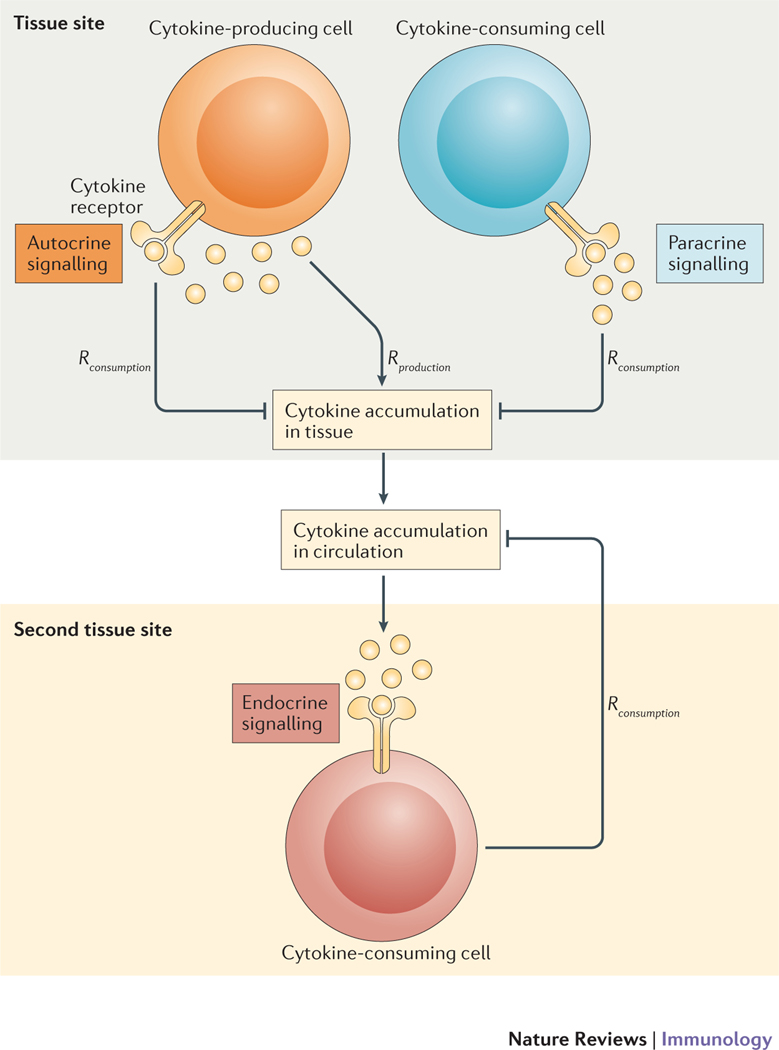
To mount an efficient and accurate response, immune cells must coordinate their individual activation into global tissue-level responses⁹: this requirement underscores the crucial relevance of cell-to-cell communication. Cross-talk between immune cells would remain local if it was only mediated by cell-to-cell contacts; consequently, the global regulation of inflammation requires long-range intercellular communication, as mediated by cytokines. Cytokines function by strongly binding to specific receptors on target cells and activating a cascade of downstream signaling events that culminate in the expression of a set of genes necessary for a specialized task. The mode of action of cytokines on their target cells can be autocrine [G], paracrine [G] or even endocrine [G]. Understanding the quantitative length scales at which cytokines function can provide new insights into the mechanisms by which immune responses can be fine-tuned.

In this Review, we first make a case for the need to obtain a dynamic understanding of cytokine secretion and cytokine consumption by immune cells over time as a tool to predict whether a given cytokine is of functional relevance during an immune response. Second, we present recent quantitative analyses that show how differences in the spatial distributions of cytokines regulate cell-to-cell variability in lymphocyte activation and differentiation. Third, we summarize studies that have investigated the mechanisms of cytokine secretion by immune cells and we discuss the possible implications for cytokine-mediated communication. Fourth, we review experimental studies that show how competition for cytokines between cell types can regulate the balance between immune tolerance and immune response, thus contributing to the maintenance of immune homeostasis. Finally, we discuss general quantitative aspects of signal integration involved in converting individual cell activation to collective, global responses. We conclude by arguing that a dynamic understanding of the cytokine network between immune cells can potentially lead to deeper immunological insights and the development of novel therapeutic strategies.

Time integration

To obtain a quantitative understanding of inflammation in lymphoid organs and tissues can seem initially to be a daunting task. Knowledge of the biophysics, biochemistry and cell biology of cytokine signaling has been accumulated (Table 1), but static maps of the dense and rich cytokine network¹⁰ seem to complicate any effort to understand cell-to-cell communication. However, recent efforts (building on previous work from biochemical and pharmaco-kinetic studies) are starting to show results in model systems^9,11–14. The premise of these studies is that cytokine-mediated communication is complicated but not mysterious a priori: leukocytes and their surrounding tissues respond to molecular cues, become activated, then produce and consume cytokines. Hence, the accumulation of a soluble cytokine in lymphoid organs and peripheral tissues is the result of two simple yet fundamental biochemical and cellular events of production and consumption, as shown in FIG. 1 and encapsulated by Equation 1.

Table 1 |.

Major cytokines of the immune system: sources and sinks

Cytokine	Signalling pathways	Molecular massa (kDa)	EC50a (pM)	Primary producing cells	Primary consuming cells	Refs
IL-1β	NF-κB, JNK and p38 MAPK	17.5	0.008–0.710	Monocytes, epithelial cells	Macrophages	80–82
IL-2	JAK1, JAK2, STAT5	15.5	3.2–16.0	CD4+T cells, NK cells	Treg Cells	12,13,83
IL-3	JAK2, STAT5	15	6.67–16.00	T cells, mast cells, eosinophils	HPCs, myeloid cells, lymphoid cells, erythroid cells	83,84
IL-4	JAK1, JAK3, STAT6	15	3.3–26.7	T cells, NKT cells, yδT cells, mast cells	B cells, T cells, macrophages	83,85
IL-5	JAK2, STAT5	13	3.08–15.40	TH2 cells, mast cells, eosinophils, NK cells	B cells, eosinophils	83,86
IL-6	JAK1, STAT3, STAT1, STAT5	21	0.38–38.00	T cells, macrophages, fibroblasts, endothelial cells	B cells, T cells, thymocytes	83,87
IL-7	JAK1, STAT5	17	5.9–117.0	Bone marrow stromal cells, epithelial cells	T cells, B cells, DCs	83,88
IL-8	p38 MAPK-ERK-AKT, NF-κB and JAK-STAT (JAK2, STAT3)	8	62.5–312.5	Monocytes,T cells, neutrophils, fibroblasts, endothelial cells	Neutrophils	83,89
IL-9	JAK1, JAK3, STAT5, STAT3	16	6.25–37.50	Mast cells, TH2 cells, TH17 cells, TH9 cells	T cells, B cells, mast cells, HPCs	83,90
IL-10	TYK2, JAK1, STAT3, STAT1	18.6	8.06–53.80	TH2 cells, macrophages, DCs, B cells	T cells, macrophages	83,91
IL-11	JAK1, STAT3, STAT1	19	1.05–6.31	Bone marrow stromal cells	HPCs, stromal cells	83,92
IL-12	TYK2, JAK2, STAT4	34.7 (p40) and 22.5 (p35)	0.14–2.90	Activated macrophages, DCs	Activated T cells, NK cells	83,93
IL-13	JAK1, STAT6	12.5	40–200	TH2 cells	B cells, eosinophils, fibroblasts, mast cells, macrophages	83,94
IL-15	JAK1, JAK3, STAT3, STAT5	13	153.8–769.2	DCs, monocytes, epithelial cells	T cells, NK cells, NKT cells	83,95
IL-17	NF-κB, ERK1 and ERK2, and p38 MAPK	15.5	129–387	TH17 cells, NK cells, NKT cells	Fibroblasts, endothelial cells, epithelial cells, keratinocytes, macrophages, DCs	83,96
IL-18	NF-κB, JNK and p38 MAPK	18	83.33–500.00	Macrophages	T cells, NK cells	97
IL-20	JAK1, JAK2, STAT3	17.6	11.36–34.00	Monocytes, granulocytes, keratinocytes, DCs, fibroblasts	Keratinocytes, endothelial cells, adipocytes	83,98
IL-21	JAK3, STAT3, STAT5	17	47	CD4+T cells,Th17 cells, NKT cells	B cells, NK cells, T cells	83,99–102
IL-23	TYK2, STAT3, STAT4, STAT5	55	0.9–5.4	DCs, macrophages, B cells, endothelial cells	TH17 cells, γδT cells, NKT cells, ILCs	83,93
G-CSF	JAK1, JAK2, STAT3	18.8	0.53–3.00	Monocytes, macrophages	Neutrophils	41,83,103–105
GM-CSF	JAK2, STAT5	14	0.43–2.10	Activated T cells, NK cells, macrophages	Granulocytes, monocyte precursors	83,106–108
CSF1	PI3K-AKT, ERK1 and ERK2, and JAK-STAT	37	13.5–40.5	Fibroblasts, endothelial cells, stromal cells, macrophages, osteoblasts	Monocytes, macrophages	109,110
IFNα	TYK2, JAK1, STAT1, STAT2	19.2	40	pDCs, NKcells.Tcells, B cells, macrophages, fibroblasts, endothelial cells, osteoblasts	Macrophages, NK cells	83,111
IFNγ	JAK1, JAK2, STAT1	17	2.9–44.0	T cells, NK cells, NKT cells	T cells, monocytes, macrophages	83,112–114
TNF	NF-κB, JNK, ERK1 and ERK2, and p38 MAPK	17.5	1.42–5.71	T cells, B cells, NK cells, macrophages	T cells, B cells, endothelial cells	115
TGFβ	JNK, p38 MAPK and SMAU	25	1.6–8.0	T cells, macrophages	T cells	116

^aMolecular masses and EC₅₀ values for human cytokines are obtained from R&D Systems. The given EC₅₀ values are converted from units of mass per volume to molar concentrations by the following formula: Molar concentration (pM)=1, 000*[concentration in picograms per millilitre] MM where MM is the molecular mass of the given cytokine.

Figure 1 |. Three modes of cytokine-mediated cell-to-cell communication.

Cells of the immune system communicate through the exchange of secreted cytokines. Depending on the spatial location and identity of the cytokine-consuming cell, such communication can be autocrine (signaling to self), paracrine (signaling to neighboring cells) or endocrine (signaling globally through the circulation). The key parameters that determine the signaling mode are the rate of cytokine production (R_production) and the rate of cytokine consumption (R_consumption). Recent quantitative studies in systems immunology have begun to clarify how cells switch from one mode of signaling to another.

$$\frac{d\left[Cytokine\right]}{dt}=+R_{production}-R_{consumption}$$ (1)

Time integration of the two competing processes of cytokine production and cytokine consumption (parameterized by the two rates Rproduction and Rconsumption) to give the change in cytokine concentration over time enables immunologists to understand whether a given cytokine accumulates to a sufficient level to be functionally significant (when [Cytokine] > EC50 [G]) or remains below functionally significant levels for a given cell type (see Table 1 for the key parameters for immune cytokines, and BOX 1 for some simple algebra to be applied).

Box 1 |. Quantifying cytokine consumption.

Converting cytokine measurements into molar units enables higher levels of significance when assessing their functional effects. Researchers often measure cytokines in nanograms per milliliter or in international units per milliliter [G] (IU/ml): these units complicate any interpretation of the results in terms of cytokine production, consumption and signaling potency.

As discussed in this Review, an important, yet under–appreciated, parameter in understanding inflammation is the rate of cytokine consumption for a tissue of interest. One can estimate the number of cytokine receptors per cell by exposing cells ex vivo to cytokines and estimating how much cytokine is removed from the supernatant. When the molar concentrations of a cytokine present at the start ([Cytokine]in) and end ([Cytokine]out) of a reaction are known, the number of receptors for that cytokine per cell in a reaction volume V can be computed from Equation 5, where Ncells and NAvogadro denote the total number of cells and Avogadro number, respectively.

$$N_{receptorspercell}=\frac{\left({\left[Cytokine\right]}_{in}-{\left[Cytokine\right]}_{out}\right).V.N_{Avogadro}}{N_{cells}}$$ (5)

Once this conversion into molar units and the estimate of number of receptors per cell have been carried out, one can better assess the functional significance of a cytokine under consideration. For example, when dealing with endocrine regulation, the reaction volume is the volume of blood, Vblood (2ml for mice and 5l for humans). One can then rapidly estimate the number of cytokine molecules per cell (Equation 6).

$$N_{cytokinepercell}=\frac{\left[Cytokine\right].V_{blood}.N_{Avogadro}}{N_{cells}}$$ (6)

The rate of cytokine consumption per cell is given by Equation 7.

$$k_{cytokineconsumptionpercell}=k_{endocytosis}\times N_{receptors}$$ (7)

The characteristic timescale τconsumption for cytokine disappearance is estimated by Equation 8.

$${\tau }_{consumption}=\frac{N_{cytokinepercell}}{k_{endocytosis}.q{N}_{receptors}}$$ (8)

For example, in a culture of 50,000 regulatory T (T_reg) cells in a classical 96-well suppression assay (Vassay = 200μl), 10 pMol of IL-2 can be generated, which amounts to 25,000 molecules of IL-2 per T_reg cell. Considering that each T_reg cell can express 10,000 IL-2 receptors, all IL-2 would be consumed within approximately 1 hour (assuming a typical rate of endocytosis of 1 to 5 molecules per hour per receptor). Sustained immune responses (with long-lasting response to IL-2) must therefore rely on continued IL-2 secretion. A similar conclusion can be drawn in vivo, with 10,000 T_reg cells per lymph node and a reaction volume of 20μl: again, it will take approximately 1 hour for the T_reg cells to endocytose 10pMol of cytokine. In that context, it is not surprising that IL-2-mediated communication remains confined within a lymph node and rarely achieves systemic sharing through the blood. Moreover, it should be noted here that the derivations of equations 5, 6, 7 and 8 do not depend on ligand–receptor affinities and, hence, are generalizable for all cytokines. Overall, these simple formulae should be used to better quantify how inflammatory responses are regulated dynamically.

To parameterize Equation 1, the overall rate of cytokine production (Rproduction) can in turn be broken down into the product of the density of cytokine-producing cells (nproduction) and the rate of cytokine production for each individual cell. Immunologists routinely measure nproduction by using blockers of secretory pathways (such as monensin or brefeldin A), then staining intracellularly for the accumulation of cytokine and analyzing by flow cytometry for single-cell resolution. Measuring the rate of cytokine production at the level of individual cells can be more difficult, but cytokine capture and microchip assays¹⁵ have shown that T cells produce cytokines at a constant rate while they are producing¹⁶. More systematic efforts to document the production rates of different cytokines in different cell types will be needed to generalize these observations.

To estimate the overall rate of cytokine consumption (Rconsumption), one needs to measure the number of cytokine-consuming cells and multiply it by the rate of cytokine consumption per individual cell. Both measurements can be gained by carrying out quantitative fluorescence-activated cell sorting (FACS) to determine the abundance of cytokine receptors on the surface of cells or more biochemical assays (BOX 1). Cytokine receptor abundance can be used to estimate the rate of cytokine consumption, as cytokines bind to receptors according to well-characterized biophysical models and are endocytosed at a typical rate of 1 to 5 molecules per hour¹⁴. However, it should be noted that cytokine consumption is not only the result of receptor-mediated endocytosis and that other processes, such as binding of a cytokine to the extracellular matrix (ECM) or cleavage to an inactive form, might complicate these equations. [Au:OK?] [Yes]

In other words, every immunologist already has the experimental toolbox to enable careful quantification of all of the parameters described by these simplified equations that regulate the cytokine microenvironment over long timescales (hours to days). Adding experimental measurements to Equation 1 can already illuminate whether a tissue is headed towards cytokine accumulation (if Rproduction > Rconsumption) or cytokine disappearance (if Rconsumption > Rproduction). However, the necessary time integration (as encapsulated in Equation 1) can be very complicated because the variation of each of these individual rates must be monitored at multiple time points. Experimentally parameterizing each immunological setting is driving dedicated quantitative measurements — for example, for Rproduction and Rconsumption for each cytokine and for each cell type within a given immunological milieu. We posit that such quantitative effort is becoming invaluable to translate our static observations of sparsely-resolved-in-time datasets into a more functional understanding of cytokine-mediated communication, as discussed below.

Spatial considerations

Spatial considerations — in other words, the coupling of diffusion [G] and advection [G] with the dynamics of cytokine secretion and consumption (as delineated in the previous section) — complicate our understanding of cytokine-mediated communication. We discuss here the general case whereby a secreted cytokine is free to diffuse in the intercellular space (any correction in the regime that is required when a cytokine transiently binds to surface matrices is discussed below). Equation 1 needs to be updated by replacing the global cytokine concentration [Cytokine](t) with a time-dependent, spatially heterogeneous cytokine field [Cytokine](r^→,t) in a partial-differential equation (Equation 2).

$$\frac{\partial \left[Cytokine\right]}{\partial t}=D.{\nabla }^2\left[Cytokine\right]+R_{production}-R_{consumption}$$ (2)

Extensive numerical integration has shown that the solution of this equation generically could produce sharp spatial gradients in cytokine concentration⁸. In particular, this theoretical treatment showed that, even when a cytokine is released within the context of a T cell immunological synapse, one can expect substantial leakage of the cytokine outwards from the synapse, which would enable paracrine signaling between cells. In fact, additional computational modeling showed that the diffusion field of a cytokine could be approximated as a continuous field, with cytokine-secreting and cytokine-consuming cells being point sources^8,9,12. Indeed, a simple mathematical consideration points out that the timescale τcontinuous over which cellular heterogeneities — for example, in terms of exact cell shapes and unequal distributions of cytokine receptors on the surface of cells — become negligible can be approximated as Equation 3, where rcell is the radius of the leukocyte (rcell ≈ 5–10μm) and Dcytokine is the diffusion co-efficient for the cytokine in solution (typically, D_cytokine ≈ 100 μm²/sec), as confirmed in a recent experimental study¹⁷.

$${\tau }_{continuous}\propto \frac{r_{cell}^2}{D_{cytokine}}=1s$$ (3)

In other words, when considering cytokine propagation over timescales longer than a few seconds, one can safely apply the continuous approximation encapsulated in Equation 2 and treat cells as point sources, because of the fast diffusion of cytokines compared with the spatial scale of cellular heterogeneities. This continuous approximation will facilitate the study of the extent of cytokine-mediated communication within dense tissues, although it does have limitations and its general applicability needs to be validated. For example, cytokine diffusion could be hampered by transient binding to the ECM, leading to reduced cytokine diffusion in equations (2) and (3) and a longer timescale below which non-continuous modeling of cellular structures must be carried out. Notwithstanding these limitations, the solution of the partial-derivative equation for the diffusion and consumption of cytokines amongst cytokine-consuming cells can then be derived analytically by approximating the consumption rate as a linear function [G] of the cytokine concentration¹⁶. This linear regime constitutes an approximation that has been validated in most experimentally studied systems¹⁶. The main cause of nonlinearity in a system would be the saturation of the cytokine consumption rate at high cytokine concentrations and/or low densities of consuming cells. Other nonlinearities (for example, of the cytokine secretion rate) operate over longer timescales that can be resolved in a step-wise steady-state manner (so-called adiabatic approximation). Thus, the cytokine field settles rapidly to a steady state and yields a cytokine profile around producing cells that decays as an exponential from the cytokine source. The characteristic length scale (λcytokine) at which cell-to-cell communication by a given cytokine takes place is then given by Equation 4, where Dcytokine is the diffusion coefficient for the free cytokine and nconsumer is the density of cytokine-consuming cells.

$${\lambda }_{cytokine}=\sqrt{\frac{D_{cytokine}}{n_{consumer}.R_{consumption}}}$$ (4)

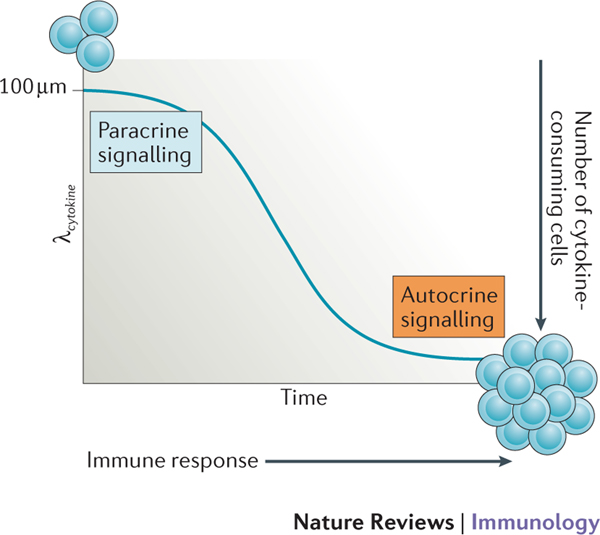
Exploring the quantitative aspects of Equation 4 leads to interesting insights into cell-to-cell communication. Indeed, the spatial compartmentalization of cytokine-mediated communication (termed ‘screening’ by analogy with electrostatic considerations¹⁶) is thus highly tunable based on molecular and cellular parameters. This theoretical result was validated experimentally ex vivo and in vivo, with λcytokine ranging from 100 μm (at the beginning of an immune response when few cells consume the cytokine of interest) down to only a few μm (when cytokine-consuming cells are generated and/or are clustered around cytokine-producing cells)¹⁶. This high tunability of cytokine-mediated communication may explain how the immune system can switch from localized cytokine niches to systemic inflammation simply by adjusting the overall rate of cytokine consumption in a given tissue (FIGS 1,2).

Figure 2 |. The rate of cytokine consumption affects signaling mode during an immune response.

The characteristic length scale (λcytokine) at which cell-to-cell communication by a given cytokine takes place is highly tunable based on molecular and cellular parameters. At the start of an immune response, when the number of cytokine-consuming cells is low, λcytokine can be in the range of 100 μm, which enables paracrine signalling. As the immune response progresses, the number of cytokine-consuming cells increases and these may cluster around cytokine-producing cells, which decreases λcytokine to only a few μm. As a result, autocrine signaling becomes dominant. [Au:OK?] [Yes]

Note that there is considerable evidence in the literature for the deposition of cytokines on the ECM, which influences the action of cytokines on target cells^18,19, thereby adding an additional layer of complexity in generalizing Equation 2 with respect to cytokine diffusion. In fact, any mechanism that influences the spatial dynamics of cytokine diffusion could potentially be a confounding factor towards laying down the mathematical rules governing the diffusibility of cytokines. A case in point is the establishment of chemokine gradients by gycosaminoglycans within the ECM^20,21 or the adsorption and subsequent slow release of some cytokines by tumour cells²². Hence, future attempts at modelling the dynamics of cytokine diffusion will have to incorporate such potential causes of variation.

In the past, theoretical studies have attempted to quantitatively model the effects of autocrine and paracrine signaling on cells across different time and length scales^23–25. A recent study further investigated the interplay between autocrine and paracrine signaling in populations of cells using a bottom-up approach²⁶. By engineering a yeast strain to secrete and sense a small protein (α factor), the authors of this study built a tunable system with which to explore all configurations of cell-to-cell communication. In particular, changing key parameters (such as the secretion rate of α factor, level of receptors for α factor, rate of extracellular degradation of α factor and strength of the positive feedback) resulted in populations of cells switching from autocrine activation, to bimodal (both autocrine and paracrine) activation to global (paracrine) activation, specifically when these parameters were changed in conjunction with decreasing cell densities. Autocrine signaling (in which cells communicate self-to-self) and quorum sensing (in which cells establish a density-dependent global response) were shown to arise from the same physico-chemical mechanisms operating in different parameter regimes. At the theoretical level, it was convincingly shown that there exist two scales with different regimes of cytokine-mediated communication: the cellular scale (< 500 μm), whereby secrete-and-sense responses are heterogeneous, and the systems-wide scale (> 500 μm), whereby the cytokine field is homogenous. Such consideration greatly simplifies the study of cytokine networks in dense tissues. Ultimately, such a synthetic biology approach — although unusual in the field of immunology — brought the clarity of a bottom-up approach and quantitatively highlighted how the interplay between production and consumption is sufficient to generate varied responses at the level of cell populations^26–28.

Short-range communication

As pointed out in the previous section, the range of cytokine-mediated communication can be highly tunable based on the rate of consumption. This is of particular relevance in the context of leukocyte cluster formation, which is a well-known phenomenon among activated immune cells. It was shown as early as 1984 that dendritic cells (DCs), T helper (T_H) cells and B cells form discrete clusters in vitro and that these clusters function as sites for the development of most antibody-forming cells²⁹. Subsequently, T cells and antigen-presenting cells (APCs) were shown to associate through immunological synapses to form functional clusters during antigen presentation^30–32. It has been shown that the targeted release of effector molecules from the T cell to the APC within an immunological synapse involves the alignment of intracellular organelles that are necessary for protein synthesis by a mechanism requiring reorientation of the Golgi apparatus with the microtubule organizing center^33,34. Furthermore, in vitro and in vivo imaging studies have shown that effector cytokines accumulate underneath the immunological synapse in APC-activated T_H cells, which offers a possible answer — assuming that immunological synapses are tight-sealed — to the question of how specificity is achieved via targeted delivery of cytokines from T cells onto their APC.

In the same context, it has been suggested that cytolytic granules remain confined to the synaptic space and function in a more specific manner³⁵. This suggestion was confirmed in natural killer (NK cells), for which a comparison of secretion of the cytolytic granule protein perforin and the cytokines IFNγ and TNF showed that they have polarized and multidirectional secretion mechanisms, respectively³⁶. Additionally, after T cells encounter APCs, as well as forming T cell–APC synaptic clusters, T cells also form tight clusters between themselves. The dynamics of cytokine-mediated communication within such T cell–T cell clusters is an interesting but poorly understood topic. An in vivo animal model of T cell activation provided evidence of the synaptic delivery of cytokines between CD4⁺ T cells in a T cell–T cell cluster³⁷. The study showed that T cells that are part of a homotypic cluster capture IL-2 and phosphorylate STAT5 more efficiently than do T cells in isolation. A possible explanation for this came with more recent studies from the same group in which CD8⁺ T cells were shown also to form homotypic clusters, and share cytokines (notably IFNγ), that are crucial for their differentiation³⁸. Further studies are needed in multiple cell types to investigate the different secretory mechanisms of cytokines produced by immune cells and the implications of these mechanisms for regulating the extent of immune responses.

Long-range communication

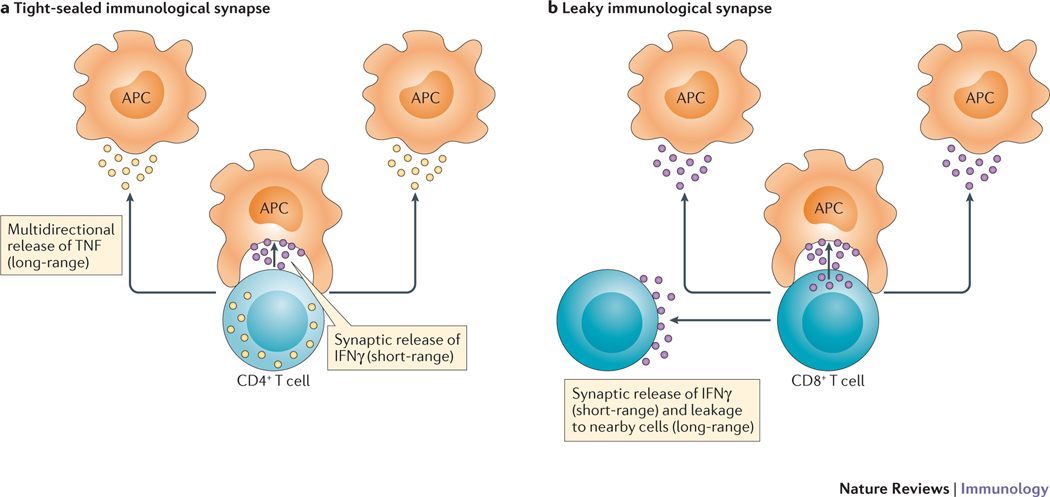
However, synaptic secretion could not explain the secretion of factors that function in an endocrine manner. One possible explanation came from a report that used in vitro imaging to show the existence of two directionally distinct paths of cytokine secretion for activated T_H cells³⁹. The study showed direct synaptic secretion of IL-2, interferon-γ (IFNγ) and IL-10, whereas tumor necrosis factor (TNF), IL-4 and CC-chemokine ligand 4 (CCL4) were secreted in a multidirectional manner³⁹. This model, termed the ‘two-pathway model’ of cytokine secretion (FIG. 3), raises interesting possibilities regarding the dynamics of cytokine-mediated communication between cell types because, in addition to the nature of the cytokine secreted, it is also imperative to understand how the cytokine is secreted to have a complete understanding of the overall effects on the immune response.

Figure 3 |. Variable confinement of cytokine-mediated communication within the T cell immunological synapse.

a | For a tight-sealed immunological synapse between a CD4⁺ T helper cell and antigen-presenting cell (APC), there are differential patterns of cytokine secretion²⁹. In this example, IFNγ is directionally released into the immunological synapse to mediate short-range communication, whereas tumour necrosis factor (TNF) is more multidirectional in its secretion pattern and thus mediates longer-range communication. b | For a leaky immunological synapse, even those cytokines such as IFNγ that are released into the synapse^73,74 can be involved in longer-range multicellular interactions as a result of a limited consumption rate by the synapsed APC. This is known as the ‘two-pathway’ model of cytokine secretion. [Au:OK?] [Actually, ‘a’ is the ‘Two-pathway’ model, whereas ‘b’ is called the ‘leaky synaptic’ model.]

A later study reported global activation of immune cells in the lymph nodes of mice infected with either Heligmosomoides polygyrus or Toxoplasma gondii⁴⁰. There was ubiquitous phosphorylation of signal transducer and activator of transcription 6 (STAT6) or STAT1, respectively, in immune cells throughout the reactive lymph nodes of these mice. These data implied that the JAK–STAT pathways associated with IL-4-mediated or IFNγ-mediated signalling in these systems must have operated in a saturated regimen. This is consistent with the fact that these two models of infection elicit hyper-activated immune responses whereby high levels of secreted cytokines overwhelm the consumption capabilities of the lymphoid organ and function in a systemic manner.

As a wide variety of immune cells form clusters upon activation, it would be of particular interest to know if such diversities in cytokine secretion pathways exist in other immune cell types, apart from CD4⁺ TH cells. Indeed, a study in CD8⁺ cytotoxic T lymphocytes (CTLs) showed that although IFNγ secretion from CTLs was polarized towards the immunological synapse, its effects were not confined to the target cell alone³⁵. This was attributed to a leakiness of the synaptic seal that allowed IFNγ to permeate out and activate nearby cells (FIG. 3). This result is consistent with the detailed molecular model described in Equation 2 and Equation 3, whereby it was shown that there exists a possibility of paracrine signalling between cells even during an immunological synapse owing to a leakage of cytokines⁸.

The above discussion makes it evident that the spatial scale of cytokine-mediated communication can be both short-range (synaptic) and long-range (throughout the tissue space), depending on the biochemical parameters (see earlier). Although it is tempting to speculate that all cytokines should follow this generic model, as the diffusion and consumption of molecules are governed by physico-chemical rules, in reality the model may have to be tweaked to take account of the diffusion mechanisms of other cytokines. In particular, the model should incorporate variabilities between cell types and different cytokines. We discussed above the impact that extracellular matrices can have on cytokine diffusion, which will need to be carefully assessed in future modelling studies.

Another example of cell-to-cell cytokine-mediated communication to consider is the formation of neutrophil clusters in response to activating signals such as wounding and inflammation, which is a well-known phenomenon referred to as neutrophil swarming. After the initiation of swarming by a few neutrophils in response to tissue injury, other cells rapidly approach the wound site resulting in an amplification of the swarm^41–43. At later stages in the response, signal relay between neutrophils within a swarm depends on leukotriene B4 and integrins⁴⁴. This amplification of the response by exchange of signals between participating neutrophils is crucial for prolonging the neutrophil swarm and it functions to extend the effective radius of neutrophil recruitment from the site of injury. However, the mechanisms by which neutrophil swarming is stopped are currently not known. A comprehensive map of cytokine and chemokine diffusion and consumption by neutrophils during swarming, coupled with mathematical analysis of feed-forward and feedback loops, will be needed to determine the quantitative principles of swarming behaviour that can then be leveraged to understand swarming dynamics.

In conclusion, it is apparent that the dynamics of cytokine-mediated communication within immune cell clusters are extremely complex and can account for the remarkable variability between different cytokines and types of immune cell. Decoding the intricacies of cytokine secretion and signaling in multiple immune cell types has revealed delicate spatio-temporal regulations, and further studies in this area will expand our understanding of immune cell behaviour within specialized haematopoietic compartments.

Homeostasis by cytokine competition

Competition for cytokine is a key mechanism to mediate homeostasis and accurate decision making within the immune system. Competition for a limited resource is a recurrent mechanism in ecology to account for the maintenance of homeostasis^45,46. Here we revisit this concept within the field of haematopoietic homeostasis via cytokine competition. Indeed, many cytokines (such as erythropoietin (EPO), thrombopoietin (THPO), IL-2, IL-7 and IL-15) are crucial for the maintenance of cell-specific niches (for erythrocytes, platelets, regulatory T (T_reg) cells, naive T cells and memory T cells, respectively). This homeostatic function can be mediated by anti-apoptosis signals and/or mitotic signals driving cell proliferation: overall, the net result of cytokine availability is the accumulation of cells responding to that cytokine. The relevance of cytokine competition as a self-modulating scheme is then structurally robust: cells accumulate until they reach a critical number that divides up the available cytokine pool and becomes a stable fixed point. Above this number, some cells do not receive enough cytokine and die; below this number, cells receive a ‘homeostatic kick’ to proliferate or extend their lifespan and the population returns to its homeostatic number. Within that context, quantitative approaches become invaluable to tease apart cytokine production and consumption to understand how homeostasis becomes established.

A recent study highlighted how cytokine consumption establishes a stable dynamic scheme (termed cytokine spring [G]) for the homeostasis of multicellular populations^47,48 (BOX 2). The authors analysed the interplay between fibroblasts and macrophages for their symbiotic exchange of growth factors, such as colony-stimulating factor 1 (CSF1) and platelet-derived growth factor (PDGF). A general mathematical framework using biochemically explicit models of cytokine-mediated communication between cells of two different lineages was established: this model could be solved analytically, which enabled the authors to test the model over a broad range of parameters. They showed that, to achieve homeostatic stability, one of the cell populations must be at carrying capacity — in other words, one cell compartment must be intrinsically limited in its expansion (through cell-to-cell contacts and/or limitation of growth medium) — otherwise, the two-cell system was found to be unstable, with either both cell populations collapsing or one of the cell populations diverging in number and becoming dominant. These results are particularly insightful as they show that similar mechanisms of negative feedback are not equivalent dynamically: only the rapid endocytosis of cytokines could greatly expand the range of parameters whereby both symbiotic populations maintain stable numbers⁴⁷. Other negative feedback mechanisms, such as receptor adaptation or cytokine cross-inhibition, are always imperfect thus they cannot limit the exponential divergence in cell number associated with cytokine fluctuations and are ultimately insufficient to enforce homeostatic stability. The authors then generalized this result to larger cell systems (with three or four interacting cell types) and showed that the need for anchoring conditions does not expand in larger systems: as long as one cell type remains at carrying capacity, other cell types can be maintained at homeostasis far from being at carrying capacity, simply by having their growth factor concentration regulated by endocytosis and/or cross-regulation⁴⁷.

Box 2 |. General rules to establish a cytokine spring.

Two recent publications introduced the concept of ‘cytokine springs’^47,48, whereby cells achieve homeostasis by secreting and competing for limited cytokines. A general set of rules can be derived when analyzing cytokine springs (these update the rules originally derived for the thrombopoietin system⁵⁰). To achieve a stable cytokine spring and to maintain homeostasis, four conditions must be satisfied:

• a low basal level of free cytokine;

• circulating levels of cytokines that vary reciprocally and proportionally to changes in cell number;

• a short time delay (minutes to hours) between changes in cytokine concentration and changes in cell number (because of endocytic consumption and/or cross-inhibition);

• slower recovery (hours to days) by cell generation or apoptosis to compensate for an increase or decrease in cytokine concentration, respectively.

Such general rules will need to be tested more systematically for all of the cytokine systems documented in Table 1. The quantitative framework under development in the field (BOX 1) is fostering a better understanding of the parameters for cytokine springs that regulate inflammation at a more systemic level.

Such a result is particularly relevant biologically, as it enables the formation of complex and dynamic symbiotic tissues with multiple cell types cohabitating a tissue without being at carrying capacity, thereby maintaining the capacity of cell populations to expand or shrink in a dynamic manner according to inflammatory perturbations. These studies^47,48 constitute a proof of principle whose generality in other contexts will need to be assessed. In the following sections, we revisit classical examples of homeostasis mediated by competition for cytokines.

Regulation of erythrocyte homeostasis by EPO.

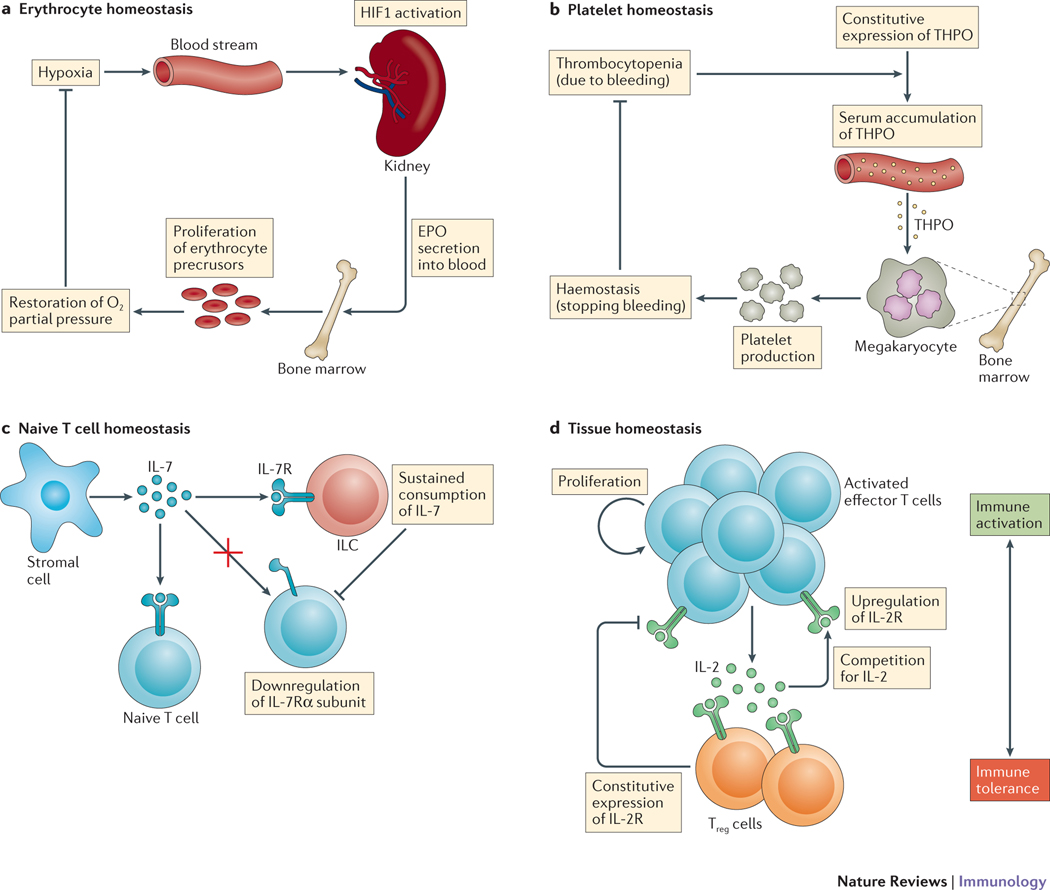
The overall function of this cytokine-mediated homeostatic system is to maintain adequate levels of oxygen in the blood supply to tissues. The feedback mechanism has been well delineated over the years, with a drop of partial oxygen pressure in the blood being detected by kidney cells (through the activation of hypoxia-induced factor 1 (HIF1)), which triggers their secretion of EPO. EPO circulates back to the bone marrow to induce the proliferation and differentiation of erythrocyte precursors and to reduce their apoptosis⁴⁹, and ultimately to boost the synthesis of haemoglobin and the restoration of oxygen pressure (FIG. 4a). Another function of EPO is to replenish the erythrocyte compartment after loss (bleeding). EPO is typically maintained at a low level during homeostasis^50–52 with approximately 6 × 10¹² molecules of free EPO circulating in the blood of a normal human individual; this equates to, at most, one EPO molecule per erythrocyte (healthy individuals have typically 20 trillion erythrocytes in their blood). In addition, this steady-state concentration of free EPO is typically 10-fold lower than the concentration that is necessary to induce 50% of a response for primary colony-forming unit erythroid cells^53,54. Note that the concentration of circulating EPO increases by a factor of 100 during trauma-induced hypoxia (for example, anaemia or blood loss). Overall, this system is thus highly responsive to fluctuations of EPO concentration (as a result of over-production of EPO or the loss of EPO-consuming cells), which are immediately detected by the erythrocyte precursors resulting in increased consumption and/or cell proliferation.

Figure 4 |. Homeostasis by cytokine competition.

a | Erythrocyte homeostasis. A drop of partial oxygen pressure in the blood (hypoxia) is detected by kidney cells (through the activation of hypoxia-induced factor 1 (HIF1)), which triggers their secretion of erythropoietin (EPO). EPO circulates to the bone marrow to induce the proliferation of erythrocyte precursors, which restores oxygen partial pressure. b | Platelet homeostasis. The rapid decrease in number of circulating platelets (thrombocytopenia) during trauma results in the serum accumulation of constitutively expressed thrombopoietin (THPO), which signals to bone marrow megakaryocytes for platelet release, thereby restoring haemostasis. c | Naive T cell homeostasis. Innate lymphoid cells (ILCs) are present at low frequencies in lymphoid organs compared with T cells but unlike T cells they do not adapt their response to IL-7 by downregulating expression of the IL-7 receptor α-subunit (IL-7Rα). The sustained consumption of IL-7 by ILCs limits the spatial extent and overall availability of IL-7 in lymph nodes. d | Tissue homeostasis. Activated effector T cells secrete IL-2, which drives their proliferation and upregulation of IL-2 receptor (IL-2R) expression. Regulatory T (T_reg) cells constitutively express IL-2R and consume IL-2, which upregulates their inhibitory functions. Competition between the production and consumption of IL-2 determines the balance between immune activation and immune tolerance. [Au:OK?] [Yes]

Regulation of platelet homeostasis by THPO.

Another classical system in which to study cytokine-regulated homeostasis is the THPO-regulated homeostasis of platelets in the blood circulation^55,56 (FIG. 4b). This system shares some dynamics features with the EPO-driven homeostasis of erythrocytes, but there are crucial differences in their molecular and cellular implementation. Platelets can be rapidly generated (by thrombocytosis), in particular during infection, but can also disappear from the circulation (acute thrombocytopenia): such fluctuations in platelet number in turn trigger feedback mechanisms to return the number of platelets to homeostasis. Specifically, fluctuations in platelet number correlate negatively with THPO levels, which in turn correlate with platelet release from megakaryocytes. One interesting aspect of this system is that THPO is constitutively expressed across various organs (mainly by liver and kidney but also by muscle and bone marrow) and its production is maintained at a steady level even during stress⁵⁷. Thus, it is the rapid change in number of circulating platelets during trauma that accounts for the rapid accumulation of THPO in the serum, which signals back to the bone marrow megakaryocytes for platelet release⁵⁸. Hence, cytokine competition is between a large number of platelets and few megakaryocytes. The general principle of cytokine-mediated homeostasis thus applies with the special feature that platelet disappearance and the ensuing cytokine over-accumulation in the circulation are corrected by platelet release (a near-instantaneous process upon THPO-induced signaling by megakaryocytes) rather than by cell proliferation and differentiation (a process that can imply a time delay)⁵⁹. This accounts for the large scale and rapid recovery (within a few hours) of platelet numbers upon trauma. We estimate that the concentration of THPO molecules in the circulation at steady state (95pMol) translates to approximately 4 occupied THPO receptors per platelet, and 100 occupied THPO receptors per megakaryocyte. Such discrepancy stems from the fact that megakaryocytes compensate for the lower affinity of their THPO receptor (Kdissociation = 90 pMol) compared with the platelet THPO receptor (Kdissociation = 20 pMol) by having 2,000 binding sites per cell, compared with only 20 binding sites per platelet⁶⁰. A five-fold decrease in platelet number thus translates directly into a five-fold increase in THPO concentration, leading to an increase in THPO receptor occupancy from 100 to 435 for megakaryocytes, but only from 4 to 10 for platelets. In other words, 5-fold platelet depletion triggers an increase of ~300 occupied receptors for megakaryocytes but only 6 occupied receptors for platelets, and hence restorative platelet production by megakaryocytes. Such biochemical considerations demonstrate how platelet homeostasis is enforced by the quantitative coupling between cell disappearance and cytokine-mediated signaling (FIG. 4b).

Naive T cell homeostasis.

IL-7 is a crucial cytokine for maintaining homeostasis in the lymphocyte compartment. Monitoring the production and consumption of IL-7 in vivo has remained elusive as existing tools are not sensitive enough to detect the exact source of IL-7 (from lymphocytes, from DCs or from radioresistant cells, such as stromal cells or fibroblastic reticular cells). Using a combination of bone marrow chimeras (with IL-7 receptor-knockout and wild-type bone marrow), as well as cell depletion by antibody tagging, it was shown that T cell homeostasis is enforced by innate lymphoid cells (ILCs)⁶¹. Although ILCs are present at a low frequency in lymphoid organs (less than 0.1%), they can sustain their consumption of IL-7, unlike T cells that adapt their response to IL-7 by downregulating expression of the IL-7 receptor α-subunit⁶². Such quantitative discrepancy between T cells and ILCs in terms of IL-7 consumption will necessitate a more fine-grained and heterogenous model of IL-7 competition (FIG. 4c). As has been pointed out by others⁶³, ILCs occupy a specific interfollicular zone in mesenteric lymph nodes that is the site of IL-7 production by stromal cells, as well as the entry point for naive T cells; hence, ILCs would be ideally located to limit the spatial extent and overall availability of IL-7 in lymph nodes, as has been described quantitatively¹⁶.

Tissue homeostasis mediated by T_reg cells.

T_reg cells are also crucial for maintaining tissue homeostasis, for example avoiding autoimmune activation, and for limiting inflammation. T_reg cells achieve these pleiotropic functions through multiple mechanisms: as cytokine sinks that consume and do not contribute pro-inflammatory cytokines, as direct blocks of autoimmune activation of T cells (through competition for IL-2^64–66 and costimulatory signals, and through the release of anti-inflammatory IL-10, IL-35 or transforming growth factor-β), and as indirect blocks of T cell activation through the induction of DCs to release anti-inflammatory metabolites such as indoleamine 2,3- dioxygenase (IDO). The complexity of T_reg cell functions is beyond the scope of this Review and has been expertly covered elsewhere^67–69. Here, we simply point out how the mathematics of competition for IL-2 or costimulatory signals has illuminated how T_reg cells decide between immune activation and tolerance at the tissue level^12,13. In summary, activated T cells secrete and accumulate IL-2 to boost their activation (by upregulating expression of IL-2 receptor, limiting apoptosis and driving proliferation); in parallel, T_reg cells (which express the complete IL-2 receptor at homeostasis), consume cytokines and upregulate their inhibitory functions (for example, consumption of IL-2 and upregulation of cytotoxic T lymphocyte antigen 4) (FIG. 4d). Such dynamic competition between the production and consumption of IL-2 determines the overall activation of effector T cells: hence, quantitative modeling^12,13 has helped us to understand how the balance between activation and regulation is determined. Similarly, the scaling of T_reg cell development with cytokine availability⁷⁰ is an intriguing feature that would benefit from further quantitative analysis.

Integrating a global response

Immune cells constantly receive various simultaneous signals, including from antigens and cytokines. The ability of individual cells to process signals at multiple levels and to integrate the obtained information into a collective response at the population level is crucial for a coordinated immune response. As such, it is important to have a quantitative understanding of how immune cells integrate the large number of signals they receive into a tailored output. This was underscored by pioneering work by Hodgkin and colleagues on the proliferation, survival and differentiation of T cells⁷¹ that described a calculus performed by T cells to convert individual signals into a linear additive effect on cell division time that in turn leads to an exponential increase in proliferation rate⁷¹. One of the key observations in the study was the effect on cell division of combined anti-CD28 and IL-4 treatment, which computed to an arithmetic sum of the individual responses. Later work from the same laboratory showed that antigen-driven T cell receptor (TCR) signaling, costimulation and cytokine-induced signals add linearly to modulate the so-called ‘division destiny’ of a T cell, which is defined as the number of divisions a cell undergoes before reaching quiescence⁷². A combined experimental and mathematical modeling approach showed that the division destiny of a T cell is regulated⁷² as a linear combination of TCR signals (signal 1) and qualitatively and quantitatively different combinations of APC-derived costimulation (signal 2) and cytokine-induced signals (signal 3). A related report showed that strongly activated CD8⁺ T cells can induce proliferation of weakly activated T cells in their microenvironment by IL-2-mediated paracrine signals⁹. Thus, these experiments, combined with mathematical modelling, provide evidence of synergistic signal integration strategies by T cells whereby a cytokine secreted by a subpopulation of strongly responding cells drives the proliferation of nearby weakly activated cells by reducing their threshold of activation. Another recent study provided insights into the effect of additive integration of multiple cytokine signals on CD4⁺ T cell differentiation⁷³. The results show that rather than having discrete phenotypes, cells responding to combinations of cytokine inputs have a continuum of differentiation fates. Mathematical modelling of the data revealed that the mean response to a combination of multiple cytokines is a linear sum of the responses elicited by the individual cytokines. This behaviour could be explained by a segmented linear regression model that could also correctly predict the response to new input conditions.

In light of the above studies, it might seem reasonable to assume that signal integration by immune cells is mainly a linear phenomenon. However, one can anticipate nonlinearity as a consequence of interactions between input conditions that elicit potentially opposite phenotypes. This was shown to be the case in a study using biological pattern-matching and a mathematical formalization to define classes of biologically similar interaction modes that mapped to the theoretical space of all possible interaction profiles of two signals⁷⁴. The theoretical model was validated by analyzing high-throughput transcriptomic data of human plasmacytoid dendritic cells (pDCs) and monocytes stimulated with a combination of microbial and host-derived ligands. The analysis shows a surprising inhibitory effect of Toll-like receptor (TLR) ligands on cytokine-induced activation of gene expression in pDCs, even though the individual stimuli (TLR ligands and cytokines given separately) strongly induced gene expression. Two more recent studies explored the concept of nonlinearity with respect to IL-2-mediated signaling in T cells^9,14. In a different study, an artificial neural network-based algorithm was developed that modeled cross talk between signaling pathways in response to multiple ligands of platelet activation⁷⁵. By training a neural network model of intracellular calcium response to binary combinations of six agonists, the authors could correctly predict the response of more complex input conditions. A similar mathematical framework will need to be tested to capture nonlinearities in the signal integration of cytokine responses.

Concluding remarks

To conclude, we have reviewed here the quantitative framework of cytokine secretion and consumption that immunologists can apply to analyze the global regulation of cytokine responses in tissues. The physico-chemical laws that determine the amplitude, spatial range, temporal extent and multiplexing of cytokine-mediated communication can be extremely complex (with feedback and nonlinearity in cytokine regulation). Yet, recent studies have reduced the complexity of the problem and delivered general results for immunological settings (using linear and continuous approximations). Namely, leukocytes can rely on cytokine springs to maintain global homeostasis; they can also modulate the extent of their cell-to-cell communications by targeting the release of their cytokines and adjusting their cytokine consumption rate through changes in cytokine receptor density and/or the number of cytokine-consuming cells. Such quantitative results can guide immunologists in assessing the delicate balance of cytokine production and consumption. Applying these laws will also help to better manipulate immune responses using combinations of cytokine treatment as a therapeutic regimen for many pathological conditions^76–79. A quantitative understanding of how immune cells integrate and respond to combinations of cytokines will become an invaluable tool to determine cytokine-mediated therapeutic strategies that are tailored to a particular individual.

Glossary

Autocrine

A form of cell-to-cell communication in which a cell secretes a cytokine (or any other soluble molecule) that binds to receptors on its own surface and elicits a signaling response

Paracrine

A form of cell-to-cell communication in which a cell secretes a cytokine that binds to receptors on the surface of neighboring cells and triggers a signaling response in these neighbouring cells

Endocrine

A form of cell-to-cell communication in which a cell secretes a cytokine that reaches the blood circulation (hence triggering a more global response). It can be considered as an extended version of paracrine communication and it applies to hormones as well as cytokines

EC₅₀

The concentration of a cytokine that yields a half-maximal response

Diffusion

The spontaneous motion of molecules down their concentration gradient (a passive mode of transport that is driven by thermal fluctuations)

Advection

The active transport of molecules driven by the flow of a fluid (blood or lymphatic fluid)

Linear function

In regimes of low cytokine concentration, the consumption rate for a given cytokine can be approximated as being proportional to the concentration of cytokine (linear dependency). When the cytokine receptors on the surface of cells are saturated with cytokines, the consumption rate reaches a plateau, becomes independent of the cytokine concentration in the extracellular milieu and introduces nonlinearities to the equations that describe its behaviour

Cytokine spring

A fundamental mechanism to achieve immune homeostasis. Cells of multiple lineages secrete and consume cytokines that drive their proliferation and death. When one of the cell populations is at carrying capacity (in other words, when its expansion has plateaued), the system behaves as a cytokine spring and achieves homeostatic stability

International units per milliliter

(IU/ml). An ad hoc unit that is the cytokine concentration for which 50% of a response can be elicited (signaling, differentiation, proliferation or survival): it practically relates to the EC₅₀ or affinity of the cytokine for its receptor and is typically in the 10 pMol range