ABSTRACT
Optimal embryonic development plays a major role in the health of an individual beyond the developmental stage. Nutritional perturbation during development is associated with cardiovascular and metabolic disease later in life. With both nutritional uptake and overall growth being risk factors for eventual health, it is necessary to understand not only the behavior of the processes during development but also their interactions. In this study, we used differential equations, image analyses, curve fittings, parameter estimation and laboratory experiments to quantify the rate of yolk absorption and its effect on early development of a vertebrate model (Danio rerio). Findings from this study establish a nonlinear functional relationship between nutrient absorption and early fish growth. We found that the rate of change in fish length and yolk utilization is logistic, that is the yolk decays rapidly for a period of time before leveling out. An interesting finding from this study is that yolk utilization reaches its maximum at 84 h post-fertilization. We validated our mathematical models against experimental observations, making them powerful tools for replication and future simulations.
KEY WORDS: Embryonic development, Zebrafish, Yolk absorption, Parameter estimation, Mathematical modeling, Logistic growth
Summary: Mathematical modeling establishes a nonlinear functional relationship between nutrient absorption and early fish growth and identifies the hour post-fertilization at which yolk metabolism reaches its maximum.
INTRODUCTION
Optimal embryonic development plays a major role in the health and longevity of an individual past the developmental stage (Wyness et al., 2013). It has long been hypothesized and since supported that nutritional and toxicological perturbation during development is associated with cardiovascular, metabolic and chronic disease later in life, known as the ‘developmental origins of health and disease’ (DOHaD) (Barker, 2004; McMillen et al., 2008). Additionally, the association between low birthweight and increased rates of coronary heart disease have been shown in various extensively replicated studies (Barker, 2004). However, most human studies rely solely on maternal nutrition as a proxy to estimate embryonic and fetal nutrition. Furthermore, the majority of these studies have been cross-sectional and do not look for specific critical windows of nutritional susceptibility during pregnancy. With both nutritional uptake and overall growth being risk factors for eventual health, it is necessary to understand not only the behavior of the processes during development but also their interactions.
Human embryonic nutrition is primarily histiotrophic until placentation during the fetal period. There is an initial maternal contribution of yolk granules in the matured oocyte, and then additional nutrition is acquired via uptake of nutrients into the yolk sac by processes such as receptor-mediated endocytosis (Burton et al., 2001; Burton et al., 2002). This histiotrophic nutrition is vital until the onset of maternal intraplacental circulation near the end of the first trimester. Because the first trimester is a dynamic period (encompassing implantation, gastrulation, embryogenesis and organogenesis), a reliable nutrient supply is vital to support these energy-intensive processes. However, our understanding of the dynamics of embryonic nutrition and their temporal impacts on growth and DOHaD is limited due to the inaccessibility of the intrauterine environment. Studies have had to rely on using maternal nutrition as a proxy for embryonic nutrition, but the appropriateness of this strategy is unknown. There is a need to understand the kinematics of embryonic nutrition, and their susceptibility to external cues such as maternal nutrition, environmental exposures and stress.
Zebrafish (Danio rerio) are an excellent model for human development and embryonic nutrition (Link and Megason, 2008). They share >70% genetic homology with humans, and are vertebrates yielding structural similarity (Howe et al., 2013). Because zebrafish eggs are laid and fertilized externally, embryonic growth can be easily visualized, unlike in mammalian models. They share a protruding yolk sac structure with human embryos, unlike rodent models which have inverted yolk sacs (reviewed by Sant and Timme-Laragy, 2018). Unlike humans, the zebrafish yolk is purely lecithotrophic, meaning that a finite amount of yolk is supplied prior to external fertilization (Kunz-Ramsay, 2013). The composition of the yolk is well-characterized, composed mostly of lipids, such as cholesterol and triglycerides, and bulk proteins, such as vitellogenins (Anderson et al., 2011; Fraher et al., 2016; Miyares et al., 2014; Quinlivan and Farber, 2017). Therefore, the zebrafish is a unique, well-controlled model in which to study the fundamental contributions of yolk nutrition to growth and development.
From zygote until about 5 days post-fertilization (dpf), zebrafish development is reliant on yolk sac metabolism for its energy. Once feeding begins to take place, the yolk plays a secondary role in nutrient uptake until full yolk absorption at 7 dpf (Wilson, 2012). Previous studies have investigated yolk sac volume perturbations at particular time points, such as 5 or 7 dpf, as a model for the amount of nutrients used (Kalasekar et al., 2015). It is believed these time points are sufficient for reasonable conclusions; however, this study aims to test this belief with a continuous time course investigation. The addition of multiple discrete time points, in comparison to just day 5 or 7, makes it possible to analyze continuous time through ordinary differential equation modeling. Not only is it important to understand how nutrient absorption occurs over time, but also how the fish is growing over time and the interaction of nutrient absorption and growth during this dynamic period of development. To address this, we used mathematical models to quantify yolk absorption from time-lapse fluorescence microscopy images of zebrafish.
Mathematical modeling is an excellent method that has been used successfully to study many developmental processes (Fletcher et al., 2017; George et al., 2015; George and Lubkin, 2018; Vasieva et al., 2013). It has significantly improved our understanding of zebrafish development (Sharpe, 2017; Wertheim and Roose, 2017; Yamaguchi et al., 2007; Zhu et al., 2017). The majority of the mathematical models that describe zebrafish development have been used to investigate the movement of pigment cells, pigment patterns and formation of zebrafish stripes (McGuirl et al., 2020; Volkening and Sandstede, 2018) and the mathematical models that have been developed to study the growth dynamics of zebrafish focus on embryonic (0-3 dpf) or early larval periods (Zhu et al., 2017). Augustine et al. (2011) described fish length over time throughout the entire juvenile stage of the fish (until about 80 dpf) using ‘dynamic energy budget’ (DEB) theory, which quantifies the uptake and use of food. DEB theory requires excess data to complete analysis and is reliant on stage transitions (e.g. larval to juvenile) to produce growth predictions, making the model invalid for the sole investigation of the embryonic stage. Investigation of yolk and length interaction during the embryonic stage has yet to be completed using continuous time mathematical models. Ramlan et al. (2017) examined fish length and yolk diameter at only 1, 2 and 3 dpf in order to evaluate the effects of ethanol exposure in an experimental group. No mathematical models were used in the study by Ramlan et al. (2017) to describe yolk and fish length independently or associatively.
In this study, we use mathematical techniques, such as differential equations modeling, image analyses, curve fittings and parameter estimation, to quantify the rate of yolk absorption over time and its effect on early fish development from 1 to 7 dpf. Findings from this study establish a nonlinear functional relationship between nutrient absorption and early fish growth. We found that the graph of the size of the fish yolk over time is a logistic decay curve. That is, it decays rapidly for a period of time and then levels out. This implies that the rate of yolk utilization in zebrafish is nonlinear.
Understanding the time at which yolk usage has its greatest impact on fish growth is of paramount importance to the DOHaD paradigm, providing a critical window of nutritional sensitivity and susceptibility during which nutritional deviance could yield the highest likelihood of adverse health effects. The goal of this study is to resolve the temporal relationship between embryonic nutrition and growth in a vertebrate model (Danio rerio), and to characterize the prioritization of yolk nutrition towards overall growth throughout the developmental period.
RESULTS
Mathematical model formulation of nutritional absorption during zebrafish development
The amount of nutrients used by the zebrafish can be inferred from the amount of yolk used at a particular time point. Using the yolk area as the measure for embryonic nutritional uptake, we determined a mathematical model that explains the yolk change during 1-7 dpf. Embryos of adult wild-type zebrafish (AB strain) were used in this study. Microscopy images from 14 zebrafish were obtained for each day of the experimentation. The yolk area in mm2 and fish length in mm was computed (Fig. 1), and each data point was normalized according to the maximum value in each set. The experimental data for yolk area and fish length are shown in Tables S1 and S2, respectively. The normalized data for yolk size and fish length are shown in Tables S3 and S4, respectively. Normalized data were used for the modeling.
Fig. 1.
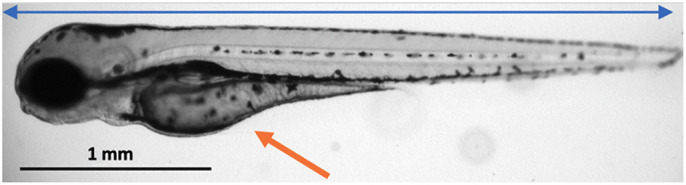
Zebrafish measurements. Example image of a zebrafish at 72 h post-fertilization (hpf). Blue line represents the fish length. Orange arrow points to the yolk sac.
The raw experimental data of yolk area plotted over time foreshadows a decreasing sigmoidal behavior. Here, we examined multiple potential mathematical models in order to conclude with a function that is indubitably the best representation of the experimental data and the inherent biological properties. The biologically relevant model restrictions that we considered were yolk depletion at 7 dpf, consistent depletion of yolk over time with no regeneration of yolk, and the initial yolk size taken at 1 dpf. Therefore, we aimed to determine a function Y(t) that describes the yolk area over time with mathematical properties 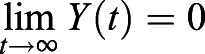 ,
,
dY/dt<0 for t∈[1, 7], and Y(1)=Yini, where Yini is the initial yolk size. The three mathematical models used in this investigation are: the exponential model, Hill function and the logistic model.
Exponential decay is commonly used to model the depletion of a substance and fits the criteria for the biological restriction of yolk depletion by 7 dpf. The function proposed is described by Eqn 1, where Y(t) describes the yolk area as a function of time, a is the yolk decay rate with dimension time−1 and A is a constant determined by the initial yolk size:
| (1) |
where 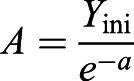 . The exponential function Y(t) is the solution of the exponential differential equation dY/dt=− aY, with Y(1)=Yini, where Yini is chosen to correspond to the experimentally measured yolk size.
. The exponential function Y(t) is the solution of the exponential differential equation dY/dt=− aY, with Y(1)=Yini, where Yini is chosen to correspond to the experimentally measured yolk size.
The sigmoidal shape of the data may be modeled using Hill function. Hill function is traditionally used to model sigmoidal ligand-binding curves in mathematical physiology, but is used widely as a model for various other processes, including dose-response curves in pharmacology (Bhaskaran et al., 2015; Gadagkar and Call, 2015; Keener and Sneyd, 1998). Hill function (Eqn 2) satisfies all of the biological restrictions we specified. Yini is the initial yolk size, b1 is the parameter that describes the time at which half the yolk has been utilized with dimension time, and n1 is the dimensionless Hill exponent:
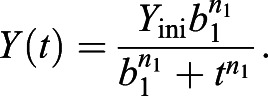 |
(2) |
The final model for consideration is the logistic decay model. The model is described by Eqn 3, where k1 is the carrying capacity with dimension 1, c is the decay constant with dimension time−1, and Yini is the initial yolk size:
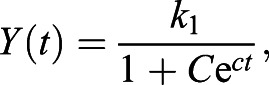 |
(3) |
where C=(k1−Yini)/Yiniec. The constant C is determined from the solution for the differential equation dY/dt=−cY(1−(Y/k1)), with Y(1)=Yini accounting for the initial day being 1 dpf.
Mathematical model formulation of fish length as a representation of growth
As with human and other vertebrate development, successful initial fish growth is an important factor in determining fish longevity and health at the adult stage. A continuous time investigation of fish length over the first 7 days of development was conducted to allow for proper analysis of nutritional effects on this developmental process and the potential adverse health effects. The fish length experimental data depict an increasing trend with a decreased growth rate near the end of the developmental stage. Therefore, we wished to determine a function, L(t), that describes the fish length during days 1-7 with L(1)=Lini, where Lini is the initial fish length, and dL/dt>0 for t∈[1, 7] dpf. In this section, we investigated two different mathematical models in order to confidently describe the experimental data in the best way possible.
The increasing Hill function was used as the first model for consideration. This function reaches a maximum limit as time reaches infinity, representing a decreased rate of growth once the developmental stage reaches its end. The function is described by Eqn 4, where Lmax is the maximum fish length during development, b2 is the time at which half of length development/growth has completed (t∈[1, 7] dpf) with dimension time, and n2 is the dimensionless Hill exponent:
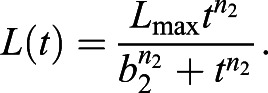 |
(4) |
In addition to using the increasing Hill function as a model of fish growth, we also investigated the logistic growth model. The logistic model is described by Eqn 5, where k2 is dimensionless and represents the maximum possible fish length during the developmental stage, d is the growth rate with dimension time−1, and Lini is the initial fish length:
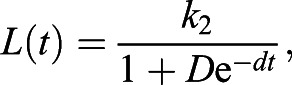 |
(5) |
where D=(k2−Lini)Linie−d. Similarly to the logistic equation represented in the previous section (Eqn 3), the constant D is determined from the solution of the differential equation dL/dt=dL(1−(L/k2)) with L(1)=Lini (Boyce et al., 2017).
Data fitting
It was necessary to determine parameter values for the unknowns in each of the preceding proposed functions (Eqns 1-5). In order to determine parameter values in agreement with the experimental data, we performed data fitting on each zebrafish individually. The experimental data was fitted to the predicted values determined by each function via a nonlinear least squares regression method in which the sum of squared residuals (SSR) is minimized. The sum of squared residuals measures the overall difference between the data and the values predicted by the estimation model. SSR is calculated using Eqn 6, where 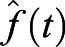 represents the value predicted by the model at time t and f(t) is the corresponding experimental data. In this case, we summed from time equal to 1-7 dpf. The method was executed in MATLAB R2019b and was performed for all functions in consideration:
represents the value predicted by the model at time t and f(t) is the corresponding experimental data. In this case, we summed from time equal to 1-7 dpf. The method was executed in MATLAB R2019b and was performed for all functions in consideration:
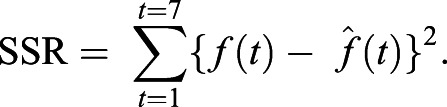 |
(6) |
Error analysis for model selection
Error analysis is used in order to determine the best model to fit the data in each scenario. We computed for each function the coefficient of determination (R-Squared). R-Squared is given by Eqn 7, where the SSR and the sum of squared totals (SST) are given by Eqn 8. In these formulae, f is the expected data, 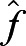 is the prediction by the model, and
is the prediction by the model, and 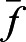 is the mean of the data set. We chose R-Squared as our comparison model because it describes the amount of variability in the data that is explained by the model. We note that R-Squared should take values between 0 and 1, with higher values indicating that the model explains the variability of the response data around its mean. If the value is out of this range or negative, the model is an insufficient fit.
is the mean of the data set. We chose R-Squared as our comparison model because it describes the amount of variability in the data that is explained by the model. We note that R-Squared should take values between 0 and 1, with higher values indicating that the model explains the variability of the response data around its mean. If the value is out of this range or negative, the model is an insufficient fit.
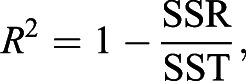 |
(7) |
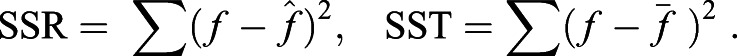 |
(8) |
Mathematical model of yolk absorption
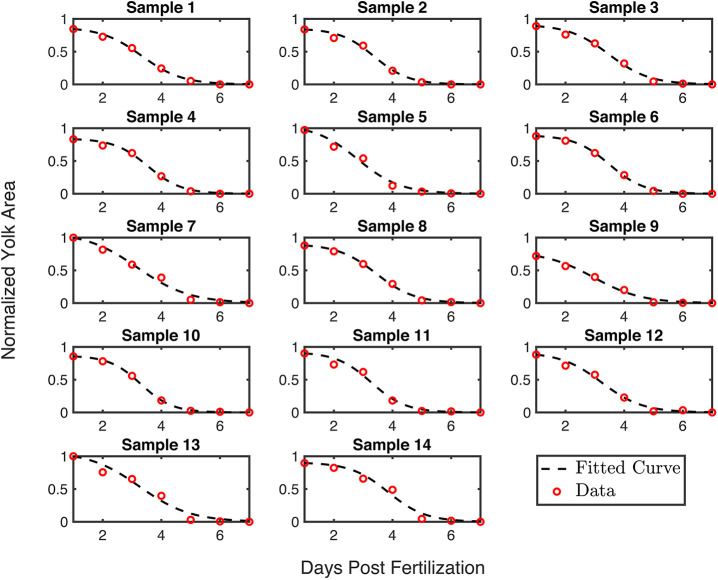
Estimated parameters, shown in Table S5, for the yolk model (Eqns 1-3) were obtained by fitting each model to individual fish experimental data. The graphs for the individual fish yolk samples are shown in Fig. 2 (for logistic model, Eqn 3), Fig. S1 (for exponential model, Eqn 1) and Fig. S2 (for Hill function, Eqn 2). Plots of the mean yolk data±s.e.m. are shown along with the mean best-fit curve in Fig. S3. After computing the errors for each model describing yolk area over time (Fig. S3), we determined the logistic decay model to be the most representative of the data (exponential model: R2=0.86; Hill function: R2=0.98; logistic model: R2=0.99). We note that even though the logistic model is the best fit for the data, the Hill function is also an excellent fit with R2=0.98. This is because both the Hill function and logistic model have sigmoidal curves and therefore can describe the sigmoidal curve for the yolk data.
Fig. 2.
Logistic fit of yolk size over time. Fish length normalized to the maximum observed at 7 dpf, for 14 fish samples. Dashed line represents the fitted curve.
The logistic model has a mean decay rate, c, of 1.5 time−1 and mean dimensionless carrying capacity, k1, of 0.92. This model shows that nutrition is being used at a faster rate during the initial stages of development but less nutrition is available near the end, as expected (Fig. 2). An interesting finding is that the rate of yolk utilization (i.e. the rate of change in yolk with respect to time) is nonlinear, inferred from the slope of the graph of the logistic model. Additionally, the logistic decay model yields insight into how fast the yolk is being absorbed.
Mathematical model of fish length
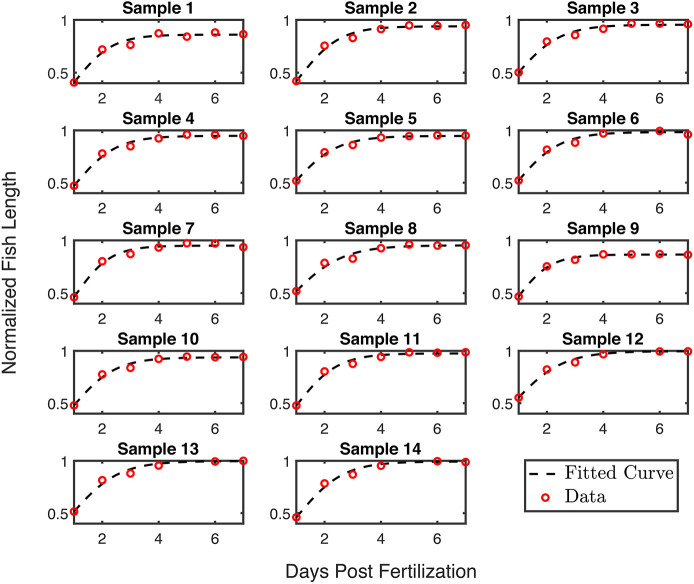
Parameter values for the models for fish length (Eqns 4 and 5) were estimated by fitting the models to the data for each individual fish sample. The graphs for the individual fish length plotted against dpf for individual fish samples are shown in Fig. 3 (for logistic model, Eqn 5) and in Fig. S4 (for Hill function, Eqn 4).
Fig. 3.
Logistic fit of fish length over time for the fish samples. Yolk area, normalized to the maximum observed at 0 dpf, for 14 fish samples. Dashed line represents the fitted curve.
Parameter estimates found using the least squares method are shown in Table S6 and plots showing each best fit model and experimental data±s.e.m. to fit the data are shown in Fig. S5. Both models taken into consideration visually fit the model well (Fig. S5), but the logistic growth model (Eqn 5) yields the least error (Hill function: R2=0.98; logistic model: R2=0.99). We made note of the logistic behavior of the fish length to be investigated in subsequent sections. Our findings showed that there is rapid growth at the early stages of development but the rate slows down near the end of the developmental (Fig. 3) time range we considered in the study. We aimed to further investigate the link between the rapid early growth and the rapid yolk absorption taking place between 1 and 4 dpf.
The interaction between nutrient uptake and fish length
Based on the preceding results, we conclude that yolk size and fish length vary with time in a logistic pattern. The equations best describing their change over time are given by Eqns 3 and 5. Knowing exactly how yolk size and fish length vary independently of each other will pave the way for studying their interactions. Here, we develop a system of two differential equations that describe the effects one developmental process has on the other.
It is known that embryonic nutrition plays a role in eventual health and longevity, but it is equally important to determine the relationship between nutrition and early fish development. The energy produced via metabolism of substrates in the yolk is the only source of energy during the embryonic period. We can then take the amount of nutrients absorbed, or the yolk depleted, as the driving force for fish length growth. The two processes are taken to influence each other; therefore, we designed a mathematical model to capture their interactions, with L denoting fish length and Y denoting the size of the yolk, or the assumed nutrients available. The rate of yolk utilization is then determined by Eqn 9, where β, α, and K1 are positive real parameters:
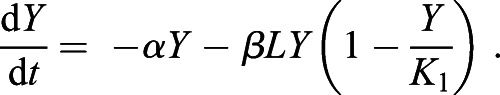 |
(9) |
The unit of β and α is day−1 and the unit of K1 is 1. The term −βLY(1−(Y/K1)) represents the yolk depleted to fuel fish length and the term −αY represents the yolk decay and/or depletion to fuel other organs/processes within the body. In this case, we see that when L=0, or there is no longer growth of the fish length, the yolk depletes exponentially to other parts of the body, with K1 representing the capacity of available nutrients. The product term βLY signifies that the absorption/depletion of the yolk varies with fish length. As the fish grows and increases in length, the amount of yolk necessary to sustain the fish increases; therefore, more yolk is consumed by the fish. The parameter α represents the rate at which nutrients are being used elsewhere in the body and the parameter β describes rate at which the interaction between yolk and length occurs. This interaction also yields Eqn 10 for the rate of fish length growth, where the unit of γ is day−1 and the unit of K2 is 1:
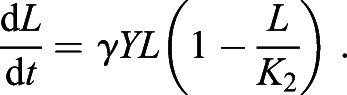 |
(10) |
In the absence of nutrients (Y=0), we see that the length growth will terminate and no longer grow. The rate parameter γ represents the rate at which the length grows with respect to the nutrients absorbed into the body that fuel the growth. We take this length growth to be logistic based on the findings in the preceding sections. The product term γYL signifies that the larger the amount of yolk available, the more the fish will grow. Fig. 3 further supports this argument because the magnitude of the rate of change in fish length decreases with time and this corresponds to a decrease in available yolk. The coupled system of equations (Eqn 11) describes the dynamics between yolk utilization and the rate of fish length growth. Initial conditions are determined by the data from 1 dpf:
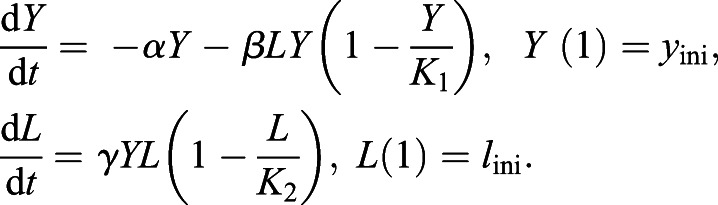 |
(11) |
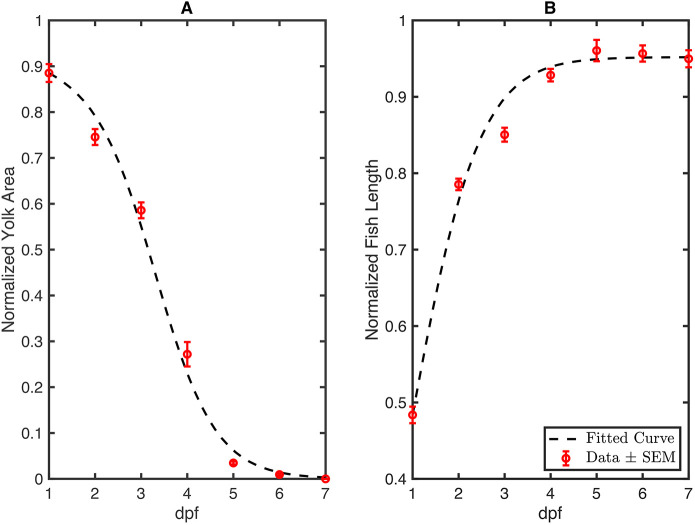
Parameter estimation for the coupled model was performed using the least squares regression method as described previously. The model to fit the data and the experimental data±s.e.m. is shown in Fig. 4 with parameter estimates for each fish shown in Table S7.
Fig. 4.
The fitted system of two ordinary differential equations. (A) Normalized yolk area over time fitted to experimental data. (B) Normalized fish length over time fitted to experimental data. Data are normalized to the maximum value for each parameter (Eqn 11).
Initial parameter estimates were inferred from the computed individual function parameters in Eqns 1-3. The Runge–Kutta-4 method was used to solve the differential equations to ensure accuracy and efficiency. The two-dimensional ordinary differential equation model (Eqn 11) proved to be a novel and accurate representation of experimental data (R2=0.99, Fig. 4).
The system of differential equations (Eqn 11) predicts that yolk depletion that fuels fish length is logistic, whereas the yolk depletion that fuels other organs and/or decay within the body is exponential. In Eqn 11, α represents the rate at which nutrients are being used elsewhere in the body. The average value of α was 0.058 day−1 computed from data in Table S7. In Eqn 11, the parameter β describes rate at which the interaction between yolk and length occurs. Similarly, the average value of β was 1.55 day−1, computed from data in Table S7. The average values for γ, K1 and K2 were 1.47 day−1, 0.891 and 0.998, respectively. The variability of parameter values across samples for the various models was determined by the percentage of sample parameters that fall within one standard deviation from the mean. This was done for each parameter in the logistic yolk over time model, the logistic length over time model and the ODE system model. The models are robust, and the variability of each parameter value was minimal across samples (Table S8).
The system of differential equations (Eqn 11) was then used to investigate the impact of yolk usage on daily growth.
The impact of yolk usage on daily growth
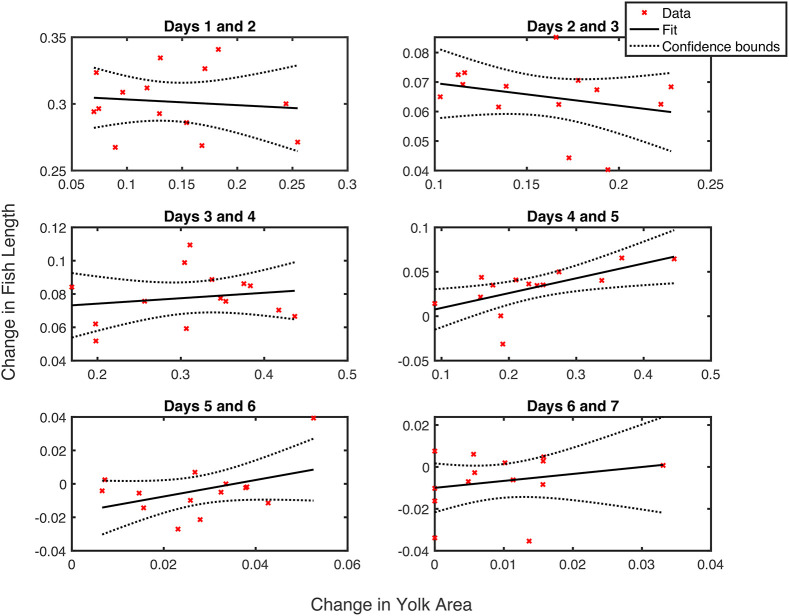
Understanding the time at which yolk usage has its largest impact on fish growth is of paramount importance because nutritional deviance at this key time point could yield the highest likelihood of adverse health effects. The first step in determining the impact on yolk usage is to look at the change in yolk over a 24-h period and compare it to the change in fish length over the same period using experimental data (Fig. 5).
Fig. 5.
Daily change in fish length and yolk area. The changes in fish length and yolk area (both normalized to the maximum value) vary daily. There is an association between the change in yolk and the change in length between 4 and 5 dpf. Linear regression analysis was performed with the fit and confidence bounds shown by the solid and dotted lines, respectively. ANOVA was performed and found to be statistically significant (P=0.017).
Our results show that there is a strong association between yolk usage and length change between 4 and 5 dpf (P=0.017) but no other time frame showed statistical significance (Fig. 5). To support this, we found the percentage change for each fish individually and determined that the same time frame is statistically significant (P=0.04) with no other time points demonstrating statistical significance. This discrete time analysis shows that yolk metabolism between 4 and 5 dpf plays a large role in successful fish growth but fails to give a precise time at which the rate of yolk usage is at its greatest.
In order to further study the rate of yolk utilization over time, we plotted |dY/dt| from Eqn 11 over time in days. This represents the rate of yolk utilization over time rather than the yolk area over time as displayed previously. After substituting the values for the parameters from the data fitting, we obtained the functions Y(t) and L(t) by solving the differential Eqn 11. These were used to determine the magnitude of the rate of yolk utilization |dY(t)/dt| from Eqn 11 over time in days. This was done for every sample and the mean values are plotted in Fig. 6A. The overall rate of yolk utilization, |dY/dt|, is nonlinear with maximum utilization occurring at 3.4 dpf.
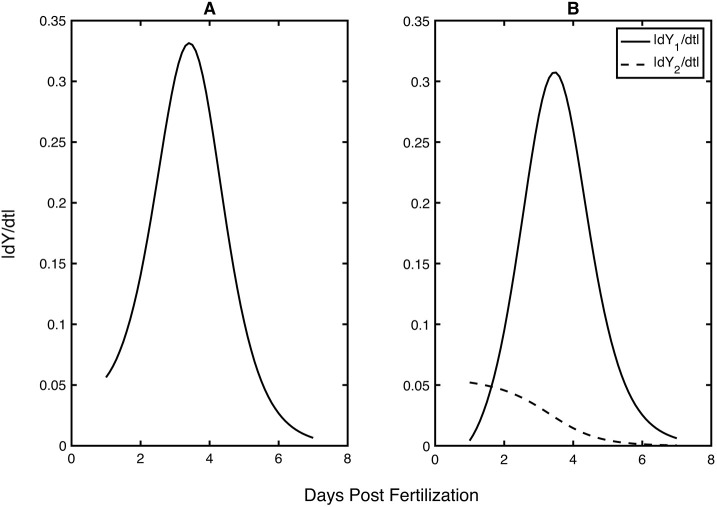
Fig. 6.
Absolute value of the rate of yolk utilization. (A) Plot of the absolute value of total yolk utilization (day−1) (|dY/dt|) versus dpf. This plot shows that the maximum rate of utilization occurs at approximately 3.4 dpf. (B) Plot of yolk utilization based on separate valuation of each of the terms in the differential equation, |dY1/dt| and |dY2/dt|.
In Fig. 6B, the two curves on the graph represent the rate of yolk utilization based on both terms in the differential equation evaluated separately. Thus, the rate of yolk utilization that drives the increase in fish length is dY1/dt=−βL(t)Y(t)(1−Y(t)/K1) whereas the rate of yolk utilization for other processes including yolk decay is dY2/dt=− αY(t), where dY/dt=dY1/dt+dY2/dt. We plotted computed values for |dY1/dt| and |dY2/dt| against dpf (Fig. 6B). The plots were generated in a similar way as described above for Fig. 6A, where Y(t) and L(t) are functions of time. The rate of change in yolk necessary for fish growth |dY1/dt| is nonlinear with maximum value at 3.5 dpf. The rate of yolk decay, |dY2/dt|, is nonlinear in time with maximum value at 1 dpf. In addition, |dY2/dt| is larger in value than |dY1/dt| until approximately 2 dpf (Fig. 6B) after which |dY2/dt| becomes larger. This implies that between 1 and 2 dpf the fraction of yolk depleted to fuel the increase in fish length was smaller than that used for other processes in the body.
Through this investigation, we were able to determine the exact time at which yolk utilization reaches its maximum for nutrition fueling the increase in fish length versus other processes, including yolk decay. In both cases, we observed that the maximum rate of utilization, (|dY/dt|, |dY1/dt|), occurs between 3 and 4 dpf (3.4 dpf and 3.5 dpf, respectively). The precise time at which maximum utilization occurs (3.5 dpf) assists in the identification of utilization sensitivity, which can be informative when determining sensitive time points for further analysis. This finding from the system of differential equations complements the results from the raw data statistical analysis approach (Fig. 5), in which the yolk usage between 4 and 5 dpf was found to be highly correlated with fish growth during 4-5 dpf. We see that once the maximum utilization rate occurs, the impact on fish growth is increased with a slight delay. These findings suggest there may be a delay between yolk usage and fish growth, which is to be discussed in a later section.
Stability analysis of the system of differential equations
The system of differential equations describing yolk utilization and length change over time was analyzed for stability to further aid our understanding of the mathematical model. Independent yolk utilization over time given in Eqn 3 can be rewritten as:
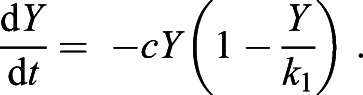 |
(12) |
The model has two ultimate potential equilibrium points, one at zero and another at its carrying capacity (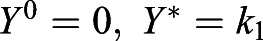 ). Algebraic stability analysis reveals that the zero equilibrium is stable whereas the maximum yolk equilibrium is unstable (see supplementary Materials and Methods). The change in length over time is given in Eqn 5 with its dynamical form given in supplementary Materials and Methods. In this case, the model has similar equilibrium points as the yolk model at zero and its carrying capacity
). Algebraic stability analysis reveals that the zero equilibrium is stable whereas the maximum yolk equilibrium is unstable (see supplementary Materials and Methods). The change in length over time is given in Eqn 5 with its dynamical form given in supplementary Materials and Methods. In this case, the model has similar equilibrium points as the yolk model at zero and its carrying capacity 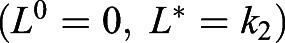 . Whereas the yolk utilization over time reaches the zero equilibrium, algebraic stability analysis reveals stability of the maximum fish length,
. Whereas the yolk utilization over time reaches the zero equilibrium, algebraic stability analysis reveals stability of the maximum fish length, 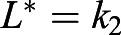 . This is consistent with our expectation, because we do not expect the fish length to increase or decrease after yolk depletion (i.e. in the absence of outer sources of nutrients).
. This is consistent with our expectation, because we do not expect the fish length to increase or decrease after yolk depletion (i.e. in the absence of outer sources of nutrients).
The system of differential equations describing the interaction between fish length and yolk utilization (Eqn 11) has two equilibrium points, E0 and 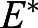 (see supplementary Materials and Methods):
(see supplementary Materials and Methods):
| (13) |
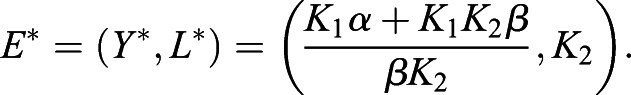 |
(14) |
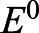 is a nonphysical equilibrium point with a zero fish length; therefore, further analysis of this steady state is unnecessary. Linearization of the system along
is a nonphysical equilibrium point with a zero fish length; therefore, further analysis of this steady state is unnecessary. Linearization of the system along 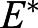 and analyzing the eigenvalues of the Jacobian matrix reveals that
and analyzing the eigenvalues of the Jacobian matrix reveals that 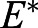 is unstable (see supplementary Materials and Methods, and Fig. S6). The instability of
is unstable (see supplementary Materials and Methods, and Fig. S6). The instability of 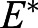 is particularly interesting due to the previous finding
is particularly interesting due to the previous finding 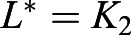 . In the independent case, we found
. In the independent case, we found 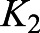 to be stable. When looking at the interactions between yolk and length, we see that stability of
to be stable. When looking at the interactions between yolk and length, we see that stability of 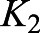 no longer exists. Although this is the case, we do see that the restriction of the model occurring solely between 1 and 7 dpf results in an unexpected ultimate tendency. At 7 dpf, yolk utilization is no longer occurring and no longer fueling fish growth. Therefore, the length at day 7 is the ultimate length possible within the model constraints. As fish receive their energy from food consumption beyond 7 dpf, further experiments may be required to investigate long-term growth following the developmental stage.
no longer exists. Although this is the case, we do see that the restriction of the model occurring solely between 1 and 7 dpf results in an unexpected ultimate tendency. At 7 dpf, yolk utilization is no longer occurring and no longer fueling fish growth. Therefore, the length at day 7 is the ultimate length possible within the model constraints. As fish receive their energy from food consumption beyond 7 dpf, further experiments may be required to investigate long-term growth following the developmental stage.
Modeling the delay between yolk usage and fish growth
Delay differential equation modeling is useful in practice when a characteristic at time t depends on t−τ, where t−τ is some previous time. In the model proposed in the preceding sections, we made the assumption that there is no delay between nutrient usage and its contribution to fish growth. In contrast, we may remove this assumption by incorporating a time delay into our mathematical model (Eqn 11). After the time at which the zebrafish uses its yolk, there are various complex processes that occur to metabolize the yolk for development. The new model with this incorporated delay can be described by Eqn 15:
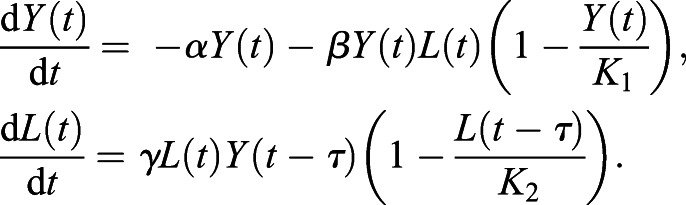 |
(15) |
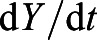 is the first order derivative representing the rate of change of yolk utilization whereas
is the first order derivative representing the rate of change of yolk utilization whereas 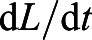 is the first order derivative representing the rate of change in fish length, as discussed previously. The variation between this model and the previous is the incorporation of the delay parameter
is the first order derivative representing the rate of change in fish length, as discussed previously. The variation between this model and the previous is the incorporation of the delay parameter 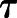 , where
, where 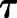 is the delay factor and
is the delay factor and 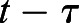 is the time delay term. This model describes the fish needing time to metabolize the yolk before growth can occur. We aimed to determine the impact of this addition to the model and to determine whether the correlation between yolk utilization and fish length changes/increases with the modification. The nonlinear least squares regression method is used to determine the best fit parameter values, including
is the time delay term. This model describes the fish needing time to metabolize the yolk before growth can occur. We aimed to determine the impact of this addition to the model and to determine whether the correlation between yolk utilization and fish length changes/increases with the modification. The nonlinear least squares regression method is used to determine the best fit parameter values, including 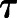 , that represent the mean data best for our delay differential equation model. This method yields
, that represent the mean data best for our delay differential equation model. This method yields 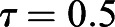 days, approximately 12 h, which implies that it takes about 12 h for yolk consumed to be metabolized for fish growth. This also implies that there is a 12-h delay between the maximum yolk utilization rate at 3.5 dpf discussed previously and the contribution of this maximum utilization to fish growth. Therefore, the maximum yolk utilization rate at 3.5 dpf will impact the increase in fish length at 4 dpf. This modification yields
days, approximately 12 h, which implies that it takes about 12 h for yolk consumed to be metabolized for fish growth. This also implies that there is a 12-h delay between the maximum yolk utilization rate at 3.5 dpf discussed previously and the contribution of this maximum utilization to fish growth. Therefore, the maximum yolk utilization rate at 3.5 dpf will impact the increase in fish length at 4 dpf. This modification yields 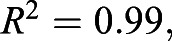 meaning that the addition of the delay within the model demonstrates the correlation between yolk utilization, fish length and the model prediction.
meaning that the addition of the delay within the model demonstrates the correlation between yolk utilization, fish length and the model prediction.
Testing the applicability of our model to an environmental condition
Through our results, we aimed to lay a foundation for further pharmacological modification studies investigating yolk utilization and fish growth rates. However, it is unknown whether our model (Eqn 11) is still applicable under conditions of stress and environmental modulation. To test this, we also exposed embryos daily to a pollutant, perfluorooctanesulfonic acid (PFOS, 32 µM). PFOS has been previously shown to disrupt yolk utilization (Jantzen et al., 2016; Sant et al., 2017, 2018), with no significant impact on fish length at the selected concentration (see supplementary Materials and Methods). Therefore, PFOS was an ideal candidate to test the robustness of our mathematical model because of the known outcome and because we can test whether our model may examine independently controlled variables. We performed a nonlinear least squares regression analysis to determine the parameter values (Table S9) for which Eqn 11 best fits the mean sample data. There was no significant increase in heterogeneity (variance) due to exposures (Levene's test; P>0.05) and the system of differential equations (Eqn 11) is still representative of the data (R2=0.99) (Fig. S7). PFOS samples displayed an increase in yolk utilization as shown by the best fit values for the rate parameters α and β (Table S9, Fig. S7). α displayed an increase of 84.47% and β increased by 51.28%. Therefore, the mathematical model (Eqn 11) can capture how pharmacological modifications affect the per capita yolk utilization rates that fuel the fish growth (β) and also the decay due to yolk use elsewhere in the body (α). This is interesting, because it demonstrates that exposure of zebrafish to the pollutant PFOS leads to the yolk being used up at an increased rate compared with control. The average rate parameter γ (i.e. per capita growth rate of zebrafish) displayed a 1.17% decrease in PFOS-exposed samples (Table S9). This little to no change in γ between controls and PFOS samples demonstrates the models’ ability to capture the similarities in fish length growth behavior between groups (Fig. S7). These results support our previous crude findings that yolk utilization, and not fish length, are impacted by this concentration of PFOS (Sant et al., 2017; Sant et al., 2018). The extension of the model (Eqn 11) to a ‘stressed’ or non-control environment demonstrates that even in the presence of toxicological modifications, logistic behavior is expected and that our model is robust enough to withstand environmental perturbation.
DISCUSSION
Embryonic development is a dynamic process, requiring a coordinated and energy-intensive continuum of events crucial for success. During this period, embryogenesis and later organogenesis lay a pattern that serves as a foundation for health throughout life.
The DOHaD paradigm has repeatedly associated the relationship between developmental nutrition, in utero environment, and prenatal growth with chronic disease outcomes. Here, we assess the relationship between embryonic nutrition and growth using the zebrafish model in order to better characterize these relationships temporally and identify key windows of metabolic development.
The impact of yolk utilization over time is a question unanswered by previous literature. Our findings demonstrate the continual time interactions between yolk utilization and fish growth through a system of two differential equations. The mathematical model is novel and it has been validated by experimental observations, making it a powerful tool for replication and future simulations. Our models show a strong association between the rates of change in yolk and fish length between 4 and 5 dpf (P=0.017), highlighting that yolk metabolism between 4 and 5 dpf plays a crucial role in successful fish growth. Therefore, disruption of yolk metabolism during this period may have the greatest impact on larval growth, and this is a critically sensitive metabolic window for DOHaD in zebrafish studies.
Modeling zebrafish growth
Zebrafish length over time has been investigated in various toxicology and biology studies, in which a mathematical model may or may not be reported to describe the experimental data (Collery et al., 2014; Dang et al., 2018; Ho and Burggren, 2012; Imrie and Sadler, 2010). Additionally, the time frame for fish length measurements varies greatly among studies with the majority of measurements being taken cross-sectionally during the embryonic stage or much later in the larval or juvenile stages (Augustine et al., 2011). As a result, the embryonic time frame lacks fish length mathematical modeling and studies investigating later time points possess few models to describe the experimental data, although one study is of particular interest (Zhu et al., 2017). Zebrafish length and body mass was assessed at 180 days post-hatching, where hatching takes place between 2 and 3 dpf (Kimmel et al., 1995). The experimental data for the study was fit to a four-parametric logistic model and it was concluded that the fish length over time behaves logistically (Zhu et al., 2017). With the embryonic stage also behaving logistically, as described extensively throughout this study, we see there may be a correlation between early and juvenile fish length development of the zebrafish. Early development studies that investigate length over time lack the necessary time points for the developed mathematical model of this study to be applied (Dang et al., 2018; Schäfers et al., 2007). One study in particular reported paired yolk and length data at 1, 2 and 3 dpf but the lack of further time points deem the data impractical for a continuous time analysis over the embryonic and larval stages (Ramlan et al., 2017). The need for a time course model of fish length throughout these embryonic and larval stages is apparent and the model proposed in this study lays a foundation for a growing body of literature surrounding this topic.
Zebrafish are an important model for developmental biology and toxicological research. Because zebrafish are lecithotrophic, the amount and rate of yolk utilization can be an important indicator of adaptive mechanisms due to environmental stressors, such as toxicant exposures or environmental modulation (temperature, pH, etc.). Yolk use is a common endpoint used in toxicological testing, and therefore we needed to ensure that our model was robust enough to withstand these stressors. Here, we showed that our model could indeed account for toxicant-induced stress (Fig. S7), and that sample heterogeneity, including differences in sample means between groups due to treatment, could be readily accounted for. Therefore, we expect this model to be applicable to diverse studies for use across disciplines, including pharmacology and toxicology.
Implications of the peak time of utilization fueling fish growth
Zebrafish have been shown to be a high-throughput, simplified model in which to study the relationship between nutrition and growth in vertebrates during the embryonic period (previously reviewed by Sant and Timme-Laragy, 2018). The majority of research relating developmental nutrition with growth outcomes has been largely associative due to the inaccessibility of the intrauterine environment in mammals. Unlike humans, who rely on maternally supplied yolk granules during early embryogenesis and histiotrophic uptake of nutrients following implantation, zebrafish are a clarified nutritional model. Because zebrafish have a finite amount of yolk available until exogenous feeding, the use of this supply over time can serve as a proxy for total embryonic nutrition.
Using our mathematical model, we were able to determine the time at which yolk metabolism fueling fish growth is at its peak. At approximately 84 hpf, the yolk utilization rate reached its maximum, with a 12 h delay until its impact on fish length growth at 96 hpf. Although this window of sensitivity requires additional validation across other vertebrate models using comparative biology (Carnegie stages), this finding is especially interesting biologically because this is a peak period of endodermal maturation in the zebrafish. During this time window, structural organogenesis wanes, but physiological functions commence. Organs and tissues that are vital for nutrient uptake, distribution and metabolism, such as the liver, become more physiologically and metabolically active between 4 and 5 dpf (reviewed by Goessling and Sadler, 2015; Wilkins and Pack, 2013). Although we cannot make any conclusions from this study about chronic disease and the relationship between exogenous feeding and growth after the developmental period, this work further supports that 4-5 dpf may be a critical metabolic window for growth and development in zebrafish. Furthermore, this window is also likely then to be a window of susceptibility (within the DOHaD paradigm) during which nutritional, toxicological or pharmacological exposures and deficiencies may produce deleterious effects that could persist throughout life.
Dynamic energy budget
Augustine et al. (2011) calculated the energy of the zebrafish using DEB theory. This method uses data on observed fish lengths, weights, reproduction and survival to estimate the cumulative energy invested in development. This cumulative maturity level is measured in millijoules and was found for the entirety of the juvenile life stage for the fish (day 1-218). For 1-7 dpf, maturity was estimated to be a linear process, which differs from the logistic behavior seen here. In our experiment, the energy invested in development was taken from the yolk area and we assume use the sole use of this deposit as energy during development. This differs from the study of Augustine et al. (2011), in which they assume a smooth transition from yolk usage to food consumption without a perturbation of the maturity level. The simplicity of the model described in this study is valuable for its accessibility for usage even with small data sets. The accessibility of the model will also allow for widespread usage of the model to investigate nutritional deviation (perturbation or supplementation) during development using measurements that are time and cost efficient (microscopy-based measurements). Further research and data collection should be executed to extend the proposed model to include the complex processes the DEB model considers while keeping the necessary data for conclusions to a minimum.
Limitations of the mathematical model
We acknowledge some limitations of this study. The mathematical model assumes that yolk metabolism occurs largely to fuel fish length, thereby using fish length as a measure of overall fish growth. Future studies obtaining growth data from various other organs could aid in the extension of the mathematical model to better incorporate growth in other areas of the body. Additionally, using 2D area as a proxy for total 3D yolk limits the exact evaluation of yolk present at a particular time. We acknowledge that other 3D methods are available, such as Oil Red O staining, that would help with the understanding of lipid-rich yolk, but Oil Red O staining would not allow for longitudinal assessment over time (Kalasekar et al., 2015). Note that when we use 2D area measurements, we measure yolk size in the x and y plane, but its size in the z plane is not taken into account (Fig. S8A,B). In the early stages of development, particularly at 2-3 dpf, the fish yolk may easily be approximated by a combination of an ellipsoid and a cylindrical tube (Fig. S8A,B). The tube at this stage may add a disproportionate amount to the area when using 2D measurements as a proxy for total 3D yolk. This is because the ellipsoidal portion holds much more mass and this may not be captured in the 2D plane (Fig. S8B). We estimated the yolk volume from sagittal and coronal images of zebrafish (Fig. S8A,B). We found that the yolk volume and yolk area are positively correlated at 2-3 dpf when the yolk has a significant depth not captured by a 2D image (see supplementary Materials and Methods and Fig. S8C). From this, we state that 2D modeling of the yolk, although not perfect, is an acceptable proxy for yolk volume in this study. Statistical analysis reveals a strong association (R2>0.85, P<0.01).
We understand that our model is only applicable to embryos and early larvae prior to the onset of exogenous feeding (during 100% yolk-supplied, lecithotrophic nutrition). Beyond that dynamic period, yolk is no longer available nor a viable predictor of overall growth. Additionally, parameter estimates made by the model are based on a relatively small data set and are setting a foundation that has not been laid before. Yolk utilization has previously been thought to be a labile process that is sensitive to perturbation, but the relationship between yolk utilization and time has not been well characterized (reviewed by Sant and Timme-Laragy, 2018). Here, we conclude that yolk utilization occurs logistically. Without a foundation for the logistic behavior, we identified the best mathematical models by using a combination of data from laboratory experiments, parameter estimations and least squares error analysis, rather than building on findings from existing literature. It is also of note the model has been made for a wild-type (AB) zebrafish line. Other strains of zebrafish may behave differently, and a larger data set is needed to overcome this limitation. Lastly, the model is able to make predictions on the first 7 days of development, without the added variable of exogenous feeding. Growth occurring from food intake may be incorporated for future extensions of the mathematical model.
Application of the model to developmental biology and health
In this study, we characterize the relationships between embryonic growth and nutrition in a controlled model. Unlike mammalian models, we are able to exclude exogenous nutrient sources in zebrafish. Although this is a simplified model that allows us to reduce the number of convoluted or extraneous variables, we are unable to account for any adaptive responses which may occur as a result. ‘Catch-up growth’ and adaptive changes in feeding behaviors, during which rapid growth is observed followed by a period of impaired or stunted growth, are well-documented pediatric observations (Boersma and Wit, 1997). Catch-up growth has been widely studied, and has been associated with increased risk for chronic disease later in life (Eriksson et al., 1999; Huxley et al., 2000; Ong et al., 2000). Because this adaptive response is a potential mechanism of the DOHaD paradigm, future studies should examine flux following the onset of exogenous diets (after 5-7 dpf). Because zebrafish do not rely on lactation and instead consume purely exogenous diets, they could be a unique tool to examine this relationship.
Here, we examined the relationship between nutrition and growth under ideal laboratory conditions for the development of zebrafish. Although this reductionist approach allowed us to construct an ideal model, this does not account for genetic or environmental diversity, which may contribute to physiological perturbations. Deviations from these ideal conditions, such as nutritional modulation (under- and over-nutrition, yolk composition and rate of use) or exposures to relevant pharmacological or toxicological agents may hinder or exacerbate the rate or timing of the relationships proposed in this study. We have previously shown that exposures to toxicants and pharmacological agents can impair embryonic uptake and availability of nutrients in rodent models, and that these exposures are associated with hindered growth (Harris et al., 2015; Sant et al., 2016a; Sant et al., 2016b; Sant et al., 2013). In future work, our laboratory will assess how these factors impact these relationships in order to show the robustness and sensitivity of our model.
Conclusion
In conclusion, this study applies mathematical techniques, such as differential equations modeling, image analyses, curve fittings and parameter estimation, to quantify the rate of yolk absorption over time and its effect on early fish development. It identifies a nonlinear functional relationship between nutrient absorption and early fish growth, and a critical window of yolk utilization at approximately 84 hpf. We highlight a susceptible time point during development at which exposures and nutrition may have deleterious and potentially lasting effects.
MATERIALS AND METHODS
Animals and husbandry
Animal care and use was performed in strict accordance with protocols approved by the San Diego State University Institutional Animal Care and Use Committee (PHS Assurance Number 16-00430). Adult wild-type zebrafish (AB strain) were obtained from existing populations at the University of California San Diego and maintained as a colony at San Diego State University. Zebrafish were maintained in an automated zebrafish habitat (Aquaneering), at 28.5°C and on a 12 h light:12 h dark cycle. Water quality conditions were monitored throughout the study, and safe levels of chemicals including total chlorine, ammonia, nitrites and nitrates were maintained. Adult zebrafish were fed a Gemma Micro 300 powdered diet (Skretting) daily, according to manufacturer's recommendations.
Embryo collection and maintenance
Embryos for each experiment were randomized from six breeding tanks containing 20 females and ten males in order to reduce clutch effects. Embryos were collected and confirmed for fertilization prior to 1 hpf. Embryos were rinsed and transferred to 100 mm polystyrene Petri dishes containing 0.3× Danieau's medium [17 mM NaCl, 2 mM KCl, 0.12 mM MgSO4, 1.8 mM Ca(NO3)2, 1.5 mM HEPES, pH 7.6], and placed into a light-cycling incubator (28.5°C) overnight. At 24 hpf, embryos were manually dechorionated using watchmaker's forceps and individually transferred into wells of a polystyrene 24-well plate containing 1 ml of 0.3× Danieau's medium supplemented with 0.01% dimethyl sulfoxide (DMSO; Thermo Fisher Scientific, BP231-100). DMSO was utilized to mimic typical vehicle control conditions for zebrafish studies, and the 0.01% v/v concentration has been previously shown to be non-toxic and have minimal impact on growth and development (Hallare et al., 2006; Maes et al., 2012; Sant et al., 2016c). Media was refreshed daily to prevent hypoxia throughout the study. To test the applicability of our model to an environmental stressor, we additionally exposed embryos to a contaminant, heptadecafluorooctanesulfonic acid (PFOS) (Sigma-Aldrich, 33607). Additional experimental details related to exposures are provided in the supplementary Materials and Methods.
Microscopy
All microscopy was performed using a Nikon Ti-2 inverted light microscope using Nikon NIS Elements Advanced software. Prior to imaging, embryos and larvae were rinsed thoroughly in 0.3× Danieau's and briefly anesthetized in 0.168 mg/ml Tricaine-S MS-222 solution. Embryos and larvae were rinsed then transferred to drops of 3% methylcellulose for imaging. Images were acquired at 20× and 40× magnification. At the conclusion of imaging, embryos and larvae were thoroughly rinsed in fresh 0.3× Danieau's medium and transferred back to their wells with fresh media. We used 2D imaging in order to decrease handling and anesthesia time for each fish and to support high-throughput microscopy for obtaining data at successive time points.
Image analysis
Visualization of the developmental processes in vivo allows for accurate analyses of nutritional uptake and fish growth. Microscopic images were used to determine yolk area and fish length in zebrafish each day during experimentation beginning at 24 hpf (n=14). Measurements were taken using the NIS Elements Advanced Research software to extract yolk area in mm2 and fish length in mm. Fish length is defined as total anterior-posterior length. The experimental data for yolk area and fish length are shown in Tables S1 and S2, respectively. For analysis, each data point was normalized according to the maximum value in each set. The normalized data for yolk size and fish length are shown in Tables S3 and S4, respectively.
Statistical analysis
Data are presented in mean fit figures as mean±s.e.m. Statistical tests for mean differences were performed using an independent two-sample t-test. For linear regression analysis, testing for association between two variables, independent ANOVAs were used to test whether the slope of the regression line is significantly different from zero using R software. In all cases, a 95% confidence level was utilized (α=0.05) to deduce statistical significance. All data used in this study are normally distributed (Kolmogorov–Smirnov test, α=0.05) and consistent with historical laboratory data.
Supplementary Material
Footnotes
Competing interests
The authors declare no competing or financial interests.
Author contributions
Conceptualization: A.V.S., K.E.S., U.Z.G.; Methodology: A.V.S., K.E.S., U.Z.G.; Software: A.V.S.; Validation: J.N.; Formal analysis: A.V.S., K.E.S., J.N., U.Z.G.; Investigation: A.V.S., J.N.; Resources: K.E.S.; Writing - original draft: A.V.S., K.E.S., U.Z.G.; Writing - review & editing: A.V.S., K.E.S., U.Z.G.; Visualization: A.V.S., K.E.S., U.Z.G.; Supervision: K.E.S., U.Z.G.; Funding acquisition: A.V.S., K.E.S., J.N., U.Z.G.
Funding
This work was done with support from the San Diego State University Grants Program (to K.E.S.), and with generous support from the National Institutes of Health (K01ES031640 to K.E.S.). U.Z.G. acknowledges support from the California State University Program for Education & Research in Biotechnology New Investigator grant. A.V.S. and U.Z.G. acknowledge support from the College of Sciences at San Diego State University. A.V.S. and J.N. acknowledge support from the Doris A. Howell Foundation and the California State University Program for Education & Research in Biotechnology Research Scholar Award. Deposited in PMC for release after 12 months.
References
- Anderson, J. L., Carten, J. D. and Farber, S. A. (2011). Zebrafish lipid metabolism: from mediating early patterning to the metabolism of dietary fat and cholesterol. Methods Cell Biol., 101, 111-141. 10.1016/B978-0-12-387036-0.00005-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Augustine, S., Gagnaire, B., Floriani, M., Adam-Guillermin, C. and Kooijman, S. (2011). Developmental energetics of zebrafish, Danio rerio. Comparative Biochemistry and Physiology Part A: Molecular & Integrative Physiology 159, 275-283. 10.1016/j.cbpa.2011.03.016 [DOI] [PubMed] [Google Scholar]
- Barker, D. J. P. (2004). The developmental origins of adult disease. J. Am. Coll. Nutr. 23, 588S-595S 10.1080/07315724.2004.10719428 [DOI] [PubMed] [Google Scholar]
- Bhaskaran, S., Umesh, P. and Nair, A. S. (2015). Hill equation in modeling transcriptional regulation. In Systems and Synthetic Biology (eds Singh V. and Dhar P.), pp. 72-92. Springer. 10.1007/978-94-017-9514-2_5 [DOI] [Google Scholar]
- Boersma, B. and Wit, J. M. (1997). Catch-up growth. Endocr. Rev. 18, 646-661. 10.1210/edrv.18.5.0313 [DOI] [PubMed] [Google Scholar]
- Boyce, W. E., DiPrima, R. C. and Meade, D. B. (2017). Elementary differential equations. John Wiley & Sons. [Google Scholar]
- Burton, G. J., Hempstock, J. and Jauniaux, E. (2001). Nutrition of the human fetus during the first trimester – a review. Placenta 22, S70-S77. 10.1053/plac.2001.0639 [DOI] [PubMed] [Google Scholar]
- Burton, G. J., Watson, A. L., Hempstock, J., Skepper, J. N. and Jauniaux, E. (2002). Uterine glands provide histiotrophic nutrition for the human fetus during the first trimester of pregnancy. J. Clin. Endocrinol. Metab. 87, 2954-2959. 10.1210/jcem.87.6.8563 [DOI] [PubMed] [Google Scholar]
- Collery, R. F., Veth, K. N., Dubis, A. M., Carroll, J. and Link, B. A. (2014). Rapid, accurate, and non-invasive measurement of zebrafish axial length and other eye dimensions using SD-OCT allows longitudinal analysis of myopia and emmetropization. PLoS One 9, e110699. 10.1371/journal.pone.0110699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dang, Y., Wang, F. E. and Liu, C. (2018). Real-time PCR array to study the effects of chemicals on the growth hormone/insulin-like growth factors (GH/IGFs) axis of zebrafish embryos/larvae. Chemosphere 207, 365-376. 10.1016/j.chemosphere.2018.05.102 [DOI] [PubMed] [Google Scholar]
- Eriksson, J. G., Forsen, T., Tuomilehto, J., Winter, P. D., Osmond, C. and Barker, D. J. (1999). Catch-up growth in childhood and death from coronary heart disease: longitudinal study. BMJ 318, 427-431. 10.1136/bmj.318.7181.427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher, A. G., Cooper, F. and Baker, R. E. (2017). Mechanocellular models of epithelial morphogenesis. Philos. Trans. R. Soc. B. Biol. Sci. 372, 20150519. 10.1098/rstb.2015.0519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraher, D., Sanigorski, A., Mellett, N. A., Meikle, P. J., Sinclair, A. J. and Gibert, Y. (2016). Zebrafish embryonic lipidomic analysis reveals that the yolk cell is metabolically active in processing lipid. Cell Rep. 14, 1317-1329. 10.1016/j.celrep.2016.01.016 [DOI] [PubMed] [Google Scholar]
- Gadagkar, S. R. and Call, G. B. (2015). Computational tools for fitting the Hill equation to dose-response curves. J. Pharmacol. Toxicol. Methods 71, 68-76. 10.1016/j.vascn.2014.08.006 [DOI] [PubMed] [Google Scholar]
- George, U. Z. and Lubkin, S. R. (2018). Tissue geometry may govern lung branching mode selection. J. Theor. Biol. 442, 22-30. 10.1016/j.jtbi.2017.12.031 [DOI] [PubMed] [Google Scholar]
- George, U. Z., Bokka, K. K., Warburton, D. and Lubkin, S. R. (2015). Quantifying stretch and secretion in the embryonic lung: Implications for morphogenesis. Mech. Dev. 138, 356-363. 10.1016/j.mod.2015.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goessling, W. and Sadler, K. C. (2015). Zebrafish: an important tool for liver disease research. Gastroenterology 149, 1361-1377. 10.1053/j.gastro.2015.08.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallare, A., Nagel, K., Köhler, H.-R. and Triebskorn, R. (2006). Comparative embryotoxicity and proteotoxicity of three carrier solvents to zebrafish (Danio rerio) embryos. Ecotoxicol. Environ. Saf. 63, 378-388. 10.1016/j.ecoenv.2005.07.006 [DOI] [PubMed] [Google Scholar]
- Harris, C., Jilek, J. L., Sant, K. E., Pohl, J., Reed, M. and Hansen, J. M. (2015). Amino acid starvation induced by protease inhibition produces differential alterations in redox status and the thiol proteome in organogenesis-stage rat embryos and visceral yolk sacs. J. Nutr. Biochem. 26, 1589-1598. 10.1016/j.jnutbio.2015.07.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho, D. H. and Burggren, W. W. (2012). Parental hypoxic exposure confers offspring hypoxia resistance in zebrafish (Danio rerio). J. Exp. Biol. 215, 4208-4216. 10.1242/jeb.074781 [DOI] [PubMed] [Google Scholar]
- Howe, K., Clark, M. D., Torroja, C. F., Torrance, J., Berthelot, C., Muffato, M., Collins, J. E., Humphray, S., McLaren, K. and Matthews, L. (2013). The zebrafish reference genome sequence and its relationship to the human genome. Nature 496, 498-503. 10.1038/nature12111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxley, R. R., Shiell, A. W. and Law, C. M. (2000). The role of size at birth and postnatal catch-up growth in determining systolic blood pressure: a systematic review of the literature. J. Hypertens. 18, 815-831. 10.1097/00004872-200018070-00002 [DOI] [PubMed] [Google Scholar]
- Imrie, D. and Sadler, K. C. (2010). White adipose tissue development in zebrafish is regulated by both developmental time and fish size. Dev. Dyn. 239, 3013-3023. 10.1002/dvdy.22443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jantzen, C. E., Annunziato, K. A., Bugel, S. M. and Cooper, K. R. (2016). PFOS, PFNA, and PFOA sub-lethal exposure to embryonic zebrafish have different toxicity profiles in terms of morphometrics, behavior and gene expression. Aquat Toxicol 175, 160-170. 10.1016/j.aquatox.2016.03.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalasekar, S. M., Zacharia, E., Kessler, N., Ducharme, N. A., Gustafsson, J.-Å., Kakadiaris, I. A. and Bondesson, M. (2015). Identification of environmental chemicals that induce yolk malabsorption in zebrafish using automated image segmentation. Reprod. Toxicol. 55, 20-29. 10.1016/j.reprotox.2014.10.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keener, J. P. and Sneyd, J. (1998). Mathematical physiology. Springer. [Google Scholar]
- Kimmel, C. B., Ballard, W. W., Kimmel, S. R., Ullmann, B. and Schilling, T. F. (1995). Stages of embryonic development of the zebrafish. Dev. Dyn. 203, 253-310. 10.1002/aja.1002030302 [DOI] [PubMed] [Google Scholar]
- Kunz-Ramsay, Y. (2013). Developmental biology of teleost fishes. Springer Science & Business Media. [Google Scholar]
- Link, B. A. and Megason, S. G. (2008). Zebrafish as a Model for Development. In Sourcebook of Models for Biomedical Research (ed. Conn P.M.) , pp. 103-112. Totowa, NJ: Humana Press. [Google Scholar]
- Maes, J., Verlooy, L., Buenafe, O. E., de Witte, P. A. M., Esguerra, C. V. and Crawford, A. D. (2012). Evaluation of 14 organic solvents and carriers for screening applications in zebrafish embryos and larvae. PLoS ONE 7, e43850. 10.1371/journal.pone.0043850 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuirl, M. R., Volkening, A. and Sandstede, B. (2020). Topological data analysis of zebrafish patterns. Proc. Natl Acad. Sci. USA 117, 5113-5124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMillen, I. C., MacLaughlin, S. M., Muhlhausler, B. S., Gentili, S., Duffield, J. L. and Morrison, J. L. (2008). Developmental origins of adult health and disease: the role of periconceptional and foetal nutrition. Basic Clin. Pharmacol. Toxicol. 102, 82-89. 10.1111/j.1742-7843.2007.00188.x [DOI] [PubMed] [Google Scholar]
- Miyares, R. L., de Rezende, V. B. and Farber, S. A. (2014). Zebrafish yolk lipid processing: a tractable tool for the study of vertebrate lipid transport and metabolism. Dis. Models Mech. 7, 915-927. 10.1242/dmm.015800 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ong, K. K., Ahmed, M. L., Emmett, P. M., Preece, M. A. and Dunger, D. B. (2000). Association between postnatal catch-up growth and obesity in childhood: prospective cohort study. BMJ 320, 967-971. 10.1136/bmj.320.7240.967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinlivan, V. H. and Farber, S. A. (2017). Lipid uptake, metabolism, and transport in the larval zebrafish. Front. Endocrinol. 8, 319. 10.3389/fendo.2017.00319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramlan, N. F., Sata, N. S. A. M., Hassan, S. N., Bakar, N. A., Ahmad, S., Zulkifli, S. Z., Abdullah, C. A. C. and Ibrahim, W. N. W. (2017). Time dependent effect of chronic embryonic exposure to ethanol on zebrafish: Morphology, biochemical and anxiety alterations. Behav. Brain Res. 332, 40-49. 10.1016/j.bbr.2017.05.048 [DOI] [PubMed] [Google Scholar]
- Sant, K. E. and Timme-Laragy, A. R. (2018). Zebrafish as a model for toxicological perturbation of yolk and nutrition in the early embryo. Curr. Environ. Health Rep. 5, 125-133. 10.1007/s40572-018-0183-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sant, K. E., Dolinoy, D. C., Nahar, M. S. and Harris, C. (2013). Inhibition of proteolysis in histiotrophic nutrition pathways alters DNA methylation and one-carbon metabolism in the organogenesis-stage rat conceptus. J. Nutr. Biochem. 24, 1479-1487. 10.1016/j.jnutbio.2012.12.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sant, K. E., Dolinoy, D. C., Jilek, J. L., Sartor, M. A. and Harris, C. (2016a). Mono-2-ethylhexyl phthalate disrupts neurulation and modifies the embryonic redox environment and gene expression. Reprod. Toxicol. 63, 32-48. 10.1016/j.reprotox.2016.03.042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sant, K. E., Dolinoy, D. C., Jilek, J. L., Shay, B. J. and Harris, C. (2016b). Mono-2-ethylhexyl phthalate (MEHP) alters histiotrophic nutrition pathways and epigenetic processes in the developing conceptus. J. Nutr. Biochem. 27, 211-218. 10.1016/j.jnutbio.2015.09.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sant, K. E., Jacobs, H. M., Xu, J., Borofski, K. A., Moss, L. G., Moss, J. B. and Timme-Laragy, A. R. (2016c). Assessment of toxicological perturbations and variants of pancreatic islet development in the zebrafish model. Toxics 4, 20. 10.3390/toxics4030020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sant, K. E., Jacobs, H. M., Borofski, K. A., Chen, P., Park, Y. and Timme-Laragy, A. R. (2017). Pancreas development and nutrient uptake and utilization are disrupted by embryonic exposures to the environmental toxicant perfluorooctanesulfonic acid in the zebrafish. FASEB J. 31, 792-798. [Google Scholar]
- Sant, K. E., Sinno, P. P., Jacobs, H. M. and Timme-Laragy, A. R. (2018). Nrf2a modulates the embryonic antioxidant response to perfluorooctanesulfonic acid (PFOS) in the zebrafish, Danio rerio. Aquat. Toxicol. 198, 92-102. 10.1016/j.aquatox.2018.02.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfers, C., Teigeler, M., Wenzel, A., Maack, G., Fenske, M. and Segner, H. (2007). Concentration- and time-dependent effects of the synthetic estrogen, 17α-ethinylestradiol, on reproductive capabilities of the zebrafish, Danio rerio. J. Toxicol. Environ. Health A 70, 768-779. 10.1080/15287390701236470 [DOI] [PubMed] [Google Scholar]
- Sharpe, J. (2017). Computer modeling in developmental biology: growing today, essential tomorrow. Development 144, 4214-4225. 10.1242/dev.151274 [DOI] [PubMed] [Google Scholar]
- Vasieva, O., Rasolonjanahary, M. and Vasiev, B. (2013). Mathematical modelling in developmental biology. Reproduction 145, R175-R184. 10.1530/REP-12-0081 [DOI] [PubMed] [Google Scholar]
- Volkening, A. and Sandstede, B. (2018). Iridophores as a source of robustness in zebrafish stripes and variability in Danio patterns. Nat. Commun. 9, 1-14. 10.1038/s41467-018-05629-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wertheim, K. Y. and Roose, T. (2017). A mathematical model of lymphangiogenesis in a zebrafish embryo. Bull. Math. Biol. 79, 693-737. 10.1007/s11538-017-0248-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkins, B. J. and Pack, M. (2013). Zebrafish models of human liver development and disease. Comprehensive Physiology 3, 1213-1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson, C. (2012). Aspects of larval rearing. ILAR J. 53, 169-178. 10.1093/ilar.53.2.169 [DOI] [PubMed] [Google Scholar]
- Wyness, L., Stanner, S. and Buttriss, J. (2013). Nutrition and development: short- and long-term consequences for health. Chichester, West Sussex: Wiley-Blackwell for the British Nutrition Foundation. [Google Scholar]
- Yamaguchi, M., Yoshimoto, E. and Kondo, S. (2007). Pattern regulation in the stripe of zebrafish suggests an underlying dynamic and autonomous mechanism. Proc. Natl Acad. Sci. USA 104, 4790-4793. 10.1073/pnas.0607790104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, Y., Su, G., Yang, D., Zhang, Y., Yu, L., Li, Y., Giesy, J. P., Letcher, R. J. and Liu, C. (2017). Time-dependent inhibitory effects of Tris(1,3–dichloro-2-propyl) phosphate on growth and transcription of genes involved in the GH/IGF axis, but not the HPT axis, in female zebrafish. Environ. Pollut. 229, 470-478. 10.1016/j.envpol.2017.06.024 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.