The voltage sensor is responsible for ΔpH dependence in H_v1 channels

Significance

Acid extrusion in various types of cells and the reactive oxygen species production by the NADPH oxidase in phagocytes and microglia are mediated by the voltage-gated proton channel (H_v1). One of the biophysical properties essential for the H_v1 function is its ΔpH-dependent gating. Here, we measured the H_v1 gating currents’ pH dependence in the monomeric nonconducting D160N Ciona intestinalis H_v1 mutant. We demonstrated that H_v1 ΔpH-dependent gating is a consequence of voltage sensor modulation by direct gating currents recordings. Around 60% of the energy stored in the ΔpH is coupled to the H_v1 voltage sensor activation. Therefore, the proton chemical energy is transduced to the voltage sensor activation in H_v1 to produce ΔpH-dependent gating.

Abstract

The dissipation of acute acid loads by the voltage-gated proton channel (H_v1) relies on regulating the channel’s open probability by the voltage and the ΔpH across the membrane (ΔpH = pH_ex − pH_in). Using monomeric Ciona-H_v1, we asked whether ΔpH-dependent gating is produced during the voltage sensor activation or permeation pathway opening. A leftward shift of the conductance-voltage (G-V) curve was produced at higher ΔpH values in the monomeric channel. Next, we measured the voltage sensor pH dependence in the absence of a functional permeation pathway by recording gating currents in the monomeric nonconducting D160N mutant. Increasing the ΔpH leftward shifted the gating charge-voltage (Q-V) curve, demonstrating that the ΔpH-dependent gating in H_v1 arises by modulating its voltage sensor. We fitted our data to a model that explicitly supposes the H_v1 voltage sensor free energy is a function of both the proton chemical and the electrical potential. The parameters obtained showed that around 60% of the free energy stored in the ΔpH is coupled to the H_v1 voltage sensor activation. Our results suggest that the molecular mechanism underlying the H_v1 ΔpH dependence is produced by protons, which alter the free-energy landscape around the voltage sensor domain. We propose that this alteration is produced by accessibility changes of the protons in the H_v1 voltage sensor during activation.

The voltage-gated proton channel (H_v1) is gated by internal and external pH changes favoring proton extrusion during acute cytosolic acidosis, an essential function for cell physiology and pathophysiology (1). The wide diversity of cell types in which H_v1 is expressed, including different immune cells, sperm, microglia, lung epithelial cells, osteoclasts, cardiac cells, and cancer cells (1), renders this channel as a promising pharmacological target. A selective H_v1 modulation can be achieved by studying the molecular mechanisms of its distinctive pH dependence; although pH modulates other voltage-gated ion channels (2–5), the pH dependence of H_v1 is unique, since the channel opening depends only on the ΔpH (pH_ex − pH_in) established across the membrane (6). Briefly, voltage-gated ion channels have a voltage-sensing domain (made up of transmembrane segments S1 to S4) coupled to a pore domain (S5 to S6) (7). Quite interestingly, H_v1 consists of only four transmembrane segments (from S1 to S4) flanked by intracellular N- and C-terminal domains (8, 9); thus, the permeation pathway, voltage sensor, and pH sensor(s) are contained in these four transmembrane segments. Moreover, the C-terminal domain folds into a coiled-coil structure between two H_v1 subunits to produce a dimer (10, 11), resulting in monomeric voltage-gated proton channels when the N- and C-terminal domains are deleted (10). Although the H_v1 monomer lacks the dimer cooperative opening (12, 13), it maintains its distinctive biophysical properties (10). However, although it has been reported that the monomeric H_v1 gating depends on pH, it is not clear whether the distinctive ΔpH-dependent gating is still present in this channel.

The remarkable pH dependence of the H_v1 opening has been observed since the first proton current measurements (14, 15). However, its detailed analysis was only possible when fine precautions to control the pH during the proton current measurement were taken into account (6). These studies showed that conductance-voltage (G-V) curves and activation kinetics shift along the voltage axis as a function of the ΔpH regardless of the internal or external pH (6, 16). Although cloning of the H_v1 gene (8, 9) facilitated the search for mutations affecting the channel’s pH dependence (16–19), its molecular mechanism has remained elusive. In this regard, the H_v1 pH dependence has been challenging to understand, because it has mainly been studied by measuring the dimer’s proton current; in fact, the pH dependence of these currents could be produced by modulating the channel cooperativity, voltage sensor activation, or channel opening. Indeed, there is evidence indicating that pH affects both the voltage sensor movement (20, 21) and the channel’s unitary conductance (22). Consequently, the simultaneous processes that occur during H_v1 gating obscure the source of this ΔpH dependence. To overcome these difficulties, we used a nonconducting mutant of the Ciona intestinalis H_v1 (CiH_v1) monomer to monitor the pH dependence exclusively on the voltage sensor activation. By measuring the voltage sensor movements directly from gating currents in the absence of cooperativity (10, 23) and proton currents (24–26), we asked whether the ΔpH-dependent gating in H_v1 originates during the voltage sensor activation or the permeation pathway opening. We found that the H_v1 voltage sensor movements are modulated by pH. In detail, the voltage sensor activation is coupled to the chemical free energy stored in the ΔpH, resulting in a ΔpH-dependent shift of the gating charge-voltage (Q-V) curves along the voltage axis. Accordingly, the H_v1 ΔpH-dependent gating is a consequence of the voltage sensor modulation. On the other hand, the gating currents kinetics depended on the internal and external pH values, indicating that the pH modulates the voltage sensor movements in a state-dependent manner.

Results

Monomeric H_v1 Is a Suitable Model for Studying the Channel pH Dependence.

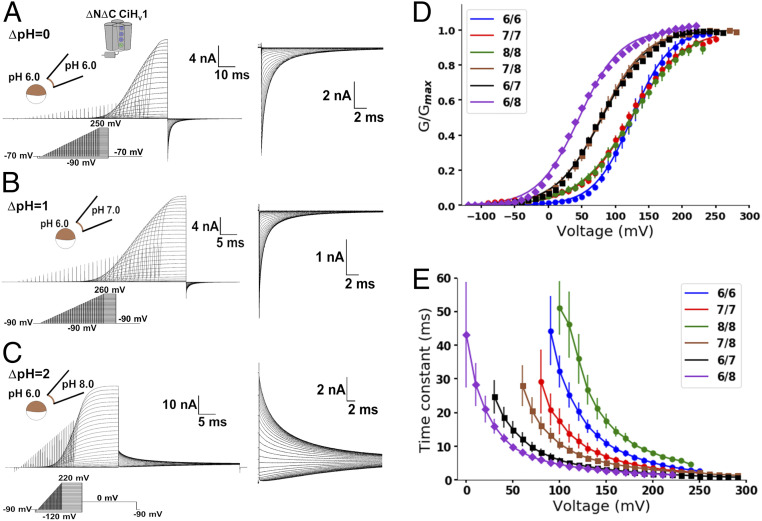
As monomeric H_v1 is a functional pH-dependent proton channel (10, 12), we envisioned this channel could be an appropriate model for investigating the H_v1 pH dependence. We first studied the pH-dependent gating of this channel to verify that it maintains the characteristic ΔpH-dependent G-V curve shifts of the dimer. We expressed the monomeric CiH_v1 in Xenopus laevis oocytes to measure the G-V curves at different pHs and ΔpHs from instantaneous tail currents (Fig. 1 A–C). We then fitted the tail currents, I_tail(V), to a two-state Boltzmann distribution model

$$I_{tail}\left(V\right)=\frac{I_{tail,max}}{1+e^{\left(\frac{-z\delta F\left(V-V_0\right)}{RT}\right)}},$$ [1]

where I_tail,max is the maximal tail current, zδ is the voltage-dependence parameter, V₀ is the voltage at which half of the channels are open, and F, R, and T are Faraday’s constant, ideal gas constant, and absolute temperature, respectively. To minimize local pH changes caused by proton fluxes, we used a high pH buffer concentration in recording solutions to increase the proton transfer rate. Additionally, as the depolarizing voltage was increased and higher currents passed through channels, the voltage pulse duration was shortened to avoid depletion or accumulation of protons. We also measured the experimental reversal potential before and after the G-V curve measurements to determine the ΔpH (SI Appendix, Fig. S1). With these precautions, the G-V curves shifted toward lower voltages as the ΔpH increased regardless of the internal or external pH value (Fig. 1D). An increment of two ΔpH units promoted a −78 ± 6 mV V₀ shift (SI Appendix, Table S1). These results are in line with previously reported data for the dimeric H_v1 (6, 16), validating the monomer to study H_v1 pH dependence. Following this, we examined the activation kinetics of proton currents (I) by fitting them to a single exponential function

$$I\left(t\right)=I_{max}\left(1-e^{-t/\tau }\right),$$ [2]

where I_max is the steady-state current and τ is the activation time constant. Interestingly, the τ(V) curves followed a different behavior than the G-V curves (Fig. 1E) since they were not superimposed at the same ΔpH. Thus, the channel opening process rate is influenced by the internal and external pH values instead of the ΔpH. Notwithstanding, the G-V curve shifts render the monomeric channel a suitable model to study this property in H_v1.

Fig. 1.

Monomeric H_v1 currents were ΔpH dependent. Representative current recordings of monomeric H_v1 at (A) ΔpH = 0, (B) ΔpH = 1, and (C) ΔpH = 2. Insets show the tail currents in an expanded time and current scale. Note the superposition of tail currents at high voltages suggesting that the open probability reached its maximum value. (D) Mean G-V curves at the indicated pH_in/pH_ex obtained from the tail currents. Curves were fitted using a two-state Boltzmann distribution model (lines; Eq. 1 in text and SI Appendix, Table S1). (E) Mean activation time constant as a function of voltage at the indicated pH_in/pH_ex (Eq. 2 in text). Data are shown as mean ± SEM.

H_v1 Gating Currents in a Nonconducting Mutant Channel.

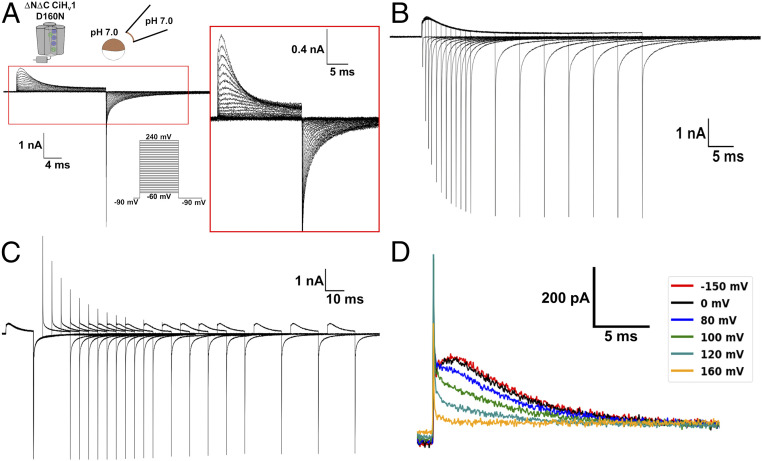
The G-V curve shifts presented in Fig. 1D and induced by a proton gradient indicate that it affects the H_v1 closed-open equilibrium. However, the voltage sensor activation and the channel opening are kinetically different processes (23); thus, the G-V curve shifts could be produced by affecting either of them. On the other hand, as the permeation pathway and voltage sensor are in the same structural domain, the activation process could also be affected by the pH gradient. To explore this possibility, we studied the pH dependence on the voltage sensor activation by measuring gating currents produced by the voltage sensor movements (27, 28). Previously, we demonstrated that the low-conducting mutant N264R could be employed to measure gating currents in the monomeric H_v1 (23). Although changes on the ΔpH modulated gating currents of the N264R mutant, it was not possible to analyze them in detail due to the presence of large proton currents (SI Appendix, Fig. S2). Since proton currents increase at higher ΔpH values, an adequate strategy to achieve our goal was to find a nonconducting H_v1 mutant. Previous works have reported that some mutations at the CiH_v1 selectivity filter D160 produced nonconducting channels (25, 26). The evidence indicates that the absence of proton currents in these mutants is not due to a defective voltage sensor given that fluorescent-labeled mutant channels exhibited voltage-dependent fluorescence changes (25, 26). To our delight, we registered robust gating currents with almost a complete absence of ion currents using the monomeric D160N H_v1 mutant (Fig. 2A). These currents were largely gating currents, since they corresponded to a nonlinear charge component (SI Appendix, Fig. S3A) and did not reverse (SI Appendix, Fig. S3 B and C). However, a small current consistently remained at the end of the depolarizing pulse in patches expressing the channel, especially at high voltages (Fig. 2A, Inset), although its small magnitude impeded a more detailed examination. Nevertheless, it was evident that the mutation D160N significantly affects the channel proton conduction. This alteration is quite useful to our purposes, but it could also modify the H_v1 voltage sensor movements. We tested this last claim’s validity by comparing the D160N mutant gating currents with the low-conducting N264R mutant (23). The D160N mutant exhibited an OFF-gating current saturation (Fig. 2B and SI Appendix, Fig. S4A), a fast and a slow component during an ON-gating current recovery (Fig. 2C and SI Appendix, Fig. S4B), and a Cole–Moore shift effect (Fig. 2D). Thus, despite the alteration of the channel opening by the D160N mutation, the distinctive H_v1 voltage sensor movements were conserved. Lastly, we quantified the gating charge displaced by numerical integration. We found that the ion residual current resulted in a higher gating charge during the ON stage when compared to the OFF stage for large depolarizing voltages. As this residual current is rather small, we fitted the ON-gating current decay, I_g(t), to a single exponential

$$I_g\left(t\right)=I_0{e}^{-t/\tau },$$ [3]

where I₀ is the current after the ON-gating current rising phase and τ is the decay time constant. Given the strong decay kinetics dependence on the applied voltage (cf. Fig. 1E), the time interval we employed for the exponential fit was short for high voltages and increased as the applied voltage decreases (SI Appendix, Fig. S5A). Residuals were used as the criterion to determine the interval of time needed for the fittings (SI Appendix, Fig. S5 B and C). Using this methodology, the displaced ON- and OFF-gating charge was equal (SI Appendix, Fig. S5D). Therefore, the perturbation in the channel opening caused by the D160N mutation did not alter the characteristic H_v1 voltage sensor movements, showing that this mutant channel can be used to study H_v1 gating currents in the absence of proton currents.

Fig. 2.

Gating currents of the monomeric D160N H_v1 mutant channel conserved their distinctive characteristics. Currents produced in patches of membranes expressing the monomeric D160N H_v1 mutant at symmetrical pH 7 are shown. A -P/8 subtraction protocol from a subholding potential of −90 mV was applied. (A) Superimposed traces of gating currents produced by depolarizations from a holding potential of −90 mV. Gating currents were elicited by voltages from −60 to 240 mV in 10 mV steps. (B) Superimposed traces of currents produced by a 200-mV depolarization pulse of increasing duration. Holding potential was −90 mV. (C) Superimposed traces of currents produced by an ON-recovery protocol consisting of two 200-mV depolarization pulses separated by returning to −90 mV at increasing durations. Holding potential was −90 mV. (D) A Cole–Moore shift effect was produced when a 200-mV depolarization was preceded by a prepulse at the indicated voltage.

The H_v1 Voltage Sensor Equilibrium Is ΔpH Dependent.

The monomeric D160N H_v1 mutant fulfills the requirements to study the pH dependence on the H_v1 voltage sensor movements. Accordingly, we measured gating currents produced from this mutant at different internal and external pH values (Fig. 3 A–C). Q-V curves were obtained from numerical integration of the OFF-gating currents for each condition (Fig. 3D) and fitted to a two-state Boltzmann distribution model

$$Q\left(V\right)=\frac{Q_{max}}{1+e^{\left(\frac{-z{\delta }_{Q}F\left(V-V_{0.5}\right)}{RT}\right)}},$$ [4]

where Q_max is the maximal charge displaced, zδ_Q is the effective valence (29), and V_0.5 is the voltage at which the probability of the active voltage sensor is 0.5; the rest of the parameters were defined in Eq. 1. Surprisingly, Q-V curves obtained at the same ΔpH superimposed, and they shifted to the left as the ΔpH increased (Fig. 3D) like the pattern exhibited by the G-V curves (compare Fig. 1D with Fig. 3D). The Q-V curve shifts indicate that the ΔpH alters the resting-active (R-A) equilibrium of the voltage sensor. This ΔpH-dependent change can be quantified as the V_0.5 shift relative to symmetrical pH:

$$\mathrm{\Delta }{V}_{0.5}=V_{0.5\left(\mathrm{\Delta }pH\right)}-V_{0.5\left(\mathrm{\Delta }pH=0\right)}.$$ [5]

The ΔV_0.5 obtained at ΔpH = 2 was −79 ± 4 mV (SI Appendix, Table S2), which can be approximated to a decrease in the free-energy difference between the voltage sensor R and A states of 7.6 ± 0.4 kJ/mol. Although this calculation makes the simplifying assumption that a two-state R-A model describes the voltage sensor displacement, it is useful to illustrate the significant difference of free energy in the voltage sensor R-A equilibrium produced by the ΔpH change.

Fig. 3.

Gating currents of monomeric D160N H_v1 mutant were ΔpH dependent. Currents produced in patches of membranes expressing the monomeric D160N H_v1 mutant at different pHs were measured. A -P/8 subtraction protocol from a subholding potential of −90 mV was applied. Representative recordings at (A) ΔpH = 0, (B) ΔpH = 1, and (C) ΔpH = 2 are shown. (D) Mean Q-V curves at the indicated pH_in/pH_ex. Curves were fitted using a two-state Boltzmann distribution model (lines; Eq. 4 and SI Appendix, Table S2). (E) Mean ON-gating current decay time constant as a function of voltage at the indicated pH_in/pH_ex. (Eq. 3 in text). Data are shown as mean ± SEM.

Next, we fitted the ON-gating current decay using the strategy discussed above for different pHs (SI Appendix, Fig. S5). The ON-gating currents’ decay kinetics were similar in symmetrical pH and became faster in a positive ΔpH (Fig. 3E). However, they markedly differed when comparing data at ΔpH = 1 (brown and black curves in Fig. 3E), indicating that the voltage sensor kinetics depend on the internal and external pH values instead of ΔpH. These changes are analogous to the proton currents of the conducting channel (Fig. 1), suggesting a state-dependent modulation. Despite this, the ΔpH-dependent shifts of the Q-V curves demonstrated that the ΔpH-dependent gating is produced by modulating the H_v1 voltage sensor activation.

A Model to Quantify the Coupling between Voltage and ΔpH.

The last result shows that the energy stored in the ΔpH is coupled with the H_v1 voltage sensor activation. Following this reasoning, we attempted to describe the Q-V curves at different ΔpHs with the empirical relation

$$\frac{Q}{Q_{max}}=\frac{1}{1+e^{\left(\frac{\mathrm{\Delta }{G}_0-2.3\epsilon RT\mathrm{\Delta }pH-zFV}{RT}\right)}}.$$ [6]

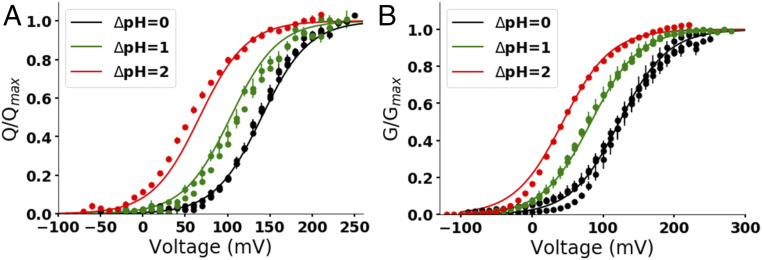
In this equation, ΔG₀ is the free energy of the voltage sensor activation when ΔpH = 0 and V = 0, and ε and z are adimensional factors quantifying how the free energy changes with ΔpH and voltage, respectively. The Q-V and G-V curves were well fitted to Eq. 6 (Fig. 4), demonstrating that the empirical equation explains the ΔpH-dependent changes in H_v1. Based on this result, we proposed that the voltage sensor free energy, G, can be expressed as

$$G=G^0+\epsilon RTln\left[H^{+}\right]+zF\psi ,$$ [7]

where G⁰ is the standard free energy of the H_v1 voltage sensor, RTln[H⁺] is the increase in the chemical potential caused by the presence of a local proton concentration [H⁺] divided by the standard state, and zFψ is the electric energy resulting from the product of the apparent gating charge z, the Faraday constant F, and the local electric potential ψ. The adimensional factor ε quantifies the effect on the voltage sensor free energy produced by the proton chemical potential. As the H_v1 voltage sensor activates, it moves from the internal side (R state) to the external side of the membrane (A state). Therefore, the free energy associated with each state is

$$G_{in}=G_{in}^0+\epsilon RTln{\left[H^{+}\right]}_{in}+zF{\psi }_{in}$$ [8]

$$G_{ex}=G_{ex}^0+\epsilon RTln{\left[H^{+}\right]}_{ex}+zF{\psi }_{ex}.$$ [9]

The change in free energy associated with the voltage sensor activation is obtained from the difference of Eqs. 8 and 9 as

$$\mathrm{\Delta }G=G_{ex}-G_{in}=\mathrm{\Delta }{G}^{0}0-2.3\epsilon RT\mathrm{\Delta pH}-zFV,$$ [10]

where V = ψ_in − ψ_ex. Eq. 10 states that the free energy decreases and the voltage sensor activates with an increase in voltage or ΔpH. The ε value of 0.57 ± 0.02 obtained from the Q-V curves’ fit (Fig. 4A) indicates that around 60% of the chemical energy stored in the ΔpH is used to stabilize the H_v1 voltage sensor active state, which corresponds to 6.4 ± 0.2 kJ/mol at ΔpH = 2.

Fig. 4.

The Q-V and G-V curves were well fitted to the empirical equation accounting for the ΔpH-dependent shifts. The normalized charge or conductance was globally fitted using a least-squares minimization method to the empirical equation 1/{1 + exp[(ΔG₀ − 2.3εRTΔpH − zFV)/RT]} (Eq. 6). (A) Q-V curves of the monomeric D160N H_v1 mutant at different ΔpHs shown in Fig. 3D were globally fitted to Eq. 6. The lines are the curves obtained from the fit at the indicated ΔpH using the parameters ΔG₀ = 12.3 ± 0.3 kJ/mol, ε = 0.57 ± 0.02, and z = 0.91 ± 0.02. (B) G-V curves of the monomeric H_v1 at different ΔpHs shown in Fig. 1D were globally fitted to Eq. 6. The lines are the curves obtained from the fit at the indicated ΔpH using the parameters ΔG₀ = 8.9 ± 0.1 kJ/mol, ε = 0.51 ± 0.01, and z = 0.75 ± 0.01. V_0.5 and V₀ values calculated from the global fit parameters using Eq. 11 are listed in SI Appendix, Table S3.

Is it possible to obtain a parameter to quantify this coupling from the curve shifts? When the probability of the active voltage sensor state is 0.5, ΔG = 0, and V = V_0.5, then

$$V_{0.5}=\frac{\mathrm{\Delta }{G}^0-2.3\epsilon RT\mathrm{\Delta pH}}{zF}.$$ [11]

In agreement with the experimental data, Eq. 11 shows that the Q-V curve should shift to the left along the voltage axis at ΔpH > 0 (SI Appendix, Table S3). Then, the ΔV_0.5 defined in Eq. 5 can be expressed as

$$\mathrm{\Delta }{V}_{0.5}=\frac{-2.3\epsilon RT\mathrm{\Delta pH}}{zF}=C\frac{-2.3RT\mathrm{\Delta pH}}{F}.$$ [12]

The factor C in Eq. 12 quantifies the coupling between the voltage sensor and ΔpH through the ratio between ε and z. From the Q-V curves (Fig. 4A), C had a value of 0.63 ± 0.03. Although the G-V curves’ ε and z values changed (Fig. 4B), the C factor was similar, with a value of 0.68 ± 0.02. This result confirms that the distinctive ΔpH-dependent gating observed in proton currents of the H_v1 is produced mainly by modulating the voltage sensor activation.

Discussion

The monomeric H_v1 contains the molecular determinant(s) necessary to sense the internal and external pH. In particular, the H_v1 voltage sensor movements are modulated by pH changes. This pH dependence has been studied previously using the dimeric W207A-N214R hH_v1 mutant (20). Like our results, an increase of pH_ex (higher ΔpH) produced a leftward shift of the Q-V curve and faster ON-gating currents decay (20). However, that study only explored one change in pH_ex, leaving the effects of ΔpH on H_v1-gating currents unknown. Recently, another report explored the pH sensitivity in the conductive CiH_v1 dimer using patch-clamp fluorometry (21). Tracking the S4 movements with fluorescence changes, they found that the S4 segment sensed the ΔpH imposed on the membrane. However, as they used the wild-type channel, the pH dependence they observed in the voltage sensor could be influenced by the high proton fluxes produced during the opening of the permeation pathway and the dimer’s cooperativity. Our results measuring gating currents of the monomeric D160N mutant channel provide direct evidence that the H_v1 voltage sensor is responsible for the channel’s ΔpH-dependent gating.

We demonstrated that the monomeric D160N mutant is a suitable model to study the ΔpH dependence in H_v1 even though others have reported different phenotypes in hH_v1 with similar modifications. Partial or complete deletions of the N-terminal domain in hH_v1 alter its pH dependence (17, 18). In contrast, the deletion of the N- and C-terminal domain in CiH_v1 shifted the G-V curve to higher voltages compared to the wild-type channel (23) but does not alter the ΔpH-dependent shifts in the range of pH values studied (Fig. 1D and SI Appendix, Table S1). Indeed, G-V curve shifts calculated from Eq. 12 result in 39.6 ± 0.9 mV per ΔpH unit, which is in line with the reported 40 mV shift per ΔpH unit (6). The N-terminal domain of H_v1 is not conserved across species, which could explain the difference observed between hH_v1 and CiH_v1. Interestingly, the mutations of the selectivity filter also show different phenotypes between these two channels. The D112N hH_v1 mutant has been reported to decrease conductance and alters proton selectivity (24). Only the D112V mutant is a nonconducting channel (24), although mutants D112A, D112N, and D112Q produce small currents (30). On the other hand, dimeric CiH_v1 mutations producing nonconducting channels include D160A, D160C, and D160N (25, 26). This difference could be explained by variations in the conductance or gating kinetics between hH_v1 and CiH_v1. Despite the different phenotypes of D112 hH_v1 mutants, they preserve their ΔpH dependence (24), and the same is true for D160N CiH_v1 as evidenced by its ΔpH-dependent Q-V curve shifts. Therefore, our results validate both the monomeric and D160N mutants in CiH_v1 to study the molecular determinants of ΔpH dependence in H_v1.

The H_v1 ΔpH-dependent gating is produced by a coupling between the voltage sensor activation and the ΔpH imposed through the membrane. Around 60% of the chemical energy stored in the ΔpH is utilized to activate the H_v1 voltage sensor. Therefore, our data demonstrated that the modulation of its voltage sensor, not the permeation pathway opening, produces the distinctive ΔpH-dependent gating in H_v1. In contrast, the voltage-sensor kinetics depended on the internal and external pH values. This result is not surprising, as monomeric H_v1 has more than one closed state and multiple steps of gating charge displacement (23). The existence of various states results in a τ(V) being a product of the voltage- and pH-dependent kinetics constants parameters of each transition, suggesting that the H_v1 voltage sensor movements during activation are modulated by pH in a state-dependent manner. A detailed study of gating-currents kinetics’ pH dependence is needed to understand this state-dependent modulation. Knowing this, we cannot rule out the possibility that the channel’s opening is also pH dependent. Despite this possibility, the ΔpH dependence is produced mainly by the modulation of the voltage sensor. The equilibrium of the voltage sensor’s R and A states is determined by the ΔpH value, while the pathway to reach this equilibrium depends on the internal and external pH values.

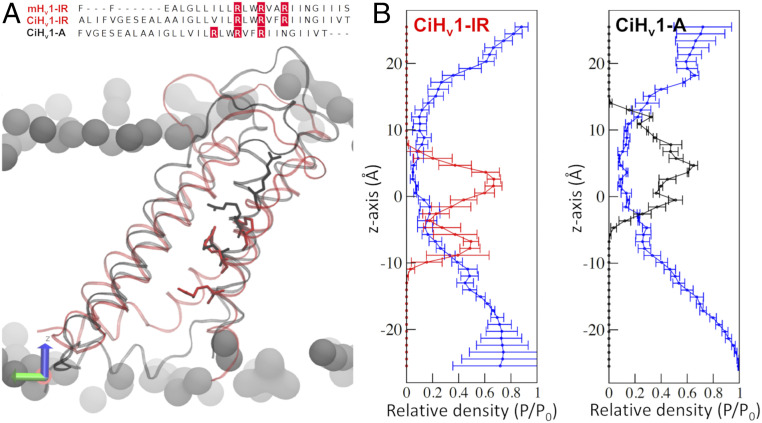
A previous proposal to explain the distinctive ΔpH dependence of H_v1 relies on an alteration of the H_v1 closed-open equilibrium due to protonation in negatively charged residues on the channel’s inner and outer surface as pH changes (1). However, this proposal involves pK_a values of such amino acids and dependence on absolute local pH values at each side of the membrane, which does not easily explain the overlap of G-V and Q-V curves at the same ΔpH. Thus, the coupling between voltage sensing and ΔpH requires a further mechanistic and microscopic explanation. We postulate a mechanism that relies on a microscopic and explicit interpretation of Eq. 10, which implies that the chemical potential stored in the pH gradient imposes a chemical work toward the voltage sensor, reducing the electrical energy needed to activate it. This is in line with the 60% coupling between the proton chemical potential and voltage sensing from Eq. 10 because it is not a specific interaction but rather a force that imposes pressure on the H_v1 structure. The fact that coupling quantification through Eq. 12 did not change between the Q-V and G-V curves showed that the chemical potential energy stored in the ΔpH is coupled mainly with the voltage sensor activation. Moreover, our model agrees with the empirical 40 mV shift per ΔpH unit (6), since replacing the parameters obtained from the fits in Eq. 12 results in a shift of 36 ± 2 and 39.6 ± 0.9 mV per ΔpH unit for the Q-V and G-V curves, respectively. Finally, the state dependence of the voltage sensor to the internal and external pH values can be explained by changes in the electrochemical potential of the different voltage sensor conformations during activation. To further explore this idea at a structural level, we constructed comparative CiH_v1 models of the intermediate resting (CiH_v1-IR) and active (CiH_v1-A) channel and simulated them via classical molecular dynamics at zero electric field conditions (SI Appendix, Supplementary Methods and Fig. 5). Interestingly, the gating-charged arginines maintained different positions along the z-axis in the CiH_v1-IR and CiH_v1-A models during the entire simulation (Fig. 5B), following the changes in accessibility demonstrated in the resting and active states in H_v1 (31). Even though the specific structural determinants of the ΔpH-sensor in the H_v1 voltage sensor are still unknown, it will involve interactions with water molecules. Therefore, we studied the water structuring of the CiH_v1 models in the form of relative densities along the z-axis (32). Both models presented hydrated structures with distinctive density profiles, especially within the region that colocalizes with the S4 arginines. In detail, for the CiH_v1-A model, the water density is very smooth and isotropic; on the contrary, the CiH_v1-IR model exhibits higher densities at the lower half and almost null for the upper one (Fig. 5B). This difference will produce state-dependent accessibilities to protons in the H_v1 voltage sensor. Similar results were obtained for simulations of the D160N mutant channel (SI Appendix, Fig. S6).

Fig. 5.

Water densities of the H_v1 voltage sensor changed during activation. (A) The crystal structure of the intermediate-resting state of the mouse H_v1 (mH_v1-IR) was used as a template to build a homology model of the intermediate-resting state of the Ciona-H_v1 (CiH_v1-IR, red). The active model of CiH_v1 (CiH_v1-A, black) was built by displacing the S4 arginines in the alignments (above; R255, R258, and R261 in red). A representative snapshot of the 100 ns molecular dynamics simulation is shown below with the S4 arginines in licorice representation for the CiH_v1-IR (red) and CiH_v1-A (black). (B) The relative densities of the arginine residues and water with respect to bulk water (P/P₀) along the cylindrical pore axis (z-axis) for the CiH_v1 models. The CiH_v1-IR model maintains the arginines in a lower position (Left, red trace) compared to the CiH_v1-A model (Right, black trace). For both models, the water density is shown in the blue traces.

We propose that protons in the H_v1 voltage sensor are the transducers of the proton chemical energy stored in the ΔpH. During the voltage sensor activation, these protons’ accessibility changes would be coupling the ΔpH chemical potential with the electrical potential imposed on the membrane. Since a proton energy change is produced by a displacement between positions with different chemical potentials just like a charge energy change is produced by a displacement between positions with different electrical potentials, our proposal does not necessarily require protonation and deprotonation, making it independent of the absolute pH values. The H_v1 voltage sensor’s unique capability to efficiently utilize the energy stored in the ΔpH, which is absent in other voltage-gated ion channels (33–35), strongly suggests that the H_v1 voltage sensor has unique structural characteristics compared to other S4-based voltage sensors. The detailed study of these differences at the structural level can be exploited in the future to design specific therapeutic drugs against H_v1, opening opportunities to treat diseases such as immune response dysfunctions or cancer.

Materials and Methods

Mutagenesis, Transcription, and Sequencing.

CiH_v1 contained in the pSP64T vector was kindly provided by Yasushi Okamura, Osaka University, Osaka, Japan. The vector was modified with a stop codon at V270 and an initiator methionine-replacing E129 to produce the monomeric CiH_v1 (10). The D160N single mutation was introduced using QuikChange kit (Promega Corp.). The resulting DNA was amplified, checked by sequencing, and then linearized with PvuII restriction enzyme. Linearized DNA was used to synthesize RNA with the mMESSAGE mMACHINE SP6 transcription kit (Ambion). RNA was quantified by absorbance at 260 nm, and its integrity was checked by electrophoresis in an agarose gel.

Oocyte Extraction and RNA Injection.

X. laevis oocytes were obtained and manipulated according to previously described methodologies (36). They were injected with 50 nL RNA at a concentration of 1 µg/µL and incubated at 18 °C for 2 to 3 d until they were used for the recordings.

Electrophysiology.

Currents were measured in patches of oocyte membranes in the inside-out modality by voltage clamp. Only one experiment was performed in each patch, as we consistently observed a change in the current kinetics—and sometimes even the shifts—of the G-V or Q-V curves when patches were repeatedly depolarized. This phenomenon has been reported by others (6, 14). The internal and external solutions contained 100 mM buffer [2-(N-morpholino)ethanesulfonic acid for pH 6.0, 4-(2-hydroxyethyl)piperazine-1-ethanesulfonic acid (HEPES) for pH 7.0, and N-(2-hydroxyethyl)piperazine-N′-(4-butanesulfonic acid) or HEPES for pH 8.0], 2 mM MgCl₂, 1 mM ethylene glycol-bis(2-aminoethylether)-N,N,N′,N′-tetraacetic acid, and 50 mM N-methyl-D-glucamine (NMDG)-methanesulfonate. The pH was adjusted with NMDG or methanesulphonate. Measurements were performed at room temperature (22 °C). Pipettes of borosilicate capillary glass (1B150F-4, World Precision Instruments) were pulled on a horizontal pipette puller (Sutter Instruments) and fire-polished until a diameter between 15 to 24 µm (resistances of 0.8-1.2 MΩ in the bath solution) was reached. Data were acquired with an Axopatch 200B amplifier (Axon Instruments). The voltage command and the current output were filtered at 20 kHz with 8-pole Bessel low-pass filters (Frequency Devices). Analog signals were sampled with a 16-bit A/D converter (Digidata 1440A, Axon Instruments) at 250 kHz. Experiments were performed using Clampex 8 acquisition software (Axon Instruments). Capacitive currents were compensated by analog circuitry, and a -P/8 subtraction protocol was used (27). Data analysis was performed using Python programming language scripts (Python Software Foundation, https://www.python.org/).

Data Availability

All study data are included in the article and/or SI Appendix.