Image-charge effects on ion adsorption near aqueous interfaces

Significance

Understanding electrostatic interactions across interfaces is of critical importance in energy storage devices and biological science. We study the adsorption of salt ions on aqueous interfaces using molecular dynamics simulations, applying an efficient algorithm that enables us to systematically control the effect of surface, solvent, and solute polarization. In the absence of applied potential difference, the image-charge attraction of the ions predicted by continuum electrostatics is shown to be screened out by the solvating water molecules, resulting in no appreciable difference in the ion profiles near a metal surface vs. a nonpolarizable surface. However, the metal surfaces promote significantly enhanced fluctuation in, and magnitude of, the charge separation across the confined electrolyte, leading to greater capacitance under applied electric field.

Abstract

Electrostatic interactions near surfaces and interfaces are ubiquitous in many fields of science. Continuum electrostatics predicts that ions will be attracted to conducting electrodes but repelled by surfaces with lower dielectric constant than the solvent. However, several recent studies found that certain “chaotropic” ions have similar adsorption behavior at air/water and graphene/water interfaces. Here we systematically study the effect of polarization of the surface, the solvent, and solutes on the adsorption of ions onto the electrode surfaces using molecular dynamics simulation. An efficient method is developed to treat an electrolyte system between two parallel conducting surfaces by exploiting the mirror-expanded symmetry of the exact image-charge solution. With neutral surfaces, the image interactions induced by the solvent dipoles and ions largely cancel each other, resulting in no significant net differences in the ion adsorption profile regardless of the surface polarity. Under an external electric field, the adsorption of ions is strongly affected by the surface polarization, such that the charge separation across the electrolyte and the capacitance of the cell is greatly enhanced with a conducting surface over a low-dielectric-constant surface. While the extent of ion adsorption is highly dependent on the electrolyte model (the polarizability of solvent and solutes, as well as the van der Waals radii), we find the effect of surface polarization on ion adsorption is consistent throughout different electrolyte models.

Interfaces of aqueous electrolytes with materials of different dielectric constant is of central importance in broad areas of science. The interplay of electrostatic interactions through the symmetry-breaking boundaries plays a major role in the thermodynamic and dynamic behavior of a wide range of systems, such as electrochemical cells (1) , air/water interfaces (2, 3), colloidal suspensions (4, 5), hydrovoltaics (6), and biological membranes (7), to name a few. Recent advances in surface-specific spectroscopic techniques have unveiled rich structural and chemical properties at interfaces that are distinct from homogeneous bulk systems (8–10); however, molecular understanding of the observed behaviors in these complex systems remains far from complete.

A key factor in determining the ion distribution and other interfacial properties is the difference in the polarization between the solvent and the bounding medium (e.g., electrodes or air). Continuum electrostatics accounts for this difference via the construct of image–charge interaction (ICI): A charged particle feels attractive/repulsive force from the interface when the bounding medium has a higher/lower dielectric constant than the solvent, respectively, due to its image charge on the other side of the interface. The ICI depends only on the dielectric constants of the adjacent media and the charge of ions and was invoked in the pioneering work by Wagner (11) and Onsager and Samaras (12) to explain the increase of water surface tension with salt concentration. However, simulation (8, 13–28) and experimental (9, 29–38) evidence indicates that the ion distribution in the interfacial region is strongly ion-specific, with larger and more polarizable ions tending to accumulate near the air/water interface. The ion-specific adsorption at the air/water interface has been attributed to a number of factors including cavity formation (15, 24), ionic polarizability (14, 39, 40), capillary fluctuations (41–43), and electrochemical surface potential (44), but the quantitative extent of these effects remains a matter of discussion and disagreement (10, 44, 45). Furthermore, recent experiments by Saykally and coworkers showed similar adsorption free energy of the thiocyanate (${\mathrm{S}\mathrm{C}\mathrm{N}}^{-}$) ion for two dielectric interfaces with nominally opposite ICI (air/water vs. graphene/water) (46). The apparent similarity between air/water and graphene/water interfaces raises question on the nature and effects of ICI at aqueous interfaces.

Molecular simulations incorporating both polarization effects—the surface polarization represented by ICI and the molecular polarization of the ions and water—are thus warranted to elucidate the physical origin of these interfacial behaviors. Molecular dynamics (MD) studies addressing the surface polarization effect for metallic surfaces have been attempted by several methods. The constant potential condition of the conducting surfaces was achieved either by an iterative method (47–50) or by the method of image charge (51–53). Ion distribution near the electrode in these simulations, which are measured either with an implicit solvent model or under external electric potential difference, have supported the traditional view of attractive ICI toward metallic or graphene interfaces. On the other hand, MD studies by Jungwirth and Tobias highlighted the importance of using polarizable ion/water force fields (FFs) to capture the enhanced surface concentration of large halide ions at bulk solution interface (14). It has also been shown that simulations with optimized nonpolarizable FFs exhibit increased surface concentration for iodide ions but not for chlorides (14, 15, 54, 55), which claimed that the conventional polarizable FFs overestimate the surface ion concentration (39, 45). The quantitative enhancement of the ions at the air/water interface (especially for the moderately sized chloride ion) is a matter of active discussion (26, 41, 56–58), but the general consensus is that both greater polarizability and larger van der Waals radius of the ion enhance surface enrichment (10). Notably, an MD study accounting for both the surface and molecular polarization has been reported recently for an ionic liquid in its pure state and in organic solvent under an applied external electric field (59), but such simulations for aqueous electrolytes have not been reported yet due largely to the computational expense associated with each of the polarization methods.

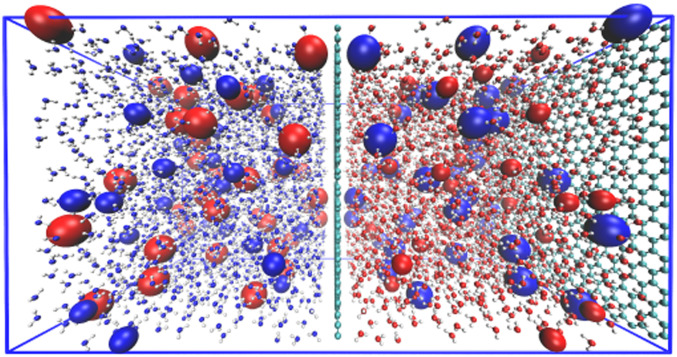
In this work, we perform systematic analysis of the surface and molecular polarization effects on the ion distribution near aqueous interfaces with different ICI, by controlling each of the polarization effects independently. As shown in Fig. 1, the system consists of an electrolyte [1 M NaCl(aq) aqueous solution] placed between two parallel graphene-like model surfaces located at $z=0$ and $z=L$ (walls at the center and the right in Fig. 1, respectively). The effect of molecular polarization is analyzed by comparing simulations with a polarizable FF (60, 61) and a nonpolarizable FF (62, 63). The surface polarization effect is accounted for by using the known symmetry of the exact solution of ICI (51), where the ICI due to the perfectly conducting wall boundary (CW, mimicking graphene/water interface) can be captured by using image-charge particles (ICPs). The ICPs are the mirror reflections of the real charges about the conducting surface (at $z=0$), with charges having the same magnitude but opposite sign with respect to their parent particles (represented as the blue and red particles in Fig. 1). When both surfaces are conducting, the real system and its image are repeated ad infinitum in a periodic manner in the $z$ direction. Note that the partial charges on the water molecules also generate image charges, an effect that is missing in the dielectric continuum treatment of the solvent. When the ICI is turned off, the surface is treated as a pure van der Waals atomic wall with a nonpolarizable wall (NPW) boundary. An efficient integration algorithm is implemented with the massively parallel MD simulation package OpenMM (64) using graphical processing units (GPUs), which enabled us to use Drude-oscillator polarizable FFs along with the ICI with moderate computational cost. To see the effect of the capillary fluctuations we also consider the case where one of the surfaces is free.

Fig. 1.

Schematic drawing of the expanded unit cell to simulate aqueous electrolytes placed between two conducting surfaces. The unit cell is composed of the primary cell that contains the actual electrolyte and the conducting wall boundary is treated with ICPs reflected in the image cell on the left that mirrors all charged particles in the primary cell. Applying a three-dimensional periodic boundary condition accounts for the exact ICI induced by the parallel conducting surfaces (51). Large and medium-sized spheres in blue and red in the primary cell represent the anions and cations, respectively. Water molecules and their ICPs are represented with balls and sticks. The water oxygen atoms are represented with red and blue in the primary and image cell, respectively, while the colors for hydrogen atoms are omitted for clarity. Opposite colors (blue–red) of the same sized ions and water oxygen atoms on the primary and image cell indicate that the ICPs carry the charge of the same magnitude but opposite sign with respect to the primary particles.

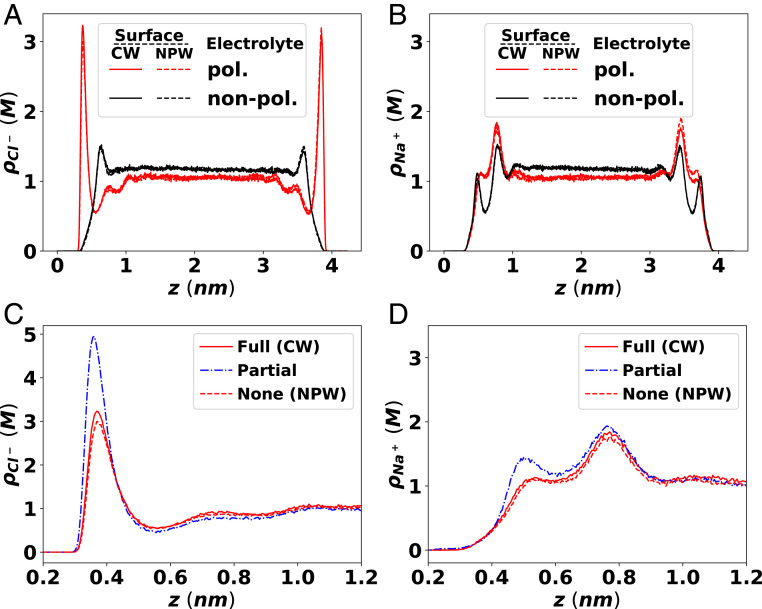
Fig. 2 compares the ion distribution in 1 M NaCl(aq) solution under different electrostatic conditions, where the surface polarization (CW vs. NPW analogous to graphene/water vs. air/water) and the molecular polarization (pol. vs. nonpol.; polarizable FF vs. nonpolarizable FF) are controlled independently. The confining surfaces are modeled as atoms fixed on the lattice points of single flat graphene sheets, which are treated as completely inert electronically. The fixed surfaces are introduced simply to confine the system and reduce the surface fluctuations at the aqueous interfaces, allowing a rigorous comparison of purely electrostatic effects on the ion distribution; as such, we do not include the strong cation–pi interaction reported for the sodium ions and the real graphene surfaces (65). The medium outside of the confining surfaces is assumed to be either a perfect conductor (conducting wall boundary or CW) or vacuum (nonpolarizable wall boundary or NPW), to study the effect of surface polarization; the boundaries are taken to be located at the plane where the confining surface atoms reside.

Fig. 2.

Effect of different polarization models on the distribution of the (A and C) chloride and (B and D) sodium ions in 1 M NaCl(aq) solution between two parallel plates under no applied electric field (0 V). (A and B) Ion distribution near the fully polarizable graphene/water-like surface (CW, solid lines) shows almost no noticeable difference from nonpolarizable air/water-like surface (NPW, dotted lines). Electrolytes modeled with polarizable FF (pol., red color) show strong adsorption of chloride ions on the surfaces, while nonpolarizable FF (nonpol., black color) predicts depletion of both sodium and chloride ions from the surfaces. (C and D) Effect of ICI of the ions and water molecules on the ion density profile simulated with polarizable FF. When ICI is included partially for the ions but not the water molecules (partial, blue dashed-dotted lines), both ions’ density near the interface increases significantly compared to the simulation results with either no ICI (NPW, red dotted lines) or the full ICI (CW, red solid lines), suggesting the strongly attractive ICI induced by the ions is almost completely screened by the ICI induced by the water molecules.

The most striking feature in Fig. 2 is that there is apparently no effect of the ICI, as indicated by the nearly complete overlap in the ion distribution profile between the CW case (solid lines) and the NPW case (dashed lines). This observation is consistent with the experimental observation by Saykally and coworkers (46) but contrary to the conventional view of ICI based on the implicit solvent treatment of water (i.e., as a continuum dielectric), which would predict strong ion accumulation near a conducting surface (52, 53). We note that simulations incorporating both explicit solvent molecules and the surface polarization effect have been performed previously (66); however, the importance of the combined ICI effects induced by the explicit solvent molecules and the ions—which should strongly alter the nature of surface–water (67) and surface–ion (68) interactions—has not been addressed.

To analyze the influence of the explicit water and its image charges, we performed a simulation with partial ICI, in which only image charges of the ions are included but not those of water. Note that the primary cell still contains explicit water molecules and is treated with polarizable FF. Fig. 2 C and D compares this simulation with the previous two simulations that accounted for full ICI (CW) and no ICI (NPW). The blue dashed-dotted line representing partial ICI (ions only) shows strong influence of ICI of the ions, where both the chloride and the sodium ion concentrations are significantly enhanced near the surface. Thus, we can conclude that the polarizable surface indeed induces strong attractions to all ions when the ICI of the water is suppressed, but when the ICI of water is present, due to the partial charges as a result of the large dipole moment of water, there seems to be nearly complete cancellation of the attraction to the ions, resulting in apparently indistinguishable ion distribution between the CW surfaces and NPW surfaces. This striking result offers a possible explanation of the experimental findings of Saykally and coworkers (46); it also calls for new theoretical explanations for some interfacial phenomena that were previously explained based on ICI using an implicit water model, such as the salt dependence of surface tension of aqueous electrolytes. (12).

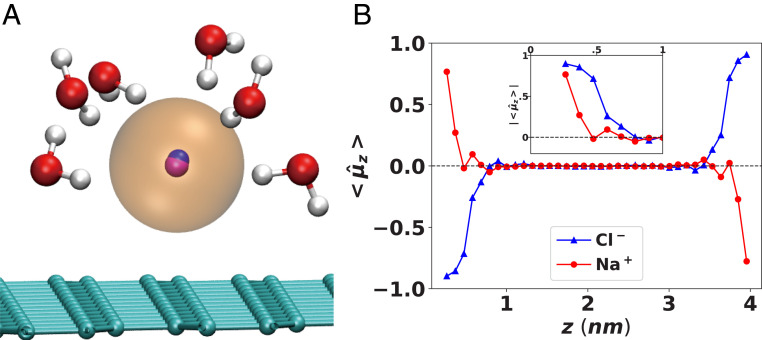
The ICI between a single dipole and its image dipole is much shorter-ranged than the ICI induced by a single ion (SI Appendix, Fig. S2). Thus, the apparent cancellation of the ion ICI effect by the inclusion of water ICPs is unlikely due to the competitive adsorption of the water molecules vs. the ions on the conducting surface. Rather, the heterogeneous solvation environment of the surface-exposed ions and the strong screening by the water molecules in their first solvation shell are responsible for this cancellation. The surface ions at the outermost molecular layer of the electrolyte carry water molecules in the half-solvation shell (Fig. 3A). The ICPs generated by these half-solvating water molecules are closely located to the ICP of the ion and counteract the strong attractive ICI by the ion; the water ICPs are preferrentially oriented such that the electrostatic force between these oriented image dipoles and the original surface ion is in the opposite direction to the ICI by the image ion. The combined effect is nearly complete screening of the ICI even for the outermost surface ions as seen in Fig. 2. Thus, we emphasize that including explicit solvent molecules in treating the surface polarization effect is essential to properly account for the delicate balance among complex electrostatic contributions.

Fig. 3.

Orientation of the polarization dipoles of the ions near the interface. (A) A snapshot of an interfacial chloride ion (sphere at center) and its half-solvation shell adsorbed on the surface. Blue and violet at the core of the anion show strong polarization dipole (directing from blue to violet) of the ion due to inhomogeneous solvation environment. (B) Average alignment of the dipole moment vector of each ions along the z axis, simulated for 1 M NaCl(aq) with polarizable FF under no applied electric field. The two boundary surfaces are located at z = 0 and z = 4.3 nm.

Another interesting feature in Fig. 2 is that only the chloride ion modeled with polarizable FF shows enhanced ion concentration at the surface. The importance of molecular polarization on the interfacial behavior has been known for more than a decade since the study by Jungwirth and Tobias (14), who provided a qualitative explanation based on asymmetric solvation at the air/water interface; the loss of solvation free energy for the surface-exposed ion is thought to be compensated by the strong ion polarization. As shown in Fig. 3A the asymmetric water structure in the half-solvation shell surrounding the surface chloride ion generates a strong local electric field that creates an induced dipole moment in the ion pointing toward the surface. This highly preferential water orientation near ions is in accord with the excess ion polarizability (i.e., the change of solvent polarizability due to the ion) of most ions (including large anions) being negative in aqueous electrolytes (69). However, the magnitude of the actual polarizability of an ion strongly affects the extent of the asymmetric polarization and the stabilization of the surface ion.

In Fig. 3B we provide a quantitative measure of the interfacial solvation and asymmetric polarization by calculating the orientation distribution of the induced ion dipole (modeled by the Drude oscillator in the polarizable FF). Here, ${\widehat{\mu }}_z=\cos \left(\theta \right)$ characterizes the cosine angle ($\theta$) of the dipole vector along the positive $z$ direction perpendicular to the parallel electrodes. If present at the outermost surface (within $\sim$4 Å from the electrodes), both the cation and anion can be characterized with strongly preferential dipole orientation (${\widehat{\mu }}_z=\pm 1$), which dies after about 1-nm distance from the electrodes. For the more polarizable chloride ion, the polarization-induced stabilization of the surface ion is enough to compensate for the loss of half of the solvation free energy, thus resulting in enhanced ion concentration on the outermost surface layer compared to the bulk region. On the other hand, the depletion of sodium ions from the outermost surface layer can be explained based on weaker orientational preference as well as much smaller magnitude of the ion-induced dipole. As shown in Fig. 3B, Inset, sodium ions lose much of the alignment of the induced dipole very quickly (at z = 4 Å, where the surface chloride ions reside, the order parameter already has decreased to ${\widehat{\mu }}_z<0.5$). Moreover, the average magnitude of the induced dipole for sodium ions is 40 times lower than for chloride ions (SI Appendix, Fig. S3D). Notably, the sodium ions at $z=0.8,3.5$ nm, which corresponds to the second peak with the highest local density in the Na⁺ ion distribution profile (Fig. 2B), shows the same dipole orientation as the surface chloride ions but in opposite direction to the outermost sodium ions near $z=0.4,3.8$ nm (Fig. 3B and SI Appendix, Fig. S3B). The highest peak in the distribution profile of sodium ions is due to the formation of the electric double layer, where the sodium ions are attracted by the surface-adsorbed chloride ions; thus, their induced dipoles point toward the surface chloride ions, which is the same direction as the induced dipoles in the surface chloride ions.

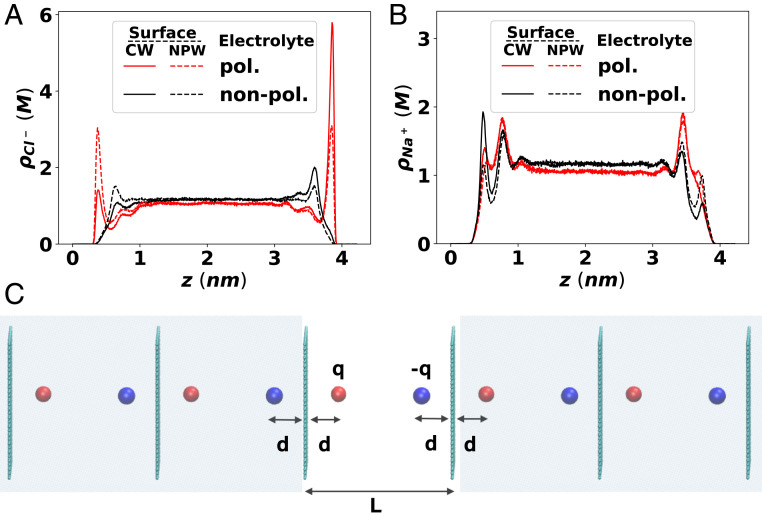
We now turn to the case of applied potential difference between the two conducting surfaces, which has obvious implications for electrochemical systems such as energy-storage devices. This can be modeled by applying a uniform electric field of magnitude $\mathrm{\Delta }V/L$ along the $z$ axis in the primary cell (51, 53). Alternatively, the potential difference can be effected by assigning surface charge (70) of the same magnitude but opposite sign to the atoms of the two bounding surfaces. The density profiles obtained from the two methods—Fig. 4 with an imposed constant electric field and SI Appendix, Fig. S6 with fixed surface charges—are fully consistent with each other. These figures show the density profile of the two types of ions under the electrostatic potential difference of 1 V between the electrodes, obtained with either nonpolarizable (NP) or polarizable (P) FFs, each with CW and NPW conditions. The electric field is directed toward the left electrode, and thus the right electrode is charged positive while the left electrode is charged negative. Under this electric field, the effect of the ICI due to the polarizable surface is immediately noticeable, unlike the earlier zero-field case shown in Fig. 2; both the anion and cations accumulate more strongly toward the oppositely charged surfaces when the attractive ICI is accounted for (CW, solid lines in Fig. 4 A and B). Interestingly, the surface ion concentration near the like-charged surfaces is lower for the polarizable surface (CW) than for the nonpolarizable surface (NPW, dashed lines), despite the attractive ICI in the case of CW. Thus, in the presence of an applied electric field, the primary net effect of the CW is the increased “charge separation” instead of increased “total net adsorption” of ions toward the surfaces.

Fig. 4.

Effect of ICI on the ion distribution of the (A) chloride and (B) sodium ions in 1 M NaCl(aq) solution placed between two surfaces under 1-V electrostatic potential difference (higher on the right surface). Under external electric field, allowing surface polarization (CW, solid lines) significantly enhances charge separation. The solid/dashed lines indicate CW/NPW surface, respectively, while the colors of the curves distinguishes polarizable/nonpolarizable water and ion FF, analogous to Fig. 2 A and B. (C) Schematic drawing of the infinite series of ICPs generated by a symmetrically placed pair of opposite-charged ions. As shown in Eq. 1 and SI Appendix, Fig. S2, larger separation of an ion pair is always preferred by the ICI.

To understand these counterintuitive results that the ion concentration near the like-charged surface is lower for the CW than for the NPW surfaces, we quantify the contribution of the ICI to the electrostatic energy of the system under the CW and NPW boundary conditions by considering a simple ion pair that is symmetrically separated between the two surfaces as shown in Fig. 4C. The difference between electrostatic energies calculated with CW and NPW characterizes the contribution from ICI, i.e., the energies of all possible pair interactions between the real charges (the two oppositely charged ions in the central real cell) and the ICPs (all other charges in the shaded area in the figure). As noted by Hautman et al. (51), only half of the Coulombic energy of these real–ICP pair interactions should be included in the system energy, while the direct-pair interactions between ICPs in the image cell do not contribute to the system energy. Thus, the ICI contribution to the system energy for the symmetric ion pair becomes

$$\begin{array}{cc}\hfill E^{ICI}\left(x\right)& =\frac{q^2}{ϵL}\sum _{n=1}^{\infty }\left(\frac{2}{n}-\frac{1}{n+1-2x}-\frac{1}{n-1+2x}\right)\hfill \\ \hfill & =\frac{q^2}{ϵL}\left(2\gamma +\psi \left(2-2x\right)+\psi \left(2x\right)\right)\hfill \end{array},$$ [1]

where $x=d/L<1/2$, $\gamma =0.5772\dots$ is the Euler–Mascheroni constant, and $\psi \left(x\right)$ is the digamma function defined as the logarithmic derivative of the gamma function $\psi \left(x\right)={\mathrm{\Gamma }}^{\prime }\left(x\right)/\mathrm{\Gamma }\left(x\right)$. In Eq. 1, only the interactions between the real particles and ICPs on the right of the real cell are summed over due to the symmetry. Eq. 1 is a monotonically increasing function in the range $0<x<1/2$ (SI Appendix, Fig. S2), which converges to zero as the ions meet at the center and diverges to negative infinity if the ions are separated to touch the surfaces.

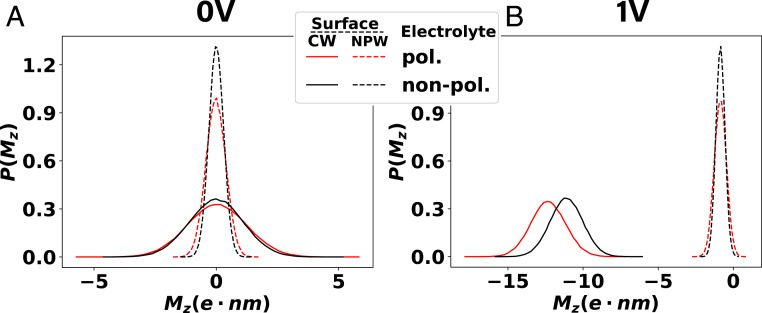
The negativity of Eq. 1 indicates that including the ICI with CW promotes charge separation by lowering the electrostatic energy of the system dipole; the larger the separation between the oppositely charged ions, the stronger this stabilization. In the absence of an applied external field, this charge separation by the ICI can be in either direction, resulting in a symmetric ion distribution with greater fluctuations than in the absence of ICI. To see this, we calculate the instantaneous system dipole, $M_z={\sum }_i{q}_i{z}_i$, including the contributions from partial charges of water molecules, from the simulation trajectories of 1 M NaCl(aq) performed under different polarization and external electric field conditions already discussed in Figs. 2 and 4.

The distribution of system dipole shown in Fig. 5 reveals a strong influence of surface polarization effect even under zero applied electric field condition that is hidden in the ion density profiles. The calculated $M_z$ shows much wider distribution when the surface polarization is accounted for (CW, solid lines) than that measured without the effect (NPW, dashed lines). Unlike the ion density profile, the effect of ion/molecular polarization on this fluctuation of system dipole is only moderate. While the increased fluctuation in the system dipole for the CW does not lead to charge separation in the absence of applied potential difference, this enhanced fluctuation makes the system more susceptible to applied potential difference, resulting in a greater degree of charge separation compared to the NPW case. For the 1 M NaCl(aq) simulated with 1-V potential difference between the electrodes, the average system dipole, which is directly related to the capacitance of the electrolytic cell, is increased to more than 10 times higher value under CW than under NPW (Fig. 5B).

Fig. 5.

Enhanced fluctuation and stabilization of net system dipole due to ICI observed from different simulations of 1 M NaCl(aq) with (A) 0-V and (B) 1-V electrostatic potential drop across the electrolyte. Each figure contains four probability density curves of the total system dipole along the z axis that are obtained with different surface (CW vs. NPW) and electrolyte (polarizable vs. nonpolarizable) polarization models.

The increased system dipole fluctuation and stabilization of charge separation by ICI can help understand several recent experiments of the interfacial aqueous electrolytes. For instance, breakdown of electroneutrality in aqueous electrolytes under nanoconfinement has been reported in uncharged graphitic nanoporous carbon (71), which is analogous to our zero-field simulation results. The ICI induced by the graphitic surfaces promotes microstates with charge separated ion distributions across the carbon electrode, where the local electroneutrality can be violated due to nanoconfinement while global neutrality is still maintained across the system. Furthermore, the enhanced charge fluctuation in the longitudinal direction induced by ICI under CW boundary is also applicable to nonaqueous electrolytes and pure ionic systems; for example, this enhanced charge fluctuation is likely to play a role in the recently proposed spontaneous charge separation in solvent-free ionic liquid capacitors predicted by field-theoretic models (72–74).

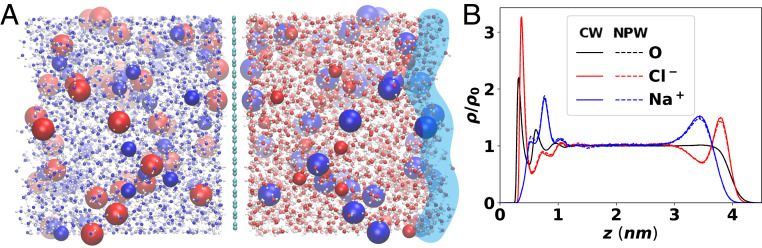
An important aspect of the air/water interface that we (intentionally) omitted in the results discussed so far (by using hard planar surface) is the fluctuation in the free surface of water (41–43, 75). To see the role of the surface fluctuation on the ion distribution and the role of ICI in such systems, we constructed a system with only a single graphene-like surface on the left, while allowing the vacuum/water interface on the right to fluctuate freely (Fig. 6A). Similar to the previous systems we have discussed, polarization on the left graphene-like surface is controlled by including (CW) or excluding (NPW) the ICPs mirrored to the left side of the system. The surface atoms are again inert and neutral, similar to Fig. 2.

Fig. 6.

Effect of surface fluctuation at the air/water interface on the interfacial ion and water distribution. (A) The simulation snapshot of the two-boundary system simulated with a polarizable FF and full ICI (CW) on left hard graphene-like surface. A simulation without ICI (NPW) is also performed by not including any ICPs on the left side of the wall atoms. The right surface is allowed to freely fluctuate, mimicking an air/water interface. (B) Relative ion/water distribution as a function of the distance from the left hard surface. Allowing surface fluctuation on the right surface reduces the peak height and broadens the interfacial ion/water concentration peak, but the relative position of the surface species is consistent on both surfaces, showing both chloride and water molecules are exposed to both of the surfaces but sodium ions are solvent-separated (one water molecule apart) from the surfaces. Similar to Fig. 2, effect of ICI under zero external field is almost perfectly screened, resulting in two overlapping curves for each color.

In Fig. 6B we compare the distribution of the ions and the water oxygen in this two-surface system with either CW or NPW conditions (for the left surface). The measured ion/water distributions in simulations with either CW (solid lines) or NPW (dotted lines) are almost indistinguishable, similar to the electrolyte between uncharged parallel surfaces in Fig. 2. Thus, the nearly perfect screening of ion ICI by the water ICI holds for this system with a single conducting wall as well, indicating the strong cancellation of ICI by explicit solvent molecules is a general phenomenon in aqueous electrolytes and is not caused by the confined geometry. Also, the qualitative effect of ion polarizability on ion distribution is consistent between the hard and fluctuating surfaces, namely, only the ${\text{Cl}}^{-}$ ions with large polarizability are able to reside at the outermost surface layer (large blue spheres near both surfaces on the right side of Fig. 6A), while the Na⁺ ions show only solvent-separated surface adsorption next to an outermost surface water layer. The ion distribution in Fig. 6B corresponds to the formation of electric double layers consisting of the surface ${\text{Cl}}^{-}$ layer followed by the solvent-separated Na⁺ layer. Quantitatively, fluctuation of the vacuum/water interface relaxes the oscillation in the number density along the $z$ axis, resulting in a smoothly decaying concentration profile for the water oxygen on the right. We note the density profile at the air/water interface in Fig. 6B is in semiquantitative agreement with earlier simulation results using other polarizable FF (14, 76), with a significantly reduced uncertainty in our calculation due to larger system size and longer simulation time. The oscillatory high concentration peak on the left interface is due to the size of ions and water molecules. Allowing the surface atoms to move in the $z$ direction reduces the intensity and broadens the width of the surface concentration peaks but does not alter the qualitative effect of the molecular polarizability.

The effect of surface polarization discussed above (either with or without external electric field) is independent of the ion/water FF or the driving force for ion adsorption. This can be illustrated with halides larger than chloride ions, where simulations with carefully optimized nonpolarizable FFs can reproduce the enhanced ion adsorption at the air/water interface (15, 44, 54). As shown in SI Appendix, Figs. S7 and S8, simulation results using such FFs for a set of alkali halides predict surface enrichment of the iodide for both CW/NPW boundaries, and the role of surface polarization is consistent regardless of the types of ions and the extent of the surface propensity: The ICI is always nearly perfectly screened under zero external field but strongly increased charge separation is observed under applied field.

We also note that there are considerable debates on the degree of the ion enrichment at the air/water interface, especially for the moderately sized chloride ion. Simulation studies with nonpolarizable FFs (15, 44) along with continuum-based theoretical studies (39, 58, 77) predict depletion of chloride ions from the air/water interface, which appeared to be consistent with the surface tension measurements based on the Wagner–Samaras–Onsager picture (12). On the other hand, simulations using polarizable FFs (14, 23, 25, 26, 78) and ab initio computations (79) propose less depletion or even enrichment of chloride ions at the air/water interface, which is (partly) supported by surface-specific vibrational spectroscopy (30, 57, 80) and photoelectron spectroscopy (31) measurements. These experiments estimated neutral to enhanced surface concentration than the bulk solution concentration for chloride and larger halides. In particular, using surface-specific femtosecond vibrational spectroscopy, Bonn and coworkers estimated the concentration of chloride and iodide ions at the air/water interface to be about 1.8 and 3.5 times higher, respectively, than the concentration in bulk solution (57). The increased surface concentration of chloride and iodide ions is in near-quantitative agreement with our simulation results for the dual surface with polarizable FFs, where the surface peak in the anion density profile is 1.5 and 3.2 times larger than the bulk concentration for chloride and iodide, respectively (Fig. 6 and SI Appendix, Fig. S9). Direct comparison of simulated density profile with experiments is not trivial due to the underlying approximations in estimation of the surface excess and the surface tension (54). The development of highly accurate water and ion FFs would provide an alternative route to directly compare the simulation results with experimental bulk solution properties and interfacial spectroscopic data (81–83). Nevertheless, the robustness of strong screening of ICI by explicit solvent molecules, which is observed for all tested electrolytes simulated with either polarizable or nonpolarizable FFs, calls for new theoretical development to describe the effect of dielectric interfaces.

In conclusion, by controlling surface and molecular polarization in the simulations of aqueous electrolytes with interfaces we obtain a simple unified explanation for interfacial ion distribution observed in air/water and graphene/water interfaces. High molecular polarizability and/or large size of the halide ions stabilizes the surface-exposed anions, followed by surface excluded sodium ions forming a clear electric double layer at the interface. The strong attractive ICI for all ions induced by the polarizable surface is found to be almost perfectly canceled by the ICI induced by the water molecules, resulting in interfacial density profiles that are not sensitive to the nature of the boundary surface. However, applied external field results in much greater charge separation for the CW surface than for the NPW surface, due to enhanced system dipole fluctuation induced by the ICI in the CW case. Allowing capillary fluctuation in the NPW surface reduces the sharp interfacial peak of ion/water distribution function.

Our simulation explains many recent experimental observations including the identical ion adsorption free energy of thiocyanate anion to both a conducting graphene surface and a low dielectric air/water interface (46) and electroneutrality breakdown in nanoconfined aqueous electrolytes (71). At the same time, the cancellation of ICIs induced by the ions and the explicit water molecules calls for development of new theories of aqueous electrolyte phenomena that have been explained based on ICI, such as non–ion-specific salt concentration dependence of surface tension (12). We hope this work stimulates such development which fully accounts for both molecular and surface polarization effects as well as ICI for both the ions and the solvents. An anticipated extension of our work is to study polyelectrolyte adsorption near dielectric interfaces, where simulations using implicit solvation model has shown the importance of the surface polarization effect (84). Also warranted are new simulation studies accounting for the ICI on graphene oxide membranes under electrostatic potential, which has received great attention as desalination membrane (85, 86). The efficient simulation code developed in this work fully utilizes massive parallelization with GPUs and is freely available to download at https://github.com/scychon/openmm_constV.

Materials and Methods

We initialize our simulation by preparing an orthorhombic unit cell of 1 M NaCl(aq) solution and placed it between two parallel planar layers made of Lennard-Jones particles arranged in a two-dimensional graphene structure. The system consists of 2,046 water molecules and 38 pairs of NaCl ions, with 640 fixed atoms on each of the two surfaces. The $x$ and $y$ dimensions of the unit cell were chosen to accommodate the atom periodicity in a perfectly planar graphene sheet, and the $z$ dimension was allowed to fluctuate during first equilibrium process. The system was equilibrated at ambient condition (298 K and 1 atm) for 6 ns without including any polarization effects. The equilibrated system results in a unit cell dimension of (3.9, 4.3, 4.2) nm. After density equilibration, each set of polarizable/nonpolarizable FFs, surface polarization (CW vs. NPW vs. partial), and the electric potential drop across the electrolyte (0 V vs. 1 V) and the van der Waals atomic wall boundary vs. free boundary simulations are performed for 110 ns in canonical ensemble, where the first 10 ns was excluded from the analysis of density distribution and system dipole. SI Appendix provides the FF parameters used for all simulations and additional simulation results for 1 M NaBr(aq) and 1 M NaI(aq) solutions with optimized nonpolarizable FFs, as well as the simulation results for 1 M NaI(aq) solution under a two-surface system with Drude polarizable FFs. Additional discussion on the different contributions from ion polarization vs. water polarization to the ion adsorption, as well as simulation results of nonpolarizable FFs with partial ICI, are provided in SI Appendix. SI Appendix also contains more detailed description on the ICI contribution to system energy.

Data Availability

All study data are included in the article and/or SI Appendix.