Cognitive impairment after focal brain lesions is better predicted by damage to structural than functional network hubs

Significance

Hubs are highly connected brain regions that are important for coordinating processing in brain networks and supporting cognition. There are several different methods for characterizing network hubs in gray and white matter, yet it is unclear which of these hub measures identify sites that are most critical for supporting cognition. Here, we use data from two large cohorts of patients with focal brain damage to show that lesions of white matter regions with dense structural connections have the strongest association with cognitive impairment, while gray matter functional centrality measures have weaker associations. These findings highlight the critical role of densely connected white matter regions in supporting cognition, which helps to explain interindividual differences in cognitive outcomes following brain damage.

Abstract

Hubs are highly connected brain regions important for coordinating processing in brain networks. It is unclear, however, which measures of network “hubness” are most useful in identifying brain regions critical to human cognition. We tested how closely two measures of hubness—edge density and participation coefficient, derived from white and gray matter, respectively—were associated with general cognitive impairment after brain damage in two large cohorts of patients with focal brain lesions (N = 402 and 102, respectively) using cognitive tests spanning multiple cognitive domains. Lesions disrupting white matter regions with high edge density were associated with cognitive impairment, whereas lesions damaging gray matter regions with high participation coefficient had a weaker, less consistent association with cognitive outcomes. Similar results were observed with six other gray matter hubness measures. This suggests that damage to densely connected white matter regions is more cognitively impairing than similar damage to gray matter hubs, helping to explain interindividual differences in cognitive outcomes after brain damage.

The importance of different brain regions in supporting large-scale brain networks is not uniformly distributed. Hub regions are especially critical in forming a backbone of global network architecture and, by extension, are thought to be critical in supporting human cognition. However, there are competing ideas regarding what measures of “hubness” are most relevant for cognition (1, 2). Much of the evidence linking structural and functional hubs to cognition is correlational in nature, showing associations of imaging measures with task performance in healthy participants (3). While informative, it is difficult to draw causal inferences from these studies. As such, studies of neurological patients with focal pathology have been helpful in further clarifying the role of network hubs in cognition (4–7).

Influential studies have shown that focal brain damage involving network hubs causes widespread changes in brain networks (8–10). In addition, some studies have related hub damage with cognitive impairment, either in a single domain (7, 11) or spanning multiple cognitive domains (6, 12). These studies have largely focused on either gray matter measures (6) or white matter measures of hubness (13) but have not compared the two. Here, we aim to extend this line of research by quantifying the degree to which individuals’ focal brain lesions map onto both functional and structural network measures of hubness in two large cohorts. We focus on two well-established network metrics, participation coefficient and edge density—derived from gray and white matter, respectively—to test the association of these network measures with general cognitive performance.

Participation coefficient describes the involvement of a brain region within multiple brain systems. It is often considered the preferred measure of “hubness” in networks derived from correlated patterns of brain activity, including those derived from resting state functional connectivity MRI (8). Regions with higher participation coefficient are thought to be important for integrating and coordinating processing between networks, a feature that may be important for general cognitive processes (14–16). For instance, Warren and colleagues (6) assessed the postlesion performance of 30 patients with focal damage to regions either high or low in participation coefficient, derived from normative functional connectivity MRI data. Patients with lesions in high participation coefficient regions showed broad cognitive impairments in multiple domains, beyond what was expected by clinicians based on lesion location alone (6, 17).

Alternatively, regions with a high density of white matter connections also form structural network hubs, as these regions are critical for facilitating the flow of information in brain networks. Edge density provides an important metric of this kind of structural hubness, indexing the number of white matter connectome edges that link gray matter regions on a voxel-wise basis (18). Introducing lesions to regions high in edge density in the posterior periventricular white matter was disruptive to distributed brain networks in simulated lesion analyses (19, 20), but this has yet to be tested with data from patients with brain lesions.

The relative importance of these gray and white matter network measures in identifying brain regions important for human cognition is unclear. Lesion studies that have looked at this topic have relatively small sample sizes and focus on gray or white matter network measures, but not both. There is some evidence to suggest, however, that white matter network metrics might be more predictive of cognitive outcomes than those derived from gray matter (13, 21–23). For instance, a study by Griffis and colleagues (7) found that damage to white matter “bottlenecks” underlying the temporal lobe was more predictive of language impairment than damage to canonical cortical regions involved in language. However, a systematic evaluation that evaluates both structural and functional network hubness measures as they relate to cognitive outcomes is needed to further evaluate the relative importance of each.

Here, we extend this line of investigation by evaluating the real-world functional importance of different types of structural and functional network hubs based on their association with cognitive impairment following focal brain lesions. In two large cohorts of individuals with focal, acquired brain lesions (N = 402 and 102), we estimated the degree to which the brain lesions disrupt brain networks based on the extent of the lesion’s overlap with population-derived, brain-wide maps of edge density and participation coefficient. We estimated general cognition in each subject based on shared variance in a structural equation model among 17 neuropsychological tests spanning different domains of cognition. Based on the evidence reviewed above, we hypothesized that greater cognitive deficits would be seen in association with 1) lesions of gray matter regions that participate in multiple networks (represented as higher participation coefficient), 2) lesions of densely connected white matter (represented as higher edge density), and 3) a regression model combining edge density and participation coefficient would provide a stronger prediction than either measure alone, with edge density explaining more variance in cognitive outcomes relative to participation coefficient (8, 9, 21). Prior to conducting any analyses, we preregistered these three main hypotheses and the proposed analytic approach on the Open Science Framework (OSF) (https://osf.io/kpc2b/?view_only=a38cd1e09a4f4735b02cb36955c3f933).

Results

Lesions of Densely Connected White Matter Predicts Greater Cognitive Impairment.

The relationship between the location of each patient’s lesion relative to the edge density and participation coefficient maps was investigated using three hierarchical regression models. This served as the main analysis and test of the preregistered hypotheses. These results are reported in detail in Table 1. On the first step of each of the three models, lesion volume was a significant predictor of cognitive outcome, with larger lesions associated with greater cognitive impairment (β = −0.193, ΔR² = 0.037, P < 0.001). Lesion volume was log-transformed to reduce a positive skew and avoid problems with multicollinearity with the other variables. The main hypotheses were tested in the second step of the regression models. The first model was the most comprehensive and included both edge density lesion load (the sum of all voxel-wise edge density values contained within each individual lesion) and participation coefficient lesion load (the sum of all voxel-wise participation coefficient values contained within each individual lesion). The second step of this regression model significantly improved the predictive variance (ΔR² = 0.045, P < 0.001), but only edge density was significantly associated with cognitive impairment (β = −0.233, P = 0.018), and participation coefficient lesion load failed to reach significance (β = −0.084, P = 0.401).

Table 1.

Iowa cohort: Hierarchical linear regressions with lesion volume, edge density load/peak, and participation coefficient load/peak predicting post-lesion g scores

	Step and Variable		95% CI for b
		b	Lower bound	Upper bound	β	t	p	df	R2	ΔR2	Sig. ΔF	AIC
Raw g Scores
Lesion Load
Model 1	Step 1
	Total Lesion Volume (log mm3)	−0.119	−0.179	−0.059	−0.193	−3.926	<0.001	400	0.035	0.037	<0.001	−80.006
	Step 2
	Total Lesion Volume (log mm3)	0.019	−0.067	0.104	0.030	0.429	0.668	398	0.076	0.045	<0.001	−95.439
	Edge Density Load	−0.214	−0.391	−0.037	−0.233	−2.378	0.018	398	0.076	0.045	<0.001	−95.439
	Participation Coefficient Load	−0.077	−0.603	0.121	−0.084	−0.841	0.401	398	0.076	0.045	<0.001	−95.439
Model 2	Step 1
	Total Lesion Volume (log mm3)	−0.120	−0.181	−0.058	−0.188	−3.818	<0.001	396	0.033	0.035	<0.001	−79.304
	Step 2
	Total Lesion Volume (log mm3)	0.002	−0.086	0.089	0.003	0.037	0.970	395	0.065	0.034	<0.001	−91.498
	Participation Coefficient Load	−0.243	−0.369	−0.117	−0.265	−3.787	<0.001	395	0.065	0.034	<0.001	−91.498
Model 3	Step 1
	Total Lesion Volume (log mm3)	−0.119	−0.179	−0.059	−0.193	−3.926	<0.001	400	0.035	0.037	<0.001	−80.006
	Step 2
	Total Lesion Volume (log mm3)	0.008	−0.074	0.089	0.013	0.187	0.852	399	0.076	0.044	<0.001	−96.725
	Edge Density Load	−0.269	−0.391	−0.148	−0.293	−4.361	<0.001	399	0.076	0.044	<0.001	−96.725
Lesion Peak	Step 1
	Total Lesion Volume (log mm3)	−0.119	−0.179	−0.059	−0.193	−3.926	<0.001	400	0.035	0.037	<0.001	−80.006
	Step 2
	Total Lesion Volume (log mm3)	−0.038	−0.153	0.076	−0.062	−0.659	0.510	398	0.063	0.033	0.001	−89.901
	Lesion Peak Edge Density	−0.022	−0.033	−0.010	−0.220	−3.739	<0.001	398	0.063	0.033	0.001	−89.901
	Lesion Peak Participation Coefficient	−0.046	−1.105	1.013	−0.007	−0.085	0.932	398	0.063	0.033	0.001	−89.901
g Scores Controlled for Crystallized Intelligence
Lesion Load	Step 1
	Total Lesion Volume (log mm3)	−0.092	−0.127	−0.058	−0.255	−5.266	<0.001	400	0.063	0.065	<0.001	−521.118
	Step 2
	Total Lesion Volume (log mm3)	0.008	−0.040	0.057	0.023	0.341	0.733	398	0.127	0.069	<0.001	−547.870
	Edge Density Load	−0.138	−0.239	−0.037	−0.256	−2.691	0.007	398	0.127	0.069	<0.001	−547.870
	Participation Coefficient Load	−0.075	−0.177	0.028	−0.138	−1.430	0.154	398	0.127	0.069	<0.001	−547.870
Lesion Peak	Step 1
	Total Lesion Volume (log mm3)	−0.092	−0.127	−0.058	−0.255	−5.266	<0.001	400	0.063	0.065	<0.001	−521.118
	Step 2
	Total Lesion Volume (log mm3)	−0.079	−0.146	−0.013	−0.219	−2.353	0.019	398	0.081	0.023	0.007	−527.140
	Lesion Peak Edge Density	−0.010	−0.017	−0.003	−0.174	−2.984	0.003	398	0.081	0.023	0.007	−527.140
	Lesion Peak Participation Coefficient	0.278	−0.337	0.893	0.076	0.889	0.374	398	0.081	0.023	0.007	−527.140

Note: R² represents adjusted R². AIC = Akaike Information Criterion. Four patients had lesions that did not intersect with the participation coefficient map and were thus excluded from Model 2 (n = 402). Bold text indicates variable P < .05.

The regression analysis was repeated, combining lesion volume with individual lesion load values of either participation coefficient (model 2) or edge density (model 3). In model 2, higher participation coefficient lesion load was associated with greater cognitive impairment, as hypothesized (β = −0.265, ΔR² = 0.034, P < 0.001). In model 3, higher edge density was again associated with greater cognitive impairment, as hypothesized (β = −0.293, ΔR² = 0.044, P < 0.001). In comparing the three models, we hypothesized that more variance would be explained with the first, most comprehensive model relative to models 2 and 3, but the adjusted R² in models 1 and 3 was the same (0.076), suggesting that the inclusion of participation coefficient did little to improve the overall model. The results were similar using the actual lesion volume, without log transformation, but participation coefficient was no longer significantly associated with cognitive impairment in step 2 of model 2 (SI Appendix, Table S1).

Validation in an Independent Sample.

Next, we repeated these same hierarchical regression models in an independent sample collected at Washington University in St. Louis (WU cohort; Table 2). These regression analyses mirrored the pattern of results from the Iowa cohort. For step 1 in each model, larger lesions were associated with greater cognitive impairment (β = −0.386, ΔR² = 0.149, P < 0.001). In contrast to the main analysis, step 2 in models 1 through 3 did not reach statistical significance in predicting cognitive outcome. Higher edge density lesion load was associated with greater cognitive impairment similar to the Iowa sample (model 1 P = 0.025; model 3 P = 0.055, ΔR² = 0.031), whereas the same association between participation coefficient lesion load and cognitive impairment was negligible (ΔR² = 0.002, P = 0.661). Edge density did explain significant variance in cognitive outcome above and beyond lesion volume when raw lesion volume was used in model 1, while step 2 of models 2 and 3 did not reach significance (SI Appendix, Table S2).

Table 2.

WU cohort: Hierarchical linear regressions with log-transformed lesion volume, edge density load, and participation coefficient load predicting post-lesion g scores

	Step and Variable		95% CI for b
		b	Lower bound	Upper bound	β	t	p	Df	R2	ΔR2	Sig. ΔF	AIC
Model 1	Step 1
	Total Lesion Volume (log mm3)	−0.228	−0.335	−0.120	−0.386	−4.189	<0.001	100	0.141	0.149	<0.001	−13.498
	Step 2
	Total Lesion Volume (log mm3)	−0.145	−0.311	0.022	−0.246	−1.726	0.087	98	0.169	0.044	0.074	−14.906
	Edge Density Load	−0.421	−0.788	−0.053	−0.421	−2.272	0.025	98	0.169	0.044	0.074	−14.906
	Participation Coefficient Load	0.231	−0.137	0.599	0.231	1.244	0.217	98	0.169	0.044	0.074	−14.906
Model 2	Step 1
	Total Lesion Volume (log mm3)	−0.221	−0.338	−0.104	−0.357	−3.742	<0.001	96	0.118	0.127	<0.001	−10.100
	Step 2
	Total Lesion Volume (log mm3)	−0.191	−0.369	−0.012	−0.309	−2.122	0.036	95	0.111	0.002	0.661	−8.300
	Participation Coefficient Load	−0.063	−0.350	0.223	−0.064	−0.441	0.661	95	0.111	0.002	0.661	−8.300
Model 3	Step 1
	Total Lesion Volume (log mm3)	−0.228	−0.335	−0.120	−0.386	−4.189	<0.001	100	0.141	0.149	<0.001	−13.498
	Step 2
	Total Lesion Volume (log mm3)	−0.112	−0.271	0.046	−0.191	−1.406	0.163	99	0.164	0.031	0.055	−15.308
	Edge Density Load	−0.263	−0.533	0.006	−0.263	−1.941	0.055	99	0.164	0.031	0.055	−15.308

Note: R² represents adjusted R². Four patients had lesions that did not intersect with the participation coefficient map and were thus excluded from Model 2 (n = 98).

As an additional validation method, we evaluated whether the regression model equations generated from the Iowa data could be used to predict cognitive performance scores in the WU cohort, using their lesion volume and lesion load values as inputs. The correlation between the predicted and actual scores, as well as the root mean squared error (RMSE), are reported in SI Appendix, Table S3. The predicted score was significantly correlated with observed score in each regression model. The statistical significance was determined using permutation testing—comparing r values of actual versus randomly generated correlations across 10,000 permutations, with the P value derived from the proportion of randomly generated correlations greater than the observed correlation. The only model more predictive than lesion volume alone was lesion volume + edge density: (lesion volume: r(102) = 0.386, RMSE = 0.938, P < 0.001; edge density + lesion volume: r(102) = 0.401, RMSE = 0.922, P < 0.001). The inclusion of participation coefficient increased the RMSE and reduced the correlation strength of observed and predicted g relative to models using only lesion volume.

Additional Analyses and Investigating Possible Confounds.

The main analyses partially supported the main hypotheses, with edge density lesion load predicting a significant amount of the variance in cognitive outcomes (ΔR² = 0.044). However, participation coefficient lesion load was less consistently associated with cognitive outcomes (ΔR² = 0.034). While participation coefficient lesion load was a significant predictor in a stand-alone regression model using the Iowa data, it did not approach significance in models that included edge density from either cohort. We performed a number of additional analyses on the Iowa cohort to further evaluate these findings, including examining peak edge density and participation coefficient values within each lesion and attempting to control for patients’ premorbid intellect (SI Appendix, Fig. S5). Details of these analyses are reported in the SI Appendix. Similar to the main analyses, both analyses found a significant relationship between edge density and cognitive performance, while participation coefficient did not significantly predict cognitive performance when edge density was included in the model (Table 1).

Furthermore, we investigated whether lesions that occur at the locations in the brain with the highest overall edge density—MMNI (Montreal Neurological Institute) coordinate (−37, −43, 3)—and highest participation coefficient—the midline cerebellum (2, −62, −24), thalamus (9, −4, 8), and precuneus (−6, −62, 56)—were associated with impaired cognition. Damage to the edge density peak region was associated with significantly more cognitive impairment than damage elsewhere (n = 11, M = −0.604 compared to N = 391; M = 0.017, t(400) = 2.221, P = 0.027). Patients with lesions to the peak participation coefficient hubs, however, did not significantly differ from those with lesions to other regions (n = 5, M = −0.692 compared to n = 397, M = −0.009, t(400) = 1.698, P = 0.090).

Alternative parcellation schemes and normative data sets do not change results.

To test whether the weaker findings for participation coefficient may be attributed to the parcellation schemes or the normative dataset used to calculate participation coefficient, we repeated the analyses with alternative participation coefficient maps produced using a different parcellation scheme [Yeo 17 network parcellation of cerebral cortex, basal ganglia, thalamus, and cerebellum (24, 25, 26)] and two alternative normative data sets: 62 subjects from the Nathan Kline Institute-Rockland Sample (NKI) (27) and 100 Human Connectome Project-related subjects (HCP) (28). Total participation coefficient lesion load was then recalculated using the same processing pipeline, and the analyses repeated with the new values. The results remained largely unchanged by the different parcellation scheme or the alternative functional connectivity data sets used to calculate participation coefficient (SI Appendix, Table S4).

We also evaluated whether the higher resolution of the edge density map relative to the participation coefficient map may have driven their differences in predictive strength due to the fact that edge density weights were calculated on a voxel-wise basis, and participation coefficient was derived from parcellated regions containing many voxels. To this end, we recalculated participation coefficient on a voxel-wise basis, using a 4 mm³ voxel size and down-sampled the edge density map to 4 mm³. Lesion load and lesion peak values were recalculated for all patients. These reanalyses did not meaningfully change any of our results—edge density continued to explain significantly more variance in cognitive outcomes above and beyond lesion volume. Participation coefficient was a significant predictor only in those models that did not include edge density (SI Appendix, Table S5).

Other gray matter network measures are not as predictive as edge density.

There is debate about which gray matter metrics provide the best estimate of the importance of a region for maintaining information flow in a functional network. To address the possibility that measures other than participation coefficient may be a more suitable metric of hubness in association with cognition, we tested the relationship of six other potential measures of network centrality derived from functional connectivity MRI: eigenvector centrality, weighted degree, gateway coefficient, subgraph centrality, within module degree z-score, and community density (29–33). Each analysis was preregistered as exploratory follow-up analyses to the main analysis of participation coefficient, with the postregistration addition of community density (6). Just as with edge density and participation coefficient, we calculated a standardized lesion load measure by summing the weight of every voxel within each lesion for each network measure. Each measure in turn was entered into a hierarchical linear regression on the second step, with lesion volume on the first step as a covariate. All six measures added significant predictive value over lesion volume (Table 3). However, when edge density lesion load was entered into the second step of each model, none of these measures remained statistically significant.

Table 3.

Iowa cohort: Hierarchical linear regressions with log-transformed lesion volume, eigenvector centrality load, gateway centrality load, subgraph centrality load, weighted degree, within-module degree, and community density predicting post-lesion g scores

Step and Variable		95% CI for b
	B	Lower bound	Upper bound	β	t	p	df	R2	ΔR2	Sig. ΔF	AIC
Step 1
Total Lesion Volume (log mm3)	−0.119	−0.179	−0.059	−0.193	−3.926	<0.001	400	0.035	0.037	<0.001	−80.006
Step 2
Total Lesion Volume (log mm3)	−0.044	−0.116	0.027	−0.072	−1.219	0.224	399	0.062	0.030	<0.001	−90.525
Eigenvector Centrality Load	−0.193	−0.300	−0.086	−0.210	−3.553	<0.001	399	0.062	0.030	<0.001	−90.525
Step 1
Total Lesion Volume (log mm3)	−0.119	−0.179	−0.059	−0.193	−3.926	<0.001	400	0.035	0.037	<0.001	−80.006
Step 2
Total Lesion Volume (log mm3)	−0.017	−0.102	0.067	−0.028	−0.400	0.689	399	0.058	0.025	0.001	−88.775
Gateway Centrality Load	−0.211	−0.337	−0.085	−0.229	−3.291	0.001	399	0.058	0.025	0.001	−88.775
Step 1
Total Lesion Volume (log mm3)	−0.119	−0.179	−0.059	−0.193	−3.926	<0.001	400	0.035	0.037	<0.001	−80.006
Step 2
Total Lesion Volume (log mm3)	−0.040	−0.112	0.031	−0.066	−1.107	0.269	399	0.064	0.032	<0.001	−91.614
Subgraph Centrality Load	−0.202	−0.309	−0.095	−0.220	−3.707	<0.001	399	0.064	0.032	<0.001	−91.614
Step 1
Total Lesion Volume (log mm3)	−0.119	−0.179	−0.059	−0.193	−3.926	<0.001	400	0.035	0.037	<0.001	−80.006
Step 2
Total Lesion Volume (log mm3)	−0.010	−0.094	0.073	−0.017	−0.241	0.810	399	0.063	0.030	<0.001	−90.925
Weighted Degree Load	−0.228	−0.352	−0.104	−0.248	−3.610	<0.001	399	0.063	0.030	<0.001	−90.925
Step 1
Total Lesion Volume (log mm3)	−0.119	−0.179	−0.059	−0.193	−3.926	<0.001	400	0.035	0.037	<0.001	−80.006
Step 2
Total Lesion Volume (log mm3)	−0.019	−0.102	0.064	−0.030	−0.444	0.657	399	0.059	0.027	0.001	−89.240
Within-Module Degree Load	−0.211	−0.335	−0.088	−0.230	−3.363	0.001	399	0.059	0.027	0.001	−89.240
Step 1
Total Lesion Volume (log mm3)	−0.118	−0.178	−0.058	−0.191	−3.867	<0.001	395	0.034	0.036	<0.001	−80.006
Step 2
Total Lesion Volume (log mm3)	−0.023	−0.108	0.061	−0.037	−0.537	0.592	393	0.074	0.044	<0.001	−86.189
Community Density Load	−0.202	−0.330	−0.073	−0.215	−3.085	0.002	393	0.074	0.044	<0.001	−86.189

Note: R² represents adjusted R². AIC = Akaike Information Criterion.

Discussion

In line with our overall hypothesis, the main finding from these analyses is that damage to critical white matter regions containing the highest density of structural connections is associated with worse cognitive outcomes. This finding was robust to multiple analytic approaches, and the main findings were similar in an independent sample of patients with focal lesions. The fact that the regression model derived from the original cohort was predictive of cognitive outcomes in the second cohort, despite a different testing epoch (subacute versus chronic) and different sample demographic characteristics (primarily White participants in the Iowa cohort, majority Black participants in the WU cohort), strengthens the generalizability of these findings.

Our second major hypothesis was that the extent to which a lesion damages functional network hubs as defined by high participation coefficient would be a significant predictor of cognitive impairment. This was only weakly supported. Regression models that included participation coefficient alone were significant in the Iowa sample but not the WU sample. Relative to edge density, participation coefficient was more weakly associated with cognitive performance when the two were analyzed in conjunction. Our final hypothesis was that combining edge density and participation coefficient in a single regression model would improve upon either variable tested alone. This hypothesis was not supported, as the addition of participation coefficient did not explain variance beyond a model with lesion volume and edge density alone. This unexpected lack of association between cognitive outcomes and participation coefficient in models that included edge density was similar using different normative resting state functional magnetic resonance imaging (fMRI) data sets, with different parcellation schemes, or when calculated on a voxel-wise basis. Furthermore, the results were similar when repeating the same analysis with six other measures of functional network “hubness”—eigenvector centrality, gateway centrality, subgraph centrality, weighted degree, weighted median degree, and community density; each was significantly associated with cognitive impairment only when edge density was not included in the model. The predictive value of these functional network measures increased when estimated premorbid cognitive ability was regressed from cognitive performance, although not enough to reach statistical significance in the overall model containing edge density lesion load.

A possible explanation for these findings is that damage to important white matter tracts is more associated with impairment in distributed brain functions than damage to gray matter functional network hubs. Historically, much of the research on human cognition has focused on the cerebral cortex (34). Yet the importance of white matter for cognition has been highlighted by others. Our findings are in alignment with prior work that has shown that white matter lesions disrupt networks measured with functional connectivity MRI (8, 9, 35), cause widespread changes in brain structure (36–38), and are associated with cognitive impairment (7, 13, 21). Here, we extend these findings, showing that lesions to densely packed white matter hubs in structural networks are more closely associated with cognitive deficits than damage to highly connected gray matter network hubs defined using participation coefficient.

It is important to note that the observed effect size of our primary model was small, explaining about 7.6% of the variance in cognitive scores. However, this effect size is consistent with most other brain-wide correlates of interindividual differences in domain-general cognition and consistent with the observation that effect sizes tend to be smaller with larger samples (39). One of the most robust and replicated biological correlates of cognitive ability to date has been overall brain volume, which explains about 7.6% of the variance in a sample of >29,000 individuals (40). Lesion volume is also a consistent and robust correlate of cognitive outcomes (41–44), and our results show that edge density lesion load outperforms lesion volume in predicting more variance in cognitive ability when entered independently for both samples (Iowa cohort: lesion volume explains 3.5%, edge density 7.9%; WU cohort: lesion volume explains 14.1%, edge density 15.6%). Further, the two are additive such that edge density predicted significant variance after accounting for lesion volume (Iowa cohort: 4.4%; WU cohort: 3.1%). Although these percentages are of questionable clinical utility in isolation, we anticipate future research will begin to combine these predictive variables to begin to make clinically meaningful predictions of cognitive outcome after focal brain lesions.

One major strength of this analysis was the large sample size of patients with focal, acquired brain lesions. This approach of using patients with focal brain lesions allows for a stronger inference of brain regions that are critical to cognition, relative to methods that rely on correlational measures like fMRI. In addition, extensive neuropsychological testing was conducted in each of the participants across multiple cognitive domains, and we were able to use structural equation modeling to derive a robust estimate of cognitive ability that captured variance across individual domains. Finally, we were able to validate the key findings in an independent cohort that showed remarkable similarity in results.

There are also limitations to this study. First, our primary focus was on two network measures, participation coefficient and edge density, with a follow-up analysis that included six additional measures. However, we acknowledge that this is not a comprehensive list. A variety of alternative measures exist, and each would be of interest for future analyses, but they fell outside the scope of the current analysis (13, 35, 45, 46). Relatedly, it is also important to note that edge density and participation coefficient are derived differently and a head-to-head comparison of the two must take this into consideration. For example, they are derived using different imaging modalities (resting state functional connectivity and diffusion tractography), and the spatial resolution of participation coefficient is lower than that of edge density because it is acquired at a lower resolution and has a granularity limited to the parcellated brain regions as opposed to the voxel-wise mapping of edge density. Notably, however, attempting to match the resolution of edge density and participation coefficient on a voxel-wise basis did not alter our main findings. Furthermore, these findings are specifically relevant to our estimate of general cognitive ability that spans multiple domains. Future analyses focused on how network measures predict impairment in specific domains will also be important. Furthermore, although our study employed standard hierarchical linear models to test for a relationship between hub measures and cognitive outcomes, future research could also examine this within a Bayesian framework or use mixed-effect modeling or machine learning techniques to build more sophisticated predictive models of postlesion cognitive impairments.

Finally, we used network measures derived from group-averaged results. It is possible that individualized maps of participation coefficient or edge density within the lesion site could be estimated from the healthy hemisphere or from prelesion scans, in rare instances when this is possible, and this personalization of network metrics may improve the strength of association between these measures and cognitive outcomes.

The fact that our results did not align fully with those of Warren and colleagues (6, 17)—who found that patients with damage to regions high in participation coefficient had worse cognitive outcomes—may be due to a few factors. First, because they limited their participants to those with smaller lesions of cortical regions with high or low participation coefficient, it is possible that participation coefficient was a better predictor of cognitive deficits within this more restricted sample, but these findings don’t generalize as well to a broader sample with lesions that vary more in volume and are more evenly distributed throughout the brain. Additionally, their use of expert ratings as their dependent variable may have been sensitive to information that was not included in our general cognition calculation or vice versa. Twenty-three patients from Warren and colleagues’ (6) sample had adequate neuropsychological testing to calculate a similar g score, and a t test comparing the g scores of their target lesion group against their control lesion group was nonsignificant, (n = 14 versus 8; mean g = −0.21 and 0.37; t (20) = −1.978, P = 0.063). However, their outcome measures assessed executive function, personal adjustment/emotional function, and adaptive function—domains that did not factor into our calculation of general cognition, which was focused solely on cognitive ability. It is possible that participation coefficient is associated with noncognitive domains to a greater extent than it is with our g construct. Moreover, the patients included in that study were selected using a combination of participation coefficient and another measure, community density, and our study evaluated each measure separately. Finally, it is possible that the particular hubs that Warren et al. (6) focused on—the anterior insula, posterior middle frontal gyrus, and anterior medial prefrontal cortex—are more important to brain function or cognition than other regions that also have a high participation coefficient.

Future Directions

These results generate a number of research questions that could be tested in future studies. First, this research demonstrates that predictions derived from computational and theoretical research on the human connectome can help to advance our understanding of how focal brain lesions influence cognition. This work also highlights the utility of the lesion method in evaluating construct validity among various network importance measures as they relate to cognition. Additionally, these data show the emerging possibility of how network neuroscience and connectomics can contribute to clinical advances. Cognitive abilities after brain damage are closely related to quality of life and survival (47–49). Our findings indicate that edge density can be used to predict the likelihood of cognitive impairments, above and beyond the predictive utility of well-established predictors like lesion volume. As such, this information could be incorporated into prognostic tools to more accurately predict cognitive outcomes after an acquired brain lesion, helping to inform treatment and rehabilitation plans for patients with focal brain damage.

Conclusion

In this study, we examined whether brain lesion location relative to measures of “hubness” derived from the functional and structural connectome of healthy participants were associated with general cognitive impairment. We found that, across two distinct patient cohorts, lesions involving densely connected white matter regions were associated with impaired cognitive performance to a greater extent than lesions of highly connected gray matter regions. These findings serve to underscore the importance of white matter in supporting cognitive processing, and how measures of hubness can be leveraged to better understand cognitive outcomes after brain lesions.

Materials and Methods

Participants.

The primary analysis included 402 individuals with focal brain lesions from the Iowa Cognitive Neuroscience Patient Registry. Demographic information is presented in SI Appendix, Table S6. Each individual had detailed neuropsychological testing and structural neuroimaging with manual delineation of the lesion boundaries. Patients with focal brain lesions have been inducted into the Iowa registry for more than three decades. These patients were screened to exclude individuals with a history of learning disabilities, psychiatric disorders, substance abuse, premorbid personality disorders, developmental epilepsy, and other neurological conditions not related to their focal lesion (50). Each participant included in the current analysis also had 1) a focal brain lesion with visible boundaries evident from research-quality structural imaging performed in the chronic epoch (>3 mo since lesion onset), 2) lesion onset at age 18 or older, and 3) test scores for at least 75% of the selected neuropsychological assessments listed in SI Appendix, Table S7. All participants provided informed consent for involvement in research. In accordance with federal and institutional guidelines, all procedures were approved by the University of Iowa Institutional Review Board and are in accordance with the Declaration of Helsinki.

Assessment of cognitive outcomes.

A comprehensive neuropsychological assessment was completed using the standard procedures of the Benton Neuropsychology Laboratory (SI Appendix, Table S7) (51). When a patient had more than one recorded test score, we selected the score most contemporaneous with the date of the patient’s neuroimaging. Patients’ scores for each assessment were adjusted for age using available normative and metanormative data. The age-corrected scores were then standardized onto the same scale using a Z-transformation. Missing assessment scores were imputed using multiple imputation by chained equations using the MICE package available in R (52, 53).

A measure of cognitive function was estimated for each individual using structural equation modeling, as used previously by our group (details provided in SI Appendix). The Z-transformed scores drawn from 17 neuropsychological tests were evaluated in a hierarchical model of cognitive abilities to estimate a latent variable of general cognitive ability (g) that explained variance across specific cognitive domains of visuospatial ability, learning/memory, processing speed, crystallized intelligence, and working memory.

Neuroimaging and lesion analysis.

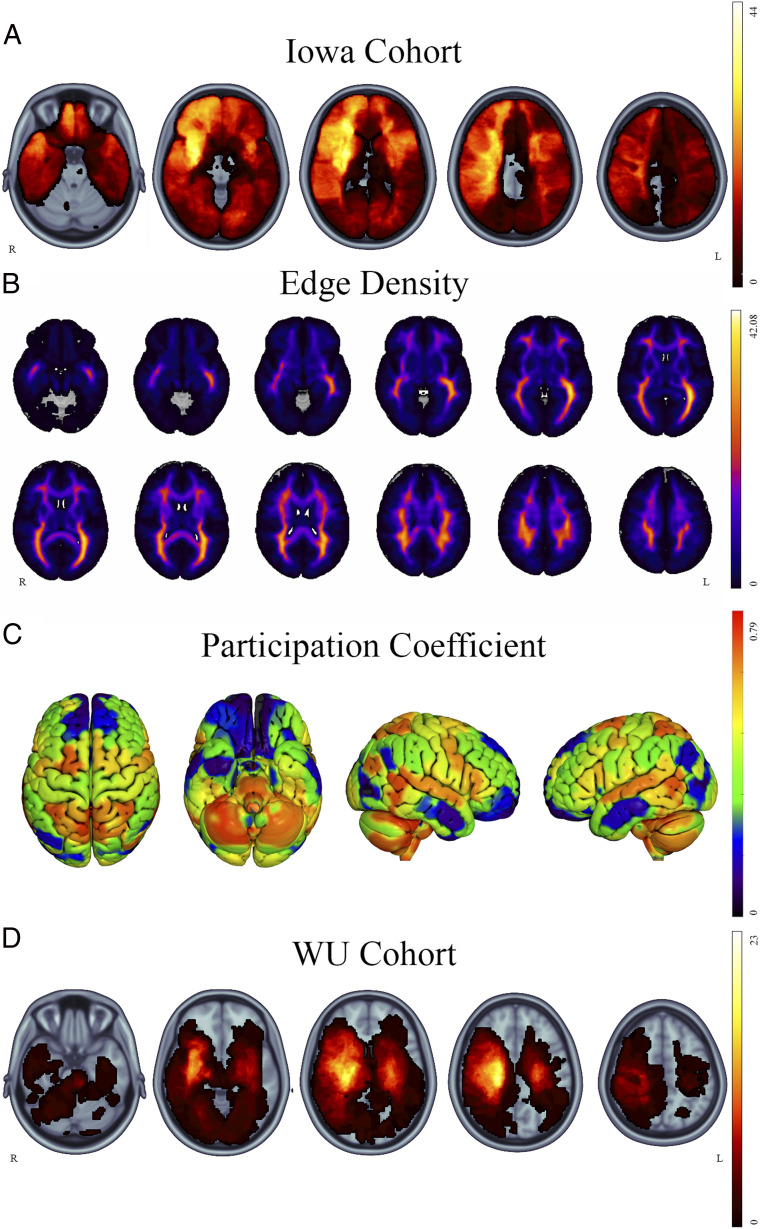
Structural neuroimaging was acquired at least three months after lesion onset, and lesion boundaries were segmented manually for all 402 scans according to standard procedures (54, 55). For scans prior to 2006, the lesion volume was traced directly onto a template brain upon visualizing the three-dimensional anatomy of the lesion on the subject’s scan using Brainvox and MAP-3 techniques (55, 56). With improvements in the accuracy of methods to coregister lesioned brains to a template, lesions since 2006 have been manually traced directly on the native T1-weighted scans using FSL (57) and then transformed to MNI152 space. Because lesions negatively affect the accuracy of the transformation to MNI space, we used enantiomorphic normalization, which extracts the voxel intensities from the nondamaged homolog of the lesion volume and inserts it in place of the manually defined lesion mask. As such, normal voxel intensity values were artificially inserted into the lesion space for the purpose of transforming the brain. For bilateral lesions, the lesion mask was converted to a cost-function mask and used to aid in spatial normalization following the methods of Brett et al. (58). The native MRI was then coregistered to the MNI152 1 mm atlas using nonlinear registration using Advanced Normalization Tools (ANTs) (59), and the spatial transformation warp was applied to the native lesion mask. The anatomical accuracy of each lesion mask was reviewed in both native and MNI space and edited as needed by a neurologist blinded to the cognitive data. The overlap map of all lesions in the Iowa Cohort is shown in Fig. 1A.

Fig. 1.

Lesion overlaps and network measures. Overlap map of all participants’ lesions in (A) the Iowa cohort. The distribution of edge density and participation coefficient are represented in B and C, respectively. Validation analyses were carried out in the WU cohort (D). The images are presented in radiological orientation.

Estimating the level of network disruption caused by the lesion.

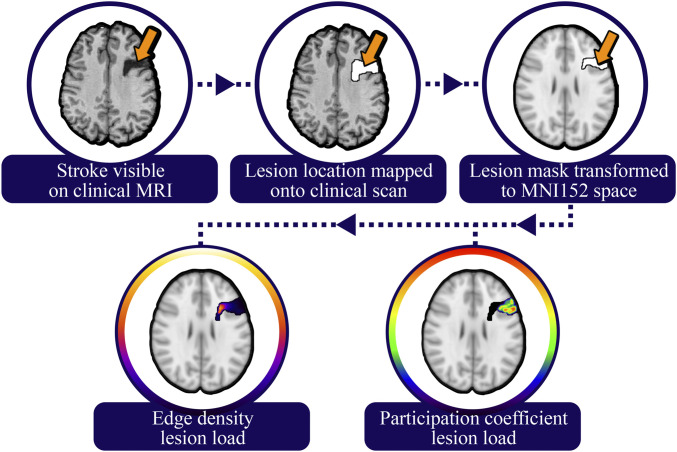
We estimated the degree to which each brain lesion disrupted brain networks using brain-wide maps of edge density and participation coefficient. Edge density is a simple count of the number of structural edges that pass through a given voxel, derived from diffusion tensor imaging (18, 19). For this analysis, we used an average edge density map produced using diffusion-weighted imaging and structural MRIs from 10 individuals, each scanned twice (Fig. 1B). Imaging was performed on a 3T Siemens TIM Trio MR scanner with a 32-channel phased-array radiofrequency head coil. Axial rapid-acquisition gradient-echo (MPRAGE) T1-weighed sequence (echo time [TE] =1.64 ms, repetition time [TR] = 2,530 ms, inversion time [TI] = 1,200 ms, flip angle of 7°) with a 256 mm field of view (FOV), and 160 1.0 mm contiguous partitions at a 256 × 256 matrix was used for the anatomical imaging. Diffusion-weighted images (b = 1,000 s/mm², 30 directions) were collected with a multislice 2D single-shot twice-refocused spin-echo echo-planar sequence, the iPAT (integrated Parallel Acquisition Techniques) technique for parallel imaging with a reduction factor of 2; NEX (number of excitations) = 1; interleaved 2 mm axial sections with no gap; in-plane resolution of 2 × 2 mm with a 128 × 128 matrix; and a FOV of 256 mm. The TE and TR were 80 and 10,000 ms, respectively. The brain tissue was extracted from surrounding tissues, and motion and eddy current correction was performed with FSL’s linear registration tool FLIRT. The fractional anisotropy diffusion image was registered to the T1 using a 12 parameter linear registration with the b = 0 s/mm² as the reference. Parcellation of 68 cortical and 14 subcortical gray matter regions were delineated using FreeSurfer and the Desikan–Killiany atlas applied to the T1 sequence (60). Probabilistic tractography was then performed with probtrackx2 (61), with 1,000 streamlines from each parcellated voxel. Direct connections between each seed node and a target node were selected by excluding streamlines with connections to any of the other 80 nodes. The connectivity of each node was considered independently by performing 82 × 81 = 6,642 tractography runs. Streamlines representing direction connections between two nodes were binarized, and the edge density for each individual subject was calculated as the summation of all binarized streamlines the pass each voxel in the brain. The final edge density map for this analysis was the average of 20 scans across 10 subjects, each transformed to a common MNI152 template. Further details of the calculations can be found in the original publication by Owen et al. (19). For this study, we summed the edge density values within the three-dimensional volume of each lesion to generate an edge density lesion load, and this value was standardized across subjects with a Z-transformation (Fig. 2).

Fig. 2.

Lesion load calculation pipeline. Lesions were traced on the patient’s structural MRI, then transformed to a template brain. The resulting lesions were then overlaid on the edge density and participation coefficient maps, which were derived from healthy subjects, and the sum of all voxels within the lesion volume was calculated.

Participation coefficient was calculated from resting state functional connectivity MRI (rs-fMRI) data from 303 healthy adults (mean age = 21.28 y, SD = 2.64; age range = 19 to 27 y; 128 males) that were acquired as part of the Brain Genomics Superstruct data set (62). Two runs of 6.2 min each were acquired using a gradient-echo echo-planar imaging sequence with the following parameters: TR = 3,000 ms; TE = 30 ms; flip angle = 85°; and 3 mm³ isotropic voxels with 47 axial slices. Structural data were acquired using a multi-echo T1-weighted MPRAGE sequence (TR = 2,200 ms; TE = 1.54 ms [image 1] through 7.01 ms [image 4]; flip angle = 7°; 1.2 mm³ isotropic voxel).

We replicated our main analyses with two other publicly available rs-fMRI data sets. This included a cohort of 62 healthy adults (mean age = 23.96 y, SD = 5.24; age range = 18 to 37 y; 27 males) that was acquired as part of the Nathan Kline Institute (NKI)-Rockland sample (27) and a cohort of 100 healthy adults (mean age = 29.11 y, SD = 3.66; age range = 22 to 36 y; 46 males) acquired as part of the Human Connectome Project (28). For this cohort, 9 min and 35 s of rs-fMRI data were acquired using a multiband gradient-echo echo-planar imaging sequence. For both data sets, subjects were instructed to stay awake and keep their eyes open.

Functional MRI Data Preprocessing.

Image preprocessing was performed with the Configurable Pipeline for the Analysis of Connectomics software (63). First, brain images were segmented into white matter, gray matter, and cerebrospinal fluid (CSF). Rigid body motion correction was then performed to align each volume to a temporally averaged volume with coregistration of anatomical and functional data. ANTs were used to register the images to the MNI152 template using a nonlinear normalization procedure (59). All images were spatially resampled to a 2 mm voxel resolution, and a nuisance regression was performed to further reduce nonneural noise and artifacts. To reduce motion-related artifacts, we used the Friston-24 regressors model during nuisance regression (64). White matter and CSF signals were regressed using the anatomical CompCor approach with five components for each tissue class (65). Linear and quadratic drifts were also removed. Data were bandpass filtered from 0.009 to 0.08 Hz and scaled to a whole-brain mean value of 10,000. Next, mean rs-fMRI time series were extracted from 333 cortical regions of interest (66) and concatenated across runs for subjects with multiple rs-fMRI scans.

We extracted the blood-oxygenation-level–dependent (BOLD) signal using either the preprocessed signal of each individual voxel or the averaged voxel-wise BOLD signal within each parcellated subdivision of the cortex and subcortex. We used these processed data to calculate participation coefficient (PC) of each brain region. PC was calculated as $PC=1-\hspace{0.17em}{\displaystyle \sum }_{s=1}^{N_M}{\left(\frac{K_{is}}{K_i}\right)}^2$, where $K_i$is the sum of connectivity weight of region i, $K_{is}$is the sum of connectivity weight between region i and function network s, and N_M is the total number of networks. As such, a region that is connected equally to all networks will have a value close to 1, while a region that is strongly connected to a single network will have a value closer to 0. PC was plotted in separate adjacency matrices across subjects and across a range of thresholds (D = 0.01 to 0.15) to ensure results were not biased by a specific threshold. The average values across subjects and across thresholds were used to produce the final PC values. PC was also recalculated separately for follow-up analyses using a different network parcellation scheme [Yeo 17 network parcellation of cerebral cortex, basal ganglia, thalamus and cerebellum (24, 25, 26)] and using a voxel-wise approach. The voxel-wise calculations followed the same process as detailed above, but images were instead resampled to a 4 mm³ voxel resolution before rs-MRI time-series were extracted from individual voxels, and functional connectivity was calculated between voxels rather than between regions of interest. As was performed for the edge density maps, PC voxel-wise values were summated within each lesion to create PC lesion load values, then standardized across individual lesions using a Z-transformation.

Independent validation.

The main hypotheses were also tested in an independent validation cohort, which was part of the preregistered analysis. This was done using previously collected data from 102 individuals with focal brain lesions from stroke, recruited from Washington University in St. Louis by Corbetta and colleagues (WU cohort) (21). Demographic details are described in SI Appendix, Table S6. Imaging was acquired and cognition was assessed in these subjects within the first 3 mo following the stroke, as opposed to the Iowa cohort where imaging and assessments were conducted in the chronic epoch, 3 mo or more after the lesion onset. Similar to the Iowa cohort, a large battery of cognitive tests was administered to the WU cohort (SI Appendix, Table S7), and a similar process was used to calculate g with structural equation modeling—after correcting scores for age, imputing missing scores (<1% of data), and standardizing to a common Z-scale. Lesion segmentation was performed on the subject’s MRI scan and transformed to MNI152 space, with anatomical review performed by a neurologist as described previously (21). The distribution of lesions is shown in Fig. 1A. All participants provided informed consent for involvement in research, and all procedures were approved by the Institutional Review Boards in accordance with the Declaration of Helsinki.

Statistical analyses.

Our analyses were preregistered on the Open Science Framework and included three hierarchical linear regressions (models 1 through 3) to test the three main hypotheses. We hypothesized that, above and beyond variance predicted by lesion volume 1) densely connected white matter regions defined by high edge density lesion load would predict greater cognitive impairment, 2) highly connected gray matter regions defined by high participation coefficient lesion load would predict greater cognitive impairment, and 3) a combined model that included both edge density and participation coefficient lesion load would predict more variance in cognitive outcome than either variable alone and that edge density would predict more variance than participation coefficient. In each regression model the g score estimate of cognitive impairment was the outcome variable and lesion volume was entered as the first step. Higher lesion volume has been associated with worse cognitive impairment, and thus we attempted to covary for this variable in step 1 (42–44). Model 1 was the most comprehensive and included both edge density and participation coefficient lesion load in step 2, whereas model 2 and model 3 only included participation coefficient lesion load and edge density lesion load in step 2, respectively. For each analysis any patient with a lesion that did not intersect the edge density and participation coefficient maps were excluded from that respective analysis.

OSF preregistration.

As noted, the main hypotheses were preregistered on OSF. At the time of preregistration, the lesion data and cognitive data existed. These data have accrued over a period of several years and were not collected prospectively for this study specifically. At the time of the preregistration, we had not conducted any analyses or testing of our hypotheses with regard to edge density and participation coefficient maps.

Data Availability

Anonymized .csv data have been deposited in Open Science Framework (https://osf.io/6a7tq/?view_only=3c7a0ee0a3834633bb9d30837118c31c).