Towards a General Model of Temporal Discounting

Abstract

Psychological models of temporal discounting have now successfully displaced classical economic theory due to the simple fact that many common behavior patterns, such as impulsivity, were unexplainable with classic models. However, the now dominant hyperbolic model of discounting is itself becoming increasingly strained. Numerous factors have arisen that alter discount rates with no means to incorporate the different influences into standard hyperbolic models. Furthermore, disparate literatures are emerging that propose theoretical constructs that are seemingly independent of hyperbolic discounting. We argue that although hyperbolic discounting provides an eminently useful quantitative measure of discounting it fails as a descriptive psychological model of the cognitive processes that produce intertemporal preferences. Instead, we propose that recent contributions from cognitive neuroscience indicate a path for developing a general model of time discounting. New data suggest a means by which neuroscience-based theory may both integrate the diverse empirical data on time preferences and merge seemingly disparate theoretical models that impinge on time preferences.

1. Introduction

A tremendous variety of decisions faced by humans and animals require selecting between actions whose outcomes are realized at different times in the future. Moreover, it is quite commonly the case that more desirable outcomes can only be had at the expense of greater time or effort. As such, doing well in many behavioral contexts requires the ability to forego immediate temptations and to delay gratification.

Given the ubiquity and importance of delaying gratification, there has been a longstanding interest is understanding and describing how humans and other animals respond to such decisions. The standard approach to investigating these phenomena is to present intertemporal choices – decisions, for example, between an immediate and a delayed reward – and to describe mathematically how choices are made. Both humans and other animals often prefer the immediate reward even when the delayed reward is larger. Mathematically, this can be summarize by asserting that the subjective value of a reward is discounted by an amount that depends on the delay until receipt (Ainslie, 1975; Rubinstein, 2003; Samuelson, 1937). From a research standpoint, the critical question is the nature of this delay discounting function. Fundamentally, this question can be satisfied by establishing a mathematical formulation of discounting that accounts for the diversity of behaviors involving choices over delays. Identifying such an equation seems likely to benefit from a close coupling between the mathematical function and the psychological and cognitive processes that underlie decision-making.

Advances in understanding the delay discounting equation have been tremendous. In the next section we review these efforts that ultimately culminate in quasi-hyperbolic discounting models that capture behavior with impressive precision (published r² values commonly greater that 0.9). However, hyperbolic models are clearly limited in the range of discounting phenomena that they account for. In particular, the models capture behavior well in isolated contexts but are unequipped to account for how discounting varies across situations. These contextual effects can be profound. We believe this limitation arises from the fact that hyperbolic discounting models are distant from the basic cognitive processes that underlie decision-making. We review some highly cited models of discounting. However, our primary focus is on neuroscience, with the goal of proposing a brain-inspired model of discounting that (a) preserves the overall structure of hyperbolic discounting, but (b) is linked to neuroscience findings in such a way as to easily incorporate many contextual effects on discounting, and (c) links to psychological and process models of discounting. In the end, we argue that neuroscience may provide a framework for a next generation of delay discounting models that account for behavior across a broader spectrum of situations than has been possible with hyperbolic discounting models alone.

1.1. A history of delay discounting in mathematical models

A central assumption in decision science is that when selecting between alternatives, choices are predominantly made for the option with the largest subjective value. In the context of delay discounting, outcomes in their most reduced form are composed of reward (or punishments) of a certain magnitude (amount, A) available after some delay (τ) relative to the present time (t). The subjective value of outcomes is then given by the discounting applied on the basis of delay (τ) multiplied by the reward magnitude (A_t+τ, for reward available at time t+τ):

$$V_t=A_{t+\tau }{D}_{\tau }.$$ Equation 1

D_τ is an individual-specific discount function and can depend on a number of external and internal state variables (which we collectively call state or contextual factors). Of course, the discounting factor D is generally less than one in value (0 ≤ D_τ ≤ 1 for all τ) otherwise preferences would be to delay receipt of reward (but see Loewenstein & Prelec, 1993; Radu, Yi, Bickel, Gross, & McClure, 2011).

Describing preferences in intertemporal choices reduces to understanding the character of D_τ. The classical approach to modeling D_τ begins from a normative stance and asks how we ought to behave. For example, we would all like to be consistent in our preferences. If we would prefer to abstain from drug or alcohol use for the sake of long-term wellness, then this preference should always be true, even when substances are readily available and highly tempting. The only discount function that ensures consistent preferences is the standard in economic theory (Samuelson, 1937), in which the discount factor D_τ is assumed to consist of single exponential function:

$$D_{\tau }={\delta }^{\tau }$$ Equation 2

Smaller values for parameter δ indicate greater impatience, whereas larger values for δ capture behavior of more patient individuals, with the limit case being δ = 1 for which the future is not discounted at all.

Although the exponential discounting model was initially not meant to provide a descriptive account of behavior or the mechanisms underlying decision-making, it was quickly adapted as such (Frederick, Loewenstein, & O’Donoghue, 2002). However, in time it became clear that both humans (Kirby, 1997; Thaler, 1981) and other animals (Ainslie & Herrnstein, 1981; Green, Fisher, Perlow, & Sherman, 1981) discount rewards in a non-exponential manner. First of all, empirical studies indicated that discount rates are not constant over time, but appear to decline. For instance, Thaler (1981) showed that people are indifferent to receiving $15 today and $20 in one month, $50 in one year or $100 in 10 years. This is consistent with annual discount rates of 345% over the one-month period, 120% over the one-year period and only 19% over the ten-year period. Secondly, the exponential discounting model does not predict the all-too-common “dynamic inconsistencies,” or preference reversals that are evident in daily behavior (Ainslie, 1975). In simplified laboratory form, people may prefer $101 in one year and one day over $100 in one year, but a year later they will often prefer $100 today over $101 tomorrow. Holding both such preferences implies preferring one outcome ($101) only to change preference later on when the more proximate outcome ($100) approaches “today.” This pattern of behavior is especially problematic in self-control situations such as addiction, in which preferences to abstain from drug use are difficult to maintain when drugs are immediately at hand.

To accommodate these and other patterns of behavior, a hyperbolic discounting model has emerged as the dominant model of behavior. This function is most commonly written as

$$D_{\tau }=1/(1+k\tau ).$$ Equation 3

The individually determined k is known as the discount factor. Larger values for k reflect greater relative impatience. The finding that temporal discounting is better described by a hyperbola than by an exponential has been replicated in innumerable studies (Frederick et al., 2002; Green & Myerson, 2004).

The hyperbolic function in Equation 3 has one small blemish: it tends to overestimate subjective value at shorter delays and under-predict values at longer delays. To accommodate this, alternative two-parameter extensions models have been suggested (Green & Myerson, 2004). One common version suggested by Green and colleagues takes the form:

$$D_{\tau }=1/{(1+k\tau )}^{\text{s}}.$$ Equation 4

In this and similar (Rachlin, 2006) equations, s reflects individual differences in the scaling of delay or individual differences in time-perception (Green & Myerson, 2004; Rachlin, 2006; Zauberman, Kim, Malkoc, & Bettman, 2009). When s is less than 1.0, subjective value is more sensitive to changes at shorter delays and less sensitive to changes at longer delays.

It is difficult to adequately emphasize the success or importance of the hyperbolic model of discounting. In most experiments it provides a superb fit to individually expressed preferences. Moreover, especially for the version in Equation 3, the hyperbolic model captures behavior in an extremely useful manner. There is only one free parameter, k, that can be easily and appropriately understood as a measure of impulsivity. Greater k implies greater impulsivity and a reduced tolerance for delay.

One problem with the hyperbolic equation is that, for common values of k, the discounted value of outcomes at moderately long delays is very small (e.g. delays of one to several years). A reward of $1 typically gives a subjective value of a few cents when delays are a year or more. This does not produce a problem in predicting relative preference. However, empirically measured subjective values at such delays are typically much large than predicted by the hyperbolic function (Laibson, 1997). Moreover, the critical feature of the hyperbolic model is that it has high discount rates over the near term and much more moderate discount rates over the long term. This is equivalent to saying that there is something special about “now” (or the very near term) that makes near-term reward disproportionately valuable. One well-known model that summarizes these features of behavior is the β-δ model. The discount function in this formulation takes the form

$$D_{\tau }=\{\begin{array}{cc}1& \text{when }\tau =0\\ \beta {\delta }^{\tau }& \text{when }\tau >0\end{array}$$ Equation 5

where the parameter β encapsulates the special value placed on immediate rewards relative to rewards received at any other point in time (Laibson, 1997; McClure, Laibson, Loewenstein, & Cohen, 2004a) and the δ parameter is the discount rate in the standard exponential equation (compare with Equation 2). Note that although the additional parameters of quasi-hyperbolic models can, post hoc, be associated with psychological variables, the main motivation for the development of these models was to find a mathematical solution to better fit the data (particularly the subjective value of rewards at long delays). For instance, while it may be true that there is something special about immediate gratification (Magen, Dweck, & Gross, 2008; Prelec & Loewenstein, 1991), it is unlikely that, psychologically, “now” is discontinuous in the manner expressed by the β-δ model (McClure, Ericson, Laibson, Loewenstein, & Cohen, 2007b).

1.2. Towards a general model

Although the discounting paradigm has been criticized for not capturing several important features of real-world intertemporal decision-making (Rick & Loewenstein, 2008), hyperbolic discounting models have gained much credibility by (1) showing that groups that exhibit real-world temporally myopic behavior, such as drug addicts (Bickel & Marsch, 2001; Kirby & Petry, 1999), pathological gamblers (Dixon, Marley, & Jacobs, 2003) and ADHD patients (Scheres, Tontsch, Thoeny, & Kaczkurkin, 2010), have steeper discount rates than healthy controls; and (2) showing that the task has high stability (Kirby, 2009; see Koffarnus, Jarmolowicz, Mueller, & Bickel, this issue, for a review).

Despite these successes there is currently no consensus on which of the modeling alternatives presented above is superior. Although studies have suggested that two parameter models (Equation 4) may fit the discounting behavior slightly better than single parameter hyperbolic functions (Equation 3), controlling for increased model complexity (McKerchar et al., 2009; Takahashi, Oono, & Radford, 2008). However, these kinds of model comparisons fall short of addressing what we consider to be an important limitation of the hyperbolic model: the vast and systematic variability in discount rates observed within individuals across contexts (and between individuals across experiments), which none of the current models is able to explain (Frederick et al., 2002)¹. To be more explicit: although most discounting behavior can be described very well by hyperbolic or quasi-hyperbolic functions, this has invariably been shown in limited experimental and behavioral contexts. Certainly, discounting (D_τ) is well approximated by a hyperbolic function at any given moment, but the nature of this hyperbolic function is highly variable across contexts, so as to lose the majority of its predictive power across contexts.

Systematic changes in individual discount rates have been shown to result from the framing of the choice, the type of goods under consideration and temporary differences in the state of the individual (e.g. whether they are emotionally aroused or hungry; see Section 3, below). Given this known variation in discount rate across contexts, and across “frames” of the same context, the usefulness of attempting to produce any single parametric specification of discounting has been questioned (Frederick et al., 2002; Monterosso & Luo, 2010). Our motivating belief, which underlies the remainder of this article, is that this view is overly pessimistic. Instead, we propose that incorporating known psychological and neural processes into theories of discounting provides a path towards a more general model of time discounting. Moreover, we hope to show that known properties of the brain systems involved in delay discounting already provide an account for many contextual effects on behavior.

Our optimism is not unique or particularly new. Frederick and Loewenstein urged for efforts to understand the processes that underlie discounting instead of aiming to capture something approximating an individuals’ “fixed discount rate” (Frederick et al., 2002; Frederick & Loewenstein, 2008). Rubinstein (2003) suggested that we need to open “the black box of decision makers instead of modifying functional forms.” We agree, except that we expect that the contents of the black box will be amenable to mathematical description.

Working towards a more general model of discounting, we propose a new formulation that preserves much of the form of the hyperbolic discount function but is grounded in neuroscience. We demonstrate how this model is able to account for a broader body of data than the hyperbolic equation does on it own. Additionally we indicate how such a brain-based mechanistic account can also help to understand how some cognitive models are related to the hyperbolic function.

2. Neurobiology of temporal discounting

Neurobiological frameworks of decision-making divide the required computations into several basic processes or stages (Rangel, Camerer, & Montague, 2008). First is the representational stage in which a representation of the relevant decision variables is constructed. This includes detecting internal states (e.g. hunger level), external states (e.g. reward distribution in environment) and potential actions (e.g. take reward now or wait). Second, in the valuation stage, each action under consideration is assigned a value. The final stage of decision-making consists of comparing the different values and selecting the action that optimizes benefits for the individual. Note that the computations in the three stages of the decision process need not necessarily be performed sequentially but may operate in parallel². Additionally, it is possible that when action selection fails, the representational processes may be engaged again to provide more details. Note also that the current description is agnostic about the phenomenological status of these processes; they may or may not reach conscious awareness. Finally, all decisions are followed by an outcome phase in which the outcome of the selected action is evaluated so as to improve future decisions. In this review we will focus on the phases involved in the decision process, which includes representation, valuation and action selection, given that this has been the target of most, if not all, neuroimaging studies on temporal discounting³.

The neural basis of valuation is complicated by the fact that the brain functions in a parallel manner, with cognition reflecting the combined function of multiple qualitatively different systems. Consonant with this, several theories have proposed that there are multiple types of valuation processes that operate to a certain extent independently (Frank, Cohen, & Sanfey, 2009; McClure, Laibson, Loewenstein, & Cohen, 2004a; Peters & Büchel, 2010). One well-known example is the tripartite division of (1) a Pavlovian system which learn relationships between stimuli and outcomes; (2) a habitual system, which learn relationships between stimuli and responses; and (3) a goal-directed system, which learn relationships between responses and outcomes (Balleine, Daw, & O’Doherty, 2008). Another related set of models builds on a distinction between brain valuation systems that learn direct associations between stimuli or actions and rewards and more sophisticated systems in which actions are planned in a goal-direction manner using prospective reasoning (Botvinick, Niv, & Barto, 2009; Daw, Niv, & Dayan, 2005; Frank & Badre, 2012). Importantly, these systems may yield conflicting valuations of the same actions. For example, when a smoker considers lighting a cigarette, a habitual system may value this action highly, whereas the goal-directed system may value this action negatively in relation to the goal of quitting.

In the past decade numerous imaging studies have examined temporal discounting using a variety of intertemporal choice tasks (see Peters & Buchel, 2011 for a review). Although the discounting tasks used across experiments have differed on various important aspects (e.g. choice set, choice presentation, type of reward), the findings have converged on a common set of subcortical and cortical regions that are involved in temporal discounting. Commonly, these regions are divided into two networks: a valuation network that is involved in estimating the incentive value of the different options, and a control network that is involved in action selection, considering and maintaining future goals, exerting top-down modulation over the valuation network, and inhibiting prepotent responses (Peters & Büchel, 2011). More recently, a role has been proposed for the hippocampus and the declarative memory system. We expect that memory processes will certainly be critical for fully explaining delay discounting, but omit further discussion in this paper because the amount of empirical data is still rather small.

2.1. The valuation network

Important nodes in the valuation network include the ventromedial prefrontal cortex (VMPFC; including the orbitofrontal cortex, OFC), ventral regions of striatum (VS), amygdala, and the posterior cingulate cortex (PCC; Hariri, Brown, & Williamson, 2006; Kable & Glimcher, 2007; Knutson & Ballard, 2009; Luhmann, Chun, Do-Joon, Lee, & Wang, 2009; McClure et al., 2007b; McClure, Laibson, Loewenstein, & Cohen, 2004a; Peters & Büchel, 2009; Pine, Shiner, Seymour, & Dolan, 2010; Sripada, Gonzalez, & Phan, 2011; Weber & Huettel, 2008). These areas are all closely associated with the mesolimbic dopamine system and numerous studies (including human neuroimaging studies) have shown that they play a central role in the representation of incentive value for both primary (e.g. sweet juice) as wells as secondary (e.g. money) rewards (e.g. Chib, Rangel, & Shimojo, 2009). The VS and VMPFC are particularly highly studied in this regard. These brain areas are the primary afferent targets of dopaminergic (DA) neurons of the substantia nigra (SN) and the ventral tegmental area (VTA), and are believed to be the fundamental brain areas associated with reinforcement learning and reward representation (Haber & Knutson, 2009).

An association between impulsivity and dopamine function is clearly demonstrated by patients with dopamine related disorders such as addiction, attention-deficit/hyperactivity disorder (ADHD), and dopamine dysregulation syndrome. Although these disorders differ in many respects, they are all thought to be associated with abnormal levels of dopamine in the fronto-striatal circuitry. With regard to time discounting, these patient groups have consistently been shown to have steeper discount rates than controls (Dagher & Robbins, 2009; O’Sullivan, Evans, & Lees, 2009; Winstanley, Eagle, & Robbins, 2006). More recently, Pine and colleagues provided more direct evidence for the relationship between DA and discounting by showing that individuals given the DA agonist L-Dopa show higher discount rates compared placebo (Pine et al., 2010).

The mechanism by which DA influences time discounting and behavior is fairly well established. Dopamine neurons are known to fire in proportion to prediction errors in the associations between stimuli or actions and linked, subsequent rewards (Schultz, Dayan, & Montague, 1997). These errors are used to modify synaptic connections so that neurons in the striatum come to drive action selection in favor of stimuli or actions with greatest associated reward (Montague, Dayan, & Sejnowski, 1996). This form of learning is clearly evident in rats with lesions in the VS. In a free-operant task, rats with VS lesions learned the association between pressing a certain lever and the delivery of a reward only when reward was concurrent with the action. Learning was impaired when the reward was introduced with a delay, even with a perfect action-outcome contingency (Cardinal, Winstanley, Robbins, & Everitt, 2004). Thus, the magnitude of perceived rewards was normal in these animals, but the lesions produced deficits in the ability to learn associations between actions and subsequent rewards over short time scales.

Several human neuroimaging studies have shown that brain areas associated with the brain’s dopamine system, particularly the VS, VMPFC, and PCC, are more active when presented with a choice set containing an immediate option versus a choice set with two delayed options (Albrecht et al., 2011; Luo, Ainslie, & Giragosian, 2009; McClure et al., 2007b; McClure, Laibson, Loewenstein, & Cohen, 2004a). Initially these results were interpreted in terms of the β–δ model, suggesting that the VS, VMPFC and PCC network was primarily involved in the evaluation of the immediate rewards (β system), whereas the value of more delayed rewards is preferentially represented in lateral control regions such as the DLPFC and PPC (δ system; McClure et al., 2007b; McClure, Laibson, Loewenstein, & Cohen, 2004a). However, DA-related brain reward areas do not respond only to immediate rewards. VS, VMPFC, and PCC activity is greater than zero even for choices involving only rewards delayed by 2 weeks or more (McClure et al., 2004a). Moreover, activity in these same structures has been shown to correlate with the discounted value of future rewards, even in the absence of immediate rewards (Kable & Glimcher, 2007; Kable & Glimcher, 2010; Peters & Büchel, 2009; Sripada et al., 2011). Nonetheless, the VS, VMPFC, and PCC show a clear present bias in signaling future rewards, which would be expected if these responses are learned from direct associative learning. Moreover, greater activity in the VS, VMPFC, and PCC is associated with more impulsive choices (McClure et al., 2004a; Hare, Camerer, & Rangel, 2009).

It is worth pausing briefly at this point to discuss some of the complexities in the neuroscience data, particularly with respect to the VMPFC. Greater activity in the VMPFC is associated with more impulsive decision-making (McClure et al., 2004a; Hare et al., 2009). At the same time, it was recently shown that individuals with VMPFC lesions show increased, rather than decreased discounting (Sellitto, Ciaramelli, & di Pellegrino, 2010). Similarly, lesions to (possibly different) parts of the VMPFC in rats both increase (Mobini et al., 2002; Rudebeck, Walton, Smyth, Bannerman, & Rushworth, 2006) and decrease (Kheramin, Body, Mobini, & Ho, 2002; Mar et al., 2011; Winstanley, 2004) discount rates. Based on these and other findings, several researchers have suggested that the VMPFC integrates information that is encoded elsewhere in the brain into one or more value signals (Monterosso & Luo, 2010; Peters & Büchel, 2010). This interpretation is consistent with findings by Roesch, Taylor, and Schoenbaum (2006) who identified two types of neurons in the VMPFC: one class that fired more strongly to immediate rewards compared with delayed rewards and another class that showed the opposite effect, responding more strongly for rewards that were delivered after a long delay. The absence of such integrative value comparisons due to VMPFC damage may affect delay-discounting by requiring adoption of simple choice strategies that may then lead to more or less impulsive decisions depending on the nature of the task (Mar, Walker, Theobald, Eagle, & Robbins, 2011). A dominant idea in cognitive neuroscience is that the VMPFC lies at the intersection of the valuation and control networks, integrating information from each system to determine behavior. It may be that the VS, or other structures, are more central components of a valuation network that biases behavior towards immediate rewards.

2.2. The control network

Important nodes in the control network include the dorsal anterior cingulate cortex (dACC), dorsal and ventral lateral prefrontal cortex (DLPFC/VLPFC), and the posterior parietal cortex (PPC). These brain areas have long been believed to underlie executive processes generally, including controlling attention, working memory, and maintaining behavioral goals. Such processes seem fundamental to conceiving of and guiding behavior to seek rewards available after any significant delay (McClure et al., 2004a).

A dominant account for how control is triggered posits a critical role for conflict in response selection (Botvinick, Braver, Barch, Carter, & Cohen, 2001). In the context of intertemporal choice, response conflict occurs when individuals have to choose between two options that have similar discounted subjective values (McClure, Botvinick, Yeung, Green, & Cohen, 2007a). The level of response conflict has been associated with a slowing of responses and an increase in activity of the dACC (Carter et al., 1998; Kennerley, Walton, Behrens, Buckley, & Rushworth, 2006). This same pattern of dACC activity and response slowing has been found in temporal discounting tasks (McClure, Botvinick, Yeung, Green, & Cohen, 2007a; Pine et al., 2009). Although the function of the conflict signal in the dACC is still under debate, one recent theory suggest that dACC supports the selection and maintenance of context specific sequences of behavior directed toward long-term goals (Holroyd & Yeung, 2012). As such, in context of intertemporal choice the dACC may bias behavior towards different decision strategies that yield less decision conflict and therefore may result in less or more impulsive behavior depending on the nature of the task. This interpretation is consistent with recent findings showing that individual differences in patterns of dACC activity are related to the effect of context on discount rates (Ersner-Hershfield, Wimmer, & Knutson, 2008; Peters & Büchel, 2010).

In addition to the dACC, activity in the LPFC and PPC has also been shown to increase on the basis of choice difficulty. In intertemporal choice, difficulty is defined based on indifference: LPFC and PPC activity is greatest when the discounted values of immediate and delayed rewards are equal, and declines as the value of one option grows in relation to the other (Hoffman et al., 2008). Moreover, increased LPFC and PPC activity has been shown to be associated with an increase in the likelihood of selecting larger delayed outcomes over smaller sooner outcomes (Peters and Büchel, 2011). The hypothesis that DLPFC and PPC are involved in response selection is supported by imaging studies showing that activation in DLPFC and PPC relative to areas in the valuation network is associated with selection of delayed rewards (McClure et al., 2004a), and that the disruption of left DLPFC through repetitive transcranial magnetic stimulation (rTMS)⁴ leads to increased selection of immediate rewards (Figner et al., 2010).

Several possible mechanisms for how the control network may influence discount rates have been suggested. (1) There could be direct interactions of the LPFC with valuation regions in the VMPFC; (2) the DLPFC could bias attention (possibly via the PPC) to different aspects of the choice; (3) the DLPFC could directly inhibit automatic, prepotent responses that tend to be short-sighted (Figner et al., 2010; Hare et al., 2009; Miller & Cohen, 2001). Future research is needed to determine whether some or all of these processes are involved in temporal discounting, and develop methods to determine when each is engaged.

Overall, in most situations studied to date, the control network is involved in self-regulation process necessary for guiding behavior based on overriding behavioral goals. In the context of intertemporal choice the dominant effect of increased control is to bias behavior in favor of larger later outcomes. Following from this, for our purposes we simply assume that increased recruitment of control processes tends to reduce net discount rates.

2.3. A brain-inspired mathematical model

While knowingly blurring over many details, we can summarize the above discussion by asserting that the brain possesses parallel systems that differ in how they respond to delayed rewards. Parallel system architectures are a common motif in the brain. This is true even at the level of basic sensory processing: there are at least three parallel pathways in vision beginning with outputs from the retina (Hendry & Reid, 2000). For the valuation of future rewards, there seems to exist at least a valuation system and a control system. For modeling, our primary assumption is that the valuation system is myopic relative to the control system.

At this point in time, the precise nature of discounting for each of these systems is unclear. Since behavioral output in intertemporal choice is fully summarized by a discount function, we can only capture the function of different systems by their net effect on discounting. We therefore make another simplification in modeling the valuation and control systems, using a summary discount rate to capture these net effects on behavior. For the valuation system, we assign a discount rate δ₁ that is less than the discount rate, δ₂, for the control system. Again, this assumption is made to stay within what is commonly accepted about the function of these brain systems – that increasing activity in the valuation system tends to increase selection of smaller, sooner outcomes, and increasing activity in the control system tends to increase selection of larger, later outcomes. Put together, we have a discount function given by

$$D_{\tau }=\omega {\delta }_1^{\tau }+(1-\omega ){\delta }_2^{\tau }$$ Equation 6

where ω indicates the relative involvement of each system in a given decision (McClure et al., 2007b). Manipulations that prime the recruitment of one system naturally account for differences in intertemporal preferences (Radu et al., 2011).

Some technical details regarding Equation 6 are worth noting. First, as in Equation 1, both δ₁ and δ₂ must be at least 0 and no greater than 1 in value. Second, δ₁ < δ₂, by assumption. Finally, the weighting parameter ω must be between 0 and 1. The inclusion of a ω and a (1-ω) term is not necessarily intended to indicate an antagonistic relationship between the two systems. Decision-making imposes a normalization of subjective values (choice is for the largest valued option, so only relative values are relevant for modeling preferences). Including ω and (1-ω) builds this normalization into the model and simultaneously imposes that the discount function (D_τ) is 1 for immediate rewards (τ=0).

This dual system model has a number of attractive features. First, the equation closely approximates quasi-hyperbolic discounting. This implies that Equation 6 can fit behavior with the same impressive precision that has been repeatedly shown for hyperbolic discounting models. To demonstrate this feature, we reproduced the best-fitting hyperbolic discount function from Pine et al. (2010) in Figure 2A. The dashed line is the best fitting hyperbolic function, and the solid line is the best fitting double exponential model (Equation 6; δ₁=0.395, δ₂=0.965, ω=0.257). Data were extracted from Pine et al. (2010) and fitting was done to minimize the sum-squared difference between the hyperbolic and dual system model.

Figure 2.

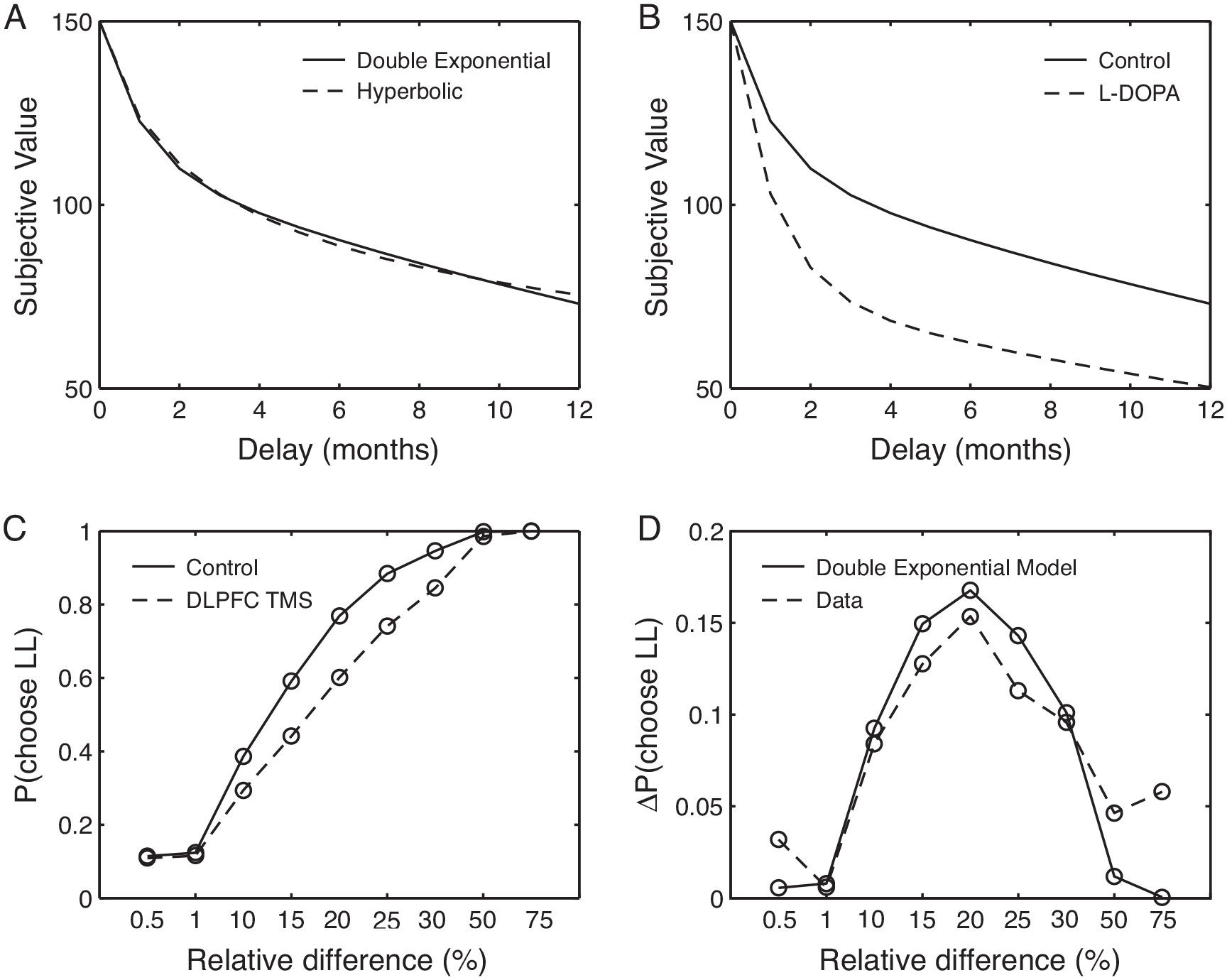
(A) Dual system models of discounting closely approximate quasi-hyperbolic models. (B) Moreover, the models can account for the effects of dopamine agonists on discounting (adapted from Pine et al., 2010). (C) Manipulations to the DLPFC also influence discounting, but only for intermediately values of delayed reward (relative difference is percent difference between larger, later rewards relative to smaller, sooner alternatives; adapted from Figner et al., 2010). (D) Our dual system model fits this behavioral effect by changing the relative weight of the valuation and control systems in decision-making.

Second, the double exponential model easily fits data in which the valuation and control systems have been experimentally manipulated (Figner et al., 2010; Pine et al., 2010). Figure 2B demonstrates the effect of systemic dopamine agonists on discounting, adapted from Pine et al. (2010). Again, we used an optimization algorithm to minimize the difference between the dual model discount function and that published in Pine et al. We held δ₁ and δ₂ fixed at the values determined above. Allowing ω to vary, the best fit of the dual system model was achieved by increasing the relative impact of the valuation system via an increase ω (from 0.257 to 0.488).

Manipulations that inhibit the function of the DLPFC increase the selection of smaller, sooner rewards in a value-dependent manner (Figner et al., 2010). These data are reproduced in Figure 2C, where the x-axis indicates the percent difference in the magnitude of the later reward compared to the smaller, immediate rewards. TMS to the DLPFC increase selection of smaller, sooner (decrease selection of larger, later or LL choices) only for intermediate values of larger, later rewards. This effect is also easily captured by Equation 6 as an increase in the value of ω (that is, a decrease in the value of the weight, 1-ω, on the control system). Increasing ω from 0.257 to 0.425 (and again holding δ₁ and δ₂ fixed), minimizes the difference between the dual system model of discounting and the data from Figner et al., thereby capturing the behavioral impact of inhibiting the control system (Figure 2D).

There is one final comment that should be made before moving on. Figner and colleagues interpreted their findings to indicate that the DLPFC is recruited in a reactive manner, based on the presence of conflict in the choice. On first view, this seems to be a natural interpretation of the data. Certainly, conflict should only be high for intermediate values of delayed rewards and likewise manipulating DLPFC activity only has an effect for these values of reward. However, we are able to produce an excellent fit to their results without assuming any reactivity (Figure 2C, 2D). A second piece of data marshaled by Figner and colleagues to support their claims was the finding that TMS to the DLPFC did not influence valuation of individually presented outcomes, when participants valued them using a visual-analog scale. We find these data difficult to interpret. First, TMS produces famously subtle behavioral effects so that the likelihood of false negatives is high. Second, the use of visual-analog scales is notoriously finicky and context sensitive. Given the duration of the effects of TMS, participants rated items in long blocks that were well separated in time. It is reasonable to suspect that use of the scale differed across blocks making comparison difficult. Finally, TMS to the DLPFC has been shown to influence valuation for other stimuli in which delay is a primary consideration of subjective value (Camus et al., 2009). This argument is not to say that recruitment of the control system does not depend on response conflict in some manner. We simply point out that we are unaware of data that require this addition to the model and so we have stuck with a simpler model in which the valuation systems work entirely in parallel (as a sum). We fully expect that future models will have to include interaction terms, but for now we stick with the simpler model because it maintains significant new explanatory power, as discussed next.

3. Generality of a neuroscience-based model

With a brain-based model in hand, understanding the direction of many known context effects can be reduced to understanding the effects of context on the function of the valuation and control system. We discuss several known context effects below for which the concomitant neural difference can be inferred from extant data. Additionally, we point out that our simplified brain-based model provides a natural bridge between many cognitive models of delay discounting and quantitative measures of discounting behavior.

3.1. Context effects

It is well known that temporary personal state factors can have large influences on discount factors. For example, discounting is elevated when people are hungry, tired, or emotionally aroused so that emotional responses that underlie impulsivity are exaggerated (Giordano et al., 2002; Li, 2008; Van den Bergh, Dewitte, & Warlop, 2008; Wang & Dvorak, 2010; Wilson & Daly, 2004). These effects are fully anticipated by the dual system model. For instance, dopamine is known to regulate food intake by modulating its rewarding effects through the VS (Volkow, Wang, Fowler, & Logan, 2002). It has been shown that hunger results in a decrease in extracellular dopamine levels in the animal’s brain (Vig, Gupta, & Basu, 2011). This decrease is believed to trigger a series of reactions that increase the responsivity of the phasic dopamine system. For a cue that predicts future reward such as the promise of money and a temporal delay, we would expect that the valuation system is enhanced relative to control (non-hungry) conditions. Directionally, this makes the right prediction with respect to the sign of the effect direction – an increase in net discount rate.

The same argument can be made for other similar effects. For instance, emotional priming increases discounting (Li, 2008; Van den Bergh et al., 2008; Wilson & Daly, 2004). Emotionally evocative stimuli, such as sexually arousing stimuli, are known to increase VS activity in a manner that predicts effects on behavior (Knutson, Wimmer, Kuhnen, & Winkielman, 2008). These results are again are easily incorporated by our model as an increase in ω and net discount rates.

Other context effects are known to modulate discount rates by affecting the control system. For instance, discounting is elevated when distracted by a secondary task that competes for attention (Hinson, Jameson, & Whitney, 2003; Shiv & Fedorikhin, 1999). From neuroimaging studies it is known that such secondary tasks put a load on DLPFC and parietal cortex (Szameitat, Schubert, Müller, & Cramon, 2002), suggesting that these manipulations may have the same effect on discounting as the temporary shut down of the control system by TMS (Figner et al., 2010)⁵.

The biggest benefit to a brain based account may be in understanding contextual effects that have so far evaded process-level description. For example, consider the date/delay effect in which discounting is less when delays are expressed in definite terms (November 1^st) as opposed to relative terms (4 weeks; Read, Frederick, Orsel, & Rahman, 2005). Recent neuroimaging data indicate that a similar manipulation increases recruitment of the hippocampus and DLPFC (Peters & Büchel, 2010). On the basis of these brain data, Peters & Büchel speculate on the cognitive (control) processes that may give rise to the effect. We suspect that such neurally-inspired accounts may become the norm in research on delay discounting.

3.2. Multiple selves

It is beyond the scope of the current review to discuss cognitive theories of delay discounting with any semblance of completeness. However, we believe it is a worthy challenge for mathematical models of discounting to incorporate conceptual models of the psychological process that underlie intertemporal choice. We briefly discuss some prominent cognitive models – specifically those that fall under the broad heading of “multiple selves” – that seem to align particularly well with our proposed brain-based model.

There is a long tradition of framing intertemporal choice as the outcome of a conflict between multiple selves (Ainslie, 1992). These multiple-selves models can by subdivided in (1) “synchronic” models that posit that the agents’ behavior is the product of multiple, possibly conflicting, sub-agents, and (2) “asynchronic” models that see the agent as the product of a temporal series of agents, which are sometimes engaged in strategic opposition to each other (Monterosso & Luo, 2010). Most synchronic multiple selves models conceptualize intertemporal choice, or self-control in general, as the struggle between two distinct sub-agents that value the same outcomes differently, one being myopic and the other future-oriented. For instance, Shefrin and Thaler (1981) suggested a “planner-doer” model in which the myopic “doer” cares only about their own immediate gratification, but interacts with the future-oriented “planner” that cares equally about the present and the future. Similarly, Loewenstein (1996) contrasts non-visceral with visceral motivations and Metcalfe and Mischel (1999) propose a cool “know-system” that interacts with a hot “go-system”. In each of these multiple selves models, the different selves compete for control of choice, with a common motif of a future-oriented system trying to tone down or suppress a myopic, present-oriented, system.

In contrast to synchronic multiple self models, diachronic multiple self models do not suppose that there are multiple selves in any moment in time, but rather poses that the self may not have consistent preferences over time (Ainslie, 1992; Schelling, 1984). Importantly, the current self can, to a certain extent, be aware of its future change in preference. As a result, an individual can at one moment prefer to lose weight, while at the same time know that the future self will succumb to the delicious items on the dessert menu.

The strength of both “synchronic” and “asynchronic” models is that they each predict that individuals will develop strategies to deal with future choices that will involve self-control, such as pre-commitment. However, few of these multiple-self models have been expressed formally, and it has therefore not been possible to derive testable implications that go beyond the initial intuitions they were based upon (Frederick et al., 2002). The outstanding questions for these frameworks concern how the multiple selves may interact and why one agent may dominate choice behavior in one situation but not in others. We believe that our brain-based model provides some insights in the mechanisms underlying these dynamics.

The ventral striatum is believed to control behavior by manipulating motivational drive in a relatively automatic, stimulus-specific, and stereotyped manner. Increased reliance on this system is fundamental to addiction and compulsive behaviors that are sub-consciously driven and often beyond deliberative control. Such definite, concrete behaviors supported by the ventral striatum contrasts starkly with processes supported by the DLPFC and PPC. The DLPFC is well recognized to maintain and support high-order, abstract goals. By monitoring performance and guiding attention, the DLPFC is able to direct behavior to satisfy goals in a manner that is largely divorced of the specifics of the required behaviors. This understanding of VS versus DLPFC/PPC activity is strikingly similar to the conceptual distinctions made between “doers” and “planners” and other multiple-selves accounts.

Finally, in line with our suggested conceptual mapping, some human neuroimaging studies have found that manipulations that increase consideration of the future self modulate VMPFC in a manner that predicts changes in discount rates (Ersner-Hershfield et al., 2008; Mitchell, Schirmer, Ames, & Gilbert, 2010). The VMPFC has been associated with self-relevant cognition. Self-relevant cognition includes those processes implicated in self-referential thought and self-reflection. For instance, the cortical mid-line structures, including the medial prefontal cortex, have been shown to be engaged during tasks that involve relatively unstructured self-reflection, as well as tasks which require making specific judgments about one’s own traits compared to judgments of others or semantic judgments (for a review see Lieberman, 2007). It is hard at this point to link self-relevant processes with reward processing, except for the obvious fact that rewards are naturally self-relevant stimuli, but the link at the level of the brain is clear (van den Bos, McClure, Harris, Fiske, & Cohen, 2007). Of course, lumping the VS, VMPFC and other structures into a singular, ill-specified valuation system is almost certain to be inadequate. Once we better understanding the computations supported by these different brain structures, the connection between reward and self-relevant cognitions ought to become clearer.

Importantly this brain based model shows how these cognitive models can be linked to hyperbolic discounting curves in a very natural way. Furthermore, as we have showed above, the model can help clarify why one agent may dominate choice behavior in one situation but not in others.

6. Conclusions

Hyperbolic discounting has been a tremendously influential model in describing intertemporal preferences. In most ways, the model maintains most of its potency. It provides an excellent fit to behavior in (commonly) a single parameter (k) that is directly interpretable as a measure of impulsivity. This aspect of the model seems impossible to displace, and we hope it is never displaced.

However, hyperbolic discounting is severely limited in important ways. Of particular interest for this paper is the fact that the hyperbolic model has no means to account for the various contextual influences that are known to influence a person’s intertemporal preferences. Moreover, the model does not connect with increasingly influential cognitive models of discounting.

We have outlined a first, if simplistic, brain-based model of discounting that overcomes these limitations while preserving much of the functional form of the hyperbolic discount equation. Our model is certainly overly simplistic. We capture discounting as arising from two parallel systems. However, there are likely to be several other valuation processes involved in making intertemporal choices. Furthermore, the decision-making process itself is likely to include interactions between different systems. Nonetheless, the two parallel system model that we propose already shows the promise afforded by a neuroscience-based approach. The model easily accounts for many known contextual effects based on what is independently known about the function of the underlying brain systems. Furthermore, the nature of these systems indicates links to psychological models of discounting.

Figure 1.

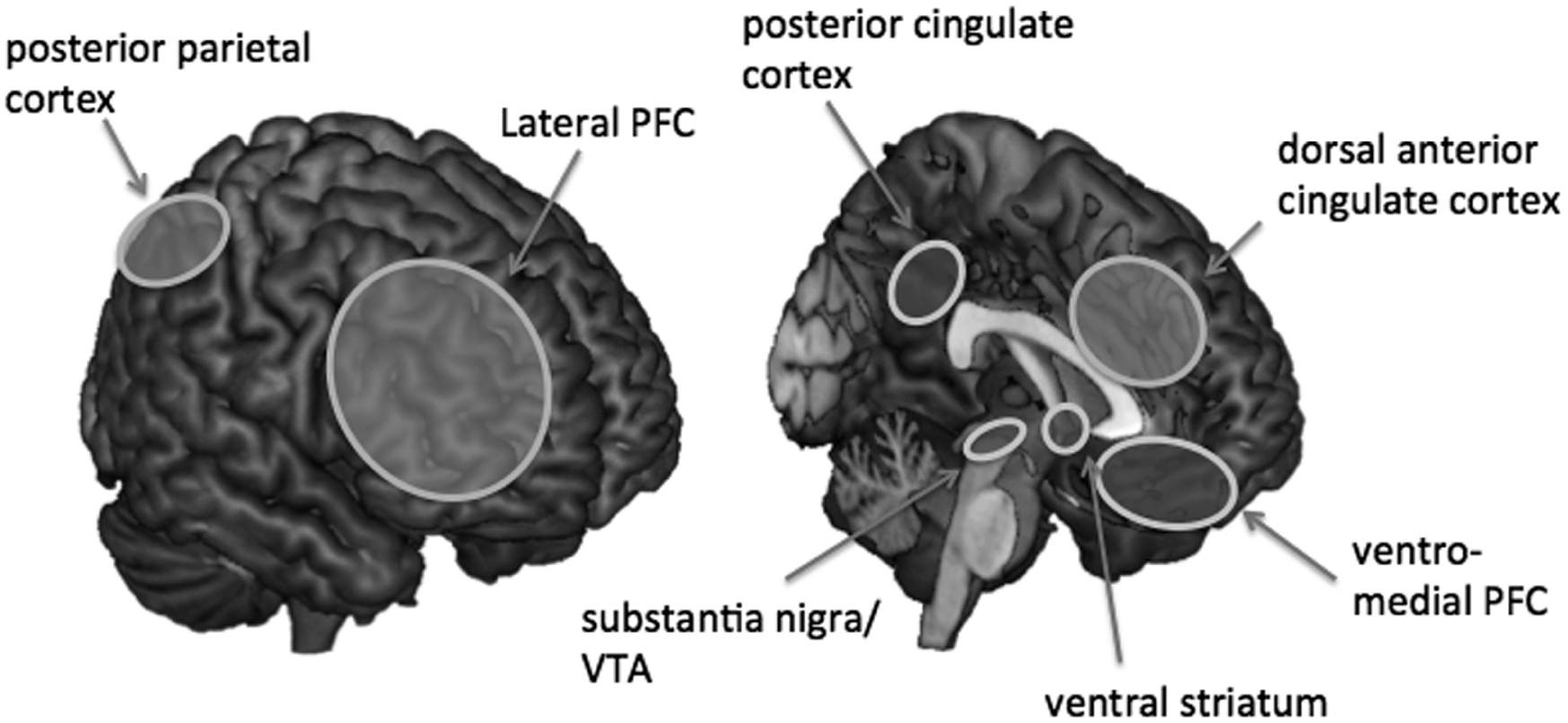
Brain regions associated with intertemporal choice can be separated into (left) a control and (B) a valuation system.