Adaptive non-inferiority margins under observable non-constancy

Abstract

A central assumption in the design and conduct of non-inferiority trials is that the active-control therapy will have the same degree of effectiveness in the planned non-inferiority trial as in the prior placebo-controlled trials used to define the non-inferiority margin. This is referred to as the ‘constancy’ assumption. If the constancy assumption fails, decisions based on the chosen non-inferiority margin may be incorrect, and the study runs the risk of approving an inferior product or failing to approve a beneficial product. The constancy assumption cannot be validated in a trial without a placebo arm, and it is unlikely ever to be met completely. When there are strong, observable predictors of constancy, such as dosing and adherence to the active-control product, we can specify conditions where the constancy assumption will likely fail. We propose a method for using measurable predictors of active-control effectiveness to specify non-inferiority margins targeted to the planned study population characteristics. We describe a pre-specified method, using baseline characteristics or post-baseline predictors in the active-control arm, to adapt the non-inferiority margin at the end of the study if constancy is violated. Adaptive margins can help adjust for constancy violations that will inevitably occur in real clinical trials, while maintaining pre-specified levels of type I error and power.

Introduction

Non-inferiority (NI) trials are designed to determine whether a new therapy is as effective as, or at least not meaningfully worse than, an existing standard-of-care therapy. By using previously approved therapies as controls, NI trials are used to infer whether a new therapy is effective without a placebo arm, given that placebo controls are unethical when effective treatments exist. Without a placebo arm, however, strong assumptions must be made about the effectiveness of the active-control therapy in the NI trial. Specifically, it must be assumed that the active-control therapy will be as effective in the planned NI trial as it was in prior placebo-controlled trials. This is referred to as the ‘constancy’ assumption. If the constancy assumption fails, inferences made from the NI trial could be invalid. For example, if the active-control is not as effective as expected, an NI trial could lead to approval of an ineffective or harmful therapy. Conversely, if the active-control is more effective than expected, an NI trial could fail to achieve approval for an effective therapy.

To mitigate the effects of non-constancy, various authors suggest modifications to the non-inferiority margin when evidence of constancy failure exists. Everson-Stewart [4] proposed a model for assessing constancy based on heterogeneous effectiveness in population subgroups, and recommended tightening the margin, or moving to a superiority design, if constancy is violated. Koopmeiners and Hobbs [9] developed a Bayesian approach to adjusting the NI margin based on inter-trial heterogeneity. Nie and Soon [12, 13] published a regression-model approach for identifying potential non-constancy, and use baseline population characteristics to define a non-inferiority margin appropriate for the enrolled study participants.

In this article we extend Nie and Soon’s idea of a regression-based non-inferiority margin to include trial-level data and post-randomization factors in the active-control arm. We then propose several methods for post-trial adaptation of the margin, and evaluate how each method influences operating characteristics such as Type-I error and power. A trial testing a novel HIV pre-exposure prophylaxis (PrEP) agent compared to an established effective daily oral pill is used for illustration.

Defining the NI Margin

A non-inferiority margin δ is the amount by which an experimental product E can be worse than a standard of care therapy C and still be considered clinically useful. Statistical inference in a non-inferiority trial is based on the null hypotheses that the treatment effect is equal to δ, as opposed to superiority trials where the null hypothesis represents ‘no effect’ (e.g., RR=1.0). In a trial estimating RR_E/C, the relative risk comparing E to C, the statistical hypotheses are

$$\begin{gathered} H_0:R{R}_{E/C}=\delta \\ {H}_1:R{R}_{E/C}<\delta \end{gathered}$$ (1)

and provided that the observed value ${\widehat{RR}}_{E/C}$ is significantly less than δ, the new product is considered ‘non-inferior’ to C. If δ = 1.1, for example, then E is allowed to have a 10% higher risk than C and still be considered clinically important. (Note that although the parameter ‘relative risk’ is used here for illustration, non-inferiority margins can be specified on any scale, and the methods we propose can be applied generally to any treatment-comparison parameter.)

To protect against falsely declaring non-inferiority (inflated type I error) if the active control is not as effective as in prior trials, non-inferiority margins are often chosen to be conservative (i.e., less likely to produce a statistically significant result). Defining the margin typically involves estimating the effect of an active-control therapy based on prior placebo-controlled trials, and choosing a margin that conserves some proportion ρ of the active-control effect [5]. For example, consider a series of two arm trials comparing the active-control therapy C to placebo P, and let ${\widehat{RR}}_{C/P}$ be the estimated relative risk based on a meta analysis. The non-inferiority margin δ can be defined, conservatively, to preserve at least (100 × ρ)% of the active-control benefit (on the log scale) by setting

$$\delta ={\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\right)\right)}^{1-\rho }$$ (2)

where LCL₉₅ is the lower limit of the 95% confidence interval and${\widehat{RR}}_{P/C}={\widehat{RR}}_{C/P}^{-1}$.

The lower confidence limit can be thought of as the ‘assured effect’, i.e. evidence from prior trials rules out a smaller effect, but does not assure anything larger. The assured effect is typically referred to as ‘M1’. Using the LCL₉₅ as the estimated active-control effect acknowledges the uncertainty associated with the meta-analytic estimate and provides a degree of protection against non-constancy. Values for ρ can range between 0 and 1, where ρ = 0 preserves none of the benefit of C but assures that the experimental therapy E is at least minimally better than placebo. Choosing ρ = 1 gives a margin of 1.0 which is equivalent to requiring superiority of E over C. The value for ρ is often taken to be 0.50, yielding a margin that preserves at least 50% of the benefit provided by C (on the log relative risk scale). A margin that preserves at least some of the active-control benefit is commonly referred to as the ‘M2’ margin. If the results of a non-inferiority trial comparing E to C satisfy

$$UC{L}_{95}\left({\widehat{RR}}_{E/C}\right)<\delta$$ (3)

where UCL₉₅ is the upper limit of the 95% confidence interval, then the trial results are consistent with non-inferiority. Appropriate values for ρ will depend on context and should be justified for any individual trial.

Population-specific NI margins

Non-constancy can occur for many reasons, including differences in participant characteristics, differences in dosing or adherence, changes in background supportive care, or actual declines in biological benefit of the active control (e.g., due to antibiotic resistance.) The meta-analysis-based margin δ in (2) effectively assumes that the active-control effect in the planned trial will correspond to the average effect observed in prior trials, and ignores predictive factors that might provide a more precise specification of the margin. While some sources of non-constancy are unobservable, when observable participant characteristics are known to be modifiers of effectiveness for the active-control therapy, they can be used to specify margins appropriate to the (assumed) characteristics of the planned study population.

Effect modifiers are often identified using post hoc subgroup analyses within individual trials. Although informative, subgroup analyses are generally underpowered and exploratory in nature. In addition, analyses of effectiveness based on post-randomization factors such as drug adherence do not benefit from the protection of randomization. Effect modifiers are more reliably identified by using meta-analysis regression to aggregate results across multiple studies. Meta-analysis regression can improve power and precision by virtue of the combined, increased sample size [17]. While it is well recognized that cross-trial comparisons may be influenced by ecological bias [7], by comparing post-randomization effects across studies, rather than within studies, the meta-analysis approach can reduce the potential for confounding. By treating factors such as drug adherence as trial-level variables in a meta-regression model, post-randomization effect modifiers can be identified and estimated with reduced risk of the confounding usually associated with analysis of post-randomization subgroups.

To estimate the size and importance of potential effect modifiers, we use mixed-effects meta analysis extended to a regression model that includes study-level, fixed-effects covariates [15]. Predictive factors are divided into two categories: (1) fixed population attributes such as race and gender that are measured at baseline, and (2) dynamic features, such as dosing and drug adherence, that could change during the course of a trial and cannot be assessed until the trial is underway. The following model is used for RR_j, the relative risk comparing P to C for study j:

$$\log \left(R{R}_j\right)={\beta }_0+{\beta }_1{x}_j+{\beta }_2{z}_j+b_j+{\epsilon }_j$$ (4)

where x_j is a set of population attributes, z_j is a set of dynamic features, b_j are the study-specific random effects with b_j ∼ N(0,τ²), τ² represents between-study heterogeneity not explained by x_j and z_j, and ε_j are error terms with ${\epsilon }_j\sim N\left(0,{\sigma }_j^2\right)$ where ${\sigma }_j^2$ represent within-trial sampling variability. Fixed-effect parameter estimates ${\widehat{\beta }}_0$, ${\widehat{\beta }}_1$, and ${\widehat{\beta }}_2$ are used to estimate effectiveness in a new study with anticipated attributes x^A and features z^A, by setting

$${\widehat{RR}}_{P/C}\left(x^A,z^A\right)=\exp \left({\widehat{\beta }}_0+{\widehat{\beta }}_1{x}^A+{\widehat{\beta }}_2{z}^A\right).$$ (5)

A population-specific NI margin is computed based on the lower 95% confidence limit of the regression model estimate (population-specific M1), preserving at least the fraction ρ of the active control benefit, by setting

$$\delta \left(x^A,z^A,\rho \right)={\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)\right)}^{1-\rho },$$ (6)

which represents a population specific value for M2. Recall that because the NI trial is a comparison of experimental versus active control, somewhat counterintuitively the active-control effect is formulated as the placebo-versus-control relative risk (i.e., a measure of how much worse the placebo performs as compared to the active control therapy.) The NI margin defines how much worse the experimental therapy can be as compared to the active-control therapy.

Case study: HIV pre-exposure prophylaxis (PrEP)

HIV/AIDS remains a global pandemic with no vaccine or cure; prevention strategies are therefore desperately needed. Daily oral TDF/FTC, used as pre-exposure prophylaxis (PrEP), has been shown in multiple randomized, placebo-controlled trials to reduce the risk of HIV infection [1, 2, 6, 10, 11, 16, 18]; however the estimated benefit varies widely across different studies. Because many people are unable to take daily oral PrEP consistently, there is strong impetus for developing long-acting products. Given the established effectiveness of TDF/FTC, it is unethical to use placebo controls, and hence active-control trials are now the most appropriate design for testing new prevention therapies.

Based on the meta-regression analysis including all prior PrEP trials, two factors are predictive of oral PrEP effectiveness: adherence and gender. Fitting model (5) to the PrEP-trial data gives the following:

$${\widehat{RR}}_{P/C}(sex\text{,}adherence)=\exp (0.7520-0.1058\times sex-2.276\times adherence)$$ (7)

where sex is an indicator variable of sex at birth with 1 = male and 0 = female, and adherence is a measure between zero and one of the proportion of active-arm participants with detectable plasma levels of PrEP.

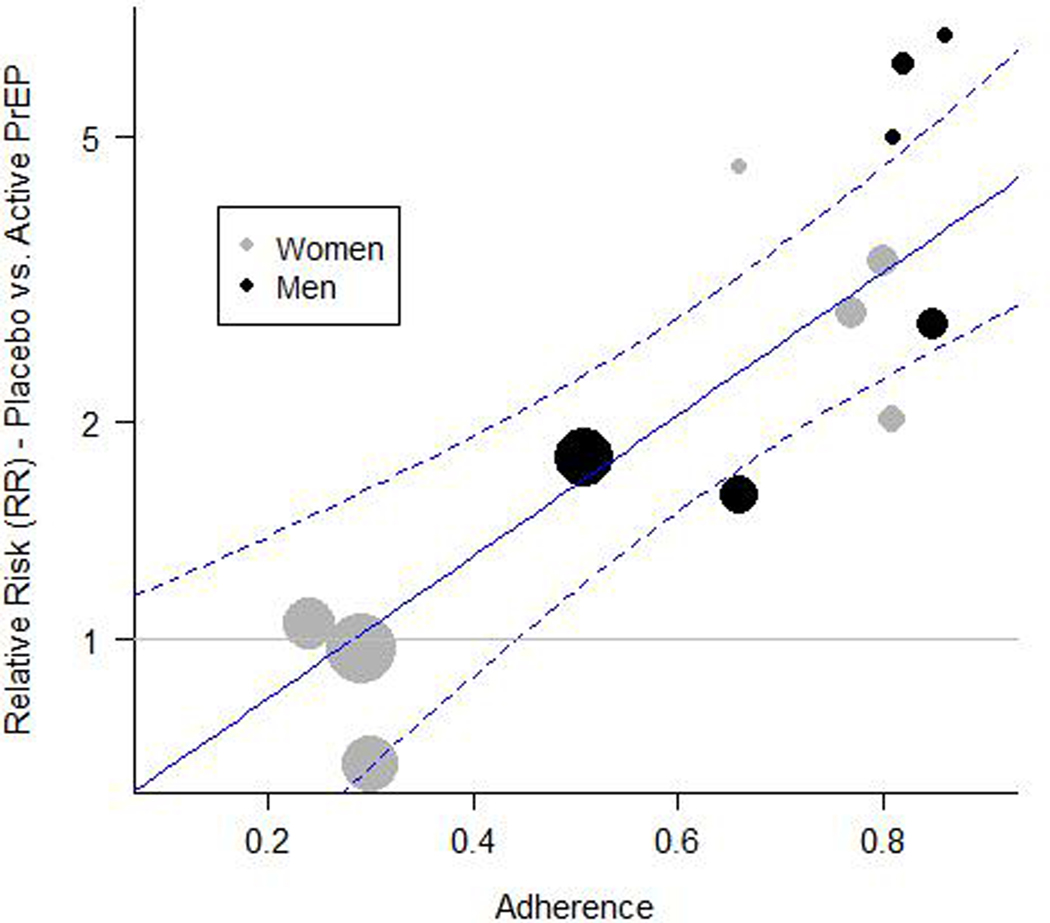
Figure 1 shows a scatterplot of trial-level results as a function of adherence, as well as the fitted regression line for men, along with confidence bounds. For a planned study in men, the lower confidence limit represents M1 and would be used as the basis for computing an NI margin, depending on expected adherence. The regression line in Figure 1 drops below 1.0 at 0.3, suggesting a threshold effect whereby PrEP provides little observable protective benefit in a population where adherence is below 30%. A similar fitted line and confidence bound could be generated for a study in women, or in a study with a mix of men and women.

Figure 1.

PrEP effectiveness plotted against trial-level adherence, as measured by estimated proportion of active-arm participants with detectable plasma TDF, for all randomized trials of oral PrEP versus placebo where an objective adherence measure was available. Circle sizes are proportional to the number of incident HIV infections during the trial. The fitted regression line and 95% confidence bounds (dashed lines) are shown for men.

A range of margins – derived from the fitted model – are shown in Table 1 based on different levels of assumed adherence in the study population. Low adherence requires lower (stricter) margins and higher adherence allows larger margins. When projected adherence is lower than approximately 40%, the value M1 is below 1.0, indicating that there is not strong evidence for effectiveness, and that a superiority trial is recommended. (A non-inferiority trial with a margin of 1.0 is equivalent to a superiority trial.) This suggests that the meta-regression model may be used not only to set population-specific NI margins, but also to determine under what circumstances an NI trial is appropriate.

Table 1.

Predicted oral-PrEP effectiveness in men (based on the lower confidence limits in Figure 1) for different assumed adherence, and suggested NI margins that preserve at least 50% of the benefit (ρ = 0.5).

Adherence	Effectiveness (M1)	NI Margin (M2)
0.40	<1.0	1.0
0.50	1.17	1.08
0.60	1.50	1.23
0.70	1.89	1.37
0.80	2.30	1.52

Type I error and power under non-constancy

Even if a population-specific approach is used to select the margin, the observed values of the effect modifiers in the study population may not match the values used in the planning phase. If the observed values are substantially different from the planning phase, the predicted efficacy of the active control will be different than planned, and the constancy assumption will not hold. With the pre-planned NI margin the trial runs the risk of declaring support for a product that doesn’t work (type I error), or failing to support a product that does work (type II error).

To illustrate, consider a trial that is designed under the assumed values x = x^A and z = z^A, with corresponding NI margin δ(x^A, z^A, ρ) as in (6). The statistical hypotheses are

$$\begin{gathered} H_0:R{R}_{E/C}=\delta \left(x^A,z^A,\rho \right) \\ {H}_1:R{R}_{E/C}<\delta \left(x^A,z^A,\rho \right) \end{gathered}$$ (8)

where δ() will typically be larger than 1.0. Re-expressing these hypotheses in terms of incidence rates helps illustrate the impact of non-constancy. The relative effectiveness RR_E/C can be written as ${\lambda }_E/{\lambda }_C^A$, where λ_E is the incidence rate in E, and ${\lambda }_C^A$ is the incidence rate in C when x = x^A and z = z^A. The null hypothesis in (8) can then be written as

$$H_0:{\lambda }_E={\lambda }_E^0={\lambda }_C^A\delta \left(x^A,z^A,\rho \right),$$ (9)

where ${\lambda }_E^0$ is defined to be the highest allowable incidence under E that would be considered clinically acceptable.

The alternative hypothesis used to compute sample size and power is often based on the desire to reject H₀ if E is equivalent to C, i.e., if H₁ : RR_E/C = 1.0. If there is reason to expect that E may outperform C then the study may be powered to establish a somewhat stronger effect, say H₁ : RR_E/C = ξ, where ξ ∈ [0, 1]. The alternative hypothesis can then be expressed in terms of incidence rates as

$$H_1:{\lambda }_E={\lambda }_E^1={\lambda }_C^A\xi .$$ (10)

Note that since an NI trial is designed to rule out the margin, not equality, the trial is powered to detect an effect size (ratio of the alternative to the null) equal to ξ/δ(x^A, z^A, ρ).

If the true study population characteristics are x^T ≠ x^A and z^T ≠ z^A such that RR_C/P(x^T, z^T) ≠ RR_C/P(x^A, z^A) then the planned margin δ(x^A, z^A, ρ) will be incorrect and the study will not retain desired levels of type I error and power. By expressing RR_E/C in terms of incidence rates, and using the fact that ${\lambda }_C^T={\lambda }_{P}R{R}_{C/P}\left(x^T,z^T\right)$, where λ_P is incidence in a hypothetical placebo arm, type I error and power can be expressed as a function of RR_C/P(x^T, z^T):

$$\begin{array}{c}P[\text{Type}\text{I}\text{error}]=P\left[UC{L}_{95}\left(\frac{{\lambda }_E}{{\lambda }_{P}R{R}_{C/P}\left(x^T,z^T\right)}\right)<\delta \left(x^A,z^A,\rho \right)\mid {\lambda }_E={\lambda }_E^0\right]\\ \text{Power}=P\left[UC{L}_{95}\left(\frac{{\lambda }_E}{{\lambda }_{P}R{R}_{C/P}\left(x^T,z^T\right)}\right)<\delta \left(x^A,z^A,\rho \right)\mid {\lambda }_E={\lambda }_E^1\right].\end{array}$$ (11)

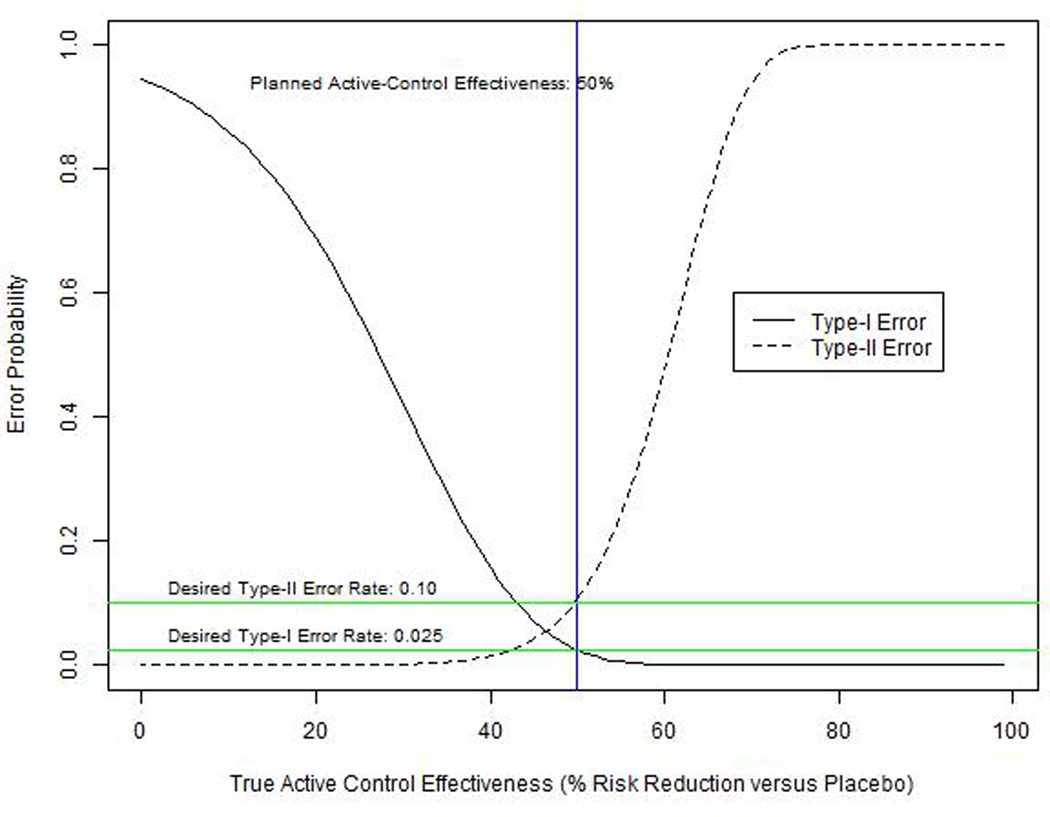
Error rates for an example trial are plotted in Figure 2 as a function of the (hypothetical) percent risk reduction provided by C (versus placebo) in the true study population, or (1 − RR_C/P(x^T, z^T)) × 100. If C is more effective than planned, E will not look as good in comparison, and the type II error rate will be high (i.e., the trial will have low power.) If C is less effective than planned, E will appear better in comparison to C, and the chances of a false-positive result will increase. Even fairly small deviations from constancy can have a substantial impact on the probability of making a false conclusion. For instance if C is 60% effective instead of the planned 50%, the type II error probability increases from 10% to 48% (i.e., power drops from 90% to 52%). Likewise, if C is only 40% effective, the type I error probability increases from 2.5% to 16%. To reduce these error probabilities we propose an adaptive NI margin approach based on the pre-specified meta-regression model used to select the study NI margin, and observed values of the effect modifiers in the NI study population.

Figure 2.

Type I and type II error probabilities according to the true level of effectiveness (% risk reduction vs. placebo) in the active-control arm. Rates are for a hypothetical NI trial with NI-margin=1.3, effect size versus active-control=0.7, sample size = 110 events, and planned active-control effectiveness=50%.

Adaptive NI Margins

Although an NI margin must be pre-specified in order to plan an NI trial, the margin used for planning may not always be the appropriate gauge to judge whether the experimental product is truly effective. As demonstrated in the previous section, using the NI margin based on planned characteristics, rather than observed, can be detrimental to the operating characteristics of a trial, and fail to ensure that the NI trial conclusions are valid.

To make certain that an NI trial will only support a therapy that meets a pre-specified level of effectiveness, we propose adapting the planned margin using equation (5) together with observed study-population characteristics. The adaptive margin is based on the idea of simply inserting the observed values x^T and z^T into equation (6) to compute the adapted margin

$${\delta }^a={\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)\right)}^{1-\rho }.$$ (12)

We define a more general notation that encompasses multiple approaches to adapting the margin. Let Δ be the relative risk defining the amount of benefit an experimental therapy is required to provide over a (hypothetical, unobserved) placebo. The adaptive M2 margin, expressed in terms of Δ, is

$${\delta }^a=\text{Δ}\times LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right),$$ (13)

and (1 − Δ) × 100 represents the required percent risk reduction over placebo. Δ can also be thought of as the ratio M2/M1. The general approach will use meta-regression to compute M1 for the observed study population, and then use a pre-specified method to compute Δ and generate the adapted M2 margin based on equation (13).

There are two general strategies for specifying Δ: the first pre-specifies the desired percent risk reduction relative to placebo (fixed Δ); and the second pre-specifies the proportion of (observed) active-control benefit that must be preserved by the experimental therapy (fixed ρ).

For method one, a fixed level of benefit Δ is chosen, which could be either (a) the amount of benefit over placebo required by the planned margin, or (b) an investigator-defined minimal clinically important difference (MCID). For example, if the planned margin is the meta-regression-based margin δ(x^A, z^A, ρ) described in (6), the planned value for Δ is

$$\begin{array}{c}{\text{Δ}}_{\text{Plan}}=\delta \left(x^A,z^A,\rho \right)\times LC{L}_{95}{\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)}^{-1}\\ ={\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)\right)}^{1-\rho }\times LC{L}_{95}{\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)}^{-1}\\ ={\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)\right)}^{-\rho },\end{array}$$ (14)

which uses the planned values x^A and z^A in relation (13). If x^T = x^A and z^T = z^A then δ^a = δ(x^A, z^A, ρ). This strategy may be used by investigators who wish to keep constant the required benefit over placebo, regardless of enrolled-participant characteristics.

An NI trial might also be planned using a fixed MCID, based on investigator consensus and/or expert opinion. For example, it might be determined that regardless of study population characteristics, it is essential that the experimental product provide a reduction in risk of at least 10% (RR_E/P = 0.90) over what would be expected with placebo. In this case Δ would be defined as

$${\text{Δ}}_{MCID}=R{R}_{MCID}=0.90,$$ (15)

where RR_MCID is the risk reduction corresponding to the pre-specified MCID. Since relative risks increase in value as benefit decreases, RR_MCID is actually the maximum allowable relative risk.

The second strategy defines Δ based on a fixed proportion ρ of the benefit provided by the active-control therapy in the observed study population. Substituing x^T and z^T into equation (14), yields

$${\text{Δ}}_{\text{Estimated}}={\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)\right)}^{-\rho },$$ (16)

which can be used in (13) to generate the adjusted margin in (12).

This second approach may be desirable when the active-control therapy has different levels of effectiveness in different populations. For example, assume that the active-control treatment has been shown to be more effective in adults than in adolescents, and that, despite plans to recruit adults, the NI study population is mostly adolescents. Because the study population has more adolescents than planned, the effectiveness of the active-control therapy is assumed to be lower than planned. Nevertheless, investigators may still be content with an experimental therapy that preserves at least 50%, say, of the benefit achievable by the active-control among adolescents. By using the planned, fixed value for ρ (0.5) and the estimated value for M1, Δ can be adapted using equation (16). The value of M1 (i.e.,$LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)$) will be lower than originally planned, giving a higher than planned value of Δ_Estimated, and although this corresponds to a smaller required percent risk reduction than planned (i.e., a smaller value of (1 − Δ) × 100), it still ensures that the new therapy preserves 50% of active-control benefit in the enrolled study population.

Placing limits on change in NI margins

Both of the approaches defined above have undesirable properties when there are extreme changes in effect modifier characteristics from the planned trial. In the second approach using Delta_Estimated, if active-control effectiveness in the NI trial is much lower than expected, the adapted NI margin fails to ensure that the experimental therapy provides any benefit over placebo. In both approaches, if active-control effectiveness in much higher than expected, the adapted margin can be arbitrarily high. Both problems can be controlled by placing limits on the margin.

If low active-control effectiveness is a concern, Δ may be defined by selecting the more stringent of the two choices Δ_MCID or Δ_Estimated, which is accomplished by choosing the minimum:

$$\begin{gathered} {\text{Δ}}_{Min}=\min \left({\text{Δ}}_{MCID},{\text{Δ}}_{Estimated}\right) \\ =\min \left(R{R}_{MCID},{\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)\right)}^{-\rho }\right) \end{gathered}$$ (17)

This will typically mean using Δ_Estimated when the active-control effect is as planned or larger, and using Δ_MCID when the effect of the active-control effect is estimated to be relatively small. Using this method prevents the level of required effectiveness from diminishing too far in a study population where the active-control therapy is thought to be not working well, for example due to low adherence.

Investigators or regulators may also wish to impose an upper limit on the NI margin, but allow adaptation of the margin below the maximum level. In this case Δ may be defined by considering Δ_Estimated in combination with a maximum value for the NI margin, δ^Max. The value of Δ corresponding to the desired margin is

$${\text{Δ}}_{Max}={\delta }^{Max}/(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right),$$ (18)

which may then be combined with Δ_Estimated to place a cap on δ by setting

$${\text{Δ}}_{\text{Cap}}=\min \left({\text{Δ}}_{\text{Max}},{\text{Δ}}_{\text{Estimated}}\right).$$ (19)

This strategy will typically mean using Δ_Estimated when the active-control effect is as planned or smaller, and using Δ_Max when the effect of the active control is estimated to be relatively large. Setting a maximum prevents the margin from increasing to a point where the experimental therapy is allowed to be substantially worse than the active control. Although this technique will effectively require the proportion of preserved active-control benefit ρ to increase as active-control effectiveness increases, investigators and/or regulators may feel more comfortable placing a cap on the absolute magnitude of the NI margin.

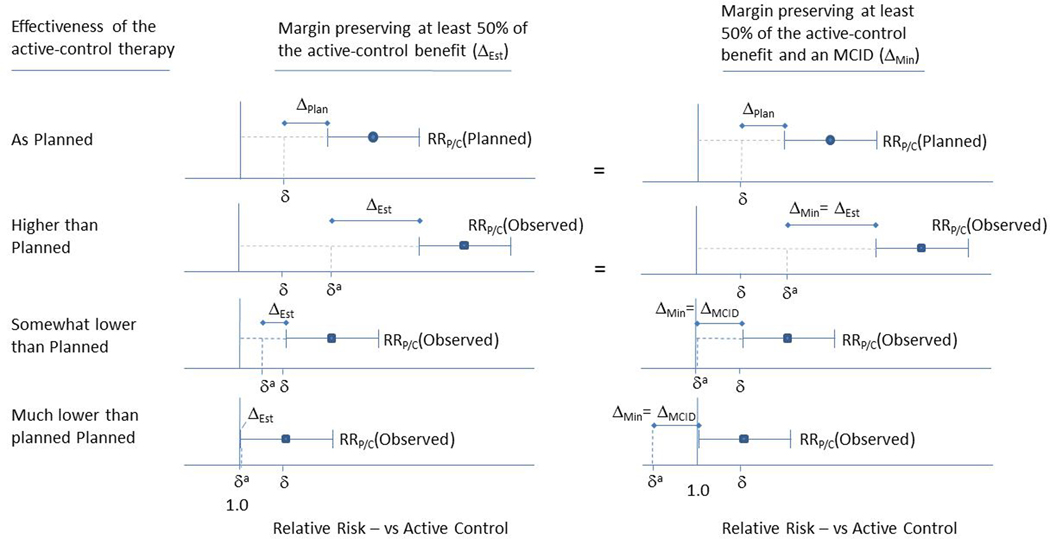
Figure 3 illustrates how varying levels of effectiveness in the active-control arm leads to different adaptive NI margins using Δ_Estimated and Δ_Min. If effectiveness is higher than planned, δ^a will shift to the right relative to δ, thereby relaxing the NI margin. Since Δ_Estimated is smaller than Δ_MCID in this case, Δ_Min = Δ_Estimated and the adapted margin is same for both approaches. If active-control effectiveness is somewhat lower than planned the adapted margin preserving proportional benefit will become correspondingly more stringent. If we require the margin to preserve an MCID, this reduces δ^a to 1.0, effectively requiring the experimental intervention to be superior to the active control.

Figure 3.

Adaptive non-inferiority margins preserving proportional (50%) benefit (Δ_Est, Column 1), and preserving at least the MCID (Δ_Min = Min(Δ_Est, Δ_MCID), Column 2), depending on the planned and observed effectiveness of the active control therapy. Point estimates for active control effectiveness (quantified by the relative risk comparing placebo to active control, RR_P/C), and 95% confidence interval bars are derived from a meta-regression model. When the observed level of active-control effectiveness is as planned or higher, Δ is the same for both methods. (We assume that Δ_Plan <= Δ_MCID, i.e., that a trial would not be planned with a Δ that was less substantial than the MCID.) When the observed level of active-control effectiveness is less than planned, the adapted margin δ_a preserving the MCID is less than (more restrictive) the adapted margin δ_a preserving proportional benefit.

The bottom row in Figure 3 shows a scenario where active-control effectiveness is so low that there is no assured effect (i.e.,$LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)=1.0$) and Δ_Estimated = 1.0. This implies a requirement of superiority when using Δ_Estimated, but a requirement of ‘super superiority’ (δ^a < 1.0) when using Δ_Min = Δ_MCID. Super superiority simply means that the experimental product must not only be superior to the active control, but that the $UC{L}_{95}\left({\widehat{RR}}_{E/C}\right)$ must rule out small benefits. For example, if δ^a = 0.90, $UC{L}_{95}\left({\widehat{RR}}_{E/C}\right)$ must be less than 0.90, thus assuring the experimental intervention reduces risk by an additional 10% compared to the active control. Note that whenever Δ is fixed in advance (e.g., when using Δ_Plan or Δ_MCID), super superiority may be required.

Adapting the Statistical Hypotheses

Once the adapted margin δ^a has been specified, this margin becomes the null hypothesis for statistical inference. Although the nominal value of the null hypothesis will have changed from the planning stage, the adapted null still corresponds to the pre-planned amount of benefit that the experimental therapy is required to provide relative to a hypothetical placebo. When active-control effectiveness depends on observable effect modifiers, and the null hypothesis is expressed in relation to the active-control therapy, the nominal value of the null hypothesis must change to ensure that the experimental treatment produces the required level Δ of effectiveness over placebo. Note that if a trial is planned based on (6), the analysis margin (and hence the null hypothesis) will be the same as the planning margin if the constancy assumption is met, i.e., if x^T = x^A and z^T = z^A.

Just as the nominal value of the null hypothesis can change under an adaptive NI margin strategy, so too can the nominal value of the alternative hypothesis. Although the alternative hypothesis is typically expressed in relation to the active control, it is the alternative hypothesis in relation to the NI margin that determines power and sample size. We define the effect size Ω as the ratio ξ/δ, which represents the ratio of the null and alternative hypotheses. For example, if the alternative hypothesis is ξ = 0.90 and the NI margin δ is 1.1, the effect size used to compute power and sample size is Ω = ξ/δ = 0.82.

Because active-control effectiveness – and hence the NI margin – is a moving target under non-constancy, it is useful to anchor the alternative hypothesis to the hypothetical placebo arm, just as we did for the null. Let Ω_Plan be defined as the target effect size of the experimental treatment over placebo, defined as

$${\text{Ω}}_{\text{Plan}}=\xi /LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right).$$ (20)

The effect size Ω_Plan can be thought of as the target benefit of the experimental product over placebo, as opposed to the target benefit over the active-control therapy, and this target remains fixed even when the active-control effect changes as a result of non-constancy. The planned alternative hypothesis for computing power can be expressed as a function of Ω_Plan as

$$\xi ={\text{Ω}}_{\text{Plan}}\times LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right),$$ (21)

and once the values for x^T and z^T have been observed we can adjust the nominal value of ξ to reflect the pre-planned target effect. Using the observed study population characteristics gives the following adaptive alternative hypothesis:

$${\xi }^a={\text{Ω}}_{\text{Plan}}\times LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right).$$ (22)

Although the nominal value of ξ will have changed, by fixing Ω we preserve the initial, planned target effect of the experimental treatment over placebo. The adapted value ξ^a can now be used to compute power under the new hypotheses, as discussed in the next section.

Investigators may not want to change the alternative hypothesis, even when faced with non-constancy. For example, a common non-inferiority alternative hypothesis is ξ = RR_E/C = 1.0, meaning that trial is designed to establish non-inferiority in the situation where experimental and active-control treatments are equally effective. This is a natural choice, however it will have important effects on power, as we will see in the next section.

Updating Type-I Error and Power

In the context of potential non-constancy we think of the type-I error rate as the probability of declaring non-inferiority when the true RR_E/C is just at the point of being unacceptable, i.e., when RR_E/C is equal to an NI margin appropriate for the study population. In other words, the null hypothesis of interest is the adjusted null hypothesis reflecting enrolled study participants. If a fixed NI margin is used that is too high (too permissive), type-I error will be too high, and vice-versa for a margin that is too low. Adjusting the NI margin to reflect the observed study population removes the mismatch between the desired null hypothesis and fixed NI margin, and thereby prevents inflation and reduction in Type-I error. A fundamental assumption is that the adjusted NI margin is a reasonable estimate of the point at which a new therapy would be unacceptable. The validity of this assumption will depend on the quality of the trials used to construct the meta-regression model.

Statistical power will depend on the ratio of the adjusted alternative and null hypotheses, i.e., the adjusted effect size. Provided that this ratio does not change, power will be not be affected. For example, if the NI margin is planned using the meta-analysis regression in (6), the planned effect size can be written as the ratio of (21) and (6) as follows,

$$\begin{array}{c}\frac{\xi }{\delta }=\frac{{\text{Ω}}_{Plan}\times LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)}{{\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)\right)}^{1-\rho }}\\ ={\text{Ω}}_{Plan}\times {\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)\right)}^{\rho }.\end{array}$$ (23)

If δ^a is computed using the pre-specified value Δ_Plan, the adjusted effect size does not change:

$$\begin{array}{c}\frac{{\xi }^a}{{\delta }^a}=\frac{{\text{Ω}}_{Plan}\times LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)}{{\text{Δ}}_{Plan}\times LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)}\\ =\frac{{\text{Ω}}_{Plan}}{{\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)\right)}^{-\rho }}\\ ={\text{Ω}}_{Plan}\times {\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^A,z^A\right)\right)\right)}^{\rho }.\end{array}$$ (24)

In other words, if the null and alternative hypotheses are adjusted by using the pre-specified values for Ω_Plan and Δ_Plan, the effect size ratio remains the same, and there is no loss or gain in power. However, if Δ is allowed to vary depending on observed population characteristics, the effect size will no longer remain constant. Using estimated effectiveness to define Δ as in (16), the adjusted effect becomes

$$\begin{array}{c}\frac{{\xi }^a}{{\delta }^a}=\frac{{\text{Ω}}_{Plan}\times LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)}{{\text{Δ}}_{Estimated}\times LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)}\\ ={\text{Ω}}_{Plan}\times {\left(LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)\right)}^{\rho },\end{array}$$ (25)

which is a function of observed population characteristics. This means that on the one hand, if the active-control therapy is observed to be more effective than planned, the effect size, and consequently the power, will be lower than planned. On the other hand, if the active-control therapy is estimated to be worse than planned, the effect size will be larger than planned and power will be greater than planned.

Similarly, if the null hypothesis is adjusted but the alternative hypothesis remains constant at, for example, ξ = 1.0, the effect size, and hence power, will vary depending on the adjusted null, following the equation

$$\frac{\xi }{{\delta }^a}=\frac{1}{\text{Δ}\times LC{L}_{95}\left({\widehat{RR}}_{P/C}\left(x^T,z^T\right)\right)},$$ (26)

where Δ could be ΔPlan, ΔAdjusted, ΔMCID, ΔMin, or ΔCap. In this case the effect size is just the inverse of the non-inferiority margin. Stronger observed effects in the active-control arm (i.e., larger values for placebo-versus-control relative risk) will imply larger effect sizes (smaller absolute value of the relative risk) and hence higher power. Conversely, weaker than expected effects in the active-control arm would yield smaller effect sizes and reduced power. This is intuitive, since if the two interventions are equally effective, it is more difficult to establish non-inferiority using a narrower margin.

Case Study: HIV PrEP

Returning to the example of HIV PrEP, assume a trial is planned to evaluate a new long-acting therapy in men, and adherence to oral PrEP in the active-control arm is projected to be 60%. The planned NI margin can be taken from Table 1 as δ = 1.23. Assuming a planned alternative hypothesis ξ = 0.80, the effect size Ω would be 0.80/1.23 = 0.52, and the study would achieve 90% power with a sample size of 231 new HIV infections.

Table 2 illustrates how the four ways of defining Δ would influence the adapted margin δ^a at the end of a trial, depending on observed active-control arm adherence, and also how power is affected by the choice of alternatives. In approach one (first three rows of Table 2), Δ is maintained at the planned level (Δ_Plan = 1.23/1.5 = 0.82). If adherence is higher than planned (70%) or lower than planned (50%) the margin changes substantially to 1.54 or 0.95, respectively. Although Δ_Plan is constant, these margins preserve very different proportions (ρ) of the active control benefit as compared to the planned level; equivalent to ρ = 0.32 and ρ = 1.33 respectively. (Note that the value ρ = 1.33 corresponds to the requirement that the benefit of the experimental agent be 33% larger than the assured effect of the active control, and is equivalent to requiring super superiority.) If instead the target benefit Ω over placebo is held constant at 0.53 (middle four columns of Table 2), the effect size will not change and the target of 90% power will be achieved regardless of observed effectiveness. And finally, if the alternative hypothesis is fixed (last four columns of Table 2), higher than planned active-control effectiveness leads to too much power (nearly 100%) and lower than planned effectiveness results in low power (26%).

Table 2.

Planned and adaptive hypotheses, effect sizes, and power for varying levels of estimated active-control effectiveness in an example trial comparing and experimental HIV PrEP agent to an active control (oral HIV PrEP). Four methods of computing the required benefit over placebo (Δ) are shown, including (1) Δ_pian which is defined to preserve 50% of the active-control benefit at the planned level of effectiveness, (2)Δ_Est which preserves 50% of the estimated active-control benefit at the observed level of effectiveness, (3)Δ_Min which preserves both 50% of the estimated benefit at the observed level of effectiveness and an MCID (defined here as 0.90), and (4) Δ_Max which preserves 50% of the estimated benefit at the observed level of effectiveness and places a maximum on the Nl margin. Also shown are two methods for specifying the alternative hypothesis ξ), the first fixing Ω. based on the pre-planned alternative ξ=0.80, and the second method holding ξ constant at 0.80. Bolded values are fixed by design and determine the adaptive margins, hypotheses, and effect sizes. All values are relative risks exceptp and power. The pre-planned sample size is 231 HIV-infection events.

						Fixed target benefit over placebo				Fixed target benefit over active control
	Active-control effectiveness†	Assured active-control benefit -LCL,s(RRp/c)‡	Required benefit over Placebo -Δ	Adaptive Null / Nl margin -δa	Proportion of Benefit Preserved -ρ	Fixed/planned target benefit over placebo -Ω	Adaptive Alternative* -ξa	Effect size ξa/δa	Power	Effective target benefit over placebo -Ω	Fixed alternative -ξ	Effect size ξ/δa	Power
Preserve planned benefit Δ=ΔPlan	Higher than planned	1.89	0.82	1.54	0.32	0.53	1.00	0.65	0.90	0.42	0.80	0.52	1.00
	As planned	1.50	0.82	1.23	0.50	0.53	0.80	0.65	0.90	0.53	0.80	0.65	0.90
	Lower than planned	1.17	0.82	0.95ϕ	1.33	0.53	0.62	0.65	0.90	0.69	0.80	0.84	0.26
Preserve proportional benefit Δ=ΔEst	Higher than planned	1.89	0.73	1.37	0.50	0.53	1.00	0.73	0.66	0.42	0.80	0.58	0.98
	As planned	1.50	0.82	1.23	0.50	0.53	0.80	0.65	0.90	0.53	0.80	0.65	0.90
	Lower than planned	1.17	0.93	1.08	0.50	0.53	0.62	0.57	0.99	0.69	0.80	0.74	0.63
Preserve proportional benefit and MCID Δ=min(ΔMCID, ΔEst), ΔMCID=0.90	Higher than planned	1.89	0.73	1.37	0.50	0.53	1.00	0.73	0.66	0.42	0.80	0.58	1.00
	As planned	1.50	0.82	1.23	0.50	0.53	0.80	0.65	0.90	0.53	0.80	0.65	0.90
	Lower than planned	1.17	0.90	1.05	0.69	0.53	0.62	0.59	0.98	0.69	0.80	0.76	0.54
Preserve proportional benefit and limit the maximum margin ΔMax= min(1.23/LCL95(RRp/c), ΔEst)	Higher than planned	1.89	0.65	1.23	0.67	0.53	1.00	0.82	0.34	0.42	0.80	0.65	0.90
	As planned	1.50	0.82	1.23	0.50	0.53	0.80	0.65	0.90	0.53	0.80	0.65	0.90
	Lower than planned	1.17	0.93	1.08	0.50	0.53	0.62	0.57	0.99	0.69	0.80	0.74	0.63

^†Planned effectiveness is based on 60% adherence, higher than planned is based on 70% adherence, and lower than planned is based on 50% adherence.

^‡The "assured benefit" is the Lower Confidence Limit(LCL) of the 95% confidence interval surrounding the relative risk (RR) of HIV infection comparing placebo to active-control (oral PrEP), as estimated by the meta-regression model for oral PrEP effectiveness as a function of drug adherence and sex.

^*When adherence is as planned, the alternative is also as planned (fixed at 0.80).

^ϕA margin less than one indicates that super superiority is required. In this example, in order to maintain the pre-planned benefot over placebo, the experimental therapy must be at least 5% better than the active control.

If instead the investigators wish to adapt δ^a to maintain proportional benefit (Δ = Δ_Estimated and ρ = 0.5) as shown in the middle three rows of Table 2, changes to the margin will be less dramatic, with higher and lower than planned effectiveness leading to margins of 1.37 and 1.08 respectively. If the target benefit Ω is held constant at 0.53, the adapted alternative will change by the same amount as when preserving planned benefit, and the effect size will no longer remain stable. Higher than planned effectiveness leads to a smaller effect size (RR=0.73) while lower than planned effectiveness leads to a larger effect size (RR=0.57), with corresponding reductions and increases in power. If, on the other hand, a fixed alternative is selected (ξ = 0.80), the effect size responds to changes in effectiveness much the same way it does when using Δ_Plan, only the changes in power are less extreme (power becomes 98% and 63% for higher and lower effectiveness, respectively).

When a minimum benefit requirement (Δ_MCID = 0.90) is also imposed on the adapted margin, as shown in the third set of results in Table 2, the results match those of previous example when effectiveness is higher than planned, but differ when effectiveness is lower than planned. For lower than planned active-control effectiveness, we have

$$\text{Δ}=\min \left({\text{Δ}}_{Estimated},{\text{Δ}}_{MCID}\right)=\min (0.93,0.90)=0.90,$$ (27)

which reduces the margin to 1.05 and increases the required proportion ρ to 0.69. The effect size for the fixed Ω scenario is slightly reduced, although power is similar, and the effect size is also reduced for the fixed ξ scenario, with power correspondingly dropping from 63% to 54%.

If a maximum NI margin δ^Max is imposed, as shown in the final section of Table 2, δ^a is constrained at 1.23 even when active-control effectiveness is higher than planned. The proportion of benefit preserved increases to 0.67, and power drops dramatically under the adapted alternative hypothesis.

Dynamic features and sampling variation

It will not always be possible to measure dynamic features in the entire study cohort. Lab-based drug adherence assessment, for example, requires costly collection and testing of samples. Typically it will be sufficient to generate an unbiased estimate of adherence using a random subset of participants, at a random set of time points. To compute the adapted margin, a sample-based estimate ẑ^T may be substituted into (13) in place of z^T. The degree to which sampling variation may influence the margin depends on both the estimated regression coefficients in (5) and the sampling distribution of z^T. Potential bias in δ(x^T, z^T, ρ) introduced by sampling can be quantified by

$$\delta \left(x^T,z^T,\rho \right)-\int \delta \left(x^T,{\widehat{z}}^T,\rho \right)f\left({\widehat{z}}^T\right)d{\widehat{z}}^T$$ (28)

where f() is the sampling distribution of ẑ^T and δ() is defined as in equation (6). The true value of z^T will generally not be known, but sample sizes for ẑ^T should be chosen to provide precise estimates of z^T and minimize potential bias.

Discussion

In regulatory settings, NI margins must be set in advance. However, specifying non-inferiority margins is an imprecise and subjective process, and the validity of these margins relies heavily on the assumption of constancy. A pre-specified adaptive margin approach, included as a secondary or sensitivity analysis in a trial, could have considerable credibility where the trial data suggest non-constancy. Once the trial is complete, the pre-specified regression model and pre-specified adaptive method can be used to update the end-of-study margin according to observed effect modifiers in the study population, preserving planned levels of Type-I error and assuring pre-planned levels of benefit over placebo.

We have proposed two different approaches for defining an adaptive NI margin, and the rationale for each choice is slightly different. Decisions to limit the potential change in the margin need to be specified in advance. Determining the most appropriate strategy for adapting the margin will depend on the goals of the trial, the factors that influence non-constancy, and the investigators’ perspective.

The International Council for Harmonization draft E9(R1) guidelines recommend defining study estimands with respect to events that occur after randomization [8]. Our proposed approach involves two estimands, (1) the relative effectiveness of the experimental therapy compared to the active-control, and (2) the effectiveness of the active-control therapy compared to a hypothetical placebo arm. We assume that estimand (1) will be estimated using the intent-to-treat (ITT), or ‘treatment policy’ strategy, which recognizes that post-randomization events, such as non-adherence, may directly influence the estimates. Estimand (2) is also constructed based on ITT estimates from prior placebo-controlled trials, and represents an average effect given observed study-population behavior. Combining these estimates allows investigators to infer whether the experimental treatment provides sufficient clinical benefit as compared to what would have been experienced under placebo.

A key element of our approach is that NI-margin adaptation is not based on observed effectiveness data from within the trial. Meta-regression parameters are estimated prior to starting the trial, and depend entirely on external efficacy data. The end-of-study M1 margin depends only on the pre-specified model for active-control arm effectiveness and observed effect modifiers at baseline and post-randomization in only the active-control arm of the NI trial. The NI margin (M2) will depend on M1 and a pre-defined amount of preserved benefit. It may be reasonable to update the meta-regression with data from external trials that conclude during the conduct of the NI trial, but the decision to update the model and the decision about which adaptive approach will be selected should be explicitly pre-specified.

Just as historical trials may show that participant characteristics can influence active-control efficacy, experimental-therapy efficacy may similarly depend on characteristics of participants in the experimental arm. In the context of an NI trial there is no historical information regarding effect modification in the experimental arm, but exploratory analyses may be possible. For example, a secondary objective of the trial might be to assess whether key baseline and post-randomization factors also modify experimental-arm effectiveness; such assessments might include subgroup analyses or tests for interaction.

Our meta-analysis regression method is an important extension of Nie and Soon’s approach [13] in that it allows for the inclusion of post-randomization dynamic features, which in some settings may be the most influential effect modifiers. In trials where the active-control arm medication is controlled by the participant, the importance of medication adherence likely outweighs any known effect modifier that could be measured at baseline.

Rohmel and Kieser [14] address the idea of “variable margins” which have been proposed as way to construct more reasonable NI margins for binaryend-point trials when failure rates in the active-control arm are substantially different than expected. The variable-margin approach allows the end-of-study margin to depend on observed failure rates, and when these rates are lower than a preset threshold, the margin switches from a difference-in-proportions scale to the odds-ratio scale. Although changing the scale provides some flexibility in the face on non-constancy, unlike the meta-analysis approach it does not address the question of how to define an appropriately sized margin based on observed levels of active-control effectiveness.

The choice of endpoint-assessment scale is nevertheless important. Although our development of the adaptive NI margin approach uses the relative risk scale, the same approach can be used for risk differences, differences in means, or any outcome scale. For example, by applying the log transformation to (6), so that the conserved proportion ρ becomes a multiplier on a risk difference instead of an exponent on a risk ratio. The required benefit Δ and target benefit Ω would then become additive differences instead of multipliers. In applications where event rates are fairly high (a threshold 20% is often used in the variable-margin approach) the risk-difference scale may be more intuitive and useful. Similarly, when comparing the mean value of continues measures, defining the margin in terms of absolute differences may often be appropriate.

Meta-analysis based adaptive NI margins have important limitations. First, meta-analysis results are only as good as the trials upon which they are based, and it is not always the case that multiple, high-quality trials are available. Particularly for meta-analysis regression, multiple trials with accurate measures of important effect modifiers are necessary to achieve a reliable regression model. While some fields of study are rich with existing, high-quality trial data, others are not.

Critical effect modifiers such as adherence can be measured in very different ways, yielding different results; for example, self-reported drug adherence has been shown to be consistently higher than lab-based adherence measures [10, 18]. It is therefore essential that assessment of effect modifiers in the new trial be consistent with the prior studies used to construct the margin. If measurement is not consistent, regression-based estimates of active-control effectiveness are unlikely to be accurate, in which case the adapted NI margin will not result in the desired trial characteristics.

In addition, if measurement methods are not clearly pre-specified, the opportunity could arise for inappropriate manipulation of the margin. For example, if it is known that higher measured adherence corresponds to higher effectiveness, one need only choose an inflated adherence measure, such as self-report, to increase the estimated active-control effect and relax the NI margin, thus making drug approval more likely. Trial integrity will depend on the use of carefully pre-specified procedures that incorporate independently and objectively measured effect modifiers.

Relying on between-trial effect-modifier estimates will not always prevent confounding. Unmeasured differences in study populations can introduce ecological bias [7], such as might occur with gender in the PrEP example. If drug adherence were not included in model (7), it would likely appear that oral PrEP is much less effective in women than in men. This result, however, would be due primarily to the fact that in several large PrEP trials in women, adherence was very low, whereas in most trials that include men, adherence was moderate or high (Figure 1). It is therefore important to use caution when using trial-level data to evaluate effect modifiers, and if post-randomization factors are not included in the model, consider using individual participant data as proposed by Hua et al. [7].

Sampling error may also introduce bias to an adapted NI margin. In situations where it is difficult to obtain sufficiently precise estimates of z^T, the potential for bias may be higher. We would suggest assessing the potential for bias by evaluating (28) using a variety of reasonable values for x^T and f(). Ideally, the sampling plan would sample randomly among participants across study time to account for temporal trends.

Even if effect modifiers could be measured and modelled perfectly, unmeasured effect modifiers always may exist. If non-constancy results from factors that cannot be measured or have otherwise not been included in the model, the adaptive margin cannot make appropriate corrections. In the study of HIV prevention, for instance, it is not possible to measure sexual exposure to HIV. If exposure to HIV is substantially less than expected based on prior efficacy trials, active-control effectiveness may be lower than is predicted by the model [3].

In the presented results we assumed a fixed study design, adapting the NI margin at the conclusion of the trial. In future work we will investigate the possibility of adapting NI margins based on interim analyses in group sequential trials, and appropriate ways to update sample sizes as a result of interim updates to the margin and hypotheses.

Meta-analysis regression methods offer a way to define NI margins appropriate to a specific study population, and to adapt end-of-study margins to observed characteristics of study populations. In the presence of known, measurable effect modifiers, these methods can substantially reduce the undesirable consequences of violating the assumption of constancy.