Diffusion Tensor MR Imaging and Fiber Tractography: Technical Considerations

Abstract

SUMMARY:This second article of the 2-part review builds on the theoretic background provided by the first article to cover the major technical factors that affect image quality in diffusion imaging, including the acquisition sequence, magnet field strength, gradient amplitude, and slew rate as well as multichannel radio-frequency coils and parallel imaging. The sources of many common diffusion image artifacts are also explored in detail. The emphasis is on optimizing these technical factors for state-of-the-art diffusion-weighted imaging and diffusion tensor imaging (DTI) based on the best available evidence in the literature. An overview of current methods for quantitative analysis of DTI data and fiber tractography in clinical research is also provided.

In this article, the major technical factors that affect image quality in diffusion MR imaging are evaluated in detail. The first half focuses on diffusion-weighted imaging (DWI). The strengths and weaknesses of single-shot echo-planar imaging, by far the most popular sequence for brain DWI, are considered, and alternative sequences are presented for special purpose applications. The effect of hardware and software variables such as magnetic field strengths, gradient amplitudes and slew rates, radio-frequency coils, and parallel imaging reconstruction methods is reviewed. The causes of common DWI artifacts are explained, and strategies are provided for minimizing artifacts and optimizing image quality.

The second half of the article focuses on technical considerations specific to diffusion tensor imaging (DTI) and fiber tractography, including optimizing the b-values, the number and orientations of diffusion-weighted acquisitions, as well as the fiber tracking parameters. The undesirable effects of common problems such as low signal intensity–to-noise ratio (SNR) and pulsation artifact are reviewed. An overview is provided of current methods for analyzing quantitative DTI data for clinical research, including the reproducibility of DTI measurements. Throughout this review, the emphasis is on optimizing the many technical factors needed for state-of-the-art DWI and DTI based on the best available evidence in the literature.

Technical Considerations for State-of-the-Art DWI

Echo-Planar DWI

Advantages of Single-Shot Echo-Planar DWI.

Because even minimal bulk patient motion during acquisition of DWIs can obscure the effects of the much smaller microscopic water motion due to diffusion, ultrafast imaging sequences are necessary for successful clinical DWI. Most commonly, diffusion imaging is performed by using spin-echo single-shot echo-planar imaging (SS-EPI) techniques. The term “single shot” means that an entire 2D image is formed from a single radio-frequency excitation pulse. Images can be acquired in a fraction of a second; therefore, artifact from physiologic cardiac and respiratory pulsatility and from patient motion is greatly reduced, including motion between acquisitions with different orientations of the diffusion-sensitizing gradients. Another advantage of SS-EPI is its relatively high SNR per unit of scanning time. This is particularly important for DWI because diffusion gradients at high b-values cause considerable signal-intensity loss (equation 2 in Part I¹); hence, DWI is more SNR-limited than conventional MR imaging such as T2-weighted imaging. Because of the speed and high SNR efficiency of the SS-EPI acquisition, DWI has been among the shortest sequences in a typical brain imaging protocol, typically requiring only 1–2 minutes. This is very beneficial for applications such as hyperacute stroke imaging, in which the time window for MR imaging is very short. The motion insensitivity of SS-EPI means that DWI can often produce diagnostic results in ill uncooperative patients, in whom all other sequences are too motion-degraded to be useful.

Shortcomings of SS-EPI DWI.

However, limitations of SS-EPI include low spatial resolution, blurring effects of T2* decay and T2 decay occurring during image readout, and sensitivity to artifacts due to Nyquist ghosting, chemical shift, magnetic field inhomogeneity, and local susceptibility effects. With current MR imaging hardware and software limitations, the single-shot technique limits matrix size for a typical 2D DWI to 128 × 128, which is much less than that for standard T1- and T2-weighted scans, which can have matrix sizes of 256 × 192 or greater. Blurring of T2-weighted and T2*-weighted contrast is another shortcoming of the single-shot approach; this also occurs in single-shot fast spin-echo (SS-FSE) and half-Fourier acquired single-shot turbo spin-echo (HASTE) sequences due to their extended echo-train lengths. The Nyquist ghost is an artifact that is specific to EPI, because it results from the fact that EPI traverses k-space in opposite directions on alternate echoes. Errors in the phase of the MR imaging signal intensity from sources such as fat-water chemical shift can cause a second “ghost” image to be overlaid on the original image, where the ghost image is shifted by one half of the FOV in the phase-encoding direction. Because of the Nyquist ghost phenomenon, chemical shift can be particularly troublesome in DWI. Fortunately for head imaging, fat-containing regions are usually limited to the scalp, the orbits, and the bone marrow of the calvarium, including the skull base. These artifacts are minimized by frequency-selective fat-saturation pulses incorporated into the SS-EPI sequence. Perhaps the worst artifacts inherent to SS-EPI, especially at high fields of 3T or greater, are those from magnetic field inhomogeneities, primarily caused by local susceptibility differences between adjacent structures. These often result in marked distortion and signal intensity dropout near air-filled cavities such as the paranasal and mastoid sinuses, particularly at the skull base and the posterior fossa, limiting the sensitivity of DWI with SS-EPI in these areas.

Optimizing SS-EPI DWI: b-Values.

As reviewed previously (equation 5, Part 1¹), for clinical b-values in the range of 0–1000 s/mm², only 2 different b-values need to be measured to estimate ADC: 1 at a very low b-value (or zero) and the other at a high b-value. Acquisition of DWIs at additional intermediate values of b is redundant. A high b-value of 1000 s/mm² has become the standard for clinical DWI. The brains of neonates and infants have much longer T2 relaxation times and much higher ADC values than those of adults^2–5; therefore, it is common practice to use less diffusion-weighting, for example, b = 600 s/mm² for premature neonates and b = 700 s/mm² for term neonates and infants younger than 1 year of age. A simple rule of thumb is that the optimal b-value multiplied by the ADC of the tissue under investigation should be close to 1.

Optimizing SS-EPI DWI: Gradients.

One of the most important hardware factors influencing the quality of DWI is the gradient performance of the MR imaging scanner, for both the diffusion gradients and the EPI readout gradients. Stronger and faster gradients enable stronger diffusion-weighting in a shorter period of time as well as reducing the time required to form an EPI image. This permits DWIs to be acquired at a shorter TE, which improves SNR and reduces geometric warping artifacts from susceptibility effects. Gradient strength is often measured in milliteslas per meter. The switching speed of gradients is referred to as “slew rate” and is measured in milliteslas per meter per millisecond. Higher gradient amplitudes and slew rates are desirable for DWI; however, there are US Food and Drug Administration (FDA) limits on the maximal rate at which the magnetic field can be changed, referred to technically as dB/dt. Gradient performance that exceeds the federal dB/dt guidelines risks peripheral nerve stimulation due to induced electric currents, which can lead to involuntary skeletal muscle contractions. Taller patients would be more likely to be affected due to the longer length of their peripheral nerves. All clinical MR imaging scanners meet FDA safety guidelines for dB/dt limits. The current generation of MR imagers with 40–80 mT/m maximal gradient amplitude and 150–200 mT/m per millisecond maximal slew rate enables DWI with better anatomic fidelity than older MR imaging systems. Some newer MR imaging scanners are equipped with even stronger and faster gradients that have a reduced FOV, to stay within dB/dt guidelines, and are suitable for head imaging but not for spine or body imaging. Besides maximal amplitude and slew rate, another important factor is the gradient duty cycle, which can be limited by heating constraints. Larger duty cycles permit more 2D diffusion-weighted sections to be acquired in a given TR. Modern MR imaging systems have water-cooled gradients with larger duty cycles than older systems, which allow faster DWI.

As gradients become more powerful, they may exacerbate problems such as eddy currents and mechanical vibration. All MR imaging gradient coils are self-shielded to prevent eddy currents, which are residual magnetic fields induced by gradient switching that persist after the gradients are turned off. However, self-shielding is inadequate for the large amplitude and rapid onset and offset of diffusion-sensitizing gradients at high b-values. Eddy currents cause 3 different types of image artifacts in DWI: scaling, shift, and shear.⁶ “Scaling” refers to expansion or contraction of the DWI. “Shift” describes displacement of the image along the phase-encoding direction (Fig 1). “Shear” denotes shifting of the image in opposite directions on the left and right sides. Therefore, additional eddy current compensation strategies are needed for DWI. Most DWI sequences now use bipolar diffusion gradients, which have positive and negative lobes to cancel eddy currents.⁷ Another option available on the current generation of MR imaging scanners is the twice-refocused spin-echo (TRSE) or dual spin-echo (DSE) diffusion-weighted sequences, which use 2 consecutive radio-frequency refocusing pulses, each with a pair of bipolar diffusion gradients to further break up the time that eddy currents have to arise and decay.⁸ However, these sequences may slightly increase TE, which reduces SNR and increases susceptibility artifacts. TRSE/DSE sequences have also been shown to dramatically increase mechanical vibration at 3T.⁹ These shortcomings should be weighed against the adverse effect of eddy currents in deciding whether to use the TRSE/DSE option.

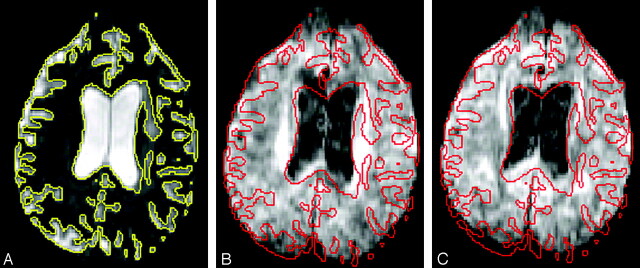
Fig 1.

Shift of DWIs due to eddy currents. A, The b = 0 s/mm² image with the brain-CSF interface outlined (yellow). B, Corresponding DWI with the same outline (red), unchanged in position compared with A, shows a shift of the brain anteriorly, most easily seen at the ventricular margins and at the occipital lobes. C, Another DWI with the diffusion gradient pointing in a different direction than in B shows a different degree of anterior shift.

Diffusion gradients are powerful enough to shake the entire MR imaging scanner and its platform too. These mechanical vibrations may be transmitted to the patient and cause characteristic artifacts in the DWIs (Fig 2). A systematic study of vibrations induced by diffusion-encoding gradients showed that they increase strongly with b-value.⁹ It might be expected that heavier patients would be less affected because their weight would more effectively damp the vibrations; however, this 3T study showed that the movement might actually increase with greater weight on the patient table. Advances in gradient design and magnet stabilization may help in mitigating these vibration artifacts.

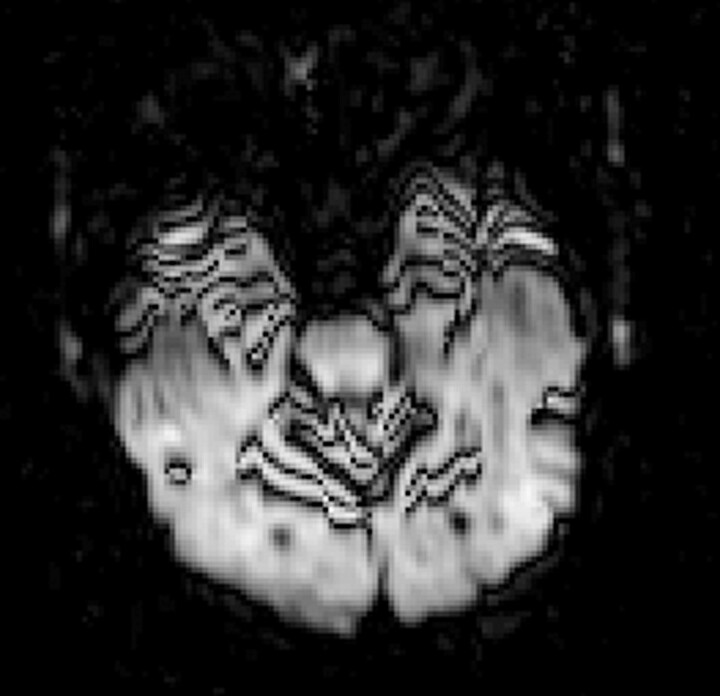
Fig 2.

Combined DWI image shows pronounced artifacts at the anterior temporal lobes and around the superior cerebellar vermis (black lines) due to mechanical vibration.

Optimizing SS-EPI DWI: Multichannel Coils and Parallel Imaging.

New multichannel phased-array head radio-frequency coils with better SNR characteristics than the standard birdcage head radio-frequency coils have also enhanced DWI, which is an SNR-limited technique. Unlike birdcage head coils, which have relatively uniform sensitivity throughout their imaging volume, the phased-array head coils have better sensitivity in the periphery of the volume than in the center. Hence, the SNR gain is greater in the cerebral cortex than for central brain structures such as the thalamus. Besides their better overall SNR, another advantage of phased-array head coils is their multiple independent receiver channels, which enable parallel imaging on modern MR imaging systems, which are equipped to handle parallel data streams.^10,11

Parallel imaging techniques such as sensitivity encoding (SENSE), array spatial sensitivity encoding technique (ASSET), and generalized autocalibrating partially parallel acquisition (GRAPPA) can all be used to shorten the echo-train length of EPI (Figs 3 and 4), thereby mitigating susceptibility-induced geometric warping artifacts and reducing the blurring of T2 and T2* image contrast that occurs with extended EPI echo trains.^12,13 Moreover, due to the shorter readout, the TE may be decreased; this decrease has the effect of improving SNR and further reducing susceptibility and off-resonance artifacts as well as T2 shinethrough (Figs 3 and 4). These substantial improvements increase with the acceleration factor used in parallel imaging but must be balanced against the greater loss of SNR at higher acceleration. With current 8- to 12-channel head radio-frequency coil designs, acceleration factors of 2–3 are optimal.^14–16 Even at 1.5T, both SENSE and GRAPPA with twofold acceleration have been shown to improve subjective DTI image quality and objective DTI parameter measurements compared with DTI acquisition without parallel imaging.¹⁶

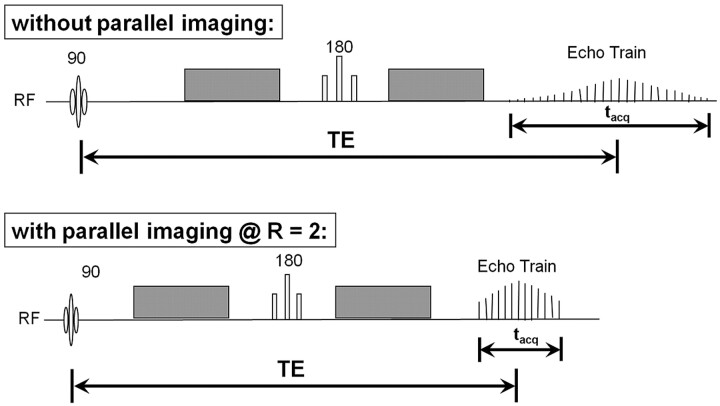
Fig 3.

Pulse sequence diagrams show the benefits of parallel imaging for DWI. At an acceleration factor of R = 2, the echo-train length for the single-shot EPI acquisition is only half as long. This is reflected in a shorter readout time (t_acq) and allows the echo train to be better centered at the peak of the spin-echo, improving SNR, decreasing T2 and T2* contrast blurring, and reducing off-resonance artifacts that cause geometric distortions. The shorter readout time also enables a reduction of TE, further improving SNR and reducing geometric distortion. However, the use of parallel imaging results in an intrinsic loss of SNR that may offset the aforementioned SNR gains. RF indicates radio-frequency.

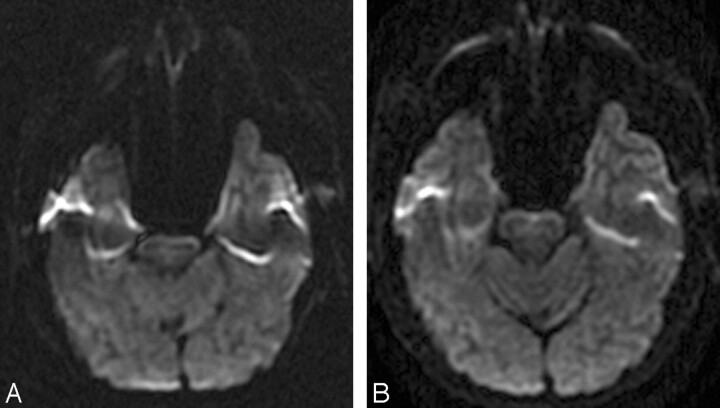
Fig 4.

Parallel imaging ameliorates susceptibility-induced geometric distortions and T2 and T2* contrast blurring in 3T DWI performed with a single-shot echo-planar sequence. A, The b = 1000 s/mm² DWI image acquired at 3T without parallel imaging shows warping of the pons and anterior temporal lobes. There is also signal-intensity void with adjacent regions of signal-intensity pileup in the temporal lobes. These are typical artifacts encountered with 3T ssEPI DWI due to susceptibility effects from the adjacent air-filled mastoid sinuses and sphenoid sinus. B, The b = 1000 s/mm² 3T DWI image acquired at the same axial level with ASSET parallel imaging (R = 2) demonstrates reduced foreshortening of the pons and reduced warping and signal-intensity distortions in the temporal lobes. There is also mitigation of contrast blurring, seen as improved definition of the cerebellar fissures and folia as well as better gray-white matter differentiation in the occipital lobes.

Parallel imaging is even more helpful for ameliorating the stronger EPI susceptibility artifacts that occur at 3T¹⁴ and is absolutely essential at 7T,¹⁷ thereby permitting high-field and ultra-high field DWI with superior image quality (Fig 5). Conversely, higher field strength enables greater acceleration factors for parallel imaging because the shorter radio-frequency wavelengths, in conjunction with larger numbers of phased-array receiver elements, improve the ability to reconstruct images with fewer phase-encoding steps without incurring an unacceptable loss of SNR.^18–20 Hence, high-field highly accelerated SS-EPI with 16, 32, or an even greater number of head coil elements may be a promising avenue for improving DWI.

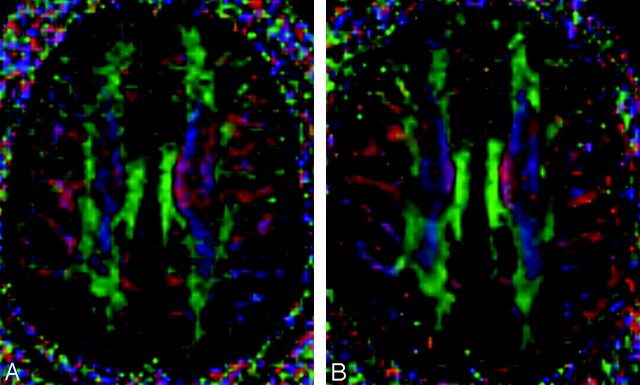
Fig 5.

3T-versus-7T DTI with 36 diffusion-encoding directions at b = 3000 s/mm² and 2.0 × 2.0 × 2.0 mm isotropic voxel resolution. Directionally encoded color FA maps at the axial level of cingulum bundles and the callosal striations are shown for 3T (A) and for 7T (B) in a healthy adult volunteer. Both scanners were equipped with 40 mT/m gradients and 8-channel phased-array head coils, and ASSET parallel imaging was used with an acceleration factor of 2. The standard DTI color conventions are used, with red representing left-right fiber orientation, green representing anteroposterior, and blue representing craniocaudal. With this combination of high spatial resolution and very strong diffusion weighting, the 3T image appears grainy because of inadequate SNR. However, with identical scanning parameters, the additional SNR at 7T produces a higher quality image. Parallel imaging is essential for SS-EPI at ultra-high field to combat the increased susceptibility artifacts as well as the signal intensity loss and contrast blurring due to shorter T2 ad T2* relaxation times.

However, parallel imaging can also introduce new types of artifacts into DWI. A common problem encountered for methods that operate in the image domain, such as SENSE and ASSET, is unfolding artifact. The images that are acquired by each receiver element in a multichannel array are aliased (ie, have wraparound) due to their small FOV. Image domain parallel imaging techniques work by unfolding and combining these images to form the full FOV image. However, SENSE and ASSET both require a calibration scan performed before DWI to estimate the sensitivity profiles of each of the coil elements. This calibration scan is usually a proton-density-weighted gradient-echo acquisition, which does not have the susceptibility-induced geometric distortions common to SS-EPI. Therefore, the calibration may be inaccurate in areas of warping on DWI, especially at high field in which the geometric distortions are more pronounced, leading to unfolding errors in the parallel imaging reconstruction that appear as ghosting along the phase-encoding direction.

Unfolding artifacts emanating from the orbits can be especially exaggerated in DWI performed with SENSE or ASSET (Fig 6) and may be mistaken for lesions.²¹ They can be eliminated by a saturation band over the orbits or by using a fluid-attenuated inversion recovery pulse in conjunction with DWI, though the latter solution would lead to a significant loss of SNR. Patient movement between the calibration scan and the DWI acquisition can also lead to artifacts; hence it is advisable to perform DWI immediately after the calibration scan, without any intervening sequences. GRAPPA does not have this specific type of unfolding artifact because it operates in k-space rather than the image domain and also because it is autocalibrated (ie, the calibration scanning is incorporated into the DWI acquisition itself). However, other types of reconstruction errors might occur with GRAPPA, which may be less predictable.

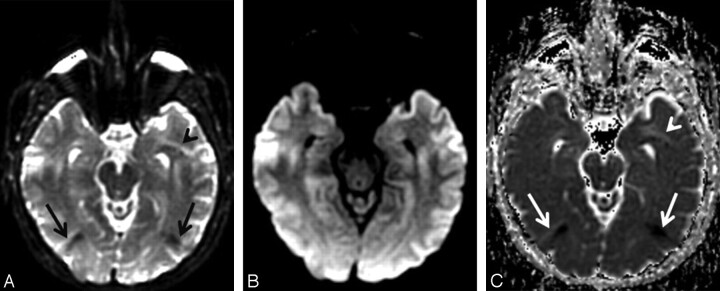
Fig 6.

Unfolding artifacts from the globes in ASSET-accelerated DWI. A, The b = 0 s/mm² image acquired at 3T with an ASSET acceleration factor of R = 2 shows unfolding artifacts from the distorted high-signal-intensity globes appearing as dark bands in the occipital regions (black arrows) as well as a bright band in the anterior left temporal lobe (black arrowhead). B, The unfolding artifacts are not apparent on the combined DWI image because the globes contain fluid with high diffusivity; therefore, the globes signal intensity is suppressed by the diffusion gradients. C, However, the unfolding artifacts are again apparent on the ADC map (white arrows and arrowhead) because the b = 0 s/mm² image is required for ADC calculation (equation 5, Part I¹).

Another method for reducing the echo-train length of SS-EPI is through partial-Fourier encoding of k-space. Due to conjugate symmetry, only half of k-space actually needs to be measured, and the other half can be inferred. This cuts the SS-EPI echo train in half, entailing the same benefits as parallel imaging with an acceleration factor of 2. The interaction between partial-Fourier encoding and parallel imaging is complex, and their joint effect on the quality of DWI and DTI has been explored in detail by Jaermann et al,¹⁵ who recommended an optimal acceleration factor of approximately 2 in combination with 60% partial-Fourier encoding for 3T acquisitions at b = 1000 s/mm².

Alternatives to SS-EPI DWI.

Other pulse sequences have also been applied to diffusion imaging, including variants of fast spin-echo (FSE) or turbo spin-echo imaging, multishot EPI, spiral imaging, and line-scanning methods. Single-shot methods other than SS-EPI, such as SS-FSE or HASTE, can be used to perform DWI. Because these are also ultrafast sequences, they share the relative immunity to bulk patient motion like SS-EPI, but they do not have nearly as much susceptibility or chemical shift artifacts. For this reason, they may represent a good alternative to SS-EPI in regions in which susceptibility or chemical shift effects are particularly profound, such as the spine or neck.^22,23 However, SS-FSE and HASTE have not proved popular for brain DWI because of their low SNR per unit of time compared with SS-EPI, resulting in longer scanning times.

Multishot methods also have much reduced susceptibility artifacts compared with SS-EPI. However, they are not as fast as single-shot methods, and this also makes them intrinsically more sensitive to artifacts arising from bulk motion during image acquisition. Motion artifacts can be ameliorated by the use of navigator echoes, especially in combination with cardiac and respiratory gating. One increasingly popular technique for DWI is a multishot FSE sequence called periodically rotated overlapping parallel lines with enhanced reconstruction (PROPELLER), which continually oversamples the center of k-space (ie, self-navigation) to mitigate motion artifacts without the need for gating.²⁴ This has been shown to improve detection of small acute infarcts, especially at the skull base and in the posterior fossa, where SS-EPI has the greatest susceptibility-induced distortions.^25,26 However, PROPELLER has not overtaken SS-EPI for routine brain DWI, likely because of its much longer scanning times.

Further improvements in speed, such as in the more recently developed Turboprop sequence,²⁷ may continue to narrow this gap. Moreover, a similar self-navigated k-space trajectory can be applied to multishot EPI to yield the desired combination of high SNR per unit of time and reduced susceptibility artifacts. This new technique is called PROPELLER EPI²⁸ and can be further enhanced by parallel imaging.²⁹ Alternatively, parallel imaging can be directly incorporated into multishot EPI for improved-quality DWI without loss of SNR efficiency compared with SS-EPI; for this purpose, GRAPPA was found to produce fewer off-resonance and motion artifacts than SENSE.³⁰

Technical Considerations for State-of-the-Art DTI

All of the factors reviewed previously for optimizing DWI also apply for optimizing DTI acquisitions. However, there are a number of additional considerations that are specific to DTI. Because diffusion imaging is an SNR-limited technique and DTI measures such as fractional anisotropy (FA) and relative anisotropy (RA) are more affected by measurement noise than DWI measures such as ADC, the ability to acquire DTI with adequate SNR for clinical applications is limited by time constraints. Thus, optimizing image acquisition parameters is an essential step for producing high-quality DTI. There is no fixed set of parameters optimal for every application; optimization depends on the MR imaging hardware configuration, available scanning time, anatomic coverage needed, and specific anatomic structures to be investigated. For instance, when studying less compliant subjects such as children, minimizing the scanning time is crucial, whereas high spatial resolution (leading to long scanning times) is essential for delineating relatively small white matter tracts. Factors to consider for application-specific optimization of DTI are emphasized below.

Optimizing Clinical DTI

Optimizing the Number of Diffusion-Encoding Directions.

To estimate the diffusion tensor, one needs DWIs with high b-values along at least 6 noncollinear directions in addition to a low-b DWI or a T2-weighted (b = 0 s/mm²) image. However, for most applications, many more images are usually required to boost SNR to acceptable levels. It has been a common practice simply to repeat acquisition of the same DWIs (ie, increasing NEX) to achieve this. However, acquiring more distinct diffusion-encoding directions without any repeated acquisitions is becoming more widespread. There has been debate in the literature about the optimal number and orientational distribution of diffusion-encoding directions^31–38; however, the emerging consensus is that diffusion tensor estimation is more robust with data acquired from many diffusion-encoding directions rather than repeated scanning of the minimal number (ie, 6) of directions.

The rationale for sampling more directions is that this reduces the orientational dependence and increases the accuracy and precision of diffusion tensor parameters such as FA, mean diffusivity, and the eigenvalues and eigenvectors. In other words, measurement errors will not be as dependent on relative orientation of the measured diffusion tensor compared with the set of diffusion-gradient directions. According to 1 Monte Carlo computer simulation study,³⁶ at least 20 unique directions are necessary for a robust estimation of anisotropy, whereas at least 30 directions are required for a robust estimation of tensor orientation (ie, the primary eigenvector) and mean diffusivity. The benefit of sampling more than 30 unique directions is not established for DTI, assuming that the total number of diffusion-weighted acquisitions is constant (ie, acquiring 60 directions would not be expected to be superior to sampling 30 directions at 2 NEX). Thus, using 30 directions is recommended for routine clinical DTI studies as long as time permits, and even more directions would be useful primarily when more sophisticated diffusion modeling such as high angular resolution diffusion imaging (HARDI) is contemplated to better delineate connectivity in regions of complex white matter architecture such as crossing fiber tracts.^39–41

In addition to optimizing the number of diffusion-encoding directions at high b-values, there is a need to decide the best number of b = 0 s/mm² T2-weighted image acquisitions, though image sets acquired at a very low b-value are sometimes used instead to crush artifacts from residual magnetization. The best available evidence indicates that the optimal ratio of M / (N + M), where M is the number of low-b acquisitions and N is the number of high-b acquisitions, ranges from 0.1⁴² to 0.2.⁴³ This translates to having 1 low-b image set for every 5–10 high-b image sets; hence, 3–6 low-b image sets would need to be acquired in addition to 30 high-b diffusion-encoding directional images sets. Unfortunately, prescribing multiple b = 0 s/mm² image sets can be complicated when using older MR imaging hardware and software, which often only permit a single b = 0 s/mm² acquisition. Also, the total number of DWIs that can be acquired in a series may be limited on older MR imaging systems, placing constraints on the number of diffusion-encoding directions if both thin sections and large anatomic coverage in the section-select dimension are required. One solution is to split the DTI scanning into multiple series, though this might prove cumbersome in practice, in addition to slightly increasing the scanning time.

Optimizing the Geometric Configuration of the Diffusion-Encoding Directions.

Besides the number of unique diffusion-encoding directions at high b, the orientational distribution of these diffusion-sensitizing gradients also needs to be taken into account. In general, the optimal geometric configuration of the sampling directions is one that is uniformly distributed along the surface of a sphere, to minimize the orientational dependence of the estimated DTI parameters. Approximating this optimal distribution is often achieved in practice for an arbitrary number of diffusion-encoding directions by using an electrostatic repulsion scheme⁴² or through various geometric polyhedral schemes.^33,44 The diffusion-gradient directions provided with older vendor-supplied MR imaging software may not be optimized; it is advisable in these cases to check the standard diffusion-gradient table and replace it if necessary. One recent study has suggested that as long as the distribution of directions is optimized, the exact directions that are prescribed matter less.³⁸

Optimizing the Acquisition Order of the Diffusion-Encoding Directions.

The order in which diffusion-encoding directions are acquired does not matter if it is anticipated that the scanning will not be corrupted or terminated by factors such as patient motion during the time it takes to acquire the total number of DWI sets. However, for certain applications such as unsedated pediatric imaging or imaging of dementia, in which patient noncompliance is common, it is preferable for lengthy DTI scanning to use a progressive ordering scheme for acquiring the diffusion-encoding directions.^45,46 Compared with unordered acquisitions, partial scans from these optimized ordering schemes are more likely to contain a relatively uniform distribution of diffusion-encoding directions from which DTI parameters can be derived, albeit with lower SNR and more orientational dependence than the full scan. This represents an improvement over acquiring the directions in random order, because partial scans will then have uneven spherical coverage and the resulting DTI parameters will be biased.

The Effect of Low SNR on DTI.

As a rule of thumb, the SNR of the b = 0 s/mm² images of a DTI acquisition should be at least 20 to derive relatively unbiased measures of parameters such as FA. Methods to measure the SNR of a DWI or DTI sequence, including the more complicated cases in which parallel imaging is used, have recently been reviewed by Dietrich et al.⁴⁷

Insufficient SNR is undesirable because weak diffusion-weighted signals close to the background noise level bias the estimated diffusion tensor parameters.⁴⁸ Very small signals tend to be pushed upward (overestimated) by noise, because MR imaging signals are reconstructed as the magnitude of complex values and they are forced to be non-negative. Overestimation of diffusion signals results in the underestimation of diffusivity (affecting eigenvalues and mean diffusivity) and, in anisotropic structures, underestimation of anisotropy (because diffusivities along the directions of fiber bundles are larger and more underestimated). Highly anisotropic white matter structures, such as the corpus callosum, can be especially vulnerable to insufficient SNR because the lack of restriction of water diffusion along the fiber orientation of the white matter tracts leads to strongly attenuated diffusion-weighted signals.

Even if this noise floor effect is not a concern, anisotropy indices such as FA or RA can be significantly overestimated (biased) at low SNR, especially when measuring low FA values. Indeed, infinite SNR would be required to measure zero anisotropy reliably. Hence, the minimum measurable FA, for example within a stationary water phantom in which there should be no anisotropy, is a good indication of the SNR of the DTI acquisition. This phenomenon, explained as eigenvalue repulsion, has been well documented by Monte Carlo simulation studies as well as by real in vivo data.^49–53 If the degree of bias is different between 2 groups of research subjects, this can create a statistically significant difference in FA between the groups even when the groups are not biologically distinct. Also, at low SNR, coregistration of diffusion-weighted images to correct subject motion and eddy current distortion becomes more problematic.

The Effect of Physiologic Motion on DTI.

Diffusion-weighted images are designed to capture microscopic water self-diffusion, but they are sensitive to macroscopic movements as well, such as bulk subject motion and cardiac pulsation. Bulk motion occurring during the acquisition causes additional dephasing of the magnetization that leads to more attenuated diffusion-weighted signals. The ADC is then overestimated, and anisotropy and eigenvectors may be biased as well, especially if the displacement occurs preferentially in certain directions. SS-EPI effectively freezes bulk patient motion, but signal-intensity dropout from CSF pulsation induced by the cardiac cycle can often be found even with this fast imaging technique, especially in certain anatomic regions such as the posterior fossa and the corpus callosum.

Previous studies have shown the benefit of cardiac gating with single-shot EPI.^54–58 It was claimed that the gain in the SNR by cardiac gating is actually larger than the increased scanning time required for cardiac gating⁵⁵ and that the bias in the mean diffusivity or eigenvectors without cardiac gating can be substantial.^56,57 Still, cardiac gating is not widely used for clinical DTI acquisitions due to the longer scanning time as well as the increased time for patient preparation. Also, the advent of parallel imaging and partial-Fourier encoding has reduced the sensitivity of DTI to pulsation artifacts by shortening the EPI echo train, though these artifacts have not been entirely eliminated. The fact that pulsation artifact is often not apparent visually in the DTI-derived parameter maps might also contribute to the underuse of cardiac gating.

The Reliability of Quantitative DTI Measurements.

As outlined previously, there are many potential sources of variation in quantitative DTI parameters. Therefore, it is very important to be consistent in data acquisition, reconstruction, and processing across subjects and groups in clinical DTI research. This is also why comparing reported DTI measurements from studies with differences in methodology calls for great caution. Multicenter DTI studies are very challenging, especially those with different MR imaging scanner types at different sites. A study of the replicability of trace and FA measurements found much better within-scanner reliability than between-scanner reliability, even for 2 different 1.5T scanner models from the same vendor.⁵⁹ FA measurements on the same scanner were reproducible to within 1.9%, and trace was reproducible to within 2.6%; however, there was a systematic FA difference of 4.5% between scanners and a larger between-scanner bias of 7.5% for trace. Hence, multicenter DTI studies need extensive standardization testing with identical phantoms and human volunteers scanned across sites to ensure that the DTI measurements are comparable.

Optimizing DTI for Fiber Tracking

Although tips for optimizing DTI acquisition for fiber tracking are similar to those for DTI optimization in general, there are a few issues that are specific to fiber tracking. Unlike routine clinical DTI, acquisitions for fiber tractography must be contiguous in 3D, with no gaps between sections. Another point is that making the voxel isotropic (ie, section thickness is the same as the in-plane pixel length) is more important with fiber tracking. This generally requires much thinner sections and, therefore, many more sections for whole-brain coverage than with routine clinical DTI. With these thinner sections, it is typical to interleave the acquisition to prevent cross-talk between adjacent contiguous sections.

The voxel size is 1 of the factors affecting the error of fiber tracking,⁶⁰ and the degree of partial volume averaging will also depend on the voxel size. Larger voxels are more likely to contain more than 1 fiber tract. The presence of multiple intravoxel fiber populations with different orientations will cause errors in the estimation of fiber direction using DTI. This limitation is inherent to the diffusion tensor, which can only model 1 fiber orientation per voxel, and can be overcome only by adopting more sophisticated HARDI approaches.^39–41 Fiber tracking typically relies on the primary eigenvector estimated at each voxel, and the accuracy of this measurement is insensitive to the number of b = 0 s/mm² images. Thus, unlike the situation for DTI parameter quantitation, it is optimal for DTI fiber tracking to acquire as many strongly diffusion-weighted images as possible rather than increasing the number of low-b or b = 0 s/mm² images.⁴³

However, the real power of DTI comes from combining complementary information from both sources: 1) the scalar parameters such as FA and ADC that reveal the microstructural organization of tissue, and 2) the main vector parameter, specifically the primary eigenvector, that can be used to infer fiber orientation and thereby delineate the 3D connectivity of specific tracts by using fiber tracking algorithms. This is necessary if tractography-based quantitation of DTI parameters is contemplated. Recent studies have indicated that tract-based quantitation of ADC and FA is more reproducible across subjects than conventional manual region-of-interest measurements.^61,62 Hence, securing sufficient b = 0 s/mm² images and adopting isotropic voxel dimensions at high spatial resolution is the optimal approach to DTI acquisition, provided that sufficient scanning time is available. Examples of typical DTI acquisition parameters optimized for 1.5T and 3T scanners equipped with 8-channel head coils and capable of parallel imaging are shown in the Table.

Typical optimized whole-brain DTI acquisition parameters in a 1.5T or 3T MR imaging system^*

Acquisition Parameters	3T	1.5T
Spatial resolution	2.0 × 2.0 × 2.0 mm	2.5 × 2.5 × 2.5 mm
Acquisition matrix	128 × 128 × 60	96 × 96 × 50
FOV	256 mm	240 mm
No. DWIs	30	30
No. minimally weighted images	5	5
No. repetitions (NEX)	1	1
b-value	1000 s/mm2	1000 s/mm2
TE/TR	70 ms/<12 seconds	70 ms/<10 seconds
Total acquisition time	<8 minutes	<7 minutes

^*The hardware is assumed to be equipped with an 8-channel head coil and gradients of 40 mT/m. It is also assumed that parallel acquisition is done with a SENSE reduction factor of 2, partial k-space acquisition of 62.5% (only 5/8 of the phase-encoding lines after a reduction to half by parallel acquisition is acquired), and an interleaved multisection SS-EPI sequence with no gap.

Optimizing Fiber Tracking Methodology

There are a multitude of DTI tractography algorithms that have been reported to date, and many more are being introduced every year. Comparing their specific attributes is beyond the scope of this review, and the reader is referred to Mori and van Zijl⁶³ for a basic overview of deterministic streamline fiber tracking methods. However, the original fiber assignment by continuous tracking (FACT) method,⁶⁴ using the multiple region-of-interest “virtual dissection” technique^65,66 for isolating specific anatomic pathways, remains the most popular approach for both scientific and clinical applications. All of the fiber tractography software currently supplied by the major MR imaging manufacturers for DTI postprocessing is based on FACT with multiple region-of-interest targeting.

There are 2 ways of placing seed points for initiating tractography. The first is to seed only the voxels within a region of interest manually placed within the tract of interest.⁶⁴ The other is to seed every voxel in the entire 3D volume containing the head above a certain threshold anisotropy value, thereby generating all the white matter streamlines in the brain in 1 computation, from which specific tracks are selected by using manually placed regions of interest.⁶⁵ This latter so-called “brute force” approach is considered technically superior because it may find some tracks that are missed by region-of-interest–based seeding and produces a better balance of streamline density along the delineated tract. However, the brute force approach is also much more computationally demanding in terms of compute time, memory requirements, and, potentially, also disk space if the whole-brain fiber tracks are to be stored for later postprocessing.

Two important parameters that affect the results of FACT and other deterministic streamline algorithms are the following: 1) the minimum FA threshold within a voxel for propagation of streamlines, and 2) the maximum streamline turning angle between voxels. Typical minimum FA thresholds used for the adult brain range from 0.1 to 0.3. For fiber tracking in the neonate or infant brain, where FA values are much lower than those in the mature brain, the minimum FA threshold may be lowered to below 0.1. With all other parameters being equal, lower minimum FA thresholds will produce more and longer streamlines; however, values that are too low for the SNR of the DTI acquisition will produce more spurious (ie, false-positive) fiber tracks. Typical values for the maximum turning angle between voxels range from 40° to 70°. Larger values may be necessary to define pathways properly with hairpin turns, such as the uncinate fasciculus or Meyer loop. However, larger maximum turning angles may dramatically increase the number of spurious tracks and also, for brute force whole-brain tracking, dramatically increase the computational load.

Quantitative Analysis of DTI Data

At present, there is no consensus on the best way to analyze quantitative DTI data for clinical research, and this remains an active area of technical development. Manually placed region-of-interest analysis has been widely used in the DTI literature but has intrarater and inter-rater variability and is very time-consuming if many white matter tracts are to be analyzed in many subjects. Also, only a part of each tract can be assessed. Voxel-based analysis (VBA) techniques such as statistical parametric mapping, popular for unbiased whole-brain analysis of 3D structural MR imaging data, have also been applied to DTI. However, these methods are not yet designed to manage the special characteristics of tensor datasets and therefore have numerous pitfalls. For example, the underlying statistical model of random Gaussian fields in VBA is not appropriate for non-normal DTI data, even with moderate levels of smoothing. Furthermore, varying the smoothing filter size in VBA can lead to completely different results of the VBA analysis of FA data.⁶⁷ Achieving adequate coregistration of DTI data across subjects for group analysis can also be challenging, given individual differences in brain size and shape and in white matter and gyral anatomy. To avoid the problem of non-normality, one can use nonparametric statistics such as permutation testing to perform whole-brain DTI analysis.⁶⁸ To avoid the pitfalls of group spatial normalization, one can even perform this testing in single subjects to examine DTI changes across serial examinations, though this has less statistical power than comparisons between large groups.

Tract-based spatial statistics (TBSS) is an automated method of detecting group-wise changes in diffusion metrics from the white matter of the entire brain.⁶⁹ FA maps from each subject in an experiment are registered to construct a mean FA map. The mean FA map is skeletonized to identify the core of white matter tracts containing the highest FA values. FA values from individual subjects are then projected onto the FA skeleton, and voxel-wise statistics are applied. The TBSS method can detect changes in FA simultaneously throughout the white matter of the brain, whereas DTI fiber tracking measurements are derived from individual white matter tracts. However, like VBA, TBSS is also dependent on an accurate registration, which may not be possible with diseases or congenital malformations resulting in large anatomic shifts.

3D DTI fiber tracking can be used as the basis for quantitatively assessing the microstructure of a specific white matter tract. Diffusion metric maps including FA, ADC, and the eigenvalues are inherently registered to the resultant DTI fiber tracks. The general strategy of quantitative DTI fiber tracking is to create a 3D region of interest based on the voxels through which the fiber tracks pass. Quantitative DTI fiber tracking can be performed in conjunction with deterministic or probabilistic fiber tracking. The connectivity metric produced by probabilistic tracking methods can be used to threshold a 3D region of interest, restricting measurements to voxels most likely to contain the desired white matter tract. Alternatively, the contribution of each voxel to the tract measurement can be weighted by the connectivity metric generated by probabilistic fiber tracking. Thus, voxels with a low probability of containing the white matter tract of interest will contribute little to the final measurement.

Studies have shown the reproducibility of quantitative DTI fiber tracking^62,70 as well as the accuracy of the technique and improved intrarater reliability as compared with manually drawn regions of interest.⁶¹ A chief advantage of 3D tractography is that it can delineate a large portion of the tract of interest, as opposed to only a small region for a manual region of interest. Other algorithms have been reported that perform semiautomated region-growing and chain-linking to produce 3D regions of interest of white matter tracts without explicitly performing fiber tracking.⁷¹ These are also more reproducible and less time-consuming than manual 2D region-of-interest analysis. Many other methods for analyzing DTI data have been described or are currently in development, but an exhaustive treatment is beyond the scope of this review.

Conclusion

Tremendous progress in diffusion MR imaging technology during the past decade has enabled high-quality DWI and DTI of the brain in clinically feasible scanning times, for use in routine diagnostic evaluation and in clinical research. However, these same advances have also increased the number and complexity of the technical factors that must be understood and properly controlled to achieve a consistently high level of quality in diffusion imaging. The goal of this review article has been to consolidate this expanding body of knowledge for optimization of DWI and DTI, including 3D fiber tractography.

However, continued improvements in the technology of diffusion MR imaging will ensure that the current state-of-the-art will be rapidly superseded. One major avenue for future progress is newer mathematic models such as HARDI^39–41 and diffusion spectrum imaging,⁷² which promise to overcome the shortcomings of the diffusion tensor for representing complex white matter architecture such as crossing fibers and intravoxel partial volume averaging. They are a more natural fit than DTI for the emerging fields of probabilistic tractography^73–75 and whole-brain connectivity analysis.⁷⁶ These newer methods also take better advantage of ongoing MR imaging hardware developments, including the synergistic combination of 7T diffusion¹⁷ with highly accelerated parallel imaging,^18–20 which should lead to new scientific and clinical applications in neuroradiology.