Structure-based QSAR Models to Predict Repeat Dose Toxicity Points of Departure

Abstract

Human health risk assessment for environmental chemical exposure is limited by a vast majority of chemicals with little or no experimental in vivo toxicity data. Data gap filling techniques, such as quantitative structure activity relationship (QSAR) models based on chemical structure information, can predict hazard in the absence of experimental data. Risk assessment requires identification of a quantitative point-of-departure (POD) value, the point on the dose-response curve that marks the beginning of a low-dose extrapolation. This study presents two sets of QSAR models to predict POD values (POD_QSAR) for repeat dose toxicity. For training and validation, a publicly available in vivo toxicity dataset for 3592 chemicals was compiled using the U.S. Environmental Protection Agency’s Toxicity Value database (ToxValDB). The first set of QSAR models predict point-estimates of POD values (POD_QSAR) using structural and physicochemical descriptors for repeat dose study types and species combinations. A random forest QSAR model using study type and species as descriptors showed the best performance, with an external test set root mean square error (RMSE) of 0.71 log₁₀-mg/kg/day and coefficient of determination (R²) of 0.53. The second set of QSAR models predict the 95% confidence intervals for POD_QSAR using a constructed POD distribution with a mean equal to the median POD value and a standard deviation of 0.5 log₁₀-mg/kg/day, based on previously published typical study-to-study variability that may lead to uncertainty in model predictions. Bootstrap resampling of the pre-generated POD distribution was used to derive point-estimates and 95% confidence intervals for each POD prediction. Enrichment analysis to evaluate the accuracy of POD_QSAR showed that 80% of the 5% most potent chemicals were found in the top 20% of the most potent chemical predictions, suggesting that the repeat dose POD QSAR models presented here may help inform screening level human health risk assessments in the absence of other data.

1. Introduction

Human health risk assessment due to environmental chemical exposure is limited by the tens of thousands of chemicals with little or no experimental in vivo toxicity data [1]. A complete battery of regulatory tests for risk assessment associated with a single chemical relies on multiple animal tests and can costs millions of dollars [2]. A more effective way to evaluate a large number of environmental chemicals is to prioritize them for additional testing based on the results of new approach methodologies (NAMs) for predicting experimental data [3–5]. NAMs, including quantitative structure activity relationship (QSAR) models based on chemical structure information, are commonly used to predict chemical toxicity in the absence of experimental data [4, 6–10]. NAMs are increasingly being used for chemical safety evaluation and prioritization in accordance with the directive set forth by the Frank R. Lautenberg Chemical Safety for the 21st Century Act that encourages reduction in the animal testing and replacing them with computational or alternative approaches whenever applicable. The impetus to use NAMs is further supported by the 2019 memo by the EPA Administrator that directs the EPA to channel its efforts towards, “reducing requests for, and funding of, mammal studies by 30 percent by 2025, and eliminate all mammal study requests and funding by 2035” [11].

Toxicity in repeat dose studies includes a range of adverse effects on one or more systems in adult animals, such as changes in body weight, or gross and/or histopathological changes in organs. Toxicity can be measured in terms of different levels of effects based on a dose-response assessment, including the dose at which effects were first observed, i.e. lowest effect level (LEL), lowest observed effect level (LOEL) and low observed adverse effect level (LOAEL), and at the doses at which no effects were observed, i.e. the no effect level (NEL), no observed effect level (NOEL), or no observed adverse effect level (NOAEL). The NOAEL and LOAEL are defined via expert toxicological review to determine a critical effect level, whereas the LEL signifies the lowest dose at which a statistically significant effect was observed and the NEL is the next lowest dose in the dose index [12]. Throughout, we will use the term “effect level” to mean any dose in a study that showed a statistically significant treatment-related effect relative to study-level controls. These study-level effect level values (NOAEL/NEL/LOAEL/LEL) can be reviewed together to derive a chemical-level value of the dose where treatment-related effects may occur, i.e. a quantitative point-of-departure (POD) value, or the point on the dose-response curve that marks the beginning of a low-dose extrapolation for risk assessment. Prediction of this POD value using QSAR methods in the absence of a complete in vivo study battery of tests could provide a rapid screening result.

Repeat dose toxicity data for a chemical can come from several different sources with similar or different experimental designs that measure the same or different effect levels in repeat dose studies. Effect levels are experimental values of toxicity from individual studies. Therefore, a chemical with multiple studies could have multiple effect levels associated with it. To maximize the dataset available for training models, it is advantageous to combine all of these effect level data to overcome the effects of potential outliers on quantitative estimates of effect levels (or doses) and effect level variability. Consequently, a repeat dose toxicity dataset for a single chemical may include several observed effect levels and effect level types, with variability in these values. Variability in experimental in vivo data can arise from sources including biological variability (test species, environmental conditions, etc.) and/or systematic error (measurement errors, different experimental protocols, or measurement tools and/or metrics, etc.) [13–15].

The goal of the current analysis is to develop methods to predict a POD using QSAR methods (POD_QSAR) based on training set data from chemicals with multiple studies across multiple species and study types, with large dose ranges and small dose spacing. These predicted POD_QSAR could be used for prioritization or screening level risk assessments. Predicting POD_QSAR is challenging given the variability in experimental data, as even in an idealized battery of studies there would still be uncertainty in the POD due to experimental and biological variability. When computational models are developed using such variable data, the predictions are inherently subject to prediction uncertainty since the model performance will be evaluated using variable experimental data. Thus, uncertainty in the training data will lead to uncertainty in the computational model and in its performance estimates. Incorporation of variability in computational model development, and subsequent quantification of data-driven uncertainty in model predictivity, are critically needed to improve the reliability and acceptance of computational models for screening level risk assessment.

Several in silico models have been developed in the past to predict repeat-dose PODs. Mumtaz et al. developed a regression model to predict LOAELs using rat chronic toxicity data for a dataset of 234 chemicals. They report a standard error of 0.41 log₁₀-mg/kg/day and coefficient of determination (R²) of about 84% [16]. Hisaki et al. published a set of QSAR models to predict NOELs for repeat dose (421 chemicals), developmental (156 chemicals), and reproductive (315) toxicities using the data on environmental chemicals from Japan’s existing chemical database [17]. They reported 10-fold cross-validated root mean square error values (RMSE, log₁₀-mg/kg/day units) of 0.53, 0.56 and 0.51 for repeat-dose, developmental and reproductive toxicities, respectively [18]. Toropova et al. published a set of regression models developed using the Monte Carlo technique to predict NOAELs using a dataset of 218 chemicals. They report a RMSE in the range of 0.51–0.63 (log₁₀-mg/kg/day) and R² in the range of 0.61–0.67 on three randomly split validation sets of 19–21 chemicals [19]. Like the previous models, Veselinovic et al. published a set of QSAR models for predicting LOAELs using the Monte Carlo technique on a dataset of 341 organic chemicals. They report RMSE in the range of 0.46–0.76 (log₁₀-mg/kg/day units) and R² in the range of 0.49–0.70 on five randomly split validation sets of 11–30 chemicals [20]. These studies report models to predict different effect levels for repeat dose toxicity using relatively small datasets (<500 chemicals) and illustrate the limited accuracy of the models. A public and crowd-sourced challenge was also organized in 2013 by the United States Environmental Protection Agency (U.S. EPA) to develop models to predict repeat dose LELs using traditional animal toxicity data from ToxRefDB version 1 for 1800 chemicals [21–23]. The challenge had 436 registrants from over 32 countries. The winning model was built using 10 different LEL models utilizing different in silico descriptor packages available in OCHEM (online chemical database and modeling environment). The final model was built as a simple average consensus over the ten individual models. The consensus models were evaluated on the final test subset (80 chemicals) with reported RMSE of 1.12 ± 0.08 log₁₀-mg/kg/day and R² of 0.31 [22]. Recently, Truong et al. published models to predict repeat dose effect levels using a much larger dataset of 1247 chemicals. They developed a consensus model using a combination of study-level information (as descriptors) in addition to chemical, biological, and kinetic descriptors, and reported an external test set RMSE of 0.69 log₁₀-mg/kg/day and R² of 0.43 [24]. Examining these models suggests that several different modeling approaches for small datasets were unable to achieve a coefficient of determination (R²) greater than 43–70%, and RMSE values in log₁₀-mg/kg/day of less than approximately 0.5 log₁₀-mg/kg/day. However, none of these models considered the variability in underlying data in model development to subsequently characterize the uncertainty in model predictions. Presentations of QSAR predictions as a confidence interval may be useful in understanding not only model performance but also in performing preliminary safety assessments, where rapid identification of a range of doses for a putative POD would enable rapid estimation of hazard to exposure ratios to identify chemicals for which additional information would be informative. There are other types of in silico models (such as read-across) that are not reviewed here since they are out of scope with regards to the QSAR models developed in this work.

This study presents a set of QSAR models developed using chemical structural and physicochemical properties to provide a robust prediction for repeat dose toxicity in vivo POD using a large dataset of 3592 chemicals. Herein we present two sets of QSAR models as outlined in the schematic in Figure 1. The first set of models predict a single value as a point estimate of the POD value (POD_QSAR) for each chemical. The second set of models consider data variability in model development. These models use a bootstrap resampling technique to incorporate typical study-to-study variability (~0.5 log₁₀-mg/kg/day) previously reported by Pham et al. in the POD values for deriving confidence intervals in model predictions [12, 25]. To aid in chemical screening and prioritization efforts, all of these models were also evaluated for their ability to accurately predict the PODs for the most potent chemicals, referred to hereafter as enrichment analysis.

Figure 1.

Schematic outlining the different models developed in this work.

2. Methods

2.1. Dataset

The in vivo data used to develop the QSAR models in this study was taken from the U.S. EPA’s ToxValDB database [26], a database compiled from experimental toxicity data on ~3500 chemicals from over 40 publicly available sources. The current version of ToxValDB is accessible through the EPA’s CompTox Chemicals Dashboard [27] (https://comptox.epa.gov/dashboard) and more information on the database is provided in supplemental information (POD-QSAR_SupplementaryFile.docx, Section S1). The database was queried and filtered for in vivo data according to several criteria.

1. Study types and species: data corresponding to five study types, including chronic (CHR), subchronic (SUB), reproductive (REP), developmental (DEV), and subacute (SAC) for three different species, rat, mouse, and rabbit, based on availability of adequate data from a modeling perspective were used. The CHR studies include cancer studies, the SUB studies include repeat-dose and short-term studies, the REP studies include multigenerational reproductive studies, and the developmental studies labeled by submitters as “reproductive developmental”;

2. Lifestages: For developmental studies, effect levels include those from all generations (i.e. not limited to parental effects);

3. Effect level types (recall that effect level is a generic term for the dose where any effect is observed or for the maximum dose at which no effect was observed): data for specific effect level types included lowest effect level/concentration (LEL, LEC), lowest observed effect level/concentration (LOEL, LOEC), lowest observed adverse effect level/concentration (LOAEL, LOAEC), no effect level (NEL), no observed effect level/concentration (NOEL, NOEC), no observed adverse effect level (NOAEL, NOAEC), benchmark dose/concentration (BMD, BMC, BMC10), benchmark dose/concentration lower bound (BMDL, BMDL-01, BMDL-05, BMDL-10, BMDL-1SD, BMCL, ‘BMCL-5’, ‘BMCL-10’, ‘BMCL-1SD’); and,

4. Administration route and effect level units: effect levels measured in mg/kg/day as defined by the study authors. Most studies use oral exposures in food or water, with a small number of inhalation or dermal studies where doses have been converted to mg/kg/day by the study authors.

Following these requirements, only the study type and species combinations with data on more than 50 chemicals were used for modeling to ensure an adequate amount of data. The final number of effect level data and the number of unique chemicals per study type and species combination are listed in Table 1. QSAR models were subsequently developed for each study type and species combination (e.g., model 1: study type = chronic | species = rat; model 2: study type = chronic | species = mouse, etc.) and the complete dataset. Note that for a given study-type/species combination, a chemical may have multiple effect level values, including for instance a combination of LOEL, NEL, and BMD values. Given finite dose spacing, we assume that toxicologically relevant effects will arise within the range of these values. Alternative choices would be to only include LEL/LOEL/LOAEL values, or to only include NEL/NOEL/NOAEL values. However, either of these choices would reduce the size of the data set (both in terms of studies included and chemicals) and would bias the POD predictions either up or down in dose. Therefore, on average, the predictions from the current model should lie somewhere between the LEL/LOEL/LOAEL and the NEL/NOEL/NOAEL.

Table 1.

Summary of the dataset and random forest model performance metrics for different study types and species combinations used in this study. Only the combinations with more than 50 unique chemicals were used in this analysis. The mean standard deviation per combination reflects the underlying variability in the data and can be thought of as a theoretical lower bound on RMSE i.e. we can expect the RMSE to be higher than this.

Study Type	Species	Total number of effect level values	Number of unique chemicals with curated structure and descriptors	Training-Test set split	Theoretical lower bound on RMSE (Mean standard deviation of effect level values, Figure 2)	Random Forest Model Performance Metrics
						Internal Training Set (5-fold cross-validation)			External Test Set
						RMSE	RMSE/σ	R2	RMSE	RMSE/σ	R2
Chronic (CHR)	Rat	7172	1129	903-226	0.51	0.93	0.76	0.43	0.93	0.82	0.33
	Mouse	4029	720	576-144	0.50	0.86	0.84	0.29	0.96	0.82	0.33
	Rat, Mouse	11201	1236	988-248	0.55	0.94	0.78	0.39	0.92	0.77	0.40
Subchronic (SUB)	Rat	36017	3199	2559-640	0.48	0.81	0.82	0.33	0.86	0.85	0.28
	Mouse	5030	723	578-145	0.50	0.88	0.83	0.31	0.86	0.80	0.37
	Rabbit	1516	415	332-83	0.49	0.96	0.96	0.08	0.83	0.90	0.20
	Rat, Mouse, Rabbit	42563	3306	2644-662	0.50	0.83	0.83	0.31	0.80	0.82	0.33
Reproductive (REP)	Rat	5446	841	672-169	0.49	0.79	0.80	0.36	0.76	0.84	0.30
	Mouse	505	87	69-18	0.36	1.80	1.09	−0.19	0.88	0.71	0.50
	Rat, Mouse	5951	889	711-178	0.49	0.91	0.86	0.26	0.79	0.83	0.31
Developmental (DEV)	Rat	6021	930	744-186	0.41	0.80	0.92	0.16	0.78	0.89	0.20
	Mouse	704	116	92-24	0.34	1.05	0.96	0.09	0.80	1.05	−0.09
	Rabbit	3220	491	392-99	0.38	0.76	0.89	0.20	0.88	0.95	0.10
	Rat, Mouse, Rabbit	9945	1004	803-201	0.42	0.76	0.89	0.29	0.80	0.86	0.26
Subacute	Rat	946	160	128-32	0.58	0.92	0.98	0.05	1.04	1.05	−0.10
ALL (CHR, SUB, REP, DEV, SAC)	All (Rat, Mouse, Rabbit)	71020	3632	2905-727	0.53	0.82	0.82	0.32	0.81	0.80	0.36
*ALL (CHR, SUB, REP, DEV, SAC)	All (Rat, Mouse, Rabbit)	71020	3632	8349-2088	-	0.67	0.65	0.54	0.70	0.64	0.57

^*The numbers in this row reflect the final model (Figure 5) which use study type and species as additional descriptors and so each chemical is used more than once in the training dataset as separate instances reflected in the much larger size of training and test sets.

2.2. Structure and molecular descriptors

QSAR-ready chemical structures for the chemicals used in this study were obtained from the DSSTox database [28]. The chemical structures in the database were curated and standardized to ensure accuracy in chemical structure by correcting errors and mismatches in chemical structure formats and identifiers and structure validation issues like hypervalency. [29, 30]. These chemical structures were characterized using PubChem fingerprints [31], PaDEL physicochemical descriptors [32], and Chemistry Development Kit (CDK) molecular descriptors [33, 34]. The PubChem fingerprint is an 881-bit long vector where each bit represents the presence or absence of a specific substructure indicated by 1 and 0, respectively. The substructural units spanned by PubChem fingerprints include hierarchical element counts, rings in a canonical extended smallest set of smallest rings, ring set, simple atom pairs, simple atom nearest neighbors, detailed atom neighborhoods, simple SMARTS patterns, and complex SMARTS patterns [35]. The PubChem fingerprints were generated in KNIME analytics platform (version 3.7.1) [36]. PaDEL is a software that can calculate 1875 descriptors (1444 1D, 2D descriptors and 431 3D descriptors) and 12 types of fingerprints using the CDK toolkit [37]. For this work, only 1444 1D and 2D descriptors were calculated which include functional group counts, atom-type, e-state indices, fragmental, topological, and constitutional descriptors. CDK is an open-source freely available software designed for cheminformatics and bioinformatics applications. Eighteen CDK molecular descriptors were calculated using the CDK toolkit implemented in KNIME analytics platform (version 3.7.1). The descriptors include logP, molecular weight, number of aromatic bonds amongst many others. Chemicals for which the descriptors could not be calculated were not considered in model development.

Next, feature cleaning and selection was performed to select features that contribute most to model performance. Constant or near constant fingerprint bits (i.e., fingerprint bits contained by >80% of the chemicals in this study) were removed since they do not provide any added value in the modeling process. Only one fingerprint bit from a pair of correlated bits was retained if the correlation coefficient was greater than 80%. Supervised recursive feature elimination algorithm (recursively considering smaller and smaller sets of features) was used to select 5 descriptors from PaDEL and CDK descriptors each to reduce the number of descriptors.

2.3. Experimental data variability and uncertainty quantification analysis

The experimental effect level data for most of the chemicals was obtained from more than one primary data source as recorded in ToxValDB. Figure 2 shows the distribution of the number of effect level values for each chemical per study type and species combination (referred to as a combination hereafter), as outlined in Table 1. To understand the variability in available experimental data, a two-step procedure was employed. First, the range of effect level values was calculated for each chemical for each combination. Second, the variance and standard deviation in the effect level values for each chemical was calculated to understand the variance in experimental data due to study-to-study variation.

Figure 2.

Number of effect level values (experiments/studies) per chemical with data across different study types and species combinations with data on more than 50 chemicals.

2.4. Development of QSAR models

QSAR models were developed for each training data combination using the molecular descriptors described above and several machine learning algorithms including k nearest neighbors [38, 39], support vector machines [40, 41], random forests [42, 43] and gradient boosting regression [44, 45]. More details on the algorithms are provided in supplemental information (POD-QSAR_SupplementaryFile.docx, Section S2). All the QSAR models were developed within a 5-fold cross-validation scheme, where the dataset was randomly split into 80% training and 20% test set, respectively. The models were built using the training set and were evaluated using 5-fold internal cross validation. The hyper-parameters for each model were tuned using 5-fold cross-validated parameter search, where the model was developed over a grid of parameter values (in Python, function “gridsearch”), and the parameter values with the best model performance were selected as the final algorithm hyper-parameters. Once the model was developed on the training dataset, external validation was performed on the test set. The consistently best performing algorithm in terms of RMSE, R², and estimated error across the training and test set, Random forest, was chosen as algorithm of choice for final model development.

Random forest is an example of an ensemble machine learning method, which constructs modified bagging ensembles of random decision trees for classification and regression problems. Each tree gives a predicted response for an instance, and the final predicted response is the consensus or an average prediction from all the trees in the ensemble [42, 43]. The hyper-parameters for the model optimized in this work are: number of trees in the forest (values used: 500, 750, 1000, 1250 and 1500) and number of features to consider when looking for the best split (values used: auto and sqrt). Finally, two types of models were developed for each experimental dataset combination as described below.

2.4.1. Point-estimate QSAR models

Point-estimate QSAR models use a single representative effect level value for each chemical in the training set. This is in distinction to confidence interval QSAR models, described in the next section. This point estimate approach is what is typically used in QSAR modeling. To be clear on terminology, models are trained on effect levels, but the output is a prediction of a POD (POD_QSAR) by chemical-study type- species combination. The training data for these models uses the median log₁₀(effect level mg/kg/day) value across all experimental effect level values for a chemical for a given combination of study type and species. In addition to models for each combination, two sets of models were developed using the complete dataset where all the chemicals are pooled together as a single dataset. In the first of these models, study type and species are not used to distinguish between effect levels for a given chemical. For each chemical, the median of all the experimental effect level values was used as the training effect level value. In the second of these models, chemicals are grouped by study type and species, and the median effect level value for that group was used as the training effect level value for that group. Thus, a single chemical can be used more than once in the training dataset, and the different instances are distinguished by using study type and species as additional descriptors in these models. Table 1 summarizes the different combinations and types of models developed. Throughout this paper, effect levels are represented as their log base 10 values, i.e. log₁₀-mg/kg/day.

2.4.2. Point-estimate with confidence interval models

The process for deriving a point-estimate of POD (POD_QSAR) with confidence intervals is illustrated and summarized in Figure 4 using Bisphenol A as an example chemical. A log-normal distribution of effect level values was constructed for each chemical where the mean of the distribution was set as the median experimental log₁₀-mg/kg/day effect level value for each chemical, and the standard deviation of the distribution was set as 0.5 log₁₀-units (typical study to study variability) based on the observations in this study (Figure 3(b)) and as previously reported by Pham et al. [25, 46]. The reason for using a single standard deviation value is that the chemicals in the current data set have variable numbers of effect values, including chemicals with a single value. Therefore, estimates of the chemical-specific standard deviation would be prone to significant uncertainty. This distribution of effect level values was used to develop 100 bootstrap models such that for each model, the effect level value for a chemical was randomly sampled from the constructed POD distribution. Each cross-validated bootstrap model then results in 100 POD_QSAR predictions per chemical. The final predicted POD_QSAR value is the mean of the 100 predictions, and the 95% confidence interval is calculated as ±2 standard deviations of the predictions. In case of models where study type and species are used as additional descriptors in the model, each chemical is assigned a mean value within that group, and the final summary POD_QSAR prediction for the chemical is calculated as the median of the bootstrapped means for each group of predictions.

Figure 4.

Schematic outlining the bootstrapping process for development of effect level point estimate and confidence interval models using Bisphenol A as an example chemical and using of effect level data from all study types and species. A POD (log₁₀-transformed) distribution is constructed where the mean (μ) of the distribution is set as the median effect level value (= 1.57) and the standard deviation (σ) is set equal to 0.50 (based on typical lab-to-lab variability). Next, for each (of n) bootstrapped models the POD value for Bisphenol A is randomly drawn from the pre-constructed POD distribution. Finally, each cross-validated bootstrapped model predicts a POD_QSAR value resulting in n POD_QSAR predictions. The final point-estimate POD_QSAR value is the mean of the n predictions and the confidence interval derived as the one standard deviation of the n predictions. In this work, n = 100.

Figure 3.

(a) Distribution of the range of effect level values per chemical as obtained from the ToxValDB database for each study type combination. As seen, the distribution of effect level values can range from 0–4 for all dataset combinations. (b) Distribution of the standard deviation (σ) of the effect level values for each chemical per study type and species combination. As seen, the standard deviation per chemical ranges between −0.34–0.58 for all dataset combinations. The mean standard deviation (μ_σ) gives an estimate of the experimental variability in the underlying data for each combination which limits the predictive ability of any model developed on this data. The mean (μ_σ) of the distribution is used as an estimate of theoretical lower bound on RMSE values for the QSAR models developed using these data (Table 1).

A third set of models was developed using a reconstructed dataset that aimed to reduce the skewness in the underlying data. However, these models did not yield any performance improvement and have not been discussed in the main manuscript; results and discussion for these models are included as part of supplemental information (POD-QSAR_SupplemtntaryFile.docx, Section S3).

2.5. Enrichment analysis

Enrichment analysis evaluated the ability of the models to accurately identify the most potent chemicals in the dataset. This is an important element because successful utilization of any QSAR for a POD in prioritization and screening level risk assessment applications requires that the most potent chemicals be identified; failure to identify these most potent chemicals could result in failure to employ protective exposure limits for these chemicals. The external test set for each training dataset combination (i.e. species, study type) was rank-ordered according to the median effect level value for each chemical, with the most potent chemical (lowest median effect level value) ranked 1 and the least potent (highest median effect level value) ranked last. This sorted list is referred to as the experimental rank list. Next, the point-estimate QSAR models were developed for each training data combination, and the resultant models were used to predict a point POD_QSAR value for each chemical in the external test set. The chemicals in the external test set were then rank ordered according to their predicted POD_QSAR values. This sorted list is referred to as the predicted rank list. Finally, the fraction of the N% experimental rank list that was found (enriched) in X% of the predicted rank list was calculated for each model.

2.6. Code and Data Availability

The software code for data analysis and model development was written in Python 3.2 [47, 48]. The models were developed using the sklearn package and the hyper-parameters for each machine learning language were tuned using the gridsearch function. The Python code and KNIME workflow for generating the descriptors are available as supplementary information.

3. Results

3.1. Data variability analysis

Most chemicals with data in each study type-species combination have a range of repeat dose toxicity data effect level values. Figure 3(a) shows the distribution of effect level range of log₁₀-mg/kg/day values for chemicals in each of the study type-species combinations. Chemicals with only one log₁₀-mg/kg/day effect level value have a range of zero and were excluded from this analysis. In general, the log₁₀-mg/kg/day effect level value range can vary up to 4 orders of magnitude, and the average range tends to be about 1 order of magnitude for the bulk of chemicals. Mean standard deviation of the effect level per combination gives an estimate of variability in the underlying data and can be considered as a theoretical lower bound on the RMSE of the models developed using these data. Thus, RMSE of the predictive models are expected to be at least as large as the mean standard deviation of these effect level values. For example, the mean standard deviation per chemical in the CHR-rat combination is 0.51 log₁₀-mg/kg/day, and so one would expect the models to have errors close to 0.51 log₁₀-mg/kg/day, solely due to the variability in the dataset being modeled. Figure 3(b) shows the distribution of standard deviations of the effect level in log₁₀-mg/kg/day values for chemicals in each of the combinations. Chemicals with only one effect level have were excluded from this analysis. In general, the peaks in these distributions are around 0.5 log₁₀-mg/kg/day, which is similar to what has been observed in recent works on variability in in vivo studies by Pham et al. (data restricted to studies with oral exposure) [25, 46].

3.2. Point-estimate models

QSAR models were developed for each dataset combination using machine learning algorithms described in the Supplemental File (POD-QSAR_SupplementaryFile.docx). Predictive performance of individual models was evaluated using RMSE, ratio of RMSE to the standard deviation of the modeled dataset (RMSE/σ), and coefficient of determination (R²). The predictive performance of the best model for each dataset combination were compared. Random forest models had the best metrics across all the dataset combinations (results not shown for other algorithms). A summary of the best model metrics is given in Table 1. There is not much variation in the metrics across different dataset combinations; RMSE ranged from 0.76–1.80 log₁₀-mg/kg/day (training) and 0.76–1.04 (test); RMSE/ σ ranged from 0.76–1.09 (training) and 0.71–1.05 log₁₀-mg/kg/day (test); and, R² ranged from −0.19–0.43 (training) and 0.09–0.40 (test). The final models were, therefore, developed using a complete dataset across all study types and species, and using study types and species as descriptors to the model in addition to chemical fingerprints and physicochemical descriptors.

Adding species and study types as additional descriptors to the complete (all study type-species combinations) dataset of 3632 chemicals resulted in the best overall model (Table 1). The effect level distribution in the dataset is 7.83% rat, 14.7% mouse and 7% rabbit, and 59.9% subchronic, 15.9% chronic, 14% developmental, 8.4% reproductive and 1.8% subacute studies. The fingerprints, descriptors, and model hyperparameters of the model are listed in supplemental information Table S1 (POD-QSAR_SupplementaryFile.docx, Section S5). Figure 5(a) shows the distribution of the training and test set relative to each other used for training and validating the complete dataset model. In all, there were 8349 chemical instances in the training set and 2088 chemical instances in the external test set. Note that each chemical within a study type-species combination is considered a separate instance in this model. Figure 5(b) and (c) show the plots of observed versus predicted point POD values for the 5-fold cross-validated training set (red scatter plot) and the external test set (green scatter plot), respectively. The performance metrics for the 5-fold internal cross-validation were RMSE = 0.70 log₁₀-mg/kg/day, RMSE/σ = 0.67, and R² = 0.53, and for the external test set were RMSE = 0.71 log₁₀-mg/kg/day, RMSE/σ = 0.67 and R² = 0.53.

Figure 5.

Data and model performance results for the best model (random forest) developed using a combination of all study types (CHR, SUB, DEV, REP and SUB) and all species (rat, mouse and rabbit) and using species and study type as additional descriptors in the model. (a) Distribution of the training and training and test dataset relative to each other, (b) observed versus predicted POD_QSAR values (transformed scale) for 5-fold internal cross-validation (red scatter plot), and (c) observed versus predicted POD_QSAR values (transformed scale) for external validation (green scatter plot). The legend shows the performance metrics of each set where RMSE = root mean-squared error, σ = standard deviation of the dataset, and R² = coefficient of determination. The blue dotted lines indicate an error interval of one standard deviation of the dataset. The points within the error interval are predicted within one standard deviation of the observed values.

The impact of each descriptor can be assessed by averaging the results across all the trees in the forest. By such an analysis, it is possible to calculate the importance of each fingerprint and descriptor that is used to develop the model and the variability based on inter-trees performance shown in supplemental information (POD-QSAR_SupplementaryFile.docx, Figure S2). A summary of the top 10 descriptors as determined by the feature importance analysis are listed in Table 2. While none of the descriptors seem to have a huge amount of impact on their own, study type (chronic, developmental etc.) turns out to be the most significant descriptor of putative POD values. It is also well known that there is a strong effect of the study type and species on POD values [12,25].

Table 2:

Summary of the top 10 descriptors that drive POD predictions identified using feature selection analysis in the Random forest model.

DescriptorNumber	Relevant Descriptors	Description	Feature Importance Value	Descriptor Source
1	Study Type	The type of study conducted (chronic, subchronic etc.)	0.10	Study data
2	Molar Mass	Molar mass	0.06	CDK
3	Molecular Weight	Molecular weight	0.06	CDK
4	Species	Species in which the study was conducted (rat, mouse, rabbit)	0.06	Study data
5	VABC Volume Descriptor	Volume descriptor using the method implemented in the VABCVolume class.	0.05	CDK
6	Atomic Polarizabilities	Sum of the atomic polarizabilities (including implicit hydrogens)	0.05	CDK
7	Sv	2D constitutional descriptor (Sum of atomic van der Waals volumes scaled on carbon atom)	0.05	PaDEL
8	ATS0i	Autocorrelation descriptor (Broto-Moreau autocorrelation - lag 0/weighted by first ionization potential)	0.05	PaDEL
9	Si	Constitutional descriptor (Sum of first first ionization potentials scaled on carbon atom)	0.05	PaDEL
10	Sse	Constitutional descriptor (Sum of atomic Sanderson electronegativities scaled on carbon atom)	0.05	PaDEL

Figure 6 shows the results of the enrichment analysis on the test dataset. The enrichment analysis was done for 5%, 20% and 50% most potent chemicals. As seen, over 75% of the 5% most potent chemicals were found in the 10% most potent predicted chemicals and over 80% of the 5% most potent chemicals were found in 20% of the most potent predicted chemicals.

Figure 6.

Enrichment analysis for 5%, 20% and 50% most potent chemicals (observed) in the predicted set from the random forest model developed using the dataset with all study types and species and using study type and species as additional descriptors in the model. Over 75% of the 5% most potent chemicals were enriched within 10% of predicted potent chemicals.

3.3. Point-estimate with confidence interval models

The hyperparameters of the random forest model for the final point-estimate model was used to develop 100 bootstrap models. Figure 7 shows the observed versus predicted plot for 50 chemicals chosen randomly from the training and test dataset. Each dot on the plot represents a chemical and is associated with 95% confidence interval (CI) bars reflecting underlying experimental variability and model predicted uncertainty. The observed 2-sided CI is calculated as the ±2 times the average standard deviation of the experimental effect levels for each chemical i.e. each chemical has an associated experimental uncertainty due to the variability in effect level measurements. The predicted 2-sided CI for each chemical is calculated as ±2 times the standard deviation of the predictions from the models. The blue dotted lines indicate an error margin of ±1 log₁₀ unit. The bootstrap models did not result in improved performance as compared to the point-estimate models. However, the benefit of this approach is that each point-prediction could be associated with a 95% confidence interval.

Figure 7:

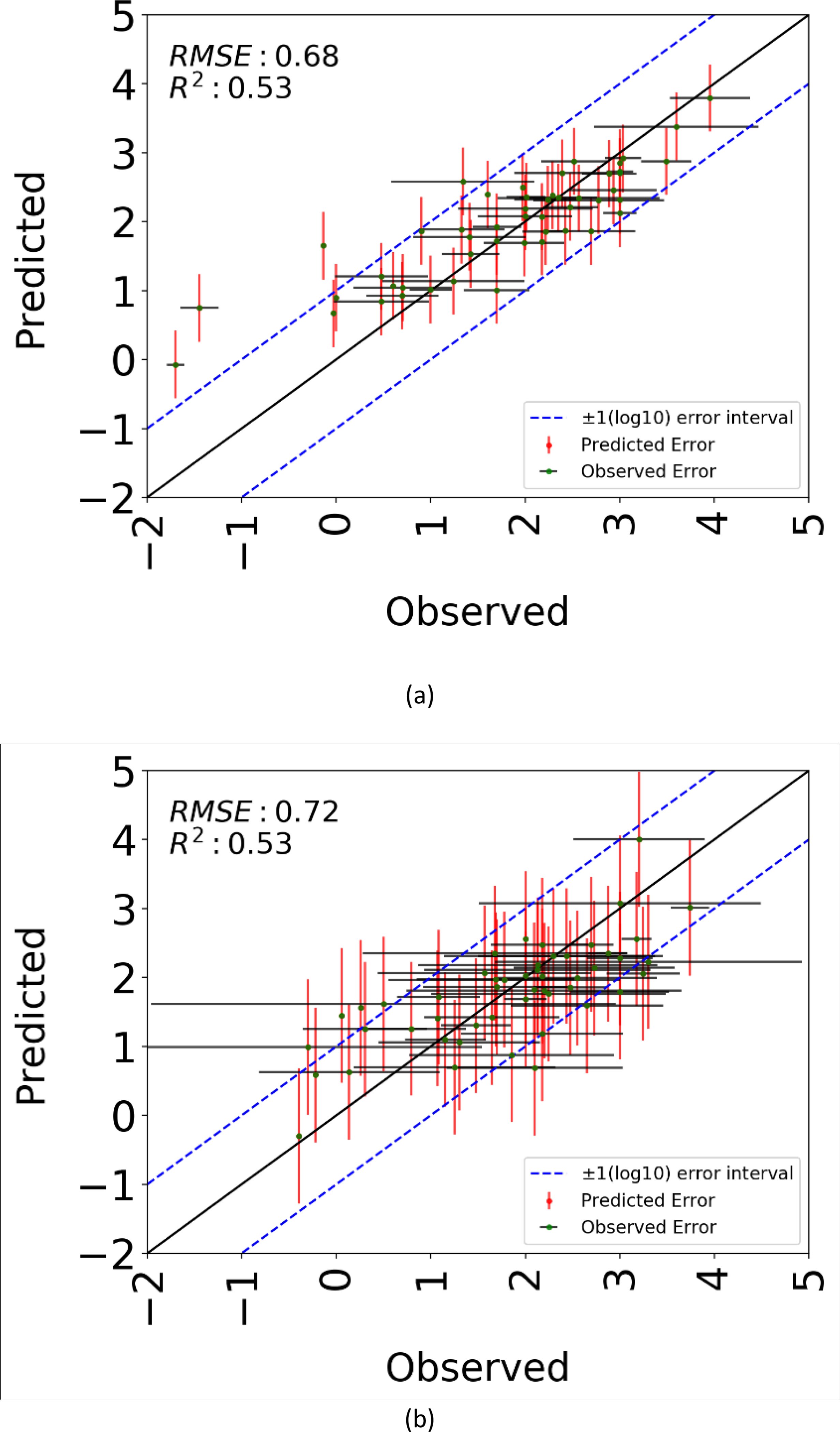
Model performance results for point-estimate with confidence intervals models calculated using n=100 bootstrap models for (a). training set, and (b). test set. 50 chemicals from each, training and test, set were randomly selected and plotted along with the observed and predicted confidence intervals. The predicted 95% confidence interval (error bar) for each chemical is calculated as two standard deviations of the predictions from the models. The observed 95% confidence interval (error bar) is calculated as two standard devisations of the experimental data for each chemical. The blue dotted lines indicate an error margin of ±1-log₁₀ unit.

The final models with instructions to help derive predictions for a new chemicals are included as part of supplemental information (PredictPradeepPOD-QSAR_HelpFile.docx).

4. Discussion

This study presents simple structure-based QSAR models for predicting repeat dose toxicity PODs using a large, diverse dataset of 3632 chemicals spanning various use classes. Overall, the novelty of this work lies in: (1) compilation and use of the largest dataset of environmentally relevant chemicals to date for use in the development of POD models, (2) assessment of underlying variability in the experimental data coming from a variety of in vivo studies and incorporation of that variability to understand model uncertainty and derivation of confidence intervals for each prediction, and (3) enrichment analysis to evaluate the suitability of these models from a screening level risk assessment and prioritization perspective. These models provide a robust support framework for chemical screening and prioritization efforts to aid human health risk assessment.

Multiple point-estimate QSAR models were built initially to evaluate model performance when the data were partitioned by different study type-species combinations. Interestingly, the results demonstrated that the best performing point estimate model resulted from using the largest dataset possible that included all study type-species combinations. In this model, species and study type were still considered as model descriptors. This result suggests that for prediction of repeat dose toxicity using a QSAR approach, the best model performance is obtained using the largest dataset possible; this result makes sense given that the potential impact of any putative outliers or influential values in these models would likely be dampened by the size of the dataset for all study type and species combinations. The dataset for all combinations of study type and species is far larger (over 71,000 effect level values) than the number of values in any of the other datasets partitioned by study type-species combination (ranging from approximately 500 to 43,000 values depending on the combination, see Table 1). This is also consistent with previous work that suggested that similar amounts of variance could be explained in datasets with any study type and species combination as well as datasets partitioned by study type and species [12].

The performance of the current model can be compared with previously published models summarized in the introduction [16–22, 24]. Summary statistics for this comparison are provided in Table 3. Overall, the current model RMSE appears slightly higher and R² value appears lower than many of the previously published models. However, it should be noted that (1) the current model is built using a significantly larger data set, indicating that the domain of applicability should be larger, and (2) it is different from previously published models in that it predicts an overall chemical level POD value and not various effect levels (e.g., NOAEL or LOAEL specifically) specific to study type or type of toxicity observed, which renders the comparison somewhat biased. Additionally, this model, like that of Truong et al., has explicitly taken account of the variability in the underlying experimental data, so the performance metrics may more accurately reflect the reality of the variable experimental data.

Table 3:

Comparison of performance of the current model with previous publications.

Study	Reference	Number of chemicals	RMSE (log10-mg/kg/day)	R2
Current	Current	3592	0.70	0.57
Mumtaz et al.	[17]	234	0.41	0.84
Hisaki et al.	[18], [19]	421	0.53, 0.56, 0.51	-
Toropova et al.	[20]	218	0.51–0.63	0.61–0.67
Veselinovic et al.	[21]	341	0.46–0.76	0.49–0.70
Novotarskyi et al.	[23]	1,854	1.12 ± 0.08	0.31
Truong et al.	[25]	1247	0.69	0.43

A primary novel finding in this work is that a 95% confidence interval (± 2 standard deviations) around each POD_QSAR prediction of repeat dose toxicity approaches ± 1 log₁₀-mg/kg/day, based on the variability in the training set values. Quantitative prediction of POD within ± 1 log₁₀-mg/kg/day when the training set POD values typically range approximately 1–2 log₁₀-mg/kg/day per chemical (Figure 3) indicates that variability in the POD values clearly limits QSAR accuracy. It is also worth noting that the majority of experimental effect levels span only about 4 orders of magnitude (Figure 5(a)). Supporting the use of the POD_QSAR approach presented here is the additional finding that over 75% of the 5% most potent chemicals were found in the 10% most potent predicted chemicals and over 80% of the 5% most potent chemicals were found in 20% of the most potent predicted chemicals. Thus, the POD_QSAR approach accounts for the variability in the reference data and the QSAR model by representing values with a confidence interval and still manages to identify the most potent chemicals.

The dataset refined from ToxValDB is the largest of its kind to date in the public domain. However, there are limitations in its use, including potential errors in the underlying experimental data. ToxValDB is undergoing a multi-year curation effort, where the database values (study type, species, chemical identity, duration, effect level and units, etc.) will be compared with those in the original study reports. One issue is the use of variable terminology by the multiple sources used by ToxValDB. An example is the designation of study type. Different sources may call studies run under a particular protocol either “subchronic” or “repeat dose.” In the development of the database, all values of this type are mapped to common terms, but further manual curation will be required to make sure that these mappings are correct. Another identified issue is the presence of a limited number of studies that are brought into the database from more than one source. An example are studies from the National Toxicology Program (NTP), which have been compiled by different sources (e.g. HESS and ToxRefDB), leading to replication of effect level values; however, this kind of replication issue would minimize estimates of variability. Yet another possible data curation issue is that the same study may have been reviewed by different regulatory authorities to result in different effect level value determinations; this issue would require resolution of study and report mapping.

The QSAR model reported here will have utility in screening level chemical safety assessment for human health hazard. It is important to note that the POD_QSAR values predicted here are mean values on the log₁₀ scale. To get the lower 95% confidence interval, one would need to subtract 2 times the standard deviation or about 1.4 log units. The values predicted by this model could be used in the context of exposure predictions to understand a hazard to exposure ratio for relative prioritization of chemicals for further data gathering [49, 50]. The work reported herein also informs expectations regarding model performance and accuracy in the prediction of repeat dose toxicity, confirming the observations reported previously that R² is unlikely to exceed 40–70% and RMSE is likely to approach 0.5 log₁₀-mg/kg/day for any model of a large repeat dose toxicity dataset (see Table 2 and references therein).