Use of fractal analysis in dental images for osteoporosis detection: a systematic review and meta-analysis

Abstract

Fractal dimension (FD) calculated on oral radiographs has been proposed as a useful tool to screen for osteoporosis. This systematic review and meta-analysis firstly aimed at assessing the reliability of FD measures in distinguishing osteoporotic patients (OP) from healthy controls (HC), and secondly, to identify a standardized procedure of FD calculation in dental radiographs for the possible use as a surrogate measure of osteoporosis. A comprehensive search was conducted up to September 2020 using PubMed, Web of Science, and SCOPUS databases. The Preferred Reporting Items for Systematic reviews and Meta-Analyses (PRISMA) statement was followed. Meta-analysis was performed on FD values calculated for HC and OP. Overall, 293 articles were identified. After a three steps screening, 19 studies were included in the qualitative appraisal and 12 were considered for meta-analysis. The methodological quality of the retrieved studies was generally low. Most of the studies included used White and Rudolph and box counting to process the images and to calculate FD, respectively. Overall, 51% of the studies found a meaningful difference between HC and OP groups. Meta-analyses showed that to date, FD measures on dental radiographs are not able to distinguish the OP from HC group significantly. From the current evidence, the use of FD for the identification of OP is not reliable, and no clear conclusion can be drawn due to the heterogeneity of studies. The present review revealed the need for further studies and provided the fundamentals to design them in order to find a standardized procedure for FD calculation (regions for FD assessment; images processing technique; methods for FD measurement). More effort should be made to identify osteoporosis using dental images which are cheap and routinely taken during periodic dental examinations.

Supplementary Information

The online version contains supplementary material available at 10.1007/s00198-021-05852-3.

Introduction

Osteoporosis is a major and growing health problem worldwide. It is a skeletal systemic disease characterized by low bone mass and deterioration of the microarchitectural structure of the bone which results in the increased risk of fractures [1]. On 1994, World Health Organization (WHO) provided diagnostic criteria on the assessment of fracture risk and its application for screening the postmenopausal osteoporosis. These criteria are based on the measurement of bone mineral density (BMD) [1], which is the amount of the bone mass per unit volume (volumetric density, g/cm³), or per unit area (areal density, g/cm²). BMD is assessed by dual-energy X-ray absorptiometry (DEXA) and it is recommended for all women who come to menopause age [2]. Osteoporosis is diagnosed if the patient’s femoral neck BMD is 2.5 standard deviations (SDs) below the average of a young and healthy individual (T-score). Low BMD, or osteopenia, is defined as a BMD value of more than 1 SD but 2.5 SDs below the normal range.

At present, the assessment of BMD is the only aspect that is readily measured in clinical practice which forms the cornerstone for the general management, risk prediction, and treatment of osteoporotic patients (OP) [3, 4]. Ideally, the clinical assessment of the skeleton should also capture other features of the bone, since other abnormalities such as micro-architectural deterioration can also contribute to skeletal fragility. The only BMD cannot capture all these assessments. As a consequence, it sometimes happens that there is an overlap in BMD scores of patients who do and do not sustain osteoporotic fractures. For example, patients undergoing a long duration of treatment with bisphosphonates show an increased risk of atypical femur fractures despite a decrease in osteoporotic and hip fractures [5]. Therefore, BMD alone cannot be considered an optimal index to monitor the effects of osteoporosis or treatments and to predict the risk of fracture [6]. Thus, there is a necessity to develop new techniques for better assessment of trabecular structures and cortical bone [7–9].

Dental radiographs are cheap and routinely taken during periodic dental examinations and checkups on a large population. Dental radiographs may provide a window into the composition and condition of the jawbone over a long period with minimal exposure or risk [10] as well as the chance for screening individuals with low BMD or risk of bone fractures. For example, the OSTEODENT project [11–16] used an image analysis software for automatic quantification of mandibular cortical width (MCW) from dental panoramic X-rays and showed that there is a correlation between MCW and BMD. These results suggest a possible use of dental radiographs for the evaluation of the BMD if acceptable specificity and sensitivity are achieved.

A possible useful method to analyze the radiographs is fractal analysis (FA), a mathematical method describing and analyzing complex shapes and structural patterns such as the bone tissue. Specifically, the fractal dimension (FD) is a quantitative measure of image complexity. Since coining the term fractal by Mandelbrot and devising sets of mathematical approaches to calculate FD [17], FA was applied in different fields including dentistry [18]. FA has been shown to be useful to quantify trabecular changes after jaw bone regeneration [19] and implant positioning [20]; to measure the roughness of implant surfaces [21, 22]; to evaluate the healing process of endodontic lesions after root canal treatment [23, 24]; to assess staging, grading, and survival on histological samples of individuals affected by oral squamous cell carcinoma; to diagnosis caries [25]; and to characterize and diagnose the epithelial-connective tissue interface malignant and premalignant lesions [18, 26]. That being said, the main application of FA in dentistry is the evaluation of the morphological pattern of jawbones and its possible change over time [27]. Some reports have shown the promising application of FD in differentiating healthy individuals (HC) from osteoporotic patients (OP) [10, 28–30]. The bone is a fractal tissue, and the FA may be the ideal non-invasive method of detecting and quantifying changes in the bone mineral content and architecture of jawbone in OP.

However, there is still a lack of literature on standardized methods to apply FA in radiographic images. There are some reviews in the literature about the FA of medical radiographs; however, these are focused on the application of FD in evaluating the bone microstructure using non-dental radiographs [31–34] or focused on the broad application of FD obtained from dental images. These reviews did not reach a conclusion about the applicability of dental radiographs for osteoporosis diagnosis [18, 27, 35, 36].

Therefore, this systematic review firstly aimed at evaluating the accuracy of FD obtained from dental radiographs in distinguishing HC from OP. Secondly, the authors intended to identify the appropriate site and technique to differentiate HC from OP by means of FD measurements on dental radiographs with the final goal to suggest a standardized procedure.

Materials and methods

Protocol

This systematic review was prepared according to the guidelines of the Preferred Reporting Items for Systematic Reviews and Meta-analyses (PRISMA) statement [37]. The current review addresses clearly a focused question by using the participant, intervention, comparison, and outcomes (PICO) criteria [38, 39].

Search strategy

Three electronic databases (PubMed, Scopus, and Web of Science) were used to identify publications that met the inclusion criteria. The search was conducted up to September 2020, using the following terms and keywords: dental radiography OR dental image OR panoramic OR cone-beam computed tomography OR CBCT OR periapical OR computed tomography AND fractal analysis OR fractal dimension OR lacunarity AND osteoporosis OR osteopenia OR bone. The search was limited to the English language. In addition to the electronic search, reference lists of the selected studies were manually screened.

Eligibility criteria

Original research articles in which FD was used for bone texture analysis of dental images from at least 5 HC and 5 OP were included. Only studies published in peer-reviewed journals were included, without any publication date restriction. In vitro or ex vivo studies, evaluating radiographs from regions other than the orofacial region and being about the effect of medical drugs on osteoporosis were excluded. Moreover, studies involving patients with systemic conditions that would affect bone metabolism (i.e., parathyroidism, hypoparathyroidism, Paget’s disease, osteomalacia, renal osteodystrophy, osteogenesis imperfecta, chronic renal disease, anemia, hyperthyroidism), cancers with bone metastasis or significant renal impairment, and/or involving patients using specific drugs or hormones (i.e., corticosteroids, excess thyroid hormone) which are known to have adverse effects on bone metabolism were excluded (Appendix Table 1).

Focused PICO question

Is FD from oral radiographs able to distinguish OP from HC?

Participants: patients with a history of bone loss due to osteoporosis confirmed by chart information, and/or BMD, and/or rate of fracture

Intervention: radiographs from the orofacial region and the corresponded FD

Comparison: FD mean values computed for HC and OP

Outcomes: Ability of FD values calculated from dental images to separate OP from HC (primary); the best procedure (i.e., location of the region of interest (ROI), technique of measurement) in the estimation of the FD for the identification of patients affected by osteoporosis (secondary)

Selection of studies

A three-stage screening (titles, abstract, and full text) was carried out by two authors (M.M. and V.P) independently. Title management was performed electronically by a commercially available software program (Endnote X7, Thomson, London, UK). Removal of duplicate studies was conducted internally in each database and by comparing the results against other databases. The full texts of potentially relevant articles were then obtained and assessed using an eligibility form. Any disagreements on the selection of studies were resolved by discussion, and the reasons for excluding irrelevant articles were reported.

Data extraction

The following information was extracted independently from each study by the two authors (M.M. and V.P.), using a predesigned data extraction form: title, authors’ names, contact address, study location, language of publication, year of publication, published or unpublished data, study design, method of randomization, duration of study, number of patients, ration of women to men, method of measuring the FD, type of radiograph, radiographic indices besides FD, non-radiographic indices, ROI, image processing method, outcome variables, and authors conclusion.

Risk of bias assessment

Quality assessment was conducted independently and in duplicate by two authors (M.M. and V.P.). The Quality Assessment of Diagnostic Accuracy Studies (QUADAS-2) criteria were followed, as suggested by Cochrane guidelines for diagnostic test accuracy [40]. Specifically, the QUADAS-2 tool adjusted by Calciolari et al. [36] was applied; each domain was evaluated in terms of risk of bias (low, high, or unclear), but not in terms of applicability. Only if all signaling questions for a domain were answered “yes,” then the risk of bias was judged as “low”; if any of the signaling questions was answered no, then the risk was considered “high.” The unclear answer was used only when insufficient data were presented to allow a judgment.

Data analysis

Data analysis was performed in order to review all selected studies which passed the eligibility criteria and to perform the meta-analysis on studies that reported FD values in HC and OP groups.

Review analysis

The review analysis summarized all important features of each study, including both demographic (number, sex, and age of participants) and methodological characteristics (type of image, non-radiographic indices, radiographic indices besides FD, methods for measuring FD, shape and location of the selected ROIs, image processing method). In addition, we summarized the analysis performed to estimate the ability of FD to distinguish HC from OP: analysis of specificity and sensibility (ROC analysis on FD values) or statistical comparisons between FD values in the two groups, or correlation analyses.

Meta-analysis

We selected all studies which measured FD from dental radiographs of HC and OP. Due to the heterogeneity of the studies in FD calculation (i.e., different sites and shapes of the selected ROIs, different methods to process the images), we calculated for each study, the mean difference of FD between HC and OP as effect index and the weight of the study according to the sample size (n_HC, number of HC and n_osteoporotic, number of OP) and standard deviations on FD measures in HC (SD(FD_HC)) and in OP (SD(FD_osteoprotic) groups). Specifically, for each i-th study:

$$\begin{array}{c}{\text{Effect}}_{\mathrm{i}}={\left({\text{mean FD}}_{\mathit{HC}}-{\text{mean FD}}_{\mathit{\text{osteoporotic}}}\right)}_{\mathrm{i}}\\ {\mathit{\text{weight}}}_i={\left(\frac{1}{\frac{\mathit{SD}\left({\mathit{FD}}_{\mathit{HC}}\right)}{n_{\mathit{HC}}}+\frac{\mathit{SD}\left({\mathit{FD}}_{\mathit{\text{osteoporotic}}}\right)}{n_{\mathit{\text{osteoporotic}}}}}\right)}_i\end{array}.$$

In the first meta-analysis, the ability of FD to differentiate HC from OP was estimated regardless the location and shape of the selected ROIs involved in the FD calculation and regardless the method for image processing and FD calculation. Secondly, meta-analysis was used to identify the best site and the best technique for the measurement of FD in dental radiographs to separate HC from OP. When fewer than 3 studies were retrieved, meta-analysis was not performed.

For each effect index and for the overall effect, 95% confidence interval (CI) was estimated.

Results

Review analysis

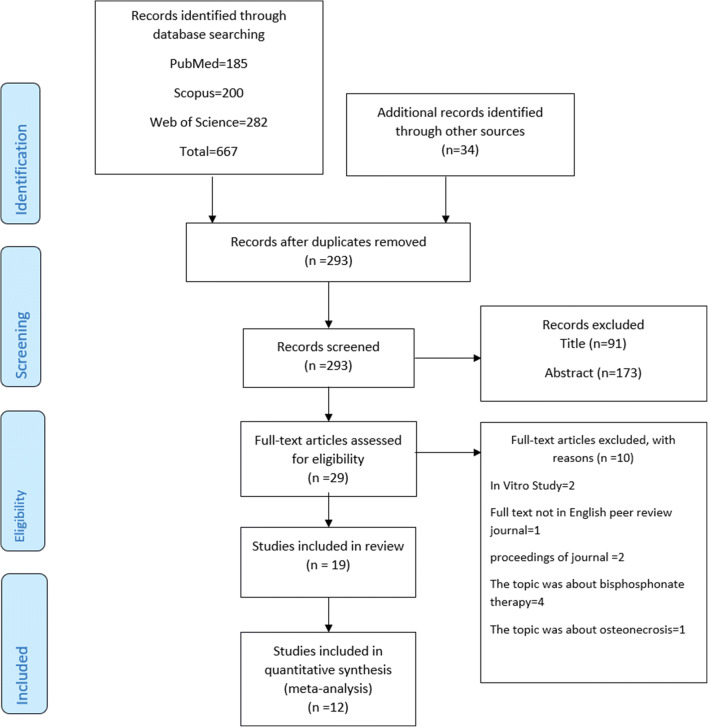
The search resulted in 293 unique articles. The initial screening of the titles and abstracts identified 29 full texts. After reading the full-text articles, 10 articles were excluded. The summary of the search strategy is depicted in Fig. 1. Nineteen articles [10, 28, 30, 41–56] were identified through the database, hand search, and bibliography check that met the inclusion/exclusion criteria. The reasons for study exclusions and characteristics of the included studies are presented in Appendix Tables 2 and 3.

Fig. 1.

Flow chart of the search process

Assessment of methodological quality

There was no study complying with all the QUADAS-2 items (Table 1). The patient selection and index test domains raised most of the methodological concerns being inadequate in all the studies. Sixteen articles (84%) did not specify how the patients were enrolled and 16% [28, 51, 53] showed a high risk of bias; indeed, demographic data of the population were often missed, and when provided, they were incomplete for an accurate assessment of the risk of bias. In addition, most authors did not report if the examiners were blinded to patients’ skeletal BMD and if both intra- and inter-observer agreement for index measurement were conducted. Sixteen studies [10, 28, 30, 41, 43, 45, 47–49, 51–56] out of 19 showed a low risk of bias regarding the reference standard domain indicating that skeletal BMD measured by DEXA is a well-established scientific criterion for the diagnosis of osteoporosis. Only 4 studies [42, 44, 46, 50] did not follow the WHO guidelines because in two of them the osteoporotic changes were secondary to other diseases (type 2 diabetes mellitus [46] and Sheehan’s syndrome [44]); therefore, the patients were classified according to their primary disease, and in the remaining two studies [46, 50], it has not been stated if the patients were classified as HC or OP based on the T-score. Finally, regarding flow and timing, only 26% of the authors [10, 30, 45, 51, 53, 54] stated that FD was measured on radiographs performed within 12 months from the date of the DEXA.

Table 1.

Detailed quality assessment for the 19 studies included in the qualitative appraisal

Author/year	Patient selection	Index test	Reference standard	Flow and timing
Alam/2020 [38]	?	?	☺	?
Alman/2012 [7]	?	?	☺	☺
Bollen/2001 [39]	?	?	☹	?
Camargo/2016 [40]	?	?	☺	?
De Sà Cavalcante/2019 [41]	?	☹	☹	?
Gungor/2016 [25]	☹	?	☺	?
Hwang/2017 [42]	?	☹	☺	☺
Kavitha/2015 [44]	?	☹	☺	?
Kavitha/2016 [45]	?	☹	☺	?
Kayipmaz/2017 [43]	?	?	☹	?
Koh/2012 [46]	?	?	☺	?
Law/1996 [47]	?	?	☹	?
Mostafa/2016 [48]	☹	?	☺	☺
Oliveira/2013 [49]	?	?	☺	?
Roberts/2013 [50]	☹	☹	☺	☺
Sindeaux/2014 [27]	?	?	☺	☺
Tosoni / 2006 [51]	?	☹	☺	☹
Vijayalakshmi/2017 [52]	?	?	☺	?
Yasar/2006 [53]	?	?	☺	?

☹high ☺risk; low risk; ? unclear risk

Study characteristics

Fractals may be calculated from digitized images, after a mandatory pre-processing analysis. Except for two studies [50, 53] that did not report the image processing method, the other 17 studies [10, 28, 30, 41–49, 51, 54–56] applied binarization before FD calculation. Moreover, 14 studies (74%) used the White and Rudolph image processing method. The participants in 12 out of 19 studies [41, 43, 47–56] were 100% women, 2 studies [10, 46] recruited a mix of men and women, and 5 studies [28, 30, 42, 44, 45] did not report the sex of the participants. The square form (48%) followed by rectangular (33%) was the most common shape for the ROI. The most common imaging technique was panoramic which was used in 15 studies (68%) [10, 30, 42, 43, 45, 47–50, 52–54, 56]. FD values for panoramic images showed the highest values among all the modalities with values ranging from 1.065 to 3.19 for HC and from 1.049 to 3.24 for OP. Overall, 19 measurements of FD (51%) found a meaningful difference between HC and OP groups [28, 30, 45, 47, 49, 50, 52], while 18 estimations of FD (49%) found no difference between HC and OP [28, 30, 41, 45, 51, 54–56]. The details of the main findings of the study are shown in Table 2.

Table 2.

Main characteristics and findings of the included articles for the review

Method of FD calculation	Articles % (n)
Box counting	73.68 (14)
Differential box counting	10.52 (2)
Power spectra	5.26 (1)
Others	10.52 (2)
Images processing method	Articles % (n)
White and Rudolph	73.68 (14)
Others	26.31 (5)
ROI shape	Articles % (n)
Rectangular	33.33 (7)
Square	47.61 (10)
Irregular	9.52 (2)
Not specified	9.52 (2)
Imaging techniques	Articles % (n)
PR	68.18 (15)
PA	18.18 (4)
CBCT	13.63 (3)
Main results on FD	Measurements % (n)
Significant difference between HC and OP	51.35 (19)
No difference between HC and OP	48.64 (18)
Accuracy higher than 80%	100 (2)
Accuracy lower than 80%	//
Significant correlation between FD and BMD	50 (1)
Absence of correlation between FD and BMD	50 (1)
Dental images	FD values (min-max)
PR	HC: 1.065–3.190 OP: 1.049–3.240
PA	HC: 0.834–3.190 OP: 0.823–3.240
CBCT	HC: 0.91–1.40 OP: 0.93–1.39

Abbreviations: CBCT cone beam computed tomography; FD fractal dimension; HC healthy control; OP osteoporotic patients; PR panoramic radiographs; PA periapical radiographs

Meta-analysis

Twelve studies [28, 30, 41, 45, 47, 49–52, 54–56] met the criteria for the meta-analysis. All FD values shown in each study were considered for the computation of the effect index and the weight. All FD values were shown in Table 3.

Table 3.

Summarizes fractal dimension (FD) values for the studies (#12) included in the meta- analyses

First author/year	Region/subregion 1: mandible; 2: maxilla; 3: condyle (a: molar; b: premolar; c: canine)	Healthy individuals		Osteoporotic patients		Method for measuring FD
		FD mean (sd)	N	FD mean (sd)	N
Alam/2020 [41]	1/b	1.64 (0.02)	30	1.65 (0.02)	30	Box counting by White and Rudolph
Gungor/2006 [28]	2/c	0.91 (0.17)	25	0.94 (0.08)	29	Box counting by Mandelbrot
	2/c	0.96 (0.04)		0.93 (0.05)
	3	1.4 (0.02)		1.37 (0.07)
	3	1.39 (0.07)		1.39 (0.04)
Hwang/2017 [45]	3	1.27 (0.06)	227	1.27 (0.07)	227	Box counting by White and Rudolph
	1/a	1.29 (0.07)		1.28 (0.07)
	1/b	1.22 (0.07)		1.21 (0.06)
Kavitha/2015 [47]	1/b	1.69 (0.03)	120	1.66 (0.04)	21	Differential Box Counting by Sarkar and Chauduri
	1/b	1.38 (0.04)		1.37 (0.04)
	1/b	1.15 (0.05)		1.11 (0.05)
	1/b	1.41 (0.03)		1.38 (0.03)
	1/b	1.69 (0.03)	121	1.66 (0.03)	20
	1/b	1.38 (0.04)		1.36 (0.03)
	1/b	1.15 (0.03)		1.14 (0.09)
	1/b	1.41 (0.02)		1.39 (0.04)
Koh/2012 [49]	2/c	1.16 (0.13)	31	1.17 (0.12)	25	Box counting by White and Rudolph
	2/b	1.08 (0.07)		1.10 (0.09)
	2/a	1.11 (0.08)		1.08 (0.10)
	1/c	1.16 (0.1)		1.11 (0.12)
	1/b	1.13 (0.09)		1.10 (0.08)
	1/a	1.16 (0.08)		1.13 (0.09)
Law/1996* [50]	1/b	1.13 (0.03)	44	3.24 (0.07)	60	Power spectra
Mostafa/2016 [51]	1/c	1.17 (0.04)	25	1.19 (0.04)	25	Box counting by White and Rudolph
Oliveira/2013 [52]	1/a	1.41 (0.08)	38	1.36 (0.10)	35	Box counting (Minkowski-Bouligand dimension)
	1/a	1.40 (0.07)		1.35 (0.11)
	1/c	1.40 (0.08)		1.38 (0.08)
	1/c	1.42 (0.05)		1.37 (0.08)
Sindeaux/2014 [30]	1/c	1.14 (0.081)	22	1.14 (0.122)	62	Box counting by White and Rudolph
	1/c	1.17 (0.11)	24	1.15 (0.09)	25
	1/c	1.18 (0.11)	22	1.15 (0.13)	62
	1/c	1.16 (0.15)	24	1.18 (0.10)	25
	1/c	1.13 (0.12)	22	1.13 (0.15)	62
	1/c	1.16 (0.15)	24	1.15 (0.12)	25
	1/a	1.42 (0.05)	22	1.34 (0.08)	62
	1/a	1.42 (0.05)	24	1.38 (0.06)	25
	1/b	1.429 (0.07)	22	1.354 (0.09)	62
	1/b	1.373 (0.06)	24	1.371 (0.05)	25
Tosoni/2006 [54]	1/a	1.33 (0.03)	15	1.34 (0.04)	17	Box counting by White and Rudolph
	1/c	1.16 (0.03)		1.14 (0.05)
	1/a	1.55 (0.03)		1.56 (0.03)
	1/c	1.3 (0.07)		1.33 (0.06)
Vijayalakshmi/2017 [55]	1/a	0.83 (0.10)	30	0.82 (0.09)	30	Box counting by White and Rudolph
	1/b	0.84 (0.09)		0.84 (0.13)
	1/c	0.83 (0.11)		0.82 (0.12)
Yasar/2006 [56]	1/b	1.39 (0.05)	21	1.4 (0.07)	27	Box counting by White and Rudolph

Abbreviations: FD fractal dimension; N number of individuals/patients; sd standard deviation

The first meta-analysis included 12 articles [28, 30, 41, 45, 47, 49–52, 54–56] which compared FD values for HC vs OP groups regardless of site and technique used for obtaining FD. For the studies showing more than one FD value, the best result (in terms of largest difference between FD values in HC and OP group and minor SDs) was chosen for the computation of the overall effect. Each study showed that FD mean-difference values were just a little lower or higher than zero and the CI overlapped the y-axis for all the studies (Fig. 2). Meta-analysis results showed that no conclusion can be suggested on the difference in FD values between HC and OP groups. Indeed, the overall effect of the mean difference was near zero (0.005) and the CI overlapped the y-axis (− 0.023; 0.034). Thus, this meta-analysis suggested no clear conclusion on FD values in HC and the OP groups when different ROIs and techniques were used for the computation of FD.

Fig. 2.

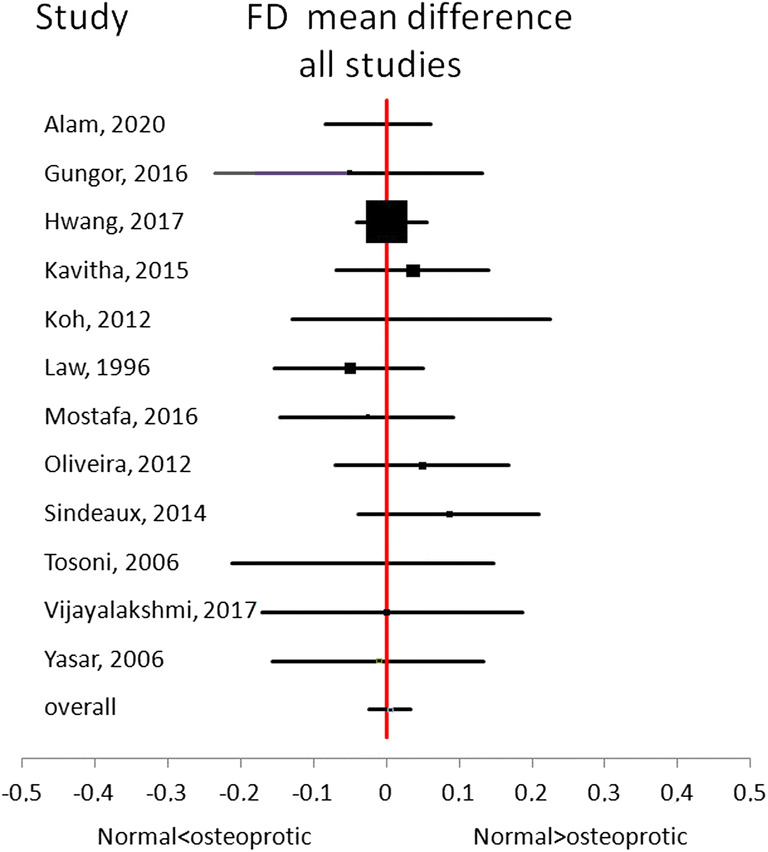
Forest plot of the results obtained from all 12 studies. For each study, the best result in terms of the largest effect index was shown

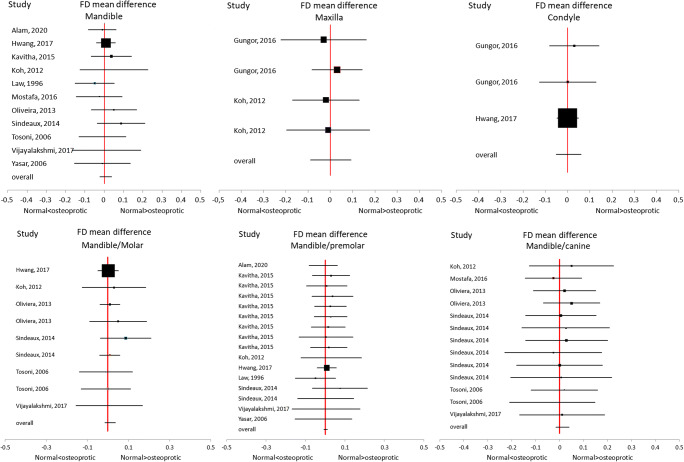
The second meta-analysis had the aim to summarize the results of all studies which used the same regions among mandible, maxilla, and condyle for the computation of the FD. Eleven studies [30, 41, 45, 47, 49–52, 54–56] used mandible as selected ROI, while only 2 studies chose maxilla [28, 49] and condyle [28, 45]. Thus, the meta-analysis was performed on mandible accounting on the best effect index obtained for each study, whereas for maxilla and condyle, all effect indexes were used for the meta-analyses (Fig. 3).

Fig. 3.

Forest plot of the results obtained from mandible, maxilla, and condyle. For the mandible, the best result in terms of the largest effect index was shown. For the mandible subregions (molar, premolar, and canine), if the same study showed more than one FD value, we included all effect index values. For maxilla and condyle, all effect indexes were shown

For the mandible region, the effect index was lower than 0 for 5 studies [41, 50, 51, 54, 56] and higher than zero for 6 studies [30, 45, 47, 49, 52, 55] and CI overlapped the y-axis for all studies. The overall effect of the meta-analysis showed that the FD mean-difference was also around zero, suggesting no evidence of a possible significant difference between HC and OP group on FD values computed on the mandible region. For maxilla and condyle regions, the results showed that the FD mean-difference between HC and OP group was around zero for all studies (Fig. 3).

According to the authors of the included studies [30, 41, 45, 47, 49–52, 54–56], the mandible region was divided into 3 subregions (molar, premolar, and canine) and we performed meta-analysis on the 3 subregions separately to understand if differences among studies on FD values could be ascribed to different subregions chosen in the calculation. To highlight the reliability of the results, if the same study showed more than one FD value, we included all effect indices in the meta-analysis. In the molar subregion of the mandible, 5 studies [30, 45, 49, 52, 55] showed a slightly greater value of FD in HC than in OP group whereas 1 study [54] showed the opposite. However, the results were quite reliable within each study. Oliveira et al. [52], Sindeaux et al. [30], and Tosoni [54] showed the same trend for two different measures in the same subregion (i.e., mandible/molar). Reliable results in the same study were also found for the premolar subregion of the mandible; indeed Kavitha et al. [47] showed FD values which were slightly greater in HC than in OP for the 8 different measures of FD in the same subregion. Instead, for the canine subregion of the mandible, 2 different studies [30, 54] showed no trend in the difference of FD mean values between the HC and OP. The overall effect, which is near zero, did not show, thus, promising results in the distinction of OP from HC for each subregion of the mandible (Fig. 4).

Fig. 4.

Forest plot of the results obtaining from 10 studies that used the box-counting technique for FD measurements on HC and OP groups

For the maxilla subregion, 3 values of FD were reported for HC and OP groups for the anterior maxilla subregion. Two values were reported by the same study [28] and showed similar values of FD for HC and OP, but with an opposite trend.

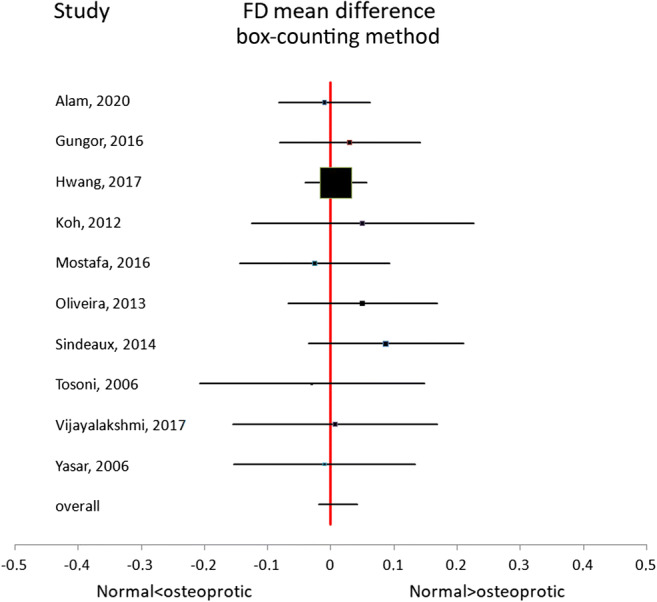
The last meta-analysis had the aim to evaluate if the same technique among box counting, power spectra, and the differential box counting (DBC) provided reliable results on FD among studies. For the selected 12 studies, 10 studies used box counting [28, 30, 41, 45, 49, 51, 52, 54–56], 1 power spectra [50], and 1 the DBC method proposed by Sarkar and Chauduri [47]. Meta-analysis was performed on the 10 studies [28, 30, 41, 45, 49, 51, 52, 54–56] which used box-counting technique. The results showed no trend in the effect index, and the overall effect was near zero with the CI which overlapped the y-axis.

In conclusion, meta-analysis results suggest that FD measured with the features mentioned above is not able to separate OP from HC group.

Discussion

To the authors’ knowledge, this is the first systematic review on the application of FD obtained from dental images for the screening and the diagnosis of osteoporosis. Also, unlike previous reviews [18, 27, 33], a comprehensive meta-analysis was conducted which also took into account the role of possible moderators such as ROIs and FD calculation methods. Controversial findings have been reported in the literature for the application of FD as a supportive marker in the diagnosis of osteoporosis. Some authors suggested that with a loss of BMD, the complexity of trabecular structure increases with the consequent increase of FD values [42, 50]. Some other authors, instead, showed a correlation between simulated model of osteoporosis and decreased FD values [57] and also decreased FD with low BMD [10, 53, 58]. The ability to screen possible OP in dental settings is of great importance since dental check-ups are performed routinely, and dental radiographs are an inseparable part of it. Dental radiographs are noninvasive, inexpensive, and widely available; therefore, if the obtained FD values were found to be reliable and with high values of sensibility and specificity, it would be considered a supportive tool in the identification of OP and in the progression of osteoporosis.

The overall analysis of the included studies in our review showed that to date FD cannot be used to identify patients affected by osteoporosis. In addition, the heterogeneity of the studies suggests the necessity for the standardization of the whole procedure for the calculation of FD from dental images. The conflicting findings among studies may be explained by differences in ROIs size, shape, and location; dissimilar images processing methods (which can lead to difficulties in controlling magnification/distortion), anatomical variations, discrepancies between two-dimensional or three-dimensional images, different methods for FD measurements [59], and non-consistent FD output for cortical and trabecular bone [30].

The numerical representation of FA is not affected by variations in X-ray exposure and small variations in beam alignment, but the image pre-processing before FD evaluation and the choice of the ROI (i.e., shape and size) can affect the final results [60, 61]. There was high variability in the size, shape, and sites of the ROIs in the included studies. To overcome these differences in our meta-analysis, a general categorization was done based on the most common sites: mandible, maxilla, and condyles. Mandible region was the most used site for the measurement of FD; indeed eleven studies reported FD values from mandible and only 2 studies chose maxilla and condyle. However, taking the mandible region as a whole, the overall effect of meta-analysis showed no evidence of a possible significant difference between HC and OP because the studies reported conflicting results. Indeed, 5 studies [41, 50, 51, 54, 56] showed that FD values were higher in OP than in HC and 6 studies [30, 45, 47, 49, 52, 55] showed the opposite. The lack of consensus among studies on FD result can be partly explained by differences of trabecular and cortical regions architecture which were not be taken into account. The lack of an adequate number of studies on maxilla and condyle cannot allow us to infer any conclusion about these regions and their reliability for the computation of FD values. Nevertheless, when adjusted on the ROIs sites, dividing maxilla into three subregions (i.e., molar, premolar, and canine), more consistent results were found among FD measurements. Indeed, for molar subregion of maxilla, 5 studies [30, 45, 49, 52, 55] showed a slightly lower value of FD in OP than in HC group whereas only 1 study [54] showed the opposite. Some previous studies found that small changes in X-ray exposure, beam alignment, and ROI position do not change FD values calculated from digital radiographic images significantly, and hence, exact positioning of ROIs may not be necessary [61]. Our results agree with these previous findings showing the same trend for different studies on the measures in the same subregions of the mandible.

When using the term FD, it is important to keep in mind that it is not something unique or absolute since the FD values depend on several factors such as processing and calculation methods [18]. On the other side, FD can overcome the limitations related to unequal magnification and geometric distortion produced by different equipment. However, to analyze the dental radiographs, first, a ROI is selected using appropriate software such as NIH’s ImageJ (Image J; US National Institutes of Health, Bethesda, MD). Then, fractals may be calculated from digitalized images after a mandatory pre-processing analysis. Steps, such as cropping of the ROI, duplication of the ROI and removal of large-scale variations in brightness with a blurred Gaussian filter, the subtraction of ROI from the original image, and the addition of 128 gray values to each pixel location, binarization, erosion, dilatation, inversion, and skeletonization, should be taken before evaluating the FD [61]. Most of the authors used the proposal of White and Rudolph [62].

After pre-processing, several methods can be used for FD calculation such as the power spectral density, triangular prism surface area, blanket method, intensity difference scaling or variogram, and the box-counting algorithm [62]. However, calculation and interpretation of FD are always challenging since all the calculation methods work based on estimation, and since each method has its theoretical basis, different FD values may be obtained for the same region [63]. Also, since there is no gold standard for the estimators, the best approach is to consider the relative discrepancies of all estimators together to form the best understanding [59]. Among all the methods, box counting seems to be the most commonly used probably due to its simplicity and availability [30, 44]. However, similar to other methods, there are some limitations to box counting including difficulty in obtaining error bounds [64], possibility of overestimation or underestimation [65], construction of empty boxes, box-size dependency of the FD computation, grid effect, process of signal binarization required for this method [63], and lengthy computation time [65]. Moreover, box counting is not appropriate for rough-textured surfaces since it has limitations in covering the image surface completely [66]. Our meta-analysis showed that the results of studies that applied box counting, which was the most common method for calculating FD, were not in line with each other, meaning that other possible factors might have played role in the final results.

Finally, panoramic was the most common imaging modality followed by periapical X-ray and CBCT. However, a comparison of the results between studies with different imaging modalities was not feasible since FD can only be reliably compared when the imaging systems have the same spatial resolution [67]. For example, a previous study on rat bones found that FD values obtained from digitized film radiographs were higher than direct digital images [68]. Also, more studies with CBCT as imaging modality is needed since three-dimensional and high-resolution images are considered more accurate than panoramic in evaluating bone quality because of the low dose of radiation, minimized distortion, and the opportunity to work with real-size images. However, only three studies in our review [28, 46, 51] used CBCT as the method of choice.

BMD results were used to separate the OP from HC group in most of the studies evaluating FD on dental radiographs, but it would be even more interesting to explore the association of FD with the risk of fractures. These studies may lead in the future to the development of a tool that calculates FD values from dental radiographs with a standardized pipeline. In this manner, the measurement could be more accessible for the practitioner to evaluate the diagnostic potential of FD measures on dental radiographs in the evaluation and/or progression of osteoporosis.

In conclusion, from the current evidence, the applicability of FD should be very carefully considered since the average methodological quality of the studies is low and none of them complied with all 4 QUADAS domains. Moreover, the wide heterogeneity of the results strongly suggested standardizing the protocol used for FD calculation.

Funding

Open Access funding provided by Università degli Studi G. D'Annunzio Chieti Pescara. The authors declare that the study was self-funded by the authors and their institutions.

Data availability

All authors agreed to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Compliance with ethical standards

Consent for publication

All the authors are aware of the manuscript content and have contributed to the study meeting all three of the following criteria for authorship, thereby accepting public responsibility for appropriate portions of the content:

1. Substantial contributions to conception and design, or acquisition of data, or analysis and interpretation of data.

2. Drafting the article or revising it critically for important intellectual content.

3. Approval of the version to be published and all subsequent versions.

Ethics approval

N/A

Consent to participate

N/A

Competing interests/Conflict of interest

The authors declare no competing interests.

Code availability

N/A