Abstract
Long-range Lennard-Jones (LJ) interactions have been incorporated into the CHARMM36 (C36) lipid force field (FF) using the LJ particle-mesh Ewald (LJ-PME) method in order to remove the inconsistency of bilayer and monolayer properties arising from the exclusion of long-range dispersion [Yu, Y.; Semi-automated Optimization of the CHARMM36 Lipid Force Field to Include Explicit Treatment of Long-Range Dispersion. J. Chem. Theory Comput. 2021, 10.1021/acs.jctc.0c01326.]. The new FF is denoted C36/LJ-PME. While the first optimization was based on three phosphatidylcholines (PCs), this paper extends the validation and parametrization to more lipids including PC, phosphatidylethanolamine (PE), phosphatidylglycerol (PG) and ether lipids. The agreement with experimental structure data is excellent for PC, PE and ether lipids. C36/LJ-PME also compares favorably with scattering data of PG bilayers but less so with NMR deuterium order parameters of 1,2-dimyristoyl-sn-glycero-3-phospho-(1’-rac-glycerol) (DMPG) at 303.15 K, indicating a need for future optimization regarding PG-specific parameters. Frequency dependence of NMR T1 spin-lattice relaxation times is well described by C36/LJ-PME and the overall agreement with experiment is comparable to C36. Lipid diffusion is slower than C36 due to the added long-range dispersion causing a higher viscosity, although it is still too fast compared to experiment after correction for periodic boundary conditions. When using a 10 Å real-space cutoff, the simulation speed of C36/LJ-PME is roughly equal to C36. While more lipids will be incorporated into the FF in the future, C36/LJ-PME can be readily used for common lipids and extends the capability of the CHARMM FF by supporting monolayers and eliminating the cutoff dependence.
1. Introduction
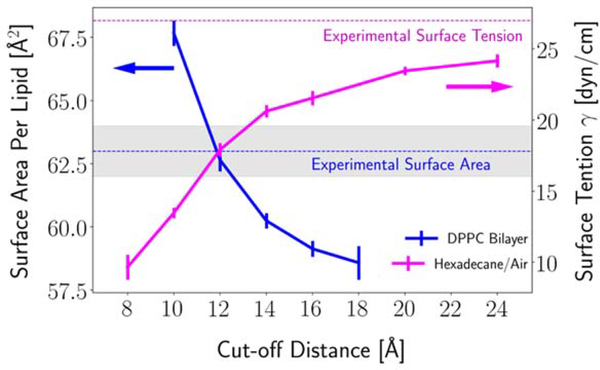
Since its release in 2010, the CHARMM36 (C36) lipid force field (FF) [1] has been extended to include anionic lipids [2], ether lipids [3], ceramides [4, 5], glycolipids [6], plasmalogens [7], and polyunsaturated tails [8]. The C36 lipid FF is heavily utilized due to the diversity of lipids it covers and the well-parametrized potential parameters. Like other commonly used FFs, C36 was parametrized considering specific treatment of nonbonded interactions. The C36 lipid FF uses the Particle Mesh Ewald (PME) method [9] for the electrostatic interactions and a force-based switching function ranging from 8 to 12 Å for the Lennard-Jones (LJ) potential. Hence, the long-range dispersion is excluded from the energy calculation. Although standard for C36 and most other FFs, this way of treating the LJ potential leads to an inconsistency between bilayers and monolayers, because the acyl chain/air interface of monolayers, similar to alkane/air interfaces, requires long-range dispersion to reproduce experiment; i.e., the LJ interactions must be summed to infinity, similar to the electrostatic terms (Fig. 1) [3, 10, 11]. However, as also shown in Figure 1, any deviation from the 12 Å cutoff in LJ leads to dramatic change in bilayer surface areas, and, as follows from the hexadecane results, surface tensions of alkane/air interfaces. This inconsistency was recognized in the original publication of C36 [1], but it was not possible to rectify the problem at that time because an efficient method for calculating long-range LJ interactions was not supported in CHARMM [12] and other major simulation programs. The situation has changed and the inclusion of long-range LJ terms using a Particle Mesh Ewald method similar to that used for electrostatics called LJ-PME has been added to Gromacs [13, 14], OpenMM [15], and CHARMM [16].
Figure 1.
Influence of Lennard-Jones cutoff distance on the surface area per lipid of a dipalmitoylphosphatidylcholine (DPPC) bilayer at 323.15 K (blue line) and the surface tension of hexadecane/air interface at 298.15 K (magenta line) simulated with the C36 FF. Hexadecane/air data from Leonard et al. [16]
This work presents the reparametrization of the C36 lipid FF with LJ-PME on common biologically relevant lipids and the extended validation of the newly optimized FF. The optimization of the new FF used a semi-automated workflow to fit the nonbonded parameters (partial atomic charges and LJ parameters) starting from the C36 parameters, which is described in detail in our preceding paper [17] (henceforth denoted Paper I). Since the hydrocarbon parameters utilized in lipid tails are well validated [16], this reparametrization is restricted to the head groups. The water model, TIP3P [18, 19], also remains unaltered to maintain consistency with the CHARMM-family of FFs. The experimental targets used in the parametrization include surface areas per lipid for bilayers, monolayer isotherms of the surface area, area compressibilities, NMR deuterium order parameters and radial distribution functions between water molecules and specific atoms in the head groups. While the lipids used for the parametrization are phosphatidylcholines (PCs) (Paper I) and ether lipids (this paper), the validation of the new FF also covers phosphatidylethanolamines (PEs) and phosphatidylglycerols (PGs) (see Table 1). The optimized parameter set maintains the same level of accuracy for bilayer as C36, while correctly reproducing the pressure/area isotherm for monolayers.
Table 1.
Name, abbreviation, and chain structure of lipids noted in this paper
| lipid name | abbreviation | sn1 | sn2 |
|---|---|---|---|
| 1,2-dipropionyl-sn-glycero-3-phosphocholine | C3-PC | 3:0 | 3:0 |
| 1,2-dilauroyl-sn-glycero-3-phosphorylcholine | DLPC | 12:0 | 12:0 |
| 1,2-dimyristoyl-sn-glycero-3-phosphorylcholine | DMPC | 14:0 | 14:0 |
| 1,2-dipalmitoyl-sn-glycero-3-phosphocholine | DPPC | 16:0 | 16:0 |
| 1,2-dimyristoyl-sn-glycero-3-phospho-(1'-rac-glycerol) | DMPG | 14:0 | 14:0 |
| 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine | POPC | 16:0 | 18:1 |
| 1,2-dioleoyl-sn-glycero-3-phosphocholine | DOPC | 18:1 | 18:1 |
| 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine | POPE | 16:0 | 18:1 |
| 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine | POPG | 16:0 | 18:1 |
| 1-stearoyl-2-docosahexaenoyl phosphatidylethanolamine | SDPE | 18:0 | 22:6 |
| 1,2-di-O-hexadecyl-sn-glycero-3-phosphocholine | DHPC | 16:0 | 16:0 |
Although this paper focuses on adding LJ-PME into the C36 lipid FF, a brief review of all CHARMM lipid FFs is important. Currently, CHARMM includes both all-atom (AA) and united-atom (UA) lipid models. The first AA model, C22, by Schlenkrich et al. [20], was developed in the early 1990s, the parametrization was based on small molecules and QM calculations at Hartree-Fock level. The validation of this early model was limited to the microcanonical ensemble. Its successor, C27 [21], improved the LJ and torsional parameters of alkanes, and also the partial atomic charges and torsional parameters of the phosphate. The alkane torsions in this set were further refined to reproduce the experimental aliphatic chain order parameters, leading to the revised set, C27r [22]. C27 and C27r are generally not suitable for constant pressure simulations, as they yield surface tensions of ~20 dyn/cm/side for DPPC bilayers at the experimental surface area [23]. This problem was solved with the most recent parametrization by Klauda et al. [1], i.e., C36. C36 also yields the correct head groups order parameters, which are not captured by most existing lipid FFs [24]. The UA model was first introduced by Hénin et al. [25], which matches the C27r lipid FF [26]; Lee et al. [27] reparametrized it in 2013 to match the C36 head groups. Recently, it has been updated with the optimized hydrocarbon parameters [28]. Besides the additive FFs mentioned above, CHARMM also has its own polarizable lipid FF, known as the Drude lipid FF [29, 30]. In principle, a polarizable lipid FF can better describe events and membrane properties where dielectric response is important, for example, the dipole potential at the membrane water interface and the permeability of small molecules through the membrane [31, 32]. However, the Drude lipid FF is presently only available for a limited number of lipid types, and perhaps more importantly, the area compressibilities of lipid bilayers are overestimated by nearly two-fold. The current study provides valuable insights into the parametrization of the CHARMM lipid FF, and the methodology can be readily applied to the reparametrization of the Drude lipid FF and is a topic of future work.
By way of outline, Section 2 describes the training and validation sets, followed by system set-ups, simulation protocols and methods of analyzing the trajectories. Section 3 provides the results, including the new parametrization of the ether-linked lipid 1,2-di-O-hexadecyl-sn-glycero-3-phosphocholine (DHPC), and validation for the other lipids. Section 4 discusses benefits of including LJ-PME and summarizes the work.
2. Methods
As noted in the Introduction, the semi-automated workflow to optimize the parameter set starting from C36 is described in Paper I, and it will not be reproduced here. Instead, the Methods section focuses on the range of lipids covered by this reparametrization, the systems used for training and validation, and computational details.
2.1. Lipids Covered and Nomenclatures.
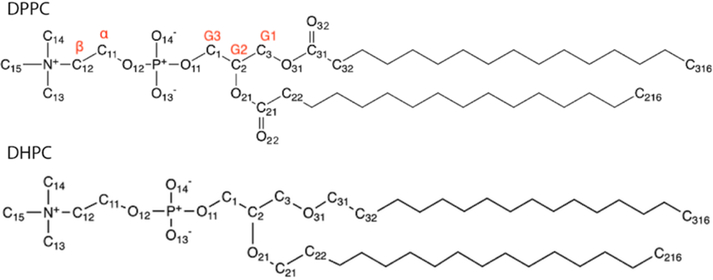
The current study includes PC, PE, PG, and ether lipids. Optimized parameters are primarily tested on single component lipid bilayers and monolayers. 1,2-dipropionyl-sn-glycero-3-phosphocholine (C3-PC) in solution phase is also simulated to study the head group hydrations. Table 1 provides the abbreviations and chain structures for the assorted lipids used in this study. The atom notations used by C36/LJ-PME are the same as C36 and follow the Sundaralingam nomenclature [33], where the numbering of the glycerol carbons is inverted with respect to the sn nomenclature [34, 35]. Examples of atom notation based on DPPC and DHPC can be found in Figure 2. In addition, a table of clarification can be found in the original publication of C36 (Table 5) [1]. For consistency, CHARMM atom notations are used for all discussions in this paper.
Figure 2.
Chemical structure of DPPC and DHPC, nomenclature follows CHARMM convention.
Table 5.
Adjusted dihedral parameters for the ether linkage.
| dihedral | Kφ | n | δ |
|---|---|---|---|
| C-O-C-C | 0.25 | 2 | 0.0 |
| 0.43 | 3 | 0.0 | |
| 0.26 | 4 | 0.0 | |
| 0.08 | 5 | 0.0 | |
| O-C-C-O | 1.23 | 1 | 180.0 |
| 1.02 | 2 | 0.0 |
2.2. Training Set.
The training targets were selected to be representative of lipid systems. There are two major considerations when selecting the training targets. The first is the lipid type. While various tails were used in every parametrization stage to explore effects of unsaturation and carbon number, different head groups and linkages were parametrized sequentially. PC was the first head group optimized (see Paper I for details), and the ether linkage (DHPC) is optimized here. PE and PG lipids were tested using the new parameters (linkage region) from the PC optimization and a decision on whether to further optimize them was made based on the tests. The reason behind this is that PE and PG head groups share the same phosphate and glycerol backbone moieties with PC, hence it can be optimized easily after PC (if needed). For the ether lipid, DHPC, the only difference from DPPC is the linkage between the head group and tails, which can be parametrized separately as indicated by the parametrization of C36 lipid FF for ether lipids [3].
The second consideration is what properties should be covered in the training set. As commonly used benchmarks for lipid FF development, surface areas and membrane thicknesses were included. The correct surface area is difficult to parametrize (because the large negative and positive oscillations in the tangential pressure must sum to zero [36]) and is critical to other properties. For this reason, we gave relatively high weight factors to the surface areas in the optimizations. The monolayer surface areas at different applied surface tensions were also included in the training set, which historically has not been the case in parametrizations. This was inspired by the known inconsistency of bilayer and monolayer surface tensions for C36. Another set of properties considered were the deuterium order parameters (SCD). Order parameters are sensitive to bond orientations and chain order and are important metrics for membrane structure. In this study, order parameters from head group and tails were included as long as the experimental data was available. Since there is no published experimental data for ether lipids to our knowledge, only the PC optimization utilized order parameters (see Paper I for details).
The radial distribution functions (RDFs) between PC headgroup and water were recently determined by Foglia et al. [37] using 1,2-dipropionyl-sn-glycero-3-phosphocholine (C3-PC) in solution. Using neutron diffraction with isotopic substitution (NIDS) augmented by empirical potential structure refinement (EPSR) modeling, RDFs for unique atom-atom pairs between functional groups in C3-PC and water were resolved. While the data itself is meaningful, the usefulness of it is debatable in our case for several reasons. The first is that the TIP3P water model used by the CHARMM FF cannot reproduce experimental RDFs accurately, especially for the O-O pairs [38]. Secondly, electrostatic polarization is not included in our model, which may influence the interaction strengths between water and lipid atoms. Lastly, it was noted by Foglia et al. that EPSR only provides a model which is consistent with the diffraction data, but it is not necessarily unique. However, the inclusion of this set of data can avoid overfitting in parameters which may lead to unwanted strong interactions between water and lipid atoms when the optimizer tries to increase the hydration. To balance all the uncertainties, we assigned low weights to this data. Another concern is how to use the RDF data. Our preliminary test using C36 indicated that integrals of the RDF curve (coordination numbers of water) are in good agreement with experiment, so that only the RMSD ranging from 2 to 6 Å were used (see Paper I).
Apart from properties extracted from single simulation, the training set also included three additional properties which were determined from multiple simulations. The most important one is the area compressibility (KA) of DPPC bilayer at 323.15 K. As discussed in previous publications [1, 36], KA can be determined by the fluctuation of the surface area, or through the surface tension dependence of the surface area at a given temperature as
| (1) |
where 〈A〉 is the average total area per leaflet, 〈δA2〉 is the mean square fluctuation, kB is Boltzmann’s constant, T is the temperature, and γ is the total surface tension applied tangential to the bilayer surface. The second one is the area difference between 323.15 K and 333.15 K for DPPC bilayer, which was used to extract the temperature dependence of the surface area. The last one is the area difference between bilayers of DMPC and DPPC, which was used to train the tail length dependence of the surface area. The weights for these properties were relatively low, because their uncertainties were large from simulations.
Table 2 details the systems simulated in this study and the training targets associated with them. The weight factors used for these targets are listed in Table 1 of Paper I.
Table 2.
Systems simulated in this study.
| System | T (K) | Ensemble | Nlipid | Nwater/lipid | Use |
|---|---|---|---|---|---|
| DPPC bilayer | 323.15 | NPT | 72 | 30.4 | optimization, validation |
| NPγT (−5 dyn/cm) | 72 | optimization | |||
| NPγT (5 dyn/cm) | 72 | optimization | |||
| NPT | 288 | validation | |||
| NPT | 648 | validation | |||
| NPT | 1152 | validation | |||
| 333.15 | NPT | 72 | optimization, validation | ||
| DPPC monolayer | 321 | NLzγT (18 dyn/cm) | 72 | 30.4 | optimization, validation |
| NLzγT (40 dyn/cm) | 72 | optimization, validation | |||
| NLzγT (55 dyn/cm) | 72 | optimization, validation | |||
| DMPC bilayer | 303.15 | NPT | 72 | 25.7 | optimization, validation |
| DLPC bilayer | 303.15 | NPT | 72 | 30.4 | validation |
| POPC bilayer | 303.15 | NPT | 72 | 31.1 | optimization, validation |
| DOPC bilayer | 303.15 | NPT | 72 | 33.5 | validation |
| 303.15 | NPT | 288 | 30.4 | validation | |
| 303.15 | NPT | 648 | 33.5 | validation | |
| POPE bilayer | 303.15 | NPT | 80 | 32.0 | validation |
| 308.15 | NPT | 80 | 32.0 | validation | |
| DMPG bilayer | 303.15 | NPT | 72 | 75.0 | validation |
| 323.15 | NPT | 72 | validation | ||
| 333.15 | NPT | 72 | validation | ||
| POPG bilayer | 303.15 | NPT | 72 | 45.0 | validation |
| DHPC bilayer | 321 | NPT | 80 | 30.0 | optimization, validation |
| 333 | NPT | 80 | optimization, validation | ||
| C3-PC solution | 298.15 | NPT | 9 | 250 | optimization, validation |
2.4. Simulation Details.
Table 2 lists the details of the systems simulated in this study. Initial structures of small (less than 100 lipids) bilayers and monolayers were built from CHARMM-GUI [39] Membrane Builder [40–42]. Systems containing 288 lipids were built by duplicating the 72-lipid systems at the end of 200 ns simulations 4 times. The initial coordinates of the 648-lipid and 1152-lipid systems were end-of-simulation frames taken from Venable et al. [36] and unpublished simulations using the C36 FF. In addition, the building procedure of the 1,2-dipropionyl-sn-glycero-3-phosphocholine (C3-PC) aqueous solution is detailed by Paper I. All PC bilayers were fully hydrated using the same hydration numbers found in the original publication of C36 [1]. The hydration numbers of PE and PG bilayers are consistent with two previous studies by Venable et al. [2, 36] DHPC bilayers were hydrated in the same way as Leonard et al. [3] For DPPC monolayers, lipid head groups from different leaflets were separated by a water slab, and the tails were separated by vacuum which measures about 180 Å in the monolayer normal direction. For all systems, the modified TIP3P water model [18, 19] was used to keep consistency with the rest of the CHARMM FF. Simulations of PG bilayers included 0.1 M of NaCl. Bilayers were simulated in tetragonal boundary conditions in one of two ensembles: NPT (constant number, pressure of 1 atm, and temperature), or NPγT (constant number, normal pressure, surface tension, and temperature). Monolayers were simulated in the NLz,γ,T (constant number, cell length normal to the surface, surface tension, and temperature).
In each optimization cycle, small PC bilayers and monolayers were simulated for 200 ns except the two NPγT simulations of DPPC bilayers used to calculate the area compressibility, which were simulated for 300 ns. The simulation of C3-PC aqueous solution was 100 ns in each optimization cycle. All simulations were run in OpenMM 7.4.1 using the Langevin Integrator with a friction coefficient of 1/ps and a 2 fs timestep. Pressure was controlled by the Monte Carlo Membrane Barostat at 1 atmosphere for membranes and by the Monte Carlo Barostat at 1 bar for the C3-PC solution. The real-space cutoff (rcut) was set to be 10 Å for LJ-PME. The Ewald error tolerance was set to be 10-4. The simulation method used for validation was the same as the optimization except the 288/648-lipid bilayers and an extra set of 72-lipid bilayers (DPPC and DOPC) used to study lipid diffusion, for which a Nosé-Hoover chain velocity Verlet integrator was applied. In addition to the LJ-PME simulations, two monolayers were simulated using the C36 FF and a force-switching function ranging from 8 to 12 Å for the LJ, and the NPγT ensemble was used in which γ was set to be 18 and 41 dyn/cm.
2.5. Property Calculations.
The following properties were evaluated during the optimization for the training set and after for the validation set:
The surface area per lipid (Al) was calculated as the area of the simulation cell in the x-y plane (tangential to the membrane surface) divided by the number of lipids per leaflet.
Area compressibility, KA. As discussed in Section 2.3 (Eq. 1), KA can be calculated in two ways. For parameter optimization, KA was obtained from dγ/dA, and the reweighting was done to the surface area of the two DPPC bilayers under applied surface tensions of ±5 dyn/cm.
- Deuterium order parameters were computed from
where θ is the angle between the C-H vector and the bilayer normal, the angular bracket denotes the time and ensemble average.(2) The overall bilayer thickness, DB, was estimated by the distance between the two midpoints (one for each side of the bilayer) of water electron density profile (EDP) along the bilayer normal, for which a bin size of 0.2 Å was used. EDPs for lipid atoms were also calculated in the validation process, from which the headgroup-to-headgroup distance (DHH) and the hydrophobic thickness (DC) were estimated. DHH is defined as the distance between the peaks in the overall EDP, and DC is half of the distance between the midpoints of EDP for the acyl chain. From EDPs, X-ray and neutron form factors were generated using the SIMtoEXP program [43], which were compared directly to experiments.
Dynamic properties of lipid bilayers were studied as model validation. The first set of properties are the NMR spin lattice relaxation time T1 of C-H bonds. T1 was calculated assuming pure dipolar relaxation between the 13C nucleus and its N attached protons using the formula [44]
| (3) |
where h is the Plank’s constant, rC−H is the effective C-H bond length, γC and γH are the gyromagnetic ratios of the 13C and H nuclei, ωC and ωH are the angular Larmor frequencies. J(ω) is the spectral density of the second rank reorientational correlation function (P2) of the C-H bond direction, where is the unit vector along the C-H bond at time t.
Another set of properties are the lipid diffusion constants. Comparing simulated diffusion constants with experiments faces two major challenges. The first is the artifact introduced by the period boundary conditions (PBC) common to molecular dynamics (MD) simulations [45]. For membrane spanning proteins, Camley et al. [46] predicted that the diffusion constant would be underestimated by factors 3–10, and recent studies by Venable et al. [47] and Zgorski et al. [48] indicate that lipid diffusion could be affected by similar factors. To overcome this challenge, DPPC and DOPC bilayers of different sizes were simulated and the periodic Saffman-Delbrück (PSD) model developed by Camley et al. [46] was used to extrapolate diffusion constants at infinite system size. The second challenge is determining the viscosity of the lipid molecule in a membrane environment, which must be used as an input parameter in the PSD model. More details on this will be discussed in Sections 3.4 and 4. In diffusion constant calculations, the center of mass (COM) motion of the bilayer should be removed in order to get the motions of individual lipids relative to the bilayer. It was found in previous MD simulations [28, 49] that the two leaflets of small bilayers (36 lipids/leaflet) have fast relative motions, so that COM motions for individual leaflets were removed instead of the COM motion of the whole bilayer. Two-dimensional (2D) mean-squared displacement (MSD) for each lipid as a function of time was computed via a difference correlation function using the x and y components of the lipid COM [47]. The 2D diffusion constants were computed from the slopes of 〈msd〉LIPID vs. time, for 10 ns < t < (ti – 10)/2, where ti is the analysis interval (80 ns). The lower cutoff removes the sub-diffusive dynamics, which is significantly faster than the diffusion in all-atom simulations [47]. Standard errors were estimated based on 3 replicas for each system, and each replica contains 4 (72- and 288-lipid systems) or 2 (648-lipid systems) trajectory blocks of 80 ns.
3. Results
3.1. Parametrization of the Ether Linkage.
Using the C36 ether parameters [3] with LJ-PME, we observed a too low Al for DHPC at 333.15 K (62.4 ± 0.3 Å2 compared to 67.2 Å2 in experiment [50]), implying a reparametrization for the ether linkage was needed. The reparametrization was based on properties of DHPC bilayer at two different temperatures (see Table 3) and conformational energies of 1,2-diethoxyethane (C6H14O2; hereafter DEOE). In each optimization cycle, partial charges of the ether linkage were fitted to the experimental Al and overall thickness DB of DHPC bilayers using the same strategy described in Paper I. LJ parameters were set to those of C36 and not allowed to change. After that, parameters for the C-O-O-C and O-C-C-O dihedrals were fitted to the QM potential energy scan (PES) of DEOE from Leonard et al. [3] In CHARMM, the form of the dihedral potential for a single dihedral is
| (4) |
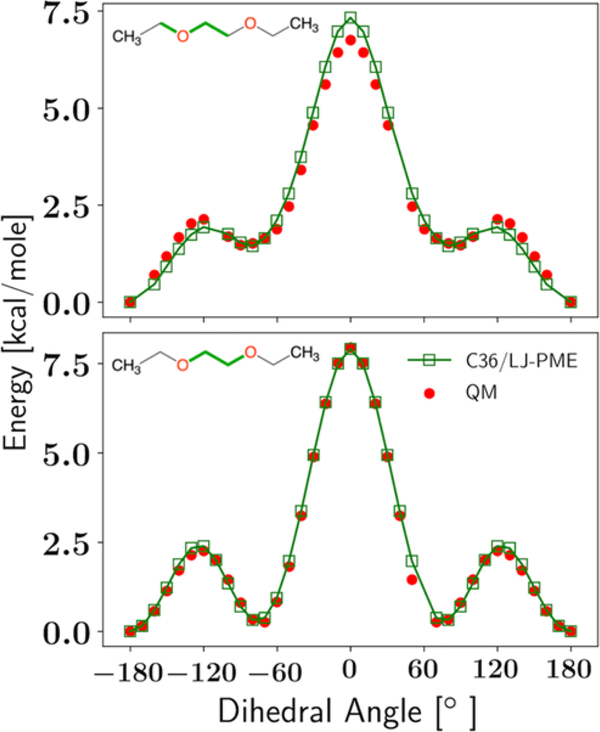
where φ is the dihedral angle and Kφ, n, and δ are fitting parameters. The multiplicity n can take values from 1 to 6. In the dihedral fittings, n was fixed as in C36 and only changes in Kφ and δ were allowed. We found that only one optimization cycle was needed to obtain good agreement with experimental observables (although two cycles were run to confirm). PES based on the optimized parameters are compared to QM in Figure 3, and bilayer properties can be found in Section 3.4.
Table 3.
Training targets, along with their scaling factors and weight factors for the ether linkage reparametrization. All bilayers are fully hydrated. Surface Area per Lipid (Al), Overall Bilayer Thickness (DB). Definitions of scaling factor and weight factor are in Paper I.
Figure 3.
Dihedral fittings for the C-O-C-C and O-C-C-O dihedrals. The chemical structure of DEOE and the positions of the two dihedrals (green) are shown on the upper left of each panel. All dihedrals not used for the scan are fixed at 180°.
3.2. Optimized Parameters.
The optimized parameters for the PC head group are listed in Table 4 and compared to C36. As noted in Paper I, the parametrization of C36/LJ-PME only introduced changes to the glycerol region and the ester linkage. For partial charges, the changes are all within 0.06 e. There are also small but unneglectable changes to the Rmin/2 of carbonyl oxygens (O22/O32) and ester oxygens (O21/O31); ε for ester oxygens also changed. These changes in LJ parameters can be partially explained by the presence of the pairwise RDFs (between these atoms and water) in the training set. Figure S1 compares the RDFs for C36/LJ-PME and C36. Due to the fixed phosphate parameters and regularizations imposed during the optimization, only small differences can be observed for the ester group and they are discussed in Paper I.
Table 4.
Comparison of partial charges and LJ parameters for C36/LJ-PME and C36.
| atom | C36 | C36/LJ-PME |
|---|---|---|
| partial charges (e): PC lipids | ||
| C2 | 0.17 | 0.1339 |
| HS | 0.09 | 0.1023 |
| O21 | −0.49 | −0.4739 |
| C21 | 0.90 | 0.8445 |
| O22 | −0.63 | −0.6272 |
| C22 | −0.22 | −0.1652 |
| H2R | 0.09 | 0.0928 |
| H2S | 0.09 | 0.0928 |
| C3 | 0.08 | 0.0302 |
| HX | 0.09 | 0.1030 |
| HY | 0.09 | 0.1030 |
| O31 | −0.49 | −0.4739 |
| C31 | 0.90 | 0.8445 |
| O32 | −0.63 | −0.6272 |
| C32 | −0.22 | −0.1652 |
| H2X | 0.09 | 0.0928 |
| H2Y | 0.09 | 0.0928 |
| Rmin/2 (Å): PC lipids | ||
| O21 | 1.65 | 1.6809 |
| O22 | 1.70 | 1.6470 |
| O31 | 1.65 | 1.6809 |
| O32 | 1.70 | 1.6470 |
| ε (kcal/mol): PC lipids | ||
| O22 | −0.120 | −0.1192 |
| O32 | −0.120 | −0.1192 |
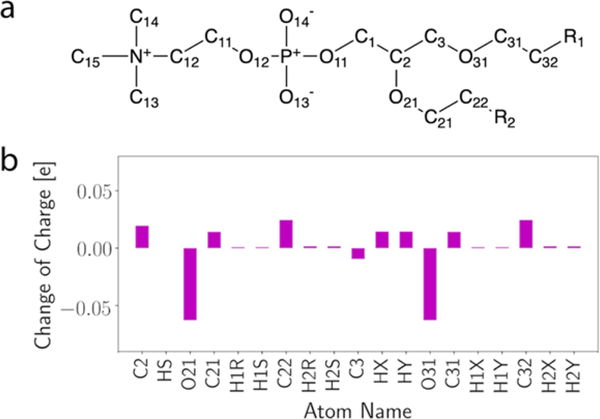
Changes of partial charge for the ether linkage are shown in Figure 4, while exact numbers of the charges are compared with C36 in Table S1. In fact, these changes are very small and comparable to the difference between QM calculations using different model compounds [3]. The adjusted dihedral parameters for C-O-C-C and O-C-C-O are listed in Table 5, and the partial charges of DEOE atoms used for the PES are shown in Figure S2.
Figure 4.
(a) Chemical structure of ether lipids where R1 and R2 represent the acyl chains, atom notations follow CHARMM convention. (b) changes of partial charge in C36/LJPME relative to C36.
3.3. Membrane Structure and Area Compressibility.
As presented in Paper I, reparametrization of the PC head group solved the inconsistency between bilayers and monolayers in C36. In this study, validation of the new parameter set is extended to the PE and PG head groups. In principle, the PE/PG-specific nonbonded parameters only need to be reparametrized if they do not work well with the new linkage parameters. The overall bilayer structure measured by Al (Table 6) and membrane thicknesses (Table 7) implies that PE and PG lipids are well modeled by C36/LJ-PME. However, there might be a potential issue for DMPG at relatively lower temperatures (e.g., 303.15 K) as indicated by the higher-than-experiment chain order parameters, which will be discussed in Section 4.
Table 6.
Al from NPT and NPγT simulations. Available C36 and experimental data included for comparison. Standard errors are given in parentheses.
| System | Temperature (K) | Ensemble | C36/LJ-PME (Å2/lipid) | C36 (Å2/lipid) | Experiment (Å2/lipid) |
|---|---|---|---|---|---|
| DPPC bilayer | 323.15 | NPT | 62.7 (0.2) | 62.9 (0.1) [36] | 63.1 (1.3) [53] |
| 333.15 | 63.3 (0.2) | 65.0 (1.3) [53] | |||
| DMPC bilayer | 303.15 | NPT | 62.4 (0.2) | 61.5 (0.1) [36] | 60.6 [54], 59.9 (1.2) [53] |
| DLPC bilayer | 303.15 | NPT | 64.3 (0.4) | 63.1 (0.3) [55] | 60.8 (1.2) [53] |
| DOPC bilayer | 303.15 | NPT | 69.4 (0.2) | 68.9 (0.1) [36] | 67.4 [56], 72.4 [57] |
| POPC bilayer | 303.15 | NPT | 65.4 (0.5) | 66.0 (0.1) [36] | 64.4 (1.3) [53] |
| POPE bilayer | 308.15 | NPT | 58.9 (0.4) | 58.8 (0.1) [36] | 58.0 (1.2) [58] |
| DMPG bilayer | 303.15 | NPT | 59.8 (0.4) | 64.0 (0.2) [2] | 62.5 (1.3) [59, 60] |
| 323.15 | 65.3 (0.5) | 66.0 (1.3) [59, 60] | |||
| 333.15 | 66.0 (0.4) | 67.5 (1.4) [59, 60] | |||
| POPG bilayer | 303.15 | NPT | 65.4 (0.3) | 68.0 (0.1) [36] | 64.3 (1.3) [59, 60] |
| DHPC bilayer | 321.15 | NPT | 63.5 (0.2) | 63.2 (0.3) [3] | 65.1 [51] |
| 333.15 | 65.5 (0.3) | 65.4 (0.2) [3] | 67.2 [50] | ||
| DPPC monolayer | 321.15 | NPγT (γ=18 dyn/cm) | 55.7 (0.2) | 60.0 (0.2) | 54.0 [61] |
| 321.15 | NPγT (γ=41 dyn/cm) | 63.9 (0.2) | 72.1 (0.2) | 64.0 [61] | |
| 321.15 | NPγT (γ=55 dyn/cm) | 76.5 (0.3) | 80.0 [61] |
Table 7.
Overall thickness (DB), headgroup-headgroup distance (DHH) and hydrophobic thickness (2DC) for each lipid bilayer from C36/LJ-PME, C36 and experiments (Expt.). Standard errors are given in parentheses. The experimental values with uncertainties for saturated PC lipids and POPC from 2011, Kučerka et al. [53] DOPC experimental values from earlier study of same group published in 2008 [56]. PE experimental values from their later study in 2015 [58]. PG experimental values from their 2014 paper [60]. DHPC experimental values from two separate publications [50, 51]. C36 values are from Zhuang et al. [52, 55] and Leonard et al. [3], and standard errors are less than 0.3 Å if not provided.
| Lipid | Temperature (K) | DB (Å) | DHH (Å) | 2DC (Å) | |||||
|---|---|---|---|---|---|---|---|---|---|
| C36/LJPME | C36 | Expt. | C36/LJPME | Expt. | C36/LJPME | C36 | Expt. | ||
| DPPC | 323.15 | 38.5 (0.1) | 39.6 | 39.0 (0.8) | 37.6 (0.2) | 38.4 | 28.2 (0.1) | 28.9 | 28.5 (0.6) |
| 333.15 | 38.3 (0.1) | 38.9 | 38.1 (0.7) | 38.0 (0.1) | 34.6 | 28.1 (0.2) | 28.5 | 27.9 (0.6) | |
| DMPC | 303.15 | 34.6 (0.2) | 36.2 | 36.7 (0.7) | 33.6 (0.2) | 35.3 | 24.7 (0.1) | 25.6 | 25.7 (0.5) |
| DLPC | 303.15 | 29.7 (0.1) | 31.0 | 32.6 (0.7) | 29.8 (0.2) | 29.8 | 20.3 (0.1) | 20.9 | 21.7 (0.4) |
| POPC | 303.15 | 37.1 (0.2) | 37.4 | 39.1 (0.8) | 37.3 (0.3) | 36.5 | 27.7 (0.2) | 28.1 | 28.8 (0.6) |
| DOPC | 303.15 | 36.0 (0.2) | 38.7 | 37.2 (0.1) | 37.0 | 27.4 (0.1) | 28.8 | ||
| Absolute Deviation (PC) | 4.8% | 2.9% | 1.9% | 3.5% | 2.0% | ||||
| DHPC | 321.15 | 36.6 (0.3) | 38.7 (0.1) | 38.4 (0.4) | 38.2 | 27.8 (0.3) | 28.9 (0.1) | 27.6 | |
| 333.15 | 35.7 (0.3) | 37.7 (0.3) | 36.8 | 37.8 (0.3) | 38.0 | 27.3 (0.2) | 28.4 (0.1) | 27.1 | |
| Absolute Deviation (Ether) | 3.0% | 3.3% | 0.5% | 0.7% | 4.8% | ||||
| POPE | 308.15 | 40.7 (0.3) | 43.0 | 40.5 (0.8) | 39.8 (0.3) | 38.3 | 31.1 (0.2) | 32.6 | 32.1 (0.6) |
| Absolute Deviation (PE) | 0.5% | 6.2% | 3.9% | 3.1% | 1.6% | ||||
| DMPG | 303.15 | 34.2 (0.3) | 33.3 | 33.8 (0.7) | 34.5 (0.3) | 34.6 | 25.6 (0.3) | 24.0 | 24.5 (0.5) |
| 323.15 | 32.3 (0.3) | 31.5 | 32.6 (0.7) | 33.2 (0.3) | 34.6 | 24.5 (0.3) | 23.0 | 23.7 (0.5) | |
| 333.15 | 32.2 (0.2) | 31.1 | 32.0 (0.7) | 32.8 (0.1) | 33.8 | 24.2 (0.1) | 22.8 | 23.4 (0.5) | |
| POPG | 303.15 | 36.8 (0.3) | 36.2 | 37.6 (0.8) | 37.2 (0.2) | 36.6 | 28.3 (0.2) | 27.2 | 28.5 (0.5) |
| Absolute Deviation (PG) | 1.2% | 2.9% | 2.2% | 3.0% | 3.0% | ||||
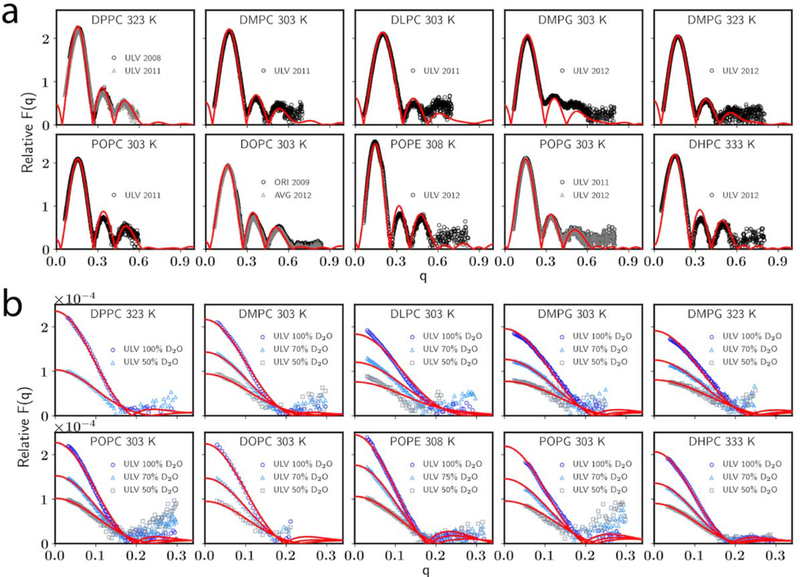
Table 6 also compares the Al for PC membranes and DHPC bilayers. Generally speaking, the overall agreement with experiment for C36/LJ-PME is just as good as C36 in terms of bilayers. While Al of DMPC bilayer is higher than experiment, X-ray and neutron form factors (Figure 5) agree well with experiment and are comparable to those calculated using C36 [52]. The situation is more complicated for DLPC, for which the neutron form factors deviate from experiment by noticeable amounts, indicating the potential deficiency of the FF to describe shorter tails. As the only ether lipid optimized and tested in this study, Al of DHPC bilayers match the experimental data pretty well and are comparable to C36.
Figure 5.
(a) X-ray and (b) neutron form factors for bilayers. C36/LJ-PME in red line and experiments [50, 53, 56–59, 62, 63] in open symbol.
Table 7 compares membrane thicknesses calculated using C36/LJ-PME to experiments. Overall, C36/LJ-PME agrees well with experiments for all tested lipids, though under- and overestimations exist for some lipids. For DMPC, DLPC, POPC and DOPC bilayers, DB is underestimated, which is consistent with their slightly overestimated Al. While the average underestimation of DB is small, this implies an overhydration is needed to generate the accurate Al for bilayers, and this overhydration can be visualized directly using EDP (Figure S3), as the distribution of water is shifted slightly inward compared to experiment. Nevertheless, comparison with the experimental form factors indicates that structures of these bilayers are well-modeled. The head-to-head distance DHH and the hydrophobic thickness 2DC follow the same trend of DB for most lipids. One exception is POPE, for which DHH is higher than the experiment despite a close-to-experiment DB. This indicates that head group size and intermolecular hydrogen bonds may influence DHH and thus the difference between DB and DHH.
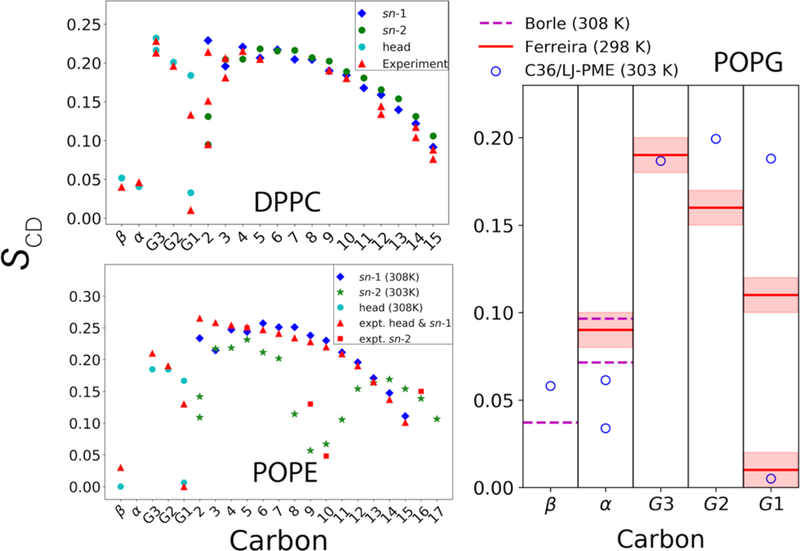
Another important metric of membrane structure is the deuterium order parameter (SCD). C36 is the first lipid FF to accurately capture the chain order splitting for all carbons [1, 24]. As described in Paper I, dihedral fitting for the PC head group was conducted in a way maximizing the consistency with C36, and post-fit refinement was used to further improve the agreement with experiment. Hence, head group SCD for PCs are nearly identical as C36 and in perfect agreement with experiment (Figure 6, upper left). Furthermore, because the parametrization also included the nonbonded parameters of the first two carbons in the acyl chain and dihedral parameters extending to the fourth carbon, the splitting of C2 from the sn-2 chain is well preserved.
Figure 6.
(upper left) NMR deuterium order parameters (SCD) for DPPC bilayer from experiments [66–68] and C36/LJ-PME at 323 K; (lower left) SCD for POPE bilayer. Experimental temperatures are 308 K for the sn-1 chain [64], 303 K for the sn-2 chain [69] and 310 K for the head group (Unpublished data from the NMRLipid Project [70]). Simulation temperatures shown in legend. (Right) SCD for POPG head group, experimental data from Borle et al. [65] and the NMRLipid project [70].
When it comes to PE and PG, the experimental data is less accessible. The lower left panel of Figure 6 compares the SCD of POPE bilayer simulated using C36/LJ-PME with several independent experiments. It is clear that the agreement with experiment is good for the head group region. When interpreting the experimental data for the sn-1 chain, extra caution should be exercised because the experiment assumed a monotonic variation of SCD toward the disordered center of the bilayer [64]. However, the overall agreement for the sn-1 chain is decent, indicating that the structure of the hydrophobic core is well described by C36/LJ-PME, and that the overall structure of the bilayer is well captured. For the sn-2 chain, the drop of SCD around the double bond (C9=C10) is evident for C36/LJ-PME and it agrees qualitatively with the experiment. SCD for the POPG head group are also compared to experiment in Figure 6. There is no reported error from Borle et al. [65], but the comparison with Ferreira’s data indicates that further refinement of PG-specific parameters might be needed, and it will be a focus of future updates to the FF.
KA calculated based on area fluctuation are listed in Table 8. Considering the standard errors, KA from C36/LJ-PME simulations are highly consistent with C36 values, asserting that the reparametrization only introduced minimal changes to the C36 lipid FF. KA also compare favorably with available experimental values for PC and PE lipids, demonstrating the two head groups were well parametrized. While a direct comparison with experiment is not available for DHPC, KA for DHPC is close to DPPC, which is reasonable considering the two molecules are very similar to each other in chemical structure.
Table 8.
Area compressibility moduli (KA) in dyn/cm for selected bilayers compared to C36 simulations using same system sizes and experimental values. Standard errors are given in parentheses.
| lipid | temperature (K) | C36/LJ-PME | C36 | experiment |
|---|---|---|---|---|
| DPPC | 323.15 | 240 (20) | 230 (20) [36] | 231 [71] |
| DMPC | 303.15 | 210 (20) | 210 (30) [36] | 234 [72] |
| DLPC | 303.15 | 260 (20) | ||
| DOPC | 303.15 | 300 (40) | 280 (10) [36] | 300 [73] |
| POPC | 303.15 | 230 (30) | 240 (10) [36] | 180–330 [74] |
| POPE | 308.15 | 260 (40) | 280 (20) [36],a | 233 [75] |
| DMPG | 303.15 | 200 (20) | ||
| POPG | 303.15 | 250 (20) | 220 (20) [36] | |
| DHPC | 321.15 | 240 (30) | 214 (18) [3] | |
| 333.15 | 240 (30) | 230 (15) [3] |
Data obtained at 310 K.
3.4. Dynamic Properties.
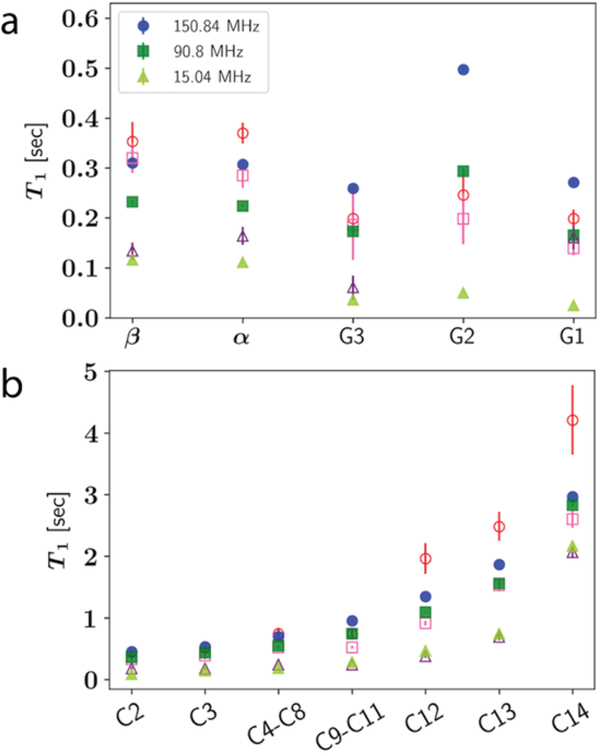
The last part of the validation focuses on dynamic properties of lipid bilayers. The NMR spin-lattice relaxation times of C-H bonds are shown in Figure 7 for DMPC. Overall, C36/LJ-PME agrees well with the experiment at all three carbon Larmor frequencies, except carbon G2 (C2) under high frequency (150.84 MHz). The same trend has been detected for C36 in previous publications [52, 68] and will be further discussed in Section 4. In fact, the overall pattern for the headgroup T1 from C36/LJ-PME is very similar to C36, despite the small differences for the α and β carbons. Again, this similarity is related to the dihedral fitting protocol maximizing the consistency with C36. It should be noted that dihedrals in the glycerol region are highly coupled and direct fits to QM data are impractical. An alternative approach was taken by Klauda et al. in the original C36 FF [1], where the order parameters of that region were used as additional targets to parametrize the dihedrals. This can potentially lead to unphysical description of the energy landscape in that region since the dihedral parameters that can generate the experimental order parameters might not be unique. In terms of the tail region, better agreement with experiment is seen for carbons closer to the head group, while the last three carbons (C12, C13 and C14) are underestimated at high frequency (150.84 MHz).
Figure 7.
T1 for DMPC at 303.15 K from experiment [76] (open symbols) and simulation (closed symbols). (a) Headgroup carbons; (b) Tail carbons.
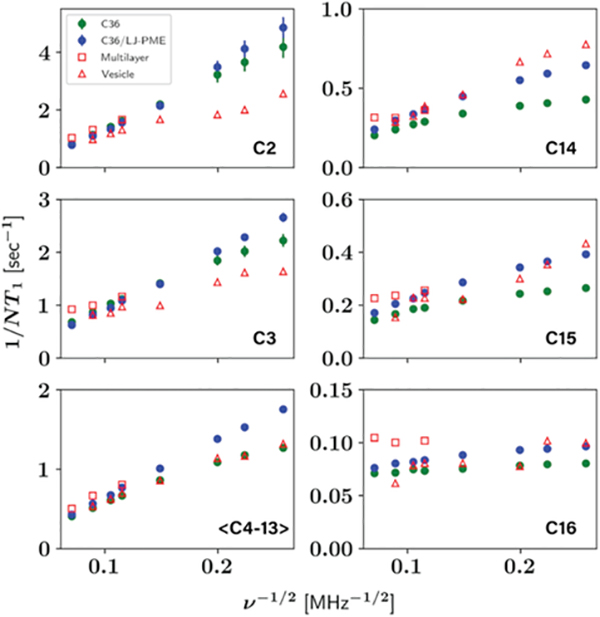
To further study the frequency dependence for the tail region, T1 of DPPC tail carbons were computed and compared to both experiments and C36 (see Figure 8). There are two sets of experiments. One is from Brown et al. [77] measured with small vesicles, the other is from Klauda et al. [68] measured with large multilamellar liposomes (multilayers) at relatively higher frequencies. It should be noted that experimental 1/NT1 from multilamellar liposomes are, on average, 13% higher than those from small vesicles at 75.4 MHz, and 28% higher at 125.7 MHz. Possible causes are the waters remaining between the bilayers in the multilamellar liposomes and the different curvatures as discussed by Klauda et al. [68] In general, 1/NT1 for C36/LJ-PME agree well with the experiments, though slightly higher values are observed for <C4-C13> at lower frequencies compared to the vesicle data. There is also a trend that 1/NT1 for C36/LJ-PME at lower frequencies are higher than C36. These trends can be understood following Szabo’s [78] analysis of the frequency dependence of vesicle data using his a “model-free” formalism [44]. Specifically, the spectral density for the ith carbon in a chain, Ji(ω) is written
| (5) |
where τi is the fast relaxation time associated with gauche-trans isomerization, is the generalized order parameter for each carbon, and τs is a slow relaxation common to all of the acyl chain carbons. Since both the dihedral parameters (which are related to the fast motion) and the order parameter profiles (Figure S4) for the acyl chain are identical for C36/LJ-PME and C36, the difference must arise from τs which here is the slow relaxation associated with of wobble [79]. To verify this, the second rank reorientational correlation function C2(t) of the unit vector formed by C22 and C32 carbons (second carbons from the two acyl chains) were computed. C2(t) is defined as
| (6) |
where P2 is the second Legendre polynomial. This correlation function is then fit with two exponentials in the form of eq 7 to extract the time constants corresponding to different modes of motion, and the slow relaxation time is assigned to wobble [80].
Figure 8.
Frequency dependence of NMR T1 for DPPC tail carbons. Vesical data from Brown et al. [77], and multilayer data from Klauda et al. [68]
| (7) |
Fitting to eq 7 gives a slow relaxation time of 2.79 ± 0.12 ns for C36 and 4.15 ± 0.2 ns for C36/LJ-PME, which supports our assertion that the larger 1/NT1 of C36/LJ-PME at lower frequencies are caused by slower wobble. In fact, the second term on the right-hand side of eq 5 is a monotonically increasing function of τs within the frequency range studied here; besides, the lager τs of C36/LJ-PME makes the frequency dependence sharper than C36. Similar analysis can be conducted to explain the difference between C36 and C36/LJ-PME for DMPC T1. Investigations into the chain order parameters (Figure S4) show that C36/LJ-PME is less ordered near the lipid head compared to C36 but more ordered for the terminal carbons. For carbons near the head, the influence of lower order parameter might be canceled by the slower wobble, thus T1 for this region are similar between the two FFs. However, the relatively higher order parameters for the terminal carbons impose the same effect as the slower wobble, causing larger Ji(ω) and hence shorter T1 for that region.
Another dynamic property studied is the diffusion constant of single lipids in a homogenous bilayer. The self-diffusivity of lipid has been a popular target for FF validation. However, obtaining meaningful diffusion constants from simulation to compare with experiments is not straightforward due to the strong effect of PBC on translational diffusion. Instead, extrapolation using knowledge of membrane shear viscosity (ηm) and interleaflet friction (b) is needed to get the diffusion constants to infinite system size. Based on the continuum hydrodynamic theory of Saffman-Delbrück, Camley et al. [46, 47] developed the periodic Saffman-Delbrück (PSD) model to predict the diffusion constant of single leaflet spanning or monotonic cylinder in a membrane, which states
| (8a) |
| (8b) |
where DPBC is the diffusion constant for a periodic simulation box which measures L in x/y, and D∞ is the diffusion constant for infinite system size, β is a constant, R is the (effective) radius of the cylinder, H is the average height of water layers above and below the membrane, ηmono = ηm/2 is the monolayer surface viscosity, ηf is the bulk viscosity of the surrounding fluid (water), and b is the inter-leaflet friction. D∞ can be computed for a specific set of R, ηm, and b (the other parameters can be precisely determined from the simulation) using https://diffusion.lobos.nih.gov. Using a R of 0.45 nm for DPPC and fixing b at 1 × 107 P/cm [81], Venable et al. [47] found that the best ηm to match the three C36 systems of different sizes is 4.4 × 10−8 P⋅cm. In a recent study of Zgorski et al. [48], the surface viscosity ηm for DPPC is calculated to be (12.26 ± 0.50) × 10−8 P⋅cm, which is significantly larger than the fitted value by Venable et al. By fixing ηm at this value, Zgorski et al. found the best R to match the simulation results is 0.15 nm, a number much smaller than the radius estimated from the average area occupied by a single lipid in bilayer (0.45 nm as mentioned above). One explanation for this inconsistency is that an effective hydrodynamic radius might be smaller than one consistent with the surface area since a lipid is not a solid cylinder.
Here, we fit ηm to the simulated results of DPPC using both R=0.45 nm and R=0.15 nm but those of DOPC only using R=0.47 nm, a radius consistent with the surface area. Table 9 lists the diffusion constants of DPPC and DOPC calculated from C36/LJ-PME simulations and those from fitting. Remaining parameters used in the fitting are listed in Table S2. Using a R of 0.45 nm for DPPC, ηm is determined to be 5.7 × 10−8 P⋅cm, which is at least 30% larger than the value obtained by Venable et al. [47] The fitted ηm of DOPC is 10.0 × 10−8 P⋅cm, a value 12% larger than Venable et al. This trend of higher viscosity is expected because of the added long-range dispersion in C36/LJ-PME and it is consistent with the slower diffusion. When changing R to 0.15 nm, ηm of DPPC becomes 11.3 × 10−8 P⋅cm, a value much larger than 5.7 × 10−8 P⋅cm but smaller than the surface viscosity calculated by Zgorski et al. using C36. This indicates that effective radius of DPPC in C36/LJ-PME might be different from C36, since a higher-than-C36 surface viscosity is expected. D∞ of DPPC from fitting are 3.89 × 10−7 cm2/s for R=0.45 nm and 2.87 × 10−7 cm2/s for R=0.15 nm, which are still substantially larger than the experiment (1.5 × 10−7 cm2/s) [82]. D∞ for DOPC is 2.24 × 10−7 cm2/s, while the experimental value is 0.825 × 10−7 cm2/s [83].
Table 9.
Diffusion constants from C36/LJ-PME simulations (Dsim) and fittings using the PSD model (DPBC and D∞) for DPPC and DOPC.
| lipid, temperature (K) | R (nm) | ηm (10−8 P⋅cm) | # lipid | Dsim (10−7 cm2/s) | DPBC (10−7 cm2/s) | D∞ (10−7 cm2/s) |
|---|---|---|---|---|---|---|
| DPPC, 323.15 | 0.45 | 5.7 | 72 | 1.12 ± 0.05 | 1.01 | 3.89 |
| 288 | 1.45 ± 0.04 | 1.44 | ||||
| 648 | 1.59 ± 0.07 | 1.70 | ||||
| 0.15 | 11.3 | 72 | 1.12 ± 0.05 | 1.18 | 2.87 | |
| 288 | 1.45 ± 0.04 | 1.42 | ||||
| 648 | 1.59 ± 0.07 | 1.55 | ||||
| DOPC, 303.15 | 0.47 | 10.0 | 72 | 0.60 ± 0.04 | 0.58 | 2.24 |
| 288 | 0.87 ± 0.03 | 0.82 | ||||
| 648 | 0.89 ± 0.03 | 0.96 |
4. Discussion
Long-range dispersion has been incorporated into the CHARMM36 lipid FF through the LJ-PME method, resulting in a new FF denoted C36/LJ-PME. C36/LJ-PME was validated against a wide range of structural and dynamic properties using various lipids. While the overall agreement with experiment is similar to C36, the explicit inclusion of the long-range dispersion eliminates the sensitivity of the FF to the truncation of the LJ. Proceeding beyond lipids, simulations [84] using the CHARMM36m protein parameter set show the presence of LJ-PME does not impact assorted properties of ubiquitin. This is consistent with the use of an isotropic long-range LJ correction in condensed phase simulations during optimization of the model compounds (e.g., N-methylacetamide, methanol, dimethyldisulfide) that are the foundation of the C36 force field. Hence, it is reasonable to add proteins to membrane simulations carried out with C36/LJ-PME, though some testing would be prudent. Similar testing is also recommended for simulations of membranes and nucleic acids and other compounds with the CHARMM force fields. The TIP3P water model is used to keep the balance between solvent-solvent and solvent-solute interactions and the long-range dispersion would not impact this balance because the dominant interaction is the short-range hydrogen bonding. Another significant improvement over C36 is that C36/LJ-PME achieves consistency between bilayer and monolayer isotherms because of the long-range dispersion and the reparametrization targeting both bilayer and monolayer properties. This makes it possible to compare simulations to monolayer experiments directly (see the Discussion of Paper I for more details). Since LJ-PME is based on the efficient particle-mesh Ewald (PME) algorithm, the simulation speed should be comparable to the electrostatic PME method when using a proper real-space cutoff. Using the 72-lipid DPPC bilayer as a benchmark, the speed on a single NVIDIA V100 GPU is 179 ns/day when using a real-space cutoff of 10 Å and a time step of 2 fs in OpenMM 7.4.1. This is 10 ns/day faster than the electrostatic PME combined with a force-switching function ranging from 8–12 Å for the LJ interactions (other settings remain the same). While reducing the real-space cutoff can further speed up the simulation, a cutoff smaller than 9 Å is not recommended because our tests (Table S8 of Paper I) have shown that the surface area of bilayer starts to deviate from its optimized value when the real-space cutoff is smaller than 9 Å.
In this study, glycerophospholipids (GPLs) and ether lipids were parametrized separately because there is no overlap between the parameters. PCs were used for the parametrization of GPLs, where only the glycerol and ester groups were changed with respect to C36. This topologically restricted parametrization maximizes the consistency with the rest of the CHARMM FF by keeping the phosphate unchanged. It also allows freedom for future optimization targeting head-specific groups like the serine group in phosphatidylserine (PS) and the glycerol group in PG. The ether linkage was parametrized by targeting the DHPC bilayer surface area and thickness. Both parametrizations only introduced minimal changes to the C36 parameters, demonstrating the high quality of the C36 lipid FF and the efficiency of the semi-automated optimization approach.
The validation set for GPLs consists of a total of nine lipid types covering PC, PG and PE heads and saturated/unsaturated chains. Surface areas for these nine lipids agree very well with experiments, with the largest deviation being DLPC (+5.8%). Similar to the C36 lipid FF, there is an overhydration of bilayers compared to experiment, especially for PCs with relatively short chains. The overall thickness DB, which is calculated based on the water distribution, deviates from experimentally fitted values by 4.8% on average. As discussed in the original publication of C36, such an overhydration facilitates the improved estimate in the surface area. As the only PE bilayer simulated in this study, POPE has excellent agreement with experimentally measured structural data. The test for PG is based on DMPG bilayer at three different temperatures (303.15 K, 323.15 K and 333.15 K) and POPG bilayer at 303.15 K. C36/LJ-PME is able to reproduce the experimental surface area and thickness, as well as the scattering data. However, concern is raised when comparing the DMPG (303.15 K) chain order parameter to experiment (see Figure S5). The average over the 12 largest values from both chains is 0.24 for C36/LJ-PME, while the NMR experiment measures about 0.21 [85]. This higher order parameter is consistent with the lower surface area compared to experiment (59.8 Å2 versus 62.5 Å2). In fact, the gel to fluid phase transition temperature of the DMPG bilayer is 297.15 K (close to the simulated temperature) [85], and C36/LJ-PME fails to accurately predict properties at 303.15 K where transient domain(s) containing extended hydrocarbon chains are formed (Figure S6). This indicates that further refinement of the PG head group is needed for a more accurate treatment of the phase transition temperature and lipid packing. This will be a focus of future updates to the C36/LJ-PME FF.
NMR spin lattice relaxation time T1 of C-H bonds were compared to experiments. The head group region is well described by C36/LJ-PME. At high frequency (150.84 MHz), T1 of carbon G2 is overestimated compared to the sonicated vesicle data from Brown et al. [76] However, a more recent measurement [86] using multilamellar vesicles obtained by centrifuge is in favor of C36/LJ-PME and C36. At 13C Larmor frequency of 125 MHz, Antila et al. detected a T1 of 0.38 ± 0.04 s, a value right between the T1 at 90.8 MHz and 150.84 MHz predicted by C36/LJ-PME. Considering the monotonic increasing of T1 with respect to the Larmor frequency within the range studied here, this indicates that C36/LJ-PME predicts the T1 of carbon G2 precisely. However, the same authors pointed out in another paper [87] that C36 underestimates the T1 for the β and α segments due to the high weights of motion at the 0.1–1 ns timescale. An explanation for this could be the too fast diffusion of the TIP3P water considering these segments are close to the aqueous phase, though it is hard to quantify the influence. The frequency dependence of the chain is also well described by C36/LJ-PME as shown in Figure 7–8. The small difference with C36 can be explained by the slower wobble and rotational diffusion about the long axis of the lipid due to the increased viscosity at the presence of long-range dispersion.
Lipid diffusion calculated by C36/LJ-PME is slower than C36. Extrapolating the simulated results using the PSD model with an effective hydrodynamic radius of 0.15 nm generated a D∞ of 2.87 × 10−7 cm2/s for DPPC, which is still 90% faster than experiment. As discussed by Zgorski et al.[48], the underestimated viscosity of water and interleaflet coupling accounts for approximately 20% of this error, and the dominant modulator to diffusion is ηm within a hydrodynamic treatment.
The lower fluidity compared to C36 raises the concern that bilayers simulated with C36/LJ-PME will remain in the fluid phase above the transition temperature. To examine this problem, microsecond-long simulations were conducted for the 72-lipid DPPC bilayer at 323.15 K and 317.15 K (approximately 3 °C above the ripple (Pβ) to liquid-crystalline (Lα) phase transition temperature) [88]. The areas per lipid for the two simulations are reported in Figure S7. It is clear from Figure S7 that the bilayer remained in the liquid-crystalline phase during the microsecond-long simulations. To study the influence of system size, 1152-lipid bilayers were simulated for seven lipid types, and the results are shown in Figure S8. Among the seven simulations, three used C36/LJ-PME and the other four used parameters from the Global parametrization in Paper I. The Al indicates that all these large bilayers stayed in the fluid phase during the 400 ns simulations.
While successful in many aspects, C36/LJ-PME has its limitations as an additive FF. For example, the electrostatic potential drop from the center of bilayer to water is about twice the experimental measures (Figure S9) [89] suggesting polarization is needed. Other situations a polarizable FF include water permeation, solvation free energy of apolar molecules in polar solutions or vice versa. While C36/LJ-PME and other popular additive lipid FFs will likely remain popular, a reliable polarizable FF for lipid membrane is in urgent need. Methods developed in this paper could be used to parametrize such a force field. Likewise, these methods could be used to replace the TIP3P model in an additive FF. Hence, C36/LJ-PME represents a major update to the C36 lipid FF by resolving the inconsistency between bilayer and monolayer and eliminating the “cutoff” dependence of the FF thereby increasing the range of systems that can be studied using the CHARMM FF.
Supplementary Material
Acknowledgements:
This research was supported by the Intramural Research Program of the NIH, the National Heart, Lung, and Blood Institute, and the use of the high-performance computational capabilities at the National Institutes of Health, Bethesda, MD (NHLBI LoBoS and Biowulf clusters). JBK acknowledges support from NSF (CHE-2003912).
Footnotes
Supporting Information Available:
Table comparing partial charges of the ether linkage for C36 and C36/LJ-PME; table listing the extra fitting parameters used for the PSD model; figure comparing the atom-pair-specific RDFs for C36 and C36/LJ-PME; figure showing the partial atomic charges of DEOE used for PES; figure showing the electron density profile for DPPC and DMPC bilayers; figure comparing the SCD profiles of DPPC and DMPC bilayers for C36 and C36/LJ-PME; figure showing the chain SCD of DMPG bilayer; figure containing snapshots from the DMPG bilayer (303.15 K) simulation; figures showing surface areas during microsecond-long and 400 ns-long simulations; and figure showing the electrostatic potential drop for DPPC bilayer.
References:
- 1.Klauda JB, Venable RM, Freites JA, O’Connor JW, Tobias DJ, Mondragon-Ramirez C, et al. Update of the CHARMM All-Atom Additive Force Field for Lipids: Validation on Six Lipid Types. J Phys Chem B. 2010;114(23):7830–43. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Venable RM, Luo Y, Gawrisch K, Roux B, Pastor RW. Simulations of Anionic Lipid Membranes: Development of Interaction-Specific Ion Parameters and Validation Using NMR Data. J Phys Chem B. 2013;117(35):10183–92. doi: 10.1021/jp401512z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Leonard AN, Pastor RW, Klauda JB. Parameterization of the CHARMM All-Atom Force Field for Ether Lipids and Model Linear Ethers. J Phys Chem B. 2018;122(26):6744–54. doi: 10.1021/acs.jpcb.8b02743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Venable Richard M, Sodt Alexander J, Rogaski B, Rui H, Hatcher E, MacKerell Alexander D Jr., et al. CHARMM All-Atom Additive Force Field for Sphingomyelin: Elucidation of Hydrogen Bonding and of Positive Curvature. Biophys J. 2014;107(1):134–45. doi: 10.1016/j.bpj.2014.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wang E, Klauda JB. Molecular Dynamics Simulations of Ceramide and Ceramide-Phosphatidylcholine Bilayers. J Phys Chem B. 2017;121(43):10091–104. doi: 10.1021/acs.jpcb.7b08967. [DOI] [PubMed] [Google Scholar]
- 6.Wu Emilia L, Engström O, Jo S, Stuhlsatz D, Yeom Min S, Klauda Jeffery B, et al. Molecular Dynamics and NMR Spectroscopy Studies of E.coli Lipopolysaccharide Structure and Dynamics. Biophys J. 2013;105(6):1444–55. doi: 10.1016/j.bpj.2013.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.West A, Zoni V, Teague WE, Leonard AN, Vanni S, Gawrisch K, et al. How Do Ethanolamine Plasmalogens Contribute to Order and Structure of Neurological Membranes? J Phys Chem B. 2020;124(5):828–39. doi: 10.1021/acs.jpcb.9b08850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Klauda JB, Monje V, Kim T, Im W. Improving the CHARMM force field for polyunsaturated fatty acid chains. J Phys Chem B. 2012;116(31):9424–31. doi: 10.1021/jp304056p. [DOI] [PubMed] [Google Scholar]
- 9.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A smooth particle mesh Ewald method. J Chem Phys. 1995;103(19):8577–93. doi: 10.1063/1.470117. [DOI] [Google Scholar]
- 10.Klauda JB, Wu X, Pastor RW, Brooks BR. Long-Range Lennard-Jones and Electrostatic Interactions in Interfaces: Application of the Isotropic Periodic Sum Method. J Phys Chem B. 2007;111(17):4393–400. doi: 10.1021/jp068767m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mecke M, Winkelmann J, Fischer J. Molecular Dynamics Simulation of the Liquid-Vapor Interface: The Lennard-Jones Fluid. J Chem Phys. 1997;107:9264–70. doi: 10.1063/1.475217. [DOI] [Google Scholar]
- 12.Brooks BR, Brooks CL, Mackerell AD, Nilsson L, Petrella RJ, Roux B, et al. CHARMM: The biomolecular simulation program. J Comput Chem. 2009;30(10):1545–614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wennberg CL, Murtola T, Páll S, Abraham MJ, Hess B, Lindahl E. Direct-Space Corrections Enable Fast and Accurate Lorentz-Berthelot Combination Rule Lennard-Jones Lattice Summation. J Chem Theory Comput. 2015;11(12):5737–46. doi: 10.1021/acs.jctc.5b00726. [DOI] [PubMed] [Google Scholar]
- 14.Wennberg CL, Murtola T, Hess B, Lindahl E. Lennard-Jones Lattice Summation in Bilayer Simulations Has Critical Effects on Surface Tension and Lipid Properties. J Chem Theory Comput. 2013;9(8):3527–37. doi: 10.1021/ct400140n. [DOI] [PubMed] [Google Scholar]
- 15.Eastman P, Swails J, Chodera JD, McGibbon RT, Zhao Y, Beauchamp KA, et al. OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLoS Comput Biol. 2017;13(7):e1005659. doi: 10.1371/journal.pcbi.1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Leonard AN, Simmonett AC, Pickard FC, Huang J, Venable RM, Klauda JB, et al. Comparison of Additive and Polarizable Models with Explicit Treatment of Long-Range Lennard-Jones Interactions Using Alkane Simulations. J Chem Theory Comput. 2018;14(2):948–58. doi: 10.1021/acs.jctc.7b00948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Yu Y, Krämer A, Venable RM, Simmonett AC, MacKerell AD, Klauda JB, et al. Semi-automated Optimization of the CHARMM36 Lipid Force Field to Include Explicit Treatment of Long-Range Dispersion. J Chem Theory Comput. 2021. doi: 10.1021/acs.jctc.0c01326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Durell SR, Brooks BR, Ben-Naim A. Solvent-Induced Forces between Two Hydrophilic Groups. J Phys Chem. 1994;98(8):2198–202. doi: 10.1021/j100059a038. [DOI] [Google Scholar]
- 19.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79(2):926–35. doi: 10.1063/1.445869. [DOI] [Google Scholar]
- 20.Schlenkrich M, Brickmann J, MacKerell AD, Karplus M. An Empirical Potential Energy Function for Phospholipids: Criteria for Parameter Optimization and Applications. In: Merz KM, Roux B, editors. Biological Membranes: A Molecular Perspective from Computation and Experiment. Boston, MA: Birkhäuser Boston; 1996. p. 31–81. [Google Scholar]
- 21.Feller SE, MacKerell AD. An Improved Empirical Potential Energy Function for Molecular Simulations of Phospholipids. J Phys Chem B. 2000;104(31):7510–5. doi: 10.1021/jp0007843. [DOI] [Google Scholar]
- 22.Klauda J B, Brooks B R, MacKerell A D, Venable R M, Pastor R W. An ab Initio Study on the Torsional Surface of Alkanes and Its Effect on Molecular Simulations of Alkanes and a DPPC Bilayer. J Phys Chem B. 2005;109(11):5300–11. doi: 10.1021/jp0468096. [DOI] [PubMed] [Google Scholar]
- 23.Pastor RW, MacKerell AD. Development of the CHARMM Force Field for Lipids. J Phys Chem Lett. 2011;2(13):1526–32. doi: 10.1021/jz200167q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Botan A, Favela-Rosales F, Fuchs PFJ, Javanainen M, Kanduč M, Kulig W, et al. Toward Atomistic Resolution Structure of Phosphatidylcholine Headgroup and Glycerol Backbone at Different Ambient Conditions. J Phys Chem B. 2015;119(49):15075–88. doi: 10.1021/acs.jpcb.5b04878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hénin J, Shinoda W, Klein ML. United-Atom Acyl Chains for CHARMM Phospholipids. J Phys Chem B. 2008;112(23):7008–15. doi: 10.1021/jp800687p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Klauda JB, Brooks BR, MacKerell AD, Venable RM, Pastor RW. An ab Initio Study on the Torsional Surface of Alkanes and Its Effect on Molecular Simulations of Alkanes and a DPPC Bilayer. J Phys Chem B. 2005;109(11):5300–11. doi: 10.1021/jp0468096. [DOI] [PubMed] [Google Scholar]
- 27.Lee S, Tran A, Allsopp M, Lim JB, Hénin J, Klauda JB. CHARMM36 United Atom Chain Model for Lipids and Surfactants. J Phys Chem B. 2014;118(2):547–56. doi: 10.1021/jp410344g. [DOI] [PubMed] [Google Scholar]
- 28.Yu Y, Klauda JB. Update of the CHARMM36 United Atom Chain Model for Hydrocarbons and Phospholipids. J Phys Chem B. 2020;124(31):6797–812. doi: 10.1021/acs.jpcb.0c04795. [DOI] [PubMed] [Google Scholar]
- 29.Chowdhary J, Harder E, Lopes PEM, Huang L, MacKerell AD, Roux B. A Polarizable Force Field of Dipalmitoylphosphatidylcholine Based on the Classical Drude Model for Molecular Dynamics Simulations of Lipids. J Phys Chem B. 2013;117(31):9142–60. doi: 10.1021/jp402860e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Li H, Chowdhary J, Huang L, He X, MacKerell AD, Roux B. Drude Polarizable Force Field for Molecular Dynamics Simulations of Saturated and Unsaturated Zwitterionic Lipids. J Chem Theory Comput. 2017;13(9):4535–52. doi: 10.1021/acs.jctc.7b00262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Venable RM, Krämer A, Pastor RW. Molecular Dynamics Simulations of Membrane Permeability. Chem Rev. 2019;119(9):5954–97. doi: 10.1021/acs.chemrev.8b00486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lamoureux G, Roux Bt. Modeling induced polarization with classical Drude oscillators: Theory and molecular dynamics simulation algorithm. J Chem Phys. 2003;119(6):3025–39. doi: 10.1063/1.1589749. [DOI] [Google Scholar]
- 33.Sundaralihgam M DISCUSSION PAPER: MOLECULAR STRUCTURES AND CONFORMATIONS OF THE PHOSPHOLIPIDS AND SPHINGOMYELINS. Ann N Y Acad Sci. 1972;195(1):324–55. Epub 1972/06/01. doi: 10.1111/j.1749-6632.1972.tb54814.x. [DOI] [PubMed] [Google Scholar]
- 34.Nomenclature of Lipids. J Lipid Res. 1967;8(5):523–8. [PubMed] [Google Scholar]
- 35.The Nomenclature of Lipids (Recommendations 1976). IUPAC-IUB Commission on Biochemical Nomenclature. J Lipid Res. 1978;19(1):114–28. [PubMed] [Google Scholar]
- 36.Venable RM, Brown FLH, Pastor RW. Mechanical Properties of Lipid Bilayers from Molecular Dynamics Simulation. Chem Phys Lipids. 2015;192:60–74. doi: 10.1016/j.chemphyslip.2015.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Foglia F, Lawrence MJ, Lorenz CD, McLain SE. On the Hydration of the Phosphocholine Headgroup in Aqueous Solution. J Chem Phys. 2010;133(14):145103. doi: 10.1063/1.3488998. [DOI] [PubMed] [Google Scholar]
- 38.Mark P, Nilsson L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J Phys Chem A. 2001;105(43):9954–60. doi: 10.1021/jp003020w. [DOI] [Google Scholar]
- 39.Jo S, Kim T, Iyer VG, Im W. CHARMM-GUI: A Web-Based Graphical User Interface for CHARMM. J Comput Chem. 2008;29(11):1859–65. doi: 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
- 40.Jo S, Lim JB, Klauda JB, Im W. CHARMM-GUI Membrane Builder for Mixed Bilayers and Its Application to Yeast Membranes. Biophys J. 2009;97(1):50–8. doi: 10.1016/j.bpj.2009.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wu EL, Cheng X, Jo S, Rui H, Song KC, Dávila-Contreras EM, et al. CHARMM-GUI Membrane Builder toward realistic biological membrane simulations. J Comput Chem. 2014;35(27):1997–2004. doi: 10.1002/jcc.23702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lee J, Cheng X, Swails JM, Yeom MS, Eastman PK, Lemkul JA, et al. CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field. J Chem Theory Comput. 2016;12(1):405–13. doi: 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kučerka N, Katsaras J, Nagle JF. Comparing Membrane Simulations to Scattering Experiments: Introducing the SIMtoEXP Software. J Membr Biol. 2010;235(1):43–50. doi: 10.1007/s00232-010-9254-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lipari G, Szabo A. Model-Free Approach to the Interpretation of Nuclear Magnetic Resonance Relaxation in Macromolecules. 2. Analysis of Experimental Results. J Am Chem Soc. 1982;104(17):4559–70. doi: 10.1021/ja00381a010. [DOI] [Google Scholar]
- 45.Yeh IC, Hummer G. System-size dependence of diffusion coefficients and viscosities from molecular dynamics simulations with periodic boundary conditions. J Phys Chem B. 2004;108(40):15873–9. doi: 10.1021/jp0477147. [DOI] [Google Scholar]
- 46.Camley BA, Lerner MG, Pastor RW, Brown FLH. Strong Influence of Periodic Boundary Conditions on Lateral Diffusion in Lipid Bilayer Membranes. J Chem Phys. 2015;143(24):243113. doi: 10.1063/1.4932980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Venable RM, Ingólfsson HI, Lerner MG, Perrin BS, Camley BA, Marrink SJ, et al. Lipid and Peptide Diffusion in Bilayers: The Saffman-Delbrück Model and Periodic Boundary Conditions. J Phys Chem B. 2017;121(15):3443–57. doi: 10.1021/acs.jpcb.6b09111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zgorski A, Pastor RW, Lyman E. Surface Shear Viscosity and Interleaflet Friction from Nonequilibrium Simulations of Lipid Bilayers. J Chem Theory Comput. 2019;15(11):6471–81. doi: 10.1021/acs.jctc.9b00683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Klauda JB, Brooks BR, Pastor RW. Dynamical motions of lipids and a finite size effect in simulations of bilayers. J Chem Phys. 2006;125(14):144710-. doi: 10.1063/1.2354486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pan J, Cheng X, Heberle FA, Mostofian B, Kučerka N, Drazba P, et al. Interactions between Ether Phospholipids and Cholesterol As Determined by Scattering and Molecular Dynamics Simulations. J Phys Chem B. 2012;116(51):14829–38. doi: 10.1021/jp310345j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Guler SD, Ghosh DD, Pan J, Mathai JC, Zeidel ML, Nagle JF, et al. Effects of Ether vs. Ester Linkage on Lipid Bilayer Structure and Water Permeability. Chem Phys Lipids. 2009;160(1):33–44. doi: 10.1016/j.chemphyslip.2009.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Zhuang X, Dávila-Contreras EM, Beaven AH, Im W, Klauda JB. An extensive simulation study of lipid bilayer properties with different head groups, acyl chain lengths, and chain saturations. Biochim Biophys Acta. 2016;1858(12):3093–104. doi: 10.1016/j.bbamem.2016.09.016. [DOI] [PubMed] [Google Scholar]
- 53.Kučerka N, Nieh MP, Katsaras J. Fluid phase lipid areas and bilayer thicknesses of commonly used phosphatidylcholines as a function of temperature. Biochimica et Biophysica Acta - Biomembranes. 2011;1808(11):2761–71. doi: 10.1016/j.bbamem.2011.07.022. [DOI] [PubMed] [Google Scholar]
- 54.Kučerka N, Liu Y, Chu N, Petrache HI, Tristram-Nagle S, Nagle JF. Structure of fully hydrated fluid phase DMPC and DLPC lipid bilayers using x-ray scattering from oriented multilamellar arrays and from unilamellar vesicles. Biophys J. 2005;88(4):2626–37. doi: 10.1529/biophysj.104.056606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zhuang X, Makover JR, Im W, Klauda JB. A Systematic Molecular Dynamics Simulation Study of Temperature Dependent Bilayer Structural Properties. Biochim Biophys Acta. 2014;1838(10):2520–9. doi: 10.1016/j.bbamem.2014.06.010. [DOI] [PubMed] [Google Scholar]
- 56.Kučerka N, Nagle JF, Sachs JN, Feller SE, Pencer J, Jackson A, et al. Lipid Bilayer Structure Determined by the Simultaneous Analysis of Neutron and X-Ray Scattering Data. Biophys J. 2008;95(5):2356–67. doi: 10.1529/biophysj.108.132662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Pan J, Tristram-Nagle S, Kučerka N, Nagle JF. Temperature Dependence of Structure, Bending Rigidity, and Bilayer Interactions of Dioleoylphosphatidylcholine Bilayers. Biophys J. 2008;94(1):117–24. doi: 10.1529/biophysj.107.115691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kučerka N, Van Oosten B, Pan J, Heberle FA, Harroun TA, Katsaras J. Molecular Structures of Fluid Phosphatidylethanolamine Bilayers Obtained from Simulation-to-Experiment Comparisons and Experimental Scattering Density Profiles. J Phys Chem A. 2015;119(5):1947–56. doi: 10.1021/jp511159q. [DOI] [PubMed] [Google Scholar]
- 59.Pan J, Heberle FA, Tristram-Nagle S, Szymanski M, Koepfinger M, Katsaras J, et al. Molecular Structures of Fluid Phase Phosphatidylglycerol Bilayers as Determined by Small Angle Neutron and X-ray Scattering. Biochim Biophys Acta. 2012;1818(9):2135–48. doi: 10.1016/j.bbamem.2012.05.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Pan J, Marquardt D, Heberle FA, Kučerka N, Katsaras J. Revisiting the Bilayer Structures of Fluid Phase Phosphatidylglycerol Lipids: Accounting for Exchangeable Hydrogens. Biochim Biophys Acta. 2014;1838(11):2966–9. doi: 10.1016/j.bbamem.2014.08.009. [DOI] [PubMed] [Google Scholar]
- 61.Somerharju PJ, Virtanen JA, Eklund KK, Vainio P, Kinnunen PKJ. 1-Palmitoyl-2-Pyrenedecanoyl Glycerophospholipids as Membrane Probes: Evidence for Regular Distribution in Liquid-Crystalline Phosphatidylcholine Bilayers. Biochemistry. 1985;24(11):2773–81. doi: 10.1021/bi00332a027. [DOI] [PubMed] [Google Scholar]
- 62.Kučerka N, Holland BW, Gray CG, Tomberli B, Katsaras J. Scattering Density Profile Model of POPG Bilayers As Determined by Molecular Dynamics Simulations and Small-Angle Neutron and X-ray Scattering Experiments. J Phys Chem B. 2012;116(1):232–9. doi: 10.1021/jp208920h. [DOI] [PubMed] [Google Scholar]
- 63.Pan J, Tristram-Nagle S, Nagle JF. Effect of cholesterol on structural and mechanical properties of membranes depends on lipid chain saturation. Phys Rev E. 2009;80:021931-. doi: 10.1103/PhysRevE.80.021931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Shaikh SR, Brzustowicz MR, Gustafson N, Stillwell W, Wassall SR. Monounsaturated PE Does Not Phase-Separate from the Lipid Raft Molecules Sphingomyelin and Cholesterol: Role for Polyunsaturation? Biochemistry. 2002;41(34):10593–602. doi: 10.1021/bi025712b. [DOI] [PubMed] [Google Scholar]
- 65.Borle F, Seelig J. Ca2+ Binding to Phosphatidylglycerol Bilayers as Studied by Differential Scanning Calorimetry and 2H- and 31P-nuclear Magnetic Resonance. Chem Phys Lipids. 1985;36(3):263–83. doi: 10.1016/0009-3084(85)90007-6. [DOI] [Google Scholar]
- 66.Seelig A, Seelig J. Dynamic structure of fatty acyl chains in a phospholipid bilayer measured by deuterium magnetic resonance. Biochemistry. 1974;13(23):4839–45. doi: 10.1021/bi00720a024. [DOI] [PubMed] [Google Scholar]
- 67.Seelig A, Seelig J. Bilayers of dipalmitoyl-3-sn-phosphatidylcholine. Conformational differences between the fatty acyl chains. Biochim Biophys Acta. 1975;406(1):1–5. doi: 10.1016/0005-2736(75)90037-1. [DOI] [PubMed] [Google Scholar]
- 68.Klauda JB, Eldho NV, Gawrisch K, Brooks BR, Pastor RW. Collective and Noncollective Models of NMR Relaxation in Lipid Vesicles and Multilayers. J Phys Chem B. 2008;112(19):5924–9. doi: 10.1021/jp075641w. [DOI] [PubMed] [Google Scholar]
- 69.Perly B, Smith ICP, Jarrell HC. Acyl chain dynamics of phosphatidylethanolamines containing oleic acid and dihydrosterculic acid: deuteron NMR relaxation studies. Biochemistry. 1985;24(17):4659–65. doi: 10.1021/bi00338a027. [DOI] [PubMed] [Google Scholar]
- 70.NMRlipids/NMRlipidsIVPEandPG [cited 2020 12/15]. Available from: https://github.com/NMRLipids/NMRlipidsIVPEandPG/blob/master/Figs/HGorderparametersPCPSPEPG-eps-converted-to.pdf.
- 71.Nagle JF, Tristram-Nagle S. Structure of Lipid Bilayers. Biochim Biophys Acta. 2000;1469(3):159–95. doi: 10.1016/S0304-4157(00)00016-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Rawicz W, Olbrich KC, McIntosh T, Needham D, Evans EA. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys J. 2000;79(1):328–39. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Evans E, Rawicz W, Smith BA. Concluding remarks back to the future: Mechanics and thermodynamics of lipid biomembranes. Faraday Discuss. 2012;161:591–611. doi: 10.1039/c2fd20127e. [DOI] [PubMed] [Google Scholar]
- 74.Binder H, Gawrisch K. Effect of Unsaturated Lipid Chains on Dimensions, Molecular Order and Hydration of Membranes. J Phys Chem B. 2001;105(49):12378–90. doi: 10.1021/jp010118h. [DOI] [Google Scholar]
- 75.Rand RP, Parsegian VA. Hydration forces between phospholipid bilayers. Biochim Biophys Acta. 1989;988(3):351–76. doi: 10.1016/0304-4157(89)90010-5. [DOI] [Google Scholar]
- 76.Leftin A, Brown MF. An NMR Database for Simulations of Membrane Dynamics. Biochim Biophys Acta. 2011;1808(3):818–39. doi: 10.1016/j.bbamem.2010.11.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Brown MF, Ribeiro AA, Williams GD. New View of Lipid Bilayer Dynamics from 2H and 13C NMR Relaxation Time Measurements. Proc Natl Acad Sci U S A. 1983;80(14):4325–9. doi: 10.1073/pnas.80.14.4325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Szabo A Nuclear Magnetic Resonance Relaxation and the Dynamics of Proteins and Membranes: Theory and Experiment. Ann N Y Acad Sci. 1986;482(1):44–50. doi: 10.1111/j.1749-6632.1986.tb20935.x. [DOI] [PubMed] [Google Scholar]
- 79.Szabo A Theory of Fluorescence Depolarization in Macromolecules and Membranes. J Chem Phys. 1984;81(1):150–67. doi: 10.1063/1.447378. [DOI] [Google Scholar]
- 80.Klauda JB, Roberts MF, Redfield AG, Brooks BR, Pastor RW. Rotation of Lipids in Membranes: Molecular Dynamics Simulation, 31P Spin-Lattice Relaxation, and Rigid-Body Dynamics. Biophys J. 2008;94(8):3074–83. doi: 10.1529/biophysj.107.121806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Camley BA, Brown FLH. Diffusion of Complex Objects Embedded in Free and Supported Lipid Bilayer Membranes: Role of Shape Anisotropy and Leaflet Structure. Soft Matter. 2013;9(19):4767–79. doi: 10.1039/C3SM00073G. [DOI] [Google Scholar]
- 82.Scheidt HA, Huster D, Gawrisch K. Diffusion of Cholesterol and Its Precursors in Lipid Membranes Studied by 1H Pulsed Field Gradient Magic Angle Spinning NMR. Biophys J. 2005;89(4):2504–12. doi: 10.1529/biophysj.105.062018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Lindblom G, Orädd G. Lipid Lateral Diffusion and Membrane Heterogeneity. Biochim Biophys Acta. 2009;1788(1):234–44. doi: 10.1016/j.bbamem.2008.08.016. [DOI] [PubMed] [Google Scholar]
- 84.You X, Jing H. On the Transferability of CHARMM36m Protein Force Field with LJ-PME: Hydrogen Bonding Dynamics under Elevated Pressures 2021. [DOI] [PMC free article] [PubMed]
- 85.Loew C, Riske KA, Lamy MT, Seelig J. Thermal Phase Behavior of DMPG Bilayers in Aqueous Dispersions as Revealed by 2H- and 31P-NMR. Langmuir. 2011;27(16):10041–9. doi: 10.1021/la201027p. [DOI] [PubMed] [Google Scholar]
- 86.Antila HS, Wurl A, Ollila OHS, Miettinen MS, Ferreira TM. Quasi-uncoupled rotational diffusion of phospholipid headgroups from the main molecular frame. arXiv:200906774 2020. [Google Scholar]
- 87.Antila HS, Ferreira M T, Ollila, Miettinen MS. Using Open Data to Rapidly Benchmark Biomolecular Simulations: Phospholipid Conformational Dynamics. J Chem Inf Model. 2021. doi: 10.1021/acs.jcim.0c01299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Mabrey S, Sturtevant JM. Investigation of phase transitions of lipids and lipid mixtures by high sensitivity differential scanning calorimetry. Proc Natl Acad Sci U S A. 1976;73(11):3862–6. doi: 10.1073/pnas.73.11.3862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Clarke RJ. The dipole potential of phospholipid membranes and methods for its detection. Adv Colloid Interface Sci. 2001;89–90:263–81. doi: 10.1016/S0001-8686(00)00061-0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.