A Many-Body, Fully Polarizable Approach to QM/MM Simulations

Abstract

We present a new development in quantum mechanics/molecular mechanics (QM/MM) methods by replacing conventional MM models with data-driven many-body (MB) representations rigorously derived from high-level QM calculations. The new QM/MM approach builds on top of mutually polarizable QM/MM schemes developed for polarizable force fields with inducible dipoles and uses permutationally invariant polynomials to effectively account for quantum-mechanical contributions (e.g., exchange-repulsion and charge transfer and penetration) that are difficult to describe by classical expressions adopted by conventional MM models. Using the many-body MB-pol and MB-DFT potential energy functions for water, which include explicit two-body and three-body terms fitted to reproduce the corresponding CCSD(T) and PBE0 two-body and three-body energies for water, we demonstrate a smooth energetic transition as molecules are transferred between QM and MM regions, without the need of a transition layer. By effectively elevating the accuracy of both the MM region and the QM/MM interface to that of the QM region, the new QM/MB-MM approach achieves an accuracy comparable to that obtained with a fully QM treatment of the entire system.

Graphical Abstract

1. INTRODUCTION

Quantum mechanics/molecular mechanics (QM/MM) approaches that integrate quantum chemistry (QM) with molecular mechanics (MM) have been used to describe systems that cannot be completely modeled by a pure QM or MM approach. These methods, which treat a smaller subsystem (S) via a quantum mechanical framework and the surrounding environment (E) using a force field, were initially described by Warshel and Karplus in 1972, wherein they partitioned the σ and π electrons of a molecule into separate empirical and semi-empirical treatments.¹ The current QM/MM formalism was originally proposed in the seminal 1976 study by Warshel and Levitt, where a protein was split into separate QM and MM subsystems, which interacted via a dielectric coupling.²

In their infancy, these QM/MM approaches were used to study small chemical reactions, such as halide exchange reactions of the form CH₃Cl + Cl⁻, which needed a solvent to be accurately modeled.³ Following the development of efficient interfaces between popular QM and MM software,³ along with advances in computational power, it became possible to simulate larger and more complex systems, such as enzymatic and other biomolecular reactions.^4,5 Furthermore, QM/MM saw success in the simulation of spectroscopic experiments of complex molecular systems.⁶

With regards to the formalism, most QM/MM approaches rely on an “effective Hamiltonian″ which couples the properties of the electronic density of the subsystem S to a set of point charges representing the environment E. This coupling, known as the electrostatic embedding (EE), is commonly used with non-polarizable force-fields, as all electrostatic interactions between the two regions can be taken into account in a relatively straightforward and cost-effective way. However, in EE, only the QM density is polarized by the environment and not vice versa. In particular, this implies that the interaction between the QM subsystem and the environment is the same, independent of the electronic state of the QM subsystem and/or the effects of an external field. The solution to this conundrum, known as a “polarizable embedding″ (PE), allows for the self-consistent equilibration of the classical degrees of freedom used to represent the electrostatic distribution of the environment, described with a polarizable force field^7–10 with the electronic density in the QM region. Early approaches to the PE method involved simple iterations over an electrostatic embedding scheme where the inducible dipoles could be back-polarized by point charges fit to the electronic density until the system converged.^11–14 A related approximation to the polarizable embedding was introduced with the LICHEM interface, which couples generic QM and MM software using a partially self-consistent polarization scheme, compromising some accuracy for a more generalized interface and greater computational efficiency.^15,16

By solving the QM equations and the MM polarization equations in a fully coupled fashion, some recent approaches adopt a more intimate coupling between the electron density in the QM region and the polarization in the MM region, with the latter being modeled by inducible point dipoles (IPD),^17–25 fluctuating charges,^26–31 Drude oscillators,^32–37 or using a response kernel.^38,39 In this contribution, we limit our discussion to IPD-based approaches, as this is the polarization model adopted by both the MB-pol^40–42 and AMOEBA^43,44 models used in this analysis. We note, in passing, that an IPD polarization scheme is also present in other advanced QM/MM methods, such as the effective fragment potential method⁴⁵ and the X-pol method.⁴⁶ Several implementations exist of fully polarizable IPD-based QM/MM schemes.^{17,21,23,47–49} Over the years, these implementations have been extended to simulations of various molecular properties, with the QM subsystem in either the ground or an excited state, hydration properties and, more recently, ab initio multiscale molecular dynamics.^{22,23,30,31,35–37,50,51}

Beyond the issues associated with coupling the QM and the MM regions, QM/MM faces another methodological road-block: diffusive breakup of the QM region. During a molecular dynamics simulation in solution, molecules that were originally assigned to the QM region can diffuse apart, which lead to an effective exchange between QM and MM molecules. Such situations can result in low-accuracy MM molecules, which, by construction, cannot undergo any chemical transformation, moving into the original QM region of interest, while high-accuracy QM molecules are dispersed in the original MM region. So-called adaptive QM/MM schemes attempt to overcome this limitation by adaptively partitioning the molecules in the QM and MM regions at each step.^52–55 Although appealing, adaptive QM/MM schemes suffer from some drawbacks associated with the inherent differences between QM and MM descriptions of the energies and corresponding forces. Due to this, when a molecule is switched between QM and MM treatments during re-partitioning, the whole system can experience a large change in energy, causing a discontinuity in the force. This can, for example, happen if the minima of the QM and MM energy landscapes are shifted relative to each other, which implies that a molecule located in a minimum energy configuration on the MM energy landscape can be thrust into a high-energy configuration when transitioned to the QM energy landscape.^52,53,56 In simulations, this behavior is manifested as unphysical dynamics along with structural artifacts at the QM/MM boundary.^{4,52,53,56,57} In this thread, advances in adaptive QM/MM have focused on suppressing and reducing energetic discontinuities at the QM/MM boundary, often by using a transition layer to smoothly transition atoms between QM and MM treatments.⁵⁵ These techniques range from simple smoothing functions to more complex distance-based partitioning approaches, which have been shown to conserve energy and smooth forces.^{4,53–56,58–71}

Unfortunately, while these adaptive approaches improve energy conservation and alleviate some of the discontinuities in the forces, which, consequently, smooth out boundary artifacts that may occur, they do not solve the underlying issue in that the system is being represented by two different potential energy functions.⁵⁵ Furthermore, adoption of transition layers increases the computational cost of QM/MM simulations, as some schemes can result in up to 2^N additional QM calculations for N molecules in the transition layer, though more modern partitioning schemes have been shown to significantly reduce that number.^{53,55,56,63,67}

Other approaches using advanced representations of the energy landscape have attempted a more rigorous treatment of QM/MM systems. Effective and exchange fragment models (EFP and XFP respectively) partition the system into ab initio and effective fragment (EF) components, where the two regions interact via one electron integrals between ab initio and EF molecules.^72–76 Recent EFP approaches have further developed this by integrating exchange-repulsion style interaction potentials across the QM/MM boundary in order to account for some quantum effects missing from the core EFP interaction.⁷⁷ The Gaussian electrostatic model (GEM) uses a density fitting formalism to represent the MM region using molecular electron densities.⁷⁸ Incorporated into a QM/MM approach, GEM allows both the QM and the MM regions to be represented by an electron density, and thus affords the scheme much greater accuracy when evaluating QM/MM interactions.^79,80 Building on these previous QM/MM approaches, we propose a new development, QM/MB-MM, in which the MM region is represented by data-driven models rigorously derived from the many-body expansion of the interaction energy. In this study, we describe the QM/MB-MM scheme using water as a prototypical example where the MB-MM region is described by the MB-pol^40–42 and MB-DFT⁸¹ models. MB-pol and MB-DFT are many-body water models that include explicit terms fitted to reproduce two-body and three-body energies calculated at the CCSD(T) and DFT levels of theory, respectively. We demonstrate that QM/MB-MM combined with a polarizable embedding scheme effectively elevates QM/MM calculations to quantum mechanical levels of accuracy, specifically, CCSD(T) for MB-pol and PBE0 for MB-DFT. Importantly, by combining a PBE0 representation of the QM region with a MB-DFT model fitted to PBE0 two-body and three-body data to represent the MM region, we demonstrate that energy discontinuities at the QM/MM boundary are largely suppressed and reduced to negligible effects.

2. THEORY AND COMPUTATIONAL DETAILS

All QM/MM calculations were carried out with the PBE0 functional along with the D3 dispersion correction using the aug-cc-pVQZ basis set.^82–85 Gaussian16⁸⁶ was used for the QM calculations, while an in-house code was used to handle the MB-pol and MB-DFT components incorporated into the QM/MM coupling framework.

2.1. Explicit Many-Body Models: MB-Pol and MB-DFT.

MB-pol and MB-DFT are explicit many-body models based on the many-body expansion (MBE), which represents the energy of a system as the sum of individual n-body contributions in a system of N molecules with n ≤ N.^40–42 This is formally expressed as:⁸⁷

$$\begin{gathered} E_N\left(r_1,\cdots ,r_N\right)=\sum _{i=1}^N{\epsilon }_{1B}\left(r_i\right)+\sum _{i<j}^N{\epsilon }_{2B}\left(r_i,r_j\right) \\ +\sum _{i<j<k}^N{\epsilon }_{3B}\left(r_i,r_j,r_k\right)+\cdots \\ +{\epsilon }_{NB}\left(r_1,\cdots ,r_N\right) \end{gathered}$$ (1)

where ε_1B represents the energy required to distort an individual monomer from its equilibrium geometry and ε_nB with n>1 are the n-body energies that are recursively defined as:

$$\begin{gathered} {\epsilon }_{NB}={\epsilon }_n(1,\cdots ,n)-\sum _{i=1}^N{\epsilon }_{1B}\left(r_i\right)-\sum _{i<j}^N{\epsilon }_{2B}\left(r_i,r_j\right) \\ -\sum _{i<j<k<\cdots <n-1}^N{\epsilon }_{(n-1)B}\left(r_i,r_j,\cdots ,r_{n-1}\right) \end{gathered}$$ (2)

For molecules with localized electron density and a large band gap, such as water, this expansion converges very quickly, with the sum of two-body and three-body energies contributing approximately 90–95% to the total interaction energy.

The MB-pol^40–42 and MB-DFT⁸¹ models include explicit representations for the first three terms of the MBE, while implicitly accounting for all higher order, n > 3 body terms through a classical polarization term,

$$\begin{gathered} E_N\left(r_1,\cdots ,r_N\right)=\sum _{i=1}^N{\epsilon }_{1B}\left(r_i\right)+\sum _{i>j}^N{\epsilon }_{2B}\left(r_i,r_j\right) \\ +\sum _{i>j>k}^N{\epsilon }_{3B}\left(r_i,r_j,r_k\right)+E_{\text{pol}} \end{gathered}$$ (3)

In these models, the 1B term is described by the Partridge–Schwenke potential energy surface, which was originally calculated at the configuration interaction level of theory and subsequently refined to quantitatively reproduce the experimental rovibrational transitions.⁸⁸ The two-body term consists of three contributions:

$${\epsilon }_{2B}=E_{2B}^{\text{sr}}+E_{\text{elec}}+E_{\text{disp}}$$ (4)

where $E_{2B}^{\text{sr}}$ is a fourth-degree permutationally invariant polynomial (PIP)⁸⁹ representing short-range interactions within a water dimer. E_elec is described by Coulomb interactions between geometry-dependent point charges, which reproduce the ab initio dipole moment surface of a water molecule.⁸⁸ Lastly, the two-body dispersion interaction is expressed as

$$E_{\text{disp}}=-\sum _{i,j}f\left({\delta }_{ij}\right)\frac{C_{6,ij}}{R_{ij}^6}$$ (5)

where i and j are indices for atoms on two separate water monomers, f(δ_ij) is the Tang–Toennies damping function with a fitted parameter δ_ij,⁹⁰ and C_{6, ij} are the dispersion coefficients calculated from the asymptotic reference energies of the water dimer as in CC-pol.⁹¹ The explicit three-body term,

$${\epsilon }_{3B}=E_{3B}^{\text{sr}}$$ (6)

represents short-range three-body interactions and is represented by a fourth-degree PIP.⁸⁹ In MB-pol, these explicit 2B and 3B terms were fitted on top of an implicit many-body polarizable term (E_pol in eq 3) to reproduce 2B and 3B energies calculated at the CCSD(T) level of theory in the complete basis set (CBS) limit.^40,41 In the MB-DFT model, the explicit ε_2B and ε_3B terms were instead fitted to 2B and 3B energies calculated at the PBE0-D3/aug-cc-pVQZ level of theory using the same procedure described in ref 81.

2.2. The QM/MM Interaction with MB-pol and MB-DFT.

In this section, we briefly overview the theory of IPD-based polarizable QM/MM at the self-consistent field level of theory, i.e., Hartree–Fock (HF) or DFT. A more detailed overview can be found in a recent review.⁹² The MB-pol and MB-DFT polarization energy is variational with respect to the polarization degrees of freedom, which means that the coupled QM/MM equations and energy can be conveniently obtained starting from a variational energy functional^21,24 of the SCF density P and the IPDs μ

$$\epsilon (P,\mu )={\epsilon }^{\text{QM}}(P)+{\epsilon }^{\text{MM}}(\mu )+{\epsilon }^{\text{Coup}}(P,\mu )$$ (7)

where ε^QM(P) and ε^MM(μ) represent the purely quantum mechanical and classical contributions to the energy, and ε^Coup(P, μ) describes the coupling between the two regions. The MM and coupling terms can then be combined into a general “environmental″ ε^Env(P, μ) term:

$$\epsilon (P,\mu )={\epsilon }^{\text{QM}}(P)+{\epsilon }^{\text{Env}}(P,\mu )$$ (8)

which is expressed as a sum of the MM contribution (ε^FF), the polarization energy $\left({\tilde{\epsilon }}^{\text{Pol}}\right)$, and the electrostatic QM/MM coupling (ε^QM/MM):

$${\epsilon }^{\text{Env}}(P,\mu )={\epsilon }^{\text{FF}}+{\tilde{\epsilon }}^{\text{Pol}}(P,\mu )+{\epsilon }^{\text{QM}/\text{MM}}(P)$$ (9)

The first term in eq 9 represents the energy of the MM region as described by a force field, which depends on neither the electron density nor the induced dipoles on the MM atoms, as well as any non-electrostatic interactions between the QM and MM regions, such as van der Waals interactions between molecules in the QM and MM regions:

$${\epsilon }^{\text{FF}}=E_{\text{non}-\text{elec }}^{\text{MM}}+E_{\text{non}-\text{elec}}^{\text{QM}/\text{MM}}$$ (10)

For the MB-pol and MB-DFT models which, besides the standard dispersion energy term, also incorporate 2B and 3B PIPs to account for short-range quantum-mechanical effects (e.g., charge transfer and penetration) missing in standard force fields, the first term of eq 10 becomes

$$E_{\text{non}-\text{elec }}^{\text{MB}-\text{pol}}=E_{\text{disp}}+E_{2b,\text{sr}}+E_{3b,\text{sr}}$$ (11)

Here, $E_{\text{non}-\text{elec }}^{\text{MB}-\text{pol}}$sums up all the dispersion and short-range 2B and 3B terms for the MM region alone, as well as all possible cross terms for pairs and triples of molecules split between the QM and MM regions. The 2B and 3B PIPs included in the QM/MM interaction, therefore, act as correction terms, allowing, in principle, the QM/MM energy to achieve the same accuracy as in purely QM calculations. In contrast, when the MM region is described with a standard polarizable force field, such as AMOEBA, the non-electrostatic QM/MM interaction only includes a van der Waals term represented by a force-field specific functional force, such as a standard 12–6 potential, or, for AMOEBA, a buffered 14–7 potential:^{15,21,24,43,44}

$$E_{\text{non}-\text{elec }}^{\text{AMOEBA }}=E_{\text{vdW}}$$ (12)

We note here that in the QM/MB-pol scheme, the non-electrostatic interactions are modeled in a purely classical fashion; i.e., the associated energy contribution does not depend on the QM density but only on geometrical parameters. This allows one to achieve high accuracy on the energy and structures without complicating the QM equations but cannot reproduce quantum confinement effects on the QM density, which might be relevant to compute properties and model spectroscopies.^45,93,94 A density-dependent correction for MB-pol and MB-DFT is currently under active investigation.

The second term of eq 9 is the most relevant one for the coupling of the QM and classical subsystems, as it describes the QM/MM polarization:

$${\tilde{\epsilon }}^{\text{Pol}}(P,\mu )=\frac{1}{2}{\mu }^{†}T\mu -{\mu }^{†}\left(E^{\text{MM}}+E^{\text{QM}}(P)\right)$$ (13)

where μ is a vector that collects all the IPD, T describes the Thole-damped dipole interaction tensor, and

$$\begin{gathered} E_i^{\text{QM}}(P)=\sum _{\alpha }{Z}_{\alpha }\frac{R_{\alpha }-r_i}{{\left|R_{\alpha }-r_i\right|}^3} \\ -\sum _{\mu \nu }{P}_{\mu \nu }\int {\chi }_{\mu }(r){\chi }_{\nu }(r)\frac{r-r_i}{{\left|r-r_i\right|}^3} {\text{d}}^{3}r \end{gathered}$$ (14)

is the electric field due to the QM density at the ith polarizable site.^40,49 We remark that the QM field is the sum of the contributions of the nuclei, with charges Z_α at positions R_α and of the electronic density, that has been expanded in a basis of atomic orbitals χ. Finally, the third term in eq 9 represents the interaction of the electron density with the static charges:

$${\epsilon }^{\text{QM}/\text{MM}}(P)=q^{†}{V}^{\text{QM}}(P)$$ (15)

where V^QM is the QM electrostatic potential and q is a vector that collects all the point charges that represent the permanent electrostatic distribution in MB-pol and MB-DFT. The coupled QM/MM equations are easily obtained by minimizing the variational energy functional in eq 7 with respect to the QM density and the IPDs, taking into account the constraints on the density. In particular, by differentiating with respect to the elements of the density matrix, we get the QM/MM Fock (Kohn–Sham, KS) matrix:

$$F_{\mu \nu }=F_{\mu \nu }^{\text{vac}}+q^{†}{V}_{\mu \nu }-{\mu }^{†}{E}_{\mu \nu }$$ (16)

where F^vac is the standard Fock (KS) matrix and V_μν and E_μν are the standard potential and electric field one-electron integrals, respectively.²¹ The polarization equations are obtained by differentiating with respect to the IPD:

$$T\mu =E^{\text{MM}}+E^{\text{QM}}(P)$$ (17)

We note that the QM and polarization equations are coupled, as the Fock (KS) matrix depends on the IPDs, while the right-hand side of the polarization equations depends on the QM density. Within an SCF approach, the coupled equations are solved by computing the IPDs at each SCF cycle by solving eq 17 either with a direct method or iteratively and then using them to assemble the environment contribution to the Fock (KS) matrix, which is in turn diagonalized to get a new density until convergence is achieved.

For the QM/AMOEBA polarizable QM/MM scheme, a few modifications need to be introduced, as the model is non variational and includes higher order multipolar moments into the permanent electrostatic distribution. A detailed derivation of the electrostatic and polarization interactions can be found in the relevant literature.^21,24

In our analysis, we also consider a simplified polarizable embedding scheme implemented in the LICHEM software.^15,16 In this scheme, the electrostatic interaction between the QM and MM regions is separated into two components. The first component accounts for the polarization of the QM region induced by the point charges in the MM region, while the second component accounts for the back-polarization of the MM region induced by the polarized QM charges. For multipolar models that contain permanent dipoles and quadrupoles, such as AMOEBA, a set of six point charges are octahedrally distributed about each atom to guarantee that the permanent multipole moments are correctly described.¹⁵

In this work, the fully self-consistent polarizable QM/MM scheme is referred to as fsc-QM/MB-MM, and the partially self-consistent polarizable QM/MM scheme implemented in LICHEM is referred to as psc-QM/MB-MM.

3. RESULTS AND DISCUSSION

3.1. Water Dimer.

As an initial demonstration, Figure 1 shows the QM/MB-MM interaction energies of the water dimer calculated along MP2/aug-cc-pVQZ scans obtained by optimizing the positions of the hydrogen atoms for each fixed oxygen–oxygen distance. In this analysis, both possible QM/MB-MM partitions were examined, with the QM region containing either the hydrogen-bond donor or the hydrogen-bond acceptor. The QM/MB-MM energies, calculated using both the fully self-consistent polarizable (fsc-QM/MB-MM)^21,24,25 and the partially self-consistent polarizable (psc-QM/MB-MM)^15,16 schemes, are compared against the corresponding full MB-MM and QM values calculated with MB-pol and PBE0-D3, respectively. The kink in the plot occurring at ~2.7 Å corresponds to configurations that shift from a “sheared″ geometry, where the two water molecules are symmetrically flipped, to a “hydrogen-bonded″ geometry, as displayed in the upper left panel of Figure 1.

Figure 1.

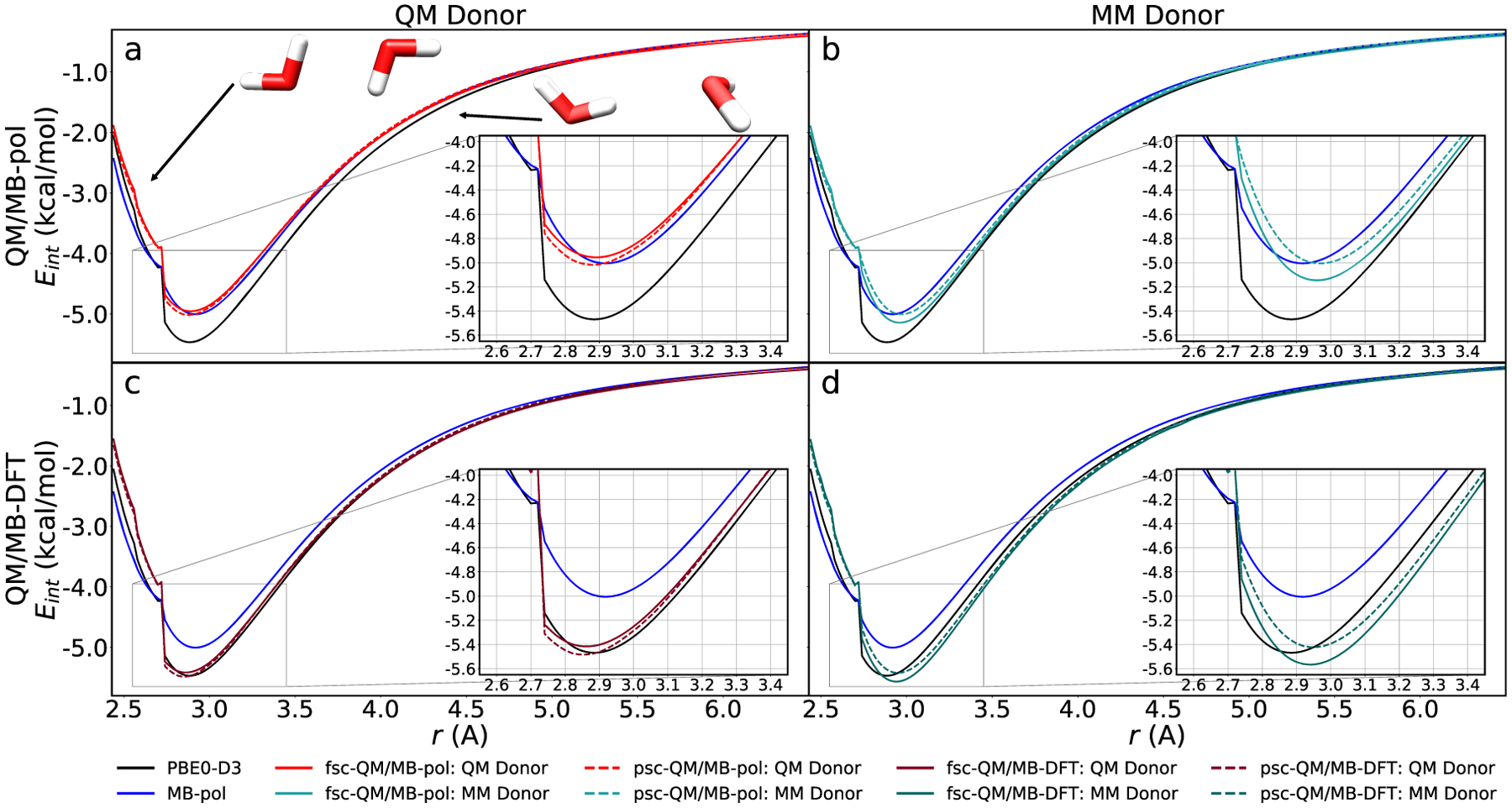
Comparison of the QM/MM interaction energy against the MB-pol and PBE0-d3 values over the MP2/aug-cc-pvqz optimized dimer scan. (a) QM/MB-pol results with the QM water molecule as the hydrogen-bond donor. (b) QM/MB-pol results with the MM water molecule as the hydrogen-bond donor. (c) QM/MB-DFT results with the QM water molecule as the hydrogen-bond donor. (d) QM/MB-DFT results with the MM water molecule as the hydrogen-bond donor.

When the QM water molecule donates the hydrogen bond, the fsc-QM/MB-pol energies lie close to the MB-pol reference values in the neighborhood of minimum-energy geometry (between 2.7 and 3.2 Å), with the largest deviation of ~0.1 kcal/mol occurring near the kink at 2.7 Å. The psc-QM/MB-pol scheme yields comparable results, although it tends to slightly overestimate the interaction strength, giving rise to a larger maximum error of ~0.25 kcal/mol in correspondence with the kink. When the partition is reversed, such that the QM water molecule becomes the hydrogen-bond acceptor, a much larger overall error is observed in both QM/MB-MM schemes. In this case, the fsc-QM/MB-pol scheme overestimates the interaction energy by ~0.3 kcal/mol at the kink, while underestimating the interaction energy at the minimum by about 0.2 kcal/mol. The psc-QM/MB-pol scheme predicts a larger error of ~0.5 kcal/mol at the kink but reproduces the minimum energy within 0.05 kcal/mol of the reference MB-pol value.

The bottom panels of Figure 1 compare the reference MB-pol and PBE0-D3 interaction energies to the corresponding QM/MB-DFT values where, as described in section 2, the MB-DFT model was fitted to reproduce 2B and 3B PBE0-D3/aug-cc-pVQZ energies. Similar to the QM/MB-pol case, when the QM water molecule is the hydrogen-bond donor, the fsc-QM/MB-DFT scheme underestimates the PBE0-D3 interaction energies, with the largest error of about 0.1 kcal/mol found at the kink. The psc-QM/MB-DFT scheme predicts an error of ~0.2 kcal/mol for the same configuration. When the QM/MM partition is switched and the QM water molecule becomes the hydrogen-bond acceptor, both the fully and partially self-consistent schemes overestimate the reference PBE0-D3 interaction energy at the kink, with the errors being ~0.3 and ~0.5 kcal/mol, respectively. The fsc-QM/MB-DFT scheme underestimates the interaction energy at the minimum by ~0.1 kcal/mol, while the psc-QM/MB-DFT scheme overestimates it by ~0.1 kcal/mol.

Because QM/MB-pol and QM/MB-DFT only differ in the identity of the 2B and 3B PIPs (along with the Tang–Toennies damped dispersion), the shift in the interaction energies from QM/MB-pol, which closely reproduces the MB-pol values, to QM/MB-DFT, which instead closely reproduces the PBE0-D3 values, is due to the MB-DFT PIPs correctly compensating the core QM/MM electrostatic interaction. If the QM/MM electrostatic interaction is sufficiently similar to the core MM electrostatic interaction, these results suggest that the 2B and 3B corrections used in MB-pol and MB-DFT can be successfully integrated into a QM/MM scheme to correctly account for the deficiencies in the core QM/MM interaction. In both QM/MB-pol and QM/MB-DFT, smaller overall deviations from the corresponding MB-pol and PBE0-D3 reference values are observed when the QM water molecule donates the hydrogen bond compared to those found when the QM water is the hydrogen-bond acceptor. Furthermore, between these two partitions, the QM hydrogen-bond donor case predicts a minimum that is slightly shifted to a shorter distance, indicating a slightly more attractive interaction between water molecules. On the other hand, in the QM hydrogen-bond acceptor case, the minimum is shifted significantly to a larger distance (by ~0.15 Å), indicating that both QM/MB-pol and QM/MB-DFT overall predict a more repulsive interaction relative to the MB-pol and PBE0-D3 references, respectively. This“repulsive shift″ observed in the QM hydrogen-bond acceptor case carries out to the region beyond the minimum, where both QM/MB-pol and QM/MB-DFT consistently underestimate the interaction energies as the two water molecules are taken apart. This indicates that, depending on which molecule (QM or MM) is the hydrogen-bond donor, the difference between the QM/MB-MM and MB-MM descriptions of the underlying electrostatic interactions may become significant and possibly incompatible with the corrections provided by the PIPs at short range.

In the short-range region, where the two water molecules are closer than 2.7 Å, they adopt a symmetrically flipped “sheared″ geometry. Due to the symmetry of these dimer configurations, the two possible QM/MM partitions are virtually identical and, consequently, predict the same QM/MM energies. The close vicinity of the water molecules in these configurations makes the distinction of the QM and MM regions somewhat blurred, which implies that the QM/MM electrostatic interaction become more quantum mechanical in nature, with the point charges and dipoles of the MM molecule penetrating the electron density of the QM molecule. The consistently higher error of ~0.5 kcal/mol observed for these configurations can thus be attributed to the expected incompatibility of the short-range PIPs, which were optimized for a purely MB-MM description of the interaction energies, with the QM/MM electrostatics.

3.2. Water Two-Body Energies.

With the previous section evaluating the performance of QM/MB-pol and QM/MB-DFT for an optimized water dimer scan where the geometries of the two water molecules lied close to the corresponding minimum-energy conformation, this section explores the performance of QM/MB-pol and QM/MB-DFT for a set of 1000 dimers with more distorted molecular geometries randomly extracted from the original MB-pol 2B training set.⁴⁰ Figure 2 shows correlations between two-body energies calculated with the QM/MB-pol, QM/MB-DFT, and QM/AMOEBA14 schemes and the corresponding CCSD(T) and PBE0-D3 reference values for this set of distorted dimers. For this analysis, the CCSD(T) 2B energies in the complete basis set limit were taken from the original MB-pol reference,⁴⁰ while the corresponding PBE0-D3 values were calculated with Gaussian16 using the aug-cc-pVQZ basis set. In order to exclude from this analysis overly distorted dimers whose CCSD(T)-based geometry-dependent MB-pol charges may significantly deviate from those predicted by PBE0-D3 and thus provide a more electrostatically consistent QM/MM interaction, the RMSDs reported in Figure 2 are calculated considering only configurations whose maximum intramolecular OH bond length is shorter than 1.16 Å, corresponding to the 90th percentile of the entire set. It should be emphasized that in actual QM/MM simulations, these distorted dimers with elongated OH bonds should effectively be included in the QM region since they represent configurations involved in the water autoionization process.

Figure 2.

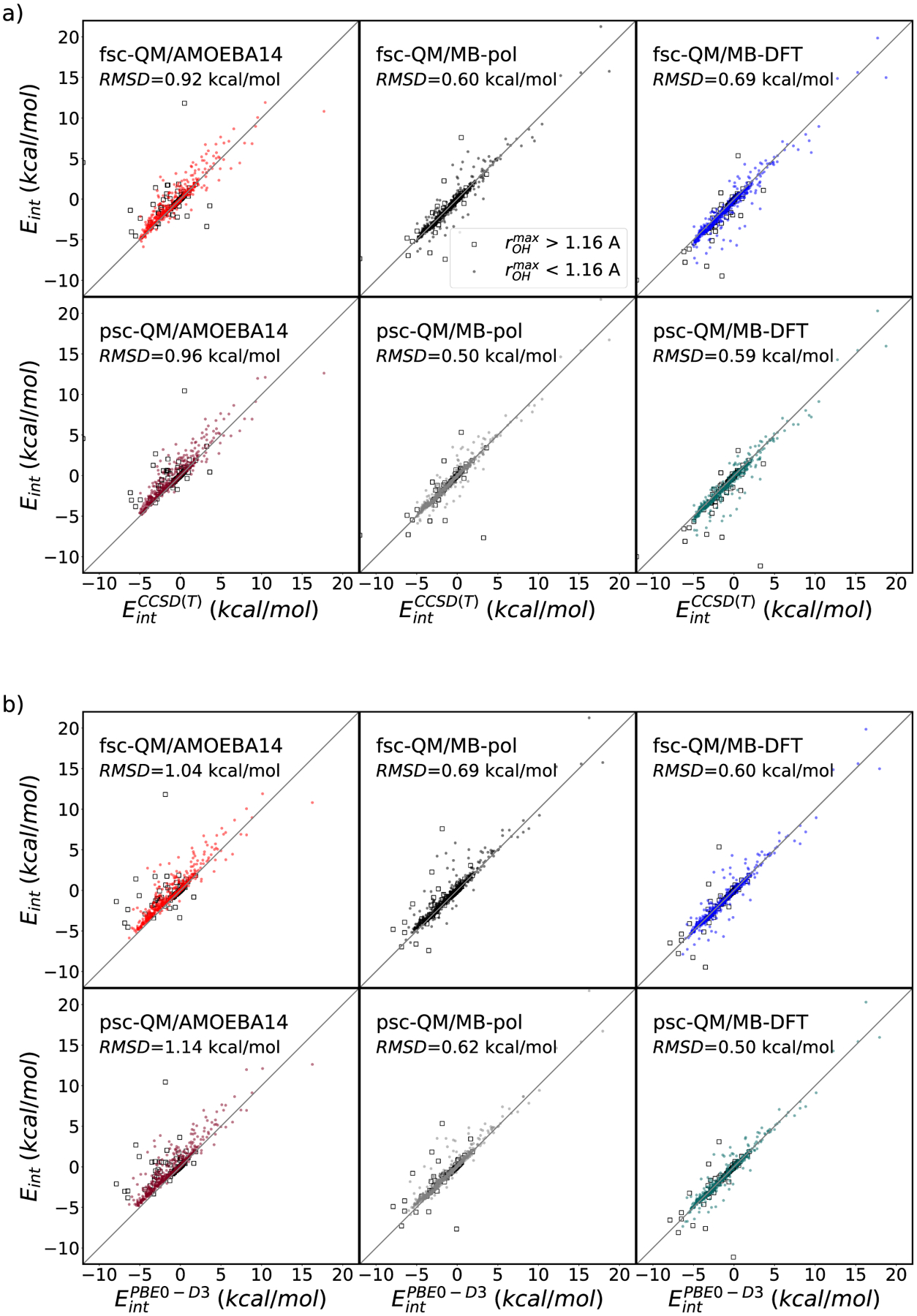
Correlations between the QM/MM interaction energies of 1000 water dimers calculated with AMOEBA14, MB-pol, and MB-PBE0 representing the MM region, and PBE0-D3 representing the QM region, and the corresponding CCSD(T) (panels a) and PBE0-D3 (panels b) values. Each RMSD is calculated for configurations whose maximum intramolecular OH bond length is shorter than 1.16 Å.

The RMSDs relative to the CCSD(T) 2B energies are 0.92, 0.60, and 0.69 kcal/mol for the fsc-QM/AMOEBA14, QM/MB-pol, and QM/MB-DFT schemes, respectively. A similar trend is found for the RMSDs calculated relative to the PBE0-D3 2B energies, with values of 1.04, 0.69, and 0.60 kcal/mol for QM/AMOEBA14, QM/MB-pol, and QM/MB-DFT, respectively. Slightly smaller values are obtained using the partially self-consistent scheme, with QM/AMOEBA14, QM/MB-pol, and QM/MB-DFT being associated with RMSDs of 0.96, 0.50, and 0.59 kcal/mol, respectively, relative to the CCSD(T) 2B energies, and 1.14, 0.62, and 0.50 kcal/mol, respectively, relative to the PBE0-D3 2B energies.

The overall decrease in the RMSD values observed for the QM/MB-pol and QM/MB-DFT schemes relative to QM/AMOEBA14 is attributed to the ability of the PIPs adopted by the explicit many-body models to account for short-range quantum-mechanical effects (e.g., charge transfer and penetration), which cannot be quantitatively recovered by the purely classical expressions used in the QM/AMOEBA14 scheme. QM/MB-pol, which employs PIPs specifically fitted to account for the difference in 2B energies between the 2B CCSD(T) reference energies and the classical components of the 2B MB-pol energies, shows the smallest RMSD relative to CCSD(T). Correspondingly, QM/MB-DFT, which uses the same PIPs as MB-pol but fitted to PBE0-D3 2B reference energies, shows the smallest QM/MM RMSD relative to PBE0-D3. These results, which hold for both the fully and partially self-consistent schemes, suggest that respective to their references, the PIPs fitted to CCSD(T) and PBE0-D3 are able to compensate, at least in part, for the differences between the actual quantum-mechanical 2B energies (ε_2B in eq 4) and the corresponding classical 2B terms (i.e., E_elec and E_disp in eq 4), even for distorted dimer configurations.

It is particularly interesting to note that the psc-QM/MB-pol and QM/MB-DFT exhibit lower RMSDs than their fully consistent counterparts. This apparently counterintuitive result can be understood by considering that the partially self-consistent QM/MM scheme may benefit from a more “MM-like″ representation of the QM/MM electrostatics, as part of the QM/MM polarization is evaluated using the MM functional form. Specifically, in the psc-QM/MB-MM, the MB-MM region gets back-polarized by the polarized QM point charges, instead of the electron density as in the fully self-consistent QM/MB-MM scheme, which makes part of the QM/MM polarization more similar to that of the MM model. As a result, this more MM-like treatment of the QM/MM electrostatics within the psc-QM/MM scheme is, by construction, more compatible with the PIPs of the MB-pol and MB-DFT models, which were fitted to the differences between the 2B CCSD(T) and PBE0-D3 energies, respectively, and the classical electrostatic and dispersion terms.

3.3. QM/MM Partitions for the Water Hexamer.

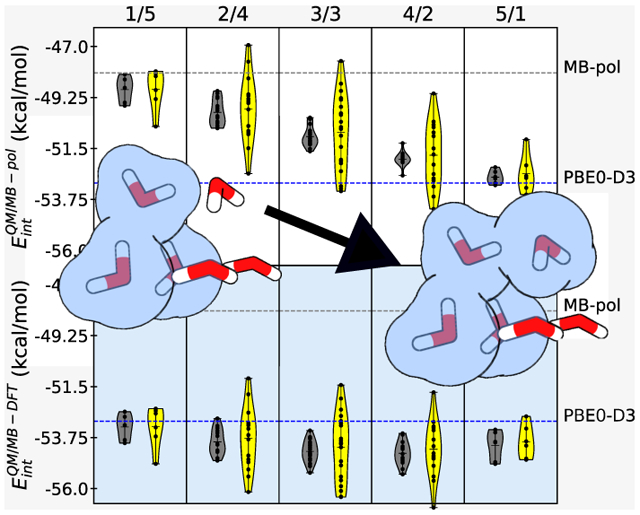
With the the two previous sections focusing on dimer configurations, which report at most on two-body contributions to the interaction energies, in this section, we examine the ability of the QM/MB-MM scheme to reproduce the energetics of the water hexamer isomers. Here, it should be emphasized that as MB-pol and MB-DFT were explicitly trained only up to the 3B energy, they do not have any prior knowledge of systems containing more than three water molecules.^40,41,81 While the analysis described in the following will specifically focus on the prism isomer, which is the lowest-energy isomer of the water hexamer,⁹⁵ analogous analyses for other low-lying isomers are reported in the Supporting Information. Starting with the cluster containing one water molecule in the QM region, water molecules are successively included in the QM region until a total of five water molecules are placed in the QM region. As water molecules are added one at a time, all possible QM/MM partitions are examined. This analysis thus examines the effects of adding (subtracting) water molecules to (from) the QM region, as it might happen during adaptive QM/MM simulations in solution. The interaction energies calculated for the different QM/MM partitions as a function of number of water molecules in the QM region are shown in Figure 3 where they are compared with the corresponding MB-pol and PBE0-D3 values. Within each column of Figure 3, the QM/MM partitions keep the number of QM and MM molecules constant but permute the QM and MM indices, which allow us to assess the performance of the QM/MB-pol and QM/MB-DFT schemes depending on all possible spatial arrangements of the QM and MM water molecules within the prism cluster.

Figure 3.

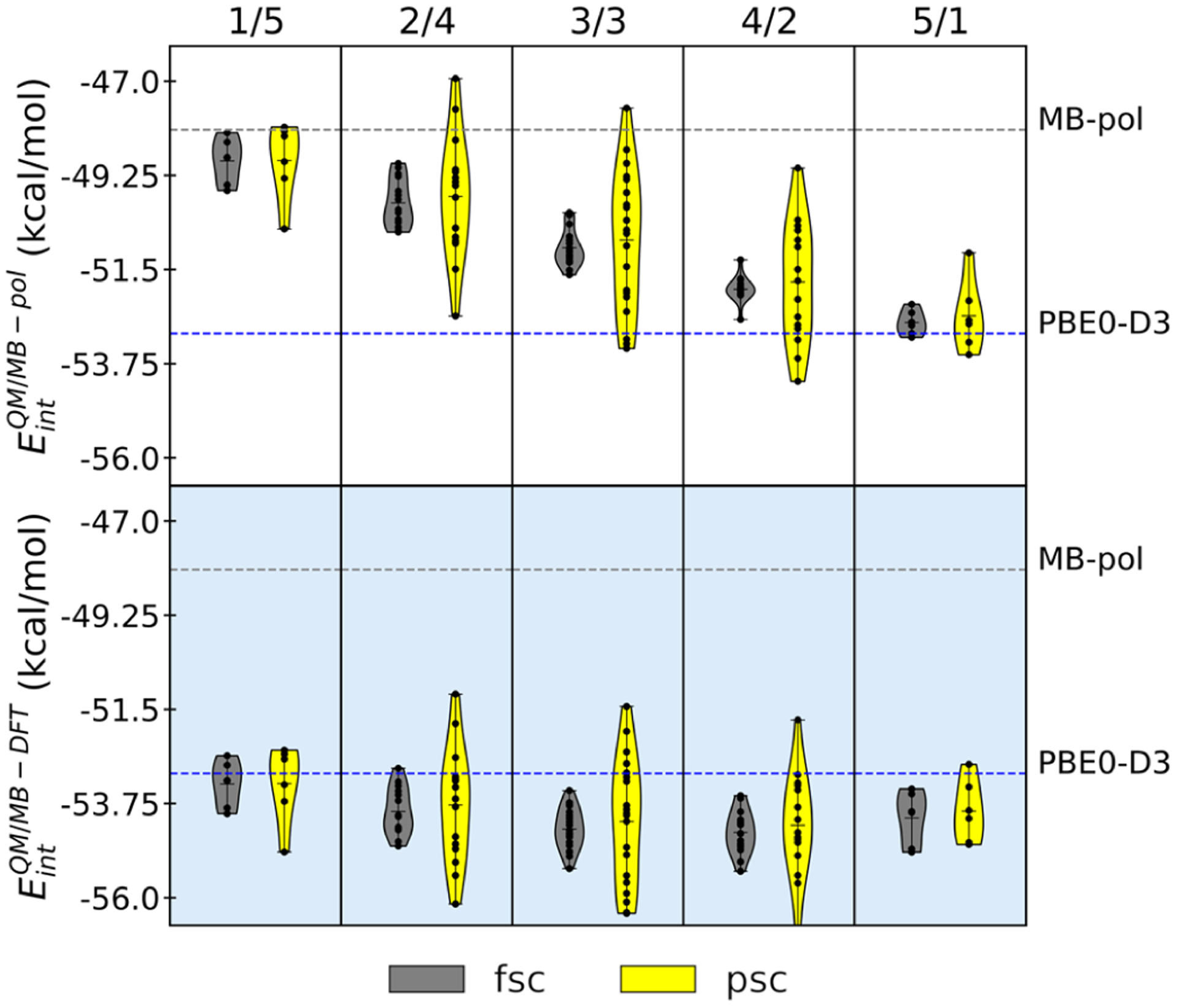
Interaction energies of the prism isomer (isomer 1 in ref 96 of the water hexamer calculated using QM/MB-pol and QM/MB-DFT for all possible QM/MM partitions involving one to five water molecules in the QM region using fully self-consistent (fsc) and partially self-consistent (psc) cross-polarization between the QM and MM regions. The grey line is the MB-pol reference energy, and the blue line is the PBE0-D3 reference energy. The numbers at the top of each column determine the number of water molecules in the QM and MM regions (num QM/num MM).

With one water in the QM region, the interaction energies calculated for the different QM/MM partitions using both the fully and partially self-consistent QM/MB-pol schemes lie, on average, within ~1.5 kcal/mol of the reference MB-pol energies, with only one partition of the psc-QM/MB-pol scheme displaying a deviation of ~2.3 kcal/mol. Successively including one water to the QM region linearly shifts the distribution of QM/MB-pol energies toward the QM value. When the QM/MM partition contains five water molecules in the QM region, the QM/MB-pol energies lie within 0.6 and 1.5 kcal/mol of the PBE0-D3 value for the fsc-QM/MB-pol and psc-QM/MB-pol schemes, respectively. On the other hand, fsc-QM/MB-DFT and psc-QM/MB-DFT calculations for the partition with one water molecule in the QM region predict interaction energies that are within 1.0 and 2.0 kcal/mol, respectively, of the reference PBE0-D3 value. The successive addition of water molecules results in fsc-QM/MB-DFT and psc-QM/MB-DFT interaction energies that are within 1.5 and 1.3 kcal/mol, respectively, of the PBE0-D3 reference value for the partition containing five water molecules in the QM region. The largest deviations (up to 2.25 kcal/mol for fsc-QM/MB-DFT and up to 3.54 kcal/mol for psc-QM/MB-DFT) relative to the PBE0-D3 value are found for the symmetric partition with three water molecules in both the QM and MM regions. Furthermore, independent of the usage of the partially or fully self-consistent schemes, the largest deviations in the distributions of both QM/MB-pol and QM/MB-DFT interaction energies are associated with configurations in which the QM water molecule is a double hydrogen-bond acceptor from two MM water molecules. This is consistent with the results in section 3.1 where the case of the MM donor (QM acceptor) displays the largest error in the scan of the water dimer potential energy surface.

Compared to the QM/MB-pol interaction energies, which are increasingly weighted toward the PBE0-D3 reference value as the number of water molecules in the QM region increases, the QM/MB-DFT results remain relatively close to the PBE0-D3 reference value, independent of how the water molecules are partitioned in the QM and MM regions. The different trend found for interaction energies calculated with QM/MB-pol and QM/MB-DFT as a function of the number of water molecules in the QM region can be explained by considering that the only differences between the MB-pol and MB-DFT potential energy functions derive from the differences in the corresponding 2B and 3B PIPs. Since the MB-pol PIPs were fitted to CCSD(T)/CBS 2B and 3B energies, this implies that when the QM/MM partition includes only one water molecule in the QM region, all possible 2B and 3B energies within the hexamer contains contributions from the corresponding MB-pol PIPs. In the opposite limit, when five water molecules are placed in the QM region, only 6 out of 15 2B energies and 10 out of 20 3B energies include contributions from the corresponding MB-pol PIPs. As a result, the QM/MB-pol interaction energy approaches the PBE0-D3 reference value as the number of water molecules in the QM region increases because the contributions from the MB-pol PIPs become progressively smaller. In contrast, since the MB-DFT PIPs were fitted to PBE0-D3 2B and 3B energies, all possible 2B and 3B contributions to the QM/MB-DFT interaction energy, independent of the QM/MM partition, are effectively described at the PBE0-D3 level (either through actual PBE0-D3 calculations in the QM region or through the MB-DFT PIPs in the MM region). As a result, the QM/MB-DFT interaction energies remain relatively close to the PBE0-D3 reference value for all different partitions in which the QM/MB-DFT scheme enables smooth transitions between QM regions described by an arbitrary DFT model and MM regions described by the corresponding MB-DFT potential energy function, which is particularly appealing for QM/MM simulations in solution.

Figure 3 shows that while the psc-QM/MB-pol and psc-QM/MB-DFT scheme displayed smaller RMSDs than the corresponding fully self-consistent schemes for energetics of water dimers (Figure 2), they predict wider spread than the corresponding fully self-consistent schemes in the interaction energies of the prism hexamer, depending on the spatial arrangements of the water molecules in the QM and MM regions. In particular, the psc-QM/MB-pol and psc-QM/MB-DFT calculations predict the largest spread of 4.5 kcal/mol for the symmetric QM/MM partition, with three water molecules in both QM and MM regions, which must be compared with a spread of ~1.5 kcal/mol predicted by the corresponding fully self-consistent schemes. This symmetric QM/MM partition contains the largest number of different spatial arrangements of the QM and MM molecules, resulting in 20 total permutations, as well as the largest number of 2B (9) and 3B (18) QM/MM energies. The large number of 2B and 3B QM/MM interactions serves to amplify possible inaccuracies of the 2B and 3B PIPs as even relatively small errors in the description of individual 2B and 3B energies add up, resulting in larger total errors and, consequently, wider spreads for interaction energies calculated for different QM/MM partitions. Importantly, as shown in Figures S10 and S11 of the Supporting Information, both psc-QM/MB-DFT and fsc-QM/MB-DFT are able to reproduce, on average, the interaction energies and relative stabilities of the water hexamers predicted by PBE0-D3, independently of the QM/MM partition. This suggests that when employed in adaptive QM/MM simulations, QM/MB-DFT would correctly sample the same water configurations as in fully QM simulations.

The analysis reported in Figure 3 underscores the importance of many-body polarization effects in QM/MM calculations. In particular, the relatively wider spreads associated, on average, with interaction energies of the water hexamer calculated with the psc-QM/MB-pol and psc-QM/MB-DFT schemes are due to the neglect of fully self-consistent polarization effects between the QM and MM regions, which are included in the corresponding fsc-QM/MB-pol and fsc-QM/MB-DFT schemes. These findings are further underscored by observing that both fully and partially self-consistent polarization schemes predict similar spreads of the interaction energies for the two limiting QM/MM partitions, with one and five water molecules in the QM region, respectively, which correspond to the two QM/MM partitions with the smallest contributions from mutual polarization between the QM and MM regions.

4. CONCLUSIONS

We presented here a new development in QM/MM, integrating the MB-pol and MB-DFT models into a polarizable embedding, allowing the dipoles in the MM region to self-consistently equilibrate with the density in the QM region. On top of this embedding, the PIPs used in MB-pol and MB-DFT, which are fitted to recover the CCSD(T) and PBE0-D3 energies at the 2B and 3B levels, are incorporated into the QM/MM interaction. We show that use of both QM/MB-pol and QM/MB-DFT increases the overall accuracy of the QM/MM interaction, as the PIPs account for the leading order dispersion and repulsion energies. Using both partially and fully self consistent mutual polarization between the QM and MM regions, we show that a fully self-consistent scheme is required to fully capture the polarization effects in larger and more complex water clusters. More importantly, we demonstrate a consistent treatment between the QM and MM regions. Using MB-DFT, the MM region can be represented at the same level of accuracy as an arbitrary DFT functional used in the QM region. In our case, using PBE0-D3 as the functional of choice, we can consistently represent an entire QM/MM system, with the pure MM, QM, and QM/MM interactions at the PBE0-D3 level of theory. The QM/MB-DFT scheme offers the advantage that, since both QM and MM components as well as the QM/MM interaction are treated at the same level of accuracy, the need for a transition layer is reduced or eliminated, though it should be noted that some levels of QM theory do not have analytical gradients, and can thus become prohibitively expensive for dynamical QM/MM simulations. In more succinct terms, this approach can be thought of as treating the entire system under the same ″effective″ Hamiltonian with different but numerically equivalent representations for the QM and MM components.