Abstract
Selective stable isotope labeling has transformed structural and dynamics analysis of RNA by NMR spectroscopy. These methods can remove 13C-13C dipolar couplings that complicate 13C relaxation analyses. While these phenomena are well documented for sites with adjacent 13C nuclei (e.g. ribose C1′), less is known about so-called isolated sites (e.g. adenosine C2). To investigate and quantify the effects of long-range (> 2 Å) 13C-13C dipolar interactions on RNA dynamics, we simulated adenosine C2 relaxation rates in uniformly [U-13C/15N]-ATP or selectively [2-13C]-ATP labeled RNAs. Our simulations predict non-negligible 13C-13C dipolar contributions from adenosine C4, C5, and C6 to C2 longitudinal (R1) relaxation rates in [U-13C/15N]-ATP labeled RNAs. Moreover, these contributions increase at higher magnetic fields and molecular weights to introduce discrepancies that exceed 50%. This will become increasingly important at GHz fields. Experimental R1 measurements in the 61 nucleotide human hepatitis B virus encapsidation signal ε RNA labeled with [U-13C/15N]-ATP or [2-13C]-ATP corroborate these simulations. Thus, in the absence of selectively labeled samples, long-range 13C-13C dipolar contributions must be explicitly taken into account when interpreting adenosine C2 R1 rates in terms of motional models for large RNAs.
Supplementary Information
The online version contains supplementary material available at 10.1007/s10858-021-00368-8.
Keywords: Dipolar coupling, Relaxation, Dynamics, NMR spectroscopy, Nucleic acids
Introduction
RNAs are important macromolecules that function in a wide range of cellular roles (Cech and Steitz 2014; Mortimer et al. 2014; Sharp 2009). Despite being composed of only four ribonucleotide building blocks, RNAs are capable of adopting complex three-dimensional structures that impart functionality (Dethoff et al. 2012; Ganser et al. 2019). Moreover, RNAs are dynamic and can sample numerous conformations on various time scales that might be important for function (Zhao et al. 2017; Marušič et al. 2019). Solution nuclear magnetic resonance (NMR) spectroscopy is a high-resolution biophysical technique that is well suited to probe these dynamic RNA structures. Three commonly measured dynamics parameters are the longitudinal (R1) and transverse (R2) relaxation rates and the heteronuclear Overhauser effect (hNOE) (Marušič et al. 2019; Palmer 2004; Wagner 1993). The R1 rate measures the return of the longitudinal magnetization to thermal equilibrium whereas R2 measures the decay of transverse magnetization, and the hNOE measures the change in heteronuclear spin magnetization in response to saturating proton spins (Yamazaki et al. 1994; Peng and Wagner 1992; Abragam 1961).
RNA motions directly influence these R1, R2, and hNOE relaxation parameters (Marušič et al. 2019; Palmer 2004; Wagner 1993; Yamazaki et al. 1994; Peng and Wagner 1992; Abragam 1961; Spiess 1978; Hansen and Al-Hashimi 2007; Nirmala and Wagner 1988; Palmer et al. 1991). Depending on the probed nuclei, dipolar interactions and chemical shielding anisotropy (CSA) mechanisms contribute predominantly to R1 and R2 relaxation, and dipolar interactions to the hNOE. These three relaxation measurements can be fit to extract motional variables such as overall correlation time () and the square of the generalized order parameter (S2) that describe fast (ps-ns) dynamics in RNA within a Model Free formalism (Spiess 1978; Lipari and Szabo 1982) or combined Model Free and reduced spectral density mapping implemented in ROTDIF (Berlin et al. 2013). Therefore, accurate R1, R2, and hNOE measurements are crucial for obtaining precise dynamics information and drawing valid conclusions about RNA molecular recognition events.
These dynamic RNA motions are most often measured by using 13C (Boisbouvier et al. 1999; Dayie et al. 2002) and 15N (Dayie et al. 2002; Akke et al. 1997) nuclei as indirect probes. However, imino and amino 15N nuclei experience solvent exchange and are only visible in structured regions, making non-protonated 15N (e.g. purine N7) and protonated 13C (e.g. adenosine C2) nuclei attractive probes. The latter sites are present in both the nucleobase and ribose moieties and therefore provide more coverage of RNA structure. Still, large 13C-13C scalar and dipolar couplings in uniformly 13C/15N labeled RNA can complicate analyses of these sites (Yamazaki et al. 1994; Kay et al. 1989; Alvarado 2014; Johnson et al. 2006; Thakur and Dayie 2012; Nam et al. 2020; Thakur et al. 2012). Indeed, the effect of dipolar couplings on RNA relaxation has been studied for sites with adjacent 13C nuclei (e.g. ribose C1′). These investigations demonstrate that dipolar interactions from attached 13C atom(s) lead to deviations from monoexponential decay and discrepancies in the extracted R1 rate for ribose C1′ (Alvarado 2014; Thakur and Dayie 2012; Nam et al. 2020; Thakur et al. 2012), C2′ and C4′ (Johnson et al. 2006), as well as for pyrimidine C6 (Nam et al. 2020; Thakur et al. 2012). However, much less is known about isolated sites such as purine C8 or adenosine C2. We recently showed that purine C8 may experience non-negligible dipolar contributions to R1 relaxation from non-adjacent coupling partners (Nam et al. 2020). The extent to which adenosine H2-C2 approximates an isolated spin pair remains unclear.
To investigate and quantify the effects of long-range (> 2 Å) 13C-13C dipolar coupling on RNA dynamics, we simulated adenosine C2 relaxation rates in uniformly [U-13C/15N]-ATP or selectively [2-13C]-ATP labeled RNAs. Our simulations predict non-negligible 13C-13C dipolar contributions from adenosine C4, C5, and C6 to C2 R1 rates in [U-13C/15N]-ATP labeled RNAs that increase with higher magnetic fields and molecular weights. To empirically test our simulations, we measured adenosine C2 relaxation in the 61 nucleotide (nt) human hepatitis B virus encapsidation signal ε (HBV ε) RNA (Flodell et al. 2006; Lee 1997; Knaus and Nassal 1993; Hirsch et al. 1990) labeled with [U-13C/15N]-ATP or [2-13C]-ATP. To this end, we used our recently synthesized [2-13C, 7-15N]-ATP (Olenginski and Dayie 2020) as a selective adenosine 13C2 labeled probe. We demonstrate that the removal of long-range 13C-13C dipolar coupling partners reveals discrepancies in measured adenosine C2 R1 values between uniformly and selectively labeled samples. Moreover, R1 measurements at lower temperature (mimicking increased molecular weight) revealed exacerbated R1,C2 discrepancies, which further corroborates our simulations and argues that selective 13C2 labeled probes obviates the need to account for the significant contributions to meausured R1,C2 that arise from neighboring 13C atom(s) in RNAs with a > 20 ns. Our [2-13C, 7-15N]-ATP (Olenginski and Dayie 2020) also showed better spectroscopic properties than [U-13C/15N]-ATP, providing and additional advantage to using selectively labeled samples to measure RNA dynamics.
Materials and methods
Theoretical simulations
13C R1 and R2 relaxation rates and steady-state 13C{1H} hNOE values were simulated using Eqs. 1–6, (Palmer 2004; Peng and Wagner 1992; Abragam 1961). We assumed isotropic tumbling. These relaxation parameters were simulated for adenosine C2 in [U-13C/15N]-ATP or [2-13C]-ATP labeled RNAs and included dipolar contributions from adenosine C4, C5, C6, N1, and N3 at average distances of 2.20, 2.70, 2.30, 1.40, and 1.30 Å, respectively. In addition, adenosine C2 experiences dipolar contributions with the following protons: (1) the attached H2, (2) those within the same nucleotide, (3) those 3′-same strand, and (4) those 3′-cross-strand contacts (Wijmenga and Buuren 1998). Protons in (2) are H1′ and H2′ at average distances of 4.35 and 4.20 Å. Protons in (3) are H1, H2, amino (N)H2, and H1′ at average distances of 4.00, 4.40, 4.33, and 4.45 Å. Protons in (4) are H1, H3, amino (N)H2, and H1′ at average distances of 4.10, 4.50, 4.40, and 4.95 Å. All proton distances above were calculated from pdb 2ixy (Flodell et al. 2006) as a representative A-helical RNA. Solution NMR derived CSA values (σ11 = 89, σ22 = 15, σ33 = − 104) (Ying et al. 2006) and an aromatic CH bond length of 1.104 Å (Fiala et al. 2000) were used in these simulations.
RNA sample preparation
In vitro transcriptions of RNA were performed as previously described (Milligan and Uhlenbeck 1989). In brief, transcriptions were carried out in 40 mM Tris–HCl pH 8 (at 37 °C), 1 mM spermidine, 0.01% Triton X-100, 80 mg/ml PEG, 0.3 μM DNA template, 1 mM 1,4-dithiothreitol, 2 U/μl thermostable inorganic pyrophosphatase, 5–20 mM rNTPs, 5–20 mM MgCl2, and 0.1 mg/mL T7 RNA polymerase. Reactions proceeded for 3 h at 37 °C. For each RNA transcribed, the concentrations of MgCl2 and rNTPs were optimized. DNA template and [U-13C/15N]-ATP were purchased from Integrated DNA Technologies and Cambridge Isotope Laboratories, respectively. The [2-13C, 7-15N]-ATP was synthesized as recently described (Olenginski and Dayie 2020). After transcription, samples were extracted with acid-phenol:chloroform, ethanol precipitated, purified by preparative denaturing gel electrophoresis, and electroeluted. The samples were subsequently dialyzed five times against UltraPure ddH2O, folded in NMR buffer (10 mM Na3PO4 pH 6.5, 0.1 mM EDTA), lyophilized, and resuspended in 100% D2O. NMR samples of HBV ε labeled with [U-13C/15N]-ATP or [2-13C, 7-15N]-ATP had a final concentration of 0.35 mM in 0.30 ml (calculated using a molar extinction coefficient of 768.3 mM−1 cm−1).
NMR spectroscopy
All NMR experiments were performed on an 800 MHz Avance III Bruker spectrometer equipped with a triple resonance cryogenic probe. NMR relaxation data were collected at either 5 or 25 °C as specified in the text and figure legends. TROSY-detected measurements of 13C R1 and R1ρ relaxation rates and steady-state 13C{1H} hNOE values were adapted from previous pulse sequences (Hansen and Al-Hashimi 2007; Lakomek et al. 2013). For R1 experiments at 25 °C, relaxation delays of 0.10, 0.20 (× 2), 0.36, 0.50, 0.90, and 1.20 s (with both [U-13C/15N]-ATP and [2-13C, 7-15N]-ATP labeled sample) were used. For R1 experiments at 5 °C, relaxation delays of 0.10, 0.20 (× 2), 0.80, 1.00, 1.20 (with [U-13C/15N]-ATP labeled sample) or 0.10, 0.20 (× 2), 0.90, 1.10, 1.30 (with [2-13C, 7-15N]-ATP labeled sample) were used. For R1ρ experiments, relaxation delays of 1.5, 2.4, 3.4, 4.6, 6.1, 8.0, and 11.0 ms (at 25 °C) or 1.0, 2.0, 4.0, 5.0, and 6.0 ms (at 5 °C) were used and the strength of the spin-lock field (ω1) was 1.9 kHz. R1 and R1ρ experiments were acquired in an interleaved manner as a pseudo-three-dimensional experiment and using a recycle delay of 2.5 s. For 13C{1H} hNOE (saturation) experiments, recycle and saturation delays of 1.5 and 7 s were used and proton saturation was achieved using a train of hard 180° pulses. In the 13C{1H} hNOE (no saturation) experiments, a delay of 8.5 s was used in order to match the time of both recycle and saturation delays from the saturation experiment. For experiments on [U-13C/15N]-ATP labeled HBV ε, selective pulses were applied as previously described (Hansen and Al-Hashimi 2007; Nam et al. 2020). Shape pulses used for on-resonance 13C inversion, on-resonance 13C refocusing, and off-resonance 13C inversion were Q3 (Emsley and Bodenhausen 1992), RSNOB (Kupče et al. 1995), and IBURP2 (Geen and Freeman 1991), respectively. Q3 pulse selectively inverts the 13C magnetization of interest, whereas RSNOB and IBURP2 selectively refocus (invert) 13C magnetization to eliminate 13C-13C scalar coupling evolution. Pulse lengths for each pulse were 937.5, 1000, and 450 μs, respectively. The offset and bandwidth for IBURP2 were − 40 and 50 ppm, respectively. 15N was decoupled.
Data analysis
NMR spectra were processed and analyzed using TopSpin 4.0, NMRFx Processor, and NMRViewJ (Norris et al. 2016; Johnson and Blevins 1994). R1 and R1ρ relaxation rates were determined by fitting peak intensities to a monoexponential decay. Uncertainties in R1 rates were estimated by propagating the error in peak intensities from duplicated delay points (indicated by “ × 2” above). R2 rates were corrected for the off-resonance ω1 using Eqs. 7 and 8. Uncertainties in R1ρ rates were determined by the RELAXFIT (Fushman et al. 1997) Matlab program. The steady-state 13C{1H} hNOE was obtained using (1 + η) (Peng and Wagner 1992; Palmer et al. 1991; Clore et al. 1990a, b; Weaver et al. 1988). Uncertainties in 13C{1H} hNOE values were estimated by propagating the error in peak intensities in duplicated experiments.
Results and discussion
Effects of long-range dipolar couplings on adenosine C2 relaxation
Before quantifying the effects of dipolar couplings on RNA dynamics, it is informative to consider the various relaxation contributions to our targeted nuclei. The 13C R1 and R2 rates of adenosine C2 (R1,C2 and R2,C2) are given by
| 1 |
| 2 |
wherein the auto R1,C2 () and R2,C2 () rates and cross-relaxation () are functions of the underlying spectral density function (Palmer 2004; Peng and Wagner 1992; Abragam 1961):
| 3 |
| 4 |
| 5 |
Rex is the chemical exchange contribution to R2, DC,i and CC are the dipolar coupling (/) and CSA () constants, respectively, where is the gyromagnetic ratio of spin i (where i can be 1H, 13C, or 15N), r is the distance between the two spins, is the permeability of free space, is Plank’s constant divided by 2p, and . Here, σx = σ33 − σ11, σy = σ33 − σ22 and σ11, σ22, and σ33 are the principal components of the chemical shielding tensor (Ying et al. 2006; Fushman et al. 1998) and is the spectral density function assuming isotropic tumbling. The auto- and cross-relaxation rates combine to give the steady-state 13C{1H} hNOE (η) (Peng and Wagner 1992; Palmer et al. 1991; Clore et al. 1990a, b; Weaver et al. 1988)
| 6 |
where Isat and Ieq are signal intensities of the 13C resonances when the 1H resonances are saturated or not.
As seen in Eqs. 1–5, adenosine R1,C2 and R2,C2 rates incorporate dipolar interactions with nearby 1H, 13C, and 15N nuclei, as well as the 13C CSA. For small-to-medium sized RNAs with a < 10 ns, 1H-13C dipolar and 13C CSA contributions dominate adenosine R1,C2 and R2,C2 relaxation. At 800 MHz, the 1H-13C dipolar and 13C CSA contribution to adenosine R1,C2 is 43–71% and 29–52%, respectively, whereas their contribution to adenosine R2,C2 is 43–64% and 36–57%, respectively (13C CSA and dipolar contributions are defined as [100*(13C2 CSA/R1/2,C2)] and [100*(1H-13C dipolar/R1/2,C2)], [100*(13C-13C dipolar/R1/2,C2)], or [100*(13C-15N dipolar/R1,C2)], respectively, where the CSA and dipolar terms are those found in Eqs. 3 and 5) (Supplementary Fig. S1a and b). Therefore, for these RNAs, the dipolar contributions from surrounding 13C (< 4%) and 15N (< 1%) nuclei are negligible and can likely be ignored. However, 13C-13C dipolar interactions contain an additional term arising from , which increases as a function of and magnetic field strength. Moreover, the bonafide term in R2,C2 is pre-multiplied by 4 and is linked with the direct H2-C2 dipolar vector that is larger than any 13C-13C dipolar vector by ~ 16 due to the contribution from the gyromagnetic ratios alone. Taken together, 13C-13C dipolar interactions are expected to negligibly contribute to adenosine R2,C2 (< 0.1%) and significantly contribute to R1,C2 as RNAs increase in size and higher magnetic fields are used. Indeed, at 800 MHz, these 13C-13C dipolar contributions to adenosine R1,C2 rise to 20, 50, and 80% in larger RNAs with a of 25, 50, and 100 ns (Supplementary Figs. S1c and d). Moreover, these contributions further increase at higher magnetic fields (Supplementary Figs. S1c and d).
In [U-13C/15N]-ATP labeled RNAs, adenosine C2 is dipolar coupled to the attached H2, the adjacent N1 and N3, and the long-range (> 2 Å) C4, C5, and C6 atoms (Fig. 1a, inset). Moreover, in fully protonated RNA, adenosine C2 also experiences long-range dipolar contributions from protons within the same nucleotide, those 3′ and on the same strand, and those 3′ and on the cross-strand (Wijmenga and Buuren 1998). If these long-range dipolar couplings contribute significantly to RNA relaxation, theoretical simulations should reveal discrepancies in adenosine R1,C2 and R2,C2 rates and steady-state 13C{1H} hNOE values in [U-13C/15N]-ATP and [2-13C]-ATP labeled RNAs. To test this hypothesis, we used previously reported CSA values derived from solution NMR (Ying et al. 2006) and Eqs. 1–6, (Palmer 2004; Peng and Wagner 1992; Abragam 1961) to simulate adenosine R1,C2 and R2,C2 relaxation rates and steady-state 13C{1H} hNOE values in [U-13C/15N]-ATP or [2-13C]-ATP labeled RNAs (see “Materials and Methods” section). For simplicity, our simulations assume isotropic tumbling as the effects of long-range dipolar couplings are more readily quantifiable.
Fig. 1.
Adenosine R1,C2 simulations in [U-13C/15N]-ATP or [2-13C]-ATP labeled RNAs. a Simulated adenosine R1,C2 rates with a scheme of adenine (numbered by atom and with interatomic distances (Å) to C2) shown as an inset. b Simulated adenosine R1,C2 percent difference (diff.) [100*(R1,C2(uniform) − R1,C2(selective))/R1,C2(uniform)]. c Simulated adenosine R1,C2 percent difference for each dipolar coupling partner (C4, C5, C6, N1, and N3). All simulations assume isotropic tumbling and those in b were carried out with increasing magnetic field strengths and overall correlation times () whereas those in a and c are at 800 MHz. Solution NMR derived CSA values (σ11 = 89, σ22 = 15, σ33 = − 104) (Ying et al. 2006) and an aromatic CH bond length of 1.104 Å (Fiala et al. 2000) were used. Our simulations suggest that dipolar interactions result in overestimated R1,C2(uniform) rates that increase with higher magnetic fields and molecular weights
We do not observe differences in the simulated R2,C2 rates or steady-state 13C{1H} hNOE values (Supplementary Fig. S2), in agreement with previous studies (Yamazaki et al. 1994; Hansen and Al-Hashimi 2007; Nam et al. 2020). However, our simulations do predict discrepancies in R1,C2 rates (Fig. 1a) between uniformly and selectively labeled samples (R1,C2(uniform) and R1,C2(selective), respectively), an observation similar to that recently reported for purine C8 sites (Nam et al. 2020). Specifically, dipolar interactions result in overestimated R1,C2(uniform) rates that increase with higher magnetic fields and molecular weights (Fig. 1a), as predicted by Eq. 3 (Supplementary Fig. S1a). Moreover, the percent difference in R1,C2 (defined as [100*(R1,C2(uniform) − R1,C2(selective))/R1,C2(uniform)]) is predicted to be as large as 80% at 1.2 GHz and a of 100 ns (Fig. 1b). While RNAs of this size are rarely probed by NMR, the simulated discrepancies are still significant for smaller RNAs. As highlighted by our simulations, 13C-13C dipolar interactions dominate the discrepancy whereas N1 and N3 have almost no effect. Moreover, the 13C-13C contributions scale with atomic distance from C2, with C4 (2.2 Å) having the greatest effect followed by C6 (2.3 Å) and then C5 (2.7 Å) (Figs. 1a, inset and c).
Adenosine C2 R1 measurements in uniformly and selectively labeled RNA
Our newly synthesized [2-13C, 7-15N]-ATP (Olenginski and Dayie 2020) removes unwanted 13C-13C and 13C-15N dipolar interactions and was therefore used along with commercially available [U-13C/15N]-ATP to empirically test our simulations. To this end, we measured adenosine R1,C2 rates for [U-13C/15N]-ATP or [2-13C, 7-15N]-ATP labeled HBV ε (Fig. 2) at 800 MHz and 25 °C using TROSY-detected pulse sequences (Hansen and Al-Hashimi 2007; Lakomek et al. 2013; Weigelt 1998; Pervushin et al. 1997). In agreement with our simulations (Fig. 1a), R1,C2(uniform) was significantly higher than R1,C2(selective) for 6 of the 8 HBV ε adenosine residues (Fig. 3a). Explanations for why A29 and A55, in particular, differ from the other residues requires detailed structural information which is currently lacking. Nevertheless, our simulated and experimental trends show good agreement on the whole. That is, the average percent difference in measured R1,C2 rates was 4.7% (Fig. 3b) compared to the simulated 5.4% (Fig. 2b) for an RNA with a of 11 ± 1 ns at 800 MHz (measured from R2/R1 (Fushman et al. 1994; Thakur et al. 2010)) (Supplementary Fig. S3). While this discrepancy is small and can likely be ignored, our simulations suggest that this is no longer true as RNAs increase in size.
Fig. 2.
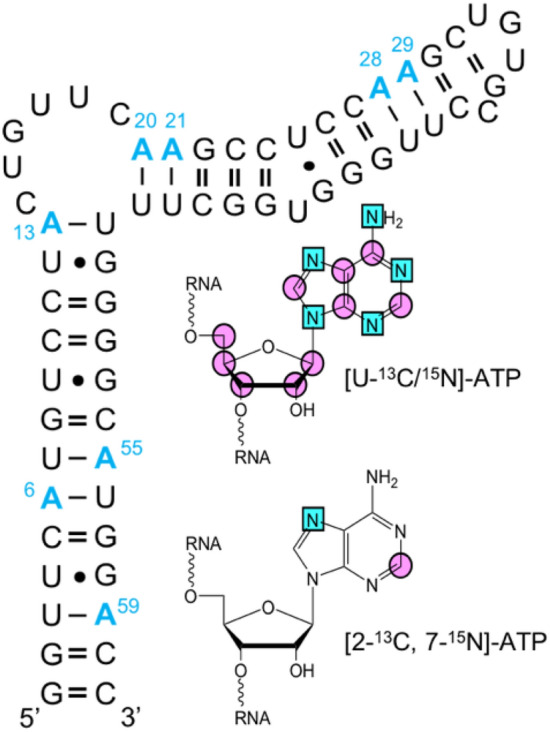
Selective and uniform RNA labeling. Sequence of the 61 nt HBV ε RNA with all [U-13C/15N]-ATP or [2-13C, 7-15N]-ATP labeled adenosine residues shown in blue and numbered. Magenta circle = 13C and cyan square = 15N
Fig. 3.
Experimental adenosine R1,C2 measurements in [U-13C/15N]-ATP or [2-13C, 7-15N]-ATP labeled HBV ε RNA. a Adenosine R1,C2(uniform) and R1,C2(selective) rate measurements in HBV ε at 800 MHz and 5 or 25 °C. Mean rates are shown with dashed lines and error bars represent ± standard deviation (s.d.). Experimental R1,C2(uniform) rates at 25 °C were larger (outside experimental error) than R1,C2(selective) for all adenosine residues except A29 and A55 (designated no significance, n.s.). Experimental R1,C2(uniform) rates at 5 °C were larger than R1,C2(selective) for all 4 resolved adenosine residues. b Average R1,C2 percent difference (diff.) [100*(R1,C2(uniform) − R1,C2(selective))/R1,C2(uniform)] for the data at different temperatures (temp.) shown in a. The average percent difference in measured R1,C2 rates at 25 °C was 4.7%, which agrees well with the simulated 5.4% difference for an RNA with a of 11 ± 1 ns [measured from R2/R1 ratio (Fushman et al. 1994; Thakur et al. 2010)]. The average percent difference in measured R1,C2 rates at 5 °C was 25.5%, compared to the simulated 15.6% difference for an RNA with a of 21 ± 1 ns [measured from R2/R1 ratio (Fushman et al. 1994; Thakur et al. 2010)]. Taken together, our simulations and experimental measurements suggest that the discrepancy between R1,C2(uniform) and R1,C2(selective) increases with higher molecular weights
To experimentally verify that the discrepancy in R1,C2 increases at higher molecular weights, we repeated our R1,C2 measurements in [U-13C/15N]-ATP or [2-13C, 7-15N]-ATP labeled HBV ε at 5 °C to simulate an RNA with a higher molecular weight (larger ). To maximize signal-to-noise and minimize experimental time, we reduced the sweep-width and time-domain points while increasing the number of scans. Therefore, only 4 of 8 adenosine C2-H2 resonances were resolved (Supplementary Fig. S4). Nevertheless, R1,C2(uniform) was again observed to be significantly higher than R1,C2(selective) for all 4 resolved HBV ε adenosine residues (Fig. 3a). Moreover, the average percent difference in measured R1,C2 at 5 °C was significantly higher than those measured at 25 °C (Fig. 3b), in agreement with our simulations (Fig. 1b). Specifically, the average percent difference in measured R1,C2 rates was 25.5% (Fig. 3b), compared to the simulated 15.6% (Fig. 1b) for an RNA with a of 21 ± 1 ns at 800 MHz (measured from R2/R1 (Fushman et al. 1994; Thakur et al. 2010)) (Supplementary Fig. S3).
Taken together, while relatively isolated, adenosine C2 experiences long-range 13C-13C dipolar couplings that can neither be wholly ignored nor circumvented with selective pulses in [U-13C/15N]-ATP labeled samples. That is, these dipolar contributions must be explicitly taken into account (Hansen and Al-Hashimi 2007) when interpreting adenosine R1,C2 rates in terms of motional models for large RNAs.
Adenosine C2 R1ρ relaxation and steady-state 13C{1H} hNOE measurements in uniformly and selectively labeled RNA
As previously described, R1, R2, and hNOE measurements are a prerequisite to a robust analysis of RNA ps-ns dynamics (Marušič et al. 2019; Palmer 2004; Wagner 1993; Lipari and Szabo 1982). We have already quantified the discrepancies that exist in adenosine R1,C2 measurements derived from [U-13C/15N]-ATP labeling. While we did not observe such differences in the simulated adenosine R2,C2 rates or steady-state 13C{1H} hNOE values (Supplementary Fig. S2), we sought to experimentally verify this for completeness. We therefore measured adenosine R2,C2 rates and 13C{1H} hNOE values for [U-13C/15N]-ATP or [2-13C, 7-15N]-ATP labeled HBV ε (Fig. 2) at 800 MHz and 25 °C using TROSY-detected pulse sequences (Hansen and Al-Hashimi 2007; Lakomek et al. 2013; Weigelt 1998; Pervushin et al. 1997). Observed R1ρ rates contain contribution from both R1 and R2 relaxation, which are accounted for according to the relations (Hansen and Al-Hashimi 2007; Lakomek et al. 2013; Akke and Palmer 1996; Davis et al. 1994)
| 7 |
| 8 |
Here, is the strength of the spin-lock field and is the offset from the spin-lock carrier frequency. We used an R1ρ experiment (Hansen and Al-Hashimi 2007; Lakomek et al. 2013; Akke and Palmer 1996; Peng et al. 1991; Korzhnev et al. 2002) to extract R2 rates in HBV ε. In agreement with our simulations, adenosine R2,C2 rates and steady-state 13C{1H} hNOE values did not differ significantly between uniformly or selectively labeled samples (Supplementary Fig. S5). For straightforward analysis, we will interpret dynamics data from our [2-13C, 7-15N]-ATP labeled sample.
As such, adenosine R1,C2 and R2,C2 rates measured in helical regions of HBV ε were all close to the mean, except for residues A13 and A21 (Fig. 4). Specifically, residue A13 shows high R1,C2 and low R2,C2 rates suggestive of increased internal motions (Fig. 4). Residue A21, on the other hand, has a high R2,C2 rate indicative of possible Rex contributions (Fig. 4). In addition to R1 and R2 rates, accurate measurements of steady-state 13C{1H} hNOE values can provide further information on RNA dynamics (Marušič et al. 2019; Palmer 2004; Wagner 1993; Lipari and Szabo 1982). Consistent with adenosine R1,C2 and R2,C2 rates, residue A13 shows the highest hNOE value suggestive of increased internal motions (Fig. 4). All other adenosine C2 nuclei have hNOE values close to the mean indicative of helical residues (Fig. 4). Taken together, our [2-13C, 7-15N]-ATP label simplified probing of adenosine C2 spin relaxation measurements in HBV ε without the need for selective pulses (Emsley and Bodenhausen 1992; Kupče et al. 1995; Geen and Freeman 1991) or explicit spectral density modeling with assumed models of motion (Hansen and Al-Hashimi 2007). As an added benefit, 1H-13C TROSY spectra collected on selectively labeled HBV ε showed better signal-to-noise and narrower 1H linewidths compared to its [U-13C/15N]-ATP counterpart (Supplementary Fig. S6).
Fig. 4.
Experimental adenosine C2 relaxation measurements for [2-13C, 7-15N]-ATP labeled HBV ε at 800 MHz and 25 °C. Adenosine R1,C2 and R2,C2 (calculated from R1ρ,C2 using Eqs. 6 and 7) rates and steady-state13C{1H} hNOE measurements are shown. Error bars represent ± s.d. and the mean relaxation parameters are shown with dashed lines with a shaded box representing ± s.d. above and below the mean. Residue A13 shows high R1,C2 and hNOE suggestive of increased internal motions whereas A21 has a high R2,C2 rate indicative of possible Rex
Conclusion
We investigated and quantified the effect of long-range 13C-13C dipolar couplings on adenosine C2 relaxation in [U-13C/15N]-ATP and [2-13C, 7-15N]-ATP labeled RNAs. Selective 13C-labeling of adenosine C2 removed unwanted dipolar interactions with C4, C5, and C6 found in [U-13C/15N]-ATP. Theoretical simulations and experimental measurements revealed non-negligible overestimates in adenosine R1,C2 rates derived from [U-13C/15N]-ATP labeled samples that increase with higher magnetic fields and molecular weights. The agreement between our experimental and simulated R1,C2 rates and discrepancies at 25 °C support the predictions from our simulations. Moreover, R1,C2 measurements at 5 °C (increased molecular weight) revealed exacerbated R1,C2 discrepancies, which further confirms our simulations and argues that selective 13C2 labeled probes simplify R1,C2 measurements in RNAs with a > 20 ns.
It is important to note that auto-relaxation due to the 13C-13C dipolar interaction does not lead to deviation from the expected monoexponential relaxation and can be explicitely taken into account by using the appropriate spectral density function (Hansen and Al-Hashimi 2007). Therefore, elimination of these unwanted 13C-13C dipolar contributions permits the use of simple spectral density modeling, offering advantages in data analysis. We also observed better signal-to-noise and narrower 1H linewidths in 1H-13C TROSY spectra collected on selectively labeled samples compared to its uniformly labeled counterpart. To take advantage of these benefits, our atom-selectively labeled [2-13C, 7-15N]-ATP was also used to measure 13C R2 relaxation rates and steady-state 13C{1H} hNOE values in HBV ε. These spin relaxation measurements provide a starting point to a robust understanding of HBV ε dynamics and suggest that residue A13 has increased flexibility whereas A21 may have Rex contributions.
Supplementary Information
Below is the link to the electronic supplementary material.
Acknowledgements
This research was financially supported by NSF for 800 MHz NMR instrumentation (DBI1040158 to T.K.D.) and for support of labeling work (1808705 to T.K.D.).
Data availability
All results generated in this study are included in this published article and its Supplementary Materials.
Declarations
Conflict of interest
The authors declare no competing interests.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Abragam A. Principles of nuclear magnetism. Oxford: Clarendon Press; 1961. [Google Scholar]
- Akke M, Palmer AG. Monitoring macromolecular motions on microsecond to millisecond time scales by R1p–R1 constant relaxation time NMR spectroscopy. J Am ChemSoc. 1996;118:911–912. [Google Scholar]
- Akke M, Fiala R, Jiang F, Patel D, Palmer AG. Base dynamics in a UUCG tetraloop RNA hairpin characterized by 15N spin relaxation: correlations with structure and stability. RNA. 1997;3:702–709. [PMC free article] [PubMed] [Google Scholar]
- Alvarado LJ, et al. Regio-selective chemical-enzymatic synthesis of pyrimidine nucleotides facilitates RNA structure and dynamics studies. ChemBioChem. 2014;15:1573–1577. doi: 10.1002/cbic.201402130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berlin K, Longhini A, Dayie TK, Fushman D. Deriving quantitative dynamics information for proteins and RNAs using ROTDIF with a graphical user interface. J Biomol NMR. 2013;57:333–352. doi: 10.1007/s10858-013-9791-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boisbouvier J, Brutscher B, Simorre J-P, Marion D. 13C spin relaxation measurements in RNA: sensitivity and resolution improvement using spin-state selective correlation experiments. J Biomol NMR. 1999;14:241–252. [Google Scholar]
- Cech TR, Steitz JA. The noncoding RNA revolution—trashing old rules to forge new ones. Cell. 2014;157:77–94. doi: 10.1016/j.cell.2014.03.008. [DOI] [PubMed] [Google Scholar]
- Clore GM, et al. Deviations from the simple two-parameter model-free approach to the interpretation of nitrogen-15 nuclear magnetic relaxation of proteins. J Am ChemSoc. 1990;112:4989–4991. [Google Scholar]
- Clore GM, Driscoll PC, Gronenborn AM, Wingfield PT. Analysis of the backbone dynamics of interleukin-1β using two-dimensional inverse detected heteronuclear 15N–1H NMR spectroscopy. Biochemistry. 1990;29:7387–7401. doi: 10.1021/bi00484a006. [DOI] [PubMed] [Google Scholar]
- Davis DG, Perlman ME, London RE. Direct measurements of the dissociation-rate constant for inhibitor-enzyme complexes via the T1ρ and T2 (CPMG) methods. J MagnResonSer B. 1994;104:266–275. doi: 10.1006/jmrb.1994.1084. [DOI] [PubMed] [Google Scholar]
- Dayie KT, Brodsky AS, Williamson JR. Base flexibility in HIV-2 TAR RNA mapped by solution 15N, 13C NMR relaxation. J MolBiol. 2002;317:263–278. doi: 10.1006/jmbi.2001.5424. [DOI] [PubMed] [Google Scholar]
- Dethoff EA, Chugh J, Mustoe AM, Al-Hashimi HM. Functional complexity and regulation through RNA dynamics. Nature. 2012;482:322–330. doi: 10.1038/nature10885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emsley L, Bodenhausen G. Optimization of shaped selective pulses for NMR using a quaternion description of their overall propagators. J MagnReson. 1992;97:135–148. [Google Scholar]
- Fiala R, Czernek J, Sklenář V. Transverse relaxation optimized triple-resonance NMR experiments for nucleic acids. J Biomol NMR. 2000;16:291–302. doi: 10.1023/a:1008388400601. [DOI] [PubMed] [Google Scholar]
- Flodell S, et al. Solution structure of the apical stem-loop of the human hepatitis B virus encapsidation signal. Nucleic Acids Res. 2006;34:4449–4457. doi: 10.1093/nar/gkl582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fushman D, Weisemann R, Thüring H, Rüterjans H. Backbone dynamics of ribonuclease T1 and its complex with 2′GMP studied by two-dimensional heteronuclear NMR spectroscopy. J Biomol NMR. 1994;4:61–78. doi: 10.1007/BF00178336. [DOI] [PubMed] [Google Scholar]
- Fushman D, Cahill S, Cowburn D. The main-chain dynamics of the dynaminpleckstrin homology (PH) domain in solution: analysis of 15N relaxation with monomer/dimer equilibration. J MolBiol. 1997;266:173–194. doi: 10.1006/jmbi.1996.0771. [DOI] [PubMed] [Google Scholar]
- Fushman D, Tjandra N, Cowburn D. Direct measurement of 15N chemical shift anisotropy in solution. J Am ChemSoc. 1998;120:10947–10952. [Google Scholar]
- Ganser LR, Kelly ML, Herschlag D, Al-Hashimi HM. The roles of structural dynamics in the cellular functions of RNAs. Nat Rev Mol Cell Biol. 2019;20:474–489. doi: 10.1038/s41580-019-0136-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geen H, Freeman R. Band-selective radiofrequency pulses. J MagnReson. 1991;93:93–141. [Google Scholar]
- Hansen AL, Al-Hashimi HM. Dynamics of large elongated RNA by NMR carbon relaxation. J Am ChemSoc. 2007;129:16072–16082. doi: 10.1021/ja0757982. [DOI] [PubMed] [Google Scholar]
- Hirsch RC, Lavine JE, Chang LJ, Varmus HE, Ganem D. Polymerase gene products of hepatitis B viruses are required for genomic RNA packaging as well as for reverse transcription. Nature. 1990;344:552–555. doi: 10.1038/344552a0. [DOI] [PubMed] [Google Scholar]
- Johnson BA, Blevins RA. NMR view: a computer program for the visualization and analysis of NMR data. J Biomol NMR. 1994;4:603–614. doi: 10.1007/BF00404272. [DOI] [PubMed] [Google Scholar]
- Johnson JE, Julien KR, Hoogstraten CG. Alternate-site isotopic labeling of ribonucleotides for NMR studies of ribose conformational dynamics in RNA. J Biomol NMR. 2006;35:261–274. doi: 10.1007/s10858-006-9041-x. [DOI] [PubMed] [Google Scholar]
- Kay LE, Torchia DA, Bax A. Backbone dynamics of proteins as studied by 15N inverse detected heteronuclear NMR spectroscopy: application to staphylococcal nuclease. Biochemistry. 1989;28:8972–8979. doi: 10.1021/bi00449a003. [DOI] [PubMed] [Google Scholar]
- Knaus T, Nassal M. The encapsidation signal on the hepatitis B virus RNA pregenome forms a stem-loop structure that is critical for its function. Nucleic Acids Res. 1993;21:3967–3975. doi: 10.1093/nar/21.17.3967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korzhnev DM, Skrynnikov NR, Millet O, Torchia DA, Kay LE. An NMR experiment for the accurate measurement of heteronuclear spin-lock relaxation rates. J Am ChemSoc. 2002;124:10743–10753. doi: 10.1021/ja0204776. [DOI] [PubMed] [Google Scholar]
- Kupče Ē, Boyd J, Campbell ID. Short selective pulses for biochemical applications. J MagnResonSer B. 1995;106:300–303. doi: 10.1006/jmrb.1995.1049. [DOI] [PubMed] [Google Scholar]
- Lakomek N-A, et al. Internal dynamics of the homotrimeric HIV-1 viral coat protein gp41 on multiple time scales. AngewChemieInt Ed. 2013;52:3911–3915. doi: 10.1002/anie.201207266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee WM. Hepatitis B virus infection. N Engl J Med. 1997;337:1733–1745. doi: 10.1056/NEJM199712113372406. [DOI] [PubMed] [Google Scholar]
- Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J Am ChemSoc. 1982;104:4546–4559. [Google Scholar]
- Marušič M, Schlagnitweit J, Petzold K. RNA dynamics by NMR spectroscopy. ChemBioChem. 2019;20:2685–2710. doi: 10.1002/cbic.201900072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milligan JF, Uhlenbeck OC. Synthesis of small RNAs using T7 RNA polymerase. Methods Enzymol. 1989;180:51–62. doi: 10.1016/0076-6879(89)80091-6. [DOI] [PubMed] [Google Scholar]
- Mortimer SA, Kidwell MA, Doudna JA. Insights into RNA structure and function from genome-wide studies. Nat Rev Genet. 2014;15:469–479. doi: 10.1038/nrg3681. [DOI] [PubMed] [Google Scholar]
- Nam H, et al. Deleterious effects of carbon-carbon dipolar coupling on RNA NMR dynamics. J Biomol NMR. 2020;74:321–331. doi: 10.1007/s10858-020-00315-z. [DOI] [PubMed] [Google Scholar]
- Nirmala NR, Wagner G. Measurement of 13C relaxation times in proteins by two-dimensional heteronuclear correlation 1H–13C spectroscopy. J Am ChemSoc. 1988;110:7557–7558. [Google Scholar]
- Norris M, Fetler B, Marchant J, Johnson BA. NMRFx Processor: a cross-platform NMR data processing program. J Biomol NMR. 2016;65:205–216. doi: 10.1007/s10858-016-0049-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olenginski LT, Dayie TK. Chemo-enzymatic synthesis of [2-13C, 7–15 N]-ATP for facile NMR analysis of RNA. Monatshefte fur Chemie. 2020;151:1467–1473. [Google Scholar]
- Palmer AG. NMR characterization of the dynamics of biomacromolecules. Chem Rev. 2004;104:3623–3640. doi: 10.1021/cr030413t. [DOI] [PubMed] [Google Scholar]
- Palmer AG, Rance M, Wright PE. Intramolecular motions of a zinc finger dna-binding domain from xfin characterized by proton-detected natural abundance 13c heteronuclearnmr spectroscopy. J Am ChemSoc. 1991;113:4371–4380. [Google Scholar]
- Peng JW, Wagner G. Mapping of the spectral densities of N-H bond motions in Eglin c using heteronuclear relaxation experiments. Biochemistry. 1992;31:8571–8586. doi: 10.1021/bi00151a027. [DOI] [PubMed] [Google Scholar]
- Peng JW, Thanabal V, Wagner G. Improved accuracy of heteronuclear transverse relaxation time measurements in macromolecules. Elimination of antiphase contributions. J MagnReson. 1991;95:421–427. [Google Scholar]
- Pervushin K, Riek R, Wider G, Wüthrich K. Attenuated T2 relaxation by mutual cancellation of dipole-dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. ProcNatlAcadSci USA. 1997;94:12366–12371. doi: 10.1073/pnas.94.23.12366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp PA. The centrality of RNA. Cell. 2009;136:577–580. doi: 10.1016/j.cell.2009.02.007. [DOI] [PubMed] [Google Scholar]
- Spiess HW. Dynamic NMR spectroscopy. Berlin, Heidelberg: Springer; 1978. Rotation of molecules and nuclear spin relaxation; pp. 55–214. [Google Scholar]
- Thakur CS, Dayie TK. Asymmetry of 13C labeled 3-pyruvate affords improved site specific labeling of RNA for NMR spectroscopy. J Biomol NMR. 2012;52:65–77. doi: 10.1007/s10858-011-9582-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thakur CS, Sama JN, Jackson ME, Chen B, Dayie TK. Selective 13C labeling of nucleotides for large RNA NMR spectroscopy using an E. coli strain disabled in the TCA cycle. J Biomol NMR. 2010;48:179–192. doi: 10.1007/s10858-010-9454-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thakur CS, Luo Y, Chen B, Eldho NV, Dayie TK. Biomass production of site selective 13C/15N nucleotides using wild type and a transketolaseE. coli mutant for labeling RNA for high resolution NMR. J Biomol NMR. 2012;52:103–114. doi: 10.1007/s10858-011-9586-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner G. NMR relaxation and protein mobility. CurrOpinStructBiol. 1993;3:748–754. [Google Scholar]
- Weaver AJ, Kemple MD, Prendergast FG. Tryptophan sidechain dynamics in hydrophobic oligopeptides determined by use of 13C nuclear magnetic resonance spectroscopy. Biophys J. 1988;54:1–15. doi: 10.1016/S0006-3495(88)82925-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weigelt J. Single scan, sensitivity- and gradient-enhanced TROSY for multidimensional NMR experiments. J Am ChemSoc. 1998;120:10778–10779. [Google Scholar]
- Wijmenga SS, Van Buuren BNM. The use of NMR methods for conformational studies of nucleic acids. ProgNuclMagnResonSpectrosc. 1998;32:287–387. [Google Scholar]
- Yamazaki T, Muhandiram R, Kay LE. NMR experiments for the measurement of carbon relaxation properties in highly enriched, uniformly 13C,15N-labeled proteins: application to 13Cα carbons. J Am ChemSoc. 1994;116:8266–8278. [Google Scholar]
- Ying J, Grishaev A, Bryce DL, Bax A. Chemical shift tensors of protonated base carbons in helical RNA and DNA from NMR relaxation and liquid crystal measurements. J Am ChemSoc. 2006;128:11443–11454. doi: 10.1021/ja061984g. [DOI] [PubMed] [Google Scholar]
- Zhao B, Guffy SL, Williams B, Zhang Q. An excited state underlies gene regulation of a transcriptional riboswitch. Nat ChemBiol. 2017;13:968–974. doi: 10.1038/nchembio.2427. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All results generated in this study are included in this published article and its Supplementary Materials.





