Characterization of the Force Production Capabilities of Paralyzed Trunk Muscles Activated with Functional Neuromuscular Stimulation in Individuals with Spinal Cord Injury

Abstract

Paralysis of the trunk results in seated instability leading to difficulties performing activities of daily living. Functional neuromuscular stimulation (FNS) combined with control systems have the potential to restore some dynamic functions of the trunk. However, design of multi-joint, multi-muscle control systems requires characterization of the stimulation-driven muscles responsible for movement.

Objective:

This study characterizes the input-output properties of paralyzed trunk muscles activated by FNS, and explores co-activation of muscles.

Methods:

Four participants with various spinal cord injuries (C7 AIS-B, T4 AIS-B, T5 AIS-A, C5 AIS-C) were constrained so lumbar forces were transmitted to a load cell while an implanted neuroprosthesis activated otherwise paralyzed hip and paraspinal muscles. Isometric force recruitment curves in the nominal seated position were generated by inputting the level of stimulation (pulse width modulation) while measuring the resulting muscle force. Two participants returned for a second experiment where muscles were co-activated to determine if their actions combined linearly.

Results:

Recruitment curves of most trunk and hip muscles fit sigmoid shaped curves with a regression coefficient above 0.75, and co-activation of the muscles combined linearly across the hip and lumbar joint. Subject specific perturbation plots showed one subject is capable of resisting up to a 300N perturbation anteriorly and 125N laterally; with some subjects falling considerably below these values.

Conclusion:

Development of a trunk stability control system can use sigmoid recruitment dynamics and assume muscle forces combine linearly.

Significance:

This study informs future designs of multi-muscle, and multi-dimensional FNS systems to maintain seated posture and stability.

I. Introduction

AN estimated 288,000 people live with a spinal cord injury (SCI) in the United States, and approximately 17,700 new cases occur each year [1]. SCI that results in paralysis can limit independence and reduce quality of life. Specifically, cervical to low thoracic injuries can cause paralysis of the trunk muscles resulting in reduced or complete loss of trunk stability [2]. This hampers the ability to perform many activities of daily living and reduces the seated stability necessary for tasks such as efficiently propelling a manual wheelchair or manipulating objects in the environment. Paralysis can also lead to secondary health problems such as pressure ulcers [3], and scoliosis, lordosis, and kyphosis due to the passive seated postures assumed by affected individuals [4]. Restoration of trunk stability was reported as the third highest priority to improve quality of life in both individuals with quadriplegia and tetraplegia, which gains in importance with increasing time post injury [5]. Current methods to improve trunk stability in this population involve use of straps and assistive pads that constrain movements, or constant use of the upper extremities which restricts bilateral hand use.

Recently, methods have been proposed to control trunk posture using functional neuromuscular stimulation (FNS) [6]–[13]. FNS is the application of low-level electrical currents applied to the motor nerves to elicit contractions of the otherwise paralyzed muscles. FNS can be applied through many methods including electrodes placed on the surface of the skin and electrodes implanted near the motor points of nerves. Implanted electrodes have the advantage of improved muscle selectivity and access to deep muscle structures [14]. Such external interventions that serve as inputs to activate otherwise paralyzed muscles are called neuroprostheses. Implementation of FNS systems can restore movement in a wide range of applications, such as walking [15]–[17], upper extremity hand grasping and reaching [18]–[20], stationary cycling [21]–[23], etc. In regards to trunk stability, FNS has been used in combination with closed loop control systems to restore upright seated posture and maintain seated balance while resisting external perturbations [8], [11]. Most of these studies have been confined to one degree of freedom, extension and flexion movements in the sagittal plane. Because muscles can act across multiple degrees of freedom, expansion of these techniques to the full range of motion around the whole workspace of a seated operator will require knowledge of the directional aspects of trunk muscle forces.

Due in part to the large range of motion capable by the trunk, dynamic trunk stability requires the synergistic activities of a multitude of muscles. Even during quiet upright sitting, the trunk muscles display tonic levels of activation that are necessary to maintain postural stability, [24], [25] which are unique to each muscle [26], [27]. In the presence of external perturbations, common in certain environments such as when riding in a motor vehicle or in a wheelchair, the EMG responses of the trunk muscles reveal a highly direction-dependent system with unique muscle synergies activated for perturbations in different directions [26]–[28]. EMG responses also vary depending on the given motor task being performed during a perturbation [29]. Replication of both the base tonic activation and synergistic responses to external perturbations with FNS will require knowledge of the force production capabilities that can be elicited from muscles activated individually and simultaneously with current trunk based neuroprostheses.

To further maximize controller performance in closed-loop FNS applications, an accurate model of the nonlinear input-output relationships of paralyzed muscles activated by neural stimulation is essential for more accurate and smoother control [30]. Stimulated muscle activities generally display nonlinear recruitment properties [30], [31], which were approximated with linear behaviors in a number of previous closed-loop control systems for restoring trunk stability [8], [11]. Linear models lack sufficient generality to capture a larger range of muscle behavior [31], and failing to correct for nonlinear muscle dynamics can degrade controller performance [32]. Several methods to incorporate non-linear characteristics into control strategies have been proposed, which include sigmoid functions [20], neural networks [33], and Hammerstein models [34], [35] all of which require subject-specific parameters obtained from the recruitment properties of each muscle. Creation of a robust closed-loop trunk control system will benefit from knowledge of these subject and muscle-specific properties.

Activation of multiple muscles simultaneously is crucial for control of a multi-muscle joint, both to change the direction of movement and precisely control the resulting force. Control patterns have often been simplified by assuming the force produced by two or more muscles results in a linear combination of the resultant force vector produced by each muscle when activated alone [11], [20]. This assumption has been confirmed in rat [36], and cat [37] muscles, and in muscles that cross the human shoulder joint [20]. However, this has never been confirmed in muscles that cross the human hip or lumbar joints. We hypothesize that if paralyzed synergistic muscles crossing the lumbar spine are co-activated the resulting force output will be a linear combination of the individual forces from the muscles acting alone.

The goals of this study were (1) to characterize the recruitment and directional properties of paralyzed trunk and hip muscles which are activated by an implanted FNS neuroprostheses, (2) to determine if activation of multiple muscles resulted in a linear combination of muscle force vector outputs, and (3) to estimate the maximum disturbing force each subject can resist across all directions while sitting erect.

II. Methods

A. Participants

Four individuals with a SCI at varying thoracic and cervical levels lacking volitional control of their trunk were recruited for the study. Each volunteer had previously been implanted with a neuroprosthesis for other studies intended to restore standing, stepping or seated balance that included the muscles controlling the trunk and hips. The neuroprosthesis utilizes intramuscular, epimysial, or nerve cuff electrodes to excite the motor nerves of the hip and trunk muscles connected to an implanted stimulator–telemeter developed at Case Western Reserve University [38], [39]. Table I lists the anthropometric and neurological characteristics of each volunteer at the time of testing, along with the muscles activated by their implanted FNS systems. Additionally, surface stimulation was applied to activate the quadratus lumborum and erector spinae of one of the subjects (S2). The results from surface stimulation was only assessed for a sigmoid fit and not directly compared to the results obtained from intramuscular electrode activation. At the time of the experiements, two of the subjects (S2, S4) were taking Baclofen to reduce hypertonia and unwanted muscle spasms [40]. Subject S4 has some volitional motor control on the left side of his body. All electrodes, except those targeting the left erector spinae and left quadratus lumborum, are implanted on the right side of his body and during all experiments S4 was told to relax and to not intervene. Due to the unique nature of each of the subjects and the relatively small sample size, a single-subject experimental design was used and data were analyzed individually with subjects as their own controls. All subjects signed a consent form approved by the local institutional review board before participation (IRB: VA Northeast Ohio Healthcare System, Protocol Number: 07101-H36, Approval Date: 9/7/2010 or IRB: VA Northeast Ohio Healthcare System, Protocol Number: 18037-H20, Approval Date: 11/2/2018 ).

TABLE I:

Clinical characteristics of study participants and the muscles activated. Muscles shown indicate stimulation of both sides of the body unless otherwise stated.

Subject	Age (y)	Gender	Height (cm)	Weight (kg)	Injury level	AIS# scale	Time post injury (y)	Time post implant (y)	Relevant medication	Muscles stimulated
S1	48	F	167.6	58.5	C7	B	22	21	None	ES, QL, PA, HS, GX, GM
S2	63	M	175.3	77.1	T4	B	11	8	Baclofen	ES*, QL*, IL, PA, GX, GM, HS
S3	44	F	172.7	84.9	T4	A	8	5	None	ES, QL, IL, PA, GX
S4	48	M	175.3	82	C5	C	5	1	Baclofen	ES, QL, IL+, GX+, GM+, HS+

ES lumbar erector spinae, QL quadratus lumborum, PA posterior portion of adductor magnus, GX gluteus maximus, GM gluteus medius, IL iliopsoas, HS hamstring semimembranosus

^#American Spinal Injury Association Impairment Score (AIS)

^*Tests performed using surface stimulation

⁺Only implanted/tested on the right side of the body

For all subjects, the main focus in this study was on electrodes implanted on nerves targeting muscles that cause movement of the hip and lumbar joints while seated. The function of the erector spinae (ES) is extension and lateral bending of the lumbar vertebral column [41]. The posterior portion of adductor magnus (PA) mainly causes adduction of the thigh along with extension of the hip [42]. The main function of the gluteus maximus (GX) is to extend and laterally rotate the hip joint [41]. The gluteus medius (GM) is responsible for abduction at the hip joint [41]. The function of the hamstrings or semimembranosus (HS) is extension of the hip [41]. The iliopsoas (IL) causes flexion of the hip [41]. The quadratus lumborum (QL) causes lateral bending and extension of the lumbar spine [41]. When referring to a specific muscle on one side of the body we will precede the abbreviation with left (L) or right (R), for example the right erector spinae will be abbreviated as the RES. It should be noted that whereas each electrode of the neuroprosthesis was named based on the muscle that it was ideally expected to activate, there is always the potential of unintended current spillover to nerve fibers activating other surrounding muscles which could result in actions that may not be associated with the ideal anatomical action of the targeted muscle alone.

B. Trunk Force Transducer

Figure 1a shows a custom trunk force transducer, of which the design and validation has previously been reported [43]. Briefly, the device was designed to rigidly constrain the femurs and thorax and isolate the actions of the hip and paraspinal muscles on the lumbar spine. The device was constructed predominantly of aluminum frames to allow for both a rigid and modular setup. Form fitting pads at the interfaces between the subject’s trunk and the trunk force transducer, and a dense foam seat cushion on the seating surface protected the soft tissues, minimized subject discomfort, and prevented pressure sore development. Adjustability to various subject sizes was assured by lockable sliding joints that allowed adjustments in Anterior/Posterior (A/P), Medial/Lateral (M/L), and Superior/Inferior (S/I) directions. A six-axis load cell (Model 160M50A-I100, JR3 Inc., Woodland, CA) was attached to the device to capture the A/P, M/L, and S/I forces (Figure 1c) exerted by the trunk when any particular muscle was activated. The load cell, which was rigidly attached to the Trunk Force Transducer, was itself bolted to the dynamometer measurement head of the Biodex Pro System (Biodex Medical Systems, Shirley, NY) with a custom machined adapter to provide a mechanically grounded base. Orthotic thigh cuffs constrained the legs and a pelvic strap minimized rotation of the pelvis and ensured that hip muscle actions were transferred to the pelvis and lumbar spine. Each subject was seated upright on the device, which was adjusted to place the form fitting pads under the axillae, wrapping around the chest as shown in Figure 1b. This constrained the trunk sufficiently to prevent movement, thereby ensuring the force effects from isometric contraction of the muscles were transmitted to the load cell.

Fig. 1:

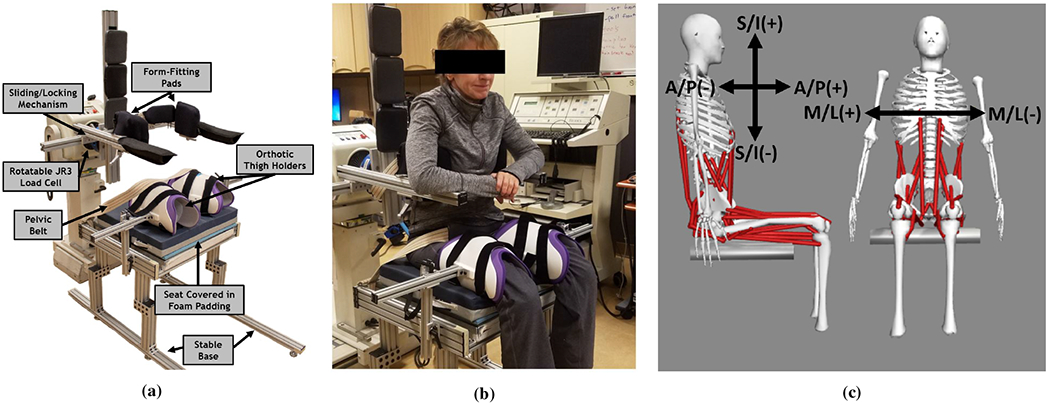
(a) The Trunk Force Transducer designed to hold any size subject with form fitting pads and adjustable sliding/locking mechanisms and transmit all forces to a six axis load cell. (b) With a seated subject. (c) The directions (A/P - Anterior/Posterior, M/L - Medial/Lateral, S/I - Superior/Inferior) and signs measured by the load cell attached to the Trunk Force Transducer.

C. Collection of Isometric Recruitment Curves

Each subject was seated in the Trunk Force Transducer and strapped to ensure that their trunk remained rigidly constrained. Before each experiment, the subject was told to minimize movements of the upper extremities, to relax their trunk muscles, and not intervene. Isometric pulse width (PW) modulated recruitment curves were obtained with the steady-state step response method [44]. Overall tetanic contractile force output of the hip and trunk muscles were recorded as functions of stimulation PW. Both PW modulation and amplitude modulation can recruit the full dynamic range of muscle force [44], PW modulation was chosen over amplitude modulation because the implanted neuroprostheses had greater resolution of PW (0 to 250μs in 1 increments) than current amplitude (8 discrete current levels from 2 to 20mA). Initially, to allow the subject to get used to the device and to avoid possible potentiation effects, each muscle was primed with 10 pulses of stimulation lasting half a second every five seconds at 20% of maximum PW reported to be comfortable for the subject. Stimulation was initiated at zero μs and increased linearly over 26 discreet steps to the maximum PW. The maximum PW was determined before the experiment by applying increasing values until it was reported uncomfortable by the subject or the hardware maximum was reached (250μs). Stimulation was limited due to discomfort in 13 of 44 channels across all subjects (S1{RES, RQL, LQL}, S2{RIL, RPA, LGM}, S3{RES, LES}, S4{RES, RQL, RIL, LES, LQL}), and hardware limits to stimulation were reached in the remaining 31 channels. The amplitude was kept unchanged during the experiments and was typically set at 20mA. Stimulation was applied for two seconds followed by five seconds of rest starting with the lowest activation level, followed sequentially by higher PW values. This was repeated three times per electrode. Stimulation frequency was set to 20 Hz, as frequencies in this range have been shown to result in slower fatigue rate while maintaining strong force production [45], [46]. Force measurements were collected, for the entire pulse train, from the load cell. The force data were sampled at 40 Hz using a DAQ (NI PCI-6031E, National Instruments) and collected by a MATLAB Simulink program running in the xPC Host-Target real-time environment. These data were filtered offline with a 4th order zero-phase Butterworth filter with a low-pass cutoff of 10 Hz [47]. The cutoff value was empirically determined by a fast Fourier transform analysis showing that greater than 99.9% of the power of stimulation-evoked-forces fell below 10 Hz. To ensure steady state, measured force was averaged over the last one second of stimulation in each direction, and any drift in baseline was removed by subtracting the average force measured for a one second interval prior to each application of stimulation.

The recruitment curve data were fit to a modified sigmoid curve (Equation 1) [48].

$$F\left(PW\right)=d(\frac{F_{\mathit{max}}}{1+e^{m\left(P{W}_{50\%}-PW\right)}}-\frac{F_{\mathit{max}}}{1+e^{m\left(P{W}_{50\%}\right)}})$$ (1)

In this equation, F is the force output of the muscle, d is a directional adjustment term allowing for negative forces to be retained, F_max is the maximum output from the sigmoid function, PW_50% is the input at half of the maximum force, m is the slope at 50% of the maximum output, and PW is the activation input to the system. The second term on the right side of the equation is an offset term that forces the output to be zero when the input is zero. The directional component (d) was set as either −1 or 1 depending on the sign of the last collected force. This was necessary to distinguish between right (positive) and left (negative) lateral forces, anterior (positive) and posterior (negative) forces, and superior (positive) and inferior (negative) forces. A recruitment curve was generated for each muscle and for all 3 directions (A/P, M/L and I/S) so long as the force output in that direction was above a 15N threshold. This threshold was determined to account for any noise caused by respiration or subtle, unintended voluntary movements made by the subject, the majority of which varied within the range ±15N. Assessment of fit was determined using root-mean-square error (RMSE) and the coefficient of determination (R²) [49].

D. Effect of Muscle Co-Activation

We performed additional experiments on two subjects (S2, S4) to test if co-contraction of multiple muscles resulted in a linear vector addition of muscle force output. The subjects were seated in the trunk force transducer and a set of muscles were chosen to be activated simultaneously in various co-activations. For subject S2, we chose the RGM, RHS, LIL, and LGX because each of these muscles produced forces in four different directions allowing analysis of antagonist muscles. The co-activations tested were as follows:

• Single: Every muscle alone

• Double: Every possible double co-activation (RGM-RHS, RGM-LIL, RGM-LGX, RHS-LIL, RHS-LGX, LIL-LGX)

• Triple: Every possible triple combination (RGM-RHS-LIL, RGM-RHS-LGX, RGM-LIL-LGX, RHS-LIL-LGX)

• Quadruple: One quadruple combination (RGM-RHS-LIL-LGX)

For subject S4 we chose five muscles the LQL, LES, RHS, RIL, and RGX. The combinations tested were as follows:

• Single: Every muscle alone

• Double: Every possible double co-activation (LQL-LES, LQL-RHS, LQL-RIL, LQL-RGX, LES-RHS, LES-RIL, LES-RGX, RHS-RIL, RHS-RGX, RIL-RGX)

• Triple: The three lumbar muscles (LQL-LES-RIL)

• Quadruple: The four muscles that produce both extension and left lateral forces (LQL-LES-RHS-RGX)

• Quintuple: All five muscles (LQL-LES-RHS-RIL-RGX)

Activation level was chosen based on the PW that resulted in the largest force observed during the experiments described in the previous section. Stimulation was applied for 2 seconds at a frequency of 20 Hz followed by 10 seconds of rest. Each combination was repeated 10 times in random order. Output force components were obtained using the same procedure described in the previous section. The forces in the transverse plan (A/P and M/L forces) were converted to polar coordinates to provide both a direction and magnitude. We defined 0° as directly to the subject’s right, 90° is purely anterior, 180° is directly right, and 270° is purely anterior. S/I forces were excluded because most trunk movements occur in the A/P and M/L directions and S/I forces are small with a low signal to noise ratio. The magnitude and direction of each of the co-activations was compared to the theoretical magnitude and direction calculated through vector addition of the measured forces from each of the muscles acting alone. Percent difference was calculated using Equation 2 to determine the difference between the measured combination force and the theoretical vector addition of each muscle in both magnitude and direction.

$$\mathit{PD}=(\frac{V_{\mathit{mea}}-V_{\mathit{vec}}}{\frac{V_{\mathit{mea}}+V_{\mathit{vec}}}{2}})\ast 100$$ (2)

Where PD is the percent difference, V_mea is the measured magnitude or direction, and V_vec is the magnitude or direction resulting from linear vector addition of the muscles activated alone. Additionally, we quantified the linearity of the co-activated muscles, both in magnitude and direction, by using root-mean-square error (RMSE) and the coefficient of determination (R²) [49] with respect to a line that indicates perfect linear vector addition.

E. Maximum Perturbation Resistance

To analyze the maximum possible perturbations each individual can withstand in a seated upright position, we calculated every possible linear combination of the measured force values from the isometric recruitment curves collected in section C. This included the resulting muscle force from 26 different stimulation levels applied to each channel. For example, the resulting force from one muscle at one stimulation level in the recruitment pattern was combined with the force produced at a single stimulation level from every other muscle’s recruitment pattern within the same subject. This was repeated until every possible permutation was calculated. Only forces in the A/P and M/L directions were considered, I/S forces were excluded because perturbations in this direction will automatically be countered by the weight of the individual. Forces in the A/P and M/L were then converted to polar coordinates and shown as a magnitude and direction. The resulting values show the amount of force the subject would be able to apply in any direction. A more useful measure is the ability of the subject to resist externally applied perturbations in any direction, as this has been used in the past to access FNS modulated trunk stability [8], [11]. To reflect the equal and opposite perturbation force that the co-activating muscles would be able to resist, the force components were first multiplied by −1 before conversion to polar coordinates.

III. Results

A. Isometric Recruitment Curves

Figure 2 shows a typical force recruitment curve of the LQL of S1. Data are displayed in the A/P, M/L, and S/I directions (Figure 1c) with sigmoid function fits. A/P forces represent extension and flexion forces around the lumbar spine. A negative A/P force results from the trunk pressing on the device in the posterior direction, which would move the trunk into extension if unimpeded. A positive A/P force pushing forward on the device which if unimpeded would cause flexion. M/L forces cause lateral bending, with positive forces bending the trunk to the right, and negative forces the left. S/I forces exerted on the device indicate actions tending to move the trunk upward or downward. Thus, a positive S/I force would indicate the muscles were acting to straightening the lumbar spine and elevate the trunk. Figure 2 shows that stimulation of the LQL channel resulted in extension forces, left lateral bending, and straightening of the posterior lumbar spine. The response of this muscle shows that the high slope region of the recruitment curve begins at the same activation level in the A/P and M/L direction. While the response in the S/I direction is slightly delayed and has a much shallower slope. Responses from other muscles show that this high slope region can begin at different levels of activation.

Fig. 2:

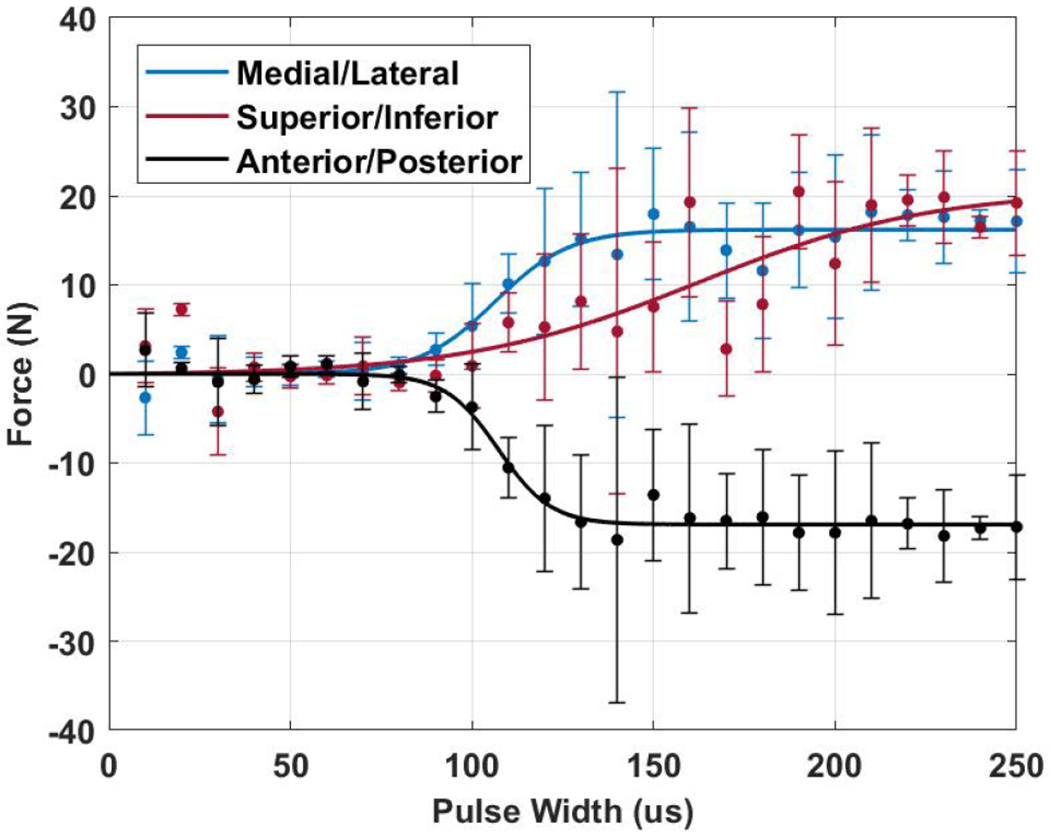
Representative recruitment curves in the M/L, S/I, and A/P directions from the left quadratus lumborum (LQL) of subject S1. The points indicate measured values with error bars of standard deviation (n=3). Solid lines indicate sigmoid curve fits.

The R² and RMSE from the sigmoid function fits of each subject in each direction are summarized in Table II. The results are separated by the direction of force and the RMSE and R² values of each subject were averaged. Across all subjects, the average R² for A/P, M/L and S/I are 0.83, 0.85 and 0.44 respectively. This suggests a strong relationship between the fitted curve and the experiment results in the A/P and M/L directions in particular. The sigmoid function was unable to represent forces in the S/I direction. Forces were generally lower in this direction. The RMSE showed similar trends, with average values of 3.68N, 2.55N, and 6.56N respectively in those directions. Only four values had R² below 0.75, bolded in Table II. An R² value of 0.39 was found in the A/P direction of S3. Recruitment curves in the A/P direction of S3 reached a maximum force and then changed direction with additional stimulation (Figure 3c).

TABLE II:

Root-mean-square error (RMSE) and coefficient of determination (R²) for the sigmoid fit in the Anterior/Posterior, Medial/Lateral, and Superior/Inferior directions. Subject specific R² values below 0.75 are bolded for discussion.

Subject	Force Direction
	Anterior/Posteror		Medial/Lateral		Superior/Inferior
	R2	RSME (N)	R2	RSME (N)	R2	RSME (N)
S1	0.96	1.34	0.95	1.54	0.64	5.48
S2	0.87	3.68	0.75	3.3	0.3	7.35
S3	0.39	5.85	0.80	2.68	0.37	7
S4	0.9	3.74	0.93	2.37	0.82	4.15
Mean	0.83	3.68	0.85	2.55	0.44	6.56

Fig. 3:

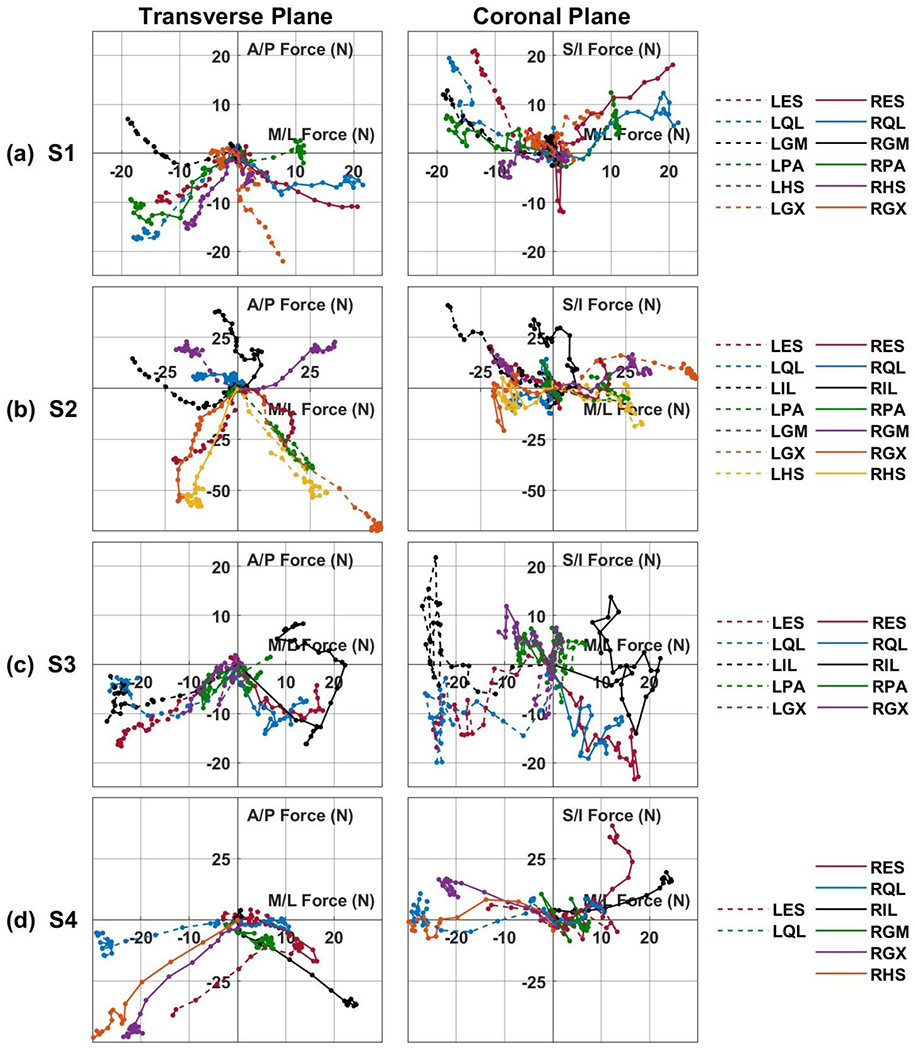
Muscle recruitment curves of all subjects plotted against each other in the force space. (a) Shows subject S1, (b) shows subject S2, (c) shows subject S3, and (d) shows subject S4. Anterior/posterior forces (positive is anterior, negative is posterior) plotted against medial/lateral forces (positive is right, negative is left). Superior/inferior (positive is superior; negative is inferior) plotted against medial/lateral force. A moving average of three was used to smooth the presented data. Acronyms: RES, LES - right or left lumbar erector spinae, RQL, LQL - right or left quadratus lumborum, RPA, LPA - right or left posterior portion of adductor magnus, RGX, LGX - right or left gluteus maximus, RGM, LGM - right or left gluteus medius, RIL, LIL - right or left iliopsoas, RHS, LHS - right or left hamstring semimembranosus.

To examine the directionality of each of the tested muscles, the recruitment curves were plotted against each other in the force space as depicted in Figure 3. These plots allow visualization of the force production from stimulation of each channel. From a holistic view a majority of channels resulted in forces being applied in the posterior direction with deviation to the right or left sides depending on which side of the body the electrode is located. Channels targeting muscles located around the lumbar spine (ES, QL, IL) typically displayed the largest forces in the S/I direction. These generalizations are most evident in S1 (Figure 3a), where only the LGM caused an anterior force and the ES and QL channels showed the largest superior forces. More specific examples are expanded upon below.

Not all muscles produced forces on the ipsilateral side to where the electrode was located. For example, in Figure 3b the RHS, RGX and RPA results in contralateral forces on the left side of the body. Further observation shows that contralateral forces occur primarily in muscles crossing the hip joint (PA, HS, GM, GX). Out of 23 tested hip muscles, 7 had little response at all under 15N, 13 had responses on the contralateral side, and three resulted in ipsilateral forces. All three of the hip muscles that produced ipsilateral forces were GM, with no GM resulting in contralateral forces. The IL muscle classically causes flexion of the hip, however as observed in this study, two out of five IL muscles tested did not result in flexion as observed in Figures 3c and 3d, instead resulting in trunk extension. In some cases, the produced forces change their direction of action. This is evident in S3 (Figure 3c) when the RIL initially results in posterior forces and then changes to anterior forces with increased stimulation. This change in force direction can also be observed in the LQL, RQL, and RES of S3 to a lesser extent.

B. Muscle Co-Activations

The magnitude and direction of a single muscle response and co-activation of muscles is depicted in Figure 4 for subject S2 and Figure 5 for subject S4. The muscle direction is shown in the transverse plane where a direction of 0° is directly right, 90° is purely anterior, 180° is directly left, and 270° is purely posterior. We calculated the percent difference between the measured co-activation force and the theoretical linear addition of the two muscles, shown as a black bar on the bars labeled Com. For S2 the average percent difference for magnitude (Figure 4a) and direction (4b) was 26.2% and 4.8%, respectively. The LIL appears to be responsible for all differences above 20%. Exclusion of co-activations involving the LIL drastically reduced the average percent difference to 7.15% and 1.4%, respectively. For subject S4 the average percent difference of the magnitude was 4.9% (Figure 5a) and 2% in the muscle direction (Figure 5b). For S4, differences decreased to near zero when more muscles were combined from a magnitude percent difference of −1.5% with three muscles, to 0.37% with four and finally 0.25% with five muscles. Similarly, the direction had minimal differences of −2.9%, −3.7% and −1.4%, respectively.

Fig. 4:

Subject S2: Magnitude (a) and directions (b) of possible double and triple, quadruple, and quintuple muscle combinations. Magnitude and direction were calculated from measured force in the A/P and M/L directions. Each graph shows the result when the muscle is activated alone followed by the result when the muscles are co-activated (Com) along with a black line indicating perfect vector addition. Percent difference between the linear combination and measured combination is shown above each graph. Error bars are standard deviation (n=10). A direction of 0° is directly right, 90° is purely anterior, 180° is directly left, and 270° is purely posterior. Acronyms: LGX - left gluteus maximus, RGM - right gluteus medius, LIL - left iliopsoas, RHS - right hamstring semimembranosus.

Fig. 5:

Subject S4: Magnitude (a) and directions (b) of possible double and triple, quadruple, and quintuple muscle combinations. Magnitude and direction were calculated from measured force in the A/P and M/L directions. Each graph shows the result when the muscle is activated alone followed by the result when the muscles are co-activated (Com) along with a black line indicating perfect vector addition. Percent difference between the linear combination and measured combination is shown above each graph. Error bars are standard deviation (n=10). A direction of 0° is directly right, 90° is purely anterior, 180° is directly left, and 270° is purely posterior. Acronyms: LES - left lumbar erector spinae, LQL - left quadratus lumborum, RGX - right gluteus maximus, RIL - right iliopsoas, RHS - right hamstring semimembranosus.

Figure 6 shows the magnitude and direction of the co-activated muscles plotted against the magnitude and direction that resulted from a linear vector addition of each of the muscles activated alone. When the linearity was assessed against a line representing a perfect linear addition the force magnitude from subject S2 resulted in an R²=0.68 and a RMSE=11.1N (Figure 6a). The force direction of S2 resulted in an R²=0.97 and an RMSE=13.7° (Figure 6b). For S4, the force magnitude resulted in R²=0.98 and a RMSE=3.8N (Figure 6a). The force direction of S4 resulted in an R²=0.80 and an RMSE=7.3° (Figure 6b). These results support the assumption that forces from multiple muscles combine additively.

Fig. 6:

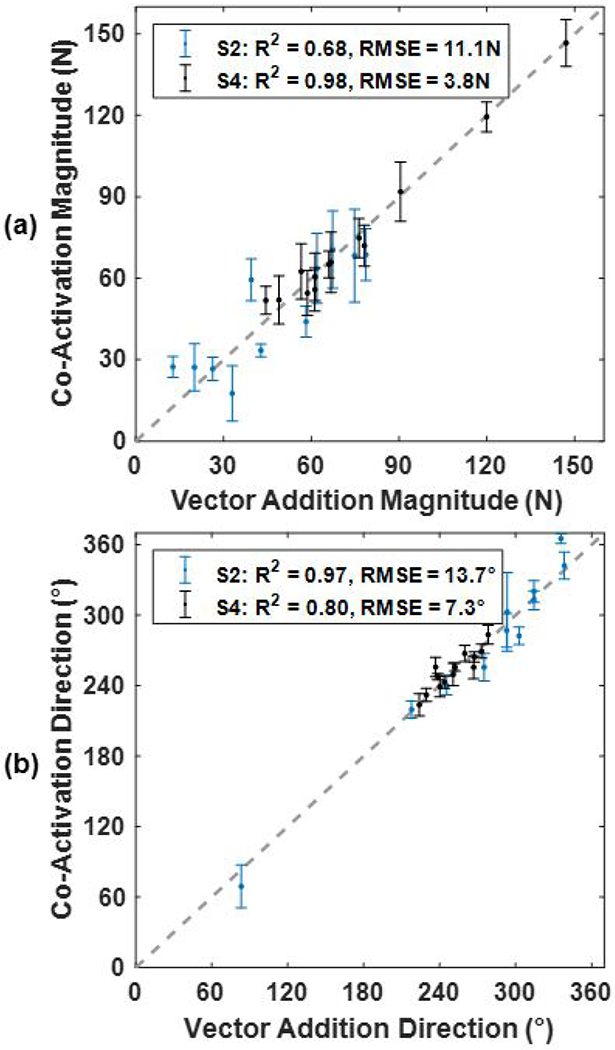
Linear regression of the force magnitude (a) and direction (b) of every muscle co-activation compared to the vector addition of the force from each muscle activated alone. The dashed grey line shows the perfect linear addition of muscle forces. Linear fit is accessed, for both S2 and S4, using root-mean-square error (RMSE) and coefficient of deter-mination (R2). Error bars are standard deviation (n=10). A direction of 0° is directly right, 90° is purely anterior, 180° is directly left, and 270° is purely posterior.

C. Maximum Perturbation Resistance

Based on the assumption that muscle forces add linearly, we used the isometric recruitment curve data from Figure 3 to estimate perturbation resistance plots (Figure 7). Each grey dot indicates a possible co-activation of two or more muscles. A solid grey area shows that there are many different co-activations that can result in that amount of force, a more diffuse area shows that fewer combinations of co-activated muscles can achieve that amount of force. The solid grey line shows the maximum magnitude and direction of external perturbations each subject can resist. For example, Figure 7 shows that S2 should be able to resist a perturbation of just over 300N directly anterior and 125N directly laterally. Resistance to perturbations was highest from directions between 30° and 150°. Subject S1, S3, and S4 would be unable to resist even minimal perturbations greater than 25N directly posterior. The maximum perturbation resistance values are 105N at 50° for subject S1, 328N at 99° for subject S2, 103N at 45° for subject S3, and 206N at 75° for subject S4.

Fig. 7:

Polar plots of all possible muscle combinations showing the maximum perturbation resistance of each subject. Each grey dot indicates one possible co-activation of two or more muscles. The grey line indicates the maximum perturbation that can be resisted in that direction. A direction of 0° is directly right, 90° is purely anterior, 180° is directly left, and 270° is purely posterior.

IV. Discussion

Here, we presented results on the force production characteristics of muscles activated by an implanted trunk neuroprostheses. Due to the nature of this multi-joint, multi-muscle system, force was recorded in three dimensions to account for both the magnitude and direction from the elicited muscle contraction. Multiple muscles were then activated simultaneously to determine if their actions add linearly both in magnitude and direction through vector addition. This assumption, combined with the recruitment curves, was then used to approximate the maximum external perturbations each individual can withstand in every direction which would indicate the theoretical limits of control of their trunk posture.

Analysis of the produced forces revealed the direction of action of each muscle, important for control of a multi-directional joint, and also which muscles had relatively little impact on trunk forces. This information offers insight into the design of sophisticated control systems to alter seated posture and automatically maintain sitting balance. The sigmoid function was able to capture the profile of the recruitment curves of trunk muscles in the A/P and M/L directions as it has been able to do for other animal and human muscles [20], [44], [50]. However, several notable exceptions occurred when the resultant force from a specific stimulus channel changed direction as stimulation increased, evident with the LIL, RIL, LQL, RQL, and RES channels of S3 that initially caused extension forces however, increasing stimulation resulted in reduced extension forces and even flexion forces in the LIL channel (Figure 3c). The initial trunk extension forces is likely caused by spillover to other back muscles, such as the ES, in addition to fibers of the IL that are known to be innervated by similar spinal nerves. The IL is innervated by spinal nerves from L1 to L4 and the lumbar ES is innervated by spinal nerves from L1 to L5 [41]. This was possibly caused by current spillover to nerves of other neighboring muscles in close approximation to the original target, which has been reported before with intramuscular electrodes targeting trunk and hip muscles [14].

Accurately accounting for these directional changes will require a more complex curve fit or limiting the maximum stimulation. Current spillover could be avoided via more exact electrode placement, or better shaping of the electric field via techniques such as field steering or multipolar stimulation. Nevertheless, the simplicity of the sigmoid approximation of the recruitment curves of the trunk muscles allows for real time feedback control. In fact, a sigmoid approximation has already been used in feed-forward control of a FNS arm system [20].

The results suggest that force vectors of multiple muscles activated simultaneously add linearly, supporting the idea that the trunk muscles are independent actuators, when activated by FNS. This greatly simplifies implementation of future control systems in multi-joint, multi-muscle systems, as the accurate predictions of resultant forces can be determined without the use of complex models. This finding is unsurprising because each of these muscles are activated through separate nerves sometimes on opposite sides of the body [41]. There is currently some evidence for muscles being independent actuators in rats [36], cats [37], and a FNS arm system [20]. However, this premise has not been confirmed across the lumbar spine and hips. Any nonlinear addition of force could be due to transmission of muscles forces that occur via pathways other than the muscular origin and insertion point. Such epimuscular myofascial transmission of force occurs through connective tissue between synergistic muscles [51], [52]. Substantial contribution of epimuscular myofascial forces would lead to nonlinear addition of force and could have contributed to observed percent differences. Additionally, we are likely activating afferent fibers along with the targeted efferent fibers. Stimulation of afferent reflex loops can activate various synergistic or antagonistic muscles. Activation of the reflex loop is observed more rarely than current spillover with intramuscular electrodes, however it can still occur [14]. Contribution of unexpected reflex activated muscles would impact linear addition of forces; however, it is unclear if co-activation of afferent nerves would amplify or possibly dampen the reflex response. If the reflex response does not change with co-activation then the effect on these results would be minimal. The effect of muscle reflexes is further reduced here because both subjects S2 and S4 take Baclofen that has an inhibitory effect [53].

Both epimuscular myofascial and reflex effects could explain the increased differences observed in subject S2 when the LIL was activated along with other muscles. However, these nonlinear factors appear to be small relative to the produced forces. Interestingly, the linear addition still holds true with co-activation of antagonistic muscles which is important for control of joint stiffness which may result in improved controller performance [30], [54]. Trunk stiffness has been shown to be a significant factor for trunk stability [55], [56]. This study both identifies antagonistic muscles and confirms their forces can be effectively canceled to only increase trunk stiffness.

For the individuals tested here, predicted perturbation resistance was greatest between 30° and 150°, which is desirable because perturbation of the intact trunk is largest in diagonal directions [57] and combinations of the muscles tested in this study can withstand forces ranging from 100N to 330N in these directions (Figure 7). To gain perspective of similar musculoskeletal modeling results, Lambrecht et al. [7] performed a sum of moments calculations at the lumbar joint to assess the weight an individual with the neuroprosthesis system could hold. Performing a similar calculation here, assuming a trunk height of 30cm, subject S2 would be able to hold a 30kg weight with his arms stretched out 30cm anteriorly, double what Lambrecht et al. predicted for a similar system. S1 on the other hand would only be able to hold a 10kg weight. The absence of perturbation resistance for three of the subjects (less than 25N) in the posterior direction can easily be counteracted by the presence of a backrest on the wheelchair. Similarly, the use of a backrest can act as an antagonistic force to counter excess extension forces while maintaining the lateral forces from the activated muscles to better counteract lateral perturbations. This in total will allow resistance of perturbations from 0° to 180°. These findings bode well for dynamic trunk control in this region and will require confirmation with a dynamic control system.

The perturbation resistance plots (Figure 7) shows that each subject has unique force production characteristics. S1 showed a well-balanced system by being able to resist the same size perturbations from 30° to 150°, S2 and S4 were both skewed in the anterior direction, and S3 skewed towards the right. Just as the design and implantation of a stimulation neuroprosthesis is highly customized to each individual user [58], so are the resulting functional capabilities of the systems. For these reasons, control systems have to be designed taking cognizance of the limits of the system for each individual in order to fully leverage the capabilities of the neuroprosthesis for that individual. A major use of these results is to inform the development of robust subject-specific musculoskeletal models, which in turn will serve as solid platforms for the design of control systems for each individual subject without use of lengthy controller tuning sessions.

Despite the uniqueness of each system, there appears to be some generalizations that can be gained from this study. First, as mentioned above, sigmoid fits can be used to model recruitment. Second, when these hip muscles (GX, PA, HS) are used in lateral movements of the trunk they likely apply forces to the contralateral side, which should be further quantified. Third, FNS control systems of multiple muscles across the multiple joints of the hips and trunk can assume that the muscle forces add with linear vector addition when appropriate stimulation levels avoid spillover to nerves activating undesired muscle groups. As linear addition has been confirmed previously with the human arm [20] and in this study with the human lumbar and hip joints.

While fatigue is always a consideration when dealing with FNS, a number of steps are taken with our implanted subjects to minimize its effects in these experiments. First, after implantation all subjects underwent an extensive six-month exercise program specifically designed to strengthen and improve the fatigue resistance of their stimulated contractions. Thus, all subjects participating in this study were well conditioned and regular users of their stimulation systems. Second, the paraspinal muscles are postural muscles that contain a high concentration of fatigue resistant muscle fibers [59]. In general, we have observed that they tend to fatigue more slowly than the larger muscles of the lower extremities. Subjects report routinely turning their paraspinal and hip muscles on for long periods of time to help stabilize their sitting during driving or other daily activities without noticeable loss in output. Third, the method for collecting recruitment curves followed similar steps employed in the past whereby fatigue effects were minimized by keeping “on” times short and allowing sufficient rest between contractions [44], [60]. In general, fatigue would have been evident as a drop in force output during the plateau region of the recruitment, which was not observed during any contractions due to these precautions. A randomized recruitment pattern, or other strategies such as twitch recruitment or application of increasing tetanic PW values followed by decreasing vales, could be implemented in the future to further ensure against the potentially confounding influence of fatigue on the results.

One limitation of this study is that all experiments were performed in an upright seated position with isometric contractions. Muscle force changes depending on the muscle length and the contraction velocity. Muscle recruitment curves scale with length [61] suggesting that the results shown here will scale similarly and would only require a scaling factor. This could be beneficial for trunk control in a position away from erect as an upright seated position often results in suboptimal muscle length. Extension torque generation has been shown to increase with increasing trunk pitch in a FNS system [62] and had even been shown to double in strength from 0° to 50° flexion in able bodied individuals [63]. This characteristic would help compensate for the additional effect of gravity on the trunk with increasing trunk pitch. Nevertheless, these experiments should be repeated at other sitting postures and with additional subjects. Whether an increase in muscle strength is enough to counteract the increased effect of gravity remains to be determined.

Another limitation was not accounting for forces in the S/I direction in the combination analysis and the perturbation resistance plots. This was excluded under the assumption that any perturbations in the S/I direction would be resisted by gravity or the presence of the platform on which the subject sat. This could have an effect on muscle combinations as the LIL of subject S2 has S/I forces of 40N, inclusion of this in analysis of the combined magnitude could reduce the observed percent difference. Further consideration of the compressing or lifting forces exerted on the lumbar spine is required, as they can impact the linear combination of separate muscles at the lumbar joint. Additionally, the muscle combinations and perturbation plots calculations were made assuming the upper chest is a point mass and do not account for the distributed mass of each individual. Lastly, voluntary movements of the subject could have impacted the results. The potential influences of any voluntary muscle activity was minimized by subject instruction (limit upper extremity movement, relax trunk muscles, and do not intervene) and with repeated measures to reduce the influence of random noise.

V. Conclusion

In this study, we characterized the force production capabilities of an implanted trunk neuroprosthesis to gain insight that would facilitate the design of future multi-muscle control systems. Recruitment curves of these muscles followed a sigmoid relationship unless the current spilled over to adjacent musculature causing a change in the resultant force direction, beyond the capabilities of a sigmoid. These results indicate that in the majority of muscle pairs, activation of multiple muscles results in a linear vector addition of forces even across the complex lumbar and pelvic joint with both agonist and antagonist muscle systems. We predict that the neuroprosthesis tested here can resist perturbations up to 300N anteriorly and 125N laterally, unique to each person. These results demonstrate the necessity of identifying the directional and recruitment properties of muscles in multi-muscle, multi-dimensional FNS applications to inform future design of robust control systems for maintaining trunk posture to widen the workspace of the seated operator.